Mathematical modeling of the apo and holo transcriptional regulation in Escherichia coli

Abstract

Transcription factors (TFs) modulate gene expression as a consequence of internal or exogenous changes in cell signaling. TFs can bind to DNA either with their effector bound (holo conformation), or as free proteins (apo conformation). With the aim of contributing to the understanding of the evolutionary fitness and organizational principles behind the different TF conformations, we inquire into the origins of these conformational differences by analyzing these two TF conformations from the perspective of Savageau's demand theory. For the control of a gene whose function is in high demand, we found that evolutionary constraints are responsible for activator TFs binding to DNA mainly in holo conformation whereas apo activation is under-represented. The mathematically controlled comparison of the apo and holo conformations reveals formal and evolutionary arguments in favor of this TF control asymmetry, which suggests that evolution favors holo activation under environmental conditions commonly found by E. coli in the human digestive tract. Specifically, the sensibility analysis performed for the holo conformation, in the positive mode of regulation, shows that the wild-type is more robust for situations where realizable changes in the model's parameters favored a better performance under non-stressful environmental conditions commonly found by E. coli in the human digestive tract. By contrast, the positive apo conformation is better adapted to adverse situations. On the other hand, the sensibility analysis performed for the negative mode of regulation showing none of the TF active conformations presents an advantage.

---

Introduction

Based on the active conformation of 149 TFs collected from the RegulonDB database, Balderas-Martínez et al.¹ reported a general trend for activator TFs to bind in holo conformation in Escherichia coli K-12, suggesting that apo activation is under-represented.

Why is the transcription factor in holo conformation dominant in the Escherichia coli K-12 bacteria as the mode of regulation? Why is the apo active conformation under-represented? Are these alternative TFs conformations historical accidents or have they been evolved in base of their functional differences?

In this work, we inquire into the possible evolutionary origins of this asymmetry from a population genomics perspective. We explored how mutations and selection could affect the preference for certain TF active conformations, and present evolutionary and mathematical arguments for the apo–holo asymmetry as a product of adaptations allowing the bacteria to respond optimally to the challenges it faces inside the mammalian gut.

Warm-blooded animals provide a favorable habitat and reproduction niche for Escherichia coli.^2,3 However, even inside the host this enterobacteriaceae member faces stress-induced situations such as host diet, competition with other microbiota, etc.⁴

We evaluate the possible influence of the TF–DNA protective interaction on the different TF active conformations and modes of regulation of the environmental conditions for E. coli inside the gut.

Theoretical studies have suggested a functional explanation for the demand theory of gene regulation (DTGR) predictions, claiming that the TF can protect the DNA from errors produced by unspecific interactions between DNA and proteins or other biological components.⁵ Recently, the possibility of TF–DNA error minimization has been tested experimentally with synthetically engineered organisms.⁶

Model description

The DTGR establishes an evolutionary framework predicting a positive control if the expression of a structural gene is necessary for the majority of the organism's cycle time (high demand) and a negative control if that gene is only necessary during a small fraction of the cycle time (low demand).^7–9 Gerland and Hwa¹⁰ analyzed genetic robustness as a possible evolutionary-driving force when transcriptional functionality is minimally used during definite biological periods. This group found that both modes of gene regulation (i.e. DTGR driven by the transcriptional rate and the regulation driven by genetic robustness) can have an effect on the organism, depending on the time scales and nutrient fluctuations involved. They showed that DTGR is more appropriate in describing relatively small populations and long-time scales of environmental variation.

Nevertheless, metabolism and gene regulation are strongly coupled by allosterism in bacteria. Interactions between metabolic effectors and their cognate TFs play a fundamental role in controlling genetic output,^11,12 given that genetic response not only depends on the presence/absence of the TF but also on the combinatorial control exerted by both the TF and the metabolic effector. Based on information collected from the RegulonDB database¹³ a recent study found that activator TFs mainly regulate in holo conformation, and provided evidence of statistical under-representation of the apo activation in Escherichia coli K-12.¹

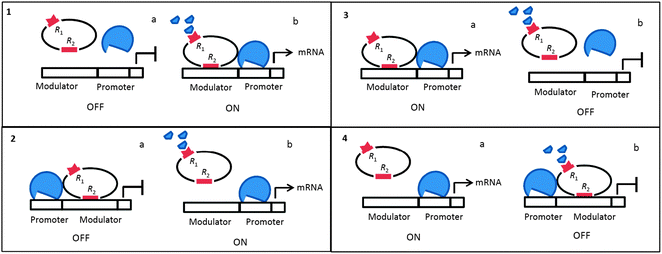
Four types of gene control circuits were previously analyzed in DTGR: induction with positive and negative controls, and repression with positive and negative controls. These combinations define the anatomy of the molecular switches that modulate gene expression levels in bacteria when allosterism is neglected⁸ (Fig. 1). Therefore, this model depends only on the presence/absence of the TF and excludes the possibility of combinatorial control exerted by both the TF and metabolism.

Fig. 1 Simple gene control circuits. (case 1) Induction with positive control. (a) In the first condition, the expression level of the regulated genes is OFF due to the activator being in the inactive state. (b) When the effector appears, it binds to the activator, changing it to a holo-functional conformation allowing the gene expression, e.g., MalT bound to maltotriose induces the maltose operon. (case 2) Induction with negative control. (a) The repressor is functional in apo-conformation, so the system is repressed in the absence of the effector. (b) The appearance of the effector and its binding to the TF change it to an inactive conformation, inducing the system, e.g., LacI bound to allolactose induces the lactose operon. (case 3) Repression with positive control. (a) In the absence of the effector, the system is ON with the activator in apo-functional conformation. (b) When the effector appears the system is deactivated, e.g., Cbl activates tau and ssi operons when it is unbound from adenosyl 5′-phosphosulphate. (case 4) Repression with negative control. (a) The repressor is inactive, so there is gene expression. (b) When the effector appears, it allows the TF bound to DNA to repress the transcription, e.g., TrpR bound to tryptophan in holo-conformation represses this aminoacid biosynthesis. Symbols: ON indicates gene expression and OFF indicates no gene expression. Oval: TF in oval with the regions R₁ and R₂ in brown, blue figure: RNA polymerase, effector: blue pyramidal triangles.

To take this into account, we developed the transcription factor conformation (TFC) model (Fig. 2), which considers the mutation and growth rates of single and double mutant populations after mutations affect: the ability of the TFs to bind an effector or allosteric binding site (r₁), TF's DNA recognition site (r₂), TF's DNA binding site (m), and the operon promoter. Fig. 2 clearly shows that each double mutant population has two different routes to be generated. Note that the mutation sequence is important for the parameter assignation and the final gene expression (Table S1, ESI†).

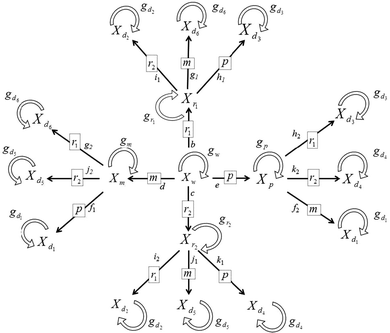Fig. 2 Schematic diagram representing the wild-type and mutant populations. The symbols are as follows: X_w the number of wild-type organisms; X_p the number of promoter mutants; X_m the number of modulator mutants; X_r1 the number of regulator mutants at the ligand binding domain; X_r2 the number of regulator mutants at the DNA binding domain; X_d1⋯X_d2 double mutants. The growth rates are represented by g_i where i can take the symbols {w, m, p, r₁, r₂, d₁, d₂, d₃, d₄, d₅, and d₆}. The symbols inside the square frames correspond to the mutation taking place. The alpha-numbers at one side of the arrows correspond to the mutation rates in Table S1 (ESI†) key.

Our TFC model includes two new variables X_r1 and X_r2 that correspond to the population of mutants in the allosteric binding site (R₁) and the DNA recognition site (R₂), respectively, (Fig. 2). We also include two new mutant rate parameters: the DNA protection exerted by the TF (ψ) and the allosteric binding site mutation rate (ω) (Table S1, ESI†). To model the combinatorial control exerted by both the TF and the effector, TFs are now divided into two regions: the first is named rho (ρ), defined as the rate of loss of the functional TF's DNA recognition site (R₂ or r₂), and the second, omega (ω), defined as the mutation rate for the loss of the allosteric binding site (R₁ or r₁) (Fig. 3 and Fig. S1–S6 and Table S1, ESI†). TF dissection is essential for appropriate modelling of the apo and holo conformations. As a consequence, our TFC model does not present the additive parameters for the rate of loss of the modulator target site (τ) with the rate of loss of the functional TF (ρ) as collapsed in Savageau's seminal model (see Table 1 from ref. 9). We used three values for modelling the allosteric binding site mutation rate (ω = {1, 20, and 40}). These values are directly related to the average number of critical bases involved in the interaction between TFs and their cognate metabolic effectors, and correspond to around 1, 10, and 20 amino acids, respectively, because the third codon position is the wobble position. We chose these values in agreement with experimental data for LacI showing that the region encoding the essential residues involved in the interaction with allolactose is in the range of 20 to 40 critical bases.¹⁴ Please note that ω = 1 is an extreme value that assumes that a single base mutation could disturb the functionality of a fragile TF interaction with its effector.

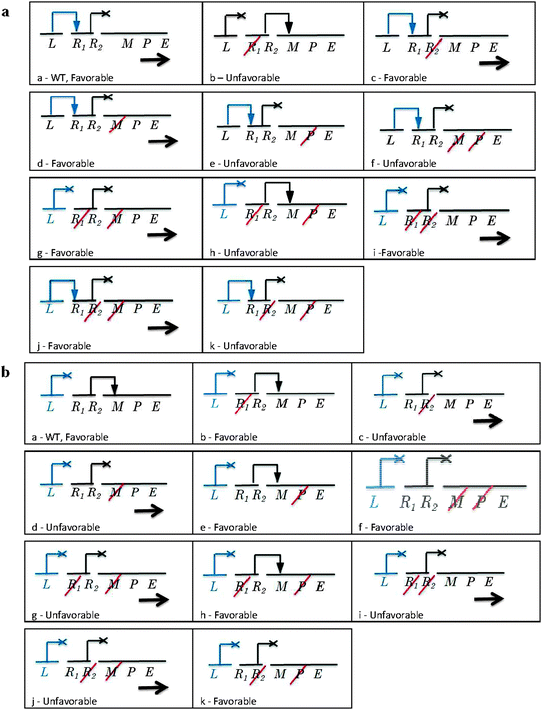Fig. 3 Regulation for LacI of an inducible system with negative control during high (a) and low demands (b). The DNA can mutate (diagonal red line) in the modulator (M), promoter (P), and/or in the regulator site R₁ if the mutation occurs in the TF-ligand domain or in R₂ if the mutation occurs in the TF–DNA binding domain. The horizontal arrow represents the gene expression of the structural gene (E). A blue line starting from R₂ and ending in an arrowhead indicates the interaction of the TF with the DNA; if the blue line ends in an X, it represents no TF–DNA interaction with the operon. (a) High demand; (a) wild type, (b–e) four single mutants, (f–k) six double mutants. (b) Low demand; (a–k) similar to Fig. 3a.

Model assumptions

To perform a mathematically controlled comparison between regulatory modes (repressor and activator) of TFs and the two possible active conformations (holo and apo), we selected four TFs, each representative of a corresponding combination of the regulatory mode and active conformation: LacI (repressor, apo) and MalT (activator, holo), TrpR (repressor, holo) and Cbl (activator, apo). LacI and MalT numerical parameters were collected from ref. 8, and extrapolated to TrpR and Cbl (Table S3, ESI†), given the limited amount of information on the specific TF parameter values, especially for Cbl.

For all the TF conformations analyzed, it is assumed that the TF–effector interaction produces a conformational change in the TF that affects the TF–DNA binding site. In mathematical terms, this implies an additive effect of ω and ρ over the mutation rates, c, i₁, j₂, and k₂, (Table S1, ESI†). This intrinsic TF interaction has been experimentally reported, at least for the well-documented LacI, by molecular structure analysis,¹⁵ and by changing residues that affect the binding site,¹⁶ among others.

In all the TFs analyzed, it is assumed that the regulatory proteins follow a classical coupled circuit regulation where the TF itself is unregulated,¹⁷ as has been experimentally reported for LacI operon regulation.¹⁸ Mathematically, the implication is that epsilon's (ε) mutation rate does not affect the TF expression when the structural gene expression is enhanced (Table S1, ESI†).

Following the same assumption as in the DTGR model, we did not include the analysis of possible combinations of double, triple or quadruple mutant populations due to the low probability of their occurrence. Nevertheless the universe of double mutants is presented in Fig. 2 and eqn (S25)–(S30) (ESI†).

As represented by the unidirectional arrows in Fig. 2, it is assumed that the possible reverse mutations restoring the original DNA functionality or compensating the mutation effects are low and were neglected.

It is also assumed that the TF–modulator interaction reduces the basal rate of the mutation by a factor of ψ = 1/10. The parameter ψ represents the DNA mutation rate reduction as a consequence of DNA protection under extreme environmental conditions. This protein–DNA protection can occur under oxidative stress or starvation (e.g.ref. 19 and 20) and is associated with the non-specific binding of other TFs, metabolites, and/or other proteins to the free binding site.⁵

The growth parameter delta (δ) was assigned according to the more nutritionally deficient environment along the proximal and distal portions of the human digestive tract (Table S2, ESI†).

In the case of Cbl, the δ assignation during the high demand fraction of the E. coli cycle was made in spite of the presence of sulphur nutrients in the colon,²¹ under the assumption of starvation for sulphur scavenging as a consequence of competition with other sulphur-specialized microorganisms and/or by competition with the host²² (see Discussion for details).

Given that the idea was to make mathematically-controlled comparisons of the active conformations within the activator and repressor modes of regulation, the TFs with dual modes of control are not included in this work.

Results and discussion

The diagrams in Fig. 3 and Fig. S1–S6 (ESI†) represent all the different possible conditions under which the wild-type and single or double mutant regulate or deregulate the expression of the structural genes during high and low demand.

Thresholds of selection (TS) for the wild-type regulatory mechanism

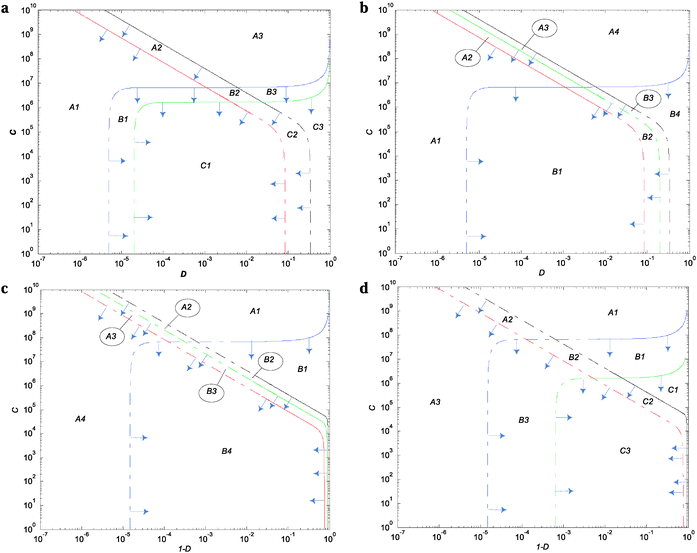
The thresholds of selection from Fig. 4 and 5 and Fig. S7–S10 (ESI†) define the population's boundary between the wild type and the corresponding single mutant. These were obtained by equating eqn (S33) and (S34) (ESI†) with the criterion of selection (θ) (whichever gives the maximum ratio) and solved by using the method of bisection to find C with respect to D (or D with respect to C) (see ESI† for details).

Fig. 4 TS of the wild-type regulatory mechanism. Curves when ω = 40, region for the wild-type and mutants as C_i,j with i = {1…3}; j = {1…3}. The thresholds are represented on a logarithmic scale as functions of the demand for gene expression (D) and the cycle time (C). The thresholds are for the promoter (p) in blue, modulator (m) in black, TF-effector regulatory section (r₁) in green, and TF-DNA regulatory section (r₂) in red. The solid and dotted line intervals for each curve represent the low- and high-C asymptotes, respectively, where the root finding method was implemented. The blue arrows, perpendicular to the TS, point in the direction of the population's realizable regions. (a) LacI; (b) TrpR; (c) MalT; and (d) Cbl.

Fig. 5 TS of a wild-type regulatory mechanism. The demand (D) vs. total cycle (C) are represented in linear and logarithmic scales, respectively. Dynamics with ω = 20. (a) LacI; (b) TrpR, curves for the thresholds for X_r1/X_w and X_m/X_w are superimposed; (c) MalT, curves for X_r1/X_w and X_m/X_w are superimposed; and (d) Cbl.

LacI threshold of selection. LacI is negatively regulated in apo conformation when the demand for lactose catabolism is low.²³

Fig. 4a and Fig. S7 (ESI†) show that LacI wild-type TS are similar to Savageau's seminal model with respect to their shapes and demand extreme values (Fig. 2A from ref. 8) but different with respect to the TS enclosing the wild-type region. When omega equals 20 and 40, the wild-type boundaries are delimited by X_r1/X_w and X_r2/X_w with the TS for X_m/X_w and promoter X_p/X_w at the periphery. When ω increases, the X_r1/X_w curve moves to the right and the X_r2/X_w curve is displaced slightly to the left; these two migrations act in conjunction, narrowing the wild-type region.

TrpR thresholds of selection. The TrpR regulon is involved in tryptophan biosynthesis, transport, and regulation.²⁴ It is negatively regulated in holo conformation when the demand for tryptophan is low.

Fig. 4b and Fig. S8 (ESI†) show the following: first, that the curves of the modulator and promoter are similar in shape to those obtained with LacI (Fig. 4a and Fig. S7, ESI†); second, that when ω increases, the X_r2/X_w threshold moves inwards through smaller values of the demand, narrowing the wild-type region; and third, that in all the simulations, the wild-type region is delimited by X_p/X_w on the left side of the demand and by X_r2/X_w on the right side.

MalT thresholds of selection. The MalT regulon is active when the demand for the maltose catabolism is high.²⁵ During high demand, MalT is holo positively regulated, acting over the site of action of regulatory DNA.

Fig. 4c and Fig. S9 (ESI†) show that the shapes for the threshold of selection for the modulator and promoter are similar to those obtained with Savageau's model (ref. 8, Fig. 3A). However, the wild-type boundaries X_p/X_w and X_r2/X_w are delimited now. When ω is increased, the X_r2/X_w thresholds shift to the left increasing the wild-type region.

Cbl thresholds of selection. In the colon, Cbl activates two transcription units, tauABCD and ssuEADCB, coding for proteins responsible for the transport and catabolism of taurine and aliphatic sulphonates, respectively – two alternative sources of sulphur.²⁶

Cbl regulation is intimately associated with the hierarchical preference of E. coli for sulphur sources: cysteine > sulphate > sulphonates.²⁷ In the presence of cysteine, the preferred sulphur source, the Cbl associate regulon is not expressed. This is because CysB, the major regulator of sulphur utilization, is inactive.

When sulphur is present, N-acetyl-L-serine (NAS) binds to CysB to change its state into the functional holo conformation.²⁸ In the absence of sulphur, the APS concentration decreases, so Cbl can regulate its regulon in its functional apo conformation.

Fig. 4d and Fig. S10 (ESI†) show the wild-type TS boundaries of the wild-type region delimited by X_r1/X_w and X_r2/X_w. When ω increases, X_r1/X_w and X_r2/X_w thresholds shift to the right and the left, respectively, narrowing the wild-type region.

Overlapping between the TF wild-type areas. Fig. 5 presents the TS with the abscissa in a linear scale for ease of comparison between the TF wild-type regions. As in the seminal Savageau model, there are no wild-type regions overlapping between the negative (Fig. 5a and b) and positive (Fig. 5c and d) modes of regulation. Please note that the X_r2/X_w threshold determines for all the cases the boundary for the wild type between the positive and negative modes of regulation.

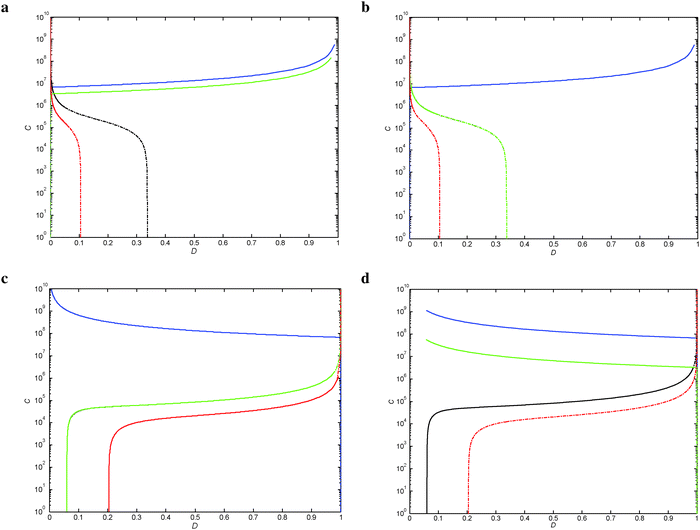
Within the two modes of regulation, there is an almost complete overlapping of the wild-type regions, indicating that the apo and holo conformations do not differentiate in this aspect (Fig. 5).

Tables S4–S6 (ESI†) offer an overview of the population areas framed by the TS from Fig. 4 and Fig. S7–S10 (ESI†) after ω variation. They mark the wild-type as well as the realizable favorable (F) and unfavorable (U) single mutant population regions under high demand. The regions not marked represent zones of coexistence of single mutants.

Influence of parameters on minimum and maximum values of demand

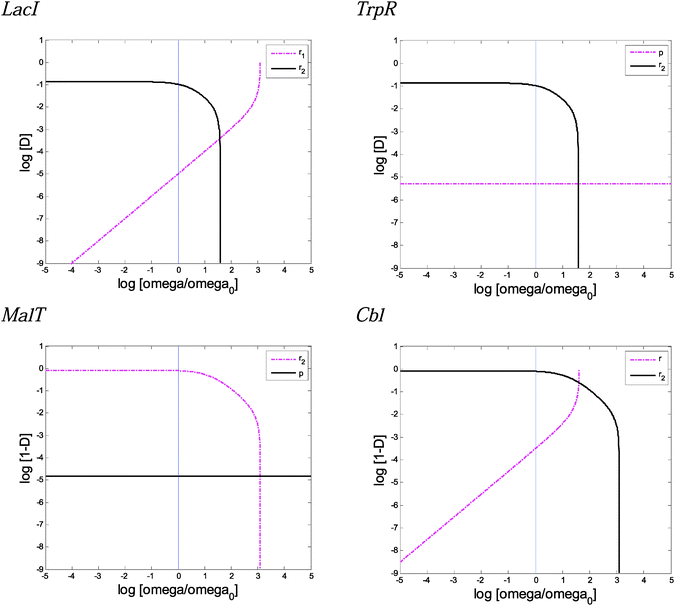
Wild-type TS from Fig. S7–S10 (ESI†), when ω = 20, were used along this sensitivity analysis.

Fig. 6 and Fig. S15 (ESI†) display the influence of the parameter change on the extreme values of the demand. Fig. S16 (ESI†) presents the influence of the parameters over the TS not surrounding the wild-type region.

Fig. 6 Influence of the constituent parameters on the values of the wild-type D_min and D_max. The parameter is varied around its nominal value, and the resulting lower (D_min) and upper (D_max) values are calculated. Solid lines correspond to the D_max and magenta dashed-dotted lines correspond to the D_min. LacI and TrpR represent the TF negative mode of regulation for apo and holo, respectively. MalT and Cbl represent the TF positive mode of regulation for holo and apo, respectively. Mutation rate ω = 20 was used along these analysis. The axes are represented in decimal logarithmic scale.

Each TFC model parameter (Table 1 and Table S3, ESI†) was evaluated around its nominal value and its influence over D_min and D_max were analyzed (see the ESI† Model description for details).

Table 1 Definition for the model mutation and growth rate parameters

Mutation rate parameters
μ	Reference mutation rate
π	Relative to μ, for loss of a strong promoter with negative control
υ	Relative to μ, for gain of an up-promoter with positive control
τ	Relative to μ, for loss of a regulator's functional target site
ρ	Relative to μ, for loss of the transcription factor DNA binding domain
ω	Relative to μ, for loss of the transcription factor ligand domain
ε	Relative to μ, when expression is increased 100-fold
ψ	Relative to μ, for a 10-fold decrease in μ when the transcription factor interacts with its functional DNA binding domain

---

Growth rate parameters
γ	Reference growth rate in the nutritionally richer of the two environments
δ	Relative to γ, for the more nutritionally deficient of the two environments
λ	Relative to γ, when there is a loss of expression with negative control
λ	Relative to γδ, when there is a loss of expression with positive control
σ	Relative to γ, when there is superfluous expression with positive control
σ	Relative to γδ, when there is superfluous expression with negative control

---

The sensitivities were analyzed by comparing their effect over the area of the wild-type region. A change that produces an increase in the wild-type region is considered to be advantageous over other changes that do not have discernible effects or that produce a decrease of the wild-type region. If no discernible difference is found, then no advantage is selected for any TF conformation.

Negative mode of regulation

With the exception of π and ω, there is almost complete equilibrium of the advantages between the two TF conformations (Table 2 and Table S7 and S8, ESI†). When the parameters π and ω increase in value, they present advantages for LacI and TrpR; the opposite is true when π and ω decrease in their nominal values.

Table 2 Summary of the advantages from Tables S8 and S9 (ESI) after subdivisions. Advantages are classified according to the increase and decrease around the nominal value, sub-grouped according to the extremes of the demand and further sub-grouped between mutation or growth parameters

			Negative		Positive
			LacI	TrpR	MalT	Cbl
Increase (→)	D min	Mutation	π	ω	—	μ, ρ, ω
		Growth	—	—	σ, θ	δ, λ
	D max	Mutation	—	—	—	μ, υ, ρ, ω, ε
		Growth	—	—	λ, θ	δ, σ
Decrease (←)	D min	Mutation	ω	π	μ, ρ, ω	—
		Growth	—	—	δ, λ	σ, θ
	D max	Mutation	—	—	μ, υ, ρ, ω, ε	—
		Growth	—	—	δ, σ	λ, θ

---

These TF mirror advantages for π and ω are for both the D_min sides of the demand (Table 2). However, because there is no significant room to additionally increase the wild-type region from the D_min side, there is no practical implementation or advantage, even if it is theoretically possible (see Fig. 4a, b, 5a, b and Fig. S7, S8, ESI†).

On the whole, from the point of view of the parameter sensitivities, the apo and holo conformations are both well-adapted at the negative mode of regulation. At least, this is the case if one does not take into consideration other factors that could bias the advantages. Possible examples of this might involve mechanisms not included in the model, such as the TrpR attenuation^29,30 or gene regulation by auto-regulation.^13,24,31

Positive mode of regulation. Table 2 and Tables S7 and S9 (ESI†) show that the advantages of one parameter frequently appears in tandem for both extremes of the demand.

Globally, the parameters with advantages are equally distributed between the two conformations, with 16 cases each (first row Table S10, ESI†). In addition, Table S10 (ESI†) shows that the advantages are equally distributed after grouping with respect to the extremes of the demand or according to the mutation and growth parameters.

Marked differences are evident only when the parameters are grouped according to the increase or decrease in their nominal parameter values (Table 2 and Table S10, ESI†). This includes a bias for the apo conformation when the parameters increase (12 of 16) and for the holo conformation when they decrease (12 of 16).

The classification in Table 2 allows for a better visualization of the advantages after sub-collecting the extremes of the demand within the parameters that increase or decrease their basal values.

It is important to note that the MalT and Cbl wild-type areas almost completely cover the upper extreme of the demand with no practical room for further increase (Fig. 5c and d). This implies that parameters with D_max advantages, though mathematically feasible, do not offer realistic advantages, and are therefore are not analyzed here.

In Table 2, the D_min extreme of demand shows a bias for MalT advantages when the parameters decrease their nominal value with three mutation and two growth parameters. The mutation parameters correspond to the reference mutation rate (μ), loss of the transcription factor DNA-binding domain (ρ), and the loss of the transcription factor ligand domain (ω). Growth parameters encompass the more nutritionally deficient environment of the two environments (δ), and the loss of expression with positive control (λ).

By contrast, the D_min advantages when the parameters increase their nominal value show a bias for Cbl with the same mutation (μ, ρ, ω) and growth (δ, λ) parameters.

Table 2 shows that Cbl presents advantages in the growth parameters delta (δ) and lambda (λ) when the parameters increase their nominal value. For MalT, the growth parameters with advantages are sigma (σ) and theta (θ). These Cbl and MalT parameter results are reversed when their nominal value is decreased.

The individual analysis of the parameters from Table S7 (ESI†) highlight the advantage of Cbl under stress conditions when there is an increase in the basal mutation rate mu (μ). Also, Cbl presents an advantage after increasing omega (ω), reflecting a better adaptation or flexibility for the apo conformation over the holo to mutations in the DNA region coding for the effector TF binding site. In addition, Cbl better tackles mutations that increase rho (ρ) than MalT. The parameter rho (ρ) represents the rate of mutations at the level of the TF-site of interaction with the DNA (Table 1).

The criterion of selection theta (θ) represents the minimal fraction a mutant population can decrease with respect to the wild type before it disappears in a given environment.³² A low value of θ indicates better adaptation under extreme conditions. Table S9 (ESI†) shows that a decreasing θ is advantageous for Cbl over MalT.

In summary, individual analyses of the parameter sensitivities indicate that Cbl apo conformation is better adapted to stress situations where the rates of the mutation are likely to be increased and the selection coefficient theta (θ) decreased.

Two parameters, gamma (ψ) and psi (Ψ), exhibit no influence in any of the cases (Fig. S15h and S16i, ESI†). The parameter γ represents the reference mutation rate in the richer of the two environments.

The parameter ψ represents the decrease in the mutation basal rate when the TF interacts with the DNA binding site (Table 1). Fig. S15g and S16h (ESI†) do not reveal sensibility effects to the changes in ψ around their nominal value. However, Fig. S16h (ESI†) shows that a 20-fold and 40-fold increase in the nominal value for the negative and positive modes of regulation, respectively, produces an abrupt decrease in the threshold of selection modulator sensitivities. In addition, simulations (not shown) can reproduce these abrupt sensitivity changes around the nominal value if the basal mutation rate (μ) is increased 100-fold. These simulations indicate that ψ can become an important parameter that affects the boundaries delimited by X_m/X_w in stress situations when the basal mutation rate is incremented (e.g. under heat shock, starvation, or oxidative stress).

From an evolutionary standpoint, the results indicate that the positive apo conformation (Cbl) has been under selective pressure, likely due to the particular stress suffered due to sulfate limitation in the distal digestive tract. By contrast, positive holo conformation (MalT) adapts better to the “normal” conditions that E. coli more frequently faces in the colon of the digestive tract.

Conclusions

To the best of our knowledge, this is the first mathematical model explicitly comparing the evolutionary adaptations of the apo–holo TF conformations in any organism.

Thresholds of selection

There is no wild type region overlap between negative (Fig. 5a and b) and positive (Fig. 5c and d) modes of regulation. In contrast, within each of the separate modes of regulation there is almost complete overlap.

With the exception of LacI, where the D_min threshold of selection changes from X_p/X_w (when ω = 1) to X_r1/X_w (when ω = 20 and 40), the rest of the TFs analyzed maintain the same TS boundaries for the wild-type region along the different ω values studied (Fig. 4 and 5 and Fig. S7–S10, ESI†).

In Fig. 4, 5 and Fig. S7–S10 (ESI†), it can be seen that the X_m/X_w TS are never part of the boundary limits for the wild-type population in either mode of regulation. Rather, X_p/X_w is frequently the wild-type lower limit of the demand. In many cases, at least one of the TS enclosing the wild-type regions corresponds to X_r1/X_w or X_r2/X_w.

As expected, the promoter and modulator LacI and MalT TS presented in Savageau's model⁸ have shapes similar to those obtained with the TFC model, although slight differences can be observed with respect to the wild-type extent of selections. The reason behind these differences can be found in the increase in the details of the regulation, as seen with the dissection of the TF in two sectors r₁ and r₂.

Sensitivity analysis

Within the positive mode of regulation, there is a marked difference between the two conformations when they are grouped according to the parameter increase or decrease and further subdivided according to the extremes of the demand (Table 2).

The parameter advantages for the positive mode of regulation are biologically realizable from the D_min side (see Fig. 5c and d), which indicates that the organism can deal well with mutations related to short periods of high demand. The reverse is true for the case of negative regulation, which is better adapted to dealing with increasing periods of high demand (D_max); in this case, the sensibility parameters do not exhibit a bias for either transcriptional configuration (Table 2), which is in accordance with the more balanced frequencies reported in ref. 1. The selection of one or the other transcriptional mechanism is probably made on the basis of other selectionist arguments.

Exploratory studies for the six LacI double mutants (not shown) produced a range of different TS but with low-level total life cycle (C) curves as the common denominator. These results would indicate a better adaptation of these mutants to larger total life cycles or, in other words, a predominant presence of the wild type for shorter life cycles.

Cbl positive apo active conformation

The reported presence of inorganic sulfate along the mammalian intestine²¹ predicts that Cbl should be in its non-functional holo conformation when E. coli colonizes the colon.

In principle, this is in contradiction with our model assumption that Cbl should be in its functional apo conformation in that later section of the intestine. A possible reason behind this assumption is that E. coli could face starvation for inorganic sulphur during the period spent in the distal region of the intestine as a consequence of competition for the element with sulfate-reducing bacteria in the large intestine³³ (see delta assignation (δ) for Cbl in Table S2, ESI†). This is a highly competitive environmental situation where cysteine and sulphate could be effectively unavailable for E. coli (or with low scavenging capacity). This would force the organism to use other sulphate sources such as taurine, which is found in high concentrations in the colon, where it is key for chelating bile acids, or sulphonates, whose assimilation and catabolism into sulfite are activated by Cbl under its active apo conformation. This situation for Cbl apo conformation could also probably occur in unpredictable sulphate detrimental situations outside of the host as well.

In conclusion, the results presented here furnish evolutionary arguments favoring the holo conformation over the apo TF representation under the positive modes of control, as reported recently.¹ In addition, the observed unbiased distribution for the negative apo or holo frequencies is also in accordance with the no-preference model parameter sensitivities for the two TF configurations studied.

Future considerations

Other E. coli genetic regulations such as the dual TF or attenuation can encompass control systems of relevance not analyzed here. The extension of the TFC model to the other transcriptional mechanisms of regulation is an open research topic that might be developed.

A better comprehension of the apo and holo transcriptional regulation connected to an organism's life cycle is fundamental for improving the design of “à la carte” bacteria that may not be as robust as the wild type,³⁴ but will offer specific fitness advantages of human interest. In this respect, there is evidence in the literature for E. coli systems built on the basis of a deep understanding of the transcriptional regulation mechanisms.³⁵

The TFC model consists of a set of binary S-system equations (eqn (S20)–(S30)) and can be log-transformed into linear equations allowing for reverse engineering with classic linear optimization techniques for the design of mutants able to grow in the demand and total cycle ranges of human interest.³⁶ This technique promises to rationalize the search for mutants able to live during a given period of time and under certain environmental conditions from a universe of bacteria with different modes of transcriptional regulation.

Acknowledgements

We acknowledge fruitful discussions with Dr Néstor Torres Darias, Dr Martín Peralta Gil, and members of the Computational Genomics Research Program from the CCG-UNAM. This work was partially supported by grant IA200614-2 from PAPIIT-UNAM to JAF-G. YIB-M acknowledges the PDCB of CCG-UNAM and her support by a PhD fellowship (228320/210360) from CONACyT-México.

References

1. Y. I. Balderas-Martínez, M. Savageau, H. Salgado, E. Perez-Rueda, E. Morett and J. Collado-Vides, PLoS One, 2013, 8, e65723.
2. M. Savageau, Am. Nat., 1983, 122, 732–744.
3. G. W. Tannock and D. C. Savage, Infect. Immun., 1974, 9, 591–598.
4. M. T. Bailey, Horm. Behav., 2012, 62, 286–294.
5. G. Shinar, E. Dekel, T. Tlusty and U. Alon, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 3999–4004.
6. V. Sasson, I. Shachrai, A. Bren, E. Dekel and U. Alon, Mol. Cell, 2012, 46, 399–407.
7. M. A. Savageau, Proc. Natl. Acad. Sci. U. S. A., 1977, 74, 5647–5651.
8. M. A. Savageau, Genetics, 1998, 149, 1677–1691.
9. M. A. Savageau, Genetics, 1998, 149, 1665–1676.
10. U. Gerland and T. Hwa, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 8841–8846.
11. V. Baldazzi, D. Ropers, Y. Markowicz, D. Kahn, J. Geiselmann and H. de Jong, PLoS Comput. Biol., 2010, 6, e1000812.
12. O. Kotte, J. B. Zaugg and M. Heinemann, Mol. Syst. Biol., 2010, 6, 355.
13. H. Salgado, M. Peralta-Gil, S. Gama-Castro, A. Santos-Zavaleta, L. Muniz-Rascado, J. S. Garcia-Sotelo, V. Weiss, H. Solano-Lira, I. Martinez-Flores, A. Medina-Rivera, G. Salgado-Osorio, S. Alquicira-Hernandez, K. Alquicira-Hernandez, A. Lopez-Fuentes, L. Porron-Sotelo, A. M. Huerta, C. Bonavides-Martinez, Y. I. Balderas-Martinez, L. Pannier, M. Olvera, A. Labastida, V. Jimenez-Jacinto, L. Vega-Alvarado, V. Del Moral-Chavez, A. Hernandez-Alvarez, E. Morett and J. Collado-Vides, Nucleic Acids Res., 2013, 41, D203–D213.
14. P. Markiewicz, L. G. Kleina, C. Cruz, S. Ehret and J. H. Miller, J. Mol. Biol., 1994, 240, 421–433.
15. M. Lewis, G. Chang, N. C. Horton, M. A. Kercher, H. C. Pace, M. A. Schumacher, R. G. Brennan and P. Lu, Science, 1996, 271, 1247–1254.
16. S. Tungtur, S. M. Egan and L. Swint-Kruse, Proteins, 2007, 68, 375–388.
17. M. Savageau, in Coupled circuits of gene regulation. In: Sequence specificity in transcription and translation, ed. A. R. Liss, New York, 1985.
18. B. Muller-Hill and J. Kania, Nature, 1974, 249, 561–563.
19. M. Almiron, A. J. Link, D. Furlong and R. Kolter, Genes Dev., 1992, 6, 2646–2654.
20. A. Martinez and R. Kolter, J. Bacteriol., 1997, 179, 5188–5194.
21. T. Florin, G. Neale, G. R. Gibson, S. U. Christl and J. H. Cummings, Gut, 1991, 32, 766–773.
22. F. Carbonero, A. C. Benefiel, A. H. Alizadeh-Ghamsari and H. R. Gaskins, Front. Physiol., 2012, 3, 448.
23. J. H. Miller and W. S. Reznikoff, The Operon, Cold Spring Harbor Laboratory, Cold Spring Harbor, NY, 2nd edn, 1980.
24. I. M. Keseler, J. Collado-Vides, A. Santos-Zavaleta, M. Peralta-Gil, S. Gama-Castro, L. Muniz-Rascado, C. Bonavides-Martinez, S. Paley, M. Krummenacker, T. Altman, P. Kaipa, A. Spaulding, J. Pacheco, M. Latendresse, C. Fulcher, M. Sarker, A. G. Shearer, A. Mackie, I. Paulsen, R. P. Gunsalus and P. D. Karp, Nucleic Acids Res., 2011, 39, D583–D590.
25. O. Raibaud and E. Richet, J. Bacteriol., 1987, 169, 3059–3061.
26. T. Bykowski, J. R. van der Ploeg, R. Iwanicka-Nowicka and M. M. Hryniewicz, Mol. Microbiol., 2002, 43, 1347–1358.
27. E. Stec, M. Witkowska-Zimny, M. M. Hryniewicz, P. Neumann, A. J. Wilkinson, A. M. Brzozowski, C. S. Verma, J. Zaim, S. Wysocki and G. D. Bujacz, J. Mol. Biol., 2006, 364, 309–322.
28. A. Lochowska, R. Iwanicka-Nowicka, D. Plochocka and M. M. Hryniewicz, J. Biol. Chem., 2001, 276, 2098–2107.
29. E. Merino and C. Yanofsky, Trends Genet., 2005, 21, 260–264.
30. C. Yanofsky, J. Bacteriol., 2000, 182, 1–8.
31. R. Hermsen, B. Ursem and P. R. ten Wolde, PLoS Comput. Biol., 2010, 6, e1000813.
32. J. E. LeClerc, B. Li, W. L. Payne and T. A. Cebula, Science, 1996, 274, 1208–1211.
33. B. Deplancke, K. R. Hristova, H. A. Oakley, V. J. McCracken, R. Aminov, R. I. Mackie and H. R. Gaskins, Appl. Environ. Microbiol., 2000, 66, 2166–2174.
34. M. E. Csete and J. C. Doyle, Science, 2002, 295, 1664–1669.
35. M. R. Atkinson, M. A. Savageau, J. T. Myers and A. J. Ninfa, Cell, 2003, 113, 597–607.
36. N. V. Torres and E. O. Voit, Pathway analysis and optimization in metabolic engineering, Cambridge University Press, New York, 2002.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4mb00561a

‡ Current address: Facultad de Ciencias, Universidad Nacional Autónoma de México, Mexico City, Mexico.

---