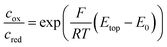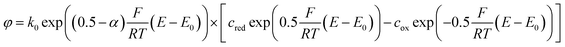Redox cycling in nanoporous electrochemical devices

Abstract

Nanoscale redox cycling is a powerful technique for detecting electrochemically active molecules, based on fast repetitive oxidation and reduction reactions. An ideal implementation of redox cycling sensors can be realized by nanoporous dual-electrode systems in easily accessible and scalable geometries. Here, we introduce a multi-electrode array device with highly efficient nanoporous redox cycling sensors. Each of the sensors holds up to 209 000 well defined nanopores with minimal pore radii of less than 40 nm and an electrode separation of ∼100 nm. We demonstrate the efficiency of the nanopore array by screening a large concentration range over three orders of magnitude with area-specific sensitivities of up to 81.0 mA (cm⁻² mM⁻¹) for the redox-active probe ferrocene dimethanol. Furthermore, due to the specific geometry of the material, reaction kinetics has a unique potential-dependent impact on the signal characteristics. As a result, redox cycling experiments in the nanoporous structure allow studies on heterogeneous electron transfer reactions revealing a surprisingly asymmetric transfer coefficient.

---

Introduction

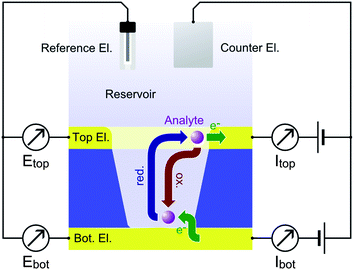
Electrochemical redox cycling on the nanoscale is a very efficient technique for the amplification of Faradaic currents. It provides a high sensitivity by means of repetitive oxidation and reduction events of an analyte molecule. A convenient way to achieve repetitive electrode reactions is the usage of a two closely spaced and individually addressable electrodes. The target molecules can then shuttle between these electrodes, driven by Brownian motion.¹ As one electrode is biased to a reducing potential and the other one to an oxidizing potential, a certain number of electrons is transferred from the cathode to the anode with each shuttling cycle. The recurring electron transport is detected as a current (see Scheme 1).

Scheme 1 Redox cycling within a nanopore for an oxidizing top (E_top) and a reducing bottom electrode potential (E_bot). The flux of reduced and oxidized molecules participating in redox cycling is indicated by blue and red arrows, respectively. Green arrows denote the electron transfer at the electrodes. Accordingly, the redox active molecules repetitively transfer electrons from the bottom of the pore to its periphery. A continuous redox cycling current |I_bot| ∼ |I_top| is detected at both electrodes.

The redox cycling current is typically proportional to the number of molecules contributing to the signal. It can therefore be used for quantitative analyte detection² and may even reach single-molecule resolution under well-defined conditions.^3–7 The principle of redox cycling is utilized in multiple configurations. A probe-based configuration is employed in scanning electrochemical microscopy (SECM), which allows characterizations of electrochemical interface reactions to be locally resolved.⁸ SECM has been used in a variety of applications ranging from topographic and reactivity studies on solid-state surfaces to the electrochemical imaging of living cells.^9–14

Other techniques aim for on-chip implementations of redox cycling devices for electrochemical detection.^15–17 The advances of micro- and nanofabrication techniques during the last decades have greatly contributed to the efficiency of on-chip redox cycling devices. Lateral sensor arrangements, such as interdigitated electrode arrays, have profited from fabrication techniques that allow closely spaced electrodes to be produced on the micron- and sub-micron scale opening up a variety of applications in sensing and fundamental electrochemistry.^18–30 However, reducing gap sizes in lateral electrode arrangements to the nanometer scale usually requires advanced fabrication methods. A convenient way to implement 20–100 nm gaps in between individually addressable electrodes is achieved by arranging the sensor in a vertical architecture using a layer-by-layer deposition process. This concept has been exploited by the group of Lemay for the fabrication of highly sensitive nanofluidic or nanocavity redox cycling devices using a chromium sacrificial layer in between the electrodes.^31–33 Here, two electrodes form the upper and lower boundaries of a nanochannel being separated only by a thin film of electrolyte. The high redox cycling efficiency of strongly confined cavity devices can be exploited for sensing applications^31,34,35 as well as investigations on fundamental electrochemical phenomena such as electron transfer characteristics³³ and species adsorption.³⁶ The redox cycling effect specifically amplifies the signal of molecules, which are capable of repetitively changing their oxidation states. This feature is of particular importance when the analyte of interest is to be detected in solutions containing other electrochemically active molecules that do not efficiently participate in redox cycling. In this case, the redox cycling amplification and limited bulk access of the sensor help to discriminate relevant signals from background interference.^31,37 Furthermore, sweeping electrode potentials at a constant offset enables the quantitative detection of different redox active compounds in redox cycling mode.²⁶ Choosing the potential window of both electrodes accordingly, the response of one analyte can be amplified while the signal derived from the other analytes is restricted to mass exchange with the reservoir only. In on-chip fabrication of redox cycling devices, the working electrodes are easily stacked in vertical layers. This way, no lateral structuring limitations have to be considered. Instead, the electrode distance is only limited by the thickness of the spacing layer preventing a shortcut of the sensor electrodes. A convenient approach to implement this strategy is the usage of porous redox cycling sensors.^38–49 Typically, an upper electrode is facing the electrolyte directly. A lower electrode is accessible via individual apertures in the top electrode and a separating insulator film. Porous redox cycling systems combine the easy accessibility of surface bound electrodes with the close spacing of vertical alignment. Thus, small fluctuations of analyte concentrations or kinetic behaviour can be monitored in high temporal resolution. Additionally, the porous structure allows experiments related to specific binding events. Here, the redox active species serve as a tracer and the actual analyte causes blocking of the pores suppressing the redox cycling current. Preferably for this application, the pores should feature diameters comparable to the size of the blocking molecules. However, also standard detection benefits from pore radii far below the micrometer range as long as the interpore distances are equally decreased.

The consideration above led to the development of porous redox cycling devices with pore diameters of 500 nm and electrode separations of 100–200 nm.⁴¹ Recently, the group of Bohn presented investigations on the electrochemical sensing properties in porous redox cycling devices with an interpore spacing of ∼1 μm and pore radii of ∼250 nm.⁴⁷ In the work presented here, we cross the line at which smaller pores simply imply an improved signal quality. Thus, we protrude to a regime where the specific pore geometry becomes crucial for quantitative and qualitative redox cycling processes, shedding light on fundamental aspects of electrochemistry. In particular, we present investigations performed on arrays of up to 209 000 pores with an electrode spacing of ∼100 nm, minimal pore radii below 40 nm and a pore density of ∼2.9 × 10⁹ cm⁻². We demonstrate the applicability of the nanoporous sensors to the detection of redox-active Fc(MeOH)₂ molecules with high sensitivity up to 81.0 mA (cm⁻² mM⁻¹) and reveal a surprisingly asymmetric transfer coefficient for the electrode reactions. We further elucidate the impact of geometric aspects, which provide the opportunity to gain a comprehensive picture of redox cycling phenomena inside nanoporous devices. The theoretical explanations for the observed phenomena are supported by numerical simulations to aid in developing advanced nanoscaled sensor geometries.

Methods

A detailed description of the fabrication process, data acquisition, data analysis, and the numerical simulations are provided in the ESI.† The main experimental procedures are described below.

Fabrication

Devices are fabricated in the clean room using oxidized 4′′-silicon wafers as substrates. The platinum bottom electrodes (70 nm Pt and 10 nm Ti adhesion layer) are structured via optical lithography and lift-off using a dual-layer resist stack to reduce edge effects. A 100 nm Si₃N₄ spacer layer is deposited by plasma enhanced chemical vapor deposition on top of the bottom electrode. Subsequently, the top electrodes (30 nm Pt and 10 nm Ti adhesion layers) are patterned again by optical lithography and lift-off. The whole device is passivated in an 800 nm stack of alternating SiO₂/Si₃N₄ layers. Nanopores are introduced into the sensor by electron beam lithography and subsequent reactive ion etching down to the bottom platinum layer. Individual sensor arrays are diced from the wafer and contacted via bond-pads at the outer edge of each chip. For the recorded concentration-dependent series, glass rings are attached to the chip using a two-component PDMS adhesive. Curing of the PDMS is facilitated by applying moderate baking temperatures of 60–80 °C for 30 minutes.

Characterization

All experiments are carried out using redox-active Fc(MeOH)₂ in a 100 mM KNO₃-electrolyte. The potential sweeps are performed at rates of 50 mV s⁻¹ using a CHI1030B multi-channel potentiostat (CH-Instruments). The structure's top and bottom electrodes operate as separate working electrodes. A platinum wire serves as a counter electrode. Either a housed Ag/AgCl electrode (BASi Inc) or a Warner Instruments “Leak-Free Reference Electrode” (WPI) is used as a reference electrode. The current traces used for plotting and analysis are obtained from the 3^rd sweep of a particular experiment. The experiments were performed at room temperature (∼21 °C).

Numerical simulation

The numerical calculations are performed with a finite element method using COMSOL 4.2a. The sensor is represented by a single pore, its closest surrounding (r_vol = 105 nm) and the overlaying reservoir (h_vol = 800 nm). This method is known as the “diffusion cell approach”. The geometry is adapted from SEM recordings and FIB cuts. Radial symmetry of the cell is assumed. In the free volume Fick's laws of diffusion are applied. At electrically inactive boundaries the flux of both species being perpendicular to the surface is set to zero. At the electrodes the flux is defined by the Butler–Volmer equation. Sweep rate and analyte concentrations are chosen according to the experiments emulated.

Results and discussion

Nanoporous sensor geometry

A typical nanoporous sensor array is shown in Fig. 1. The 1 inch chip holds an array of 32 redox cycling sensors, which are arranged on a square grid at an inter-sensor spacing of 400 μm. The electrode radius of individual sensors is 25 μm, 35 μm or 50 μm, depending on the sensor type. The inner part of the electrode is porous while the top electrode is planar at an outer rim of 2 μm. The inter-pore distance of the hexagonally arranged pores is d_int = 200 nm. This leads to a number of 48 000, 98 900 and 209 200 pores for the sensors of varying diameters. The pore arrangement is shown in Fig. 1c. Fig. 1d shows the cross-section of a single pore. From bottom to top we see the lower platinum electrode (bright) and the 100 nm silicon nitride spacer (grey). The top electrode (dark grey) blends into a platinum protection layer, which has been evaporated for cutting the pore with a focused ion beam. Between the insulator and electrodes a 10 nm adhesion layer of titanium is deposited. Consequently, the electrode distance of our sensor sums up to 120 nm.

Fig. 1 Design of the sensors: (a) photograph of a chip holding 32 dual-electrode sensors, (b) a top view on a 35 μm dual-electrode, (c) a close-up upon the electrode pores and (d) the cross section of a single pore cut via focused ion-beam etching. Images (b–d) are recorded with scanning electron microscopy.

Interestingly, the pores exhibit a conical shape with a larger aperture at the top electrode than at the bottom electrode. The radii at the pore's top amount to r_top = 57 nm while the bottom radii average to r_bot = 40 nm. Considering a 35 μm sensor, the active electrode surfaces within the nanoporous area sum up to about 500 μm² for the bottom electrode and 2620 μm² for the top electrode. The top electrode's rim amounts to additional 430 μm². For different batches of sensors these values can vary. We ascribe this fact to slight variations during the reactive ion etching (RIE) process used to transfer the porous pattern onto the chip. The apertures of the smallest functional pores amount to radii of r_top = 40 nm at the top and r_bot = 29 nm at the bottom. Aperture sizes and electrode areas of the sensors presented within this work are summarized in the ESI.†

Basic electrochemical characterization

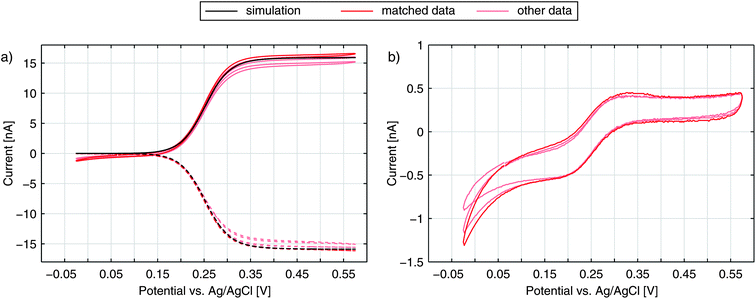
The graphs in Fig. 2a show the typical cyclic voltammogram obtained by sweeping the nanoporous top electrode of our nanoporous device versus the bottom electrode, which is held at a reducing potential of −25 mV vs. Ag/AgCl. For comparison we present data of three different sensors. The recordings are all derived from 35 μm sized electrodes on a chip with pore radii of 57 nm at the top and 40 nm at the bottom.

Fig. 2 The signal of a redox cycling sensor: (a) top currents (straight lines) and bottom currents (dashed) for the experimentally derived values (red) in 50 μM Fc(MeOH)₂ and 100 mM KNO₃ supporting electrolyte and for the theoretical approximation (black) with k₀ = 6.0 cm s⁻¹ and α = 0.49, (b) experimental difference between the top and the inverted bottom currents (I_top − |I_bot|) representing non-redox cycling currents towards the top electrode.

As long as top and bottom electrodes of a sensor are both in a reducing state there is no redox cycling current to be detected. For opposing electrode potentials of −25 mV and +575 mV vs. Ag/AgCl a maximum redox cycling current is observed. The switching between cycling on- and off-state mainly occurs in a sharp transition regime of about 150 mV. Therefore, in a first approximation, we can assume that the ratio of oxidized and reduced molecules at the top electrode is essentially set according to the Nernst equation. With F, R, and T respectively denoting Faraday constant, gas constant, and temperature the equation reads:

We obtain the redox potential E₀ of Fc(MeOH)₂ at the potential where the slope of the current reaches its maximum. To avoid uncertainties caused by capacitive effects of the sweeping top electrode we use the bottom current and determine the redox potential, which corresponds to E₀ = 250 mV versus the Ag/AgCl reference electrode. The observed behaviour is in accordance with what we expect for Fc(MeOH)₂ in aqueous solutions.^33,50 As the electron transfer rates are fast (typical values lie in the range of several cm s⁻¹) the redox cycling process can be assumed to be mainly diffusion limited.

To test if the signals are congruent with the special geometry of our sensor we perform numerical simulations of a sensor's pore with electrode boundary conditions based on the Butler–Volmer equation (see Methods). With an electron transfer rate k_top,bot = 6.0 cm s⁻¹ and a transfer coefficient α = 0.49 for Fc(MeOH)₂ in aqueous 250 mM KCl,³³ the theoretically predicted values for the bottom current seem to fit the obtained current (Fig. 2a). The simulated redox cycling current particularly matches the recorded bottom electrode currents. For the top currents we find certain deviations. This is due to the applied model, which does not include effects other than redox cycling in individual pores. The increasing current at negative potentials, however, is not a redox cycling effect but is caused by the reduction of oxygen and possibly includes the reduction of nitrates from the electrolyte.⁵¹ At positive potentials we see a slight increase of the oxidative branch exceeding the redox cycling current, which can be explained by the exchange of Fc(MeOH)₂-species between the reservoir and the top electrode. This explanation is confirmed by the trace in Fig. 2b, where the additional current exhibits the same characteristic that is generally derived from recordings at microdisc electrodes. As the majority of molecules diffuse radially towards the sensor, the flux arriving from the bulk volume is largely caught by the top electrode's non-porous rim. The porous part, which is lying closer to the top electrode's centre, in contrast, is affected less by mass exchange with the reservoir. Here, the concentration ratio can be easily set by the top electrode potential. In sum, the exposed position of the top electrode leads to a shielding of the bottom electrode from the reservoir at high overpotentials. This is visible in the discussed additional oxidation currents as well as in the top electrode's larger reduction currents (Fig. 2b).

Accordingly, as shown in Fig. 3, the Fc(MeOH)₂-molecules at the upper surface are almost exclusively in their oxidized state when applying a potential of 450 mV. At the bottom electrode the molecules of the Fc(MeOH)₂-couple are easily converted as well. Consequently, we find a steep gradient between top and bottom electrodes being the condition for high redox-cycling currents.

Fig. 3 Simulated concentration distribution (c_ox) of the oxidized species in a nanopore for electrode potentials of E_top = 450 mV and E_bot = −25 mV. The overall analyte concentration amounts to 50 μM. The transfer rate and coefficient are k₀ = 6.0 cm s⁻¹ and α = 0.49, respectively.

In principle, the signal characteristics can be described quite well assuming standard electrochemical parameters in a simple model. However, we will show later in a more detailed analysis that depending on the geometry and configuration of the sensors, parametric fits can be highly misleading if no further data are taken into account.

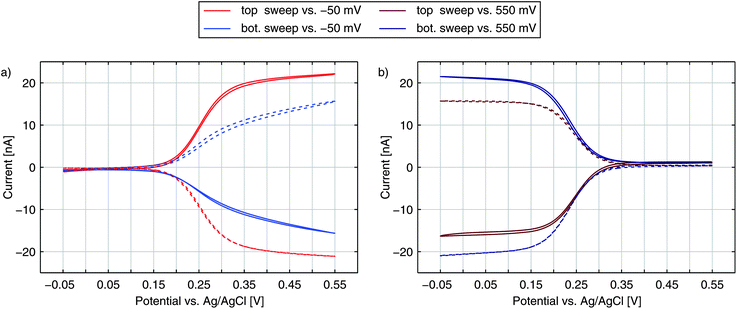
Amplification and sensitivity of nanoporous sensors

As discussed above, the current of the bottom electrode represents almost exclusively contributions by redox cycling. The top electrode, in contrast, depicts both redox cycling current and current deriving from bulk diffusion (Fig. 2b). The additional current should be the same as obtained from a free single disk electrode. Calculating the ratio of both currents therefore yields a characteristic value:

As this value describes the current multiplication due to redox cycling for this kind of nanoporous sensor we call γ the amplification factor. To preferably include the currents originating from the electrochemical conversion of the Fc(MeOH)₂-couple we only consider the current increase between +50 mV and +450 mV. For the nanoporous devices we find amplification factors of 16–18 (25 μm electrodes) and 30–40 (50 μm electrodes). The amplification is directly affected by the lateral size of the sensor. While the redox cycling flux scales with the active area of the sensor and thus with r², the flux from the reservoir in the steady state scales with the electrode radius r for microscopic devices.^52,53 Consequently, the relative gain of redox cycling current vs. reservoir current increases linearly with the electrode's radius. This is what we observe for the smallest and the largest electrodes. Surprisingly, the maximum amplification factors amount to γ = 31–46 for the 35 μm sized sensors. The high amplification factors for these devices are presumably the consequence of variances in fabrication. The differences in pore radii can have a significant impact on the redox cycling current. It should further be noted that if the amplification factor is defined by the ratio of the bottom electrode currents in redox cycling on- and off-state as described in ref. 40 and 47, the nanoporous sensors presented here exhibit amplification factors of about 500, which significantly exceeds previously reported values obtained with porous redox cycling devices.

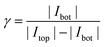
Independent of the exact amplification factor we expect a linear correlation between analyte concentration and signal amplitude for each electrode. Fig. 4 shows the response of the nanoporous sensors for three concentration series ranging from 500 nM to 175 μM. In Fig. 4a we see the resulting cyclic voltammograms of one concentration series using a 50 μm sensor. As the absolute values at 500 mV indicate, we find the expected linear behaviour for all electrode sizes (Fig. 4b). For the 50 μm electrodes the sensitivity amounts to 161.4 nA mM⁻¹. The redox cycling currents with respect to the sensor's nanoporous area are between 2.1 and 2.6 mA (cm⁻² mM⁻¹) for the differently sized sensors presented here. The observed variations are attributed to differences of the pore radii. Even on a single chip variances of roughly 5% for the overall current are found. Interestingly, our simulations show that varying an average pore by only 1 nm already leads to an appropriate change in current.

Fig. 4 (a) Cyclic voltammograms recorded for a 50 μm electrode with varying Fc(MeOH)₂ concentrations. The top electrode (straight lines) is swept versus the bottom electrode (dashed lines). The potential of the latter is fixed to E_bot = −50 mV. (b) Concentration series for currents of the top electrode at E_top = 450 mV for different electrode sizes.

The sensors presented here show some aging effects, which push the signal below the theoretically expected values. These effects are suspected to arise from adsorption of inactive species to the electrode surfaces. The associated decrease in transfer kinetics is identified by a broadened on-step of the redox cycling current, which can eventually lead to incomplete analyte conversion at the applied maximum overpotentials. Freshly finished and un-encapsulated sensors, however, feature the theoretically predicted sensitivity, which is limited only by the diffusion of Fc(MeOH)₂. For pores with a size of r_top = 57 nm and r_bot = 40 nm (Fig. 1 and 2) we reach per-area sensitivities of about 9.0 mA (cm⁻² mM⁻¹). With respect to the actual electrode area at the bottom electrode, the sensitivity reaches 81.0 mA (cm⁻² mM⁻¹) which is the maximum value of all chips produced. Since we investigate redox cycling on the nanoscale we are able to detect the subsequent changes in reaction probability even for a redox-molecule like Fc(MeOH)₂ with generally high transfer rates. After encapsulation and first sweeps the current usually stabilizes. Reliable long term measurements can then be performed as demonstrated by the linear current–concentration relation shown in Fig. 4b.

Signal characteristics caused by asymmetric electron transfer

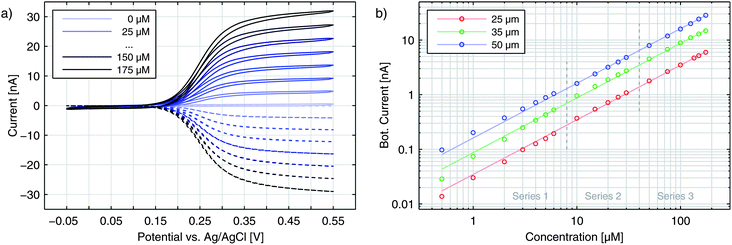
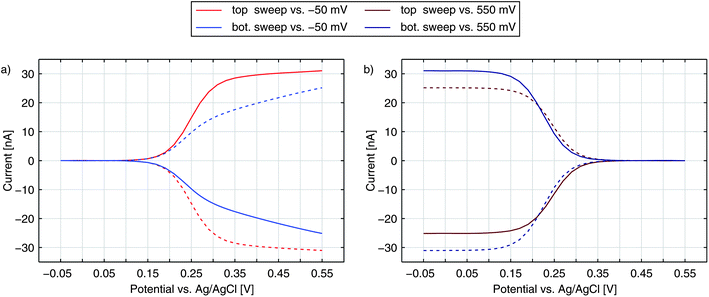
Until now, we have only discussed the signals obtained by sweeping the top electrode versus a reducing bottom electrode. In Fig. 5 we see a more detailed characterization of a nanoporous sensor. For the traces in Fig. 5a one electrode is constantly held at a reducing potential of −50 mV while the other electrode is swept over the potential range. Fig. 5b shows data taken with one electrode being fixed to an oxidizing potential (+550 mV). Solid and dashed curves represent the currents of the top and bottom electrodes, respectively. The color indicates whether the top (red) or the bottom (blue) is swept over the voltage range while the other electrode is set to a constant potential. The traces were recorded with an aged 50 μm sensor holding pore radii of r_top = 57 nm and r_bot = 40 nm.

Fig. 5 Top (solid) and bottom (dashed) currents obtained for 100 μM Fc(MeOH)₂ and 100 mM KNO₃ supporting electrolyte. Either the top electrode (red) or the bottom electrode (blue) is swept over the potential range. The other electrode is set to a constant reducing (a) or oxidizing (b) potential.

For the currents of the top electrode sweeping versus −50 mV (Fig. 5a, red traces) we can once again see the familiar behaviour previously shown in Fig. 1a. Yet, when sweeping the bottom electrode and keeping the top electrode at −50 mV (Fig. 5a, blue traces), the curves display an interesting feature with a decreased slope. At first thought, one might expect the graphs of a sweeping top electrode and a sweeping bottom electrode to be identical. In this case, however, the geometric factors of the nanoporous sensor have to be considered. One important factor is the difference in surface size for the top and bottom electrodes. The area ratio A_top/A_bot amounts to values larger than 5 even for chips, which hold the largest pores fabricated. This disparity can already qualitatively explain a slower increase of the current during a bottom sweep: due to the limited area the integrated kinetics of the lower electrode is rather small. At the larger top electrode the concentration ratio of the Fc(MeOH)₂-species can approximately follow Nernstian behaviour. As a consequence, the concentrations at the bottom electrode are significantly affected by the upper electrode's concentrations. One has to apply higher overpotentials at the bottom electrode to reach the limiting current, than at the top electrode. Thus, the slope for a sweeping bottom electrode is less steep. Differing integrated kinetics, however, cannot solely explain the distinct current at maximum overpotentials. Assuming a symmetric transfer coefficient α, the magnitude of the redox cycling current should not depend on the orientation of the potential at one electrode as long as both electrodes are biased to opposing overpotentials of the same magnitude. The graphs for the two electrodes in the reducing state (Fig. 5a) should therefore meet at +550 mV. We can also exclude species exchange with the reservoir as a possible reason. Comparing the currents of top and bottom electrodes for opposing concentrations we find the difference to be rather small. Variances between the two potential configurations are significantly larger. This can only be described by a symmetry factor α being significantly larger than 0.5.

To understand the effects of α on the electrode reactions, we can rewrite the Butler–Volmer equation:

We see that the transfer coefficient, which is actually a measure for the asymmetry of the reduction and oxidation reactions of the mediator, can also be seen as part of a potential dependent transfer rate. For α > 0.5, for example, the transfer probability will be increased at potentials below E₀, while it will decrease with rising potential.

Considering a variable rate constant k̃₀ (E) = k₀ exp((0.5 − α) F/RT (E − E₀)), the differences between the two configurations mentioned above become perfectly clear: in the configuration, at which the larger top electrode is biased to the oxidation potential, the hindered electron transfer described by α ≫ 0.5 is compensated by the relatively large area. At the other electrode the transfer kinetics is enhanced. The kinetics of the bottom electrode does not influence redox cycling and the process is diffusion limited. If both electrodes are switched to the inverse overpotentials the situation differs completely. Along with its larger surface area, the top electrode features the improved transfer rate. On the other hand, the reaction at the bottom electrode, which is already restricted by the geometry, suffers from additional limitations by the asymmetric transfer coefficient. Thus, the redox cycling current is limited by the bottom electrode's kinetics.

The either restricting or enhancing qualities of α can also be seen when comparing the bottom electrode sweeps versus −50 mV and versus +550 mV. As described above, the current is limited by decreased kinetics when sweeping the bottom electrode versus −50 mV. Sweeping the electrodes potential versus +550 mV the effective reaction rate below E₀ is increased. Accordingly, we see a sharp rise and the maximum current is larger than the maximum current for the inverse configuration.

When sweeping the top electrode versus the bottom electrode biased to +550 mV (red curves in Fig. 5b) we also obtain a clear step. Referring to this curve as being diffusion limited is still misleading. As discussed above, the maximum current is limited by the bottom electrode's integrated kinetics. This allows the concentrations at the top electrode to follow the Nernstian behaviour even more easily as during the sweep versus −50 mV. Though the concentrations at the bottom electrode are gradually brought out of equilibrium, the concentration ratio reaches a constant value as soon as the ratio at the top electrode is constant. Thus, the Nernstian behaviour at the upper electrode is what is eventually reflected in our signals as the step width.

Numerical analysis

After elucidating the experimentally observed current behaviour we are able to reproduce our data by numerical calculations. In Fig. 6 we show the bottom current in response to a sweeping top electrode. The additional curve shown is the best fit derived by a finite element simulation. Treating electron transfer rate and transfer coefficient as free parameters we obtain k_top,bot = 5.2 cm s⁻¹ and α = 0.88. As we can see from the graph these kinetic parameters lead to an almost perfect agreement of theoretical and experimental results. Especially the slight increase at higher potentials is matched. Also the characteristically similar curves presented in Fig. 2a are fitted best by α = 0.88. Their transfer coefficients amount to k_top,bot = 4.4 cm s⁻¹ and k_top,bot = 1.2 cm s⁻¹.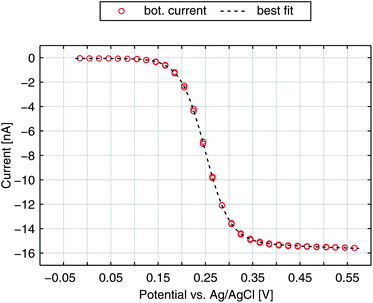

Fig. 6 Redox-cycling current of the bottom electrode for a non-aged sensor and the best fit with α = 0.88 and k_top,bot = 5.2 cm s⁻¹.

We further simulate the current response for the four sweep configurations of the aged electrode from Fig. 5. The best fitting curves, which are shown in Fig. 7, are in good agreement with the shapes of the voltammograms recorded. Their kinetic parameters are α = 0.90 for the transfer coefficient and k_top = 0.80 cm s⁻¹, k_bot = 0.60 cm s⁻¹ for the reaction constants. The curves are allowed to scale by a common factor to fit the characteristic shape rather than the exact current magnitudes. In general, values for the transfer coefficient are in the range of α = 0.78–0.90.

Fig. 7 Redox-cycling currents of the top and bottom electrodes at an aged sensor. Data from Fig. 5 are fitted with a transfer coefficient of α = 0.90 and transfer rates of k_top = 0.8 cm s⁻¹ and k_bot = 0.6 cm s⁻¹.

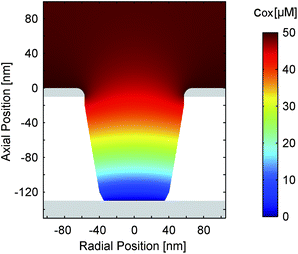
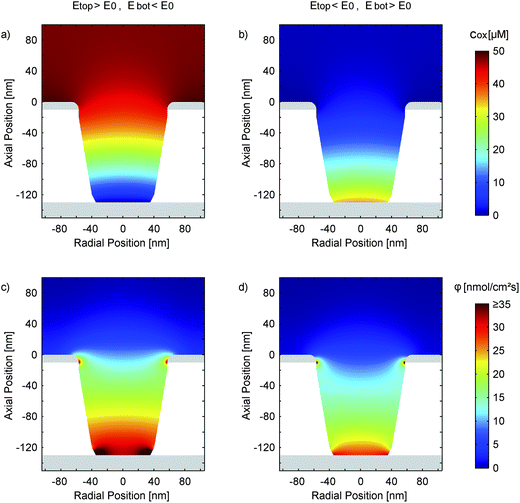
Fig. 8a and b present the simulated distribution of the redox species in a nanopore. The two configurations with maximum opposing overpotentials are shown. As mentioned above, the top electrode can easily set the concentration ratio in both cases. The bottom electrode, in contrast, is only capable of full species conversation when it is in the reducing state (Fig. 8a). Being set to an oxidizing potential (Fig. 8b) almost one out of four Fc(MeOH)₂ molecules at the electrode surface is still reduced. Due to the small area and the high transfer coefficient the reaction probability is just too low in relation to the rapid molecule exchange with the top electrode.

Fig. 8 Simulation of the concentration distribution (c_ox) of the oxidized species (a and b) and the corresponding diffusive flux (c and d) in a nanopore at electrode potentials of E_top = 550 mV and E_bot = −50 mV (a and c) and E_top = −50 mV and E_bot = 550 mV (b and d). The electrochemical parameters are k_top = 0.8 cm s⁻¹, k_bot = 0.6 cm s⁻¹ and α = 0.90. With the asymmetric transfer coefficient the species at the oxidizing bottom electrode (b and d) are not fully converted and the redox-cycling process is partially suppressed. In the opposing configuration (a and c) we have a rapid conversion at the bottom electrode, which is primarily located at the lower aperture's edge. The overall reaction at the top electrode is barely influenced.

Interestingly, differing surface sizes of top and bottom electrodes are not the only significant feature of the porous sensor. Other than for a nanochannel, for instance, the amount of species conversion is not equally distributed over the active sites. This fact is illustrated by Fig. 8c, which shows the flux of the oxidized redox-active molecules for a reducing bottom electrode and an oxidizing top electrode. The conversion will preferably happen where the electrode spacing is minimal. These points are located at the intersections of the electrodes with the pore walls. Consequently, the expansion of the areas close to these electrode edges can be more important than the overall size of the electrodes. This specifically applies to the case of a reducing bottom electrode (Fig. 8c). Switching to oxidizing mode we see a more homogeneous flux distribution along the pore bottom (Fig. 8d). Again, this is the result of the diminished rate of electrode reactions described by the high transfer coefficient (α ≫ 0.50).

Aspects of varying kinetics, transfer coefficient, and redox potential

The experimental (Fig. 2 and 5) and numerical (Fig. 6) results feature similar characteristics that can directly be ascribed to a highly asymmetric transfer coefficient. Although nanoelectrode studies on other ferrocene derivatives have also suggested asymmetric transfer coefficients,^54–58 previous redox cycling investigations of Fc(MeOH)₂ have reported symmetric transfer coefficients in aqueous electrolytes around α = 0.5.³³

Regarding the discrepancy towards a range of α = 0.78–0.90 we might point out that a nanoporous redox cycling sensor is a very sensitive tool for the investigation of kinetic behaviour. Due to the characteristic geometry of nanoporous sensors with differently scaled reaction sites the asymmetric nature of transfer reactions is clearly identified. Experiments performed in a nanochannel, in contrast, yield curves, which can be fitted with comparable quality either with α = 0.5 or significantly higher values (e.g. α = 0.85, see ESI†). This makes it very difficult to discern deviations from a symmetric transfer coefficient from experimental uncertainties. Here, a multi-sweep experiment including varying potential configurations in the asymmetric porous sensor can provide clarity. The observed effect can be understood in terms of molecular reorganization energy and conformational confinement of reduced and oxidized species^59,60 (asymmetric Marcus–Hush). It might also be attributed to electrophoretic effects (Frumkin) of the polarized electrodes.^61–66 The influence of these and other factors, such as long-range electron transfer probabilities at the electrode interface,⁶⁷ potential-dependent anion adsorption,^61,68 unequal diffusion coefficients of oxidized and reduced species,⁶⁹ and effects of adhesion layers as well as geometric aspects are discussed in the ESI.†

Generally, however, the numerical investigations presented in the ESI† show that no electrochemical parameter other than α can describe the observed behaviour using the fundamental Butler–Volmer model. Besides advantages for electrochemical sensing, the introduced nanoporous dual-electrode sensors therefore provide a unique way to clearly identify asymmetric transfer reactions.

Conclusions

We have introduced a new nanoporous redox cycling device capable of highly efficient electrochemical sensing. The sensors were fabricated via electron beam lithography, which represents a suitable approach for introducing regular pores with radii well below 50 nm. We demonstrated the high sensitivity and versatility of the device by investigating the response over a large concentration range spanning three orders of magnitude. The lateral distance of the electrodes is short enough to observe the distinct impact of a highly asymmetric transfer coefficient, which can be interpreted as a potential-dependent transfer rate. We have performed numerical investigations and elucidated the influence of specific geometric features on the recorded signal shape. Due to the high sensitivity and strong coupling to the reservoir, which is associated with short response times, nanoporous sensors hold great potential especially for real-time measurements at high resolution.

Acknowledgements

We thank Serge Lemay and Enno Kätelhön for helpful discussion on the manuscript and acknowledge funding by the Helmholtz Young Investigator Program.

Notes and references

1. E. Kätelhön, K. J. Krause, P. S. Singh, S. G. Lemay and B. Wolfrum, J. Am. Chem. Soc., 2013, 135, 8874–8881.
2. L. B. Anderson and C. N. Reilley, J. Electroanal. Chem., 1965, 10, 295–305.
3. F.-R. F. Fan and A. J. Bard, Science, 1995, 267, 871–874.
4. P. Sun and M. V. Mirkin, J. Am. Chem. Soc., 2008, 130, 8241–8250.
5. M. A. G. Zevenbergen, P. S. Singh, E. D. Goluch, B. L. Wolfrum and S. G. Lemay, Nano Lett., 2011, 11, 2881–2886.
6. P. S. Singh, E. Kätelhön, K. Mathwig, B. Wolfrum and S. G. Lemay, ACS Nano, 2012, 6, 9662–9671.
7. S. G. Lemay, S. Kang, K. Mathwig and P. S. Singh, Acc. Chem. Res., 2013, 46, 369–377.
8. A. J. Bard, F. R. Fan, J. Kwak and O. Lev, Anal. Chem., 1989, 61, 132–138.
9. J. V. Macpherson and P. R. Unwin, Anal. Chem., 2000, 72, 276–285.
10. P. Sun, F. O. Laforge and M. V. Mirkin, Phys. Chem. Chem. Phys., 2007, 9, 802–823.
11. M. A. Edwards, S. Martin, A. L. Whitworth, J. V. Macpherson and P. R. Unwin, Physiol. Meas., 2006, 27, R63–R108.
12. S. Amemiya, A. J. Bard, F.-R. F. Fan, M. V. Mirkin and P. R. Unwin, in Annual Review of Analytical Chemistry, Annual Reviews, Palo Alto, 2008, vol. 1, pp. 95–131.
13. A. Schulte, M. Nebel and W. Schuhmann, Annu. Rev. Anal. Chem., 2010, 3, 299–318.
14. Y. Takahashi, A. I. Shevchuk, P. Novak, B. Babakinejad, J. Macpherson, P. R. Unwin, H. Shiku, J. Gorelik, D. Klenerman, Y. E. Korchev and T. Matsue, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11540–11545.
15. L. Rassaei, P. S. Singh and S. G. Lemay, Anal. Chem., 2011, 83, 3974–3980.
16. C. Batchelor-McAuley, E. J. F. Dickinson, N. V. Rees, K. E. Toghill and R. G. Compton, Anal. Chem., 2012, 84, 669–684.
17. E. Kätelhön and B. Wolfrum, Rev. Anal. Chem., 2012, 31, 7–14.
18. O. Niwa, M. Morita and H. Tabei, Anal. Chem., 1990, 62, 447–452.
19. P. Van Gerwen, W. Laureyn, W. Laureys, G. Huyberechts, M. Op De Beeck, K. Baert, J. Suls, W. Sansen, P. Jacobs, L. Hermans and R. Mertens, Sens. Actuators, B, 1998, 49, 73–80.
20. H. Schift, R. W. Jaszewski, C. David and J. Gobrecht, Microelectron. Eng., 1999, 46, 121–124.
21. E. Nebling, T. Grunwald, J. Albers, P. Schäfer and R. Hintsche, Anal. Chem., 2004, 76, 689–696.
22. V. N. Goral, N. V. Zaytseva and A. J. Baeumner, Lab Chip, 2006, 6, 414.
23. V. A. T. Dam, W. Olthuis and A. van den Berg, Analyst, 2007, 132, 365.
24. E. Goluch, B. Wolfrum, P. Singh, M. Zevenbergen and S. Lemay, Anal. Bioanal. Chem., 2009, 394, 447–456.
25. P. M. Lewis, L. B. Sheridan, R. E. Gawley and I. Fritsch, Anal. Chem., 2010, 82, 1659–1668.
26. M. Odijk, J. Wiedemair, M. J. J. van Megen, W. Olthuis and A. van den Berg, in 2010 IEEE Sensors, 2010, pp. 918–922.
27. K. Ino, Y. Kanno, T. Nishijo, T. Goto, T. Arai, Y. Takahashi, H. Shiku and T. Matsue, Chem. Commun., 2012, 48, 8505–8507.
28. K. Ino, T. Nishijo, T. Arai, Y. Kanno, Y. Takahashi, H. Shiku and T. Matsue, Angew. Chem., Int. Ed., 2012, 51, 6648–6652.
29. Y. Liu, B. Wolfrum, M. Hüske, A. Offenhäusser, E. Wang and D. Mayer, Angew. Chem., Int. Ed., 2013, 52, 4029–4032.
30. L. Le Thi Ngoc, M. Jin, J. Wiedemair, A. van den Berg and E. T. Carlen, ACS Nano, 2013, 7, 5223–5234.
31. B. Wolfrum, M. Zevenbergen and S. Lemay, Anal. Chem., 2008, 80, 972–977.
32. M. A. G. Zevenbergen, P. S. Singh, E. D. Goluch, B. L. Wolfrum and S. G. Lemay, Anal. Chem., 2009, 81, 8203–8212.
33. M. A. G. Zevenbergen, B. L. Wolfrum, E. D. Goluch, P. S. Singh and S. G. Lemay, J. Am. Chem. Soc., 2009, 131, 11471–11477.
34. E. Kätelhön, B. Hofmann, S. G. Lemay, M. A. G. Zevenbergen, A. Offenhäusser and B. Wolfrum, Anal. Chem., 2010, 82, 8502–8509.
35. M. G. Straver, M. Odijk, W. Olthuis and A. van den Berg, Lab Chip, 2012, 12, 1548.
36. P. S. Singh, H.-S. M. Chan, S. Kang and S. G. Lemay, J. Am. Chem. Soc., 2011, 133, 18289–18295.
37. A. Aggarwal, M. Hu and I. Fritsch, Anal. Bioanal. Chem., 2013, 405, 3859–3869.
38. C. S. Henry and I. Fritsch, Anal. Chem., 1999, 71, 550–556.
39. C. S. Henry and I. Fritsch, J. Electrochem. Soc., 1999, 146, 3367–3373.
40. S. Neugebauer, U. Müller, T. Lohmüller, J. P. Spatz, M. Stelzle and W. Schuhmann, Electroanalysis, 2006, 18, 1929–1936.
41. T. Lohmüller, U. Müller, S. Breisch, W. Nisch, R. Rudorf, W. Schuhmann, S. Neugebauer, M. Kaczor, S. Linke, S. Lechner and others, J. Micromech. Microeng., 2008, 18, 115011.
42. D. Menshykau, A. M. O'Mahony, F. J. del Campo, F. X. Munõz and R. G. Compton, Anal. Chem., 2009, 81, 9372–9382.
43. M. Hüske and B. Wolfrum, Phys. Status Solidi A, 2011, 208, 1265–1269.
44. F. Zhu, J. Yan, M. Lu, Y. Zhou, Y. Yang and B. Mao, Electrochim. Acta, 2011, 56, 8101–8107.
45. S. P. Branagan, N. M. Contento and P. W. Bohn, J. Am. Chem. Soc., 2012, 134, 8617–8624.
46. L. R. Gibson, S. P. Branagan and P. W. Bohn, Small, 2013, 9, 90–97.
47. C. Ma, N. M. Contento, L. R. Gibson and P. W. Bohn, ACS Nano, 2013, 7, 5483–5490.
48. A. Oleinick, F. Zhu, J. Yan, B. Mao, I. Svir and C. Amatore, Chemphyschem Eur. J. Chem. Phys. Phys. Chem., 2013, 14, 1887–1898.
49. C. Ma, N. M. Contento, L. R. Gibson and P. W. Bohn, Anal. Chem., 2013, 85, 9882–9888.
50. D. Krapf, B. M. Quinn, M.-Y. Wu, H. W. Zandbergen, C. Dekker and S. G. Lemay, Nano Lett., 2006, 6, 2531–2535.
51. M. de Groot and M. T. Koper, J. Electroanal. Chem., 2004, 562, 81–94.
52. K. Aoki and J. Osteryoung, J. Electroanal. Chem. Interfacial Electrochem., 1981, 122, 19–35.
53. D. Shoup and A. Szabo, J. Electroanal. Chem. Interfacial Electrochem., 1982, 140, 237–245.
54. W. Miao, Z. Ding and A. J. Bard, J. Phys. Chem. B, 2002, 106, 1392–1398.
55. J. J. Watkins, J. Chen, H. S. White, H. D. Abruña, E. Maisonhaute and C. Amatore, Anal. Chem., 2003, 75, 3962–3971.
56. P. Sun and M. V. Mirkin, Anal. Chem., 2006, 78, 6526–6534.
57. J. Velmurugan, P. Sun and M. V. Mirkin, J. Phys. Chem. C, 2009, 113, 459–464.
58. Y. Li, D. Bergman and B. Zhang, Anal. Chem., 2009, 81, 5496–5502.
59. E. Laborda, M. C. Henstridge and R. G. Compton, J. Electroanal. Chem., 2012, 667, 48–53.
60. M. C. Henstridge, E. Laborda, Y. Wang, D. Suwatchara, N. Rees, Á. Molina, F. Martínez-Ortiz and R. G. Compton, J. Electroanal. Chem., 2012, 672, 45–52.
61. B. Timmer, M. Sluyters-Rehbach and J. H. Sluyters, Surf. Sci., 1969, 18, 44–61.
62. D. J. Gavaghan and S. W. Feldberg, J. Electroanal. Chem., 2000, 491, 103–110.
63. X. Yang and G. Zhang, Nanotechnology, 2007, 18, 335201.
64. Y. Liu, R. He, Q. Zhang and S. Chen, J. Phys. Chem. C, 2010, 114, 10812–10822.
65. E. J. F. Dickinson and R. G. Compton, J. Electroanal. Chem., 2011, 661, 198–212.
66. M. van Soestbergen, Electrochem. Commun., 2012, 20, 105–108.
67. R. J. White and H. S. White, Langmuir, 2008, 24, 2850–2855.
68. S. Kang, K. Mathwig and S. G. Lemay, Lab Chip, 2012, 12, 1262.
69. D. Mampallil, K. Mathwig, S. Kang and S. G. Lemay, Anal. Chem., 2013, 85, 6053–6058.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3nr03818a

---