Evolutionary game theory: molecules as players

Abstract

In this and an accompanying paper we review the use of game theoretical concepts in cell biology and molecular biology. This review focuses on the subcellular level by considering viruses, genes, and molecules as players. We discuss in which way catalytic RNA can be treated by game theory. Moreover, genes can compete for success in replication and can have different strategies in interactions with other genetic elements. Also transposable elements, or “jumping genes”, can act as players because they usually bear different traits or strategies. Viruses compete in the case of co-infecting a host cell. Proteins interact in a game theoretical sense when forming heterodimers. Finally, we describe how the Shapley value can be applied to enzymes in metabolic pathways. We show that game theory can be successfully applied to describe and analyse scenarios at the molecular level resulting in counterintuitive conclusions.

---

1 Introduction

The application of game theory has been extremely successful at the level of multicellular organisms, especially to understand animal behaviour.^1–6 Its application to cellular and subcellular levels of life is much less common, but of increasing interest and importance. We feel, however, that the power of respective approaches is still seriously underestimated. To motivate more researchers to use the tools of game theory, we outline its potential in this and an accompanying review.⁷ While this review is delimited to deal with the subcellular level, the accompanying review⁷ covers game-theoretical approaches at the cellular level.

Life is based on molecules and molecules have certainly been the first entities to cooperate in evolution.^8,9 However, the lowest level of life is by far not as well explored by game theory as interactions among organisms on a macroscopic scale or interactions among cells. In the following, we review future potential areas as well as successful examples of the application of game theory to interactions among molecules. We interpret this term in a broad sense, also including macromolecular complexes such as viruses.

Not only organisms as a whole, but also all macromolecules that have (indirect) influence on their reproductive success can be considered as players in the sense of game theory. Many of their properties can then be regarded as strategies, such as rigidity versus flexibility of a protein. The change between strategies can occur by mutations or epigenetic modifications in themselves, as is the case for ribonucleic acid (RNA) or deoxyribonucleic acid (DNA), or, as for proteins, in their coding sequences. Cognitive and rational capabilities are no prerequisites of players in game-theoretical models. It is unimportant if the player has chosen the strategy by using cognitive and rational capabilities or if the strategy is an intrinsic property. Molecules with different strategies reproduce to a different extent and, thus, have a different payoff.

The strategies can be classified into four different types of “social” behaviour according to the effects on direct fitness of its player. “Direct fitness” is the fitness component gained by a player through the impact on the own reproduction. Following Hamilton^10–12 and West et al.,¹³ “selfishness” is a behaviour beneficial to the actor (increasing direct fitness) while being costly to the recipient (decreasing direct fitness). Two other behaviours, which can both be regarded as kinds of “cooperation”, are selected for their positive effects on the recipient; these two types are called “mutual benefit” (if beneficial to the actor) and “altruism” (if costly to the actor). The fourth type of behaviour is “spite”, bearing costs (in terms of direct fitness) for both recipient and actor. Thus, besides being mutually beneficial, molecules can be altruistic, spiteful and selfish.

Additionally, a player can gain indirect fitness by influencing the reproduction of related players. Behaviour causing negative effects on direct fitness can be selected for during evolution because of its indirect fitness benefits. A genetic element can be seen as maximizing its inclusive fitness¹⁴ which comprises direct and indirect fitness.

An important point is that one and the same molecule can be involved in different games and can show different social behaviour, depending on the interaction partner.

Games on the molecule level have not been studied so intensely as games on the cell or organism level. Bringing into focus the study of interactions of molecules from their point of interest in the light of game theory is a major intention of this review.

We structured this paper according to biological applications, similar to the accompanying review.⁷ There, an outline of the mathematical fundamentals of game theory is given in the Appendix and in particular, all symmetric two-player two-strategy games are listed.

2 Catalytic RNA games

A game close to the origin of life, involving macromolecules of the prominent class of ribonucleic acid (RNA) as primaeval types of replicators, has been experimentally studied by Vaidya et al.⁸ (see also Attwater and Holliger⁹). They used RNA fragments of ribozymes that have the ability to self-assemble in a cooperative cycle. Ribozyme 1 cooperates in assembling ribozyme 2, ribozyme 2 helps in completing 3 and 3 closes the cycle in aiding assembly of 1. The two strategies are here “cooperating = aiding assembly” and “not cooperating”. Vaidya et al.⁸ observed that cooperative RNA replicators gain a benefit through cooperation, facilitating them to outcompete non-cooperative RNA replicators. Furthermore, cooperation between small RNA molecules leads to the emergence of longer, more complex RNAs. An extension of this idea is the concept of hypercycles, meaning that larger cycles of catalytic RNAs and enzymes have arisen in prebiotic evolution.¹⁵

Paradoxically, parasitic replicators may have been advantageous for the evolution of cooperative molecular communities of catalytic replicators. Modelling the evolutionary initiation of prebiotic enzymatic replicator diversity, Könnyu and Czárán¹⁶ observed the interplay of replicators with different enzymatic activities – efficient “specialists”, less efficient “generalists” and fast-replicating, non-enzymatic “parasites”. Provided that the replicators can slowly migrate on the hosting mineral surface, the evolved replicator community will be usually composed of specialists as well as a minority of parasites. Könnyu and Czárán¹⁶ speculate that the persistence of the parasite, lacking any positive selection to maintain its sequence information, allows it to freely mutate and pre-adapt numerous possible beneficial functions, including new enzymatic activities in metabolism, replicase activity, or membrane assembly, which can later be adopted by the cooperating replicator community.

Game-theoretical approaches are also used for the prediction of the 3D structures of RNA. These are based on the observation that macromolecules often do not attain the global minimum of free energy. Therefore, Lamiable et al.¹⁷ replaced the global optimization by a local optimization, where each component of the RNA molecule “selfishly” maximizes its own payoff function. The theoretical justification of such a decomposition of the energy function is not yet, however, fully clear.¹⁸

3 Gene games

Genes, modern replicators consisting of deoxyribonucleic acid (DNA), can be considered like RNA as players in a game on success in replication. Cooperation of genes in sexual organisms is based on a “fair” transmission of genes.¹⁹ In diploid individuals, each allele usually faces the chance of reaching the next generation in 50% of the progeny. Thus, the process of gene-transmission to the next generation does not in itself lead to a change in allele frequencies. The frequencies of alleles are altered if their carrier organisms reproduce to a different extent, mediated by natural selection.

The success of a carrier organism in reproduction is based on its genes – which is a bunch of different genetic elements – and their interactions. Genes that are able to cooperate in making its carrier organism more successful in reproduction, thus, have been selected for during evolution.

Yet, some genetic elements managed to spread and persist without contributing to organismal fitness or even worse, being harmful to the carrier organism. These genetic elements benefit from actions of cooperating genes within their carrier organism at the expense of the organism. In this sense, they are parasites of the genome. Their designation in the literature is sometimes confusing. Some authors have called them “selfish genetic elements”,²⁰ “selfish DNA”^21,22 or “self-promoting elements”.²³ However, one of the first to propose the existence of “parasitic DNA”, Dawkins, pointed out in his famous book “The Selfish Gene”²⁴ that each gene can be seen as “selfish”. Using the same notation, different aspects are meant by entitling genetic elements “selfish”. Dawkins²⁴ emphasized that each gene can be regarded as being self-interested – being cooperative or not. The focus lies on the genetic element as a fitness-maximizing agent. The other aspect meant is the “social behaviour” of the genetic element. Depending on the environment (i.e., other genetic elements in the genome, other organisms than the carrier organism as well as the abiotic environment), different behaviours lead to success in fitness-maximization and are selected for.

Since we here look at genetic elements in the context of game theory, their strategies in interactions with other genetic elements are highlighted, which essentially means their social behaviour. Accordingly, we attribute “selfish” to parasitic genetic elements including parasitic transposons. They will be discussed in Sections 3.5 and 3.6.

3.1 Games at transmission

The book “Genes in conflict” by Burt and Trivers¹⁹ documents strategies of selfish genetic elements in eukaryotic organisms to enhance their reproduction at the cost of others. Three main strategies to increase the own transmission “unfairly” have evolved multiple times – “interference”, “overreplication” and “gonotaxis”.

“Interfering” genetic elements disrupt the transmission of other gene variants (Fig. 1). They are able to direct behavior against others according to their relatedness in a kind of “kinship” discrimination. From sabotaging gametes and killing offspring that lacks their own copy to altering a species' genetic system, they show a broad repertoire of selfish behavior.

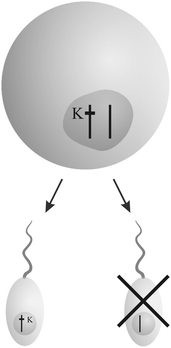Fig. 1 Example for the “interference” strategy: a killer gene K eliminates sperm that does not bear its copy. Thus, the chance of sperm carrying a copy of K in fertilizing an egg increases. The figure was adopted from Burt and Trivers.¹⁹

“Overreplicating” genetic elements succeed in enhancing their rate of transmission (Fig. 2). While most genes are replicated exactly once per cell cycle, they manage to be replicated more often. Transposable elements (see Section 3.6), the most abundant class of selfish genetic elements, follow that strategy. Entire organelle genomes like that of mitochondria and chloroplasts can enhance their replication rate in a competition in germinal tissue. An example is provided by the “petite” mutation in yeast.²⁵ Finally, replication rates can diverge on the cell level. Genetically different cells in an organism, stemming from spontaneous mutation and mitotic recombination, can replicate faster than others, such as in the case of cancer (see the accompanying review⁷).

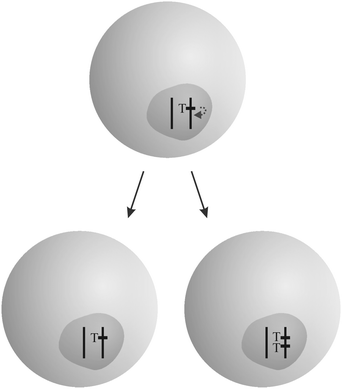Fig. 2 Example for the “overreplication” strategy: a transposable element T succeeds in replicating more often than other genes in the cell by gaining an additional copy in one daughter cell. The figure was adopted from Burt and Trivers.¹⁹

“Gonotaxis” is the third strategy used by selfish genetic elements (Fig. 3). When possible, they move towards the germline, away from somatic cells. Female meiosis, where only one of the resulting cells – the egg or ovule – has the chance to pass replicators to the next generation, is prone to parasitic invaders. Genetic elements that are able to avoid the nonfunctional “polar bodies” in favour of the egg or ovule, will increase in frequency. A well-studied example is the evolution of “knobs” on the chromosomes of maize, acting as centromeres during meiosis and pulling themselves along the spindle.¹⁹ Additional “B” chromosomes in many species of plants and animals that are not a necessary part of the genotype use the same strategy (among others).¹⁹

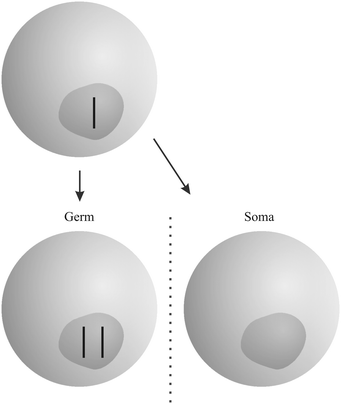Fig. 3 Example for the “gonotaxis” strategy: both copies of a chromosome move to the germline. The somatic cell contains no copy. The figure was adopted from Burt and Trivers.¹⁹

3.2 Genomic imprinting

Besides distorting transmission of genes, selfish genetic elements may use another main mechanism in enhancing their spreading. They distort the carrier organism's behaviour towards its relatives.¹⁹ A well-known example is “genomic imprinting”.¹⁹ Genes can carry the information of their origin – maternal or paternal – in an “epigenetic” way – they are said to be imprinted. Thus, the gene's degree of relatedness to its parents (and, thus, to all other relatives) is precisely determinable – 1 to the parent-of-origin and 0 to the other parent.

Two kinds of conflict arise from the awareness of descent. Over (evolutionary) time active selfish genes stemming from one parent select for opposing active genes originating from the other. Within an individual those opposing genes can create a conflict, how much to help or hinder a given relative.

Sakai²⁶ modeled the interaction of genes in the female parent, and maternally as well as paternally derived genes in her growing offspring in the competition on maternal resources, comprising parent-offspring conflict as well as intragenomic conflict. Parent-offspring conflict arises since female parents are equally related to all of their offspring and, thus, tend to allocate resources equally, while each offspring is more closely related to itself than to its siblings, trying to exploit maternal resources.²⁷ In view of parent-offspring conflict, maternally and paternally derived genes have the same interest. Their interests diverge if their relatedness to their siblings differs, causing intragenomic conflict. Paternally derived genes are on average less related to other offspring than maternally derived genes are, if more than one male parent contributes to offspring production.²⁸

Sakai²⁶ derived different situations of conflict, depending on the costs caused by abortions due to overgrowth. With increasing costs, the situation alters from harmony in interaction via patterns of parent-offspring conflict to patterns of genomic imprinting. The evolutionarily stable size and number of offspring greatly vary with the “abortion cost of overgrowth” when resource allocation is merely weakly controlled by maternal genes. A strong maternal control stabilizes both.

3.3 Alleles in diploid genomes play two-player games

As we have seen, genetic elements show a broad repertoire of dynamic social behaviour, depending on their abiotic as well as their biotic environment, thus, providing playground for evolutionary game theory. In this sense, Traulsen and Reed²⁹ encourage to combine population genetics with evolutionary game theory. They revisit the formerly rarely considered interpretation of interactions between alleles in a diploid genome as a two-player game. For the example of “meiotic drive”, where a gene is said to “drive” when being transmitted at a higher probability than fair 50%, Traulsen and Reed²⁹ set up the following payoff matrix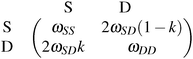where k is the probability that the driving allele D is transferred from a heterozygous parent to the offspring instead of the susceptible allele S. ω_DD, ω_SS and ω_SD are the relative fitnesses of the different genotypes over an entire life cycle. Meiotic drive is maximal for k = 1, when only the driving allele D is transmitted to the gametes of a heterozygote. For k = 1/2 both alleles have the same chance of 50% to be transmitted, thus, no meiotic drive occurs. In between, for 1/2 < k < 1, meiotic drive exists in varying degrees. Depending on the order of payoffs in the payoff matrix (3.1), four different situations arise corresponding to four distinct games:²⁹ (I) a Prisoner's Dilemma when the drive allele can invade and reach fixation, (II) a snowdrift game when the allele can invade but not reach fixation, (III) a harmony game when the allele can neither invade nor reach fixation and (IV) a coordination game when the allele cannot invade but can reach fixation when starting at a sufficiently high initial frequency. In Fig. 8 in the accompanying review⁷ the transition between different game types upon parameter change can be seen. Invading alleles resistant to the process of meiotic drive can lead to cyclic dominance as in the rock–paper–scissors game²⁹ (see Appendix of ref. 7).

3.4 Games between two supergenes

In the work of Brown and Levin³⁰ the interaction of two supergenes rather than two alleles has been modelled using a series of game-theoretic models. Genomes consisting of two distinct chromosome complexes (supergenes) always present in the heterozygous state are found in some plant species, one example being evening primrose Oenothera.^31,32 Brown and Levin³⁰ show that the association of the respective supergenes with transmission either via pollen or the egg represents a risk of intragenomic conflict over resource allocation to reproductive functions. Sexual transmission of genes by outcrossing leads to instability of mutual cooperation of supergenes.³⁰ Clonal self-fertilization, which can be viewed as a form of functional asexuality, paves a route out of conflict in that it restores the coupling of the interests of each gene with that of the entire organism which is normally done by recombination in fair meiosis.

3.5 Selfish genetic elements: suppressed, domesticated, or enhancing cooperation

Selfish genetic elements usually impose some cost on the host organism, thus, attracting the evolution of suppressors. An example is the common presence of “addiction” gene complexes in bacterial genomes that code for both a toxin and a corresponding antitoxin (TA complex).³³ TA complexes, where the antitoxin gene presumably has no function besides suppressing toxin expression by means of an antisense RNA, are supposed to have evolved in a “toxin-first” scenario.³³ In a former environment, the toxin coding gene was beneficial to the organism and, thus, to its accompanying genes within the organism, while later, the toxin and its coding gene became a fitness burden – a selfish gene. Genetic elements can have different “social” effects, depending on the environment.

The other way round, selfish genetic elements can be recruited for host functions, which is referred to as “domestication”, “co-option” or “exaptation”.³⁴ Furthermore, they can serve as a basis for cooperation in relating non-related individuals. Mobile genetic elements that spread through horizontal gene transfer increase genetic relatedness of their carriers (at the focal mobile loci). Since costly cooperative behaviours like the secretion of public goods are favoured within groups of related individuals,^10,11 mobile selfish genetic elements can become beneficial by enhancing cooperation, which benefits the organism.^33,35 The following subsection is specifically devoted to transposons.

3.6 Transposon games

Transposable elements (TEs; “jumping genes”) represent a class of DNA sequences that can move (“jump”) from one location in the genome of a single cell to another. TEs are often considered as “junk DNA” or as “selfish” genetic elements that “live” as molecular “parasites” in the genomes of their hosts.³⁶ There is growing evidence, however, that they occasionally have been “domesticated” for host functions (see, e.g., Souza et al.,³⁷ Kokošar and Kordiš,³⁸ Feschotte and Pritham,³⁹ Volff,⁴⁰ Rebollo et al.⁴¹). Bundock and Hooykaas⁴² have reported the example of a gene, termed DAYSLEEPER, derived from a transposon that has an essential function in the host. Arabidopsis plants lacking DAYSLEEPER show severe growth effects, indicating its indispensability for normal plant growth. A frequently discussed scenario is that TE insertions have provided transcription factor binding sites that serve as new promoters or enhancers of host genes, but also exaptations of coding-sequences are known.^37,43 TEs may even have been crucial for the origin of some major evolutionary novelties of eukaryotes, a spectacular example being the placenta of the mammals.³⁸ Also many traits of domesticated plants, including the colour of some grapes and blood oranges, the shape of some tomato fruits and the growth habit of maize owe their origin to TE activity (reviewed by Lisch⁴³).

However, even though TEs obviously can benefit the host, such cases are quite certainly relatively rare, given the enormous number of TEs that have swamped eukaryotic genomes. Especially some plants such as gymnosperms appear to have a “one way ticket towards genome obesity”, possibly because they lack an efficient elimination mechanism for TEs.⁴⁴

One may think that the ambivalent character of TEs – sometimes beneficial, but mostly selfish – immediately provokes investigations based on game theory, but little has been done so far in this direction. A pioneering study aiming at a better understanding of some eubacterial TEs was done by Wagner.⁴⁵

Many TEs (termed “class II elements”) move from one genomic locus to another via a “cut and paste” mechanism. The arguably simplest class II TEs are the insertion sequences (IS) of eubacteria such as Escherichia coli. They typically consist of one or more genes encoding an enzyme called transposase, flanked by two short (10–40 bp) inverted repeats. The transposase catalyzes the transposition event by generating a staggered cut at the target site producing “sticky ends”, cutting out the TE and ligating it into the target site.

Two ISs (IS_L and IS_R) in inverted orientation can constitute a composite transposon by flanking another genetic element (G) on the left and on the right side, respectively: IS_L-G-IS_R. The additional genetic element can be almost any kind of gene. Of special interest are genes that allow bacteria to survive toxic compounds, such as industrial waste or antibiotics. In fact, composite transposons that act as vehicles for the spreading of antibiotic resistance are a global threat to our health system.

Each IS of a composite transposon can either transpose alone (“selfishly”) or jointly with the other IS (“cooperatively”), thus taking the gene G with them. In order to describe the behavior of IS elements, Wagner⁴⁵ has argued that game theory is advantageous over population genetics, mainly for three reasons: first, whether selfishness, cooperativity, or a mix thereof is an ESS can be easily determined by just focusing on the individual transposon. Second, game theory is well suited to reflect the fact that a composite transposon comprises two “agents”, i.e. the two IS elements, that can behave independently of each other while trying to maximize a payoff, but whose interaction is relevant for the fate of the whole transposon. Third, game theory naturally captures the fact that the two IS elements (IS_L and IS_R) of a composite transposon can have different structures and functional features and thus different “interests” in propagating the whole transposon.

Using game theory to model the behavior of ISs revealed that the conditions under which cooperative transposition is an ESS are not biological realistic.⁴⁵ According to the analysis, cooperativity can only be maintained shortly after a selection pressure first arises. A good case in point is the spreading of antibiotic resistance, which may thus represent a fleeting moment in evolution in which cooperation among selfish ISs has provided a means of survival.

Analyzing the distribution of IS spacing of 28 different IS families in more than 200 bacterial genomes, Wagner⁴⁵ found very few closely linked IS pairs that might represent composite transposons, and no excess of such pairs from what would be expected by pure chance. This provides empirical evidence for the predictions of the model of Wagner.⁴⁵ It thus seems that most ISs are most of the time indeed simply selfish loners rather than cooperative team players.

4 Virus games

Viruses are intracellular parasites that exploit the host cell's metabolism and gene expression machinery for reproduction. To complete their life cycle, viruses generate products (RNA, proteins) that diffuse within the host cell and prevent an individual virus from having exclusive access to its own gene products. This potentially creates a “conflict of interest” whenever more than one virus infects a single host cell (Turner and Chao;⁴⁶ and references cited therein). A virus that generates excess amounts of gene products benefits other co-infecting genotypes; such a virus can be considered being a “cooperator”. In contrast, a virus that synthesizes less but specializes in appropriating a larger share of the gene products can be considered being a “defector” (or “cheater”).

For studying the games viruses play the bacteriophage (phage) Φ6 has become a model system.^46–49 Φ6 is a double-stranded RNA virus of the family Cystoviridae that infects the eubacterium Pseudomonas phaseolicola. To investigate competitive interactions among viruses in a game-theoretical framework, Turner and Chao^48,49 conducted experiments that controlled the ratio of infecting phages to host cells (also termed “multiplicity of infection”, MOI). It turned out that some phages at a high MOI (but not low MOI) gained an added advantage during coinfection, suggesting that these viruses evolved a defection strategy for intracellular competition. However, under circumstances where high MOI viruses became fixed and hence intracellular competition with other viral genotypes was removed, these phages showed evolution of lowered fitness. When the authors generated the payoff matrix for the high MOI phages (defectors) relative to their ancestors (cooperators), they realized that under these conditions the selfish genotypes of the bacteriophage Φ6 outcompete their progenitors while at the same time lowering population fitness.⁴⁹ This seemed to be a good example for the classical clash between individual advantage and collective benefit that is typical for the Prisoner's Dilemma⁵⁰ (see Appendix B of the accompanying review by Hummert et al.⁷).

However, since the outcome may depend on the conditions of high MOI, and little is known about the opportunity of co-infection of Φ6 in the wild, the authors carried out additional experiments to test whether the phage Φ6 gets generally trapped in a Prisoner's Dilemma.⁴⁶ They reasoned that the evolution of phages at other MOIs may alter the fitness payoffs associated with cooperation and defection. Therefore, they investigated the change in payoff matrix variables by propagating the phages under strictly clonal conditions and thus improving the chances for cooperation to evolve. In competition experiments involving derived cooperators and their cheating counterparts a new outcome was observed where cooperation and defecting are predicted to coexist in a mixed polymorphism.⁴⁶ This reveals that for Φ6 the payoff matrix is not a constant, and that clonal selection allows viruses like Φ6 to escape the Prisoner's Dilemma.

These findings are remarkable, but raise the question as to how relevant laboratory studies of cheating phages are for the interaction of viruses under natural conditions.⁵¹ A frequent case in nature is the infection of plants by two or more viruses; it can have very different consequences, ranging from the amelioration of symptoms to synergistic exacerbation (Martín and Elena,⁵² and references cited therein). For example, Cauliflower Mosaic Virus (CaMV; a caulimovirus) has often been found in mixed infections with Turnip Mosaic Virus (TuMV, a potyvirus) in plants belonging to the genus Brassica, including important crops such as Brassica oleracea (cabbage, broccoli, cauliflower, kale, Brussels sprouts), Brassica napus (oilseed rape) and Brassica rapa (canola, turnip). The two viruses have a double-stranded DNA genome (CaMV) or a single-stranded RNA genome (TuMV), respectively, and the results of the interaction between viruses that are so different are notoriously difficult to predict; strikingly, in some species CaMV suppresses TuMV accumulation (Martín and Elena,⁵² and references cited therein). To better understand the long-term results of interactions between TuMV and CaMV during infection of the model plant Arabidopsis thaliana (like Brassica belonging to the family Brassicaceae), Martín and Elena⁵² determined the accumulation, infectivity and symptoms of the two viruses and then applied basic rules of game theory. The authors report that, when co-inoculated at equal concentrations, TuMV behaved as a defector and benefited from the presence of CaMV, whereas CaMV behaved as a candid cooperator and paid a fitness penalty by accumulating at significantly lower levels.⁵² Constructing a payoff matrix for the TuMV and CaMV interaction revealed that TuMV always showed higher fitness than CaMV, indicating that the CaMV strategy is unstable and will always be outcompeted, rendering a strict Nash monomorphic equilibrium that departs from a Prisoner's Dilemma.⁵²

Using similar methods, Chen et al.⁵³ analyzed the interaction between Hibiscus Latent Singapore Virus (HLSV) and Tobacco Mosaic Virus (TMV), two Tobamoviruses, in Nicotiana benthamiana (a wild tobacco relative) under co-infection. Both game theoretical predictions and experimental evidence indicated that under these conditions TMV dominates the game on the long run.⁵³ This is interesting in the light of the observation that in super-inoculation experiments, Nicotiana benthamiana can be protected against TMV by HLSV.⁵³

Findings like this might be of great practical importance, not least because co-infecting viruses might be used to counter virulent plant viruses in a scenario termed “cross protection”.⁵³ Cross protection, a type of induced resistance, describes the long-known phenomenon that an infection of a mild strain virus protects plants against subsequent infections by a severe strain of a closely related virus.⁵⁴ Even though cross protection has been applied to a number of crops already (such as cocoa, tomato, tobacco, citrus, cucurbits, grapevine, soybean and papaya), its molecular mechanisms are not well understood. Several hypotheses have been put forward, but none of them could comprehensively explain all the various facets of cross protection. We suggest that evolutionary game theory could provide a unifying framework for understanding the interaction between viruses, including the phenomenon of cross protection. Consequently, evolutionary game theory should also be used to model subsequent rather than simultaneous infection events.

In addition to competitive interactions during viral infections also a simple developmental decision of a virus has been analyzed in the framework of game theory. After having been infected by phage λ an E. coli bacterium goes either into a lytic state, where the phage particles rapidly replicate and eventually lyse the cell and thus kill it, or into a lysogenic state, where the phage goes dormant and replicates along with the cell. Experimental data obtained already 40 years ago indicated that the decision between lysis and lysogeny depends on the MOI, with a single phage infection (MOI is 1) deterministically choosing lysis and double infection (MOI is 2) resulting in a stochastic choice (reviewed by Avlund et al.⁵⁵). To obtain a better understanding of this puzzling observation from the perspective of game theory, Avlund et al.⁵⁵ considered the set of all phages in an infected bacterial cell to be one player in a game where the choice is between lysis and lysogeny. The authors argue that λ is playing a game of minimizing the chance of extinction and that the observed shift from determinism to stochasticity is due to a shift from a single-player to a multiplayer game.⁵⁵

5 Protein games

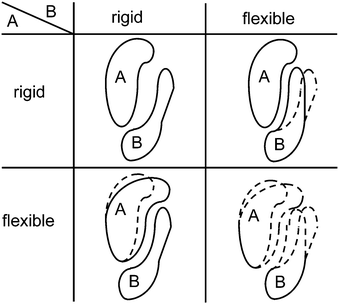
Usually, proteins are not regarded to be replicative units. Nevertheless, since they are encoded by genes, they can be regarded as players in the same sense as genes can.

Kovács et al.⁵⁶ suggested that the formation of a protein complex from two proteins can be considered as a “game” in which both proteins have two possible strategies. Assume that each of the proteins can be either flexible or rigid in the sense of adopting many different conformations or only a few, respectively (see Fig. 4). If both are rigid and their shapes do not coincidentally match to each other, binding is impossible. If one of the proteins is rigid and the other is flexible, they are able to bind. If both are flexible, they can bind, but with no fixed resulting shape of the complex. So, speaking in anthropomorphic terms, it is best if one of them is rigid and dictates the shape while the other surrenders (see also Csermely et al.⁵⁷). This is the classical hawk-dove game (see the Appendix of the accompanying review Hummert et al.⁷).

Fig. 4 The four different situations of the protein heterodimer game, arranged like in a payoff matrix. Dashed lines indicate possible alternative shapes. Upper left, two rigid proteins cannot bind to each other unless they coincidentally have shapes that match; lower left and upper right, a flexible protein can bind to a rigid protein by adopting its shape, these are the two Nash equilibria; lower right, two flexible proteins can bind to each other but the shape of the dimer is indeterminate.

It has been observed that many transcription factors form heterodimers rather than homodimers (cf. Lenser et al.⁵⁸). The asymmetric Nash equilibria of the hawk-dove game may provide one explanation (besides others) for this observation because a homodimer could only adopt the strategy pairs “rigid, rigid” or “flexible, flexible” but no asymmetric type.

In the light of the ideas of Kovács et al.,⁵⁶ new experimental findings on protein structure are worth mentioning. While it was assumed earlier that most proteins are mainly formed by well-defined secondary structures such as the α-helix and β-sheet, in recent years, more and more proteins have been found that involve disordered regions (cf. Moesa et al.⁵⁹). In many cases, these regions adopt their secondary structure only upon binding to other, well-structured proteins. In this context, the early theory of induced fit proposed by Koshland–Nemethy–Filmer is worth mentioning.⁶⁰

An experimental method frequently used in biology is to perform knockouts and perturbations. The majority of studies perturbed a single element at a time, yet in biological systems single perturbations will fail to reveal the complete functional organization, owing to interactions and redundancies. Deutscher et al.⁶¹ analysed multiple knockouts by calculating the Shapley value for each enzyme. The Shapley value, a concept from game theory called after 2012 Nobel prize winner Lloyd Shapley, quantifies the contribution of players in a coalition to the overall performance (cf. Myerson et al.⁶²). Deutscher and coworkers used an in silico network of Saccharomyces cerevisiae metabolism and found that single-perturbations analysis misses at least 33% of the genes that contribute significantly to the growth potential of this organism. The concept of the Shapley value has also been applied to computational neuroscience, with different brain areas considered as “players”.⁶³

The results of such approaches at the molecular level are interesting and promising. Although “the end justifies the means”, the theoretical grounds for considering proteins and, in particular, enzymes, as players in game theory are not, however, that clear as in the case of cells or species. It is an interesting task in future studies to clarify the conceptional basis for games played by molecules.

6 Challenges and future prospects

While the idea that cells can pursue different strategies is quite intuitive,⁷ this is less so in the case of macromolecules. However, from the examples reviewed above, it becomes understandable that the concept of strategy can also be applied in many situations at the molecular level. This is especially obvious for the major information carrying macromolecules of cells, that is, DNA, RNA and protein molecules.

As DNA molecules carrying genes are units of replication, they are subject to mutation and selection, as are the proteins encoded by them. Thus one may consider the result of some mutations or epigenetic modifications as changes in strategy, if only metaphorically, and thus evolutionary game theory can be applied in quite a straightforward way. A number of examples outlined in this article, including the “behaviour” of DNA-based transposons as well as protein molecules and viruses, bear witness to the fact that this is a valuable heuristic approach, notwithstanding epistemological issues that have been discussed earlier.¹⁸

Along the same lines of reasoning, the concept of the “selfish gene” proposed by Richard Dawkins (see, e.g. the 2006 edition of his book⁶⁴) is worth mentioning. If genes are considered as acting quite independently and self-interested, they may well be considered as players in the sense of game theory and so can the corresponding gene products, for example, proteins or regulatory RNAs. For instance, a protein that is quite flexible can, by mutation, become more rigid in the next generation of the organism harbouring that protein. As outlined in Section 5, also the concept of Shapley value can be used at the molecular level, in particular, to assess the relevance of enzymes within a metabolic network.⁶¹

One useful condition of applying game theory to molecules is that the molecules have, at least in principle, several possible states or dynamic patterns. If there were no alternatives, the term of “strategy” would be meaningless. Whereas in contrast, macromolecules that can, for example, adopt several possible conformations, may be describable by game theory. It is an interesting question for future studies to find out what the smallest entities are to which game theory can be applied. Another challenge is to see what processes usually described by physics can be analysed in the light of strategies and games. Quantum game theory is worth mentioning in both respects.⁶⁵

An important aspect of game theoretical descriptions is that sub-optimal states can be stable, as in the paradigmatic Prisoner's Dilemma. This is due to interference between different entities (agents, players) which hinder each other to reach optimal states. This phenomenon can occur at such a low level as that of molecules, as shown above by several examples. In many cases more work is needed to transform the descriptive representations of these games at the molecular level into mathematical models. To cope with the complexity of living cells it is certainly worth studying games with more than two players and multiple or continuous strategies. To include the temporal aspect the classical description by payoff matrices can be combined with differential equation systems.⁶⁶

We are convinced that evolutionary game theory can fruitfully be applied to many more examples of molecular interactions and subcellular complexes such as viruses than reviewed here and that, thus, its use has only just begun. Beyond providing a better understanding of some basic principles and processes of life, evolutionary game theory is also a promising tool for practical applications in medicine and biotechnology, producing counter-intuitive results where conventional approaches fail. This aspect is discussed in more detail in the accompanying review.⁷

Acknowledgements

Financial support by the International Max Planck Research School (Jena), the Leibniz Institute for Natural Product Research and Infection Biology – Hans-Knöll-Institute (Jena), the Jena School of Microbial Communication, and the Virtual Liver Network funded by the BMBF (Germany) is gratefully acknowledged. We thank Ina Weiß for helpful literature search and Sebastian Germerodt for stimulating discussions.

References

1. J. Maynard Smith and G. R. Price, Nature, 1973, 246, 15–18.
2. K. C. Clements and D. W. Stephens, Anim. Behav., 1995, 50, 527–535.
3. M. Broom and G. Ruxton, Behav. Ecol., 1998, 9, 397–403.
4. J. Brown and T. Vincent, Evolution, 1992, 46, 1269–1283.
5. D. W. Dickins and R. A. Clark, J. Theor. Biol., 1987, 125, 301–305.
6. R. Poulin and W. L. Vickery, J. Theor. Biol., 1995, 175, 63–70.
7. S. Hummert, K. Bohl, D. Basanta, A. Deutsch, S. Werner, G. Theißen, A. Schroeter and S. Schuster, Mol. BioSyst., 2014 10.1039/c3mb70602h.
8. N. Vaidya, M. L. Manapat, I. A. Chen, R. Xulvi-Brunet, E. J. Hayden and N. Lehman, Nature, 2012, 491, 72–77.
9. J. Attwater and P. Holliger, Nature, 2012, 491, 48–49.
10. W. D. Hamilton, J. Theor. Biol., 1964, 7, 17–52.
11. W. D. Hamilton, J. Theor. Biol., 1964, 7, 1–16.
12. W. D. Hamilton, Nature, 1970, 228, 1218–1220.
13. S. A. West, A. S. Griffin and A. Gardner, J. Evol. Biol., 2007, 20, 415–432.
14. A. Gardner and J. J. Welch, J. Evol. Biol., 2011, 24, 1801–1813.
15. M. Eigen and P. Schuster, Naturwissenschaften, 1977, 64, 541–565.
16. B. Könnyu and T. Czárán, PLoS One, 2011, 6, e20931.
17. A. Lamiable, F. Quessette, S. Vial, D. Barth and A. Denise, IEEE/ACM Trans. Comput. Biol. Bioinf., 2013, 10, 193–199.
18. S. Schuster, J. U. Kreft, A. Schroeter and T. Pfeiffer, J. Biol. Phys., 2008, 34, 1–17.
19. A. Burt and R. Trivers, Genes in Conflict: The Biology of Selfish Genetic Elements, Belknap Press of Harvard University Press, Cambridge, Mass, 2006.
20. J. H. Werren, U. Nur and C. I. Wu, Trends Ecol. Evol., 1988, 3, 297–302.
21. W. F. Doolittle and C. Sapienza, Nature, 1980, 284, 601–603.
22. L. E. Orgel and F. H. Crick, Nature, 1980, 284, 604–607.
23. L. D. Hurst, A. Atlan and B. O. Bengtsson, Q. Rev. Biol., 1996, 71, 317–364.
24. R. Dawkins, The Selfish Gene, Oxford University Press, Oxford, UK, 1976.
25. K. A. Clark, D. K. Howe, K. Gafner, D. Kusuma, S. Ping, S. Estes and D. R. Denver, PLoS One, 2012, 7, e41433.
26. S. Sakai, J. Theor. Biol., 2010, 266, 367–373.
27. R. L. Trivers, Am. Zool., 1974, 14, 249–264.
28. D. Haig, J. Evol. Biol., 1996, 9, 357–380.
29. A. Traulsen and F. A. Reed, J. Theor. Biol., 2012, 299, 120–125.
30. S. P. Brown and D. A. Levin, Evolution, 2011, 65, 3360–3367.
31. W. Wagner, P. Hoch and P. Raven, Revised classification of the Onagraceae, American Society of Plant Taxonomists, 2007.
32. M. T. J. Johnson, S. D. Smith and M. D. Rausher, New Phytol., 2010, 186, 769–779.
33. D. J. Rankin, L. A. Turner, J. A. Heinemann and S. P. Brown, Proc. R. Soc. B, 2012, 279, 3706–3715.
34. J. H. Werren, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(suppl 2), 10863–10870.
35. D. J. Rankin, E. P. C. Rocha and S. P. Brown, Heredity, 2011, 106, 1–10.
36. C. Biémont and C. Vieira, Nature, 2006, 443, 521–524.
37. F. S. de Souza, L. F. Franchini and M. Rubinstein, Mol. Biol. Evol., 2013, 30, 1239–1251.
38. J. Kokošar and D. Kordiš, Mol. Biol. Evol., 2013, 30, 1015–1031.
39. C. Feschotte and E. J. Pritham, Annu. Rev. Genet., 2007, 41, 331–368.
40. J.-N. Volff, BioEssays, 2006, 28, 913–922.
41. R. Rebollo, M. T. Romanish and D. L. Mager, Annu. Rev. Genet., 2012, 46, 21–42.
42. P. Bundock and P. Hooykaas, Nature, 2005, 436, 282–284.
43. D. Lisch, Nat. Rev. Genet., 2013, 14, 49–61.
44. B. Nystedt, N. R. Street, A. Wetterbom, A. Zuccolo, Y.-C. Lin, D. G. Scofield, F. Vezzi, N. Delhomme, S. Giacomello, A. Alexeyenko, R. Vicedomini, K. Sahlin, E. Sherwood, M. Elfstrand, L. Gramzow, K. Holmberg, J. Hallman, O. Keech, L. Klasson, M. Koriabine, M. Kucukoglu, M. Kaller, J. Luthman, F. Lysholm, T. Niittyla, A. Olson, N. Rilakovic, C. Ritland, J. A. Rossello, J. Sena, T. Svensson, C. Talavera-Lopez, G. Theißen, H. Tuominen, K. Vanneste, Z.-Q. Wu, B. Zhang, P. Zerbe, L. Arvestad, R. Bhalerao, J. Bohlmann, J. Bousquet, R. Garcia Gil, T. R. Hvidsten, P. de Jong, J. MacKay, M. Morgante, K. Ritland, B. Sundberg, S. Lee Thompson, Y. Van de Peer, B. Andersson, O. Nilsson, P. K. Ingvarsson, J. Lundeberg and S. Jansson, Nature, 2013, 497, 579–584.
45. A. Wagner, PLoS Comput. Biol., 2006, 2, e162.
46. P. E. Turner and L. Chao, Am. Nat., 2003, 161, 497–505.
47. L. Chao, Nature, 1990, 348, 454–455.
48. P. E. Turner and L. Chao, Genetics, 1998, 150, 523–532.
49. P. E. Turner and L. Chao, Nature, 1999, 398, 441–443.
50. M. A. Nowak and K. Sigmund, Nature, 1999, 398, 367–368.
51. P. E. Turner, Am. Sci., 2005, 93, 428–435.
52. S. Martín and S. F. Elena, J. Gen. Virol., 2009, 90, 2815–2820.
53. Z. Chen, J. Y. Tan, Y. Wen, S. Niu and S.-M. Wong, PLoS One, 2012, 7, e37007.
54. S. Pennazio, P. Roggero and M. Conti, New Microbiol., 2001, 24, 99–114.
55. M. Avlund, I. B. Dodd, S. Semsey, K. Sneppen and S. Krishna, J. Virol., 2009, 83, 11416–11420.
56. I. Kovács, M. Szalay and P. Csermely, FEBS Lett., 2005, 579, 2254–2260.
57. P. Csermely, R. Palotai and R. Nussinov, Trends Biochem. Sci., 2010, 35, 539–546.
58. T. Lenser, G. Theißen and P. Dittrich, PLoS Comput. Biol., 2009, 5, e1000264.
59. H. A. Moesa, S. Wakabayashi, K. Nakai and A. Patil, Mol. BioSyst., 2012, 8, 3262–3273.
60. J.-P. Changeux and S. Edelstein, F1000 Biol. Rep, 2011, 3, 19.
61. D. Deutscher, I. Meilijson, S. Schuster and E. Ruppin, BMC Syst. Biol., 2008, 2, 50.
62. R. B. Myerson, Game Theory: Analysis of Conflict, Harvard University Press, 1991.
63. A. Keinan, B. Sandbank, C. Hilgetag, I. Meilijson and E. Ruppin, Artif. Life, 2006, 12, 333–352.
64. R. Dawkins, The Selfish Gene, Oxford University Press, Oxford, UK, 2006.
65. J. Eisert, M. Wilkens and M. Lewenstein, Phys. Rev. Lett., 1999, 83, 3077–3080.
66. J. Hofbauer and K. Sigmund, Evolutionary Games and Population Dynamics, Cambridge University Press, Cambridge, 1998.

---