Continuum- and particle-based modeling of shapes and dynamics of red blood cells in health and disease
Xuejin
Li
a,
Petia M.
Vlahovska
b and
George Em
Karniadakis
*a
aDivision of Applied Mathematics, Brown University, Providence, RI 02912, USA. E-mail: george_karniadakis@brown.edu
bSchool of Engineering, Brown University, Providence, RI 02912, USA
First published on 22nd October 2012
Abstract
We review recent advances in multiscale modeling of the mechanics of healthy and diseased red blood cells (RBCs), and blood flow in the microcirculation. We cover the traditional continuum-based methods but also particle-based methods used to model both the RBCs and the blood plasma. We highlight examples of successful simulations of blood flow including malaria and sickle cell anemia.
 Xuejin Li | Xuejin Li received his Ph.D. in 2009 from the University of Science and Technology of China and is a postdoctoral research associate at the Brown University since 2010. His research interests focus on the self-assembly of amphiphilic block copolymers in solution, the dynamics of DNA chain translocation through microchannels, and multiscale modeling of red blood cells. |
 Petia M. Vlahovska | Petia M. Vlahovska received a Ph.D. in chemical engineering in 2003 from Yale University. Before joining the faculty at Brown University, she was a post-doctoral fellow at the Max Planck Institute of Colloids and Interfaces and an assistant professor in the Thayer School of Engineering at Dartmouth College. Her research interests are in the area of non-equilibrium soft matter. |
 George Em Karniadakis | George Em Karniadakis received his Ph.D. in 1987 from Massachusetts Institute of Technology. He joined the Division of Applied Mathematics of Brown University in 1994. His research interests include diverse topics in computational science both on algorithms and applications. A main current thrust is stochastic simulations and multiscale modeling of physical and biological systems. |
Blood is composed primarily of RBCs suspended in plasma with volume fraction (hematocrit) about 40%. Progress towards realistic computer simulations of blood flow hinges on accurately resolving the mechanics of RBCs over a wide range of spatial and temporal scales: from membrane microstructure to collective behavior of many cells. This is a very active research area, see for recent reviews.1–5 Here we overview the theoretical and computational approaches towards the modeling of healthy and diseased RBCs with focus on the most recent contributions, as summarized in Table 1.
| Particle-based model | Continuum-based model | ||
|---|---|---|---|
| RBC equilibrium shapes | √ | √ | |
| RBC fluctuations | √ | × | |
| RBC dynamics | TT motion | √ | √ |
| TB motion | √ | √ | |
| SW motion | √ | √ | |
| RBC dynamics in disease | √ | × | |
The healthy human RBC is a nucleus-free cell; it is essentially a membrane encapsulating hemoglobin solution. The membrane consists of a lipid bilayer supported by an attached spectrin-based skeleton, see Fig. 1a. They are connected by different transmembrane proteins. Traditionally, continuum models based on elasticity theory and fluid dynamics have been used for studying blood dynamics on macroscopic length and time scales. However, particle-based approaches are gaining popularity in recent years as a promising tool for multiscale computational simulations. Fig. 1b illustrates the basic idea behind the continuum- and particle-based approaches. The continuum framework treats the RBC membrane and embedding fluids as homogeneous materials,6,7 while particle-based models either account for the membrane structure, e.g., by describing it as a network of springs8,9 or represent the bulk fluids as particulate medium,10,11 or both.12,13 Currently, there is a great variety of modeling approaches since there is no universal solution for all blood flow related problems. Eventually, the cross-fertilization between continuum and particle-based methods will lead to practical yet physics- and biology-accurate, and computationally efficient methods that can tackle a broad range of hemodynamics problems relevant to human health.
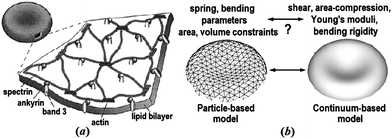 | ||
| Fig. 1 The equilibrium shape of a healthy human RBC is a biconcave disk approximately 8.0 μm in diameter and 2.0 μm in width. (a) A schematic view of the RBC membrane; reproduced from ref. 14 with permission from Elsevier. (b) A sketch of the particle- and continuum-based RBC models; adapted from ref. 15. | ||
1 Equilibrium shapes and fluctuations
1.1 Continuum-based models
The composite bilayer-spectrin membrane is very thin (∼10 nm), hence on length scale of the cell (microns) the membrane can be treated as a 2D viscoelastic interface embedded in a 3D space. Under stress, the lipid bilayer stores elastic energy in bending, while the cross-linked polymer network in stretching and shearing. The development of a continuum-based computational model then centers at the choice of material laws to describe the energy–strain relation of the 2D membrane.The cost for bending is described by several models based on the Helfrich energy:16 the SCM, the BCM and the ADE model.17 For example, the SCM energy of a membrane patch with area A is
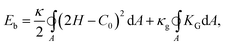 | (1) |
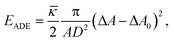 | (2) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) is a material parameter and D is the monolayer thickness.
is a material parameter and D is the monolayer thickness.
A classic model for the elastic energy associated with the stretch and shear of the spectrin polymer network is19–21
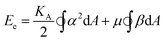 | (3) |
The lipid bilayer endows the RBC membrane with large resistance to changes in area. Accordingly, the main control factor in cell deformability is the surface area-to-volume ratio. The more deflated the cell, the more shape configurations it can adopt. The departure of the cell shape from a sphere (which is the least deformable shape), is quantified by the reduced volume
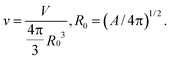 | (4) |
The reduced volume of the healthy RBC is v ∼ 0.65. Accordingly, RBCs display a rich palette of shapes under equilibrium and non-equilibrium conditions. Next, we discuss the equilibrium ones, while in Section 2.1 we analyze RBC shapes under flow.
Equilibrium RBC shapes correspond to minima of the sum of the bending and elastic energies eqn (1)–(3) as a function of the reduced volume. Minimizing only the bending energy highlights features of the RBC shape arising from the properties of the lipid bilayer alone, without the presence of the cytoskeleton. The discocyte equilibrium shape of the RBC corresponds to a minimum of the bending energy at the reduced volume of the healthy RBC.17 However, there are shapes which can not be explained solely by bending energy such as the spiculated morphology known as echinocyte (Fig. 2, upper right three pictures). Lim et al.22 proposed the combination of the bending and elastic energies to model the stomatocyte-discocyte-echinocyte sequence. Membrane elasticity implies memory, and models incorporating elastic energy depend on the choice of unstressed (rest) configuration. Khairy and Howard23 recently explored the role of the resting shape of the cytoskeleton and found that prolate ellipsoid resting shape gives rise to a larger variety of echinocytic shapes (I–III), see Fig. 2. However, the issue regarding the stress-free shape of the RBC has not yet been settled.26 Khairy et al.27 found that disruption of the spectrin network leads to the formation of the elliptocyte, which led to the conclusion that even though the discocyte is a minimal shape, the membrane-associated cytoskeleton is needed to stabilize it.
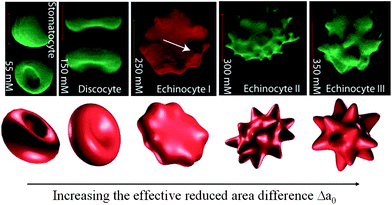 | ||
| Fig. 2 Shape transformation pathways of RBCs obtained from experimental investigations (upper) and theoretical predictions (lower). Reproduced from ref. 23. | ||
1.2 Particle-based models
The RBC membrane is very soft; its bending rigidity lies between 25 and 195 kBT (here kB is the Boltzmann constant and T is the room temperature), similar to that of lipid bilayers.28,29 As a result, the membrane is easily bent by thermal noise and the RBC shape fluctuates. The structure and dynamics of lipid bilayer membranes has received a lot of attention.30,31 The composite nature of the RBC membrane brings about new challenging features. Experiments show that fluctuations are not isotropic on the RBC surface, with smaller amplitudes in the RBC center and on the side.32 Moreover, it appears that RBC fluctuations may be sensitive to ATP concentration although this is still an open issue.33,34 These experimental observations challenge the continuum view of the RBC membrane. Since the spectrin cytoskeleton is only sparsely connected to the lipid bilayer, nonthermal (ATP-driven) shape fluctuations may reflect topological defects induced in the cytoskeleton network by ATP.35The architecture of the spectrin network was first incorporated in studies of equilibrium states.8,9 Hydrodynamic effects needed to describe dynamic fluctuations were recently included.36,37 These spectrin-based models are limited by high computational cost. A possible solution to this problem is to reduce the number of degrees of freedom through mapping of a spectrin-based model onto coarse-grained structures. In fact, some simple particle-based models have been used extensively in modeling deformable particles such as RBCs.38,39 More recently, DPD method was employed in a systematic CG procedure for modeling RBCs,40 which served as a basis of a general MS-RBC model12 that included membrane viscosity and external/internal fluid viscosity contrast. The MS-RBC simulations predicted that the RBC membrane fluctuations depend on location,41 in agreement with experiment.32
In the MS-RBC model, the RBC membrane is represented by a 2D triangulated network with Nv vertices, where each vertex is represented by a DPD particle. The vertices are connected by Ns visco-elastic bonds to impose proper membrane mechanics. Specifically, the elastic part of bond is represented by
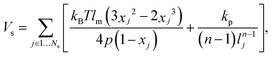 | (5) |
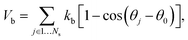 | (6) |
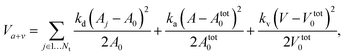 | (7) |
The MS-RBC model is multiscale, as the RBC can be represented on the spectrin level, where each spring in the network corresponds to a single spectrin tetramer with the equilibrium distance between two neighboring actin connections of ∼75 nm. On the other hand, for more efficient computation, the RBC network can also be highly coarse-grained with the equilibrium spring lengths of up to 500–600 nm. The internal and external fluids are modeled by free DPD particles. External/internal fluid separation is enforced by bounce-back reflections of fluid particles at a moving membrane surface.
The RBC membrane network consists of triangles whose edges have different lengths; this may cause local stress artifacts in simulations, thus, the triangulation method employed is important. The triangulation quality is affected by edge lengths and by vertex angles. Several different types of triangulation strategies such as point charges,42 advancing front,43 and energy relaxation methods,15 can be employed to generate the mesh of RBC membrane network. Fig. 3a–c shows the RBC shapes at equilibrium for different triangulation strategies. The RBC triangulated by the point charges method and by the advancing front method show pronounced buckling (Fig. 3a) and a non-biconcave shape (Fig. 3b) for realistic bending and elastic RBC properties due to strong local stresses. The characteristic biconcave RBC shape is achieved by using the energy relaxation method with the advancing front triangulation.
 | ||
| Fig. 3 RBC shape evolution for different triangulation strategies (a–c). Reproduced from ref. 15. Simulated sickle RBC with elongated shape (d), classical sickle shape (e), and granular shape (f). Adapted from ref. 44 with permission from Elsevier. | ||
The MS-RBC model can be applied to study RBCs in disease like SCA. For example, Lei and Karniadakis44,45 employed the MS-RBC model to quantify the morphology of sickle-shaped RBCs. In their simulations, the RBC membrane is deformed by exerting surface tension at different anchor points to mimic the distortion effect of HbS fibers on the RBC membrane. Starting from the original biconcave shape, the RBC membrane undergoes various deformations, and several different types of sickle cell membranes typically observed in experiments46 are constructed, see Fig. 3d–f. The sequence of events in SCA is: nucleation, polymerization, cell deformation, and then vaso-occlusion, revealing that HbS polymerization is the primary cause of the clinical disease manifestations. Numerical models may be helpful to understand how sickling occurs and how it affects RBC dynamics. To this end, the self-assembly of coarse-grained models of HbS was simulated with DPD in ref. 47. Chain chirality was confirmed to be the main driver for the formation of HbS fibers. Li and Lykotrafitis48,49 simulated the thermal behavior of HbS fibers and proposed that the continuous polymerization of HbS fibers and additional unzippering of these fibers can explain the formation of HbS fiber networks.
2 RBC shapes and dynamics in flow
Experimental observations of RBC behavior in flows mimicking the microcirculation reveal dramatic deformations and rich dynamics. A RBC in steady shear flow deforms into an ellipsoid that can TT (the cell shape and orientation with respect to the flow direction remains steady, while the membrane rotates as a TT), TB, or SW (TT accompanied by oscillations in the inclination angle).50 Oscillatory shear gives rise to chaotic dynamics.51 In capillary flows, RBCs adopt symmetric parachute or asymmetric slipper shapes depending on confinement and flow rate.1,52 Similar behavior is also exhibited by other membrane bound particles such as vesicles2 and capsules.6,7 For example, vesicles made of pure lipid bilayer can undergo TT or TB in linear (shear) flows,53,54 and can adopt parachute- and slipper-shapes in quadratic (capillary) flows.55The explanation of these behaviors has been attempted with various theoretical approaches, ranging from reduced analytical models to detailed numerical simulations. Since the problem is inherently non-equilibrium, energy minimization is not applicable; instead the cell shape and motion is determined by the balance of membrane and viscous flow stresses.
2.1 Continuum-based models
| τκ = −κ[(2H − C0)(2H2 − 2KG + C0H) + 2∇s2H]n. | (8) |
The area-incompressibility constraint is treated by the use of a local Lagrange multiplier, which adds an additional term to the free energy of the membrane ∫γdA. The corresponding stress is
| τγ = 2γHn − ∇sγ. | (9) |
The elastic behavior can be described by various constitutive laws,7,56 which for small membrane deformations reduce to a linear stress–strain relation (a 2D equivalent of Hooke's law)57,58
| τμ = 2(KA − μ)(∇s·d)Hn − (KA − μ)∇s∇s·d − μ∇s·[∇sd·Is + Is·(∇sd)†] | (10) |
| ∇s·d = 0, ∇s·vm = 0, | (11) |
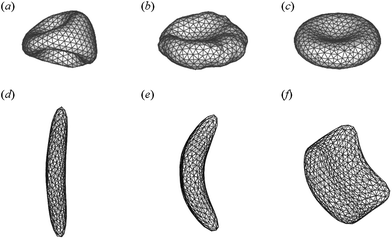
Under stress, energy can be stored by the membrane in elastic deformation or dissipated by viscous friction. Membrane viscous stresses depend not on the strain (d) but on the rate of strain (vm); for a Newtonian interface, the expression for the viscous stress is analogous to eqn (10) but with the surface velocity vm instead of d, and the surface shear viscosity ηm in place of μ.
Dimensional analysis of the governing equations shows that RBC dynamics is controlled by several dimensionless parameters. One subset depends solely on cell geometry and fluid properties: reduced volume v and viscosity ratio λ = ηi/ηo. The rest are flow-dependent: capillary number based on the bending rigidity Caκ = ηoR03G/κ, and capillary number based on the shear elasticity Caμ = ηoR0G/μ, where G is the shear rate. In the case of Poiseuille flow, the curvature of the flow is another relevant parameter.
In the case of pure lipid bilayer, the model demonstrates that vesicle TB motion in simple shear flow originates from the area-incompressibility of the membrane, which gives rise to shape-dependent tension.59–61 The theoretical phase diagram of vesicle behaviors (TT, TB, and SW) depends on three control parameters, v, λ, and Caκ.62 This prediction was questioned by experiments,54 but the discrepancies appear to be due to membrane thermal undulations, which are not included in the model. This conclusion is supported by the fact that a more accurate, higher-order theory agreed with the numerical results for the phase diagram.63,64 Further analytical work of vesicle dynamics showed that TB can be suppressed by bilayer slippage65 or application of a uniform electric field in the velocity gradient direction.66
In the case of the RBC, cell behavior in shear flow also depends on the shear elasticity, Caμ, and reduced volume of the rest shape v0. At low shear rates, Caμ ≪ 1, the resistance to shearing immobilizes the surface and the cell tumbles. As the shear rate increases, the dynamics changes from TB to SW, and the SW amplitude decreases with increasing shear rate. The SW motion was attributed to a non-spherical rest shape, v0 ≠ 1. However, cell behavior near the transition generated some controversy. Phenomenological models,50,67–69 which approximate the RBC by an ellipsoid of fixed shape, predicted intermittent behavior (SW periodically interrupted by a TB), for which no evidence was found in the numerical simulations.70–72 A deformable cell was considered in the analyses by ref. 73–75. The deformable capsule model73 showed that near the transition, intermittent behavior is found only if the capsule deforms in the shear plane and does not undergo stretching or compression along the vorticity direction; the intermittency disappears if deformation along the vorticity direction occurs, i.e., if the capsule “breathes”.
The small-deformation asymptotic theory has been applied to study vesicles in Poiseuille flow76 or sedimentation.77 Intriguingly, despite the axial symmetry of the ambient flow, non-axisymmetric solutions for the vesicle shapes are possible. For example, in Poiseulle flow, in addition to centered symmetric (parachute or bullet) shapes, off-centered asymmetric (slipper) shapes exist at low flow strengths. These findings have been supported by numerical simulations,78 but in experiments55 asymmetric slippers seem to be unstable. While the problem for cell shapes and dynamics in capillary flows is far from being fully solved, the analytical results suggest that the cytoskeleton and the confinement due to channel walls are not essential for the appearance of the slipper.
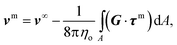 | (12) |
A major challenge in the numerical simulations is to enforce the local inextensibility of the membrane eqn (11); it results in a very stiff problem with high computational cost.82 Recently, efficient schemes for the BIM have been developed to study pure lipid vesicles (shear-free interface μ = 0),64,83–87 multicomponent membrane vesicles,88 and RBCs.55,89,90 These computations have allowed to explore the behavior of an isolated vesicle in wall-bounded shear flows,83 quadratic flows,78,91 and capillary flows.92 Collective dynamics of many vesicles has also been considered,93,94 but only to a limited extent and a systematic numerical study of suspension rheology is still lacking. Such simulations are needed to interpret the experiments on hydrodynamic interactions between vesicles95 and the effective viscosity of suspensions of RBCs and vesicles,96 which was found to depend non-monotonically on λ.
A great advantage of the BIM is the accurate computation of the interface evolution. However, the method can not handle topological changes such as budding, and it is restricted to zero-Reynolds number (no inertia). To treat these effects, other computational approaches are being developed, e.g., level-set,97,98 phase-field,99 immersed finite element,100 and front-tracking.101,102 A simulation using the level-set method recently showed that inertia suppresses vesicle TB motion in simple shear flow.103 Another computational challenge is to include the membrane thermal undulations; progress in this direction has been made only for planar membranes.31,104,105
Finally, due to space restrictions, we do not discuss the large body of literature on numerical simulations of capsules7,81 as they mostly deal with area-extensible (e.g., neo-Hookean) membranes.
2.2 Particle-based models
Particle-based computational methods come in several flavors.11 One option is to integrate the continuum membrane with particle model for the fluid, e.g., as in LB method.71,106–108 Another approach is to model both the fluid and the membrane as particulate materials, using SPH,109–111 MPCD,112,113 and DPD. The latter is a mesoscopic particle method in which each particle represents a molecular cluster rather than an individual atom. In a DPD simulation, the RBC membrane and surrounding plasma can be seamlessly represented. Next, we focus our attention to the DPD approach and some applications.The DPD approach simulates flow by interactions between discrete particles. Early attempts to simulate blood flow modeled the RBC as an elastic particle with an inner skeleton, which is represented by a rectangular lattice of particles connected by elastic springs.114,115 The MS-RBC is more physically accurate model,12 but it is quite expensive computationally in blood flow simulations. To simulate the flow of a dense RBC suspension, a LD-RBC model, also based on DPD, was constructed as a closed torus-like ring of only ten colloidal particles simulated as rigid DPD particles.13,116
An important characteristic of the dynamics of an individual RBC in shear flow is the TT frequency. Simulations with continuum models90,101,117,118 suggest that the membrane viscosity needs to be accounted for in order to agree with the experiments.119 Indeed, the MS-RBC model with membrane viscosity12 captures this effect, see Fig. 4a.
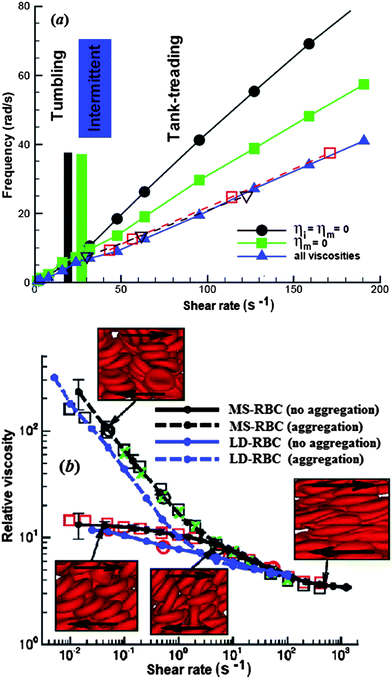 | ||
| Fig. 4 (a) TB and TT frequency of a RBC in shear flow for different cases: (1) ηo = 0.005 Pa s, ηi = ηm = 0 (circles); (2) ηo = ηi = 0.005 Pa s, ηm = 0 (squares); (3) ηo = ηi = 0.005 Pa s, ηm = 0.022 Pa s (triangles); reproduced from ref. 12 with permission from Elsevier. In this figure, ηm is the membrane viscosity, and ηo and ηi are the viscosities of the external solvent and the internal cytoplasm, respectively. (b) Plot of non-Newtonian relative viscosity (the cell suspension viscosity normalized by the solvent viscosity) as a function of shear rate at H = 45% and 37 °C; reprinted with permission from ref. 116. Symbols represent experimental results from three different laboratories. | ||
DPD simulations have become quite practical to analyze the flow of dense RBC suspensions.116 The simulations for shear flow accurately predicted the dependence of blood viscosity on shear rate, see Fig. 4b. A novel feature is the inclusion of attractive cell–cell interactions which allows to investigate cell aggregation and formation of rouleaux. Simulations in larger tubes with diameters ranging from 10 μm to 40 μm successfully reproduced several hemodynamic phenomena, including cell migration towards the flow centerline, cell-free layer near the wall and blunt velocity profile.12,13,120,121 Recently, more complex geometries have been considered, e.g. the flow in a bifurcating microfluidic channel.122 The results quantified the blood-plasma separation as a function of RBC deformability and feed hematocrit level, which is agreement with experiment.123
In addition to DPD, the collective dynamics of RBCs has also been studied with hybrid methods. For example, Noguchi and Gompper112 employed MPCD, which combined a particle-based hydrodynamics model for the solvent and a coarse-grained, dynamically triangulated surface model for the membrane, for efficiency in blood flow simulations. Simulations of small clusters of RBCs with the MPCD method113,124 predicted three distinct phases, one consisting of disordered biconcave RBCs, another with parachute-shaped RBCs, and a third with slipper-shaped RBCs. The LB-based methods have also successfully simulated dense RBC suspensions.106,125–128 A coupled LB-FE method, which combined the LB method for the fluid phase with a linear FE analysis describing RBC deformation, has been developed for blood flows. The LB-FE method could not resolve extreme deformations associated with RBC passage through small tubes and TT regime. To overcome these problems, more recently, the LB method was coupled with a spectrin-level based model for the membrane.129
2.3 Dynamics of diseased RBCs
Numerical simulations may be used for qualitative and quantitative interpretation and predictions of mechanical properties and dynamic behaviors of RBCs in malaria and other hematological diseases. The particle-based RBC models are an ideal tool to study the RBC dynamics in malaria.130–134 For example, Fedosov et al.132 used the MS-RBC model in combination with adhesive interactions to simulate the adhesive dynamics of Pf-RBCs. Their simulation results revealed several types of cell dynamics such as firm adhesion, RBC peeling off the surface followed by flipping from one side to the other or by detachment from the wall, and very slow slipping along the wall. They also simulated the effect of the solid parasite inside the Pf-RBCs on their adhesive dynamics and found the presence of a rigid body inside a RBC significantly affects the RBC adhesive dynamics.133 Imai et al.130 employed a mesh-free particle method to study the microvascular hemodynamics arising from the malaria infection. They examined flows in a circular microchannel and found that the hydrodynamic interaction between HRBCs and Pf-RBCs causes a train formation.131Quantitative measurement of dynamic cell deformability for various stages of Pf-RBCs and other types of blood cells is significant. Bow et al.134 combined experimental and computational methods to characterize the biomechanical properties of cells in a high-throughput manner. In their experiment, they introduced the flow cytometer device (Fig. 5a) to measure dynamic mechanical responses of individual RBCs. In simulations, they employed the MS-RBC model to translate the experimental measurements into quantitative data describing the mechanical properties of individual RBCs. Snapshots from simulations showing passage of Pf-RBC through channels with converging and diverging pore geometries were shown in Fig. 5b. Their simulations were able to capture the effects of pore geometry and changes of RBC properties arising from parasitization quite well, see Fig. 5c and d.
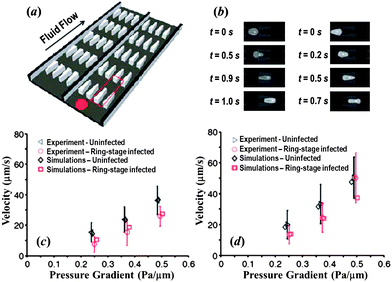 | ||
| Fig. 5 (a) Illustration of the flow cytometer device. (b) DPD simulation images of Pf-RBCs traveling in channels of converging (left) and diverging (right) pore geometry at 0.48 Pa μm−1. Velocity vs. pressure for uninfected and ring-stage-infected RBCs in the diverging (c) and converging (d) pore geometries. Adapted from ref. 134. | ||
3 Challenges and open questions
Continuum models allow the study of blood flow on macroscopic length and time scales; however, currently they do not include membrane fluctuations although there is recent ongoing research towards this end.31,105 On the other hand, particle-based methods can resolve cellular and sub-cellular scales, and can model accurately membrane fluctuations and the cytoskeleton structure; however, they are computationally very expensive to scale up to large domains. For example, 1 mm3 of blood contains about five million RBCs that would require more than a billion particles to be resolved accurately. Hybrid (continuum–particle) models maybe the best solution for effective simulations, balancing biophysical fidelity and computational efficiency. Recent efforts have been directed towards this approach, e.g., using particle-based plasma and continuum-based RBCs. Given the discussion of this paper, the opposite would be a better approach, i.e., combine the continuum description to model the blood plasma with the particle description for the RBCs. Technically this is quite difficult and it would require combining particle-based methods with immersed boundary method as was done recently in ref. 135. Another challenge would be to develop a more realistic RBC representation, e.g. to endow the spectrin-based RBC models with more accurate structure, e.g., account separately for the lipid bilayer and cytoskeleton but also include explicitly the transmembrane proteins.No matter what type of combination of continuum–particle methods prevails in the future, ultimately, computations which encompass all scales would require integration of both approaches. Such simulations would potentially answer questions concerning the coupling of biochemistry and mechanics, for example shear-induced ATP release5,136 and the mechanics of diseased RBCs,137e.g., the link between HbS polymerization and mechanics of sickled RBCs.138
Abbreviations
| ADE | Area-difference elasticity |
| BIM | Boundary integral method |
| BCM | Bilayer-coupling model |
| CG | Coarse-graining |
| DPD | Dissipative particle dynamics |
| HbS | Sickle hemoglobin |
| LB | Lattice-Boltzmann |
| LB-FE | Lattice-Boltzmann-finite-element |
| LD-RBC | Low-dimensional red blood cell |
| MPCD | Multiparticle collision dynamics |
| MS-RBC | Multiscale red blood cell |
| Pf-RBC | Plasmodium falciparum red blood cell |
| RBC | Red blood cell |
| HRBC | Healthy red blood cell |
| SCA | Sickle cell anemia |
| SCM | Spontaneous curvature model |
| SPH | Smoothed particle hydrodynamics |
| SW | Swinging |
| TB | Tumbling |
| TT | Tank-treading |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
Acknowledgements
X.L. and G.E.K. are grateful for the financial support provided by the National Institute of Health (NIH) Grant R01HL094270 and the National Science Foundation (NSF) Grant CBET-0852948. P.M.V. acknowledges partial financial support by NSF Grant CBET-1117099.References
- M. Abkarian, M. Faivre, R. Horton, K. Smistrup, C. A. Best-Popescu and H. A. Stone, Biomed. Mater., 2008, 3, 034011 CrossRef.
- M. Abkarian and A. Viallat, Soft Matter, 2008, 4, 653–657 RSC.
- P. M. Vlahovska, T. Podgorski and C. Misbah, C. R. Phys., 2009, 10, 775–789 CrossRef CAS.
- S. Guido and G. Tomaiuolo, C. R. Phys., 2009, 10, 751–763 CrossRef CAS.
- J. Wan, A. M. Forsyth and H. A. Stone, Integr. Biol., 2011, 3, 972–981 RSC.
- D. Barthes-Biesel, C. R. Phys., 2010, 10, 764–774 CrossRef.
- D. Barthes-Biesel, Curr. Opin. Colloid Interface Sci., 2011, 16, 3–12 CrossRef CAS.
- D. E. Discher, D. H. Boal and S. K. Boey, Biophys. J., 1998, 75, 1584–1597 CrossRef CAS.
- J. Li, M. Dao, C. T. Lim and S. Suresh, Biophys. J., 2005, 88, 3707–3719 CrossRef CAS.
- S. M. Hosseini and J. J. Feng, Chem. Eng. Sci., 2009, 64, 4488–4497 CrossRef CAS.
- T. Yamaguchi, T. Ishikawa, Y. Imai, N. Matsuki, M. Xenos, Y. F. Deng and D. Bluestein, Ann. Biomed. Eng., 2010, 38, 1225–1235 CrossRef.
- D. A. Fedosov, B. Caswell and G. E. Karniadakis, Biophys. J., 2010, 98, 2215–2225 CrossRef CAS.
- W. X. Pan, B. Caswell and G. E. Karniadakis, Soft Matter, 2010, 6, 4366–4376 RSC.
- J. C. Hansen, R. Skalak, S. Chien and A. Hoger, Biophys. J., 1996, 70, 146–166 CrossRef CAS.
- D. A. Fedosov, Ph.D. thesis, Brown University, 2010.
- W. Helfrich, Z. Naturforsch., C: Biochem., Biophys., Biol., Virol., 1973, 28, 693–703 CAS.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- H. Dobereiner, Curr. Opin. Colloid Interface Sci., 2000, 5, 256–263 CrossRef CAS.
- E. A. Evans and R. Skalak, Mechanics and Thermodynamics of Biomembranes, CRC Press, Boca Raton, Florida, 1980 Search PubMed.
- E. A. Evans, Methods Enzymol., 1989, 173, 3–35 CrossRef CAS.
- R. Mukhopadhyay, H. W. G. Lim and M. Wortis, Biophys. J., 2002, 82, 1756–1772 CrossRef CAS.
- H. W. G. Lim, M. Wortis and R. Mukhopadhyay, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 16766–16769 CrossRef.
- K. Khairy and J. Howard, Soft Matter, 2011, 7, 2138–2143 RSC.
- M. Dao, C. T. Lim and S. Suresh, J. Mech. Phys. Solids, 2003, 51, 2259–2280 CrossRef.
- Z. L. Peng, R. J. Asaro and Q. Zhu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031904 CrossRef.
- T. Svelc and S. Svetina, Cell. Mol. Biol. Lett., 2012, 17, 217–227 CrossRef CAS.
- K. Khairy, J. Foo and J. Howard, Cell. Mol. Bioeng., 2008, 1, 173–181 CrossRef.
- D. Marsh, Chem. Phys. Lipids, 2006, 144, 146–159 CrossRef CAS.
- R. Dimova, S. Aranda, N. Bezlyepkina, V. Nikolov, K. A. Riske and R. Lipowsky, J. Phys.: Condens. Matter, 2006, 18, S1151–S1176 CrossRef CAS.
- M. Muller, K. Katsov and M. Schick, Phys. Rep., 2006, 434, 113–176 CrossRef.
- F. L. H. Brown, Q. Rev. Biophys., 2011, 44, 391–432 CrossRef CAS.
- Y.-K. Park, C. A. Best, T. Auth, N. S. Gov, S. A. Safran, G. Popescu, S. Suresh and M. S. Feld, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1289–1294 CrossRef CAS.
- T. Betz, M. Lenz, J.-F. Joanny and C. Sykes, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15320–15325 CrossRef CAS.
- Y. Yoon, J. Kotar, A. T. Brown and P. Cicuta, Soft Matter, 2011, 7, 2042–2051 RSC.
- S. A. Safran, N. Gov, A. Nicolas, U. S. Schwarz and T. Tlusty, Phys. A, 2005, 352, 171–201 CrossRef CAS.
- Q. Zhu, C. Vera, R. J. Asaro, P. Sche and L. A. Sung, Biophys. J., 2007, 93, 386–400 CrossRef CAS.
- R. Zhang and F. L. H. Brown, J. Chem. Phys., 2008, 129, 065101 CrossRef.
- G. Marcelli, K. H. Parker and C. P. Winlove, Biophys. J., 2005, 89, 2473–2480 CrossRef CAS.
- J. P. Hale, G. Marcelli, K. H. Parker, C. P. Winlove and P. G. Petrov, Soft Matter, 2009, 5, 3603–3606 RSC.
- I. V. Pivkin and G. E. Karniadakis, Phys. Rev. Lett., 2008, 101, 118105 CrossRef.
- D. A. Fedosov, H. Lei, B. Caswell, S. Suresh and G. E. Karniadakis, PLoS Comput. Biol., 2011, 7, e1002270 CAS.
- Y. B. Shan, J. L. Klepeis, M. P. Eastwood, R. O. Dror and D. E. Shaw, J. Chem. Phys., 2005, 122, 054101 CrossRef.
- P. L. George and E. Seveno, Int. J. Numer. Meth. Eng., 1994, 37, 3605–3619 CrossRef.
- H. Lei and G. E. Karniadakis, Biophys. J., 2012, 102, 185–194 CrossRef CAS.
- H. Lei and G. E. Karniadakis, Soft Matter, 2012, 8, 4507–4516 RSC.
- D. K. Kaul and H. Xue, Blood, 1991, 77, 1353–1361 CAS.
- X. J. Li, B. Caswell and G. E. Karniadakis, Biophys. J., 2012, 103, 1130–1140 CrossRef CAS.
- H. Li and G. Lykotrafitis, J. Mech. Behav. Biomed. Mater., 2011, 4, 162–173 CrossRef CAS.
- H. Li, V. Ha and G. Lykotrafitis, J. Biomech., 2012, 45, 1947–1951 CrossRef.
- M. Abkarian, M. Faivre and A. Viallat, Phys. Rev. Lett., 2007, 98, 188302 CrossRef.
- J. Dupire, M. Abkarian and A. Viallat, Phys. Rev. Lett., 2010, 104, 168101 CrossRef.
- G. Tomaiuolo, M. Simeone, V. Martinelli, B. Rotoli and S. Guido, Soft Matter, 2009, 5, 3736–3740 RSC.
- J. Deschamps, V. Kantsler and V. Steinberg, Phys. Rev. Lett., 2009, 102, 118105 CrossRef CAS.
- N. J. Zabusky, E. Segre, J. Deschamps, V. Kantsler and V. Steinberg, Phys. Fluids, 2011, 23, 041905 Search PubMed.
- G. Coupier, A. Farutin, C. Minetti, T. Podgorski and C. Misbah, Phys. Rev. Lett., 2012, 108, 178106 CrossRef.
- C. Pozrikidis, Modeling and Simulation of Capsules and Biological Cells, CRC Press, London, 2003 Search PubMed.
- D. Barthes-Biesel and J. M. Rallison, J. Fluid Mech., 1981, 113, 251–267 CrossRef.
- D. A. Edwards, H. Brenner and D. T. Wasan, Interfacial Transport Processes and Rheology, Butterworth-Heinemann, Boston, 1991 Search PubMed.
- C. Misbah, Phys. Rev. Lett., 2006, 96, 028104 CrossRef.
- P. M. Vlahovska and R. Gracia, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 016313 CrossRef.
- V. V. Lebedev, K. S. Turitsyn and S. S. Vergeles, New J. Phys., 2008, 10, 043044 CrossRef.
- B. Kaoui, A. Farutin and C. Misbah, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061905 CrossRef.
- A. Farutin, T. Biben and C. Misbah, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 061904 CrossRef.
- T. Biben, A. Farutin and C. Misbah, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 031921 CrossRef.
- J. T. Schwalbe, P. M. Vlahovska and M. J. Miksis, J. Fluid Mech., 2010, 647, 403–419 CrossRef.
- J. T. Schwalbe, P. M. Vlahovska and M. J. Miksis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 046309 CrossRef.
- J. M. Skotheim and T. W. Secomb, Phys. Rev. Lett., 2007, 98, 078301 CrossRef CAS.
- S. Kessler, R. Finken and U. Seifert, Eur. Phys. J. E, 2009, 29, 399–413 CrossRef CAS.
- H. Noguchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021902 CrossRef.
- S. Kessler, R. Finken and U. Seifert, J. Fluid Mech., 2008, 605, 207–226 CrossRef.
- Y. Sui, Y. T. Chew, P. Roy, Y. P. Cheng and H. T. Low, Phys. Fluids, 2008, 20, 112106 CrossRef.
- P. Bagchi and R. M. Kalluri, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 016307 CrossRef.
- P. M. Vlahovska, Y.-N. Young, G. Danker and C. Misbah, J. Fluid Mech., 2011, 678, 221–247 CrossRef CAS.
- S. S. Vergeles and P. E. Vorobev, JETP Lett., 2011, 94, 513–518 CrossRef CAS.
- R. Finken, S. Kessler and U. Seifert, J. Phys.: Condens. Matter, 2011, 23, 184113 CrossRef CAS.
- A. Farutin and C. Misbah, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 011902 CrossRef.
- G. Boedec, M. Jaeger and M. Leonetti, J. Fluid Mech., 2012, 690, 227–261 CrossRef.
- B. Kaoui, G. Biros and C. Misbah, Phys. Rev. Lett., 2009, 103, 188101 CrossRef.
- C. Pozrikidis, Boundary Integral and Singularity Methods for Linearized Viscous Flow, Cambridge University Press, Cambridge, 1992 Search PubMed.
- C. Pozrikidis, Ann. Biomed. Eng., 2005, 33, 165–178 CrossRef CAS.
- C. Pozrikidis, Computational Hydrodynamics of Capsules and Biological Cells, CRC Press, Boca Raton, Florida, 2010 Search PubMed.
- H. Zhou and C. Pozrikidis, J. Fluid Mech., 1995, 283, 175–200 CrossRef.
- H. Zhao, A. P. Spann and E. S. G. Shaqfeh, Phys. Fluids, 2011, 23, 121901 CrossRef.
- G. Boedec, M. Leonetti and M. Jaeger, J. Comput. Phys., 2011, 230, 1020–1034 CrossRef.
- S. K. Veerapaneni, A. Rahimian, G. Biros and D. Zorin, J. Comput. Phys., 2011, 230, 5610–5634 CrossRef CAS.
- S. K. Veerapaneni, D. Gueyffier, G. Biros and D. Zorin, J. Comput. Phys., 2009, 228, 7233–7249 CrossRef.
- A. Rahimian, S. K. Veerapaneni and G. Biros, J. Comput. Phys., 2010, 229, 6466–6484 CrossRef CAS.
- J. Sohn, Y. Tseng, S. Li, A. Voigt and J. Lowengrub, J. Comput. Phys., 2010, 229, 119–144 CrossRef CAS.
- H. Zhao, A. H. G. Isfahani, L. N. Olson and J. B. Freund, J. Comput. Phys., 2010, 229, 3726–3744 CrossRef CAS.
- W. R. Dodson III and P. Dimitrakopoulos, Biophys. J., 2010, 99, 2906–2916 CrossRef.
- B. Kaoui, N. Tahiri, T. Biben, H. Ez-Zahraouy, A. Benyoussef, G. Biros and C. Misbah, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041906 CrossRef CAS.
- B. Kaoui, J. Harting and C. Misbah, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 066319 CrossRef.
- G. Ghigliotti, A. Rahimian, G. Biros and C. Misbah, Phys. Rev. Lett., 2011, 106, 028101 CrossRef.
- H. Zhao, E. S. G. Shaqfeh and V. Narsimhan, Phys. Fluids, 2012, 24, 011902 CrossRef.
- M. Levant, J. Deschamps, E. Afik and V. Steinberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 056306 CrossRef.
- V. Vitkova, M. A. Mader, B. Polack, C. Misbah and T. Podgorski, Biophys. J., 2008, 95, L33–L35 CrossRef CAS.
- D. Salac and M. Miksis, J. Comput. Phys., 2011, 230, 8192–8215 CrossRef CAS.
- E. Maitre, C. Misbah, P. Peyla and A. Raoult, Phys. D, 2012, 241, 1146–1157 CrossRef CAS.
- Q. Du, C. Liu and X. Wang, J. Comput. Phys., 2006, 212, 757–777 CrossRef.
- Y. Liu and W. K. Liu, J. Comput. Phys., 2006, 220, 139–154 CrossRef.
- A. Z. K. Yazdani, R. M. Kalluri and P. Bagchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 046305 CrossRef.
- A. Z. K. Yazdani and P. Bagchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 026314 CrossRef.
- A. Laadhari, P. Saramito and C. Misbah, Phys. Fluids, 2012, 24, 031901 CrossRef.
- P. J. Atzberger, P. R. Kramer and C. S. Peskin, J. Comput. Phys., 2007, 224, 1255–1292 CrossRef.
- P. J. Atzberger, J. Comput. Phys., 2011, 230, 2821–2837 CrossRef CAS.
- E.-J. Ding and C. K. Aidun, Phys. Rev. Lett., 2006, 96, 204502 CrossRef.
- C. K. Aidun and J. R. Clausen, Annu. Rev. Fluid Mech., 2010, 42, 439–472 CrossRef.
- F. Janoschek, F. Mancini, J. Harting and F. Toschi, Philos. Trans. R. Soc., A, 2011, 369, 2337–2344 CrossRef CAS.
- N. Tanaka and T. Takano, Int. J. Comput. Meth., 2005, 2, 558–568 CrossRef.
- K. Tsubota, S. Wada and T. Yamaguchi, Comput. Meth. Programs Biomed., 2006, 83, 139–146 CrossRef.
- S. M. Hosseini and J. J. Feng, Biophys. J., 2012, 103, 1–10 CrossRef CAS.
- H. Noguchi and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 14159–14164 CrossRef CAS.
- J. L. McWhirter, H. Noguchi and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6039–6043 CrossRef CAS.
- K. Boryczko, W. Dzwinel and D. A. Yuen, J. Mol. Model., 2003, 9, 16–33 Search PubMed.
- W. Dzwinel, K. Boryczko and D. A. Yuen, J. Colloid Interface Sci., 2003, 258, 163–173 CrossRef CAS.
- D. A. Fedosov, W. X. Pan, B. Caswell, G. Gompper and G. E. Karniadakis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11772–11777 CrossRef CAS.
- P. Dimitrakopoulos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 058301 CrossRef CAS.
- Z. L. Peng, R. J. Asaro and Q. Zhu, J. Fluid Mech., 2011, 686, 299–337 CrossRef.
- T. M. Fischer, Biophys. J., 2007, 93, 2553–2561 CrossRef CAS.
- D. A. Fedosov, B. Caswell, A. S. Popel and G. E. Karniadakis, Microcirculation, 2010, 17, 615–628 CrossRef.
- W. X. Pan, D. A. Fedosov, B. Caswell and G. E. Karniadakis, Microvasc. Res., 2011, 82, 163–170 CrossRef.
- X. J. Li, A. S. Popel and G. E. Karniadakis, Phys. Biol., 2012, 9, 026010 CrossRef.
- S. Yang, A. Ündar and J. D. Zahn, Lab Chip, 2006, 6, 871–880 RSC.
- J. L. McWhirter, H. Noguchi and G. Gompper, Soft Matter, 2011, 7, 10967–10977 RSC.
- M. M. Dupin, I. Halliday, C. M. Care, L. Alboul and L. L. Munn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 066707 CrossRef.
- R. M. MacMeccan, J. R. Clausen, G. P. Neitzel and C. K. Aidun, J. Fluid Mech., 2009, 618, 13–39 CrossRef.
- F. Janoschek, F. Toschi and J. Harting, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 056710 CrossRef CAS.
- S. Melchionna, Macromol. Theory Simul., 2011, 20, 548–561 CrossRef CAS.
- D. A. Reasor, J. R. Clausen and C. K. Aidun, Int. J. Numer. Methods Fluids, 2012, 68, 767–781 CrossRef.
- Y. Imai, H. Kondo, T. Ishikawa, C. T. Lim and T. Yamaguchi, J. Biomech., 2010, 43, 1386–1393 CrossRef.
- Y. Imai, K. Nakaaki, H. Kondo, T. Ishikawa, C. T. Lim and T. Yamaguchi, J. Biomech., 2011, 44, 1553–1558 CrossRef.
- D. A. Fedosov, B. Caswell and G. E. Karniadakis, Biophys. J., 2011, 100, 2084–2093 CrossRef CAS.
- D. A. Fedosov, B. Caswell, S. Suresh and G. E. Karniadakis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 35–39 CrossRef CAS.
- H. Bow, I. V. Pivkin, M. Diez-Silva, S. J. Goldfless, M. Dao, J. C. Niles, S. Suresh and J. Han, Lab Chip, 2011, 11, 1065–1073 RSC.
- L. Grinberg, V. Morozov, D. Fedosov, J. A. Insley, M. E. Papka, K. Kumaran and G. E. Karniadakis, A New Computational Paradigm in Multiscale Simulations: Application to Brain Blood Flow, International Conference for High Performance Computing, Networking, Storage and Analysis, 2011 Search PubMed.
- A. M. Forsyth, J. Wan, P. D. Owrutsky, M. Abkarian and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10986–10991 CrossRef CAS.
- S. Suresh, J. Mater. Res., 2006, 21, 1871–1877 CrossRef CAS.
- G. A. Barabino, M. O. Platt and D. K. Kaul, Annu. Rev. Biomed. Eng., 2010, 12, 345–367 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2013 |
