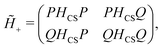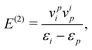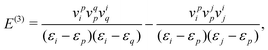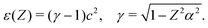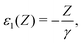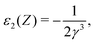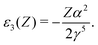Perspectives of relativistic quantum chemistry: the negative energy cat smiles
Received
26th May 2011
, Accepted 29th September 2011
First published on 14th November 2011
Abstract
Given the remarkable advances in relativistic quantum chemistry, some conceptual aspects still remain to be addressed. Among others, the role of negative energy states (NES) in electron correlation and other properties requires most attention. Based on critical assessments of the configuration space (CS), no-photon (and no-time) Fock space (FS) and quantum electrodynamics (QED) approaches, it is concluded that only QED provides the correct prescription for the contributions of NES to correlation, while both CS and FS give rise to wrong results. This essentially means that one should work either with the no-pair approximation (which has an intrinsic error of order (Zα)3) or with QED. Whether a consistent relativistic many-electron theory does exist in between remains an open question. Even under the no-pair approximation, there still exists an issue arising from that the no-pair Hamiltonian is incompatible with explicitly correlated methods. It turns out that this can nicely be resolved by introducing the concept of extended no-pair projection. Apart from these take-home messages, other immediate prospects of relativistic quantum chemistry are also highlighted for guiding future developments and applications.

Wenjian Liu
| Wenjian Liu is a Cheung Kong Professor of theoretical chemistry at Peking University (since 2001). After receiving his PhD at Peking University in 1995, he spent 6 years as a postdoc at Max Planck Institute Dresden and Ruhr University Bochum, Germany. His research interests focus on the development of relativistic quantum mechanical theories and methods for molecular electronic structure and magnetic properties. Besides strong publication and citation records, he has gained several worldwide distinctions, including the Friedrich Wilhelm Bessel Research Award of the Alexander von Humboldt Foundation (2007), the Annual Medal of International Academy of Quantum Molecular Science (2006), and the Pople Medal of Asian Pacific Association of Theoretical and Computational Chemists (2006). |
1 Introduction
Modern quantum chemistry is a “3+1” dimensional problem, as schematically illustrated in Fig. 1. The extra “1” dimension here refers to the electroweak, parity non-conserving (PNC) interaction that is responsible for molecular parity violation. Although PNC effects are of great interest in their own right,1 they are only of 10−11 J mol−1 magnitude in energy and are hence completely irrelevant to thermodynamics and kinetics of chemistry. The other “3”-dimensions consist of the Hamiltonian (equation) axis, going from the Schrödinger through the approximate two-component (A2C), exact two-component (X2C),2 quasi-four-component (Q4C)3,4 and four-component Dirac equations to quantum electrodynamics (QED), the method axis going from Hartree–Fock (HF) to full configuration-interaction (FCI), as well as the one-particle basis axis going from minimal to complete basis sets. As QED effects also do not play any role in chemistry, it is then the non-retarded no-pair Dirac–Coulomb–Breit (DCB) Hamiltonian, represented in a restricted kinetically balanced (RKB) basis set,5 that serves as the basis of relativistic quantum chemistry for electronic structure calculations. It can then be shown6 that four- and two-component calculations, whether uncorrelated or correlated, can be made fully equivalent in all aspects of simplicity, accuracy and efficiency. In particular, various variants of the X2C Hamiltonian can be formulated in a very simple manner. That is, they can be obtained in one step, either at matrix level3,4,7–9 or equivalently at operator (more precisely, operator-like) level.10 The former starts directly from the matrix Dirac equation represented in a RKB basis and makes a single block-diagonalization, whereas the latter amounts to reversing the matrix representation and the block-diagonalization steps, viz., first block-diagonalizing the Dirac operator via the Foldy–Wouthuysen unitary transformation and then making the matrix representation in a RKB basis via resolution of the identity, which is just a formal step, not an approximation even for a finite basis. Other two-step or multiple-step block-diagonalizations of the Dirac equation are found6 to share the same decoupling condition as the one-step approach and the three differ only in the renormalization of the eigenvectors when going from the Dirac to the Schrödinger picture. Based on the so-obtained mean-field X2C Hamiltonian and its eigenstates, a second-quantized and normal-ordered two-component relativistic many-electron Hamiltonian can be formed4 for accurate molecular calculations. The same procedure can also be employed to formulate an X2C theory for magnetic properties.11 The (no-pair) Hamiltonian axis can hence be viewed as completed. For further discussions of the Hamiltonians and strategies for computational efficiency, see ref. 6. As for the method axis, the know-how developed in the nonrelativistic realm can directly be adopted (for a recent review see ref. 12). It appears, at this stage, that the major “bottleneck”, an engineering issue, remains efficient implementations of such methods for investigating relativistic effects in heavy-element (REHE) chemistry and physics.
 |
| | Fig. 1 Schematic illustration of the “3+1” dimensions of modern quantum chemistry. | |
However, there do exist some problems with the no-pair approximation. That is, there are situations where the negative energy cat† raises its head. Nuclear magnetic resonance (NMR) shieldings represent a first example where the no-pair approximation becomes very crude: The sizeable contributions of negative energy states (NES) even survive to the nonrelativistic limit in the standard sum-over-states (SOS) formulation such that the diamagnetism is entirely missed under the no-pair approximation. Even though the diamagnetism shows up naturally when the magnetic balance is explicitly incorporated,13–17 the contributions of NES still amount to order (Zα)2 or (Zα)4, which cannot be ignored for accurate absolute shieldings. It is even the case that, neglecting terms of (Zα)2, a first order coupling approximation, provides very accurate estimates of relative shieldings, whereas neglecting terms of (Zα)4, a second order coupling approximation, leads to spurious results due to imbalanced treatment of NES.13,14 A second example is that, at variance with nonrelativistic FCI, the no-pair FCI energy is always dependent on the potential used to generate the orbitals,18 which is a direct consequence of ignoring the correlation space spanned by NES. In other words, the no-pair FCI is actually a CAS-CI (complete active space CI) instead of the genuine FCI. An immediate question is, then, whether the combination of a no-pair calculation with only radiative QED corrections is meaningful at all: The missing contributions of NES to correlation are of the same order of (Zα)3 as the leading QED corrections. A recent numerical study19 indeed shows that, for the first ionization potential of the gold atom, the already good agreement between the no-pair calculation and experiment is actually worsened when the corrections due to electron self-energy and vacuum polarization are included. Moreover, the no-pair Hamiltonian, just like any second-quantized Hamiltonian, is incompatible with explicitly correlated methods, which aim to generate a complementary correlation space outside the spectrum of the Hamiltonian.
To address the contributions of NES to electron correlation, we will compare three approaches (i.e., configuration space (CS), Fock space (FS) and QED) in Section 2. The analysis shows that neither CS nor FS provides the correct prescription whereas only QED, an intrinsically time-dependent approach, does the job. Nevertheless, for one-electron properties, the three approaches give rise to the same expressions and differ only in the interpretations (Section 3). An extended no-pair Hamiltonian is proposed in Section 2.4 for explicitly correlated calculations. Further prospects of relativistic quantum chemistry will finally be highlighted in Section 4 to close the account.
2 The role of NES in electron correlation
2.1 The configuration space approach
The point of departure is the configuration space (CS) DCB Hamiltonian for N-electrons moving in the field of the clamped nuclei| | 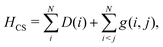 | (1) |
| | D0 = c![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) · ·![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) + βmc2, + βmc2, | (3) |
| | 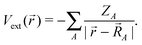 | (4) |
Here, the SI-based atomic units have been employed (ℏ = m = e = 4πε0 = 1), although the electron mass m is still spelt out explicitly. D0 is the free particle Dirac operator, Vext the nuclear attraction, c = 1/α the speed of light, 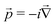 the linear momentum operator, and
the linear momentum operator, and ![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) and β the usual 4 × 4 Dirac matrices. The two-electron interaction g(1,2) in the Coulomb gauge takes the following form:
and β the usual 4 × 4 Dirac matrices. The two-electron interaction g(1,2) in the Coulomb gauge takes the following form:| | | g(1,2) = gC(1,2) + gB(1,2), | (5) |
| | 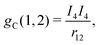 | (6) |
| | | gB(1,2) = gG(1,2) + gg(1,2), | (7) |
| | 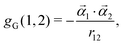 | (8) |
| | 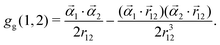 | (9) |
For the purpose of perturbative treatment of electron correlation, the full Hamiltonian HCS can be partitioned as| | 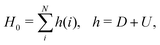 | (11) |
| | 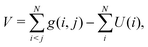 | (12) |
where the effective one-electron operator h is to be employed to generate the unperturbed orbitals {φp} and energy levels {εp}, viz.,Various choices of h can be made, each of which defines accordingly a no-pair projected (npp) N-electron Hamiltonian:
(a) U = −Vext, the free-particle npp20
(b) U = 0, the external-field npp (known as the Furry picture21)
(c) U = VHF, the mean-field npp with the nonlocal HF potential (also known as the Fuzzy picture22)
(d) U = Vloc, the mean-field npp with some local (e.g., Kohn–Sham) potential
The most salient feature of the Dirac operator h (11) is that it has a negative energy continuum and is therefore unbounded from below. Yet, this imposes no particular problem on solving eqn (13) represented in a finite basis, as long as the basis is constructed according to, e.g., the RKB prescription5 and meanwhile the electrons are, in each iteration cycle, assigned to the lowest positive energy stats (PES). Even full variational safety23 can be guaranteed via the dual kinetic balance (DKB) prescription.24 However, the situation is changed dramatically when going beyond the mean-field level. To see this more clearly, we consider second order Rayleigh–Schrödinger perturbation theory for electron correlation. In terms of the eigenfunctions (|n〉, n = 0, 1,…) and eigenvalues (E(0)n) of H0, the SOS expressions for the ground state energy of an N-electron system can generally be written as
| | | E = E(0) + E(1) + E(2) +…, | (14) |
| | 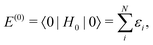 | (15) |
| | | E(1) = 〈0|V|0〉 = (½VHF − U)ii, | (16) |
| | 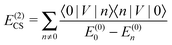 | (17) |
| | | = E(2)CS,1 + E(2)CS,2, | (18) |
| | | E(2)CS,1 = E(2)CS,1+ + E(2)CS,1−, | (19) |
| | 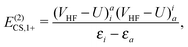 | (20) |
| | 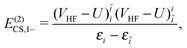 | (21) |
| | | E(2)CS,2 = E(2)CS,++ + E(2)CS,−− + E(2)CS,+−, | (22) |
| | 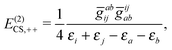 | (23) |
| | 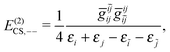 | (24) |
| | 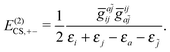 | (25) |
Apart from the Einstein summation convention over repeated indices, the following convention has been adopted to label the orbitals: indices {
i,
j,…} and {
a,
b,…} for the occupied and unoccupied
PES, and {
ĩ,
![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif)
,…} for the unoccupied NES. Unspecified orbitals are denoted as {
p,
q,
r,
s}. When necessary, NES will explicitly be designated by {
![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif)
,
![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif)
,
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif)
,
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif)
}. The above one- and two-electron integrals are defined as
| | hqp = ∫ d![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 3φp†( 3φp†(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )h( )h(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )φq( )φq(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), ), | (26) |
| | grspq = ∫∫ d![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 31d 31d![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 32φp†( 32φp†(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1)φq†( 1)φq†(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2)g(1,2)φr( 2)g(1,2)φr(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1)φs( 1)φs(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2), 2), | (27) |
| |  rspq = grspq − gsrpq = grspq − grsqp. rspq = grspq − gsrpq = grspq − grsqp. | (28) |
The two-body second order energy
E(2)CS,2 consists of three terms,
E(2)CS,++ involving two virtual
PES,
E(2)CS,1−− involving two virtual NES, and
E(2)CS,+− involving one virtual
PES and one virtual NES. The first two terms are always negative and positive, respectively, where the third term is troublesome: If
εa =
εi + |
X| and
ε![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif)
=
εj − |
X|, the denominator would vanish and there exist an infinite number of such “+−” intermediates. This kind of instability of many-electron systems was first discussed by Brown and Ravenhall
25 and is usually called the continuum dissolution problem or simply the Brown–Ravenhall disease (BRD). A direct deduction made was that the many-electron DC Hamiltonian
(1) has no bound states and even its discrete states are characterized by complex energies and are hence resonances of finite life times. This further implies that the DC Hamiltonian is
not self-adjoint (Hermitian). If one knows that the one-electron Dirac operator
D itself is essentially self-adjoint on the dense domain
C∞0(
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3
3\{
O})
4 (
i.e., the space of infinitely differentiable functions with compact support of the field of triples of real numbers excluding the origin) and self-adjoint on the first Sobolev space
H1(
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3
3)
4 for nuclear charge
Z ≤ 118 in the case of a point nuclear model and becomes self-adjoint on
C∞0(
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3
3)
4 for all
Z in the case of a finite nuclear model,
26 one ought to ask the following questions:
Is the BRD a real one? Isn't it a mathematical failure of applying a non-degenerate perturbation theory to a degenerate problem? Consider two non-interacting 1s2 electrons, each of which is strongly bounded by the attraction −Z/ri of a heavy nucleus. Is it really possible that the interaction 1/r12, which is much weaker than the nuclear attraction, would completely spoil their stability?
Actually, these questions were already addressed by Jáuregui,27 who carried out careful DC-FCI calculations on helium-like ions and found that, thanks to the McDonald interleaving (interlacing) theorem, the DC Hamiltonian does have bona fide positive energy bound states, which are bounded from below by those of the no-pair DC Hamiltonian. However, this strong statement was recently challenged by Watanabe28,29 and Pestka,30,31 who demonstrated that the discrete states of the DC Hamiltonian are instead characteristic of Feshbach resonances. The former carried out DC-FCI calculations on helium-like ions with huge Gaussian basis sets and found that the wave functions of 1s2 for all the ions are composed predominantly of the “++” components, but of very small “−−” and “+−” components as well. As the energies are real-valued, the resonance nature of the states can only be inferred indirectly by the stabilization analysis. There could be two uncertainties here. First, the RKB prescription is somewhat biased toward the PES such that care should be taken when speaking of the precise amount of the BRD “+−” components. This problem can be avoided by going to the DKB prescription for constructing the basis sets.23,24 Second, no attempt has been made to see whether the “+−” components would vanish by optimizing the basis sets, as done by Jáuregui.27 By contrast, Pestka30,31 provided more direct evidence on the resonance nature of the 1s2 states of helium-like ions. They obtained in their DC-Hylleraas-CI calculations only complex energies, the imaginary parts of which can nicely be fitted as −0.0064(Zα)3 in atomic unit. However, instead of the original Hamiltonian HCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )(1), a dilated (also called ‘complex-coordinate-rotated’, CCR) Hamiltonian HCS(
)(1), a dilated (also called ‘complex-coordinate-rotated’, CCR) Hamiltonian HCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) eiθ) was employed therein. Mathematically, such a dilation would not change the bound states of HCS(
eiθ) was employed therein. Mathematically, such a dilation would not change the bound states of HCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) but only rotates those unbound states to the complex energy plane. That only complex energies have been obtained with HCS(
) but only rotates those unbound states to the complex energy plane. That only complex energies have been obtained with HCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) eiθ) implies immediately that HCS(
eiθ) implies immediately that HCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) has no bound states. However, this point should be viewed with caution: The bound states remain unchanged only if both the Hamiltonian and the square-integrable basis functions are scaled simultaneously, e.g., gμ(r) = exp(−ημr2) → gμ(ρ) = exp(−ημr2e2iθ). Otherwise, in principle a complete set of unscaled gμ(r) functions is required for HCS(
) has no bound states. However, this point should be viewed with caution: The bound states remain unchanged only if both the Hamiltonian and the square-integrable basis functions are scaled simultaneously, e.g., gμ(r) = exp(−ημr2) → gμ(ρ) = exp(−ημr2e2iθ). Otherwise, in principle a complete set of unscaled gμ(r) functions is required for HCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) eiθ) to reproduce the matrix eigenvalues of HCS(
eiθ) to reproduce the matrix eigenvalues of HCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) represented just in a small basis. This is because a scaled function gμ(ρ) is highly oscillatory and can hardly be simulated by the real radial functions gν(r). To confirm this viewpoint, we carried out a set of calculations for the ground state of the Xe53+ ion for which the existence of bound states is out of question. It is seen from Table 1 that, for 30s and 40s even-tempered Gaussian functions, the dilated Dirac operator D(
) represented just in a small basis. This is because a scaled function gμ(ρ) is highly oscillatory and can hardly be simulated by the real radial functions gν(r). To confirm this viewpoint, we carried out a set of calculations for the ground state of the Xe53+ ion for which the existence of bound states is out of question. It is seen from Table 1 that, for 30s and 40s even-tempered Gaussian functions, the dilated Dirac operator D(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) eiθ) does give rise to a spurious imaginary part in the energy even with a rotation angle as small as 0.03 rad. The convergence toward the exact energy is slowed down when the angle is enlarged, e.g., to 0.30 rad. It was also observed in the course of experimentation that all the states above +mc2 (below −mc2) have large negative (positive) imaginary parts in the energies, whereas the imaginary parts in the energies for the states below +mc2 and above −mc2 can be both positive and negative and tend to vanish only when the basis is sufficiently large. Although only a one-electron system is considered here, the observation should also apply to many-electron cases. Therefore, it cannot be excluded that the complex energies obtained by Pestka30,31 are due to incompleteness errors in the basis set. Given such uncertainties, the conclusion28–31 that the DC Hamiltonian has no bound states may be premature. What can really be concluded at this stage is that the BRD is much less virulent than originally claimed, and that the no-pair projection, as recommended by Sucher32 for avoiding the BRD, is not really needed. At this moment a mathematician may debate that the non-interacting Hamiltonian D(1) + D(2) does not have any gap in the continuous spectrum of (−∞, +∞) such that any weak interaction would result in the BRD. However, what is in mind here is an electron in the PES and the other in the NES, not a physical process where both the initial and final states are of positive energies.
eiθ) does give rise to a spurious imaginary part in the energy even with a rotation angle as small as 0.03 rad. The convergence toward the exact energy is slowed down when the angle is enlarged, e.g., to 0.30 rad. It was also observed in the course of experimentation that all the states above +mc2 (below −mc2) have large negative (positive) imaginary parts in the energies, whereas the imaginary parts in the energies for the states below +mc2 and above −mc2 can be both positive and negative and tend to vanish only when the basis is sufficiently large. Although only a one-electron system is considered here, the observation should also apply to many-electron cases. Therefore, it cannot be excluded that the complex energies obtained by Pestka30,31 are due to incompleteness errors in the basis set. Given such uncertainties, the conclusion28–31 that the DC Hamiltonian has no bound states may be premature. What can really be concluded at this stage is that the BRD is much less virulent than originally claimed, and that the no-pair projection, as recommended by Sucher32 for avoiding the BRD, is not really needed. At this moment a mathematician may debate that the non-interacting Hamiltonian D(1) + D(2) does not have any gap in the continuous spectrum of (−∞, +∞) such that any weak interaction would result in the BRD. However, what is in mind here is an electron in the PES and the other in the NES, not a physical process where both the initial and final states are of positive energies.
Table 1 The ground state energy of Xe53+ calculated with the dilated Dirac Hamiltonian hD(θ). The exponents of the restricted kinetically balanced s-Gaussian functions are ηi = exp[−0.84 + 0.52(i − 1)]. The point nuclear model and a value of 137.0359895 a.u. for the speed of light are adopted. ΔE: deviation of ℜE from the exact energy −1519.4733528183 a.u. All calculations were performed using Mathematica
|
N
|
ℜE |
ℑE |
ΔE |
| |
θ = 0 rad |
| 30 |
−1519.3561352764 |
|
0.1172175419 |
| 40 |
−1519.4724092505 |
|
0.0009435678 |
| 50 |
−1519.4733449155 |
|
0.0000079028 |
| 60 |
−1519.4733527510 |
|
0.0000000673 |
| 70 |
−1519.4733528168 |
|
0.0000000015 |
| 80 |
−1519.4733528174 |
|
0.0000000009 |
| 90 |
−1519.4733528174 |
|
0.0000000009 |
| |
θ = 0.03 rad |
| 30 |
−1519.3563243499 |
6.62E-03 |
0.1170284684 |
| 40 |
−1519.4724106919 |
5.21E-05 |
0.0009421264 |
| 50 |
−1519.4733449275 |
4.36E-07 |
0.0000078908 |
| 60 |
−1519.4733527511 |
3.64E-09 |
0.0000000672 |
| 70 |
−1519.4733528168 |
1.46E-11 |
0.0000000015 |
| 80 |
−1519.4733528174 |
−1.59E-11 |
0.0000000009 |
| 90 |
−1519.4733528174 |
−1.61E-11 |
0.0000000009 |
| |
θ = 0.30 rad |
| 30 |
−1519.3745128342 |
6.26E-02 |
0.0988399841 |
| 40 |
−1519.4725497336 |
4.95E-04 |
0.0008030847 |
| 50 |
−1519.4733460371 |
4.13E-06 |
0.0000067812 |
| 60 |
−1519.4733527104 |
2.02E-08 |
0.0000001079 |
| 70 |
−1519.4733527665 |
−1.43E-08 |
0.0000000518 |
| 80 |
−1519.4733527669 |
−1.46E-08 |
0.0000000514 |
| 90 |
−1519.4733527669 |
−1.46E-08 |
0.0000000514 |
What has been discussed so far is a purely mathematical issue of the DC Hamiltonian. Even if one can someday prove that the DC Hamiltonian is indeed self-adjoint (a very difficult mathematical problem) and does have bound states, it does not imply that the CS approach provides a correct prescription for the contributions of NES to electron correlation (vide post). A good indicator for this doubt is that such contributions are “anti-correlating”, leading to a reduction in the correlation energy although the correlation space is enlarged.
For later comparison, we now introduce the second-quantized Hamiltonian
| | | HCS = Dqpapq + ½grspqapqrs | (29) |
| | | = εpapp − Uqpapq + ½grspqapqrs, | (30) |
| | | ap = a†p, apq = a†paq, apqrs = a†pa†qasar, | (31) |
which is obtained from the first-quantized form
(1) upon the introduction of the field operator
| | ϕ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = apφp( ) = apφp(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), ap|0; ), ap|0; 〉 = 0, 〉 = 0, | (32) |
where
φp(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
) are the eigenvectors of
h (13). Note that the Hamiltonian
HCS(29) is already normal ordered with respect to the vacuum |0;
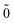
〉 but not yet to the reference state |
N;
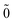
〉 of
N positive energy electrons and zero negative energy electrons. If the
ai and
aa operators in
(30) are rearranged to the right of
ai and
aa, we would obtain a Hamiltonian that is also normal ordered with respect to |
N;
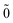
〉,
viz.,
| | | HCS = H0 + V0 + V1 + V2, | (33) |
| | 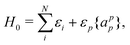 | (34) |
| | 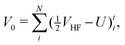 | (35) |
| | | V1 = (VHF − U)qp{apq}, | (36) |
where the braces indicate that the operators have been normal-ordered. The particle–hole picture (
i.e.,
aa =
ba,
aa =
ba,
ai =
bi,
ai =
bi) may further be introduced to facilitate the graphical representation of the operators. Effectively, this would turn the reference |
N;
〉 into a genuine vacuum |0;
〉 of no particles or holes,
viz.,
| | ϕ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = bpφp( ) = bpφp(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), bp|0; ), bp|0; 〉 = 0. 〉 = 0. | (38) |
Note that the indices {
a,
p,
q,
r,
s} starting from
eqn (29) include both
PES and NES.
The no-pair approximation32‡ amounts to taking only the part of the Hamiltonian (33) where all the indices are PES, viz.,
| | 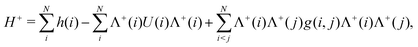 | (39) |
where the PES projector Λ
+ is defined as
| | 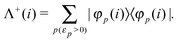 | (40) |
Obviously,
H+ is dependent on the potential
U generating the orbitals.
2.2 The no-photon Fock space approach
It is well known26 that, given the existence of an empty Dirac sea, no collapse can occur in the case of one electron subject to an arbitrarily strong static field, whether electric or magnetic. As discussed before this holds, to a large extent, also for many-electron cases. However, the situation is changed completely when the electron is coupled to a radiation field: Any electron would fall down into the sea emitting radiation. To overcome this radiation catastrophe, Dirac postulated33 that the negative energy sea be filled with electrons and the hole left by exciting an electron from the sea be a positron. This bold prediction was soon confirmed experimentally.34 However, this filled Dirac picture (also known as hole theory) has a number of defects:
(1) It is asymmetric with respect to electrons and positrons
(2) It characterizes a positron as a hole rather than a real particle. The propagation of the hole is reflected only indirectly by that of the remaining electrons in the sea
(3) It involves an infinite negative electric charge filling the whole space even if only one electron is under consideration
(4) It has to assume that the negative energy electrons do not generate any potential acting on the positive energy electrons
(5) It does not, in a strict sense, explain the stability of a positive energy electron: Being infinitely large, the sea can always accept infinitely many electrons. In other words, the Pauli exclusion principle does not really hold for a system of an infinite number of fermions
(6) It does not apply to spin zero particles which do not satisfy an exclusion principle
Such problems can be resolved by the so-called no-photon Fock space (FS) formulation,35–39 which involves three steps:
Step (1) Define the Dirac vacuum as a state in which all the NES are occupied, symbolically expressed as |0;Ñ〉 = ΠÑĩaĩ|0;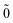 〉
〉
Step (2) Introduce the particle-hole picture, i.e., ap = bp and ap = bp for εp > 0 and a![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) = b
= b![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) and a
and a![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) = b
= b![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) for ε
for ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) < 0. This effectively turns the |0;Ñ〉 state into the genuine vacuum |0;
< 0. This effectively turns the |0;Ñ〉 state into the genuine vacuum |0;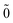 〉 of no particles or holes, i.e., bp|0;
〉 of no particles or holes, i.e., bp|0; 〉 = b
〉 = b![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) |0;
|0; 〉 = 0. It also amounts to writing the field operator as
〉 = 0. It also amounts to writing the field operator as
| | ϕ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = bpφp( ) = bpφp(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) + b ) + b![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) φ φ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), ), | (41) |
which is to be contrasted with the naive second quantization
(38) associated with the empty Dirac picture
Step (3) Introduce the concept of normal ordering. Effectively, this will change the sign of the negative energy ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) and get rid of the infinite energy of the otherwise filled sea
and get rid of the infinite energy of the otherwise filled sea
The above procedure can be depicted by Fig. 2. Steps (1) and (3) define the FS Hamiltonian as
| | | HFS = Dqp{apq}n + ½grspq{apqrs}n | (42) |
| | | = εp{app}n − Uqp{apq}n + ½grspq{apqrs}n, | (43) |
where the subscript
n emphasizes that the normal ordering is taken only with respect to the NES. This is the Hamiltonian that was advocated by Kutzelnigg
39 as the only acceptable relativistic many-electron Hamiltonian under the no-
photon approximation. It has a very complicated structure when the particle-hole picture is also taken: The one-body part
V1 consists of 4 terms,
viz.,
bpbq,
b![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) bq
bq,
bpb![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif)
, and −
b![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) b
b![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif)
, the second and third of which correspond to pair annihilation and creation, respectively. The two-body part
V2 is composed of 16 terms, not to be documented here. Moreover, care should also be taken of the polarization of the vacuum |0;
〉.
Let us start with a zeroth order state |N; 〉(0) of N bound electrons alongside with the zeroth order vacuum |0;
〉(0) of N bound electrons alongside with the zeroth order vacuum |0; 〉(0). The zeroth and first order energies of the system can easily be obtained as shown in eqn (15) and (16), respectively. To derive the first order correction |N;
〉(0). The zeroth and first order energies of the system can easily be obtained as shown in eqn (15) and (16), respectively. To derive the first order correction |N; 〉(1) to the state, we first notice that the intermediate states include zero, one, and two electron-positron (ep) pairs, viz.,
〉(1) to the state, we first notice that the intermediate states include zero, one, and two electron-positron (ep) pairs, viz.,
| | |N; 〉(1) = |N; 〉(1) = |N; 〉(1)0ep + |N; 〉(1)0ep + |N;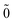 〉(1)1ep + |N; 〉(1)1ep + |N;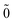 〉(1)2ep. 〉(1)2ep. | (44) |
So does the first order correction |0;
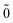
〉
(1) to the vacuum:
| | 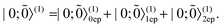 | (45) |
After straightforward manipulations we obtain
| | 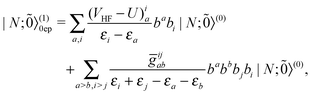 | (46) |
| | 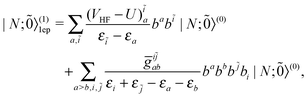 | (47) |
| | 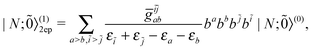 | (48) |
| | |0; 〉(1)0ep = 0, 〉(1)0ep = 0, | (49) |
| | 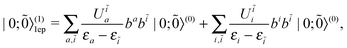 | (50) |
| | 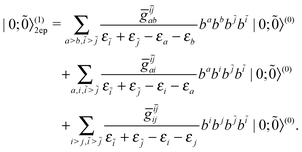 | (51) |
The second order energy is then obtained as
| | E(2)FS = (0) 〈N; |V|N; |V|N; 〉(1) − (0) 〈0; 〉(1) − (0) 〈0;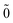 |V|0; |V|0;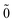 〉(1), 〉(1), | (52) |
| | | = E(2)FS,1 + E(2)FS,2, | (53) |
| | | E(2)FS,1 = E(2)FS,1+ + E(2)FS,1−, | (54) |
| | 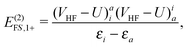 | (55) |
| | 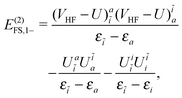 | (56) |
| | | E(2)FS,2 = E(2)FS,++ + E(2)FS,X1 + E(2)FS,−− + E(2)FS,X2, | (57) |
| | 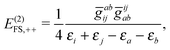 | (58) |
| | 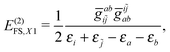 | (59) |
| | 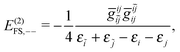 | (60) |
| | 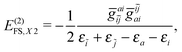 | (61) |
where all the terms with a global negative sign stem from the vacuum |0;
〉 whereas the others from the |
N;
〉 state. Such a rearrangement is to make a better comparison with those by the CS approach. It is seen that
E(2)FS,1+ arising from the first term of
(46) agrees with
E(2)CS,1+ in
(20),
E(2)FS,++ arising from the second term of (46) agrees with
E(2)CS,++ in
(23), and
E(2)FS,−− arising from the third term of
(51) agrees with
E(2)CS,−− in
(24). It is just that
E(2)FS,−− is now interpreted as a double-pair vacuum term instead of the previous transitions from the occupied PES to the virtual NES. The vexing BRD term
E(2)CS,+−(25) does not show up by construction. However,
E(2)FS,1− arising from both the first term of
(47) and the two terms of
(50) is different from
E(2)CS,1− in
(21). Moreover, the
E(2)FS,X1 arising from the second term of
(47) and the
E(2)FS,X2 from the second term of
(51) are absent in the CS. It is therefore clear that the CS (associated with the empty Dirac picture) and FS (associated with the filled Dirac picture) approaches are intrinsically different, which can only be uncovered by examining two-electron properties such as electron correlation. Also, the meaning of ‘no-pair approximation’ now becomes clear: Retaining the terms involving only the PES does correspond to no virtual pairs.
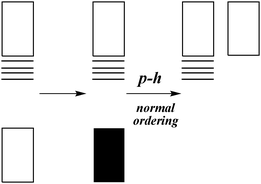 |
| | Fig. 2 Schematic illustration of the Fock space formalism: The one-particle states are generated by solving eqn (13) under the assumption of an empty Dirac sea (leftmost). The sea is then filled up with non-interacting electrons. Upon introduction of the particle–hole picture and the concept of normal ordering, the sea is turned into an empty space of positive energy (rightmost) representing virtual positrons. | |
As a matter of fact, manipulating the FS Hamiltonian (43) in terms of the b-operators and the associated vacuum polarization is completely equivalent to directly calculating the energy difference between the Ψ(N;Ñ) and Ψ(0;Ñ) states with the second-quantized CS Hamiltonian ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) , viz.,
, viz.,
| | E = 〈Ψ(N;Ñ)|![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |Ψ(N;Ñ)〉 − 〈Ψ(0;Ñ)| |Ψ(N;Ñ)〉 − 〈Ψ(0;Ñ)|![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |Ψ(0;Ñ)〉, |Ψ(0;Ñ)〉, | (62) |
| | 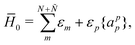 | (64) |
| | 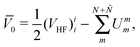 | (65) |
| | V1 = (VHF − U)qp{apq}, (VHF)qp = ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) qipi qipi | (66) |
where the normal ordering has been taken for both the occupied PES (
i,
j) and the occupied NES (
ĩ,
![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif)
), as indicated by the summation over
m in
(64) and
(65). Note that the
VHF term in
(66) emerges only for systems of more than one positive energy electron. Another caveat here is that, when deriving the normal-ordered Hamiltonian
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif)
, no contractions among the NES are allowed. Otherwise, the following terms would arise
| | Ṽ1 = ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) qĩpĩ {apq}, qĩpĩ {apq}, | (69) |
which give rise to infinite energies,
e.g.,
E(1) = (½
VHF −
U)
ii +
![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) i
i![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) i
i![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif)
, to be compared with the correct result
(16). That is, the negative energy electrons must be regarded as non-interacting, a very weird feature of the filled Dirac picture. Such contractions have been excluded automatically by the normal ordering with respect to the NES, see
eqn (42). At this stage it should be emphasized that the same set of mean-field NES (
cf.eqn (13)) has been employed here for describing the state and the (floating) vacuum, such that the vacuum polarization arises only from the fluctuation potential, starting from second order in energy. The so-called renormalization procedure is not needed as every term is finite individually. In contrast, in the so-called `no-
photon variational mean-field QED' approach,
35–38 the mean-field and free-particle NES are used for the state and the (frozen) vacuum, respectively, such that the vacuum polarization arises also from the mean-field potential, starting from first order in energy. Thereby, suitable regularization and renormalization have to be performed in each iteration step. To the best of our knowledge, no actual applications of this approach have yet been made. The corresponding second order correlation energy can also be derived in the same way as above. It is just that some additional terms would arise thanks to the use of different NES for the state and the vacuum.
2.3 The QED approach
As discussed in the previous section, although it provides a useful picture of how virtual NES, emerged from the mean-field eqn (13), are related to physical positrons of positive energy, the filled Dirac sea has some severe limitations. It is superseded by modern field theory such as QED, which allows only positive energy states. This is facilitated by charge (field) conjugation| | 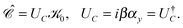 | (70) |
Its action on the Dirac equation| | 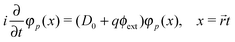 | (71) |
yields the charge conjugated equation | | 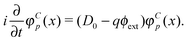 | (72) |
It follows that, for the same time-independent external potential ϕext(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), if φp(
), if φp(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )e−iεpt is a stationary solution of the Dirac equation for an electron (q = −1) of energy εp, φCp(x) = φCp(
)e−iεpt is a stationary solution of the Dirac equation for an electron (q = −1) of energy εp, φCp(x) = φCp(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )eiεpt would be a stationary solution of the Dirac equation for a positron (q = +1) of energy −εp. Note in particular that the probability density of a negative energy (−|ε
)eiεpt would be a stationary solution of the Dirac equation for a positron (q = +1) of energy −εp. Note in particular that the probability density of a negative energy (−|ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) |) electron φ
|) electron φ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )e−i|ε
)e−i|ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) |(−t) is indistinguishable from that of a positive energy (|ε
|(−t) is indistinguishable from that of a positive energy (|ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) |) positronφC
|) positronφC![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )e−i|ε
)e−i|ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) |t, i.e.,
|t, i.e., 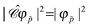 . Because of this feature, negative energy electrons can be regarded as mirror images of positive energy positrons propagating in opposite direction and time.
. Because of this feature, negative energy electrons can be regarded as mirror images of positive energy positrons propagating in opposite direction and time.
As any operator must be expanded in a complete basis consisting of both the PES and NES of the same equation, we ought to write the field operator ϕ(x) in the interaction representation as
| | ϕ(x) = bpφp(x) + d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) φ φ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (x) (x) | (73) |
| | = bpφp(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )e−iεpt + d )e−iεpt + d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) φ φ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )e−iε )e−iε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) t, t, | (74) |
where
bp (
bp) annihilates (creates) an electron of positive energy
εp, whereas
d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif)
(
d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif)
) creates (annihilates) a
positron of positive energy |
ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif)
| = −
ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif)
.
That the operator d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (instead of d
(instead of d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) ) must accompany bp is required by charge conservation. Both bp and d
) must accompany bp is required by charge conservation. Both bp and d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) increase the charge of a state by one unit; bp does this by destroying an electron whereas d
increase the charge of a state by one unit; bp does this by destroying an electron whereas d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) does this by creating a positron. Thus the field operator ϕ(x) always increases one unit of charge. Similarly, the field operator ϕ†(x) always decreases one unit of charge. Therefore, the operator ϕ†(x)ϕ(x) conserves the charge. Had d
does this by creating a positron. Thus the field operator ϕ(x) always increases one unit of charge. Similarly, the field operator ϕ†(x) always decreases one unit of charge. Therefore, the operator ϕ†(x)ϕ(x) conserves the charge. Had d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) been chosen to accompany bp, the operator ϕ†(x)ϕ(x) would not conserve the charge: It would include terms like bpd
been chosen to accompany bp, the operator ϕ†(x)ϕ(x) would not conserve the charge: It would include terms like bpd![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) and d
and d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) bp which decrease and increase two units of charge, respectively.
bp which decrease and increase two units of charge, respectively.
To further understand the particular form of the field operator (73), we may generalize the charge conjugation transformation (70) to field theory by introducing a unitary operator 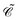 , which transforms the field ϕ(x) as
, which transforms the field ϕ(x) as
| | 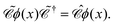 | (75) |
The distinctions between
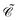
and
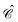
are as follows. Just like a rotation operation in point group theory, the
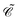
operator is unitary and acts only on the
b and
d operators but not on the functions
φp(
x). In contrast, as a product between the unitary matrix
UC and the complex conjugation
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) 0
0, the
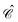
operator
(70) is anti-unitary and acts also on the functions. Spelling out the left and right hand sides of
eqn (75) leads to
| | 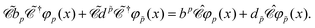 | (76) |
In the case of free particles, where
φp represent a PES of momentum
![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif)
and spin projection
s while
φ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif)
represent a NES of momentum −
![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif)
and spin projection −
s, the following identities can be obtained:
| | 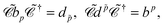 | (77) |
| | 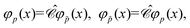 | (78) |
showing that
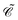
interchanges particles and antiparticles of the same momentum
![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif)
and spin projection
s,
viz.,
| | 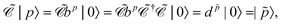 | (79) |
| | 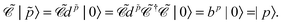 | (80) |
The charge conjugation symmetry is of course broken by any external potential. However, what really matters is that annihilation operators must go with PES whereas creation operators must go with NES in order for field theory to describe only PES states. That is, electronic NES should still be employed as a basis to describe real positrons even if the charge conjugation symmetry no longer holds. This leads to the same spectrum as the previous FS formalism starting with the filled Dirac picture (see the rightmost part of Fig. 2). At this moment it deserves to be mentioned that the charge conjugation transformation 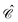 proceeds through Kramers pairs (φp and
proceeds through Kramers pairs (φp and 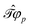 ) thanks to the simple relationship23 between
) thanks to the simple relationship23 between 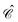 and the time reversal operator
and the time reversal operator 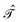 , i.e.,
, i.e., 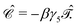
Having prepared the above background, we now follow the S-matrix formulation40 of QED to calculate up to second order energies. The relevant Feynman diagrams are given in Fig. 3, where a double line between two interaction vertices represents the bound state Feynman propagator SF defined algebraically as a Wick time-ordered contraction, viz.,
| | | SF(x2,x1) = −i〈0|T[ϕ(x2)ϕ†(x1)]|0〉 | (81) |
| | | = −i〈0|Θ(t2 − t1)ϕ(x2)ϕ†(x1) − Θ(t1 − t2)ϕ†(x1)ϕ(x2)|0〉 | (82) |
| | = −i{Θ(t2 − t1)φp(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2)φ†p( 2)φ†p(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1)e−iεp(t2−t1) − Θ(t1 − t2)φ 1)e−iεp(t2−t1) − Θ(t1 − t2)φ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2)φ† 2)φ†![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1)e−iε 1)e−iε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (t2−t1)}. (t2−t1)}. | (83) |
The last line shows clearly that the PES, associated with the Heaviside function Θ(
t2 −
t1) , propagate forward in time, while the NES, associated with Θ(
t1 −
t2), propagate backward in time. At first glance, the latter sounds very strange but is plausible if we can turn the direction of motion around and think of an electron–
positron pair being created at time
t2 and annihilated at a later time
t1. Therefore, the idea that NES propagate backward in time actually enables us to reinterpret them as
positrons of positive energy propagating forward in time. This has been achieved mathematically by charge conjugation as outlined above. By analytical continuation the propagator can be written as an integral in the complex plane
| | 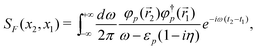 | (84) |
where the implicit summation over index
p is now understood to include both
PES and NES. The correct ordering of times, previously associated with the Θ functions, is now assured by the signs of the
iηεp terms or equivalently the locations of the poles of the propagator,
i.e., the positive energy pole in the lower half plane and the negative energy pole in the upper half plane.
Since the primary interest here is the contributions of NES to correlation mediated by the instantaneous Coulomb interaction, we only need to introduce the Coulomb photon propagator in the Coulomb gauge
| | 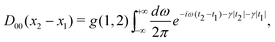 | (85) |
where adiabatic damping factors have been introduced to turn on and off the interaction. Note in passing that the instantaneous Breit term can also be included here although it formally arises from the zero frequency limit of the transverse
photon propagator. A plausible argument for this choice is that it can also be derived in a semiclassical manner. The adiabatically damped counter term −
U in the perturbation
V (12) reads
| | t(x) = −U(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )e−γ|t|, )e−γ|t|, | (86) |
which is represented by a hatched circle in the Feynman diagrams. The Sucher expression
41 of the adiabatic
S-matrix can then be employed to calculate the energy shifts to the unperturbed state |α〉 = Π
Nibi|0〉 of energy
E(0) (see
eqn (15) and
Fig. 3(a)). The first order energy
E(1), corresponding to
Fig. 3(b) and (c), is the same as
eqn (16). The second order energy
E(2) consists of contributions from all the remaining diagrams in
Fig. 3. In particular,
Fig. 3(d) (ladder, L) and (e) (crossed ladder, X) correspond respectively to the uncrossed and crossed two Coulomb
photons. After some straightforward manipulations (see
ref. 42 for more details) we get the following results for the ladder
| | 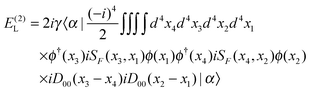 | (87) |
| | 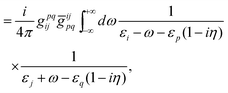 | (88) |
and the crossed ladder
| | 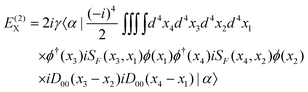 | (89) |
| | 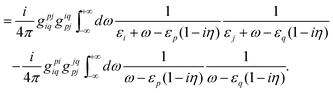 | (90) |
Because of the locations of the poles, only the “++” and “−−” combinations of the intermediates contribute to
E(2)L, whereas only the “+−” combinations contribute to
E(2)X. The results can be organized as
| | | E(2)L = E(2)L,1+ + E(2)L,1++ + E(2)L,−−, | (91) |
| | 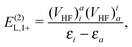 | (92) |
| | 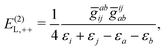 | (93) |
| | 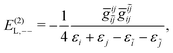 | (94) |
| | 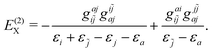 | (95) |
It is somewhat surprising that the QED literature (
e.g.,
ref. 18) has only documented specific expressions for few-electron systems, from which the general
expressions (88) and (90) to (95) cannot be obtained.
As for the counter Hamiltonian (86), Fig. 3(f) and its complex conjugate (g) give rise to
| | 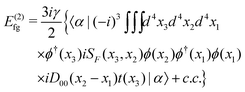 | (96) |
| | 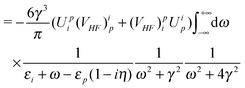 | (97) |
| | | = E(2)fg,1+ + E(2)fg,1−, | (98) |
| | 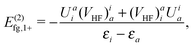 | (99) |
| | 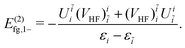 | (100) |
Likewise,
Fig. 3(h) leads to
| | | E(2)h = iγ〈α∣(−i)2∫∫d4x2d4x1 × ϕ†(x2)iSF(x2,x1)ϕ(x1)t(x2)t(x1)∣α〉 | (101) |
| | 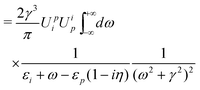 | (102) |
| | | = E(2)h,1+ + E(2)h,1−, | (103) |
| | 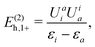 | (104) |
| | 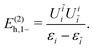 | (105) |
The one-body terms in
(92),
(98) and
(103) can be regrouped as
| | | E(2)QED,1+ = E(2)CS,1+, | (106) |
| | 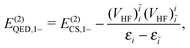 | (107) |
with
E(2)CS,1+ and
E(2)CS,1− given in
eqn (20) and (21), respectively.
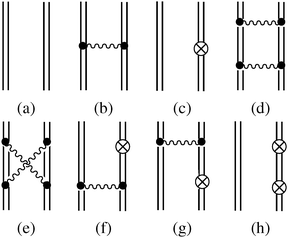 |
| | Fig. 3 Feynman diagrams associated with the zeroth (a), first (b, c), and second (d–h) order energy. | |
The results obtained so far can be summarized as follows.
(I) The CS, FS and QED approaches agree with each other only for the energy components involving the PES manifold, including the zeroth order E(0)(15), first order E(1)(16), and second order E(2)++ (see E(2)CS,++(23), E(2)FS,++(58) and E(2)L,++(93)). Such an agreement holds for arbitrary orders.
(II) As for the energy components involving the NES manifold, the three approaches differ from each other in both the one- and two-body terms. In the Fuzzy picture, i.e., U = VHF, the one-body terms E(2)CS,1+(20) and E(2)CS,1−(21) both vanish in CS but the last two terms of E(2)FS,1−(56) and the second term of E(2)QED,1−(107) still survive in FS and QED, respectively. What is more intriguing is that the QED term E(2)L,−−(94) differs by a negative sign from the corresponding CS term E(2)CS,−−(24) (or the FS term E(2)FS,−−(60)). The former is correlating whereas the latter is “anti-correlating”. It has been demonstrated18 that, for helium-like systems, E(2)X(95) is positively valued such that the total contributions of NES are still “anti-correlating”, notwithstanding that E(2)L,−−(94) is correlating. In particular, it is the terms E(2)fg,1−(100) and E(2)h,1−(105) arising from the counter Hamiltonian (86) that are mainly responsible for removing the potential dependence of the no-pair energy composed of E(2)L,1+(92) and E(2)L,1++(93). Instead, the sum of E(2)L,1−−(94) and E(2)X(95) is virtually potential independent. This might suggest a pragmatic ansatz, where the no-pair energy is to be corrected by the simple one-body counter terms involving the NES for ensuring potential independence. All beyond this can then be ascribed to QED corrections.
(III) It is interesting to note that, if iηεp was set to iη in eqn (84) regardless of the sign of εp, one would ‘recover’ the CS approach. That is, E(2)L,−− would equal to E(2)CS,−− and the term E(2)X(95) would vanish. This amounts to rewriting the electron propagator (81) as
| | ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) F(x2,x1) = −i〈0|T[ϕ(x2)ϕ†(x1)]|0〉 F(x2,x1) = −i〈0|T[ϕ(x2)ϕ†(x1)]|0〉 | (108) |
| | | = −iΘ(t2 − t1)〈0|ϕ(x2)ϕ†(x1) + ϕ†(x1)ϕ(x2)|0〉, | (109) |
which is completely unphysical. Therefore, irrespective of its Hermiticity or bounds discussed in Section 2.1, the previous numerical assessments
27–31 of the CS DCB Hamiltonian are pointless. Rather unexpectedly, we find no ‘mechanism' to go from QED back to FS, given the fact that they share the same working space (see the rightmost part of
Fig. 2) and the same interpretation of the NES. In the first place, QED is intrinsically time dependent whereas the FS formalism is time independent, but we have seen that the direction of time flow is an essential ingredient: In relativistic quantum mechanics we must allow time to flow backwards. It is a general standpoint that a time (or frequency) dependent treatment of particles and antiparticles is mandatory, even if the target (two-particle) property is formally time independent. This can further be understood as follows. The system of electrons is a closed and stationary system under the no-pair approximation and can hence be treated with both time dependent and time independent approaches. However, upon lifting the PES projection, the number of electrons is no longer conserved and the system becomes hence an open and non-stationary subsystem coupled to the negative energy sea, just like the well-known Schrödinger cat entangled with the environment. A time dependent treatment is hence necessary, particularly because the positive and negative energy electrons propagate in opposite directions in both space and time. This feature has tacitly been assumed in QED (through the electron propagator
(84), a Wick time-ordered contraction
(81)) but not in the (no-
photon and no-time) FS approach. Moreover, it is the sum of
E(2)L(91) and
E(2)X(95) that is gauge invariant but the latter is, by construction, missed by the FS approach. Therefore, it can be concluded that it is only safe to leave the negative energy cat in the hands of QED.
(IV) The term ‘no-pair approximation’ has been employed as an effective means in the CS approach to avoid the BRD or convergence problems encountered in multiconfiguration Dirac–Fock calculations43 or regarded as an approximation to the FS Hamiltonian. This is rather unfortunate for if it were merely an approximation, the inclusion of virtual pairs would lead to the correct result. Since this is not the case, it had better be replaced with ‘non-QED approximation’ for conceptual consistency. In other words, one should work with either the no-pair approximation (possibly corrected for ensuring potential dependence, see above) or QED, not anything in between.
(V) As only QED provides the correct prescription for the contributions of NES to correlation, one can in practice think of the following ansatz
| | | E = EHLNPP,++(valence) + E(2)QED,+−(core′) + EPTQED, | (110) |
where the first term stands for a high-level treatment of valence electrons within the PES manifold (see Section 2.4), the second term for the second order QED treatment (
i.e.,
E(2)L +
E(2)X +
E(2)fg +
E(2)h) of core–core and core–valence electrons involving both the PES and NES manifolds, whereas the third term for a perturbative treatment of effects due to retardation, recoil, and quantization of the electromagnetic field. It is the second term that will eliminate the often mentioned
31,39 intrinsic uncertainty of order (Z
α)
3 in the eigenenergies of the DC or DCB equation. It has been considered in accurate nonrelativistic QED calculations of light atoms
44 but not in relativistic QED calculations of heavy atoms.
19 Note that, to be internally consistent, the last two terms are either both included or both neglected as they are of the same leading order of magnitude.
2.4 Relativistic explicitly correlated methods: The extended no-pair projection
Non-relativistic quantum chemistry has in the last years witnessed fast progress in explicitly correlated methods, where the conventional expansion of the wave function in terms of antisymmetrized orbital products (Slater determinants) is augmented by a small number of r12-dependent two-electron basis functions (geminals). A particular stimulus for the development is the Slater-type correlation factor| | 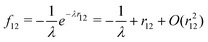 | (111) |
introduced by Ten-no.45 Attempts toward scalar relativistic explicitly correlated R12 methods have also been made recently by Bischoff et al.46 However, none of the recipes proposed therein is really useful for heavy elements. The reason is that integrals like 〈pq|ĥrelf12|rs〉 and 〈pq|f12ĥrelf12|rs〉 must be evaluated analytically to achieve fast convergence, but the required operator ĥrel is not available in the algebraic no-pair Hamiltonian (39) or its two-component counterpart. More seriously, just like any second-quantized Hamiltonian, the no-pair Hamiltonian has only a finite spectrum defined by the given basis such that the effect of the correlation factor f12 is just null. To really incorporate the correlation factor, one ought to pick up the original CS Hamiltonian (1) alongside a carefully designed two-electron projection operator Q12. To see this more clearly, we decompose the identity operator as| | 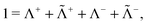 | (112) |
where Λ+ and Λ− are the PES and NES projectors defined by a given basis while 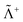 and
and 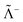 are the respective complements. The
are the respective complements. The 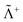 subspace is to be simulated by Q12f12|0〉 but the whole NES subspace has to be projected out explicitly. However,
subspace is to be simulated by Q12f12|0〉 but the whole NES subspace has to be projected out explicitly. However, 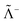 is inaccessible, meaning that the contaminations of NES cannot strictly be avoided. To minimize such contaminations we propose to construct ‘dual basis projectors’, i.e., Λ+L and Λ−L with a large basis set (BasL) and Λ+S and Λ−S with a subset (BasS) of BasL. We then assume that the residual
is inaccessible, meaning that the contaminations of NES cannot strictly be avoided. To minimize such contaminations we propose to construct ‘dual basis projectors’, i.e., Λ+L and Λ−L with a large basis set (BasL) and Λ+S and Λ−S with a subset (BasS) of BasL. We then assume that the residual 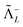 is negligible and that conventional correlation is to be carried out within the Λ+S subspace. Such a partitioning of the complete configuration space is depicted in Fig. 4, which gives rise to the following definition of Q12
is negligible and that conventional correlation is to be carried out within the Λ+S subspace. Such a partitioning of the complete configuration space is depicted in Fig. 4, which gives rise to the following definition of Q12| | 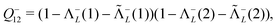 | (114) |
| | | ≈(1 − Λ−L(1))(1 − Λ−L(2)), | (115) |
| | | Q+12 = (1 − Λ+S(1))(1 − Λ+S(2)), | (116) |
where Q−12(115) projects out essentially the whole NES space while Q+12 further projects out the ‘active’ PES subspace within which the conventional correlation is performed. Although there is no degree of freedom left with Q−12, other choices of Q+12 are possible, e.g.,| | | Q+12 = (1 − O+S(1))(1 − O+S(2))(1 − V+S(1)V+S(2)), | (117) |
where O+S and V+S are projectors onto the occupied and virtual PES defined by BasS. This Q+12(117) ensures strong orthogonality to the reference and orthogonality to the conventional products of virtual PES.
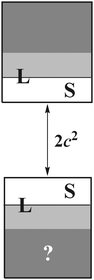 |
| | Fig. 4 Partition of the complete configuration space for explicit correlation. L/S: subspace spanned by a large/small basis. The question-marked area cannot be projected out by Q12. | |
In practice, the required projector Λ−L can be obtained as follows. If the molecular mean-field calculation with BasL is affordable, both Λ−L and Λ+S can readily be constructed. Otherwise, the molecular mean-field calculation can first be done with BasS. After convergence, the Fock matrix over BasL is constructed and diagonalized. The eigenvectors are then employed to construct the Λ−L. Alternatively, the Λ−L can simply be approximated as the superposition of the atomic ones in the spirit of “from atoms to molecule”.3,4 As a matter of fact, due to the large energy gap between the occupied orbitals and the NES, the differential effects between Λ−L and Λ−S may be so small that Λ−L can simply be replaced with Λ−S. Then, only a single basis set is needed. Anyhow, any approximations to two-electron integrals involving the small components would bring in some effects of NES.
With the so-defined projectors we can write, e.g., the CI wave function as
| | 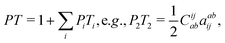 | (120) |
| | 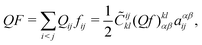 | (121) |
where the coefficients
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ijkl
ijkl may be fixed by symmetry argument as done in the nonrelativistic case.
45 The
P and
Q projectors in the wave
function (118) can likewise be folded into the first-quantized Hamiltonian
HCS(1), leading to an
extended no-pair Hamiltonian
| | 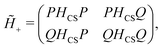 | (122) |
which acts on the unprojected many-electron basis functions
T|0〉 and
F|0〉 and is independent of the wave function ansatz. This is an important generalization of the original no-pair Hamiltonian
(39) which is otherwise incompatible with explicitly correlated methods. Note in passing that the present
extended no-pair projection is conceptually different from the one
47 formed by the positive energy part of the CCR spectrum of the core Hamiltonian, the first term of
eqn (1). The former works with the original Hamiltonian
(1) and is hence closely parallel to nonrelativistic explicitly correlated methods whereas the latter invokes the CCR Hamiltonian.
For a first implementation of the above idea, one may take only the spin-free part of the DC Hamiltonian, which is a two-component scalar relativistic Hamiltonian in the spirit of the ‘modified Dirac equation’.48,49 The spin–orbit effects can then be accounted for at a lower level of theory. The basis of this hybrid is the short-range and quasi-one-particle nature of spin–orbit operators. That is, the cross terms between spin–orbit coupling and electron correlation are not of very high orders.
3 The role of NES in one-electron properties
The previous analysis shows that neither the CS nor the FS approach agrees with QED on the contributions of NES to electron correlation (and other two-electron properties in general), a remaining question is what happens in the case of a one-electron perturbation. Very fortunately, the three approaches agree with each other up to arbitrary orders in this case such that the simplest CS approach can be adopted.
Consider a perturbation v on a non-interacting system. The first three order energies are found to be
| | 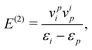 | (124) |
| | 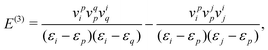 | (125) |
where the implicit summation over
p includes both
PES and NES.
There is a simple application of these results, viz., the perturbation expansion50 of the energy ε(Z) of a hydrogenic ion with the nuclear charge perturbed from Z to Z + Z′. This model can be solved exactly by a Taylor expansion of ε(Z)
| | 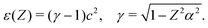 | (126) |
The results read
| | | ε(Z + Z′) = ε(Z) + ε1(Z)Z′ + ε2(Z)Z′2 + ε3(Z)Z′3 +…, | (127) |
| | 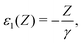 | (128) |
| | 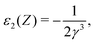 | (129) |
| | 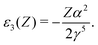 | (130) |
To use the general expressions (123) to (125) for the present model, one can just set v = −1/r and restrict the indices i and j to the 1s orbital. The results for Z up to 100 are given in Table 2, where the contributions of NES are explicitly documented. A least-squares fitting reveals that E(2)− scales roughly as Z3 for Z > 60. As Z is always accompanied by α, it is anticipated that E(2)− should scale grossly as (Zα)3, at variance with the leading order of (Zα)4. This can actually be confirmed by an analytical analysis: Taking the nonrelativistic limit of the hydrogenic function φ1s and the plane wave representation of the NES, one can find that E(2)− is indeed proportional to (Zα)3 after integration over the wave vectors. This result is in line with the order of magnitude of the contributions of NES to electron correlation.30,31 The E(3)−− in Table 2 denotes two virtual NES while E(3)+− denotes one virtual PES and one virtual NES in the summations (125). Least-squares fittings reveal that both E(3)+− and E(3)−− also scale roughly as Z3 for Z > 60. The contributions of NES to NMR parameters described by odd (off-diagonal) operators are even more significant as elucidated before.13–16
Table 2 Perturbed hydrogenic 1s state. The exponents of the restricted kinetically balanced s-Gaussian functions are ηi = 10−5 × 1.72i−1, i = 1,…,120. For Z = 100, this basis set can reproduce the exact second (129) and third (130) order energies up to the 11th and 7th decimal places, respectively
|
Z
|
E
(1)
|
E
(2)
|
E
(2)+
|
E
(2)−
|
| 10 |
−10.0267324 |
−0.5040206 |
−0.5041258 |
0.0001052 |
| 20 |
−20.2164698 |
−0.5164115 |
−0.5170541 |
0.0006425 |
| 30 |
−30.7458110 |
−0.5382252 |
−0.5399916 |
0.0017663 |
| 40 |
−41.8212905 |
−0.5714553 |
−0.5750227 |
0.0035674 |
| 50 |
−53.7022668 |
−0.6194950 |
−0.6256552 |
0.0061602 |
| 60 |
−66.7369382 |
−0.6880422 |
−0.6977764 |
0.0097342 |
| 70 |
−81.4246208 |
−0.7869427 |
−0.8015599 |
0.0146172 |
| 80 |
−98.5335792 |
−0.9342278 |
−0.9556214 |
0.0213935 |
| 90 |
−119.347864 |
−1.1659674 |
−1.1971327 |
0.0311653 |
| 100 |
−146.256615 |
−1.5642874 |
−1.6105179 |
0.0462305 |
|
Z
|
E
(3)
|
E
(3)++
|
E
(3)−−(×10−5) |
E
(3)+−
|
| 10 |
−0.0002698 |
−0.0002981 |
−0.02466 |
0.0000286 |
| 20 |
−0.0005619 |
−0.0006441 |
−0.15105 |
0.0000837 |
| 30 |
−0.0009031 |
−0.0010498 |
−0.40887 |
0.0001507 |
| 40 |
−0.0013306 |
−0.0015514 |
−0.80707 |
0.0002288 |
| 50 |
−0.0019027 |
−0.0022119 |
−1.35754 |
0.0003227 |
| 60 |
−0.0027197 |
−0.0031408 |
−2.08656 |
0.0004420 |
| 70 |
−0.0039690 |
−0.0045429 |
−3.04653 |
0.0006043 |
| 80 |
−0.0060375 |
−0.0068370 |
−4.33660 |
0.0008428 |
| 90 |
−0.0098266 |
−0.0109928 |
−6.14907 |
0.0012277 |
| 100 |
−0.0178187 |
−0.0196595 |
−8.89084 |
0.0019297 |
As shown by the SOS expressions (124) and (125), neglecting the contributions of NES to one-electron properties is simply a truncation of the basis composed of both PES and NES. Yet, in the parlance of FS or QED, this is precisely the no-pair approximation. Likewise, in mean-field calculations with the empty Dirac picture, the rotations between the occupied PES and virtual NES can be called either orbital relaxation or pair creation effects. Neglecting such orbital rotations (pair creations) results always in energy lowering.
4 Conclusions and outlook
As an attempt to bridge the gap between relativistic quantum chemistry and QED, the distinctions between the DC/DCB-based no-photon-no-time CS and FS formulations of relativistic quantum chemistry as well as the with-photon-with-time QED approach for electronic structure and properties have carefully been addressed. Although they agree with each other on electron correlation within the PES manifold as well as one-electron properties involving both the PES and NES manifolds, there is no consensus among the three approaches on the contributions of NES to electron correlation. In this regard, only QED, but neither CS nor FS, provides the correct prescription. The previous numerical assessments of the CS Hamiltonian (associated with the empty Dirac picture), as well as the formal arguments in favor of the FS formalism (associated with the filled Dirac picture), are hence pointless. In essence, a time dependent treatment of particles and antiparticles is mandatory even if the target (two-particle) property is formally time independent. On the other hand, it can be argued that the contributions of NES to correlation and the leading order radiative QED corrections (Lamb shift) are either both neglected or both included as they are of the same leading order of magnitude. Since both of them come from the atomic cores, it may well be possible to derive some local or semi-local potential to simplify their calculations.
The above arguments essentially mean that one should work either with the no-pair approximation (which has an intrinsic error of order (Zα)3) or with QED. Whether there exists an intermediate relativistic many-electron theory remains an open question.
Staying within the no-pair approximation, the major challenge is still the slow convergence of the determinant-based expansions of the wavefunction. Explicitly correlated methods do help but an extended no-pair projection of the first-quantized DC/DCB Hamiltonian has to be introduced for doing so. The spin-free counterpart can readily be implemented into a nonrelativistic code that already contains some explicitly correlated methods. Nonetheless, the behavior of the relativistic wave function at the coalescence of two electrons remains to be uncovered. For this purpose, the ‘Dirac spherium’ (i.e., two Dirac electrons on a sphere), particularly its spin-free counterpart, may be taken as a good start, in analogy with the ‘Schrödinger spherium’.51 Yet, it remains difficult, if not impossible, to adapt algebraic two-component Hamiltonians to explicitly correlated methods.
Notably, the known X2C Hamiltonians have all been derived from the parent Dirac equation with the restricted kinetic balance incorporated either explicitly or implicitly.6 It is worthwhile to reformulate them in terms of the dual kinetic balance24 for it furnishes full variational safety.23 Moreover, at variance with such a ‘top down' reduction, one may wonder if there exists a ‘bottom up' procedure, in the context of relativistic Hamiltonian dynamics, to build up such Hamiltonians without recourse to the Dirac equation.
As for magnetic properties such as NMR shielding, problems associated with the ‘missing' relativistic diamagnetism have only been understood rather recently52 (for a recent review see ref. 53). How to combine the idea of magnetic balance with gauge invariant correlated wave function methods, with or without the no-pair approximation, remains to be explored. Another important observable is the nuclear spin-rotation (NSR) constant. Its nonrelativistic formulation54,55 has been in existence for more than six decades but the relativistic counterpart is still missing. According to the unpublished work by Y. Xiao and the present author, there is no direct relationship between the NSR constant and the NMR shielding in the relativistic regime, although they are related in a simple way in the nonrelativistic limit. The implications of such findings deserve great attention. Moreover, there has been little attempt to solve the Dirac equation in the presence of a strong magnetic field. In this regard, the combination of magnetic balance and dual kinetic balance (i.e., ‘dual magnetic balance’53) could be very rewarding.
Finally, it deserves to be mentioned that modern two-component relativistic Hamiltonians, as well as the novel reformulations of magnetic properties, have been developed by chemists instead of physicists. They are not known to the community of computational physics. It would be nice if such relativistic theories could be exported back to where they come from.
Acknowledgements
The research of this work is supported by the National Natural Science Foundation of China (Project No. 21033001).
Notes and references
- M. Quack, J. Sohner and M. Willeke, Annu. Rev. Phys. Chem., 2008, 59, 741–769 CrossRef CAS.
- The generic acronym “X2C” (pronounced as “ecstasy”) for exact two-component Hamiltonians resulted from intensive discussions among H. J. A. Jensen, W. Kutzelnigg, W. Liu, T. Saue and L. Visscher during the Twelfth International Conference on the Applications of Density Functional Theory (DFT-2007), Amsterdam, 26–30 August, 2007. Note that the “exact” here means only that all the solutions of the Dirac-based Hamiltonian can be reproduced up to machine accuracy. It is particularly meaningful when compared with finite order quasirelativistic theories.
- W. Liu and D. Peng, J. Chem. Phys., 2006, 125, 044102 CrossRef; W. Liu and D. Peng, J. Chem. Phys., 2006, 125, 149901 CrossRef.
- D. Peng, W. Liu, Y. Xiao and L. Cheng, J. Chem. Phys., 2007, 127, 104106 CrossRef.
- R. E. Stanton and S. Havriliak, J. Chem. Phys., 1984, 81, 1910–1918 CrossRef CAS.
- W. Liu, Mol. Phys., 2010, 108, 1679–1706 CrossRef CAS.
- K. G. Dyall, J. Chem. Phys., 1997, 106, 9618–9626 CrossRef CAS.
- W. Kutzelnigg and W. Liu, J. Chem. Phys., 2005, 123, 241102 CrossRef.
- M. Iliaš and T. Saue, J. Chem. Phys., 2007, 126, 064102 CrossRef.
- W. Liu and D. Peng, J. Chem. Phys., 2009, 131, 031104 CrossRef.
- Q. Sun, W. Liu, Y. Xiao and L. Cheng, J. Chem. Phys., 2009, 131, 081101 CrossRef.
- T. Fleig, Chem. Phys., 2011 DOI:10.1016/j.chemphys.2011.06.032 , in press.
- Y. Xiao, D. Peng and W. Liu, J. Chem. Phys., 2007, 126, 081101 CrossRef.
- Y. Xiao, W. Liu, L. Cheng and D. Peng, J. Chem. Phys., 2007, 126, 214101 CrossRef.
- L. Cheng, Y. Xiao and W. Liu, J. Chem. Phys., 2009, 130, 144102 CrossRef.
- L. Cheng, Y. Xiao and W. Liu, J. Chem. Phys., 2009, 131, 244113 CrossRef.
- S. Komorovsky, M. Repisky, O. L. Malkina, V. G. Malkin, I. M. Ondk and M. Kaupp, J. Chem. Phys., 2008, 128, 104101 CrossRef.
- J. Sapirstein, K. T. Cheng and M. H. Chen, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 259–266 CrossRef CAS ; a negative sign was missed in eqn (21) therein.
- C. Thierfelder and P. Schwerdtfeger, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 062503 CrossRef.
- G. Hardekopf and J. Sucher, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 30, 703–711 CrossRef.
- W. H. Furry, Phys. Rev., 1951, 81, 115–124 CrossRef.
- M. H. Mittelman, Phys. Rev. A: At., Mol., Opt. Phys., 1981, 24, 1167–1175 CrossRef.
- Q. Sun, W. Liu and W. Kutzelnigg, Theor. Chem. Acc., 2011, 129, 423–436 CrossRef CAS.
- V. M. Shabaev, I. I. Tupitsyn, V. A. Yerokhin, G. Plunien and G. Soff, Phys. Rev. Lett., 2004, 93, 130405 CrossRef CAS.
- G. E. Brown and D. G. Ravenhall, Proc. R. Soc. London, Ser. A, 1951, 208, 552–559 CrossRef CAS.
-
B. Thaller, The Dirac Equation, Springer-Verlag, Berlin, 1992, pp. 114, 130, & 298–299 Search PubMed.
- R. Júregui, C. Bunge and E. Ley-Koo, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 55, 1781–1784 CrossRef.
- Y. Watanabe, H. Nakano and H. Tatewaki, J. Chem. Phys., 2007, 126, 174105 CrossRef.
- Y. Watanabe, H. Nakano and H. Tatewaki, J. Chem. Phys., 2010, 132, 124105 CrossRef.
- G. Pestka, M. Bylicki and J. Karwowski, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, 2979–2987 CrossRef CAS.
- G. Pestka, M. Bylicki and J. Karwowski, J. Phys. B: At., Mol. Opt. Phys., 2007, 40, 2249–2259 CrossRef CAS.
- J. Sucher, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 348–362 CrossRef CAS; J. Sucher, Int. J. Quantum Chem., 1984, 25, 3–21 CrossRef.
- P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1931, 133, 60–72 CrossRef.
- C. D. Anderson, Phys. Rev., 1932, 41, 405–421 CrossRef CAS.
- P. Chaix and D. Iracane, J. Phys. B: At., Mol. Opt. Phys., 1989, 22, 3791–3814 CrossRef.
- P. Chaix, D. Iracane and P. L. Lions, J. Phys. B: At., Mol. Opt. Phys., 1989, 22, 3815–3828 CrossRef.
-
T. Saue and L. Visscher, in Theoretical Chemistry and Physics of Heavy and Superheavy Elements, ed. U. Kaldor and S. Wilson, Kluwer Academic, Dordrecht, 2003, p. 211 Search PubMed.
-
E. Eliav and U. Kaldor, in Relativistic Methods for Chemists, ed. M. Barysz and Y. Ishikawa, Springer, Dordrecht, 2010, pp. 279–349 Search PubMed.
- W. Kutzelnigg, Chem. Phys., 2011 DOI:10.1016/j.chemphys.2011.06.001 , in press.
- P. J. Mohr, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 1949–1957 CrossRef CAS.
- J. Sucher, Phys. Rev., 1957, 107, 1448–1449 CrossRef CAS.
- S. A. Blundell, P. J. Mohr, W. R. Johnson and J. Sapirstein, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 48, 2615–2626 CrossRef CAS.
- P. Indelicato and J. P. Desclaux, Phys. Scr., 1993, T46, 110–114 CrossRef CAS.
- J. Komasa, K. Piszczatowski, G. Lach, M. Przybytek, B. Jeziorski and K. Pachucki, J. Chem. Theor. Comput., 2011, 7, 3105–3115 CrossRef CAS.
- S. Ten-no, J. Chem. Phys., 2004, 121, 117–129 CrossRef CAS; S. Ten-no, Chem. Phys. Lett., 2004, 398, 56–61 CrossRef.
- F. A. Bischoff, E. F. Valeev, W. Klopper and C. L. Janssen, J. Chem. Phys., 2010, 132, 214104 CrossRef.
- M. Bylicki, G. Pestka and J. Karwowski, Phys. Rev. A, 2008, 77, 04450 CrossRef.
- W. Kutzelnigg, Int. J. Quantum Chem., 1984, 25, 107–129 CrossRef CAS.
- K. G. Dyall, J. Chem. Phys., 1994, 100, 2118–2127 CrossRef CAS.
- I. P. Grant and H. M. Quiney, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 62, 022508 CrossRef.
- P.-F. Loos and P. M. W. Gill, Phys. Rev. Lett., 2009, 103, 123008 CrossRef.
- W. Kutzelnigg and W. Liu, J. Chem. Phys., 2009, 131, 044129 CrossRef.
- Y. Xiao, Q. Sun and W. Liu, Theor. Chem. Acc., 2011 Search PubMed , in press.
- G. C. Wick, Phys. Rev., 1948, 73, 51–57 CrossRef CAS.
- N. F. Ramsey, Phys. Rev., 1950, 78, 699–703 CrossRef CAS.
Footnotes |
| † The term ‘negative energy cat’ is introduced here to draw a loose analogy with the Schrödinger cat. Both appear mysterious (at least at first glance) and demand proper time dependent treatments. |
| ‡ Strictly speaking, one should not speak of ‘no-pair approximation’ here, since the CS Hamiltonian preserves the number of electrons such that virtual pairs never arise. It is more appropriate to use ‘positive energy state projection’ or simply ‘basis set truncation’ as an equivalent of ‘no-pair approximation’. |
|
| This journal is © the Owner Societies 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. 

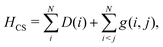
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) ·
·![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) + βmc2,
+ βmc2,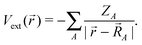
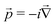 the linear momentum operator, and
the linear momentum operator, and ![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) and β the usual 4 × 4 Dirac matrices. The two-electron interaction g(1,2) in the Coulomb gauge takes the following form:
and β the usual 4 × 4 Dirac matrices. The two-electron interaction g(1,2) in the Coulomb gauge takes the following form: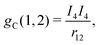
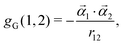
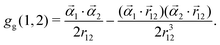
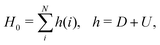
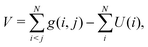
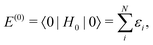
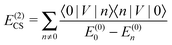
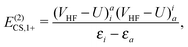
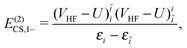
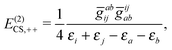
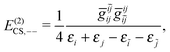
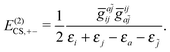
![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) ,…} for the unoccupied NES. Unspecified orbitals are denoted as {p,q,r,s}. When necessary, NES will explicitly be designated by {
,…} for the unoccupied NES. Unspecified orbitals are denoted as {p,q,r,s}. When necessary, NES will explicitly be designated by {![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) ,
,![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) ,
,![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) ,
,![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) }. The above one- and two-electron integrals are defined as
}. The above one- and two-electron integrals are defined as![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 3φp†(
3φp†(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )h(
)h(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )φq(
)φq(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ),
),![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 31d
31d![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 32φp†(
32φp†(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1)φq†(
1)φq†(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2)g(1,2)φr(
2)g(1,2)φr(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1)φs(
1)φs(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2),
2), rspq = grspq − gsrpq = grspq − grsqp.
rspq = grspq − gsrpq = grspq − grsqp.![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) = εj − |X|, the denominator would vanish and there exist an infinite number of such “+−” intermediates. This kind of instability of many-electron systems was first discussed by Brown and Ravenhall25 and is usually called the continuum dissolution problem or simply the Brown–Ravenhall disease (BRD). A direct deduction made was that the many-electron DC Hamiltonian (1) has no bound states and even its discrete states are characterized by complex energies and are hence resonances of finite life times. This further implies that the DC Hamiltonian is not self-adjoint (Hermitian). If one knows that the one-electron Dirac operator D itself is essentially self-adjoint on the dense domain C∞0(
= εj − |X|, the denominator would vanish and there exist an infinite number of such “+−” intermediates. This kind of instability of many-electron systems was first discussed by Brown and Ravenhall25 and is usually called the continuum dissolution problem or simply the Brown–Ravenhall disease (BRD). A direct deduction made was that the many-electron DC Hamiltonian (1) has no bound states and even its discrete states are characterized by complex energies and are hence resonances of finite life times. This further implies that the DC Hamiltonian is not self-adjoint (Hermitian). If one knows that the one-electron Dirac operator D itself is essentially self-adjoint on the dense domain C∞0(![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3\{O})4 (i.e., the space of infinitely differentiable functions with compact support of the field of triples of real numbers excluding the origin) and self-adjoint on the first Sobolev space H1(
3\{O})4 (i.e., the space of infinitely differentiable functions with compact support of the field of triples of real numbers excluding the origin) and self-adjoint on the first Sobolev space H1(![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3)4 for nuclear charge Z ≤ 118 in the case of a point nuclear model and becomes self-adjoint on C∞0(
3)4 for nuclear charge Z ≤ 118 in the case of a point nuclear model and becomes self-adjoint on C∞0(![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3)4 for all Z in the case of a finite nuclear model,26 one ought to ask the following questions:
3)4 for all Z in the case of a finite nuclear model,26 one ought to ask the following questions:
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )(1), a dilated (also called ‘complex-coordinate-rotated’, CCR) Hamiltonian HCS(
)(1), a dilated (also called ‘complex-coordinate-rotated’, CCR) Hamiltonian HCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) eiθ) was employed therein. Mathematically, such a dilation would not change the bound states of HCS(
eiθ) was employed therein. Mathematically, such a dilation would not change the bound states of HCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) but only rotates those unbound states to the complex energy plane. That only complex energies have been obtained with HCS(
) but only rotates those unbound states to the complex energy plane. That only complex energies have been obtained with HCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) eiθ) implies immediately that HCS(
eiθ) implies immediately that HCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) has no bound states. However, this point should be viewed with caution: The bound states remain unchanged only if both the Hamiltonian and the square-integrable basis functions are scaled simultaneously, e.g., gμ(r) = exp(−ημr2) → gμ(ρ) = exp(−ημr2e2iθ). Otherwise, in principle a complete set of unscaled gμ(r) functions is required for HCS(
) has no bound states. However, this point should be viewed with caution: The bound states remain unchanged only if both the Hamiltonian and the square-integrable basis functions are scaled simultaneously, e.g., gμ(r) = exp(−ημr2) → gμ(ρ) = exp(−ημr2e2iθ). Otherwise, in principle a complete set of unscaled gμ(r) functions is required for HCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) eiθ) to reproduce the matrix eigenvalues of HCS(
eiθ) to reproduce the matrix eigenvalues of HCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) represented just in a small basis. This is because a scaled function gμ(ρ) is highly oscillatory and can hardly be simulated by the real radial functions gν(r). To confirm this viewpoint, we carried out a set of calculations for the ground state of the Xe53+ ion for which the existence of bound states is out of question. It is seen from Table 1 that, for 30s and 40s even-tempered Gaussian functions, the dilated Dirac operator D(
) represented just in a small basis. This is because a scaled function gμ(ρ) is highly oscillatory and can hardly be simulated by the real radial functions gν(r). To confirm this viewpoint, we carried out a set of calculations for the ground state of the Xe53+ ion for which the existence of bound states is out of question. It is seen from Table 1 that, for 30s and 40s even-tempered Gaussian functions, the dilated Dirac operator D(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) eiθ) does give rise to a spurious imaginary part in the energy even with a rotation angle as small as 0.03 rad. The convergence toward the exact energy is slowed down when the angle is enlarged, e.g., to 0.30 rad. It was also observed in the course of experimentation that all the states above +mc2 (below −mc2) have large negative (positive) imaginary parts in the energies, whereas the imaginary parts in the energies for the states below +mc2 and above −mc2 can be both positive and negative and tend to vanish only when the basis is sufficiently large. Although only a one-electron system is considered here, the observation should also apply to many-electron cases. Therefore, it cannot be excluded that the complex energies obtained by Pestka30,31 are due to incompleteness errors in the basis set. Given such uncertainties, the conclusion28–31 that the DC Hamiltonian has no bound states may be premature. What can really be concluded at this stage is that the BRD is much less virulent than originally claimed, and that the no-pair projection, as recommended by Sucher32 for avoiding the BRD, is not really needed. At this moment a mathematician may debate that the non-interacting Hamiltonian D(1) + D(2) does not have any gap in the continuous spectrum of (−∞, +∞) such that any weak interaction would result in the BRD. However, what is in mind here is an electron in the PES and the other in the NES, not a physical process where both the initial and final states are of positive energies.
eiθ) does give rise to a spurious imaginary part in the energy even with a rotation angle as small as 0.03 rad. The convergence toward the exact energy is slowed down when the angle is enlarged, e.g., to 0.30 rad. It was also observed in the course of experimentation that all the states above +mc2 (below −mc2) have large negative (positive) imaginary parts in the energies, whereas the imaginary parts in the energies for the states below +mc2 and above −mc2 can be both positive and negative and tend to vanish only when the basis is sufficiently large. Although only a one-electron system is considered here, the observation should also apply to many-electron cases. Therefore, it cannot be excluded that the complex energies obtained by Pestka30,31 are due to incompleteness errors in the basis set. Given such uncertainties, the conclusion28–31 that the DC Hamiltonian has no bound states may be premature. What can really be concluded at this stage is that the BRD is much less virulent than originally claimed, and that the no-pair projection, as recommended by Sucher32 for avoiding the BRD, is not really needed. At this moment a mathematician may debate that the non-interacting Hamiltonian D(1) + D(2) does not have any gap in the continuous spectrum of (−∞, +∞) such that any weak interaction would result in the BRD. However, what is in mind here is an electron in the PES and the other in the NES, not a physical process where both the initial and final states are of positive energies.![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = apφp(
) = apφp(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), ap|0;
), ap|0; 〉 = 0,
〉 = 0,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) are the eigenvectors of h (13). Note that the Hamiltonian HCS(29) is already normal ordered with respect to the vacuum |0;
) are the eigenvectors of h (13). Note that the Hamiltonian HCS(29) is already normal ordered with respect to the vacuum |0;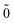 〉 but not yet to the reference state |N;
〉 but not yet to the reference state |N;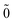 〉 of N positive energy electrons and zero negative energy electrons. If the ai and aa operators in (30) are rearranged to the right of ai and aa, we would obtain a Hamiltonian that is also normal ordered with respect to |N;
〉 of N positive energy electrons and zero negative energy electrons. If the ai and aa operators in (30) are rearranged to the right of ai and aa, we would obtain a Hamiltonian that is also normal ordered with respect to |N;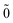 〉, viz.,
〉, viz.,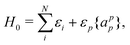
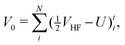
 〉 into a genuine vacuum |0;
〉 into a genuine vacuum |0; 〉 of no particles or holes, viz.,
〉 of no particles or holes, viz.,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = bpφp(
) = bpφp(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), bp|0;
), bp|0; 〉 = 0.
〉 = 0.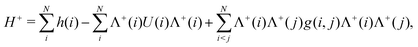
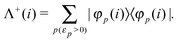
 〉
〉![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) = b
= b![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) and a
and a![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) = b
= b![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) for ε
for ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) < 0. This effectively turns the |0;Ñ〉 state into the genuine vacuum |0;
< 0. This effectively turns the |0;Ñ〉 state into the genuine vacuum |0; 〉 of no particles or holes, i.e., bp|0;
〉 of no particles or holes, i.e., bp|0; 〉 = b
〉 = b![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) |0;
|0; 〉 = 0. It also amounts to writing the field operator as
〉 = 0. It also amounts to writing the field operator as![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = bpφp(
) = bpφp(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) + b
) + b![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) φ
φ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ),
),![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) and get rid of the infinite energy of the otherwise filled sea
and get rid of the infinite energy of the otherwise filled sea![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) bq, bpb
bq, bpb![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) , and −b
, and −b![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) b
b![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) , the second and third of which correspond to pair annihilation and creation, respectively. The two-body part V2 is composed of 16 terms, not to be documented here. Moreover, care should also be taken of the polarization of the vacuum |0;
, the second and third of which correspond to pair annihilation and creation, respectively. The two-body part V2 is composed of 16 terms, not to be documented here. Moreover, care should also be taken of the polarization of the vacuum |0; 〉.
〉.
 〉(0) of N bound electrons alongside with the zeroth order vacuum |0;
〉(0) of N bound electrons alongside with the zeroth order vacuum |0; 〉(0). The zeroth and first order energies of the system can easily be obtained as shown in eqn (15) and (16), respectively. To derive the first order correction |N;
〉(0). The zeroth and first order energies of the system can easily be obtained as shown in eqn (15) and (16), respectively. To derive the first order correction |N; 〉(1) to the state, we first notice that the intermediate states include zero, one, and two electron-positron (ep) pairs, viz.,
〉(1) to the state, we first notice that the intermediate states include zero, one, and two electron-positron (ep) pairs, viz., 〉(1) = |N;
〉(1) = |N; 〉(1)0ep + |N;
〉(1)0ep + |N;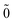 〉(1)1ep + |N;
〉(1)1ep + |N;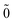 〉(1)2ep.
〉(1)2ep.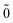 〉(1) to the vacuum:
〉(1) to the vacuum: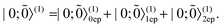
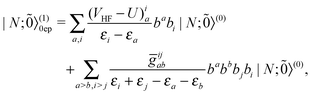
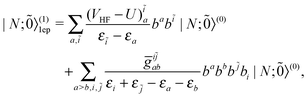
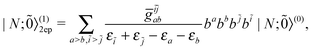
 〉(1)0ep = 0,
〉(1)0ep = 0,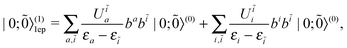
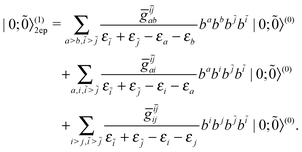
 |V|N;
|V|N; 〉(1) − (0) 〈0;
〉(1) − (0) 〈0;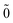 |V|0;
|V|0;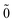 〉(1),
〉(1),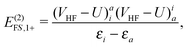
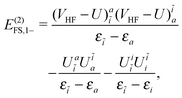
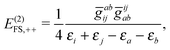
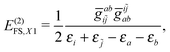
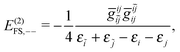
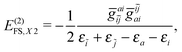
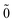 〉 whereas the others from the |N;
〉 whereas the others from the |N;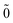 〉 state. Such a rearrangement is to make a better comparison with those by the CS approach. It is seen that E(2)FS,1+ arising from the first term of (46) agrees with E(2)CS,1+ in (20), E(2)FS,++ arising from the second term of (46) agrees with E(2)CS,++ in (23), and E(2)FS,−− arising from the third term of (51) agrees with E(2)CS,−− in (24). It is just that E(2)FS,−− is now interpreted as a double-pair vacuum term instead of the previous transitions from the occupied PES to the virtual NES. The vexing BRD term E(2)CS,+−(25) does not show up by construction. However, E(2)FS,1− arising from both the first term of (47) and the two terms of (50) is different from E(2)CS,1− in (21). Moreover, the E(2)FS,X1 arising from the second term of (47) and the E(2)FS,X2 from the second term of (51) are absent in the CS. It is therefore clear that the CS (associated with the empty Dirac picture) and FS (associated with the filled Dirac picture) approaches are intrinsically different, which can only be uncovered by examining two-electron properties such as electron correlation. Also, the meaning of ‘no-pair approximation’ now becomes clear: Retaining the terms involving only the PES does correspond to no virtual pairs.
〉 state. Such a rearrangement is to make a better comparison with those by the CS approach. It is seen that E(2)FS,1+ arising from the first term of (46) agrees with E(2)CS,1+ in (20), E(2)FS,++ arising from the second term of (46) agrees with E(2)CS,++ in (23), and E(2)FS,−− arising from the third term of (51) agrees with E(2)CS,−− in (24). It is just that E(2)FS,−− is now interpreted as a double-pair vacuum term instead of the previous transitions from the occupied PES to the virtual NES. The vexing BRD term E(2)CS,+−(25) does not show up by construction. However, E(2)FS,1− arising from both the first term of (47) and the two terms of (50) is different from E(2)CS,1− in (21). Moreover, the E(2)FS,X1 arising from the second term of (47) and the E(2)FS,X2 from the second term of (51) are absent in the CS. It is therefore clear that the CS (associated with the empty Dirac picture) and FS (associated with the filled Dirac picture) approaches are intrinsically different, which can only be uncovered by examining two-electron properties such as electron correlation. Also, the meaning of ‘no-pair approximation’ now becomes clear: Retaining the terms involving only the PES does correspond to no virtual pairs.

![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) , viz.,
, viz.,![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |Ψ(N;Ñ)〉 − 〈Ψ(0;Ñ)|
|Ψ(N;Ñ)〉 − 〈Ψ(0;Ñ)|![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |Ψ(0;Ñ)〉,
|Ψ(0;Ñ)〉,![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) =
= ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0 +
0 + ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) 0 + V1 + V2,
0 + V1 + V2,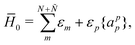
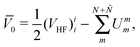
![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) qipi
qipi![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) ), as indicated by the summation over m in (64) and (65). Note that the VHF term in (66) emerges only for systems of more than one positive energy electron. Another caveat here is that, when deriving the normal-ordered Hamiltonian
), as indicated by the summation over m in (64) and (65). Note that the VHF term in (66) emerges only for systems of more than one positive energy electron. Another caveat here is that, when deriving the normal-ordered Hamiltonian ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) , no contractions among the NES are allowed. Otherwise, the following terms would arise
, no contractions among the NES are allowed. Otherwise, the following terms would arise![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) i
i![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) i
i![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) + ½
+ ½![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) ĩ
ĩ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) ĩ
ĩ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) ,
,![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) qĩpĩ {apq},
qĩpĩ {apq},![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) i
i![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) i
i![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) , to be compared with the correct result (16). That is, the negative energy electrons must be regarded as non-interacting, a very weird feature of the filled Dirac picture. Such contractions have been excluded automatically by the normal ordering with respect to the NES, see eqn (42). At this stage it should be emphasized that the same set of mean-field NES (cf.eqn (13)) has been employed here for describing the state and the (floating) vacuum, such that the vacuum polarization arises only from the fluctuation potential, starting from second order in energy. The so-called renormalization procedure is not needed as every term is finite individually. In contrast, in the so-called `no-photon variational mean-field QED' approach,35–38 the mean-field and free-particle NES are used for the state and the (frozen) vacuum, respectively, such that the vacuum polarization arises also from the mean-field potential, starting from first order in energy. Thereby, suitable regularization and renormalization have to be performed in each iteration step. To the best of our knowledge, no actual applications of this approach have yet been made. The corresponding second order correlation energy can also be derived in the same way as above. It is just that some additional terms would arise thanks to the use of different NES for the state and the vacuum.
, to be compared with the correct result (16). That is, the negative energy electrons must be regarded as non-interacting, a very weird feature of the filled Dirac picture. Such contractions have been excluded automatically by the normal ordering with respect to the NES, see eqn (42). At this stage it should be emphasized that the same set of mean-field NES (cf.eqn (13)) has been employed here for describing the state and the (floating) vacuum, such that the vacuum polarization arises only from the fluctuation potential, starting from second order in energy. The so-called renormalization procedure is not needed as every term is finite individually. In contrast, in the so-called `no-photon variational mean-field QED' approach,35–38 the mean-field and free-particle NES are used for the state and the (frozen) vacuum, respectively, such that the vacuum polarization arises also from the mean-field potential, starting from first order in energy. Thereby, suitable regularization and renormalization have to be performed in each iteration step. To the best of our knowledge, no actual applications of this approach have yet been made. The corresponding second order correlation energy can also be derived in the same way as above. It is just that some additional terms would arise thanks to the use of different NES for the state and the vacuum.
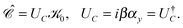
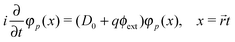
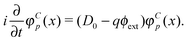
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), if φp(
), if φp(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )e−iεpt is a stationary solution of the Dirac equation for an electron (q = −1) of energy εp, φCp(x) = φCp(
)e−iεpt is a stationary solution of the Dirac equation for an electron (q = −1) of energy εp, φCp(x) = φCp(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )eiεpt would be a stationary solution of the Dirac equation for a positron (q = +1) of energy −εp. Note in particular that the probability density of a negative energy (−|ε
)eiεpt would be a stationary solution of the Dirac equation for a positron (q = +1) of energy −εp. Note in particular that the probability density of a negative energy (−|ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) |) electron φ
|) electron φ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )e−i|ε
)e−i|ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) |(−t) is indistinguishable from that of a positive energy (|ε
|(−t) is indistinguishable from that of a positive energy (|ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) |) positronφC
|) positronφC![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )e−i|ε
)e−i|ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) |t, i.e.,
|t, i.e., 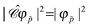 . Because of this feature, negative energy electrons can be regarded as mirror images of positive energy positrons propagating in opposite direction and time.
. Because of this feature, negative energy electrons can be regarded as mirror images of positive energy positrons propagating in opposite direction and time.
![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) φ
φ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (x)
(x)![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )e−iεpt + d
)e−iεpt + d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) φ
φ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )e−iε
)e−iε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) t,
t,![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (d
(d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) ) creates (annihilates) a positron of positive energy |ε
) creates (annihilates) a positron of positive energy |ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) | = −ε
| = −ε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) .
.
![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (instead of d
(instead of d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) ) must accompany bp is required by charge conservation. Both bp and d
) must accompany bp is required by charge conservation. Both bp and d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) increase the charge of a state by one unit; bp does this by destroying an electron whereas d
increase the charge of a state by one unit; bp does this by destroying an electron whereas d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) does this by creating a positron. Thus the field operator ϕ(x) always increases one unit of charge. Similarly, the field operator ϕ†(x) always decreases one unit of charge. Therefore, the operator ϕ†(x)ϕ(x) conserves the charge. Had d
does this by creating a positron. Thus the field operator ϕ(x) always increases one unit of charge. Similarly, the field operator ϕ†(x) always decreases one unit of charge. Therefore, the operator ϕ†(x)ϕ(x) conserves the charge. Had d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) been chosen to accompany bp, the operator ϕ†(x)ϕ(x) would not conserve the charge: It would include terms like bpd
been chosen to accompany bp, the operator ϕ†(x)ϕ(x) would not conserve the charge: It would include terms like bpd![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) and d
and d![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) bp which decrease and increase two units of charge, respectively.
bp which decrease and increase two units of charge, respectively.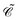 , which transforms the field ϕ(x) as
, which transforms the field ϕ(x) as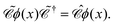
 and
and  are as follows. Just like a rotation operation in point group theory, the
are as follows. Just like a rotation operation in point group theory, the 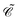 operator is unitary and acts only on the b and d operators but not on the functions φp(x). In contrast, as a product between the unitary matrix UC and the complex conjugation
operator is unitary and acts only on the b and d operators but not on the functions φp(x). In contrast, as a product between the unitary matrix UC and the complex conjugation ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) 0, the
0, the 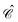 operator (70) is anti-unitary and acts also on the functions. Spelling out the left and right hand sides of eqn (75) leads to
operator (70) is anti-unitary and acts also on the functions. Spelling out the left and right hand sides of eqn (75) leads to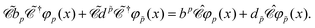
![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) and spin projection s while φ
and spin projection s while φ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) represent a NES of momentum −
represent a NES of momentum −![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) and spin projection −s, the following identities can be obtained:
and spin projection −s, the following identities can be obtained: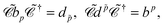
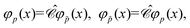
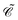 interchanges particles and antiparticles of the same momentum
interchanges particles and antiparticles of the same momentum ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) and spin projection s, viz.,
and spin projection s, viz.,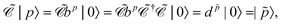
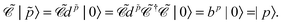
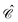 proceeds through Kramers pairs (φp and
proceeds through Kramers pairs (φp and 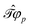 ) thanks to the simple relationship23 between
) thanks to the simple relationship23 between 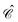 and the time reversal operator
and the time reversal operator 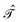 , i.e.,
, i.e., 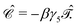
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2)φ†p(
2)φ†p(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1)e−iεp(t2−t1) − Θ(t1 − t2)φ
1)e−iεp(t2−t1) − Θ(t1 − t2)φ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2)φ†
2)φ†![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1)e−iε
1)e−iε![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (t2−t1)}.
(t2−t1)}.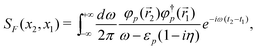
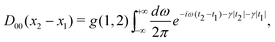
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )e−γ|t|,
)e−γ|t|,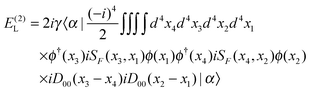
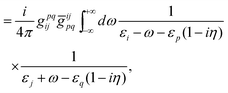
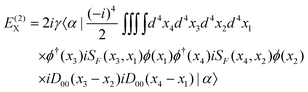
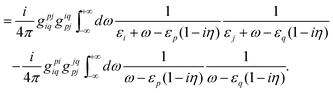
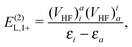
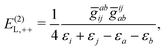
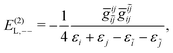
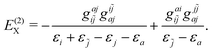
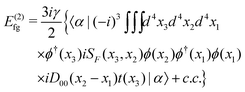
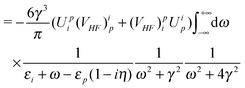
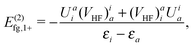
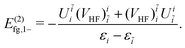
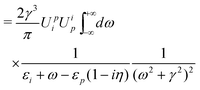
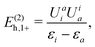
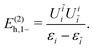
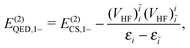

![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) F(x2,x1) = −i〈0|T[ϕ(x2)ϕ†(x1)]|0〉
F(x2,x1) = −i〈0|T[ϕ(x2)ϕ†(x1)]|0〉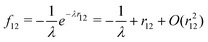
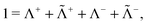
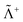 and
and 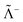 are the respective complements. The
are the respective complements. The 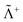 subspace is to be simulated by Q12f12|0〉 but the whole NES subspace has to be projected out explicitly. However,
subspace is to be simulated by Q12f12|0〉 but the whole NES subspace has to be projected out explicitly. However, 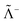 is inaccessible, meaning that the contaminations of NES cannot strictly be avoided. To minimize such contaminations we propose to construct ‘dual basis projectors’, i.e., Λ+L and Λ−L with a large basis set (BasL) and Λ+S and Λ−S with a subset (BasS) of BasL. We then assume that the residual
is inaccessible, meaning that the contaminations of NES cannot strictly be avoided. To minimize such contaminations we propose to construct ‘dual basis projectors’, i.e., Λ+L and Λ−L with a large basis set (BasL) and Λ+S and Λ−S with a subset (BasS) of BasL. We then assume that the residual 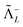 is negligible and that conventional correlation is to be carried out within the Λ+S subspace. Such a partitioning of the complete configuration space is depicted in Fig. 4, which gives rise to the following definition of Q12
is negligible and that conventional correlation is to be carried out within the Λ+S subspace. Such a partitioning of the complete configuration space is depicted in Fig. 4, which gives rise to the following definition of Q12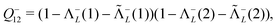

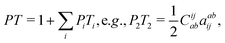
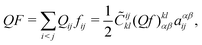
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ijkl may be fixed by symmetry argument as done in the nonrelativistic case.45 The P and Q projectors in the wave function (118) can likewise be folded into the first-quantized Hamiltonian HCS(1), leading to an extended no-pair Hamiltonian
ijkl may be fixed by symmetry argument as done in the nonrelativistic case.45 The P and Q projectors in the wave function (118) can likewise be folded into the first-quantized Hamiltonian HCS(1), leading to an extended no-pair Hamiltonian