Molecular knots, links, and fabrics: prediction of existence and suggestion of a synthetic route

Abstract

The possible existence and formation of molecular knots, molecular links, and molecular fabrics, built from quite arbitrary monomers, is discussed. General theoretical considerations lead to the conclusion that such molecular species are likely to represent local minima on potential energy hypersurfaces and, therefore, should be stable and able to exist, if once formed. A surface template technique is suggested as a possible experimental avenue to actually form molecular knots and links. This technique may open the door to the directed and controlled synthesis of knots, thus transcending present-day methods based on self-assembly of constituting monomers or oligomers.

---

1. Introduction

THE SERPENT  You see things; and you say “Why?” But I dream things that never were; and I say “Why not?”¹ Knots, which are considered in this work as objects without loose ends, e.g. closed space curves or closed loops of strings, can be combined to form composite knots and links (see Fig. 1 for some illustrative examples of different types of knots and links, further details will be given below). The subject of the present work is the search for answers to the following general question: can such objects exist on a molecular scale? Or, with much broader scope: is the existence of arbitrary molecular knots possible? In general, such a molecular knot has typically a size of molecular dimension, it can be of arbitrary knot type, and it can be constituted of quite arbitrary monomers. And if our answer to the previous questions is ‘yes’, then how can such systems be studied by theory and realized experimentally? The latter requires an experimental method (or a set of methods) for the directed or undirected synthesis of knotted and linked molecules. Is it possible to generate more complicated structures, like links or fabrics, familiar to us from everyday life, on a molecular scale as well? These questions will be answered, but before doing so let us briefly consider knots, links and fabrics at a more familiar size, to demonstrate the importance of these objects in everyday life.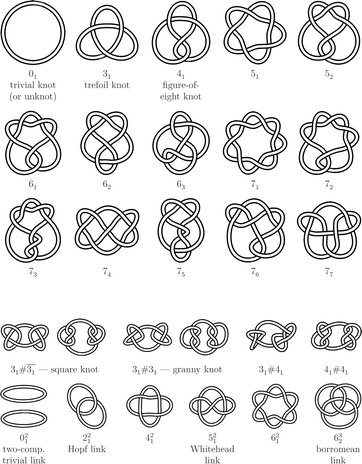

Fig. 1 Graphical representation of knots and links (generated with KnotPlot²). Upper part: the trivial knot 0₁ and all prime knots n_k for 3 ≤ n ≤ 7. Lower part: some composite knots n_k#m_j and l-component prime links n^l_k.

The making of knots and links from fibres, threads or yarn and the weaving of threads or yarn, to make fabrics, are well-known and important techniques developed since the earliest times in the cultural history of mankind.³ The development of techniques in this area led always to improvements in the survival and living conditions of man. Examples from prehistoric times are the making of nets for fishing, the weaving of vegetable material by hand to produce shoes or baskets, and the invention of distaff and spindle for hand spinning and of the manually operated loom to produce textiles for clothing. The spinning wheel, probably invented in India and known in Europe since the late Middle Ages, mechanized the spinning process but still required operation by hand. With the beginning of industrialization in the 18th century there began also the development of automatic machines for spinning, weaving and other operations. In turn, several places, first in Europe, evolved into centres of textile manufacturing and textile industry. The invention of synthetic fibres in the first half of the 20th century simplified the mass production of yarn and fabric even further, at the cost of the global mineral oil resources (the consumption of these fossil resources by our traffic systems and for heating purposes is much larger, of course). In a completely different realm, namely communication, knots gained high importance as well. Probably the best known example for their use in such a non-written form of communication is given by the quipus of the pre-Columbian Peruvian Incas.³ A record of the large diversity of knots and links invented by man for various purposes is beautifully presented in ref. 4.

It is called to the attention of the reader that the ability to form knotted or woven objects is not restricted to the culture of man. Several examples from the animal kingdom are known. Let us mention the formation of cocoons by the silkworm larvae (Bombyx mori) and the nest-building by various kinds of weaverbirds (family Ploceidae, and others).⁵ Spiders (order Araneidae) can produce various kinds of silk (up to six kinds, at least, for individuals of some orb weaver species).³ They use this silk also to make a cocoon for their brood. Their highly specialized spinning apparatus, and the properties of the produced silk, still exceed the abilities of human fibre spinning technology by far. The eel-like Atlantic hagfish (Myxine glutinosa) is able to tie a knot into its body and to let this move from the tail to the head.⁶ There is also a hint that chimpanzees may be able to tie simple knots.⁷

So far we have considered knots, links and fabrics only as macroscopic objects. We learned that a tool (a hand, a bill, a machine) is required, in general, to handle the object or the material (thread, yarn, blade of grass) from which a knot, link, or fabric is to be formed.

Let us turn now from the practical aspects to more theoretical ones, and briefly summarize some important facts from the mathematical theory of knots and links. This theory, called knot theory, interestingly evolved from chemical physics. At the beginning of the last third of the 19th century, W. Thomson (later to become Lord Kelvin) seriously considered knots (or, precisely, vortices in the ether) as a promising atomic model.⁸ Subsequently, tabulations of knots with low crossing number n, so-called prime knots n_k, were prepared (k is just a counting index, see Fig. 1 for all prime knots n_k with 3 ≤ n ≤ 7). Prime knots may be combined to form more complicated objects, known as composite knots, n_k#m_l, or l-component links, n^l_k (see Fig. 1 for examples). Today, knot theory⁹ is a well-developed branch of topology, largely devoted to the classification of knots and to the search for so-called knot invariants. The latter allow one to decide, more or less easily, whether two given knots are identical (and thus interconvertible) or not. The universal knot invariant has not yet been found (and may not even exist), but hierarchies of knot invariants are known, so that more powerful invariants may be used when simpler ones fail. From a topological point of view, the particular kind of representation of a knot or link, e.g., with a rope (cf. Fig. 1), with a string, or in a necklace-like style with sticks and beads (Fig. 2), is completely unimportant.

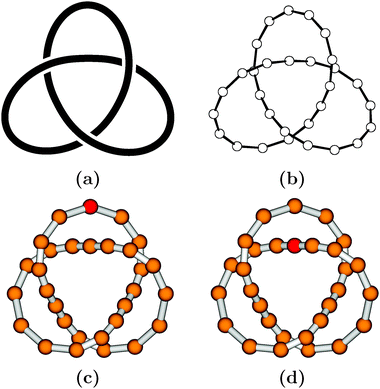Fig. 2 Some topologically equivalent representations of the trefoil knot 3₁: (a) as a smooth space curve in 3-space (generated with KnotPlot²), see also Fig. 1; (b) as a simple polygonal representation with beads (generated with ORTEP¹⁰); (c, d) similar to (b), but with shaded beads and a single bead labelled by a different shade (generated with MOLDEN¹¹). Every bead may be replaced by some monomeric unit, to obtain a molecular representation of the knot.

Numerous connections between knot theory and various branches of science have been discovered in the last 40 years. In physics,¹² string theory and statistical mechanics are deeply related to knot theory. In the 1960s, the preparation of [2]-catenanes¹³ (molecular representations of the Hopf link 2²₁, see Fig. 1) and the observation of knotted and linked forms of nucleic acids from natural sources¹⁴ initiated the interaction between knot theory, on one side, and chemistry and biochemistry, on the other side. We remark that, as for the macroscopic objects discussed above, a tool is required to obtain knotted or linked forms of nucleic acids. It has been known since the early 1970s that special enzymes (topoisomerases)¹⁵ play the rôle of the tool. There is also now evidence for the existence of knotted proteins in Nature.^16,17 In one case¹⁷ the resulting object, a bacteriophage capsid, consists of catenated protein chains and can be considered as a piece of the finest-possible fabric of almost spherical shape. Due to the bias induced by the current research focus, organic (especially biochemical) examples of molecular knots or links are much more numerous than inorganic ones. Topologically interesting structures, however, are not uncommon in inorganic and organometallic chemistry. An illustrative example¹⁸ shows sheets of interlocked (or catenated) rings in the crystal structure of a polymeric copper complex. The detection of helical forms of carbon nanotubes provides another example, which led to a theoretical study¹⁹ of both toroidal and helical forms of nanotubular carbon.

Topological chemistry and biochemistry are now well-established fields of research,²⁰ with close relations to, e.g., supramolecular chemistry and molecular biology. Currently, the activity in topological and supramolecular chemistry is quite high, since these areas of research hold a key position for ‘nanoscience’ and ‘nanotechnology’, see ref. 21 for examples.

Today, the controlled synthesis of various types of knotted and linked molecules can be achieved. All these syntheses, however, rely on self-assembly and template effects in three-dimensional space, in one way or the other. Advantage is taken (i) of the template effect in metal–ligand complexes in the work of Sauvage et al.,²² (ii) of the directing action of hydrogen bonds in the work of Seeman et al.,²³ (iii) of the aromatic π–π-stacking interaction in the work of Stoddart et al.,²⁴ and (iv) of the self-assembly of amide bonds in the work of Vögtle et al.²⁵ Despite all these achievements, we are still far away from being able to prepare molecular knots of arbitrary knot type from arbitrarily chosen organic or inorganic monomers.

The ideas presented in this work may help to change this situation in the future. The suggested technique is also based on template effects, but on a surface (i.e., in a two-dimensional space). The reduction of dimensionality opens a way to assemble molecular knots in a directed and controlled way. It may become possible then, for example, to study by experiment the molecules shown in Fig. 3, which are up to now only accessible to theory. Fig. 3 shows, from top to bottom, hydrogenated sections of single-walled carbon nanotubes, new molecular forms of phosphorus²⁶ and sulfur, and a [2]-catenane formed from a pair of cycloalkanethiole molecules.

Fig. 3 Some as yet unknown molecular knots and links. The structures (generated with MOLDEN¹¹) are primarily meant to be illustrative, and do not necessarily represent optimized equilibrium structures. Upper part: molecular representations of the trivial knot 0₁ by saturated sections of single-walled carbon nanotubes, (para-C₆H₄)_n (point group D_nh, n = 15) and (C₄H₂)_n (D_nh, n = 30), and by a cyclic form of phosphorus, [(P₈)(P₂)]_n (D_nh, n = 14). Lower part: molecular representations of the trefoil knot 3₁ (by a chain of sulfur atoms, S_6n, point group D₃, n = 9) and of the Hopf link 2²₁ (by a [2]-catenane built from a cycloalkanethiole, (C₃₀H₆₀S)₂, point group D₂).

This paper is organized as follows. The question of the possible existence of molecular knots, links and fabrics is addressed in general in the next section, together with related questions concerning molecular and electronic structure. Then, in section 3, a suggestion is made for a possible experimental avenue to actually form molecular knots. This route may be explored further from the experimental side. Concluding remarks are made at the end.

For reasons of brevity and readability we frequently write only ‘knot’ in the following, where the terms ‘link’ and ‘fabric’ may obviously be included as well. Pictures of knots and links, and of their molecular realizations were generated with the programs KnotPlot^2,27, ORTEP,¹⁰ and MOLDEN.^11,28

2. Theoretical considerations

2.1. The existence of molecular knots

Is it possible for arbitrary molecular knots, links, or fabrics, to exist? Arbitrariness is meant here to indicate freedom with respect to both knot type and choice of constituting monomers, respectively. Will such species be stable, if they are formed?

Chemistry has accumulated a vast knowledge about groups of atoms (molecular fragments) capable of forming linear oligomers, and even polymers. The constituting building blocks, or monomers, M, may be of a single kind, to give homo-oligomers, or of two or more kinds, thus leading to hetero-oligomers. A schematic short-hand notation for these species is X–M_l–Y, where X and Y are terminal groups, and the l monomers M may all be different. The terminal groups X and Y need not necessarily be single-valent. As an example we consider a chain of l carbon atoms (M = C), for even l, l = 2k. We may have either X = Y = H (this yields the polyynes C_2kH₂), or X = Y = H₂ (this leads to the cumulenes C_2kH₄). Obviously, in this case, the terminal groups strongly influence (or even determine to a large extent) the molecular electronic structure. Frequently, the monomers M are known to form not only linear oligomers, but even cyclic oligomers, cyclo-M_l. Well known examples are the cycloalkanes (M = CH₂, l ≥ 3), the cyclosulfur species (M = S, allotropes with 6 ≤ l ≤ 13 and for some larger values of l are known), or the cyclodextrins (M is the α-(1→4)-linked glucopyranose unit, 6 ≤ l ≤ 8). These are already molecular representations of the trivial knot 0₁.

We make now the following general statements: any monomer M (or set of monomers, if different ones are considered), which forms linear oligomeric or polymeric molecular structures, X–M_l–Y (l < ∞), can also form molecular knots n_k-M_l, of arbitrary knot type n_k. Once formed, such knots are likely to represent local minima of sufficient depth on potential energy hypersurfaces, and therefore should be stable. The number of monomers l required to actually generate a particular knot type n_k for the given monomer M is not specified by these statements.

We do not claim that such molecular knots can be formed easily from the monomers, or that they can be formed, in general, by self-assembly. As for their macroscopic counterparts from daily life, the actual formation of a molecular knot or link from an open oligomeric chain or from chain-like oligomeric fragments is likely to require a suitable tool, which necessarily has to be of molecular size itself.

Now an important related question arises: what size will these knots have? We know from the mere existence of linear oligomers and polymers, X–M_m–Y, that the local situation for any monomer M in the knotted molecular chain n_k-M_l approaches the situation of the linear polymer as closely as we please when the size of the knot is increased, simply by increasing the monomer number l. Experience from polymer and solid state research, where linear and three-dimensional periodic structures are important (though admittedly idealized) limiting cases, shows that for a reasonably chosen sequence of smaller systems (like linear oligomers, for example) several physical properties of the monomers, like monomeric molecular structure, energy per monomeric unit etc., approach the situation of the limiting cases reasonably quickly and well.

The identification of methylene units (M = CH₂) as building blocks, both in n-alkanes, CH₃(CH₂)_l−2CH₃, and in polyethylene, (CH₂)_n, may serve as an example where it is even possible to assign a prototypic (or averaged) molecular structure to the monomeric unit, i.e. the methylene unit. This does not mean that individual monomers will not show variations from this prototypic structure, but that is not of importance here. The important point is that the mere existence of linear oligomeric and polymeric saturated hydrocarbon chains and of cycloalkanes allows us to predict, in this special case, that knotted and linked hydrocarbons (of any knot or link type) are likely to be able to exist, if they are once formed from a sufficiently large number l of monomers. This point of view is supported by chemical experience, which allows us to consider suitable small fragments as building blocks for large and stable molecules, and qualitative quantum chemical knowledge, which tells us that stable molecules populate sufficiently deep potential energy hypersurface minima. It has in fact been known for more than 20 years²⁹ that molecular representations of the Hopf link 2²₁, i.e. [2]-catenanes, with methylene as the monomeric unit, can actually be formed. Whereas a pure hydrocarbon version of the simplest link is thus known, a hydrocarbon version of the simplest knot, the trefoil knot, still awaits its realization. However, a sufficiently large number of methylene units, say l = 120, allows not only a cycloalkane and [2]-catenanes (with equal or unequal cycloalkanes as constituents) to be formed, but quite likely also a molecule representing a trefoil knot, 3₁-(CH₂)₁₂₀. And if l = 120 should turn out to be too small to form a trefoil knot, then one may just raise this number to a sufficiently large value.

As far as the formation of linear or cyclic oligomeric structures is concerned, there is nothing special about the methylene group (except, perhaps, that after almost 180 years of systematic development in organic chemistry, since Wöhler’s synthesis of urea in 1828, quite a lot of experience in forming organic molecules has been accumulated). Hence, our conclusion is that knots should be able to exist, if they are once formed, irrespective of the particular monomer M chosen for their realization. The only prerequisite is that M must form linear oligomers.

Given a knot or link type, like 3₁ (the trefoil knot) or 2²₁ (the Hopf link), and a chosen monomer M, say D-glucose (or a set of monomers), a question of direct chemical interest is then: what is the smallest possible molecular realization of the chosen type of knot (a knotted or catenated topological isomer of a cyclodextrin is obtained here)? This question cannot be answered in general, but a combination of theory and experiment may be able to give a definite answer in this and many other cases.

On the theoretical side, the study of knotted or linked systems requires some further development of existing tools. Once the atom types and positions are known, any quantum chemical or force field method can be applied to study the electronic and molecular structure of molecular knots without too much difficulty. With an initial guess of the molecular structure (molecular ‘geometry’) at hand, we only need to choose a method (quantum mechanical or classical mechanical), run the optimization (hopefully successful), and get the desired results for the optimized molecular structure and other properties of interest.

Nevertheless, special tools for the easy set-up of knotted or linked structures are still missing. The building-up of such molecular structures is, in general, difficult to achieve with existing tools. Therefore we present in the next subsection a method to systematically build up the geometric structure of a knotted or linked molecule in a standardized way. Then, subsequently, some aspects related to electronic structure calculations of such systems are discussed.

2.2. Defining the geometric structure of molecular knots

As for any other molecule, the geometric structure of a molecular knot is completely defined when the positions of all atomic nuclei in 3-dimensional space are known. Traditionally, this task is accomplished in terms of Cartesian coordinates or with the so-called Z matrix (representing a concatenated sequence of spherical polar coordinates).³⁰ Alternatively, and equivalently, other types of coordinates may be used. The resulting data set allows one to generate, in particular, all desired structural parameters of the molecular chain, including, in particular, those required for the standardized description of biopolymers, i.e., polypeptides,³¹ polysaccharides,³² and polynucleotides.³³ Additional parameters, used for the standardized description of conformation and configuration of the double-stranded polynucleotide chain,^34,35 are also obtainable from Cartesian or internal coordinates.

There seems to be, up to now, no general method to define the geometric structure of molecular knots and links. To arrive at a method of general applicability, we consider the case where a molecular knot n_k-M_l is given. The case of links can be treated analogously, by considering separately every single strand. The geometric structure of a molecular knot can be defined as follows:

(1) Associate a point (position vector) r_i (i = 0, 1, …, l − 1) with each of the l monomers. This chosen point could be the position of an atomic nucleus, a bond midpoint, or any other suitable position. With completion of this step, we have at hand already a piecewise linear (or polygonal) representation of the underlying knot of type n_k.

(2) Define a local right-handed orthonormal coordinate system at each of the l points from step (1). This requires the definition of sets of unit vectors {e_i,m} (i = 0, 1, …, l − 1; m = 1, 2, 3). If we take the points from step (1) to represent points on a smooth space curve r(t), r_i = r(t_i), then we might like to choose the unit vectors e_i,m according to the Frenet–Serret frame (tangent, normal and binormal unit vectors) at r_i. This choice, however, is not optimal. In fact, this choice cannot be made when the space curve has vanishing curvature at point r_i (inflection points, points on straight line parts), and has other additional drawbacks. Better choices for the local axis systems are known,^27,36 and may be used. It is, however, not essential to actually relate the local axis system to a (piecewise linear or smooth) representation of the knot. A completely independent choice is possible, in principle.

(3) For each of the l monomers in the molecular knot: represent the positions R_i,j of all N_i atomic nuclei belonging to monomer i (j = 1, 2, …, N_i) as R_i,j = r_i + s_i,j, with

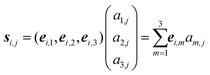where the column vectors a_j = (a_1,j, a_2,j, a_3,j)^T represent the nuclear coordinates in the local coordinate system of monomer i (as defined in the two previous steps). The total number of atomic nuclei is ∑_iN_i = N.

We have thus accomplished our task: the positions R_i,j of all atomic nuclei (i = 0, 1, …, l − 1; j = 1, 2, …, N_i) are specified in a manner which accounts for the fact that the molecule under study represents a knot (or link). To draw a parallel to the description of crystal structures: the piecewise linear (or polygonal) representation of the knot n_k corresponds to the crystal lattice, and the l monomers M_i correspond to the basis to be placed in the unit cells of the lattice. Here, however, there is in general no symmetry operation (translation, rotation, reflection, or combination thereof), which transfers a monomer, say M_i, onto some other monomer, M_j (i ≠ j).

2.3. Generating an initial guess for the geometric structure of a molecular knot

The approach presented in the last subsection can be modified to build up an initial guess for the molecular structure of a knotted molecule. This initial guess is a necessary starting point, required for all subsequent theoretical work, irrespective whether this is based on quantum mechanical or classical (force field) methods.

We assume that the following pieces of information are available:

(a) A set of l monomers {M_i} (i = 0, 1, …, l − 1), possibly of m different types (m ≥ 1), together with local nuclear coordinates a_j (j = 1, 2, …, N_m) for all N_m nuclei in a monomer-fixed right-handed coordinate system (origin , sets of orthonormal unit vectors {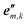}) for each of the m different types of monomers.

(b) A sequence list specifying the desired sequence of the l monomers in the knot.

(c) An oriented, piecewise linear (or polygonal) representation of the desired knot type n_k,³⁷ with l vertices and edges. The lengths of the edges are properly chosen, so that there is enough space to place monomer M_i along edge i (for all i). Fulfillment of this requirement provides the set of points r_i from step (1) of the previous subsection. Also required is a set of right-handed orthonormal unit vectors {e_i,k} attached to each point r_i.

An initial guess for the geometric structure of the molecular knot can be obtained then in the following way:

(1) Formation, and optional equilibration, of a linear chain X–M_l–Y with desired monomer sequence: an initial linear structure is readily prepared from the sets of nuclear coordinates of the l monomers with standard ‘molecule editors’.¹¹ A first pre-equilibration of the molecular structure may be performed, after saturation of the molecular chain with suitable terminal groups, X and Y. To this end, force field or low-level quantum chemical methods may be used. With or without pre-equilibration, this step yields an updated set of reference points 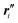, unit vector sets {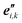}, and global nuclear coordinates 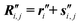, 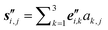(by application of the procedure explained in detail in the previous subsection).

(2) Formation, and optional equilibration, of a cyclic structure, cyclo-M_l or 0₁-M_l: from the previous step (or from the initial data) a set of l distances d_k (k = 1, 2, …, l) can be obtained, such that d_k specifies the length of monomer M_k−1. These lengths, together with their known sequence, define a polygon (irregular in general) with l vertices and edges, inscribed in a circle with suitably chosen radius R. The vertices of the polygon serve as new reference points 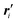, and a new set of unit vectors {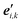} is chosen at each of them. Hence, new global nuclear coordinates can be written as 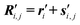, 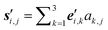. Again, an equilibration step can be performed, to obtain updated vectors and coordinates.

(3) Formation of the desired knot, n_k-M_l: the nuclear coordinates a_j from one of the previous steps are taken to define global nuclear coordinates as R_i,j = r_i + s_i,j, 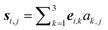. Use of nuclear coordinates from the initial data set yields a molecular structure built from rigid isolated monomers. Use of data obtained in the previous step may yield a more suitable initial guess, due to optional pre-equilibration.

Thus, eventually, an initial guess for the geometric structure of the desired knotted molecule is obtained. The last step of this controlled structure-generation procedure, from structures of individual monomers via linear and cyclic forms to the desired knotted form, is schematically shown in Fig. 4 (monomers are represented simply as beads, without presenting any further internal details accounting for their possibly multinuclear nature). Mathematically speaking, the interrelation between knotted and cyclic forms of M_l, n_k-M_l ⇄ 0₁-M_l, shown in Fig. 4, is based on a homeomorphism in three-dimensional space. This matching of three-dimensional space onto itself has, of course, nothing to do with an actual, physically effected isomerization of M_l.

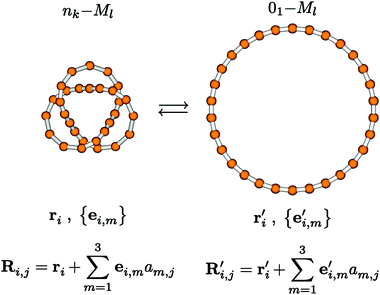Fig. 4 The relation between knotted and cyclic forms of M_l. This relation can be used to systematically build up the geometric structure of a knotted molecule, and to simplify electronic structure calculations for molecular knots. Every bead may represent a possibly multinuclear monomeric unit. See text for further details (pictures generated with MOLDEN¹¹).

2.4. The electronic structure of molecular knots

With the geometric structure of the desired molecular knot at hand, we are now ready to study its electronic structure. As mentioned above, standard quantum chemical methods can be readily applied, in principle. However, an ‘old problem’ of electronic structure calculations arises again: as the size of M_l increases, by increasing the monomer number l, the limits of hard- and software are quickly approached and exceeded (imagine knots or links of moderate size, with only about hundred monomers, but each monomer being a multinuclear metal complex). Therefore, additional tools are welcome.

The knotted and cyclic forms of M_l can be related (mathematically at least), n_k-M_l ⇄ 0₁-M_l. This has been used above to build up the geometric structure of the molecular knot in a systematic way. This relationship also opens a possibility to handle the electronic structure problem in an approximate, but efficient and in many cases still reliable way.

As long as the various parts of the molecular chain do not strongly interact with each other, we may expect to find no great differences between the electronic structures of the knotted and cyclic isomers of M_l. The electronic structure of the cyclic form of M_l, 0₁-M_l, is likely to exhibit many or all of the essential features of the electronic structure of the knotted form, n_k-M_l. The cyclic form, however, may exhibit high rotational symmetry, due to the presence of a rotation axis C_l of high order l (usually l ≥ 10, see the examples shown in the upper part of Fig. 3). Perhaps additional symmetries are present. The efficiency of the electronic structure calculations will then be increased by the ability to handle rotation axes C_l of arbitrarily high order l.

It is suggested, therefore, to perform the electronic structure calculations on cyclic isomers of M_l, where usually l ≥ 10, and to take advantage in this task of the Abelian point groups C_l, C_lh, and S_l³⁸ (with restriction to even values of l in the last case). To the best of the author’s knowledge, none of the currently available standard quantum chemical program codes is able to handle rotation axes C_l with order l ≥ 10, though several codes are probably not too difficult to extend to this case. We remark that in the limit l → ∞, the periodic polymer is approached. This opens a possibility for comparison with results from crystal structure calculations for the linear periodic polymer.

We have discussed, in this section, several questions related to molecular knots and links from the theoretical point of view. We turn now to experimental aspects of the subject, and suggest a route for the actual synthesis of arbitrary knots, built from arbitrary (not necessarily organic or bio-organic) monomers.

3. The synthesis of molecular knots and links

In this section, we make a suggestion for a synthetic route to molecular knots, links, or fabrics. We can present just the principles, of course, and do not have an experimental proof of applicability. The reader may thus consider the following as speculative, or visionary, depending on his or her point of view. Nevertheless, we consider these ideas worth communicating, as they might help others to develop more efficient and more generally applicable methods for the directed and controlled synthesis of molecular knots and links.

The suggested synthetic route works on a surface regularly covered with linker groups. The regular arrangement of these linker groups provides a template for the systematic directed and controlled synthesis of molecular knots. Thus, the suggested technique is called the surface template technique.

Successful application of this technique requires, as prerequisites, the mastering of various sophisticated chemical and physical experimental techniques, some of which are already quite well developed, others are currently under development in areas related to ‘nanoscience’ and ‘nanotechnology’, and yet others still have to be developed in the future. So, further development will be necessary before the surface template technique, as described below, will become applicable with ease.

Particularly needed are protection group techniques (for a much broader range of groups, not only from organic chemistry or biochemistry, but also for inorganic groups), tunneling microscope techniques (like scanning tunneling microscopy/atomic force microscopy) and single-molecule detection and manipulation techniques (to detect, manipulate and perform chemical reactions with individual surface-fixed molecules in a controlled manner). It will then become possible to use a variety of organic and inorganic monomers to generate homo- and hetero-oligomeric forms of molecular knots and links over a wide range of sizes.

We call to the attention of the reader that some of these techniques are already being developed. Manipulation on a surface has been achieved for single atoms^39,40 and for small molecules.⁴¹ Molecular tweezers⁴² have already been designed and synthesized, but cannot yet be used as reliably and easily as their macroscopic counterparts from daily life. The selective breaking of the carbon–iodine bond in single iodobenzene molecules, attached to Cu(111) step-edges, has been achieved through action of the scanning tunneling microscope tip.⁴³

In the following, we give a detailed description of the principles of the surface template technique. The related Fig. 5 illustrates this technique with four examples of the formation of molecular knots: the trivial knot 0₁, the trefoil knot 3₁, the Hopf link 2²₁, and a knot resembling a piece of fabric in plain weave. In each case, four steps of the surface template technique are sketched.

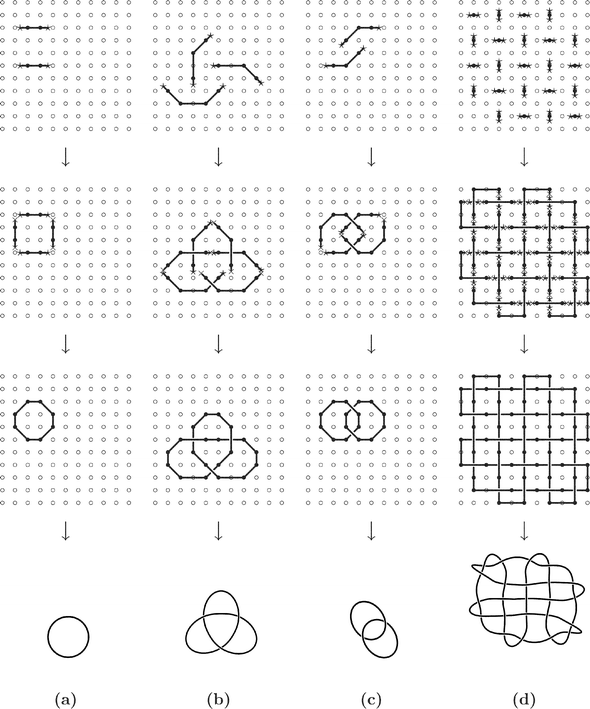Fig. 5 Schematic representation of the surface template technique for the actual synthesis of arbitrary knots and links. The linker groups on the surface (∘) are assumed to be arranged in a square lattice. Only the backbone of the molecular chain is represented, for simplicity. For molecules attached or linked to the surface, this representation is made with (open or closed) polygons. Examples are given for the synthesis of molecular representations of (a) the trivial knot 0₁, (b) the trefoil knot 3₁, (c) the Hopf link 2²₁, and (d) a knot resembling a piece of fabric in plain weave (see text for further details).

Initially given is a surface regularly covered with linker groups. These linker groups have to be suitably selected for every type of monomer that is used in subsequent steps to build up the knot. Regularity of linker groups is not mandatory, but makes the following steps easier, since the position of the linker groups is predictable only in a regular arrangement. In Fig. 5 a square lattice arrangement of linker groups was chosen.

Also required at the beginning are two sets (or assortments) of oligomers, X–M_i–X and Y–M_j–Y, of different but well-chosen chain lengths (such sets have been called, inappropriately, molecular ‘libraries’). The required chain lengths, i and j, can be estimated with sufficient accuracy from geometrical considerations of the molecular structure of the monomers when these monomers, the linker group arrangement, and the desired knot type have been specified. Some of the monomers M in these oligomers are assumed to have side chains carrying special groups (not shown in the schematic presentation of Fig. 5) that can bind or react under controlled conditions only with the linker groups on the surface. It is further assumed that the chemical bonds thus formed can be easily cleaved at the end. Finally, the oligomers are required to carry reactive terminal groups, different from the ones used to link them to the surface.

Now, in a first step, oligomers of the type X–M_i–X are linked to the surface at all places where later the molecular knot or link has a crossing point. The chemical bonds made by the linking reaction in this and also in the next step must be such that they can be easily broken at the end, but stay stable during the intermediate steps to come. Suitable reactions must be selected, depending on the type of monomers, to accomplish this task. The molecules fixed in this step still carry their reactive terminal groups X, which are assumed to be of such a kind that they cannot react with each other (these groups are shown as asterisks in Fig. 5).

In the second step, all other, remaining molecular chains are linked to the surface. The oligomers Y–M_j–Y used here also constitute the upper parts at all crossing points. The reaction used to link the oligomer to the surface should be the same as in the previous step, to simplify the release of the molecular knot at the end. The molecules fixed in this step carry another type of reactive group at their ends, Y (shown as crosses in Fig. 5), which again shall not be able to react with each other.

All pieces of the molecular chain of the knot (or link) are now fixed on the surface. The third step requires the connection of these pieces by reaction between their end groups (those shown as asterisks, X, with those shown as crosses, Y, in Fig. 5). Since there is always only a single pair of reactive groups at a place, with no others in the close neighbourhood, this reaction is likely to lead directly to the formation of the desired knotted or linked molecular chain, which is then, however, still fixed on the surface.

Finally, the release of the knot or link from the surface is required. In this step the bonds formed between the oligomers and the linker groups on the surface in the previous steps must be cleaved. This reaction shall not destroy the knot or link, and, ideally, might even reconstitute the regular arrangement of linker groups on the surface.

Both bond formation and bond breaking processes, appearing in the different steps of the surface template technique, may be performed by e.g. condensation or addition reactions, or photochemically. However, the set of reactions and reagents needs to be chosen with great care, depending on the monomer type(s) and linker groups to be used.

The surface template technique has the advantage to offer a direct and controlled way to the synthesis of molecular knots and links. However, it is not omnipotent. For example, it is impossible to apply in those cases where the monomers M in the oligomers X–M_i–X and Y–M_j–Y are unable to carry side chains, or to directly form bonds to the linker groups themselves. Thus, the sulfur knot from Fig. 3 cannot be synthesized in this way, whereas organic molecular chains meet all the requirements for the surface template technique, due to the high development of protection group techniques in organic chemistry. But this does not exclude the application of this technique to inorganic cases. It only means that we first have to learn the necessary chemistry.

4. Concluding remarks

From a theoretical point of view, molecular knots, links and fabrics, once formed, are expected to exist in many more cases than have been found up to now. Such molecules are likely to represent local minima of sufficient depth on potential energy hypersurfaces, and should possibly be realizable for any monomer (or set of monomers) that forms linear oligomers or polymers.

On the theoretical side, algorithms are described for the convenient build-up of the geometric structure of molecular knots and links, from a given geometric structure for the monomers and a piecewise linear (polygonal) representation of the desired knot or link. Essential features of the electronic structure of such molecules can be obtained from cyclic forms, as long as different parts of the molecular chain can be assumed to interact only weakly. The cyclic form, cyclo-M_l, likely exhibits rotational symmetry, due to presence of a rotation axis C_l of high order l (l ≥ 10). Additional symmetry elements may possibly be present, so that the electronic structure calculations should take advantage of the Abelian point groups C_l, C_lh, and S_l (with even l in the last case) to largest possible extent.

The actual experimental generation, i.e. the chemical synthesis of molecular knots, links, and fabrics, may be accomplished with a surface template technique suggested in this work. The principles of this technique are expected to be applicable not only to organic or biochemical cases, but to inorganic cases as well. A surface, regularly covered with linker groups, is used as a template. In a first step, only those pieces of the molecular chain(s) are chemically fixed to the surface which represent the lower parts at the crossing points of the desired knot or link. The remaining parts of the chain(s), including the upper parts at the crossing points, are linked to the surface in a second step. The bonds between the linear oligomers and the surface must be stable towards reagents used in the intermediate steps, until the desired molecular knot or link has been formed on the surface. Finally then, it is released from the surface by breaking all the bonds that fixed the chain(s) to the surface. The latter has to be regenerated, unless this has already been achieved during release of the knots or links.

If one considers chemistry and physics (including biochemistry and molecular biology) as sciences mastering the arrangement of atoms in three-dimensional space, to form molecules, polymers, crystals, etc., trying to understand the properties of these structures and making reliable use of this knowledge for the benefit and cultural development of man, then a toolbox for the study of molecular knots and links is simply a must. This toolbox has to be equipped with both theoretical and experimental tools. Once established, such a toolbox may be likely to help improve the living conditions on Earth, not only for man, as did the various textile manufacturing aids and tools mentioned at the beginning.

 

THE SERPENT   You imagine what you desire; you will what you imagine; and at last you create what you will.

EVE  How can I create out of nothing?

THE SERPENT  Everything must have been created out of nothing.¹

Acknowledgements

The author is thankful to Professor Juergen Hinze, Bielefeld, Germany, for critical reading of the manuscript, to Professor Roald Hoffmann, Ithaca, NY, USA, for bringing the work of N. C. Seeman and his group to his attention, and to Professor Alain Dedieu, Strasbourg, France, for helpful discussion. Some pictures of molecular knots were prepared by Ralf Brodbeck and Volker Koch. Their cooperation is gratefully acknowledged.

References

1. G. B. Shaw, Back to Methuselah. A Metabiological Pentateuch, Constable, London, 1921, repr. 1949, pp. 7 & 9.
2. R. G. Scharein, KnotPlot, Department of Computer Science, University of British Columbia, Vancouver, Canada, 1995–2004 (http://www.pims.math.ca/knotplot/).
3. Encyclopædia Britannica, Macropædia, Chicago, 15th edn, 1974–2002, articles on ‘Araneida’, ‘Textile Industry’ and ‘Writing, Forms of’.
4. C. W. Ashley, The Ashley Book of Knots, Faber and Faber, Boston, 1979.
5. M. H. Hansell, Animal Architecture and Building Behaviour, Longman, London, 1984.
6. (a) H. Adam, Nature (London), 1960, 188, 595; (b) R. Strahan, in The Biology of Myxine, ed. A. Brodal and R. Fänge, Universitetsforlaget, Oslo, 1963, pp. 22–32; (c) F. H. Martini, in The Biology of Hagfishes, ed. J. M. Jørgensen, J. P. Lomholt, R. E. Weber and H. Malte, Chapman & Hall, London, 1998, pp. 57–77.
7. W. C. McGrew and L. F. Marchant, Pan Africa News, 1998, 5, 8.
8. (a) W. Thomson, Proc. R. Soc. Edinburgh, 1867, 6, 94; (b) W. Thomson, Trans. R. Soc. Edinburgh, 1869, 25, 217.
9. (a) D. Rolfsen, Knots and Links, Publish or Perish, Berkeley, CA, 1976; (b) R. H. Crowell and R. H. Fox, Introduction to Knot Theory, Springer, New York, 1977; (c) G. Burde and H. Zieschang, Knots, de Gruyter, Berlin, 1985; (d) C. C. Adams, The Knot Book, Freeman, New York, 1994; (e) C. Livingston, Knot Theory, Mathematical Association of America, Washington, DC, 1993; (f) W. B. R. Lickorish, An Introduction to Knot Theory, Springer, New York, 1997; (g) V. V. Prasolov and A. B. Sossinsky, Knots, Links, Braids and 3-Manifolds: An Introduction to the New Invariants in Low Dimensional Topology, American Mathematical Society, Providence, RI, 1997; (h) P. R. Cromwell, Knots and Links, Cambridge University Press, Cambridge, 2004.
10. M. N. Burnett and C. K. Johnson, ORTEP-III, Oak Ridge National Laboratory Report ORNL-6895, USA, 1996 ( http://www.ornl.gov/sci/ortep/ortep.html).
11. G. Schaftenaar, MOLDEN, Centre for Molecular and Biomolecular Informatics (CMBI), University of Nijmegen, Netherlands, 2000–2005 (http://www.cmbi.ru.nl/molden/molden.html).
12. (a) M. Atiyah, The Geometry of Physics and Knots, Cambridge University Press, Cambridge, 1993; (b) L. H. Kauffman, Knots and Physics, World Scientific, Singapore, 3rd edn, 2001.
13. (a) E. Wasserman, J. Am. Chem. Soc., 1960, 82, 4433; (b) H. L. Frisch and E. Wasserman, J. Am. Chem. Soc., 1961, 83, 3789; (c) G. Schill and A. Lüttringhaus, Angew. Chem., 1964, 76, 567.
14. (a) B. Hudson and J. Vinograd, Nature (London), 1967, 216, 647; (b) D. A. Clayton and J. Vinograd, Nature (London), 1967, 216, 652.
15. (a) J. C. Wang, J. Mol. Biol., 1971, 55, 523; (b) L. F. Liu, R. E. Depew and J. C. Wang, J. Mol. Biol., 1976, 106, 439.
16. (a) C. Liang and K. Mislow, J. Am. Chem. Soc., 1994, 116, 11189; (b) C. Liang and K. Mislow, J. Am. Chem. Soc., 1995, 117, 4201; (c) W. R. Taylor, Nature (London), 2000, 406, 916.
17. W. R. Wikoff, L. Liljas, R. L. Duda, H. Tsuruta, R. W. Hendrix and J. E. Johnson, Science, 2000, 289, 2129.
18. D. M. L. Goodgame, P. D. Lickiss, S. J. Rooke, A. J. P. White and D. J. Williams, Inorg. Chim. Acta, 2001, 324, 218.
19. S. Ihara and S. Itoh, Carbon, 1995, 33, 931.
20. (a) G. Schill, Catenanes, Rotaxanes, and Knots, Academic Press, New York, 1971; (b) D. M. Walba, Tetrahedron, 1985, 41, 3161; (c) S. A. Wasserman and N. R. Cozzarelli, Science, 1986, 232, 951; (d) Fractals, Quasicrystals, Chaos, Knots and Algebraic Quantum Mechanics, ed. A. Amann, L. Cederbaum and W. Gans, Kluwer, Dordrecht, 1988; (e) R. E. Merrifield and H. E. Simmons, Topological Methods in Chemistry, Wiley-Interscience, New York, 1989; (f) J.-P. Sauvage, New J. Chem., 1993, 17(10–11), special issue on topology in molecular chemistry; (g) M. C. T. Fyfe and J. F. Stoddart, Acc. Chem. Res., 1997, 30, 393; (h) V. Balzani, M. Gómez-López and J. F. Stoddart, Acc. Chem. Res., 1998, 31, 405; (i) Molecular Catenanes, Rotaxanes and Knots. A Journey Through the World of Molecular Topology, ed. J.-P. Sauvage and C. Dietrich-Buchecker, Wiley-VCH, Weinheim, 1999; (j) E. Flapan, When Topology Meets Chemistry. A Topological Look At Molecular Chemistry, Cambridge University Press, Cambridge, 2000; (k) O. Lukin and F. Vögtle, Angew. Chem., Int. Ed., 2005, 44, 1456.
21. (a) Molecular Self-Assembly. Organic versus Inorganic Approaches, ed. M. Fujita, Springer, Berlin, 2000; (b) Molecular Machines and Motors, ed. J.-P. Sauvage, Springer, Berlin, 2001; (c) V. Balzani, A. Credi and M. Venturi, Molecular Devices and Machines—A Journey into the Nano World, Wiley-VCH, Weinheim, 2003; (d) The Chemistry of Nanostructured Materials, ed. P. Yang, World Scientific, New Jersey, 2003; (e) Supramolecular Assembly via Hydrogen Bonds I & II, ed. D. M. P. Mingos, Springer, Berlin, 2004; (f) Functional Molecular Nanostructures, ed. A. D. Schlüter, Springer, Berlin, 2005; (g) Templates in Chemistry I & II, ed. C. A. Schalley, F. Vögtle and K. H. Dötz, Springer, Berlin, 2005.
22. (a) C. O. Dietrich-Buchecker and J.-P. Sauvage, Chem. Rev., 1987, 87, 795; (b) C. O. Dietrich-Buchecker and J.-P. Sauvage, Angew. Chem., 1989, 101, 192; (c) C. O. Dietrich-Buchecker, C. Hemmert, A.-K. Khémiss and J.-P. Sauvage, J Am. Chem. Soc., 1990, 112, 8002; (d) C. Dietrich-Buchecker and J.-P. Sauvage, New J. Chem., 1992, 16, 277.
23. (a) J. E. Mueller, S. M. Du and N. C. Seeman, J. Am. Chem. Soc., 1991, 113, 6303; (b) J. Chen and N. C. Seeman, Nature (London), 1991, 350, 631; (c) S. M. Du and N. C. Seeman, J. Am. Chem. Soc., 1992, 114, 9652; (d) N. C. Seeman, J. Chen, S. M. Du, J. E. Mueller, Y. Zhang, T.-J. Fu, Y. Wang, H. Wang and S. Zhang, New J. Chem., 1993, 17, 739; (e) S. M. Du, B. D. Stollar and N. C. Seeman, J. Am. Chem. Soc., 1995, 117, 1194; (f) N. C. Seeman, Acc. Chem. Res., 1997, 30, 357; (g) N. C. Seeman, Nature (London), 2003, 421, 427.
24. (a) D. B. Amabilino and J. F. Stoddart, Chem. Rev., 1995, 95, 2725; (b) S. J. Cantrill, K. S. Chichak, A. J. Peters and J. F. Stoddart, Acc. Chem. Res., 2005, 38, 1.
25. (a) O. Safarowsky, M. Nieger, R. Fröhlich and F. Vögtle, Angew. Chem., Int. Ed., 2000, 39, 1616; (b) F. Vögtle, A. Hünten, E. Vogel, S. Buschbeck, O. Safarowsky, J. Recker, A.-H. Parham, M. Knott, W. M. Müller, Y. Okamoto, T. Kubota, W. Lindner, E. Francotte and S. Grimme, Angew. Chem., Int. Ed., 2001, 40, 2468.
26. The possible existence of this and similar compounds could have been anticipated already from the crystal structure analysis of Hittorf phosphorus,⁴⁴ see also the recent discovery of new phosphorus allotropes⁴⁵.
27. R. G. Scharein, Thesis, Department of Computer Science, University of British Columbia, Vancouver, Canada, 1998.
28. G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123.
29. G. Schill, N. Schweickert, H. Fritz and W. Vetter, Angew. Chem., 1983, 95, 909.
30. I. N. Levine, Quantum Chemistry, Prentice-Hall, Englewood Cliffs, New Jersey, 5th edn, 2000.
31. IUPAC-IUB Commission on Biochemical Nomenclature, Pure Appl. Chem., 1974, 40, 291.
32. IUPAC-IUB Joint Commission on Biochemical Nomenclature, Pure Appl. Chem., 1983, 55, 1269.
33. IUPAC-IUB Joint Commission on Biochemical Nomenclature, Pure Appl. Chem., 1983, 55, 1273.
34. R. E. Dickerson, M. Bansal, C. R. Calladine, S. Diekmann, W. N. Hunter, O. Kennard, E. von Kitzing, R. Lavery, H. C. M. Nelson, W. K. Olson, W. Saenger, Z. Shakked, H. Sklenar, D. M. Soumpasis, C.-S. Tung, A. H.-J. Wang and V. B. Zhurkin, EMBO J., 1989, 8, 1.
35. W. K. Olson, M. Bansal, S. K. Burley, R. E. Dickerson, M. Gerstein, S. C. Harvey, U. Heinemann, X.-J. Lu, S. Neidle, Z. Shakked, H. Sklenar, M. Suzuki, C.-S. Tung, E. Westhof, C. Wolberger and H. M. Berman, J. Mol. Biol., 2001, 313, 229.
36. F. Klok, Comput. Aided Geom. Des., 1986, 3, 217.
37. A piecewise linear (or polygonal) representation of a knot of type n_k, with an arbitrary number l of vertices and edges, can be readily obtained with the help of, e.g., the KnotPlot²⁷ program. It is even possible to pre-equilibrate the polygon.
38. The two-fold degenerate representations in the groups C_n, C_nh and S_2n are reducibly degenerate, i.e., they can be split into two one-dimensional irreducible representations, at the affordable cost of appearance of complex characters.
39. D. M. Eigler and E. K. Schweizer, Nature (London), 1990, 344, 524.
40. M. F. Crommie, C. P. Lutza and D. M. Eigler, Science, 1993, 262, 218.
41. J. A. Stroscio and D. M. Eigler, Science, 1991, 254, 1319.
42. A. Petitjean, R. G. Khoury, N. Kyritsakas and J.-M. Lehn, J. Am. Chem. Soc., 2004, 126, 6637.
43. S.-W. Hla, G. Meyer and K.-H. Rieder, Chem. Phys. Lett., 2003, 370, 431.
44. H. Thurn and H. Krebs, Acta Crystallogr., Sect. B, 1969, 25, 125.
45. A. Pfitzner, M. F. Bräu, J. Zweck, G. Brunklaus and H. Eckert, Angew. Chem., 2004, 116, 4324.

---