 Open Access Article
Open Access ArticleAchieving high performance triboelectric nanogenerators simultaneously with high-voltage and high-charge energy cycle†
Yikui
Gao‡
ab,
Jiaqi
Liu‡
ac,
Linglin
Zhou
*ab,
Lixia
He
ab,
Di
Liu
ab,
Peiyuan
Yang
a,
Bingzhe
Jin
ab,
Zhong Lin
Wang
*abdef and
Jie
Wang
 *abd
*abd
aBeijing Institute of Nanoenergy and Nanosystems, Chinese Academy of Sciences, Beijing 101400, China. E-mail: zhoulinglin@binn.cas.cn; wangjie@binn.cas.cn
bSchool of Nanoscience and Engineering, University of Chinese Academy of Sciences, Beijing, 100049, P. R. China
cCangzhou Normal University, Cangzhou 061001, P. R. China
dGuangzhou Institute of Blue Energy, Knowledge City, Huangpu District, Guangzhou 510555, P. R. China
eGeorgia Institute of Technology, Atlanta, GA 30332, USA. E-mail: zhong.wang@mse.gatech.edu
fYonsei Frontier Lab, Yonsei University, Seoul 03722, Republic of Korea
First published on 9th October 2024
Abstract
Triboelectric nanogenerators (TENGs), serving as an innovative energy harvesting technology, have garnered significant attention and demonstrated promising potential applications across internet of things and artificial intelligence. However, developing an efficient and rational power management circuit (PMC) remains a significant challenge, primarily attributed to the limited energy transmission efficiency. Here, we propose a universal and effective strategy that can achieve lossless energy transmission between TENGs and PMCs by using the inherent capacitor of the TENG as the excitation source for the PMC. Additionally, we attain high-charge output (1.24 mC m−2) and high-voltage output (7200 V) simultaneously by harnessing the space charge accumulation effect and increasing the thickness of the triboelectric layer. More importantly, a high energy output of 4.24 J m−2 cycle−1 is achieved in the HV–HQ energy cycle by eliminating spark discharge at the synchronous switch. This groundbreaking work perfectly addresses the unavoidable low energy transmission efficiency issue, and provides a new methodology for achieving high-performance TENGs to power electrical devices.
Broader contextIn the age of the internet of things (IoTs), there's a growing need for dependable power sources for distributed electronics. Triboelectric nanogenerators (TENGs) have attracted broad attention due to their superior merits. However, their inherent electrical characteristics of low current and high voltage do not match the typical electronic device requirements. Therefore, an efficient power management circuit (PMC) is indispensable to bridge the gap between the TENG and electronic devices. This work comprehensively analyzes the energy transmission relationship between TENGs’ maximum energy cycle and various energy extraction methods by utilizing the V–Q plot. It indicates that taking the inherent capacitor of the TENG as the excitation source for the PMC can not only greatly reduce the costs but also achieve lossless energy transmission. Additionally, this work also demonstrates that increasing the thickness of the triboelectric layer is a feasible strategy to enhance output voltage without charge loss caused by electrostatic breakdown, achieving a HV–HQ energy cycle with an energy density of 4.24 J m−2 cycle−1. This work not only provides a new approach for improving the performance of the TENG but also offers a typical paradigm for the efficient utilization and storage of TENG output energy. |
Introduction
With the rapid development of internet of things (IoTs) and artificial intelligence (AI), the demand for distributed energy has skyrocketed due to the increasing number of portable electronic devices.1–3 Based on the conjunction of triboelectrification and electrostatic induction effects, triboelectric nanogenerators (TENGs) can effectively convert ubiquitous mechanical motions into electricity,4–9 and thereby provide an alternative solution to replace the conventional batteries and have the merits of low cost,10–14 wide selection of materials,15,16 environmental friendliness17–19 and easy fabrication.20,21 However, the TENG has low-current and high-voltage characteristics induced by its high internal resistance, which mismatches the requirement of power supply with only several volts for common electronic devices.22,23 Hence, an efficient power management circuit (PMC) is indispensable to bridge the gap between the TENG and electronic devices.Generally, for the conventional PMC, an appropriate input capacitor (Cin) is necessary to extract the electrical energy generated by the TENG, and then serve as the excitation source for the subsequent circuit. Take the LC buck circuit as an example,24–29 which is a commonly used PMC in the TENG's field; its energy transmission path can be expressed as CT–Cin–L–Cout (CT is the inherent capacitor of the TENG, L is the inductance, and Cout is the output capacitor). It is worth noting that the first stage energy transmission path composed of CT and Cin often causes massive energy loss. Theoretically, Cin can only capture approximately 25% of the maximum output energy from the TENG; even when Cin is employed as the constant-voltage excitation source for the PMC, its energy capture efficiency remains limited to about 50%. Currently, by directly using the CT as the excitation source for the PMC (a new energy transmission path of CT–L–Cout), the limitation of maximum energy transmission efficiency in the dual-capacitor system (CT–Cin) can be overcome.29–31 However, without the suppressive effect of Cin on electrostatic breakdown,24,29 the concurrent increase of both output voltage and output charge will further exacerbate the electrostatic breakdown, i.e. only the HV–LQ energy cycle (high-voltage output but low-charge output) or LV–HQ energy cycle (low-voltage output but high-charge output) can be obtained,30 which greatly limits the improvement of TENG energy density (ET = 0.5 × QSC × VOC). In addition, even if the HV–HQ energy cycle with high-voltage output and high-charge output is realized, the inevitable energy loss caused by spark discharge at the synchronous switch will also result in an obvious decrease in energy transmission efficiency.32 Therefore, there is an urgent need to simultaneously achieve lossless energy transmission between TENGs and PMCs, along with the design of high-performance TENGs with high-charge output and high-voltage output, to further broaden their practical applications.
Here, we propose a comprehensive and effective approach that simultaneously achieves high-voltage output and high-charge output for TENGs, while maintaining lossless energy transmission between the TENG and the PMC. Through rigorous analysis of the capacitance model and structural parameters of the sliding-mode TENG (S-TENG), we demonstrate that increasing the thickness of the triboelectric layer is a feasible strategy to enhance output voltage without charge loss. Specifically, by employing polytetrafluoroethylene (PTFE) and nylon (PA) as tribo-material pairs, we achieve a voltage of 7200 V and a charge density of 1.24 mC m−2via increasing the PTFE thickness to 150 μm. Moreover, apart from utilizing CT as the direct excitation source for the PMC, we incorporate a synchronous switch within a specifically designed oil-based medium to eliminate spark discharges, thus ensuring lossless energy transmission. Finally, a high-voltage and high-charge energy cycle (HV–HQ energy cycle) with a record-breaking energy density of 4.24 J m−2 cycle−1 is obtained. Furthermore, by matching an appropriate PMC, the output power of the S-TENG is enhanced by at least two orders of magnitude under low voltage conditions (0.5–5 V). As a demonstration, 16 hygrothermographs operating in parallel and three wireless sensors are continuously powered by a small TENG with an electrode area of just 10 cm2, operating at a low frequency of 1 Hz. This work not only provides a new approach to improving the performance of TENGs, but also offers a typical paradigm for efficient utilization and storage of TENG output energy.
Results
The strategy of energy transmission of TENGs
To effectively utilize and store the energy generated by TENGs, a compatible and efficient power management strategy is crucial. As shown in Fig. 1a, the energy transmission process within conventional strategies can be broadly categorized into three stages. In the first stage, the input capacitor (Cin) extracts energy from the TENG, serving as the excitation source for the PMC. In the second stage, the stored energy in Cin is released through a synchronous switch to the PMC, which then transfers it to the output capacitor (Cout). In the third stage, the energy stored in Cout is utilized to power electrical appliances. Improving the PMC energy transmission efficiency of the second stage can be achieved by optimizing inductors,28 freewheeling diodes,33 and Cout to minimize energy losses.30 However, a common question that is overlooked is how to improve the energy transmission efficiency from TENG to PMC.The V–Q plot directly visualizes the TENG's output energy cycle across various loads, thus serving as a valuable tool to investigate the energy transmission efficiency of different energy extraction methods.34–36 As shown in Fig. 1b, VOC represents the open-circuit voltage, while QSC represents the short-circuit charge. Cin1, Cin2, and Cin3 represent Cin with different capacity values, and Vin1, Vin2, and Vin3 indicate different output voltages. Additionally, the CMEO curve (the black line in Fig. 1b(i) and (ii)) illustrates the theoretical maximum output energy cycle achievable by TENGs. Notably, regardless of the electronic components being powered, such as resistors, capacitors, batteries, etc., the output energy cycles generated by TENGs never exceed this CMEO curve.
C in is often utilized to directly extract energy from the TENG, and the energy of Cin can be calculated as
 | (1) |
C T is the inherent capacitor of the TENG (the detailed calculated process is presented in Note S1, ESI†). When Cin is equal to CT, the maximum energy can be obtained. Obviously, the energy transmission efficiency is just 25% (Fig. 1b(i)).
Furthermore, more energy can be obtained from the TENG when the voltage of Cin remains fixed at 0.5 × VOC. As shown in Fig. 1b(ii), the area enclosed by the V–Q curve of Cin transforms from a triangle to a rectangle. The energy can be calculated as
| E = Vin(QSC − VinCT) | (2) |
The dual-capacitor energy transmission system, comprised of the TENG and Cin, is limited to a transfer efficiency of 50%, making it not an optimal choice for developing a highly efficient power management circuit. It is clear that the energy generated by the TENG is stored within the inherent capacitor (CT), as shown in Fig. 1c (ET = 0.5 × QSC × VOC). When the TENG itself functions as the excitation source for the PMC, we not only enable the lossless energy transmission between the TENG and the PMC (Fig. 1d), but also greatly reduce the cost of finding the optimum Cin or Vin in previous works and simplify the design process of the power management circuit. However, without the suppressive effect of Cin on electrostatic breakdown,24,29 by conventional methods it is difficult for TENG to simultaneously possess the characteristics of high-voltage output and high-charge output so that the TENG can only achieve the HV–LQ energy cycle28,37 (increasing the air gap between triboelectric layers or decreasing the overlap area of electrodes) or the LV–HQ energy cycle29–32 (decreasing the air gap between triboelectric layers or decreasing the thickness of triboelectric layers) (Fig. 1e), which greatly limits the further improvement of TENG energy density.
We propose that it is indeed crucial to achieve efficient energy transmission of TENGs, but it is even more important to simultaneously achieve an energy cycle with higher energy density, as this not only enhances the overall performance of the system but also paves the way for a broader adoption and utilization of TENGs across diverse scenarios. Therefore, the ultimate goal of this work is to achieve lossless energy transmission between the TENG and the PMC while simultaneously achieving the HV–HQ energy cycle (Fig. 1f). By analyzing the structural parameters of the S-TENG, here we demonstrate that increasing the thickness of the triboelectric layer can effectively enhance the output voltage without charge loss due to air breakdown. Furthermore, the arc-extinguishing effect of oil medium aids in preventing energy loss at the synchronous switch, and then an HV–HQ energy cycle with a maximum energy density of 4.24 J m−2 cycle−1 is ultimately achieved (Fig. 1g). Detailed analysis is presented in the following sections.
Achieving high-charge output
To achieve the HV–HQ energy cycle, obtaining a high charge density is crucial. Here, the S-TENG is utilized to achieve this, and its working mechanism is shown in Fig. 2a. Briefly, the triboelectric layers accumulate surface charges due to the triboelectrification effect, and then the S-TENG generates current during the periodic motion by changing the relative position of triboelectric layers. Compared to other mode TENGs, the S-TENG offers two distinct advantages:On the one hand, the shielding electrode (Fig. 2b(i)) effectively suppresses electrostatic breakdown between triboelectric layer 1 (TL1) and triboelectric layer 2 (TL2). Commonly, insufficient contact at the interface results in the formation of numerous air gaps between triboelectric layers (Fig. 2b(ii)), ultimately leading to inevitable air breakdown and charge loss. As demonstrated in Fig. 2c and d, regardless of the upper slider's position, the electric field strength within air gaps is significantly reduced when a shielding electrode is present compared to when it is absent (Fig. S2, ESI†). The parameters of finite element simulated calculations are detailed in Table S1 (ESI†). Consequently, the surface charge density of the S-TENG rises from 0.35 mC m−2 to 1.24 mC m−2 with the introduction of the shielding electrode.
On the other hand, the dissipation of surface charge in triboelectric layer 2 enables triboelectric layer 1 to quickly accumulate a higher surface charge density,38 as shown in Fig. 2f. In the first cycle, prior to the atomic-scale contact between TL1 and TL2, their respective electron clouds remain separate without overlap (Fig. 2f(i)). Once TL1 comes in contact with TL2, an electron transition occurs from TL2 to TL1, resulting in a decrease in the energy potential barrier difference between the two materials (Fig. 2f(ii)), which has been confirmed by atomic force Kevin probe microscopy.39,40 If the surface charge of TL2 remains stable, then in the following cycles, fewer electrons would transit from TL2 to TL1 due to the already reduced energy potential barrier difference. Actually, the positive surface charge on TL2 will dissipate through either air breakdown or material leakage, i.e. electrons return to TL2 (Fig. 2f(iii)), which allows the energy potential barrier difference to re-form between TL1 and TL2 (Fig. 2f(iv)). Thus, electrons will continuously transfer from TL2 to TL1 in the following cycles, resulting in a higher surface charge density in TL1 (Fig. 2f(v) and (vi)). This assumption has been confirmed by the surface charge density of triboelectric layers in different regions, as shown in Fig. 2g. It is evident that the surface charge density in region A, B and C of TL2 is two orders of magnitude smaller than that in region D of TL1.
To further increase the output charge of the S-TENG, three representative negative polarity materials (PTFE, fluorinated ethylene propylene (FEP), fluoroplastics (ETFE)) and three positive polarity materials (polycarbonate (PC), thermoplastic polyurethane (TPU), PA) are selected as different material pairs (PTFE-PC, PTFE-TPU, FEP-PA, ETFE-PA and PTFE-PA) to fabricate the S-TENG. The corresponding output charges are shown in Fig. 2h, which are 0.44 mC m−2, 0.52 mC m−2, 0.49 mC m−2, 1.13 mC m−2 and 1.24 mC m−2 respectively. The corresponding currents at 0.5 Hz work frequency are 3.3 μA, 4.2 μA, 4.3 μA, 6.4 μA, and 11.3 μA, as shown in Fig. 2i. The experimental results indicate that PTFE has stronger electron acquisition ability compared to FEP and ETFE, and PA is more likely to lose electrons compared to TPU and PC. Therefore, the PTFE–PA pair is selected as the optimum material to fabricate the S-TENG and the corresponding photograph is shown in Fig. S3 (ESI†). Additionally, the output performance of the S-TENG at different operating frequencies was also measured. With the operating frequency increasing from 0.25 Hz to 1 Hz, the corresponding charge almost remains stable (Fig. 2j), and the current increases with increasing operating frequency (Fig. 2k). In addition, the result (Fig. S4, ESI†) indicates that the output charge of the S-TENG still maintains 91.9% of its initial value after 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, showing good durability.
000 cycles, showing good durability.
Achieving high-voltage output
The other essential factor for achieving a HV–HQ energy cycle is increasing the output voltage of the S-TENG while ensuring a stable output charge. Therefore, we conducted an analysis of the impact of S-TENG's device parameters on QSC and VOC.The open-circuit voltage (VOC) of the S-TENG can be calculated as
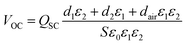 | (3) |
According to Paschen's law, as the air gap increases, the threshold electric field at the air gap gradually decreases, which would reduce the upper limit of the surface charge density of the S-TENG (Fig. 3c and Fig. S5 and Note S4, ESI†). Additionally, based on eqn (4), even if the surface charge density (σ) of TL1 remains constant, increasing dair or d2 will lead to a decrease in QSC (Fig. 3c and d and Fig. S6, ESI†).
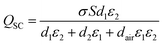 | (4) |
Furthermore, a decrease in the overlap area of the electrodes will also sharply increase the electric field intensity of the air gap. Due to the concentrated distribution of induced charges at the electrodes (Fig. S7, ESI†), the electric field strength in the overlapping area of the electrodes in open-circuit state is much higher than that in short-circuit state (the maximum electric field strength under short circuit conditions is the threshold electric field of air breakdown, as shown by the dashed line in Fig. 3e), which means that the high surface charge of TL1 can no longer be maintained when the S-TENG is in the open-circuit state (Fig. 3e, the parameters of simulation are presented in Table S1, ESI†). Therefore, increasing d2 and dair or decreasing S to increase VOC is not advisable.
By increasing d1, we can also increase the VOC of the S-TENG, and the charge distribution is shown in Fig. S8 (ESI†). Benefiting from the induced charges generated by the grounded electrode, we observe a notable attenuation in the electric field of the air gap when the S-TENG operates in an open-circuit state compared to that in a short-circuit state (Fig. 3f). Notably, this attenuation phenomenon persists even as VOC continues to increase (Fig. 3f). This implies that by adopting this approach, we can effectively enhance the output voltage without compromising the output charge (Fig. 3g and h, Note S5, ESI†). The experimental results in Fig. 3i demonstrate that, when the thickness of PTFE is increased from 30 μm to 150 μm, VOC reaches 7200 V without any obvious decrease in QSC (Fig. 3j), which is consistent with the previous simulation results (the parameters of simulation are presented in Note S6 and Table S2, ESI†).
Achieving a HV–HQ energy cycle
Taking advantage of the high voltage and high charge density of the S-TENG, the energy stored in CT can be completely released by a synchronous switch to achieve a HV–HQ energy cycle. The detailed working mechanism of the S-TENG with synchronous switch is shown in Fig. 4a. Fig. 4a(i) shows the initial state of charge distribution of the S-TENG. When the slider moves to the right or the left of the stator (Fig. 4a(ii) and Fig. S9, ESI†), positive charges will transfer from the bottom electrode to the top electrode by the diode, and the energy will be stored in the PTFE film. During this process, the S-TENG operates in a short-circuit state, which can prevent excessive electric field at the air gap from reducing the surface charge of PTFE. Then, when the slider moves to the initial position gradually, there is no charge transfer in the external circuit because the diode is not conducting (Fig. 4a(iii)). Once the top electrode overlaps with the bottom electrode, the synchronous switch will close and energy will be released from the TENG (Fig. 4a(iv)). In order to clearly understand the energy release process of the S-TENG, an equivalent circuit diagram for the S-TENG when the electrodes overlap is constructed (Fig. 4b and Fig. S10, ESI†), which includes the switch, resistor (Rload), and equivalent capacitors CPTFE, Cair, and CPA formed by PTFE, air and PA, respectively. Before the switch closes (Fig. 4b(i)), energy is stored in CPTFE, and the initial voltage of CPTFE is σ*S/CPTFE, while the initial voltage of Cair and CPA is zero. When the switch closes (Fig. 4b(ii)), energy will be released from CPTFE to Cair, CPA and Rload until the entire circuit reaches a steady state (the sum of the voltage of CPTFE, Cair, and CPA is 0 at this time). Therefore, by calculating the dynamic equation of the circuit (Note S7 and Fig. S11, ESI†), the energy that can be utilized during this process is equivalent to the energy stored in CT with an initial charge of QSC.Fig. 4c presents the structural schematic diagram of the S-TENG equipped with a synchronous switch, which is located at the center of both the stator and the slider, ensuring that the switch closes when the electrodes overlap. The test circuit and the method are shown in Fig. S12 and Note S8 (ESI†). Actually, with the decrease of the switch gap, multiple spark discharges will occur at the switch gap, resulting in energy loss. As shown in Fig. 4d(i) and Movie S1 (ESI†), it can be observed that the first spark discharge occurs before the switch closes, as the voltage of the S-TENG is higher than the withstand voltage of the gap of switch. During this process, partial charges are released (Fig. S13, ESI†) and the residual charges are still in CT to maintain the high voltage of the S-TENG. Therefore, as the switch gap decreases, the withstand voltage of the gap also continuously decreases, and spark discharge occurs again once the voltage of the S-TENG again exceeds the withstand voltage (Fig. 4e(i)). In order to avoid this phenomenon, the switch was soaked in an oil medium with high electrical insulation to eliminate spark discharge and achieve complete energy utilization. As shown in Fig. 4d(ii), Movie S1 (ESI†) and Fig. 4e(ii), compared with the switch in air, only one spark discharge occurs when the switch soaked in oil. Therefore, the output energy of the S-TENG with the switch soaked in oil is nearly twice higher than that in air (Fig. 4f, the shaded area refers to the output energy).
Moreover, Fig. 4g further shows the advantage of the synchronous switch in the energy utilization of TENGs. In the low impedance range (0.01–10 MΩ), the experimental results show that the output energy density of the S-TENG with switch is much higher than that without switch. Especially, compared with the switch put in air, the output energy density of the S-TENG with the switch immersed in oil is at least doubled. Furthermore, the energy cycle of the S-TENG with different QSC was also measured as shown in Fig. S13 (ESI†). It is obvious that the output voltage increases from 1.02 kV to 4.45 kV and the output energy also increases from 0.09 J m−2 to 2.52 J m−2 with QSC increasing from 0.18 μC to 1.18 μC, which means that higher energy output can be achieved by increasing the output charge density. In addition, consistent with previous analysis about the relationship between the voltage and film thickness in Fig. 4i, the output voltage can increase from 3.4 kV to 7.2 kV with a stable output charge of 1.11 μC as the thickness of PTFE increases from 30 μm to 150 μm, which leads to an output energy density as high as 4.24 J m−2 cycle−1 (Fig. 4h). Benefitting from the HV–HQ energy cycle, this work achieved the highest output energy density in one energy cycle compared with the previous works (Fig. 1g).
Application demonstration of the S-TENG with PMC
Although the S-TENG exhibits high energy density, it still cannot drive electronic devices directly due to its inherent characteristics of high voltage and low current output that does not match the impedance of electronic devices. Therefore, the PMC is necessary to decrease the voltage and increase the current of the S-TENG for matching the requirement of electronic devices (the photo of the S-TENG with synchronous switch and PMC is shown in Fig. S14, ESI†). The circuit diagram of the PMC is displayed in Fig. 5a, which can be divided into three stages. In the first stage, the TENG collects mechanical energy from the environment and converts it into electrical energy for storage in CT. In the second stage, the switch closes, and energy transmission from CT to the inductor (L) occurs instantaneously, where L acts as an energy storage unit. In the third stage, the energy stored in L (L acts as the power source) is slowly released to the output capacitor (Cout). In particular, by changing the capacitance of Cout, the S-TENG can provide both stable direct current (DC) and pulse DC to satisfy the need of different applications. As shown in Fig. 5b, when the load is 10 kΩ and the capacitance varies from 1 μF to 1000 μF, the current gradually changes from a pulsed current of 3.5 mA to a constant current of 0.22 mA. This is related to the time constant (τ) of the RC circuit. Therefore, if τ is very small, the energy of Cout will be released in a very short period of time and a high peak current can be achieved. Fig. 5c gives the average power density of the S-TENG with PMC. When the output voltage is in the common range of 0.5–5.0 V, the average power density increases at least two orders of magnitude compared to the case without PMC, which indicates that the S-TENG can drive common electrical appliances more efficiently with PMC (Fig. S15 and Note S9, ESI†). Moreover, the S-TENG with PMC can easily charge a 100 μF capacitor to 13.3 V in 10 s, a voltage 100 times higher than that without PMC (Fig. 5d), and also can achieve a high energy storage rate that is 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times greater than that without PMC (Fig. S16, ESI†), laying a firm foundation for driving electronic devices.
000 times greater than that without PMC (Fig. S16, ESI†), laying a firm foundation for driving electronic devices.
Based on the excellent output performance and various output characteristics of the S-TENG with PMC, it can be a power source for different applications. As shown in Fig. S17 (ESI†), when Cout is 2.2 μF, a high peak current is achieved, and ten bulbs (10 W) in parallel can be easily powered (Movie S2, ESI†). Moreover, the S-TENG with PMC can not only generate peak current, but can also produce direct current to stably power electronics. As shown in Fig. 5g and Movie S3 (ESI†), when the S-TENG operates at a motion frequency of 1 Hz and with a Cout of 4.7 mF, it is capable of powering 16 hygrothermographs with the required operating voltage of 1.5 V (Fig. 5e), which ensures that the hygrothermographs operate steadily. Furthermore, when Cout increases to 15 mF, the S-TENG can not only simultaneously drive multiple sensors, including hygrothermograph, vibration sensor and light intensity sensor, but can also achieve wireless transmission functionality (Fig. 5h and Movie S4, ESI†). Fig. 5f shows the detailed voltage changes during this process and the subsequent stable operating state.
Conclusions
Here, we comprehensively analyzed the energy transmission relationship between the maximum energy cycle of the TENG and different energy extraction methods, utilizing the direct visualization tool, the V–Q plot. Based on our analysis, we proposed that by using the inherent capacitor of the TENG as the excitation source for the PMC, we can not only greatly reduce the cost of finding the optimum capacitance/voltage but can also avoid the massive energy loss caused by the dual-capacitor system, thereby achieving lossless energy transmission between the TENG and the PMC. Furthermore, by utilizing the characteristics of bottom triboelectric layer's charge dissipation of the S-TENG and material optimization, a high charge density of 1.24 mC m−2 was obtained. More importantly, through rigorous analysis of the capacitance model and structural parameters of the S-TENG, we found that increasing the thickness of the top triboelectric layer is a feasible method to enhance output voltage while avoiding the charge loss caused by the electrostatic breakdown. Specifically, a voltage up to 7200 V can be obtained by increasing the PTFE thickness to 150 μm. Finally, by combining with a synchronous switch submerged in oil to eliminate spark discharge, the HV–HQ energy cycle with a high energy density of 4.24 J m−2 cycle−1 was achieved. Due to the high performance of the S-TENG and lossless energy transmission between the TENG and the PMC, the output power of the S-TENG can be enhanced by at least two orders of magnitude under low voltage conditions (0.5–5 V) by matching an appropriate PMC, and 16 hygrothermographs operating in parallel or three wireless sensors can be continuously powered by a small TENG with an electrode area of just 10 cm2. Overall, this work provides a typical paradigm for efficient utilization and storage of TENG output energy and sets the foundation for further applications and industrialization of TENG technology.Experimental section
Fabrication of the S-TENG
Slider: (1) Cut a piece of acrylic sheet with dimensions of 30 × 60 × 4 mm as a substrate using a laser cutter. (2) Stick a 1 mm thick piece of foam on the top of the acrylic sheet. (3) Place a conductive fabric on top of the sponge and use a laser cutter to cut it into 20 × 50 mm. (4) Cut a piece of PTFE with dimensions of 30 × 60 mm and place it on the conductive fabric as a triboelectric layer.Stator: (1) Cut a piece of acrylic sheet with dimensions of 90 × 60 × 4 mm as a substrate using a laser cutter. (2) Stick a 2 mm thick piece of foam on the top of the acrylic sheet. (3) Place a conductive fabric on top of the sponge and use a laser cutter to cut it into 20 × 50 mm. (4) A 50 μm thick Kapton is affixed to both sides of the conductive fabric for a flat surface. (5) Cut a piece of PA with dimensions of 90 × 60 mm and place it on the conductive fabric as a triboelectric layer.
Characterization and electrical measurement
The sliding process was driven by a linear motor (TSMV120-1S). The short-circuit current and transferred charges of the TENG were measured with a programmable electrometer (Keithley model 6514). The open-circuit voltage was obtained by using the mixed domain oscilloscope (MDO3024). The acrylic sheet was cut using a laser cutter.Author contributions
Y. G. and J. W. conceived the idea. Y. G. and J. L. designed the experiments and performed data measurements. Y. G., J. L., L. Z. and D. L analyzed the data. L. H., D. L., P. Y. and B. J. helped with the experiments. Y. G., J. L., L. Z. and J. W. drafted the manuscript. L. Z., J. W. and Z. L. W. supervised this work. All the authors discussed the results and commented on the manuscript.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no competing interests.Acknowledgements
The research was supported by the National Key R & D Project from the Minister of Science and Technology (2021YFA1201602), the National Nature Science Foundation of China (No. 22109013, U21A20147, 62204017, 52302214, and 62304024), the China Postdoctoral Science Foundation (2021M703171), and the Fundamental Research Funds for the Central Universities (E2E46803).References
- A. Alagumalai, W. Shou, O. Mahian, M. Aghbashlo, M. Tabatabaei, S. Wongwises, Y. Liu, J. Zhan, A. Torralba, J. Chen, Z. Wang and W. Matusik, Joule, 2022, 6, 1475–1500 CrossRef CAS.
- W. Xu, H. Zheng, Y. Liu, X. Zhou, C. Zhang, Y. Song, X. Deng, M. Leung, Z. Yang, R. X. Xu, Z. L. Wang, X. C. Zeng and Z. Wang, Nature, 2020, 578, 392–396 CrossRef CAS.
- R. Hinchet, H.-J. Yoon, H. Ryu, M.-K. Kim, E.-K. Choi, D.-S. Kim and S.-W. Kim, Science, 2019, 365, 491–494 CrossRef CAS.
- J. Chen, Y. Huang, N. Zhang, H. Zou, R. Liu, C. Tao, X. Fan and Z. L. Wang, Nat. Energy, 2016, 1, 16138 CrossRef CAS.
- H. Li, A. Berbille, X. Zhao, Z. Wang, W. Tang and Z. L. Wang, Nat. Energy, 2023, 8, 1137–1144 CrossRef CAS.
- H. Guo, X. Pu, J. Chen, Y. Meng, M.-H. Yeh, G. Liu, Q. Tang, B. Chen, D. Liu, S. Qi, C. Wu, C. Hu, J. Wang and Z. L. Wang, Sci. Robot., 2018, 3, eaat2516 CrossRef.
- J. Wang, C. Wu, Y. Dai, Z. Zhao, A. Wang, T. Zhang and Z. L. Wang, Nat. Commun., 2017, 8, 88 CrossRef.
- C. Zhang, L. Zhou, P. Cheng, X. Yin, D. Liu, X. Li, H. Guo, Z. L. Wang and J. Wang, Appl. Mater. Today, 2020, 18, 100496 CrossRef.
- J. H. Park, H. E. Lee, C. K. Jeong, D. H. Kim, S. K. Hong, K.-I. Park and K. J. Lee, Nano Energy, 2019, 56, 531–546 CrossRef CAS.
- L. Zhou, Y. Gao, D. Liu, L. Liu, Z. Zhao, S. Li, W. Yuan, S. Cui, Z. L. Wang and J. Wang, Adv. Energy Mater., 2021, 2101958 CrossRef.
- L. Zhou, D. Liu, Z. Zhao, S. Li, Y. Liu, L. Liu, Y. Gao, Z. L. Wang and J. Wang, Adv. Energy Mater., 2020, 10, 2002920 CrossRef CAS.
- A. Chen, Q. Zeng, L. Tan, F. Xu, T. Wang, X. Zhang, Y. Luo and X. Wang, Energy Environ. Sci., 2023, 16, 3486–3496 RSC.
- D. Liu, X. Yin, H. Guo, L. Zhou, X. Li, C. Zhang, J. Wang and Z. L. Wang, Sci. Adv., 2019, 5, eaav6437 CrossRef CAS.
- H. E. Lee, J. H. Park, D. Jang, J. H. Shin, T. H. Im, J. H. Lee, S. K. Hong, H. S. Wang, M. S. Kwak, M. Peddigari, C. K. Jeong, Y. Min, C. H. Park, J.-J. Choi, J. Ryu, W.-H. Yoon, D. Kim, K. J. Lee and G.-T. Hwang, Nano Energy, 2020, 75, 104951 CrossRef CAS.
- D. Liu, L. Zhou, S. Cui, Y. Gao, S. Li, Z. Zhao, Z. Yi, H. Zou, Y. Fan, J. Wang and Z. L. Wang, Nat. Commun., 2022, 13, 6019 CrossRef CAS.
- H. Zou, Y. Zhang, L. Guo, P. Wang, X. He, G. Dai, H. Zheng, C. Chen, A. C. Wang, C. Xu and Z. L. Wang, Nat. Commun., 2019, 10, 1427 CrossRef.
- L. He, C. Zhang, B. Zhang, Y. Gao, W. Yuan, X. Li, L. Zhou, Z. Zhao, Z. L. Wang and J. Wang, Nano Energy, 2023, 108, 108244 CrossRef CAS.
- B. Zhang, L. He, J. Wang, Y. Liu, X. Xue, S. He, C. Zhang, Z. Zhao, L. Zhou, J. Wang and Z. L. Wang, Energy Environ. Sci., 2023, 16, 3873–3884 RSC.
- B. Zhang, L. He, R. Zhang, W. Yuan, J. Wang, Y. Hu, Z. Zhao, L. Zhou, J. Wang and Z. L. Wang, Adv. Energy Mater., 2023, 13, 2301353 CrossRef CAS.
- S. Niu, Y. Liu, S. Wang, L. Lin, Y. S. Zhou, Y. Hu and Z. L. Wang, Adv. Funct. Mater., 2014, 24, 3332–3340 CrossRef CAS.
- S. Niu, S. Wang, L. Lin, Y. Liu, Y. S. Zhou, Y. Hu and Z. L. Wang, Energy Environ. Sci., 2013, 6, 3576–3583 RSC.
- J. Liu, L. Zhou, Y. Gao, P. Yang, D. Liu, W. Qiao, B. Zhang, Z. Zhao, Z. L. Wang and J. Wang, Adv. Energy Mater., 2023, 13, 2300410 CrossRef CAS.
- W. Liu, Z. Wang, G. Wang, Q. Zeng, W. He, L. Liu, X. Wang, Y. Xi, H. Guo, C. Hu and Z. L. Wang, Nat. Commun., 2020, 11, 1883 CrossRef CAS.
- Z. Cao, Z. Wu, R. Ding, S. Wang, Y. Chu, J. Xu, J. Teng and X. Ye, Nano Energy, 2022, 93, 106891 CrossRef CAS.
- W. Harmon, H. Guo, D. Bamgboje, T. Hu and Z. L. Wang, Nano Energy, 2021, 85, 105956 CrossRef CAS.
- W. Harmon, D. Bamgboje, H. Guo, T. Hu and Z. L. Wang, Nano Energy, 2020, 71, 104642 CrossRef CAS.
- H. Zhang, F. Marty, X. Xia, Y. Zi, T. Bourouina, D. Galayko and P. Basset, Nat. Commun., 2020, 11, 3221 CrossRef CAS.
- Z. Wang, Q. Tang, C. Shan, Y. Du, W. He, S. Fu, G. Li, A. Liu, W. Liu and C. Hu, Energy Environ. Sci., 2021, 14, 6627–6637 RSC.
- Z. Cao, J. Teng, R. Ding, J. Xu, C. Ren, S.-H. Lee, X. Guo and X. Ye, Energy Environ. Sci., 2024, 17, 5002–5012 RSC.
- Y. Gao, D. Liu, Y. Li, J. Liu, L. Zhou, X. Li, Z. Zhao, S. Li, P. Yang, Z. L. Wang and J. Wang, Energy Environ. Sci., 2023, 16, 2304–2315 RSC.
- Z. Guo, P. Yang, Z. Zhao, Y. Gao, J. Zhang, L. Zhou, J. Wang and Z. L. Wang, Energy Environ. Sci., 2023, 16, 5294–5304 RSC.
- H. Wu, S. Wang, Z. Wang and Y. Zi, Nat. Commun., 2021, 12, 5470 CrossRef CAS.
- Z. Zhang, G. Gu, W. Zhang, G. Gu, W. Shang, Y. Liu, G. Cheng and Z. Du, Nano Energy, 2023, 110, 108360 CrossRef CAS.
- Y. Zi, S. Niu, J. Wang, Z. Wen, W. Tang and Z. L. Wang, Nat. Commun., 2015, 6, 8376 CrossRef CAS.
- Y. Zi, J. Wang, S. Wang, S. Li, Z. Wen, H. Guo and Z. L. Wang, Nat. Commun., 2016, 7, 10987 CrossRef CAS.
- Y. Gao, L. He, D. Liu, J. Zhang, L. Zhou, Z. L. Wang and J. Wang, Nat. Commun., 2024, 15, 4167 CrossRef CAS.
- Z. Wang, W. Liu, W. He, H. Guo, L. Long, Y. Xi, X. Wang, A. Liu and C. Hu, Joule, 2021, 5, 441–455 CrossRef.
- W. He, W. Liu, J. Chen, Z. Wang, Y. Liu, X. Pu, H. Yang, Q. Tang, H. Yang, H. Guo and C. Hu, Nat. Commun., 2020, 11, 4277 CrossRef CAS.
- S. Lin, C. Xu, L. Xu and Z. L. Wang, Adv. Funct. Mater., 2020, 30, 1909724 CrossRef CAS.
- S. Lin, L. Xu, C. Xu, X. Chen, A. C. Wang, B. Zhang, P. Lin, Y. Yang, H. Zhao and Z. L. Wang, Adv. Mater., 2019, 31, 1808197 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee02447h |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |





