Universal descriptors for zeolite topology and acidity to predict the stability of butene cracking intermediates

Abstract

The influence of pore topology and acid strength on the adsorption of (iso)butene in Brønsted acid zeolites is investigated using a combination of static calculations and ab initio molecular dynamics simulations at operating conditions. The nature and lifetime of the adsorbed intermediates – a physisorbed alkene, a chemisorbed carbenium ion or an alkoxide – is assessed for a series of one-dimensional and three-dimensional zeolite topologies as well as metal substituted aluminophosphates with varying acid site strength. While alkoxides are elusive intermediates at high temperature, irrespective of the pore dimensions or acidity, the carbenium ion stabilization is highly correlated with the zeolite confinement and acid site strength. The impact of both topology and acidity can be nicely predicted by identifying universal descriptors such as the dispersion component of the isobutene adsorption energy (topology) and the ammonia adsorption energy (acidity). It is shown that the isobutene adsorption energies and protonation barriers follow clear linear correlations with these descriptors. Our findings yield essential insight into the reactivity differences for frameworks with a different topology and acidity. The activity of a zeolite for alkene conversion can for a large part be ascribed to variations in adsorption strength and its protonation ability.

---

1. Introduction

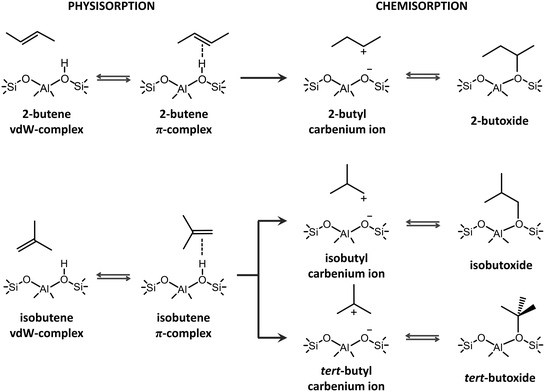
The catalytic transformation of alkenes in acid zeolites plays a predominant role in both traditional chemical processes and emerging alternatives for light olefin production such as catalytic cracking, biomass upgrading, methanol-to-hydrocarbons (MTH) or CO₂ valorization.^1–6 The conversion of C₄₊ alkenes occurs through a complex mechanism involving isomerization, alkylation, β-scission, etc.^7–10 Prior to the actual transformations, alkenes need to diffuse into the zeolite pores, adsorb at active sites and form reactive species. Due to the highly elusive nature of alkene intermediates, tracking the prevailing species experimentally remains challenging.^1,11 Nevertheless, the performance of a zeolite framework hinges on its ability to properly accommodate and activate the alkenes. Molecular modeling techniques are ideally suited to evaluate the stability of adsorbed alkene intermediates in different zeolites and to predict trends in reactivity by constructing structure–property relationships.^12,13

Upon interaction of butene with the Brønsted acid site of the catalyst, four different adsorption states can be formed (see Scheme 1). If the alkene interacts with the zeolite wall solely via dispersion interactions, a physisorbed van der Waals (vdW) complex is formed. A physisorbed π-complex is characterized by interaction of the alkene double bond with the acid proton. The acid site can protonate the alkene, resulting in a chemisorbed carbenium ion, which in turn can covalently bind to a framework oxygen of the active site, forming an alkoxide.

Scheme 1 Different intermediates formed upon 2-butene and isobutene adsorption.

The true nature of the chemisorbed intermediates remains a point of discussion.^1,14,15 Alkoxides have been identified as stable intermediates by a series of NMR^16,17 and FT-IR^18,19 spectroscopy studies at relatively low temperatures. Combining IR spectroscopy and calorimetry, Schallmoser et al. provided a full description of pentene adsorption in ZSM-5 and suggested that stable pentene alkoxides will be formed via a carbenium ion transition state.²⁰ Static DFT calculations on cluster models also pointed to the existence of alkoxide species.^21–24 These observations led to the conclusion that carbenium ions should rather be seen as activated species for the interconversion between two stable states. However, the employed small cluster models – consisting of just a few T atoms – were unable to properly describe the long-range non-covalent interactions with the zeolite environment. Furthermore, the influence of temperature and entropy effects was often ignored. Due to the large entropic penalty, alkoxide stability decreases while carbenium ion stability increases with temperature. De Moor et al. showed that the entropy loss upon alkene adsorption is notably larger for chemisorbed alkoxides.^25,26 Carbenium ions have a higher mobility compared to alkoxy species and are stabilized by long-range van der Waals interactions with the surrounding zeolite wall and electrostatic interactions between the positively charged alkyl carbocation and the negatively charged framework. Although direct experimental observation of small alkyl carbenium ions has not been successful to date, several computational studies demonstrated the plausible existence of alkyl carbenium ions as true intermediates in the zeolite pores.^27–37

The particular case of isobutene adsorption has received a lot of attention in computational studies.^38–47 Sauer and coworkers performed accurate hybrid MP2:PBE-D + CCSD(T) calculations on isobutene in H-FER.⁴² While a physisorbed isobutene π-complex was still identified as the most stable intermediate at 623 K, the tert-butyl carbenium ion was also found to become more stabilized than the tertiary butoxide. Nguyen et al. predicted that the tert-butyl carbenium ion will become more stable than the alkoxide at temperatures around 500 K in H-ZSM-5.⁴³ Dai et al. combined DFT calculations with NMR spectroscopy to find evidence for the existence of the tert-butyl carbenium ion in H-ZSM-5 by capturing it with ammonia.^45,46 The current authors also investigated the nature of linear and branched C₄–C₈ intermediates in H-ZSM-5 at cracking conditions (773 K) using ab initio molecular dynamics simulations.^36,37 Herein, linear, secondary carbenium ions were found to be metastable states, yet, tertiary carbenium ions were identified as stable intermediates. Irrespective of the applied methodology, these studies clearly demonstrated the necessity of including finite temperature and entropy effects to properly model the stability and lifetime of the butene intermediates at actual process conditions.

Next to operating conditions, the zeolite pore structure and composition will have a critical impact on the nature of the intermediates. Ramirez et al. discovered that different frameworks may show a varying reactivity for alkene protonation while screening bifunctional catalysts for CO₂ conversion.⁴⁸ The influence of pore size on alkene adsorption is governed by a compensation effect between the adsorption enthalpy on the one hand and the entropy loss upon adsorption on the other hand.^49,50 The zeolite confinement is particularly important to facilitate the formation of carbenium ions.^50–52 DFT calculations demonstrated that bulkier carbocations may fit well within large-pore zeolites, while smaller carbocations such as the tert-butyl carbenium ion experience a more optimal fit in narrow-pore zeolites.^43,53 Sarazen and Iglesia have shown that the pore shape and framework flexibility also play a vital role in the accommodation of alkoxides through local lattice deformations.^54,55 These observations have important repercussions on the alkene reactivity as zeolite topologies closely resembling the adsorbate size were found to show the best catalytic performance.^{47,50,56–58}

Furthermore, the zeolite acidity also has a significant effect on the stability of alkene intermediates.^59–61 The stability of ion pair structures is highly sensitive to the zeolite acid strength. Fang et al. concluded from static DFT calculations that the stability of carbenium ions relative to alkoxides and π-complexes increases for more acidic materials.⁶² Iglesia et al. confirmed the increase in stability of ion pair structures with increasing acid strength⁶³ and suggested the alkoxide stability to be insensitive to the acid strength due to the predominantly covalent nature of these intermediates.⁵⁴

Interestingly, the product selectivity of alkene conversions can be tuned by altering the zeolite topology or by modifying the zeolite acidity.^48,64–67 Several researchers also established structure–activity relations in zeolite catalysis to predict reactivity trends with either acidity descriptors^68–74 or topological descriptors.^58,74–82 Given its ubiquitous application, a fundamental understanding of alkene adsorption is essential to select or design an optimal catalyst. Nevertheless, a comprehensive study of the influence of zeolite topology and acidity on the stability of alkoxides and carbenium ions at operating conditions is still lacking.

In this study, we aim to identify universal descriptors which can predict the stability and sensitivity of the (iso)butene intermediates for the zeolite pore architecture and acid site strength. The adsorption characteristics of the intermediates are evaluated in various one- and multi-dimensional framework topologies (see Fig. 1) at room temperature (323 K) and typical cracking conditions (773 K). Furthermore, to address the influence of the acid site strength, we consider a series of metal substituted aluminophosphates (see Fig. 1), where the nature of the metal dopant results in a varying Brønsted acidity. This paper is organized as follows: After outlining the computational details, the results section consists of two parts. First, the influence of the zeolite topology and secondly, the influence of the acid strength on the adsorption properties of (iso)butene is discussed. In both parts, we assess the relative stability of the C₄ intermediates in the different materials by a multi-level approach with the aim to propose structure–activity relations. Static DFT calculations are performed to quantify adsorption energies and ab initio molecular dynamics simulations, combined with enhanced sampling techniques, are carried out to evaluate the lifetime of the intermediates at operating conditions and to reconstruct free energy profiles for isobutene protonation. To the best of our knowledge, it is shown for the first time that highly accurate structure–activity relations with elementary descriptors for the zeolite topology and acidity can be derived from ab initio molecular dynamics simulations.

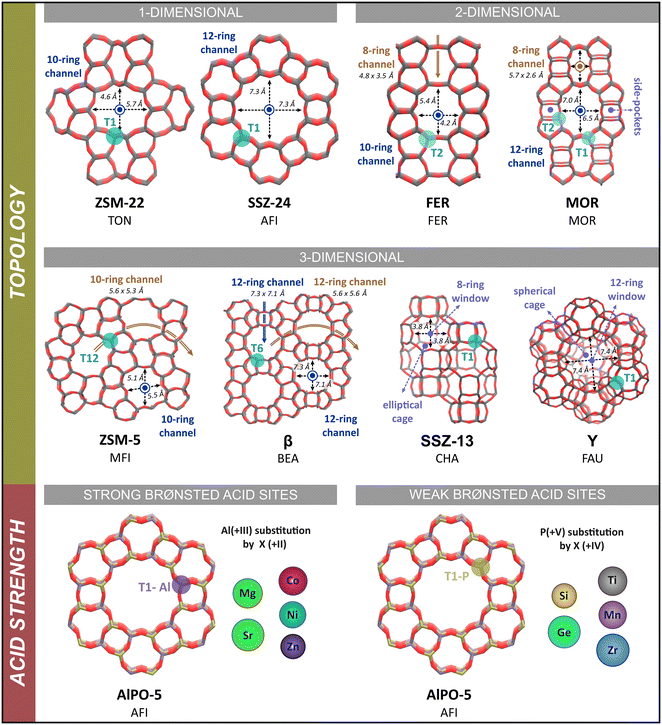Fig. 1 Schematic representation of the investigated zeolite topologies. The channel/cage dimensions are taken from the database of the International Zeolite Association (IZA).⁸³

2. Computational methodology

2.1. Zeolite models

All calculations in this study are performed on fully periodic models of the zeolite catalysts to properly account for the confinement induced by the multi-dimensional zeolite pore architecture. The influence of the pore structure is investigated by considering eight different zeolite topologies. These topologies have a broad variation in pore size and include both zeolites with a one-dimensional channel system (ZSM-22 and SSZ-24) or a multi-dimensional channel system (FER, MOR, ZSM-5 and β) as well as zeolites that are composed of cages connected by smaller windows (SSZ-13 and Y). Each zeolite framework contains a single Brønsted acid site per unit cell, which is created by substitution of a Si atom by an Al atom and adding a charge-compensating proton. The influence of the Brønsted acid site strength is studied by considering ten metal substituted AlPO-5 zeotype frameworks with Mg, Sr, Zn, Co, Ni, Si, Ge, Ti, Zr or Mn as metal substituents. This way, a series of isostructural frameworks with the same AFI topology, but with varying acid site strength are created. A complete overview of the employed zeolite models is shown in Fig. 1. Detailed information on the models and acid site positions can be found in section S1 of the ESI.†

2.2. Static DFT calculations

Static geometry optimizations are conducted with the Vienna Ab Initio Simulation package (VASP 5.4),^84–87 using the Projector Augmented Wave (PAW) method^88,89 and the PBE functional⁹⁰ as level of theory. Dispersion corrections are added by the Grimme D3 formalism.⁹¹ A plane wave basis set with kinetic energy cutoff of 600 eV and the recommended GW PAW potentials are used.⁹² Sampling of the Brillouin zone is restricted to the Γ-point only. The ionic and electronic convergence criteria are set at 10⁻⁴ eV and 10⁻⁵ eV respectively for all relaxations. The local minima of the adsorption states are optimized with the conjugate gradient algorithm. The cell shape and volume are kept fixed during the optimization. A normal mode analysis is carried out to verify the true nature of the stationary states. The vibrational modes are obtained by applying a partial Hessian vibrational analysis (PHVA)^93–95 on the adsorbate and an 8T cluster of the zeolite framework, centered around the acid site. Thermal corrections and thermodynamic quantities at finite temperature are estimated based on the harmonic oscillator (HO) approximation using the in-house developed TAMkin package.⁹⁶ Within this study, we mainly want to show a proof-of-concept for the possibilities of ab initio calculations to construct structure–activity relations. In this sense, the PBE-D3 level of theory is chosen, albeit being less performant in predicting accurate adsorption energies compared to high-level methods such as MP2.⁹⁷ Nevertheless, executing all calculations in this work at the MP2 level of theory is computationally unfeasible.

2.3. Molecular dynamics simulations

Ab initio molecular dynamics simulations have been performed with the CP2K software package.⁹⁸ All simulations employ the revPBE functional^90,99 with additional Grimme D3 dispersion corrections.⁹¹ To approximate the interaction of valence electrons with the atomic cores, GTH pseudopotentials are applied.^100,101 A combination of a double zeta valence polarized (DZVP) Gaussian functions and plane wave functions with an energy cutoff of 320 Ry (GPW)^102,103 are used as basis set.¹⁰⁴ The self-consistent field convergence criterion was set at 10⁻⁶ Ha. The MD simulations are carried out in the canonical ensemble at a temperature of 323 K or 773 K, which is controlled by a chain of 5 Nosé–Hoover thermostats.^105,106 The system is equilibrated for 5 ps, before starting a production run of 100 ps with a time step of 0.5 fs for integrating the Newtonian equations of motion.

2.4. Umbrella sampling

Umbrella sampling (US) simulations^107,108 are carried out to construct free energy profiles for isobutene protonation. Within the US technique, the reaction coordinate or collective variable (CV) is divided into a number of equidistant windows, for which individual MD simulations are carried out in parallel to ensure that each point along the reaction coordinate is sampled equally well. A harmonic bias potential is employed to restrict the sampling to a specific window along the reaction coordinate only. To describe the protonation of isobutene, a one-dimensional CV is selected, defined as the CN between the oxygen atoms of the acid site and all hydrogen atoms of the alkene (cf. Fig. S2†).

All US simulations have been performed with the CP2K software package interfaced with the PLUMED module.^98,109 Simulations are carried out at the revPBE-D3 level of theory^90,91,99 with a triple zeta valence polarized (TZVP) basis set for improved accuracy of the host–guest interactions.¹⁰⁴ For a proper quantitative comparison, this is essential as the DZVP basis set may overestimate the stability of charged species like carbenium ions and is therefore less accurate. The free energy surface is reconstructed by combining the sampling distributions of all windows via the in-house developed ThermoLib software.¹¹⁰ Phenomenological protonation free energy barriers are calculated according to the procedure described by Bučko et al.¹¹¹ and Bailleul et al.,¹¹² which takes into account the particular shape of the free energy valleys. By combining the intrinsic protonation barriers with the statically determined adsorption free energies of isobutene, a rough estimate of the apparent protonation barriers is obtained. Detailed information on the computational methods can be found in section S2 of ESI.†

3. Results and discussion

3.1. Influence of zeolite topology

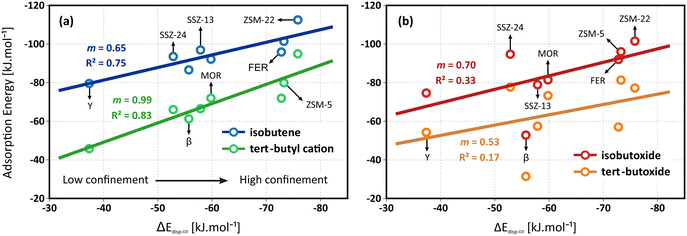
In this section, we focus on the role of the zeolite framework topology and micropore dimensions on the adsorption of C₄ alkenes. A number of framework topologies are included which all exhibit a distinctly different pore architecture, hence it may result in a pronounced influence on the stability of the isobutene intermediates. The latter will be governed by an interplay of both enthalpic and entropic effects, such as stabilizing dispersion interactions with the zeolite walls, electrostatic interactions with the acid sites, destabilizing framework repulsion, constraints in the conformational freedom of the adsorbates,… An additional complicating factor is the presence of acid sites at different framework positions, potentially experiencing different interactions with the local zeolite environment.

Identifying a universal descriptor, capable of capturing these intricate effects for all intermediates is far from trivial. While seminal work on scaling relations has been performed in the context of catalysis on metal surfaces, defining a suitable descriptor for zeolite catalysts, which can cover a broad range of cage and/or channel based topologies has proven to be less trivial. Previously, structural parameters (e.g., pore-limiting diameter, hydrogen affinity,…) or thermodynamic quantities (e.g., adsorption/reaction entropies or free energies,…) have been suggested, some of which were also tested for the current problem, as illustrated in section S7 of ESI.† Furthermore, van der Waals contributions have been shown to yield linear correlations with transition state energies for small alkene conversions in different zeolite frameworks.^74,79 Despite the broad range of suggestions, quantifying these descriptors for various frameworks is often difficult or computationally expensive. Given the major importance of van der Waals interactions in the stabilization of the weakly bound physisorbed and chemisorbed butene species, we suggest using the dispersion component of the isobutene adsorption energy as a descriptor for the topology. This relatively straightforward and easily accessible descriptor allows to distinguish between highly confined topologies (such as ZSM-22, ZSM-5 and FER), moderately confined topologies (such as MOR and SSZ-13) and large pore topologies (such as SSZ-24, β and Y). Note that this descriptor is computed by averaging the D3 dispersion contributions to the isobutene adsorption energies from 10 significantly different adsorbate conformations that are extracted from regular MD simulations (see section S7 of ESI†).

3.1.1. Static calculations of isobutene adsorption. To assess the relative stability of the butene intermediates in the different framework topologies, static DFT calculations have been carried out. In Fig. 2a, the adsorption energies of the isobutene π-complex and tert-butyl carbenium ion are plotted as a function of the dispersion energy descriptor, ΔE_disp-D3. The adsorption energy of the isobutene π-complex shows some correlation with the dispersion energy, which in itself forms the main contribution to the total isobutene adsorption energy. The slope m of 0.65 for the linear fit points to a high dependency of the isobutene adsorption strength on the pore dimensions. Furthermore, also the tert-butyl carbenium ion correlates with the dispersion energy with a slope m of 0.99 for the linear fit. The higher slope indicates that the carbenium ion stability is much more sensitive to the zeolite confinement compared to the physisorbed π-complex. Consequently, dispersion interactions with the surrounding zeolite wall will play a more important role in the stabilization of carbocation intermediates and the relative stability between both intermediates will thus be significantly influenced by the framework topology.

Fig. 2 Linear scaling relations between the isobutene adsorption dispersion energies and static adsorption electronic energies for (a) the isobutene π-complex and tert-butyl carbenium ion; (b) the tert-butoxide and isobutoxide intermediates in the various topologies.

In clear contrast, no reliable linear correlation with the dispersion energy descriptor can be established for the alkoxide intermediates (see Fig. 2b). The zeolite topology has no evident influence on the adsorption strength of the isobutoxide or tert-butoxide. The lack of a distinct trend might be understood by considering that the dispersion descriptor is mainly targeted to the enthalpic interactions of weakly adsorbed species. The stability of alkoxides, however, is also governed by more local effects such as the framework repulsion by close interaction with the alkoxy species and local framework deformation to form an optimal C–O covalent bond distance. These specific features are not only influenced by the pore dimensions but also by the curvature and shape of the pores, as well as the framework flexibility around the acid sites, which may not be properly captured in this single descriptor.

It can be noticed that the linear correlation for the isobutene π-complex and tert-butyl carbenium ion adsorption energies are not perfect with R² values of 0.75 and 0.83 respectively. Next to dispersion and the energetic contributions, also the configurational freedom of the adsorbates and the entropic contributions will play a role in the stabilization of the intermediates. Naturally, the varying confinement and pore architecture of the frameworks is expected to have a major impact on the adsorption entropy components. Since the conformational freedom and entropy of the adsorbates are also linked to the pore dimensions, it can be anticipated that the dispersion energy is still a functional descriptor for the relation between the pore topology and the stability of physisorbed alkenes and carbenium ions at finite temperature.

A complete overview of all thermodynamic quantities for isobutene adsorption can be found in section S3 of the ESI.† Due to the variations in mobility and configurational freedom between the isobutene π-complex and tert-butyl carbenium ion, the adsorption entropies of both species will be different and the established topology correlations will therefore have a pronounced temperature dependency. The isobutene adsorption free energies are expected to yield even improved linear correlations with the dispersion energy descriptor. However, estimating adsorption entropies using a static approach is far from trivial and often results in substantial error bars. Indeed, counterintuitively, the adsorption entropies of the isobutene intermediates vary only slightly among the different framework topologies (cf. section S3†). Consequently, the correlation of the adsorption free energies with the dispersion descriptor shows no improvement compared to the electronic adsorption energies. To obtain more accurate estimates for the entropy and free energy of the adsorbed intermediates, one would need to rely on MD simulations (vide infra).

Independent of the specific zeolite topology, it is predicted that a physisorbed isobutene π-complex is the most strongly adsorbed intermediate at cracking temperature (773 K), in agreement with previous findings.^36,37 In Fig. 3, the optimized isobutene π-complex geometries are shown in the various topologies, highlighting the different degree of confinement for the frameworks. The alkoxide intermediates suffer from the highest entropic penalty of all intermediates (cf. section S3†) due to the covalent bond formation with the framework. As a result, at 773 K, alkoxides will experience a much lower stability compared to the physisorbed isobutene or the tert-butyl carbenium ion, which can retain a considerable degree of conformational freedom and mobility. In the most confined framework, ZSM-22, the one-dimensional 10-ring channels provide the most optimal fit for the tert-butyl carbenium ion, resulting in a free energy difference of only 16 kJ mol⁻¹ at 773 K between the carbenium ion and the π-complex. The slightly more spacious ZSM-5 (free energy difference of 18 kJ mol⁻¹ at 773 K) and FER (free energy difference of 14 kJ mol⁻¹ at 773 K) topologies can accommodate adsorbates at the intersection of two narrow channels, resulting in a slightly lower confinement but still with a relatively high carbenium ion stability. In MOR, the presence of side pockets allows partially for strong interactions with the zeolite walls and therefore leads to moderate adsorption energies of the physisorbed isobutene and tert-butyl carbenium ion. The weakest adsorption strength is found inside the large 12-ring channels of SSZ-24 or β, with a free energy difference between the isobutene π-complex and tert-butyl carbenium ion of 33 kJ mol⁻¹ and 25 kJ mol⁻¹ respectively, and inside the supercages of zeolite Y.

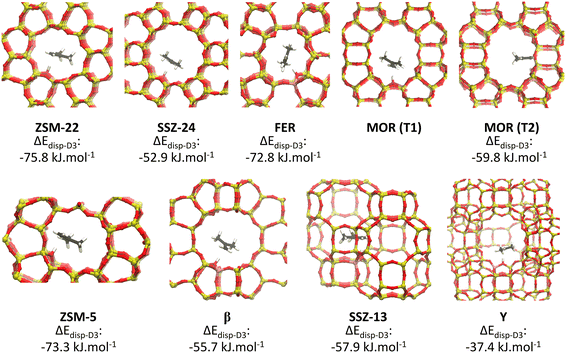Fig. 3 Optimized geometries of the isobutene π-complex adsorbed in the different framework topologies.

Finally, note that the applied level of theory and the choice of dispersion scheme may have a significant influence on the absolute values of the adsorption energies and on the sensitivity of the intermediate stabilities for the pore topologies. For example, it has been argued that the PBE-D3 level of theory may systematically overestimate the stability of ion pair intermediates compared to high-level coupled cluster calculations.^113,114,97 On the other hand, it was also shown that these DFT functionals are capable to accurately predict trends among different catalysts, thus supporting their use for a computational screening.¹¹⁵

3.1.2. MD analysis of the isobutene intermediates. A major shortcoming of the static approach is the limited exploration of the energy surface which typically exhibits multiple, often nearly-isoenergetic local minima and maxima for zeolite host-guest systems.^36,44 Typically only a small number of configurations are taken into account despite the high dependency of the adsorption free energies on the specific orientation of the adsorbates in the zeolite pore system.^36,42,116 Furthermore, the a posteriori entropy correction to the free energy, based on the harmonic oscillator approximation, may result in significant error bars for the adsorption free energies. Especially the stability of weakly bound species such as carbenium ions may be significantly underestimated.^36,37,44 Indeed, the confinement and molecular fitting inside the zeolite pores forms a major contribution in the stabilization of cationic intermediates. Therefore, to fully account for the configurational freedom at finite temperature, ab initio MD simulations are performed on the C₄ intermediates adsorbed in the different zeolite topologies. A complete analysis of the MD simulations can be found in section S4 in ESI.†

In the course of the MD simulations, regular transitions between the intermediates can take place. The lifetime and sampling probability of each intermediate are related to its stability, provided each state is sampled sufficiently long to achieve ergodicity. In reality, due to finite simulation lengths, equivalent simulations often result in a different sampling distribution of the intermediates. Reaching converged values for the sampling probability is difficult, hence the MD analysis rather presents a qualitative insight into the relative stability of the intermediates.

The sampling probabilities in the various framework topologies are displayed for isobutene in Fig. 4 and for 2-butene in Fig. S7.† Note that the displayed results are averaged from two regular MD simulations with either the π-complex or carbenium ion as starting configuration to reduce the dependency of the sampling probability on the initial state of the MD simulations (cf. section S4 in ESI†). Also note that the sampling fractions should solely be regarded as a qualitative comparison as the employed double zeta basis set tends to somewhat overestimate the stability of carbenium ions.

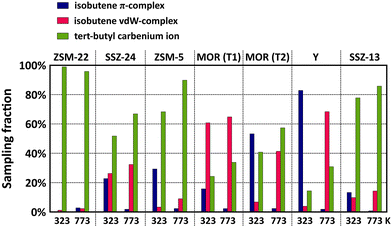Fig. 4 Sampling probability of the isobutene π-complex, isobutene vdW-complex and tert-butyl carbenium ion intermediates during MD simulations in different zeolite topologies at 323 K and 773 K.

While the influence of the zeolite pore dimensions on the stability of the physisorbed 2-butene π-complex and the chemisorbed 2-butoxide is rather limited, the sampling probabilities of the isobutene intermediates are highly dependent on the zeolite topology. For linear butene, the framework effect is rather subtle but most pronounced when comparing the 10-ring channel zeolite, ZSM-22, and the 12-ring channel zeolite, SSZ-24, which form an interesting case study since they both are composed only of one-dimensional straight channels with different radii. In the narrow ZSM-22 channels, the 2-butene π-complex exists as a very stable intermediate, with a sampling probability of around 40% at 773 K, however, in the large SSZ-24 channels, the freely adsorbed 2-butene vdW-complex is significantly more favored with a sampling probability of more than 90% at 773 K. This trend can be explained by the combination of a greater enthalpic stabilization in the higher confinement of ZSM-22, and simultaneously, the entropy loss upon formation of a physisorbed π-complex will be much lower in ZSM-22 than in the spacious channels of SSZ-24, thus explaining the higher preference for a 2-butene vdW-complex in the latter. In contrast to n-butene, isobutene can get easily protonated in the course of the simulations thanks to the higher stability of the tertiary carbocation. A large variation in the sampling probability of the tert-butyl carbenium ion can be distinguished with a sampling fraction between 90 and 100% in ZSM-22 while in the SSZ-24 topology this is reduced to about 70% at 773 K. Since van der Waals interactions with the surrounding zeolite wall are crucial for the stabilization of ion pair intermediates, the tert-butyl carbenium ion evidently experiences a greater adsorption strength in the more confined 10-ring channels of ZSM-22 than in the large 12-ring channels of SSZ-24.

Similar trends can be observed when comparing the multi-dimensional channel zeolites ZSM-5 and MOR. At 773 K, the tert-butyl carbenium ion sampling in ZSM-5 amounts to ca. 90%, slightly lower than in the one-dimensional ZSM-22 topology. Although the strongly stabilizing interactions are also present in ZSM-5, the tert-butyl carbenium ion is somewhat less common which can be attributed to the dimensionality of the zeolite pore system. The 1D straight channels of ZSM-22 provide an optimal confinement as the carbocation is entirely surrounded by the zeolite wall, while the straight and sinusoidal channel intersections of ZSM-5 result in a slightly more spacious environment. Also in the encapsulating 1D 12-ring channels of SSZ-24, the tert-butyl carbenium ion intermediates are markedly more stable than in the channel intersections of MOR. Note that for zeolite MOR, the location of the Brønsted acid site has a large influence on the sampling of the carbenium ion. For the T2 site, the proximity of the 8-ring side pocket provides a partial confinement which allows for an enhanced stabilization of the carbocations compared to the large 12-ring channel environment of the T1 position.

Finally, in the cage topologies, SSZ-13 and Y, the tert-butyl carbenium ion is clearly the prevailing intermediate in SSZ-13 (sampling probability around 85% at 773 K), while it is much less prominent in Y (sampling probability around 30% at 773 K). Next to the large difference in free pore volume of both zeolites, this variation might also be related to the specific shape of the cages. The SSZ-13 elliptical cages provide better dispersion interactions with the zeolite walls due to the high curvature of the cages, while the large spherical cages of Y, on the other hand, exhibit a wide curvature, resulting in the lowest confinement of all investigated zeolites. Therefore, the carbenium ion will experience less stabilizing dispersion interactions with the zeolite wall, as evidenced by the lowest tert-butyl carbenium ion sampling probabilities of all topologies.

3.1.3. Free energy profiles for isobutene protonation. While regular MD simulations present some interesting qualitative insight into the relative stability of physisorbed and protonated isobutene in different frameworks, quantitative trends can hardly be discerned. Therefore, to assess reactivity differences for the various topologies, the protonation of isobutene into a tert-butyl carbenium ion is quantified by performing umbrella sampling simulations, which will allow to deduce protonation barriers and free energies of protonation at cracking conditions. Furthermore, it allows to check if the previously identified topology descriptors are indeed capable to reliably predict reactivity trends for reaction free energies determined from accurate MD simulation techniques.

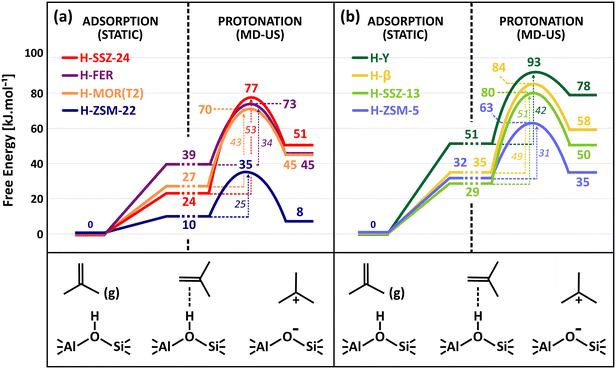
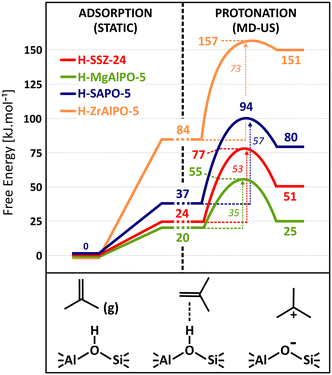
Fig. 5 shows the isobutene protonation free energy profiles at 773 K for the different topologies, also including the preliminary isobutene adsorption step from static calculations. In agreement with the pore dimensions, the lowest intrinsic protonation barriers are found for ZSM-22 (25 kJ mol⁻¹), ZSM-5 (31 kJ mol⁻¹) and FER (34 kJ mol⁻¹). The multi-dimensional channel system and intersections of ZSM-5 and FER apparently result in a slightly lower stabilization of the protonation transition state. Other topologies are characterized by considerably higher intrinsic barriers. The lowest barrier for the 12-ring channel and cage zeolites is observed for MOR (43 kJ mol⁻¹) where the partial confinement of the side pocket clearly enhances interactions with the zeolite wall and aids in the stabilization of the protonation transition state and carbenium ion products. The one-dimensional 12-ring channel zeolite SSZ-24 (53 kJ mol⁻¹) has a slightly higher barrier than the three-dimensional zeolite β (49 kJ mol⁻¹), in agreement with its slightly larger channel diameter. It is also noteworthy that the activation barrier is lower for zeolite Y (42 kJ mol⁻¹) than for SSZ-13 (51 kJ mol⁻¹) despite the much more voluminous cages of the former. This curiosity might be a consequence of the large degree of conformational freedom of the protonation transition state in the supercages of H–Y, thus resulting in a greater entropic stabilization.

Fig. 5 Free energy profile for the adsorption (from static PBE-D3 calculations) and protonation (from AI-US simulations) of an isobutene π-complex into a tert-butyl carbenium ion at 773 K in (a) the one- and two-dimensional zeolite topologies; (b) the three-dimensional zeolite topologies, with reference to the empty framework and isobutene in gas phase.

To fully assess the ability of the zeolite framework to protonate isobutene, also the adsorption strength should be considered. In Fig. 5, the adsorption data from the static PBE-D3 calculations are combined with the free energy profiles from umbrella sampling to compute apparent protonation barriers. Notice however that these are rough estimates for the apparent barriers as the free energy levels for the π-complex are not directly comparable since they are extracted using two different methods, static calculations and MD simulations. The static adsorption free energy relies on a single conformation of the adsorbate, while the free energy level from MD actually entails a whole ensemble of π-complex configurations and can therefore be considered to be more accurate. Nevertheless, it becomes quite clear that the apparent barriers will be even more sensitive to the pore topology and that the distinction between the different zeolites is even further magnified.

The reaction free energy of isobutene protonation, i.e., the free energy difference between physisorbed isobutene and the tert-butyl carbenium ion is also highly sensitive to the pore structure and dimensions. In the 10-ring channel zeolites (ZSM-22 and ZSM-5), the tert-butyl carbenium ion stability is on par with the stability of physisorbed isobutene, as evidenced by a free energy difference of −2 kJ mol⁻¹ and +3 kJ mol⁻¹ respectively. In the more spacious 12-ring channel zeolites (SSZ-24, MOR and β), the free energy difference increases to about 18–28 kJ mol⁻¹. The tert-butyl carbenium ion is clearly more stabilized with respect to physisorbed isobutene in the narrow pore topologies which provide a high degree of confinement and dispersion stabilization for the carbocation intermediates. As a result, the tert-butyl carbenium ion will on average interact more closely with the zeolite walls than in large pore zeolites, resulting in a greater enthalpic stabilization and hence explaining also their high sampling probability in regular MD simulations for these topologies.

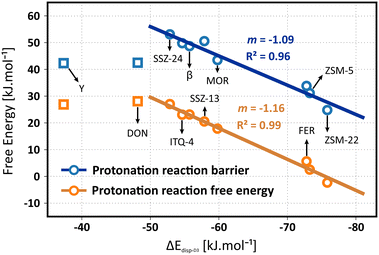
The question remains whether the correlation with the dispersion energy descriptor holds true for the free energies, obtained from molecular dynamics simulations which properly account for adsorbate mobility and finite temperature effects. In Fig. 6, the correlation of the isobutene protonation barriers and reaction free energies are plotted as a function of the dispersion descriptor. A perfect linear trend with the topology descriptor can be distinguished for all frameworks, except for zeolite Y. Although a specific reason for this outlier is hard to identify, it may be explained by the size of the supercages in the FAU topology which induces important effects on the adsorption entropy that may not be properly captured by the dispersion descriptor. To validate this hypothesis, two additional large-pore frameworks were included in the data set, namely the IFR topology (ITQ-4) exhibiting one-dimensional 12-ring channels with slightly smaller channel dimensions (d_max 7.24 Å) compared to SSZ-24 and the DON topology, exhibiting one-dimensional 14-ring channels with significantly larger channel dimensions (d_max 8.79 Å) compared to SSZ-24. While ITQ-4 still follows the linear trend, zeolite DON does not obey the trend anymore. A comparison of the translational entropy – as a measure for the mobility – of the reactant and transition states yields further insight (see Table S24 in ESI†). The reduction in translational entropy going from the adsorbed isobutene reactant state to the protonation transition state is significantly higher for zeolite Y (35 J mol⁻¹ K⁻¹) and DON (33 J mol⁻¹ K⁻¹) compared to all other frameworks (< 20 J mol⁻¹ K⁻¹). These observations demonstrate that for the zeolite topologies consisting of extra-large pores, the effect of adsorbate mobility and entropy on the stabilization of the intermediates becomes considerably more important. A one-dimensional descriptor based on only dispersion interactions seems therefore insufficient to properly describe and predict trends in the stability of alkene intermediates inside these topologies.

Fig. 6 Linear scaling relations between the isobutene adsorption dispersion energies and the isobutene protonation free energy barriers or reaction free energies (i.e., the free energy difference between physisorbed isobutene and the tert-butyl carbenium ion) at 773 K in the different framework topologies, obtained from umbrella sampling simulations.

The linear fit for the protonation barriers (Fig. 6) is characterized by a slope m of 1.09, which is higher than both the static isobutene and tert-butyl carbenium ion adsorption energies, suggesting an even higher topology sensitivity for activation than for adsorption of alkenes. Furthermore, the relative stability of physisorbed isobutene and the tert-butyl carbenium ion also correlates well with the dispersion energy descriptor. The slope m of 1.16 for the linear fit is very similar to the slope of the protonation barriers, suggesting that the effect of the pore environment is similar for both the stabilization of the protonation transition state and the carbenium ion product. Consequently, the barriers for deprotonation of the carbenium ion will be rather independent on the pore topology. Again, note that the chosen level of theory will have a major influence on the absolute protonation barriers and that the PBE-D3 level of theory may likely underestimate these barriers significantly. Nevertheless a similar offset can be expected for all topologies and therefore the predicted trends are still reliable.¹¹⁵

The sensitivity of the alkene adsorption and protonation for the zeolite pore dimensions is a crucial element in the selection of a framework topology as carbenium ions are key intermediates in many zeolite-catalyzed conversions. The stability of guest species is governed by the balance between the stabilizing enthalpic interactions with smaller pore dimensions and the stabilizing entropic contributions with increasing pore dimensions. Our results demonstrate that the enthalpic effects are the dominant factor in the ultimate carbenium ion stability. The more confined 10-ring channel zeolites seem particularly well suited for isobutene protonation and conversion, especially compared to the large 12-ring channel zeolites. Note, however, that this will not necessarily result in a more effective catalyst, as the dimensionality of the pore system will also have a considerable impact on product diffusion and pore blocking or deactivation by large aromatics.^57,117–120 Finally, it should be mentioned that the stability of larger and bulkier carbenium ions is expected to improve in the more spacious topologies, i.e., when the pore dimensions provide an optimal fit for the guest species.^50,51,82,121

3.2. Influence of zeolite acid site strength

Next to the topology, the zeolite acidity may also have a pronounced influence on the stability of the alkene intermediates and protonation barriers. The acidity of the framework encompasses multiple factors such as the individual acid site strength, acid site density and acid site proximity.^122,123 Herein, we focus on the role of the Brønsted acid site strength by considering a series of isostructural metal substituted AlPO-5 frameworks (AFI topology) with different elemental compositions, resulting in a varying acid site strength (see Fig. 1). For comparison, the aluminosilicate SSZ-24, also exhibiting the AFI topology, is included as well.

Since all metal substituted AlPO-5 frameworks exhibit the same structural topology, it can reasonably be assumed that the entropic contributions upon butene adsorption are similar for all materials and that any variation in the adsorption thermodynamics can solely be attributed to the enthalpic stabilization of the guest species and its interaction with the acid site. This assumption appears valid as the adsorption entropies at 773 K lie in general within a relatively narrow range for most materials (cf. Table S17†).

The strength of isolated acid sites is defined as the deprotonation energy of the framework. However, this measure is highly dependent on the computational method and ignores solvation effects caused by the zeolite framework.^63,124 Therefore, to establish acidity trends in zeolites, the adsorption energies of basic probe molecules like ammonia or pyridine are commonly used as descriptors.¹²⁵ Previous studies demonstrated that well-fitted linear correlations can be derived between the ammonia adsorption energy and activation energies in the context of the methanol-to-olefins process.^70,71,73,126

3.2.1. Static calculations of butene adsorption. In Fig. 7, the static adsorption energies of the 2-butene and isobutene intermediates in the isostructural AFI frameworks with different acidities are plotted as a function of the ammonia adsorption energy descriptor. Note that the 2-butyl carbenium ion could not be localized statically in any of the considered materials and that the tert-butyl carbenium ion could not be localized for the weakly acidic frameworks (with a lower acid strength than SAPO-5). Only electronic energies are reported in the discussion below to eliminate the uncertainty on the static thermal corrections within the HO approximation. For the complete data set of the butene adsorption thermodynamics at 773 K the reader is referred to section S3 of the ESI.†

Fig. 7 Linear scaling relations between the ammonia adsorption energies and (a) the static 2-butene π-complex and 2-butoxide adsorption electronic energies; (b) the static isobutene π-complex, tert-butyl carbenium ion, tert-butoxide and isobutoxide adsorption electronic energies in the metal substituted H-MeAlPO-5 frameworks and zeolite H-SSZ-24.

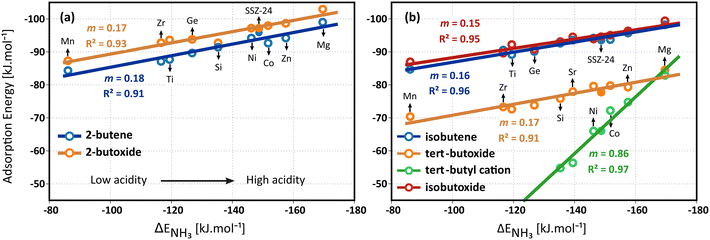
Unsurprisingly, the strongest adsorption for all intermediates is found in the most acidic material, MgAlPO-5, and the weakest adsorption in the framework with the lowest acid strength, MnAlPO-5. Due to the strong covalent interaction with the framework, the 2-butoxide is slightly stronger adsorbed than the 2-butene π-complex which has only a weaker π–H interaction. The adsorption energies of the butene intermediates nicely correlate with the acid strength. The formation of the alkene π-complexes and alkoxides is only slightly sensitive to the acid site strength, as confirmed by the low slopes for the linear fit of these species. The slopes m of the linear fit of the butene π-complexes and butoxides are nearly equal, varying between 0.14 and 0.18, indicating a similar dependency on the acidity of the framework. The relative stability of the alkene π-complexes and alkoxides remains therefore unaltered in all materials and appears to be invariant for the acid strength.

Interestingly, on the other hand, the tert-butyl carbenium ion adsorption energy is significantly more influenced by the acidity, as evidenced by the slope of 0.86 for the linear fit. Clearly, the difference in stability between the isobutene π-complex and the tert-butyl carbenium ion has a very high sensitivity for the acid site strength. For MgAlPO-5, the tert-butyl carbenium ion adsorption energy is predicted to be on par with the tert-butoxide and only 15 kJ mol⁻¹ higher in energy than the isobutene π-complex, while for SAPO-5, it is predicted to be 38 kJ mol⁻¹ higher in energy than the π-complex. At cracking conditions, finite temperature and entropy effects will become determining for the adsorption free energies of the intermediates. For example, the stability of the tert-butyl carbenium ion will significantly increase and the stability of the alkoxide intermediates will significantly decrease relative to the physisorbed isobutene. Nevertheless, the entropic effects are expected to be similar for all materials and hence the acidity correlation of the intermediates adsorption free energy will be nearly invariant for temperature.

Finally, it can be remarked that the aluminosilicate SSZ-24 obeys the same linear trends with acidity as the aluminophosphates materials despite their different chemical composition. Compared to SAPO-5, the slightly more acidic SSZ-24 zeolite clearly results in stronger adsorption of the isobutene intermediates. Furthermore, the higher stability of the tert-butyl carbenium ion in SSZ-24 implies a higher tendency for alkene activation and cracking, in agreement with previous findings.^59,127 The current observation indicates that for materials with identical topologies and similar pore dimensions, the same acidity correlation for alkene adsorption can be applied, irrespective of the constituting framework elements.

3.2.2. MD analysis of the butene intermediates. While static calculations yield interesting insight into the role of acid strength on the adsorption energy of the (iso)butene intermediates, the thermal corrections and hence adsorption free energies for zeolite host-guest systems are known to be highly dependent on the specific orientation of the adsorbates, possibly resulting in relatively large errors.^36,116 Indeed, counterintuitively, the static free energy differences between the isobutene π-complex and tert-butyl carbenium ion (cf. section S3†) show far from a clear correlation with the Brønsted acidity. Therefore, ab initio MD simulations are performed for the butene intermediates in MgAlPO-5, SAPO-5, ZrAlPO-5 and SSZ-24 at 323 K and 773 K. Section S4 in ESI† summarizes the most important results from the analysis of these MD simulations.

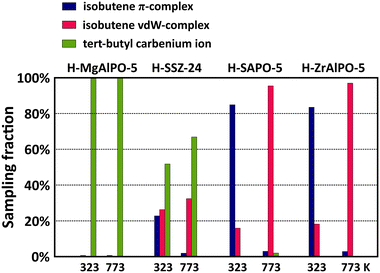
The acidity effect is quite pronounced for the branched intermediates. Fig. 8 shows the sampling fractions of the isobutene π-complex, vdW-complex and tert-butyl carbenium ion for the four materials at 323 K and 773 K. The sampled tert-butyl carbenium ion fractions show a clear correlation with the acid strength. While the tertiary carbocation is stable throughout the entire simulation on MgAlPO-5, its sampling probability is reduced to about 70% in SSZ-24 at cracking temperatures, and on the weaker acidic SAPO-5 and ZrAlPO-5 frameworks, the tert-butyl carbenium ion is only rarely observed and will readily deprotonate into isobutene. Clearly, the carbocation intermediates can interact more tightly with strong acid sites, resulting in lower adsorption enthalpies. Also notice that the tert-butoxide is stable throughout the entire simulation in ZrAlPO-5 at 323 K, indicating that the alkoxide intermediates may also experience enhanced stabilization in the less acidic materials (cf. section S4†).

Fig. 8 Sampling probability of the isobutene π-complex and vdW-complex and the tert-butyl carbenium ion intermediates during MD simulations at 323 K and 773 K in the H-MgAlPO-5, H-SSZ-24, H-SAPO-5 and H-ZrAlPO-5 zeolites.

In contrast, the effect of acidity on the linear 2-butene intermediates in the AFI materials (Fig. S8 in ESI†) is negligible. At low temperature, both the 2-butoxide and 2-butene π-complex are stable intermediates, while at high temperature, these intermediates become entropically unfavored and the 2-butene van der Waals-complex is the most sampled intermediate in all frameworks. The only noticeable trend with acid strength is the sampling probability of the 2-butene π-complex at low temperature. Due to a stronger attraction, physisorbed alkenes will bind more tightly to the more acidic sites. As a result, the butene π-complex configuration is sampled to a greater extent on the strongly acidic MgAlPO-5 compared to the weakly acidic ZrAlPO-5. At high temperature, this effect is erased since entropy contributions will become prevailing, thus favoring a more freely adsorbed conformation.

3.2.3. Free energy profiles for isobutene protonation. To quantitatively assess the impact of acid strength on the reactivity at cracking conditions, again umbrella sampling simulations for isobutene protonation are performed. Fig. 9 shows the reconstructed free energy profiles at 773 K for the four materials, also including the preceding isobutene adsorption step from static calculations. The influence of the acid strength is not only apparent on the isobutene adsorption energy but also on the intrinsic protonation barrier which increases from 35 kJ mol⁻¹ for MgAlPO-5 to 73 kJ mol⁻¹ for ZrAlPO-5. Since the entropy barriers are expected to be similar for the isostructural frameworks, it can be concluded that the acid strength mainly affects the enthalpy barriers and the interaction of the transition state with the acid site. Taking into account the adsorption strength of isobutene as well, the apparent protonation barriers (with respect to gas phase reactants) will even be more sensitive to the zeolite acidity.

Fig. 9 Free energy profile for the adsorption (from static PBE-D3 calculations) and protonation (from AI-US simulations) of an isobutene π-complex into a tert-butyl carbenium ion in the zeolite topologies with different acid strength at 773 K with reference to the empty framework and isobutene in gas phase.

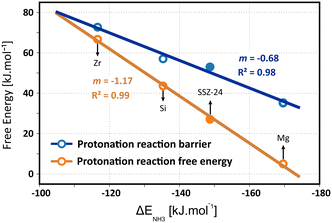
The intrinsic protonation barriers and protonation free energies (the relative stability of physisorbed isobutene and the tert-butyl carbenium ion), as displayed in Fig. 10, follow a perfect linear trend with the ammonia adsorption energy as acid strength descriptor. The slope m of 0.68 for the linear correlation point to a high impact of the acid site strength on the protonation barrier. Also the free energy difference between the neutral isobutene and the tert-butyl carbenium ion has a very high dependency on the acid strength, as evidenced by the slope of 1.17 for the linear fit. There exists a clear positive correlation between the barrier height and the reaction free energy difference, since the most acidic material (Mg) with the lowest protonation barrier also exhibits the lowest free energy difference between the tert-butyl carbenium ion and the physisorbed isobutene, which corroborates the observation from regular MD simulations that carbenium ions have a higher sampling probability in zeolites with a higher acidity. The free energy difference between both states decreases from 67 kJ mol⁻¹ for ZrAlPO-5 to only 5 kJ mol⁻¹ for MgAlPO-5. The trend is even more pronounced than suggested by the static results (slope of 0.70), which might be due to the rather weak description of carbocation intermediates with static calculations. The current observation also reflects Hammond's postulate of early transition states, resembling more closely the reactant state for exergonic reactions and late transition states, resembling more closely the product states for endergonic reactions, which is confirmed by the location (CV value) of the transition state along the reaction profile for these materials (cf. Fig. S12 in ESI†).

Fig. 10 Linear scaling relations between the ammonia adsorption energies and the isobutene protonation free energy barriers or reaction free energies (i.e., the free energy difference between physisorbed isobutene and the tert-butyl carbenium ion) at 773 K in the metal substituted H-MeAlPO-5 frameworks and zeolite H-SSZ-24, obtained from umbrella sampling simulations.

In ZrAlPO-5, the protonation barrier and free energy difference approach similar values, indicating that carbenium ions will likely be unable to form in these weakly acidic materials. The high sensitivity of the carbenium ion stability for the acid strength is in particular important for the reactivity of alkene conversions in zeolites such as catalytic cracking since carbenium ions are crucial intermediates in the activation and transformation of alkenes. Our results confirm that a higher acidity will lead to an increase in the reactivity of the catalyst for alkene conversion. Note, however, that this will not necessarily result in higher product selectivities as side reactions or catalyst deactivation might also be enhanced by a higher acid strength.^128,129

4. Conclusion

Understanding the influence of the zeolite pore topology and acidity on the stability of alkene intermediates is essential to design or select a proper catalyst for alkene conversions with an optimal lifetime and selectivity. The adsorption of n-butene and isobutene, as model components for alkene cracking, has been studied on a number of zeolite materials with varying pore topologies and acid strengths by a combination of static DFT calculations and ab initio molecular dynamics simulations, coupled with umbrella sampling to quantify the isobutene protonation barriers at operating temperature. Static calculations may lead to an underestimation of the conformational freedom of weakly bound species, like carbenium ions, especially at high temperature. Therefore, MD simulations might be better suited to explain the subtle trends of alkene conversion with pore size and acid strength at actual reaction conditions. Universal descriptors have been identified which are capable to predict the link between the stability of the physisorbed and chemisorbed alkene intermediates as a function of the pore topology or the zeolite acidity in a broad set of materials. Our results show that these elementary descriptors can accurately predict trends in protonation barriers and protonation free energies that are extracted from MD simulations.

The role of the zeolite topology on the stability of butene intermediates was established by considering a set of frameworks with varying pore dimensions and dimensionality. The stability of adsorbed isobutene in these topologies is governed by the balance between counteracting enthalpic and entropic stabilization and is therefore temperature dependent. At high temperature, the entropic penalty of the covalent framework bond renders alkoxides unstable. We demonstrated that the tert-butyl carbenium ion stability is critically determined by the dispersion stabilization with the zeolite wall and therefore highly dependent on the pore dimensions. The dispersion component of the isobutene adsorption energy can serve as a proper descriptor for the pore dimensions. The dispersion energy correlates generally well with the isobutene adsorption free energies and protonation barriers, with the exception for frameworks with very large pores, such as zeolite Y, for which configurational freedom and entropy contributions become of much higher importance.

The role of the zeolite acid strength on the stability of butene intermediates was established by considering a series of metal substituted aluminophosphates materials, H-MeAlPO-5, leading to catalysts exhibiting the same one-dimensional AFI topology but with markedly different acid site strengths. Thanks to their isostructural frameworks, the stability of the adsorbed isobutene intermediates in these materials is solely governed by the enthalpy effects and the guest interactions with the acid sites. While the alkoxide and π-complex intermediates are both only slightly sensitive to the acid site strength, the isobutene protonation barrier and tert-butyl carbenium ions are largely affected by the acidity. Strong acid sites lead to lower protonation barriers and higher carbenium ion lifetimes. The tendency to form carbenium ions will thus be much higher in more acidic materials. The ammonia adsorption energy is proven to be a useful descriptor to assess and predict the relative stability of all isobutene intermediates as function of acid site strength.

The ability to protonate isobutene and form tert-butyl carbenium ion products is highly sensitive to both the zeolite pore dimensions and the acidity. The current investigation highlights how carbenium ion stability is mainly governed by electrostatic and van der Waals interactions with the surrounding zeolite wall and only to a smaller extent by the configurational freedom and mobility of the guest species. Our results suggest that highly confined frameworks containing strong acid sites provide an optimal fit for the carbocation intermediates. Such frameworks appear to be efficient zeolites for the activation and conversion of isobutene, an observation that can likely be extended to other alkenes as well. Exploiting the clear correlations for the influence of the zeolite topology and acidity may therefore be an interesting element to aid in the prediction or design of efficient catalysts with improved selectivity.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

P. C. gratefully acknowledges financial support from the Fund for Scientific Research Flanders (FWO – grant no. 1246922N). V. V. S. thanks the Research Fund of Ghent University (BOF) for financial support. The authors thank Louis Vanduyfhuys for the fruitful discussions on this work. Computational resources and services used in this work were provided by the VSC (Flemish Supercomputer Centre), funded by Ghent University, the FWO and the Flemish Government – department EWI.

References

1. V. Van Speybroeck, K. Hemelsoet, L. Joos, M. Waroquier, R. G. Bell and C. R. A. Catlow, Chem. Soc. Rev., 2015, 44, 7044–7111.
2. E. T. C. Vogt and B. M. Weckhuysen, Chem. Soc. Rev., 2015, 44, 7342–7370.
3. Q. Zhang, J. Yu and A. Corma, Adv. Mater., 2020, 32, 2002927.
4. P. Sudarsanam, E. Peeters, E. V. Makshina, V. I. Parvulescu and B. F. Sels, Chem. Soc. Rev., 2019, 48, 2366–2421.
5. I. Yarulina, A. D. Chowdhury, F. Meirer, B. M. Weckhuysen and J. Gascon, Nat. Catal., 2018, 1, 398.
6. P. Tian, Y. Wei, M. Ye and Z. Liu, ACS Catal., 2015, 5, 1922–1938.
7. J. S. Buchanan, J. G. Santiesteban and W. O. Haag, J. Catal., 1996, 158, 279–287.
8. Y. V. Kissin, Catal. Rev.: Sci. Eng., 2001, 43, 85–146.
9. M. Bjørgen, S. Svelle, F. Joensen, J. Nerlov, S. Kolboe, F. Bonino, L. Palumbo, S. Bordiga and U. Olsbye, J. Catal., 2007, 249, 195–207.
10. S. Standl, T. Kühlewind, M. Tonigold and O. Hinrichsen, Ind. Eng. Chem. Res., 2019, 58, 18107–18124.
11. K. De Wispelaere, S. Bailleul and V. Van Speybroeck, Catal. Sci. Technol., 2016, 6, 2686–2705.
12. L. Grajciar, C. J. Heard, A. A. Bondarenko, M. V. Polynski, J. Meeprasert, E. A. Pidko and P. Nachtigall, Chem. Soc. Rev., 2018, 47, 8307–8348.
13. C. Chizallet, Top. Catal., 2022, 65, 69–81.
14. X. Gong, M. Çağlayan, Y. Ye, K. Liu, J. Gascon and A. D. Chowdhury, Chem. Rev., 2022, 122, 14275–14345.
15. V. Nieminen, M. Sierka, D. Y. Murzin and J. Sauer, J. Catal., 2005, 231, 393–404.
16. J. F. Haw, J. B. Nicholas, T. Xu, L. W. Beck and D. B. Ferguson, Acc. Chem. Res., 1996, 29, 259–267.
17. A. G. Stepanov, S. S. Arzumanov, M. V. Luzgin, H. Ernst and D. Freude, J. Catal., 2005, 229, 243–251.
18. F. Geobaldo, G. Spoto, S. Bordiga, C. Lamberti and A. Zecchina, J. Chem. Soc., Faraday Trans., 1997, 93, 1243–1249.
19. E. Yoda, J. N. Kondo and K. Domen, J. Phys. Chem. B, 2005, 109, 1464–1472.
20. S. Schallmoser, G. L. Haller, M. Sanchez-Sanchez and J. A. Lercher, J. Am. Chem. Soc., 2017, 139, 8646–8652.
21. A. M. Rigby, G. J. Kramer and R. A. van Santen, J. Catal., 1997, 170, 1–10.
22. M. Boronat, P. Viruela and A. Corma, J. Phys. Chem. A, 1998, 102, 982–989.
23. P. J. Hay, A. Redondo and Y. Guo, Catal. Today, 1999, 50, 517–523.
24. A. Bhan, Y. V. Joshi, W. N. Delgass and K. T. Thomson, J. Phys. Chem. B, 2003, 107, 10476–10487.
25. B. A. De Moor, M.-F. Reyniers, O. C. Gobin, J. A. Lercher and G. B. Marin, J. Phys. Chem. C, 2011, 115, 1204–1219.
26. C. M. Nguyen, B. A. De Moor, M.-F. Reyniers and G. B. Marin, J. Phys. Chem. C, 2011, 115, 23831–23847.
27. L. Benco, T. Demuth, J. Hafner, F. Hutschka and H. Toulhoat, J. Catal., 2002, 205, 147–156.
28. A. L. L. East, T. Bučko and J. Hafner, J. Chem. Phys., 2009, 131, 104314.
29. C. J. A. Mota and N. Rosenbach Jr, J. Braz. Chem. Soc., 2011, 22, 1197–1205.
30. G. A. Ferguson, L. Cheng, L. Bu, S. Kim, D. J. Robichaud, M. R. Nimlos, L. A. Curtiss and G. T. Beckham, J. Phys. Chem. A, 2015, 119, 11397–11405.
31. J. Rey, A. Gomez, P. Raybaud, C. Chizallet and T. Bučko, J. Catal., 2019, 373, 361–373.
32. J. Rey, P. Raybaud, C. Chizallet and T. Bučko, ACS Catal., 2019, 9813–9828.
33. J. Rey, C. Bignaud, P. Raybaud, T. Bučko and C. Chizallet, Angew. Chem., 2020, 132, 19100–19104.
34. W. Chen, X. Yi, Z. Liu, X. Tang and A. Zheng, Chem. Soc. Rev., 2022, 51, 4337–4385.
35. J. Hajek, J. Van der Mynsbrugge, K. De Wispelaere, P. Cnudde, L. Vanduyfhuys, M. Waroquier and V. Van Speybroeck, J. Catal., 2016, 340, 227–235.
36. P. Cnudde, K. De Wispelaere, J. Van der Mynsbrugge, M. Waroquier and V. Van Speybroeck, J. Catal., 2017, 345, 53–69.
37. P. Cnudde, K. De Wispelaere, L. Vanduyfhuys, R. Demuynck, J. Van der Mynsbrugge, M. Waroquier and V. Van Speybroeck, ACS Catal., 2018, 8, 9579–9595.
38. N. Rosenbach Jr., A. P. A. dos Santos, M. Franco and C. J. A. Mota, Chem. Phys. Lett., 2010, 485, 124–128.
39. K. Ren, J. Long, Q. Ren, Y. Li and Z. Dai, Mol. Simul., 2017, 43, 1348–1355.
40. C. Tuma and J. Sauer, Angew. Chem., 2005, 117, 4847–4849.
41. C. Tuma, T. Kerber and J. Sauer, Angew. Chem., Int. Ed., 2010, 49, 4678–4680.
42. Q. Ren, M. Rybicki and J. Sauer, J. Phys. Chem. C, 2020, 124, 10067–10078.
43. C. M. Nguyen, B. A. De Moor, M.-F. Reyniers and G. B. Marin, J. Phys. Chem. C, 2012, 116, 18236–18249.
44. K. De Wispelaere, P. N. Plessow and F. Studt, ACS Phys. Chem. Au, 2022, 2, 399–406.
45. W. Dai, C. Wang, X. Yi, A. Zheng, L. Li, G. Wu, N. Guan, Z. Xie, M. Dyballa and M. Hunger, Angew. Chem., Int. Ed., 2015, 54, 8783–8786.
46. M. Huang, Q. Wang, X. Yi, Y. Chu, W. Dai, L. Li, A. Zheng and F. Deng, Chem. Commun., 2016, 52, 10606–10608.
47. X. Rozanska, R. A. van Santen, T. Demuth, F. Hutschka and J. Hafner, J. Phys. Chem. B, 2003, 107, 1309–1315.
48. A. Ramirez, A. D. Chowdhury, A. Dokania, P. Cnudde, M. Caglayan, I. Yarulina, E. Abou-Hamad, L. Gevers, S. Ould-Chikh, K. De Wispelaere, V. Van Speybroeck and J. Gascon, ACS Catal., 2019, 9, 6320–6334.
49. T. Bučko and J. Hafner, J. Catal., 2015, 329, 32–48.
50. R. Gounder and E. Iglesia, Acc. Chem. Res., 2012, 45, 229–238.
51. R. Gounder and E. Iglesia, Chem. Commun., 2013, 49, 3491–3509.
52. F. Leydier, C. Chizallet, D. Costa and P. Raybaud, J. Catal., 2015, 325, 35–47.
53. H. Fang, A. Zheng, J. Xu, S. Li, Y. Chu, L. Chen and F. Deng, J. Phys. Chem. C, 2011, 115, 7429–7439.
54. M. L. Sarazen and E. Iglesia, Proc. Natl. Acad. Sci., 2017, 114, E3900–E3908.
55. M. L. Sarazen and E. Iglesia, ChemCatChem, 2018, 10, 4028–4037.
56. L. A. Clark, M. Sierka and J. Sauer, J. Am. Chem. Soc., 2004, 126, 936–947.
57. B. Smit and T. L. M. Maesen, Chem. Rev., 2008, 108, 4125–4184.
58. J. Van der Mynsbrugge, A. Janda, S. M. Sharada, L.-C. Lin, V. Van Speybroeck, M. Head-Gordon and A. T. Bell, ACS Catal., 2017, 7, 2685–2697.
59. M. Westgård Erichsen, K. De Wispelaere, K. Hemelsoet, S. L. C. Moors, T. Deconinck, M. Waroquier, S. Svelle, V. Van Speybroeck and U. Olsbye, J. Catal., 2015, 328, 186–196.
60. L. Lin, C. Qiu, Z. Zhuo, D. Zhang, S. Zhao, H. Wu, Y. Liu and M. He, J. Catal., 2014, 309, 136–145.
61. M. L. Sarazen, E. Doskocil and E. Iglesia, ACS Catal., 2016, 6, 7059–7070.
62. H. Fang, A. Zheng, S. Li, J. Xu, L. Chen and F. Deng, J. Phys. Chem. C, 2010, 114, 10254–10264.
63. A. J. Jones, R. T. Carr, S. I. Zones and E. Iglesia, J. Catal., 2014, 312, 58–68.
64. V. Blay, B. Louis, R. Miravalles, T. Yokoi, K. A. Peccatiello, M. Clough and B. Yilmaz, ACS Catal., 2017, 7, 6542–6566.
65. S. Bailleul, I. Yarulina, A. E. J. Hoffman, A. Dokania, E. Abou-Hamad, A. D. Chowdhury, G. Pieters, J. Hajek, K. De Wispelaere, M. Waroquier, J. Gascon and V. Van Speybroeck, J. Am. Chem. Soc., 2019, 141, 14823–14842.
66. A. Dokania, A. D. Chowdhury, A. Ramirez, S. Telalovic, E. Abou-Hamad, L. Gevers, J. Ruiz-Martinez and J. Gascon, J. Catal., 2020, 381, 347–354.
67. F. Eder and J. A. Lercher, J. Phys. Chem. B, 1997, 101, 1273–1278.
68. S. Siahrostami, H. Falsig, P. Beato, P. G. Moses, J. K. Nørskov and F. Studt, ChemCatChem, 2016, 8, 767–772.
69. P. Deshlahra and E. Iglesia, Chem. Commun., 2020, 56, 7371–7398.
70. C.-M. Wang, R. Y. Brogaard, B. M. Weckhuysen, J. K. Nørskov and F. Studt, J. Phys. Chem. Lett., 2014, 5, 1516–1521.
71. C.-M. Wang, R. Y. Brogaard, Z.-K. Xie and F. Studt, Catal. Sci. Technol., 2015, 5, 2814–2820.
72. C. Liu, I. Tranca, R. A. van Santen, E. J. M. Hensen and E. A. Pidko, J. Phys. Chem. C, 2017, 121, 23520–23530.
73. M. Mortén, T. Cordero-Lanzac, P. Cnudde, E. A. Redekop, S. Svelle, V. van Speybroeck and U. Olsbye, J. Catal., 2021, 404, 594–606.
74. M. L. Sarazen, E. Doskocil and E. Iglesia, J. Catal., 2016, 344, 553–569.
75. Y. Chen, X. Zhao, Z. Qin, S. Wang, Z. Wei, J. Li, M. Dong, J. Wang and W. Fan, J. Phys. Chem. C, 2020, 124, 13789–13798.
76. A. A. Latimer, A. R. Kulkarni, H. Aljama, J. H. Montoya, J. S. Yoo, C. Tsai, F. Abild-Pedersen, F. Studt and J. K. Nørskov, Nat. Mater., 2017, 16, 225–229.
77. Y. Gu, Z. Liu, C. Yu, X. Gu, L. Xu, Y. Gao and J. Ma, J. Phys. Chem. C, 2020, 124, 9314–9328.
78. J. H. Kang, F. H. Alshafei, S. I. Zones and M. E. Davis, ACS Catal., 2019, 9, 6012–6019.
79. M. Fečík, P. N. Plessow and F. Studt, ChemCatChem, 2021, 13, 2451–2458.
80. F. Berger, M. Rybicki and J. Sauer, J. Catal., 2021, 395, 117–128.
81. A. Janda, B. Vlaisavljevich, L.-C. Lin, B. Smit and A. T. Bell, J. Am. Chem. Soc., 2016, 138, 4739–4756.
82. A. Janda, B. Vlaisavljevich, B. Smit, L.-C. Lin and A. T. Bell, J. Phys. Chem. C, 2017, 121, 1618–1638.
83. Database of zeolite structures, https://www.iza-structure.org/databases/, 2019.
84. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
85. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
86. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
87. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
88. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
89. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
90. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
91. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
92. K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. D. Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. D. Marco, C. Draxl, M. Dułak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Grånäs, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iuşan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Küçükbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G.-M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G.-X. Zhang and S. Cottenier, Science, 2016, 351, aad3000.
93. A. Ghysels, D. Van Neck, V. Van Speybroeck, T. Verstraelen and M. Waroquier, J. Chem. Phys., 2007, 126, 224102.
94. M. T. Reetz, A. Meiswinkel, G. Mehler, K. Angermund, M. Graf, W. Thiel, R. Mynott and D. G. Blackmond, J. Am. Chem. Soc., 2005, 127, 10305–10313.
95. P. J. Donoghue, P. Helquist, P.-O. Norrby and O. Wiest, J. Chem. Theory Comput., 2008, 4, 1313–1323.
96. A. Ghysels, T. Verstraelen, K. Hemelsoet, M. Waroquier and V. Van Speybroeck, J. Chem. Inf. Model., 2010, 50, 1736–1750.
97. T. J. Goncalves, P. N. Plessow and F. Studt, ChemCatChem, 2019, 11, 4368–4376.
98. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
99. Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890–890.
100. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
101. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662.
102. G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–488.
103. G. Lippert, J. Hutter and M. Parrinello, Theor. Chem. Acc., 1999, 103, 124–140.
104. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
105. S. Nosé, Mol. Phys., 1984, 52, 255–268.
106. G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643.
107. G. M. Torrie and J. P. Valleau, Chem. Phys. Lett., 1974, 28, 578–581.
108. G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199.
109. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
110. ThermoLIB|Center for Molecular Modeling, https://molmod.ugent.be/software/thermolib.
111. T. Bučko, S. Chibani, J.-F. Paul, L. Cantrel and M. Badawi, Phys. Chem. Chem. Phys., 2017, 19, 27530–27543.
112. S. Bailleul, K. Dedecker, P. Cnudde, L. Vanduyfhuys, M. Waroquier and V. Van Speybroeck, J. Catal., 2020, 388, 38–51.
113. S. Svelle, C. Tuma, X. Rozanska, T. Kerber and J. Sauer, J. Am. Chem. Soc., 2009, 131, 816–825.
114. F. Göltl, A. Grüneis, T. Bučko and J. Hafner, J. Chem. Phys., 2012, 137, 114111.
115. P. N. Plessow and F. Studt, J. Phys. Chem. Lett., 2020, 11, 4305–4310.
116. T. Bučko, L. Benco, J. Hafner and J. G. Ángyán, J. Catal., 2011, 279, 220–228.
117. P. Cnudde, R. Demuynck, S. Vandenbrande, M. Waroquier, G. Sastre and V. Van Speybroeck, J. Am. Chem. Soc., 2020, 142, 6007–6017.
118. P. Cnudde, E. A. Redekop, W. Dai, N. G. Porcaro, M. Waroquier, S. Bordiga, M. Hunger, L. Li, U. Olsbye and V. Van Speybroeck, Angew. Chem., 2021, 133, 10104–10110.
119. P. Ferri, C. Li, R. Millán, J. Martínez-Triguero, M. Moliner, M. Boronat and A. Corma, Angew. Chem., 2020, 59, 1–9.
120. U. Olsbye, S. Svelle, M. Bjørgen, P. Beato, T. V. W. Janssens, F. Joensen, S. Bordiga and K. P. Lillerud, Angew. Chem., Int. Ed., 2012, 51, 5810–5831.
121. P. Ferri, C. Li, C. Paris, A. Rodríguez-Fernández, M. Moliner, M. Boronat and A. Corma, ChemCatChem, 2021, 13, 1578–1586.
122. E. G. Derouane, J. C. Védrine, R. R. Pinto, P. M. Borges, L. Costa, M. A. N. D. A. Lemos, F. Lemos and F. R. Ribeiro, Catal. Rev.: Sci. Eng., 2013, 55, 454–515.
123. M. Boronat and A. Corma, Catal. Lett., 2015, 145, 162–172.
124. A. Zecchina, G. Spoto and S. Bordiga, Phys. Chem. Chem. Phys., 2005, 7, 1627–1642.
125. M. Boronat and A. Corma, ACS Catal., 2019, 9, 1539–1548.
126. R. Y. Brogaard, C.-M. Wang and F. Studt, ACS Catal., 2014, 4, 4504–4509.
127. C. Ahoba-Sam, M. W. Erichsen and U. Olsbye, Chin. J. Catal., 2019, 40, 1766–1777.
128. J. S. Martinez-Espin, M. Mortén, T. V. W. Janssens, S. Svelle, P. Beato and U. Olsbye, Catal. Sci. Technol., 2017, 7, 2700–2716.
129. I. Yarulina, K. D. Wispelaere, S. Bailleul, J. Goetze, M. Radersma, E. Abou-Hamad, I. Vollmer, M. Goesten, B. Mezari, E. J. M. Hensen, J. S. Martínez-Espín, M. Morten, S. Mitchell, J. Perez-Ramirez, U. Olsbye, B. M. Weckhuysen, V. Van Speybroeck, F. Kapteijn and J. Gascon, Nat. Chem., 2018, 10, 804.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cy00642e

---