Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetic square scheme in oxygen-redox battery electrodes†
Kosuke
Kawai‡
 a,
Xiang-Mei
Shi
a,
Xiang-Mei
Shi
 a,
Norio
Takenaka
a,
Norio
Takenaka
 ab,
Jeonguk
Jang
a,
Benoit Mortemard
de Boisse
a,
Akihisa
Tsuchimoto
a,
Daisuke
Asakura
ab,
Jeonguk
Jang
a,
Benoit Mortemard
de Boisse
a,
Akihisa
Tsuchimoto
a,
Daisuke
Asakura
 c,
Jun
Kikkawa
c,
Jun
Kikkawa
 d,
Masanobu
Nakayama
d,
Masanobu
Nakayama
 be,
Masashi
Okubo‡
be,
Masashi
Okubo‡
 ab and
Atsuo
Yamada
ab and
Atsuo
Yamada
 *ab
*ab
aDepartment of Chemical System Engineering, School of Engineering, The University of Tokyo, Hongo 7-3-1, Bunkyo-ku, Tokyo 113-8656, Japan. E-mail: yamada@chemsys.t.u-tokyo.ac.jp
bElemental Strategy Initiative for Catalysts and Batteries (ESICB), Kyoto University, Nishikyo-ku, Kyoto 615-8245, Japan
cNational Institute of Advanced Industrial Science and Technology, Tsukuba, Ibaraki 305-8568, Japan
dNational Institute of Materials Science (NIMS), Tsukuba, Ibaraki 305-0047, Japan
eFrontier Research Institute for Materials Science (FRIMS), Nagoya Institute of Technology, Showa-ku, Nagoya, Aichi 466-8555, Japan
First published on 18th May 2022
Abstract
Integrating an anionic-redox (or oxygen-redox) capacity with a conventional cationic-redox capacity is a promising strategy for large-capacity battery cathodes exceeding present technical limits. However, most oxygen-redox cathodes exhibit a large charge/discharge voltage hysteresis (>0.5 V), resulting in poor energy efficiency and impractical implementation. Here, we show that nonpolarizing O− ↔ O2− (4.4 V vs. Li/Li+) and polarizing O22− → O2− (3.3 V vs. Li/Li+) coexist and kinetically compete in O2-type Li1.12–yNi0.17Mn0.71O2. The oxygen-redox reaction is described as a square scheme, involving bond-forming 2O− → O22− and bond-cleaving O24− → 2O2− processes, where preventing the formation of O22− is essential to realize non-polarizing and energy-efficient oxygen-redox reactions.
Broader contextDevelopment of high-performance energy storage systems is of vital importance for realizing a sustainable society. Although lithium-ion batteries (LIBs) are the state-of-the-art energy storage technology, a modest cathode capacity relying solely on transition-metal redox severely limits their energy density. An additional oxygen-redox capacity, which possesses a high promise to enhance the energy density, normally causes an unacceptably large voltage hysteresis during charge/discharge, rendering their use impractical. This work identifies the origin of the voltage hysteresis as a ‘square scheme’ involving both thermodynamic and kinetic issues, providing a standard landscape for extra oxygen redox in battery electrodes. |
Introduction
The rapid market growth of electric vehicles (EVs) has significantly increased the industrial demands for their improved performance, such as longer driving distance, longer calendar life, and lower cost.1–3 For example, the driving distance of an EV is determined by the energy density of in-vehicle lithium-ion batteries (LIBs). However, current LIBs possess an unsatisfactory gravimetric energy density of 200–250 W h kg−1, powering typical EVs for 300–400 km per charge, which is below most consumers’ requirements.4,5 Thus, increasing the energy density of LIBs is crucial for the widespread use of EVs.The energy density of LIBs is limited in part by the specific capacity of the positive electrode (cathode) material. Conventional cathode materials, i.e., layered transition-metal oxides LiMO2 (M = transition metal), deliver a modest capacity of approximately 160 mA h g−1, where the dominant mechanism of charge compensation for lithium-ion (de)intercalation is the valence change of the transition metal.6–8 Further increase in the cathode capacity requires an additional redox center. To activate redox reactions of oxide ions (oxygen redox), lithium-rich transition-metal oxides (Li1+xM1−xO2) have been extensively studied for over a decade as they deliver much larger reversible capacities (> 200 mA h g−1).9–12
Redox-active oxygen is generated by specific Li–O–Li and Li–O–□ (□; vacancy) local configurations in Li1+xM1−xO2, where non-bonding O 2p states just below the Fermi level undergo oxidation to increase the charge capacity.13–15 When oxidized oxide ions O− are stabilized through an M–O bond, a nonpolarizing discharge capacity of an O−/O2− redox couple is obtained, as reported for Na2Mn3O7 (Scheme 1).16 However, most Li1+xM1−xO2 electrodes exhibit polarizing reduction of peroxo-like O22− (e.g., Li2Ru0.5Sn0.5O3) or trapped O2 molecules (e.g., Li1.2Ni0.13Co0.13Mn0.54O2) to deliver the discharge capacity at a lower voltage.11,15,17–25 Considering immediate electron transfer (O2− → O− + e−) against subsequent structural deformation (O–O dimerization), the overall hypothetical mechanism of the oxygen-redox reactions is described as a square scheme (Scheme 1): if an oxidized oxide ion (O−) is stable, it directly contributes to a non-polarizing discharge capacity (non-polarizing O redox). Meanwhile, unstable O− dimerize to form stable peroxo-like O22−, which may be accelerated by cation migration. The O22− dimers provide a polarizing discharge capacity (polarizing O redox) and an unstable reduced dimer (e.g., O24−) decomposes to O2−. The O–O dimerization is prone to result in release of O2 gas (O2 evolution) by their excessive oxidation. This sequential square-type mechanism explains the fragmental experimental observations such as a large voltage hysteresis during charge/discharge, spectroscopic detection of O22− or O2 in bulk after the charging process, O2 gas release upon charge, and different enthalpies on charge versus discharge.18–30 However, experimental verification of the square scheme is limited in part due to complicated structural changes during the oxygen-redox reactions.31–36 For example, O3-Li1.2Ni0.2Mn0.6O2 (O3: lithium ions occupy octahedral sites between the MO2 layers, and the packing arrangement of the oxide ions is ABCABC) exhibits irreversible structural degradation such as layered-to-spinel transformation and surface cation densification upon cycling.31,32 For reliable analysis, electrode materials that possess structural integrity against the oxygen-redox reactions should be considered.
 | ||
| Scheme 1 Reaction paths of an oxygen-redox reaction. ‘Non-polarizing’ and ‘polarizing’ correspond to reversible and irreversible processes, respectively. | ||
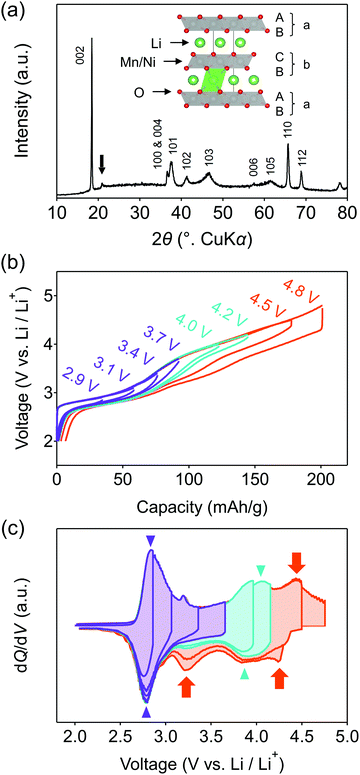
This work focuses on O2-type lithium-rich layered transition-metal oxides as cathode materials with structural integrity (Fig. 1a inset, O2: lithium ions occupy octahedral sites between the MO2 layers and the packing arrangement of the oxide ions is ABCBA), which is an emerging class of oxygen-redox electrode materials.37–41 In the O2-type oxides, the structural degradation upon cycling is suppressed because migration of M to the Li+ layers is unfavorable: M in a Li+ layer suffers from strong Coulombic repulsion from face-sharing Mn+ in an adjacent MO2 layer.39 Moreover, O2-type Li-rich layered oxides exhibit negligible O2 gas release.40 As a consequence, O2-Li1.12−yNi0.17Mn0.71O2 provides a large reversible capacity greater than 200 mA h g−1 with minimal voltage decay and capacity fading upon cycling.38
Taking advantage of the structural integrity of O2-Li1.12−yNi0.17Mn0.71O2, multi-angle analyses were performed to identify the chemical states of oxygen (O2−, O−, O22−, O24−) and their inter-state transformation, using X-ray absorption/emission spectroscopy, magnetic susceptibility measurements, and density functional theory calculations. Based on the electrochemical kinetic analysis, particularly for the 2O2− → O22− transformation, technical strategies to realize non-polarizing and energy-efficient oxygen redox will be discussed.
Results and discussion
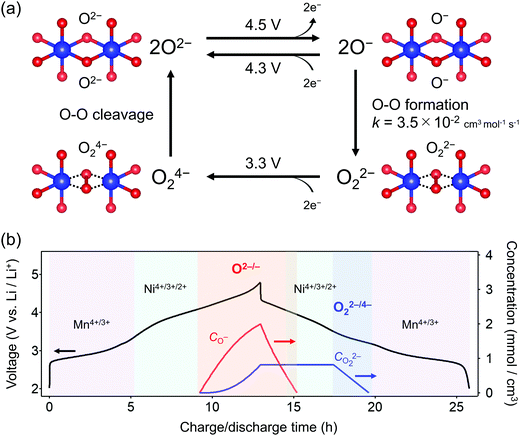
O2-Li1.12−yNi0.17Mn0.71O2 was synthesized by the Na+/Li+ ion-exchange method using P2-Na0.71[Li0.12Ni0.17Mn0.71]O2 (Fig. S1, ESI†) as a precursor.38 The powder X-ray diffraction pattern of O2-Li1.12−yNi0.17Mn0.71O2 (Fig. 1a) shows Bragg peaks indexed to a hexagonal system (space group: P62mc, typical of the O2 phase37,42,43), indicating the successful transformation of the P2-type sodium layered oxide to the O2-type lithium layered oxide (i.e., ‘aba’ stacking of the transition-metal layers in an ‘ABCBA’ oxide-ion packing arrangement, Fig. 1a inset). Indeed, a high-angle annular dark-field scanning transmission electron microscopy image confirms the ‘aba’ stacking of the transition–metal layers (Fig. S2, ESI†). The elemental analyses (inductively coupled plasma atomic emission and absorption spectroscopy) for the pristine compound determined the chemical composition of Li0.78Mn0.72Ni0.13O2. Galvanostatic charge/discharge measurements show that O2-Li1.12−yNi0.17Mn0.71O2 delivers a large discharge capacity of approximately 210 mA h g−1, exceeding the M-redox capacity (193 mA h g−1) (Fig. S3a, ESI†). After 80 cycles, 98% of the discharge capacity in the second cycle is retained, while the decay of the average discharge voltage is negligibly small (<5 mV) (Fig. S3b and c, ESI†). Typically, conventional O3-type oxygen-redox layered oxides exhibit structural degradation initiated by the migration of M to Li+ layers.33,34 In contrast, in O2-type layered oxides, Mn+ ions migrated to Li+ layers would be subjected to strong Coulombic repulsion from face-sharing Mn+ ions in the adjacent MO2 layers, such that the migration of M would be energetically unfavorable to mitigate both capacity fading and voltage decay during the charge/discharge cycles.39 These observations are consistent with those reported previously, i.e., O2-Li1.12−yNi0.17Mn0.71O2 exhibits a stable oxygen-redox reaction.38This stable oxygen-redox reaction was further investigated by measuring the charge/discharge curves under incremental upper cut-off voltages from 2.9 to 4.8 V vs. Li/Li+ (Fig. 1b). Under the cut-off voltages below 4.2 V vs. Li/Li+, dQ/dV plots (Fig. 1c) show two reversible redox reactions occurring at approximately 2.8 and 3.9 V vs. Li/Li+ with small polarizations of 0.05 and 0.13 V (purple and cyan triangles in Fig. 1c), respectively. These two nonpolarizing dQ/dV peaks should be attributed to the conventional redox reactions of Mn and Ni. With an increase in the cut-off voltage above 4.2 V vs. Li/Li+, a new anodic dQ/dV peak emerges at 4.5 V vs. Li/Li+. Correspondingly, two additional cathodic dQ/dV peaks emerge at 4.3 and 3.3 V vs. Li/Li+ (orange arrows in Fig. 1c), with the emergence of this anodic peak, which can be attributed to the oxygen-redox reactions. For most O3-type oxides, the oxygen-redox reaction proceeds simultaneously with the cationic-redox reactions such as Mn4+/Mn3+ and Ru5+/Ru4+.27,44 In contrast, the cathodic reaction at 3.3 V vs. Li/Li+ in O2-Li1.12−yNi0.17Mn0.71O2 can be ascribed solely to the polarizing oxygen reduction coupled with oxygen oxidation at 4.5 V vs. Li/Li+, allowing its systematic investigation.
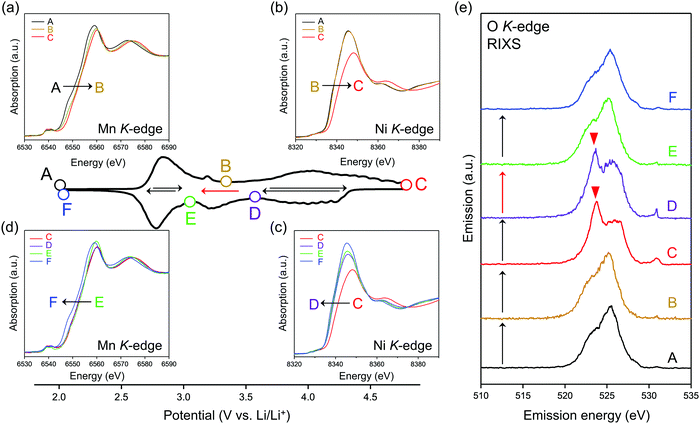
To identify the redox center for each dQ/dV peak, ex situ X-ray absorption/emission spectroscopy measurements were conducted. Fig. 2a–d shows Mn and Ni K-edge X-ray absorption near-edge structure (XANES) spectra during the second cycle. The redox reaction at 2.8 V vs. Li/Li+ causes a reversible shift of the Mn K-edge XANES spectra (Fig. 2a and d), indicating that the oxidation and reduction of Mn occur at the dQ/dV peaks of A → B and E → F, respectively. As the Ni K-edge XANES spectra show a reversible shift at 3.9 V vs. Li/Li+ (Fig. 2b and c), the dQ/dV peaks of B → C and C → D can be attributed to the oxidation and reduction of Ni, respectively. These attributions (Mn and Ni redox reactions at 2.8 and 3.9 V vs. Li/Li+, respectively) are double-confirmed by Mn and Ni L2,3-edge absorption spectra. (Fig. S4 and S5, ESI†).
After charging to 4.8 V vs. Li/Li+, O K-edge X-ray absorption spectroscopy shows the emergence of new absorption at approximately 531 eV (Fig. S6, ESI†), while resonant inelastic X-ray scattering (RIXS) spectrum with the incident photon energy of 531 eV shows intense emission at 524 eV (spectrum C in Fig. 2e), both of which are characteristic features of charged oxygen-redox electrode materials.14,15,19–21,33,39,45–47 Thus, the anodic dQ/dV peak at 4.5 V vs. Li/Li+ corresponds to the oxidation of oxide ions. These signals for oxidized oxygen do not completely disappear even after discharging to 3.6 V vs. Li/Li+. Instead, the disappearance is confirmed after discharging to 3.1 V vs. Li/Li+. Considering the similar emission peaks observed for Li2O2, CaO2, and O2 molecule,19,28,48 dimerized oxygen species O2n− (n = 0 or 2) exists in charged O2-Li1.12−yNi0.17Mn0.71O2 at 4.5 V. It is noteworthy that an enhancement in the elastic peak region was observed after charge (spectrum C and D in Fig. 2e). A possible explanation is the Raman scattering arising from the vibrational transition of O–O bond19–21 although its origin is still under debates.49,50
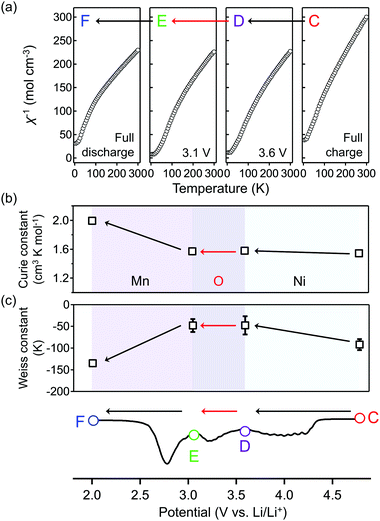
To obtain firm evidence of the above-mentioned sequential chemical states of oxygen during the oxygen-redox reaction, the magnetic properties of O2-Li1.12−yNi0.17Mn0.71O2 were measured along the C → D → E → F discharging process (Fig. 3). Analyses of the temperature dependence of magnetic susceptibility (χ) at high temperature (T > 200 K) (Fig. 3a and Fig. S7, ESI†) provide two important physical quantities, the Curie constant (C) and Weiss temperature (Θ), for each state of discharge (C: 4.8 V, D: 3.6 V, E: 3.1 V, and F: 2.0 V vs. Li/Li+, Fig. 3b and 3c) according to the Curie–Weiss law (χ = C(T − Θ)−1). Upon discharging from 4.8 to 3.6 V (C → D in the dQ/dV plot) and from 3.1 to 2.0 V vs. Li/Li+ (E → F), the value of C increases (observed ΔC = 0.04 and 0.42 cm3 K mol−1) mainly due to the reduction of Ni4+ to Ni2+ (S = 0 → 1, calculated ΔC = 0.13 cm3 K mol−1) and Mn4+ to Mn3+ (S =3/2 → 2, calculated ΔC = 0.37 cm3 K mol−1), respectively. A small difference between the observed and calculated ΔC at the C–D region is owing to the nonpolarizing reduction of O− to O2− (S = 1/2 → 0, ΔC < 0). The spin-state changes of the transition metals from 4.8 to 3.6 V (C → D) and from 3.1 to 2.0 V (E → F) vs. Li/Li+ induce a large change in Θ (Fig. 3c) through the drastic modulation of super-exchange interactions. Contrarily, both C and Θ remain almost unchanged from 3.6 to 3.1 V (D → E) vs. Li/Li+, indicating the redox reaction of diamagnetic species, i.e., the reduction of O22− to O2− (S = 0 → 0, ΔC = 0), verifying the square scheme of the oxygen-redox reaction, including the polarizing reduction of O22− (Scheme 1). No signature is identified to support the existence of paramagnetic O2 molecules in the bulk. Therefore, the cathodic dQ/dV peaks at 4.3 and 3.3 V (Fig. 1c) are ascribed to the existence of two types of reduction processes: (i) the nonpolarizing reduction of O− (4.3 V) and (ii) the polarizing reduction of O22− (3.3 V), respectively.
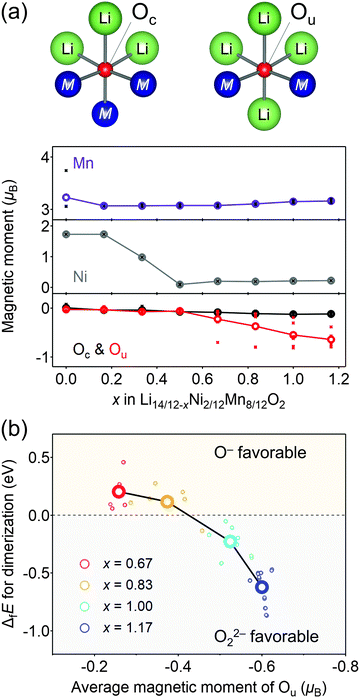
Considering that O22− formation is the origin of the voltage hysteresis, it is crucial to minimize the polarizing discharge capacity of O22− by decelerating the dimerization process of 2O− → O22− to maximize the energy efficiency of a battery cell. To quantify and visualize the energetic competition for the formation of O−versus O22−, density functional theory (DFT) calculations were conducted, where the model structures of O2-Li14/12−xNi2/12Mn8/12O2 were obtained using the genetic algorithm (GA; Fig. S8–S11, ESI†). Fig. 4a shows the plots of the magnetic moments of Mn, Ni, and O in hypothetical model structures without O–O dimerization. The oxygen atom coordinated by two transition metals is labelled as Ou, which possesses non-bonding O 2p state, while those coordinated by three transition metals are labelled as Oc. The magnetic moment of Ou changes from 0μB to −0.64μB at x = 0.50 → 1.17 (O2− → O− (S = 0 → 1/2)), whereas that of Oc remains constant during the entire process (x = 0 → 1.17), which is consistent with the other oxygen-redox cathode materials.13,15,51 In contrast, the magnetic moments of Mn and Ni increase at x = 0 → 0.50 (Ni2+ → Ni4+ (S = 1 → 0) and Mn3+ → Mn4+ (S = 2 → 3/2)). These calculation results are consistent with the attributions of redox centers for the dQ/dV plots, and emphasis should be placed on the conclusion that the non-polarizing redox reaction of O2−/O− occurs only above the potential of the M redox reactions.
The formation of O22− (2O− → O22−) was then simulated by decreasing the distances of several oxygen pairs in the model structure. For the model structures with x < 0.67, the O–O bonds immediately cleave during structural optimization owing to their thermodynamic instability. In contrast, the O–O dimers survive in the optimized structures of x ≥ 0.67 with the bond lengths of 1.4–1.5 Å, close to the typical experimental values of O22− (1.56 Å) observed in Li2O2.52 In addition, these bond lengths are in good agreement with those obtained by the DFT calculations for Li2MnO3.53 Importantly, O22− formation energy (ΔfE) is negative (O22− favorable) for the oxygen pairs with average magnetic moments below −0.5μB at highly oxidized states (Fig. 4b). Bader charge analysis (Fig. S12, ESI†) also indicates that over-oxidized oxide ions (<−0.5μB) are thermodynamically prone to undergo the dimerization of 2O− → O22−.
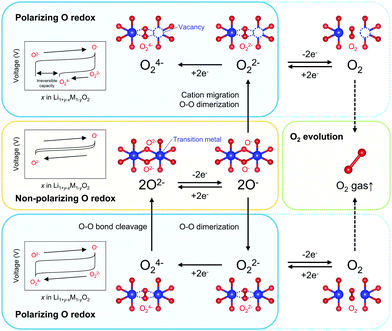
Overall, the O–O dimerization in O2-Li1.12−yNi0.17Mn0.71O2 can be summarized by the square scheme in Fig. 5a. Upon charge, Ou2− with non-bonding 2p states is oxidized to O− above 4.2 V vs. Li/Li+. At the early stage of oxygen oxidation, O− is thermodynamically more favorable than O22−. However, with further oxygen oxidation, the over-oxidized oxide ions dimerize to form O22−. If a constant voltage is applied for a time duration, Δt, after galvanostatic charge (float mode) and the dimerization proceeds with a rate constant, k, the corresponding discharge capacity (Q, in region D–E in Fig. 2) of O22− is expected to increase according to the additional dimerization during constant-voltage application as Q = jt1 − FCr(t1)ρ−1{1 + kΔtCr(t1)}−1, where j is the specific current density, t = t1 is the time to start applying the constant voltage, F is the Faraday constant, ρ is the density of the electrode material, and Cr(t1) is the concentration of O− after charge (t = t1). The kinetic analysis of this float-time dependence successfully provides the dimerization rate constant as k = 3.5 × 10−2 cm3 mol−1 s−1 (‘Rate constant for dimerization of O− under a CCCV (float) mode’, Fig. S13–S18, ESI†). Indeed, DFT calculations using a climbing image nudged elastic band (CI-NEB) method provide an energy barrier of 0.2–0.4 eV for O–O dimerization in the delithiated structures, implying the possible occurrence of the dimerization process (Fig. S19, ESI†). Fig. 5b depicts the calculated concentrations of O− and O22− in O2-Li1.12−yNi0.17Mn0.71O2 during the charge/discharge at C/20 using the square scheme shown in Fig. 5a. The chemical state at the end of charge is estimated as O2-Li1.12−yNi0.17Mn0.71O1.75(O−)0.13(O22−)0.06. Upon discharge, the sequential reduction of O−, Ni, O22−, and Mn occurs, where the reduction of O22− induces immediate O–O bond cleavage to regenerate O2−.
It is widely accepted that O–O dimerization is accelerated by transition-metal migration to alkali-ion layers.20,29 This is clearly not the case for O2-Li1.12−yNi0.17Mn0.71O2 because the MO6 octahedra share a face with the LiO6 octahedra in adjacent Li layers, which prohibits M migration. However, as demonstrated through the DFT calculations (Fig. 4b), the suppression of M migration alone cannot completely mitigate O–O dimerization. As shown in Fig. 5b, 12.5% of the oxide ions (0.25 oxide ions per 2 oxide ions) are oxidized at the end of charge, corresponding to an oxygen-redox capacity of 42 mA h g−1, and then the O–O dimerization of the 48% oxidized oxide ions (0.12 oxide ions per 0.25 oxidized oxide ions) occurs even without M migration. Recently, Na2Mn3O7 was reported to exhibit nonpolarizing oxygen-redox reaction (O−/O2−), where 14% of the oxide ions (1 oxide ion per 7 oxide ions) are oxidized but stably exist as O− without dimerization.16 One possible explanation is the effect of large Na+ to significantly mitigate the M migration to the alkaline-metal layers and hence the formation of peroxo-like O22−, where large prismatic sites of Na+ layers are unfavorable for much smaller Mn+ (radii ratio Na+/Mn+ ∼ 1.6 vs. Li+/Mn+ ∼ 1.2).54,55 Alternatively, or in parallel, covalent Ni4+–O22− interaction (strong ligand-to-metal charge transfer) promotes the O–O dimerization as compared to ionic Mn4+–O22− interaction. Indeed, average O22− formation energy (ΔfE) for the O pairs coordinated to Ni is lower than that for the O pairs coordinated to Mn (Fig. S20, ESI†). Therefore, in addition to mitigating the M migration, selecting less electronegative transition metals (e.g., Ti, Mn), which can suppress O–O dimerization is crucial to maximize the non-polarizing oxygen-redox capacity.
Conclusions
Kinetic formation of the peroxo-like O22− dimer was identified as the origin of a voltage hysteresis in O2-type Li1.12–yNi0.17Mn0.71O2. Even in O2-type layered oxides that prohibit M migration, O22− is thermodynamically favorable under certain high-voltage conditions where the oxide ions are over-oxidized. Multiple experimental and theoretical investigations have revealed that (i) O2− → O− is dominant at an early stage of oxygen oxidation, while (ii) 2O− → O22− becomes energetically favorable at over oxidation. However, (iii) 2O− → O22− requires O–O bond formation, causing (iv) coexistence of O− and O22− at charged states, followed by simultaneous emergence of non-polarizing direct O− → O2− reduction at 4.3 V and polarizing O22− → O24− reduction at 3.2 V upon discharge, where (v) the O22− → O24− reduction capacity at 3.2 V is pronounced by prolonged float charging at 4.8 V. However, as O–O dimerization is a kinetic process that occurs after oxidation of O2− to O−, a part of O− survives to contribute to the nonpolarizing discharge capacity through reversible O2−/O− redox reaction. These insights emphasize the importance of suppressing the formation of O22− and maximizing the contribution of the nonpolarizing O2−/O− redox couple to develop energy-efficient oxygen-redox battery electrodes. The square scheme confirmed in this work, involving both thermodynamic and kinetic issues, encompasses all the reaction models proposed thus far in the literature and provides a standard landscape for extra oxygen redox in battery electrodes.Methods
Materials
O2-type Li1.12−yNi0.17Mn0.71O2 was synthesized by the Na+/Li+ ion-exchange method.32 Stoichiometric amounts of NiSO4·6H2O (Wako Pure Chemical Industries, Ltd, min. 98.0%) and MnSO4·5H2O (Wako Pure Chemical Industries, Ltd, min. 99.9%) were dissolved in distilled water with a total metal concentration of 0.5 mol dm−3. In parallel, a 0.5 mol dm−3 Na2CO3 (Wako Pure Chemical Industries, Ltd, min. 99.8%) aqueous solution was prepared. The two solutions were slowly dropped into a beaker of distilled water at 70 °C and stirred continuously. After 1 h, the precipitate was filtered and washed with distilled water and ethanol to remove sodium. The product was dried overnight in vacuum at 120 °C. The resulting metal carbonate was mixed with stoichiometric amounts of Na2CO3 and Li2CO3 (Wako Pure Chemical Industries, Ltd., min. 99.0%) to obtain an intermediate P2-Na0.71[Li0.12Ni0.17Mn0.71]O2 phase. The mixture was pressed into a pellet and heated at 800 °C for 8 h under dry air. Ion-exchange from Na+ to Li+ was conducted using the molten-salt method.38 The P2-Na0.71[Li0.12Ni0.17Mn0.71]O2 powder was mixed with LiNO3 (Wako Pure Chemical Industries, Ltd) and LiCl (Wako Pure Chemical Industries, Ltd, min. 99.0%) in a molar ratio of 82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 to obtain a Na
18 to obtain a Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li ratio of 1
Li ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 in an Ar-filled glovebox. This mixture was heated at 280 °C for 4 h in air. The final product was filtered and washed with distilled water and ethanol. The powder was dried overnight in vacuum at 120 °C.
10 in an Ar-filled glovebox. This mixture was heated at 280 °C for 4 h in air. The final product was filtered and washed with distilled water and ethanol. The powder was dried overnight in vacuum at 120 °C.
Materials characterization
Powder X-ray diffraction patterns were measured using Rigaku RINT-TTR III (Cu Kα radiation) in 0.02° steps over a 2θ range of 10°–80°. The P2 and O2 phases were analyzed under an Ar atmosphere using an airtight sample holder. The crystal structures were drawn by VESTA.56 A high-angle annular dark-field scanning transmission electron microscope image was recorded using Themis Z (Thermo Fisher Scientific) with an acceleration voltage of 300 kV. A thin specimen was prepared using a focused ion beam of Ga using JIB-4501 (JEOL) at −180 °C. The elemental analyses were carried out using the inductively coupled plasma atomic emission spectroscopy (ICP-AES) (Seiko SPS4000) and ICP atomic absorption spectroscopy (ICP-AAS) (Hitachi Z-2300).Electrochemical measurements
Electrochemical measurements were performed using 2032-type coin cells assembled in an Ar-filled glovebox. To prepare the working electrodes, a slurry composed of active material (80 wt%), acetylene black (10 wt%) (Li-400, DENKA) and poly(vinylidene fluoride) (10 wt%) (KUREHA) mixed in N-methyl pyrrolidone (Kanto Chemical Co., Inc., min. 99.0%) was coated onto an Al foil and then dried overnight at 65 °C in air. The counter electrodes were Li foil (Honjo Metal Co., Ltd). The electrolyte was 1 mol dm−3 LiPF6 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) mixture of ethylene carbonate and dimethyl carbonate (battery grade, Kishida Chemical Co., Ltd). The separators used were glass fibers (GB-100R, Advantec) dried overnight at 180 °C in vacuum. Galvanostatic charge/discharge measurements were performed using a potentio-galvanostat, TOSCAT (TOYO Corporation). For ex situ analyses, the cells were disassembled in the Ar-filled glovebox. The electrodes were rinsed with dimethyl carbonate (Kishida Chemical) three times and dried in vacuum at 25 °C.
1 (v/v) mixture of ethylene carbonate and dimethyl carbonate (battery grade, Kishida Chemical Co., Ltd). The separators used were glass fibers (GB-100R, Advantec) dried overnight at 180 °C in vacuum. Galvanostatic charge/discharge measurements were performed using a potentio-galvanostat, TOSCAT (TOYO Corporation). For ex situ analyses, the cells were disassembled in the Ar-filled glovebox. The electrodes were rinsed with dimethyl carbonate (Kishida Chemical) three times and dried in vacuum at 25 °C.
Hard X-ray spectroscopy
Ex situ Mn and Ni K-edge X-ray absorption near edge structure (XANES) spectra were collected at room temperature in a transmission mode at BL-9C in Photon Factory, High Energy Accelerator Research Organization (KEK), Tsukuba, Japan. For Mn K-edge XAFS measurements, initial and final energy were 6502.6 and 6607.6 eV with an energy step of 0.3 eV. Photon energy was calibrated by setting a peak top of first derivative of K-edge XANES spectrum for Mn foil at 6539 eV. For Ni K-edge XAFS measurements, initial and final energy were 8296.7 and 8401.7 eV with an energy step of 0.3 eV. Photon energy was calibrated by setting a peak top of first derivative of K-edge XANES spectrum for Ni foil at 8333 eV. The electrodes after charging/discharging were wrapped with a Kapton tape to prevent exposure to air. Thereafter, data analysis was performed using Athena software.57Soft X-ray spectroscopy
Ex situ soft X-ray absorption spectra (XAS) and resonant inelastic X-ray scattering (RIXS) spectra were measured at room temperature in vacuum at BL07LSU and BL27SU in Spring-8, Hyogo, Japan.58 All the samples were transferred from an Ar-filled glovebox into a vacuum chamber using a transfer vessel without air exposure. A partial fluorescence yield (PFY) mode was adopted for the O K-edge and Ni L2,3-edge XAS and inverse PFY mode for the Mn L2,3-edge XAS using inversed intensity of O Kα emission to prevent the distortion of spectra due to self-absorption and saturation effect.59,60 The RIXS spectra were collected for the O K-edge. A silicon-drift detector was used for Mn and Ni L2,3-egdge XAS and O K-edge XAS measurements. The total energy resolution of the RIXS measurement at BL07LSU was ΔE ∼ 160 meV at 530 eV. Mass loading of electrodes was 1.06 mg cm−2 and thickness of electrode was approximately 15 μm for soft XAS/RIXS measurements.Magnetic measurements
Magnetic susceptibility measurements were performed using an MPMS-5S SQUID magnetometer (Quantum Design) in the temperature range of 5–300 K under an applied field of 0.1 T. All the samples were packed into capsules to prevent exposure to air. The obtained data were corrected considering the core diamagnetism based on Pascal's constants.Ab initio calculations
Ab initio calculations were performed using the Vienna ab initio simulation package with the projected augmented-wave method.61–65 To model O2-type Li1.12–yNi0.17Mn0.71O2, Li14Ni2Mn8O24 (Z = 12) was prepared as a unit cell. The arrangements of Li/Ni/Mn in the transition-metal layers were determined using the genetic algorithm (GA) approach. The GA calculation details are introduced in the next section. The total energies were calculated based on density functional theory (DFT) using the generalized gradient approximation of Perdew–Burke–Ernzerhof exchange–correlation functional with Hubbard U = 5.04 and 5.10 eV for Ni and Mn, respectively, to correct the self-interaction error of correlated d electrons.66 The energy cut-off and the number of k-points in the reciprocal cell were 300 eV and unity (Γ-point sampling), respectively. All the calculations were performed considering the initial ferromagnetic ordering of the Ni and Mn atoms. The lattice parameters and atomic positions were relaxed until the forces on each atom were less than 0.01 eV Å−1. After the GA procedure, the five lowest-energy structures were recalculated with an energy cut-off of 520 eV and a k-point mesh of 4 × 3 × 3. Similarly, the Li/vacancy arrangements in the delithiated phases of Li14–zNi2Mn8O24 (4 ≤ z ≤ 10 at intervals of 2) were also determined using the GA approach, and the total energies of the five lowest-energy structures were recalculated for each Li composition. In the case of z = 2 and 12, the total energies for all the Li/vacancy arrangements were calculated for possible structures. For electronic structure analysis, the hybrid functional introduced by Heyd–Scuseria–Ernzerhof (HSE) was used with the exact exchange fraction in the Hartree–Fock/DFT hybrid functional and range-separation parameter of 0.25 and 0.2, respectively (HSE06).67 The Bader charge was calculated using the script provided by Henkelman's group.68–71 Dimerization energy (ΔfE) is defined as follows:| ΔfE = E(Li14–zNi2Mn8O22(O2n−)) − E(Li14–zNi2Mn8O24) |
Details of genetic algorithm
The arrangements of Li/vacancy/Ni/Mn in O2-type Li14–zNi2Mn8O24 were optimized by the genetic algorithm (GA). A molar ratio of Li/Ni/Mn in a fully lithiated phase was set to reproduce the experimental composition (Li1.12Ni0.17Mn0.71O2). Layered O2-type LiCoO2 in a hexagonal structure (a space group of P63mc, 8 atoms) was used to prepare a supercell (48 atoms). Six cationic octahedral sites in each transition-metal layer contain one Li, one Ni, and four Mn atoms, while twelve octahedral sites in the Li layers were occupied by only Li atoms. In the GA procedure, a Li/Ni/Mn arrangement is regarded as a tertiary string consisting of four labels, 0 (Li), 1 (Ni), and 2, (Mn) and each cationic site was assigned to a specific string index. We prepared 20 configurations with random Li/Ni/Mn arrangements in the cationic sites and calculated the total electron energies based on DFT with a low energy cut-off (300 eV) and single k-point mesh to accelerate the calculations. Twelve lowest-energy structures among twenty candidates (60%) were selected as survivors and their structural features were inherited to the next generation by following the four points. First, the three best structures survived without any changes. Second, eight new structures were produced using the two-point crossover technique. Third, eight structures were produced by the half-uniform crossover technique. Fourth, four structures were produced by the mutation technique. The algorithm for the travelling salesman problem was adopted to maintain the molar ratio of Li/Ni/Mn during the above four genetic manipulations. The generated structures were selected to be inconsistent with the previously calculated configuration (a random cation arrangement is chosen if the above genetic operation cannot produce a new structure). Repeating this procedure determines the lowest-energy structure heuristically. The Li/vacancy arrangements in the delithiated phases of Li14-zNi2Mn8O24 (4 ≤ z ≤ 10 at intervals of 2) were also determined with the secondary strings in the GA approach but the number of structures per generation was reduced to 10 for z = 4 and 10.Author contributions
M. O. and A. Y. conceived and directed the project. K. K., J. J., and B. M. B. synthesized and characterized Li1.12−yNi0.17Mn0.71O2. K. K., X. M. S., N. T., and M. N. conducted theoretical calculations. K. K. and J. K. measured TEM images. K. K., A. T., and D. A. conducted synchrotron X-ray absorption/emission spectroscopy. All authors wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan; Grant-in-Aid for Specially Promoted Research No. 15H05701 and Grant-in-Aid for Scientific Research (S) No. 20H05673. This work was also supported by “Elements Strategy Initiative for Catalysts and Batteries (ESICB)”. M. O. was financially supported by JPSP KAKENHI (Grant Number: 19H05816, 18K19124, and 18H03924), and the Asahi Glass Foundation. M. N. was financially supported by Grant-in-Aid for Scientific Research on Innovative Areas “Interface Ionics” (Grant Number: 19H05815). K. K. was financially supported by JPSP KAKENHI (Grant Number: 20J14291). Soft X-ray absorption/emission spectroscopy at BL07LSU of SPring-8 was performed by joint research in SRRO and ISSP, the University of Tokyo (Proposal No. 2020A7474, 2019B7456, 2019A7452, 2018B7590, 2018A7560, 2018B1514, 2017B1328, and 2016B1503). Soft X-ray absorption/emission spectroscopy at BL27SU of SPring-8 was performed under the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal No. 2018A1359). XAFS was performed under the approval of the Photon Factory Program Advisory Committee (Proposal No. 2018G082). Magnetic measurements were performed using facilities of the Cryogenic Research Center, the University of Tokyo. The computations partly conducted in this study have been partly pursued by using the facilities of the Supercomputer Center at the Institute for Solid State Physics at the University of Tokyo. The authors are grateful to J. Miyawaki and Y. Harada at the University of Tokyo and K. Tsuruta and Y. Tamenori at JASRI for their support on the X-ray absorption/emission experiments.Notes and references
- D. Larcher and J.-M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- P. Adelhelm, Angew. Chem., Int. Ed., 2018, 57, 6710–6711 CrossRef CAS PubMed.
- G. Crabtree, Science, 2019, 366, 422–424 CrossRef CAS PubMed.
- R. Schmuch, R. Wagner, G. Hörpel, T. Placke and M. Winter, Nat. Energy, 2018, 3, 267–278 CrossRef CAS.
- M. Li, J. Lu, Z. Chen and K. Amine, Adv. Mater., 2018, 30, 1800561 CrossRef PubMed.
- K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Mater. Res. Bull., 1980, 15, 783–789 CrossRef CAS.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- A. Manthiram, Nat. Commun., 2020, 11, 1550 CrossRef CAS PubMed.
- Z. Lu, L. Y. Beaulieu, R. A. Donaberger, C. L. Thomas and J. R. Dahn, J. Electrochem. Soc., 2002, 149, A778–A791 CrossRef CAS.
- H. Koga, L. Croguennec, M. Ménétrier, K. Douhil, S. Belin, L. Bourgeois, E. Suard, F. Weill and C. Delmas, J. Electrochem. Soc., 2013, 160, A786–A792 CrossRef CAS.
- M. Sathiya, G. Rousse, K. Ramesha, C. P. Laisa, H. Vezin, M. T. Sougrati, M.-L. Doublet, D. Foix, D. Gonbeau, W. Walker, A. S. Prakash, M. Ben Hassine, L. Dupont and J.-M. Tarascon, Nat. Mater., 2013, 12, 827–835 CrossRef CAS PubMed.
- N. Yabuuchi, M. Nakayama, M. Takeuchi, S. Komaba, Y. Hashimoto, T. Mukai, H. Shiiba, K. Sato, Y. Kobayashi, A. Nakao, M. Yonemura, K. Yamanaka, K. Mitsuhara and T. Ohta, Nat. Commun., 2016, 7, 13814 CrossRef CAS PubMed.
- D.-H. Seo, J. Lee, A. Urban, R. Malik, S. Y. Kang and G. Ceder, Nat. Chem., 2016, 8, 692–697 CrossRef CAS PubMed.
- K. Luo, M. R. Robert, R. Hao, N. Guerrini, D. M. Pickup, Y.-S. Liu, K. Edström, J. Guo, A. V. Chadwick, L. C. Duda and P. G. Bruce, Nat. Chem., 2016, 8, 684–691 CrossRef CAS PubMed.
- T. Sudayama, K. Uehara, T. Mukai, D. Asakura, X.-M. Shi, A. Tsuchimoto, B. Mortemard de Boisse, T. Shimada, E. Watanabe, Y. Harada, M. Nakayama, M. Okubo and A. Yamada, Energy Environ. Sci., 2020, 13, 1492–1500 RSC.
- A. Tsuchimoto, X.-M. Shi, K. Kawai, B. Mortemard de Boisse, J. Kikkawa, D. Asakura, M. Okubo and A. Yamada, Nat. Commun., 2021, 12, 631 CrossRef CAS PubMed.
- E. McCalla, A. M. Abakumov, M. Saubanère, D. Foix, E. J. Berg, G. Rousse, M.-L. Doublet, D. Gonbeau, P. Novák, G. V. Tendeloo, R. Dominiko and J.-M. Tarascon, Science, 2015, 350, 1516–1521 CrossRef CAS PubMed.
- Z. N. Taylor, A. J. Perez, J. A. Coca-Clemente, F. Braga, N. E. Drewett, M. J. Pitcher, W. J. Thomas, M. S. Dyer, C. Collins, M. Zanella, T. Johnson, S. Day, C. Tang, V. R. Dhanak, J. B. Claridge, L. J. Hardwick and M. J. Rosseinsky, J. Am. Chem. Soc., 2019, 141, 7333–7346 CrossRef CAS PubMed.
- R. A. House, U. Maitra, M. A. Pérez-Osorio, J. G. Lozano, L. Jin, J. W. Somerville, L. C. Duda, A. Nag, A. Walters, K.-J. Zhou, M. R. Roberts and P. G. Bruce, Nature, 2020, 577, 502–508 CrossRef CAS PubMed.
- R. A. House, G. J. Rees, M. A. Pérez-Osorio, J.-J. Marie, E. Boivin, A. W. Robertson, A. Nag, M. Garcia-Fernandez, K.-J. Zhou and P. G. Bruce, Nat. Energy, 2020, 5, 777–785 CrossRef CAS.
- R. Sharpe, R. A. House, M. J. Clarke, D. Förstermann, J.-J. Marie, G. Cibin, K.-J. Zhou, H. Y. Playford, P. G. Bruce and M. S. Islam, J. Am. Chem. Soc., 2020, 142, 21799–21809 CrossRef CAS PubMed.
- C. Zhao, C. Li, H. Liu, Q. Qiu, F. Geng, M. Shen, W. Tong, J. Li and B. Hu, J. Am. Chem. Soc., 2021, 143, 18652–18664 CrossRef CAS PubMed.
- R. A. House, H. Y. Playford, R. I. Smith, J. Holter, I. Griffiths, K.-J. Zhou and P. G. Bruce, Energy Environ. Sci., 2022, 15, 376–383 RSC.
- H. Umeno, K. Kawai, D. Asakura, M. Okubo and A. Yamada, Adv. Sci., 2022, 9, 2104907 CrossRef CAS PubMed.
- M. Okubo, K. Kawai, Z. Ma and A. Yamada, Acc. Mater. Res., 2022, 3, 33–41 CrossRef CAS.
- J. R. Croy, K. G. Gallagher, M. Balasubramanian, B. R. Long and M. M. Thackeray, J. Electrochem. Soc., 2014, 161, A318–A325 CrossRef CAS.
- G. Assat, D. Foix, C. Delacourt, A. Iadecola, R. Dedryvère and J.-M. Tarascon, Nat. Commun., 2017, 8, 2219 CrossRef PubMed.
- W. E. Gent, I. I. Abate, W. Yang, L. F. Nazar and W. C. Chueh, Joule, 2020, 4, 1369–1397 CrossRef CAS.
- A. R. Armstrong, M. Holzapfel, P. Novák, C. S. Johnson, S.-H. Kang, M. M. Thackeray and P. G. Bruce, J. Am. Chem. Soc., 2006, 128, 8694–8698 CrossRef CAS PubMed.
- G. Assat, S. L. Glazier, C. Delacourt and J.-M. Tarascon, Nat. Energy, 2019, 4, 647–656 CrossRef CAS.
- J. Hong, D.-H. Seo, S.-W. Kim, H. Gwon, S.-T. Oh and K. Kang, J. Mater. Chem., 2010, 20, 10179–10186 RSC.
- B. Xu, C. R. Fell, M. F. Chi and Y. S. Meng, Energy Environ. Sci., 2011, 4, 2223–2233 RSC.
- J. Hong, W. E. Gent, P. Xiao, K. Lim, D.-H. Seo, J. Wu, P. M. Csernica, C. J. Takacs, D. Nordlund, C.-J. Sun, K. H. Stone, D. Passarello, W. Yang, D. Prendergast, G. Ceder, M. F. Toney and W. C. Chueh, Nat. Mater., 2019, 18, 256–265 CrossRef CAS PubMed.
- K. Ku, B. Kim, S.-K. Jung, Y. Gong, D. Eum, G. Yoon, K.-Y. Park, J. Hong, S.-P. Cho, D.-H. Kim, H. Kim, E. Jeong, L. Gu and K. Kang, Energy Environ. Sci., 2020, 13, 1269–1278 RSC.
- P. M. Csernica, S. S. Kalirai, W. E. Gent, K. Lim, Y.-S. Yu, Y. Liu, S.-J. Ahn, E. Kaeli, X. Xu, K. H. Stone, A. F. Marshall, R. Sinclair, D. A. Shapiro, M. F. Toney and W. C. Chueh, Nat. Energy, 2021, 6, 642–652 CrossRef CAS.
- Y. Yu, P. Karayaylali, D. Sokaras, L. Giordano, R. Kou, C. J. Sun, F. Maglia, R. Jung, F. Gittleson and Y. Shao-Horn, Energy Environ. Sci., 2021, 14, 2322–2334 RSC.
- N. Yabuuchi, R. Hara, M. Kajiyama, K. Kubota, T. Ishigaki, A. Hoshikawa and S. Komaba, Adv. Energy Mater., 2014, 4, 1301453 CrossRef.
- B. Mortemard de Boisse, J. Jang, M. Okubo and A. Yamada, J. Electrochem. Soc., 2018, 165, A3630–A3633 CrossRef CAS.
- D. Eum, B. Kim, S. J. Kim, H. Park, J. Wu, S. P. Cho, G. Yoon, M. H. Lee, S. K. Jung, W. Yang, W. M. Seong, K. Ku, O. Tamwattana, S. K. Park, I. Hwang and K. Kang, Nat. Mater., 2020, 19, 419–427 CrossRef CAS PubMed.
- H. Shang, Y. Zuo, F. Shen, J. Song, F. Ning, K. Zhang, L. He and D. Xia, Nano Lett., 2020, 20, 5779–5785 CrossRef CAS PubMed.
- C. Cui, X. Fan, X. Zhou, J. Chen, Q. Wang, L. Ma, C. Yang, E. Hu, X.-Q. Yang and C. Wang, J. Am. Chem. Soc., 2020, 142, 8918–8927 CrossRef CAS PubMed.
- J. M. Paulsen and J. R. Dahn, Solid State Ionics, 1999, 126, 3–24 CrossRef CAS.
- D. Carlier, I. Saadoune, L. Croguennec, M. Ménétrier, E. Suard and C. Delmas, Solid State Ionics, 2001, 144, 263–276 CrossRef CAS.
- G. Assat, C. Delacourt, D. A. Dalla Corte and J.-M. Tarascon, J. Electrochem. Soc., 2016, 163, A2965–A2976 CrossRef CAS.
- R. A. House, L. Jun, U. Maitra, K. Tsuruta, J. W. Somerville, D. P. Förstermann, F. Messel, L. Duda, M. R. Robert and P. G. Bruce, Energy Environ. Sci., 2018, 11, 926–932 RSC.
- U. Maitra, R. A. House, J. Somerville, N. Tapia-Ruiz, J. G. Lozano, N. Guerrini, R. Hao, K. Luo, L. Y. Jin, M. A. Perez-Osorio, F. Massel, D. M. Pickup, S. Ramos, X. Y. Lu, D. E. McNally, A. V. Chadwick, F. Giustino, T. Schmitt, L. C. Duda, M. R. Roberts and P. G. Bruce, Nat. Chem., 2018, 10, 288–295 CrossRef CAS PubMed.
- J. Xu, M. Sun, R. Qiao, S. E. Renfrew, L. Ma, T. Wu, S. Hwang, D. Nordlund, D. Su, K. Amine, J. Lu, B. D. Mccloskey, W. Yang and W. Tong, Nat. Commun., 2018, 9, 947 CrossRef PubMed.
- Z. Zhuo, C. D. Pemmaraju, J. Vinson, C. Jia, B. Moritz, I. Lee, S. Sallies, Q. Li, J. Wu, K. Dai, Y.-D. Chuang, Z. Hussain, F. Pan, T. P. Devereaux and W. Yang, J. Phys. Chem. Lett., 2018, 9, 6378–6384 CrossRef CAS PubMed.
- Q. Li, Z. W. Lebens-Higgins, Y. Li, Y. S. Meng, Y. Chuang, L. F. J. Piper, Z. Liu and W. Yang, J. Phys. Chem. Lett., 2021, 12, 1138–1143 CrossRef CAS PubMed.
- M. J. Zuba, A. Grenier, Z. Lebens-Higgins, G. J. Paez Fajardo, Y. Li, Y. Ha, H. Zhou, M. S. Whittingham, W. Yang, Y. S. Meng, K. W. Chapman and L. F. J. Piper, ACS Energy Lett., 2021, 6, 1055–1064 CrossRef CAS.
- M. Ben Yahia, J. Vergnet, M. Saubanère and M.-L. Doublet, Nat. Mater., 2019, 18, 496–502 CrossRef CAS PubMed.
- L. G. Cota and P. de la Mora, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 133–136 CrossRef PubMed.
- Z. Chen, J. Li and X. C. Zeng, J. Am. Chem. Soc., 2019, 141, 10751–10759 CrossRef CAS PubMed.
- X. Rong, J. Liu, E. Hu, Y. Liu, Y. Wang, J. Wu, X. Yu, K. Page, Y.-S. Hu, W. Yang, H. Li, X.-Q. Yang, L. Chen and X. Huang, Joule, 2018, 17, 125–140 CrossRef.
- B. Song, M. Tang, E. Hu, O. J. Borkiewicz, K. M. Wiaderek, Y. Zhang, N. D. Phillip, X. Liu, Z. Shadike, C. Li, L. Song, Y.-Y. Hu, M. Chi, G. M. Veith, X.-Q. Yang, J. Liu, J. Nanda, K. Page and A. Huq, Chem. Mater., 2019, 31, 3756–3765 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- Y. Harada, M. Kobayashi, H. Niwa, Y. Senba, H. Ohashi, T. Tokushima, Y. Horikawa, S. Shin and M. Oshima, Rev. Sci. Instrum., 2012, 83, 013116 CrossRef PubMed.
- A. J. Achkar, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 2–5 Search PubMed.
- H. Wadati, et al. , Appl. Phys. Lett., 2012, 100, 193906 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235121 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee03503g |
| ‡ Present address: Department of Electrical Engineering and Bioscience, School of Advanced Science and Engineering, Waseda University, Okubo 3-4-1, Shinjuku-ku, Tokyo 169-0555, Japan. |
| This journal is © The Royal Society of Chemistry 2022 |