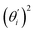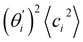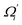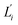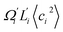Open Access Article
Open Access ArticleStructure-mechanics statistical learning unravels the linkage between local rigidity and global flexibility in nucleic acids†
Yi-Tsao
Chen
 a,
Haw
Yang
a,
Haw
Yang
 b and
Jhih-Wei
Chu
b and
Jhih-Wei
Chu
 *c
*c
aInstitute of Bioinformatics and Systems Biology, National Chiao Tung University, Hsinchu, Taiwan 30068, Republic of China
bDepartment of Chemistry, Princeton University, Princeton, NJ 08544, USA
cInstitute of Bioinformatics and Systems Biology, Department of Biological Science and Technology, Institute of Molecular Medicine and Bioengineering, National Chiao Tung University, Hsinchu, Taiwan 30068, Republic of China. E-mail: jwchu@nctu.edu.tw; Tel: +886 3 5712121 ext. 56996
First published on 23rd April 2020
Abstract
The mechanical properties of nucleic acids underlie biological processes ranging from genome packaging to gene expression, but tracing their molecular origin has been difficult due to the structural and chemical complexity. We posit that concepts from machine learning can help to tackle this long-standing challenge. Here, we demonstrate the feasibility and advantage of this strategy through developing a structure-mechanics statistical learning scheme to elucidate how local rigidity in double-stranded (ds)DNA and dsRNA may lead to their global flexibility in bend, stretch, and twist. Specifically, the mechanical parameters in a heavy-atom elastic network model are computed from the trajectory data of all-atom molecular dynamics simulation. The results show that the inter-atomic springs for backbone and ribose puckering in dsRNA are stronger than those in dsDNA, but are similar in strengths for base-stacking and base-pairing. Our analysis shows that the experimental observation of dsDNA being easier to bend but harder to stretch than dsRNA comes mostly from the respective B- and A-form topologies. The computationally resolved composition of local rigidity indicates that the flexibility of both nucleic acids is mostly due to base-stacking. But for properties like twist-stretch coupling, backbone springs are shown to play a major role instead. The quantitative connection between local rigidity and global flexibility sets foundation for understanding how local binding and chemical modification of genetic materials effectuate longer-ranged regulatory signals.
1 Introduction
Mechanical properties of nucleic acids are critical to their biological functions. In chromosome packaging, DNA repair, gene expression, and many other biological processes, the linear biopolymers are bent, twisted, and stretched by proteins.1–6 Deforming dsDNA and dsRNA (Fig. 1) can induce local structural variation to facilitate enzyme catalysis, and the sequence-dependent mechanical responses provide cues for protein recognition.7–11 Local chemical modification such as methylation, too, can change the physical properties, structures, and hence functional behaviors of nucleic acids.12–14 To understand these phenomena calls for the linkage between chemical interactions at the molecular scale and the apparent behavior related to function. Beyond biology, how does nanometer- to micron-scale flexibility arrive from atomic details is also an important question to address for using nucleic acids to build engineered nanostructures.15,16Experimental characterization of nucleic acid mechanics, for which single-molecule techniques play an important role, however, primarily focus on global deformation by treating the biopolymers as a linear rod using continuum mechanics17–21 (Fig. 1(b)), where the local chemical composition is ignored. Mechanical response parameters such as persistence length and elastic modulus have been reported to vary with sequence and chemical modification,22–29 but there does not appear to be an obvious trend and a consistent physical picture is yet to emerge. A key bottleneck is the lack of an effective approach to evaluate the local rigidity in terms of backbone, ribose puckering, base-pairing, and base-stacking whereby a linkage from the molecular scale to global flexibility can be established. Indeed, to be able to explain shape flexibility in terms of molecular interactions is essential to address issues such as the interplay between base-specific interactions and backbone electrostatics in governing nucleic acid mechanics.30,31 With growing interests in small scale flexibility of nucleic acids,32–38 resolving local force responses and their connections to global flexibility is in urgent need. Such linkage is of particular relevance to understand the increasingly appreciated phenomena of DNA-mediated allostery where proteins bound to distant DNA sites exhibit apparent cooperative interactions.39–41
In principle, the molecular and phenomenological scales of nucleic acid mechanics can be studied and linked by computer simulations. All-atom molecular dynamics (MD) simulation42–46 in particular, is a powerful method to provide detailed atomic configurations.47–57 Computing molecular scale rigidity from structural fluctuations, however, requires consideration of the coupling between many degrees of freedom in the high-dimensional space that includes combination of numerous covalent and non-bound interactions. Therefore, a coarse-grained (CG) model containing mechanical parameters is often employed to assist with analyzing MD data. Such an approach can be used to characterize small scale stiffness from MD trajectories58–60 and structure databases;61,62 however, studies using that approach were mostly conducted with base geometries only, and the contributions from backbone and ribose puckering could not be identified.
To model the probabilistic structure connecting the global flexibility of nucleic acids to their atomic fluctuations, we devise a structure-mechanics statistical learning scheme. Using this approach based on machine learning, the objective is to determine molecular scale rigidity as the basis for analyzing the different aspects of global flexibility in nucleic acids. To test and illustrate this new method, we chose B-form dsDNA and A-form dsRNA as specific examples. The distinct mechanical properties of dsDNA and dsRNA are experimentally known63–76 and serve here for contrasting local rigidity in different structural forms and characterizing global deformation in terms of chemical interactions. In the following, the structure-mechanics statistical learning framework is introduced followed by the results of systems analysis for nucleic acid mechanics.
2 Materials and methods
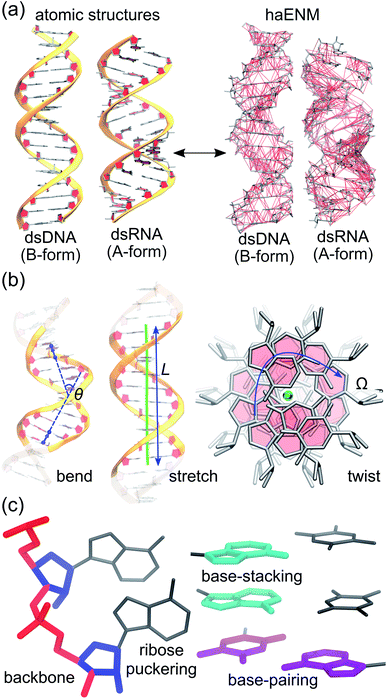
With the goal of developing a systems view for global deformation in terms of local rigidity, we adopt two unexplored strategies to extract information about nucleic acid mechanics from all-atom MD trajectories. First, the structural topologies of dsDNA and dsRNA and the mechanical responses therein are represented using the potential energy function of an elastic network model77 of heavy atoms, haENM. The structure-mechanics statistical learning based on fluctuation matching78,79 is then applied to compute the local rigidity parameters, namely spring constants of elastic bonds in haENM, from the dynamical fluctuations sampled with full atomic details. Second, the vibrational modes of structural topologies are used as orthonormal basis to expand the order parameters for bend, twist, and stretch (see Fig. 1). In the remainder of this section, the protocols of all-atom MD simulations and computation of mechanical properties of global deformation are sketched whereas the two new strategies are discussed.2.1 All-atom MD simulations
We consider the 16-basepair sequence (GCGCAATGGAGT-ACGC) as in an earlier work.56 The Nucleic Acid Builder80 is used to generate atomic coordinates in the canonical A- and B-form structures for dsRNA and dsDNA, respectively. Both systems are solvated in explicit water and K+ and Cl− ions at 0.15 M, and there are 30 more cations in the simulation box for neutralizing the negatively charged nucleic acids. All MD simulations are carried out using the GROMACS software81 and the AMBER nucleic acid force field.43,44 After initial minimization and 12 ns equilibration period, the production run of 1 μs is conducted at constant temperature (310 K) by Langevin dynamics and pressure (1.013 bar) by the Parrinello–Rahman barostat.82 A snapshot is saved every 0.1 ns for structural analysis and computing mechanical properties. The other details are reported in ESI.†2.2 Calculation of mechanical properties
As shown in Fig. 1(b), the similarity between tangent vectors along the polymer chain is analyzed to calculate the persistence length Lp83 of dsDNA and dsRNA. The details of computing the bending angle θ from MD and the calculation of Lp from the distribution of θ are described in ESI.† The stretch deformation is measured via contour length L, and the global twist Ω is the order parameter of twist deformation. Both L and Ω are calculated for each snapshot in all-atom MD using the 3DNA program.84 Next, the two-by-two covariance matrix C56 of L and Ω is calculated to determine the stretching modulus (ηs), twisting modulus (ηs), and stretching-twisting coupling (ηts) as detailed in ESI.† To compare the mechanical properties of dsDNA and dsRNA with our 16-basepair nucleic acid model, fluctuation in θ, L, and Ω are computed for the central 10 base pairs to avoid fraying effects. Mechanical properties can also be computed for shorter base pair in this model to characterize their dependence on length, and the details of this analysis are discussed in ESI.†2.3 Structure-mechanics statistical learning of local rigidity
We aim to compute haENM spring constants (km's) from all-atom MD trajectories; m is the index of springs. In this approach, haENM is an approximate free-energy function for the protein heavy atoms as the other degrees of freedom in all-atom MD are effectively marginalized. Therefore, parameters in the haENM are specific to the thermodynamic condition imposed in the all-atom MD simulation, such as temperature, pressure, and ionic strength. If a spring was isolated, km can be determined from the atomic coordinates sampled at a given temperature by computing the fluctuation of its length, as km is inversely proportional to 〈δbm2〉. Since springs are connected, learning the rigidity parameters from MD requires consideration of the coupled fluctuations in their lengths. In this structure-mechanics statistical learning, the following self-consistent iteration of fluctuation matching78,79 is conducted to update km: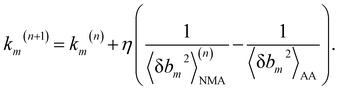 | (1) |
At iteration (n), the fluctuation of every spring, 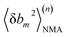 , is calculated by normal mode analysis (NMA)85 and compared with the targeted value from all-atom MD (AA) to adjust the spring constant. For equilibrium length b0m, the average inter-atomic distance in the trajectory data is taken, and η is the learning rate.
, is calculated by normal mode analysis (NMA)85 and compared with the targeted value from all-atom MD (AA) to adjust the spring constant. For equilibrium length b0m, the average inter-atomic distance in the trajectory data is taken, and η is the learning rate.
Typically, a few hundreds of iterations are performed to reach convergence. A non-negative constraint is imposed for km, and the final list of inter-atomic restraints is the mechanical coupling network deduced from the MD data. The cutoff radius of including an inter-atomic pair in haENM is another necessary parameter, and its determination is based on the comparison with several observables from quasi-harmonic analysis85 of the all-atom MD data. Details of parameterizing haENM can be found in ESI.†
2.4 Orthonormal expansion for systems analysis of global deformation
To utilize the local rigidity of inter-atomic restraints as the basis to understand how the different aspects of global flexibility emerge from molecular interactions, we employ the vibrational modes of heavy atoms as an orthonormal basis to characterize structural fluctuations. At a given temperature, 〈ci2〉 is the flexibility along mode i and is inversely proportional to it eigenvalue λi.85 As derived in ESI,† the variance of an order parameter Φ due to thermal energy can be expanded linearly as: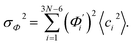 | (2) |
The mode couplings terms are omitted since the calculated values are orders of magnitude smaller and hence negligible. The orthonormal basis may be obtained from quasi-harmonic analysis85 of the all-atom MD trajectory or normal mode analysis85 of haENM. The specific contribution from mode i to the fluctuation of an order parameter involves 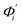 , its vector derivative with respect to mode i. The details of calculating
, its vector derivative with respect to mode i. The details of calculating 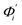 for various types of global deformation are reported in ESI.† Orthonormal expansion can also be applied to twist-stretching coupling as derived in ESI.†
for various types of global deformation are reported in ESI.† Orthonormal expansion can also be applied to twist-stretching coupling as derived in ESI.†
2.5 Computation of the chemical interaction profile for linking local rigidity and global flexibility
As derived in ESI,† the potential energy function of haENM allows its eigenvalues to be expressed as the summed contributions from each spring using Wilson's B matrix.86 Characterizing the eigenvalues of dsDNA and dsRNA for the compositions of inter-atomic restraints can thus reveal the molecular determinants of their mechanical properties. Using this approach to analyze nucleic acid mechanics is unprecedented to the best of our knowledge. In this regard, springs in haENM are categorized according to the atom types that they connect, Fig. 1(c).3 Results and discussion
The mechanical properties in bend, stretch, and twist of dsDNA and dsRNA calculated from all-atom MD trajectories are first presented. To unravel how the details of molecular interactions affect the different modes of global deformation, the rigidity of inter-atomic restraints is analyzed based on the calculation of structure-mechanics statistical learning. The systems analysis by orthonormal expansion allows the flexibility of different types of global deformation to be dissected under the same footing; that is, in terms of backbone, ribose puckering, base-stacking, and base-paring interactions. Finally, the new insights emerged from this analysis are discussed.3.1 Mechanical properties calculated from all-atom MD are consistent with experiments
The A-form and B-form contents of dsDNA and dsRNA during the 1 μs production runs are characterized as in Fig. S1.† An A-form dominant distribution is observed for dsRNA and dsDNA is mostly in the B-form as in experiments87–89 and earlier simulations.49–51 The mechanical properties calculated from the trajectory data are summarized in Table 1. For comparison, the values obtained from experiments and pulling MD simulations using the same force field are also listed.| dsDNA | dsRNA | ||||||
|---|---|---|---|---|---|---|---|
| This work | Pulling MD57 | Exp.63–75 | This work | Pulling MD57 | Exp.72–76 | ||
| Bend | L p (nm) | 39.17 ± 0.82 | 45–50 | 78.9 ± 3.4 | 60–100 | ||
| Stretch | η s (pN) | 1435 ± 61 | 1280 ± 70 | 1450–1750 | 634 ± 15 | 480 ± 11 | 350, 500 |
| Twist | η t (pN nm2) | 448 ± 16 | 303 ± 23 | 160–448 | 443 ± 14 | 310 ± 24 | 409 |
| Twist-stretch coupling | η ts | −52.0 ± 9.0 | −54.0 ± 3.0 | −39 to −17 | 27.0 ± 1.0 | 34.0 ± 1.0 | 11.5 |
The calculated values of Lp are around those from experiments, and Lp of dsRNA being ∼2 times longer than that of dsDNA71–76 is captured, Table 1. The stretch modulus ηs of dsDNA is also within the range of reported values, while ηs of dsRNA is moderately overestimated. Nonetheless, the observation of dsDNA having 2–3 times higher ηs74,75 is reproduced. The twist modulus ηt from our simulations are around the measured values.74,75 The twist-stretch coupling ηts is also calculated to be negative for dsDNA and positive for dsRNA as in experiments, although the magnitudes are overestimated as in pulling MD simulations using the same force field,57Table 1. In summary, the mechanical properties obtained from our unconstrained all-atom MD simulations are consistent with experiments and earlier simulation works.
3.2 Local rigidity in dsDNA and dsRNA
To dissect the diverse behaviors in global deformation with chemical interactions, we start by computing the local rigidity in dsDNA and dsRNA. As reported in ESI,† a 4.7 Å cut-off radius for including an inter-atomic pair in haENM is obtained based on the comparison between normal mode analysis of haENM and quasi-harmonic analysis of all-atom MD trajectories. With fluctuation matching, consistent behaviors are observed over the tested range of cut-off radius between 4–10 Å. Given similar performance in reproducing atomic fluctuations, a shorter cutoff is preferred as fewer numbers of parameters are involved in the model.The atom types for annotating local rigidity are shown in Fig. 2, and the springs are categorized into backbone, ribose puckering, base-stacking, and base-pairing groups accordingly. For each group, the sub-groups of springs are based on their equilibrium lengths and the connected atom types. For example, the PP0 and PP1 springs are sub-groups of backbone linking phosphate atoms. PP0 springs have lengths around 1.5 Å, while the lengths of PP1 springs are around 2.5 Å. The values of km and b0m in each sub-group are shown in Fig. S2.†
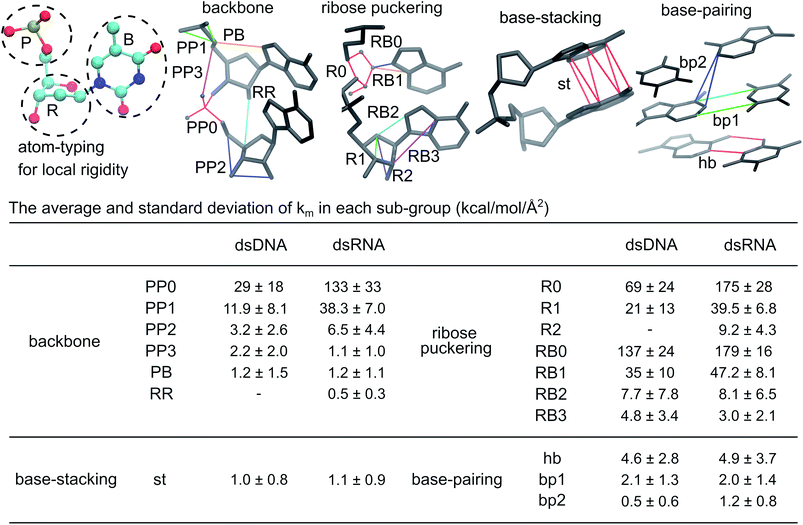 | ||
| Fig. 2 Local rigidity in dsDNA and dsRNA. According to the atom typing on top-left, the springs are categorized into four groups, backbone, ribose puckering, base-stacking, and base-pairing. For the sub-groups in a category, a few springs are shown to illustrate the kind of connections in the structure. A larger integer in a sub-group name indicates longer equilibrium lengths, Fig. S2.† The average and standard deviation of spring constants in each sub-group in kcal mol−1 Å−2 are listed to indicate the strengths of local rigidity. | ||
The average and standard deviation of km's in each sub-group are listed in Fig. 2. The closer distances between negatively charged phosphates in dsRNA reflect in 2–4 times higher averages for PP0, PP1, and PP2 sub-groups. The ribose related R0 and R1 springs in dsRNA are also 2–3 times more rigid, while the R2 and RR sub-groups are not found in dsDNA. The RB0 and RB1 springs between ribose and its side-chain are also ∼30% more rigid in dsRNA. The backbone and ribose puckering springs showing significantly higher strengths in dsRNA are mostly shorter than 3.5 Å as shown in Fig. S2.†
For PP3, RB2, RB3, and PB sub-groups with lengths around 3.5 Å and longer, the calculated values of spring constants are lower. Furthermore, their km averages in dsDNA and dsRNA are rather similar, Fig. 2 and S2.† The PP, RR, and PB sub-groups together are the backbone group whereas the R and RB sub-groups are categorized as the ribose puckering group of springs.
In base-stacking springs that only contain the st (short for stacking) sub-group, dsDNA and dsRNA have similarly low km averages around 1.0 kcal mol−1 Å−2, Fig. 2. Base-stacking springs are mostly longer than 3.5 Å (Fig. S2†). Base-pairing springs in dsDNA and dsRNA also have similar strengths in the hb sub-group for canonical hydrogen bonds and the bp1 sub-group for other inter-atomic restraints linking a basepair, Fig. 2. In general, the hb and bp1 sub-groups of base-paring springs are stronger than base-stacking restraints. Both dsDNA and dsRNA also contain springs linking second-nearest bases across strands. With the base-pairs in dsRNA being more inclined to the helical axis, the calculated km average for the bp2 sub-group is higher than that in dsDNA.
In the structure-mechanics statistical learning, the km values of all springs are adjustable. The spread of strengths in the inter-atomic restraints of each sub-group, Fig. 2 and S2,† thus contain sequence-dependent information. The potential of this framework for addressing the complexities of local rigidity in nucleic acids due to sequence variation, though, is not explored in the present work. Nevertheless, the inter-atomic spring constants calculated from all-atom MD reveal clear signatures for different chemical structures in dsDNA and dsRNA.
3.3 Systems analysis of global flexibility with orthonormal expansion
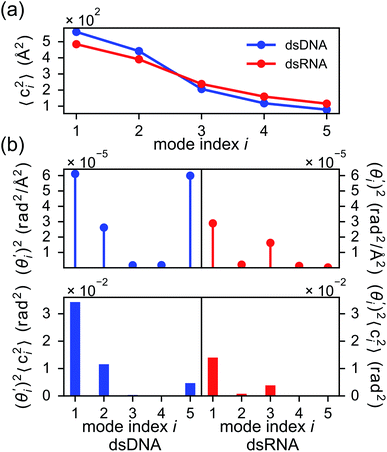
To establish linkage between local rigidity and global deformation, we conduct orthonormal expansion using eqn (2) and the quasi-harmonic modes85 of heavy atoms calculated from the all-atom MD trajectories. The first five modes of dsDNA and dsRNA displayed in Fig. 3 showcase the collective directions with increasing rigidity starting from the softest mode. The values of 〈ci2〉 shown in Fig. 4(a) indicate that the lowest-frequency modes of dsDNA and dsRNA are similarly flexible and do not deviate as much as their mechanical properties in Table 1. The RMSF (root-of-mean-squared-fluctuation) from summing over all 〈ci2〉's is 1.79 Å for dsDNA. Given the much stronger backbone and ribose springs, dsRNA is only slightly more rigid with 1.65 Å RMSF.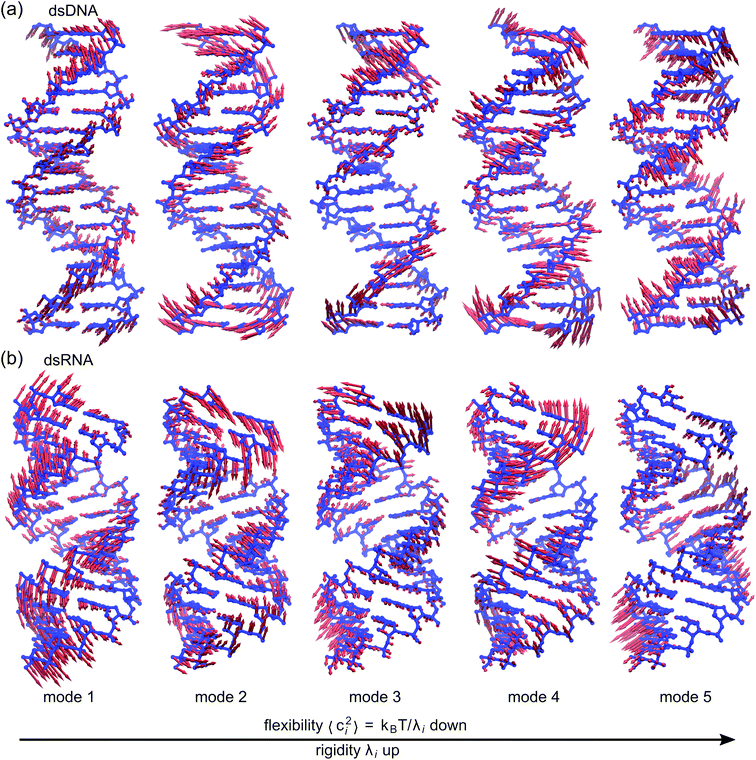 | ||
| Fig. 3 The first five vibrational modes of (a) dsDNA and (b) dsRNA via quasi-harmonic analysis of the 1 μs all-atom MD trajectories. The modes are arranged in ascending order of eigenvalue and hence descending order of flexibility. Comparing mode 1 of dsDNA and dsRNA, the former is more relevant to bending and latter is more pronounced in stretching (Movies S1 and S2 in ESI†). Mode 3 and mode 5 of dsDNA contribute most to its twist flexibility and twist-stretch coupling, while such roles are played by mode 3 and mode 4 of dsRNA. More of these results are discussed later. | ||
Fig. 4(b) shows the orthonormal expansion of bending angle over the first five modes to illustrate how the θ flexibility in all-atom MD emerges. The vector derivative with respective to mode i, 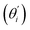 , indicates the sensitivity of θ to movement along the collective direction. The product
, indicates the sensitivity of θ to movement along the collective direction. The product 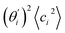 is the contribution of mode i to the overall bending flexibility according to eqn (2). It can be seen that the first mode dsDNA was ∼2 times more relevant to bending than that of dsRNA based on their values of
is the contribution of mode i to the overall bending flexibility according to eqn (2). It can be seen that the first mode dsDNA was ∼2 times more relevant to bending than that of dsRNA based on their values of 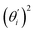 . For both biopolymers, mode 1 contributes most to the overall bending flexibility. The direction of the softest motion can also be seen in Movies S1 and S2 in the ESI† for dsDNA and dsRNA, respectively. Since the low-frequency modes of dsDNA are more relevant to bending, dsRNA has much smaller σθ2. The full-spectrum expansion of θ is shown in Fig. S3.†
. For both biopolymers, mode 1 contributes most to the overall bending flexibility. The direction of the softest motion can also be seen in Movies S1 and S2 in the ESI† for dsDNA and dsRNA, respectively. Since the low-frequency modes of dsDNA are more relevant to bending, dsRNA has much smaller σθ2. The full-spectrum expansion of θ is shown in Fig. S3.†
The orthonormal expansion of contour length L over the first five modes are shown in Fig. 5 and S4† illustrates the full-spectrum expansion. Since dsRNA has larger 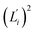 in its low-frequency modes, it is significantly more deformable in stretching. The first mode of dsRNA also contributes the most to its stretching flexibility as in bending. For dsDNA, on the other hand, mode 5 gives the largest portion to σL2, Fig. 5.
in its low-frequency modes, it is significantly more deformable in stretching. The first mode of dsRNA also contributes the most to its stretching flexibility as in bending. For dsDNA, on the other hand, mode 5 gives the largest portion to σL2, Fig. 5.
In dsDNA, mode 3 and mode 5 are the most relevant directions to total twist angle Ω and they contribute most to σΩ2 as shown in Fig. S5.† The orthonormal expansion of σΩL illustrated in Fig. 6 indicates that positive coupling is largely due to competition between mode 3 and mode 5 that have opposite signs in 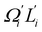 . Since the former is more flexible, the apparent twist-stretch coupling of dsDNA is positive. Modes 1, 2, and 4 also contribute positively to σΩL albeit with much lower magnitudes. Mode 5 of dsDNA is thus an outliner among the collective directions for its negative twist-stretch coupling. The apparent sign in σΩL for dsDNA thus emerges from competing over a few modes. Similar behaviors are also observed in dsRNA, Fig. S5(a)† and 6, and its negative σΩL is mainly due to competition between mode 3 and mode 4. The full-spectrum expansion of σΩL for dsDNA and dsRNA is shown in Fig. S6.† Orthonormal expansion of order parameters with haENM normal modes also reaches the same conclusions as shown in Fig. S7 to S10.†
. Since the former is more flexible, the apparent twist-stretch coupling of dsDNA is positive. Modes 1, 2, and 4 also contribute positively to σΩL albeit with much lower magnitudes. Mode 5 of dsDNA is thus an outliner among the collective directions for its negative twist-stretch coupling. The apparent sign in σΩL for dsDNA thus emerges from competing over a few modes. Similar behaviors are also observed in dsRNA, Fig. S5(a)† and 6, and its negative σΩL is mainly due to competition between mode 3 and mode 4. The full-spectrum expansion of σΩL for dsDNA and dsRNA is shown in Fig. S6.† Orthonormal expansion of order parameters with haENM normal modes also reaches the same conclusions as shown in Fig. S7 to S10.†
3.4 Chemical interaction profile shows dominant contribution of base-stacking to global flexibility
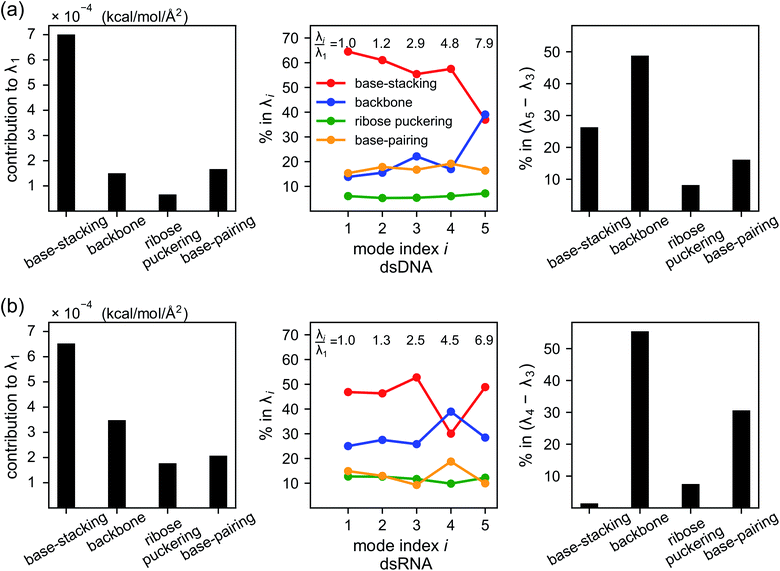
As derived in ESI,† an eigenvalue in the normal mode analysis of haENM can be expressed as contributions from local rigidity, i.e., the values of km of different inter-atomic springs. The geometrical factor multiplied with km in its contribution comes from the dot-product of eigenvector components with those in Wilson's B-matrix of the nucleic acid structure, ESI.† Therefore, a particular form of deformation would cause higher force responses if more springs of stronger rigidity were perturbed, and the softest mode is the direction that mechanically affects springs to the least extent in the structural network.Compositions of different spring groups in the eigenvalue of mode 1 in dsDNA indicate that the lowest rigidity in the B-form structure predominantly comes from base-stacking, which accounts for 63% of λ1, left and middle panels of Fig. 7(a). Although the backbone group has a similar number of springs, they only contribute one-fifth the portion of base-stacking. Base-pairing springs supply slightly more to λ1 than the backbone restraints do, and the ribose puckering group is the least relevant.
In dsRNA, base-stacking springs also contribute most to its λ1, albeit with a lower percentage of 46%, left and middle panels of Fig. 7(b). With significantly stronger backbone and ribose puckering springs, the two groups in dsRNA account for higher percentages in λ1 than they do in dsDNA. Base-pairing springs in dsDNA and dsRNA show similar percentage in λ1, Fig. 7.
Base-stacking springs giving the highest contribution to the rigidity of lower-frequency modes can be seen in the middle panels of Fig. 7, which also label the growing eigenvalues with mode index. The exception is mode 5 in dsDNA and mode 4 in dsRNA. In both cases, the contribution from backbone springs to the eigenvalue exceeds that from the base-stacking spring group. Mode 5 of dsDNA and mode 4 of dsRNA also show the non-native sign of twist-stretching coupling in Fig. 6. More detailed compositions of sub-group springs as defined in Fig. 2 are shown in Fig. S11† to indicate more extensively how global flexibility is arrived from molecular interactions.
3.5 Structural topology imposes preference on global deformation
Despite the weaker strengths of base-stacking springs (Fig. 2), they contribute more to low-frequency eigenvalues. It is likely that the double-helix structures encode certain information for the dominance of base-stacking in the soft directions. To test whether the structural topologies of dsDNA and dsRNA impose preference on global deformation, we compute the eigenvectors of a reference haENM that a universal value is used for all spring constants within the 4.7 Å cut-off radius. Dot-products of the eigenvectors of the locally homogeneous haENM with the modes from using fluctuation-matched spring constants provide a metric for the resilience of collective directions to chemical details. The objective is to analyze how much does structural topology affect the direction of low-frequency motions. In the case of using a universal value for all spring constants, eigenvectors of the haENM are independent of the specified magnitude.90The results shown in Table S1† indicate that elimination of chemical specificities does not drastically affect the directions of modes 1 to 3 in dsDNA with 0.834 similarity remains for mode 1. The similarity drops low though, for higher-frequency modes 4 and 5. For dsRNA, the first two modes are not sensitive to the chemical details of local rigidity, but significant alteration in the direction is observed starting from mode 3.
Therefore, the structural topologies of dsDNA and dsRNA do encode information about global deformation over the first few of modes. As discussed earlier, mode 1 of dsDNA contributes most to its bending flexibility and its lower relevance to L makes stretching dsDNA harder. Similarly, mode 1 of dsRNA contributes most to its stretching flexibility but it has lower relevance to bending, leading to the significantly higher bending rigidity of dsRNA. The distinct topologies of A-form and B-form structures thus impose preference on global deformation that dsDNA is easier to bend but harder to stretch than dsRNA is. The structural topologies of nucleic acids have been found to correlate with functional properties in different genome elements, and compelling evidence indicate that they are under evolutionary selection.91–94 This proposition is in coherent with our results that the preference in global flexibility for functionally distinct dsDNA and dsRNA is indeed closely related to their structural topologies.
3.6 Backbone springs playing a major role in the chemical interaction spectrum of twist-stretch coupling
Although the weak restraints of base-stacking contribute most to low-frequency eigenvalues, backbone springs are important from a different perspective—they encode higher-rigidity loci in the structural network. Therefore, it is likely that the inter-atomic restraints involving charged phosphates become prominent in twist-stretch coupling. As shown in Fig. 6, competition between mode 3 and mode 5 is key to the positive twist-stretch coupling in dsDNA. Therefore, the difference in their eigenvalues, (λ5 − λ3), can be employed to characterize the importance of local rigidity in affecting twist-stretch coupling. For the negative σΩL of dsRNA, (λ4 − λ3) was used according to Fig. 6. The compositions of different spring groups in (λ5 − λ3) of dsDNA indeed show that backbone springs give the highest contribution while the base-stacking group take the second highest place, right panel of Fig. 7(a). For (λ4 − λ3) in dsRNA, base-stacking is essentially irrelevant for its very low contribution, right panel of Fig. 7(b), while backbone springs contribute more than 50% to σΩL. Another noticeable feature of dsRNA is that the base-pairing group play a more significant role in σΩL.4 Conclusion
Using the structure-mechanics statistical learning scheme developed here, we show that the molecular scale rigidity in nucleic acids can be computed from all-atom MD trajectories. This allows establishing the previously unreachable linkage from the molecular scale to global flexibility. Further, we found that a very useful general quantitative descriptor for analyzing different types of global deformation is the orthonormal basis of vibrational normal modes. By combining these two, the chemical interaction profile in the global flexibility of nucleic acids can be calculated based on the statistically learned heavy-atom elastic network model. A key observation is that different modes of deformation exhibit specific combinations of inter-atomic springs through the nucleic acid structure. Base-stacking interactions contribute most to shape flexibility, but for properties such as twist-stretch coupling, it is possible that the inter-atomic restraints in backbone play a major role instead. Furthermore, we demonstrate that the B- and A-form topologies impose preference on global deformation that dsDNA is easier to bend and harder to stretch than dsRNA is. With the enabling capacity to compute and link chemical interactions at the molecular level to flexibility in global shape, an immediate extension of the present work is sequence-dependent behaviors in nucleic mechanics and analysis of the impact of various chemical modification, such as methylation, on structural and mechanical properties. Our results also suggest that physical chemistry-based machine learning has great potential for uncovering the chemical origin of functional behaviors in complex molecular systems.Conflicts of interest
There are no conflicts to declare statement.Acknowledgements
This work was supported by the Princeton University, the Global Networking Talent 3.0 Plan of the National Chiao Tung University, the Ministry of Science and Technology of Taiwan (No. 106-2113-M-009-020, 107-2113-M-009-003, and 108-2113-M-009-001), and the “Center for Intelligent Drug Systems and Smart Bio-devices (IDS2B)” from The Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE) in Taiwan. Computational resources were supported in part by the National Center for High-Performance Computing of Taiwan.Notes and references
- R. Schleif, Annu. Rev. Biochem., 1992, 61, 199–223 CrossRef CAS PubMed.
- A. B. Conway, T. W. Lynch, Y. Zhang, G. S. Fortin, C. W. Fung, L. S. Symington and P. A. Rice, Nat. Struct. Mol. Biol., 2004, 11, 791–796 CrossRef CAS PubMed.
- N. R. Cozzarelli, G. J. Cost, M. Nöllmann, T. Viard and J. E. Stray, Nat. Rev. Mol. Cell Biol., 2006, 7, 580–588 CrossRef CAS PubMed.
- J. T. P. Yeeles, K. van Aelst, M. S. Dillingham and F. Moreno-Herrero, Mol. Cell, 2011, 42, 806–816 CrossRef CAS PubMed.
- K. C. Dong and J. M. Berger, Nature, 2007, 450, 1201–1205 CrossRef CAS PubMed.
- D. Dulin, I. D. Vilfan, B. A. Berghuis, M. M. Poranen, M. Depken and N. H. Dekker, Nucleic Acids Res., 2015, 43, 10421–10429 CAS.
- T. Lionnet, A. Dawid, S. Bigot, F.-X. Barre, O. A. Saleh, F. Heslot, J.-F. Allemand, D. Bensimon and V. Croquette, Nucleic Acids Res., 2006, 34, 4232–4244 CrossRef CAS PubMed.
- R. Rohs, X. Jin, S. M. West, R. Joshi, B. Honig and R. S. Mann, Annu. Rev. Biochem., 2010, 79, 233–269 CrossRef CAS PubMed.
- T. Siggers and R. Gordan, Nucleic Acids Res., 2014, 42, 2099–2111 CrossRef CAS PubMed.
- M. Slattery, T. Zhou, L. Yang, A. C. Dantas Machado, R. Gordan and R. Rohs, Trends Biochem. Sci., 2014, 39, 381–399 CrossRef CAS PubMed.
- T. Zeiske, N. Baburajendran, A. Kaczynska, J. Brasch, A. G. Palmer, L. Shapiro, B. Honig and R. S. Mann, Cell Rep., 2018, 24, 2221–2230 CrossRef CAS PubMed.
- T. T. M. Ngo, J. Yoo, Q. Dai, Q. Zhang, C. He, A. Aksimentiev and T. Ha, Nat. Commun., 2016, 7, 1–9 Search PubMed.
- P. M. D. Severin, X. Zou, H. E. Gaub and K. Schulten, Nucleic Acids Res., 2011, 39, 8740–8751 CrossRef CAS PubMed.
- X. Teng and W. Hwang, Biophys. J., 2018, 114, 1791–1803 CrossRef CAS PubMed.
- P. Guo, Nat. Nanotechnol., 2010, 5, 833–842 CrossRef CAS PubMed.
- N. C. Seeman and H. F. Sleiman, Nat. Rev. Mater., 2018, 3, 17068 CrossRef CAS.
- J. F. Marko and E. D. Siggia, Macromolecules, 1994, 27, 981–988 CrossRef CAS.
- C. Bustamante, Z. Bryant and S. B. Smith, Nature, 2003, 421, 423–427 CrossRef PubMed.
- P. C. Nelson, M. Radosavljevic and S. Bromberg, Biological Physics: Energy, Information, Life, W.H. Freeman and Co., New York, 2008 Search PubMed.
- J. R. Moffitt, Y. R. Chemla, S. B. Smith and C. Bustamante, Annu. Rev. Biochem., 2008, 77, 205–228 CrossRef CAS PubMed.
- I. De Vlaminck and C. Dekker, Annu. Rev. Biophys., 2012, 41, 453–472 CrossRef CAS PubMed.
- B. S. Fujimoto and J. M. Schurr, Nature, 1990, 344, 175–177 CrossRef CAS PubMed.
- F. Lankaš, J. Šponer, P. Hobza and J. Langowski, J. Mol. Biol., 2000, 299, 695–709 CrossRef PubMed.
- J. P. Peters and L. J. Maher, Q. Rev. Biophys., 2010, 43, 23–63 CrossRef CAS PubMed.
- S. Geggier and A. Vologodskii, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 15421–15426 CrossRef CAS PubMed.
- H.-M. Chuang, J. G. Reifenberger, H. Cao and K. D. Dorfman, Phys. Rev. Lett., 2017, 119, 227802 CrossRef PubMed.
- J. Y. Lee, Y.-J. Kim, C. Lee, J. G. Lee, H. Yagyu, O. Tabata and D.-N. Kim, Nucleic Acids Res., 2019, 47, 93–102 CrossRef CAS PubMed.
- J. D. Yesselman, S. K. Denny, N. Bisaria, D. Herschlag, W. J. Greenleaf and R. Das, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 16847–16855 CrossRef CAS PubMed.
- J. P. Peters, S. P. Yelgaonkar, S. G. Srivatsan, Y. Tor and L. James Maher, Nucleic Acids Res., 2013, 41, 10593–10604 CrossRef CAS PubMed.
- J. P. Peters, L. S. Mogil, M. J. McCauley, M. C. Williams and L. J. Maher III, Biophys. J., 2014, 107, 448–459 CrossRef CAS PubMed.
- T. Dršata and F. Lankaš, J. Phys.: Condens. Matter, 2015, 27, 323102 CrossRef PubMed.
- T. E. Cloutier and J. Widom, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3645–3650 CrossRef CAS PubMed.
- P. A. Wiggins, T. van der Heijden, F. Moreno-Herrero, A. Spakowitz, R. Phillips, J. Widom, C. Dekker and P. C. Nelson, Nat. Nanotechnol., 2006, 1, 137–141 CrossRef CAS PubMed.
- A. J. Mastroianni, D. A. Sivak, P. L. Geissler and A. P. Alivisatos, Biophys. J., 2009, 97, 1408–1417 CrossRef CAS PubMed.
- A. Vologodskii and M. D. Frank-Kamenetskii, Nucleic Acids Res., 2013, 41, 6785–6792 CrossRef CAS PubMed.
- N. Ma and A. van der Vaart, J. Am. Chem. Soc., 2016, 138, 9951–9958 CrossRef CAS PubMed.
- R. Fritzsch, G. M. Greetham, I. P. Clark, L. Minnes, M. Towrie, A. W. Parker and N. T. Hunt, J. Phys. Chem. B, 2019, 123, 6188–6199 CrossRef CAS PubMed.
- R. Pawlak, J. G. Vilhena, A. Hinaut, T. Meier, T. Glatzel, A. Baratoff, E. Gnecco, R. Perez and E. Meyer, Nat. Commun., 2019, 10, 685–687 CrossRef CAS PubMed.
- J. B. Chaires, ACS Chem. Biol., 2008, 3, 207–209 CrossRef CAS PubMed.
- S. Kim, E. Brostroemer, D. Xing, J. Jin, S. Chong, H. Ge, S. Wang, C. Gu, L. Yang, Y. Q. Gao, X.-d. Su, Y. Sun and X. S. Xie, Science, 2013, 339, 816–819 CrossRef CAS PubMed.
- A. Balaceanu, A. Pérez, P. D. Dans and M. Orozco, Nucleic Acids Res., 2018, 46, 7554–7565 CrossRef CAS PubMed.
- K. Hart, N. Foloppe, C. M. Baker, E. J. Denning, L. Nilsson and A. D. MacKerell, J. Chem. Theory Comput., 2012, 8, 348–362 CrossRef CAS PubMed.
- I. Ivani, P. D. Dans, A. Noy, A. Pérez, I. Faustino, A. Hospital, J. Walther, P. Andrio, R. Goñi, A. Balaceanu, G. Portella, F. Battistini, J. L. Gelpí, C. González, M. Vendruscolo, C. A. Laughton, S. A. Harris, D. A. Case and M. Orozco, Nat. Methods, 2015, 13, 55–58 CrossRef PubMed.
- M. Zgarbová, J. Šponer, M. Otyepka, T. E. Cheatham, R. Galindo-Murillo and P. Jurečka, J. Chem. Theory Comput., 2015, 11, 5723–5736 CrossRef PubMed.
- R. Galindo-Murillo, J. C. Robertson, M. Zgarbová, J. Šponer, M. Otyepka, P. Jurečka and T. E. Cheatham, J. Chem. Theory Comput., 2016, 12, 4114–4127 CrossRef CAS PubMed.
- D. Tan, S. Piana, R. M. Dirks and D. E. Shaw, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E1346–E1355 CrossRef CAS PubMed.
- T. E. Cheatham, P. A. Kollman and S. Francisco, J. Am. Chem. Soc., 1997, 119, 4805–4825 CrossRef CAS.
- A. Noy, A. Pérez, F. Lankas, F. Javier Luque and M. Orozco, J. Mol. Biol., 2004, 343, 627–638 CrossRef CAS PubMed.
- U. D. Priyakumar and A. D. MacKerell, J. Phys. Chem. B, 2008, 112, 1515–1524 CrossRef CAS PubMed.
- I. Faustino, A. Pérez and M. Orozco, Biophys. J., 2010, 99, 1876–1885 CrossRef CAS PubMed.
- R. Galindo-Murillo, D. R. Roe and T. E. Cheatham, Biochim. Biophys. Acta, Gen. Subj., 2015, 1850, 1041–1058 CrossRef CAS PubMed.
- C. Gu, J. Zhang, Y. I. Yang, X. Chen, H. Ge, Y. Sun, X. Su, L. Yang, S. Xie and Y. Q. Gao, J. Phys. Chem. B, 2015, 119, 13980–13990 CrossRef CAS PubMed.
- X. Teng and W. Hwang, ACS Nano, 2016, 10, 170–180 CrossRef CAS PubMed.
- L. Bao, X. Zhang, Y.-Z. Shi, Y.-Y. Wu and Z.-J. Tan, Biophys. J., 2017, 112, 1094–1104 CrossRef CAS PubMed.
- A. Reymer, K. Zakrzewska and R. Lavery, Nucleic Acids Res., 2018, 46, 1684–1694 CrossRef CAS PubMed.
- K. Liebl, T. Drsata, F. Lankas, J. Lipfert and M. Zacharias, Nucleic Acids Res., 2015, 43, 10143–10156 CAS.
- A. Marin-Gonzalez, J. G. Vilhena, R. Perez and F. Moreno-Herrero, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7049–7054 CrossRef CAS PubMed.
- F. Lankaš, J. Šponer, J. Langowski and T. E. Cheatham, Biophys. J., 2003, 85, 2872–2883 CrossRef.
- O. Gonzalez, D. Petkevičiūtė and J. H. Maddocks, J. Chem. Phys., 2013, 138, 055102 CrossRef CAS PubMed.
- D. Petkevičiūtė, M. Pasi, O. Gonzalez and J. H. Maddocks, Nucleic Acids Res., 2014, 42, e153 CrossRef PubMed.
- W. K. Olson, A. A. Gorin, X. J. Lu, L. M. Hock and V. B. Zhurkin, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 11163–11168 CrossRef CAS PubMed.
- A. Pérez, A. Noy, F. Lankas, F. J. Luque and M. Orozco, Nucleic Acids Res., 2004, 32, 6144–6151 CrossRef PubMed.
- C. Rivetti, M. Guthold and C. Bustamante, J. Mol. Biol., 1996, 264, 919–932 CrossRef CAS PubMed.
- J. D. Moroz and P. Nelson, Macromolecules, 1998, 31, 6333–6347 CrossRef CAS.
- Z. Bryant, J. Gore, C. Bustamante, M. D. Stone, S. B. Smith and N. R. Cozzarelli, Nature, 2003, 424, 338–341 CrossRef CAS PubMed.
- J. Gore, Z. Bryant, M. Nöllmann, M. U. Le, N. R. Cozzarelli and C. Bustamante, Nature, 2006, 442, 836–839 CrossRef CAS PubMed.
- M. Y. Sheinin and M. D. Wang, Phys. Chem. Chem. Phys., 2009, 11, 4800–4803 RSC.
- P. Gross, N. Laurens, L. B. Oddershede, U. Bockelmann, E. J. G. Peterman and G. J. L. Wuite, Nat. Phys., 2011, 7, 731–736 Search PubMed.
- P. Lebel, A. Basu, F. C. Oberstrass, E. M. Tretter and Z. Bryant, Nat. Methods, 2014, 11, 456–462 CrossRef CAS PubMed.
- O. D. Broekmans, G. A. King, G. J. Stephens and G. J. L. Wuite, Phys. Rev. Lett., 2016, 116, 258102 CrossRef PubMed.
- P. J. Hagerman, Annu. Rev. Biophys. Biophys. Chem., 1988, 17, 265–286 CrossRef CAS PubMed.
- S. P. Edmondson and D. M. Gray, Biopolymers, 1984, 23, 2725–2742 CrossRef CAS PubMed.
- M. A. Livshits, O. A. Amosova and Y. L. Lyubchenko, J. Biomol. Struct. Dyn., 1990, 7, 1237–1249 CrossRef CAS PubMed.
- E. Herrero-Galán, M. E. Fuentes-Perez, C. Carrasco, J. M. Valpuesta, J. L. Carrascosa, F. Moreno-Herrero and J. R. Arias-Gonzalez, J. Am. Chem. Soc., 2013, 135, 122–131 CrossRef PubMed.
- J. Lipfert, G. M. Skinner, J. M. Keegstra, T. Hensgens, T. Jager, D. Dulin, M. Köber, Z. Yu, S. P. Donkers, F.-c. Chou, R. Das and N. H. Dekker, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15408–15413 CrossRef CAS PubMed.
- P. J. Hagerman, Annu. Rev. Biophys. Biomol. Struct., 1997, 26, 139–156 CrossRef CAS PubMed.
- M. M. Tirion, Phys. Rev. Lett., 1996, 77, 1905–1908 CrossRef CAS PubMed.
- J. W. Chu and G. a. Voth, Biophys. J., 2006, 90, 1572–1582 CrossRef CAS PubMed.
- J. Silvestre-Ryan, Y. Lin and J. W. Chu, PLoS Comput. Biol., 2011, 7, e1002023 CrossRef CAS PubMed.
- J. Macke Thomas and A. Case David, Molecular Modeling of Nucleic Acids, Modeling Unusual Nucleic Acid Structures, 1997, vol. 682, pp. 379–393 Search PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–7, 19–25 CrossRef.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- J. Howard, Mechanics of Motor Proteins and the Cytoskeleton, Sinauer Associates, 2001 Search PubMed.
- X. J. Lu and W. K. Olson, Nucleic Acids Res., 2003, 31, 5108–5121 CrossRef CAS PubMed.
- B. R. Brooks, D. Janežič and M. Karplus, J. Comput. Chem., 1995, 16, 1522–1542 CrossRef CAS.
- E. B. Wilson, J. C. Decius and P. C. Cross, Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, McGraw-Hill, New York, 1955 Search PubMed.
- V. I. Ivanov, L. E. Minchenkova, A. K. Schyolkina and A. I. Poletayev, Biopolymers, 1973, 12, 89–110 CrossRef CAS PubMed.
- H. R. Drew, R. M. Wing, T. Takano, C. Broka, S. Tanaka, K. Itakura and R. E. Dickerson, Proc. Natl. Acad. Sci. U. S. A., 1981, 78, 2179–2183 CrossRef CAS PubMed.
- A. Dock-Bregeon, B. Chevrier, A. Podjarny, J. Johnson, J. de Bear, G. Gough, P. Gilham and D. Moras, J. Mol. Biol., 1989, 209, 459–474 CrossRef CAS PubMed.
- A. R. Atilgan, S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin and I. Bahar, Biophys. J., 2001, 80, 505–515 CrossRef CAS PubMed.
- S. C. J. Parker, L. Hansen, H. O. Abaan, T. D. Tullius and E. H. Margulies, Science, 2009, 324, 389–392 CrossRef CAS PubMed.
- S. C. J. Parker and T. D. Tullius, Curr. Opin. Struct. Biol., 2011, 21, 342–347 CrossRef CAS PubMed.
- M. Kellis, B. Wold, M. P. Snyder, B. E. Bernstein, A. Kundaje, G. K. Marinov, L. D. Ward, E. Birney, G. E. Crawford, J. Dekker, I. Dunham, L. L. Elnitski, P. J. Farnham, E. A. Feingold, M. Gerstein, M. C. Giddings, D. M. Gilbert, T. R. Gingeras, E. D. Green, R. Guigo, T. Hubbard, J. Kent, J. D. Lieb, R. M. Myers, M. J. Pazin, B. Ren, J. A. Stamatoyannopoulos, Z. Weng, K. P. White and R. C. Hardison, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 6131–6138 CrossRef CAS PubMed.
- B. Schneider, P. Božíková, P. Čech, D. Svozil and J. Černý, Genes, 2017, 8, 278 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc00480d |
| This journal is © The Royal Society of Chemistry 2020 |