The relative stability of SCM-14 germanosilicate with different distributions of germanium ions in the absence and presence of structure-directing agents

Abstract

We report a computational study of the distribution of germanium ions among the double four-membered rings (D4Rs) in SCM-14 germanosilicate and the influence of a structure-directing agent (SDA) on the stability of the as-synthesized material. For the pure zeolite structure, the calculations suggested clustering of Ge ions and the formation of D4Rs populated entirely by Ge heteroatoms, while part of the D4Rs contain only Si as T-atoms. As a general trend, structures with more Ge–O–Ge bridges are more stable. Variations in the stabilization energy of the zeolite due to the presence of the SDA are larger in magnitude than the variations due to different germanium distributions. For this reason, the presence of the SDA was found to affect the stability order of the individual structures with different germanium distributions but the structures with clustered germanium remain the most stable. The location of the fluoride anion in D4Rs composed of silicon T-atoms or outside the D4Rs results in strong destabilization of the structure. The simulated ¹⁹F NMR chemical shift of fluorine in D4Rs with different germanium contents suggested similar values of the shifts for models with different compositions and different shifts for models with the same composition. The calculated chemical shifts for most of the models with two to eight germanium atoms are in the range of −15 to −5 ppm. Thus, the ¹⁹F NMR chemical shift may not be a reliable method for the determination of the germanium content of the D4Rs in germanosilicates.

---

1. Introduction

Germanosilicates are a unique class of crystalline microporous materials in which germanium atoms are incorporated at tetrahedral atom (T-atom) positions in a zeolite framework.^1,2 The main role of germanium in these materials is the promotion of the formation and stabilization of double four-membered ring (D4R) units during zeolite synthesis, which consequently allows the synthesis of new zeolite structures with large pore sizes.^3–7 While the preferential location of the germanium in the D4R units of the zeolite framework has been confirmed by various groups, its distribution among different D4Rs of the germanosilicate structure and the relative positions of the germanium T-atoms in those units are still under debate. For germanosilicate with the AST framework, Pulido et al.⁸ proposed that Ge atoms tend to locate far apart, avoiding Ge–O–Ge links. On the other hand, Kamakoti et al.⁴ suggested that Ge–O–Si and Ge–O–Ge linkages stabilize the D4R units in the BEC zeolite structure, in contrast to the Si–O–Si linkages. This is explained by the deformability of all former angles toward lower values. For UTL germanosilicate, Odoh et al.⁹ observed a cooperative effect for Ge incorporation in one D4R. Fischer et al. modelled germanosilicates with AST and ITH framework types with different germanium contents and found the preference for the formation of Ge–O–Ge bridges only in the presence of fluoride anions in the D4R.^10,11

This aspect is particularly important in connection with the post-synthetic modifications of germanosilicates meant to transform them in other zeolite structures or to substitute germanium by other elements. Both directions are based on the ability of germanium to be extracted from the zeolite framework more easily than silicon. The methodology for the synthesis of zeolites with new types of frameworks using ADOR (assembly–disassembly–organisation–reassembly) is based on the extraction of labile D4R units and the reassembly of the obtained zeolite layers.¹² This process would be facilitated by a large amount of germanium in those D4Rs. Another post-synthetic treatment may include germanium substitution for aluminum, which has two benefits – on the one hand stabilizing the zeolite framework by removing the labile germanium, and on the other hand generating Brønsted acid sites which may be used in catalytic applications.^13,14 The utilization of this type of post-synthetic modification requires well-separated germanium atoms among different D4Rs since the structure may collapse if germanium atoms are clustered.

Germanium distribution among the D4Rs of germanosilicate zeolites is studied by ¹⁹F NMR of the fluoride anions located in the D4Rs of the as-synthesized material. Since the content of germanium in the D4R cannot be directly derived from the measured chemical shift, those studies are complemented by relevant computational modeling. An earlier study of Pulido et al. using anionic D4R fragments with different Ge contents suggested that the calculated values of the chemical shifts are in general higher (e.g. lower in absolute value) when the germanium content of the D4R is higher, but there are some deviations of this trend for intermediate germanium content.⁸ A later study of Rigo et al. employed periodic density functional modeling of a STW zeolite structure with a structure-directing agent (SDA) inside and calculated the corresponding ¹⁹F chemical shifts.¹⁵ Although the computed values deviate notably from the experimentally measured values, based on the observed trend, they defined four groups of D4R with different germanium contents with chemical shifts for the experimental maxima at −35.7, −16.6, −7.5, −10.5 ppm. Liu et al. reported a combined computational and 2D NMR study and grouped the D4R into three groups – D4R composed only of Si T-atoms, D4R in which all Ge atoms are surrounded by Si T-atoms, and D4R containing at least one Ge–O–Ge bridge with resonances around −38, −20, and −9 ppm.¹⁶

The goal of this work is to investigate the relative stability of the germanosilicate zeolite SCM-14 (SOR framework type) depending on the location of Ge heteroatoms in the framework and the location and orientation of the SDAs in the as-synthesized zeolite.⁶ Similar to that of other Ge-containing zeolite structures, the X-ray powder diffraction (XRD) data show that Ge occupies only the T-atom positions in the D4R.⁶ In order to check if Ge is evenly distributed among different D4Rs or the germanium atoms are clustered close to each other, we applied the approach used earlier for ITQ-44 germanosilicate¹⁷ – comparison of the relative energies of the periodic zeolite structures with the same chemical composition but different distributions of the germanium T-atoms. In addition, we carried out structural optimization of the location of the SDA in the pores of the germanosilicate zeolites and investigated their influence on the relative stability of the zeolites, depending on the location of Ge heteroatoms in the framework. From these calculations, we obtained the relative stability of the optimized as-synthesized structure and the interaction energy of SDA in different orientations and frameworks. In the final part of the article, we calculated the ¹⁹F NMR chemical shift for the fluoride anion inside D4Rs with different Ge contents and distributions in order to analyze the applicability of this shift in the determination of Ge distribution among D4Rs in germanosilicates.

2. Computational method and models

For the modeling, we employed a state-of-the-art computational method, used currently for computational studies of zeolite structures. Periodic structures were optimized with calculations, based on density functional theory (DFT), with the exchange–correlation functional suggested by Perdew–Burke–Ernzerhof (PBE)¹⁸ with the additional empirical dispersion correction proposed by Grimme¹⁹ as implemented in the VASP package.^20,21 For calculations we used PAW pseudopotentials^22,23 and the valence wave functions were expanded in a plane-wave basis with a cutoff energy of 415 eV. The Brillouin zone was sampled using only the Γ point.²³

The unit cell of the SCM-14 zeolite framework was optimized for the pure periodic silicate structure with dimensions a = 20.92770 Å, b = 17.70280 Å, c = 7.58770 Å; α = β = γ = 90°. Since the unit cell in direction c was small, we also modeled the structure with a doubled unit cell in that direction, e.g. with c = 15.17540 Å. The results for this model, containing 288 atoms, are reported in the present work. The size of the unit cell was taken from the experimental CIF file, reported earlier.⁶ The germanium content of the modeled structures, 12 Ge per unit cell, corresponds to that of the experimentally synthesized materials.

For the models containing SDA, the amount of SDA in the zeolite cavities was based on the chemical composition of the as-synthesized material. For the SCM-14 zeolite, the composition was (C₉N₂H₁₃F)_1.99(H₂O)_0.84[Si_37.8Ge_10.2O₉₆], i.e. two protonated 4-pyrrolidinopyridine molecules, two fluoride anions, and one water molecule per unit cell. Since we used a doubled unit cell along the c-axis, our models involved 4 SDA molecules and 2 water molecules. The initial orientations of the SDAs were extracted from the experimental CIF files of the as-synthesized material. The extraction of the SDA position from the CIF files was somewhat complicated since the as-synthesized materials contain several different locations and orientations of the SDAs in the zeolite pores, which overlap in the CIF file. For this reason, we modeled various orientations of the SDAs in the two zeolite frameworks using structures with different germanium distributions.

All atoms in the zeolite framework, SDAs and water were allowed to relax until the force on each atom was less than 5 × 10^–4 eV pm⁻¹ during the geometry optimization procedure. The relative stability of the structures was evaluated by the electronic energy difference between the structures with the same composition as one of the structures is selected as the reference. The interaction/stabilization energies of the SDAs with the zeolite framework (equivalent to the stabilization of the models with SDAs with respect to those without SDAs) are calculated with respect to 4-pyrrolidinopyridine·HF complexes, water molecules and the corresponding zeolite framework. The relative energies are calculated with respect to the most stable models, those with the lowest energy or lowest stabilization energy, thus all relative energies are positive. A lower value of the relative energy corresponds to a more stable structure.

The simulation of ¹⁹F NMR chemical shifts was done by the gauge-independent atomic orbitals (GIAOs) method²⁴ as implemented in ORCA, an ab initio, DFT and semiempirical electronic structure package (vers. 4.1.2).^25,26 We used the hybrid gradient-corrected PBE0 exchange–correlation functional¹⁸ and def2-TZVP basis set.^27,28 For the chemical shift simulations, finer grid and tighter SCF convergence criteria were used. The calculations were performed with a fragment of the SCM-14 framework including one D4R with all five-membered rings surrounding it (see Fig. S1 in the ESI†). The positions of all atoms were allowed to relax, except that of four silicon centers, which are the most distant from the D4R (one per each five-ring). The chemical shifts for fluorine were obtained by subtraction from the calculated isotropic chemical shielding value for trichlorofluoromethane (CCl₃F). Since the experimental ¹⁹F chemical shift of fluorine in CClF₃, −28.6 ppm,²⁹ falls in the region of the measured fluorine chemical shifts in zeolite D4Rs, we calculated the corresponding value using the same computational protocol as for zeolite models and obtained the value of −33.0 ppm, i.e. by 4.4 ppm lower than the experiment. Based on this result we corrected the calculated values for the ¹⁹F chemical shift in zeolite models by 4.4 ppm and those values are reported and discussed in the article.

3. Results and discussion

3.1. Germanium distribution in the SCM-14 framework

The SCM-14 zeolite structure has six T-atom positions, each of them with a multiplicity of 8. Four of those positions participate in the D4R units of the zeolite structure. The single unit cell of SCM-14 has four D4Rs, while in the double unit cell model we have eight D4Rs. In order to evaluate the preferred Ge distribution in the SCM-14 zeolite framework in the absence of SDAs, nine structures with different distributions of Ge ions were constructed initially in the single unit cell model. All the structures contain an experimentally determined amount of germanium – 12 Ge T-atoms distributed at the four T-atom positions – participating in the D4R. The experimentally determined germanium content in those positions is very similar, 38.6% at T2, 33.0% at T3, 39.5% at T4 and 32.1% at T5. Based on this result, in all our models we have three germanium ions in each of the four T-atom positions, i.e. the germanium content in each position is 37.5%, similar to the experimental values. The modeled structures differ in the relative location of germanium among D4Rs:

– Ge heteroatoms are evenly distributed among the D4Rs with 5 silicon and 3 germanium joining in each D4R, e.g. D4R (5Si,3Ge), which results in a small number of Ge–O–Ge linkages;

– structures containing D4R units completely made up of germanium ions, D4R (8Ge) and completely made up of silicon ions, D4R (8Si), which have a high number of Ge–O–Ge linkages;

– models denoted as D4R (4Si,4Ge), which include one square wall of the D4R made of germanium ions, denoted as 4R (Ge-4R), and the other square wall of the same D4R made only of silicon ions, 4R (Si-4R), as the two squares are connected via four Ge–O–Si linkages.

A summary of the relative stability and some structural parameters for SCM-14 germanosilicate models with different Ge distributions is provided in Table 1.

Table 1 Summary of the relative stability and some structural parameters for SCM-14 germanosilicate with different Ge distributions using a double cell model: relative stability with respect to the most stable structure (in eV), number of Ge–O–Ge linkages per unit cell, number of D4R(8Ge) per unit cell containing only Ge as T-atoms, number of 4R(4Ge) containing only Ge as T-atoms without those in D4R(8Ge) per unit cell, average Ge–O–Ge angles, standard deviation of the Ge–O–Ge angles

Structure	ΔE	N(Ge–O–Ge)	D4R(8Ge)	4R(4Ge)	Ge–O–Ge	St. dev.
S14a	0.00	16	1	1	130.5	2.2
S14b	0.44	14	1	0	129.9	2.9
S14c	1.12	7	0	0	129.5	1.9
S14d	1.23	9	0	2	131.1	4.9
S14e	1.35	2	0	0	130.7	1.8
S14f	1.36	9	0	1	130.2	1.9
S14g	1.43	9	0	1	130.9	6.8
S14h	1.49	8	0	0	129.7	2.5
S14i	1.50	7	0	0	130.6	2.2

---

In the most stable structure, denoted as S14a, all 12 Ge atoms per unit cell are located in one D4R unit containing 8 Ge T-atoms, D4R(8Ge), and one square wall composed only of Ge T-atoms in another D4R, D4R(4Ge,4Si). The other two D4Rs are composed only of Si T-atoms, i.e. D4R(8Si). Next in stability is the structure denoted as S14b, which also contains one D4R(8Ge) but not additional 4R(Ge) units. The other modeled structures do not have D4R(8Ge) and are by more than 1.0 eV less stable than the structure S14a.

The results suggest some qualitative trends connecting the Ge distribution and the relative stability of the structures. The structures with completely germanium and completely silicon D4Rs, D4R(8Ge) and D4R(Si), are more stable than the structures with rings containing both Ge and Si T-atoms, and in particular than the structure with an even distribution of Ge among the D4Rs. As can be seen in Fig. 2A, in general, the structures with a larger number of Ge–O–Ge moieties are more stable. However, some structures containing an intermediate number of Ge–O–Ge contacts deviate from the latter trend, which may be caused to some extent by the larger standard deviation of the Ge–O–Ge angle in some of those structures (see Table 1) since it was shown earlier that variations of the Ge–O–Ge angle affect the framework stability.^4,17,30

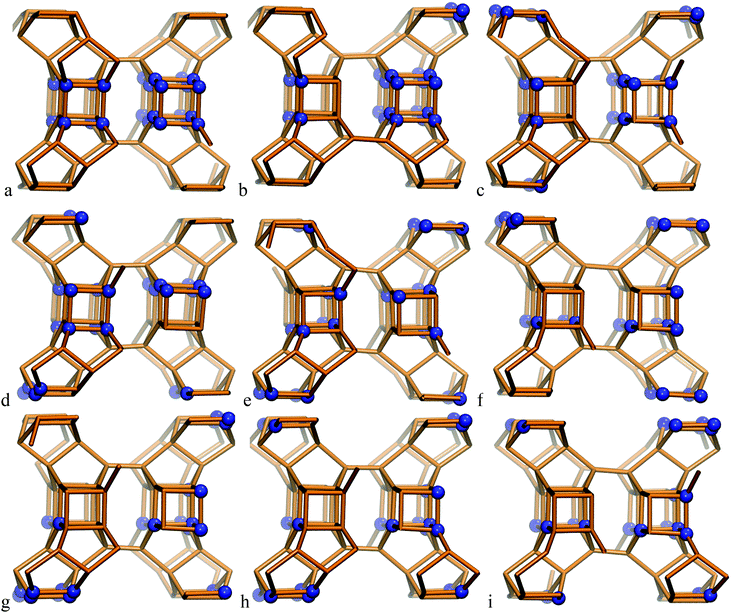Fig. 1 Modeled structures of SCM-14 germanosilicate with different relative distributions of germanium ions in the D4R; structures are denoted with letters a–i according to the notation, used in Table 1.

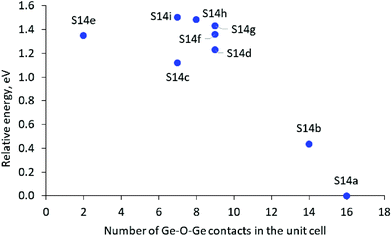Fig. 2 Relative stability of the SCM-14 structure with different germanium distributions in the D4Rs versus the number of the Ge–O–Ge contacts in the unit cell.

We tested also other potential correlations of the relative stability with Ge–Ge or Si–Si distances, or with average values of the Ge–O–Ge, Si–O–Si or Si–O–Ge angles, but no clear trends were found.

From the optimized structures, we derived some typical structural parameters, interatomic distances between T-atoms and T–O–T angles. In the left panel of Table 2, the average structural parameters for the two most stable and four least stable structures of SCM-14 germanosilicate are listed. As can be seen, the average values for all those structures are very similar, as the largest difference is observed between two most stable structures S14a and S14b, and thus, variations in the average distances and angles cannot be a factor influencing the structural stability. The obtained trend for the parameters involving different T-atoms is similar to those observed in previous studies – the Ge–O–Si and Ge–O–Ge angles are 10–15 degrees sharper than the Si–O–Si angles, and the Ge–Ge and Ge–Si distances are by 0.14 and 0.07 Å longer than the Si–Si distances.

Table 2 Interatomic distances (in Å) and angles (in degrees) of SCM-14 germanosilicate structures: left panel – average values of the parameters of six (most and least) stable structures of SCM-14 germanosilicate with different Ge distribution; right panel – some individual distances/angles within the S14b structure

Average values for the structure							Individual values within S14b structure
Structure	Ge–O–Ge	Ge–O–Si	Si–O–Si	Ge–Ge	Ge–Si	Si–Si	Ge–O–Ge	Ge–O–Si	Si–O–Si	Ge–Ge	Ge–Si	Si–Si
S14a	131	133	146	3.24	3.13	3.11	130	140	146	3.14	3.20	3.18
S14b	130	140	146	3.23	3.20	3.11	129	140	141	3.10	3.15	3.23
S14f	130	136	144	3.23	3.17	3.10	133	136	140	3.08	3.22	3.20
S14g	131	136	144	3.25	3.17	3.09	131	153	141	3.19	3.16	3.23
S14h	130	137	145	3.23	3.17	3.10	135	140	152	3.10	3.21	3.18
S14i	131	136	145	3.24	3.17	3.10	127	135	138	3.06	3.18	3.27

---

Although the average values between the structures with different germanium distributions are similar, both individual angles and distances within one structure varies in a wider range. For example, in the S14b structure, the Si–O–Si and Ge–O–Si angles vary by 14–18 degrees, while the distances between the T-atoms vary by about 0.10 Å (part of the individual values are shown in the right panel of Table 2).

3.2. Structure directing agent in the as-synthesized SCM-14

To evaluate the effect of the SDA on the stability of the SCM-14 germanosilicate structure with different germanium distributions, we used the already optimized geometries (with eight D4Rs) in which we introduced 4 molecules of 4-pyrrolidinopyridine protonated by HF and two water molecules. The experimental CIF file suggests that the organic template preferably occupies four different orientations, while the location of the water molecules is essentially the same.⁶ From the CIF file we extracted four different orientations of each of the two symmetrically inequivalent SDA molecules, which can be described with the position of the pyridine ring in the model: front-right (pyridine ring is closer to the viewer and directed towards the right-hand side), front-left, back-right, and back-left, with short notations fr, fl, br, and bl, respectively. In addition, the fluoride anion may occupy D4Rs with different Ge and Si contents.

Due to the various possible combinations of Ge distribution in the zeolite, different orientations of the SDA and locations of fluoride, we simulated in total 35 models, grouped in three series:

Series 1 (9 models): all nine SCM-14 structures with different distributions of germanium centers, reported in Table 1 and shown in Fig. 1, using the same initial orientation of the SDA – all SDAs are oriented front-right. In the models in this series, the fluoride anion is located in the D4R containing different amounts of Ge centers.

Series 2 (14 models): in the most stable SCM-14 structure, denoted as S14a, we included various orientations of the SDAs and in some cases different locations of the fluoride anion. The idea for this series was to check to what extent different orientations of the SDA and different locations of the fluoride affect the stability of the structure.

Series 3 (12 models): in the last series, we selected four SCM-14 structures with different distributions of germanium centers, denoted as S14b, S14c, S14e, and S14i. In those models, we incorporated the SDAs with orientations bl/br and fr/fl. For the bl/br models, we considered two locations of the fluoride anion in different D4Rs.

General information about the models with SDAs inside the pores of SCM-14 in the three series is provided in Table 3. The relative energies of the structures with SDAs and the relative energies of the stabilization due to the SDAs are calculated with respect to the most stable structures with SDAs, denoted as S14a_2 and S14a_3, which have essentially the same stability. The orientation of the SDA molecules in the corresponding model is also provided using the notation described above. In addition, information about the Ge content in the D4Rs in which F⁻ is located is shown (per unit cell). Note that according to the chemical composition of the as-synthesized zeolite the number of fluoride anions is twice less than the number of the D4Rs.

Table 3 General information about the models with SDAs inside the pores of SCM-14: calculated relative energies of the structures with SDAs (Rel. E with SDA); energies of the stabilization due to the SDAs (E_stab); relative energies of stabilizations (Rel. E_stab); relative energies without SDAs (from Table 1); orientation of the SDAs (notation is described in the text); number of Ge in each of the D4Rs in which F⁻ is located. All energies are in eV

Structure	Rel. E with SDA	E stab	Rel. Estab	Rel. E without SDA	SDA orient.	Ge in F/D4R	Ge in F/D4R
Series 1
S14a_1	1.84	−10.53	1.84	0.00	fr/fr	8	0
S14b_1	2.63	−10.17	2.19	0.44	fr/fr	8	0
S14c_1	2.60	−10.89	1.48	1.12	fr/fr	5	3
S14d_1	3.48	−10.12	2.25	1.23	fr/fr	4	3
S14e_1	3.10	−10.61	1.75	1.35	fr/fr	3	3
S14f_1	1.91	−11.83	0.54	1.36	fr/fr	4	2
S14g_1	2.33	−11.47	0.90	1.43	fr/fr	4	4
S14h_1	2.38	−11.47	0.90	1.49	fr/fr	4	4
S14i_1	2.62	−11.24	1.12	1.50	fr/fr	4	2
Series 2
S14a_2	0	−12.37	0	0	fr/fr	8	4
S14a_3	0	−12.36	0	0	fr/bl	8	4
S14a_4	0.26	−12.11	0.26	0	fr/br	8	4
S14a_5	0.27	−12.1	0.27	0	fr/br	8	4
S14a_6	0.44	−11.93	0.44	0	bl/br	8	4
S14a_7	1.71	−10.66	1.71	0	fr/fr	8	Outside D4R
S14a_8	1.75	−10.62	1.75	0	fl/bl	8	0
S14a_1	1.84	−10.53	1.84	0	fr/fr	8	0
S14a_9	1.84	−10.53	1.84	0	fr–bl/fr	8	0
S14a_10	1.96	−10.4	1.96	0	bl/fl	8	0
S14a_11	2.13	−10.24	2.13	0	fl/br	8	0
S14a_12	2.15	−10.22	2.15	0	fr/fr	4	0
S14a_13	2.35	−10.02	2.35	0	br/bl	8	0
S14a_14	2.36	−10.01	2.36	0	fr/fr	8	0
S14a_15	2.43	−9.94	2.43	0	br/br	8	0
S14a_16	4.1	−8.27	4.1	0	fr/fr		Outside D4R
Series 3
S14b_4	1.56	−11.25	1.12	0.44	fr/br	8	2
S14b_6	1.59	−11.21	1.15	0.44	bl/br	8	2
S14b_17	2.56	−10.25	2.12	0.44	bl/br	8	2
S14e_4	3.63	−10.09	2.28	1.35	fr/br	3	3
S14e_6	3.64	−10.07	2.30	1.35	bl/br	3	3
S14e_17	4.01	−9.71	2.66	1.35	bl/br	3	3
S14i_4	3.73	−10.14	2.23	1.50	fr/br	4	2
S14i_6	3.91	−9.96	2.41	1.50	bl/br	4	2
S14i_17	3.23	−10.64	1.73	1.50	bl/br	4	4
S14c_4	2.69	−10.79	1.58	1.12	fr/br	5	2
S14c_6	3.04	−10.45	1.92	1.12	bl/br	5	2
S14c_17	3.63	−9.85	2.51	1.12	bl/br	5	2

---

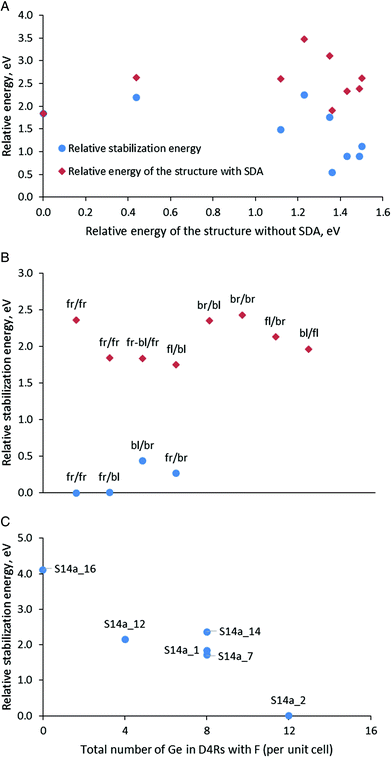
After optimization of the models in Series 1 containing protonated organic molecules and fluoride anion, the structure S14a_1 with the maximal number of Ge–O–Ge contacts was found to be the most stable (Table 3 and Fig. 3A). The stability order of the other models, however, was influenced by the presence of the SDA and is modified with respect to the structures with the same Ge distribution but without SDA, as can be seen from the lack of linear arrangement of the brown symbols in Fig. 3A. This is due to the different stabilization of the models with different germanium distributions in the presence of SDA with this specific orientation in the zeolite channels. The stabilization energy of the zeolite in the presence of SDAs (four protonated 4-pyrrolidinopyridine species, four fluoride anions and two water molecules per two SCM-14 unit cells) in this series varies between −10.12 and −11.83 eV for structures denoted as S14d_1 and S14f_1, respectively.

Fig. 3 (A) Relative energies (brown rhombus) and relative interaction energies (blue circles) of the structures with SDAs for the models in Series 1 – models with different Ge distributions with the same orientation of the SDA; (B) relative stabilization energies for a part of the models in Series 2 with different orientations of the SDAs (for the notation see the text) in the S14a structure and different locations of the fluoride anions, blue circles – in D4R(8Ge) and in D4R(4Ge4Si), brown rhombus – in D4R(8Ge) and in D4R(8Si); (C) relative stabilization energy for models with a fr/fr orientation in the S14a structure of the SDA versus the total number of Ge atoms in the D4Rs, in which fluoride anions are located (per unit cell).

In Series 2 we used an S14a structure to introduce SDAs with different orientations and fluoride anion in different locations since this structure has been found to be the most stable both in the absence of SDA and also in the presence of SDA in Series 1. In that model, twelve Ge atoms are included in one D4R containing only Ge T-atoms and one D4R with four Ge and four Si T-atoms per unit cell. Since we use the same Ge distribution in all models in this series, we can focus on the influence of the SDA orientation and fluoride location on the stability of the models.

Fig. 3B shows the calculated relative stabilization energies for some of the models in Series 2 with different orientations of the SDA using the notation described above. The models are arranged in two groups: (i) with one fluoride anion inside D4R(8Ge), composed only of Ge T-atoms, and one inside D4R(4Ge4Si) per unit cell; and (ii) with one fluoride anion also inside D4R(8Ge) but the second anion is inside D4R(8Si), composed only of Si T-atoms per unit cell. The models in the first group (see the blue circles) are more stable than the second one by more than 1.3 eV, which suggests the preference for the location of the fluoride anion inside D4R(4Ge4Si) with respect to its location inside D4R(8Si), where Ge is absent. In addition, the figure shows variations of the stabilization energy depending on the orientation of the template within each group of models, the energy variations are 0.44 eV for the 0.68 eV for the first and the second groups. Note that those variations are about twice lower than the variations due to different locations of the fluoride anion. In Fig. 3B we have two structures in the second group with the same orientation of the SDA, fr/fr, which correspond to models S14a_14 and S14a_1 (see also Fig. 3C). The energy difference between those two models is 0.52 eV and the structural difference between them is only the D4R(8Si) in which the second fluoride anion is located, i.e. fluoride anion location and the SDA orientations affect synchronously the stability of the structure S14a_1 with respect to S14a_14.

From the calculated stabilization energy of the structures with fr/fr orientation of the SDA and different location of the fluoride anion, shown in Fig. 3C one may conclude that fluoride in D4Rs containing more Ge centers is energetically favorable than the location in D4R with less Ge centers or in the zeolite channel close to protonated 4-pyrrolidinopyridine. The conclusions can be seen comparing the following structures:

• The structure S14a_2 is with the lowest relative energy and in it all four fluoride anions are located in D4Rs containing in total 12 Ge centers. The structure S14a_12 differs from it by the position of one fluoride anion – in D4R(8Si) instead of D4R(8Ge), thus the lack of Ge in the fluoride anion environment in the latter model leads to a decrease in its stability by 2.15 eV.

• In the least stable structure, S14a_16, the fluoride anions are located outside the D4R structural units, close to the protonated SDA.

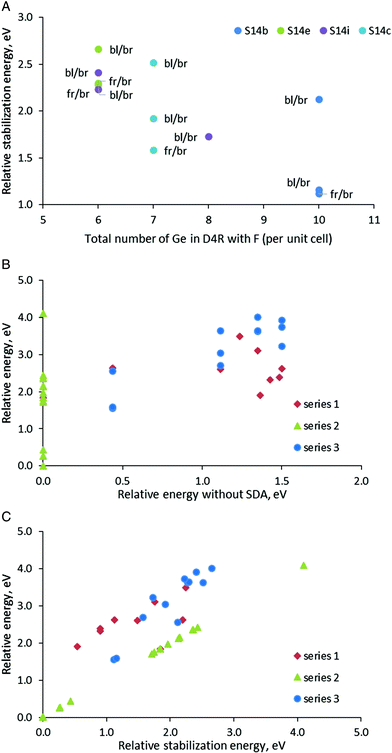
In order to have some more examples of structures with different orientations of the SDA and positions of the fluoride anion in Series 3, we used four SCM-14 structures with different distributions of germanium centers, S14b, S14c, S14e, and S14i. In each of those models, we incorporated the SDAs with orientation back-left/back-right and front-right/front-left. For the back-left/back-right model, we considered also a structure with the location the fluoride anion in different D4Rs.

Both relative stability of the modeled structures and the stabilization energy of the SDA inside them confirms the general trend discussed above that the structures in which the fluoride anion is located in D4Rs with more germanium centers are more stable (Fig. 4A). The points in the figure, however, suggest a more complex interplay between the fluoride position and the orientation of the organic moieties than simply counting the germanium centers in the D4R. If we consider the two points for the S14b model with bl/br orientation of the SDA (dark blue point), we will see a substantial difference in the relative stabilization energy by1.0 eV only due to the location of the fluoride anion in different D4Rs (although the new D4R has the same number of Ge centers, see Table 3 and Fig. S4†). For the model S14c one can observe a similar situation where the energy difference between the two structures with the same number of Ge centers in the D4R and the same orientation of the SDA is ca. 0.7 eV. On the other hand, the S14b_4 and S14b_6 models with different orientations of the SDA, fr/br and bl/br, and the same location of the fluoride anion have very similar stability, E_stab = 1.12–1.15 eV. Similarly, close values are found for the two S14e models with the same fluoride location, E_stab = 2.28–2.30 eV.

Fig. 4 Relative stabilization energies the models in Series 3 with different orientations of the SDAs versus the total number of Ge centers in the D4Rs where the fluoride anion is located per unit cell (panel A); relative energy of the structures with a SDA versus relative energy of the same structure without a SDA (panel B) or versus relative stabilization energies (panel C). For panel C the values for Series 2 are equal by definition.

After presentation of these results, one may consider all modeled structures of SDA containing SCM-14. The most stable structure without SDA, S14a, remains the most stable also with some of the models with SDA (see the green triangles in Fig. 4B and C). However, in general, Fig. 4B shows that there is no correlation between the stability of the structure without SDA and the stability of the same structure with SDA. This is due to the stronger influence of the stabilization energy of the SDA inside the structure, which correlate better with the relative energy of the structures with SDA (see the data for Series 1 and 3 in Fig. 4C). This factor dominates the total stability since the variation of the stabilization energies of different models due to the orientation of the SDA and the location of the fluoride anion is within 2.66 eV (when all fluoride anions are in D4Rs) or 4.0 eV (when one counts the model with the fluoride anion outside the D4R). For comparison, the difference in the energies of the corresponding structures without SDA due to different distributions of Ge centers in the D4R is at most 1.50 eV.

One may discuss the question whether the trend for the preference for the formation of D4R composed only of Ge T atoms and for the stabilization of the structures with more Ge–O–Ge bridges, observed here for SCM-14 germanosilicate, is specific only for this zeolite framework or is more general. In an earlier study, Pulido et al. using force field simulations for a germanosilicate with an AST framework arrived at the opposite conclusion for models with two to four Ge in one D4R that Ge atoms, when possible, tend to locate far apart, avoiding Ge–O–Ge links.⁸ This result may be due to the use of the force field but not the quantum chemistry method for this evaluation or due to a different topology of the zeolite framework. Kamakoti et al. determined the stability and structural parameters for various models with one to eight Ge atoms in the BEC zeolite structure with periodic DFT calculations and isolated fragments.⁴ They focused on the importance of the preferred values of the T–O–T angles, specific for the zeolite framework, and concluded that the site preference and energies for Ge substitution are linked to the deformability of all T–O–T angles in its vicinity toward lower values. For this reason, Ge–O–Si and Ge–O–Ge linkages stabilize the D4R units at more acute angles, while Si–O–Si linkages are disfavoured. Odoh et al. studied UTL germanosilicate with up to three Ge per unit cell and observed a cooperative effect for Ge incorporation in one D4R, which suggests that Ge atoms would become increasingly concentrated at the D4R sites of UTL as more Si/Ge substitutions are performed.⁹ For germanosilicates with AST and ITH framework types, Fischer and Fischer et al. modelled various structures with different germanium contents and relative locations and found the preference for the formation of Ge–O–Ge bridges in the presence of fluoride anions in the D4R.^10,11 Such a trend, however, is not observed in the models in the absence of fluoride and SDA. Thus, considering the previous quantum chemical studies and the results from the present work, one may conclude that the preference for the formation of Ge–O–Ge bridges in D4Rs of germanosilicates depends on the individual framework structure. For some of the modelled zeolite frameworks such preference is reported only for models in which the fluoride anion is located inside the D4R.

3.3. Simulated ¹⁹F NMR chemical shifts in germanium containing D4Rs

Our computational results, based on the relative stability of the SCM-14 structures, suggested that structures with a large number of Ge–O–Ge contacts and, respectively, with D4Rs composed mostly of germanium T-atoms or silicon T-atoms are more stable than the structures with more regular distribution of germanium in different D4Rs. Accounting for the presence of the SDA in the zeolite channels and fluoride anion in the D4R affects this stability order to some extent, but the structures with the highest number of direct Ge–O–Ge contacts remains the most stable in the presence of organic molecules in their cavities.

Several papers suggested that experimental ¹⁹F NMR spectra may provide information about the germanium content of the D4R in the zeolite materials.^8,15,16,31 The assignments of the experimentally observed bands in ¹⁹F NMR spectra is based on the comparison of the observed chemical shift with the chemical shift of the fluoride anion in D4Rs with different germanium compositions and ordering calculated by quantum chemical methods. A clear assignment from those studies is for fluoride in D4R(8Si) composed of silicon T-atoms with a chemical shift around −38 ppm as the corresponding calculated shift is between −36 and −31 ppm.^8,15 For the D4R containing germanium, different authors suggested somewhat different ranges of chemical shifts. In order to apply this approach to the SCM-14 zeolite we simulated the ¹⁹F NMR chemical shift of fluoride in D4Rs with different germanium contents using fragments of the zeolite framework. The calculations are done with hybrid density functional, which is assumed to provide more accurate electron density distribution than pure gradient-corrected functionals. In addition, in the calculations we included positively charged fragments of the SDA, in order to avoid artefacts that may arise from modeling negatively charged fragments. The obtained results were compared with the experimental data for the as-synthesized SCM-14 germanosilicates.⁶

In order to account for the presence of the SDA in our simulations we included protonated pyridine, similar to the positively charged part of the SDA used in the synthesis of SCM-14. In this way, our calculations were performed with neutral models, which avoids possible artefact with chemical shifts computed with charged models. The obtained results are shown in Table 4 together with some topological and structural data for the models. The lowest value, −30 ppm, corresponds to D4R composed only of silicon T-atoms, as the shift for one of the models with one Ge in the D4R is similar, −28 ppm. However, as shown in Fig. 5, there is no correlation between the germanium content of the D4R and the calculated fluorine chemical shift. Around −20 ppm one may see D4Rs with one and with five Ge, while between −15 and −10 ppm D4Rs with two to five germanium T-atoms may be found. In the range −10 to −5 ppm fall models with two to eight Ge, e.g. only D4R(8Si) and D4R(7Si,1Ge) have no signal in that region. By this reason, it is not surprising that for various germanosilicates the ¹⁹F chemical shift is measured in the latter region. This is also the case for the as-synthesized SCM-14 zeolite, which features a ¹⁹F shift with the maximum at −7.2 ppm.⁶ Earlier computational studies also suggested that in the same range of chemical shifts one may expect D4Rs with different germanium contents.^15,16

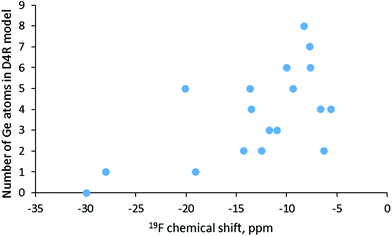Fig. 5 Calculated values for the ¹⁹F NMR chemical shift for the fluoride anion in D4Rs with different Ge contents.

Table 4 Calculated values for the ¹⁹F NMR chemical shift for the fluoride anion in D4Rs with different contents and distributions of Ge: number of Ge in the D4R, shortest T-atom – F distance (in pm), number of Ge–O–Ge bridges in the D4R model, distance between fluoride and the proton from the protonated pyridine (in pm)

Model	Corrected ^19F chemical shift	Number of Ge in D4R	Ge–F/Si–F distance	Number of Ge–O–Ge bridges	H⋯F distance
D4R(0Ge)	−30	0	187(Si)	0	446
D4R(1Ge)a	−19	1	186(Si)	0	373
D4R(1Ge)b	−28	1	189(Si)	0	413
D4R(2Ge)a	−6	2	195	1	381
D4R(2Ge)b	−14	2	197	0	417
D4R(2Ge)c	−12	2	199	0	414
D4R(3Ge)a	−11	3	194	2	405
D4R(3Ge)b	−12	3	200	0	387
D4R(4Ge)a	−7	4	197	4	384
D4R(4Ge)b	−14	4	201	0	391
D4R(4Ge)c	−6	4	201	3	384
D4R(5Ge)a	−9	5	197	5	388
D4R(5Ge)b	−14	5	199	3	389
D4R(5Ge)c	−20	5	193(Si)	4	385
D4R(6Ge)a	−8	6	199	5	387
D4R(6Ge)b	−10	6	199	7	389
D4R(7Ge)	−8	7	200	9	389
D4R(8Ge)	−8	8	200	12	390

---

For the D4R composed only of silicon T-atoms we also simulated the structure as negatively charged fragments, without the positively charged protonated pyridine moiety, and obtained a ¹⁹F chemical shift of −37 ppm, i.e. by 7 ppm lower than the value for the D4R(8Si) with a neighboring cationic moiety. This result suggests that the experimental value around −38 ppm may be due to the fluoride anion inside D4R(8Si), whose negative charge is not compensated by a cationic part of the SDA in its vicinity.

We checked some possible structural characteristics that may influence the value of the ¹⁹F NMR chemical shift for the fluoride anion in D4Rs – the shortest T-atom–F distance, the number of Ge–O–Ge bridges in the D4R model, the distance between fluoride and the proton from the protonated pyridine, and the distance of fluoride from the center of the D4R. None of those characteristics was found to correlate with the calculated shift, likely due to the complexity of the factors determining the actual chemical shift value. One may note also that D4Rs with the same number of germanium T-atoms may have notably different ¹⁹F chemical shifts due to different germanium distributions and different locations of the fluoride anion, see for example D4R(5Ge)a and D4R(5)c, the values for which differ by 11 ppm. The importance of the actual location of the fluoride inside the D4R can be seen from the different chemical shifts, −19 ppm and −28 ppm, calculated for D4R(1Ge)a and D4R(1Ge)b, as the only difference between the models is the location of the fluoride, which is on different sides of the cavity.

Recent ab initio molecular dynamic simulations, reported by Fischer et al.,^11,31 had shown that fluoride is very mobile at room temperature. This may cause additional complication for comparing the experimental values with calculated chemical shifts due to the mobility of fluoride inside the D4R, which may result in values averaged over various positions of the fluoride. On the other hand, the structures obtained from geometry optimization capture one of the various possible local minima. In some of those minima, the fluoride anion may appear closer to Ge or to Si. Goesten et al. had shown that the F–Si bond is not formed in a constrained D4R(8Si); however, in completely unconstrained optimization the F–Si bond appears.³²

4. Conclusions

The results from modeling different distributions of Ge ions in the SCM-14 germanosilicate zeolite structure suggest that the Ge ions prefer clustering together and forming D4Rs populated entirely with Ge heteroatoms, while part of the D4Rs contain only Si at T-atoms. The formation of completely germanium square walls of the D4R also partially contributes to the stability of the structures. On the other hand, the most energetically unfavorable structures are those in which the Ge heteroatoms are evenly spread among the D4R. There is a qualitative trend that the most stable structures have a large number of Ge–O–Ge linkages; however, this is not a quantitative correlation.

The presence of SDA, however, affects this stability order, obtained for the pure structures. For SCM-14, the structure with the highest number of direct Ge–O–Ge contacts remains the most stable in the presence of organic molecules in their cavities. However, for the whole set of modeled structures there is no clear correlation between the stability of the structure without a SDA and the stability of the same structure with a SDA. Both the relative stability of the modeled structures and the stabilization energy of the SDA inside them confirm the general trend that the structures in which the fluoride anion is located in the D4R with more germanium centers are more stable. The analysis of the stabilization energies of the structures suggests a more complex interplay between the fluoride position and the orientation of the organic moieties than simply counting the germanium centers in the D4R. The results have also shown that the as-synthesized models with the same distribution of germanium, combined with different orientations of the template, have significantly different relative energies. The reason for this is that the variations of the calculated energy for the stabilization of the as-synthesized zeolite due to the presence of SDA, 2.66 eV, are higher than the variations in the relative energies of the zeolite due to different Ge distributions in the D4R, 1.50 eV. Thus, the stabilization energies due to the presence of the SDA with a specific orientation may be a thermodynamic factor that influences the Ge distribution in the zeolite framework during the zeolite synthesis. In addition, the observed preference for the location of fluoride anions inside D4Rs containing more Ge atoms may suggest that fluoride stimulates the formation of D4Rs with high germanium content.

The last part of the work includes the simulation of ¹⁹F chemical shifts since the ¹⁹F chemical shifts measured by NMR spectroscopy are considered to provide information about the germanium content of the D4R in which fluoride is located. The results suggest that there is no correlation between the chemical shift and the germanium content of the D4R or with the number of the Ge–O–Ge bridges in it. Based on the results one may distinguish only the D4R, composed only of silicon T-atoms from the D4Rs containing germanium. Most of the D4Rs feature ¹⁹F between −15 and −5 ppm as those with 6 to 8 germanium per D4R are in the range −8 to −10 ppm. This result agrees with the experimentally measured value for SCM-14 germanosilicate, −7.2 ppm. In general, the ¹⁹F chemical shift cannot be used with confidence for the determination of the number of germanium T-atoms in the D4Rs where the fluoride anion is located since D4Rs with different compositions feature shifts in the same region, while fluoride in D4Rs with the same Ge content have different chemical shifts.

Author contributions

All authors participated in the planning of the research and analysing the results and have approved the manuscript. Most of the calculations have been performed by SPG, and the manuscript was drafted by GNV.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors thank Sinopec for the support and Prof. Weimin Yang and Dr Zhendong Wang for fruitful discussions.

References

1. A. Corma, M. T. Navarro, F. Rey, J. Rius and S. Valencia, Pure polymorph C of zeolite beta synthesized by using framework isomorphous substitution as a structure-directing mechanism, Angew. Chem., Int. Ed., 2001, 40, 2277–2280.
2. A. Corma, M. J. Díaz-Cabañas, J. L. Jorda, C. Martínez and M. Moliner, High-throughput synthesis and catalytic properties of a molecular sieve with 18- and 10-member rings, Nature, 2006, 443, 842–845.
3. T. Blasco, A. Corma, M. J. Díaz-Cabañas, F. Rey, J. A. Vidal-Moya and C. M. Zicovich-Wilson, Preferential Location of Ge in the Double Four-Membered Ring Units of ITQ-7 Zeolite, J. Phys. Chem. B, 2002, 106, 2634–2642.
4. P. Kamakoti and T. A. Barckholtz, Role of Germanium in the Formation of Double Four Rings in Zeolites, J. Phys. Chem. C, 2007, 111, 3575–3583.
5. B. B. Schaack, W. Schrader and F. Schüth, Structural Insight into Germanium-Containing Silicate Species by Electrospray Ionization Mass Spectrometry (ESI-MS) and ESI-MS/MS, J. Phys. Chem. B, 2009, 113, 11240–11246.
6. Y. Luo, S. Smeets, F. Peng, A. S. Etman, Z. Wang, J. Sun and W. Yang, Synthesis and Structure Determination of Large-Pore Zeolite SCM-14, Chem. – Eur. J., 2017, 23, 16829–16834.
7. Y. Luo, S. Smeets, Z. Wang, J. Sun and W. Yang, Synthesis and Structure Determination of SCM-15: A 3D Large Pore Zeolite with Interconnected Straight 12 × 12 × 10-Ring Channels, Chem. – Eur. J., 2019, 25, 2184–2188.
8. A. Pulido, G. Sastre and A. Corma, Computational Study of ¹⁹F NMR Spectra of Double Four Ring-Containing Si/Ge-Zeolites, ChemPhysChem, 2006, 7, 1092–1099.
9. S. O. Odoh, M. W. Deem and L. Gagliardi, Preferential Location of Germanium in the UTL and IPC-2a Zeolites, J. Phys. Chem. C, 2014, 118, 26939–26946.
10. M. Fischer, Local Environment and Dynamic Behavior of Fluoride Anions in Silicogermanate Zeolites: A Computational Study of the AST Framework, J, Phys. Chem. C, 2019, 123, 1852–1865.
11. M. Fischer, C. Bornes, L. Mafra and J. Rocha, Elucidating the germanium distribution in ITQ-13 zeolites by density functional theory, Chem. – Eur. J., 2022, e202104298.
12. P. Eliášová, M. Opanasenko, P. S. Wheatley, M. Shamzhy, M. Mazur, P. Nachtigall, W. J. Roth, R. E. Morris and J. Čejka, The ADOR mechanism for the synthesis of new zeolites, Chem. Soc. Rev., 2015, 44, 7177–7206.
13. F. Gao, M. Jaber, K. Bozhilov, A. Vicente, C. Fernandez and V. Valtchev, Framework Stabilization of Ge-Rich Zeolites via Postsynthesis Alumination, J. Am. Chem. Soc., 2009, 131, 16580–16586.
14. M. V. Shamzhy, P. Eliašová, D. Vitvarová, M. V. Opanasenko, D. S. Firth and R. E. Morris, Post-synthesis stabilization of germanosilicate zeolites ITH, IWW and UTL by substitution of Ge for Al, Chem. – Eur. J., 2016, 22, 17377–17386.
15. R. T. Rigo, S. R. G. Balestra, S. Hamad, R. Bueno-Perez, A. R. Ruiz-Salvador, S. Calero and M. A. Camblor, The Si-Ge substitutional series in the chiral STW Zeolite Structure Type, J. Mater. Chem. A, 2018, 6, 15110–15122.
16. X. Liu, Y. Chu, Q. Wang, W. Wang, C. Wang, J. Xu and F. Deng, Identification of double four-ring units in germanosilicate ITQ-13 zeolite by solid-state NMR spectroscopy, Solid State Nucl. Magn. Reson., 2017, 87, 1–9.
17. P. St. Petkov, H. A. Aleksandrov, V. Valtchev and G. N. Vayssilov, Framework stability of heteroatom substituted forms of large pore Ge-silicate molecular sieves: the case of ITQ-44, Chem. Mater., 2012, 24, 2509–2518.
18. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
19. S. J. Grimme, Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27, 1787–1799.
20. G. Kresse and J. Hafner, Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal-Amorphous-Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
21. G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50.
22. P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
23. G. Kresse, J. Joubert and J. From, Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
24. R. Ditchfield, Self-consistent perturbation theory of diamagnetism, Mol. Phys., 1974, 27, 789.
25. F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
26. F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327.
27. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
28. F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
29. https://nmr.chem.ucsb.edu/docs/19Fshifts.html , accessed on 27.03.2022.
30. G. Sastre and A. Corma, Predicting Structural Feasibility of Silica and Germania Zeolites, J. Phys. Chem. C, 2010, 114, 1667–1673.
31. M. Fischer and L. Freymann, Local Distortions in a Prototypical Zeolite Framework Containing Double Four-Ring Cages: The Role of Framework Composition and Organic Guests, ChemPhysChem, 2021, 22, 40–54.
32. M. G. Goesten, R. Hoffmann, F. M. Bickelhaupt and E. J. M. Hensen, Eight-coordinate fluoride in a silicate double-four-ring, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 828–833.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S6. See DOI: https://doi.org/10.1039/d2qi00697a

---