Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic order in a metal thiocyanate perovskite-analogue†
Matthew J.
Cliffe
 *a,
Oscar
Fabelo
bc and
Laura
Cañadillas-Delgado
b
*a,
Oscar
Fabelo
bc and
Laura
Cañadillas-Delgado
b
aSchool of Chemistry, University Park, Nottingham, NG7 2RD, UK. E-mail: matthew.cliffe@nottingham.ac.uk
bInstitut Laue-Langevin, 6 rue Jules Horowitz, BP 156, 38042 Grenoble Cedex 9, France
cDepartamento de Física, Universidad de La Laguna, Avda. Astrofísico Fco. Sánchez s/n, 38204 La Laguna, Tenerife, Spain
First published on 23rd June 2022
Abstract
Metal thiocyanate perovskite-analogues are a growing class of materials, but although they contain paramagnetic cations there have been no reports of their magnetic properties. Due to the large separations between the paramagnetic cations, with a shortest through-bond distance of 15.1 Å, these materials might be expected to be good examples of paramagnets. In this communication we investigate the magnetic properties of a metal thiocyanate framework Cr[Bi(SCN)6]·xH2O. We find that Cr[Bi(SCN)6]·xH2O undergoes long-range magnetic order at TN = 4.0(2) K. We use neutron powder diffraction to determine that Cr[Bi(SCN)6]·xH2O has a MnO-type {111}cubic-ordering as its ground state, consistent with frustrated nearest- and next-nearest-neighbour antiferromagnetic interactions. This suggests that appropriate design of metal thiocyanate perovskite-analogue structures may reveal a rich vein of frustrated magnetism.
Molecule-based perovskite-analogues, framework compounds built from corner-sharing octahedra with a general formula AxMX3 where at least one of A, M or X is a molecular ion, offer a diverse range of new chemistries and functionality to the solid state scientist.1,2 In particular, including molecular components generates additional degrees of freedom, which permits orderings impossible in conventional atomic analogues—for example, ordering of the electric dipole of MeNH3+ as an A-site guest can generate electrical polarisation.3,4 This polar ordering could, if combined with magnetic order generated by M-site cations, generate multiferroic materials possessing simultaneous electric and magnetic order.3,5 The magnetism of molecule-based perovskites has therefore been intensively investigated, particularly focussing on metal formates due to the diversity of A-site ammonium and M-site transition metal cations which can be incorporated. A wide range of magnetic formates have now been investigated, with particular excitement found in the wide-range of non-collinear magnets, including the perovskite A[M(CHOO)3]6–8 and niccolite mixed-metal formates A {M[M′(CHOO)6]}.9–11
A major challenge for molecular magnetism has been the weakness of the magnetic interactions between paramagnetic ions, especially compared to the pure elements and simple oxides, where strong exchange can be produced through direct overlap of the magnetic orbitals, or a single intervening anion. Developing our understanding of how crystal chemistry determines magnetic interactions will aid us realising both in producing practical magnetism, and, critically, in targeting exotic magnetic phases requiring careful balance of interactions. The cyanide Prussian Blue analogues provide an outstanding example of how crystal engineering can be used to optimise magnetic properties, with the enhancement of magnetic Curie temperatures TC from 5.6(1) K for Prussian Blue itself, Fe4[Fe(CN)6]3·xH2O,13 up to 376 K, KV[Cr(CN)6].14
Thiocyanate as a pseudohalide ligand is well-known for its optical properties,12,15 but control over its magnetism is much less developed, with most focus either on either the two dimensional pseudobinaries16–19 or frameworks incorporating additional organic coligands.17,20–22 Recently, some of us showed that the magnetism of the layered pseudobinary M(NCS)2, M = Cu, Ni, Co, Fe and Mn, can be qualitatively explained on the basis of changing orbital occupation and size, leading to enhancement of interactions and uncovering layered antiferromagnetism.18,19 Three dimensionally connected, perovskite-analogue structured materials would be of particular interest as magnets, but thus far no frameworks containing only paramagnetic metals on the M-site has been synthesised, as the sulfur terminus requires a softer metal such as Cd2+,23 Bi3+,12 or Pt4+,24 leading to the “double perovskite” structure. These sulfur-bonding metals are all diamagnetic, which suggests that the paramagnetic ions in thiocyanate Prussian Blue analogues would be magnetically isolated. However, were these paramagnetic metal ions to be magnetically connected through superexchange pathways, these frameworks would be examples of magnets with the J1 − J2 face-centered cubic model [Fig. 1(b)], which is both the source of exotic frustrated states,25,26 and shared by both rock-salt structured oxides27,28 and double perovskites.29–31
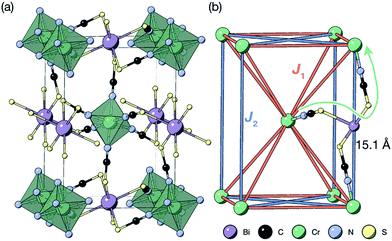 | ||
| Fig. 1 (a) Crystal structure of the Cr[Bi(SCN)6] framework. Disordered guest water omitted for clarity.12 (b) The structure showing only the magnetic Cr3+ ions and the nearest- (J1) and next-nearest-neighbour (J2) superexchange pathways, together with the through-bond distance. | ||
Here, we report the magnetic properties of a metal double-perovskite framework, Cr[Bi(SCN)6]·xH2O [Fig. 1], using a combination of bulk magnetometry and neutron powder diffraction. We show that despite the large distances (>8 Å) between paramagnetic ions, there is significant superexchange coupling between these ions: indeed, we find that it has long-range magnetic order below 4.0(2) K. We then go on to solve the magnetic structure of Cr[Bi(SCN)6]·xH2O, demonstrating that it orders with ferromagnetically correlated close-packed {111}cubic type planes, antiferromagnetically coupled, like MnO.27,32 This finding suggests that by using the extensive range of chemistry available in perovskite-analogue metal thiocyanates we could tune the magnetic interactions to realise exotic quantum states.
A multigram sample of Cr[Bi(SCN)6]·xH2O was prepared via solution precipitation, in which an aqueous solution of K3Cr(NCS)6·4H2O (5.89 g, 10 mmol) was added to a solution of Bi(NO3)3·5H2O (4.85 g, 10 mmol) in 2 M HNO3, stirred for 2 hours, filtered, washed with water and dried.12 We confirmed the structure of this compound using powder diffraction, and from the lattice parameters we determined that this sample was hydrated (x ≈ 1) [ESI† Fig. S3].12 We measured the magnetisation in a 100 Oe applied field using an MPMS-3 magnetometer on warming from a sample cooled in zero field, calculating the susceptibility using the small field approximation.
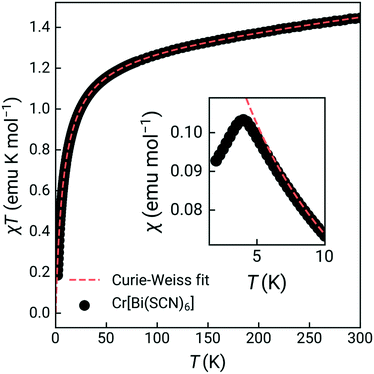
The susceptibility showed a sharp cusp at 4.0 K and Curie Weiss fitting to the high temperature susceptibility (20–300 K, including a temperature independent paramagnetism term) gave a Weiss temperature, θ, of −7.8(2) K, and an effective moment of 3.27(0.06) μB, reduced from the spin-only value of 3.87 μB [Fig. 2]. Isothermal magnetisation measurements at 2 K and 5 K showed no evidence of hysteresis, with a field-induced transition at around 1.4(1) T observed in the data measured at 2 K [ESI† Fig. S4 and S5]. Together, this suggests that Cr[Bi(SCN)6]·H2O is an antiferromagnet, with mildly frustrated ratio of f = |θ|/TN = 1.9.
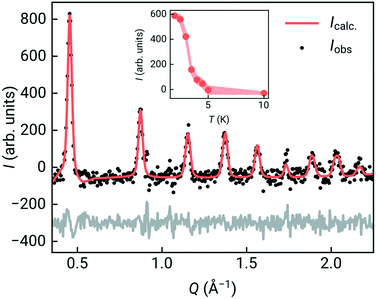
To confirm that the ground state was indeed long-range magnetic antiferromagnetic order, we carried constant wavelength powder neutron diffraction measurements on the high-intensity medium resolution D1B diffractometer at ILL, Grenoble [Fig. 3, ESI† S1 and S2].33 The incident wavelength was λ = 2.52 Å and the scattering was measured over an angular range of 2 < 2θ < 128°. We measured high quality long-acquisition time diffraction patterns at 10 K and 2 K, supplemented by shorter measurements at intermediate temperatures of 5, 4.5, 4, 3.5, 3 and 2.5 K. By subtracting the 10 K dataset from the lower temperature data we were able to confirm that additional magnetic Bragg peaks emerged between 4 and 4.5 K [Fig. 3], demonstrating that the cusp identified in bulk magnetic susceptibility was due to antiferromagnetic order. We first refined the structural model against the previously determined room temperature structure in space group P21/n of Cr[Bi(SCN)6]·xH2O to determine the overall scale and unit cell parameters using the Rietveld method and the FullProf software suite, giving a = 8.3312(16) Å, b = 8.3805(17) Å, c = 11.9723(15) Å, β = 90.30(3)° [ESI† Fig. S2].34
We began our determination of the magnetic structure by indexing the additional magnetic reflections with reference to the pseudocubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m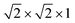 supercell, because the magnetic lattice has near-cubic metrical symmetry: sin
supercell, because the magnetic lattice has near-cubic metrical symmetry: sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = 5 × 10−6,
β = 5 × 10−6, 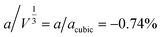 , b/acubic = −0.09%, c/acubic = +0.84%. This gave us a propagation vector of
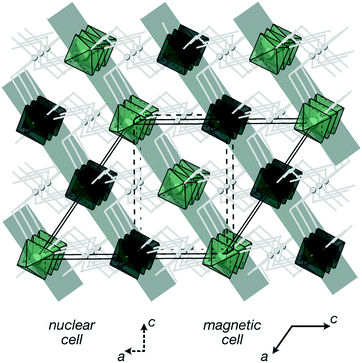
, b/acubic = −0.09%, c/acubic = +0.84%. This gave us a propagation vector of 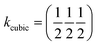 . This will correspond, for a simple collinear antiferromagnet, to ferromagnetically correlated close packed {111}cubic planes coupled antiferromagnetically. However, accounting for the true monoclinic P21/n symmetry of the nuclear structure splits this pseudocubic propagation vector into two inequivalent propagation vectors:
. This will correspond, for a simple collinear antiferromagnet, to ferromagnetically correlated close packed {111}cubic planes coupled antiferromagnetically. However, accounting for the true monoclinic P21/n symmetry of the nuclear structure splits this pseudocubic propagation vector into two inequivalent propagation vectors: 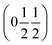 and
and 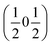 , the E and Y points on the Brillouin zone boundary, respectively. This reflects the fact the {111}cubic-type close-packed planes are symmetry- and chemically-distinct in this material. Using the k-search program included in the FullProf suite34 to quantitatively assess the propagation vectors revealed both the
, the E and Y points on the Brillouin zone boundary, respectively. This reflects the fact the {111}cubic-type close-packed planes are symmetry- and chemically-distinct in this material. Using the k-search program included in the FullProf suite34 to quantitatively assess the propagation vectors revealed both the 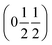 and
and 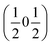 vectors, with a slightly better fit for
vectors, with a slightly better fit for 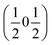 , Y, than
, Y, than 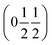 , E, (figure of merit = 0.37 vs. 0.82).
, E, (figure of merit = 0.37 vs. 0.82).
Using the ISODISTORT tool from the ISOTROPY software suite,35 we were able to identify the three distinct possible irreducible representations (irreps) consistent with this family of propagation vectors that produce a non-zero magnetic moment: mE1 + E2, mY1 and mY2 (Miller and Love notation).36 These three models correspond to the magnetic spaces groups PS![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (mE1 + E2) and Pc21/n (mY1, mY2). We were able to achieve a good Rietveld refinement fit to models for all three of these structures, in each case leading to structure consisting approximately of ferromagnetically correlated {111}cubic layers antiferromagnetically coupled. These structures are nearly collinear with moments lying nearly within the {111}cubic plane with small tilts of the moments away from the primary axis (ca. 6°), though the high degree of pseudosymmetry meant our determination of the relative angles of the moment is not completely unambiguous. We were able to refine the magnitude of the Cr3+ giving M = 2.45(20) μB, which is approximately 80% of the anticipated spin-only value. This small deviation is likely explained by the combination of some covalency and comparatively high scaled measurement temperature (T/TN = 0.5). The main difference between the models was which of the four {111}cubic type planes the spins ordered ferromagnetically within: the mY models ordered in the (1
(mE1 + E2) and Pc21/n (mY1, mY2). We were able to achieve a good Rietveld refinement fit to models for all three of these structures, in each case leading to structure consisting approximately of ferromagnetically correlated {111}cubic layers antiferromagnetically coupled. These structures are nearly collinear with moments lying nearly within the {111}cubic plane with small tilts of the moments away from the primary axis (ca. 6°), though the high degree of pseudosymmetry meant our determination of the relative angles of the moment is not completely unambiguous. We were able to refine the magnitude of the Cr3+ giving M = 2.45(20) μB, which is approximately 80% of the anticipated spin-only value. This small deviation is likely explained by the combination of some covalency and comparatively high scaled measurement temperature (T/TN = 0.5). The main difference between the models was which of the four {111}cubic type planes the spins ordered ferromagnetically within: the mY models ordered in the (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1)cubic or (10
1)cubic or (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) planes and the mE1 + E2 model ordered in the (11
) planes and the mE1 + E2 model ordered in the (11![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )cubic or (01
)cubic or (01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) planes. We found that the mY1 model fitted the data best and as the mE1 + E2 is in addition a lower symmetry triclinic structure with two symmetry independent moments, we therefore think the mY1 model is likely to be correct structure [Fig. 4]. Single crystal neutron diffraction data would allow for completely unambiguous determination of the magnetic structure but as yet single crystals of sufficient size are unavailable.
) planes. We found that the mY1 model fitted the data best and as the mE1 + E2 is in addition a lower symmetry triclinic structure with two symmetry independent moments, we therefore think the mY1 model is likely to be correct structure [Fig. 4]. Single crystal neutron diffraction data would allow for completely unambiguous determination of the magnetic structure but as yet single crystals of sufficient size are unavailable.
The most striking feature of this order is that it occurs at such accessible temperatures. The shortest through space distance between Cr atoms is d = 8.32 Å, and the shortest through-bond distance is d = 15.1 Å, and occurs through 8-bond superexchange, Cr–N–C–S–Bi–S–C–N–Cr. This can be compared to the iron cyanide Prussian Blue, which orders ferromagnetically at 5.6(1) K13 with the magnetic Fe3+ ions separated by 7.2 Å, where magnetic superexchange occurs through a six-bond Fe3+–N–C–Fe2+–C–N–Fe3+ pathway 10.2 Å long. In Prussian Blue, charge and spin delocalisation onto Fe2+ (approximately 5% of an electron) through a mixed-valence mechanism are critical to the generation of long-range order.37,38 Mixed valency is not likely in this case as the adjacent oxidation states for both Cr and Bi are not easily accessible, and the antiferromagnetic interactions we observe rule out the ferromagnetic ‘double exchange’ found in Prussian Blue. On possible explanation would be facilitation of this comparatively strong superexchange through the accessible NCS redox states—as can be see in the relatively dispersive conduction band in our previously reported DFT band-structure calculations of Cr[Bi(SCN)6].12
The importance of effective superexchange can be seen by comparison to paramagnetic salts of Cr3+, e.g. [Cr(CN)6][Co(NH3)6], where |θ| < 0.05 K and dCr–Cr = 7.4 Å.39 These comparisons also allow us to eliminate through-space dipolar coupling as a significant contributor to the observed order. Indeed, even in molecular cluster nanomagnets with similar magnet–magnet spacing but much larger total spin it is clear that superexchange rather than dipolar order drives the transition to magnetic long-range order, e.g. the S = 35/2 [Fe19 (metheidi)10(OH)14O6(H2O)12]NO3·24H2O has a shortest Fe–Fe distance of 8.3 Å and orders at 1.2 K due to superexchange interactions.40
The Cr ions form a face-centered cubic lattice, with only small chemical differences between different crystallographic directions. The interactions are likely to be primarily through-bond rather than through space, and as such the nearest neighbour (J1) and next nearest neighbour (J2) interactions are likely to be comparable in magnitude [Fig. 1(b)]. This is directly analogous to what has been found in both rocksalt transition metal monoxides, e.g. the canonical MnO,27,32 and the oxide double perovskites.29 The {111}cubic AFM order observed (Type II) occurs for J2 > 0.5J1 for an ideal J1 − J2 face-centered cubic magnet with antiferromagnetic interactions. The combination of this with the observed mild frustration, |θ|/TN = 1.9, and the presumed weakness of both further-neighbour superexchange (due to the long distances) and of non-Heisenberg effects due to the Cr3+ ion presence suggests that suggests that J2 < J1, and thus that a small (20%) reduction in J1/J2 might induce a transition into a highly frustrated state.41,42 Like other perovskites, Cr[Bi(SCN)6] has a wide-range of potential chemical possibilities for tuning its magnetic function: not only through substitution of the magnetic Cr,12 but also of the non-magnetic Bi,23,24 and the anionic ligand43 or the inclusion of A-site cations.44 This, together with the moderate exchange strength found in this material, comparable with the Zeeman splitting accessible through superconducting magnets, suggests that NCS double pervoskites are ideal platforms to engineer the complex, chiral, multi-k magnetic orderings of current interest for their potential use in magnetic computation.26,45
Author contributions
M. J. C. synthesized the samples. M. J. C., O. F., and L. C. D. carried out the neutron diffraction experiment and analysed the neutron diffraction data. M. J. C. carried out and analysed the bulk magnetic measurements. M. J. C. wrote the paper, with input from all other authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. J. C. acknowledges the School of Chemistry, University of Nottingham for support from Hobday bequest. O. F. acknowledges the Spanish Ministry of Universities (UNI/551/2021) and the European Union through the Funds Next Generation. We acknowledge the ILL for beamtime under proposal number 5-31-2676. Data are available at ILL DOI and at Nottingham DOI. Magnetic measurements were carried out in part using the Advanced Materials Characterisation Suite, funded by EPSRC Strategic Equipment Grant EP/M000524/1.Notes and references
- W. Li, Z. Wang, F. Deschler, S. Gao, R. H. Friend and A. K. Cheetham, Nat. Rev. Mater., 2017, 2, 16099 CrossRef.
- H. A. Evans, Y. Wu, R. Seshadri and A. K. Cheetham, Nat. Rev. Mater., 2020, 5, 196–213 CrossRef CAS.
- D.-W. Fu, W. Zhang, H.-L. Cai, Y. Zhang, J.-Z. Ge, R.-G. Xiong, S. D. Huang and T. Nakamura, Angew. Chem., Int. Ed., 2011, 50, 11947–11951 CrossRef CAS PubMed.
- H. L. B. Boström, M. S. Senn and A. L. Goodwin, Nat. Commun., 2018, 9, 2380 CrossRef PubMed.
- M. S. Senn and N. C. Bristowe, Acta Crystallogr., Sect. A: Found. Adv., 2018, 74, 308–321 CrossRef CAS PubMed.
- X.-Y. Wang, L. Gan, S.-W. Zhang and S. Gao, Inorg. Chem., 2004, 43, 4615–4625 CrossRef CAS PubMed.
- Z. Wang, B. Zhang, T. Otsuka, K. Inoue, H. Kobayashi and M. Kurmoo, Dalton Trans., 2004, 2209–2216 RSC.
- L. Cañadillas-Delgado, L. Mazzuca, O. Fabelo, J. Rodríguez-Carvajal and V. Petricek, Inorg. Chem., 2020, 59, 17896–17905 CrossRef.
- L. Mazzuca, L. Cañadillas-Delgado, J. A. Rodríguez-Velamazán, O. Fabelo, M. Scarrozza, A. Stroppa, S. Picozzi, J.-P. Zhao, X.-H. Bu and J. Rodríguez-Carvajal, Inorg. Chem., 2017, 56, 197–207 CrossRef CAS PubMed.
- K. S. Hagen, S. G. Naik, B. H. Huynh, A. Masello and G. Christou, J. Am. Chem. Soc., 2009, 131, 7516–7517 CrossRef CAS PubMed.
- L. Cañadillas-Delgado, O. Fabelo, J. A. Rodríguez-Velamazán, M. H. Lemée-Cailleau, S. A. Mason, E. Pardo, F. Lloret, J. P. Zhao, X. H. Bu, V. Simonet, C. V. Colin and J. Rodríguez-Carvajal, J. Am. Chem. Soc., 2012, 134, 19772–19781 CrossRef PubMed.
- M. J. Cliffe, E. N. Keyzer, M. T. Dunstan, S. Ahmad, M. F. L. De Volder, F. Deschler, A. J. Morris and C. P. Grey, Chem. Sci., 2019, 10, 793–801 RSC.
- F. Herren, P. Fischer, A. Ludi and W. Haelg, Inorg. Chem., 1980, 19, 956–959 CrossRef CAS.
- M. Verdaguer and G. S. Girolami, in Magnetism: Molecules to Materials V, ed. J. S. Miller and M. Drillon, WILEY-VCH Verlag, Weinheim, 2005, vol. 36, pp. 283–346 Search PubMed.
- J. J. Berzelius, Lehrbuch der Chemie, 1826, vol. 2, p. 771 Search PubMed.
- G. C. DeFotis, K. D. Dell, D. J. Krovich and W. W. Brubaker, J. Appl. Phys., 1993, 73, 5386–5388 CrossRef CAS.
- E. Shurdha, S. H. Lapidus, P. W. Stephens, C. E. Moore, A. L. Rheingold and J. S. Miller, Inorg. Chem., 2012, 51, 9655–9665 CrossRef CAS PubMed.
- M. J. Cliffe, J. Lee, J. A. M. Paddison, S. Schott, P. Mukherjee, M. W. Gaultois, P. Manuel, H. Sirringhaus, S. E. Dutton and C. P. Grey, Phys. Rev. B, 2018, 97, 144421 CrossRef CAS.
- E. N. Bassey, J. A. M. Paddison, E. N. Keyzer, J. Lee, P. Manuel, I. da Silva, S. E. Dutton, C. P. Grey and M. J. Cliffe, Inorg. Chem., 2020, 59, 11627–116339 CrossRef CAS PubMed.
- J. Werner, Z. Tomkowicz, T. Reinert and C. Näther, Eur. J. Inorg. Chem., 2015, 2015, 3066–3075 CrossRef CAS.
- S. Baran, A. Hoser, M. Rams, S. Ostrovsky, T. Neumann, C. Näther and Z. Tomkowicz, J. Phys. Chem. Solids, 2019, 130, 290–297 CrossRef CAS.
- E. Shurdha, C. E. Moore, A. L. Rheingold, S. H. Lapidus, P. W. Stephens, A. M. Arif and J. S. Miller, Inorg. Chem., 2013, 52, 10583–10594 CrossRef CAS PubMed.
- K.-P. Xie, W.-J. Xu, C.-T. He, B. Huang, Z.-Y. Du, Y.-J. Su, W.-X. Zhang and X.-M. Chen, CrystEngComm, 2016, 18, 4495–4498 RSC.
- H. Tabe, M. Matsushima, R. Tanaka and Y. Yamada, Dalton Trans., 2019, 48, 17063–17069 RSC.
- M. V. Gvozdikova and M. E. Zhitomirsky, JETP Lett., 2005, 81, 236–240 CrossRef CAS.
- P. Balla, Y. Iqbal and K. Penc, Phys. Rev. Res., 2020, 2, 043278 CrossRef CAS.
- A. L. Goodwin, M. G. Tucker, M. T. Dove and D. A. Keen, Phys. Rev. Lett., 2006, 96, 047209 CrossRef PubMed.
- L. Timm, M. G. Tucker, D. A. Keen, P. M. M. Thygesen, P. J. Saines and A. L. Goodwin, Phys. Scr., 2016, 91, 114004 CrossRef.
- C. R. Wiebe, J. E. Greedan, P. P. Kyriakou, G. M. Luke, J. S. Gardner, A. Fukaya, I. M. Gat-Malureanu, P. L. Russo, A. T. Savici and Y. J. Uemura, Phys. Rev. B, 2003, 68, 134410 CrossRef.
- O. H. J. Mustonen, C. E. Pughe, H. C. Walker, H. M. Mutch, G. B. G. Stenning, F. C. Coomer and E. J. Cussen, Chem. Mater., 2020, 32, 7070–7079 CrossRef CAS.
- S. Kanungo, B. Yan, C. Felser and M. Jansen, Phys. Rev. B, 2016, 93, 161116 CrossRef.
- C. G. Shull and J. S. Smart, Phys. Rev., 1949, 76, 1256–1257 CrossRef.
- I. P. Orench, J. F. Clergeau, S. Martínez, M. Olmos, O. Fabelo and J. Campo, J. Phys.: Conf. Ser., 2014, 549, 012003 CrossRef.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef.
- H. T. Stokes, D. M. Hatch and B. J. Campbell, ISOTROPY Software Suite.
- A. P. Cracknell, B. L. Davies, S. C. Miller and W. F. Love, Kronecker Product Tables, Plenum, New York, 1979, vol. 1 Search PubMed.
- B. Mayoh and P. Day, J. Chem. Soc., Dalton Trans., 1976, 1483–1486 RSC.
- P. Day, F. Herren, A. Ludi, H. U. Güdel, F. Hulliger and D. Givord, Helv. Chim. Acta, 2007, 63, 148–153 CrossRef.
- R. L. Carlin, R. Burriel, J. Pons and J. Casabo, Inorg. Chem., 1983, 22, 2832–2836 CrossRef CAS.
- F. L. Pratt, T. Guidi, P. Manuel, C. E. Anson, J. Tang, S. J. Blundell and A. K. Powell, Magnetochemistry, 2021, 7, 74 CrossRef CAS.
- Y. Yamamoto and T. Nagamiya, J. Phys. Soc. Jpn., 1972, 32, 1248–1261 CrossRef CAS.
- N.-N. Sun and H.-Y. Wang, J. Magn. Magn. Mater., 2018, 454, 176–184 CrossRef CAS.
- T. Neumann, M. Rams, Z. Tomkowicz, I. Jess and C. Näther, Chem. Commun., 2019, 55, 2652–2655 RSC.
- J. Y. Lee, S. Ling, S. P. Argent, M. S. Senn, L. Cañadillas-Delgado and M. J. Cliffe, Chem. Sci., 2021, 12, 3516–3525 RSC.
- S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii and P. Böni, Science, 2009, 323, 915–919 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Structural Rietveld refinements, infrared spectrum, isothermal magnetisation measurements and magnetic CIF files at https://doi.org/10.1039/d2ce00649a. ILL raw data available at https://doi.org/10.5291/ILL-DATA.5-31-2676. Additional raw data and analysis scripts available at https://doi.org/10.17639/nott.7224. |
| This journal is © The Royal Society of Chemistry 2022 |