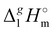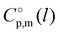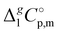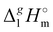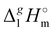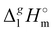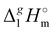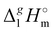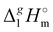Determination of the dispersion forces in the gas phase structures of ionic liquids using exclusively thermodynamic methods†
Received
16th October 2020
, Accepted 4th March 2021
First published on 9th March 2021
Abstract
Ionic liquids are described by a delicate balance of Coulomb interaction, hydrogen bonding and dispersion forces. Dissecting the different types of interactions from thermodynamic properties is still a challenge. Here, we show that comparison of vaporization enthalpies of tetra-alkyl-ammonium ionic liquids with bis(trifluoromethylsulfonyl)imide [NTf2]− anions and the related molecular liquids, trialkylamines, allows for determining dispersion interactions in the gas phase ion-pairs. For this purpose, we measured vapor pressures and vaporization enthalpies of these ionic and molecular liquids by using a quartz-crystal microbalance. For supporting these data, we determined the vaporization enthalpies additionally from experimental activity coefficients at infinite dilution. Characteristic alkyl chain length dependences of the vaporization enthalpies have been established and were used for quantifying the dispersion forces in the gas phase species. The dissected dispersion contributions suggest that the alkyl chains do not show star-like topologies but embrace the anion maximizing the dispersion interactions. For the longest alkyl chains with eight carbon atoms, the dispersion interaction is as strong as two and a half hydrogen bonds. The proportion of dispersion in the gas phase species depending on the number of methylene groups in the ammonium cations is strongly supported by quantum chemical calculations.
1. Introduction
Ionic liquids (ILs) bearing the tetra-alkyl-ammonium cation belong to the most common class of neoteric solvents. These ILs are air and water stable, and are easy to prepare from cheap amines.1 However, tetraalkylammonium based ILs have been less studied in comparison with ionic liquids based on the 1-alkyl-3-methylimidazolium cation.2 Experimental and theoretical investigations of structure-(thermodynamic) property relationships for imidazolium and ammonium based ionic liquids in combination with conventional thermodynamic methods3–7 as well as with help of the spectroscopic far-infrared measurements8,9 are some of the longstanding goals of our laboratory. In the focus of this work is an extended thermochemical study of vapor pressures and vaporization enthalpies of tetraalkylammonium based ILs (see Fig. 1).
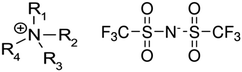 |
| | Fig. 1 Structures of cations and anions used in the present investigation: tetra-alkyl-ammonium cation based ILs (left) and the bis[(trifluoromethyl)sulfonyl]imide = [NTf2]− anion (right). | |
The textbook axiom that “function follows structure” is one of the most fundamental in science and technology. It is well established, especially in chemistry, that the properties and performance of a molecule follow from its structure. Whilst it is apparent that the structure of a molecule should contain the features responsible for its physical–chemical, thermodynamic, etc. properties, it is less obvious that these features can be discerned in any simple way.
The simplest manifestation of the structure–property relationships is the boiling temperatures’ chain-length dependence in the homologous series of n-alkanes. Consequently, the standard molar vaporization enthalpies, 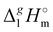 (298.15 K), of n-alkanes monotonically grow with the increasing chain-length (see Fig. 2a). Such a behavior is common with molecular compounds. And what about ionic compounds? Surprisingly, not so long ago there was a lot of controversy over this question.10 However, it is already known today that the vaporization enthalpies of aprotic ionic liquids also have the linear chain length dependencies (with the exception of a few special cases caused by a possible nanostructuring of ILs with long alkyl chains bounded to the cation).10,11 An example of such an impeccable linear dependence for 1-methyl-3-alkyl-imidazolium based ILs with the [NTf2] anion is shown in Fig. 2a.
(298.15 K), of n-alkanes monotonically grow with the increasing chain-length (see Fig. 2a). Such a behavior is common with molecular compounds. And what about ionic compounds? Surprisingly, not so long ago there was a lot of controversy over this question.10 However, it is already known today that the vaporization enthalpies of aprotic ionic liquids also have the linear chain length dependencies (with the exception of a few special cases caused by a possible nanostructuring of ILs with long alkyl chains bounded to the cation).10,11 An example of such an impeccable linear dependence for 1-methyl-3-alkyl-imidazolium based ILs with the [NTf2] anion is shown in Fig. 2a.
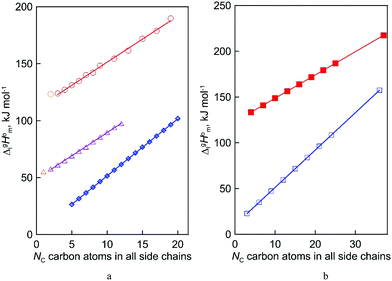 |
| | Fig. 2 Vaporization enthalpies’ at 298 K (in kJ mol−1) chain-length dependences of molecular and ionic compounds: (a) alkanes (opened diamonds,  ),12,13 alkyl-imidazoles (opened triangles, ),12,13 alkyl-imidazoles (opened triangles,  )14 and 1-methyl-3-alkyl-imidazolium based ILs (opened circles, )14 and 1-methyl-3-alkyl-imidazolium based ILs (opened circles,  );10 (b) trialkylamines15 (opened squares, );10 (b) trialkylamines15 (opened squares,  ) and tetraalkylammonium based ILs from this work (solid squares, ) and tetraalkylammonium based ILs from this work (solid squares,  ). ). | |
Coming back to the structure–property behavior of the tetraalkylammonium based ILs studied in this work, we also observe (see Fig. 2b) the already anticipated straight line as a function of the chain lengths of the enthalpy of vaporization. From this viewpoint, we should consider the results as expected and less spectacular. However, in comparison with similarly shaped ionic and molecular species and their homologous series, this observation becomes interesting. For example, for the ionic series of 1-methyl-3-alkyl-imidazolium based ILs, the similarly shaped molecular homologous series is the series of n-alkylimidazoles (see Fig. 2a).
What is interesting about the comparison of the enthalpies of vaporization in these two series? In Fig. 3, we show the differences between 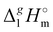 (298.15 K)-values for these ionic and the corresponding molecular compounds. As can be seen in Fig. 3, nothing surprising can be observed for the pairs 1-methyl-3-alkyl-imidazolium based ILs and alkyl-imidazoles, namely the differences between
(298.15 K)-values for these ionic and the corresponding molecular compounds. As can be seen in Fig. 3, nothing surprising can be observed for the pairs 1-methyl-3-alkyl-imidazolium based ILs and alkyl-imidazoles, namely the differences between 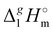 (298.15 K)-values are decreasing insignificantly with the elongation of the alkyl chain. This decrease could be understood from the competition between the corresponding van der Waals and Coulomb interactions.10 Indeed, according to Köddermann et al.,16 the Coulomb energy contribution remains unchanged as the length of the alkyl chains increases beyond n = 2. Consistent with the findings of Köddermann et al.,16 we also found experimentally that the increase in the enthalpy of vaporization for the [Cnmim][NTf2] series with increasing chain length arises completely from van der Waals interactions, which are the dominant driving force of the vaporization process.10 The finding that the
(298.15 K)-values are decreasing insignificantly with the elongation of the alkyl chain. This decrease could be understood from the competition between the corresponding van der Waals and Coulomb interactions.10 Indeed, according to Köddermann et al.,16 the Coulomb energy contribution remains unchanged as the length of the alkyl chains increases beyond n = 2. Consistent with the findings of Köddermann et al.,16 we also found experimentally that the increase in the enthalpy of vaporization for the [Cnmim][NTf2] series with increasing chain length arises completely from van der Waals interactions, which are the dominant driving force of the vaporization process.10 The finding that the 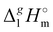 (298.15 K)-differences between pairs 1-methyl-3-alkyl-imidazolium based ILs and alkyl-imidazoles are hardly chain-length dependent can be seen as evidence that the van der Waals interactions in the ionic and molecular series are very similar even quantitatively. With this in mind, we now study the tetraalkylammonium based ILs (see Fig. 3), which are in the focus of the present work.
(298.15 K)-differences between pairs 1-methyl-3-alkyl-imidazolium based ILs and alkyl-imidazoles are hardly chain-length dependent can be seen as evidence that the van der Waals interactions in the ionic and molecular series are very similar even quantitatively. With this in mind, we now study the tetraalkylammonium based ILs (see Fig. 3), which are in the focus of the present work.
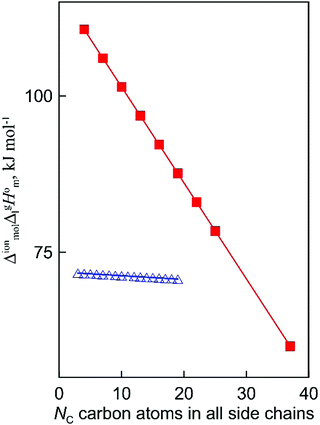 |
| | Fig. 3 Differences (in kJ mol−1) between the 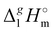 (298.15 K)-values for the ionic and molecular compounds. 1-Methyl-3-alkyl-imidazolium based ILs10 and alkyl-imidazoles14 (opened triangles, (298.15 K)-values for the ionic and molecular compounds. 1-Methyl-3-alkyl-imidazolium based ILs10 and alkyl-imidazoles14 (opened triangles,  ); tetraalkylammonium based ILs from this work and trialkylamines15 (solid squares, ); tetraalkylammonium based ILs from this work and trialkylamines15 (solid squares,  ). ). | |
In Fig. 3, we also show the differences between 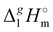 (298.15 K)-values of tetraalkylammonium based ionic liquids and the corresponding molecular tri-alkylamines. As can be seen in Fig. 3, the spectacular decrease of the
(298.15 K)-values of tetraalkylammonium based ionic liquids and the corresponding molecular tri-alkylamines. As can be seen in Fig. 3, the spectacular decrease of the 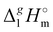 (298.15 K)-differences is observed for these pairs with the growing of the alkyl chain. What about the competition between the van der Waals and Coulomb interactions in these tetraalkylammonium-based ILs? We will address this question in the following way. First, we measure the vapor pressures and determine the molar enthalpies of vaporization by using the Quartz Crystal Microbalance (QCM) method. For consistency, we also “indirectly” determined the vaporization enthalpies with the complementary Gas Chromatography (GC) method based on measuring activity coefficients at infinite dilution of volatile solutes in these ILs. The obtained vaporization enthalpies were then related to experimental surface tensions from the literature for checking the reliability of property–property relations. Thus, we were well prepared to dissect and quantify the dispersion interactions in these ILs, in particular for the gas phase species. Finally, the dispersion contributions were confirmed using density functional theory FT) calculations showing a linear correlation between the calculated and the dissected measured dispersion interactions. Overall, we show how valuable thermodynamics methods are for better understanding non-covalent interactions, here in ammonium-based ionic liquids.
(298.15 K)-differences is observed for these pairs with the growing of the alkyl chain. What about the competition between the van der Waals and Coulomb interactions in these tetraalkylammonium-based ILs? We will address this question in the following way. First, we measure the vapor pressures and determine the molar enthalpies of vaporization by using the Quartz Crystal Microbalance (QCM) method. For consistency, we also “indirectly” determined the vaporization enthalpies with the complementary Gas Chromatography (GC) method based on measuring activity coefficients at infinite dilution of volatile solutes in these ILs. The obtained vaporization enthalpies were then related to experimental surface tensions from the literature for checking the reliability of property–property relations. Thus, we were well prepared to dissect and quantify the dispersion interactions in these ILs, in particular for the gas phase species. Finally, the dispersion contributions were confirmed using density functional theory FT) calculations showing a linear correlation between the calculated and the dissected measured dispersion interactions. Overall, we show how valuable thermodynamics methods are for better understanding non-covalent interactions, here in ammonium-based ionic liquids.
2. Experimental section
2.1 Materials
All samples of the [N(R)4][NTf2] ionic liquids were of commercial origin with ≥99% purity. Prior to vaporization experiments, samples were subjected to vacuum evaporation at 333 K and 10−2 mbar for more than 24 h to reduce possible traces of solvents and moisture. Samples used in vaporization studies were additionally conditioned inside of the vacuum chamber at the highest temperature of experiments (see in Table S1 (ESI†) with the primary results of vaporization experiments) within 12 h. This additional purification allowed for removing residual traces of volatile impurities, as well as for collecting the amount of the vaporized IL required for the FTIR analysis.
2.2 Quartz crystal microbalance (QCM)
Vapor pressures and molar enthalpies of vaporization of the [N(R)4][NTf2] samples were determined using the QCM method (details were described elsewhere17). The experiment is based on the Langmuir evaporation of an IL sample from the open surface. The sample was placed in an open cavity inside of the thermostatted block and exposed to vacuum (10−5 Pa). The QCM-sensor is mounted directly above the IL surface. After a series of isothermal steps, a certain amount of sample is evaporated into a high vacuum and condensed on the quartz crystal surface. The change of the vibrational frequency Δf of the quartz crystal is recorded and converted to the absolute vapor pressures after calibration.18 More details are given in the ESI.† The primary experimental results are summarized in Table S1 (ESI†). No sign of decomposition processes of the IL under the given experimental conditions was observed as was proven by using ATR-IR spectroscopy. The residual amount of IL in the cavity, as well as the IL-deposit on QCM were then analyzed by ATR-IR spectroscopy. No changes in the spectra were detected as can be seen in Fig. S2–S7 (ESI†).
3. Results and discussion
3.1. Vaporization enthalpies at 298.15 K
3.1.2 Vaporization enthalpies at 298.15 K from solution thermodynamics.
The total absence of vaporization studies of the ammonium based ionic liquids has prompted an “indirect” determination of vaporization enthalpies for this series with the help of an independent and complementary gas chromatography (GC) method.20,21 The latter method is based on the experimental activity coefficient of infinite dilution γ∞1 of volatile solutes (typically alkanes and alkanols denoted with a subscript (1) in an ionic liquid ([NR4][NTf2] in this work, denoted with a subscript (2) available in the literature).3,22–25 The γ∞1-values are generally related to the total solubility parameters δ1 for solutes and δ2 for the IL (details are given in the ESI†). The total solubility parameter (δT) at a temperature T is further related to the vaporization enthalpy via the following equation:26,27| | 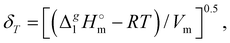 | (1) |
where 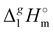 is the standard molar enthalpy of vaporization (of the solute or the solvent), R is the ideal gas constant, T is the temperature, and Vm is the molar volume (of the solute or the solvent). A simple re-arrangement of eqn (1) towards the total solubility parameter δ2 opens an independent method to derive vaporization enthalpy,
is the standard molar enthalpy of vaporization (of the solute or the solvent), R is the ideal gas constant, T is the temperature, and Vm is the molar volume (of the solute or the solvent). A simple re-arrangement of eqn (1) towards the total solubility parameter δ2 opens an independent method to derive vaporization enthalpy, 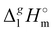 (298.15 K), of an IL using eqn (2):
(298.15 K), of an IL using eqn (2):| | 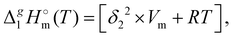 | (2) |
where all values, including Vm, are referenced to an arbitrary temperature T, which is 298.15 K in this work. We used experimental γ∞1-values for different solutes (see Tables S2–S9, ESI†) in [NR4][NTf2] available in the literature3,22–25 to obtain δ2-values (see details in the ESI†). The values 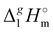 (298.15 K) were calculated from δ2 (see Table S10, ESI†). The results are in agreement within the experimental uncertainties of the QCM results (see Table 2). Such a good agreement provides more confidence to the QCM results on
(298.15 K) were calculated from δ2 (see Table S10, ESI†). The results are in agreement within the experimental uncertainties of the QCM results (see Table 2). Such a good agreement provides more confidence to the QCM results on 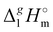 (298.15 K) and allows for a meaningful interpretation of these results at the molecular level.
(298.15 K) and allows for a meaningful interpretation of these results at the molecular level.
Table 2 Comparison of standard molar enthalpies of vaporization,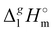 (298.15 K), of tetra-alkyl-ammonium ILs with the common anion [NTf2] derived from the QCM method at 298.15 K (in kJ mol−1)
(298.15 K), of tetra-alkyl-ammonium ILs with the common anion [NTf2] derived from the QCM method at 298.15 K (in kJ mol−1)
| Cation |
N
c
|
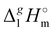
(exp)b |
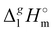
(GC)c |
Source of γ∞1-values |
N
C is the total number of C atom all alkyl chains attached to the central nitrogen atom.
From Table 1. Values in italic have been derived from the chain length dependence: 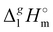 (298.15 K) = 2.545 × Nc + 123.2 (R2 = 0.976), derived from experimental vaporization enthalpies given in Table 1.
Estimated using γ∞1-values (see the text) (298.15 K) = 2.545 × Nc + 123.2 (R2 = 0.976), derived from experimental vaporization enthalpies given in Table 1.
Estimated using γ∞1-values (see the text)
|
| [N1114] |
7 |
143.7 ± 1.9 |
134.0 ± 5.2 |
3 |
| [N1116] |
9 |
146.1 ± 4.0 |
143.7 ± 4.2 |
22 |
| [N1118] |
11 |
151.2 ± 4.0 |
151.0 ± 3.7 |
23 |
| [N111,10] |
13 |
156.3 ± 4.0 |
158.3 ± 3.8 |
23 |
| [N1444] |
13 |
152.1 ± 2.7 |
157.7 ± 5.1 |
23 |
| [N2228] |
14 |
156.8 ± 3.2 |
157.0 ± 4.4 |
24 |
| [N1888] |
25 |
192 ± 6 |
208 ± 8 |
25 |
| [N8888] |
32 |
205 ± 6 |
212 ± 8 |
23 |
3.2 Structure–property and property–property correlations of vaporization enthalpies
3.2.1 Chain-length dependence.
Correlation of 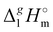 (298.15 K)-values with the number of C-atoms in the alkyl chain within the homologues series of molecular and ionic compounds is a valuable tool to study structure–property relationships. For instance, for the series [Cnmim][NTf2], the dependence of vaporization enthalpy on the number of C-atoms, n, in the alkyl chain (with n = 2–18) attached to the 3 position of the 1-methyimidazolium cation follows the linear equation:10
(298.15 K)-values with the number of C-atoms in the alkyl chain within the homologues series of molecular and ionic compounds is a valuable tool to study structure–property relationships. For instance, for the series [Cnmim][NTf2], the dependence of vaporization enthalpy on the number of C-atoms, n, in the alkyl chain (with n = 2–18) attached to the 3 position of the 1-methyimidazolium cation follows the linear equation:10| | 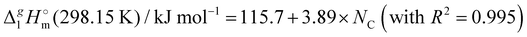 | (3) |
We also correlated the 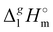 (298.15 K)-values for [N(R)4][NTf2] ionic liquids evaluated in Table 1 with the total number of C atoms, Nc, in all alkyl chains attached to the central nitrogen atom:
(298.15 K)-values for [N(R)4][NTf2] ionic liquids evaluated in Table 1 with the total number of C atoms, Nc, in all alkyl chains attached to the central nitrogen atom:
| | 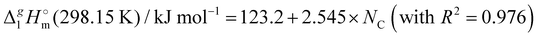 | (4) |
The high correlation coefficient R2 is an evidence of a good consistency of experimental data approximated using eqn (4). However, it is obvious from comparison of eqn (3) and (4) that slopes of the considered linear dependencies are significantly different. The slope of the vaporization enthalpy chain-length dependence generally represents the “additive” contribution of the CH2-group to the vaporization enthalpy 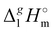 (298.15 K). In our previous studies of vaporization thermodynamics of different ionic liquids (based on imidazolium, pyridinium, and pyrrolidinium cations),10,11,28–30 we have observed that variations in the CH2-group contribution of around 4 kJ mol−1 are not pronounced and they are mostly independent of the structure of the cation and anion. Hence, the slope of 2.545 kJ mol−1 observed for the [N(R)4][NTf2] series seems to be exceptional and has to be understood while excluding possible systematic errors. However, additional proof of the consistency of the experimental data is now required to exclude a possible systematic error.
(298.15 K). In our previous studies of vaporization thermodynamics of different ionic liquids (based on imidazolium, pyridinium, and pyrrolidinium cations),10,11,28–30 we have observed that variations in the CH2-group contribution of around 4 kJ mol−1 are not pronounced and they are mostly independent of the structure of the cation and anion. Hence, the slope of 2.545 kJ mol−1 observed for the [N(R)4][NTf2] series seems to be exceptional and has to be understood while excluding possible systematic errors. However, additional proof of the consistency of the experimental data is now required to exclude a possible systematic error.
3.3 How to quantify the dispersion forces in ILs experimentally?
The 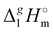 (298.15 K)-values obtained for the [NR4][NTf2] series reflect the overall bulk intensity of all the liquid phase interactions, and they are related to the quantitative amount of energetics of the disrupted inter-molecular interactions (Coulomb and dispersion forces), provided that the isolated from the liquid phase individual ionic pair does not bear any dispersion interactions occurring in the gas phase. We recently showed that for ILs with “hairy” cations such as tetraalkylammonium, the dispersion interactions of alkyl chains in the gas phase contribute significantly to the energetics of evaporation.7 It has also been shown that even with long-chain alkanes, the weak dispersion interactions between chain segments are responsible for the stability of very unusual conformers such as hairpins.7 The tetraalkylammonium ILs with the long alkyl chains investigated in this work are qualitatively predestined for intensive dispersion interactions between the chain segments. The dissection of the overall interaction energies and the quantification of the dispersion interaction are a special challenge for the polar ionic liquid systems, which are characterized by a subtle balance between Coulomb interactions and dispersion forces.7 However, we have found that the enthalpy of vaporization can be a suitable tool for quantifying the dispersion forces.7,39–41
(298.15 K)-values obtained for the [NR4][NTf2] series reflect the overall bulk intensity of all the liquid phase interactions, and they are related to the quantitative amount of energetics of the disrupted inter-molecular interactions (Coulomb and dispersion forces), provided that the isolated from the liquid phase individual ionic pair does not bear any dispersion interactions occurring in the gas phase. We recently showed that for ILs with “hairy” cations such as tetraalkylammonium, the dispersion interactions of alkyl chains in the gas phase contribute significantly to the energetics of evaporation.7 It has also been shown that even with long-chain alkanes, the weak dispersion interactions between chain segments are responsible for the stability of very unusual conformers such as hairpins.7 The tetraalkylammonium ILs with the long alkyl chains investigated in this work are qualitatively predestined for intensive dispersion interactions between the chain segments. The dissection of the overall interaction energies and the quantification of the dispersion interaction are a special challenge for the polar ionic liquid systems, which are characterized by a subtle balance between Coulomb interactions and dispersion forces.7 However, we have found that the enthalpy of vaporization can be a suitable tool for quantifying the dispersion forces.7,39–41
A “step by step” protocol based on the experimental vaporization enthalpies (see Table 1) was used to quantify dispersion interactions in the 1,3-dialkylimidazoliu based ILs. This approach was originally developed and tested for the tetra-alkylphosphonium-based ILs with [PF6] and [NTf2] anions.39 The experimental 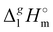 (298.15 K)-values of n-alkanes CH3–(CH2)n–CH312,13 were also included in the interpretation. The results of the calculations carried out using the “step by step” protocol are summarized in Table 4 and shown graphically in Fig. 5 and 6. The idea of the first step is simply to cut off the alkyl chains attached to the cation as they are the main cause of the dispersion interactions. The “bald” cation produced in this way can be used as a reference for quantifying the dispersion forces. In order to execute this idea, linear vaporization enthalpy chain-length dependences of a general formula:
(298.15 K)-values of n-alkanes CH3–(CH2)n–CH312,13 were also included in the interpretation. The results of the calculations carried out using the “step by step” protocol are summarized in Table 4 and shown graphically in Fig. 5 and 6. The idea of the first step is simply to cut off the alkyl chains attached to the cation as they are the main cause of the dispersion interactions. The “bald” cation produced in this way can be used as a reference for quantifying the dispersion forces. In order to execute this idea, linear vaporization enthalpy chain-length dependences of a general formula:
| | 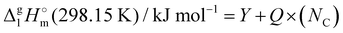 | (6) |
is developed for the IL homologous series (in this work, it is
eqn (1) for [NR
4][NTf
2]), as well as for
n-alkanes for the sake of comparison (details are given in Tables S11–S15, ESI
†). The extrapolation of these lines represents an imaginary case with the
Nc = 0 (no alkyl chain at all). The graphical interpretation of this step for ILs for
n-alkanes is given in
Fig. 5a.
Table 4 Quantification of dispersion forces for tetra-alkylammonium-based ILs with the [NTf2] anion (in kJ mol−1)
| Compound |
Y
|
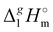
((CH2)n) |
−Edisp((CH2)ngas) |
| [N1123] |
116.4 |
24.2 |
10.9 |
| [N1114] |
27.3 |
7.8 |
| [N1115] |
29.3 |
10.8 |
| [N1224] |
31.0 |
14.1 |
| [N2225] |
33.6 |
21.5 |
| [N1444] |
35.6 |
29.6 |
| [N2228] |
40.3 |
30.0 |
| [N2666] |
56.3 |
44.0 |
| [N6666] |
66.0 |
54.4 |
| [N1888] |
75.4 |
49.9 |
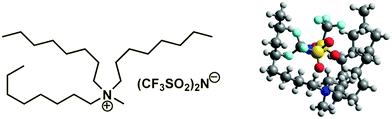 |
| | Fig. 4 Illustration of the long-chained tetra-alkylammonium based IL [N1888][NTf2] with the structurally predestinated dispersion interactions between the chain segments. | |
 |
| | Fig. 5 (a) The chain length dependence of the vaporization enthalpies for n-alkanes, CnH2n+2 (diamonds, ♦); ammonium-based ILs with the [NTf2]− anion, (squares, ■). Primary experimental data for correlations are given in Tables S11–S15 (ESI†). (b) The dispersion part of the vaporization enthalpy due to the alkyl chains. | |
 |
| | Fig. 6 The gas phase dispersive interaction between alkyl chains for ammonium-based ILs with the [NTf2]− anion, as derived from experimental vaporization enthalpies. | |
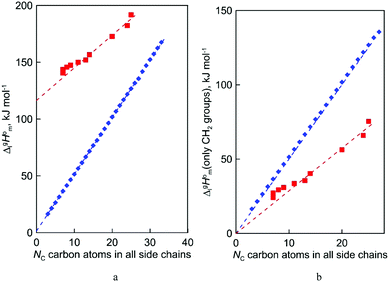
In both series taken for comparison, the intercept Y of the linear fit (see Table 4) refers to the “residual” vaporization enthalpy, that is imaginatively released from dispersion interactions by alkyl chains. From a physical point of view, the quantity of the intercept Y is very different for the molecular and ionic compounds examined. Q describes the slope with increasing number of carbons Nc and is not of relevance at this point.
In the case of ionic liquids [NR4][NTf2] (Y = 116.4 kJ mol−1), the intercept represents the vaporization enthalpy of a hypothetical “armless” [NH4][NTf2] ionic liquid. This value encompasses not only the contribution to vaporization enthalpy from the isolated “ammonium” cation, but also the overall amount of Coulomb interactions presented in the liquid phase. It is not to be overlooked that the corresponding intercept Y for [NR4][NTf2] series studied in this work is indistinguishable from those (Y = 116.0 kJ mol−1) for tetraalkylphosphonium-based ILs [Pn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) n
n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) n
n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) m][NTf2] reported in our paper,39 recently (see details in the ESI†). This observation shows that the Y intercept can be further used as a measure of Coulomb interactions between ion pairs in the liquid state.
m][NTf2] reported in our paper,39 recently (see details in the ESI†). This observation shows that the Y intercept can be further used as a measure of Coulomb interactions between ion pairs in the liquid state.
For the n-alkanes CH3–(CH2)n–CH3, the intercept Y = 1.5 kJ mol−1 was derived from the chain-length dependence of experimental vaporization enthalpies. This term can be perhaps attributed to the contribution of the terminal CH3-fragments. As a rule, the inaccuracy of the experimental data for n-alkanes is mostly below than 1 kJ mol−1 and for this reason it is reasonable to consider the intercept Y = 1.5 kJ mol−1 as an empirical factor that is not negligible for further calculations.
After we have determined the contribution Y to vaporization enthalpies of ammonium-based ILs [NR4][NTf2] by completely cutting off the alkyl chains from the real molecules, we are now ready for the second step of quantifying the dispersion forces due to the multitude of van der Waals interactions of alkyl chain segments. It seems obvious that according to eqn (7):
| | 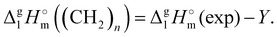 | (7) |
the subtractions of the individual contribution
Y (specific but quantified above for each series) from the real experimental vaporization enthalpies,
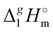
(exp), bring the desired total measure of the dispersion forces,
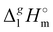
((CH
2)
n), as expressed in terms of enthalpy of vaporization. The latter values (see
Fig. 5b) could immediately be ascribed to the intensity of dispersive alkyl chains interactions in the liquid phase if the dispersive forces in the gas phase are completely absent. However, this speculation does not appear to be correct for all the series examined in this work. If the dispersion forces are only present in the liquid phase, the chain length dependency shown in
Fig. 5b for the molecular and ionic series should more or less merge with one another, in particular due to sufficiently long tails.
Fig. 5b shows, however, that if the
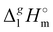
((CH
2)
n)-values for the series of molecules are only slightly different, the deviations for the ionic series are already noticeable. It seems to be that the reason is that the
n-alkanes have typical linear zig-zag structures in the gas phase, in which an occasional raveling of the chain due to dispersion forces is possible but not favorable.
16,42 Therefore, in
n-alkanes, the amount of dispersion forces drawn into the gas phase could be viewed as small, and the
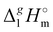
((CH
2)
n)-values are only responsible for this series of dispersion interactions in the liquid phase. The line in
Fig. 5b developed for the ammonium based ILs is significantly below the line shown for
n-alkanes. This observation is clear evidence that the remaining dispersive interactions between alkyl chains dragged from the liquid phase into the gas phase are of particular importance for the ionic compounds.
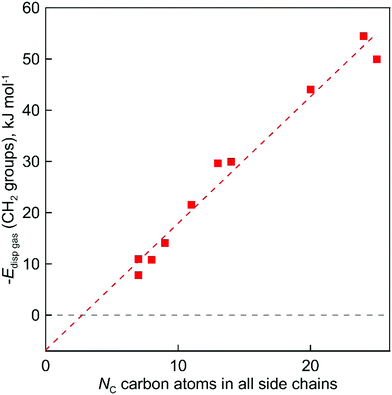
In order to determine this amount of dispersion forces, we finally propose the third step to calculate the interactions between alkyl chains Edisp((CH2)ngas)in the gas phase through space:
| | 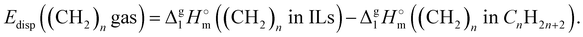 | (8) |
The evaluated values are given in Fig. 6. It is apparent from this figure that the tetra-substituted ammonium ions take a large amount of energy (up to 55 kJ mol−1) of dispersive interactions between the chains and the anion in the gas phase. First of all, this fact can explain the generally lower vaporization enthalpies of tetraalkylammonium based ILs [NR4][NTf2] compared to imidazolium-based ILs with the identical number of C-atoms in the alkyl chains. For example, the value 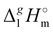 (298.15 K) = 152.1 ± 2.7 kJ mol−1 measured in this work for [N1444][NTf2] (see Table 1) is significantly lower in comparison to those
(298.15 K) = 152.1 ± 2.7 kJ mol−1 measured in this work for [N1444][NTf2] (see Table 1) is significantly lower in comparison to those 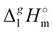 (298.15 K) = 162.2 ± 3.5 kJ mol−1 derived for [C12mim][NTf2] (the averaged result from ref. 43 and 44). Second, the gas phase dispersive interactions of alkyl chains for ammonium-based ILs with the [NTf2]− anion (see Fig. 6) are the key for the understanding of the phenomena questioned in the introduction (see Fig. 3).
(298.15 K) = 162.2 ± 3.5 kJ mol−1 derived for [C12mim][NTf2] (the averaged result from ref. 43 and 44). Second, the gas phase dispersive interactions of alkyl chains for ammonium-based ILs with the [NTf2]− anion (see Fig. 6) are the key for the understanding of the phenomena questioned in the introduction (see Fig. 3).
The dramatically decreasing differences between 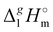 (298.15 K)-values of tetraalkylammonium based ionic liquids and the corresponding molecular tri-alkylamines are obviously the consequence of a systematic accumulation of the gas-phase dispersion interactions at the tetraalkylammonium cation with increasing chain length. These dispersion interactions are not so pronounced in the tri-alkylamines, that is why the
(298.15 K)-values of tetraalkylammonium based ionic liquids and the corresponding molecular tri-alkylamines are obviously the consequence of a systematic accumulation of the gas-phase dispersion interactions at the tetraalkylammonium cation with increasing chain length. These dispersion interactions are not so pronounced in the tri-alkylamines, that is why the 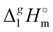 (298.15 K)-differences indicate the amount of dispersion forces disrupted in the liquid phase along the vaporisation, but taken into storage in the gaseous phase. This finding is crucial for the general reconsideration of the IL's vaporization thermodynamics, since the vaporizing molecules can no longer be regarded as a “star-shaped” conformation with the non-interacting tails (see Fig. 4a). Instead, the tetraalkyl substituted ammonium and phosphonium ILs have to be considered as entangled hairy balls (see Fig. 4b) with the significant dispersion interactions between the chain segments, as well as dispersion interactions of the long alkyl chains with the anion.
(298.15 K)-differences indicate the amount of dispersion forces disrupted in the liquid phase along the vaporisation, but taken into storage in the gaseous phase. This finding is crucial for the general reconsideration of the IL's vaporization thermodynamics, since the vaporizing molecules can no longer be regarded as a “star-shaped” conformation with the non-interacting tails (see Fig. 4a). Instead, the tetraalkyl substituted ammonium and phosphonium ILs have to be considered as entangled hairy balls (see Fig. 4b) with the significant dispersion interactions between the chain segments, as well as dispersion interactions of the long alkyl chains with the anion.
3.4 DFT approach to quantify the gas phase dispersion forces in ILs?
The contribution of the dispersion interaction in the stability of ammonium-based ionic liquids was evaluated as the difference in total energy of the molecules optimized at the B3LYP/cc-tzvp level of theory45,46 with and without the D3 dispersion correction from Grimme47 with Becky Johnson damping.48 The geometry optimization was carried out with the Gaussian16 package.
The main challenging task in the theoretical study of molecular or ionic compounds with long side alkyl chains is to correctly establish the conformational ensemble. In the presented study, we applied the Conformer Rotamer Ensemble Sampling Tool (CREST) reported by Grimme49 utilizing the GFN2-xtb method50,51 for tight optimization of the found conformers and evaluation of relative total energy. The complete evaluation of the dispersive energy for the whole ensemble of conformers is time and resource consuming. Therefore, the energies obtained using the GFN2-xtb method were used for the evaluation of the enthalpy correction of the conformational ensemble at 298.15 K. The closest by the corrected energy conformer was chosen as representative for evaluation of the dispersive contribution. The full description of the procedure is given in the ESI.† The results of dispersion energy evaluation given in Table 5 were evaluated as follows:
| | | Edisp(gas)QC = Etot(B3LYP/cc − pvtz(D3BJ)) − Etot(B3LYP/cc − pvtz) | (9) |
| | | Edisp((CH2)gas)QC = Edisp([NR4][NTf2]gas) − Edisp([NH4][NTf2]gas) | (10) |
where
Edisp(gas) corresponds to the gas phase dispersion forces in the studied ionic liquids and
Edisp((CH
2)gas) corresponds to the gas phase dispersion contribution of CH
2 groups in the studied ionic liquids.
Table 5 Quantum chemical quantification of dispersion forces for tetra-alkylammonium-based ILs with the [NTf2] anion (in kJ mol−1)
| Compound |
−Edisp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (gas)QC (gas)QC |
−Edisp((CH2)n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) gas)QC gas)QC |
−Edisp((CH2)n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) gas)exp gas)exp |
| [N1123] |
232.6 |
119.5 |
10.9 |
| [N1114] |
230.1 |
117.1 |
7.8 |
| [N1115] |
246.8 |
133.7 |
10.8 |
| [N1224] |
266.9 |
153.8 |
14.1 |
| [N2225] |
302.1 |
189.1 |
21.5 |
| [N1444] |
327.7 |
214.6 |
29.6 |
| [N2228] |
360.2 |
247.1 |
30.0 |
| [N2666] |
463.6 |
350.5 |
44.0 |
| [N6666] |
517.4 |
404.4 |
54.4 |
| [N1888] |
532.6 |
419.6 |
49.9 |
Apparently, the direct comparison of QC-evaluated and experimental dispersion forces is not relevant. The experimental values were calculated with alkanes as reference compounds and the corresponding along the chain dispersion contribution is absolutely removed from consideration. The corresponding values provide the spatial dispersion forces due to the close position of not-chemically bonded C and H atoms. The results of QC calculations provide the total dispersion interaction of all CH2 groups in the studied ILs. At the same time, the very good correlation between experimental and calculated dispersion forces obviously shows (see Fig. 7) that both the experimental “step by step” and QC methods are consistent and can quantitatively describe general trends of increasing dispersion interactions with the growing chain length:
| | | Edisp((CH2)gas)QC = 6.70 Edisp((CH2)gas)exp + 52 (R2 = 0.975) | (11) |
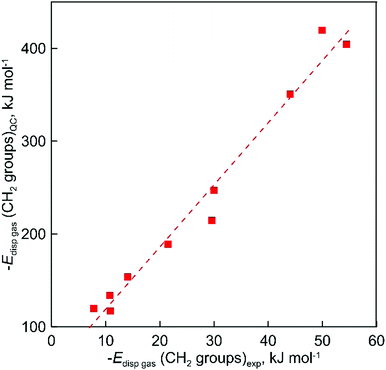 |
| | Fig. 7 The correlation of gas phase dispersive interaction between alkyl chains for ammonium-based ILs with the [NTf2]− anion calculated at the D3(BJ) corrected B3LYP level of theory and the results of experimental evaluation with the “step by step” method. | |
4. Conclusions
We measured vapor pressures and vaporization enthalpies of tetra-alkyl-ammonium ionic liquids with bis(trifluoromethylsulfonyl)imide [NTf2]− anions and related molecular liquids, trialkylamines, by using a quartz-crystal microbalance (QCM). For supporting the QCM data, we additionally determined vaporization enthalpies from experimental activity coefficients at infinite dilution. The resulting alkyl chain length dependencies for the ionic and molecular liquids allowed for quantifying the dispersion forces in the gas phase species of the ionic liquid without the use of quantum chemical calculations of ion-pairs. The purely experimental results suggest that the alkyl chains do not show star-like topologies but embrace the anion while maximizing dispersion interactions with increasing alkyl chain lengths. This way, the overall dispersion interactions in the gas phase species with the longest alkyl chains amount for the energy of two and a half hydrogen bonds. The proportion of dispersion in the gas phase structures with increasing number of methylene groups in the ammonium cations is strongly supported by quantum chemical calculations. Our careful study will help to facilitate the analysis of the thermodynamic properties of newly synthesized ionic or molecular liquids.
Author statement
Dzmitry H. Zaitsau contributed in investigation, validation, formal analysis, and original draft preparation, Ralf Ludwig contributed in conceptualization, methodology, and writing – original draft preparation, and Sergey P. Verevkin contributed in conceptualization, methodology, validation, formal analysis, and writing – original draft preparation.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work has been supported by the German Science Foundation (DFG) in the frame of the priority program SPP 1807 “Control of London Dispersion Interactions in Molecular Chemistry” (grant LU-506/12-2 for RL and grant VE 265-9/2 for SPV). DHZ acknowledges the financial support from DFG, grant ZA 872/3-1, 407078203.
References
- C. Wang, L. Guo, H. Li, Y. Wang, J. Weng and L. Wu, Green Chem., 2006, 8, 603–607 RSC.
- V. F. Scalfani, A. A. Alshaikh and J. E. Bara, Ind. Eng. Chem. Res., 2018, 57, 15971–15981 CrossRef CAS.
- A. Heintz, T. V. Vasiltsova, J. Safarov, E. Bich and S. P. Verevkin, J. Chem. Eng. Data, 2006, 51, 648–655 CrossRef CAS.
- S. P. Verevkin, V. N. Emel’yanenko, I. Krossing and R. Kalb, J. Chem. Thermodyn., 2012, 51, 107–113 CrossRef CAS.
- V. N. Emel’yanenko, G. Boeck, S. P. Verevkin and R. Ludwig, Chem. – Eur. J, 2014, 20, 11640–11645 CrossRef PubMed.
- D. H. Zaitsau, V. N. Emel’yanenko, P. Stange, S. P. Verevkin and R. Ludwig, Angew. Chem., Int. Ed., 2019, 58, 8589–8592 CrossRef CAS PubMed.
- D. H. Zaitsau, V. N. Emel’yanenko, P. Stange, C. Schick, S. P. Verevkin and R. Ludwig, Angew. Chem., Int. Ed., 2016, 55, 11682–11686 CrossRef CAS PubMed.
- A. Wulf, K. Fumino, R. Ludwig and P. F. Taday, ChemPhysChem, 2010, 11, 349–353 CrossRef CAS PubMed.
- K. Fumino, A. Wulf, S. P. Verevkin, A. Heintz and R. Ludwig, ChemPhysChem, 2010, 11, 1623–1626 CrossRef CAS PubMed.
- S. P. Verevkin, D. H. Zaitsau, V. N. Emel’yanenko, A. V. Yermalayeu, C. Schick, H. Liu, E. J. Maginn, S. Bulut, I. Krossing and R. Kalb, J. Phys. Chem. B, 2013, 117, 6473–6486 CrossRef CAS PubMed.
- S. P. Verevkin, D. H. Zaitsau, V. N. Emel’yanenko, R. V. Ralys, A. V. Yermalayeu and C. Schick, Thermochim. Acta, 2013, 562, 84–95 CrossRef CAS.
- K. Růžička and V. Majer, J. Phys. Chem. Ref. Data, 1994, 23, 1–39 CrossRef.
- J. S. Chickos and W. Hanshaw, J. Chem. Eng. Data, 2004, 49, 620–630 CrossRef CAS.
- V. N. Emel’yanenko, S. V. Portnova, S. P. Verevkin, A. Skrzypczak and T. Schubert, J. Chem. Thermodyn., 2011, 43, 1500–1505 CrossRef.
-
J. B. Pedley, R. D. Naylor, S. P. Kirby and J. B. Pedley, Thermochemical data of organic compounds, Chapman & Hall, London, 2nd edn, 1986 Search PubMed.
- T. Köddermann, D. Paschek and R. Ludwig, ChemPhysChem, 2008, 9, 549–555 CrossRef PubMed.
- S. P. Verevkin, D. H. Zaitsau, V. N. Emel’yanenko and A. Heintz, J. Phys. Chem. B, 2011, 115, 12889–12895 CrossRef CAS PubMed.
- D. H. Zaitsau, A. V. Yermalayeu, V. N. Emel’yanenko, S. Butler, T. Schubert and S. P. Verevkin, J. Phys. Chem. B, 2016, 120, 7949–7957 CrossRef CAS PubMed.
- B. Schröder and J. A. P. Coutinho, Fluid Phase Equilib., 2014, 370, 24–33 CrossRef.
- D. H. Zaitsau and S. P. Verevkin, J. Solution Chem., 2018, 47, 892–905 CrossRef CAS.
- D. H. Zaitsau, A. V. Yermalayeu, A. A. Pimerzin and S. P. Verevkin, Chem. Eng. Res. Des., 2018, 137, 164–173 CrossRef CAS.
- F. Mutelet, A.-L. Revelli, J.-N. Jaubert, L. M. Sprunger, W. E. Acree Jr. and G. A. Baker, J. Chem. Eng. Data, 2010, 55, 234–242 CrossRef CAS.
- W. E. Acree, G. A. Baker, F. Mutelet and J.-C. Moise, J. Chem. Eng. Data, 2011, 56, 3688–3697 CrossRef CAS.
- M. Wlazło and U. Domańska, Sep. Purif. Technol., 2016, 162, 162–170 CrossRef.
- N. V. Gwala, N. Deenadayalu, K. Tumba and D. Ramjugernath, J. Chem. Thermodyn., 2010, 42, 256–261 CrossRef CAS.
- C. M. Hansen, Prog. Org. Coat., 2004, 51, 77–84 CrossRef CAS.
- B. Yoo, W. Afzal and J. M. Prausnitz, Ind. Eng. Chem. Res., 2012, 51, 9913–9917 CrossRef CAS.
- D. H. Zaitsau, A. V. Yermalayeu, V. N. Emel’yanenko, S. P. Verevkin, U. Welz-Biermann and T. Schubert, Sci. China: Chem., 2012, 55, 1525–1531 CrossRef CAS.
- S. P. Verevkin, R. V. Ralys, V. N. Emel’yanenko, D. H. Zaitsau and C. Schick, J. Therm. Anal. Calorim., 2013, 112, 353–358 CrossRef CAS.
- D. H. Zaitsau, A. V. Yermalayeu, V. N. Emel’Yanenko, A. Heintz, S. P. Verevkin, C. Schick, S. Berdzinski and V. Strehmel, J. Mol. Liq., 2014, 192, 171–176 CrossRef CAS.
- D. H. Zaitsau, K. Pohako-Esko, S. Arlt, V. N. Emel’yanenko, P. S. Schulz, P. Wasserscheid, A. Schulz and S. P. Verevkin, J. Mol. Liq., 2017, 248, 86–90 CrossRef CAS.
- R. Osada, T. Hoshino, K. Okada, Y. Ohmasa and M. Yao, J. Chem. Phys., 2009, 130, 184705 CrossRef CAS PubMed.
- A. Wandschneider, J. K. Lehmann and A. Heintz, J. Chem. Eng. Data, 2008, 53, 596–599 CrossRef CAS.
- A. Bhattacharjee, A. Luís, J. H. Santos, J. A. Lopes-da-Silva, M. G. Freire, P. J. Carvalho and J. A. P. Coutinho, Fluid Phase Equilib., 2014, 381, 36–45 CrossRef CAS PubMed.
- P. Kilaru, G. A. Baker and P. Scovazzo, J. Chem. Eng. Data, 2007, 52, 2306–2314 CrossRef CAS.
- M. H. Ibrahim, M. Hayyan, M. A. Hashim, A. Hayyan and M. K. Hadj-Kali, Fluid Phase Equilib., 2016, 427, 18–26 CrossRef CAS.
- M. H. Ghatee, M. Bahrami and N. Khanjari, J. Chem. Thermodyn., 2013, 65, 42–52 CrossRef CAS.
- G. V. S. M. Carrera, C. A. M. Afonso and L. C. Branco, J. Chem. Eng. Data, 2010, 55, 609–615 CrossRef CAS.
- D. H. Zaitsau, N. Plechkova and S. P. Verevkin, J. Chem. Thermodyn., 2019, 130, 204–212 CrossRef CAS.
- V. N. Emel’yanenko, P. Stange, J. Feder-Kubis, S. P. Verevkin and R. Ludwig, Phys. Chem. Chem. Phys., 2020, 22, 4896–4904 RSC.
- D. H. Zaitsau, J. Neumann, T. Niemann, A. Strate, D. Paschek, S. P. Verevkin and R. Ludwig, Phys. Chem. Chem. Phys., 2019, 21, 20308–20314 RSC.
- N. O. B. Lüttschwager, W. N. Tobias, R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2012, 52, 463–466 CrossRef PubMed.
- S. P. S. P. Verevkin, D. H. D. H. Zaitsau, V. N. V. N. Emel’yanenko, R. V. R. V. Ralys, A. V. A. V. Yermalayeu and C. Schick, J. Chem. Thermodyn., 2012, 54, 433–437 CrossRef CAS.
- D. H. Zaitsau, S. P. Verevkin, V. N. Emel’yanenko and A. Heintz, ChemPhysChem, 2011, 12, 3609–3613 CrossRef CAS PubMed.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- K. A. Peterson, D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 7410–7415 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- P. Pracht, E. Caldeweyher, S. Ehlert and S. Grimme, ChemRxiv DOI:10.26434/chemrxiv.8326202.v1.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05439a |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  ab,
Ralf
Ludwig
ab,
Ralf
Ludwig
 *abc and
Sergey P.
Verevkin
*abc and
Sergey P.
Verevkin
 *ab
*ab

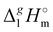 (298.15 K), of n-alkanes monotonically grow with the increasing chain-length (see Fig. 2a). Such a behavior is common with molecular compounds. And what about ionic compounds? Surprisingly, not so long ago there was a lot of controversy over this question.10 However, it is already known today that the vaporization enthalpies of aprotic ionic liquids also have the linear chain length dependencies (with the exception of a few special cases caused by a possible nanostructuring of ILs with long alkyl chains bounded to the cation).10,11 An example of such an impeccable linear dependence for 1-methyl-3-alkyl-imidazolium based ILs with the [NTf2] anion is shown in Fig. 2a.
(298.15 K), of n-alkanes monotonically grow with the increasing chain-length (see Fig. 2a). Such a behavior is common with molecular compounds. And what about ionic compounds? Surprisingly, not so long ago there was a lot of controversy over this question.10 However, it is already known today that the vaporization enthalpies of aprotic ionic liquids also have the linear chain length dependencies (with the exception of a few special cases caused by a possible nanostructuring of ILs with long alkyl chains bounded to the cation).10,11 An example of such an impeccable linear dependence for 1-methyl-3-alkyl-imidazolium based ILs with the [NTf2] anion is shown in Fig. 2a.
 ),12,13 alkyl-imidazoles (opened triangles,
),12,13 alkyl-imidazoles (opened triangles,  )14 and 1-methyl-3-alkyl-imidazolium based ILs (opened circles,
)14 and 1-methyl-3-alkyl-imidazolium based ILs (opened circles,  );10 (b) trialkylamines15 (opened squares,
);10 (b) trialkylamines15 (opened squares,  ) and tetraalkylammonium based ILs from this work (solid squares,
) and tetraalkylammonium based ILs from this work (solid squares,  ).
). (298.15 K)-values for these ionic and the corresponding molecular compounds. As can be seen in Fig. 3, nothing surprising can be observed for the pairs 1-methyl-3-alkyl-imidazolium based ILs and alkyl-imidazoles, namely the differences between
(298.15 K)-values for these ionic and the corresponding molecular compounds. As can be seen in Fig. 3, nothing surprising can be observed for the pairs 1-methyl-3-alkyl-imidazolium based ILs and alkyl-imidazoles, namely the differences between 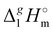 (298.15 K)-values are decreasing insignificantly with the elongation of the alkyl chain. This decrease could be understood from the competition between the corresponding van der Waals and Coulomb interactions.10 Indeed, according to Köddermann et al.,16 the Coulomb energy contribution remains unchanged as the length of the alkyl chains increases beyond n = 2. Consistent with the findings of Köddermann et al.,16 we also found experimentally that the increase in the enthalpy of vaporization for the [Cnmim][NTf2] series with increasing chain length arises completely from van der Waals interactions, which are the dominant driving force of the vaporization process.10 The finding that the
(298.15 K)-values are decreasing insignificantly with the elongation of the alkyl chain. This decrease could be understood from the competition between the corresponding van der Waals and Coulomb interactions.10 Indeed, according to Köddermann et al.,16 the Coulomb energy contribution remains unchanged as the length of the alkyl chains increases beyond n = 2. Consistent with the findings of Köddermann et al.,16 we also found experimentally that the increase in the enthalpy of vaporization for the [Cnmim][NTf2] series with increasing chain length arises completely from van der Waals interactions, which are the dominant driving force of the vaporization process.10 The finding that the 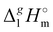 (298.15 K)-differences between pairs 1-methyl-3-alkyl-imidazolium based ILs and alkyl-imidazoles are hardly chain-length dependent can be seen as evidence that the van der Waals interactions in the ionic and molecular series are very similar even quantitatively. With this in mind, we now study the tetraalkylammonium based ILs (see Fig. 3), which are in the focus of the present work.
(298.15 K)-differences between pairs 1-methyl-3-alkyl-imidazolium based ILs and alkyl-imidazoles are hardly chain-length dependent can be seen as evidence that the van der Waals interactions in the ionic and molecular series are very similar even quantitatively. With this in mind, we now study the tetraalkylammonium based ILs (see Fig. 3), which are in the focus of the present work.
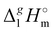 (298.15 K)-values for the ionic and molecular compounds. 1-Methyl-3-alkyl-imidazolium based ILs10 and alkyl-imidazoles14 (opened triangles,
(298.15 K)-values for the ionic and molecular compounds. 1-Methyl-3-alkyl-imidazolium based ILs10 and alkyl-imidazoles14 (opened triangles,  ); tetraalkylammonium based ILs from this work and trialkylamines15 (solid squares,
); tetraalkylammonium based ILs from this work and trialkylamines15 (solid squares,  ).
).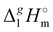 (298.15 K)-values of tetraalkylammonium based ionic liquids and the corresponding molecular tri-alkylamines. As can be seen in Fig. 3, the spectacular decrease of the
(298.15 K)-values of tetraalkylammonium based ionic liquids and the corresponding molecular tri-alkylamines. As can be seen in Fig. 3, the spectacular decrease of the 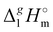 (298.15 K)-differences is observed for these pairs with the growing of the alkyl chain. What about the competition between the van der Waals and Coulomb interactions in these tetraalkylammonium-based ILs? We will address this question in the following way. First, we measure the vapor pressures and determine the molar enthalpies of vaporization by using the Quartz Crystal Microbalance (QCM) method. For consistency, we also “indirectly” determined the vaporization enthalpies with the complementary Gas Chromatography (GC) method based on measuring activity coefficients at infinite dilution of volatile solutes in these ILs. The obtained vaporization enthalpies were then related to experimental surface tensions from the literature for checking the reliability of property–property relations. Thus, we were well prepared to dissect and quantify the dispersion interactions in these ILs, in particular for the gas phase species. Finally, the dispersion contributions were confirmed using density functional theory FT) calculations showing a linear correlation between the calculated and the dissected measured dispersion interactions. Overall, we show how valuable thermodynamics methods are for better understanding non-covalent interactions, here in ammonium-based ionic liquids.
(298.15 K)-differences is observed for these pairs with the growing of the alkyl chain. What about the competition between the van der Waals and Coulomb interactions in these tetraalkylammonium-based ILs? We will address this question in the following way. First, we measure the vapor pressures and determine the molar enthalpies of vaporization by using the Quartz Crystal Microbalance (QCM) method. For consistency, we also “indirectly” determined the vaporization enthalpies with the complementary Gas Chromatography (GC) method based on measuring activity coefficients at infinite dilution of volatile solutes in these ILs. The obtained vaporization enthalpies were then related to experimental surface tensions from the literature for checking the reliability of property–property relations. Thus, we were well prepared to dissect and quantify the dispersion interactions in these ILs, in particular for the gas phase species. Finally, the dispersion contributions were confirmed using density functional theory FT) calculations showing a linear correlation between the calculated and the dissected measured dispersion interactions. Overall, we show how valuable thermodynamics methods are for better understanding non-covalent interactions, here in ammonium-based ionic liquids.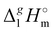 (Tav) have to be adjusted to the reference temperature T = 298.15 K. The adjustment was performed according to the Kirchhoff's Law (see Table 1, column 7). Details are given in the ESI.†
(Tav) have to be adjusted to the reference temperature T = 298.15 K. The adjustment was performed according to the Kirchhoff's Law (see Table 1, column 7). Details are given in the ESI.†
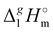 , of tetra-alkyl-ammonium ILs with the common anion [NTf2] derived from the QCM method
, of tetra-alkyl-ammonium ILs with the common anion [NTf2] derived from the QCM method
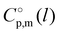 -values given in column 6 of this table according to the equation developed10 for the imidazolium based ILs:
-values given in column 6 of this table according to the equation developed10 for the imidazolium based ILs: 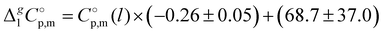 .
d Adjusted to 298.15 K using
.
d Adjusted to 298.15 K using 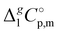 -values from column 7. The final uncertainties of vaporization enthalpies adjusted to the reference temperature T = 298.15 K are expressed as expanded uncertainties
-values from column 7. The final uncertainties of vaporization enthalpies adjusted to the reference temperature T = 298.15 K are expressed as expanded uncertainties 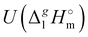 at the 0.95 level of confidence with k = 2. These uncertainties combine the experimental uncertainty and the uncertainty of the temperature adjustment. The uncertainty of the heat capacity difference
at the 0.95 level of confidence with k = 2. These uncertainties combine the experimental uncertainty and the uncertainty of the temperature adjustment. The uncertainty of the heat capacity difference 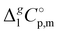 is assumed to be of ± 20 J K−1 mol−1. Values given in bold are recommended for the thermochemical calculations.
is assumed to be of ± 20 J K−1 mol−1. Values given in bold are recommended for the thermochemical calculations.
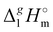 (298.15 K), [N1
(298.15 K), [N1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8][NTf2] = 191.1 kJ mol−1 calculated using COSMO-RS19 was in very good agreement with the experimental value
8][NTf2] = 191.1 kJ mol−1 calculated using COSMO-RS19 was in very good agreement with the experimental value 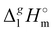 (298.15 K), [N1
(298.15 K), [N1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8][NTf2] = 191.8 ± 6.0 kJ mol−1 (see Table 1) measured in this work. It should also be mentioned that the relatively high uncertainty of our experimental value (of ± 6.0 kJ mol−1) is due to the procedure used for the adjustment of vaporization enthalpy to the reference temperature T = 298.15 K.
8][NTf2] = 191.8 ± 6.0 kJ mol−1 (see Table 1) measured in this work. It should also be mentioned that the relatively high uncertainty of our experimental value (of ± 6.0 kJ mol−1) is due to the procedure used for the adjustment of vaporization enthalpy to the reference temperature T = 298.15 K.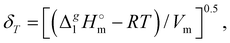
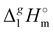 is the standard molar enthalpy of vaporization (of the solute or the solvent), R is the ideal gas constant, T is the temperature, and Vm is the molar volume (of the solute or the solvent). A simple re-arrangement of eqn (1) towards the total solubility parameter δ2 opens an independent method to derive vaporization enthalpy,
is the standard molar enthalpy of vaporization (of the solute or the solvent), R is the ideal gas constant, T is the temperature, and Vm is the molar volume (of the solute or the solvent). A simple re-arrangement of eqn (1) towards the total solubility parameter δ2 opens an independent method to derive vaporization enthalpy, 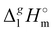 (298.15 K), of an IL using eqn (2):
(298.15 K), of an IL using eqn (2):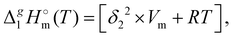
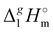 (298.15 K) were calculated from δ2 (see Table S10, ESI†). The results are in agreement within the experimental uncertainties of the QCM results (see Table 2). Such a good agreement provides more confidence to the QCM results on
(298.15 K) were calculated from δ2 (see Table S10, ESI†). The results are in agreement within the experimental uncertainties of the QCM results (see Table 2). Such a good agreement provides more confidence to the QCM results on 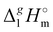 (298.15 K) and allows for a meaningful interpretation of these results at the molecular level.
(298.15 K) and allows for a meaningful interpretation of these results at the molecular level.
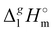 (298.15 K), of tetra-alkyl-ammonium ILs with the common anion [NTf2] derived from the QCM method at 298.15 K (in kJ mol−1)
(298.15 K), of tetra-alkyl-ammonium ILs with the common anion [NTf2] derived from the QCM method at 298.15 K (in kJ mol−1)
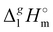 (298.15 K) = 2.545 × Nc + 123.2 (R2 = 0.976), derived from experimental vaporization enthalpies given in Table 1.
c Estimated using γ∞1-values (see the text)
(298.15 K) = 2.545 × Nc + 123.2 (R2 = 0.976), derived from experimental vaporization enthalpies given in Table 1.
c Estimated using γ∞1-values (see the text)
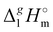 (298.15 K)-values with the number of C-atoms in the alkyl chain within the homologues series of molecular and ionic compounds is a valuable tool to study structure–property relationships. For instance, for the series [Cnmim][NTf2], the dependence of vaporization enthalpy on the number of C-atoms, n, in the alkyl chain (with n = 2–18) attached to the 3 position of the 1-methyimidazolium cation follows the linear equation:10
(298.15 K)-values with the number of C-atoms in the alkyl chain within the homologues series of molecular and ionic compounds is a valuable tool to study structure–property relationships. For instance, for the series [Cnmim][NTf2], the dependence of vaporization enthalpy on the number of C-atoms, n, in the alkyl chain (with n = 2–18) attached to the 3 position of the 1-methyimidazolium cation follows the linear equation:10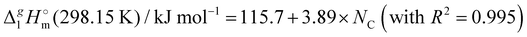
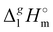 (298.15 K)-values for [N(R)4][NTf2] ionic liquids evaluated in Table 1 with the total number of C atoms, Nc, in all alkyl chains attached to the central nitrogen atom:
(298.15 K)-values for [N(R)4][NTf2] ionic liquids evaluated in Table 1 with the total number of C atoms, Nc, in all alkyl chains attached to the central nitrogen atom: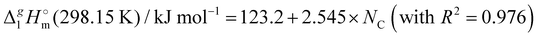
 (298.15 K). In our previous studies of vaporization thermodynamics of different ionic liquids (based on imidazolium, pyridinium, and pyrrolidinium cations),10,11,28–30 we have observed that variations in the CH2-group contribution of around 4 kJ mol−1 are not pronounced and they are mostly independent of the structure of the cation and anion. Hence, the slope of 2.545 kJ mol−1 observed for the [N(R)4][NTf2] series seems to be exceptional and has to be understood while excluding possible systematic errors. However, additional proof of the consistency of the experimental data is now required to exclude a possible systematic error.
(298.15 K). In our previous studies of vaporization thermodynamics of different ionic liquids (based on imidazolium, pyridinium, and pyrrolidinium cations),10,11,28–30 we have observed that variations in the CH2-group contribution of around 4 kJ mol−1 are not pronounced and they are mostly independent of the structure of the cation and anion. Hence, the slope of 2.545 kJ mol−1 observed for the [N(R)4][NTf2] series seems to be exceptional and has to be understood while excluding possible systematic errors. However, additional proof of the consistency of the experimental data is now required to exclude a possible systematic error. (298.15 K)-values with the surface tension within the homologues series of molecular and ionic compounds is the additional tool to establish internal consistency of the experimental data. For example, a proper linear vaporization enthalpy chain-length dependence was observed for the [Cnmim][B(CN)4] series.31 In this work, we correlated
(298.15 K)-values with the surface tension within the homologues series of molecular and ionic compounds is the additional tool to establish internal consistency of the experimental data. For example, a proper linear vaporization enthalpy chain-length dependence was observed for the [Cnmim][B(CN)4] series.31 In this work, we correlated 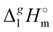 (298.15 K) for the series [NR4][NTf2] with the experimental values of surface tension σ298 at the reference temperature available for these ILs from the literature (see Table 3). It has turned out that also the linear dependence:
(298.15 K) for the series [NR4][NTf2] with the experimental values of surface tension σ298 at the reference temperature available for these ILs from the literature (see Table 3). It has turned out that also the linear dependence: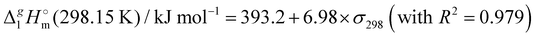
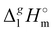 (298.15 K) with the surface tension
(298.15 K) with the surface tension
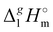 (298.15 K) = 2.545 × Nc + 123.2 (R2 = 0.976), derived from experimental vaporization enthalpies given in Table 1.
c Estimated from the equation:
(298.15 K) = 2.545 × Nc + 123.2 (R2 = 0.976), derived from experimental vaporization enthalpies given in Table 1.
c Estimated from the equation: 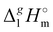 (298.15 K) = −6.98 × σ298(est) + 393.2 (R2 = 0.981)
d Difference between columns 6 and 7.
(298.15 K) = −6.98 × σ298(est) + 393.2 (R2 = 0.981)
d Difference between columns 6 and 7.
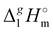 (298.15 K)-values for the [NR4][NTf2] series, they can be now applied for the interpretation of the intensity of intermolecular interactions in the ammonium based ionic liquids.
(298.15 K)-values for the [NR4][NTf2] series, they can be now applied for the interpretation of the intensity of intermolecular interactions in the ammonium based ionic liquids.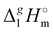 (298.15 K)-values obtained for the [NR4][NTf2] series reflect the overall bulk intensity of all the liquid phase interactions, and they are related to the quantitative amount of energetics of the disrupted inter-molecular interactions (Coulomb and dispersion forces), provided that the isolated from the liquid phase individual ionic pair does not bear any dispersion interactions occurring in the gas phase. We recently showed that for ILs with “hairy” cations such as tetraalkylammonium, the dispersion interactions of alkyl chains in the gas phase contribute significantly to the energetics of evaporation.7 It has also been shown that even with long-chain alkanes, the weak dispersion interactions between chain segments are responsible for the stability of very unusual conformers such as hairpins.7 The tetraalkylammonium ILs with the long alkyl chains investigated in this work are qualitatively predestined for intensive dispersion interactions between the chain segments. The dissection of the overall interaction energies and the quantification of the dispersion interaction are a special challenge for the polar ionic liquid systems, which are characterized by a subtle balance between Coulomb interactions and dispersion forces.7 However, we have found that the enthalpy of vaporization can be a suitable tool for quantifying the dispersion forces.7,39–41
(298.15 K)-values obtained for the [NR4][NTf2] series reflect the overall bulk intensity of all the liquid phase interactions, and they are related to the quantitative amount of energetics of the disrupted inter-molecular interactions (Coulomb and dispersion forces), provided that the isolated from the liquid phase individual ionic pair does not bear any dispersion interactions occurring in the gas phase. We recently showed that for ILs with “hairy” cations such as tetraalkylammonium, the dispersion interactions of alkyl chains in the gas phase contribute significantly to the energetics of evaporation.7 It has also been shown that even with long-chain alkanes, the weak dispersion interactions between chain segments are responsible for the stability of very unusual conformers such as hairpins.7 The tetraalkylammonium ILs with the long alkyl chains investigated in this work are qualitatively predestined for intensive dispersion interactions between the chain segments. The dissection of the overall interaction energies and the quantification of the dispersion interaction are a special challenge for the polar ionic liquid systems, which are characterized by a subtle balance between Coulomb interactions and dispersion forces.7 However, we have found that the enthalpy of vaporization can be a suitable tool for quantifying the dispersion forces.7,39–41
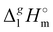 (298.15 K)-values of n-alkanes CH3–(CH2)n–CH312,13 were also included in the interpretation. The results of the calculations carried out using the “step by step” protocol are summarized in Table 4 and shown graphically in Fig. 5 and 6. The idea of the first step is simply to cut off the alkyl chains attached to the cation as they are the main cause of the dispersion interactions. The “bald” cation produced in this way can be used as a reference for quantifying the dispersion forces. In order to execute this idea, linear vaporization enthalpy chain-length dependences of a general formula:
(298.15 K)-values of n-alkanes CH3–(CH2)n–CH312,13 were also included in the interpretation. The results of the calculations carried out using the “step by step” protocol are summarized in Table 4 and shown graphically in Fig. 5 and 6. The idea of the first step is simply to cut off the alkyl chains attached to the cation as they are the main cause of the dispersion interactions. The “bald” cation produced in this way can be used as a reference for quantifying the dispersion forces. In order to execute this idea, linear vaporization enthalpy chain-length dependences of a general formula: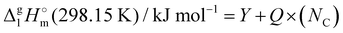



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) n
n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) n
n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) m][NTf2] reported in our paper,39 recently (see details in the ESI†). This observation shows that the Y intercept can be further used as a measure of Coulomb interactions between ion pairs in the liquid state.
m][NTf2] reported in our paper,39 recently (see details in the ESI†). This observation shows that the Y intercept can be further used as a measure of Coulomb interactions between ion pairs in the liquid state.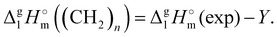
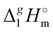 (exp), bring the desired total measure of the dispersion forces,
(exp), bring the desired total measure of the dispersion forces, 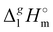 ((CH2)n), as expressed in terms of enthalpy of vaporization. The latter values (see Fig. 5b) could immediately be ascribed to the intensity of dispersive alkyl chains interactions in the liquid phase if the dispersive forces in the gas phase are completely absent. However, this speculation does not appear to be correct for all the series examined in this work. If the dispersion forces are only present in the liquid phase, the chain length dependency shown in Fig. 5b for the molecular and ionic series should more or less merge with one another, in particular due to sufficiently long tails. Fig. 5b shows, however, that if the
((CH2)n), as expressed in terms of enthalpy of vaporization. The latter values (see Fig. 5b) could immediately be ascribed to the intensity of dispersive alkyl chains interactions in the liquid phase if the dispersive forces in the gas phase are completely absent. However, this speculation does not appear to be correct for all the series examined in this work. If the dispersion forces are only present in the liquid phase, the chain length dependency shown in Fig. 5b for the molecular and ionic series should more or less merge with one another, in particular due to sufficiently long tails. Fig. 5b shows, however, that if the 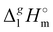 ((CH2)n)-values for the series of molecules are only slightly different, the deviations for the ionic series are already noticeable. It seems to be that the reason is that the n-alkanes have typical linear zig-zag structures in the gas phase, in which an occasional raveling of the chain due to dispersion forces is possible but not favorable.16,42 Therefore, in n-alkanes, the amount of dispersion forces drawn into the gas phase could be viewed as small, and the
((CH2)n)-values for the series of molecules are only slightly different, the deviations for the ionic series are already noticeable. It seems to be that the reason is that the n-alkanes have typical linear zig-zag structures in the gas phase, in which an occasional raveling of the chain due to dispersion forces is possible but not favorable.16,42 Therefore, in n-alkanes, the amount of dispersion forces drawn into the gas phase could be viewed as small, and the 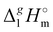 ((CH2)n)-values are only responsible for this series of dispersion interactions in the liquid phase. The line in Fig. 5b developed for the ammonium based ILs is significantly below the line shown for n-alkanes. This observation is clear evidence that the remaining dispersive interactions between alkyl chains dragged from the liquid phase into the gas phase are of particular importance for the ionic compounds.
((CH2)n)-values are only responsible for this series of dispersion interactions in the liquid phase. The line in Fig. 5b developed for the ammonium based ILs is significantly below the line shown for n-alkanes. This observation is clear evidence that the remaining dispersive interactions between alkyl chains dragged from the liquid phase into the gas phase are of particular importance for the ionic compounds.
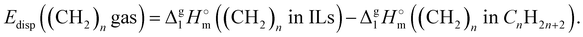
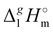 (298.15 K) = 152.1 ± 2.7 kJ mol−1 measured in this work for [N1444][NTf2] (see Table 1) is significantly lower in comparison to those
(298.15 K) = 152.1 ± 2.7 kJ mol−1 measured in this work for [N1444][NTf2] (see Table 1) is significantly lower in comparison to those 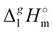 (298.15 K) = 162.2 ± 3.5 kJ mol−1 derived for [C12mim][NTf2] (the averaged result from ref. 43 and 44). Second, the gas phase dispersive interactions of alkyl chains for ammonium-based ILs with the [NTf2]− anion (see Fig. 6) are the key for the understanding of the phenomena questioned in the introduction (see Fig. 3).
(298.15 K) = 162.2 ± 3.5 kJ mol−1 derived for [C12mim][NTf2] (the averaged result from ref. 43 and 44). Second, the gas phase dispersive interactions of alkyl chains for ammonium-based ILs with the [NTf2]− anion (see Fig. 6) are the key for the understanding of the phenomena questioned in the introduction (see Fig. 3).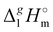 (298.15 K)-values of tetraalkylammonium based ionic liquids and the corresponding molecular tri-alkylamines are obviously the consequence of a systematic accumulation of the gas-phase dispersion interactions at the tetraalkylammonium cation with increasing chain length. These dispersion interactions are not so pronounced in the tri-alkylamines, that is why the
(298.15 K)-values of tetraalkylammonium based ionic liquids and the corresponding molecular tri-alkylamines are obviously the consequence of a systematic accumulation of the gas-phase dispersion interactions at the tetraalkylammonium cation with increasing chain length. These dispersion interactions are not so pronounced in the tri-alkylamines, that is why the 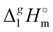 (298.15 K)-differences indicate the amount of dispersion forces disrupted in the liquid phase along the vaporisation, but taken into storage in the gaseous phase. This finding is crucial for the general reconsideration of the IL's vaporization thermodynamics, since the vaporizing molecules can no longer be regarded as a “star-shaped” conformation with the non-interacting tails (see Fig. 4a). Instead, the tetraalkyl substituted ammonium and phosphonium ILs have to be considered as entangled hairy balls (see Fig. 4b) with the significant dispersion interactions between the chain segments, as well as dispersion interactions of the long alkyl chains with the anion.
(298.15 K)-differences indicate the amount of dispersion forces disrupted in the liquid phase along the vaporisation, but taken into storage in the gaseous phase. This finding is crucial for the general reconsideration of the IL's vaporization thermodynamics, since the vaporizing molecules can no longer be regarded as a “star-shaped” conformation with the non-interacting tails (see Fig. 4a). Instead, the tetraalkyl substituted ammonium and phosphonium ILs have to be considered as entangled hairy balls (see Fig. 4b) with the significant dispersion interactions between the chain segments, as well as dispersion interactions of the long alkyl chains with the anion.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (gas)QC
(gas)QC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) gas)QC
gas)QC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) gas)exp
gas)exp