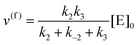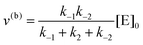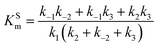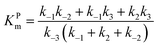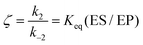DOI:
10.1039/D0CC07062A
(Feature Article)
Chem. Commun., 2021,
57, 713-720
Catalytic bias in oxidation–reduction catalysis
Received
24th October 2020
, Accepted 10th December 2020
First published on 15th December 2020
Abstract
Cataytic bias refers to the propensity of a reaction catalyst to effect a different rate acceleration in one direction versus the other in a chemical reaction under non-equilibrium conditions. In biocatalysis, the inherent bias of an enzyme is often advantagous to augment the innate thermodynamics of a reaction to promote efficiency and fidelity in the coordination of catabolic and anabolic pathways. In industrial chemical catalysis a directional cataltyic bias is a sought after property in facilitating the engineering of systems that couple catalysis with harvest and storage of for example fine chemicals or energy compounds. Interestingly, there is little information about catalytic bias in biocatalysis likely in large part due to difficulties in developing tractible assays sensitive enough to study detailed kinetics. For oxidation–reduction reactions, colorimetric redox indicators exist in a range of reduction potentials to provide a mechanism to study both directions of reactions in a fairly facile manner. The current short review attempts to define catalytic bias conceptually and to develop model systems for defining the parameters that control catalytic bias in enzyme catalyzed oxidation–reduction catalysis.
Introduction
Enzymatic reactions comprise the basic building blocks essential to the biochemical processes of cellular metabolism. While most enzymatic reactions are reversible, in conditions away from equilibrium, certain enzymes accelerate a reaction in one direction significantly differently than the reverse direction. We refer to this property as catalytic bias. For metabolic processes, biases are of paramount importance for controlled energy movement and can result in apparent irreversibility that seems to defy thermodynamics. For enzyme catalyzed oxidation–reduction reactions involving active site metal cofactors, the ability to exist in multiple oxidation states with differing reduction potentials is essential for catalysis. The immediate protein environment can effectively tune the properties of the cofactor, but little is still known about the determinants that promote the direction and magnitude of catalytic bias. Catalytic bias is not limited to enzymes, but we contend that it is a general concept applicable to both heterogeneous and homogeneous catalysis. Catalytic bias is enabled by the mechanistic complexity inherent to the multistep nature of a catalytic process, as multiple intermediates and even reaction pathways are accessible. Modifications in the catalyst environment (either in the catalyst itself or, more subtly, in the catalytic medium) can promote a pathway or another (catalytic selectivity), by simply changing the relative stability of reaction intermediates. Understanding the factors regulating the catalytic bias is of paramount important to design catalytic processes with enhanced rates and selectivity. In this review, we will discuss the parameters that define catalytic bias and recent work that supports a simple model for imposing bias in oxidation–reduction biocatalysis.
Catalytic bias
Let us consider the following reversible catalytic process| | 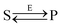 | (1) |
whereby two chemical species, S and P, are interconverted by a catalyst E. We define catalytic bias, ζ, the ratio between the forward, v(f), and backward reaction rates, v(b):| | 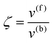 | (2) |
with v(f) = k+[S] and v(f) = k−[P], where k+ and k− are the (composite) forward and backward rate constants. If ζ > 1 then the catalyst produces preferentially P. Conversely, if ζ < 1 then the catalyst produces preferentially S. Instead, if ζ = 1 then there is not catalytic preference (bias) for either S or P.
Under thermodynamic equilibrium, there is no catalytic bias, since v(f) = v(b),
| | 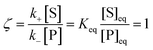 | (3) |
In non-equilibrium conditions,
ζ ≠ 1. The definition of catalytic bias adopted here differs from others provided in the recent literature (see for instance
ref. 1), based on the equilibrium (electro)chemical potential, whereby the bias is simply associated with the equilibrium constant
Keq, and a reaction is biased toward P or S if
Keq > 1 or
Keq < 1. This alternative definition masks the effect of the catalyst on the bias. Instead, the definition given in
eqn (3) is independent on the underlying thermodynamics of the process (by construction) and allows to disentangle the effect of the catalyst.
Let us now examine an important case of non-equilibrium condition, i.e., the steady state regime. Generally, the value of ζ under steady conditions depends on the underlying catalytic mechanism. We can easily show this by expanding the reaction (1) and introducing the formation of an association complex ES between the substrate and the catalyst, as shown in eqn (4).
| | 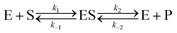 | (4) |
The steady state solution is (Haldane's equation)
2,3| | 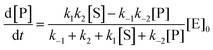 | (5) |
where [E]
0 is the initial concentration of the catalysts. A similar expression can be written for S. In enzymatic catalysis, maximal rates are typically measured working in large excess of either S or P. When [S] ≫ [P] the reaction is pushed toward P and
eqn (5) yields
| | 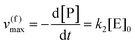 | (6) |
Instead, when [S] ≪ [P], the reaction is pushed toward S and
eqn (5) yields
| | 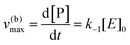 | (7) |
Using the maximal rate for the forward and backward reaction, we see that the catalytic bias under steady state conditions depends only on kinetic quantities:
| | 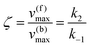 | (8) |
As can be seen from eqn (8), and in the particular case described by eqn (5), the catalytic bias is determined only by the ratio of the forward rate constant of the second step and the backward rate constant of the first step; there is no dependence on the concentration of any species involved in the catalysis (including the catalyst).
Eqn (8) clearly shows that an enzyme can be a better catalyst in one direction than the other direction depending on the relative magnitude of the rate constants.
Eqn (4) can be considered the simplest case of a catalytic reaction. Typically, a catalytic process comprises a multitude of catalytic intermediates and, likely, features branching points, which could originate a manifold of potential pathways. This complexity has important ramifications. Here we highlight what we believe is one of the most important, and somehow underappreciated, of these ramifications in enzymatic catalysis.
Let us consider a more elaborate case of reversible enzymatic reaction where the reaction proceeds through three reversible stages as indicated in eqn (9): the formation of the enzyme–substrate complex ES, its conversion to the enzyme–product complex EP and finally the dissociation to the product P.
| |  | (9) |
The steady state solution of
eqn (9) is
2,3| | 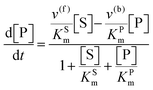 | (10) |
where
As before, we use
eqn (10) to obtain the maximal catalytic rates:
| v(f)max = v(f), when [S] ≫ [P] |
and
| v(b)max = v(b), when [S] ≪ [P] |
which yield the following expression for the catalytic bias:
| | 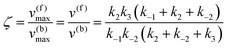 | (11) |
Eqn (11) clearly shows how every single step of the catalytic process contributes to the catalytic bias. Let us now consider the catalytic bias in the limiting situation where the reactions E + S ⇆ ES and E + P ⇆ EP are in fast equilibrium and the reaction ES ⇆ EP is rate limiting in both directions. Under this condition, k2 and k−2 are much smaller than the other rate constants and eqn (11) yields the following simple but illuminating result:
The catalytic bias corresponds to the equilibrium constant
Keq(ES/EP) of the catalytic step ES ⇆ EP,
i.e., the relative thermodynamic stability of ES and EP. Clearly, if
Keq(ES/EP) > 1 (
k2 >
k−2) then the catalytic process is biased toward the formation of P (
Fig. 1a). Instead, if ES and EP are equally stable,
i.e.,
Keq(ES/EP) = 1, there is no catalytic bias (
Fig. 1b). Finally, if
Keq(ES/EP) < 1 (
k2 <
k−2) then the catalytic process is biased toward the formation of S (
Fig. 1c).
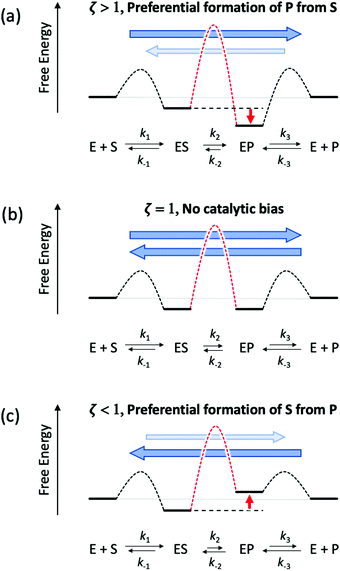 |
| | Fig. 1 Schematic representation of an ideal three-stage process for the equiergic interconversion of S and P (the equilibrium constant for S ⇆ P is 1, i.e., no thermodynamic driving force in a specific direction) by a catalyst E. Under steady state conditions, if ES ⇆ EP is rate limiting then the catalytic bias ζ, defined as the ratio between the maximal forward and backward rates, depends only on the relative stability of ES and EP. Panel a: If ES is less stable than EP (k2 > k−2) then the catalytic process is biased toward the production of P (ζ > 1); panel b: if ES and EP are equiergic (k2 = k−2) then there is no catalytic bias (ζ= 1); panel c: if ES is more stable than EP (k2 < k−2) then the process is biased toward the production of S (ζ < 1). | |
Typically, no reaction step is completely rate controlling. However, this result can be easily generalized and has a rather profound implication. Any modification of the environment that induces a stabilization or a destabilization of catalytic intermediates (e.g., ES vs. EP) can have important repercussions on the catalytic bias. Indeed, we can envision modifications that, under (non-equilibrium) steady state conditions, can change the relative propensity to generate S or P regardless of the overall underlying thermodynamic driving force, i.e., the relative stability of S and P.
Catalytic bias in enzymatic reactions
There is little known about bias in biological systems in the literature, likely as result of the overall complexity in designing effective methods to assay enzymes. More often than not, it is a challenge to design assay methods in one direction with enough accuracy to confidently determine kinetics constants. As a result, it is difficult to find examples in the literature of enzymes or catalysts where kinetic parameters have been defined in both directions in a manner that can be compared. As a consequence, it is difficult in asserting if catalytic bias is the exception or the rule in biocatalysis or catalysis in general.
There are several classes of metal-cofactor based enzymes that catalyse oxidation–reduction reactions that have been assessed in both directions. These enzymes are commonly assayed using external electron donors and acceptors that are redox active dye indicators, which span a range of reduction potentials.4 Different redox dependent dye indicators can be used to either measure oxidation or reduction spectrophotometrically as a function of a colour change, i.e. change in absorbance at a specific wavelength in the visible spectra. The particular type of dye can affect the observed catalytic rate, as they introduce different driving forces depending on the reaction. However, rates measured spectrophotometrically offer a qualitative illustrative analysis of the observed variation of catalytic bias in model systems.
Enzymes that have been measured in this manner and have reported kinetics constants for the forward and reverse directions of an oxidation–reduction reaction include: carbon monoxide dehydrogenases, formate dehydrogenases, and hydrogenases. These enzymes catalyse the reversible reduction of carbon dioxide to carbon monoxide (eqn (12)), carbon dioxide to formate (eqn (13)) and protons to dihydrogen (eqn (14)).
| | | CO2 + 2H+ + 2e− ⇆ CO + H2O | (12) |
| | | CO2 + H+ + 2e− ⇆ HCOO− | (13) |
As an example, carbon monoxide dehydrogenase/acetyl-CoA synthase (CODH/ACS) from
Carboxydothermus hydrogenoformans exhibits a bias towards CO oxidation
5,6 with a
kcat of 15,900 s
−1versus the 2 s
−1 for CO
2 reduction. Similarly, some formate dehydrogenases have been shown to have a bias toward formate oxidation.
7,8 For instance,
Thiobacillus sp. KNK65MA formate dehydrogenase exhibits a
kcat of 1.76 s
−1 for formate oxidation relative to 0.318 s
−1 for CO
2 reduction, respectively. In addition, formate dehydrogenase from
Chaetomium thermophilum exhibits formate oxidation with
kcat values of 1.8 and 0.025 s
−1 for the forward and reverse reactions, respectively.
5
Hydrogenases have long been implicated in having catalytic bias differences in rate accelerations between H+ reduction and H2 oxidation, and these differences are often linked to their physiological function.9 Although there are numerous enzymes in which H2 is a substrate or product, there are two classes of hydrogenases that formally catalyse reversible H2 oxidation termed [NiFe]-hydrogenases and [FeFe]-hydrogenases10,11 to reflect the composition of their respective active sites. These hydrogenases display a wide range of catalytic activity, with either a reaction bias for the H2 oxidation direction, H+ reduction direction, or in some cases no detectable preference at all (neutral bias). This most often is underpinned by their physiological role, which for [FeFe]-hydrogenases is generally to regenerate reduced electron carriers in anaerobic metabolism through the H+ reduction reaction or to supply electrons through the H2 uptake reaction to energy conversion processes, such as sulphate reduction, nitrogen fixation, and others.
For hydrogenases it is straightforward to measure rates of reactions using redox dependent dye indicators and/or measuring the production of H2 through gas chromatography. However, measuring Km values for H2 is technically challenging and for H+ in aqueous solutions not tractable. As a result, turnover frequency metrics are rare in the literature. Another challenge is that for a number of reports of hydrogenase activities that provide both values of H2 oxidation and H+ production, measurements of each activity are done under different pH values, i.e. activities for H2 oxidation at high pH and H+ reduction at low pH, which creates a bias within the bias. With those qualifications aside, although [NiFe]-hydrogenases have been implicated more in having a role in H2 oxidation physiologically, they display a variety of reactivity in which some are biased toward H2 oxidation, some toward H+ reduction and others where the activities in both directions are comparable (Table 1).12–27 [FeFe]-Hydrogenases have been implicated to a larger extent in the literature to functioning in H+ reduction, however the most well studied [FeFe]-hydrogenases exhibit high activities toward both H2 oxidation and H+ production with if anything a general bias toward H2 oxidation (Table 1).
Table 1 Specific activities reported for selected hydrogenases
| Enzymea |
Activityb |
Ref. |
| H2 oxidation |
H+ reduction |
Biasc |
|
Abbreviations: Hyd Tr, Thiocapsa roseopersicina; Hyn Dg, Desulfovibrio gigas; Hyn Df, D. fructosovorans; Av Hox, Anabaena variabilis ATCC 29413; Cht Hox, Chroococcidiopsis thermalis CALU 758; Ga Hox, Gloeocapsa alpicola; As(rev), Anabaena sp. strain 7120 (reversible); Ech Mb, Methanosarcina barkeri; Dd, Desulfovibrio desulfuricans; Dv, D. vulgaris (Hildenborough); Cr, Chlamydomonas reinhardtii; Cb, Clostridium beijerinckii (CbA5H); Tm, HydABC from Thermotoga maritima; Cp, Clostridium pasteurianum.
Activity expressed in μmol H2 min−1 mg−1 protein.
Bias – H2 oxidation/H+ reduction.
|
| [NiFe]-Hydrogenases |
| Hyd Tr |
53 |
63 |
0.8 |
12
|
| Hyn Dg |
50.5 |
90 |
0.6 |
13
|
| Hyn Df |
205 |
335 |
0.6 |
14
|
| HupUV |
21 |
3.7 |
5.7 |
15
|
| Av Hox |
9.0 |
10.2 |
0.8 |
16
|
| Cht Hox |
18.4 |
0.7 |
25.7 |
17
|
| Ga Hox |
0.3 |
3.6 |
0.08 |
18
|
| As(rev) |
63 |
24 |
2.6 |
19
|
| Ech Mb |
50 |
90 |
0.6 |
20
|
| [FeFe]-Hydrogenases |
| Dd |
62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
8200 |
7.5 |
21
|
| Dv |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
4800 |
10.4 |
22
|
| Cr |
271 |
728 |
0.37 |
23
|
| Cb |
158 |
751 |
0.21 |
24
|
| Tm |
500 |
270 |
1.8 |
25
|
| CpI |
24 000 |
5500 |
4.4 |
26
|
| CpII |
34 000 |
10 |
3400 |
26
|
| CpIII |
15 |
305 |
0.05 |
27
|
Like other oxidoreductases, the ability of the [FeFe]-hydrogenase active site to exist in multiple oxidation states with differing reduction potentials is essential for reversible H2 catalysis (Fig. 2). The catalytic cofactor, termed the H-cluster is strategically embedded within a protein environment which finely tunes its chemical properties and therefore the resulting catalytic bias, exploiting a variety of factors, including ligand coordination,28 non-covalent interactions,29 electrostatics,27 proton-transfer pathways and electron-transfer relays by additional metal centres.30–33 Together these effects can play an important role in modulating the catalytic activity and bias. In terms of a general reaction cycle for H2 catalysis, they can stabilize or destabilize certain catalytic steps and intermediates either in the H+ reduction direction (e.g. proton-coupled electron-transfer of HredH+ to form Hhyd) or H2 uptake direction (e.g. H2 binding to the oxidized state, Hox). Thus, as outlined above, this is a simple model for conferring catalytic bias where differential alteration of rate limiting steps in one direction relative to another would be expected to confer bias for either H+ reduction or H2 oxidation.
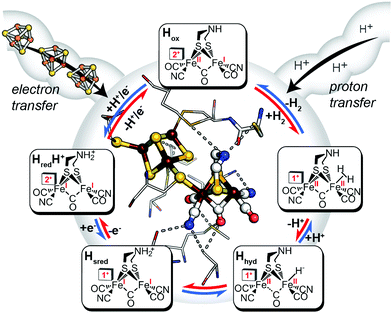 |
| | Fig. 2 Inner: catalytic active-site, the H-cluster, of CpI [FeFe]-hydrogenase depicted in its local environment and associated pathways for electron- and proton-transfer to and from the metal cofactor (X-ray crystal coordinates from PDB 3C8Y). Outer: mechanistic scheme for reversible H2 activation (blue arrows, H+ reduction direction; red arrows, H2 uptake direction) through spectroscopically defined H-cluster redox states (oxidized, Hox; reduced, HredH+, Hsred, Hhyd). Adapted from Artz et al.27 | |
A mechanism based on this concept through the differential stabilization of oxidation states of the H-cluster was recently revealed in detail by examination of a subset of three [FeFe]-hydrogenases (CpI, CpII, and CpIII) from the microorganism Clostridium pasteurianum using a combination of high-resolution X-ray diffraction techniques, biophysical analysis, and computational modelling.27 These enzymes have been shown to represent the extremes and median of bias for the reversible H2 catalytic reaction making them a truly unique model system for examining the mechanistic determinants of bias within a single system (Fig. 3). As measured through ferredoxin-based and artificial dye-coupled assays, CpI has been shown to catalyse both H+ reduction and H2 oxidation at relatively high rates, while CpII is biased toward H2 oxidation more than a thousand-fold with very low H+ reduction activity, while CpIII is biased toward the H+ reduction with very low H2 oxidation activity. Perhaps surprisingly, the differences in reactivity all occur by means of the same catalytic cofactor, but with subtle differences in the amino acid composition of the local environment of the H-cluster, as well as the complementation of additional electron-transfer clusters, termed F-clusters. For CpI, determination of the X-ray crystal structure in reduced and oxidized forms revealed several dynamic non-covalent interactions between the H-cluster and its second coordination sphere ligands, which strongly depend on the H-cluster oxidation state.27 Accompanying molecular dynamics and quantum chemical calculations further revealed that the specific conformations of these residues selectively stabilized either the oxidized (Hox) or 1-electron reduced (HredH+) intermediate of the H-cluster through modulation of its electronic properties over different redox potential regimes (Fig. 4). The results gave new understanding to the neutral bias of CpI, offering a model for redox-dependent, dynamic secondary interactions that can effectively modulate the relative ratios of active site redox intermediates in either oxidizing or reducing conditions that promote equal favourability for both the H+ reduction and H2 uptake directions.
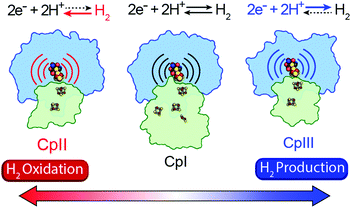 |
| | Fig. 3 Cartoon representations of CpI, CpII, and CpIII [FeFe]-hydrogenases. These enzymes span forward and reverse directional bias preferences for reversible H2 catalysis and share a modular-like arrangement of catalytic (blue) and electron-transfer (green) domains that feature the same active site H-cluster (sphere representation) embedded in different protein environments (curved lines) along with additional F-clusters (stick representations) for transferring electrons. Adapted from Artz et al.27 | |
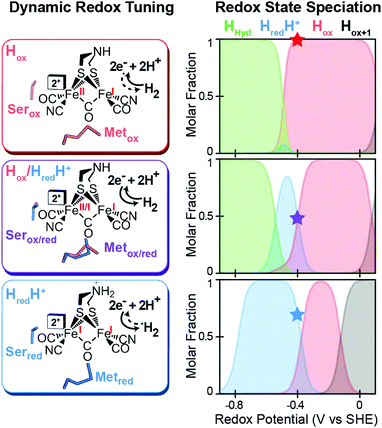 |
| | Fig. 4 Effect of dynamic, redox-dependent secondary interactions on the relative stabilization of active-site redox states for H2 catalysis. Left, stabilization of H-cluster redox states through dynamic secondary interactions by nearby serine (Ser) and methionine (Met) residues in either oxidized (ox), mixed (ox/red), or reduced (red) conformations. Right, effect of the different Met/Ser conformations on the speciation of H-cluster redox states as a function of the potential. The star at −400 mV corresponds to the redox configuration on left (voltage, V, vs. the standard hydrogen electrode, SHE at pH = 8, 25 °C and 1 atm H2). Adapted from Artz et al.27 | |
Likewise, a similar model based on the selective stabilization of active-site intermediates by the protein electrostatic fields has also emerged from the examination of CpII and CpIII [FeFe]-hydrogenases (Fig. 5).27 While X-ray crystal structures are not available for either of these enzymes, comparison of homology models reveal significant differences in the electrostatics and hydrophobicity of the surrounding H-cluster environment due to subtle changes in several non-coordinating residues. In similar fashion to CpI, quantum chemical calculations on the H-cluster, that modelled the differences in electrostatics by altering the dielectric environment at the active site, revealed significant changes in the steady-state speciation of H-cluster catalytic intermediates as a function of the redox potential. In particular, calculations revealed a destabilization of the Hox state for CpIII, which populated a narrow regime of reduction potentials compared to a wider range in CpI and CpII. This was corroborated spectroscopically as well, where only minimal signs of the Hox state were observed for CpIII when compared to CpII under similar conditions and a higher oxidation state (Hox+1) was observed instead. These findings helped explain the H+ reduction bias for CpIII, where destabilization of Hox can effectively diminish the H2 oxidation reaction rate as the state is critical to the initial H2 binding step for H2 oxidation. By similar reasoning for CpI and CpII, stabilization of Hox over a wider potential range is conducive for the H2 uptake reaction. As discussed above, it is feasible that selectively altering the kinetics of formation for certain catalytic intermediates through these effects may also lead to alternative reaction pathways that could in turn cause an overall change in reaction bias.
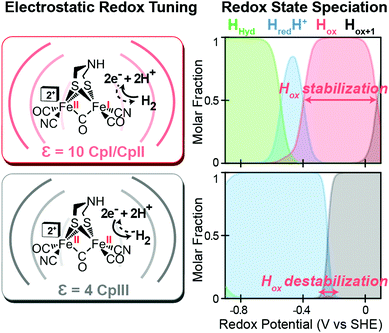 |
| | Fig. 5 Effect of electrostatic protein interactions on the relative stabilization of active site redox states for H2 catalysis. Left, stabilization or destabilization of the oxidized H-cluster redox state (Hox) by different electrostatics of the surrounding protein environment (curved lines) reflective of CpI, CpII (dielectric, ε, 10) and CpIII (dielectric, ε, 4). Right, effect of the different protein dielectrics on the speciation of H-cluster redox states as a function of the potential (voltage, V, vs. the standard hydrogen electrode, SHE at pH = 6, 25 °C and 1 atm H2). Adapted from Artz et al.27 | |
For hydrogenases, further tuning of the distribution of catalytic intermediates by electrostatic effects set in place between the H cluster and additional electron-transfer centres is also possible. This effect has been well characterized for the [NiFe]-hydrogenases, and it has been shown that the redox potential of the distal [4Fe–4S] cluster is critical for the catalytic bias.34,35 Likewise, for CpII it has been hypothesized that the more positive in potential [4Fe–4S] cluster most distal to the H-cluster can either serve as a thermodynamic bottleneck for electron-injection into the enzyme for the H+ reduction reaction or serve as a sink for electrons for the H2 oxidation reaction,36,37 with the proposed net effect being the destabilization of the reduced Hred state in relation to Hox.27 Influence on the H-cluster redox properties is also possible through cooperative interactions with nearby FeS clusters, as demonstrated on the [FeFe]-hydrogenase from Desulfovibrio desulfuricans.38 More broadly, oxidoreductases have likely evolved additional features for tuning redox reactions through altering the relative distribution of the catalytic cofactor redox intermediates. For the model Cp [FeFe]-hydrogenase summarized here, this paradigm is realized through dynamic secondary interactions, the local electrostatics, and potential effects from additional electron-transfer centres.
Catalytic bias in molecular electrocatalysts
Reversible catalysis is one of the cornerstones in the current quest for energy storage and energy utilization technologies.39 Tremendous progress has been made over the years toward efficient and reversible catalytic platforms to store in and retrieve electrons from chemical bonds, most notably for H2 production/oxidation,40,41 reversible CO2 reduction to HCO2−,42 and reversible dehydrogenation of alcohols.43 However, there is only a very limited number of examples of reversible catalytic processes for which sufficient data exist on the functional determinants at the core of reversibility and catalytic bias. Perhaps, the family of molecular electrocatalysts for H2 oxidation and H2 production developed by DuBois,44 Bullock and their co-workers45 represent the most enlightening example.
The crystal structure of the [FeFe]-hydrogenases revealed an azadithiolate bridge featuring an amine base properly positioned to transfer protons to and from the catalytic distal Fe in the H-cluster (Fig. 2). This observation led DuBois and his collaborators to develop mono-metallic [Ni(PR2NR′2)2]2+ electrocatalysts containing 1,5-diaza-3,7-diphosphacyclooctane (PR2NR′2) ligands that include positioned pendant amines in the second coordination sphere46 (Fig. 6) to facilitate proton movement and H2 molecule formation or splitting. Over the years, [Ni(PR2NR′2)2]2+ catalysts and variants of them based on different metals and different ligand sets have been synthetized with a clear propensity either for H2 oxidation or H2 production.46 Notably, some of these molecular electrocatalysts show reversible catalysis.40,47 A wealth of experimental and computational studies allowed for a full rationalization of the structural and electronic determinants that regulate the rate and directionality of catalysis. The catalytic mechanism is rather complex with multiple reactive pathways that are operative depending on the nature of the substituents and the catalytic conditions.45 In particular, and similar to [FeFe]-hydrogenases, protonation/deprotonation steps and H2 binding/dissociation steps all contribute to the rate and directionality. Nevertheless, a few general considerations can be made. Relevant to the present commentary is the observation that the free energy of binding of H2 to the metal centre, ΔG°(H2), to form a N-protonated metal hydride is the main determinant of the directionality of the catalytic process (Fig. 6). Specifically, exoergic H2 binding leads to H2 production, endoergic H2 binding leads to H2 oxidation catalysts, while an equiergic binding leads to reversible catalysts. The free energy of H2 addition is determined by two quantities: the hydride donor ability, ΔG°(H−), and the pKa of the protonated pendant amine.48,49 The higher the hydride donor ability and the lower the basicity of the pendant amine, the larger the ΔG°(H2). ΔG°(H−) is substantially affected by the twisting angle at the metal centre (dihedral angle between the planes identified by the P atoms of each ligand and the Ni atom). Generally, the bulkier the substituent R on the P atoms, the more twisted the catalyst is and the smaller ΔG°(H−). For example, ΔG°(H−) decreases along the following series of substituents: R = phenyl < cyclohexyl < tert-butyl (Fig. 6). In contrast, the pKa is mostly influenced by the basicity of the parent amine R′-NH2. The electron withdrawing capabilities of the substituent of the P atoms, R, also contribute to ΔG°(H−) and pKa. Modification of R and R′ allows for a fine-tuning of ΔG°(H2) and smoothly progressing from H2 oxidation catalysts to H2 production catalysts. The overall rate, and catalytic bias, is determined by the balance between the free energy of H2 addition and the rate of protonation/deprotonation of catalytic intermediates. Generally, the larger the absolute value of ΔG°(H2) the larger the bias toward H2 production or H2 oxidation, even if, optimization of the proton delivery process can lead to high catalytic rates also for small ΔG°(H2).
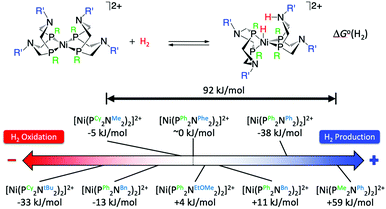 |
| | Fig. 6 Standard free energy ΔG°(H2) for H2 addition to various [Ni(PR2NR′2)2]2+ complexes. Cy = cyclohexyl, tBu = tert-butyl, Me = methyl, Bn = benzyl, Ph = phenyl, Phe = phenyl alanine, EtOMe = –CH2CH2–O–CH3. Adapted from Raugei et al.46 | |
Conclusions
Catalytic bias is probably an inherent property of many, if not most, enzymes and synthetic catalysts. However, there is really a limited amount of information available for the catalytic bias of enzymes as activities reported are typically only in one direction. This is likely a consequence of the technical challenges in developing assays for enzymes sensitive enough to obtain reliable quantitative data to extract kinetic parameters. In addition, there is a propensity in enzymatic studies to focus on a physiologically relevant reaction. Hydrogenases are perhaps a notable exception due to the ease of assaying the enzymes in both directions and the interest in both reactions (H2 oxidation and H+ reduction). From what we can glean from the literature from hydrogenases, catalytic bias is the rule rather than the exception for enzyme catalysed reversible H2 oxidation, making them an ideal model system for examining the determinants of catalytic bias experimentally. For both [NiFe]-hydrogenases and [FeFe]-hydrogenases, the active site metal clusters are the same for each class such that differences in catalytic bias are dictated by the amino acid environment of the active site cluster and/or the properties of the accessory clusters that serve as a conduit for transferring electrons to and/or from external electron donors and acceptors. The large bias observed in comparing the [FeFe]-hydrogenases can be explained by various protein design features that collectively modulate the relative stabilization/destabilization of oxidation states relevant to the rate limiting steps of the reaction in either direction. The modulation of the stability at the active site can be conferred by the electrostatics of the environment of the active site or the reduction potential and/or proximity of accessory electron transfer redox centres. The relative stabilization/destabilization of oxidations represents a simple mechanism to confer a catalytic bias in cofactor-based oxidation–reduction reactions. Data from well-studied molecular catalysts for H2 oxidation/H2 production support the generality of the concept of catalytic bias, whereby fine tuning of the first and second coordination spheres of a catalytic metal centre allows for a smooth transition from H2 production to H2 oxidation.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We would like to thank Oleg Zadvornyy for assistance in assembling the content of Table 1. Funding for research on catalytic bias in cofactor-based oxidation–reduction catalysis is provided by the National Institutes of Health (1R01GM138592-01) (J. W. P. and S. R.). Funding for research on biochemical mechanisms of redox enzymes was provided by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, Photosynthetic Systems Program (D. W. M.). The National Renewable Energy Laboratory is operated by the Alliance for Sustainable Energy, LLC., for the U.S. DOE under Contract No. DE-AC36-08GO28308. Pacific Northwest National Laboratory is operated by Battelle for DOE under Contract No., DE-AC05-76RL01830. The views expressed in this article do not necessarily represent the views of DOE or the U.S. Government. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.
Notes and references
- V. Fourmond, E. S. Wiedner, W. J. Shaw and C. Léger, J. Am. Chem. Soc., 2019, 141, 11269–11285 CrossRef CAS.
- W. W. Cleland, Biochim. Biophys. Acta, Spec. Sect. Enzymol. Subj., 1963, 67, 104–137 CrossRef CAS.
- E. L. King and C. Altman, J. Phys. Chem., 1956, 60, 1375–1378 CrossRef CAS.
- M. L. Fultz and R. A. Durst, Anal. Chim. Acta, 1982, 140, 1–18 CrossRef CAS.
- J. Seravalli, M. Kumar, W.-P. Lu and S. W. Ragsdale, Biochemistry, 1997, 36, 11241–11251 CrossRef CAS.
- J. Seravalli and S. W. Ragsdale, Biochemistry, 2008, 47, 6770–6781 CrossRef CAS.
- H. Choe, J. C. Joo, D. H. Cho, M. H. Kim, S. H. Lee, K. D. Jung and Y. H. Kim, PLoS One, 2014, 9, e103111 CrossRef.
- U. Pala, B. Yelmazer, M. Corbacioglu, J. Ruupunen, J. Valjakka, O. Turunen and B. Binay, Protein Eng., Des. Sel., 2018, 31, 327–335 CrossRef CAS.
- P. M. Vignais and B. Billoud, Chem. Rev., 2007, 107, 4206–4272 CrossRef CAS.
- W. Lubitz, H. Ogata, O. Rudiger and E. Reijerse, Chem. Rev., 2014, 114, 4081–4148 CrossRef CAS.
- J. W. Peters, G. J. Schut, E. S. Boyd, D. W. Mulder, E. M. Shepard, J. B. Broderick, P. W. King and M. W. Adams, Biochim. Biophys. Acta, 2015, 1853, 1350–1369 CrossRef CAS.
- N. A. Zorin, B. Dimon, J. Gagnon, J. Gaillard, P. Carrier and P. M. Vignais, Eur. J. Biochem., 1996, 241, 675–681 CrossRef CAS.
- C. Baffert, A. Kpebe, L. Avilan and M. Brugna, Adv. Microb. Physiol., 2019, 74, 143–189 CrossRef.
- C. E. Hatchikian, A. S. Traore, V. M. Fernandez and R. Cammack, Eur. J. Biochem., 1990, 187, 635–643 CrossRef CAS.
- P. M. Vignais, B. Dimon, N. A. Zorin, M. Tomiyama and A. Colbeau, J. Bacteriol., 2000, 182, 5997–6004 CrossRef CAS.
- L. T. Serebryakova, M. Medina, N. A. Zorin, I. N. Gogotov and R. Cammack, FEBS Lett., 1996, 383, 79–82 CrossRef CAS.
- L. T. Serebryakova, M. E. Sheremetieva and P. Lindblad, Plant Physiol. Bioch., 2000, 38, 525–530 CrossRef CAS.
- L. T. Serebryakova, M. Sheremetieva and A. A. Tsygankov, FEMS Microbiol. Lett., 1998, 166, 89–94 CrossRef CAS.
- J. P. Houchins and R. H. Burris, J. Bacteriol., 1981, 146, 215–221 CrossRef CAS.
- J. Meuer, S. Bartoschek, J. Koch, A. Kunkel and R. Hedderich, Eur. J. Biochem., 1999, 265, 325–335 CrossRef CAS.
- E. C. Hatchikian, N. Forget, V. M. Fernandez, R. Williams and R. Cammack, Eur. J. Biochem., 1992, 209, 357–365 CrossRef CAS.
- G. Fauque, H. D. Peck, Jr., J. J. Moura, B. H. Huynh, Y. Berlier, D. V. DerVartanian, M. Teixeira, A. E. Przybyla, P. A. Lespinat and I. Moura,
et al.
, FEMS Microbiol. Rev., 1988, 4, 299–344 CrossRef CAS.
- L. Kertess, A. Adamska-Venkatesh, P. Rodríguez-Maciá, O. Rüdiger, W. Lubitz and T. Happe, Chem. Sci., 2017, 8, 8127–8137 RSC.
- S. Morra, M. Arizzi, F. Valetti and G. Gilardi, Biochemistry, 2016, 55, 5897–5900 CrossRef CAS.
- N. Chongdar, K. Pawlak, O. Rudiger, E. J. Reijerse, P. Rodriguez-Macia, W. Lubitz, J. A. Birrell and H. Ogata, J. Biol. Inorg. Chem., 2020, 25, 135–149 CrossRef CAS.
- M. W. Adams, Biochim. Biophys. Acta, 1990, 1020, 115–145 CrossRef CAS.
- J. H. Artz, O. A. Zadvornyy, D. W. Mulder, S. M. Keable, A. E. Cohen, M. W. Ratzloff, S. G. Williams, B. Ginovska, N. Kumar, J. Song, S. E. McPhillips, C. M. Davidson, A. Y. Lyubimov, N. Pence, G. J. Schut, A. K. Jones, S. M. Soltis, M. W. W. Adams, S. Raugei, P. W. King and J. W. Peters, J. Am. Chem. Soc., 2020, 142, 1227–1235 CrossRef CAS.
- P. Rodriguez-Macia, L. Kertess, J. Burnik, J. A. Birrell, E. Hofmann, W. Lubitz, T. Happe and O. Rudiger, J. Am. Chem. Soc., 2019, 141, 472–481 CrossRef CAS.
- O. Lampret, A. Adamska-Venkatesh, H. Konegger, F. Wittkamp, U. P. Apfel, E. J. Reijerse, W. Lubitz, O. Rudiger, T. Happe and M. Winkler, J. Am. Chem. Soc., 2017, 139, 18222–18230 CrossRef CAS.
- O. Lampret, J. Duan, E. Hofmann, M. Winkler, F. A. Armstrong and T. Happe, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 20520–20529 CrossRef CAS.
- G. Caserta, C. Papini, A. Adamska-Venkatesh, L. Pecqueur, C. Sommer, E. Reijerse, W. Lubitz, C. Gauquelin, I. Meynial-Salles, D. Pramanik, V. Artero, M. Atta, M. Del Barrio, B. Faivre, V. Fourmond, C. Leger and M. Fontecave, J. Am. Chem. Soc., 2018, 140, 5516–5526 CrossRef CAS.
- J. H. Artz, D. W. Mulder, M. W. Ratzloff, C. E. Lubner, O. A. Zadvornyy, A. X. LeVan, S. G. Williams, M. W. W. Adams, A. K. Jones, P. W. King and J. W. Peters, J. Am. Chem. Soc., 2017, 139, 9544–9550 CrossRef CAS.
- C. Esmieu, P. Raleiras and G. Berggren, Sustainable Energy Fuels, 2018, 2, 724–750 RSC.
- S. V. Hexter, F. Grey, T. Happe, V. Climent and F. A. Armstrong, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11516–11521 CrossRef CAS.
- H. Adamson, M. Robinson, J. J. Wright, L. A. Flanagan, J. Walton, D. Elton, D. J. Gavaghan, A. M. Bond, M. M. Roessler and A. Parkin, J. Am. Chem. Soc., 2017, 139, 10677–10686 CrossRef CAS.
- M. W. Adams, E. Eccleston and J. B. Howard, Proc. Natl. Acad. Sci. U. S. A., 1989, 86, 4932–4936 CrossRef CAS.
- M. W. Adams, J. Biol. Chem., 1987, 262, 15054–15061 CAS.
- P. Rodriguez-Macia, K. Pawlak, O. Rudiger, E. J. Reijerse, W. Lubitz and J. A. Birrell, J. Am. Chem. Soc., 2017, 139, 15122–15134 CrossRef CAS.
- J.-M. Savéant, ACS Catal., 2018, 8, 7608–7611 CrossRef.
- A. Dutta, A. M. Appel and W. J. Shaw, Nat. Rev. Chem., 2018, 2, 244–252 CrossRef CAS.
- B. Ginovska-Pangovska, A. Dutta, M. L. Reback, J. C. Linehan and W. J. Shaw, Acc. Chem. Res., 2014, 47, 2621–2630 CrossRef CAS.
- D. W. Cunningham, J. M. Barlow, R. S. Velazquez and J. Y. Yang, Angew. Chem., Int. Ed., 2019, 59, 4443–4447 CrossRef.
- P. J. Bonitatibus, S. Chakraborty, M. D. Doherty, O. Siclovan, W. D. Jones and G. L. Soloveichik, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 1687 CrossRef CAS.
- D. L. DuBois, Inorg. Chem., 2014, 53, 3935–3960 CrossRef CAS.
- M.-H. Ho, R. Rousseau, J. A. S. Roberts, E. S. Wiedner, M. Dupuis, D. L. DuBois, R. M. Bullock and S. Raugei, ACS Catal., 2015, 5, 5436–5452 CrossRef CAS.
- S. Raugei, M. L. Helm, S. Hammes-Schiffer, A. M. Appel, M. O’Hagan, E. S. Wiedner and R. M. Bullock, Inorg. Chem., 2016, 55, 445–460 CrossRef CAS.
- S. E. Smith, J. Y. Yang, D. L. DuBois and R. M. Bullock, Angew. Chem., Int. Ed., 2012, 51, 3152–3155 CrossRef CAS.
- S. Chen, M.-H. Ho, R. M. Bullock, D. L. DuBois, M. Dupuis, R. Rousseau and S. Raugei, ACS Catal., 2014, 4, 229–242 CrossRef CAS.
- S. Chen, R. Rousseau, S. Raugei, M. Dupuis, D. L. DuBois and R. M. Bullock, Organometallics, 2011, 30, 6108–6118 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a,
John W.
Peters
*a,
John W.
Peters
 *b and
Simone
Raugei
*b and
Simone
Raugei
 *c
*c

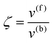
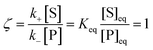
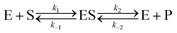
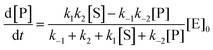
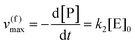
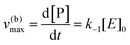
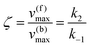


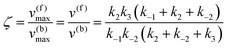
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000