Open Access Article
Open Access ArticleMeasuring the size and density of nanoparticles by centrifugal sedimentation and flotation†
Caterina
Minelli
 *a,
Aneta
Sikora
*a,
Aneta
Sikora
 a,
Raul
Garcia-Diez
b,
Katia
Sparnacci
a,
Raul
Garcia-Diez
b,
Katia
Sparnacci
 c,
Christian
Gollwitzer
b,
Michael
Krumrey
c,
Christian
Gollwitzer
b,
Michael
Krumrey
 b and
Alex G.
Shard
a
b and
Alex G.
Shard
a
aNational Physical Laboratory, Hampton Road, Teddington TW11 0LW, UK. E-mail: caterina.minelli@npl.co.uk
bPhysikalisch-Technische Bundesanstalt (PTB), Abbestr. 2-12, 10587 Berlin, Germany
cUniversità del Piemonte Orientale “A. Avogadro”, Viale T. Michel 11, I-15121 Alessandria, Italy
First published on 29th March 2018
Abstract
The successful translation of nanoparticle-based systems into commercial products depends upon the ability to reliably measure important physical and chemical properties of these particles. The density of nanoparticles is one such property, because it provides important information about the composition of the material. In this work, an analytical centrifugation approach based on line-start centrifugal sedimentation and flotation measurements is described. The two independent measurements permit both the size and the density of these nanoparticles to be determined with excellent precision. A set of monodisperse polystyrene nanoparticles of different sizes is used to demonstrate this method. The density and size measurements are validated by comparison to accurate Small Angle X-ray Scattering (SAXS) analysis for particles within the size range of SAXS, i.e. less than ∼300 nm in diameter. Both sedimentation and flotation measurements produce consistent high resolution size distributions of the particles and the measured size and density values are identical, within experimental uncertainty, to the SAXS results. This approach has the potential to provide useful characterisation of a range of particles of interest, for example, for medical application, such as liposomes and polymeric drug carriers.
Introduction
The majority of nanoparticles (NPs) used in technological applications contain internal structures with, for example, engineered coatings or compartments loaded with functional molecules. Some of the particles used in medicine have coatings that prevent protein fouling to avoid their agglomeration or elimination via the reticuloendothelial system.1 Liposomal and polymeric carriers which package drug molecules in their core have been successfully commercialised, as in the case of liposomal doxorubicin (Doxil®)2 and protein-bound paclitaxel (Abraxane®)3 for cancer treatment. A similar situation is true in other areas, for example in catalysis the NanoSelect™ technology has enabled the commercialisation of Pd catalysts as lead-free Lindlar catalyst replacements in alkyne-to-cis-alkene hydrogenations.4 Their organic coatings are essential in ensuring chemoselectivity and efficiency.The successful translation of particle-based systems into commercial products requires the ability to reliably measure the physical and chemical properties of these particles, to ensure that: the synthesis is reproducible and efficient, batch to batch variability is reduced, and the stability of the final product can be monitored. Ideally, the measurement methods should be cost effective and rapid, sufficiently precise to reliably measure differences and changes in the products, and provide statistically relevant information. For example, dynamic light scattering (DLS) is extensively used in this setting for the measurement of particle size and an expanding selection of other benchtop techniques are available.5
Size is only one characteristic of a particle system and further insight into particle properties is required. For example, combining the knowledge of particle size with that of their density can provide access to a range of additional information, such as molecular coating thickness and pack density,6–10 core porosity,5 chemical composition,11 particle deformation,12 particle encapsulation into vesicles,13 and drug loading.14 The knowledge of particle density is also useful during sample preparation for formulation and analysis. For example centrifugal sedimentation of NPs is commonly used in science and technology to separate particles of different size and density.
Differential centrifugal sedimentation (DCS), also known as centrifugal photo-sedimentation, is a benchtop technique which is commonly used to measure high resolution size distributions of NPs. DCS measures the time it takes to NPs to sediment through a fluid when exposed to a centrifugal field. This time depends on both the NP size and density. Where the size of the particles is known from an independent technique, DCS has been used with success to measure their density.5,11,12 DCS has also been used to measure both the size and density of particles by performing two independent DCS experiments using different fluid densities.5,15–17
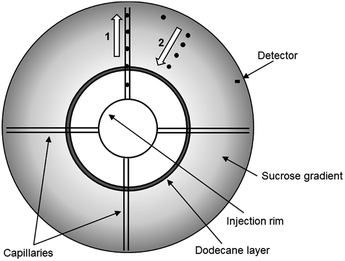
Recently, the DCS method has been developed to permit the analysis of particles which have a density close to, or below that of water. These low density particles “float” through a gradient of higher density rather than sedimenting through a gradient of lower density (Fig. 1). In a sedimentation experiment the sample is injected at the centre of a rotating disc and sediments towards the edge, where it is detected by a photodetector placed near the edge. To allow experiments by flotation, the disc has been modified so that the sample injected at the centre of the disc is delivered to the disc edge through four capillaries. From the disc edge the sample is released into the gradient and floats towards the detector. This technical innovation has opened up the possibility to measure high resolution size distributions and densities of particles such as liposomes, low density polymer particles and oil droplets. However, the literature on DCS operated in flotation mode is extremely scarce and, to our knowledge, this approach has only been briefly described in one of our previous publications.15
In this work we show the utility of the DCS technique to analyse particles with density below 1.2 g cm−3. We describe in detail the set-up which is required for this type of analysis. Furthermore, we provide examples of application to the measurement of both the diameter and density of a set of polystyrene particles ranging in size from about 120 nm to 600 nm, and to the analysis of liposomes with diameters of about 100 nm.
Experimental
Materials
The polystyrene NPs were synthesized by emulsion polymerization of styrene using sodium dodecyl sulphate (SDS) as surfactant. The amount of monomer and surfactant in the reaction mixture was properly adjusted to obtain particles with different size (Table S1 of the ESI†). The polymerization reactions were carried out in a 1 L five-neck reactor equipped with a condenser, a mechanical stirrer, a thermometer and inlets for nitrogen and styrene. 500 mL of ultrapure water containing the appropriate amount of SDS (see Table S1† for details) was introduced into the reactor at room temperature with a stirring rate of 300 rpm, then the appropriate amount of styrene (Table S1†) was added dropwise. The mixture was purged with nitrogen, and nitrogen was fluxed during the entire polymerization procedure. The reactor was heated to 80 °C, then a potassium persulfate aqueous solution (5.0 mL, 0.74 mmol) was added, and the mixture was reacted for 24 h. The obtained latex was purified from surfactant and unreacted monomer by repeated dialyses against ultrapure water (cellulose membrane, molecular weight cut-off 12 kDa). Table S1† collects the details of the various preparations, including the latex yield.Differential centrifugal sedimentation (DCS)
DCS measurements were performed with CPS Disk Centrifuge instruments, Model DC24000 (CPS Instruments, Prairieville, LA, USA), in both sedimentation and flotation configurations. Prior to the measurements a sucrose (Amresco LLC, OH, USA) gradient was built within the disc, according to manufacturer instructions. The density gradient is necessary to counteract the destabilizing effect of higher apparent density in the sample and avoid so called “streaming” i.e. the behaviour of the particle sample like a fluid of higher density, rather than like individual particles suspended in a fluid of lower density.18 The gradient was allowed to thermally equilibrate for 30 minutes before starting the measurements. The resulting average densities of the gradients were 1.011 g cm−3 (sucrose/water) for sedimentation and 1.14 g cm−3 (sucrose/D2O) for flotation experiments respectively. Turbidity measurements at the detector were performed using a diode laser at a wavelength of 405 nm. All experiments used a rotational frequency of 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm and injection volume of 100 μL. Each sedimentation measurement was calibrated using polystyrene particles of nominal size 522 nm and density 1.05 g cm−3. Each flotation measurement was calibrated using polybutadiene particles of nominal size 510 nm and density 0.91 g cm−3. The PS NP samples were diluted 20
000 rpm and injection volume of 100 μL. Each sedimentation measurement was calibrated using polystyrene particles of nominal size 522 nm and density 1.05 g cm−3. Each flotation measurement was calibrated using polybutadiene particles of nominal size 510 nm and density 0.91 g cm−3. The PS NP samples were diluted 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times from the original solution using ultrapure water for sedimentation experiments and 16% (w/w) sucrose solution in D2O for flotation experiments. The liposomes (Excytex, Zeist, The Netherlands) were also diluted 100 times in a 30% (w/w) sucrose solution in water. Each sample injection in flotation mode was followed by three 100 μL injections of 16% (w/w) sucrose in D2O to remove any sample particles retained in the disc injection rim and capillaries. Results are expressed as the arithmetic mean of the number weighted modal particle diameter from 3 repeat experiments. The uncertainty is the combined repeatability and propagated standard uncertainty.
000 times from the original solution using ultrapure water for sedimentation experiments and 16% (w/w) sucrose solution in D2O for flotation experiments. The liposomes (Excytex, Zeist, The Netherlands) were also diluted 100 times in a 30% (w/w) sucrose solution in water. Each sample injection in flotation mode was followed by three 100 μL injections of 16% (w/w) sucrose in D2O to remove any sample particles retained in the disc injection rim and capillaries. Results are expressed as the arithmetic mean of the number weighted modal particle diameter from 3 repeat experiments. The uncertainty is the combined repeatability and propagated standard uncertainty.
According to Stokes' law, the time of sedimentation t of a perfect rigid sphere as measured by DCS is:
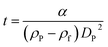 | (1) |
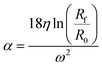 | (2) |
The parameter α is computed by means of a particle calibrant of known size and density which is run under the same experimental conditions as the sample. The time of sedimentation tc of the calibrant particles with diameter DC and density ρC is:
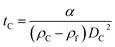 | (3) |
The ratio of eqn (1) and (3) provides the expression for the diameter of the particle DP:
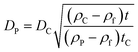 | (4) |
If the size of the particle DP is known, for example from independent measurements, the density of the particle ρP can be measured according to:
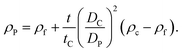 | (5) |
Dynamic light scattering (DLS)
DLS measurements were performed on a Zetasizer Nano ZS (Malvern Instruments Ltd., Malvern, UK) equipped with a max 4 mW He–Ne laser, emitting at 633 nm. Samples were diluted as appropriate and measurements performed in disposable capillary cuvettes (DTS1070, Malvern Instruments Ltd., UK). Each measurement was performed at the non-invasive backscatter angle (NIBS) of 173° at a temperature of 25 °C and preceded by a 3 min equilibration time. Particle size is expressed as the Z-ave value calculated with the cumulant method. Each value is the mean of four measurements.Scanning electron microscopy (SEM)
Particle diameter and size distribution were measured by scanning electron microscopy (SEM). The microscope was an Inspect F SEM-FEG (Field Emission Gun) from FEI Company (Hillsboro, USA), with a beam diameter of 3 nm, equipped with EDAX microanalysis. The samples were sputter coated under vacuum with a thin layer (20–30 Å) of gold. The SEM micrographs were elaborated by the ImageJ32 image processing program. From 300 to 350 individual NP diameters were measured for each sample. The results are expressed as the mean value of the distribution and the uncertainty as the standard error of the mean.Small angle X-ray scattering (SAXS)
The PS NPs in suspension were filled into vacuum-proof borosilicate glass capillaries (Hilgenberg, Malsfeld, Germany), where a solvent density gradient was achieved by bringing together two mixtures of the sample with different densities. For the bottom of the capillary, a high density mixture was prepared with a fructose (Sigma-Aldrich, Missouri, USA) mass fraction of 67% and a corresponding solvent electron density of 433 nm−3, while on the top side of the capillary a low density preparation with the same volume fraction of sample (17%) was introduced, using an ethanol mass fraction of 78.5% with a solvent electron density of 280 nm−3. The scattering experiments were performed with the SAXS setup of Helmholtz-Zentrum Berlin25 at the four-crystal monochromator beamline of PTB19 at the synchrotron radiation facility BESSY II (Helmholtz-Zentrum Berlin, Germany) with a photon energy of E = (8000.0 ± 0.8) eV. By means of the continuous contrast variation technique described elsewhere20 scattering patterns at different suspending medium electron densities were collected during 60 s at a distance L = (4539 ± 1) mm from the capillaries using a vacuum-compatible Pilatus 1 M hybrid pixel detector (Dectris Ltd, Baden, Switzerland) with a pixel size of d = (172.1 ± 0.2) μm.21 The recorded scattering patterns were circularly integrated and converted to momentum transfer q using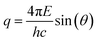 | (6) |
The diameter of the particles was determined by fitting the scattering curve measured at a solvent electron density of 290 nm−3 using a model equation describing polydisperse spherical particles with a Gaussian diameter distribution. An additive two-component background comprising a constant intensity and a term proportional to q−4 was assumed. The combined standard uncertainty associated to the particle diameter is dominated by the contribution arising from the fitting procedure, which is calculated with a confidence level of one standard deviation (k = 1) by examining the change in χ2 when varying the diameter. The average electron density of the NPs was determined by analyzing the behaviour of the scattering intensity at zero-angle as a function of the solvent electron density15 whereas the associated measurement uncertainty is related to the size of the photon beam.
Tunable resistive pulse sensing (TRPS)
TRPS measurements were performed with a qNano instrument (Izon Science Ltd, Christchurch, NZ). Based on the Coulter principle, TRPS measures the reduction in ionic current across a pore on a stretchable membrane (NP100, supplied by Izon) due to the temporary occlusion of the pore as a particle traverses it. As the exact geometry of the pore is not known, calibration particles (CPC100, nominal mean size of 118 nm, supplied by Izon) with known properties are measured at the same pore stretch as the sample and the relative values from the two measurements are compared.22 The blockade event signal is recorded by the instrument each time a particle traverses the pore. The magnitude of the measured blockade signal is directly proportional to the volume of the particle, allowing the determination of the particle diameter assuming spherical geometry. A minimum of 500 and 1000 events were recorded for each measurement of the calibrant and the sample respectively. Liposomes from Excytex (Zeist, The Netherlands) were diluted 4000 times in phosphate buffer (PBS, Sigma, St Louis, MO). The measurements were performed in duplicate for each of three different pressures. The current pulse signals were collected and exported for analysis using the Izon Control Suite software v2.2. The results were averaged and the uncertainty is expressed as the standard deviation of the values.Results and discussion
A set of 5 monodisperse PS NPs with average diameters ranging from about 120 nm to 600 nm were successfully synthesized. Fig. 2 shows some representative SEM images of the particles. The particles appear spherical and highly monodisperse in diameter. | ||
| Fig. 2 Representative SEM images of PS NPs of samples (A) PS120, (B) PS200, (C) PS250, (D) PS300 and (E) PS600. | ||
The average diameter of the particles as measured by SEM is summarised in Table 1. These are in close agreement with the particle diameters measured in water by SAXS using a spherical model, which are also summarised in Table 1. It is important to note that SAXS is a traceable technique, thus the obtained NP diameter can be related to the definition of the unit ‘meter’ in the International System of Units.23 The traceability of SAXS arises from the precise determination of the oscillation period on the q-axis, which is calibrated using SI traceable values of the X-ray wavelength and the scattering angle.24 The polydispersity of a particle sample affects SAXS accuracy, but typically, SAXS can measure particles with a polydispersity (defined as FWHM/mean) of up to 30% with high accuracy. In this work we take into account the polydispersity of the particles when computing the fit uncertainty, which is the major contribution to the measurement uncertainty. The agreement between SAXS and SEM results indicates that the SEM sample preparation and measurement conditions did not significantly affect the geometry of the particles or introduce artefacts. In fact, the sphericity values (derived from a model equation describing polydisperse spherical particles) used in the SAXS data evaluation were in good agreement with the micrograph observations. Unfortunately, SAXS could only be employed in a traceable way to determine the diameter of NPs with sizes up to 250 nm due to the limited q-range available in the experiment.
| Name | SEM diametera (nm) | SAXS | DCS | DLS diametera (nm) | ||
|---|---|---|---|---|---|---|
| Diameter (nm) | Density (g cm−3) | Diameter (nm) | Density (g cm−3) | |||
| a The estimation of the uncertainty for DLS and SEM is beyond the scope of the work. Precision was found to be ∼0.3 nm for SEM and 1% for DLS. | ||||||
| PS120 | 121 | 119.6 ± 1.6 | 1.049 ± 0.009 | 115.2 ± 4.1 | 1.050 ± 0.002 | 139 |
| PS200 | 197 | 199.3 ± 3.0 | 188.4 ± 5.8 | 1.050 ± 0.002 | 215 | |
| PS250 | 250 | 249.2 ± 3.5 | 235.9 ± 6.9 | 1.051 ± 0.002 | 260 | |
| PS300 | 305 | not measured | not measured | 298.6 ± 8.5 | 1.051 ± 0.002 | 331 |
| PS600 | 591 | not measured | not measured | 576 ± 16 | 1.047 ± 0.002 | 650 |
The size and density of the PS particles, modelled as perfect rigid spheres, were both measured by DCS. To measure the two parameters, two experiments were performed for each particle sample. One experiment involved the sedimentation of the particles through a sucrose gradient of average density 1.011 g cm−3, while a second experiment involved the flotation of the particles through a gradient of average density 1.14 g cm−3. The results of these experiments are summarised in Table S2 of the ESI.† The results of the two experiments were combined to produce a unique solution for the mode of the size distribution and the density of the particles. The number based size distributions as measured by DCS in the two modes are shown in Fig. 3 and the resulting diameter and density values are summarised in Table 1.
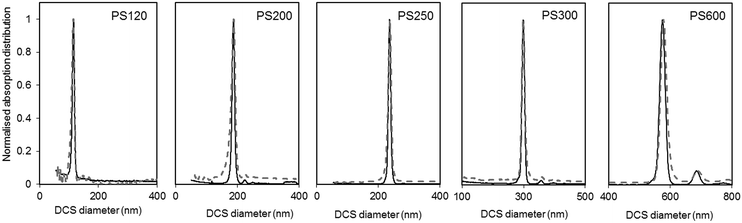 | ||
| Fig. 3 Normalised light extinction weighted size distributions of the PS NPs as measured by DCS in sedimentation (continuous black line) and flotation (dash grey line) modes. The NPs are assumed perfect spheres of density as in Table 1. | ||
The size distributions measured in flotation mode appear noisier and broader than those measured in sedimentation (see Table S3 of the ESI†), but did not exhibit the artefactual tail at smaller sizes that was observed in previous works.15 One reason for peak broadening is particle diffusion due to Brownian motion, which is more significant for smaller particles and for longer sedimentation or flotation times. This effect is typically neglected for particles larger than 200 nm. In our experiments, sedimentation times were longer than flotation times (typically 10 minutes against 8 minutes for PS120), but the size distributions measured in sedimentation had lower polydispersity index (PDI) than those measured in flotation. For this reason, it is more likely that other experimental factors contribute more significantly to peak broadening. The different width of the size distribution could be the result of a lower resolution achieved with the set up for measurements in flotation. This may relate to the typically shorter flotation times with respect to sedimentation times, which is in part due to the distance between the edge of the disc and the position of the detector through which the samples float being shorter than the equivalent distance for sedimentation. The removal of the artefactual tail in the size distribution is the result of an optimised measuring protocol aimed at removing this artefact. The rim and capillaries of the flotation disc can retain part of the sample that is released with a delay or during later injections. This causes artefactual peaks in subsequently measured size distributions or a characteristic tail at lower sizes (longer sedimentation time). In this work every sample injection was followed by an injection of the particle dispersant (i.e. 16% sucrose in D2O) to remove particles retained in the rim or capillaries. Although this procedure has the benefit of reducing artefacts in the size distributions, the injected volume should be minimised to limit changes to the density gradient. Because the dispersant has higher density than the rest of the sucrose gradient it accumulates at the edge of the disc. This causes the gradient to physically shift towards the centre of the disc. Thus, every injection of samples, calibrant particles or dispersant alters the gradient between the edge of the disc and the detector. This effect is, in part, compensated for by running a calibrant before each measurement and is considered negligible in this analysis.
The DCS modes of the particle size distributions were consistently smaller than the average diameters measured by SEM and SAXS, with differences of 5.6% or less (see Fig. 4). However, the agreement increases with increasing size of the particles. Discrepancies in the measured values, however, are expected as the two techniques do not measure the same type of size.5 Besides, the expanded uncertainty on the measurement of the DCS diameter is between 5% and 6%. When the size distributions are compared with those measured by SAXS, we observe that the width of the distributions are very close in value, with PDIs measured by DCS in sedimentation and flotation mode being lower and higher those measured by SAXS respectively (Table S3 of the ESI†). This is an indication that both SAXS and DCS have similar resolution.
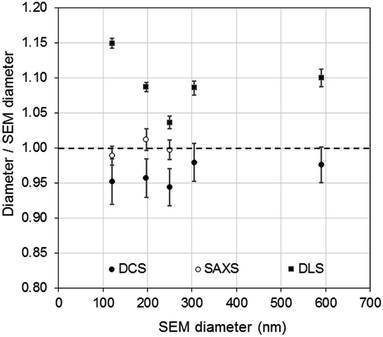 | ||
| Fig. 4 Comparison of PS NP diameters as measured by DCS (●) SAXS (○) and DLS (■) with respect to the diameters measured by SEM. | ||
The high resolution of the DCS technique permits the discrimination of non-agglomerated particles from those that are agglomerated. Some samples show the presence of a minor population of doublets whose mode appears about 1.2 times larger than the main population mode.25–27 It should be noted, in fact, that the instrument interprets every agglomerate as a sphere with equivalent sedimentation time. This time depends on the forces due to gravity, buoyancy and drag in a centrifugal field, which will depend on the volume, shape and orientation of the particles or particle agglomerates. Furthermore, particle agglomerates can have different shapes and orientations, which means that the forces need to be averaged over a range of possible configurations. The net effect, in case of dimers, is that their peak has a mode 20% larger than that of the peak of the non-agglomerated spheres. The intensities of the peaks of the size distribution measured by DCS also need correction when dealing with non-spherical objects. This is because the instrument translates the extinction-based into mass-based distribution by modelling the particles as perfect rigid spheres and applying Mie's theory. Unfortunately, applying Mie's theory to non-spherical particles can be arduous, depending on their geometry, and interpreting the results in terms of “equivalent sphere” is a convenient approximation.
Although relatively small, the presence of particle agglomeration makes the DLS measurements inaccurate. This is clearly seen in Fig. 4, where the diameters measured with the DCS, SAXS and DLS techniques are compared to those measured by SEM. As already discussed, the DCS and SAXS techniques show good agreement with the SEM results. However, the diameter measured by DLS is larger than that measured by SEM (see also Table 1) for all samples. This is somewhat expected due to DLS measuring the hydrodynamic diameter of the particles, which are modelled as perfect rigid spheres and comprises the particles plus a layer of solvent molecules within their slipping plane.5 On the other hand, we observe that the sample that shows better agreement with the other techniques is PS250, which is also the sample where no agglomeration is observed (see Fig. 3) and is therefore closer to the spherical approximation. This suggests that the accuracy of the diameter measured by DLS is affected by sample agglomeration. In DLS, doublet particles have an apparent size ∼1.4 times that of the primary population (compared to ∼1.2 in DCS25,26) and have about two times the scattering efficiency at that particle size. From the DCS trace of PS600 in Fig. 3 we evince that about 10% of the particle populations are dimers. Their DLS size is expected at ∼620 nm, which is within 5% of the measured 650 nm. This result strongly suggests that the DLS result is affected by the agglomeration of the sample. On the contrary, although SAXS and DCS are also performed on colloidal dispersions, the resolution of the techniques allows them to cope with the limited agglomeration of the samples and their results are more consistent with the SEM results. The DLS diameter of sample PS120 exhibits the largest deviation, at 15%, from the SEM results. Although agglomeration is not clearly visible in the DCS trace in Fig. 3, the baseline is not flat enough to exclude the presence of agglomerates. The 15–20% discrepancy from the diameters measured by SAXS and DCS respectively may also reflect differences in dispersant viscosity and temperature between the two techniques, which would mostly affect the smallest particles of the set.
The density of the particles measured by DCS was close to the density expected for bulk polystyrene material and showed high consistency around 1.050 g cm−3. A more significant deviation, yet still smaller than 2%, is observed for sample PS600, which is also the sample with the largest diameter of the set of particles and with the broadest size distribution. Interestingly, the experiment using flotation mode produces a measurement of the size of the particles within 0.5% of the size measured by SEM when a density of 1.050 g cm−3 is used. The measurement of the same sample in sedimentation mode produced the largest disagreement (6.6%) with the SEM measurements (Table S2 of the ESI†). It is therefore possible that the measurements performed on PS600 in sedimentation mode are slightly less accurate than the others, but the reasons for this are not yet understood.
It is interesting to observe that in the case of the dimers, and non-spherical particles in general, this approach measures the correct average density of the particles, as long as the same spherical model is applied to the objects during both sedimentation and flotation mode measurements.
The electron density of the different PS NPs was also determined with SAXS by examining the intensity at zero-angle along the large contrast range of the experiment, i.e. from 280 nm−3 to 433 nm−3. A value of (341 ± 3) nm−3 was obtained for the samples PS120, PS200 and PS250, which is slightly higher than the tabulated value of dry bulk polystyrene (339.7 nm−3).28 Because the electron density is directly proportional to the mass density, the density of the particles can be determined by employing a value of Z/A = 0.54 for this conversion, where Z and A are the average atomic number and mass of polystyrene respectively. The density of the particles determined by SAXS is (1.049 ± 0.009) g cm−3. These results are in good agreement with the density values measured by the DCS combined approach and provides further evidence that all the synthesized particles below 400 nm have a mass density very close to that of bulk polystyrene. The high accuracy achieved in the particle density determination with the DCS technique is validated by the established method of continuous contrast variation in SAXS.
These results show that DCS alone can be used to measure both the size and density of some particles with density close to that of water. This is an extension with respect to methods reported in literature for particle systems with typical density around 2 g cm−3 (e.g. silica particles), which use two measurements in sedimentation through solutions with different average densities.5,17 The range of particles the present method can be applied to depends on the density of the particle and that of the liquid the particle sediment or float through. The minimum recommended difference between the density of the particles and that of the liquid they sediment or float through is 0.03 g cm−3. Considering that deuterium oxide (D2O) can be used for the flotation measurements with typical sucrose concentrations of 30% (w/w), the range of particle densities that can be measured with this approach is between about 1.2 g cm−3 and 1.03 g cm−3. If the particles are outside this density range, a more powerful approach is to complement DCS with another technique that measures the diameter of the particles.5–7 The size of the particles also impacts the applicability of the approach. Sedimentation and flotation times should be kept within about 40 minutes not to incur baseline instabilities. To comply with these times, the density and volume of the sucrose gradient can be reduced, at the expense of loss in resolution of the size distribution.
The complementary use of the SAXS and DCS techniques opens the possibility to analyse the size distribution and density of a broad range of particles with high certainty. For example, DCS can easily be applied to larger particles and the analysis of multimodal samples is relatively straightforward. For these samples, SAXS measurements and relative data analysis can be challenging. In this case, this depends on the q-range available to SAXS which limits the diameter of particles that can be analysed to below 500 nm. As far as the density is concerned, the physical density that can be achieved with sucrose gradients as a contrast agent is 1.25 g cm−3. However, the analysis by DCS of particles with low density and diameters below, for example, 50 nm can require long sedimentation times which may be incompatible with the DCS technique. In some instances the use of the DCS set up in flotation mode can improve the measurement conditions. On the other hand, these types of samples do not pose a significant challenge to SAXS measurements.
For practical applications, it is desirable to couple DCS with a technique easily available in most laboratories. In literature, several examples have been shown for particles with densities similar to or higher than that of polystyrene.5,11,12 However, literature is scarce for particles with density close to or below that of water. The use of the DCS in flotation mode, coupled with a technique that measures particle size, opens up the possibility to measure both the size and density of these particles. To demonstrate this approach, we discuss here the measurement of the size and density of liposomes by combining the use of DCS with TRPS. TRPS is a particle-by-particle technique with the ability to measure number-based size distributions with high resolution.5 It is increasingly becoming a popular technique for the analysis of liposomes, exosomes and other biological particles. The mean diameter of the liposomes as measured by TRPS was (100.31 ± 0.52) nm, where the uncertainty represents the standard deviation measured over six repeats at three different pressures. This value is in agreement with the liposome manufacturer's specifications. The bar graph in Fig. 5 shows the normalised number based size distribution as measured by TRPS. The measured distribution has mode around 87 nm and a tail at larger sizes. However, it should be noted that TRPS cannot measure particles with size below around 70 nm and it is thus not possible to establish if particles at smaller size are present in the sample.
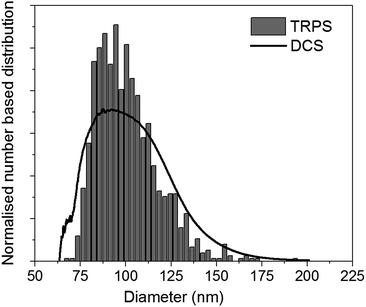 | ||
| Fig. 5 Representative normalised number based size distribution of liposomes as measured by TRPS (bar graph) and DCS (line). Both distributions have a mean diameter of 100.0 nm. | ||
The size distribution of the liposomes was also measured by DCS in flotation mode. In order to measure their density, this parameter was adjusted so that the mean of the number-based size distribution would result the same as that measured by TRPS. A representative number-based size distribution measured by DCS is plotted in Fig. 5 as a continuous line and shows very good agreement with the TRPS measurements. The resulting average density of the liposomes is 1.046 g cm−3, with uncertainty of ∼16%, which is dominated by that on the density of the calibrant particles. Recent studies have shown that the density of these calibrants may be known with better accuracy than the nominal values declared by the instrument manufacturers.29 This is an example of how well characterised and well described reference and calibrant materials can substantially reduce measurement uncertainty and allow more accurate measurements.
The DCS measurements presented in Fig. 5 were performed using a density gradient made of sucrose in water. It is also possible to perform the measurements using a gradient made of sucrose in D2O to increase the difference in density between the particles and the sucrose solution. With this set up, the average density of the gradient increases from 1.096 g cm−3 to 1.14 g cm−3, which leads to a reduction in flotation time of the liposomes from about 11 minutes to about 8 minutes. The sample was prepared by diluting the liposomes, initially in water, 100 times in 16% (w/w) sucrose in D2O. The measurements resulted in a density of the liposomes of 1.096 g cm−3. This value is higher than previously measured and reflects the fact that the molecules of D2O may penetrate and adsorb onto the liposomes. If it is the relative changes in density of these materials that is measured, the choice of the set up used for the measurements is irrelevant. However, if the absolute value of the density is measured to optimise, for example, sample preparation procedures, then it is important to consider the medium where the experiments will be carried out. This is the case, for instance, in common procedures such as liposome separation by a sucrose density centrifugation approach.
Conclusions
We have shown that the DCS technique can be used to measure both the size and density of NPs by performing two measurements. We demonstrate this by using a set of polystyrene particles with different sizes and performing the measurements by first sedimenting, and second floating the particles through fluids of different densities. This approach provides results which are identical, within the uncertainties of the methods, to SAXS measurements of the same particles. While the particle size range accessible by SAXS is limited due to instability of the samples, e.g. due to sedimentation phenomena, the DCS technique could be applied with success to a broader range of particle sizes. We use polystyrene NPs as model particles, but this approach can be easily applied to any particle with density between 1.2 g cm−3 and 1.03 g cm−3. This includes a variety of particles of interest for medical applications, such as liposomes, polymersomes24 and more generally polymer-based drug delivery systems.We also show that DCS in flotation mode can be used to measure the density of NPs when the diameter is measured by a complementary technique and provide an example of application to liposomes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr David Cant for his work of revision. This work was funded by the 14IND12 Innanopart project of the European Union through the European Metrology Programme for Innovation and Research (EMPIR). EMPIR is jointly funded by the EMPIR participating countries within EURAMET and the European Union. The work was also funded by the UK Department of Business, Energy and Industrial Strategy through the project NMS/ST17.Notes and references
- C. Minelli, S. B. Lowe and M. M. Stevens, Small, 2010, 6, 2336–2357 CrossRef CAS PubMed.
- S. E. Krown, D. W. Northfelt, D. Osoba and J. S. Stewart, Semin. Oncol., 2004, 31, 36–52 CrossRef CAS PubMed.
- W. J. Gradishar, Expert Opin. Pharmacother., 2006, 7, 1041–1053 CrossRef CAS PubMed.
- P. T. Witte, P. H. Berben, S. Boland, E. H. Boymans, D. Vogt, J. W. Geus and J. G. Donkervoort, Top. Catal., 2012, 55, 505–511 CrossRef CAS.
- N. C. Bell, C. Minelli, J. Tompkins, M. M. Stevens and A. G. Shard, Langmuir, 2012, 28, 10860–10872 CrossRef CAS PubMed.
- N. C. Bell, C. Minelli and A. G. Shard, Anal. Methods, 2013, 5, 4591–4601 RSC.
- C. Minelli and A. G. Shard, Biointerphases, 2016, 11, 04B306 CrossRef PubMed.
- R. Capomaccio, I. Ojea Jimenez, P. Colpo, D. Gilliland, G. Ceccone, F. Rossi and L. Calzolai, Nanoscale, 2015, 7, 17653–17657 RSC.
- Ž. Krpetić, A. M. Davidson, M. Volk, R. Lévy, M. Brust and D. L. Cooper, ACS Nano, 2013, 7, 8881–8890 CrossRef PubMed.
- A. M. Davidson, M. Brust, D. L. Cooper and M. Volk, Anal. Chem., 2017, 89, 6807–6814 CrossRef CAS PubMed.
- C. Minelli, R. Garcia-Diez, A. E. Sikora, C. Gollwitzer, M. Krumrey and A. G. Shard, Surf. Interface Anal., 2014, 10–11, 663–667 CrossRef.
- S. M. North, E. R. Jones, G. N. Smith, O. O. Mykhaylyk, T. Annable and S. P. Armes, Langmuir, 2017, 33, 1275–1284 CrossRef CAS PubMed.
- C. J. Mable, R. R. Gibson, S. Prevost, B. E. McKenzie, O. O. Mykhaylyk and S. P. Armes, J. Am. Chem. Soc., 2015, 137, 16098–16108 CrossRef CAS PubMed.
- D. Mehn, P. Iavicoli, N. Cabaleiro, S. E. Borgos, F. Caputo, O. Geiss, L. Calzolai, F. Rossi and D. Gilliland, Int. J. Pharm., 2017, 523, 320–326 CrossRef CAS PubMed.
- R. Garcia-Diez, A. Sikora, C. Gollwitzer, C. Minelli and M. Krumrey, Eur. Polym. J., 2016, 81, 641–649 CrossRef CAS.
- N. Kanokwan, R. Vinayak, A. F. Jeffrey and R. Vytas, Nanotechnology, 2013, 24, 155701 CrossRef PubMed.
- M. Kamiti, D. Boldridge, L. M. Ndoping and E. E. Remsen, Anal. Chem., 2012, 84, 10526–10530 CrossRef CAS PubMed.
- M. K. Brakke, Arch. Biochem. Biophys., 1953, 45, 275–290 CrossRef CAS PubMed.
- M. Krumrey and G. Ulm, Nucl. Instrum. Methods Phys. Res., Sect. A, 2001, 467, 1175–1178 CrossRef.
- R. Garcia-Diez, C. Gollwitzer and M. Krumrey, J. Appl. Crystallogr., 2015, 48, 20–28 CrossRef CAS.
- J. Wernecke, C. Gollwitzer, P. Muller and M. Krumrey, J. Synchrotron Radiat., 2014, 21, 529–536 CrossRef CAS PubMed.
- R. Vogel, G. Willmott, D. Kozak, G. S. Roberts, W. Anderson, L. Groenewegen, B. Glossop, A. Barnett, A. Turner and M. Trau, Anal. Chem., 2011, 83, 3499–3506 CrossRef CAS PubMed.
- F. Meli, T. Klein, E. Buhr, C. G. Frase, G. Gleber, M. Krumrey, A. Duta, S. Duta, V. Korpelainen, R. Bellotti, G. B. Picotto, R. D. Boyd and A. Cuenat, Meas. Sci. Technol., 2012, 23, 125005 CrossRef.
- M. Krumrey, G. Gleber, F. Scholze and J. Wernecke, Meas. Sci. Technol., 2011, 22, 094032 CrossRef.
- C. Gollwitzer, D. Bartczak, H. Goenaga-Infante, V. Kestens, M. Krumrey, C. Minelli, M. Palmai, Y. Ramaye, G. Roebben, A. Sikora and Z. Varga, Anal. Methods, 2016, 8, 5272–5282 RSC.
- D. Mehn, F. Caputo, M. Rosslein, L. Calzolai, F. Saint-Antonin, T. Courant, P. Wick and D. Gilliland, RSC Adv., 2017, 7, 27747–27754 RSC.
- L. Bondoc and S. Fitzpatrick, J. Ind. Microbiol. Biotechnol., 1998, 20, 317–322 CrossRef CAS.
- N. Dingenouts, J. Bolze, D. Potschke and M. Ballauff, in Polymer Latexes - Epoxide Resins - Polyampholytes, ed. M. Ballauff, Springer-Verlag Berlin, Berlin, 1999, vol. 144, pp. 1–47 Search PubMed.
- V. Kestens, V. A. Coleman, P.-J. De Temmerman, C. Minelli, H. Woehlecke and G. Roebben, Langmuir, 2017, 33(33), 8213–8224 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis details of PS particles, size and density measurements by DCS in sedimentation, flotation and combined mode and widths of the size distributions as measured by DCS in sedimentation and flotation modes, SEM and SAXS. See DOI: 10.1039/c8ay00237a |
| This journal is © The Royal Society of Chemistry 2018 |