Clogging of microfluidic systems
Emilie
Dressaire
*a and
Alban
Sauret
 ab
ab
aDepartment of Mechanical and Aerospace Engineering, New York University Tandon School of Engineering, Brooklyn, NY 11201, USA. E-mail: dressaire@nyu.edu
bSurface du Verre et Interfaces, UMR 125 CNRS/Saint-Gobain, 93303 Aubervilliers, France
First published on 18th October 2016
Abstract
The transport of suspensions of microparticles in confined environments is associated with complex phenomena at the interface of fluid mechanics and soft matter. Indeed, the deposition and assembly of particles under flow involve hydrodynamic, steric and colloidal forces, and can lead to the clogging of microchannels. The formation of clogs dramatically alters the performance of both natural and engineered systems, effectively limiting the use of microfluidic technology. While the fouling of porous filters has been studied at the macroscopic level, it is only recently that the formation of clogs has been considered at the pore-scale, using microfluidic devices. In this review, we present the clogging mechanisms recently reported for suspension flows of colloidal particles and for biofluids in microfluidic channels, including sieving, bridging and aggregation of particles. We discuss the technological implications of the clogging of microchannels and the schemes that leverage the formation of clogs. We finally consider some of the outstanding challenges involving clogging in human health, which could be tackled with microfluidic methods.
1 Introduction
Suspensions of microparticles occupy an important place in industrial and biological systems as the liquid phase allows the transport of the solid matter.1–6 Despite the wide use of suspensions of rigid or deformable particles, the understanding of the processes governing their flow in confined environments remains limited due to the complexity of the particle motions and interactions. In this review, we are interested in the clogging transition, i.e., the mechanisms that interrupt the transport of particles in confined geometries. In some situations, the formation of clogs can be desirable, for instance to reinforce porous and fractured substrates such as concrete and rocks7,8 or for the detection of biological cells.9 However, in many applications clogs decrease the lifetime and efficiency of micro-engineered systems that are used for the fabrication, transport and analysis of fluid samples. For example, some microfluidic processes rely on microparticles to selectively bind to target molecules or cells,10 to carry chemicals11 or to stabilize emulsions.12 Other microfluidic devices are engineered for pure fluid samples that accidentally get contaminated with impurities or suspended particles. Similarly, common macroscopic technological and biological processes involve the micro-flow of suspensions through complex networks of channels, including the filtration of water through porous membranes as illustrated in Fig. 1,13–15 the flow of ink in printers16,17 or the transport of blood cells within the microvascular system.18–20 | ||
| Fig. 1 Images of electrospun nanofibrous membranes obtained with a field-emission scanning electron microscope.21 (a) Before filtration and (b) after filtration of a suspension of 1 μm polystyrene particles. Reprinted with permission from J. Membr. Sci.21 Copyright 2006 Elsevier. | ||
The flow behavior of a suspension of hard spheres has been described at low solid volume fraction, below the jamming transition.1,2,22–24 The rheology of a suspension is strongly dependent on the solid fraction. At low solid fraction, the suspension behaves like a Newtonian fluid whose effective viscosity μeff(ϕ) increases with the solid volume fraction ϕ, and can be described through the relation
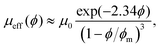 | (1) |
For particle concentrations below the jamming solid fraction, the formation of a clog is associated with complex local processes that cannot be captured through continuum rheological modeling. The description of such clogging processes has recently been the focus of a body of microfluidic research based on suspensions of microparticles whose typical diameter ranges between a hundred nanometers and a few micro-meters. Flows at the micrometer-scale are characterized by low Reynolds numbers, Re = ρU![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /μ, where ρ and μ are the density and dynamic viscosity of the fluid, respectively,
/μ, where ρ and μ are the density and dynamic viscosity of the fluid, respectively, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) the lengthscale (width or height) of the channel and U the fluid velocity. The flow dynamics in such systems can therefore generally be described through the Stokes approximation.29 In addition, the effects of diffusive, advective and colloidal forces on the particles result in the rich behavior of the suspension and the formation of clogs. The relative magnitude of Brownian and hydrodynamic effects is captured by the Peclet number: Pe = 6πμD2U/kBT, where D is the diameter of the particles, U and μ are the velocity and dynamic viscosity of the fluid, respectively, kB is the Boltzmann constant and T the absolute temperature. For micrometer-scale particles at room temperature, the critical flow velocity below which the diffusion velocity becomes comparable to the advection is of the order of 0.1 micrometer per second, which in most systems is only the case near contact at the wall and can therefore be neglected. In confined geometries, the combination of long range, steric and hydrodynamic interactions can lead to the capture of the particles on the walls of the microchannels. Particle trapping in low Reynolds number flows is exploited in industrial and natural processes including in filtration to improve the retention of solid matter.4 The deposition of particles and their subsequent assembly can eventually induce the formation of a clog, i.e., a single or multi-particle structure that spans over the cross section of the channel. When such a blockage occurs, it prevents further passage of the particles that build up a porous aggregate and reduce dramatically the flow rate of the fluid.
the lengthscale (width or height) of the channel and U the fluid velocity. The flow dynamics in such systems can therefore generally be described through the Stokes approximation.29 In addition, the effects of diffusive, advective and colloidal forces on the particles result in the rich behavior of the suspension and the formation of clogs. The relative magnitude of Brownian and hydrodynamic effects is captured by the Peclet number: Pe = 6πμD2U/kBT, where D is the diameter of the particles, U and μ are the velocity and dynamic viscosity of the fluid, respectively, kB is the Boltzmann constant and T the absolute temperature. For micrometer-scale particles at room temperature, the critical flow velocity below which the diffusion velocity becomes comparable to the advection is of the order of 0.1 micrometer per second, which in most systems is only the case near contact at the wall and can therefore be neglected. In confined geometries, the combination of long range, steric and hydrodynamic interactions can lead to the capture of the particles on the walls of the microchannels. Particle trapping in low Reynolds number flows is exploited in industrial and natural processes including in filtration to improve the retention of solid matter.4 The deposition of particles and their subsequent assembly can eventually induce the formation of a clog, i.e., a single or multi-particle structure that spans over the cross section of the channel. When such a blockage occurs, it prevents further passage of the particles that build up a porous aggregate and reduce dramatically the flow rate of the fluid.
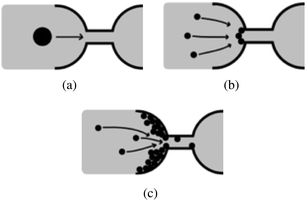
The early work of Wyss et al. established that microfluidic is a good method to study confined particle-laden flows and clogging at the pore-scale.30 Microfluidic devices are commonly designed using Computer Assisted Drawing (CAD) software and fabricated through soft lithography techniques using a clear elastomer, such as polydimethylsiloxane (PDMS).31 The simple design of the flow geometry, the low cost of the devices, and the ability to track particles with optical microscopy allow the investigation of canonical configurations to identify the relevant physical parameters and collect statistically meaningful data. This review focuses on the mechanisms of clog formation in microfluidic systems, at the pore-scale. Indeed recent advances in the flow of suspensions in confined environments rely in large part on the ability to precisely control the flow at the micrometer-scale and monitor the clogging dynamics at the pore or microchannel level. In this review, we discuss the formation of clogs in microchannels through the sieving of large particles, rigid or soft (Section 2), the jamming at constrictions (Section 3) and the clogging by aggregation of particles (Section 4) in microchannels. We focus on describing the main features of the three mechanisms represented schematically in Fig. 2. The important technological implications of clogging are discussed briefly in the relevant sections. While our review is focused on the microfluidic advances in the field of clog formation, the results presented should also provide interesting insights to the field of fouling science, which seeks to characterize the transport of particulate suspensions through complex porous structures. Finally, we summarize some of the recent work on bioclogging that constitutes a dynamic field of research both fundamental, to understand healthy and pathological clogging in biological systems and applied, to develop new diagnostic methods (Section 5).
2 Sieving: from rigid to deformable particles
Sieving refers to the blockage of particles based on size exclusion. The sieving of microparticles should however not be reduced to a simple geometrical problem, as the trapping of soft and anisotropic particles within a constriction is a complicated problem with challenging technological applications.2.1 Sieving of rigid particles
The sieving of particles contributes to the separation of solid matter from the fluid phase in filtration processes.34,35 The entrapment of micrometer-sized solid particles occurs when the width of the microchannel or the constriction, W, is equal or smaller than the particle diameter D, W ≤ D. Several studies have demonstrated that particles get sieved out of suspension at the entrance of a microchannel or constriction through direct hydrodynamic transport36,37 or after rolling on the solid surface.38,39 This method is commonly used in microfluidic technology to filter contaminants or separate particles of different sizes.40,41In practice, suspensions of particles are often polydisperse, either naturally42 or as an artifact of common fabrication methods.43,44 The size distribution is characterized by a mean diameter and a standard deviation. The sieving mechanism allows the selective trapping of the large particles, i.e., those whose diameter D satisfies D ≥ W. The clogging dynamic is thus controlled by the concentration of large particles and the flow rate in the channel.32 The probability of clog formation is measured by the mean clogging time, which is the time interval between the onset of the flow and the clog formation. Experimental measurements of the clogging times as presented in Fig. 3(a) follow a Poisson distribution, which is indicative of a random process:
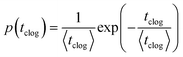 | (2) |
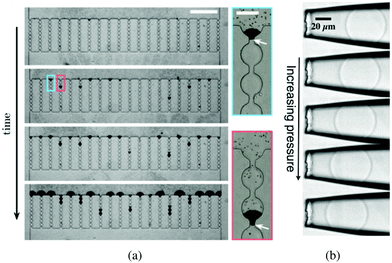 | ||
| Fig. 3 (a) Time lapse of a typical sieving experiment in a device consisting of 20 parallel microchannels. Particles are black. After clogging, the particles accumulate and form a filter cake. The suspension flows from top to bottom (scale bar is 500 μm). The close-up views show the clog formed when a large contaminant blocks a microchannel at the entrance or further inside a microchannel. The white arrows indicate the position of the large contaminants (scale bar is 50 μm). Reprinted with permission from Appl. Phys. Lett.32 Copyright 2014 AIP Publishing LLC. (b) Series of images of a microgel particle being deformed as the applied pressure increases; from top to bottom: p = 100, 150, 200, 250, 300 Pa. The fluid flow pushes the soft particle into the tapered capillary from right to left. Reprinted from Soft Matter.33 | ||
The trapping of anisotropic particles, such as fibers or ellipsoids, is possible if one of the particle dimensions exceeds the size of the channel. However, this geometrical criterion is not sufficient to determine whether a clog will form. The shape and initial orientation of the particle, the confinement and the geometry of the microchannel influence the probability and position of the clog.46 In such systems, controlling the orientation of the particle as it approaches the constriction permits to determine the clogging probability. Once the interaction between the particle and the flow is well understood, it could be leveraged to open and close constrictions at will.
2.2 Sieving of a soft particle
The flow of soft deformable particles such as microspheres of elastomer, cells, and droplets is of great significance in the food and oil industries as well as in the biological and biomedical fields.47–49 The mechanical behavior of suspensions of deformable particles leads to a wide range of flow properties. As opposed to solid particles, a soft particle can enter a microchannel whose size is smaller than the diameter of the particle at rest, W < D.50–52When the flow across the channel is controlled by a pressure difference ΔP, both the volume and the shape of a deformable object change due to the local mechanical stresses. As ΔP increases, the particle dynamics can follow different scenarii: get trapped in the tapered or narrow entrance region of the microchannel [as shown in Fig. 3(b)], or flow through the channel when the pressure exceeds the translocation pressure noted ΔPmax.53 The flow properties as well as the shape, the dimension and the mechanical features of the particle determine its behavior in such a confined environment. For instance, healthy red blood cells, which are deformable, can flow through the microvascular system.54,55 However, diseased blood cells, with reduced deformability can alter the blood flow and cause anemia and sepsis.56,57 The change in mechanical behavior of the red blood cells is key to understand, diagnose and treat the associated diseases.
The flow and eventual trapping of a soft particle in a tapered capillary or axisymmetric microchannel with an opening angle α are commonly used to measure the mechanical properties of the particle [as illustrated in Fig. 3(b)].33 Indeed the deformation of the particle is related to the elastic bulk (or compressive) and shear moduli of the material, noted K and G, respectively. Theoretically, the soft particle gets blocked when the pressure difference across the channel is lower than a threshold value. This latter can be estimated using a scaling approach to balance the deformation energy with the work of the pressure, assuming that the deformation of the particle is linearly elastic. The threshold value is thus defined as:
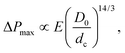 | (3) |
For pressure values ΔP < ΔPmax, the external mechanical stresses induced by the fluid balance the internal elastic stresses. The position of the stopped particle depends on the geometry of the tapered region and the particle, but also on the pressure drop imposed and the elasticity moduli (K, G).33,58 Using a linear elastic description, and assuming that the opening angle α is smaller than about 15°, it is possible to describe the deformation of the particle at equilibrium using two parameters: the average radial strain, εr, and the average axial strain, εz, defined as
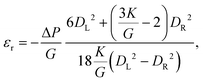 | (4) |
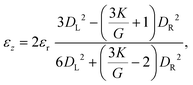 | (5) |
The formation of a clog by a soft particle in a tapered microchannel is a simple and accurate experimental method to measure the mechanical properties of individual micrometer-scale objects. This capillary micromechanics scheme has been applied to a variety of micrometer-scale objects, ranging from microgel33 and core–shell particles59 to cells.60–64 We should emphasize that the modeling of the clogging of deformable particles in microchannels is particularly relevant to biological applications.
3 Bridging in microchannels
Clogging of a constriction can also occur when the diameter of the particles D is smaller than the size of the microchannel W. A first possible mechanism when D < W is based on steric effects through the formation of an arch of particles across the width of the channel or constriction, which results in clogging. The combination of converging flow and high particle concentration generates bridge-like structures composed of a few particles, typically between 2 and 10, that span over the entire cross section of the channel.65 Such blockages occur during the confined flow of hard spheres both in suspensions and in granular materials.66–71 The latter situation has been studied in the silo geometry where dry grains are exiting a container through a small hole. Contrary to the clogging by sieving, the blockage by bridging is often intermittent as the arch can break under flow fluctuations.72While bridges are often reported for local particle concentrations reaching the jamming value, studies have examined the creation of an arch upon the simultaneous arrival of particles at the channel opening for particle concentrations lower than the jamming value.65,73 Beyond the fundamental implications of this work to describe the suspension rheology and jamming transition,74–77 understanding and controlling the bridging occurrences can improve the processing of suspensions with a high solid fraction, encountered in industrial and technological systems. Intermittent bridging is particularly disruptive as it leads to local variations of the particle concentration.
3.1 Bridging of dense suspensions
The flow of dilute suspensions is well captured with a Newtonian description.78,79 However, as the volume fraction of the particles increases, the rheology becomes more complex and the viscosity diverges near a critical or jamming volume fraction ϕm. For monodisperse hard spheres, the maximum packing fraction, ϕ ∈ [0.54,0.74], depends on the local arrangement. In addition, the flow of dense suspensions through confined environments can lead to local rearrangements of the particles and the formation of crystal structures.80 In practice, the viscosity typically rises rapidly around ϕ = 0.5 and diverges for ϕm = 0.585 for hard spheres adopting a glass phase.75,81 Jamming is therefore reported for dense suspensions, ϕ = 0.2–0.6,72,80,82,83 flowing through an increasingly confined environment in which the volume fraction locally reaches ϕm. For example, if ϕ < ϕm in the microchannel, allowing for pressure driven flow, arches or force chains can form at a constriction when the combination of geometrical and hydrodynamic effects increases the volume fraction as illustrated in Fig. 4. This transition from continuous flow to arch formation occurs over a very small range of volume fractions, of the order of a few percents and results in a sharp decrease of the average fluid velocity noted 〈U〉72 and a decrease in particle concentration downstream due to the intermittent jamming.83 This type of clogging occurs in a variety of systems in which a large number of particles, grains, pedestrians pass through a bottleneck.70 Interestingly the analogy between those systems extends to their dynamics, as demonstrated by numerical simulations of colloidal suspensions using Lattice Boltzmann methods.71 The simulations indicate that the time lapse between two consecutive bridging events follows a distribution with a power law tail, which is analogous to the flow of grains out of a hopper. Similarly, the number of particles released during the unjammed phase is well described by an exponential distribution. | ||
| Fig. 4 Flow and clogging by bridging of a neutrally buoyant suspension of PMMA particles in an axisymmetric tapered glass capillary. | ||
Consistently, experimental work shows that the pressure driven flow of dense suspensions of hard particles leads to clogging if (1) a small number of particles can form a bridge across the width of the channel and (2) the flow velocity is above a threshold value noted Uth. For example, the clogging time, i.e., the time between two consecutive bridging events is measured experimentally, and well captured by a power law:84
| tclog ∝ (〈U〉 − Uth)−β | (6) |
The intermittent nature of these clogs is due to the fragility of the bridged state: the arch can withstand large forces in only one direction, perturbations of the flow or small forces exerted in other directions can easily unjam the system. For example, the presence of rotating vortices prevents long-lived arches.72 Taking advantage of the fragility of these arches will allow the development of self lubricating flow geometries, which could prevent the formation of clogs by bridging. In summary, the clogging by bridging for dense suspensions of microparticles shares common features with the clogging in a silo for a dry granular material.70,71 However, contrary to dry grains flowing under gravity, suspensions of micrometer-scale particles can be diluted to few percents in a flowing liquid.
3.2 Arch formation in diluted suspension
Although generally associated to dense suspensions, bridging can also occurs for diluted suspensions at a small constriction. Indeed, arch formation has also been evidenced at ϕ ≤ ϕm/10.65 The bridging results from the simultaneous arrival of particles that plug a cross section of the channel, typically at the inlet or at a constriction as shown by the example in Fig. 5. The probability of arch formation increases with the particle concentration, with the flow rate and with the ratio of the particle to the channel size D/W.73,85 The complex bridging mechanism for diluted suspensions of microparticles is yet to be fully characterized. Several types of particle assemblies can constitute a stable arch, capable of interrupting the transport of particles (Fig. 5). Each of these assemblies is composed of a given number of particles arranged through the cross section. To determine the probability of formation of each assembly, it is necessary to account for both the initial position of the particles and the hydrodynamic forces as they determine the particle trajectories toward the constriction. If the particles approach the channel simultaneously, near contact, interactions involving the lubrication flow and interparticle forces determine whether an arch forms.73,86 In first approximation, it is convenient to consider an axisymmetric channel. The monodisperse suspension of particles of diameter D has a solid volume fraction ϕ. The suspension enters a constriction through a circular opening of area A, smaller than the cross section of the channel. Assuming that the particles are advected at the speed of the fluid, a clog forms when the number of particles arriving simultaneously at the opening is larger that a critical number, noted nmax, defined empirically as:87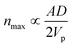 | (7) |
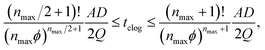 | (8) |
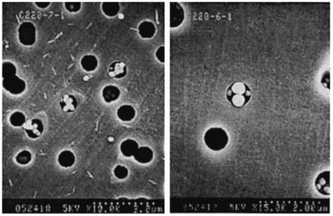 | ||
| Fig. 5 Particle arches formed at high flow velocity. Negatively charged 0.249 μm diameter polystyrene sulfate particles flow through 1 μm pores. Reprinted with permission from J. Fluid Mech.73 Copyright 2000 Cambridge University Press. | ||
Recent work has shown that particle surface properties, and therefore particle–particle and particle–wall interactions modify the clogging dynamics. Experimentally, the ionic strength of the solution allows tuning the surface interactions.89 For example, the presence of attractive interactions between particles facilitates the formation of the bridge but can also lead to the formation of aggregates. The growth of clusters of particles and the resulting blockage of the microchannel are discussed in the following section.
4 Clogging by aggregation
Whereas the two clogging mechanisms described previously, sieving and bridging, involve steric effects only, we now consider the clogging of a microchannel by successive deposition of colloidal particles. The self assembly of colloidal particles into clusters can occur in the bulk of a suspension or on a fluid interfaces.90 Driven by short-range attractive van der Waals forces, this aggregation is only possible if the particles are at close enough distance to one another. In flowing suspensions, a particle can reach the vicinity of another particle or of the surface of the channel through advection or diffusion, depending on the Peclet number. The dynamics of the clogging process by aggregation of particles thus result from the combination of hydrodynamic and surface forces, as first reported in porous media.13,15,91 Recent work on particle deposition and aggregation employs microfluidic to control the suspension flow and characterize the time evolution of the particle build-up.30,37,92–95 Several studies have focused on the characteristic timescale of the blockage of the pore.30,96,97 At low Reynolds number, as typically encountered in microfluidic channels, experiments indicate that a critical number of particles flow through the microchannel before the aggregate invades the cross section, thus preventing further passage of particles. Recent experimental work aims at describing the individual steps of the clogging process. Indeed the capture of the first particle and the growth of the aggregate determine the clogging dynamics, as the probability of deposition of individual particles varies over the different stages of the process.14,38,92,97,98 Building on those observations, quantitative models now capture some features of the clogging process but various questions remain, including on the formation of a aggregate in three dimensions around the first layer of deposited particles.4.1 Deposition of a single particle
The deposition of a single particle on the wall of a microchannel is the first step toward aggregation and clogging (see Fig. 6(a) and (f)). Numerical and experimental studies indicate that individual particles are preferentially captured at the entrance of the channel.37,38,85,96,99 In microfluidic devices, the particle deposition process can be quantified through the surface coverage of the wall, which is defined as the surface area covered by particles divided by the total surface area. When the coverage is low, the deposition events can be treated as independent. The flux of particle deposition at the wall decreases with the distance from the entrance of the channel, with the Reynolds number of the flow and with the particle size.100 The nature and intensity of the particle–wall interactions influence the rate of deposition in a complex way. Indeed, the surface forces between a particle and a wall are a combination of attractive van der Waals and repulsive electrostatic double layer interactions.101 The relative magnitude of these two forces and the resulting energy profile depend on the physico-chemical properties of the particle and the wall, and the nature of flowing phase through its composition, pH and electrolyte concentration.101 Experiments in microfluidic devices show that varying the concentration of the electrolyte typically sodium chloride, NaCl, can modify the deposition flux of particles at the wall by a factor 2.100,102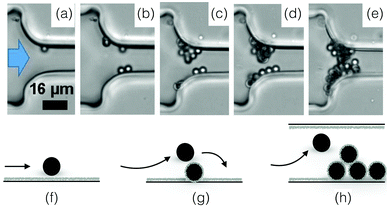 | ||
Fig. 6 Particle aggregation resulting in clog formation. (a–e) The density matched suspension of polystyrene particles (D = 3 μm) with sulphate charge groups flows through a constriction of width W = 15.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μm. The images are recorded at 3, 5, 10 and 36 minutes, with a flux of 2.8 × 104 particles per minute at the onset of the experiment. Reprinted with permission from Microfluid. Nanofluid.96 Copyright 2015 Springer. (f–h) Schematic representation of the aggregation process, from the deposition of the first particle to the clog formation. μm. The images are recorded at 3, 5, 10 and 36 minutes, with a flux of 2.8 × 104 particles per minute at the onset of the experiment. Reprinted with permission from Microfluid. Nanofluid.96 Copyright 2015 Springer. (f–h) Schematic representation of the aggregation process, from the deposition of the first particle to the clog formation. | ||
Two types of deposition behavior are reported. When the interactions between the particles and the wall are attractive for all separation distances, the deposition is favorable and the deposition flux, jdep is large, typically with a wall coverage of the order of 10% after 30 minutes of flow for a suspension of 0.25 μm-latex particles at Re = 30 and ϕ = 1.31 × 10−5 in a solution of NaCl (C = 0.01 M).100,103 When the energy profile presents a repulsive region, the deposition is unfavorable, and the flux is lower.100,104 In the latter case, the particle capture is very sensitive to surface roughness and local defects, which are difficult to describe analytically and numerically.4
To model these observations, one has to consider the flux of particles, which satisfies the mass conservation relation:100
| ∇·j = 0. | (9) |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) i and Ui, the particle diffusivity and the velocity in the i-direction, respectively, and Fi is the i-component of the resultant force acting on the particle. For a particle number concentration n, the flux in the i-direction ji is defined as100
i and Ui, the particle diffusivity and the velocity in the i-direction, respectively, and Fi is the i-component of the resultant force acting on the particle. For a particle number concentration n, the flux in the i-direction ji is defined as100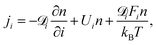 | (10) |
The resultant force F exerted on a colloidal particle is a combination of the van der Waals, electrical double layer, gravitational and hydrodynamic forces:101
| F = FvdW + FEDL + FG + FH. | (11) |
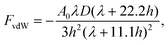 | (12) |
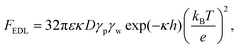 | (13) |
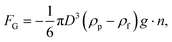 | (14) |
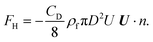 | (15) |
It is important to note that the diffusion and drag coefficients, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) and CD respectively, vary with h, when the distance between the particle and the wall becomes small, h ≤ D/2.105–108
and CD respectively, vary with h, when the distance between the particle and the wall becomes small, h ≤ D/2.105–108
At low Reynolds number, when the suspension flows between two parallel plates, the velocity profile is described by Poiseuille law, assuming that the flow is undisturbed by the particles. The flux of particles can then be obtained by solving eqn (11) numerically. The results are in good agreement with the experimental observations.100 This approach has also been used to determine the deposition rate of particles at the inlet of a channel, where the velocity field is determined numerically.38,39
For more complex flow geometries, Wyss et al.30 proposed an empirical description of the deposition probability, which describes the flux of particles at the wall. This probability, noted pdep, at a constriction of width W scales with the number of particles that flow in the vicinity of the wall, in the so-called “sticking region” of thickness εs. The probability is defined statistically as
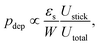 | (16) |
4.2 Successive deposition of particles: growth of an aggregate
The subsequent deposition of particles results from the same competition between hydrodynamic, diffusive and colloidal effects [see Fig. 6(b)–(d), (g) and (h)]. However the presence of previously deposited particles modifies the local geometry of the wall, the flow field and the nature of the interactions. The aggregate buildup is therefore more complex to describe analytically or numerically. Two types of deposition mechanisms have been reported depending on the local interactions.98 If the interactions between the flowing and the deposited particles are attractive for all separation distances, multiple layers of particles are deposited, which results in the formation of an aggregate and the clogging of the microchannel.93 If the interactions between flowing and deposited particles are repulsive for a range of separation distances, the electrostatic barrier reduces the probability of deposition. At low flow velocity, the particles can only stick on the wall outside a forbidden region that surrounds each deposited particle. This repulsion prevents the buildup of aggregates. At large enough velocities, the repulsion between particles can be overcome and multilayered clusters are formed resulting in the growth of aggregate.In experimental studies, the deposition of the particles and the formation of aggregates is monitored through the total size of the cluster area.92,93 This measurement records the footprint or projected area of the aggregates on the surface of the channel. For electrostatically neutral particles, the total size of the clusters varies linearly in time and with the particle concentration, until the aggregates start interacting with one another. The growth rate of an aggregate increases with the shear strain rate at the wall and the confinement.92,93 The shape of the aggregates and their growth dynamics also depend on the Peclet number, which quantifies the relative magnitude of the advective to the diffusive effects, and the ionic strength of the suspension.97,109 Using a simplified Smoluchowski equation, it is possible to define theoretically the flux of particles at the wall as
| j ∝ −nncKa, | (17) |
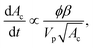 | (18) |
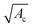 .30,92,110 These experimental results and scaling laws do not fully capture the complexity of the aggregate growth including the three dimensional geometry, which results from the complex interplay of aggregation and erosion under microfluidic flows.97
.30,92,110 These experimental results and scaling laws do not fully capture the complexity of the aggregate growth including the three dimensional geometry, which results from the complex interplay of aggregation and erosion under microfluidic flows.97
4.3 Clogging by aggregate growth
The consequence of the aggregate growth in a microfluidic device or in a confined environment is the formation of a clog. Experimental studies have described the dynamics of clog formation at a constriction through the clogging time. The clogging time aims to establish how the flow characteristics and the properties of the suspension contribute to the blockage of a microchannel. The microfluidic technology enables to reproduce the geometry of porous media in a controlled way. For example, each microchannel can present one85,94,96 or several constrictions.30,37,111 The clogging timescale is obtained by recording the fraction of blocked channels during the experiment and defining the mean clogging time as the average clogging time for all the microchannels of the device, measured from the onset of the flow. The average clogging time decreases linearly with the pressure drop across the device and the volume fraction of the suspension.30,37 Experimental results indicated that the clogging time corresponds to the passage of a critical number of particles through the channel before it clogs. The critical number of particles, N*, depends on the geometry of the microchannel and scales as W/D where W is the width of the channel and D the particle diameter.30,96 In first approximation, one can assume that the probability of deposition of the successive particles differs only because of the progressive reduction in microchannel opening. The clog is formed when N* particles have flown through the constriction, and N particles are deposited on the wall of the channel, forming a clog. Using the statistical method presented above, N* is defined as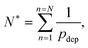 | (19) |
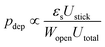 | (20) |
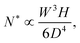 | (21) |
5 Perspectives: bio-clogging
If the microfluidic technology has been key to identify and describe the clogging mechanisms involving colloidal and micrometer-scale particles, it is also a powerful tool to study the flow of biofluids through microchannels. In biological or bioengineered systems, cells in suspensions can be transported through micrometer to centimeter-scale channels.112–115 The clogging of microchannels by cells is encountered in both healthy and pathological organisms. The complex processes involved have been the focus of recent work.115,116 Other studies have leveraged the formation of clogs to describe the behavior of cells, and proposed new schemes for diagnostic and treatment testing.117–119For example, the selective blockage or sieving of cancer cells in microchannels has been proposed to diagnose diseases.9,121,123,124 The bridging of sickle red blood cells in blood vessels has been associated with anemic crisis in millions of patients.125–127 Finally, the formation of bacterial biofilms and biofilm streamers in porous media is the result of the progressive aggregation of bacteria that can eventually lead to clogging (as illustrated in Fig. 7(a)). Indeed, the formation of biofilms has dramatic consequences including the increased resistance to bactericides which is responsible for persistent infections, and biofouling of flow systems, from catheters to pipelines.128,129 These three examples of bioclogging have been the focus of recent microfluidic studies that have led to a better understanding of the processes specific to biological systems. The use of microfluidic technology to study and leverage bioclogging is a promising emerging field of work. The richness of bioclogging mechanisms stems from the properties of individual cells that differ from solid particles in the following ways: (i) the cells are soft, most often non-isotropic objects; (ii) the cells adhere to the substrate through specific molecules that decorate the cell membranes and can selectively and strongly bind the cell to the substrate; (iii) the cells are living entities that can swim, multiply, differentiate, recruit other cells and synthesize polymeric substances. To illustrate how these differences modify the clogging dynamics and highlight the role of microfluidic advances in biological research, we describe the examples presented above. Indeed each system shows that the living nature of the cell modifies the clog formation.
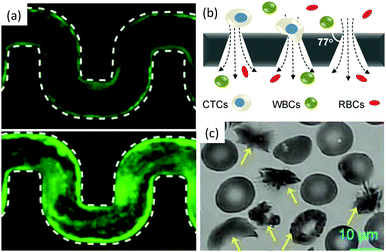 | ||
| Fig. 7 Bio-clogging. (a) Biofilm streamers of P. aeruginosa cells expressing gfp expand and clog a 200 μm wide curvy channel. Reprinted with permission from Proc. Natl. Acad. Sci. U. S. A.120 (b) Schematic of a separation method to isolate Circulating Tumour Cells (CTCs) from other blood cells such as Red Blood Cells (RBCs) and White Blood Cells (WBCs). Reprinted with permission from Sci. Rep.121 Copyright 2014 Nature Publishing Group. (c) Sickled vs. healthy red blood cells. The yellow arrows point toward the sickled RBCs. Reprinted with permission from Proc. Natl. Acad. Sci. U. S. A.122 | ||
The sieving of cells in microchannels provides information on their size and mechanical properties (see Fig. 7(b)). Biological research has shown that circulating tumor cells are transported in the peripheral blood of cancer patients and are believed to cause metastasis.130 Interestingly, the deformability of cancer cells is correlated with their metastatic potential.131 Therefore, microfluidic devices with conical and narrowing channels have been designed to take advantage of this property and have successfully been used to separate cancer cells from a blood sample using a sieving approach.9,121,123,124 Once isolated, the cells can be used for diagnostic or therapy tests. This method allows to recover up to 90% of the cancer cells. However, upon clogging, cancer cells attach on the wall of the channel, and the adsorption is irreversible, which limits the use of the device, the ability to analyse the cells trapped.124 Indeed cells, through the metastatic process adhere to the blood vessel walls. The clogging of the constriction is thus a combination of sieving of soft particles and adhesion to the wall.130
The jamming of cells has recently been observed in yeast.132 In this situation, the formation of force chains results from the growth of the cell population in a confined space and provides environmental cues, but is not associated with fluid flow. The bridging however has been associated with the flow of pathological blood cells.133 The bridge formation which causes vaso-occlusive crises does not occur when healthy red blood cells (RBCs) flow through a constriction. Yet, for patients affected with sickle cell anemia, a drop in oxygen level in the blood can trigger a series of events that go from the polymerization of hemoglobin S inside the cells to the vessel jamming [see Fig. 7(c)].125 Studies in microchannels with varying oxygen concentration in the blood flow, reproduce the conditions of the crises in a controlled environment.117,122,133,134 This work has demonstrated a correlation between the speed of the rheological response of the diseased blood cells and the severity of the crises. However questions remain on the respective role and timescale of the cell stiffness, sickled shape (see Fig. 7(c)) and adhesion properties in the vessel jamming, but the microfluidic technology offers a unique window in this complex dynamical process.
Finally, the aggregation of cells in the wall of microchannels can cause the formation of a clog. For example, the biofouling of porous filtration materials refers to the dramatic flow rate reduction due to the deposition and division of bacteria as well as the synthesis of polymeric substances during the biofilm and biofilm streamers formation.128,129 Studies in microfluidic devices have revealed information on the biofilm formation and properties and demonstrated that the biofilm streamers are porous structures that filter planktonic cells until clogging.120,135–137 The new technological platform will allow to study the transition from planktonic to biofilms and the influence of the flow features on the clogging dynamics.
6 Conclusion
In this review, we have reported on recent work that investigated the formation of clogs at the pore-scale level in microfluidic devices. Indeed, over the past decade, the microfluidic technology has been shown to be a powerful tool to control the flow of particles and record the dynamics of clog formation in different channel geometries. This new approach has led to a better description at the pore-scale, i.e., at the scale of a microchannel, of the three clogging mechanisms induced by the flow of micrometer-scale particles: sieving, bridging and aggregation (see Table 1).| Sieving | Bridging | Aggregation | |
|---|---|---|---|
| Size comparison (particle diameter D, channel width W) | D ≥ W | D ≤ W | D ≤ W |
| Solid volume fraction in suspension ϕ | Low ϕ | Large ϕ | Low ϕ |
| Interactions needed | Steric | Steric | Attractive particle–wall and particle–particle interactions |
| Clog formation | Blockage by a single particle | Blockage by an arch of particles | Successive deposition of particles leading to blockage |
In summary, sieving and bridging involve steric effects whereas the clogging by aggregation is induced by particle–particle and particle–wall attractive forces. The sieving is observed for particles that have a size D larger or comparable to the width W of the constriction, W/D ≤ 1, for any concentration of particles. The bridging occurs for suspensions having a large concentration ϕ flowing through narrow microchannel, whose width is typically of the order a few particles radii W ∼ 2–10D. Finally, clogging by aggregation can involve very diluted suspensions and fairly large constrictions but requires particle–wall and particle–particle attraction.
The recent observations performed in microfluidic systems, at the pore-scale, where the coupling between micrometer-scale particles and the microchannel walls can be finely characterized, will allow future investigations. An important step is to build on the microscopic observations performed in one microchannel and study more complex networks of channels, thus bridging the gap between the microfluidic studies and the clogging of porous media and filters that has been extensively studied in the past century at the macroscopic level.
The clogging mechanisms discussed in this review are relevant for colloidal and micrometer-scale particles. These mechanisms are also encountered in biological environments in which cells can block capillaries or microchannels and foul porous media. In particular, the technological applications of clogging to biological and biomedical systems constitute a promising research area, both fundamental as the mechanisms of biofouling are complex, and applied as the formation of biofilms and other cell aggregates have dramatic health consequences.
Acknowledgements
ED acknowledges financial support from the American Chemical Society Petroleum Research Fund under grant agreement PRF # 55845-ND9. The work of AS is partially supported by a CNRS PICS grant no. 07242.References
- E. Guazzelli and J. F. Morris, A Physical Introduction to Suspension Dynamics, Cambridge University Press, 2011 Search PubMed.
- J. Mewis and N. J. Wagner, Colloidal Suspension Rheology, Cambridge University Press, 2012 Search PubMed.
- P. Yang, S. Gai and J. Lin, Chem. Soc. Rev., 2012, 41, 3679–3698 RSC.
- M. Elimelech, J. Gregory and X. Jia, Particle Deposition and Aggregation: Measurement, Modelling and Simulation, Butterworth-Heinemann, 2013 Search PubMed.
- D. A. Fedosov, H. Noguchi and G. Gompper, Biomech. Model. Mechanobiol., 2014, 13, 239–258 CrossRef PubMed.
- F. Liang, M. Sayed, G. A. Al-Muntasheri, F. F. Chang and L. Li, Petroleum, 2016, 2, 26–39 CrossRef.
- R. G. M. van der Sman, Soft Matter, 2009, 5, 4376–4387 RSC.
- W. Zhang, X. Tang, N. Weisbrod and Z. Guan, J. Mt. Sci., 2012, 9, 770–787 CrossRef.
- L. Pang, S. Shen, C. Ma, T. Ma, R. Zhang, C. Tian, L. Zhao, W. Liu and J. Wang, Analyst, 2015, 140, 7335–7346 RSC.
- J. Gong, R. Jaiswal, P. Dalla, F. Luk and M. Bebawy, Semin. Cell Dev. Biol., 2015, 40, 35–40 CrossRef CAS PubMed.
- Y. Zhang, H. F. Chan and K. W. Leong, Adv. Drug Delivery Rev., 2013, 65, 104–120 CrossRef CAS PubMed.
- E. Vignati, R. Piazza and T. P. Lockhart, Langmuir, 2003, 19, 6650–6656 CrossRef CAS.
- W. Guo, H. H. Ngo and J. Li, Bioresour. Technol., 2012, 122, 27–34 CrossRef CAS PubMed.
- C. Henry, J. P. Minier and G. Lefevre, Adv. Colloid Interface Sci., 2012, 185–186, 34–76 CrossRef CAS PubMed.
- W. Zhang, J. Luo, L. Ding and M. Y. Jaffrin, Ind. Eng. Chem. Res., 2015, 54, 2843–2861 CrossRef CAS.
- G. D. Martin, S. D. Hoath and I. M. Hutchings, J. Phys.: Conf. Ser., 2008, 105, 012001 CrossRef.
- M. Singh, H. M. Haverinen, P. Dhagat and G. E. Jabbour, Adv. Mater., 2010, 22, 673–685 CrossRef CAS PubMed.
- I. Vermes, E. Steinmetz, L. J. J. M. Zeyen and E. van der Veen, Diabetologia, 1987, 30, 434–436 CrossRef CAS PubMed.
- S.-S. Chang, S. Tu, Y.-H. Lui, V. Savage, S.-P. L. Hwang and M. Roper, 2015, arXiv preprint.
- D. Katanov, G. Gompper and D. A. Fedosov, Microvasc. Res., 2015, 99, 57–66 CrossRef PubMed.
- R. Gopal, S. Kaur, Z. Ma, C. Chan, S. Ramakrishna and T. Matsuura, J. Membr. Sci., 2006, 281, 581–586 CrossRef CAS.
- D. V. Boger, Annu. Rev. Chem. Biomol. Eng., 2013, 4, 239–257 CrossRef CAS PubMed.
- M. M. Denn and J. F. Morris, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 203–228 CrossRef CAS PubMed.
- J. M. Brader, M. E. Cates and M. Fuchs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 1–17 CrossRef PubMed.
- I. E. Zarraga, D. A. Hill and D. T. Leighton, J. Rheol., 2000, 44, 185–220 CrossRef CAS.
- C. B. Holmes, M. Fuchs and M. E. Cates, Europhys. Lett., 2003, 63, 240–246 CrossRef CAS.
- J. F. Morris, Rheol. Acta, 2009, 48, 909–923 CrossRef CAS.
- G. During, E. Lerner and M. Wyart, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 1–12 CrossRef PubMed.
- G. K. Batchelor, An Introduction to Fluid Dynamics, Cambridge university press, 2000 Search PubMed.
- H. Wyss, D. Blair, J. Morris, H. Stone and D. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 061402 CrossRef PubMed.
- J. C. McDonald and G. M. Whitesides, Acc. Chem. Res., 2002, 35, 491–499 CrossRef CAS PubMed.
- A. Sauret, E. Barney, A. Perro, E. Villermaux, H. Stone and E. Dressaire, Appl. Phys. Lett., 2014, 105, 074101 CrossRef.
- H. M. Wyss, T. Franke, E. Mele and D. a. Weitz, Soft Matter, 2010, 6, 4550–4555 RSC.
- S. L. Sanderson, A. Y. Cheer, J. S. Goodrich, J. D. Graziano and W. T. Callan, Nature, 2001, 412, 439–441 CrossRef CAS PubMed.
- B. V. D. Bruggen, C. Vandecasteele, T. V. Gestel, W. Doyenb and R. Leysenb, Environ. Prog., 2003, 22, 46–56 CrossRef.
- B. He, L. Tan and F. Regnier, Anal. Chem., 1999, 71, 1464–1468 CrossRef CAS PubMed.
- B. Mustin and B. Stoeber, Microfluid. Nanofluid., 2010, 9, 905–913 CrossRef.
- J. Lin, D. Bourrier, M. Dilhan and P. Duru, Phys. Fluids, 2009, 21, 1–14 Search PubMed.
- P. Duru and Y. Hallez, Langmuir, 2015, 31, 8310–8317 CrossRef CAS PubMed.
- H. Wei, B.-h. Chueh, H. Wu, E. W. Hall, C.-w. Li, R. Schirhagl, J.-M. Lin and R. N. Zare, Lab Chip, 2011, 11, 238–245 RSC.
- J. Kim, J. Erath, A. Rodriguez and C. Yang, Lab Chip, 2014, 14, 2480–2490 RSC.
- S. J. Blott and K. Pye, Sedimentology, 2012, 59, 2071–2096 CrossRef.
- C. S. Chern, Prog. Polym. Sci., 2006, 31, 443–486 CrossRef CAS.
- B. Liu, M. Zhang, G. Yu, D. Chen and H. Zhang, Colloids Surf., A, 2014, 452, 159–164 CrossRef CAS.
- R. Pecora, Dynamic Light Scattering: Applications of Photon Correlation Spectroscopy, Springer Science & Business Media, 2013 Search PubMed.
- H. Berthet, M. Fermigier and A. Lindner, Phys. Fluids, 2013, 25, 103601 CrossRef.
- M. Malmsten, Soft Matter, 2006, 2, 760–769 RSC.
- A. Abbaspourrad, N. J. Carroll, S. H. Kim and D. A. Weitz, J. Am. Chem. Soc., 2013, 135, 7744–7750 CrossRef CAS PubMed.
- M. Destribats, M. Rouvet, C. Gehin-Delval, C. Schmitt and B. P. Binks, Soft Matter, 2014, 10, 6941–6954 RSC.
- M. Abkarian, M. Faivre and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 538–542 CrossRef CAS PubMed.
- S. She, C. Xu, X. Yin, W. Tong and C. Gao, Langmuir, 2012, 28, 5010–5016 CrossRef CAS PubMed.
- Y. Li, E. Kumacheva and A. Ramachandran, Soft Matter, 2013, 9, 10391–10403 RSC.
- Y. Li, O. S. Saryer, A. Ramachandran, S. Panyukov, M. Rubinstein and E. Kumacheva, Sci. Rep., 2015, 5, 17017 CrossRef PubMed.
- H. Noguchi, G. Gompper, T. C. Lubensky, H. Noguchit and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2016, 102, 14159–14164 CrossRef PubMed.
- A. S. Popel and P. C. Johnson, Annu. Rev. Fluid Mech., 2005, 37, 43–69 CrossRef PubMed.
- R. M. Bateman, M. D. Sharpe and C. G. Ellis, Crit. Care, 2003, 7, 359–373 CrossRef PubMed.
- H. Lei and G. E. Karniadakis, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 11326–11330 CrossRef CAS PubMed.
- M. Guo and H. M. Wyss, Macromol. Mater. Eng., 2011, 296, 223–229 CrossRef CAS.
- T. Kong, L. Wang, H. M. Wyss and H. C. Shum, Soft Matter, 2014, 10, 3271–3276 RSC.
- Q. Guo, S. M. McFaul and H. Ma, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 1–5 Search PubMed.
- S. M. McFaul, B. K. Lin and H. Ma, Lab Chip, 2012, 12, 2369–2376 RSC.
- P. Preira, V. Grandné, J.-M. Forel, S. Gabriele, M. Camara and O. Theodoly, Lab Chip, 2013, 13, 161–170 RSC.
- D. J. Hoelzle, B. a. Varghese, C. K. Chan and A. C. Rowat, J. Visualized Exp., 2014, e51474 Search PubMed.
- T.-H. Kim, A. C. Rowat and E. K. Sloan, Clin. Transl. Immunol., 2016, 5, e78 CrossRef PubMed.
- K. V. Sharp and R. J. Adrian, Microfluid. Nanofluid., 2005, 1, 376–380 CrossRef.
- M. E. Cates, J. Wittmer, J.-P. Bouchaud and P. Claudin, Phys. Rev. Lett., 1998, 81, 1841–1844 CrossRef CAS.
- A. J. Liu and S. R. Nagel, Nature, 1998, 396, 21–22 CrossRef CAS.
- M. van Hecke, J. Phys.: Condens. Matter, 2010, 22, 033101 CrossRef CAS PubMed.
- P. G. Lafond, M. W. Gilmer, C. A. Koh, E. D. Sloan, D. T. Wu and A. K. Sum, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 1–8 CrossRef PubMed.
- I. Zuriguel, D. R. Parisi, R. C. Hidalgo, C. Lozano, A. Janda, P. A. Gago, J. P. Peralta, L. M. Ferrer, L. A. Pugnaloni, E. Clément, D. Maza, I. Pagonabarraga and A. Garcimartín, Sci. Rep., 2014, 4, 7324 CrossRef CAS PubMed.
- I. Zuriguel, Pap. Phys., 2014, 6, 13 Search PubMed.
- A. I. Campbell and M. D. Haw, Soft Matter, 2010, 6, 4688–4693 RSC.
- V. Ramachandran and H. S. Fogler, J. Fluid Mech., 1999, 385, 129–156 CrossRef CAS.
- A. Fall, N. Huang, F. Bertrand, G. Ovarlez and D. Bonn, Phys. Rev. Lett., 2008, 100, 1–4 CrossRef PubMed.
- F. Boyer, É. Guazzelli and O. Pouliquen, Phys. Rev. Lett., 2011, 107, 188301 CrossRef PubMed.
- J. Paredes, M. A. J. Michels and D. Bonn, Phys. Rev. Lett., 2013, 111, 015701 CrossRef PubMed.
- T. Divoux, V. Lapeyre, V. Ravaine and S. Manneville, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 060301 CrossRef PubMed.
- A. Einstein, Ann. Phys., 1905, 322, 549–560 CrossRef.
- G. K. Batchelor, J. Fluid Mech., 1982, 119, 379–408 CrossRef.
- D. Genovese and J. Sprakel, Soft Matter, 2011, 7, 3889–3896 RSC.
- A. Deboeuf, G. Gauthier, J. Martin, Y. Yurkovetsky and J. F. Morris, Phys. Rev. Lett., 2009, 102, 108301 CrossRef PubMed.
- R. Ward and S. G. Whitmore, Br. J. Appl. Phys., 1950, I, 325–328 CrossRef.
- M. D. Haw, Phys. Rev. Lett., 2004, 92, 185506 CrossRef CAS PubMed.
- L. Isa, R. Besseling, A. N. Morozov and W. C. K. Poon, Phys. Rev. Lett., 2009, 102, 058302 CrossRef PubMed.
- G. C. Agbangla, E. Climent and P. Bacchin, Sep. Purif. Technol., 2012, 101, 42–48 CrossRef CAS.
- U. Zimmermann, F. Smallenburg and H. Löwen, J. Phys.: Condens. Matter, 2015, 28, 244019 CrossRef PubMed.
- G. H. Goldsztein and J. C. Santamarina, Appl. Phys. Lett., 2004, 85, 4535–4537 CrossRef CAS.
- J. R. Valdes and J. C. Santamarina, Appl. Phys. Lett., 2007, 90, 244101 CrossRef.
- Z. B. Sendekie and P. Bacchin, Langmuir, 2016, 32, 1478–1488 CrossRef CAS PubMed.
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- S. Giglia and G. Straeffer, J. Membr. Sci., 2012, 417, 144–153 CrossRef.
- M. T. Stamm, T. Gudipaty, C. Rush, L. Jiang and Y. Zohar, Microfluid. Nanofluid., 2011, 11, 395–403 CrossRef CAS.
- T. Gudipaty, M. T. Stamm, L. S. L. Cheung, L. Jiang and Y. Zohar, Microfluid. Nanofluid., 2011, 10, 661–669 CrossRef.
- S. S. Massenburg, E. Amstad and D. A. Weitz, Microfluid. Nanofluid., 2016, 20, 94 CrossRef.
- J. Linkhorst, T. Beckmann, D. Go, A. J. C. Kuehne and M. Wessling, Sci. Rep., 2016, 6, 22376 CrossRef CAS PubMed.
- B. Dersoir, M. R. de Saint Vincent, M. Abkarian and H. Tabuteau, Microfluid. Nanofluid., 2015, 19, 953–961 CrossRef CAS.
- M. R. de Saint Vincent, M. Abkarian and H. Tabuteau, Soft Matter, 2016, 12, 1041–1050 RSC.
- V. Ramachandran and H. S. Fogler, Langmuir, 1998, 14, 4435–4444 CrossRef CAS.
- G. C. Agbangla, PhD thesis, Universite Toulouse 3, 2011.
- H. N. Unni and C. Yang, J. Colloid Interface Sci., 2005, 291, 28–36 CrossRef CAS PubMed.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic press, 2011 Search PubMed.
- H. N. Unni and C. Yang, Can. J. Chem. Eng., 2007, 85, 609–616 CrossRef CAS.
- Z. Adamczyk, B. Siwek and L. Szyk, J. Colloid Interface Sci., 1995, 174, 130–141 CrossRef CAS.
- M. Elimelech and C. R. O'Melia, Environ. Sci. Technol., 1990, 24, 1528–1536 CrossRef CAS.
- H. Brenner, Adv. Chem. Eng., 1966, 6, 287–438 CAS.
- A. J. Goldman, R. G. Cox and H. Brenner, Chem. Eng. Sci., 1967, 22, 637–651 CrossRef CAS.
- A. J. Goldman, R. G. Cox and H. Brenner, Chem. Eng. Sci., 1967, 22, 653–660 CrossRef CAS.
- J. Masliyah and S. Bhattacharjee, Electrokinetic and Colloid Transport Phenomena, John Wiley & Sons, 2006 Search PubMed.
- C. P. Ortiz, R. Riehn and K. E. Daniels, Soft Matter, 2013, 9, 543–549 RSC.
- E. Brunet, G. Degré, F. Okkels and P. Tabeling, J. Colloid Interface Sci., 2005, 282, 58–68 CrossRef CAS PubMed.
- T. van de Laar, S. ten Klooster, K. Schroën and J. Sprakel, Sci. Rep., 2016, 6, 28450 CrossRef PubMed.
- M. Thiriet, Biology and mechanics of blood flows: Part I: Biology, Springer Science & Business Media, 2008 Search PubMed.
- M. Thiriet, Biology and mechanics of blood flows: Part II: Mechanics and medical aspects, Springer Science & Business Media, 2008 Search PubMed.
- T. A. Duncombe, A. M. Tentori and A. E. Herr, Nat. Rev. Mol. Cell Biol., 2015, 16, 554–567 CrossRef CAS PubMed.
- C. W. Shields IV, C. D. Reyes and G. P. López, Lab Chip, 2015, 15, 1230–1249 RSC.
- P. Patil, T. Kumeria, D. Losic and M. Kurkuri, RSC Adv., 2015, 5, 89745–89762 RSC.
- E. Loiseau, G. Massiera, S. Mendez, P. A. Martinez and M. Abkarian, Biophys. J., 2015, 108, 2623–2632 CrossRef CAS PubMed.
- J. Picot, P. A. Ndour, S. D. Lefevre, W. E. Nemer, H. Tawfik, J. Galimand, L. Da Costa, J. Ribeil, M. De Montalembert, V. Brousse and B. Le Pioufle, Am. J. Hematol., 2015, 4, 339–345 CrossRef PubMed.
- J. Ciciliano, Y. Sakurai, D. Myers, M. Fay, B. Hechler, S. Meeks, R. Li, J. Dixon, L. Lyon, C. Gachet and W. Lam, Blood, 2015, 126, 817–824 CrossRef CAS PubMed.
- K. Drescher, Y. Shen, B. L. Bassler and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4345–4350 CrossRef CAS PubMed.
- Y. Tang, J. Shi, S. Li, L. Wang, Y. E. Cayre and Y. Chen, Sci. Rep., 2014, 4, 6052 CAS.
- E. Du, M. Diez-Silva, G. J. Kato, M. Dao and S. Suresh, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 1422–1427 CrossRef CAS PubMed.
- T. Huang, C.-P. Jia, Jun-Yang, W.-J. Sun, W.-T. Wang, H.-L. Zhang, H. Cong, F.-X. Jing, H.-J. Mao, Q.-H. Jin, Z. Zhang, Y.-J. Chen, G. Li, G.-X. Mao and J.-L. Zhao, Biosens. Bioelectron., 2014, 51, 213–218 CrossRef CAS PubMed.
- E. S. Park, C. Jin, Q. Guo, R. R. Ang, S. P. Duffy, K. Matthews, A. Azad, H. Abdi, T. Todenhöfer, J. Bazov, K. N. Chi, P. C. Black and H. Ma, Small, 2016, 12, 1909–1919 CrossRef CAS PubMed.
- G. R. Serjeant and B. E. Serjeant, Sickle Cell Disease, Oxford university press, 1992 Search PubMed.
- D. Manwani and P. S. Frenette, Hematology/the Education Program of the American Society of Hematology. American Society of Hematology. Education Program, 2013, 122, 3892–3898.
- M. T. Gladwin, Lancet, 2016, 387, 2565–2574 CrossRef.
- M. E. Olson, H. Ceri, D. W. Morck, A. G. Buret and R. R. Read, Can. J. Vet. Res., 2002, 66, 86–92 Search PubMed.
- M. A. Ghannoum, M. Parsek, M. Whiteley and P. Mukherjee, Microbial Biofilms, ASM Press, 2015 Search PubMed.
- D. Wirtz, K. Konstantopoulos and P. C. Searson, Nat. Rev. Cancer, 2011, 11, 512–522 CrossRef CAS PubMed.
- R. A. Harouaka, M. Nisic and S.-Y. Zheng, J. Lab. Autom., 2013, 18, 455–468 CrossRef CAS PubMed.
- M. Delarue, J. Hartung, C. Schreck, P. Gniewek, L. Hu, S. Herminghaus and O. Hallatschek, Nat. Phys., 2016, 12, 762–766 CrossRef CAS PubMed.
- J. M. Higgins, D. T. Eddington, S. N. Bhatia and L. Mahadevan, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20496–20500 CrossRef CAS PubMed.
- D. Wood, A. Soriano, L. Mahadevan, J. Higgins and S. Bhatia, Sci. Transl. Med., 2012, 4, 123 Search PubMed.
- L. De La Fuente, E. Montanes, Y. Meng, Y. Li, T. J. Burr, H. C. Hoch and M. Wu, Appl. Environ. Microbiol., 2007, 73, 2690–2696 CrossRef CAS PubMed.
- A. P. Mosier, A. E. Kaloyeros and N. C. Cady, J. Microbiol. Methods, 2012, 91, 198–204 CrossRef PubMed.
- A. Karimi, D. Karig, A. Kumar and A. M. Ardekani, Lab Chip, 2015, 15, 23–42 RSC.
| This journal is © The Royal Society of Chemistry 2017 |