Drop morphologies on flexible fibers: influence of elastocapillary effects
Alban
Sauret†
 *a,
François
Boulogne†
b,
Katarzyna
Somszor
bc,
Emilie
Dressaire
c and
Howard A.
Stone
b
*a,
François
Boulogne†
b,
Katarzyna
Somszor
bc,
Emilie
Dressaire
c and
Howard A.
Stone
b
aSurface du Verre et Interfaces, UMR 125 CNRS/Saint-Gobain, 93303, Aubervilliers, France. E-mail: alban.sauret@saint-gobain.com
bDepartment of Mechanical and Aerospace Engineering, Princeton University, Princeton, New Jersey 08544, USA
cDepartment of Mechanical and Aerospace Engineering, New York University Tandon School of Engineering, Brooklyn, NY 11201, USA
First published on 9th November 2016
Abstract
Various materials are made of long thin fibers that are randomly oriented to form a complex network in which drops of wetting liquid tend to accumulate at the nodes. The capillary force exerted by the liquid can bend flexible fibers, which in turn influences the morphology adopted by the liquid. In this paper, we investigate through a model situation the role of the fiber flexibility on the shape of a small volume of liquid on a pair of crossed flexible fibers. We characterize the liquid morphologies as we vary the volume of liquid, the angle between the fibers, and the length of the fibers. The drop morphologies previously reported for rigid crossed fibers, i.e., a drop, a column and a mixed morphology, are also observed on flexible crossed fibers with modified domains of existence. In addition, at small tilt angles between the fibers, a new behavior is observed: the fibers bend and collapse. Depending on the volume of liquid, a thin column with or without a drop is reported on the collapsed fibers. Our study suggests that the fiber flexibility adds a rich variety of behaviors that may be important for some applications.
1 Introduction
A capillary bridge between two spheres or two surfaces is known to exert a force that tends to keep the two solid bodies together.1–3 For soft surfaces, the combination of the capillary force and the bending and/or stretching of the material leads to an elastocapillary equilibrium in which the elastic deformations of the substrate is related to the intensity of the capillary adhesion.4,5 Elastocapillary effects are, for instance, responsible for the formation of bundles with flexible beams6–8 or fibers,9,10 the collapse of beams in MEMS applications8,11–13 and in carbon nanotube14 or in biological situations such as the wetting of feathers.15Elastocapillary effects can be particularly important when considering thin elongated structures, such as fibers, whose length can be several orders of magnitude larger than their diameter; fibers are therefore prone to bend.9,16–19 In addition, fibers, rigid or flexible, can be found in a variety of applications such as in wet hair,6 in the textile industry,20–22 in filters,23,24 fog-harvesting nets25–27 or insulation materials, including glass wool.28,29 Therefore, many studies have considered the addition of liquid on an array of fibers through model systems that consist of a finite volume of wetting liquid deposited on a single or a pair of fibers.30–32 These model situations allow investigation of the equilibrium shapes of the liquid and their influence on the drying process,33,34 the capture of impacting drops,35 the condensation of liquid36 or the motion of drops along fibers.37–41
Past studies have considered the morphology adopted by a liquid drop deposited on a single fiber. For example, the addition of liquid on a single fiber can come from coating methods,32 the condensation of liquid36 or the impact of small droplets that are captured below an impact velocity threshold.35,42,43 Once on the fiber, the drop can either adopt an axisymmetric (barrel shape) morphology or an asymmetric (clamshell) morphology where the drop sits on one side of the fibers.31,44–47
Considering rigid fibers, the presence of a second fiber close to the first one leads to different morphologies that depend on the contact angle of the liquid with the fiber, the inter-fiber distance, the tilt angle between them and the volume of liquid that is deposited. For instance, for two parallel fibers separated by a distance 2d, the seminal work of Princen30 shows that the liquid can either spread in a long liquid column, whose width is of the order of the fiber diameter if the fibers are close enough, or adopt a more compact drop shape when the inter-fiber distance is increased. More recently, three different possible morphologies have been reported for fibers of radius a randomly oriented, i.e., tilted with an angle δ and separated by a minimum distance h. Depending on δ, ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) = h/a, and the dimensionless volume of liquid Ṽ = V/a3, the liquid can be in a column shape, a mixed morphology state where a drop lies at the end of a column, or a drop centered at the node, i.e., the point where the two fibers are the closest.28,48,49
= h/a, and the dimensionless volume of liquid Ṽ = V/a3, the liquid can be in a column shape, a mixed morphology state where a drop lies at the end of a column, or a drop centered at the node, i.e., the point where the two fibers are the closest.28,48,49
However, some fibrous materials, involve fibers that are very thin and long. Such high aspect ratio fibers are typically flexible. Therefore, the presence of liquid forming capillary bridges between fibers is susceptible to modify the liquid morphologies and the organization of the fibers in a randomly oriented array. Indeed, the presence of liquid can lead to the clustering of flexible structures as shown by Py et al.16 who investigated the behavior of a model brush of parallel flexible fibers withdrawn from a liquid bath. To describe their experimental findings, the authors defined an elastocapillary lengthscale:4,6
 | (1) |
Because the capillary force and the elasticity of the fibers can lead to the deformation of the fibers,50 different configurations have been investigated. In particular, Duprat et al. considered parallel fibers whose spacing and length are controlled and a known volume of wetting liquid is deposited.17 Different morphologies were observed: a drop state, a column morphology or a mixed morphology. In addition, the presence of liquid was shown to bend the fibers and influence the final liquid morphology. In their configuration, the elastocapillary length is around lEC ∼ 55 cm whereas the length of the fibers Lfib is typically a few centimeters. In such model experiments, although Lfib ≪ lEC, the effects of the flexibility can be observed experimentally and lead to the presence of new liquid morphologies.
However, the more general situation of tilted flexible fibers, encountered in arrays, has not been studied. The presence of liquid at a node is expected to introduce a capillary force and a torque that can modify the orientation of the fibers and lead to different morphologies.51 However, no systematic experimental investigations has been reported to date. To study this situation, we consider two crossed fibers, clamped at one of their ends and free to move at the other, in contact at the node and tilted with an angle δ = [0,90]°. Using experiments, we then investigate the morphologies and the equilibrium orientations of the fibers while varying the imposed initial tilt angle δ and the volume of liquid V deposited on the fibers. We highlight the presence of two new morphologies compared to the situation of crossed rigid fibers: a column collapsed state and a drop-collapsed state. In this paper, we first present the experimental method in Section 2. In Section 3, we describe the new morphologies and a morphology diagram in the (δ,Ṽ) space is reported. We then rationalize our results to explain these new morphologies. Finally, we highlight in section 4 that hysteresis effects can be large in such systems owing to capillary effects.
2 Experimental protocol
In our experiments, the fibers consist of thin capillary cylindrical tubes (purchased from VitroCom) of outer diameter 2a = 250 μm and inner diameter 2b = 150 μm. We seal the end of the tube with a small amount of epoxy glue so that no liquid can flow into the capillary tube. We have measured the bending modulus of these fibers using their deflection under their own weight and obtained B = 8.1 × 10−6 Pa m4, in agreement with the estimated theoretical value B = EI = πE(a4 − b4)/4, where I is the polar moment of inertia of the cross section of the fiber. The weight per unit length is ρl = 3.5 × 10−5 kg m−1. Therefore, the value of the elastocapillary length in our system is lEC ≃ 1.8 m, which is of the same order of magnitude as the one of previous experiments investigating elastocapillary effects between parallel fibers.17 In this paper, we study a system in which the typical drop size V1/3 is much smaller than the elastocapillary length, i.e., V1/3 ≪ lEC. As a consequence the fibers cannot bend on the lengthscale of the drop. Roman and Bico studied the opposite limit and they observed that a soft fiber coils around a liquid drop.4One extremity of each fiber is clamped on a (x,y,z) microcontroller linear stage (PT3, Thorlabs). Fibers cross at the node. One of the controllers is allowed to rotate around the node with a rotation mount (PR01, Thorlabs) to accurately tune the angle δ between the fibers. We denote Lfib the total length of a fiber and Lfree the distance between the node and the tip of the fiber (Fig. 1). In all experiments presented in this paper, the lengths Lfib and Lfree are identical for both fibers. The vertical deflection of fibers due to their own weight and the weight of the drop is limited to 3 mm for the largest fiber length (Lfib = 90 mm) and the largest drop volume (V = 8 μl). We should emphasize that we could not use longer fibers since gravity effects will then become too important.
Before each experiment, the horizontal positions of the microcontrollers are adjusted to ensure that Lfree remains constant while varying the tilt angle δ. The vertical positions of the linear microcontrollers are then adjusted to bring the fibers into contact. In all the experiments, we use a perfectly wetting fluid (5 cSt silicone oil, contact angle θ = 0°, density ρ = 918 kg m−3, surface tension γ = 19.7 mN m−1). A volume V ∈ [1,8] μl is initially dispensed with a micropipette (Eppendorf, Research Plus) at the node of the fibers. Because the fibers are flexible and bend under capillary effects, the apparent angle between the fiber ϕ can be smaller than the tilt angle without liquid δ as illustrated by the schematic in Fig. 1. In our experiments, we assume that the gravitational effects on the liquid bridge can be neglected. Indeed, the capillary length,  , is larger than the typical height H of the liquid. In addition, we neglect gravitational effects on the fibers because, in the absence of liquid, the fibers do not bend significantly under their own weight with the chosen length Lfib, as noted above.
, is larger than the typical height H of the liquid. In addition, we neglect gravitational effects on the fibers because, in the absence of liquid, the fibers do not bend significantly under their own weight with the chosen length Lfib, as noted above.
We start the experiment at a large tilt angle between the fibers (typically δ = 60°) and the angle is reduced to the desired value. The imposed tilt angle δ is directly measured on the rotation microcontroller with an uncertainty of about 0.5°. We wait for a few minutes to ensure that the final steady liquid morphology is reached and record images from the top and from the side using Nikon cameras (D5100 and D7100) and 105 mm macro lenses. The induced angle ϕ is measured using the top view images (corresponding to the schematic in Fig. 1) by image processing with an uncertainty of about 0.5°. When a steady morphology has been reached and the images recorded, we increase or decrease the angle δ between the fibers and ensure that Lfree remains constant and wait until a new steady state is reached. Using this method, we explore the influence of the volume of liquid, the tilt angle δ between the fibers, the total length Lfib and the free end Lfree of the fibers on the final morphology.
3 Morphologies and transitions
3.1 Morphology diagram
Our experimental observations highlight that the three liquid morphologies observed on rigid crossing fibers are recovered with flexible fibers as illustrated in Fig. 2(a)–(c):28 (i) the drop state for large angles (typically δ > 35°) where the liquid collects at the node of the fiber and forms a single hemispherical drop, (ii) a mixed morphology when the tilt angle is decreased and in which the liquid partially spreads into a column but a drop remains located on one side of the column (note that the side of the column where the drop is located is random and induced by perturbations present in the surrounding environment or introduced when changing the tilt angle) and (iii) a column state at small angles and small volume where the liquid spreads between the fibers and where the height of the column is typically comparable to the fiber diameter.Considering crossed flexible fibers that are clamped on one end and free to move at their other end leads to two previously unreported morphologies, shown in Fig. 2(d) and (e). This response is indeed caused by the flexibility of the crossed fibers. The presence of the wetting liquid located at the node, i.e., the point where the two fibers cross, results in capillary forces that tend to pull on fibers and cause them to deflect inwards. This elastocapillary effect decreases the local distance between the fibers and the liquid can thus continue to spread spontaneously along the fibers. The magnitude of the capillary force increases, further bending the fibers, until they stick to one another, i.e., collapse, and the liquid can form a thin long column. The interfacial and bending energies therefore lead to the observed collapsed morphology reported in Fig. 2(d). Finally, if more liquid is added to the system, the thin column keeps spreading until it reaches the full length of the sticking region, 2Lfree, and a drop grows at one end of the column. The results in the drop-collapsed morphology are shown in Fig. 2(e).
We experimentally characterize the regions of existence of the five different morphologies observed for crossed flexible fibers having a constant total length Lfib and a free length Lfree. We perform systematic experiments varying the liquid volume Ṽ = V/a3 and the tilt angle δ, and report our results in a (Ṽ, δ) morphology diagram in Fig. 2(f). Both the collapsed and drop-collapsed morphologies are observed below a tilt angle δ typically smaller than 5° for the fibers considered. Above this angle, we recover the morphology diagram of the rigid fibers as the capillary force is not sufficient to significantly bend the fibers at large tilt angle δ. Indeed, the column/mixed morphology transition described by Sauret et al.28 for rigid fibers satisfactorily captures the column/mixed morphology transition for flexible fibers as reported in Fig. 2(f). In addition, the column/drop and mixed/drop morphology transitions are also observed for a critical angle δ = 35 ± 5°, as reported for rigid fibers. The key difference is therefore that, below a critical angle, the classical column morphology is not observed but instead the fibers stick to one another in a collapsed state. In addition, in this regime of small angles, we observe a state of partial spreading for sufficiently large volume of liquid: a smaller drop remains at the edge of the collapsed region.
3.2 Transitions at large angles: drop, mixed and column morphologies
If the fibers are sufficiently rigid or the capillary force too weak to bend the fibers, the local angle at the node must be equal to the global tilt angle, that is δ = ϕ. We measure the local angle ϕ as a function of the global angle δ in our system. The results indicate that the capillary force is not sufficient to significantly bend the fibers for δ > 4° for the fibers used in our experiments, which is the angle at which the collapse transition occurs. Note that the value at which the bending of the fibers becomes important depends on the flexibility of the fibers and thus on the elastocapillary length compared to the fibers length. Therefore, the transition between the different regimes can be described by the model developed for rigid fibers, and described in previous publications.28,483.3 Transitions to the collapsed states
The transition between the column or mixed morphology (Fig. 2(b) and (c)) and the collapsed state (Fig. 2(d) and (e)) is more complex. The bending and collapse of the fibers result from an elastocapillary equilibrium. To rationalize these results, despite the complex shape of the liquid column, we can estimate the energy associated with the bending of a fiber in the collapsed state and the energy associated to the capillary bridge induced by the liquid column in the collapsed state. Different simplified situations have considered this elastocapillary equilibrium between parallel sheets or fibers.6,16,17 We denote d the distance over which the fiber needs to be deflected for the fibers to stick to one another along Lfree. Using geometrical considerations, we have | (2) |
Because the collapse happens in the limit of small angles, δ ≪ 1, we can simplify (2) to d = δLfree. Using the same notations as Bico et al.,6 we define the length of the wet segment of the fiber as Lwet = Lfib − Ldry, where Lfib and Ldry are the total length of a fiber and the dry part, respectively. The bending energy Ec associated to the deformation of the two fibers that coalesce at a distance Ldry is
 | (3) |
To simplify, we consider the capillary force induced by a liquid column when the fibers are in the collapsed state and therefore the fibers are parallel. In this situation, the liquid column has a constant cross-sectional area A ≃ πa2 on the entire free length Lwet = 2(Lfib − Ldry). Therefore, the energy associated to the capillary force is
| Es ∼ −2γa(π − 2)(Lfib − Ldry), | (4) |
 | (5) |
Using eqn (2), and considering that the fibers collapse when Lwet = 2Lfree= 2(Lfib − Ldry) we obtain the following estimate for the tilt angle δ
 | (6) |
Introducing the elastocapillary length lEC defined in eqn (1), and the ratio between the free length and the total length of the fiber α = Lfree/Lfib, this expression can be rewritten as:
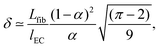 | (7) |
The experimental results obtained by varying the total length of the fiber Lfib are in qualitative agreement with this expression as illustrated in Fig. 3: the longer the fibers, the easier the collapse. Note that the order of magnitude estimate given here could be refined by considering the exact length and shape of the column for a given volume. As a result, the energy associated with the capillary bridge between the fibers could be calculated between two crossed fibers.28 However, such calculations would require to know the inter-fibers distance, which is modified by the elastocapillary equilibrium even before the collapsed state.
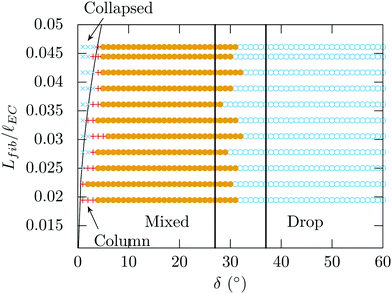 | ||
| Fig. 3 Morphologies observed for fibers of radius a = 125 μm, lEC = 1.8 m and varying Lfib/lEC. Lfree= 14 mm, the volume Ṽ = 768 and a = 125 μm are constant. The black solid curve represents eqn (7). The vertical black lines show the drop-mixed transition represented in Fig. 2(f). | ||
With typical experimental values, Lfib = 87 mm, Lfree = 18.5 mm, B = EI = 8.1 × 10−6 Pa m4, a = 125 mm, γ = 19.7 mN m−1, from (7) we obtain δ ∼ 3°. This result is satisfactorily close to the observed value and shows that elastocapillary effects are indeed responsible for the collapse of the fibers at sufficiently small angle. However, we shall see that because of our assumption of a flat shape, the transition between the column or mixed morphology and the collapsed state is only an order of magnitude. In addition, because of the shape of the capillary bridge in the column and the collapsed morphologies, the angle necessary for the fibers to release from the sticking state will be larger than the angle for the fibers to collapse. Indeed, flexible fibers that collapse owing to capillary effects present a strong hysteresis as described in Section 4.
3.4 Transition between collapsed and drop-collapsed morphologies
We now turn to the transition between the collapsed and drop-collapsed morphologies. Similarly to the situations described for parallel fibers, when the fibers collapse, the liquid shape can be assumed to be a long straight column with a cross-sectional area A ≃ πa2.17 Because the liquid can spread over a distance Lfree on each side of the node, the critical volume that describes the transition between collapsed and drop-collapsed morphologies is Vc = 2πa2Lfree leading to the critical dimensionless volume | (8) |
This expression is in agreement with our experimental observation reported on the morphology diagram in Fig. 2(f). In addition, we perform systematic experiments varying the free length of the fiber beyond the node, Lfree. The volume of liquid at the transition is thus measured and the results shown in Fig. 4 are well captured by eqn (8). Beyond the threshold value Vc, adding more liquid leads to the formation of a liquid drop at one end of the thin column.
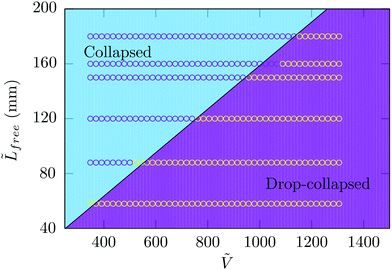 | ||
Fig. 4 Threshold value of the volume of liquid delimiting the collapsed and drop-collapsed states for varying length of the free end of the fiber ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) free = Lfree/a. The continuous black line is defined by eqn (8) and the experimental parameters kept constant are a = 125 μm and Lfib = 110 mm. free = Lfree/a. The continuous black line is defined by eqn (8) and the experimental parameters kept constant are a = 125 μm and Lfib = 110 mm. | ||
4 Hysteresis
The morphology diagram (Fig. 2(f)) presented in this article is established by starting at large tilt angle δ and then decreasing the angle for each dimensionless volume of liquid Ṽ considered. However, we also perform experiments considering the opposite situation: we start with collapsed fibers and incrementally increase the tilt angle until the collapsed to column/mixed morphology transition occurs (Fig. 2(d) and (e) then Fig. 2(b) and (c)). We observe that the critical tilt angle δr at which the fibers separate is much larger than the angle δc at which the fibers collapse. We have reported these hysteretic measurements in Fig. 5 for different volumes of liquid.We observe that the amount of liquid seems to have no influence on the coalescence and separation angles in the range of volumes considered. Indeed, when the fibers are collapsed, the liquid spreads along a thin liquid column and, the volume considered is sufficiently large for the liquid to reach the free ends of the fibers. Therefore, the energy associated with the capillary force can be assumed constant as well as the bending energy that is necessary for the fibers to be released at δr.
Finally, we explore the effects of the free length Lfree on the critical angle δr for the separation of collapsed fibers. Indeed, the capillary force associated to the wetting of parallel fibers on a distance Lfree is Es = −2γa(π − 2)Lfree. Therefore, increasing the free length of the fibers qualitatively leads to an increase of the adhesion force, increasing the critical angle for the separation of the collapsed fibers. This hysteresis effect between the column/mixed and collapsed morphologies may modify significantly the lower part of the morphology diagram shown in Fig. 2(f).
5 Conclusion
In this paper, we have experimentally illustrated that flexible crossed fibers share similar morphologies to the system of rigid fibers. In particular, at large tilt angle δ, the three morphologies obtained for rigid crossed fibers are recovered. However, when decreasing the tilt angle, the energy required to collapse the fibers decreases while the capillary force increases. The capillary force first leads to a larger deflection of the fibers, namely the tilt angle between the fibers is locally decreased (ϕ < δ) slightly modifying the column to mixed morphology transition. In addition, we have reported two new morphologies at small tilt angle δ: a column collapsed and a drop-collapsed morphology where the fibers are locally parallel. The transition between these two morphologies can be explained by considering the maximum amount of liquid that can spread into a long thin column around collapsed fibers. The transition between the column or mixed morphology and the collapsed morphologies can be captured by considering an elastocapillary equilibrium, as observed for parallel lamellae or fibers. We also observe a strong hysteresis in the system between the column/mixed and collapsed morphologies. The experiments in this study are performed in the regime where Lfib/lEC ≪ 1. Future works will need to investigate the situation Lfib/lEC > 1 where the effects of the flexibility are expected to be even greater. For instance, the influence of the flexibility of the fibers can be especially important in systems where the porosity of the fiber network needs to be large as capillary effects will tend to align fibers and form large clusters.6–8Acknowledgements
The work of AS is partially supported by a CNRS PICS grant no. 07242. KS and ED acknowledge financial support from NYU Tandon School of Engineering's Undergraduate Summer Research Program. FB acknowledges that the research leading to these results partially received funding from the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme (FP7/2007–2013) under REA grant agreement 623541.References
- L. R. Fisher and J. N. Israelachvili, J. Colloid Interface Sci., 1981, 80, 528–541 Search PubMed.
- C. H. Mastrangelo and C. H. Hsu, Systems, 1993, 2, 33–43 Search PubMed.
- C. D. Willett, M. J. Adams, S. A. Johnson and J. Seville, Langmuir, 2000, 9396–9405 Search PubMed.
- B. Roman and J. Bico, J. Phys.: Condens. Matter, 2010, 22, 493101 Search PubMed.
- J. L. Liu and X. Q. Feng, Acta Mech. Sin., 2012, 928–940 CrossRef.
- J. Bico, B. Roman, L. Moulin and A. Boudaoud, Nature, 2004, 432, 690 Search PubMed.
- K. Singh, J. R. Lister and D. Vella, J. Fluid Mech., 2014, 745, 621–646 Search PubMed.
- B. Pokroy, S. H. Kang, L. Mahadevan and J. Aizenberg, Science, 2009, 323, 237–240 Search PubMed.
- A. Boudaoud, J. Bico and B. Roman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 060102 Search PubMed.
- Q. Wang, B. Su, H. Liu and L. Jiang, Adv. Mater., 2014, 26, 4889–4894 Search PubMed.
- D. Chandra, S. Yang and A. A. Soshinsky, ACS Appl. Mater. Interfaces, 2009, 1, 1698–1704 Search PubMed.
- D. Chandra and S. Yang, Acc. Chem. Res., 2010, 43, 1080–1091 Search PubMed.
- M. De Volder and A. J. Hart, Angew. Chem., Int. Ed., 2013, 52, 2412–2425 Search PubMed.
- N. Chakrapani, B. Wei and A. Carrillo, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 4009–4012 Search PubMed.
- R. Clark, Environ. Pollut., Ser. A, 1984, 33, 1–22 Search PubMed.
- C. Py, R. Bastien, J. Bico, B. Roman and A. Boudaoud, EPL, 2007, 77, 44005 Search PubMed.
- C. Duprat, S. Protiere, A. Y. Beebe and H. A. Stone, Nature, 2012, 482, 510–513 Search PubMed.
- H. Elettro, S. Neukirch, F. Vollrath and A. Antkowiak, Proc. Natl. Acad. Sci. U. S. A., 2016, 201602451 Search PubMed.
- R. D. Schulman, A. Porat, K. Charlesworth, A. Fortais, T. Salez, E. Raphaël and K. Dalnoki-Veress, 2016, arXiv preprint arXiv:1607.05990.
- F. W. Minor, A. M. Schwartz, E. Wulkow and L. C. Buckles, Text. Res. J., 1959, 29, 931–939 Search PubMed.
- B. Miller, A. B. Coe and P. N. Ramachandran, Text. Res. J., 1967, 37, 919–924 Search PubMed.
- L. Eadie and T. K. Ghosh, J. R. Soc., Interface, 2011, rsif20100487 Search PubMed.
- B. J. Mullins, I. E. Agranovski, R. D. Braddock and C. M. Ho, J. Colloid Interface Sci., 2004, 269, 449–458 Search PubMed.
- P. Contal, J. Simao, D. Thomas, T. Frising and S. Callé, J. Aerosol Sci., 2004, 35, 263–278 CrossRef CAS.
- J. Ju, H. Bai, Y. Zheng, T. Zhao, R. Fang and L. Jiang, Nat. Commun., 2012, 3, 1247 Search PubMed.
- K. C. Park, S. S. Chhatre, S. Srinivasan and R. E. Cohen, Langmuir, 2013, 29, 13269–13277 Search PubMed.
- R. LeBoeuf and E. de la Jara, Water Int., 2014, 39, 431–450 Search PubMed.
- A. Sauret, F. Boulogne, B. Soh, E. Dressaire and H. A. Stone, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 62 Search PubMed.
- P. B. Bintein, Dynamiques de Gouttes Funambules: Applications à la Fabrication de Laine de Verre, PhD thesis, Université Pierre et Marie Curie, 2015 Search PubMed.
- H. Princen, J. Colloid Interface Sci., 1970, 34, 171–184 Search PubMed.
- B. Carroll, Langmuir, 1986, 2, 248–250 Search PubMed.
- D. Quéré, Annu. Rev. Fluid Mech., 1999, 31, 347–384 Search PubMed.
- B. Sutter, D. Bémer, J.-C. Appert-Collin, D. Thomas and N. Midoux, Aerosol Sci. Technol., 2010, 44, 395–404 Search PubMed.
- F. Boulogne, A. Sauret, B. Soh, E. Dressaire and H. A. Stone, Langmuir, 2015, 31, 3094–3100 Search PubMed.
- E. Lorenceau, C. Clanet and D. Quéré, J. Colloid Interface Sci., 2004, 279, 192–197 Search PubMed.
- K. Zhang, F. Liu, A. J. Williams, X. Qu, J. J. Feng and C. H. Chen, Phys. Rev. Lett., 2015, 115, 074502 Search PubMed.
- T. Gilet, D. Terwagne and N. Vandewalle, Appl. Phys. Lett., 2009, 95, 014106 Search PubMed.
- T. Gilet, D. Terwagne and N. Vandewalle, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 31, 253–262 Search PubMed.
- F. Boulogne, L. Pauchard and F. Giorgiutti-Dauphiné, J. Fluid Mech., 2012, 704, 232–250 Search PubMed.
- F. Weyer, M. Lismont, L. Dreesen and N. Vandewalle, Soft matter, 2015, 11, 7086–7091 Search PubMed.
- A. Bick, F. Boulogne, A. Sauret and H. A. Stone, Appl. Phys. Lett., 2015, 107, 181604 Search PubMed.
- K. Piroird, C. Clanet, E. Lorenceau and D. Quéré, J. Colloid Interface Sci., 2010, 334, 70–74 Search PubMed.
- E. Dressaire, A. Sauret, F. Boulogne and H. A. Stone, Soft Matter, 2016, 12, 200–208 Search PubMed.
- B. Carroll, J. Colloid Interface Sci., 1976, 57, 488–495 Search PubMed.
- G. McHale, M. I. Newton and B. J. Carroll, Oil Gas Sci. Technol., 2001, 56, 47–54 Search PubMed.
- G. McHale and M. I. Newton, Colloids Surf., A, 2002, 206, 79–86 Search PubMed.
- X. F. Wu, M. Yu, Z. Zhou, A. Bedarkar and Y. Zhao, Appl. Surf. Sci., 2014, 294, 49–57 Search PubMed.
- A. Sauret, A. D. Bick, C. Duprat and H. A. Stone, EPL, 2014, 105, 56006 Search PubMed.
- A. Sauret, F. Boulogne, D. Cébron, E. Dressaire and H. A. Stone, Soft Matter, 2015, 11, 4034–4040 Search PubMed.
- M. Soleimani, R. J. Hill and T. G. M. van de Ven, Langmuir, 2015, 31, 8328–8334 Search PubMed.
- J. O. Claussen, Elasticity and Morphology of Wet Fibers, PhD thesis, University of Göttingen, 2011 Search PubMed.
Footnote |
| † These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2017 |



