Discovery of neuroprotective compounds by machine learning approaches†
Jiansong Fang‡
ab,
Xiaocong Pang‡a,
Rong Yana,
Wenwen Liana,
Chao Lia,
Qi Wangb,
Ai-Lin Liu*acd and
Guan-Hua Du*acd
aInstitute of Materia Medica, Chinese Academy of Medical Sciences and Peking Union Medical College, 1 Xian Nong Tan Street, Beijing 100050, PR China. E-mail: liuailin@imm.ac.cn; dugh@imm.ac.cn; Fax: +86-10-83150885; Fax: +86-10-63165184; Tel: +86-10-83150885 Tel: +86-10-63165184
bInstitute of Clinical Pharmacology, Guangzhou University of Traditional Chinese Medicine, Guangzhou 510006, China
cBeijing Key Laboratory of Drug Target and Screening Research, Beijing 100050, PR China
dState Key Laboratory of Bioactive Substance and Function of Natural Medicines, Beijing 100050, PR China
First published on 18th January 2016
Abstract
Neuronal cell death from oxidative stress is a strong factor of many neurodegenerative diseases. To tackle these problems, phenotypic drug screening assays are a possible alternative strategy. The aim of this study is to develop the neuroprotective models against glutamate or H2O2-induced neurotoxicity by machine learning approaches, which helps in discovering neuroprotective compounds. Four different single classifiers (neural network, k nearest neighbors, classification tree and random forest) were constructed based on two large datasets containing 1260 and 900 known active or inactive compounds, which were integrated to develop the combined Bayesian models to obtain superior performance. Our results showed that both of the Bayesian models (combined-NB-1 and combined-NB-2) outperformed the corresponding four single classifiers. Additionally, structural fingerprint descriptors were added to improve the predictive ability of the models, resulting in the two best models NB-1-LPFP4 and NB-2-LCFP6. The best two models gave Matthews correlation coefficients of 0.972 and 0.956 for 5-fold cross validation as well as 0.953 and 0.902 for the test set, respectively. To illustrate the practical applications of the two models, NB-1-LPFP4 and NB-2-LCFP6 were used to perform virtual screening for discovering neuroprotective compounds, and 70 compounds were selected for further cell-based assay. The assay results showed that 28 compounds exhibited neuroprotective effects against glutamate-induced and H2O2-induced neurotoxicity simultaneously. Our results suggested the method that integrated single classifiers into combined Bayesian models could be feasible to predict neuroprotective compounds.
1 Introduction
Neurodegenerative disease is an umbrella term characterized by progressive loss of structure or function of neurons, which includes Alzheimer's, Parkinson's, and Huntington's disease.1 Oxidative stress caused by excessive reactive oxygen species (ROS) production is a common culprit of many neurodegenerative diseases.2,3The most common ROS are oxygen radicals, such as superoxide and hydroxyl radicals, and non-free radicals, such as hydrogen peroxide (H2O2). H2O2, the main form of ROS, is produced during the redox process and is recognized as a messenger in intracellular signaling cascades.4 In addition, H2O2 can cause oxidative damage to molecules such as carbohydrates, proteins, lipids, and DNA, and at last cell death.5 Besides, elevated levels of the excitatory amino acid glutamate can also lead to oxidative stress-dependent neuronal death. Glutamate is considered as the major excitatory neurotransmitter in the central nervous system (CNS), and glutamate-induced excitotoxicity is known to be a major contributor to pathological cell death within the nervous system.6 Consequently, the searching for effective treatments that prevent oxidative stress associated with neurodegenerative diseases is an issue of crucial importance.
Current drug discovery strategies include both target-based7 and phenotypic-based approaches.8 Target-based approach generally starts with target identification relevant to a disease of interest. It can guide subsequent chemical optimization of lead compounds and toxicology studies during preclinical development.9 However, the target-based drug discovery may have its limitations. Recent analysis has revealed that invalidated targets for disease lead to many failed drug candidates in Phase II and III clinical trials.10 Evaluation of approved new drugs between 1999 and 2008 has exposed that the number of approved drugs through phenotypic screens exceeded those through the target-based approach.11 The rationalization for this success was the unbiased identification of the molecular mechanism of action (MMOA). Phenotypic screening is thus gaining new momentum to improve the success rate of drug approval in drug discovery. Glutamate or H2O2-induced cultures of nerve cell, recognized as one of phenotypic screening related to neurodegenerative diseases, were employed as screening systems to find neuroprotective agents.12,13
With advances in new assay technologies, significant investment has been made towards whole-cell phenotypic screening to find active compounds against various diseases.14–16 Unfortunately, the hit rates for these costly screens are disappointing, typically ranging from less than 1% to the low single digits.17,18 To solve this question, computational approaches such as machine learning tools have been widely adopted to enhance the hit rate in drug discovery, especially for antibacterial and antitubercular compounds.18–24 Singh and co-workers developed a Bayesian classification model using structural fingerprints and physicochemical property descriptors and employed the model to virtually screen an independent data set of ∼200k compounds, which showed that the model can screen top hits of PubChem Bioassay actives with accuracy up to ∼76%.19 Ekins and his coworkers also constructed Bayesian models to predict the activity of compounds against Mycobacterium tuberculosis (Mtb), then they computationally screened 82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 403 compounds and selected 550 compounds for in vitro test, resulting in 124 actives against Mtb.22 However, up to now, there is limited research on classification predictions towards phenotypic screening of neuroprotective agents.
403 compounds and selected 550 compounds for in vitro test, resulting in 124 actives against Mtb.22 However, up to now, there is limited research on classification predictions towards phenotypic screening of neuroprotective agents.
In this investigation, a workflow for the classification models, model validations, and their application to virtual screening of neuroprotective agents is shown in Fig. 1. First, we present two large datasets containing 1260 and 900 compounds, and categorize each dataset into a training set and a test set, respectively. The two datasets are employed to develop the neuroprotective models against glutamate (1260 compounds) or H2O2 (900 compounds)-induced neurotoxicity, respectively. Additionally, four different single machine learning classifiers (neural network, k nearest neighbors, classification tree and random forest) are integrated to develop the combined naïve Bayesian models. The performances of all the models were measured by 5-fold cross-validation and a test set validation. In order to guard against the possibility of chance correlation, Y-scrambling was also performed. The best combined Bayesian models as ligand-based virtual screening tools were used to predict neuroprotective compounds from our in-house database. Finally, the selected compounds were validated by cell-based bioassay.
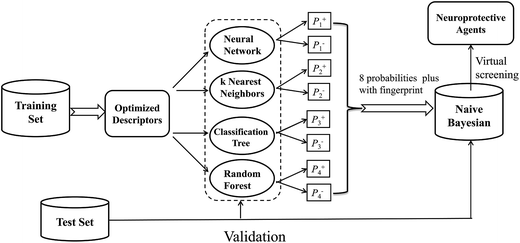 | ||
| Fig. 1 Workflow for classification model building, validation, and virtual screening (VS) as applied to neuroprotective agents. | ||
2 Material and methods
2.1 Data preparation
Two data sets were prepared. The structures for each data set were imported into ISIS_Base for deleting the duplicate compounds, then 252 neuroprotective compounds against glutamate-induced neurotoxicity in nerve cell were collected from ChEML database25 as positive data. The selection criterion is that one compound at the concentration of 10 μM should improve the cell viability significantly comparing with that of nerve cell injured by glutamate. Similarly, 200 neuroprotective compounds against H2O2-induced neurotoxicity were obtained. In addition, corresponding decoy datasets with the ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to positive compounds were generated in DUD online database26 with known neuroprotective compounds. Both the active and inactive dataset were randomly divided into two groups. Finally, for glutamate-induced models, the training set was made up of 200 active and 800 inactive compounds, and the test set contained 52 active and 208 inactive compounds, while for H2O2-induced models the training set consisted of 140 active and 560 inactive compounds, and the test set included 40 active and 160 inactive compounds (detailed information is available in the ESI, see Tables S1–S4†).
1 to positive compounds were generated in DUD online database26 with known neuroprotective compounds. Both the active and inactive dataset were randomly divided into two groups. Finally, for glutamate-induced models, the training set was made up of 200 active and 800 inactive compounds, and the test set contained 52 active and 208 inactive compounds, while for H2O2-induced models the training set consisted of 140 active and 560 inactive compounds, and the test set included 40 active and 160 inactive compounds (detailed information is available in the ESI, see Tables S1–S4†).
Before molecular descriptors were calculated, all of the inorganic salt atoms of compounds were removed, and the remaining parts were processed by the addition of hydrogen atoms, the deprotonation of strong acids, the protonation of strong bases, the generation of valid three-dimensional conformation through washing, and the minimization of energy using the software of Molecular Operating Environment (MOE).27 All active compounds are labelled as “1”, while decoys exhibiting no neuroprotective activity were labelled as “0”.
2.2 Molecular descriptors
Each compound was represented with three sets of two-dimensional (2D) descriptors using Discovery Studio 4.0 (DS 4.0)28 and MOE 2010 software.27 The first set of descriptors including 256 2D descriptors was calculated by DS 4.0, which were made up of AlogP, estate keys, molecular properties, molecular property counts, surface area and volume, and topological descriptors. MOE 2010 was another software used to calculate the second set of descriptors containing 185 2D descriptors. The last set of descriptors were composed of the first two sets of descriptors, which consisted of 441 (256+185) descriptors.Molecular fingerprints in this paper were also calculated with DS 4.0, including the SciTegic extended-connectivity fingerprints (FCFP and ECFP) and Daylight-style path-based fingerprints (FPFP and EPFP). The fingerprints used here are different from the substructures in a binary form. They stand for a much larger set of features than predefined substructures. Besides, they do not need to be preselected or predefined because they can be generated directly from the molecules. Given that the structural fragments should neither be too small nor too large, two diameters, 4 and 6, were chosen for each fingerprint.
2.3 Molecular descriptor selection
Pearson correlation analysis29 can eliminate molecular descriptors that are not significantly correlated with activity and highly correlated with each other. In this study, the descriptors exhibiting a Pearson correlation coefficient (P < 0.1) with the activity were removed. If the pairwise correlation coefficient between any two descriptors was higher than 0.9, the descriptor which had a lower correlation coefficient with the activity would be deleted. After that, genetic search in Weka 3.6 was carried out to further eliminate the descriptors.30 Genetic algorithms are search algorithms based on the mechanics of natural selection and natural genetics,31 while Weka is a collection of machine learning algorithms for data mining, including a number of methods for data preprocessing, attribute selection, classification, etc. Finally, the descriptors chosen from different sets of descriptors are listed in Table 2.| Model | Training set (ECFP2) | Test set (ECFP2) | ||||||
|---|---|---|---|---|---|---|---|---|
| Inhibitors | decoys | Total | Tanimoto index | Inhibitors | decoys | Total | Tanimoto index | |
| Glutamate-induced | 200 | 800 | 1000 | 0.125 | 52 | 208 | 260 | 0.132 |
| H2O2-induced | 140 | 560 | 700 | 0.142 | 40 | 160 | 200 | 0.162 |
| No. | Descriptor class | Number of descriptors | Descriptors |
|---|---|---|---|
| a 1–3#: neuroprotective models against glutamate-induced neurotoxicity (NGN models); 4–6#: neuroprotective models against H2O2-induced neurotoxicity (NHN models). | |||
| 1# | DS 2D | 12 | ES_Count_aasC, ES_Sum_dO, ES_Sum_ssCH2, SAscore_Complexity, HBD_Count, Num_AliphaticSingleBonds, Num_DoubleBonds, Num_RingBonds, Num_Rings6, CIC, IAC_Mean, SC_3_C |
| 2# | MOE 2D | 21 | a_don, a_ICM, balabanJ, BCUT_SMR_1, chi1_C, density, GCUT_SLOGP_1, GCUT_SLOGP_2, PEOE_RPC+, PEOE_VSA4+, PEOE_VSA0, PEOE_VSA2, PEOE_VSA3, PEOE_VSA4, PEOE_VSA5, PEOE_VSA_POL, PEOE_VSA_POS, PEOE_VSA_PPOS, SlogP_VSA4, SlogP_VSA5, SMR_VSA1, SMR_VSA5, SMR_VSA6 |
| 3# | DS 2D and MOE 2D | 26 | ES_Sum_ssCH2, SAscore_Complexity, Num_Rings6, CIC, IAC_Mean, a_don, balabanJ, BCUT_SMR_1, chi1_C, density, GCUT_SLOGP_1, GCUT_SLOGP_2, PEOE_RPC+, PEOE_VSA4+, PEOE_VSA_0, PEOE_VSA_2, PEOE_VSA_3, PEOE_VSA_4, PEOE_VSA_5, PEOE_VSA_POL, PEOE_VSA_POS, PEOE_VSA_PPOS, SlogP_VSA4, SlogP_VSA5, SMR_VSA1, SMR_VSA6 |
| 4# | DS 2D | 12 | ES_Count_aasC, ES_Count_dssC, ES_Count_ssCH2, ES_Sum_ssCH2, QED_HBD, SAscore_Complexity, HBD_Count, Num_AtomClasses, Num_H_Acceptors, Num_Rings5, IAC_Mean, SC_3_C |
| 5# | MOE 2D | 26 | a_acc, a_nN, BCUT_PEOE_0, BCUT_SLOGP_1, GCUT_SLOGP_0, GCUT_SLOGP_2, GCUT_SMR_1, opr_brigid, PEOE_VSA+2, PEOE_VSA+3, PEOE_VSA+4, PEOE_VSA0, PEOE_VSA-5, PEOE_VSA-6, PEOE_VSA_FNEG, PEOE_VSA_FPNEG, PEOE_VSA_POL, PEOE_VSA_POS, SlogP, SlogP_VSA0, SlogP_VSA1, SlogP_VSA2, SlogP_VSA3, SlogP_VSA8, SMR_VSA3, SMR_VSA6 |
| 6# | DS 2D and MOE 2D | 24 | ES_Count_ssCH2, QED_HBD, SAscore_Complexity, Num_Rings5, IAC_Mean, a_nN, a_nN, BCUT_SLOGP_1, GCUT_SLOGP_0, GCUT_SLOGP_2, GCUT_SMR_1, opr_brigid, PEOE_VSA+2, PEOE_VSA+3, PEOE_VSA+4, PEOE_VSA0, PEOE_VSA5, PEOE_VSA6, PEOE_VSA_POS, SlogP, SlogP_VSA1, SlogP_VSA2, SlogP_VSA3, SMR_VSA3, SMR_VSA6 |
2.4 Methods for model building
Five different machine learning tools, including neural network (NN), k nearest neighbors (kNN), classification tree (CT), random forest (RF) and naïve Bayesian (NB), were employed with the entire computational workflow. NN, kNN, CT and RF were performed in Orange canvas 2.7.32 NB was performed using DS 4.0. In this paper, all models developed get two probability output (positive and negative probability) as well as estimated target values (such as 1 or 0).2.4.1.1 Neural network (NN). NN is an information processing paradigm that is inspired by the way biological nervous systems, such as the brain, process information.33 In Orange canvas 2.7, neural network learner implements a multilayer perceptron. Learning is performed by minimizing an L2-regularized cost function with scipy's implementation of L-BFGS. The value of hidden layer neurons, regularization factor, and max iterations was set to 20, 1.0 and 300, respectively.
2.4.1.2 k nearest neighbors (kNN). The kNN algorithm is an algorithm to classify objects based on closest examples in the feature space.34 An object is classified by a majority vote of its neighbors, with the object being assigned to the class most common among its k nearest neighbors (k is a positive integer). In this paper, the nearness is measured by Euclidean distance metrics and the number of neighbors (k) was set to 5.
2.4.1.3 Classification tree (CT). In classification tree, leaves stand for class labels and branches represent conjunctions of features that lead to those class labels. Orange includes multiple implementations of classification tree learners. In this study, the C4.5 tree induction algorithm was implemented. C4.5 is an algorithm used to generate a decision tree developed by Ross Quinlan,35 which builds decision trees from a set of training data by means of a hill-climbing search based on the statistical property measure called information gain. The parameters here were adopted with the default setting.
2.4.1.4 Random forest (RF). RF is a classification technique that operates by constructing a multitude of decision trees at training time and outputting the class that is the mode of the classes output by individual trees. Each tree is built from a bootstrap sample from the training data. When developing individual trees, an arbitrary subset of attributes is drawn (called “random”) from which the best attribute for the split is selected. The classification is based on the majority vote from individually developed tree classifiers in the forest. A detailed descriptions of RF can be found in the original literature.36 In this work, the number of trees in forest was set to 10, while nodes were stopped splitting with 5 or fewer instances.
The naïve Bayesian classification models were developed using Discovery Studio 4.0. Bayesian is a robust classification approach that can discriminate active compounds from inactive compounds. Generally, the technique is based on the frequency of occurrence of various descriptors which are found in two or more sets of molecules that can discriminate best between these sets. Bayesian classification can process large amounts of data, learn fast, and is tolerant of random noise. For naïve Bayesian classifier, it can generate the posterior probabilities based on the core of function, which are given by eqn (1).
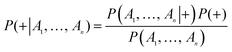 | (1) |
P(A1, …, An|+) is the conditional probability of a particular compound being classified as active; P(+) is the prior probability, a probability induced from a set of compounds in the training set; P(A1, …, An) is the marginal probability of the given descriptors that will occur in the training set.
A more detailed introduction can be found in the following ref. 42–45. In this study, the probability output (PC+1 and PC−1 i = 1, 2, 3, 4) for each compound was predicted with four single classifiers; then, all of these probability outputs were selected as new descriptors to develop the combined classifiers NB (combined-NB) model that would generate the final combination decision probability (PC+1 and PC−1).
2.5 Performance evaluation of the models
The quality of the Bayesian classifiers was measured by the quantity of true positives (TP), true negatives (TN), false positives (FP), false negatives (FN), sensitivity (SE), specificity (SP), the overall prediction accuracy (Q) and Matthews correlation coefficient (MCC), which are given by eqn (2)–(6). TP represents the number of active compounds that are predicted as the active. TN represents the number of inactive compounds that are predicted as the inactive. FP stands for the number of inactive compounds that are predicted as the active and FN is the number of active compounds that are predicted as the inactive. SE represents the prediction accuracy for active compounds and SP represents the prediction accuracy for inactive compounds.
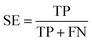 | (2) |
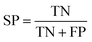 | (3) |
 | (4) |
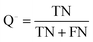 | (5) |
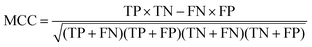 | (6) |
The value of MCC is the most important indicator for the measurement of the quality of binary classification. MCC is essentially a correlation coefficient between the observed and predicted binary classification. Its value ranges from −1 to 1, and a perfect classification gives a correlation coefficient value of 1. In addition, the receiver operating characteristic (ROC) curve was plotted. The ROC curve can graphically present the model behavior of true positive rate against false positive rate in a visual way. Performance was also measured by the area under the ROC curve (AUC). A perfect classifier gives AUC value of 1, whereas random performance gives that of 0.5.
2.6 In vitro cell-based for neuroprotective assay
3. Results and discussion
3.1 Chemical space analysis
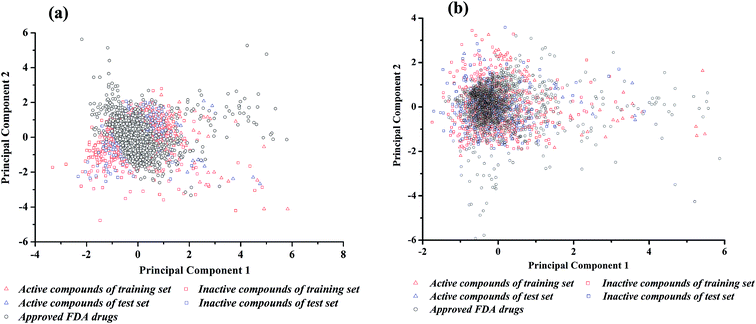
The performance of binary classifiers is related to the chemical diversity of samples utilized in the training set and test set. In general, binary classifiers that only cover a small region of chemical space limit their applications. Tanimoto similarity index and principal component analysis (PCA) are classic methods to explore the diversity of compounds within a chemical data set. The Tanimoto similarity analysis was performed with the fingerprint of ECFP_2. As shown in Table 1, for neuroprotective models against glutamate-induced neurotoxicity (NGN models), the Tanimoto index is 0.125 for training set and 0.132 for test set. For neuroprotective models against H2O2-induced neurotoxicity (NHN models), the Tanimoto index is 0.142 for training set and 0.162 for test set. Consequently, the entire data set was diverse enough.Principal component analysis (PCA) was another approach to investigate the chemical spaces of the training set and test set.48 For NGN and NHN models, the input variables were the 26 DS_MOE and 26 MOE 2D descriptors selected by Pearson correlation analysis and genetic search, respectively. Subsequently, 1630 FDA-approved drugs were downloaded from DrugBank,49 and the same properties were calculated. According to the chemical space defined by PCA (Fig. 2), there are enough diverse chemical space distributions for all compounds, and most of the compounds in test set are well within the chemical space of the training set. At the same time, there are obvious overlaps between the compounds in dataset and FDA-approved drugs in chemical space, which implies that most of the compounds have drug potential.
3.2 Performance of binary classification models by single classifier
A total of 24 single classifiers in this study (12 for each data set) were initially generated using NN, kNN, CT and RF algorithms with three sets of descriptors. Subsequently, the internal 5-fold cross validation was adopted to evaluate the performance. Additionally, the models were used to predict corresponding test set comprising 260 and 200 compounds. The performance of all the single classifiers is given in Table 3.| No. | Model | Descriptors | Training set (5-fold cross validation) | Test set | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | SP | Q+ | Q− | MCC | SE | SP | Q+ | Q− | MCC | |||
| a 1–12: neuroprotective models against glutamate-induced neurotoxicity (NGN models); 13–24: neuroprotective models against H2O2-induced neurotoxicity (NHN models); a: models built by DS_2D descriptors; b: models built by MOE_2D descriptors; c: models built by DS_MOE 2D descriptors. | ||||||||||||
| 1 | NN-a1 | 12 | 0.695 | 0.966 | 0.837 | 0.927 | 0.711 | 0.788 | 0.962 | 0.837 | 0.948 | 0.767 |
| 2 | NN-b1 | 23 | 0.755 | 0.955 | 0.807 | 0.940 | 0.728 | 0.885 | 0.986 | 0.939 | 0.972 | 0.890 |
| 3 | NN-c1* | 26 | 0.775 | 0.955 | 0.812 | 0.944 | 0.743 | 0.923 | 0.981 | 0.923 | 0.981 | 0.904 |
| 4 | kNN-a1 | 12 | 0.805 | 0.911 | 0.694 | 0.949 | 0.679 | 0.981 | 0.947 | 0.823 | 0.995 | 0.871 |
| 5 | kNN-b1 | 23 | 0.850 | 0.918 | 0.720 | 0.961 | 0.723 | 1.000 | 0.899 | 0.712 | 1.000 | 0.800 |
| 6 | kNN-c1* | 26 | 0.870 | 0.919 | 0.728 | 0.966 | 0.740 | 1.000 | 0.933 | 0.788 | 1.000 | 0.857 |
| 7 | CT-a1 | 12 | 0.660 | 0.896 | 0.614 | 0.913 | 0.542 | 0.827 | 0.933 | 0.754 | 0.956 | 0.734 |
| 8 | CT-b1 | 23 | 0.700 | 0.903 | 0.642 | 0.923 | 0.584 | 0.923 | 0.928 | 0.762 | 0.980 | 0.794 |
| 9 | CT-c1* | 26 | 0.735 | 0.898 | 0.642 | 0.931 | 0.602 | 0.904 | 0.933 | 0.770 | 0.975 | 0.790 |
| 10 | RF-a1 | 12 | 0.415 | 0.971 | 0.783 | 0.869 | 0.502 | 0.538 | 0.986 | 0.903 | 0.895 | 0.647 |
| 11 | RF-b1 | 23 | 0.615 | 0.973 | 0.848 | 0.910 | 0.667 | 0.904 | 0.976 | 0.904 | 0.976 | 0.880 |
| 12 | RF-c1* | 26 | 0.690 | 0.949 | 0.771 | 0.924 | 0.666 | 0.904 | 0.976 | 0.904 | 0.976 | 0.880 |
| 13 | NN-a2 | 12 | 0.521 | 0.959 | 0.760 | 0.889 | 0.559 | 0.725 | 0.969 | 0.853 | 0.934 | 0.739 |
| 14 | NN-b2* | 26 | 0.771 | 0.975 | 0.885 | 0.945 | 0.787 | 0.875 | 0.975 | 0.897 | 0.969 | 0.858 |
| 15 | NN-c2 | 24 | 0.714 | 0.966 | 0.840 | 0.931 | 0.724 | 0.925 | 0.988 | 0.949 | 0.981 | 0.921 |
| 16 | kNN-a2 | 12 | 0.714 | 0.914 | 0.676 | 0.928 | 0.616 | 0.950 | 0.944 | 0.809 | 0.987 | 0.843 |
| 17 | kNN-b2* | 26 | 0.857 | 0.932 | 0.759 | 0.963 | 0.755 | 1.000 | 0.938 | 0.800 | 1.000 | 0.866 |
| 18 | kNN-c2 | 24 | 0.829 | 0.923 | 0.730 | 0.956 | 0.718 | 1.000 | 0.975 | 0.909 | 1.000 | 0.941 |
| 19 | CT-a2 | 12 | 0.607 | 0.888 | 0.574 | 0.900 | 0.485 | 0.900 | 0.888 | 0.667 | 0.973 | 0.710 |
| 20 | CT-b2* | 26 | 0.721 | 0.932 | 0.727 | 0.930 | 0.655 | 0.900 | 0.913 | 0.720 | 0.973 | 0.751 |
| 21 | CT-c2 | 24 | 0.779 | 0.902 | 0.665 | 0.942 | 0.643 | 0.950 | 0.888 | 0.679 | 0.986 | 0.746 |
| 22 | RF-a2 | 12 | 0.371 | 0.964 | 0.722 | 0.860 | 0.442 | 0.525 | 0.981 | 0.875 | 0.892 | 0.623 |
| 23 | RF-b2* | 26 | 0.771 | 0.946 | 0.783 | 0.943 | 0.722 | 0.900 | 0.950 | 0.818 | 0.974 | 0.821 |
| 24 | RF-c2 | 24 | 0.707 | 0.954 | 0.792 | 0.929 | 0.690 | 0.850 | 0.956 | 0.829 | 0.962 | 0.799 |
Among the 12 NGN models, the MCC values of 5-fold cross validation ranged from 0.502 to 0.743, whereas those of test set ranged from 0.647 to 0.904. The best single classifier was NN-c1, which was developed by neural network using 26 DS_MOE descriptors. Regarding to the 12 NHN models, the MCC values of 5-fold cross validation varied from 0.442 to 0.787, whereas those of test set varied from 0.623 to 0.941. The best performance was achieved by NN-b2, neural network using 26 MOE descriptors. These data indicated that the overall predictive accuracies of 24 single classifiers from NGN and NHN were not high but acceptable. The detailed performance of the 24 single classifiers are given in Table S5.†
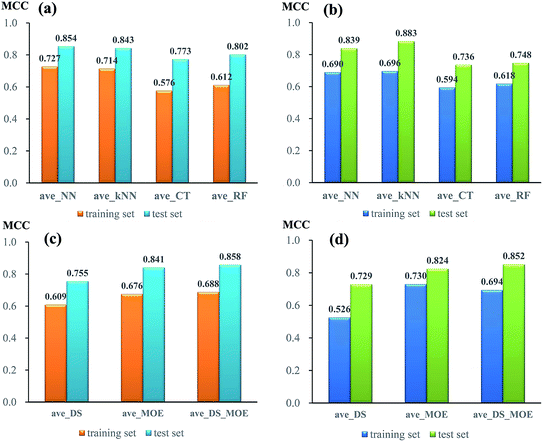
To compare the performance of single models from different algorithms, the average MCC values divided by three sets of descriptors are given in Fig. 3. For NGN single models (Fig. 3a), the performances of models from neural network (NN) and k near neighbour (kNN) are superior to those from classification tree (CT) and random forest (RF). The best performance is achieved by NN algorithm, with the average MCC value of 0.727 and 0.854 from 5-fold cross validation and test set, respectively. For NHN single classifiers (Fig. 3b), NN and kNN perform better than CT and RF, which is similar to NGN models. Among four different algorithms, kNN obtains the highest average MCC value of 0.696 from 5-fold cross validation and 0.883 from test set.
In addition, the performances of models from different sets of descriptors are also compared. As given in Fig. 3c, for single NGN models, the average MCC values from three sets of descriptors (DS, MOE, and DS_MOE) are 0.609, 0.679, and 0.688 for 5-fold cross validation as well as 0.755, 0.841, and 0.858 for test set. Obviously, here the four models derived from DS_MOE descriptors perform best and are chosen for further integration. However, for single NHN models, it is difficult to judge which performs better between models using MOE or DS_MOE descriptors. As presented in Fig. 3d, the models using DS_MOE descriptors have a higher average MCC value of 0.852 for test set, whereas the models using MOE descriptors get a better average MCC value of 0.730 in 5-fold cross validation for the training set. Considering that the models from MOE descriptors have both the desired MCC values (0.730 and 0.824) for 5-fold cross validation and test set, the single classifiers using MOE descriptors are selected for further analysis.
3.3 Performance of combined naïve Bayesian models
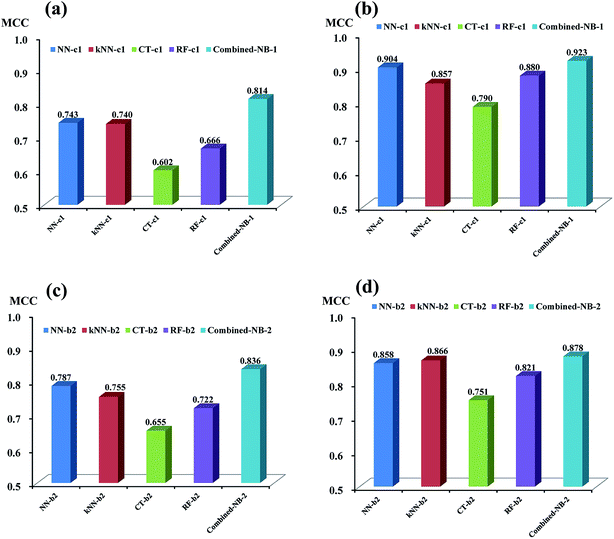
As discussed above, based on the two best sets of descriptors (DS_MOE descriptors and MOE descriptors), 4 single classifiers (NN-c1, kNN-c1, CT-c1, and RF-c1) from NGN models were chosen to develop the combined naïve Bayesian model combined-NB-1, while another 4 single classifiers (NN-b2, kNN-b2, CT-b2 and RF-b2) from NHN models were selected to build combined-NB-2. To compare the performance between single classifiers and combined naïve Bayesian model, the MCC values and AUC values via receiver operating characteristic (ROC) plot were calculated.As given in Fig. 4a and b, the performance of combined-NB-1 (MCC = 0.814) is better than any single classifiers (MCC ranging from 0.602 to 0.743) on 5-fold cross validation. At the same time, the MCC value of combined NB-1 (0.923) on test set is also significantly higher than that of 4 single classifiers (MCC ranging from 0.790 to 0.904). A similar phenomenon occurs in combined-NB-2 (Fig. 4c and d). Combined-NB-2 model obtains MCC values of 0.836 and 0.878 on 5-fold cross validation and test set, respectively, which is much higher than those of single classifiers based on 26 MOE descriptors.
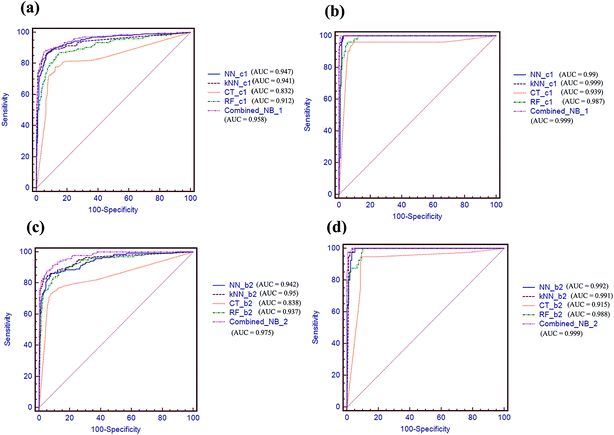
AUC values via receiver operating characteristic (ROC) plot were also compared in Fig. 5. As shown in Fig. 5a and b, the combined-NB-1 model achieves the highest AUC value of 0.958 and 0.999 among the five models on 5-fold cross validation and test set, respectively. Similarly, the combined-NB-2 obtains the highest AUC values of 0.975 and 0.999 among the five models. To sum up, after integrating different single classifiers, the combined NB models can improve the predictive performance obviously.
In order to further improve the performance of combined-NB-1 and combined-NB-2, different molecular fingerprints, together with 8 probabilities outputted by 4 single classifiers, were used simultaneously as the descriptors in Bayesian analysis to build new prediction models. The statistical results for these Bayesian classifiers are listed in Tables 4 and S6.† For NGN models, the combined-NB models using fingerprints (no. 2–13), have MCC values ranging from 0.818 to 0.975 on 5-fold cross validation, which are much higher than that of combined-NB-1 (no. 1). Given the balance performance between training set and test set, NB-1-LPFP4 (no. 12) which obtains corresponding MCC values of 0.972 and 0.953 on 5-fold cross validation and test set, is considered as the best model to predict neuroprotective activity against glutamate-induced neurotoxicity. For NHH models (no. 14–26), except for NB-2-EPFP4 (no. 17) and NB-2-FPFP4 (no. 21), all of the other ten models using fingerprints perform better than combined-NB-2 (no. 14) on 5-fold cross validation. Similarly, NB-2-LCFP6 (no. 24) with corresponding MCC values of 0.956 and 0.902 on 5-fold cross validation and test set, is recognized as the best model to predict neuroprotective activity against H2O2-induced neurotoxicity. Consequently, the addition of fingerprint can improve the performance of combined NB-1 and NB-2 models.
| No. | Model | Training set (5-fold cross validation) | Test set | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | SP | Q+ | Q− | MCC | SE | SP | Q+ | Q− | MCC | ||
| a 1–13: combined naïve Bayesian models for neuroprotection against glutamate-induced neurotoxicity; 14–26: combined NB models for neuroprotection against H2O2-induced neurotoxicity. | |||||||||||
| 1 | NB | 0.875 | 0.955 | 0.829 | 0.968 | 0.814 | 1.000 | 0.966 | 0.881 | 1.000 | 0.923 |
| 2 | NB+ECFP4 | 0.940 | 0.986 | 0.945 | 0.985 | 0.928 | 1.000 | 0.962 | 0.867 | 1.000 | 0.913 |
| 3 | NB+ECFP6 | 0.950 | 0.998 | 0.990 | 0.988 | 0.962 | 1.000 | 0.986 | 0.945 | 1.000 | 0.965 |
| 4 | NB+EPFP4 | 0.925 | 0.940 | 0.794 | 0.980 | 0.818 | 1.000 | 0.938 | 0.800 | 1.000 | 0.866 |
| 5 | NB+EPFP6 | 0.965 | 0.933 | 0.781 | 0.991 | 0.832 | 0.981 | 0.938 | 0.797 | 0.995 | 0.853 |
| 6 | NB+FCFP4 | 0.895 | 0.989 | 0.952 | 0.974 | 0.905 | 1.000 | 0.990 | 0.963 | 1.000 | 0.977 |
| 7 | NB+FCFP6 | 0.970 | 0.974 | 0.902 | 0.992 | 0.919 | 1.000 | 0.995 | 0.981 | 1.000 | 0.988 |
| 8 | NB+FPFP4 | 0.940 | 0.950 | 0.825 | 0.984 | 0.849 | 0.981 | 0.981 | 0.927 | 0.995 | 0.942 |
| 9 | NB+FPFP6 | 0.970 | 0.963 | 0.866 | 0.992 | 0.895 | 0.962 | 0.971 | 0.893 | 0.990 | 0.908 |
| 10 | NB+LCFP4 | 0.960 | 0.978 | 0.914 | 0.990 | 0.921 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 11 | NB+LCFP6 | 0.965 | 0.981 | 0.928 | 0.991 | 0.933 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 12 | NB+LPFP4 | 0.985 | 0.993 | 0.970 | 0.996 | 0.972 | 0.981 | 0.986 | 0.944 | 0.995 | 0.953 |
| 13 | NB+LPFP6 | 0.980 | 0.995 | 0.980 | 0.995 | 0.975 | 1.000 | 0.976 | 0.912 | 1.000 | 0.944 |
| 14 | NB | 0.843 | 0.975 | 0.894 | 0.961 | 0.836 | 1.000 | 0.931 | 0.784 | 1.000 | 0.855 |
| 15 | NB+ECFP4 | 0.936 | 0.996 | 0.985 | 0.984 | 0.950 | 1.000 | 0.956 | 0.851 | 1.000 | 0.902 |
| 16 | NB+ECFP6 | 0.929 | 1.000 | 1.000 | 0.982 | 0.955 | 1.000 | 0.944 | 0.816 | 1.000 | 0.878 |
| 17 | NB+EPFP4 | 0.929 | 0.927 | 0.760 | 0.981 | 0.796 | 0.925 | 0.906 | 0.712 | 0.980 | 0.758 |
| 18 | NB+EPFP6 | 0.964 | 0.930 | 0.776 | 0.990 | 0.828 | 0.975 | 0.906 | 0.722 | 0.993 | 0.794 |
| 19 | NB+FCFP4 | 0.993 | 0.925 | 0.768 | 0.998 | 0.839 | 1.000 | 0.956 | 0.851 | 1.000 | 0.902 |
| 20 | NB+FCFP6 | 0.943 | 0.991 | 0.964 | 0.986 | 0.942 | 1.000 | 0.969 | 0.889 | 1.000 | 0.928 |
| 21 | NB+FPFP4 | 0.971 | 0.884 | 0.677 | 0.992 | 0.756 | 0.975 | 0.881 | 0.672 | 0.993 | 0.755 |
| 22 | NB+FPFP6 | 0.914 | 0.970 | 0.883 | 0.978 | 0.872 | 0.975 | 0.925 | 0.765 | 0.993 | 0.826 |
| 23 | NB+LCFP4 | 0.986 | 0.980 | 0.926 | 0.996 | 0.944 | 1.000 | 0.950 | 0.833 | 1.000 | 0.890 |
| 24 | NB+LCFP6 | 0.986 | 0.986 | 0.945 | 0.996 | 0.956 | 1.000 | 0.956 | 0.851 | 1.000 | 0.902 |
| 25 | NB+LPFP4 | 0.986 | 0.964 | 0.873 | 0.996 | 0.909 | 1.000 | 0.938 | 0.800 | 1.000 | 0.866 |
| 26 | NB+LPFP6 | 0.971 | 0.986 | 0.944 | 0.993 | 0.947 | 1.000 | 0.944 | 0.816 | 1.000 | 0.878 |
The Bayesian scores based on NB-1-LPFP4 and NB-2-LCFP6 were used to evaluate the discrimination of active compounds from inactive compounds via bimodal histograms of the training and test data sets (Fig. 6). As given in Fig. 6a and b, for NB-1-LPFP4 model, the p value associated with the difference in the mean Bayesian score of training set active versus inactive compounds is 0 at the 95% confidence level as well as p value of 5.12 × 10−83 on test set, suggesting that the two distributions were significantly different. In a similar way, for NB-2-LCFP6 model (Fig. 6c and d), the corresponding p values are 3.39 × 10−261 and 2.17 × 10−79 on training set and test set, implying that Bayesian score can discriminate active compounds from inactive compounds greatly. Inspired by the two best models, we found the Bayesian score of neuroprotective agents tended to have more positive value, while the Bayesian score of inactive compounds inclined to have more negative value. The Bayesian score of a compound could be a quantitation standard to choose potential compounds as neuroprotective agents in virtual screening.
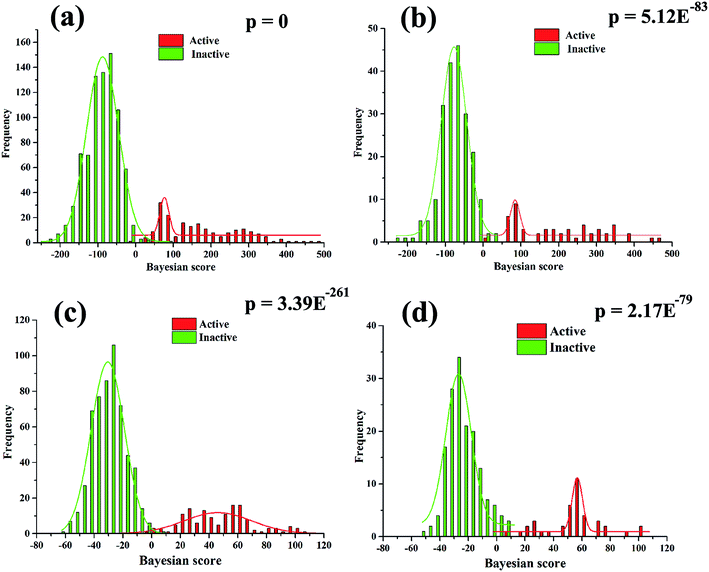 | ||
| Fig. 6 The distributions of Bayesian score predicted by the Bayesian classifier NB-1-LPFP4 (a and b) and NB-2-LCFP6 (c and d) on training set (a and c) and test set (b and d). | ||
3.4 Y-scrambling
As discussed above, NB-1-LPFP4 and NB-2-LCFP6 were regarding as the best neuroprotective models against glutamate or H2O2-induced neurotoxicity, respectively. Y-scrambling was performed to prove that it was not a result of chance correlation to have good performance for the best models. The steps are as follows. First, the activity (1 or 0) column was randomly shuffled in the training set molecules, and a new Bayesian model was developed. The procedure was repeated 50 times and the new models were expected to have low Matthews correlation coefficient (MCC) and prediction accuracy (Q). The resulting MCC and Q for the test set are presented in Fig. S1,† from which all the scrambled models have a MCC less than 0.3 and Q less than 0.8, whereas the values of MCC and Q of NB-1-LPFP4 and NB-2-LCFP6 are significantly greater.3.5 Applicability domain of the generated QSAR
An extremely important issue for classification model is the definition of the applicability domain (AD). The reason is that the reliable QSAR predictions are limited generally to the chemicals that are structurally similar to the training compounds. If the test compounds are too far away from the chemical space of AD, the predictions are usually unreliable. There are several measures for the definition of applicability domain.50–53 In this study, stepwise approach was used to determine the two best models' AD with two domain layers (Fig. S2†). The first domain layer (named “parameter range”) was extracted based on molecular weight (MW) and log(Kow) with correct predicted chemicals from training set (called good fragments). The second domain layer was “structure domain” which was extracted by the atom-centered fragment method. The atom-centered fragment is a topological sphere with center a selected atom and radius specified in any atom distance. In this work, the parameter range for NB-1-LPFP4 is MW[124.17, 862.90] as well as log(Kow)[−8.63, 12.96], while that for NB-2-LCFP6 is MW[157.17, 1165.01] as well as log(Kow)[−12.80, 11.31]. AD analysis results for training set and test set is presented in Table 5. It can be easily seen that all active compounds of test set are located in domain although a small number of the decoy compounds are located out of domain. Consequently, the predictions of the two best models (NB-1-LPFP4 and NB-2-LCFP6) are reliable.| Model | Training set | Test set | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| In domain (ID) | Out of domain (OD) | In domain (ID) | Out of domain (OD) | |||||||||
| Np | Nnon-p | Total | Np | Nnon-p | Total | Np | Nnon-p | Total | Np | Nnon-p | Total | |
| a Np: the number of positive compounds; Nnon-p: the number of decoy compounds; NB-1-LPFP4: the best model for neuroprotection against glutamate-induced neurotoxicity; NB-2-LCFP6: the best model for neuroprotection against H2O2-induced neurotoxicity. | ||||||||||||
| NB-1-LPFP4 | 199 | 797 | 996 | 1 | 3 | 4 | 52 | 178 | 230 | 0 | 30 | 30 |
| NB-2-LCFP6 | 140 | 557 | 697 | 0 | 3 | 3 | 40 | 148 | 188 | 0 | 12 | 12 |
3.6 Analysis of the important fragments given by naïve Bayesian classifier
To further explore favorable structural fragments for neuroprotective compounds, the good fragments as well as the frequency of each fragment given by NB-1-LPFP4 and NB-2-LCFP6 classifiers were summarized in Fig. 7, which were ranked by their Bayesian score. It may be useful for neuroprotective compounds design. In Fig. 7a, as to the model against glutamate-induced neurotoxicity (NB-1-LPFP4), all of the privilege fragments only contain three elements (C, H, and O), and most of fragments with oxygen atom belong to the family of esters. Therefore, hydrophobic interactions may be the main driving force for these fragments to favorably bind to the targets related to neuroprotection. As shown in Fig. 7b, for the neuroprotective compounds against H2O2-induced neurotoxicity (NB-2-LCFP6), the favorable fragments are mainly composed of sulfonic amides, polyphenols and the fragments with unsaturated side chains. This is reasonable because these groups are functional groups with reducibility which are more likely antioxidants. It is well known most of antioxidants such as vitamin E have neuroprotection against H2O2-induced neurotoxity. Besides, for sulfonic amides and polyphenols, hydrogen bonding may play a significant role in binding to the neuroprotective targets. For example, there are 14 sulfonic amides out of 140 known neuroprotective compounds on training set, while there are 8 out of 40 known neuroprotective compounds on test set.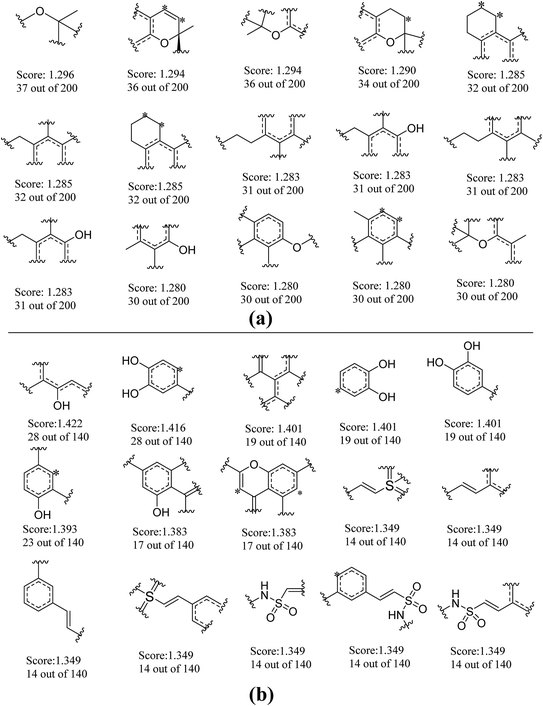 | ||
| Fig. 7 Examples of the top 30 good fragments estimated by NB-1-LPFP4 (a) and NB-2-LCFP6 (b) models. The Bayesian score (Score) and the frequency of each fragment in active compounds are given. | ||
3.7 Virtual screening of an in-house database for neuroprotective agents
Based on the two best neuroprotective models (NB-1-LPFP4 and NB-2-LCFP6), we performed a virtual screening of our in-house database (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905 compounds, National Center for Pharmaceutical Screening, Chinese Academy of Medical Sciences). The database was first filtered by the applicability domains of the two models, resulting in 20
905 compounds, National Center for Pharmaceutical Screening, Chinese Academy of Medical Sciences). The database was first filtered by the applicability domains of the two models, resulting in 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912 compounds for NB-1-LPFP4 and 20
912 compounds for NB-1-LPFP4 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832 compounds for NB-2-LCFP6, respectively. For NB-1-LPFP4 model, eight probability outputs (Pi+1 and Pi−1 i = 1, 2, 3, 4) were predicted for each compound using four single classifiers (NN-c1, kNN-c1, CT-c1, and RF-c1). Together with LPFP4 fingerprint, each compound outputted the final two combination decision probabilities (PC+1 and PC−1) with NB-1-LPFP4. Out of the 20
832 compounds for NB-2-LCFP6, respectively. For NB-1-LPFP4 model, eight probability outputs (Pi+1 and Pi−1 i = 1, 2, 3, 4) were predicted for each compound using four single classifiers (NN-c1, kNN-c1, CT-c1, and RF-c1). Together with LPFP4 fingerprint, each compound outputted the final two combination decision probabilities (PC+1 and PC−1) with NB-1-LPFP4. Out of the 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912 compounds screened, 2494 compounds were predicted as neuroprotective compounds against glutamate-induced neurotoxicity. Similarly, for NB-2-LCFP6 model, 4341 compounds were obtained against H2O2-induced neurotoxicity. Interestingly, 1614 compounds were predicted active by the two models simultaneously, and 553 out of them got both of the final probabilities PC+1 higher than 0.5 and were chosen for further study.
912 compounds screened, 2494 compounds were predicted as neuroprotective compounds against glutamate-induced neurotoxicity. Similarly, for NB-2-LCFP6 model, 4341 compounds were obtained against H2O2-induced neurotoxicity. Interestingly, 1614 compounds were predicted active by the two models simultaneously, and 553 out of them got both of the final probabilities PC+1 higher than 0.5 and were chosen for further study.
In addition, 553 compounds were clustered into 20 groups by FCFP_6 fingerprint with the Cluster ligands module in Discovery studio 4.0. Clustering is based on the root-mean-square (RMS) difference of the Tanimoto distance for fingerprinting. For each cluster, scaffold novelty as well as probability output was considered. Finally, 70 compounds (Table S7†) were obtained from our in-house sample library for in vitro neuroprotective assay.
3.8 In vitro neuroprotective assay results
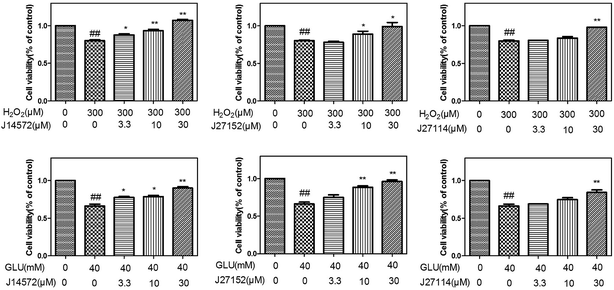
The preliminary neuroprotective assay results were given in Table S8.† Among 70 compounds screened at the concentration of 30 μM, 33 compounds showed the preliminary neuroprotective effects (cell damage inhibition higher than 40%) on monosodium glutamate-induced neurotoxicity on PC12 cell, while 28 out of these 33 compounds exhibited neuroprotective effects on H2O2-induced neurotoxicity. 40% compounds (28/70) showed neuroprotective activity against glutamate-induced and H2O2-induced neurotoxicity simultaneously, which suggested that the prediction models could greatly increase the chance of identifying neuroprotective compounds.Further evaluation results for the 28 compounds at different concentrations were given in Table 6. Vitamin E was set as reference compound and displayed neuroprotective effects.54 Most of compounds exhibit good dose–response relationship, which means cell survival increases as the concentration of compound increases. Fig. 8 displays neuroprotective effects of three representative compounds (J14572, J27152 and J27114) on monosodium glutamate-induced and H2O2-induced PC12 cells. Compared with control group, cell survival for model group injured by 40 mM monosodium glutamate or 300 μM H2O2 decreased significantly (P < 0.01). After treatment with J14572 (3.3 μM, 10 μM and 30 μM), J27152 (10 μM and 30 μM) or J27114 (30 μM), cell survival increased significantly.
| Compounda | Monosodium glutamate (40 mM) test concentration (μM) | H2O2 (300 μM) test concentration (μM) | ||||
|---|---|---|---|---|---|---|
| 3.3 μM | 10 μM | 30 μM | 3.3 μM | 10 μM | 30 μM | |
| a The data (cell viability, measured by MTT assay) were normalized and expressed as a percentage of the control group, which was set to 100%. Degree of damage of H2O2 was 69.24 ± 3.09, and degree of damage of monosodium glutamate was 66.05 ± 1.82. Data expressed as means ± SEM. Three independent experiments were carried out.b P < 0.05.c P < 0.01 vs. H2O2 group.d P < 0.05.e P < 0.01 vs. monosodium glutamate group. | ||||||
| J10216 | 76.41 ± 1.84 | 84.57 ± 4.58d | 81.75 ± 3.43d | 82.54 ± 1.53 | 83.31 ± 4.87 | 92.83 ± 0.025c |
| J10233 | 76.28 ± 3.18 | 83.81 ± 0.19e | 108.43 ± 1.76e | 68.73 ± 2.14 | 80.14 ± 1.45 | 133.15 ± 3.65c |
| J11762 | 63.29 ± 2.12 | 68.41 ± 2.67 | 89.24 ± 0.40e | 91.82 ± 0.99 c | 100.03 ± 2.58 c | 123.11 ± 0.83c |
| J12146 | 70.05 ± 4.61 | 75.97 ± 0.34 | 79.18 ± 1.73d | 82.14 ± 1.00 | 86.47 ± 2.27b | 82.19 ± 2.78 |
| J14156 | 67.83 ± 1.03 | 73.66 ± 1.01 | 79.28 ± 3.08d | 83.04 ± 3.35 | 91.16 ± 1.62 c | 100.63 ± 0.48 c |
| J14572 | 77.58 ± 1.40d | 78.66 ± 1.76d | 90.23 ± 1.25e | 87.12 ± 1.17 b | 93.04 ± 1.35 c | 106.28 ± 1.20c |
| J14581 | 71.78 ± 0.55 | 73.38 ± 0.59 | 77.41 ± 0.08d | 80.11 ± 0.66 | 85.49 ± 5.54 | 88.12 ± 3.58b |
| J14590 | 71.01 ± 3.94 | 83.56 ± 2.68e | 92.89 ± 2.35e | — | — | — |
| J14591 | 71.92 ± 1.24 | 77.51 ± 0.48d | 81.85 ± 2.95d | 99.66 ± 3.28 c | 100.90 ± 1.5 c | 103.70 ± 4.83 c |
| J14593 | 71.43 ± 5.6 | 78.36 ± 0.81d | 86.35 ± 2.88e | 78.01 ± 0.28 | 92.86 ± 2.3c | 84.86 ± 1.12 |
| J14691 | 76.25 ± 2.03 | 90.72 ± 1.50e | 101.70 ± 5.7e | 77.76 ± 0.43 | 77.28 ± 2.58 | 92.37 ± 4.19c |
| J18811 | 80.72 ± 2.96d | 93.91 ± 0.78e | 128.07 ± 5.66e | 86.63 ± 1.49b | 93.69 ± 2.5c | 93.06 ± 2.49c |
| J18836 | 85.51 ± 3.20d | 92.82 ± 3.05e | 83.62 ± 0.91e | 76.27 ± 0.68 | 92.10 ± 1.52c | 62.22 ± 0.51 |
| J18842 | 71.41 ± 0.53 | 76.12 ± 2.06 | 81.26 ± 0.65d | 79.74 ± 5.83 | 98.89 ± 3.04c | 104.32 ± 2.30c |
| J18879 | 84.44 ± 3.43d | 86.11 ± 2.05e | 99.67 ± 0.91e | 59.34 ± 5.38 | 66.92 ± 4.42 | 78.79 ± 4.86 |
| J27114 | 69.04 ± 0.067 | 74.70 ± 1.04 | 84.33 ± 0.91e | 80.78 ± 0.015 | 83.85 ± 1.38 | 98.38 ± 0.06c |
| J27115 | 76.16 ± 0.28 | 80.16 ± 4.31 | 86.13 ± 3.59d | 81.97 ± 1.16 | 75.01 ± 5.90 | 91.12 ± 2.52 c |
| J27118 | 82.64 ± 0.65d | 81.09 ± 1.78d | 84.19 ± 1.94d | 90.06 ± 2.97b | 91.65 ± 0.87c | 92.13 ± 0.62c |
| J27151 | 73.43 ± 4.87 | 77.41 ± 2.62 | 103.11 ± 6.28e | 81.64 ± 0.28 | 88.62 ± 6.16 | 114.63 ± 4.03c |
| J27152 | 77.25 ± 3.28 | 86.55 ± 1.93e | 94.63 ± 2.31e | 78.08 ± 1.31 | 86.15 ± 3.80 b | 94.02 ± 3.53b |
| J27153 | 69.65 ± 3.11 | 79.43 ± 1.70d | 98.63 ± 0.49e | 94.83 ± 2.95 c | 113.56 ± 4.94 c | 110.81 ± 4.68 c |
| J27155 | 72.49 ± 3.63 | 81.65 ± 2.91d | 90.11 ± 3.82e | 58.63 ± 4.67 | 86.97 ± 3.23 | 110.04 ± 10.33b |
| J27167 | 67.07 ± 6.79 | 59.79 ± 0.41 | 85.76 ± 3.28d | 88.41 ± 2.99b | 98.29 ± 2.3c | 88.32 ± 1.18b |
| J27198 | 67.79 ± 3.79 | 65.39 ± 1.01 | 85.54 ± 1.11e | 61.55 ± 6.34 | 82.29 ± 0.43 | 91.26 ± 2.60b |
| J27706 | 80.71 ± 1.52d | 74.77 ± 0.04 | 92.34 ± 4.37e | 81.32 ± 5.78 | 82.40 ± 4.15 | 84.12 ± 0.27 |
| J27709 | 67.02 ± 1.46 | 80.33 ± 0.35d | 80.12 ± 2.72 | 87.44 ± 0.95b | 87.27 ± 6.11 | 96.80 ± 1.70c |
| J32899 | 61.74 ± 2.22 | 68.86 ± 3.08 | 80.82 ± 1.96d | 83.78 ± 3.21 | 91.67 ± 1.98c | 86.28 ± 5.94 |
| J100313 | 66.93 ± 1.91 | 75.12 ± 3.58 | 80.31 ± 4.01 | 77.44 ± 0.43 | 86.07 ± 1.00 | 90.83 ± 0.95c |
| Vitamin E | 79.66 ± 3.77 | 85.22 ± 3.87d | 92.68 ± 5.10e | 91.29 ± 4.32b | 97.67 ± 4.44b | 106.22 ± 5.85c |
Further examination suggested five compounds (J14572, J18811, J18836, J18879 and J27118) could exhibited significant neuroprotective effects against monosodium glutamate-induced neurotoxicity at the concentration of 3.3 μM, 10 μM and 30 μM, while seven compounds (J11762, J14572, J14591, J18811, J27118, J27153 and J27167) displayed significant neuroprotective activity against H2O2-induced neurotoxicity at the same three concentration. The chemical structures of these potent compounds are shown in Fig. 9. To be exciting, three compounds (J14572, J18811, and J27118) could protect against glutamate-induced and H2O2-induced neurotoxicity at three concentrations, which showed promising prospect on neurodegenerative disease.
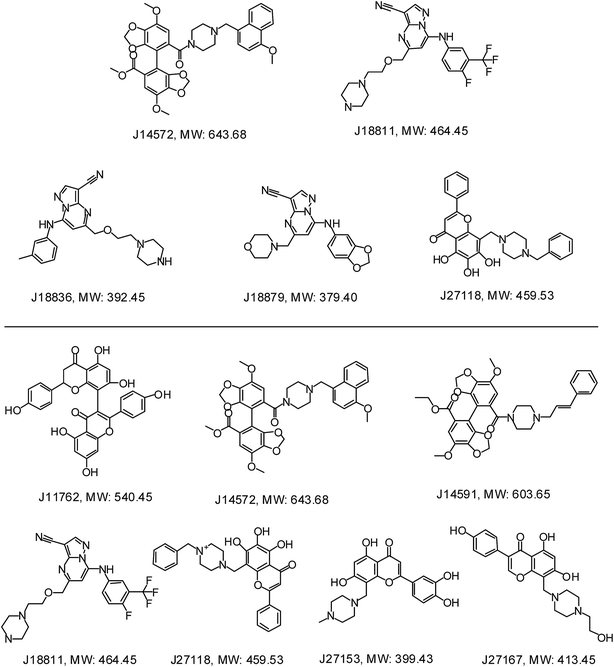 | ||
| Fig. 9 Chemical structures of representative neuroprotective compounds against glutamate-induced (top) or H2O2-induced (bottom) neurotoxicity in PC12 cell. | ||
4. Conclusion
In this study, the classification models were developed to discriminate neuroprotective compounds against glutamate or H2O2-induced neurotoxicity from inactive through machine learning approaches. Twenty four single models were generated based on four different classification algorithms (neural network, k nearest neighbors, classification tree and random forest), which were integrated to develop the combined Bayesian models to obtain superior performance. The various validations including cross validation, test set validation, and Y-scrambling confirmed the prediction reliability of the models. Finally, two best models NB-1-LPFP4 and NB-2-LCFP6 were used to perform virtual screening for discovering neuroprotective compounds.Preliminary assay results suggested that 40% (28/70) of compounds showed neuroprotective activity against glutamate-induced and H2O2-induced neurotoxicity simultaneously, and further evaluation showed that several of them could exhibit neuroprotective effects at different concentration (3.3 μM, 10 μM and 30 μM).
In short, this investigation demonstrated that in silico phenotypic-based models could efficiently identify novel neuroprotective compounds. This study provided useful suggestions for other types of rational drug discovery, and may be applied for other lead identification.
Conflict of interest
The authors declare no competing financial interest.Acknowledgements
This work was funded in part of the Research Special Fund for the National Great Science and Technology Projects (2012ZX09301002-001-001), the International Collaboration Project (2011DFR31240), and Peking Union Medical College graduate student innovation fund (2013-1007-18).References
- D. C. Rubinsztein, Nature, 2006, 443, 780–786 CrossRef CAS PubMed.
- K. J. Barnham, C. L. Masters and A. I. Bush, Nat. Rev. Drug Discovery, 2004, 3, 205–214 CrossRef CAS PubMed.
- B. Halliwell, Drugs Aging, 2001, 18, 685–716 CAS.
- C. Behl, J. B. Davis, R. Lesley and D. Schubert, Cell, 1994, 77, 817–827 CrossRef CAS PubMed.
- H. Irannejad, M. Amini, F. Khodagholi, N. Ansari, S. K. Tusi, M. Sharifzadeh and A. Shafiee, Bioorg. Med. Chem. Lett., 2010, 18, 4224–4230 CrossRef CAS PubMed.
- E. K. Michaelis, Prog. Neurobiol., 1998, 54, 369–415 CrossRef CAS PubMed.
- L. Wang, Q. Gu, X. Zheng, J. Ye, Z. Liu, J. Li, X. Hu, A. Hagler and J. Xu, J. Chem. Inf. Model., 2013, 53, 2409–2422 CrossRef CAS PubMed.
- D. C. Swinney, Clin. Pharmacol. Ther., 2013, 93, 299–301 CrossRef CAS PubMed.
- W. Zheng, N. Thorne and J. C. McKew, Drug Discovery Today, 2013, 18, 1067–1073 CrossRef CAS PubMed.
- J. Arrowsmith, Nat. Rev. Drug Discovery, 2011, 10, 87 CrossRef CAS PubMed.
- D. C. Swinney and J. Anthony, Nat. Rev. Drug Discovery, 2011, 10, 507–519 CrossRef CAS PubMed.
- J. T. Coyle and P. Puttfarcken, Science, 1993, 262, 689–695 CAS.
- Y. C. Kim, S. R. Kim, G. J. Markelonis and T. H. Oh, J. Neurosci. Res., 1998, 53, 426–432 CrossRef CAS PubMed.
- A. Vogt and J. S. Lazo, Pharmacol. Ther., 2005, 107, 212–221 CrossRef CAS PubMed.
- K. C. Peach, W. M. Bray, D. Winslow, P. F. Linington and R. G. Linington, Mol. BioSyst., 2013, 9, 1837–1848 RSC.
- R. M. Pruss, CNS Neurol. Disord.: Drug Targets, 2010, 9, 693–700 CAS.
- R. Macarron, M. N. Banks, D. Bojanic, D. J. Burns, D. A. Cirovic, T. Garyantes, D. V. Green, R. P. Hertzberg, W. P. Janzen, J. W. Paslay, U. Schopfer and G. S. Sittampalam, Nat. Rev. Drug Discovery, 2011, 10, 188–195 CrossRef CAS PubMed.
- S. Ananthan, E. R. Faaleolea, R. C. Goldman, J. V. Hobrath, C. D. Kwong, B. E. Laughon, J. A. Maddry, A. Mehta, L. Rasmussen, R. C. Reynolds, J. A. Secrist III, N. Shindo, D. N. Showe, M. I. Sosa, W. J. Suling and E. L. White, Tuberculosis, 2009, 89, 334–353 CrossRef CAS PubMed.
- N. Singh, S. Chaudhury, R. Liu, M. D. M. AbdulHameed, G. Tawa and A. Wallqvist, J. Chem. Inf. Model., 2012, 52, 2559–2569 CrossRef CAS PubMed.
- F. Tomás-Vert, F. Perez-Gimenez, M. T. Salabert-Salvador, F. Garcıa-March and J. Jaen-Oltra, J. Mol. Struct.: THEOCHEM, 2000, 504, 249–259 CrossRef.
- Y. Marrero-Ponce, R. Medina-Marrero, F. Torrens, Y. Martinez, V. Romero-Zaldivar and E. A. Castro, Bioorg. Med. Chem., 2005, 13, 2881–2899 CrossRef CAS PubMed.
- S. Ekins, R. C. Reynolds, S. G. Franzblau, B. Wan, J. S. Freundlich and B. A. Bunin, PLoS One, 2013, 8, e63240 CAS.
- E. L. Berg, J. Yang and M. A. Polokoff, J. Biomol. Screening, 2013, 18, 1260–1269 CrossRef PubMed.
- P. Prathipati, N. L. Ma and T. H. Keller, J. Chem. Inf. Model., 2008, 48, 2362–2370 CrossRef CAS PubMed.
- A. Gaulton, L. J. Bellis, A. P. Bento, J. Chambers, M. Davies, A. Hersey, Y. Light, S. McGlinchey, D. Michalovich, B. Al-Lazikani and J. P. Overington, Nucleic Acids Res., 2012, 40, D1100–D1107 CrossRef CAS PubMed.
- M. M. Mysinger, M. Carchia, J. J. Irwin and B. K. Shoichet, J. Med. Chem., 2012, 55, 6582–6594 CrossRef CAS PubMed.
- Molecular Operating Environment (MOE), version 2010.10, Chemical Computing Group Inc., Montreal, Quebec, Canada, 2010 Search PubMed.
- Discovery Studio, version 4.0, Accelrys Inc., San Diego, CA, 2013 Search PubMed.
- L. Wang, M. Wang, A. Yan and B. Dai, Mol. Diversity, 2013, 17, 85–96 CrossRef CAS PubMed.
- M. Hall, E. Frank, G. Holmes, B. Pfahringer, P. Reutemann and I. H. Witten, ACM SIGKDD explorations newsletter, 2009, 11, pp. 10–18 Search PubMed.
- D. E. Goldberg and J. H. Holland, Mach. Learn., 1988, 3, 95–99 CrossRef.
- Version 2.7, available free of charge at Web site: http://www.ailab.si/orange/.
- K. Gurney, An introduction to neural networks, CRC press, 1997 Search PubMed.
- D. T. Larose, k-Nearest Neighbor Algorithm. Discovering Knowledge in Data: An Introduction to Data Mining, 2005, pp. 90–106 Search PubMed.
- J. R. Quinlan, C4. 5: programs for machine learning, Morgan kaufmann, 1993, vol. 1 Search PubMed.
- L. Breiman, Mach. Learn., 2001, 45, 5–32 CrossRef.
- J. C. Baber, W. A. Shirley, Y. Gao and M. Feher, J. Chem. Inf. Model., 2006, 46, 277–288 CrossRef CAS PubMed.
- N. Baurin, J.-C. Mozziconacci, E. Arnoult, P. Chavatte, C. Marot and L. Morin-Allory, J. Chem. Inf. Comput. Sci., 2004, 44, 276–285 CrossRef CAS PubMed.
- F. Cheng, Y. Yu, J. Shen, L. Yang, W. Li, G. Liu, P. W. Lee and Y. Tang, J. Chem. Inf. Model., 2011, 51, 996–1011 CrossRef CAS PubMed.
- J. R. Votano, M. Parham, L. H. Hall, L. B. Kier, S. Oloff, A. Tropsha, Q. Xie and W. Tong, Mutagenesis, 2004, 19, 365–377 CrossRef CAS PubMed.
- J. Fang, R. Yang, L. Gao, S. Yang, X. Pang, C. Li, Y. He, A.-L. Liu and G.-H. Du, Mol. Diversity, 2015, 19, 149–162 CrossRef CAS PubMed.
- X. Xia, E. G. Maliski, P. Gallant and D. Rogers, J. Med. Chem., 2004, 47, 4463–4470 CrossRef CAS PubMed.
- M. Luo, T. E. Reid and X. S. Wang, Comb. Chem. High Throughput Screening, 2015, 18, 685–692 CrossRef CAS PubMed.
- J. Fang, R. Yang, L. Gao, D. Zhou, S. Yang, A.-L. Liu and G.-H. Du, J. Chem. Inf. Model., 2013, 53, 3009–3020 CrossRef CAS PubMed.
- J. Fang, Y. Li, R. Liu, X. Pang, C. Li, R. Yang, Y. He, W. Lian, A.-L. Liu and G.-H. Du, J. Chem. Inf. Model., 2015, 55, 149–164 CrossRef CAS PubMed.
- Y. Xia, J. Xing and T. Krukoff, Neuroscience, 2009, 162, 292–306 CrossRef CAS PubMed.
- K. Dong, J.-X. Pu, H.-Y. Zhang, X. Du, X.-N. Li, J. Zou, J.-H. Yang, W. Zhao, X.-C. Tang and H.-D. Sun, J. Nat. Prod., 2012, 75, 249–256 CrossRef CAS PubMed.
- S. Ma and Y. Dai, Briefings Bioinf., 2011, 12, 714–722 CrossRef CAS PubMed.
- D. S. Wishart, C. Knox, A. C. Guo, S. Shrivastava, M. Hassanali, P. Stothard, Z. Chang and J. Woolsey, Nucleic Acids Res., 2006, 34, D668–D672 CrossRef CAS PubMed.
- R. W. Stanforth, E. Kolossov and B. Mirkin, QSAR Comb. Sci., 2007, 26, 837–844 CAS.
- S. Dimitrov, G. Dimitrova, T. Pavlov, N. Dimitrova, G. Patlewicz, J. Niemela and O. Mekenyan, J. Chem. Inf. Model., 2005, 45, 839–849 CrossRef CAS PubMed.
- S. Weaver and M. P. Gleeson, J. Mol. Graphics Modell., 2008, 26, 1315–1326 CrossRef CAS PubMed.
- F. Sahigara, K. Mansouri, D. Ballabio, A. Mauri, V. Consonni and R. Todeschini, Molecules, 2012, 17, 4791–4810 CrossRef CAS PubMed.
- B. J. Josey, E. S. Inks, X. Wen and C. J. Chou, J. Med. Chem., 2013, 56, 1007–1022 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Y-scrambling result of NB-1-LPFP4 and NB-2-LCFP6 (Fig. S1), extracting applicability domain for a QSAR model-step by step (Fig. S2), the structures (in SMILE format) of the 1000 compounds of the training set and 260 compounds of the test set for glutamate-induced models (Tables S1–S2), the structures (in SMILE format) of the 700 compounds of the training set and 200 compounds of the test set for H2O2-induced models (Tables S3–S4), the detailed performance of 24 single classification models for 5-fold cross validation and test set using different combinational of molecular properties (Table S5), the detailed performance of the 26 combined Bayesian classification models for 5-fold cross validation and test set using different combinational of output probabilities and fingerprints (Table S6), and the structures (in SMILE format) (Table S7) and preliminary assay result (Table S8) for 70 virtual hits on monosodium glutamate or H2O2-induced neurotoxicity on PC12 Cell. See DOI: 10.1039/c5ra23035g |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2016 |