Open Access Article
Open Access ArticleModelling of graphene functionalization
Martin
Pykal
,
Petr
Jurečka
,
František
Karlický
 and
Michal
Otyepka
*
and
Michal
Otyepka
*
Regional Centre of Advanced Technologies and Materials, Department of Physical Chemistry, Faculty of Science, Palacký University Olomouc, tř. 17. listopadu 12, 771 46 Olomouc, Czech Republic. E-mail: Michal.Otyepka@upol.cz; Fax: +420 585 634 761; Tel: +420 585 634 756
First published on 19th August 2015
Abstract
Graphene has attracted great interest because of its remarkable properties and numerous potential applications. A comprehensive understanding of its structural and dynamic properties and those of its derivatives will be required to enable the design and optimization of sophisticated new nanodevices. While it is challenging to perform experimental studies on nanoscale systems at the atomistic level, this is the ‘native’ scale of computational chemistry. Consequently, computational methods are increasingly being used to complement experimental research in many areas of chemistry and nanotechnology. However, it is difficult for non-experts to get to grips with the plethora of computational tools that are available and their areas of application. This perspective briefly describes the available theoretical methods and models for simulating graphene functionalization based on quantum and classical mechanics. The benefits and drawbacks of the individual methods are discussed, and we provide numerous examples showing how computational methods have provided new insights into the physical and chemical features of complex systems including graphene and graphene derivatives. We believe that this overview will help non-expert readers to understand this field and its great potential.
1. Introduction
Graphene1 is a two dimensional material consisting of a hexagonal (honeycomb) lattice of covalently bound sp2 carbon atoms that are sandwiched between two π-electron clouds. Despite extensive research efforts triggered by numerous potential applications of graphene and its derivatives (Fig. 1),2 only a limited number of graphene-based products have been successfully commercialized to date. The graphene-based technology is still mainly in the research and development stage (for a more detailed discussion, please see the October 2014 issue of Nature Nanotechnology3). Among other purposes, it has diverse uses in sensing, ranging from the detection of small molecules4 to large biomacromolecules,5,6 including also DNA translocation7 and selective molecular sieving.8 The potential range of applications for graphene can be enhanced enormously by covalent and non-covalent modification.9 Covalent modification entails the formation of chemical bonds between graphene and some modifiers, which significantly change the structure and the hybridization of its carbon atoms. Such changes have profound effects on the material's physicochemical properties.10 Conversely, non-covalent modification entails the adsorption of a modifier onto the graphene surface via weak non-covalent forces. Such adsorption also changes the structure and properties, but to a lesser degree than the covalent modification; the magnitude of the changes is proportional to the modifier's binding energy. It should however be noted that the transition between covalent and non-covalent modification is rather smooth. To understand the effects of these modifications, and their behaviour in sensing applications, it is necessary to obtain an in-depth understanding of the nature and strength of the interactions between graphene and guest molecules. Computational chemistry is a valuable source of information that can be used to develop such an understanding.Modelling of the interactions between graphene and guest molecules or modifiers can provide important insights into the effects of graphene modifications. This can be achieved using either electronic structure methods based on quantum mechanics, which explicitly account for the electronic structure of the studied molecular systems, or with molecular mechanics methods (also known as empirical force fields) that simplify molecular systems by representing them as collections of covalently bound van der Waals spheres. This perspective provides an overview of electronic structure and empirical methods (Sections 3 and 4) that can be used in computational studies on graphene modifications, extended with basic simulation methods for nuclear degrees of freedom (Section 5). We also provide some guidance for non-experts to explain which methods are applicable in particular contexts and how suitable they are for predicting the behaviour and properties of functionalized graphene and graphene derivatives. Finally we present numerous illustrative examples of computational studies that have enhanced our understanding of modified graphene (Section 6).
2. Graphene models
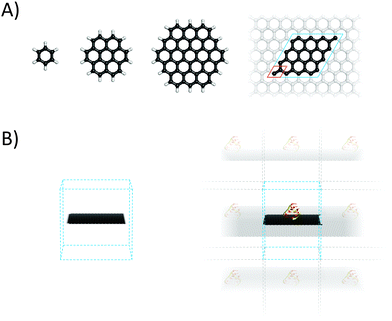
2.1 Finite molecular models of graphene
Graphene is often modelled as a finite polyaromatic hydrocarbon (PAH)11–14 such as coronene (C24H12) or circumcoronene (C54H18), both of which are shown in Fig. 2.15,16 The carbon networks of these model molecules are capped with hydrogen atoms that saturate the dangling bonds at their edges. This affects the distribution of electronic density within the system because the electrons of the hydrogens are drawn to the carbon skeleton, generating a positive electrostatic potential on the hydrogen atoms and a negative electrostatic potential above and below the carbon sheet where the π electron cloud is located. Consequently, polyaromatic hydrocarbons have significant quadrupole moments that depend on their size (Fig. 3).17 This finite quadrupolar potential means that PAHs are imperfect models for the infinite flat periodic sheet of graphene, in which the quadrupolar potential completely vanishes. It should be noted, however, that real graphene is corrugated and the quadrupolar potential may be nonzero near its surface (Fig. 3). An important advantage of using finite molecular models is that they can be studied using a wide portfolio of electronic structure methods developed for molecular systems. The only limitations come from the size of the system that can be treated in a reasonable timeframe with specific methods, and the available computational power. A systematic study by Hobza and coworkers showed that the interaction energies of tetracyanoethylene and tetracyanoquinodimethane with various PAHs decreased convergently as the size of PAH increased.18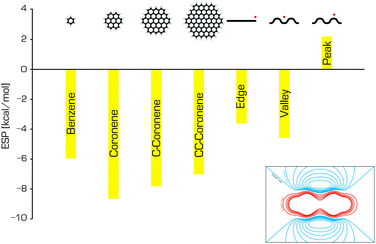 | ||
| Fig. 3 The electrostatic potentials of benzene, coronene, circumcoronene and circumcircumcoronene (calculated in the middle of the molecule, 3.4 Å above the surface), and the electrostatic potentials at specific positions relative to a graphene sheet (adapted from ref. 17). The inset shows the ESP around the benzene molecule; the red and blue contours represent positive and negative potentials, respectively. | ||
Empirical methods (Section 4) allow the use of substantially larger models of graphene flakes (up to tens of nanometers), and are therefore applicable when studying nanoscale phenomena such as exfoliation and aggregation processes in colloidal dispersions of graphene.19 In such cases edge effects as well as the effects of the system's quadrupole moment may become important.17 Shih and coworkers20 studied the stability and mechanisms of the aggregation process in exfoliated graphene solutions in several frequently used polar solvents. Based on their simulations and kinetic theory, they proposed a model of graphene aggregation in which the dominant barrier to aggregation was associated with the energetic cost of eliminating a single layer of solvent molecules confined between two graphene sheets oriented in parallel. Colloidal dispersions of graphene were also investigated by Lin et al.,21 who examined the morphology and kinetics of self-assembled structures of surfactants and graphene sheets. Their findings suggest that the surfactant molecules stabilized the colloidal graphene dispersion and prevented the re-formation of new two- and three-layered graphene aggregates. Freestanding graphene was also considered in a study on wrinkles on the graphene surface and their effect on the specific surface area.22 The results indicated that wrinkles could only change the specific surface area by 2% at most, regardless of their shape, the nature of the defects that were present, or the strain acting on the area.
2.2 Periodic graphene
Ideal graphene is an infinite two-dimensional (2D) sheet with a regular lattice structure. Such a material can be straightforwardly modelled using periodic boundary conditions (Fig. 2) in which a unit cell including two carbon atoms is replicated across space. This periodic graphene model can be studied using numerous methods, most of which are based on density functional theory (DFT) and were developed by solid-state physicists to model the physical features of crystals. When studying the adsorption of guest molecules (adsorbates) to graphene, the size of a replicating cell, which is known as the supercell, is dictated by the size and target concentration of the adsorbate because it is important to avoid unwanted interactions between replicas. Since the periodic boundary conditions are typically implemented over the three-dimensional (3D) space, graphene (which is generally assumed to lie in the xy plane) and its complexes are modelled using 3D unit cells with a large vertical length (∼1.5 nm) to avoid spurious vertical interactions between replicas. Spurious interactions could be particularly problematic if the supercell contains polar molecules or ions, because of the slow decay of Coulombic forces. It should be noted that the attractive van der Waals (vdW) forces in nanomaterials act over longer distances than was originally assumed.23Periodic models can also be used with empirical methods (Section 4). One of their advantages is that they help to avoid some artefacts that can be caused by the presence of edges. An example is the quadrupole moment, which should be considered when working with finite graphene models such as those discussed above. The electronic band structure of graphene and its derivatives can only reasonably be studied using periodic models because models that do not account the inherent extended nature of graphene neglect correlation contributions from the bands close to the Dirac point. Furthermore, the infinite model may better describe the situations encountered in some experiments, such as those involving measurements on spots of graphene flakes that may be multiple micrometers in diameter. In such cases, the presence of edge effects in a simulated finite sheet could introduce undesirable bias. An infinite periodic boundary condition (PBC) model was used to study the mechanism by which graphene dispersions are stabilized in the presence of lipids, revealing that the lipids present a kinetic barrier to graphene aggregation by forming reverse micelles on the graphene surface.24 On the other hand, PBC models may be less suitable for studying phenomena such as surface corrugation because the box size limits the scale on which corrugation effects can be studied. Another potential drawback of the periodic model that may be encountered with certain simulation configurations relates to sandwiched structures in which two graphene sheets are separated by a fixed distance; this can lead to unphysical conditions such as unreasonable pressures. It should also be noted that not every software package for performing empirical computations supports periodic models.
As mentioned above, both finite and infinite (periodic) graphene models can be described using either quantum chemical (electronic structure) or molecular mechanical (empirical) methods. The potential applications of each are delineated by the Born–Oppenheimer approximation, which enables the separation of electronic and nuclear motions inside a molecular system. Phenomena involving changes in electronic states should be modelled using electronic structure methods that explicitly account for electronic motions. Molecular mechanics can be used to model phenomena in which the electronic structure does not change or changes only slightly, such as changes in conformational states or physisorption.
3. Electronic structure methods
3.1 Methods for studying non-covalent complexes of graphene
We have already mentioned that graphene can be modified either covalently or non-covalently. However, the mode of adsorbate binding may in reality lie somewhere between these two extremes. To model such situations it is necessary to use theoretical methods that accurately describe both covalent and non-covalent forces. It should be stressed that the accurate description of non-covalent forces is quite challenging for current theoretical methods. To avoid lengthy descriptions of the many electronic structure methods that could potentially be used to describe the electronic and physical–chemical properties of graphene, we will focus here on methods that can be used to predict its non-covalent interactions with reasonable confidence. The fidelity of theoretical methods for chemical modifications of graphene will be discussed only with reference to specific cases. It is generally accepted that individual sheets of graphene are bound by London dispersion forces in graphite. London forces originate from non-local electron correlation effects.25 Any electronic structure theory must therefore account properly for these non-local correlation effects in order to reliably predict the properties of non-covalent graphene complexes such as their binding energies and geometries.3.2 Wavefunction based methods
The Hartree–Fock (HF) method fails to describe electron correlation effects because it neglects the correlation between electrons of opposite spin. It is therefore necessary to use post-HF methods to address this deficiency. The second-order Møller–Plesset perturbation method (MP2) accounts for a large fraction of the electron correlation effect, but it has some drawbacks. First, it is significantly more computationally demanding than the HF method and tends to overestimate the binding energies of non-covalent complexes that are bound mostly by London dispersive forces. Several methods that derive from MP2 but offer greater accuracy have been developed. The spin-component scaled MP2 (SCS-MP2)26 and SCS(MI)-MP227 methods are of particular note because they predict binding energies significantly more accurately than MP2 without any additional computational cost. The CCSD method itself is not suitable for the accurate description of dispersion bonded complexes. However, its spin-component scaled variants SCS-CCSD28 and SCS(MI)-CCSD, the latter of which is optimized for the study of molecular interactions,29 provide remarkably accurate results with a very good accuracy/computational cost ratio. The scaled MP2/MP3 method including higher-order correlation effects (e.g., MP2.5)30 can also be useful for obtaining very accurate binding energies for non-covalent complexes at an affordable computational cost. The current gold standard for predicting the binding energies of non-covalent complexes is undoubtedly the coupled cluster method including single, double and perturbative triple excitations – CCSD(T). Unfortunately, CCSD(T) calculations are so computationally demanding that only small systems of less than ∼35 atoms can be studied in this way (Table 1). Significant speedups of CCSD and CCSD(T) calculations have been achieved using the recently-introduced domain based local pair-natural orbital (DLPNO) approximation, yielding the modified DLPNO-CCSD31 and DLPNO-CCSD(T)32 methods. However, further testing of these methods may be required before they can be considered suitable for routine use. More detailed information on the performance of various methods for modelling non-covalent complexes can be found in a recent review.33| Method | Finite | PBC | Size | Cost | Quality |
|---|---|---|---|---|---|
| a The real performance and cost of DFT-D2, -D3, and -TS methods are determined by the underlying functional; hybrids are more expensive than GGA functionals. | |||||
| WFT | |||||
| MP2 | × | × | ** | ** | * |
| SCS(MI)-MP2 | × | × | ** | ** | ** |
| MP2.5 | × | — | ** | *** | *** |
| CCSD(T) | × | — | * | **** | **** |
| DFT | |||||
| M06-2X | × | × | *** | ** | ** |
| DFT-D2, DFT-D3a | × | × | *** | ** | ** |
| DFT-TSa | × | × | *** | ** | ** |
| vdW-DF, vdW-DF2 | × | × | *** | *** | ** |
| optB88-vdW | × | × | *** | *** | ** |
| RPA | × | × | * | **** | *** |
| Other | |||||
| QMC | × | × | ** | **** | **** |
| PM6-DH, SCC-DFTB-D | × | × | **** | * | * |
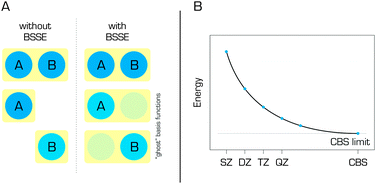
Wavefunction-based methods are always used in conjunction with a finite basis set. In the literature, combinations of a method and a basis set are typically denoted in the form of a method/basis set – for example, SCS(MI)-MP2/cc-pVTZ, where cc-pVTZ stands for the correlation consistent polarized valence triple-zeta basis set developed by Dunning and coworkers.34 Many different basis sets have been developed, and a detailed description of their construction and applicability would be beyond the scope of this review; the interested reader can find more detailed information elsewhere.35 However, it should be noted that the chosen basis set can significantly affect the quality of the results obtained in any quantum chemical calculation. It is generally accepted that larger basis sets provide better results. This idea resulted in the development of extrapolation schemes,36–38 which estimate the results for an infinite basis set that is referred to as the complete basis set (CBS). Calculations performed at the CCSD(T)/CBS level of theory provide very accurate estimates for quantities such as the interaction energies of non-covalent complexes.33,39,40 When CBS extrapolation cannot be performed and small or medium size basis sets are used, which is usually the case, it is important to apply a correction for the basis set superposition error (BSSE) (Fig. 4) such as the counterpoise (CP) correction of Boys and Bernardi.41 The BSSE arises from the fact that the basis sets used to describe non-covalent complexes are necessarily larger than those used for their individual components (in the simple case of a dimeric complex, the basis set for the dimer will necessarily be twice the size of that for the separated monomer). Failure to correct the BSSE inevitably leads to an overestimation of binding energies. However, the CP correction is imperfect and frequently overestimates the BSSE,42 so some authors use either the fractional BSSE correction or combine the CP with special extrapolation schemes.38,43
The post-HF methods were primarily developed for the study of molecular systems and they are readily applied to molecules and their assemblies. On the other hand, their applicability under periodic boundary conditions is currently very limited.44 The MP2 method has been implemented in a way that is compatible with the periodic boundary approach45–48 but calculations using this implementation are impractical for graphene because of its zero band gap. The CCSD method has been implemented in the VASP code for periodic boundary simulations49 but this update has not yet been released to the public.
3.3 Density functional methods
Classical DFT methods based on the local density approximation (LDA), the generalized gradient approximation (GGA), or hybrid functionals do not account for non-local electron correlation effects, which are critical for the correct description of London dispersion forces.50–52 In LDA the binding caused by a too strong exchange contribution to the exchange–correlation functional is very different from the dynamical correlation effects promoting dispersion interactions. Several strategies have been developed to describe London dispersion forces within the framework of DFT. These include the empirically corrected DFT methods (abbreviated as DFT-D). The first DFT-D methods were based on summation over pair-wise cij/rij6 terms (where cij represents an empirical dispersion coefficient for the electron pair ij at a distance of rij), which were multiplied by a damping function (whose parameterization critically influences the accuracy of DFT-D) to avoid double counting of dispersive contributions,53,54 which is necessary because DFT natively accounts for local electron–electron correlation. After the initial success of the DFT-D method53,55 a series of more sophisticated methods with better performance were introduced including DFT-D2,56 DFT-D357 and DFT-TS.58 In addition, it was shown that many-body dispersion methods that go beyond pair-wise vdW interactions are required to improve the description of non-covalent interactions involving graphene.59,60 Dispersion can also be accounted for by combining DFT and MP2 calculations, the latter of which naturally account for long-range correlation.61 Such methods are called double hybrids because they include some portion of HF exchange in addition to the MP2 correlation. Double hybrid methods can be very accurate.62,63 However, like MP2 calculations, they cannot be applied to periodic graphene. Note also that double hybrids somewhat underestimate long-range dispersion, although this can be corrected for by introducing empirical dispersion correction terms.64An alternative strategy resulted in the development of non-local density functionals that account directly for dispersive correlation effects. Approaches of this type include the vdW-DF method of Dion et al.,65 its improved successor vdW-DF2,66 the reparameterized version optB88-vdW,67 and the VV10 method of Vydrov et al.68 It should be noted that functionals which account for electron–electron correlation effects can be systematically improved by exploiting the adiabatic connection fluctuation–dissipation theorem69 as clearly explained by Tkatchenko.70 Yet another way of modelling mid-range intermolecular interactions accurately with DFT is to use one of the highly parameterized local, GGA or meta-GGA DFT functionals developed by Truhlar and coworkers, which are called the Minnesota functionals (e.g. M06-2X71). These functionals provide surprisingly good results at affordable cost (The comparison with other methods is shown in Table 1). The ability of some of these methods to predict the energies of interaction between graphene-based materials and molecular hydrogen has been investigated by Kocman et al.72 London dispersive forces can also be described using the random phase approximation (RPA) method, which accounts for electron–electron correlation effects from first principles. The RPA provides rather accurate predictions of surface adsorption behavior73–75 and bulk material properties.76,77 However, it is very computationally demanding. Finally, the GW approximation78 has been used for accurate quasiparticle electronic band structure calculations. This many-body method corrects DFT using a self-energy operator consisting of Green's function (G) and the screened Coulomb interaction (W), and thereby inherently accounts for electron–electron correlation effects.
The height of the activation barrier to a given chemical modification of graphene can be related to the kinetics of the corresponding process using the Eyring equation. To accurately predict activation barriers, it is necessary to address the problem of the electron self-interaction error (SIE) in DFT exchange functionals.79 This can be achieved by admixing HF or exact exchange in DFT functionals. DFT functionals containing HF exchange are known as hybrid functionals. An ideal DFT method capable of accurately describing thermodynamics, kinetics and non-covalent interaction should thus be free of SIE and account for non-local electron correlation effects. This could potentially be achieved in various ways, for example by combining RPA with exact exchange.80,81 However, this would not be trivial to achieve, and careful testing of such approaches would be essential.
3.4 Quantum Monte Carlo methods
Quantum Monte Carlo (QMC) represents another strategy for solving the electronic Schrödinger equation from first principles. QMC methods are explicit many-body approaches based on the real-space random sampling of the electron configuration space. Two QMC methods are in common use, variational Monte Carlo (VMC) and diffusion Monte Carlo (DMC). The VMC method relies on the variational principle and stochastic integration of a quantum-mechanical total energy expectation value. Its main advantage is the ability to sample complicated wave functions including explicit correlation and to improve them variationally. A more powerful alternative to VMC is the fixed-node DMC method (FN-DMC), which relies on the projection (or enhancement) of the ground-state component from a given input trial electronic wave function in imaginary time. In combination with real-space sampling (that is a complete basis set, i.e. electrons can visit any point in the real space), FN-DMC provides exact solutions within the boundaries imposed by the fixed-node (ΨT = 0) condition of the input trial state ΨT. The fixed-node approximation is the one of multiple possible strategies for simulating Pauli exchange repulsion. FN-DMC thus efficiently accounts for electron–electron correlation effects from first principles. It should be noted that the QMC results are less sensitive to the one-electron basis sets used to construct trial wave functions since the electron correlations are simulated explicitly rather than by using many-body expansions in terms of one-particle states, as is the case in traditional wave function theory. QMC results have associated error bars that only converge slowly (∝1/√K for calculations with K independent sampling points), but the method's computational cost typically scales as a low-order polynomial (of order 3–4), which is significantly better than the scaling of CCSD(T)/CBS (of order 7) and thus enables studies of larger systems with comparable accuracy (as demonstrated in ref. 82). Moreover, QMC methods can be efficiently parallelized and implemented for both finite and periodic boundary conditions (Table 1). Consequently, they have great potential for use in electronic structure calculations on graphene and related compounds. In recent years, QMC methods have been used to study small conjugated hydrocarbons (benzene/coronene) and their interactions with atoms/molecules72,82–86 and for explicit modelling of periodic graphene/graphite.84,87,88 For more details on QMC, we direct the reader to a pair of recent reviews (and references included therein).89,903.5 Semiempirical methods
Since the advent of quantum chemistry, there has been a continuous effort to develop fast electronic structure methods capable of treating large systems containing hundreds of atoms. One way of doing this is to introduce additional approximations to the HF method (Section 3.2) in the form of semiempirical parameters, which are derived by approximation or fitting to experimental results or data from higher-level calculations. Semiempirical methods such as AM1,91 PM392 and PM693 are very widely used in chemical research. In physics, the tight-binding (TB) semiempirical method is a similar approximate approach for predicting the electronic structure of periodic materials.94,95 In the TB approach, the wave function of a complex system is constructed as a superposition of the wave functions for isolated atoms located at the positions of the corresponding nuclei within the system of interest. It has been used successfully to describe graphene and its derivatives,96 achieving accuracies that rival higher level methods while enabling the simulation of systems comprising hundreds of atoms. For instance, ballistic transport in transistors based on the functionalized graphene97 were reported on the basis of the energy band calculation by high-level methods for graphane and graphone, subsequently fitted with a three-nearest neighbour sp3 tight-binding Hamiltonian. More recently, the TB approximation was used to study the electronic structures and optical properties of micrometer-scale partially and fully fluorinated graphene systems comprising 2400 × 2400 carbon atoms at GW accuracy.98 The TB approximation has also been generalized, leading to the development of density functional-based tight binding (DFTB).99 DFTB was subsequently improved by the incorporation of self-consistent redistribution of Mulliken charges (SCC-DFTB)100 to account for the Coulomb interaction between charge fluctuations, and by the addition of an empirical dispersion correction (SCC-DFTB-D).101 SCC-DFTB accounts for long-range electrostatic forces and self-interaction contributions, and has been used to investigate the correlation between the hydrogen superlattice structure on graphene and the band gap opening,102 and to explore the properties of graphene nanodots inside fluorographene.103The approximations made in the creation of current semiempirical methods mean that they cannot accurately describe non-covalent interactions. This problem can be addressed by introducing empirical dispersion corrections (D) in the same way as was done for DFT in the creation of the DFT-D methods. In keeping with the established nomenclature, the suffix -D is appended to semiempirical methods corrected in this way, which include AM1-D and PM3-D.104 The latter of these two methods was successfully used to model the interactions of small molecules with aromatic systems105 and graphite.106 Hobza and coworkers developed the semiempirical method PM6-DH, which incorporates an additional correction term to describe hydrogen-bonding107 as a function of H-bond length, donor–H⋯acceptor angle and partial charges on the H and acceptor atoms. Additional variants of the DH correction, e.g., DH+108 and DH2,109 which avoid double counting of the dispersion energy, are also available. These methods were used to model the adsorption of various molecules on graphene with quite good accuracy.110–112 A variant of the TB method incorporating an a posteriori dispersion correction has also been introduced, which performed well in the modelling of hydrogen physisorption on PAH and graphene and in predicting the bulk properties of graphite.113
4. Empirical methods
Whereas advanced quantum chemical methods provide highly accurate descriptions of systems comprising a few tens of atoms, molecular mechanics (MM) can be used to perform calculations on systems comprising thousands of atoms (Fig. 5) such as nucleic acids, proteins, and nanostructures. Of course, this advantage is counterbalanced by many simplifications and limitations resulting from the omission of the electronic degrees of freedom: molecular mechanics only accounts for the motions of nuclei. In molecular mechanics, the system is considered to be an ensemble of beads and springs that are held together by simple harmonic forces. The core of the molecular mechanics calculation is a force field (also known as an empirical potential) consisting of a set of equations and some associated parameters that are used to describe the system's energetics. The resulting energy Eff is calculated as the sum of several terms (eqn (1)) whose form and number is determined by the method's degree of simplification:Eff = Ebonded + EvdW + Eelec + (Epol) + (Eother![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) terms), terms), | (1) |
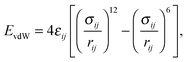 | (2) |
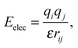 | (3) |
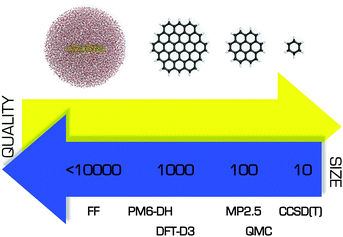 | ||
| Fig. 5 Comparison of several theoretical approaches with respect to the size of the system that can be treated efficiently and the quality of the resulting description. | ||
4.1 Current empirical force fields
Numerous force fields for various kinds of structures have been developed over the past few decades.116–119 Force fields are often very specialized and designed to target quite narrow groups of molecules. The greatest number of empirical calculations are performed on biological systems and so efforts to develop and refine force fields have largely focused on proteins, nucleic acids, and so on. While the transferability of parameters from one molecule to another is one of the principal assumptions of molecular mechanics models, their validity is far from clear when transferring parameters from biomolecules to nanomaterials. Fortunately, several modified force field parameters have been developed specifically for simulating graphene. Table 2 compares the non-bonded parameters for aromatic carbon atoms from the three most widely used biomolecular force fields to those from several modified potentials that were developed for modelling carbon allotropes and which have been used by various groups. Since in most cases the carbon atoms in graphene are treated as uncharged Lennard-Jones spheres, the molecular mechanics descriptions of the interactions between graphene and other molecules are governed exclusively by these non-bonded van der Waals parameters. Clearly, the listed force fields differ quite significantly with respect to these parameters, so it is important to choose a force field carefully if planning to use molecular mechanics to study graphene or its derivatives.4.2 Approximations employed by empirical force fields
The advantage of the molecular mechanics approach over QM models is its simplicity and low computational cost (Fig. 5). Unfortunately, its approximations mean that many phenomena cannot be explicitly accounted for by the FFs. The problem of the quadrupole moment has already been mentioned, but there are other interactions that would be challenging or impossible to describe with a classical force field. These include the charge transport involved in many of graphene's intermolecular interactions, explicit polarization, and the charge redistribution caused by wrinkling of a graphene surface.The neglect of polarization interactions is perhaps the most serious deficiency of common pairwise additive force fields when modelling graphene and its derivatives. Conventional FFs treat electrostatic interactions using effective partial charges that are constructed to match electrostatic potentials obtained from QM calculations. The point charges are located on the atomic centres and are constant (i.e. conformation- and time-independent). Consequently, it is impossible for the FF to react to changes in the molecular environment or to describe the way different solvents affect various interactions. In some force fields this problem is partly solved by adding an explicit term for electronic polarization. The contribution of polarization may be especially important in the case of nanomaterials, and it can be accounted for in several ways. A frequently used and technically simple option is the classical Drude model (the so-called “charge on spring” model), where an additional particle is attached to the atom. The particle has its own charge and, along with its attached atom, generates an induced dipole moment that depends on the external field. More detailed descriptions of the Drude model and its implementation can be found elsewhere.124 The Drude methodology was used by Ho et al.,125 who studied the effect of graphene polarization on the structural properties of water molecules at a graphene–water interface. Their results suggested that the explicit inclusion of polarizability had no significant effects on the dynamics of the graphene–water system, and that the effect became even smaller for charged graphene. However, larger effects might be expected for ions and their arrangement near the graphene surface. A similar way of including polarizability is the rigid rod model.126 Like the Drude model, this approach involves attaching a virtual interaction site to the atom, but the assigned charge is kept at a fixed distance and is only permitted to rotate. The GRAPPA force field, which was specifically designed for simulations of water–graphitic interfaces, uses the rigid rod model.127 A third way of including polarization is to assign atomic polarizabilities to the atoms and then calculate the resulting induced dipoles, whose orientation is determined by the external field felt at each atomic site in the molecule. This approach was used by Schyman et al.128 in a study on the adsorption of water and ions on carbon surfaces including graphene, where the results obtained from polarizable and non-polarizable force fields were compared to quantum calculations. The authors suggested that the use of the polarizable force field substantially improved the description of graphene-like surfaces in the condensed phase.
Another drawback of current force fields is the pairwise additive approximation of the van der Waals interactions, where the resulting energy is calculated as a sum of contributions from individual pairs of atoms up to the cutoff distance. Many-body terms involving three or more atoms are not explicitly included. Although force fields are parameterized against experimental data and thus include many-body effects implicitly, in some cases it might be desirable to include at least three-body effects explicitly. In particular, many-body effects may be important for describing the behaviour of colloidal dispersions of nanomaterials or the intermolecular interactions of graphene sheets and nanotubes.57,129
Classical force fields do not allow bond cleavage and formation because they model bonds with harmonic potentials. This is sufficient for the study of various non-covalent modifications of graphene and other materials. However, a model capable of describing bond cleavage/formation is required for the study of any process involving chemical change such as chemisorption or chemical reactions. In such cases it is necessary to use methods that explicitly account for the system's electronic structure. Unfortunately, such methods can only be applied to relatively small model systems (Fig. 5). Empirical reactive force fields such as AIREBO,130 REBO,131 and ReaxFF132 were developed to enable the study of large reacting molecular systems. These force fields use the standard force field approximations but also include terms for bond formation and dissociation. A more detailed description of individual reactive force fields is beyond the scope of this review and can be found in the specialized literature.133,134
5. Nuclear motion
As electronic structure is within Born–Oppenheimer approximation solved separately and it was described in Sections 3 and 4, this section discusses methods that account for nuclear motion and can be used to estimate the associated physical–chemical quantities. Thermodynamic quantities (internal energy, enthalpy, entropy, etc.) for processes involving nuclear motion are typically obtained from molecular dynamics (MD) and Monte Carlo (MC) simulations that involve sampling configurational space. While the first method average time sequence of the required quantity, the latter collects values of the quantity corresponding to random configuration walk.135 Simulation methods that describe the studied system in terms of position and momentum vectors can be naturally extended to quantum versions (quantum MC and quantum MD) based on the nuclear wave function/density matrix as a central point.5.1 Molecular dynamics
Molecular dynamics (MD) simulations usually use the laws of classical mechanics such as Newton's equations of motion to study the time evolution (dynamics) of a system: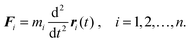 | (4) |
| Fi = −∇iE(r1, r2,…,rn). | (5) |
Once the resulting force is known, new positions and velocities at time t + δt are obtained by numerical solution of the equations. It is essential to select an appropriate time step δt. If a large time step is chosen the system may become unstable due to growing inaccuracies in the integration procedure. Time steps of 1–2 fs are typically used in classical MD simulations. This means that with current computer power it is possible to study dynamics on time scales of up to several microseconds. Perhaps the biggest benefit of this technique is its unique ability to provide information on the studied system at the atomistic level with femtosecond temporal resolutions. Moreover, specific techniques (for instance thermodynamic integration, potential of mean force, free energy perturbation, Jarzynski equality, etc.)137 have been developed for use alongside MD to estimate the thermodynamic properties of the studied systems, making MD simulations potentially useful for investigating the thermodynamic changes accompanying the non-covalent functionalization of graphene.
Sometimes, it is not possible to neglect quantum effects associated with movements of atoms and molecules (see Section 6.8 for examples). In such cases it is necessary to work with a nuclear wave function known as a wavepacket in vibrational dynamics, which must be discretized and propagated.138 The system-bath approximation is typically used when simulating quantum objects on graphene. In this approximation, the quantum system is represented by a wavepacket and the initial classical surface is implemented in a way that accounts for lattice dynamics and corrugation. A recent study on the physisorption of atomic hydrogen on graphitic surfaces139 compared four different quantum mechanical techniques: close coupling wavepacket (CCWP) and reduced density matrix (RDM) propagation methods as well as the perturbation (PT) and effective Hamiltonian (EH) theories. All four methods' descriptions of hydrogen sticking were in reasonably good agreement. The CCWP and RDM methods described desorption well, but only the RDM method correctly captured the decay of the total trapped population. On the other hand, the PT and EH methods were around two orders of magnitude faster than CCWP and RDM. In the case of chemisorption, which involves stronger atom–surface coupling, perturbation methods cannot be accurate and CCWP or RDM should be used;140 the latter may be preferable because it can describe many phonon processes. An alternative approach to fully quantum problems based on Feynman's path integral from statistical quantum mechanics can also be formulated. Path integral molecular dynamics (PIMD)141 has been used successfully to study the adsorption of hydrogen on graphene and coronene.142
5.2 Monte Carlo methods
Monte Carlo methods are based on stochastic sampling, i.e. random walks (cf. Section 3.4). Monte Carlo methods can be divided into methods which assume that classical mechanics is applicable (and energy is a continuous variable) and those which are based on the idea of discrete quantum energy levels.143 While the classical Monte Carlo (CMC) methods are less widely used than classical molecular dynamics in the modelling of graphene systems, quantum Monte Carlo (QMC) methods are commonly used to model strongly quantum interactions with graphene/graphite. The diffusion Monte Carlo (DMC) method is typically used to compute the ground vibrational state (T = 0 K) of quantum systems on graphene. Thermodynamic properties at nonzero temperatures are computed using path-integral Monte Carlo (PIMC) methods,144 which directly sample the density matrix using the path integral approach and replace integrals with averages over samples, as is also done in PIMD.6. Selected applications
6.1 Interactions of graphenes
Accurate descriptions of interactions with graphene are essential for understanding the structure and dynamics of graphene-like systems. The graphene–graphene interaction is of fundamental importance in many areas. Two graphene sheets can be stacked in a number of ways that differ in terms of the relative shifts of their basal planes. More attention is paid to the most stable AB-stacked arrangement, where half of the carbon atoms in the one layer sit directly above the centres of the hexagonal rings of the second layer. Nevertheless, determining the interlayer binding (cohesive) energy of graphene/graphite remains a significant challenge for theoreticians and experimentalists.145–149 Recently published benchmark data from thermal desorption spectroscopy suggested a value of 61 meV per atom150 and prompted further in-depth theoretical investigations into the interlayer cohesive energy and vdW interactions in graphene-like systems.151–155 AB-stacked graphene is also an attractive object of study because it is potentially amenable to band gap tuning.156Methods for modulating the band gap of graphene and its derivatives are highly desired because they make it possible to tune the material's electronic properties and could facilitate the design of a new generation of electronic devices. There are a number of ways in which the band gap of graphene could potentially be modified. One is to apply strain to the graphene.157,158 Alternatively, the adsorption of certain molecules on graphene induces symmetry breaking and hence band gap opening.159 It has been demonstrated that non-covalent functionalization of graphene with Br2 opens a relatively large band gap that can be further adjusted by using ultraviolet light to decompose the adsorbed Br2 molecules.160 A third option is the covalent modification of graphene. Fan et al. calculated that the electronic properties of graphene can be tuned by doping with either boron/nitrogen or joint BN domains.161 It was however shown that the chemical nature of B/N dopants in graphene significantly changes the final doping effect (Fig. 6).162 It has also been suggested that the reaction of graphene with atomic hydrogen is able to reversibly (by annealing) convert this highly conductive species completely into graphane, which is an insulator.163 Moreover, Singh and co-workers164 interspaced small saturated graphene islands in the graphane host and showed that the energy gap of these islands is determined by their size. Specifically, DFT calculations indicated that smaller islands had larger energy gaps. Another way of engineering the band gap of graphene is to use graphene nanoribbons of different widths; the narrower the ribbon, the wider the gap.165,166 This approach could be particularly useful in printing processes. Graphene fluorination opens the band gap in a similar way to hydrogenation,167,168 and it has been suggested that the magnitude of the band gap could be tuned by adjusting the degree of fluorination169,170 or by replacing fluorine with heavier halogens.171
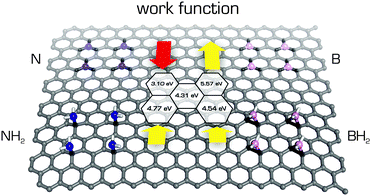 | ||
| Fig. 6 The work functions (Wfs) calculated using the PBE0 functional of B/N-doped graphenes vary with the chemical nature of doping.162 The Wf value of pristine graphene 4.31 eV (shown in the middle) increases in substitutionally B-doped graphene to 5.57 eV and decreases to 3.10 eV in substitutionally N-doped graphene. On the other hand, the Wf values increase in both graphenes with added –NH2 and –BH2 groups to 4.77 and 4.54 eV, respectively. | ||
6.2 Interactions of graphene with small molecules
Graphene was quickly identified as a powerful adsorbent172 whose interactions with various molecules often induce specific physicochemical responses that could be exploited in new types of sensors.4,5,173 Moreover, non-covalent functionalization of the graphene surface substantially increases its potential range of applications.9 Therefore the interactions of graphene with small molecules have been studied extensively, both experimentally and computationally, in order to obtain information on the strength and nature of such interactions (for some examples see Fig. 7). Using DFT symmetry adapted perturbation theory (DFT-SAPT),174 which enables the decomposition of interaction energy into meaningful components, i.e., coulombic, polarization, dispersion terms etc., Lazar and coworkers showed that the adsorption of organic molecules was driven mostly by London dispersive forces.12 The same conclusion had previously been drawn in a study on the adsorption of water molecules to graphene.175 The adsorbates, which bind to graphene weakly via London dispersion forces, change its electronic structure only slightly but reduce the mobility of its electrons,176 which can be exploited in sensing applications.4 Recently, Zhou et al.177 studied the physisorption of benzene and benzene derivatives on graphene, and suggested that the benzene derivatives adsorb more strongly than pure benzene regardless of their substituents' electronic properties.Molecules adsorbed on graphene may also affect its electronic properties by donating (n-doping) or withdrawing (p-doping) electrons and thereby shifting its Fermi level.178,179 The same also applies for graphene supports. DFT calculations provide clear information about electron fluxes and can directly determine which adsorbates/supports donate/withdraw electrons to/from graphene. This feature was also exploited to design graphene devices with a reasonably wide band gap, which can be used in graphene-based transistors.180,181 Such devices can be created from bilayer graphene sandwiched in between FeCl3 and K (Fig. 8). Calculations using the vdW-DF functional identified FeCl3 as an electron acceptor capable of providing p-doped graphene and K as a donor providing n-doped graphene.182
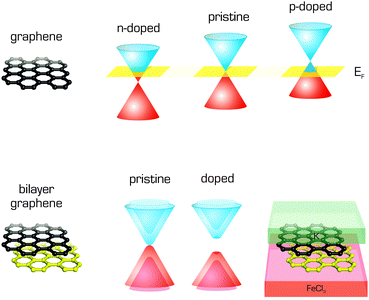 | ||
| Fig. 8 Band structure of single layer graphene showing p- and n-type doping with respect to the Fermi level, and band gap opening in bilayer graphene caused by doping. | ||
Many studies have investigated the binding energies of adsorbates to graphene using a very diverse portfolio of theoretical techniques. Unfortunately, the development of this field has been hampered by a lack of reliable experimental data, which makes it difficult to benchmark the performance of individual methods. Adsorption enthalpies are particularly suited for such comparisons because they correspond to well-defined processes, which can be modelled in a straightforward manner. Enthalpies are usually measured by temperature programmed desorption on highly oriented pyrolitic graphite (HOPG)183 or inverse gas chromatography on few-layered graphene.12,184 Calculations suggest that adsorption energies on single layer graphene are around ∼10% higher than those on few-layered graphene.184 The adsorption enthalpies derived from ab initio MD simulations using the vdW-DF (optB88-vdW) functional were in good agreement with experimental data, suggesting that this non-local functional describes the binding energies of dispersion-bound molecules to graphene reasonably well. It is worth noting that force field simulations (using the OPLS-AA force field) also accurately predicted the relative binding enthalpies of the studied molecules, indicating that the same force field could be used to obtain preliminary estimates for the interaction energies of large molecules with graphene. If highly accurate predictions of binding energies of biomacromolecules to graphene are required, one should include contributions stemming from many-body terms.129
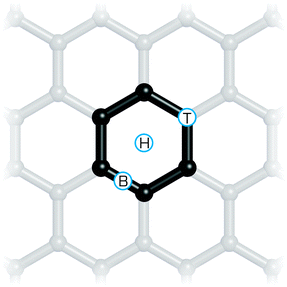
Preferred binding sites on the surface and energy differences between various binding sites can be estimated directly from theoretical calculations. Such information is important for understanding the friction on the graphene surface. Single atom adsorbates can bind at three sites (Fig. 9) referred to as on top (above the carbon atom perpendicular to the graphene sheet), on bond (above the carbon–carbon bond) and on hollow (above the centre of a “carbon hexagon”). Large molecules may have an even larger number of such high symmetry sites, as shown for tetracyanoethylene.185 Calculations can predict adsorption energies to individual sites and using the Boltzmann distribution law, the occupancy of individual sites can be estimated. Characterizing the potential energy surface of adsorbates sliding over the graphene increases the scope for understanding the friction that is generated. For example, calculations of this profile explained the contraintuitive increase in friction observed in a Pt atomic force microscopy tip moving over a graphene surface after fluorination.186
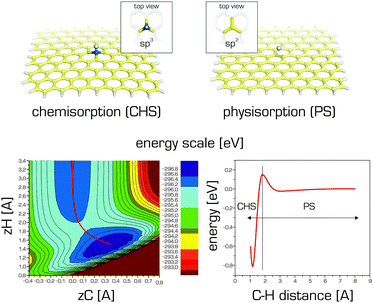
The strength of adsorption may depend not only on the adsorbate but also on its concentration and topology (the relative positions of individual adsorbates on the graphene surface). This indicates that the adsorbates significantly change the electronic structure of graphene and its binding involves some degree of covalent binding (chemisorption). The binding of fluorine or hydrogen atoms to graphene illustrates this phenomenon well.10 The bond dissociation energy of fluorine atoms at low concentration is only around 50 kcal mol−1 whereas in fully fluorinated graphene (fluorographene or graphene fluoride) it is 112 kcal mol−1.187 The attachment of a fluorine atom to a carbon atom changes its sp2 hybridization state to sp3, inducing local structural buckling (cf.Fig. 10). The degree of structural changes correlates with the strength of binding, which is reflected in the high resolution XPS spectrum of the corresponding atom. Consequently, high resolution XPS spectra can be used to decipher information about the binding of such atoms.188
The abovementioned information indicates that there is no sharp distinction between physisorption (non-covalent functionalization) and chemisorption (covalent functionalization) to graphene. In general, the interaction curve of a given adsorbate with graphene will feature two minima: one corresponding to physisorption (also known as the precursor state) and the other to chemisorption.140,142,189 These minima may be separated by an activation barrier (Fig. 10).
Density functional theory and molecular dynamics were successfully used together to explore the adsorption of the amino acid leucine on graphene,190 revealing that under certain conditions leucine molecules adsorb spontaneously from solution. Moreover, it was suggested that the properties of the graphene could be tuned by controlling the orientation of the leucine molecules when they adsorbed. The adsorption of a somewhat larger tripeptide on graphene was studied by Camden et al.191 It was shown that the presence of water at the interface strongly influenced the peptide's binding and conformation, suggesting that the inclusion of explicit solvent molecules may be essential for a proper description of the properties of peptide systems on graphene. Furthermore, some organic molecules could form highly ordered self-assembled monolayers (SAM) and bilayers on the graphene surface. O'Mahony and coworkers192 used MD techniques to study the formation of alkylamine SAMs and the effect of different layer terminations on the adsorption of proteins on these platforms. It was suggested that alkylamine SAM assemblies could be used for instance for protein immobilization and exploited in targeted binding of specific molecules.
Molecular dynamics simulations appear to be useful for studying the wetting properties of graphene (and are widely used for this purpose), which are the subject of considerable ongoing debate.193,194 The surface tension of graphene should be measured on free standing graphene, which is still quite challenging to achieve experimentally because graphene is usually prepared on a support and may be contaminated by adsorbates from the atmosphere.195 On the other hand, such conditions are readily accessible in molecular simulations, which can estimate the contact angle on pure and free standing graphene.196 The hydrophobicity of graphene is crucial for many of its potential applications (in nanomedicine, sensing, filtration, surface coatings etc.) and depends on many variables such as the purity195 of the graphene sheet and the presence of defects197,198 as well as the nature of the underlying support, whose wetting properties may affect (and be affected by) that of the graphene; this phenomenon is referred to as the wetting transparency of graphene.199,200 Li and coworkers201 suggested that graphene and other graphitic surfaces may even be slightly hydrophilic due to the adsorption of hydrocarbons commonly present in the air. Detailed studies on this behaviour could lead to the design of novel functional devices.202
6.3 Interactions of graphene with biomacromolecules
A molecular-level understanding of nucleic acids' and proteins' conformational behaviour near graphene-like supports may be important in the design and optimization of new nanoscale devices. Such interactions could be important in nanomedicine, where graphene or its derivatives could act as enzymatic inhibitors,203 or in sensing since a variety of graphene-based sensors relying on different physicochemical principles have been proposed (Fig. 11).204 One should bear in mind that molecules proposed for sensing applications have to preserve their native structure upon adsorption to graphene to maintain their function. It was shown that it is theoretically feasible to construct very sensitive graphene devices for ssDNA sequencing as a rapid and cost-effective alternative to current techniques.205 Moreover, MD simulations of nucleic acid bases in solution suggest that graphene–base interactions are stronger than base–base stacking.206 It has also been observed that DNA bases interact strongly with graphene207–209 and that interactions with graphene can induce short DNA duplexes to partially unfold, mainly from the ends.207 Such behaviour has also been reported for double stranded siRNA.210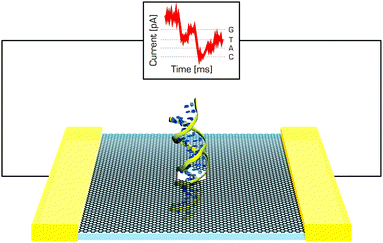 | ||
| Fig. 11 DNA passing through the graphene nanopore may induce changes in the current, which could be used in DNA sequencing. | ||
6.4 Graphene and metals
The interactions of metals with graphene are very interesting, and complex. Naturally, graphene interacts with solid metals211 in electrical circuits,212 in graphene coated metals213 and during its synthesis by chemical vapour deposition.214–218 The interactions of metal nanoparticles with graphene are also very important because graphene provides a suitable platform on which to anchor such nanoparticles for catalytic, photocatalytic and sensor applications.219–223 Moreover, graphene is being considered as a potential replacement for the widely used graphite anodes of lithium (and more generally, alkali metal) ion batteries, because it is suggested to offer a higher lithium ion storage capacity and to reduce charging times.224,225 Numerous theoretical studies dealing with the adsorption and diffusion of alkali metal ions on pristine and functionalized graphene226–229 as well as the positive influence of graphene defects on storage capacity225,230 can be found in the literature. Current progress in the use of graphene in energy applications and challenges for the field have been nicely summarized in recent reviews.231,232 Both individual metal atoms and small clusters may bond to graphene, altering its electronic and magnetic properties.227,233,234 It was suggested that graphene decorated with heavy adatoms could turn into a giant topological insulator,235 which might be used in magnetic storage devices.236,237 However, the correct description of magnetocrystalline anisotropy requires the usage of hybrid functionals238,239 and the inclusion of spin–orbit coupling.233 The nature of the metal–graphene interaction may be anywhere between non-covalent and partially covalent,240–242 indicating that any computational method used to study these interactions must reliably describe both London dispersive forces and chemical bonding.243,244 For catalytic applications involving bond-breaking and bond formation, it is also necessary to use methods that do not suffer from the electron self-interaction error, which leads to an underestimation of reaction barriers. Explicit relativistic effects245 should also be taken into account, especially when considering the interactions of heavy metals with graphene. Finally, when considering the interactions between metal adatoms and graphene, it is important to account for the spin-states of the metal and to be aware that these may change on binding.856.5 Hybrid carbon systems
The combination of graphene with other carbon allotropes such as nanotubes and fullerenes has opened up a new set of nanomaterials with many potential applications in areas such as printed electronics, conductive inks, reinforcement of polymers, etc. Computational modelling is playing an increasingly central role in studies on nanostructures because it enables the straightforward study of precisely defined structural motifs (joints) and because its atomistic resolution can help to elucidate unknown mechanisms and properties (Fig. 12). Interactions with fullerenes (mostly C60) are of particular interest. MD simulations have shown that fullerenes could potentially be used to detect defects on graphene. He et al.246 used C60 molecules to induce controlled ripples on the graphene sheet whose diffraction and interference can reveal cracks and defects on the surface. Several simulations of the diffusion of C60 molecules on graphene were performed at a constant temperature and with a temperature gradient.247,248 Moreover, Peng et al.249 suggested that C60/graphene composites could be used for gas purification especially for some binary mixtures. Numerous computational studies on graphene-hybrid systems among other things are discussed in the recent review published by Zhang et al., which focuses primarily on the computational characterization and simulation of graphene-based materials.250 It was recently demonstrated that it may be possible to combine graphene and carbon nanotubes in novel composite materials in which the graphene spontaneously rolls up around the nanotube or enters its interior.251–254 Graphene can also interact with carbon nanotubes to form 3D pillared structures where individual graphene sheets are separated by perpendicularly oriented carbon nanotubes. MD techniques were used to study the mechanical and thermal properties of these nano-networks,255,256 and there is computational evidence that such pillared graphene structures could be used in gas separation257 or hydrogen storage.258 Finally, Georgakilas et al.259 dispersed graphene sheets in aquatic media using hydrophilic functionalized carbon nanotubes and produced highly conductive graphene ink. MD simulations suggested that the formation of aggregates from graphene and hydroxyphenyl-functionalized carbon nanotubes was kinetically controlled and led to a stable colloid dispersion.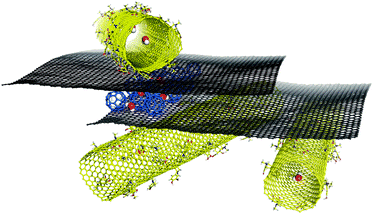 | ||
| Fig. 12 Molecular modelling may provide unique molecular insight into the structures of graphene hybrid materials, which in turn may help us to design new functional nanosystems. | ||
6.6 Graphene derivatives
While the properties of pristine graphene have attracted great interest, modified graphene derivatives may be even more interesting, at least in certain applications. The derivative that has attracted most attention is graphene oxide (GO). One obstacle to the modelling of GO stems from its complex structure, which contains epoxy, hydroxyl and carboxy groups. Even the composition of GO is quite uncertain and may depend on the conditions applied in its preparation.260 Some models have been developed for studying the structure of GO, the most well-known and widely used of which is that of Lerf and Klinowski.261,262 This model suggests that alcohol and epoxy groups are distributed randomly on the basal plane while the carboxyl groups are located on the edges. The interactions of nucleobases and several amino acids with GO were studied computationally by Vovusha et al.263 It has been shown that complexes with GO are mainly stabilized by hydrogen bonding, in contrast with graphene complexes, which are stabilized mainly through dispersion interactions. Recently, Shih et al. used both experiments and molecular dynamics to study GO in solution264 and to analyse its aggregation as a function of the pH and the protonation of its functional groups. They observed that at low pH values, GO became less hydrophilic due to protonation and formed sandwich-like aggregates in which individual sheets were separated by a confined water layer. However, separate sheets were preferred at higher pH values. Other articles have examined the electrical, structural and chemical changes accompanying GO reduction,265,266 and a few recent atomistic works have investigated the effect of different reducing atmospheres on the reduction of GO, producing the results that complemented experimental investigations.267,268 In addition, two molecular dynamics studies investigated this material's unusual mechanical properties.194,269 Another interesting class of GO-based materials with diverse potential applications are the graphene oxide framework (GOF) materials. GOF is a porous material first synthesized in 2011 that consists of GO sheets connected by linkers. Nicolaï et al. developed molecular mechanics parameters for this material and used them to investigate its dynamic properties.270 They suggested that the density of linkers connecting the GO layers can be used to tune the diffusion properties of GOF materials.Other graphene derivatives such as graphane and fluorographene have also been studied extensively by computational means. Graphane was predicted as a graphene derivative on the basis of DFT calculations.271 Fluorographene and other graphene halides have been studied in some detail:272 different investigations have focused on their band gaps and optical transitions,273 the insulating properties of fluorographene167,274 and the broad UV/VIS photoluminescence band observed experimentally (Fig. 13).275 It should however be noted that despite the use of computational methods that account for electron–electron and electron–hole correlation effects276,277 as well as the potential role of defects,98 it has not been possible to achieve satisfactory agreement between the computational results obtained to date and all of the available experimental data for fluorographene. Graphene-based materials have also been suggested for energy storage, fuel cells, and photovoltaic applications. The current state of computational chemistry methods for studying graphene-based energy materials is summarized in a review by Hughes et al.231 Furthermore, there is an intense effort led by the U.S. Department of Energy (DOE) to design novel materials for molecular storage (mainly molecular hydrogen) using graphene derivatives. Numerous computational studies have investigated the molecular interactions of hydrogen with pristine graphene and doped and substituted graphene materials with the aim of enhancing the physisorption of molecular hydrogen and increasing the adsorption capacity of these materials.72,278–281
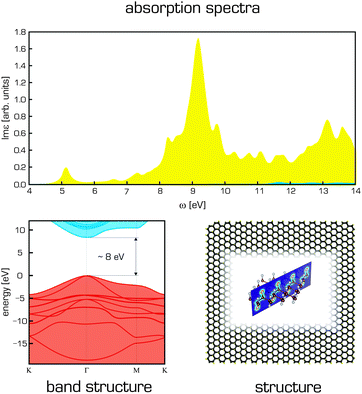 | ||
| Fig. 13 Structure of fluorographene is shown together with its electronic band structure (calculated using GW(PBE)) and BSE@GW(PBE) adsorption spectra for light polarization parallel (yellow) and perpendicular (blue) to the surface plane.276 | ||
6.7 Reactivity of graphene and graphene derivatives
Computational studies can also provide unique insights into the mechanisms underpinning the chemical modification, i.e., reactivity, of graphene and its derivatives. For example, a study on cycloaddition reactions involving graphene predicted them to be thermodynamically favoured at edges whereas the surface was predicted to be unreactive.282,283 Very recently, fluorographene, which was once considered a nonreactive counterpart of Teflon, has been identified as a reactive material187,284 and a potential source of new graphene derivatives.189,285 Analyses of its mechanisms of reaction suggested that fully fluorinated graphene preferentially undergoes SN2-type substitutions.187 This finding poses new questions about the nature of the C–F bonds in fluorographene and fluorinated graphenes.188 DFT calculations suggested that two fluorine atoms were inserted into graphene simultaneously during its reaction with XeF2. It was also shown that fluorination on one side facilitated the addition of another fluorine atom on the opposite side.286 Computations can also help to clarify the stability of graphene derivatives such as graphane,271 graphene halides273 and graphene oxide.287 For example, although the structures and distributions of oxidized and unoxidized regions of GO are currently unclear, DFT studies conducted by Yang et al.288 suggest that oxidation loci in GO are highly correlated, which is inconsistent with some previously proposed models that assume a random distribution of oxidized groups on GO.6.8 Graphene and quantum systems
Finally, we comment on the delicate problems of very light and strongly quantum systems interacting with graphene and graphite. For such specific systems as H, H2, and He as well as clusters, nanodroplets, films and layers of these substances, a full quantum treatment of both electrons and nuclei is often unavoidable. Tunnelling effects noticeably alter adsorption and diffusion barriers289 while nuclear delocalization effects change classical optimal geometrical structures and prohibit traditional approaches to computing the quantum zero-point energy.290,291Most research efforts in this area have focused on the adsorption of hydrogen on graphene and graphite. A full quantum description of hydrogen and deuterium physisorption on graphite using an MP2 potential energy surface yielded sticking probabilities of the order of a few percent for collision energies of 0–25 meV.139,292,293 Sticking increased for collision energies close to those of the relevant diffraction resonances and was also enhanced by raising the surface temperature. Desorption time constants were in the range of 20–50 ps for a surface temperature of 300 K. In contrast, graphene supported on a silicone oxide substrate or suspended over a hole in the substrate exhibited different physisorption properties.294 The sticking probabilities of hydrogen on these stabilized membranes at 10 K were high (∼50%) at low collision energies (≤10 meV), i.e. significantly larger than those for graphite. This was attributed to the different nature of the lattice vibrations in the two cases. More recently, the adsorption of hydrogen on graphene and graphite,140 and on graphene and coronene142 was studied by the wavepacket propagation method and path integral molecular dynamics. As both physisorption and chemisorption minima are present on the adsorption curve of hydrogen on graphene (Fig. 10), the barrier height between both minima contributes to the chemisorption probability. The barrier, which includes van der Waals, zero-point energy, quantum tunnelling and finite temperature effects, is approximately half or quarter of the height of the barrier predicted by DFT-GGA methods (∼0.2 eV) for graphene. The overall chemisorption probability was about 20%.
The adsorption of molecular hydrogen is often studied because of graphene's potential for hydrogen storage (cf. Section 6.6). Kowalczyk et al.295 studied hydrogen in slit-like carbon nanopores at 77 K by grand canonical classical and path-integral Monte Carlo (PIMC) simulations. The volumetric density of stored energy in optimal carbon nanopores exceeded the DOE target for 2010 (45 kg m−3). For the narrow pores (pore width H ∈ [0.59–0.7] nm), the reduction of the quantum isosteric enthalpy of adsorption at zero coverage was around 50% in comparison to the classical one and quantum confinement-inducing polymer shrinking was observed. Isosteric heats of adsorption for H2, HD and D2 as functions of coverage, and adsorption isotherms on graphite were computed by Wang and Johnson296 using the grand canonical classical PIMC method and shown to agree well with experimental results. The properties of H2 molecules adsorbed between graphite layers were also analysed by PIMD at temperatures of 300 to 900 K.297 The storage capacities of carbon foams calculated by Yakobson et al.298 met material-based DOE targets and are comparable to the capacities of a bundle of well-separated open nanotubes of similar diameter. The authors also found that quantum effects appreciably changed the foams' adsorption properties and had to be taken into account. Recently, quantum effects and anharmonicity in the H2–Li+–benzene complex, a model for hydrogen storage materials, were studied299 at zero temperature by DMC and rigid body DMC simulations at DFT PES. H2 molecules were delocalized above the Li+–benzene system and H2 binding enthalpy estimates were between 12.4–16.5 kJ mol−1.
The importance of the substrate in understanding quantum films became evident with the detailed exploration of the phases of He and H2 on graphite, originating in the late 1960s (superfluidity, Bose–Einstein condensation, and idealized 2D bosonic gas are examples of fundamental phenomena of chemistry and physics). New phenomena occurring on the new 2D substrates have been envisaged opening new fundamental questions to address. While the phase behaviour of 4He and para-H2 films (predicted by the PIMC method) on one side and both sides of graphene300,301 is expected to be similar to that on graphite,302–304 the behaviour predicted on fluorographene and graphane is different, due to different symmetry of the interaction potentials, doubled number of adsorption sites and larger corrugation for the adatom.305–307 For instance, the ground state of the He film on graphite is a 2D crystal commensurate with the substrate (the √3 × √3 R30° phase), while 3He forms an anisotropic fluid and 4He superfluid on fluorographene and graphane at the low coverage.305 At higher coverage values both the incommensurate triangular solid and the commensurate state at filling factor 2/7 are found (Fig. 14). An interested reader may find more details on behaviour of monolayer quantum gases on graphene, graphane and fluorographene in the recent review (and references therein) by Reatto et al.308
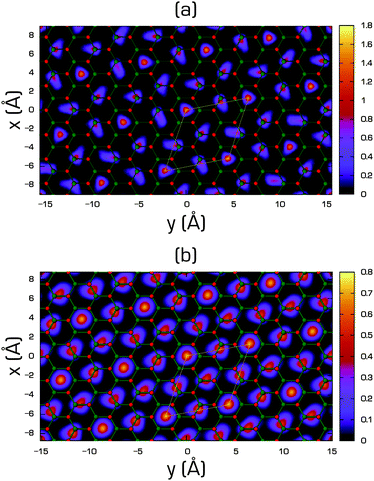 | ||
| Fig. 14 Helium density (in Å−2) on the x–y plane of the 2/7 phase of 4He on fluorographene (a) and on graphane (b) compared with the geometry of the substrate. Small red balls are centred on the position of fluorine/hydrogen atoms and the small green ones on the carbon atoms. Thin white lines enclose the unit cell of the commensurate 2/7 phase [reprinted with permission from ref. 305. Copyright 2012 by the American Physical Society]. | ||
7. Conclusions
Computational chemistry provides valuable atomistic insights into the properties of systems that are relevant in biodisciplines and nanoscience. While computational methods are constantly evolving, they have already succeeded in several tasks and are undoubtedly becoming an integral part of the basic research toolkit. Because of the on-going increases in available computing power, the sizes of the systems amenable to modelling and the lengths of the simulation times that can be handled are both increasing, meaning that computational methods will continue to get more powerful and important. We have provided several examples showing how computational methods can be used to obtain insights into the physical and chemical properties of complex molecular systems related to graphene.8. Perspectives
Despite all the great progress that has been made in modelling noncovalent interactions with graphene, many challenges remain to be addressed. There is still a need for a nonempirical theoretical method that reliably describes London dispersive forces without suffering from the electron-self interaction error and is also computationally affordable and easy to use. The recent progress in methods applying the adiabatic connection fluctuation–dissipation theorem is very promising in this respect. Robust testing of currently available methods is also highly desirable to assess their real performance. This task, is however, partially hampered by the lack of reliable experimental data addressing, e.g., the interaction energies between graphene and adsorbates.One of the key issues that need to be addressed in today's empirical force fields is the explicit inclusion of polarization. This should be very important especially in describing adsorption processes involving graphene and its derivatives. Another challenge is the correct description of the long-range (asymptotic) dispersive interactions by empirical potentials. Whereas the classical 1/R6 London formula results in a 1/R4 distance dependence of the interaction energy for a molecule interacting with an infinite graphene sheet, the real distance dependence may be significantly different.309,310 Because some empirically corrected DFT methods (e.g. those based on the DFT-D approach) use this simple dispersion model, they may also describe the asymptotic interactions incorrectly. Unfortunately, the impact of this error is not currently well understood.
Disclosure statement
The authors declare that there is no conflict of interest regarding the publication of this paper.Acknowledgements
The authors gratefully acknowledge project LO1305 of the Ministry of Education, Youths and Sports. MO acknowledges the Neuron fund to support science. We thank Matúš Dubecký, Piotr Błoński and Petr Lazar for helpful discussions.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- “Ten years in two dimensions.” Editorial, Nat. Nanotechnol., 2014, 9, 725 Search PubMed.
- F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652–655 CrossRef CAS PubMed.
- Y. Shao, J. Wang, H. Wu, J. Liu, I. A. Aksay and Y. Lin, Electroanalysis, 2010, 22, 1027–1036 CrossRef CAS.
- D. Rodrigo, O. Limaj, D. Janner, D. Etezadi, F. J. Garcia de Abajo, V. Pruneri and H. Altug, Science, 2015, 349, 165–168 CrossRef CAS PubMed.
- F. Traversi, C. Raillon, S. M. Benameur, K. Liu, S. Khlybov, M. Tosun, D. Krasnozhon, A. Kis and A. Radenovic, Nat. Nanotechnol., 2013, 8, 939–945 CrossRef CAS PubMed.
- S. P. Koenig, L. Wang, J. Pellegrino and J. S. Bunch, Nat. Nanotechnol., 2012, 7, 728–732 CrossRef CAS PubMed.
- V. Georgakilas, M. Otyepka, A. B. Bourlinos, V. Chandra, N. Kim, K. C. Kemp, P. Hobza, R. Zbořil and K. S. Kim, Chem. Rev., 2012, 112, 6156–6214 CrossRef CAS PubMed.
- D. W. Boukhvalov and M. I. Katsnelson, J. Phys.: Condens. Matter, 2009, 21, 344205 CrossRef CAS PubMed.
- M. Rubeš, P. Nachtigall, J. Vondrášek and O. Bludský, J. Phys. Chem. C, 2009, 113, 8412–8419 Search PubMed.
- P. Lazar, F. Karlický, P. Jurečka, M. Kocman, E. Otyepková, K. Šafářová and M. Otyepka, J. Am. Chem. Soc., 2013, 135, 6372–6377 CrossRef CAS PubMed.
- R. Podeszwa, J. Chem. Phys., 2010, 132, 044704 CrossRef PubMed.
- P. V. C. Medeiros, G. K. Gueorguiev and S. Stafström, Carbon, 2015, 81, 620–628 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. C, 2008, 112, 4061–4067 CAS.
- G. R. Jenness, O. Karalti and K. D. Jordan, Phys. Chem. Chem. Phys., 2010, 12, 6375–6381 RSC.
- M. Kocman, M. Pykal and P. Jurečka, Phys. Chem. Chem. Phys., 2014, 16, 3144–3152 RSC.
- S. Haldar, M. Kolář, R. Sedlák and P. Hobza, J. Phys. Chem. C, 2012, 116, 25328–25336 CAS.
- Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. T. McGovern, B. Holland, M. Byrne, Y. K. Gun'Ko, J. J. Boland, P. Niraj, G. Duesberg, S. Krishnamurthy, R. Goodhue, J. Hutchison, V. Scardaci, A. C. Ferrari and J. N. Coleman, Nat. Nanotechnol., 2008, 3, 563–568 CrossRef CAS PubMed.
- C. Shih and S. Lin, J. Am. Chem. Soc., 2010, 132, 14638–14648 CrossRef CAS PubMed.
- S. Lin, C.-J. Shih, M. S. Strano and D. Blankschtein, J. Am. Chem. Soc., 2011, 133, 12810–12823 CrossRef CAS PubMed.
- Z. Qin, M. Taylor, M. Hwang, K. Bertoldi and M. J. Buehler, Nano Lett., 2014, 29, 7271–7282 Search PubMed.
- V. V. Gobre and A. Tkatchenko, Nat. Commun., 2013, 4, 2341 Search PubMed.
- M. Pykal, K. Šafářová, K. Machalová Šišková, P. Jurečka, A. B. Bourlinos, R. Zbořil and M. Otyepka, J. Phys. Chem. C, 2013, 117, 11800–11803 CAS.
- F. London, Trans. Faraday Soc., 1937, 33, 8–26 RSC.
- S. Grimme, J. Chem. Phys., 2003, 118, 9095 CrossRef CAS.
- R. A. Distasio Jr. and M. Head-Gordon, Mol. Phys., 2007, 105, 1073–1083 CrossRef.
- T. Takatani, E. G. Hohenstein and C. D. Sherrill, J. Chem. Phys., 2008, 128, 124111 CrossRef PubMed.
- M. Pitoňák, J. Řezáč and P. Hobza, Phys. Chem. Chem. Phys., 2010, 12, 9611–9614 RSC.
- M. Pitoňák, P. Neogrády, J. Černý, S. Grimme and P. Hobza, ChemPhysChem, 2009, 10, 282–289 CrossRef PubMed.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- K. E. Riley, M. Pitonák, P. Jurecka and P. Hobza, Chem. Rev., 2010, 110, 5023–5063 CrossRef CAS PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- C. J. Cramer, Essentials of Computational Chemistry: Theories and Models, John Wiley & Sons, New York, 2nd edn, 2004 Search PubMed.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252 CrossRef CAS.
- P. L. Fast, M. L. Sanchez and D. G. Truhlar, J. Chem. Phys., 1999, 111, 2921–2926 CrossRef CAS.
- S. K. Min, E. C. Lee, H. M. Lee, D. Y. Kim, D. Y. Kim and K. S. Kim, J. Comput. Chem., 2008, 29, 1208–1221 CrossRef CAS PubMed.
- P. Jurečka and P. Hobza, J. Am. Chem. Soc., 2003, 125, 15608–15613 CrossRef PubMed.
- J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2013, 9, 2151–2155 CrossRef PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- M. Mentel and E. J. Baerends, J. Chem. Theory Comput., 2014, 10, 252–267 CrossRef PubMed.
- I. Shin, M. Park, S. K. Min, E. C. Lee, S. B. Suh and K. S. Kim, J. Chem. Phys., 2006, 125, 234305 CrossRef PubMed.
- C. Müller and B. Paulus, Phys. Chem. Chem. Phys., 2012, 14, 7605–7614 RSC.
- A. Erba, S. Casassa, L. Maschio and C. Pisani, J. Phys. Chem. B, 2009, 113, 2347–2354 CrossRef CAS PubMed.
- C. Pisani, M. Busso, G. Capecchi, S. Casassa, R. Dovesi, L. Maschio, C. Zicovich-Wilson and M. Schütz, J. Chem. Phys., 2005, 122, 094113 CrossRef CAS PubMed.
- M. Marsman, A. Grüneis, J. Paier and G. Kresse, J. Chem. Phys., 2009, 130, 184103 CrossRef CAS PubMed.
- M. Del Ben, J. VandeVondele and B. Slater, J. Phys. Chem. Lett., 2014, 5, 4122–4128 CrossRef CAS PubMed.
- G. H. Booth, A. Grüneis, G. Kresse and A. Alavi, Nature, 2013, 493, 365–370 CrossRef CAS PubMed.
- S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CrossRef CAS.
- S. Kristyán and P. Pulay, Chem. Phys. Lett., 1994, 229, 175–180 CrossRef.
- P. Hobza, J. Šponer and T. Reschel, J. Comput. Chem., 1995, 16, 1315–1325 CrossRef CAS.
- P. Jurečka, J. Černý, P. Hobza and D. R. Salahub, J. Comput. Chem., 2007, 28, 555–569 CrossRef PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- A. Tkatchenko, R. A. Distasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- A. Tkatchenko, Adv. Funct. Mater., 2015, 25, 2054–2061 CrossRef CAS.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS PubMed.
- S. Kozuch, D. Gruzman and J. M. L. Martin, J. Phys. Chem. C, 2010, 114, 20801–20808 CAS.
- T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397–3406 RSC.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- K. Lee, É. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101 CrossRef.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef PubMed.
- O. A. Vydrov and T. van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- D. Langreth and J. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1977, 15, 2884–2901 CrossRef.
- A. Tkatchenko, Adv. Funct. Mater., 2015, 25, 2054–2061 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- M. Kocman, P. Jurečka, M. Dubecký, M. Otyepka, Y. Cho and K. S. Kim, Phys. Chem. Chem. Phys., 2015, 17, 6423–6432 RSC.
- J. Harl, L. Schimka and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 115126 CrossRef.
- T. Olsen, J. Yan, J. J. Mortensen and K. S. Thygesen, Phys. Rev. Lett., 2011, 107, 156401 CrossRef PubMed.
- F. Karlický, P. Lazar, M. Dubecký and M. Otyepka, J. Chem. Theory Comput., 2013, 9, 3670–3676 CrossRef PubMed.
- H. Eshuis, J. E. Bates and F. Furche, Theor. Chem. Acc., 2012, 131, 1084 CrossRef.
- X. Ren, P. Rinke, C. Joas and M. Scheffler, J. Mater. Sci., 2012, 47, 7447–7471 CrossRef CAS.
- L. Hedin, Phys. Rev., 1965, 139, A796 CrossRef.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289–320 CrossRef CAS PubMed.
- A. Heßelmann and A. Görling, Mol. Phys., 2010, 108, 359–372 CrossRef.
- A. Heßelmann and A. Görling, Phys. Rev. Lett., 2011, 106, 093001 CrossRef PubMed.
- M. Dubecký, P. Jurečka, R. Derian, P. Hobza, M. Otyepka and L. Mitas, J. Chem. Theory Comput., 2013, 9, 4287–4292 CrossRef PubMed.
- J. Ma, D. Alf, A. Michaelides and E. Wang, J. Chem. Phys., 2009, 130, 154303 CrossRef PubMed.
- J. Ma, A. Michaelides and D. Alfè, J. Chem. Phys., 2011, 134, 134701 CrossRef PubMed.
- J. Granatier, M. Dubecký, P. Lazar, M. Otyepka and P. Hobza, J. Chem. Theory Comput., 2013, 9, 1461–1468 CrossRef CAS PubMed.
- L. Horváthová, M. Dubecký, L. Mitas and I. Štich, Phys. Rev. Lett., 2012, 109, 053001 CrossRef PubMed.
- P. Ganesh, J. Kim, C. Park, M. Yoon, F. A. Reboredo and P. R. C. Kent, J. Chem. Theory Comput., 2014, 10, 5318–5323 CrossRef CAS PubMed.
- H. Shin, S. Kang, J. Koo, H. Lee, J. Kim and Y. Kwon, J. Chem. Phys., 2014, 140, 114702 CrossRef PubMed.
- W. M. C. Foulkes, L. Mitas, R. J. Needs and G. Rajagopal, Rev. Mod. Phys., 2001, 73, 33–83 CrossRef CAS.
- M. Dubecký, Acta Phys. Slovaca, 2014, 64, 501–574 Search PubMed.
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902–3909 CrossRef CAS.
- J. J. P. Stewart, J. Comput. Chem., 1989, 10, 209–220 CrossRef CAS.
- J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173–1213 CrossRef CAS PubMed.
- F. Bloch, Z. Phys. Chem., 1928, 52, 555–600 CAS.
- J. C. Slater and G. F. Koster, Phys. Rev., 1954, 94, 1498–1524 CrossRef CAS.
- M. I. Katsnelson, Graphene: Carbon in Two Dimensions, Cambridge University Press, 1st edn, 2012 Search PubMed.
- G. Fiori, S. Lebègue, A. Betti, P. Michetti, M. Klintenberg, O. Eriksson and G. Iannaccone, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 153404 CrossRef.
- S. Yuan, M. Rösner, A. Schulz, T. O. Wehling and M. I. Katsnelson, Phys. Rev. Lett., 2015, 114, 047403 CrossRef PubMed.
- D. Porezag, T. Frauenheim, T. Köhler, G. Seifert and R. Kaschner, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 12947 CrossRef CAS.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260 CrossRef CAS.
- M. Elstner, P. Hobza, T. Frauenheim, S. Suhai and E. Kaxiras, J. Chem. Phys., 2001, 114, 5149–5155 CrossRef CAS.
- R. Balog, B. Jørgensen, L. Nilsson, M. Andersen, E. Rienks, M. Bianchi, M. Fanetti, E. Laegsgaard, A. Baraldi, S. Lizzit, Z. Sljivancanin, F. Besenbacher, B. Hammer, T. G. Pedersen, P. Hofmann and L. Hornekaer, Nat. Mater., 2010, 9, 315–319 CrossRef CAS PubMed.
- M. A. Ribas, A. K. Singh, P. B. Sorokin and B. I. Yakobson, Nano Res., 2011, 4, 143–152 CrossRef CAS.
- J. P. McNamara and I. H. Hillier, Phys. Chem. Chem. Phys., 2007, 9, 2362–2370 RSC.
- R. Sharma, J. P. McNamara, R. K. Raju, M. A. Vincent, I. H. Hillier and C. A. Morgado, Phys. Chem. Chem. Phys., 2008, 10, 2767–2774 RSC.
- A. Ramraj and I. H. Hillier, J. Chem. Inf. Model., 2010, 50, 585–588 CrossRef CAS PubMed.
- J. Řezáč, J. Fanfrlík, D. Salahub and P. Hobza, J. Chem. Theory Comput., 2009, 5, 1749–1760 CrossRef PubMed.
- M. Korth, J. Chem. Theory Comput., 2010, 6, 3808–3816 CrossRef CAS.
- M. Korth, M. Pitoňák, J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2010, 6, 344–352 CrossRef CAS PubMed.
- E. G. Gordeev, M. V. Polynski and V. P. Ananikov, Phys. Chem. Chem. Phys., 2013, 15, 18815–18821 RSC.
- M. A. Vincent and I. H. Hillier, J. Chem. Inf. Model., 2014, 54, 2255–2260 CrossRef CAS PubMed.
- S. Conti and M. Cecchini, J. Phys. Chem. C, 2015, 119, 1867–1879 CAS.
- L. Zhechkov, T. Heine, S. Patchkovskii, G. Seifert and H. A. Duarte, J. Chem. Theory Comput., 2005, 1, 841–847 CrossRef CAS PubMed.
- Y. Levy and J. N. Onuchic, Annu. Rev. Biophys. Biomol. Struct., 2006, 35, 389–415 CrossRef CAS PubMed.
- J. N. Coleman, Adv. Funct. Mater., 2009, 19, 3680–3695 CrossRef CAS.
- J. Wang, P. Cieplak and P. A. Kollman, J. Comput. Chem., 2000, 21, 1049–1074 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- N. Foloppe and A. D. MacKerell, Jr., J. Comput. Chem., 2000, 21, 86–104 CrossRef CAS.
- C. Oostenbrink, A. Villa, A. E. Mark and W. F. van Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676 CrossRef CAS PubMed.
- H. Ulbricht, G. Moos and T. Hertel, Phys. Rev. Lett., 2003, 90, 095501 CrossRef PubMed.
- L. Girifalco, M. Hodak and R. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 13104–13110 CrossRef CAS.
- A. Cheng and W. A. Steele, J. Chem. Phys., 1990, 92, 3867–3873 CrossRef CAS.
- H. Sun, J. Phys. Chem., 1998, 5647, 7338–7364 CrossRef.
- V. M. Anisimov, I. V. Vorobyov, B. Roux and A. D. MacKerell, J. Chem. Theory Comput., 2007, 3, 1927–1946 CrossRef CAS PubMed.
- T. a. Ho and A. Striolo, J. Chem. Phys., 2013, 138, 054117 CrossRef PubMed.
- F. Iori and S. Corni, J. Comput. Chem., 2008, 29, 1656–1666 CrossRef CAS PubMed.
- Z. E. Hughes, S. M. Tomásio and T. R. Walsh, Nanoscale, 2014, 6, 5438 RSC.
- P. Schyman, W. L. Jorgensen and P. F. Field, J. Phys. Chem. Lett., 2013, 4, 468–474 CrossRef CAS PubMed.
- R. A. Distasio Jr., O. A. von Lilienfeld and A. Tkatchenko, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14791–14795 CrossRef PubMed.
- S. Stuart, A. Tutein and J. Harrison, J. Chem. Phys., 2000, 112, 6472–6486 CrossRef CAS.
- D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni and S. B. Sinnott, J. Phys.: Condens. Matter, 2002, 14, 783–802 CrossRef CAS.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- T. Liang, Y. K. Shin, Y.-T. Cheng, D. E. Yilmaz, K. G. Vishnu, O. Verners, C. Zou, S. R. Phillpot, S. B. Sinnott and A. C. T. van Duin, Annu. Rev. Mater. Res., 2013, 43, 109–129 CrossRef CAS.
- M. Z. S. Flores, P. A. S. Autreto, S. B. Legoas and D. S. Galvao, Nanotechnology, 2009, 20, 465704 CrossRef CAS PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Elsevier, 2nd edn, 2001 Search PubMed.
- D. Marx and J. Hutter, NIC Series: Modern Methods and Algorithms of Quantum Chemistry, 2000, vol. 1, pp. 301–449 Search PubMed.
- W. F. van Gunsteren, X. Daura and A. E. Mark, Helv. Chim. Acta, 2002, 85, 3113–3129 CrossRef CAS.
- B. M. Garraway and K.-A. Suominen, Rep. Prog. Phys., 1995, 58, 365–419 CrossRef.
- B. Lepetit, D. Lemoine, Z. Medina and B. Jackson, J. Chem. Phys., 2011, 134, 114705 CrossRef PubMed.
- F. Karlický, B. Lepetit and D. Lemoine, J. Chem. Phys., 2014, 140, 124702 CrossRef PubMed.
- M. E. Tuckerman, NIC Series: Quantum Simulations of Complex Many-Body Systems: From Theory to Algorithms, 2002, vol. 10, pp. 269–298 Search PubMed.
- E. R. M. Davidson, J. Klimeš, D. Alfè and A. Michaelides, ACS Nano, 2014, 8, 9905–9913 CrossRef CAS PubMed.
- M. Lewerenz, NIC Series: Quantum Simulations of Complex Many-Body Systems: From Theory to Algorithms, 2002, vol. 10, pp. 1–24 Search PubMed.
- B. Bernu and D. M. Ceperley, NIC Series: Quantum Simulations of Complex Many-Body Systems: From Theory to Algorithms, 2002, vol. 10, pp. 51–61 Search PubMed.
- L. A. Girifalco and R. A. Lad, J. Chem. Phys., 1956, 25, 693–697 CrossRef CAS.
- L. Benedict, N. Chopra and M. Cohen, Chem. Phys. Lett., 1998, 2614, 490–496 CrossRef.
- N. L. Allinger, J. Am. Chem. Soc., 1977, 99, 8127–8134 CrossRef CAS.
- M. C. Schabel and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 7185–7188 CrossRef CAS.
- J.-C. Charlier, X. Gonze and J.-P. Michenaud, Europhys. Lett., 1994, 28, 403–408 CrossRef CAS.
- R. Zacharia, H. Ulbricht and T. Hertel, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155406 CrossRef.
- S. D. Chakarova-Käck, E. Schröder, B. I. Lundqvist and D. C. Langreth, Phys. Rev. Lett., 2006, 96, 146107 CrossRef PubMed.
- S. Grimme, J. Phys. Chem. C, 2007, 111, 11199–11207 CAS.
- L. Spanu, S. Sorella and G. Galli, Phys. Rev. Lett., 2009, 103, 196401 CrossRef PubMed.
- S. Lebègue, J. Harl, T. Gould, J. G. Ángyán, G. Kresse and J. F. Dobson, Phys. Rev. Lett., 2010, 105, 196401 CrossRef PubMed.
- X. Chen, F. Tian, C. Persson, W. Duan and N. Chen, Sci. Rep., 2013, 3, 3046 Search PubMed.
- J. B. Oostinga, H. B. Heersche, X. Liu, A. F. Morpurgo and L. M. K. Vandersypen, Nat. Mater., 2008, 7, 151–157 CrossRef CAS PubMed.
- Z. H. Ni, T. Yu, Y. H. Lu, Y. Y. Wang, Y. P. Feng and Z. X. Shen, ACS Nano, 2008, 2, 2301–2305 CrossRef CAS PubMed.
- G. Gui, J. Li and J. Zhong, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075435 CrossRef.
- J. Berashevich and T. Chakraborty, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 033404 CrossRef.
- X. Fan, L. Liu, J. L. Kuo and Z. Shen, J. Phys. Chem. C, 2010, 114, 14939–14945 CAS.
- X. Fan, Z. Shen, A. Q. Liu and J.-L. Kuo, Nanoscale, 2012, 4, 2157–2165 RSC.
- P. Lazar, R. Zbořil, M. Pumera and M. Otyepka, Phys. Chem. Chem. Phys., 2014, 16, 14231–14235 RSC.
- D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610–613 CrossRef CAS PubMed.
- A. K. Singh, E. S. Penev and B. I. Yakobson, ACS Nano, 2010, 4, 3510–3514 CrossRef CAS PubMed.
- L. Yang, C. H. Park, Y. W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2007, 99, 186801 CrossRef PubMed.
- M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 206805 CrossRef PubMed.
- R. Zbořil, F. Karlický, A. B. Bourlinos, T. A. Steriotis, A. K. Stubos, V. Georgakilas, K. Šafářová, D. Jančík, C. Trapalis and M. Otyepka, Small, 2010, 6, 2885–2891 CrossRef PubMed.
- D. K. Samarakoon, Z. Chen, C. Nicolas and X.-Q. Wang, Small, 2011, 7, 965–969 CrossRef CAS PubMed.
- J. T. Robinson, J. S. Burgess, C. E. Junkermeier, S. C. Badescu, T. L. Reinecke, F. K. Perkins, M. K. Zalalutdniov, J. W. Baldwin, J. C. Culbertson, P. E. Sheehan and E. S. Snow, Nano Lett., 2010, 10, 3001–3005 CrossRef CAS PubMed.
- Z. Wang, J. Wang, Z. Li, P. Gong, X. Liu, L. Zhang, J. Ren, H. Wang and S. Yang, Carbon, 2012, 50, 5403–5410 CrossRef CAS.
- F. Karlický, R. Zbořil and M. Otyepka, J. Chem. Phys., 2012, 137, 034709 CrossRef PubMed.
- J. Wang, Z. Chen and B. Chen, Environ. Sci. Technol., 2014, 48, 4817–4825 CrossRef CAS PubMed.
- Y. Liu, X. Dong and P. Chen, Chem. Soc. Rev., 2012, 41, 2283–2307 RSC.
- K. Szalewicz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 254–272 CrossRef CAS.
- G. R. Jenness and K. D. Jordan, J. Phys. Chem. C, 2009, 113, 10242–10248 CAS.
- L. Kong, A. Enders, T. S. Rahman and P. A. Dowben, J. Phys.: Condens. Matter, 2014, 26, 443001 CrossRef PubMed.
- P.-P. Zhou and R.-Q. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 12185–12193 RSC.
- S. K. Mali, J. Greenwood, J. Adisoejoso, R. Phillipson and S. De Feyter, Nanoscale, 2015, 7, 1566–1585 RSC.
- T. Hu and I. C. Gerber, J. Phys. Chem. C, 2013, 117, 2411–2420 CAS.
- F. Schwierz, Nat. Nanotechnol., 2010, 5, 487–496 CrossRef CAS PubMed.
- T. Ohta, A. Bostwick, T. Seyller, K. Horn and E. Rotenberg, Science, 2006, 313, 951–954 CrossRef CAS PubMed.
- J. W. Yang, G. Lee, J. S. Kim and K. S. Kim, J. Phys. Chem. Lett., 2011, 2, 2577–2581 CrossRef CAS.
- H. Ulbricht, R. Zacharia, N. Cindir and T. Hertel, Carbon, 2006, 44, 2931–2942 CrossRef CAS.
- P. Lazar, E. Otyepková, P. Banáš, A. Fargašová, K. Šafářová, L. Lapčík, J. Pechoušek, R. Zbořil and M. Otyepka, Carbon, 2014, 73, 448–453 CrossRef CAS.
- Y. H. Lu, W. Chen, Y. P. Feng and P. M. He, J. Phys. Chem. B, 2009, 113, 2–5 CrossRef CAS PubMed.
- Q. Li, X.-Z. Liu, S.-P. Kim, V. B. Shenoy, P. E. Sheehan, J. T. Robinson and R. W. Carpick, Nano Lett., 2014, 14, 5212–5217 CrossRef CAS PubMed.
- M. Dubecký, E. Otyepková, P. Lazar, F. Karlický, M. Petr, K. Čépe, P. Banáš, R. Zbořil and M. Otyepka, J. Phys. Chem. Lett., 2015, 6, 1430–1434 CrossRef PubMed.
- S. Zhou, S. D. Sherpa, D. W. Hess and A. Bongiorno, J. Phys. Chem. C, 2014, 118, 26402–26408 CAS.
- P. Lazar, C. K. Chua, K. Holá, R. Zbořil, M. Otyepka and M. Pumera, Small, 2015, 11, 3790–3796 CrossRef CAS PubMed.
- W. Qin, X. Li, W.-W. Bian, X.-J. Fan and J.-Y. Qi, Biomaterials, 2010, 31, 1007–1016 CrossRef CAS PubMed.
- A. N. Camden, S. a. Barr and R. J. Berry, J. Phys. Chem. B, 2013, 117, 10691–10697 CrossRef CAS PubMed.
- S. O'Mahony, C. O'Dwyer, C. A. Nijhuis, J. C. Greer, A. J. Quinn and D. Thompson, Langmuir, 2013, 29, 7271–7282 CrossRef PubMed.
- H. Zhou, P. Ganesh, V. Presser, M. C. F. Wander, P. Fenter, P. R. C. Kent, D. E. Jiang, A. A. Chialvo, J. McDonough, K. L. Shuford and Y. Gogotsi, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 035406 CrossRef.
- N. Wei, C. Lv and Z. Xu, Langmuir, 2014, 30, 3572–3578 CrossRef CAS PubMed.
- K. Xu and J. R. Heath, Nat. Mater., 2013, 12, 872–873 CrossRef CAS PubMed.
- F. Taherian, V. Marcon, N. F. A. van der Vegt and F. Leroy, Langmuir, 2013, 29, 1457–1465 CrossRef CAS PubMed.
- R. Raj, S. C. Maroo and E. N. Wang, Nano Lett., 2013, 13, 1509–1515 CAS.
- C.-J. Shih, M. S. Strano and D. Blankschtein, Nat. Mater., 2013, 12, 866–869 CrossRef CAS PubMed.
- J. Rafiee, X. Mi, H. Gullapalli, A. V. Thomas, F. Yavari, Y. Shi, P. M. Ajayan and N. A. Koratkar, Nat. Mater., 2012, 11, 217–222 CrossRef CAS PubMed.
- C.-J. J. Shih, Q. H. Wang, S. Lin, K.-C. C. Park, Z. Jin, M. S. Strano and D. Blankschtein, Phys. Rev. Lett., 2012, 109, 176101 CrossRef PubMed.
- Z. Li, Y. Wang, A. Kozbial, G. Shenoy, F. Zhou, R. McGinley, P. Ireland, B. Morganstein, A. Kunkel, S. P. Surwade, L. Li and H. Liu, Nat. Mater., 2013, 12, 925–931 CrossRef CAS PubMed.
- N. Patra, B. Wang and P. Král, Nano Lett., 2009, 9, 3766–3771 CrossRef CAS PubMed.
- X. Sun, Z. Feng, T. Hou and Y. Li, ACS Appl. Mater. Interfaces, 2014, 6, 7153–7163 CAS.
- J. Li, Y. Zhang, J. Yang, K. Bi, Z. Ni, D. Li and Y. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062707 CrossRef PubMed.
- S. K. Min, W. Y. Kim, Y. Cho and K. S. Kim, Nat. Nanotechnol., 2011, 6, 162–165 CrossRef CAS PubMed.
- V. Spiwok, P. Hobza and J. Řezáč, J. Phys. Chem. C, 2011, 115, 19455–19462 CAS.
- X. Zhao, J. Phys. Chem. C, 2011, 115, 6181–6189 CAS.
- M. Kabeláč, O. Kroutil, M. Předota, F. Lankaš and M. Šíp, Phys. Chem. Chem. Phys., 2012, 14, 4217–4229 RSC.
- Y. Cho, S. K. Min, J. Yun, W. Y. Kim, A. Tkatchenko and K. S. Kim, J. Chem. Theory Comput., 2013, 9, 2090–2096 CrossRef CAS PubMed.
- S. Mogurampelly, S. Panigrahi, D. Bhattacharyya, A. K. Sood and P. K. Maiti, J. Chem. Phys., 2012, 137, 054903 CrossRef PubMed.
- J. Wintterlin and M. L. Bocquet, Surf. Sci., 2009, 603, 1841–1852 CrossRef CAS.
- G. Giovannetti, P. A. Khomyakov, G. Brocks, V. M. Karpan, J. van Den Brink and P. J. Kelly, Phys. Rev. Lett., 2008, 101, 026803 CrossRef CAS PubMed.
- L. Hu, H. S. Kim, J. Y. Lee, P. Peumans and Y. Cui, ACS Nano, 2010, 4, 2955–2963 CrossRef CAS PubMed.
- P. W. Sutter, J.-I. Flege and E. A. Sutter, Nat. Mater., 2008, 7, 406–411 CrossRef CAS PubMed.
- X. Li, W. Cai, L. Colombo and R. S. Ruoff, Nano Lett., 2009, 9, 4268–4272 CrossRef CAS PubMed.
- Z. Sun, Z. Yan, J. Yao, E. Beitler, Y. Zhu and J. M. Tour, Nature, 2010, 468, 549–552 CrossRef CAS PubMed.
- Y. Zhang, L. Zhang and C. Zhou, Acc. Chem. Res., 2013, 46, 2329–2339 CrossRef CAS PubMed.
- P. Lacovig, M. Pozzo, D. Alfè, P. Vilmercati, A. Baraldi and S. Lizzit, Phys. Rev. Lett., 2009, 103, 166101 CrossRef PubMed.
- R. Kou, Y. Shao, D. Mei, Z. Nie, D. Wang, C. Wang, V. V. Viswanathan, S. Park, I. A. Aksay, Y. Lin, Y. Wang and J. Liu, J. Am. Chem. Soc., 2011, 133, 2541–2547 CrossRef CAS PubMed.
- C. Xu, X. Wang and J. Zhu, J. Phys. Chem. C, 2008, 112, 19841–19845 CAS.
- R. Muszynski, B. Seger and P. V. Kamat, J. Phys. Chem. C, 2008, 112, 5263–5266 CAS.
- P. V. Kamat, J. Phys. Chem. Lett., 2010, 1, 520–527 CrossRef CAS.
- S. Guo, D. Wen, Y. Zhai, S. Dong and E. Wang, ACS Nano, 2010, 4, 3959–3968 CrossRef CAS PubMed.
- J. Liu, Y. H. Xue, M. Zhang and L. M. Dai, MRS Bull., 2012, 37, 1265–1272 CrossRef CAS.
- X. Fan, W. T. Zheng and J. L. Kuo, ACS Appl. Mater. Interfaces, 2012, 4, 2432–2438 CAS.
- M. Khantha, N. A. Cordero, L. M. Molina, J. A. Alonso and L. A. Girifalco, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 1–8 CrossRef.
- K. T. Chan, J. B. Neaton and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235430 CrossRef.
- E. Lee and K. A. Persson, Nano Lett., 2012, 12, 4624–4628 CrossRef CAS PubMed.
- R. P. Hardikar, D. Das, S. S. Han, K. Lee and A. K. Singh, Phys. Chem. Chem. Phys., 2014, 16, 16502–16508 RSC.
- L.-J. Zhou, Z. F. Hou and L.-M. Wu, J. Phys. Chem. C, 2012, 116, 21780–21787 CAS.
- Z. E. Hughes and T. R. Walsh, Nanoscale, 2015, 7, 6883–6908 RSC.
- R. Raccichini, A. Varzi, S. Passerini and B. Scrosati, Nat. Mater., 2014, 14, 271–279 CrossRef PubMed.
- P. Lazar, J. Granatier, J. Klimeš, P. Hobza and M. Otyepka, Phys. Chem. Chem. Phys., 2014, 16, 20818–20827 RSC.
- P. V. C. Medeiros, G. K. Gueorguiev and S. Stafström, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 205423 CrossRef.
- J. Hu, J. Alicea, R. Wu and M. Franz, Phys. Rev. Lett., 2012, 109, 266801 CrossRef PubMed.
- A. Ehrlicher and J. H. Hartwig, Nat. Mater., 2011, 10, 12–13 CrossRef CAS PubMed.
- I. G. Rau, S. Baumann, S. Rusponi, F. Donati, S. Stepanow, L. Gragnaniello, J. Dreiser, C. Piamonteze, F. Nolting, S. Gangopadhyay, O. R. Albertini, R. M. Macfarlane, C. P. Lutz, B. A. Jones, P. Gambardella, A. J. Heinrich and H. Brune, Science, 2014, 344, 988–992 CrossRef CAS PubMed.
- P. Błoński and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 224418 CrossRef.
- I. Beljakov, V. Meded, F. Symalla, K. Fink, S. Shallcross, M. Ruben and W. Wenzel, Nano Lett., 2014, 14, 3364–3368 CrossRef CAS PubMed.
- P. A. Khomyakov, G. Giovannetti, P. C. Rusu, G. Brocks, J. van Den Brink and P. J. Kelly, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195425 CrossRef.
- J. Granatier, P. Lazar, M. Otyepka and P. Hobza, J. Chem. Theory Comput., 2011, 7, 3743–3755 CrossRef CAS PubMed.
- M. Stella, S. J. Bennie and F. R. Manby, Mol. Phys., 2015, 1–7 CrossRef.
- T. P. Hardcastle, C. R. Seabourne, R. Zan, R. M. D. Brydson, U. Bangert, Q. M. Ramasse, K. S. Novoselov and A. J. Scott, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195430 CrossRef.
- T. Olsen and K. S. Thygesen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 075111 CrossRef.
- M. Iliaš, V. Kellö and M. Urban, Acta Phys. Slovaca, 2010, 60, 259–391 Search PubMed.
- Y. Z. He, H. Li, P. C. Si, Y. F. Li, H. Q. Yu, X. Q. Zhang, F. Ding, K. M. Liew and X. F. Liu, Appl. Phys. Lett., 2011, 98, 2012–2015 Search PubMed.
- M. Neek-Amal, N. Abedpour, S. N. Rasuli, A. Naji and M. R. Ejtehadi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 051605 CrossRef CAS PubMed.
- a. Lohrasebi, M. Neek-Amal and M. R. Ejtehadi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 042601 CrossRef CAS PubMed.
- X. Peng, D. Cao and W. Wang, Ind. Eng. Chem. Res., 2010, 49, 8787–8796 CrossRef CAS.
- T. Zhang, Q. Xue, S. Zhang and M. Dong, Nano Today, 2012, 7, 180–200 CrossRef CAS.
- D. Xia, J. Xie, H. Chen, C. Lv, F. Besenbacher, Q. Xue and M. Dong, Small, 2010, 6, 2010–2019 CrossRef CAS PubMed.
- Z. Zhang and T. Li, Appl. Phys. Lett., 2010, 97, 2012–2015 Search PubMed.
- Y. Jiang, H. Li, Y. Li, H. Yu, K. M. Liew, Y. He and X. Liu, ACS Nano, 2011, 5, 2126–2133 CrossRef CAS PubMed.
- N. Patra, Y. Song and P. Král, ACS Nano, 2011, 5, 1798–1804 CrossRef CAS PubMed.
- V. Varshney, S. S. Patnaik, A. K. Roy, G. Froudakis and B. L. Farmer, ACS Nano, 2010, 4, 1153–1161 CrossRef CAS PubMed.
- L. Xu, N. Wei, Y. Zheng, Z. Fan, H.-Q. Wang and J.-C. Zheng, J. Mater. Chem., 2012, 22, 1435–1444 RSC.
- R. P. Wesołowski and A. P. Terzyk, Phys. Chem. Chem. Phys., 2011, 13, 17027–17029 RSC.
- G. K. Dimitrakakis, E. Tylianakis and G. E. Froudakis, Nano Lett., 2008, 8, 3166–3170 CrossRef CAS PubMed.
- V. Georgakilas, A. Demeslis, E. Ntararas, A. Kouloumpis, K. Dimos, D. Gournis, M. Kocman, M. Otyepka and R. Zbořil, Adv. Funct. Mater., 2015, 25, 1481–1487 CrossRef CAS.
- J. G. S. Moo, B. Khezri, R. D. Webster and M. Pumera, ChemPhysChem, 2014, 15, 2922–2929 CrossRef CAS PubMed.
- H. He, J. Klinowski, M. Forster and A. Lerf, Chem. Phys. Lett., 1998, 287, 53–56 CrossRef CAS.
- A. Lerf, H. He, M. Forster and J. Klinowski, J. Phys. Chem. B, 1998, 102, 4477–4482 CrossRef CAS.
- H. Vovusha, S. Sanyal and B. Sanyal, J. Phys. Chem. Lett., 2013, 4, 3710–3718 CrossRef CAS.
- C.-J. Shih, S. Lin, R. Sharma, M. S. Strano and D. Blankschtein, Langmuir, 2012, 28, 235–241 CrossRef CAS PubMed.
- C. Mattevi, G. Eda, S. Agnoli, S. Miller, K. A. Mkhoyan, O. Celik, D. Mastrogiovanni, C. Cranozzi, E. Carfunkel and M. Chhowalla, Adv. Funct. Mater., 2009, 19, 2577–2583 CrossRef CAS.
- A. Bagri, C. Mattevi, M. Acik, Y. J. Chabal, M. Chhowalla and V. B. Shenoy, Nat. Chem., 2010, 2, 581–587 CrossRef CAS PubMed.
- R. M. Abolfath and K. Cho, J. Phys. Chem. A, 2012, 116, 1820–1827 CrossRef CAS PubMed.
- B. Narayanan, S. L. Weeks, B. N. Jariwala, B. Macco, J.-W. Weber, S. J. Rathi, M. C. M. van de Sanden, P. Sutter, S. Agarwal and C. V. Ciobanu, J. Vac. Sci. Technol., A, 2013, 31, 040601 Search PubMed.
- J. Zhang and D. Jiang, Carbon, 2014, 67, 784–791 CrossRef CAS.
- A. Nicolaï, P. Zhu, B. G. Sumpter and V. Meunier, J. Chem. Theory Comput., 2013, 9, 4890–4900 CrossRef PubMed.
- J. O. Sofo, A. S. Chaudhari and G. D. Barber, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 153401 CrossRef.
- F. Karlický, K. Kumara Ramanatha Datta, M. Otyepka and R. Zbořil, ACS Nano, 2013, 7, 6434–6464 CrossRef PubMed.
- F. Karlický, R. Zbořil and M. Otyepka, J. Chem. Phys., 2012, 137, 034709 CrossRef PubMed.
- R. R. Nair, W. Ren, R. Jalil, I. Riaz, V. G. Kravets, L. Britnell, P. Blake, F. Schedin, A. S. Mayorov, S. Yuan, M. I. Katsnelson, H. M. Cheng, W. Strupinski, L. G. Bulusheva, A. V. Okotrub, I. V. Grigorieva, A. N. Grigorenko, K. S. Novoselov and A. K. Geim, Small, 2010, 6, 2877–2884 CrossRef CAS PubMed.
- K. J. Jeon, Z. Lee, E. Pollak, L. Moreschini, A. Bostwick, C. M. Park, R. Mendelsberg, V. Radmilovic, R. Kostecki, T. J. Richardson and E. Rotenberg, ACS Nano, 2011, 5, 1042–1046 CrossRef CAS PubMed.
- F. Karlický and M. Otyepka, J. Chem. Theory Comput., 2013, 9, 4155–4164 CrossRef PubMed.
- F. Karlický and M. Otyepka, Ann. Phys., 2014, 526, 408–414 CrossRef.
- S. Patchkovskii, J. S. Tse, S. N. Yurchenko, L. Zhechkov, T. Heine and G. Seifert, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10439–10444 CrossRef CAS PubMed.
- A. Du, Z. Zhu and S. C. Smith, J. Am. Chem. Soc., 2010, 132, 2876–2877 CrossRef CAS PubMed.
- K. C. Kemp, H. Seema, M. Saleh, N. H. Le, K. Mahesh, V. Chandra and K. S. Kim, Nanoscale, 2013, 5, 3149–3171 RSC.
- M. Seydou, K. Lassoued, F. Tielens, F. Maurel, F. Raouafi and B. Diawara, RSC Adv., 2015, 5, 14400–14406 RSC.
- Y. Cao, S. Osuna, Y. Liang, R. C. Haddon and K. N. Houk, J. Am. Chem. Soc., 2013, 135, 17643–17649 CrossRef CAS PubMed.
- I. K. Petrushenko, Monatsh. Chem., 2014, 145, 891–896 CrossRef CAS.
- K. E. Whitener, R. Stine, J. T. Robinson and P. E. Sheehan, J. Phys. Chem. C, 2015, 119, 10507–10512 CAS.
- V. Urbanová, K. Holá, A. B. Bourlinos, K. Čépe, A. Ambrosi, A. H. Loo, M. Pumera, F. Karlický, M. Otyepka and R. Zbořil, Adv. Mater., 2015, 27, 2305–2310 CrossRef PubMed.
- S. S. Lee, S. W. Jang, K. Park, E. C. Jang, J. Y. Kim, D. Neuhauser and S. Lee, J. Phys. Chem. C, 2013, 117, 5407–5415 CAS.
- S. Zhou and A. Bongiorno, Sci. Rep., 2013, 3, 2484 Search PubMed.
- J. Yang, G. Shi, Y. Tu and H. Fang, Angew. Chem., Int. Ed., 2014, 53, 10190–10194 CrossRef CAS PubMed.
- E. M. McIntosh, K. T. Wikfeldt, J. Ellis, A. Michaelides and W. Allison, J. Phys. Chem. Lett., 2013, 4, 1565–1569 CrossRef CAS PubMed.
- P. Svrčková, A. Vítek, F. Karlický, I. Paidarová and R. Kalus, J. Chem. Phys., 2011, 134, 224310 CrossRef PubMed.
- F. Calvo, F. Y. Naumkin and D. J. Wales, J. Chem. Phys., 2011, 135, 124308 CrossRef CAS PubMed.
- Z. Medina and B. Jackson, J. Chem. Phys., 2008, 128, 114704 CrossRef PubMed.
- V. Buch, J. Chem. Phys., 1989, 91, 4974 CrossRef CAS.
- B. Lepetit and B. Jackson, Phys. Rev. Lett., 2011, 107, 236102 CrossRef PubMed.
- P. Kowalczyk, P. A. Gauden, A. P. Terzyk and S. K. Bhatia, Langmuir, 2007, 23, 3666–3672 CrossRef CAS PubMed.
- Q. Wang and J. K. Johnson, Mol. Phys., 1998, 95, 299–309 CrossRef CAS.
- C. P. Herrero and R. Ramírez, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 174117 CrossRef.
- A. K. Singh, J. Lu, R. S. Aga and B. I. Yakobson, J. Phys. Chem. C, 2011, 115, 2476–2482 CAS.
- S. J. Kolmann, J. H. D'Arcy and M. J. T. Jordan, J. Chem. Phys., 2013, 139, 234305 CrossRef PubMed.
- Y. Kwon and D. M. Ceperley, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 224501 CrossRef.
- M. C. Gordillo, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 10–13 CrossRef.
- F. F. Abraham and J. Q. Broughton, Phys. Rev. Lett., 1987, 59, 64–67 CrossRef CAS PubMed.
- M. Pierce and E. Manousakis, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 3802–3814 CrossRef CAS.
- D. Sato, K. Naruse, T. Matsui and H. Fukuyama, Phys. Rev. Lett., 2012, 109, 235306 CrossRef CAS PubMed.
- M. Nava, D. E. Galli, M. W. Cole and L. Reatto, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 174509 CrossRef.
- L. Reatto, M. Nava, D. E. Galli, C. Billman, J. O. Sofo and M. V. Cole, J. Phys.: Conf. Ser., 2012, 400, 012010 CrossRef.
- M. Nava, D. E. Galli, M. W. Cole and L. Reatto, J. Low Temp. Phys., 2013, 171, 699–710 CrossRef CAS.
- L. Reatto, D. E. Galli, M. Nava and M. W. Cole, J. Phys.: Condens. Matter, 2013, 25, 443001 CrossRef PubMed.
- J. F. Dobson, A. White and A. Rubio, Phys. Rev. Lett., 2006, 96, 073201 CrossRef PubMed.
- T. Gould, E. Gray and J. F. Dobson, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 113402 CrossRef.
| This journal is © the Owner Societies 2016 |