Open Access Article
Open Access ArticleInitial reaction steps during flame synthesis of iron-oxide nanoparticles
Sebastian
Kluge
a,
Lei
Deng
b,
Omid
Feroughi
a,
Florian
Schneider
a,
Marina
Poliak
d,
Alexey
Fomin
d,
Vladimir
Tsionsky
de,
Sergey
Cheskis
d,
Irenäus
Wlokas
bc,
Igor
Rahinov
e,
Thomas
Dreier
ac,
Andreas
Kempf
bc,
Hartmut
Wiggers
ac and
Christof
Schulz
*ac
aIVG, Institute for Combustion and Gas Dynamics – Reactive Fluids, University of Duisburg-Essen, Duisburg, Germany. E-mail: Christof.schulz@uni-due.de
bIVG, Institute for Combustion and Gas Dynamics – Fluid Dynamics, University of Duisburg-Essen, Duisburg, Germany
cCENIDE, Center for Nanointegration Duisburg-Essen, University of Duisburg-Essen, Germany
dSchool of Chemistry, Tel Aviv University, Tel Aviv, Israel
eDepartment of Natural Sciences, The Open University of Israel, Raanana, Israel
First published on 7th May 2015
Abstract
Premixed, laminar H2/O2/Ar and CH4/O2/N2 low-pressure flat flames doped with iron pentacarbonyl (Fe(CO)5) were used to investigate the initial steps towards the formation of iron-oxide nanoparticles. The particles were extracted from the flame using a molecular beam sampling probe and the mass flow rate of condensed material was measured by a quartz crystal microbalance (QCM). It was observed that particles are already formed on the cold side of the flame, and vanish quickly once they pass through the flame front. To understand the process and assess the perturbations caused by the sampling probe, spatially resolved laser-based measurements of temperature, Fe and FeO concentration as well as molecular-beam sampling with particle mass spectrometry (PMS) were carried out. Numerical flow simulations of the synthesis flames, the reactor, and the sampling were performed and the simulations confirmed the experimental findings of very early particle formation. The detailed knowledge of the perturbation caused by invasive probing enabled further insight into the iron-oxide nanoparticle formation mechanism. From the results it is concluded that neither Fe atoms nor FeO molecules belong to the growth species of iron-oxide nanoparticles from flame synthesis.
Introduction
While micro-scale iron oxides in their different polymorph forms are widely used as red and brown pigments, iron-oxide nanoparticles have a wide range of advanced applications ranging from supercapacitors1 and lithium ion batteries,2 electromagnetic wave absorption3 to magnetic fluids, catalysis, biotechnology/biomedicine, magnetic resonance imaging, data storage, and environmental remediation.4 Wet-phase as well as gas-phase synthesis methods have been shown to manufacture iron oxides with specific properties in respect of the applications mentioned. Combustion synthesis provides an easy way to generate ultra-clean nanoparticles with tunable properties in scalable flow processes. By varying the flame conditions, a wide range of compositions and crystal structures can be realized including hematite (α-Fe2O3) maghemite (γ-Fe2O3), magnetite (Fe3O4), and wustite (FeO).5–7 Strobel et al.7 studied the spray-flame synthesis of iron oxides and found that both the equivalence ratio and the choice of precursor have an effect on the iron-oxide formation altering the particles between maghemite, magnetite and wustite. Buyukhatipoglu et al.6 synthesized hematite by increasing the flame temperature of their non-premixed flame.Despite the fact that many groups worldwide work on gas-phase synthesis of iron oxides, the initial steps taking place during particle formation and growth are only rudimentarily understood. For designing scalable combustion synthesis processes that reproducibly generate materials with well-defined properties, the individual processes of gas-phase reactions, interactions of intermediate species with combustion, particle nucleation, and growth must be understood in detail.
A frequently used precursor for production of iron and iron oxides is iron pentacarbonyl (Fe(CO)5) due to its purity and relatively high vapor pressure. Fe(CO)5 as an additive in flames has been the object of investigations since the 1920s, when it was applied as an anti-knock agent for fuels used in internal combustion engines. It was observed that nearly any addition of Fe(CO)5 strongly affects the flame's reaction kinetics. A good overview of recent publications on iron-containing compounds in flames was given by Wlokas et al.8 The decomposition kinetics9 of Fe(CO)5 and the formation of small clusters10 have been studied in shock tubes to provide input for modeling of the initial Fe(CO)5 pyrolysis and iron cluster formation.
Premixed low-pressure flat flames are suitable to investigate nanoparticle nucleation and growth where species concentrations and particle size can be measured as a function of the height above burner (HAB), while information about growth kinetics is available from a combination of measurements and simulations of the (ideally one-dimensional) flow.11
This paper discusses methods to characterize the initial steps towards particle formation by taking the example of iron-oxide nanoparticle synthesis from of Fe(CO)5. Two reactor systems and multiple measurement techniques are used to gather as much information as possible for the validation of fluid dynamics simulation and particle precursor kinetics. The Duisburg reactor (DU-R) was used to measure laser-induced fluorescence (LIF) of iron in combination with NO-LIF thermometry, particle mass spectrometry (PMS) and quartz crystal microbalance (QCM) measurements to determine iron atom concentration and temperature fields, particle size distribution, and aerosol mass loading, respectively, in a low-pressure flat flame. Besides for additional PMS and QCM measurements, the Tel Aviv reactor (TA-R) was used to measure temperature by OH-LIF and the concentration of FeO in the presence of particles using intra-cavity laser absorption spectroscopy (ICLAS). Experimental results are compared with simulations of fluid dynamics and species reactions covering the pyrolysis of Fe(CO)5, the formation of iron clusters, the interaction of iron-containing species with the flame radicals, and the formation of iron-oxide monomers.
Experimental
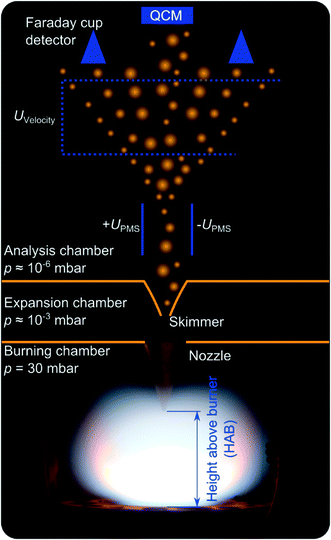
Iron-oxide nanoparticles are synthesized through the decomposition of Fe(CO)5 in almost one-dimensional, premixed, low-pressure flat flames of either H2/O2 diluted by argon (DU-R) or CH4/O2 diluted by N2 (TA-R). First experiments investigating iron-oxide formation from Fe(CO)5 trace back to PMS measurements conducted by Janzen et al.,5 and TEM images of typical particle size distributions as well as particle and agglomerate morphology are presented there. A few years later, Hecht et al.12 used Fe-LIF measurements to quantify the iron atom concentration downstream the burner head. In contrast to the previous investigations with a horizontal flow direction leading to unwanted convection, the orientation of the Duisburg reactor is now bottom-up following the recommendations of Weise et al.13 to avoid buoyancy effects. The main reactor chamber has a diameter of 100 mm with four windows enabling optical access. The water-cooled burner plate has a diameter of 36 mm. The fresh gas, constituting of 400 sccm H2, 400 sccm O2, and 600 sccm Ar is fed into the burner through a porous metal plate. The reactor used in Tel Aviv uses a top-to-bottom flame, stabilized on a McKenna burner14 having a 60 mm porous metal matrix.Properties of the flame-made materials in terms of size and the total amount of particles in the aerosol are determined in both reactors via molecular beam sampling (Fig. 1). At variable height above burner (HAB), the post-flame gas is sampled via a nozzle/skimmer setup and expands into the vacuum thus forming a particle-laden molecular beam.
The decomposition of the precursor and its influence on the flame chemistry can be studied by varying the distance of the burner head relative to the nozzle position. By replacing parts of the argon flow with a flow of Fe(CO)5 diluted in argon, the precursor concentration is varied between 0 and 200 ppm for the DU-R experiments. In the Tel Aviv reactor, precursor concentrations of 20–920 ppm are reached by adding 1–51 sccm of a mixture of Fe(CO)5 diluted in nitrogen to the flame gases.
In both reactors, particles within the gas are then either collected on a quartz-crystal microbalance (QCM)15 to study the deposition rate and thus the (relative) mass concentration of all condensable matter in the extracted gas, or they are measured with respect to their size distribution in a particle mass spectrometer.5 The PMS takes advantage of the fact that a significant fraction of the particles is singly charged. When passing a variable electric field, the particles get deflected according to their kinetic energy. Due to the narrow velocity distribution of the particles in the molecular beam the particle mass can be determined. With scanning the deflection voltage, the various particle sizes are subsequently swept across a Faraday cup charge detector and particle-size distributions are recorded.
In the absence of an electric field, all particles carried by the molecular beam hit the gold-coated crystal of the QCM and the mass of the deposited material is determined from its resonance frequency that shifts proportionally to the deposited mass. For each Fe(CO)5 concentration and measurement position, the resonance frequency of the quartz crystal is measured for several seconds. The slope of the frequency versus time is proportional to the mass deposition rate.
In parallel to PMS and QCM measurements, laser-based optical diagnostics are used to determine the spatial distribution of iron atoms (DU-R) and FeO molecules (TA-R) in the reactor chamber downstream the burner head. In addition, multiline laser-induced fluorescence (LIF) of NO (DU-R)16 and multiline OH-LIF (TA-R)17 are used for non-intrusive measurement of the gas temperature fields.
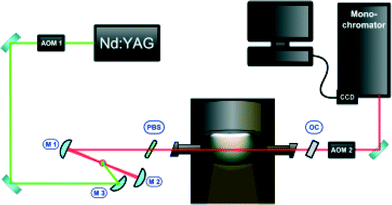
Intra-cavity laser absorption spectroscopy (ICLAS, cf.Fig. 2) is a method in which absorbing species are placed inside the cavity of a broadband laser. Due to the positive feedback mechanism in lasers, even minute quantities of a narrow-line absorber will produce holes in the spectrum where the laser output is partially quenched. The laser consists of a dye jet inside an astigmatically-compensated three-mirror folded cavity formed by M1, M2, and OC (output coupler). The central wavelength of this broadband laser source can be tuned by introducing a thin pellicle beam splitter (PBS) inside the cavity. The laser generation time tg, in the ICLAS is the time interval between the beginning of the laser generation and the sampling, which is controlled with the aid of two acousto-optic modulators (AOM1 and AOM2). The spectral output is analyzed with a high-resolution spectrograph. ICLAS is not sensitive to the broadband absorption by the nanoparticles, thus allowing monitoring FeO in a particle-laden environment.
The experimental conditions of both flame reactors are summarized in Table 1. The flames burn parallel to the gravitational axis to reduce buoyancy effects. To spatially extend the reaction zone, the pressure is kept at 30 mbar (DU-R) and 40 mbar (TA-R).
| Duisburg reactor (DU-R) | Tel Aviv reactor (TA-R) | |
|---|---|---|
| Flow rates/sccm | 400 H2, 400 O2 600 Fe(CO)5 in Ar | 450 CH4, 900 O2 1–51 Fe(CO)5 in N2 |
| Concentration Fe(CO)5 | 0–200 ppm | 20–920 ppm |
| Pressure | 30 mbar | 40 mbar |
| Orientation of the flame | Bottom to top | Top to bottom |
| Matrix diameter | 36 mm | 60 mm |
| Sampling nozzle/material | BeamDynamics model 2 0.5 mm orifice/nickel | Homemade 0.5 mm orifice/stainless steel |
| Applied measurements | PMS, QCM, Fe-LIF, multiline NO-LIF | PMS, QCM, FeO-ICLAS, multiline OH-LIF |
Modeling
Reaction mechanism
For a detailed description of the combustion process, the addition of the iron-oxide precursor must be taken into account as the presence of iron atoms strongly influences the flame chemistry. In lean conditions at low pressures, a flame-promoting effect is observed with an increased heat release from the flame.18 To capture these effects, the main reaction paths of flame radical and metal species interaction must be included in the reaction mechanism. Recently, Feroughi et al.19 developed a sub-mechanism of Fe(CO)5 reactions based on the mechanisms proposed by Wen et al.9 and Wlokas et al.8 This sub-mechanism covers the pyrolysis of Fe(CO)5, formation of initial iron clusters, the interaction of iron-containing species with the flame radicals, and the formation of iron-oxide monomers.For investigation of the Duisburg reactor (H2/O2/Ar flame), the iron sub-mechanism is merged with the C1 mechanism by Li et al.20 and contained 50 reacting species and 227 reactions. The reduced, skeletal mechanism employed for the CFD simulations is derived using a genetic algorithm method proposed by Sikalo et al.21 and contains 40 species and 66 reactions. The reduced mechanism is validated for laminar flame speeds, adiabatic flame temperatures, total iron-cluster mole fractions, and the molar fraction of iron oxide.
For investigation of the TA-R flame (CH4/O2/N2), the iron sub-mechanism is merged with the GRI 3.0 mechanism.22 For the 2D simulations, a skeletal mechanism was employed where the CH4/O2 branch was described by the DRM-19 mechanism,23 treating N2 as an inert species. The final skeletal mechanism contained 50 species and 140 reactions.
Simulation
The reacting flow is described by the conservation equations for mass, momentum, energy, and species. The mixture-averaged model for the diffusion of individual species properties is implemented into this framework due to the satisfactory accuracy and low computational effort. The laminar viscosity of the mixture is calculated from the equation developed by Wilke.24 The thermal diffusivity was considered as a fraction of thermal conductivity and heat capacity at constant pressure. The thermal conductivity was calculated following the equation introduced by Mathur et al.,25 and the heat capacity at constant pressure was treated in a mass-fraction-averaged formulation. The simulation framework is based on the open-source CFD software OpenFOAM.26 The model extensions and numerical methods are described in detail by Deng et al.27The CFD simulations are computationally very expensive and are therefore usually performed using a reduced, skeletal reaction mechanism. The error introduced by such reduced mechanisms mostly affects the resulting species concentrations while the velocity and temperature fields are predicted with high reliability. We hence used a combined two-step approach: We simulated the reactor in two dimensions with reduced chemistry using OpenFoam and corrected the results with detailed chemistry calculations from 1D simulations along a stream line27 using the open-source reaction kinetics software Cantera.28
A detailed simulation usually requires considerations of all geometric features. Here, a quasi-2D rotationally-symmetric computational domain was found to be sufficient to capture the influence caused by the metal housing of the reactor and the sampling probe for both experiments. However, there were some essential differences in the experiments which required separate sets of simulations to account for the deviation from one dimensionality of the perturbed flat flames. The computational domain of the Duisburg reactor is shown in Fig. 3 in a “to scale” sketch of the computational domain on the right side and a photo of the reactor including the burner and the probing nozzle on the left side. To capture the perturbations caused by the probing nozzle, simulations were carried out for five burner-probe distances at 2, 4, 6, 8, and 10 mm. The probe was assumed to be adiabatic27 while the outer boundary was isothermal at T = 300 K mimicking the heat losses through the reactor housing.
 | ||
| Fig. 3 The burner-probe configuration in the Duisburg rector (left: photo) and the corresponding computational geometry (right). | ||
A similar computational domain was chosen for the Tel Aviv reactor, where the distance from the burner axis to the reactor walls is much larger. However, the radial extent of the computational domain is smaller than the reactor diameter and thus an inlet–outlet boundary condition was applied allowing inflow of cooled-down gases into the domain.
Results
The intention of the investigations presented here is the characterization of the initial particle formation steps. Simple models describe particle formation in the gas phase by precursor decomposition, formation of condensable species and nucleation followed by coalescence and growth. However, gas-phase chemistry and particle formation is much more complex. Based on detailed physico-chemical characterization in combination with modeling, we were able to develop a comprehensive insight into the initial steps towards the formation of iron oxide.Flame perturbation
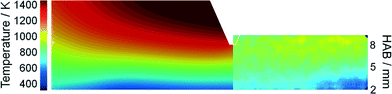
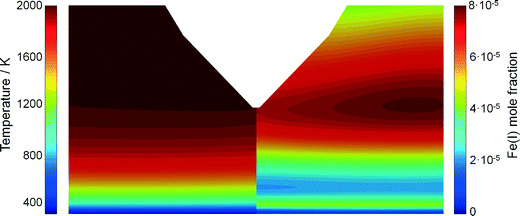
It is expected that the probing nozzle for PMS and QCM measurements perturbs the flow field and therefore influences the local species concentration, e.g., the iron atom concentration distribution. Therefore, the fluid dynamics as well as the species concentration and the temperature profile in the Duisburg reactor were simulated for several probe positions and compared with experimental data.The simulated and measured temperature fields of the perturbed flame with the sampling nozzle located at 8 mm HAB are shown in Fig. 4. Despite the fact that the temperature fields between the burner and the sampling nozzle look very similar, measurement and simulation do not match very well in their absolute values. However, both images show that the temperature field is only slightly affected by the probe – due to the adiabatic boundary condition in the simulation and the small mass of the probe. Thus, mainly aerodynamic effects (suction into the probe) will be the main source of perturbation in the experiment, while the simulation suffers from uncertainties in the boundary conditions.
Fe(CO)5 as precursor has limited thermal stability and decomposes quickly into iron atoms and CO,29 which makes it very sensitive to variations of the experimental conditions. Therefore, the spatial distribution of iron atoms was measured in the vicinity of the burner head by Fe-LIF imaging using laser excitation around 225.15 nm. As the probing nozzle for PMS and QCM measurements perturbs the fluid field and therefore the local iron atom concentration, LIF measurements were taken with burner-probe distances of 5, 7, and 9 mm. Due to geometric constraints, the first two millimeters next to the burner head are not accessible by the laser sheet.
An example for the strong perturbation of the flame by the probe is shown for a position of 5 mm HAB in Fig. 5. The large orifice diameter causes a large zone of flow acceleration, leading to a significant reduction of iron atoms directly in front of the orifice.
 | ||
| Fig. 5 Simulated iron atom concentration field for the DU-R flame perturbed with the sampling probe at HAB = 5 mm with 200 ppm Fe(CO)5 (left) and comparison with Fe-LIF measurements (right). | ||
This effect is reduced with increasing HAB as shown in Fig. 6. It is obvious, that with burner/nozzle distances of 5 and 7 mm the suction of reaction gas with the PMS nozzle located in the center of the burner head (compare Fig. 1) substantially influences the iron concentration profile while it is almost unaffected at larger distance.
Flame temperature
The addition of iron significantly influences the combustion process thus leading to an increasing temperature in the vicinity of the burner with increasing precursor concentration. Iron atoms react in a catalytic cycle with radicals in the flame (H and OH). This reaction is also responsible for the fire-suppressing properties of iron-containing compounds.In a first step we investigated the effect of the addition of Fe(CO)5 to the fresh gases without invasive probing. The simulations predict a strong increase in temperature and confirm previous observations.8,12,30Fig. 7 shows the difference in temperature between the undoped and the doped flame clearly indicating the influence of Fe(CO)5.
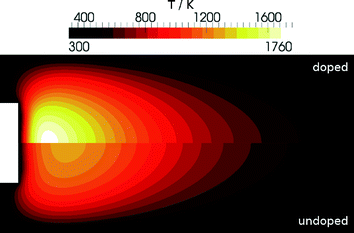 | ||
| Fig. 7 Simulated temperature distribution for the DU-R flame: Undoped (bottom) and doped (top) with 300 ppm Fe(CO)5. | ||
The temperature field was measured in parallel to the Fe-LIF measurements using multiline NO-LIF thermometry.31 As shown from the Fe-LIF measurements discussed above, the probe nozzle affects the temperature distribution in case of short burner-probe distances; however, the effect on temperature is weaker than that on the iron concentration. Fig. 8 represents the temperature distributions for 0, 100, and 200 ppm Fe(CO)5 and the respective profiles along the center line (averaged over a region ±1.5 mm around the axis). The graphs show the influence of Fe(CO)5 on the combustion kinetics leading to a significant increase in temperature with increasing Fe(CO)5 concentration.
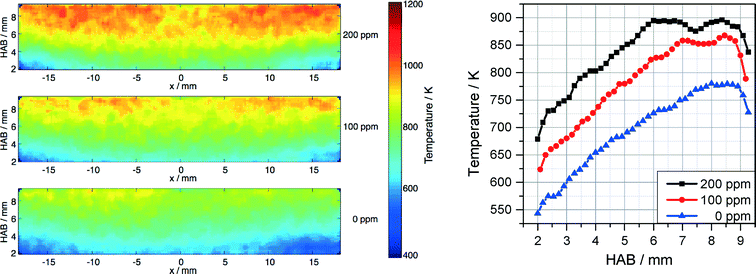 | ||
| Fig. 8 Temperature distribution measured downstream the DU-R burner for 0, 100, and 200 ppm Fe(CO)5 (left) and temperature profiles along the center line (right). | ||
Fe and FeO concentration
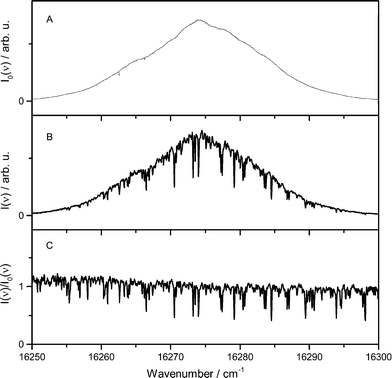
The main reaction products of iron atoms are iron oxides such as FeO, FeOOH, and Fe(OH)2 which then further react towards iron-oxide particles. While the two latter species are not easily accessible to optical measurements, we were able to monitor the FeO concentration in the Tel Aviv reactor by ICLAS in the 611 nm band range.32 Despite the fact that the setup is slightly different from the Duisburg reactor, the results from both reactors can be at least compared qualitatively. Most importantly, both, the increased burner area and the higher pressure of the TA-R lead to a reduced cold-gas velocity and a less elongated flame zone compared to the DU-R thus affecting the spatial distribution of the different species.ICLAS overcomes the disadvantage of broadband cavity losses originating from light scattering on solid particulates present in the nanoparticle synthesis reactor. A typical FeO spectrum is shown in Fig. 9. It is recorded in a flame doped with 900 ppm Fe(CO)5 and indicates a signal-to-noise ratio as high as 30 under our experimental conditions. The FeO absorbance linearly depends on the precursor concentration. This implies that FeO is detectable for Fe(CO)5 precursor concentrations as low as 30 ppm. In addition to ICLAS, temperature profiles were measured downstream the burner based on multiline OH-LIF.
The FeO absorbance was deduced by taking into account multiple spectral lines according to the fitting procedure proposed by Bryukov et al.33 and previously employed in flame studies for accurate deducing absorbance from complex dense and /or multispecies spectra in case of CN,34 HSO,35 and FeO.32 This fitting procedure allows to simultaneously account for multiple lines of the dense and irregular FeO spectrum, reducing the random noise in the extracted absorbance profile.
Fig. 10 shows the extracted (peak-normalized) absorbance profile (red circles) and the measured temperature profile as a function of the height above burner (HAB). Based on the measured temperature profile, the Fe and FeO mole fraction were simulated with the mechanism proposed by Feroughi et al.19 with a 1D model using Cantera. The simulation shows plausible agreement with the experiment, especially when considering the variation of the gas density and the molecule's partition function with temperature which would further improve the agreement of the measured profile with the shape of the simulated mole fraction distribution of FeO. Interestingly, the iron atom concentration (black line) increases directly within the first millimeter downstream the burner head, diminishes and increases again. We attribute the rise in iron concentration to the initial pyrolysis of Fe(CO)5 in the early beginning of the reaction. The intermediate decrease is somewhat unclear and may be related to the formation of iron nuclei followed by their thermal decomposition starting from about 3 mm releasing again iron atoms. It must be mentioned that the concentration of iron atoms is about five times higher than that of FeO, therefore the formation of FeO cannot be the sink for iron atoms. With the very early decomposition of Fe(CO)5 and the succeeding occurrence of Fe-atoms leading to Fe-cluster growth, the flame in the TA-R shows a different structure than the Duisburg flame. This finding is also confirmed by the detailed 2D CFD simulation, an example result is shown in Fig. 11. It predicts a higher temperature than found in the experiment. We attribute this difference to uncertainties in boundary conditions resulting from the relatively small computational domain which did not include the reactor housing and the adiabatic condition for the probe's surface. Nevertheless, the flame structure could be reconstructed and shows the same structure which results from 1D simulations based on a measured temperature profile (Fig. 10).
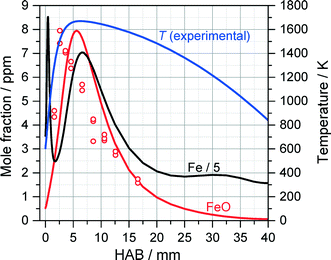 | ||
| Fig. 10 Peak-normalized FeO absorbance measured with ICLAS (open circles) compared to the result of 1D Cantera simulations of Fe and FeO concentrations (solid lines) using the detailed mechanism of Feroughi et al.19 The measured OH-LIF temperature profile (blue) was used as an input for the 1D simulation. | ||
The calculations as well as the measurements depict that gas phase FeO has almost vanished 25 mm downstream of the burner. To clarify whether an intermediate nucleation takes place, particle measurements were performed in both reactors (TA-R and DU-R) using the PMS as well as the QCM.
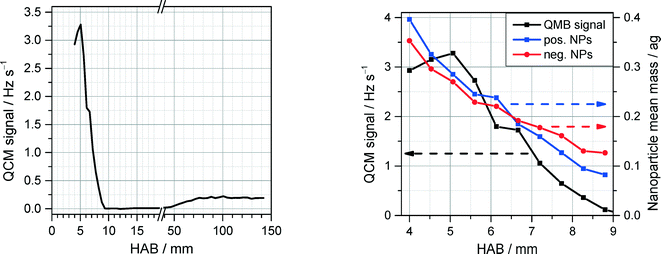
Upon addition of Fe(CO)5, the flames in both reactors exhibit strong luminosity emanating from a relatively narrow region in the vicinity of the flame front, probably due to blackbody radiation of hot, nascent nanoparticles. Consistent with this observation, QCM measurements close to the burner surface reveal substantial nanoparticle formation in the preheat zone of the flame, which then drops abruptly at about 6 mm downstream (Fig. 12, left). The QCM measurements at each HAB were synchronized with measurements of PMS current dependence on the deflection voltage, allowing to derive the m/z probability density distribution. From these data the mean nanoparticle mass was derived and shown to exhibit a four-fold decrease across the 5 mm of the mass concentration peak in the vicinity of the flame front (Fig. 12, right). The sharp drop of the nanoparticle mass concentration past the flame front and the steep decrease of nanoparticle mean mass stands in stark contrast to the existing mechanisms of nanoparticle formation5 predicting monotonic growth of the iron-oxide nanoparticle concentration with the increase of the reaction coordinate accompanied by an increase of the particle diameter.
A similar sharp peak of nanoparticle mass concentration accompanied by a drop of particle mean mass towards the flame front was observed by Fomin et al.15 for the case of a bulb-shaped flame where Fe(CO)5 was added at a central axial location rather than homogeneously seeded into the unburnt gases of the flat flame. They suggested that two competing processes can be responsible for the sharp drop in nanoparticle concentration: Evaporation/oxidation of the nascent nanoparticles in the high-temperature area downstream the nozzle, and a decrease in the particle number density due to the traveling of the particles along diverging (radial) trajectories originating from the curved front of the bulb-shaped flame.
The QCM measurements in the Tel Aviv reactor concerning the early formation of nanoparticles were reproduced in the Duisburg reactor. We also observed the formation of condensed species by means of the QCM, cf. symbols/dotted line in Fig. 13, left. It is obvious that also here particles appear only in a small range from 1 to 8 mm HAB.
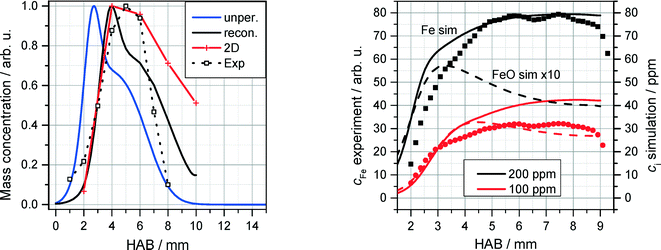 | ||
| Fig. 13 Left: normalized QCM signal (symbols/dotted line) as a function of HAB for the DU-R (200 ppm Fe(CO)5. Measured data are compared with simulations of Fen species concentrations (n = 2–8, see text). Right: normalized measured (LIF) Fe concentration for 100 and 200 ppm Fe(CO)5 (symbols) compared to 1D simulations of Fe (solid lines) and FeO (dotted lines) concentrations using the detailed mechanism of Feroughi et al.19 The measured (multi-line NO-LIF) temperature profile was used as an input for the 1D simulation. | ||
The above mentioned nucleation of iron atoms to clusters within the vicinity of the burner surface competes with gas-phase reactions such as oxidation. Therefore, sufficient precursor concentration would be required to produce an observable mass concentration of iron nanoparticles. Indeed, the experiments show that the dependence of the nanoparticle mass concentration on the concentration of Fe(CO)5 exhibits a “threshold-like” behavior. With the assumption that in the vicinity of the burner surface all iron atoms generated via the Fe(CO)5 decomposition yield nanoparticles with the exception of those that are converted to gaseous products, a simple kinetics consideration leads to the following dependence of nanoparticle mass concentration, mNP, on the initial amount of Fe(CO)5 precursor:36
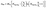 | (1) |
Where MFe is the mass of the iron atom, NFE(CO)5 is the initial concentration of iron pentacarbonyl, k1 is the rate constant of nanoparticle formation (quadratic with respect to the Fe-atom concentration) and k2 is the rate constant of the hypothetic reaction leading to gas-phase products (linear, with respect to the Fe-atom concentration).eqn (1) fits the observed dependence of the nanoparticle mass concentration on the precursor load.
These findings were further investigated with the application of a 1D simulation of the flat flame using Cantera28 with the detailed chemical mechanism proposed by Feroughi et al.19 supported by measured temperature profiles (multiline NO-LIF) to account for realistic heat losses of the reactor. This model well reproduces the shape of the nanoparticle mass concentration on the Fe(CO)5 concentration.36 2D numerical simulations were used to calculate the mass transport of iron clusters Fen with n = 2–8 (indicating all iron mass that does not appear as iron atoms or gaseous species) through the probing nozzle with burner-probe distances of 2, 4, 6, 8, and 10 mm, respectively (red line in Fig. 13, left). The blue line indicates the cluster mass transport in case of an unperturbed flame; the black line is reconstructed from the calculated 2D temperature distribution. The accordance between measurement and simulation is surprisingly good giving clear evidence that the condensed species that is sampled around 5 mm HAB by means of the QCM consists of iron nanoparticles.
Similar to Fig. 10, the concentration of Fe and FeO was calculated with Cantera based on the multiline NO-LIF temperature measurements and compared with Fe-LIF measurements of iron atoms. Measured and calculated Fe profiles match quite well, while similar to the results shown in Fig. 10, the concentration of FeO is significantly reduced by about a factor of ten.
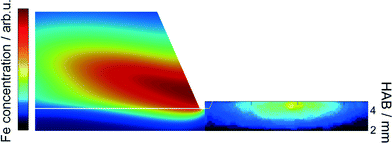
The left graph in Fig. 12 comprises one feature that has not been mentioned so far. Starting from about 50 mm HAB, nucleated species is measured by means of the QCM. Because the ICLAS measurements did not give any indication for FeO molecules at HAB >25 mm (Fig. 10) and also iron atoms have vanished before, both cannot be the origin of the nuclei. As a consequence, we assume that condensable species measured here can neither be composed of FeO nor of Fe. Most probably, condensation takes place from Fe(OH)2 and FeOOH leading to the iron-oxide polymorphs that are commonly observed from flame synthesis.5,8
Our observations can be rationalized as follows: When the Fe(CO)5 concentration is sufficiently high (less than 100 ppm is sufficient), its decomposition produces enough Fe-atoms to give rise to a homogeneous nucleation of iron nanoparticles in the vicinity of the burner surface. As the temperature increases towards the flame front (where it reaches up to 1700 K), the nascent nanoparticles decompose via evaporation and oxidation. This is consistent with the decrease in iron particle size and mass concentration occurring a few millimeter downstream of the burner. In parallel with iron particle formation, FeO molecules are formed at a ratio of about 10–20% related to the iron atom concentration. Both, Fe and FeO vanish around 30 mm HAB while in parallel no condensed species is formed. With decreasing temperature at large distances from the burner surface, iron oxide nucleates producing the “late tail.”
Summary
Sophisticated measurement and modeling techniques have been used to characterize the initial steps of iron-oxide nanoparticle formation from Fe(CO)5 in premixed flat flame reactors in Duisburg and in Tel Aviv. Laser-induced fluorescence was used to measure the spatial distribution of iron atoms downstream the burner head while intra-cavity laser absorption spectroscopy was applied to determine the concentration of FeO molecules. Molecular-beam sampling at selected heights above burner (HAB) in combination with particle mass spectrometry (PMS) and quartz crystal microbalance (QCM) measurements enabled the local measurement of solid species produced in the flame. In addition, both reactors were characterized with respect to their temperature profile using either multiline NO-LIF thermometry (DU-R) or two-line OH-LIF thermometry (TA-R). For a detailed understanding, the measurement results were evaluated taking into account 1D and 2D simulations of temperature, flow, and species concentration fields.From measurements and simulations it was concluded that the Fe(CO)5 precursor initially decomposes when leaving the burner surface, directly forming iron atoms. In case of sufficiently high precursor concentration (less than 100 ppm is sufficient), homogeneous nucleation of iron takes place within the first few millimeters downstream of the burner, resulting in significant amounts of iron nanoparticles that could be measured by PMS and QCM. In parallel to the iron nucleation, FeO molecules are formed. When passing the flame front, both, iron nanoparticles and FeO start to decompose resulting in only gaseous species from about 10 mm HAB. Further downstream with decreasing temperature, a second nucleation process develops leading to iron-oxide nanoparticles. As iron atoms as well as FeO molecules have almost vanished at this point, the experimental results suggest that the nanoparticle growth species consists of other molecules such as FeOOH and Fe(OH)2.
Acknowledgements
CS, SK, and HW acknowledge funding of this work by the German Research Foundation (grant no. SCHU 1369/13 and FOR 2284). SC acknowledges support of the Israel Science Foundation (grant no. 1149/12), IR and SC acknowledge the support by Israel Ministry of Energy and Water Resource (grant no. 211-11-007/2011-7-10), IR acknowledges the support from the Research Authority of The Open University of Israel (Grant No. 47324).References
- H.-C. Chen, C.-C. Wang and S.-Y. Lu, J. Mater. Chem. A, 2014, 2, 16955–16962 CAS.
- L. Xiao, D. Wu, S. Han, Y. Huang, S. Li, M. He, F. Zhang and X. Feng, ACS Appl. Mater. Interfaces, 2013, 5, 3764–3769 CAS.
- H. Zhang, A. Xie, C. Wang, H. Wang, Y. Shen and X. Tian, J. Mater. Chem. A, 2013, 1, 8547–8552 CAS.
- A.-H. Lu, E. L. Salabas and F. Schüth, Angew. Chem., Int. Ed., 2007, 46, 1222–1244 CrossRef CAS PubMed.
- C. Janzen and P. Roth, Combust. Flame, 2001, 125, 1150–1161 CrossRef CAS.
- K. Buyukhatipoglu and A. Morss Clyne, J. Nanopart. Res., 2010, 12, 1495–1508 CrossRef CAS.
- R. Strobel and S. E. Pratsinis, Adv. Powder Technol., 2009, 20, 190–194 CrossRef CAS PubMed.
- I. Wlokas, A. Faccinetto, B. Tribalet, C. Schulz and A. Kempf, Int. J. Chem. Kinet., 2013, 45, 487–498 CrossRef CAS PubMed.
- J. Z. Wen, C. F. Goldsmith, R. W. Ashcraft and W. H. Green, J. Phys. Chem. C, 2007, 111, 5677–5688 CAS.
- A. Giesen, J. Herzler and P. Roth, J. Phys. Chem. A, 2003, 107, 5202–5207 CrossRef CAS.
- P. Roth, Proc. Combust. Inst., 2007, 31, 1773–1788 CrossRef PubMed.
- C. Hecht, H. Kronemayer, T. Dreier, H. Wiggers and C. Schulz, Appl. Phys. B: Lasers Opt., 2009, 94, 119–125 CrossRef CAS PubMed.
- C. Weise, A. Faccinetto, S. Kluge, T. Kasper, H. Wiggers, C. Schulz, I. Wlokas and A. Kempf, Combust. Theory Modell., 2013, 17, 504–521 CrossRef CAS PubMed.
- D. W. Senser, J. S. Morse and V. A. Cundy, Rev. Sci. Instrum., 1985, 56, 1279–1284 CrossRef CAS PubMed.
- A. Fomin, M. Poliak, I. Rahinov, V. Tsionsky and S. Cheskis, Combust. Flame, 2013, 160, 2131–2140 CrossRef CAS PubMed.
- W. G. Bessler and C. Schulz, Appl. Phys. B: Lasers Opt., 2004, 78, 519–533 CrossRef CAS PubMed.
- G. P. Davis and R. A. Gottscho, J. Appl. Phys., 1983, 54, 3080–3086 CrossRef CAS PubMed.
- G. T. Linteris and V. I. Babushok, Proc. Combust. Inst, 2009, 32, 2535–2542 CrossRef CAS PubMed.
- O. M. Feroughi, S. Hardt, I. Wlokas, T. Hülser, H. Wiggers, T. Dreier and C. Schulz, Proc. Combust. Inst, 2015, 35, 2299–2306 CrossRef CAS PubMed.
- J. Li, Z. Zhao, A. Kazakov, M. Chaos, F. L. Dryer and J. J. J. Scire, Int. J. Chem. Kinet., 2007, 39, 109–136 CrossRef CAS PubMed.
- N. Sikalo, O. Hasemann, C. Schulz, A. Kempf and I. Wlokas, Int. J. Chem. Kinet., 2014, 46, 41–59 CrossRef CAS PubMed.
- G. P. Smith, D. M. Golden, M. Frenklach, N. W. Moriarty, B. Eiteneer, M. Goldenberg, C. T. Bowman, R. K. Hanson, S. Song, W. C. Gardiner, V. Lissianski and Z. Qin, GRI-Mech 3.0 web site, http://www.me.berkeley.edu/gri_mech/, 1999 Search PubMed.
- A. Kazakov and M. Frenklach, Reduced Reaction Sets based on GRI-Mech 1.2, http://combustion.berkeley.edu/drm/, 2014 Search PubMed.
- C. R. Wilke, J. Chem. Phys., 1950, 18, 517–519 CrossRef CAS PubMed.
- M. S. Mathur and S. C. Saxena, Appl. Sci. Res., 1967, 17, 155–168 CrossRef.
- OpenCFD, OpenCFD release OpenFOAM, http://www.openfoam.org/version2.1.0.
- L. Deng, A. Kempf, O. Hasemann, O. P. Korobeinichev and I. Wlokas, Combust. Flame, 2015, 162, 1737–1747 CrossRef CAS PubMed.
- D. Goodwin, Cantera: An object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes, http://code.google.com/p/cantera Search PubMed.
- D. Woiki, A. Giesen and P. Roth, Proc. 23rd Int. Symp. Shock Waves, Forth Worth, USA, 2001, pp. 447–455 Search PubMed.
- S. Staude, C. Hecht, I. Wlokas, C. Schulz and B. Atakan, Z. Phys. Chem., 2009, 223, 639–649 CrossRef CAS.
- W. G. Bessler and C. Schulz, Appl. Phys. B: Lasers Opt., 2004, 78, 519–533 CrossRef CAS PubMed.
- I. Rahinov, A. Fomin, M. Poliak and S. Cheskis, Appl. Phys. B: Lasers Opt., 2014, 117, 317–323 CrossRef CAS.
- M. G. Bryukov, A. A. Kachanov, S. I. Panov and O. M. Sarkisov, J. Phys. IV, 1991, 1(C7), 485–488 CrossRef.
- I. Rahinov, N. Ditzian, V. A. Lozovsky and S. Cheskis, Chem. Phys. Lett., 2002, 352, 169–175 CrossRef CAS.
- I. Rahinov, A. Goldman and S. Cheskis, Isr. J. Chem., 2007, 47, 131–140 CrossRef CAS.
- M. Poliak, A. Fomin, V. Tsionsky, S. Cheskis, I. Wlokas and I. Rahinov, Phys. Chem. Chem. Phys., 2015, 17, 680–685 RSC.
| This journal is © The Royal Society of Chemistry 2015 |