Small steps towards the development of chemical artificial intelligent systems
Pier Luigi
Gentili
*
Dipartimento di Chimica, Biologia e Biotecnologie, Università di Perugia, 06123 Perugia, Italy. E-mail: pierluigi.gentili@unipg.it; Fax: +39 075 585 5598; Tel: +39 075 585 5576
First published on 26th September 2013
Abstract
Researchers working in the field of Artificial Intelligence and human-level intelligent agents are driven by the ambitious projects of understanding the foundations and running mechanisms of the human mind, and trying to reproduce them artificially. These projects have been receiving a renewed spur by the research initiative named “The Decade of the Mind” since 2007. A deep understanding of how the mind perceives, thinks, and acts, and its imitation will have a revolutionary impact in science, medicine, economic growth, security, and well-being. Our intelligence grounds on the working mechanism of the human nervous system. The human nervous system is a “computational machine” based on a complex “wetware” of neuronal cells collecting, relaying, processing and storing information under the shape of electrochemical signals. It is worthwhile trying to imitate human intelligence by using chemical systems. In this review, two types of chemical artificial intelligent systems are presented: (a) the sensing and processing properties of chromogenic and fluorogenic materials; and (b) the computational power of the Belousov–Zhabotinsky reaction, which is an excellent model of the neural dynamics.
 Pier Luigi Gentili | Pier Luigi Gentili is Lecturer in Physical Chemistry at Perugia University (Italy), where he teaches “Survey on Complex Systems”. He is working on the development of chemical artificial intelligence to face the challenges of complexity and chaos. He is carrying out his research at the “Photophysics and Photochemistry Laboratory” of Perugia University (Italy). He has worked also at the “Nonlinear Dynamics Group” of the Brandeis University (USA), the “European Laboratory of Nonlinear Optics” (Florence, Italy), the “Center for Photochemical Sciences” of the Bowling Green State University (USA), and the “Laboratory of Computational Chemistry and Photochemistry” of Siena University (Italy). |
1. Introduction
Nowadays, science is spurred to win the Complexity Challenges. There are two types of Complexity Challenges. The first regards a deep understanding and a reliable prediction of the behaviour of Natural Complex Systems, like any living being, any ecosystem, human brain, the trends in macro-economics, etc. The second type of challenge concerns the Computational Complexity, i.e., the solutions of NP-problems and the recognition of variable patterns, like human faces, voices, hand-written words, etc. To try to win at least some of the Complexity Challenges, scientists are developing Artificial Intelligence and at the same time they are devising always more powerful computing machines, because dealing with complexity means in general handling a huge amount of data.Around the globe, many countries are competing with each other to develop the world's fastest supercomputers. The TOP500 supercomputer project ranks and publishes an updated list of the high-performance computers twice a year.1 In 2011, the RIKEN Advanced Institute for Computational Science in Kobe (Japan) announced at the International Supercomputing Conference the manufacturing by Fujitsu of the world's most powerful supercomputer, named as K computer (from the Japanese word “kei” that means 10 quadrillion, i.e. 1016). The K supercomputer is able to calculate at a rate of 10 petaFlop per s (one petaFlop per s corresponds to 1015 floating-point operation per second) based on 705![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 024 processor cores distributed in 672 computer racks. The K computer is also one of most energy efficient system (working at a power of 12
024 processor cores distributed in 672 computer racks. The K computer is also one of most energy efficient system (working at a power of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660 kW) and it has a memory space of 1.4 million GB. To give an idea of just how fast it is, imagine the following: all seven billion people in the world have a calculator and are asked to perform one calculation per second 24 hours per day, non stop. It would take the world's population approximately 17 days to do what the K supercomputer can do just in one second.2 Alternatively, we may understand the K computer's computational power highlighting that its performance equals that of one million desktop computers, to cite the evaluation made by the TOP500 compiler Jack Dongarra. The K supercomputer is being used to address many problems regarding Natural Complex Systems. For instance, it is exploited to perform calculations whose aims are: (i) protecting our environment more effectively and conserving natural resources; (ii) developing new renewable sources of energy; (iii) mitigating the effects of climate change; (iv) predicting natural disasters (such as earthquakes, tornados, tsunamis) and developing appropriate response plans; (v) developing new drugs to treat deadly diseases. In June 2012, TOP500 project committee announced1 that IBM manufactured a new supercomputer, named Sequoia, setting a new record in computational rate: an impressive 16 petaFlop per s. The supercomputer Sequoia has more processor cores and it is more energy efficient than K supercomputer (see Table 1 for the details). It is being used at the Lawrence Livermore National Laboratory: (i) to provide a clearer understanding of nuclear weapons performance, notably hydrodynamics and properties of materials at extreme pressure and temperatures; and (ii) to study the aging of nuclear stockpile. The high rate of calculations enables to run very large suites of calculations to test the sensitivity on initial conditions in reasonable time. Scientists have confidence to obtain accurate results avoiding real underground nuclear tests. In November 2012, TOP500 project committee1 declared that Titan, a supercomputer installed at Oak Ridge National Laboratory (USA), knocked Sequoia out of first place in the list of supercomputers, reaching a computational rate of 17.59 petaFlop per s. Its record is based on a hybrid architecture, combining traditional central processing units (CPUs) with graphic units (GPUs), the latter being faster than the former. Combining GPUs and CPUs is a way of providing a striking computational power for research in energy, climate change, and materials, as scientists at the Oak Ridge Laboratory believe. Titan is lauded as the first step towards the goal of computing at a rate of 1000 quadrillion calculations per second (exaFlop per s) at a power of 20 megawatts or less. In June 2013, during the opening session of the 2013 International Supercomputing Conference in Leipzig (Germany), it was announced that the Chinese supercomputer Tianhe-2, developed by China's National University of Defense Technology, is the world's new number 1 system with a performance of 33.86 petaFlop per s. The pace of improvement of supercomputers puts processing power within range of an exaFlop per s by 2018.1
660 kW) and it has a memory space of 1.4 million GB. To give an idea of just how fast it is, imagine the following: all seven billion people in the world have a calculator and are asked to perform one calculation per second 24 hours per day, non stop. It would take the world's population approximately 17 days to do what the K supercomputer can do just in one second.2 Alternatively, we may understand the K computer's computational power highlighting that its performance equals that of one million desktop computers, to cite the evaluation made by the TOP500 compiler Jack Dongarra. The K supercomputer is being used to address many problems regarding Natural Complex Systems. For instance, it is exploited to perform calculations whose aims are: (i) protecting our environment more effectively and conserving natural resources; (ii) developing new renewable sources of energy; (iii) mitigating the effects of climate change; (iv) predicting natural disasters (such as earthquakes, tornados, tsunamis) and developing appropriate response plans; (v) developing new drugs to treat deadly diseases. In June 2012, TOP500 project committee announced1 that IBM manufactured a new supercomputer, named Sequoia, setting a new record in computational rate: an impressive 16 petaFlop per s. The supercomputer Sequoia has more processor cores and it is more energy efficient than K supercomputer (see Table 1 for the details). It is being used at the Lawrence Livermore National Laboratory: (i) to provide a clearer understanding of nuclear weapons performance, notably hydrodynamics and properties of materials at extreme pressure and temperatures; and (ii) to study the aging of nuclear stockpile. The high rate of calculations enables to run very large suites of calculations to test the sensitivity on initial conditions in reasonable time. Scientists have confidence to obtain accurate results avoiding real underground nuclear tests. In November 2012, TOP500 project committee1 declared that Titan, a supercomputer installed at Oak Ridge National Laboratory (USA), knocked Sequoia out of first place in the list of supercomputers, reaching a computational rate of 17.59 petaFlop per s. Its record is based on a hybrid architecture, combining traditional central processing units (CPUs) with graphic units (GPUs), the latter being faster than the former. Combining GPUs and CPUs is a way of providing a striking computational power for research in energy, climate change, and materials, as scientists at the Oak Ridge Laboratory believe. Titan is lauded as the first step towards the goal of computing at a rate of 1000 quadrillion calculations per second (exaFlop per s) at a power of 20 megawatts or less. In June 2013, during the opening session of the 2013 International Supercomputing Conference in Leipzig (Germany), it was announced that the Chinese supercomputer Tianhe-2, developed by China's National University of Defense Technology, is the world's new number 1 system with a performance of 33.86 petaFlop per s. The pace of improvement of supercomputers puts processing power within range of an exaFlop per s by 2018.1
| Supercomputer | Rate (petaFlop per s) | Cores (no.) | Memory (GB) | Power (kW) |
|---|---|---|---|---|
| K | 10 | 7.05 × 105 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 410![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 048 048 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660 660 |
| Sequoia | 16 | 1.57 × 106 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 572 572![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 864 864 |
7890 |
| Titan | 17.59 | 5.6 × 105 | 710![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 144 144 |
8209 |
| Tianhe-2 | 33.86 | 3.12 × 106 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 024 024![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 808 808 |
The processing power and data storing capacity of these brand new supercomputers seem to have overcome the performances of the human brain. In fact, the computing rate and the memory capacity of our brain have been estimated to be about 1–0.1 petaFlop per s (ref. 3) and 105 of GB,4 respectively. Have we reached the “Singularity”,5i.e., the point where machines surpass human intelligence, as envisioned by Kurzweil? The answer is of course no, because human intelligence does not reside simply on its computing rate and memory space, but on its ability to learn, understand scenarios, react independently to unexpected events that come across, recognize variable patterns like human voices, faces, handwritten words, etc. Human brain loses out to computers in mathematical and recording jobs, because it is made for general purposes and it is constantly bombarded by the information coming from the human sensory system, and is distracted by emotions and thoughts. On the other hand, computers struggle to recognize human faces at airport check-ins because variations like lighting, facial expression, or accessories and details like glasses, hats, beards… upset the computer's fragile and rigid logic.
The researchers working in the field of Artificial Intelligence and human-level intelligent agents are driven by the ambitious projects of understanding the foundations and running mechanisms of the human mind, and trying to reproduce them artificially. These projects have been receiving a renewed spur by the research initiative named “The Decade of the Mind”6 since 2007. A deep understanding of how the mind perceives, thinks, and acts and its imitation will have a revolutionary impact in science, medicine, economic growth, security, and well-being. In a fairly recent book,7 the cognitive scientists Gallistel and King, in agreement with the neuroscientist Marr,8 argue that to understand a complex biological system like our brain, it is necessary to perform an analysis at three distinct levels. The first is the “computational level” and consists of describing the inputs, outputs and the task of the system. The second is the “algorithmic level” and consists of formulating algorithms that might carry out those computations. Finally, the third is the “implementation level” and consists of searching for mechanisms of the kind that would make the algorithm work. In this review, the computational and the algorithmic levels are resumed in paragraph 2. The rest of the review is dedicated to a description of a facet of the implementation level. In fact, it describes how chemists are trying to develop artificial systems to mimic the computational power of the elementary components of the human nervous system. In particular, this review focuses on the computational power of chromogenic and fluorogenic materials and that of the Belousov–Zhabotinsky (BZ) reaction. The chromogenic and fluorogenic materials are surrogates of the sensory elements we have in our nervous system. On the other hand, the BZ reaction is a remarkable model of neurons and their dynamics; its computational performances tested so far are critically analyzed. This review does not present the use of chromogenic materials and the BZ reaction as actuators, because there are already very recent reviews dealing with this subject.9–17 In the last paragraph, an outlook for future developments on the analysis of the human mind at the implementation level is traced.
2. The “computational” and “algorithmic” levels of analysis of the human nervous system
The field of neuroscience has grown dramatically in the last decades. Much research focuses on the question of how information is processed in nervous systems, from the level of individual ionic channels to large-scale neuronal networks. New interdisciplinary methodologies combine a bottom-up experimental methodology with the more top-down-driven computational and modelling approach. In the next two paragraphs (2.1 and 2.2), the main properties of the human nervous system and that of its elementary unit, i.e., the neuron, are described. More details regarding the “computational” and “algorithmic” levels of analysis of neural network can be found in the book by Koch and Segev.182.1. Neurons: the elementary computational units of the human nervous system
Our intelligence grounds on the working mechanism of the human nervous system. The human nervous system is a “computational machine” based on a “wetware” made of a complex network of billions of nerve cells (i.e., neurons) collecting, relaying, processing and storing information under the shape of electrochemical signals.19 Each neuron is electrically polarized, i.e., it is characterized by an electric potential across the cell membrane. At rest, the electric potential Vin − Vout equals −70 mV. A neuron receives chemical signals from other neurons through the dendrites. These signals can be either inhibitory or excitatory. They are collected into the cell body, i.e., the soma, and here they are transduced as electrochemical signals. The net integration of the signals received by the dendrites of the cell occurs in the axon hillock. If the overall signal is inhibitory, it promotes the closure of Na+ channels and the hyperpolarisation of the cell membrane (the potential becomes more negative). On the other hand, if the overall signal is excitatory, it promotes the opening of Na+ channels and the depolarization of the cell membrane. When the depolarization is so strong to overcome a threshold value, which is usually of −55 mV, the neuron fires an action potential, which is an electrochemical wave propagating in a unidirectional way from the hillock along the axon up to reach the bottom part of the neuron where there are the synapses. This electrochemical wave is due to voltage-gated ion channels embedded in the cell membrane, which rapidly opens when the membrane potential increases upward of the threshold value. When the channels open, they allow an inward flow of Na+, which in turn produces a further rise in the membrane potential. Then, this causes more sodium ion channels to open, in an autocatalytic step. Finally, the polarity of the membrane reverses and the Na+ channels close. K+ channels are then activated, promoting an outward current of them, returning the electrochemical gradient to the resting state. Moreover, an active mechanism transport re-establishes the original ion concentration gradient for Na+ and K+. These restoring processes prevent an action potential from travelling backwards and fix a refractory period for the electrochemical wave. The discharge of an action potential in a portion of the axon takes around 1 ms. The spike of the action potential is the ideal solution for conveying information over long distances (up to tens of cm) without weakening. The action potential is a binary event per se, because its formation follows an “all-or-nothing” law. In the case of spike trains, since spikes have similar shapes, information is encoded on their frequency, i.e., on the inter-spike intervals. The equation describing the relation between the firing frequency (ν) of action potential and the membrane voltage (ΔV) is given by the logistic function (eqn (1)):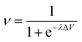 | (1) |
 | ||
| Fig. 1 Profile of the logistic function for small and large values of gain parameter λ. | ||
When the action potential reaches the bottom part of the axon, it encounters the synapses. Here the electrochemical signal is transduced into a chemical signal. The synapses release neurotransmitters to the dendrites of the neurons they are linked to. The computational power of our nervous system relies on the properties of the network of synaptic connections among neurons. The number of connections is huge: it suffices to say that a typical neuron connects with about 104 other neurons and in the brain there are billions of neurons. Moreover, the connections are plastic: they continuously change depending on the experiences. Recent advances in non-invasive neuro-imaging have enabled the measurement of connections between distant regions in the living human brain, thus opening up the new field of research called “Connectomics”.20 The combined analysis of structural and functional networks has begun to reveal components or modules with distinct patterns of connections engaged in different cognitive tasks into the brain. Collectively, advances in human Connectomics open up the possibility of studying how brain connections mediate regional brain function and hence behaviour.
2.2. The human nervous system as a special “electrochemical” computer, which processes information by using words
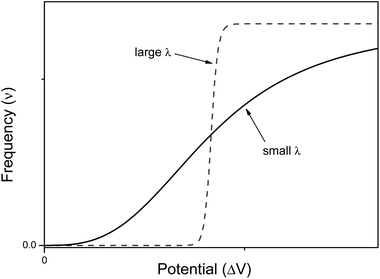
It is interesting to compare the structure and working mechanisms of our nervous system with those of current electronic computers (see Fig. 2). Current electronic computers have a design which follows the Von Neumann's original architecture.21 Computers are constituted by four main elements: (i) a memory storing information; (ii) a central processing unit (CPU) wherein information is processed (it consists of two subunits: the arithmetic logic unit, which performs arithmetic and logical operations, and the control unit, which extracts instructions from memory, decoding and executing them); (iii) an information exchanger (IE) allowing transfer of information in and out of the computer (it consists of screen, keyboards, etc.); (iv) a data and instructions bus (playing as a communication channel) binding the other three components of computer by conveying information among them. Electronic computers are general purpose computing machines because the instructions to make different types of computation tasks are stored into the memory as specific software, i.e., as sequences of bits. Information is encoded in electrical signals, and transistors are the basic switching elements of a CPU. A computer program can guide a robot, which is usually an automated electro-mechanical machine provided with at least one sensor system and a movable physical structure controlled by the CPU. All components, of course, are fed by a power supply. | ||
| Fig. 2 Schematic structures of the Von Neumann's architecture of current electronic computers (on the left) and the human nervous system (on the right). | ||
Also the human nervous system can be described as consisting of four main components: (i) the sensory system; (ii) the spinal cord; (iii) the brain; and (iv) the effectors' system. The sensory system consists of many different specialized receptor cells which either catch the stimuli coming from the external environment or monitor the inner state of the body. The receptor cells transduce the different kinds of stimuli in electrochemical signals which are sent to the spinal cord and hence to the brain. The brain processes the information coming from the sensory cells, and is based on the memory of previous experiences, it takes decisions. The final decision is communicated across the spinal cord to the tissues and organs made of effectors' cells, i.e., to glands (both exocrine and endocrine) and muscles. The brain is both the central processing unit and the memory of the computing human nervous system. The sensory system along with the effectors' cells play like the information exchanger of electronic computers, and finally the spinal cord is the data and instructions bus.
Our sensory system catches physical and chemical stimuli. It codes for four aspects of a stimulus: type (or the so called modality, M), intensity (IM), location (IM(x, y, z)), and duration (IM(t)). The power to distinguish different modalities is due to the existence of specialized receptor cells. There are photoreceptors collecting visible light; mechanoreceptors sensing mechanical stimuli; thermoreceptors perceiving thermal stimuli and chemoreceptors detecting several chemicals. Whatever the stimulus, it modifies the permeability of the ion channels present in the receptor cells membranes, whereby the receptor cells transduce any kind of stimulus in electrochemical signals. The receptors produce graded potentials whose intensities depend on those of the inputs. The graded potentials are analog signals which are finally converted in action potentials either inside the same receptor cell (like in the somatosensory system) or in afferent neurons (like, for example, in the auditory system). The stimuli triggering the discharge of action potentials are called liminal, whereas the others are called underliminal. The analog information regarding the intensity of the liminal stimuli is not lost but it is coded in the firing rate of action potential trains. The higher the intensity of a graded potential, the higher the frequency of the action potentials train. The duration of the train of impulses reflects the duration of the stimulus. Finally, the architecture of the sensory organs and the existence of distinct receptive fields for each receptor cell allow the information regarding the spatial distribution of the stimuli to be retrieved. The information regarding the spatial distribution of the stimuli is maintained inside the nervous system. In fact, each receptor cell sends electrochemical signals along different labelled pathways up to reach specific portions of the cerebral cortex.
In the cortex, association areas assemble separate perceptions, computing in parallel and not in serial as an electronic computer does, and produce a meaningful experience of the world. The experience of the world is influenced by past perceptive events, stored in the mnestic areas. These stored events confer to the humans the noticeable power of making decisions in complex situations and recognizing patterns. Of course, the information caught by the sensory system and sent to the brain is not devoid of uncertainty. Although perception is deterministic, many factors contribute to limiting the reliability of sensory information about the world. Structural constraints on neural representations and computations (for example the density of receptors or the mapping of 3D objects into 2D images as it occurs on the retina) along with the neural noise introduced in early stages of sensory coding contribute to limiting the reliability of sensory information about the world. It derives that perceptions are granular, as pointed out by Zadeh.22 Perceived values of variables are not sharply defined. In other words there are not as many receptor cells as the possible values a variable can assume (for instance, one photoreceptor cell for each colour). The human sensory system consists of seven distinct elements: the (a) visual; (b) olfactory; (c) gustatory; (d) auditory; (e) superficial somatosensory; (f1) inner somatosensory (f2) vestibular; and (g) thermosensory systems. Each of them is based on a collection of specialized sensory cells.
When a stimulus having a specific modality, intensity, duration and spatial distribution, IM(t, x, y, z), impinges on our sensory system, it interacts with one of these specialized collections, evoking activity not just in one cell but in all of them at different degrees. If x = 1, 2,…, N is the number of sensory cells disposed as a bi-dimensional array (except for the somatosensory and vestibular systems, which have a three-dimensional distribution), the stimulus will have specific degrees of membership μM,x in each sensory cell, which plays like a fuzzy set. A fuzzy set23 is more than a classical set: it can wholly include or wholly exclude elements, but it can also partially include and exclude other elements. The theory of fuzzy sets breaks the Law of Excluded Middle because an element x may belong to both set X and its complement not-X. An element x may belong to any set, but with different degrees of membership. The degree of membership (μ) of an element to a fuzzy set can be any real number included between 0 and 1. In the theory of fuzzy logic, a collection of fuzzy sets, transforming crisp input values into a vector of degrees of membership, is named as fuzzifier. Therefore, each of the seven elements of the sensory system is a fuzzifier.24 The information of a stimulus is encoded as the matrix† of degree of membership values,
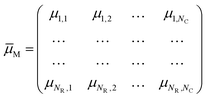 | (2) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) M represents the fuzzy information of human perception. The uncertainty into the perception induces our sensory system to group perceived values into granules, with a granule being a clump of
M represents the fuzzy information of human perception. The uncertainty into the perception induces our sensory system to group perceived values into granules, with a granule being a clump of ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) M values drawn together by indistinguishability, similarity, proximity or functionality. The human brain must deal with the resulting uncertainty to generate perceptual representations of the world. This led to the idea that perception is a process of Bayesian probabilistic inference.25,26 If IM is the stimulus of modality M, and XM represents the collection of cells sensitive to it, applying the Bayes' rule, it results that
M values drawn together by indistinguishability, similarity, proximity or functionality. The human brain must deal with the resulting uncertainty to generate perceptual representations of the world. This led to the idea that perception is a process of Bayesian probabilistic inference.25,26 If IM is the stimulus of modality M, and XM represents the collection of cells sensitive to it, applying the Bayes' rule, it results that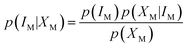 | (3) |
The term p(IM|XM) represents the “posterior probability” and is given by the product of the “prior probability” p(IM) and the “likelihood” p(XM|IM). p(IM) is the probability of each perception prior to receiving the stimulus: it represents knowledge of the regularities. p(XM|IM) can be identified with the fuzzy information, i.e., the membership functions ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) M in accordance with the theory of Bayesian inference generalized in fuzzy context.27 The term p(XM) is the “plausibility” and is merely a normalization factor. Bayes formula implies that human perception is a trade-off between p(XM|IM) and p(IM).28 Some perceptions may be more “prior probability” driven, and others more data (that is
M in accordance with the theory of Bayesian inference generalized in fuzzy context.27 The term p(XM) is the “plausibility” and is merely a normalization factor. Bayes formula implies that human perception is a trade-off between p(XM|IM) and p(IM).28 Some perceptions may be more “prior probability” driven, and others more data (that is ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) M) driven. The more noisy and ambiguous the perception features, the more relevant the role played by p(IM).‡ The population of XM sensory neurons activated by the stimulus, evokes the activity of a population of N′ downstream neurons which we here denote by a vector RM = (r1, r2,…,rN′)M (in analogy with the symbols used by Pouget).29 The terms IM, XM and RM form a chain communication system. For such a chain, the mathematical theory of information30 allows to state that
M) driven. The more noisy and ambiguous the perception features, the more relevant the role played by p(IM).‡ The population of XM sensory neurons activated by the stimulus, evokes the activity of a population of N′ downstream neurons which we here denote by a vector RM = (r1, r2,…,rN′)M (in analogy with the symbols used by Pouget).29 The terms IM, XM and RM form a chain communication system. For such a chain, the mathematical theory of information30 allows to state that
| p(IM, XM, RM) = p(IM|XM)p(RM|XM)p(XM) = p(XM|IM)p(RM|XM)p(IM) | (4) |
At each step along the communication chain, the uncertainty does not decrease. It rather increases due to the noise operating in the communication among neurons. Thus, the information that RM gives about IM cannot be greater than the information XM gives about IM, in agreement with the Law of Diminishing Information30
| inf(RM@IM) ≤ inf(XM@IM) | (5) |
Finally, after one or more of these communication steps, our brain receives information about perceptions which is fuzzy granular due to the uncertainty. The final information is properly described by propositions in natural language. Computing with words becomes the most effective way of handling uncertainty and complexity at the same time.
3. The “implementation” level of analysis of the human nervous system
Chemists are trying to develop artificial chemical systems that can mimic at least some computational properties of neurons. This review focuses the attention on the computational power of chromogenic and fluorogenic materials and the BZ reaction.3.a. Chromogenic and fluorogenic compounds as artificial sensory materials
In human sensory systems there are many types of responsive molecules catching physical and chemical stimuli. In the case of the visual system,31 the photo-sensitive molecules are four types of seven transmembrane α-helices proteins containing the same chromophore, 11-cis retinal, and differing only in the amino-acidic composition of the pocket hosting it. When 11-cis retinal absorbs a photon, it isomerizes to all-trans retinal. The cis-to-trans isomerisation triggers a conformational change of the embedding apoprotein, which activates a cascade of events ending in a modification of the transmembrane electrical potential of the sensory cell. The chemoreceptors in the olfactory32 and gustatory33 systems are proteins having odorant- or flavour-binding sites. When a ligand binds to the protein's site, it brings about a structural modification on the hosting protein, which then triggers a cascade of chemical signalling events. The senses of hearing, touch, proprioception, kinaesthesia, all rely on the activity of mechanoreceptors. They are gated ion channels34 detecting either steady or vibrating or instantaneous mechanical forces, which promote the opening or the closure of the ion channels and hence a depolarization or a hyperpolarisation of their hosting cells. The mechanical stimuli are transduced in electrochemical signals inside the neural cells. Ion channels, with an activity sensitive to temperature, are involved in the thermosensation.35 Also the sensory cells detecting noxious chemical and physical stimuli are provided with ion channels.36 These natural responsive molecules can be artificially imitated by chromogenic and fluorogenic materials. Their behaviour is schematically described in Fig. 3.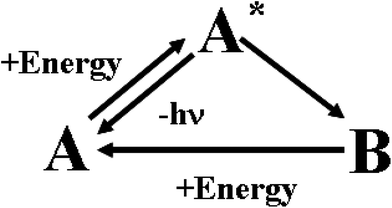 | ||
| Fig. 3 Working mechanism of chromogenic and fluorogenic materials. | ||
Initially, in the absence of any external perturbation, the chemical system is in the A structural state that can be uncoloured or coloured. If A receives an external perturbation, it stores energy from the outside and reaches an excited new state, A*. In A*, the system is like a marble on the top of a hill: it is in a state of unstable equilibrium. The intensities of forces governing the nuclear dynamics depend on the slopes of the different accessible pathways. A* evolves toward the steepest directions. In other words, the logic of the evolution is ruled by the kinetic law “the faster the process, the higher its probability”. The evolution of the A* state defines how A processes the information contained in the initial perturbation. In the case of chromogenic compounds, A* evolves to a completely new structure, B, with appearance of a new colour. In the case of fluorogenic materials, A* will decay to the initial state A by producing light. In both cases, A sends “photonic” messages (colour changes or emitted light) after the perturbation. These optical messages contain the final results of the molecular computation. The transmitted or emitted photons bridge the gap between the microscopic and macroscopic worlds. They can be quite easily collected by lenses and sent through optical fibres over long distances. In the case of chromogenic compounds, the B structure is a chemical metastable state: it can convert back to A by using the thermal energy available at room T or it may need another form of energy and hence another perturbation to go back to the A state. The best fluorogenic and chromogenic materials are those which are completely reversible and devoid of side-reactions.
Chromogenic materials are classified according to the kind of external perturbation that promotes the conversion of A to B. This perturbation can have physical or chemical nature.37,38 The different types of chromogenism are indicated by the word chromism preceded by a prefix specifying the kind of stimulus producing colour. In the case of physical perturbations, we can have:
(a1) Photochromism when the appearance of colour is induced by electromagnetic radiation. The structural transformation is due to photochemical reactions like electrocyclisation, cis–trans isomerisation, cycloaddition, electron transfer, dissociation and tautomerisation. The back reaction (from B to A) can occur thermally (photochromism of type T) or photochemically (photochromism of type P).39
(a2) Piezochromism when the perturbation is the pressure. The action of mechanical forces applied on the surface of crystalline structures can induce phase transitions (like in EuS37 that changes from NaCl-type to a CsCl-type structure or in SmS changing from semiconductor to conductor state) or chemical reactions characterized by a molecular volume contraction (ΔVr < 0);40 both bring about a thermally reversible change of colour.
(a3) Thermochromism when heat generates colour. Thermochromic materials reversibly change colour if subjected to specific variations of temperature. The change of optical properties can be due to phase transitions (like in VO2 that switches from a monoclinic to a tetragonal crystal structure at 68 °C)41 or to endothermic chemical reactions (ΔHr > 0, like the C–O spiro bond breakage in spiroheterocycles).42
(a4) Electrochromism when an electric field triggers the appearance of colour. It is a reversible and visible change in transmittance and/or reflectance that is associated with electrochemically induced oxidation–reduction reactions.43–46
In the case of chemical perturbations, we can have:
(b1) Acidichromism when it is a variation in pH to bring about colour modification. The acidic form and the conjugated basic form of some compounds may have distinctly different absorption spectra. By changing the pH, it is possible to control the colour of the system.40,47,48,49
(b2) Ionochromism, halochromism, metallochromism when a new colour appears after addition of salts. Addition of salts can either induce reversible complexation reactions49 or establish equilibria between acids and bases of Lewis, like that of eqn (6).39
| Ph3C-Cl (colourless) + AlCl3 = Ph3C+ + AlCl4− (yellow) | (6) |
(b3) Solvatochromism is the change of colour due to chemical composition and the physical properties of the solvent.50 An example is betaine that shows a very large solvatochromic effect, and on which the empirical parameter of solvent polarity, ET(30), is based.
Also the fluorogenic materials are classified according to the kind of external perturbation promoting the emission of radiation. Fluorogenic materials can be excited via photons; in this case we have either fluorescent or phosphorescent materials51 if the populated excited electronic state has the same or different spin multiplicity with respect to the ground state, respectively. When a material emits light in response to the action of an electric field, it is defined electroluminescent.52 Pyroluminescence results from the effect of high temperatures on certain molecules which, when pushed to excited electronic levels, then emit light as they return to the ground state.53 Also mechanical actions can induce the emission of light. For example, by striking two solids together, or by rubbing or applying a shearing stress, or by using ultrasound waves, we observe emission phenomena known under the general term of mechanoluminescence.53 Finally, there are certain chemical reactions, involving usually an oxidizing agent in the presence of an activator or catalyst, which give rise to excited chemical intermediates, relaxing to the ground state by emitting light. This fluorogenic phenomenon is known as chemiluminescence.54
The chromogenic and fluorogenic compounds are switchable materials, i.e., they are reversible in their functioning as shown from the closed cycle of Fig. 3. They behave like the sensory cells and the electronic transistors, which are the building blocks of modern digital computers. Electronic transistors are made of semiconductors and are based on input and output electrical signals; they implement the basic elementary YES/NOT logic functions. Two transistors in series and two transistors in parallel implement the AND and OR logic gates, respectively. Connecting the output and input terminals of several AND, NOT, and OR gates, it is possible to set up combinational logic circuits. Of course, the logic function of a circuit can be adjusted altering the number and type of basic gates and their interconnection protocol. The electrical communication among the basic AND, OR, NOT elements allows even complex logic functions to be implemented. In the case of human nervous system, complicated logic functions are processed inside the cerebral cortex, receiving relatively neat signals from the sensory cells. On the other hand, chromogenic and light-emitting materials, can be exploited to implement complicated logic functions by following three different strategies. The first strategy consists in designing multi-switchable responsive molecules, i.e., compounds having many accessible states. The other two strategies consist of employing communication among simple molecular switches: their communication can be based on either chemical or physical messages. In the next two paragraphs, a few representative examples of the three strategies are described. Further examples of chromogenic and fluorogenic molecular switches used to implement logic functions can be found in recent reviews.55–57
A recent example49 of a multiswitchable molecule allowing complicated logic functions to be implemented is the chromogenic 1,3-dihydro-1,3,3-trimethyl-8′-nitro-spiro[2H-indole-2,3′-[3H]naphth[2,1-b][1,4]oxazine] (SpO), whose chemical structure is depicted in Fig. 4. SpO is uncoloured (see its spectrum in Fig. 4(a)). UV irradiation produces the blue coloured photomerocyanine (MC) (its spectrum has a maximum at 611 nm in acetonitrile as shown in Fig. 4(b)), which is thermally unstable. It reverts back to SpO spontaneously in a few hundreds of seconds at room temperature. If SpO is UV irradiated in the presence of one equivalent of HClO4, the solution becomes orange due the formation of H+–MC, whose spectrum is shown in Fig. 4(c) exhibiting a maximum at 485 nm. H+–MC is thermally stable and can be converted to SpO by irradiating with visible light or by adding one equivalent of NaOH. When SpO is UV irradiated in the presence of one equivalent of Al3+, the solution becomes coloured in orange due to the formation of the complex Al3+–MC. Its absorption spectrum has a maximum at 485 nm (see Fig. 4(d)). Al3+–MC is thermally stable and the original SpO state can be restored by irradiating into the visible or by adding one equivalent of 4,4′-dimethyl-2,2′-bipyridyl (bpy). When SpO is UV irradiated in the presence of one equivalent of Cu(ClO4)2, the solution becomes coloured in yellow, due to production of the complex Cu2+–MC, whose spectrum has a maximum at 423 nm and is shown in Fig. 4(e). Cu2+–MC is thermally stable and the original state SpO can be recovered by adding one equivalent of ethylenediaminetetraacetic acid (EDTA). It is evident that SpO is a five-states chromogenic molecular switch.
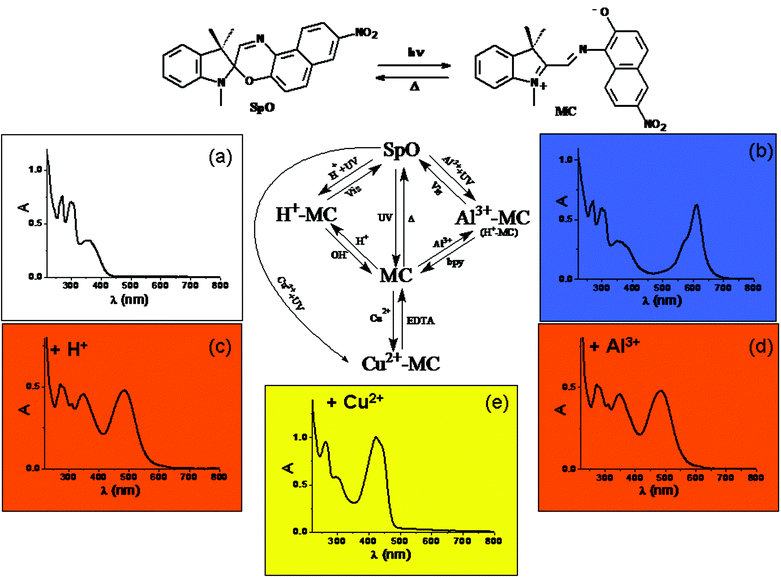 | ||
| Fig. 4 Schematic representation of the photochromic, acidichromic and metallochromic five-states molecular switch SpO. | ||
In crisp Boolean logic, data processing requires the encoding of information in the form of binary digit. Therefore, it is necessary to establish a threshold value and a logic convention for each signal. The signals can be simply high or low, becoming the digital 1 or 0, respectively, in the positive logic convention. Based upon the reversible chromogenic properties of SpO, it is possible to process binary logic by using UV radiation as power supply, HClO4, AlCl3 and Cu(ClO4)2 as chemical inputs, and the absorbance at a specific wavelength into the visible as optical output. An input is “off” (i.e., 0) when the respective chemical is not injected at all into the solution containing the molecular switch SpO, whereas it is “on” (i.e., 1) when one equivalent of the chemical reagent is added. An optical output is “on” (i.e., 1) whenever the absorbance at the analysis wavelength, A(λan), is larger than 0.4, whereas it is “off” (i.e., 0) whenever A(λan) < 0.4. SpO can be used to implement the YES logic function based on either HClO4 (In1) or AlCl3 (In2) or Cu(ClO4)2 (In3) as chemical input, UV radiation as power supply and the absorbance at either 485 nm or 423 nm as optical output. If we combine two chemical inputs, more complex logic functions can be implemented as shown in Tables 2 and 3 wherein the absorbance values at 611 nm (A(611 nm)), 485 nm (A(485 nm)) and 423 nm (A(423 nm)) are fixed as output 1 (Out1), 2 (Out2) and 3 (Out3), respectively. The combination of In1 (H+) and In2 (Al3+) allows the NOR, OR and FALSE logic gates to be implemented (see Table 2).
| In1 (H+) | In2 (Al3+) | Out1 (A(611 nm)) | Out2 (A(485 nm)) | Out3 (A(423 nm)) |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| NOR | OR | FALSE |
| In1 or 2 (H+ or Al3+) | In3 (Cu2+) | Out1 (A(611 nm)) | Out2 (A(485 nm)) | Out3 (A(423 nm)) |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| NOR | INHIBIT | TRUE |
On the other hand, by combining the action of the two inputs In1 (H+) and In3 (Cu2+), or that of In2 (Al3+) and In3 (Cu2+), the NOR, INHIBIT and TRUE logic gates are implemented (see Table 3).
It is worthwhile noticing that the three NOR, OR and FALSE logic gates (Table 2) or the other three NOR, INHIBIT and TRUE gates (Table 3) coexist simultaneously. They are superimposed logic devices. Their operation mode depends on the way information is read, e.g. it is possible to pass from one element to another simply by changing the monitored wavelength. Other examples of molecules that are multiply configurable Boolean logic elements can be found in recent reviews.55–57,60–63 The superposition of the output states is somehow close to the property of quantum logic of dealing with superimposed quantum states.
Furthermore complex binary logic functions can be implemented if the actions of all the three inputs are combined together with UV irradiation as power supply. Their truth tables are reported below (Table 4). The combinational logic circuits equivalent to these truth tables are illustrated in Fig. 5. Twenty simple logic elements AND, NOT, and OR are necessary to reproduce the functions performed by a single molecule. This is one of the most complicated logic networks reported so far in the chemical literature.
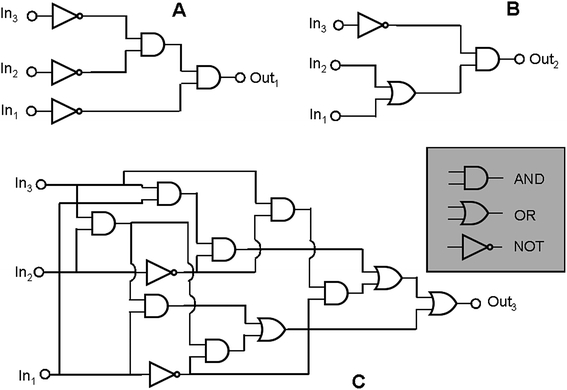 | ||
| Fig. 5 The three logic circuits that can be implemented through the chromogenic behaviour of SpO. Each circuit has HClO4, AlCl3 and Cu(ClO4)2 as chemical inputs. For the circuits A, B and C the outputs are the absorbance values at 611 nm, 485 nm and 423 nm, respectively. | ||
| In1 (H+) | In2 (Al3+) | In3 (Cu2+) | Out1 (A(611 nm)) | Out2 (A(485 nm)) | Out3 (A(423 nm)) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 |
The computational power of SpO does not stop here. By switching from a digital- to an analog-type addition of the chemical inputs H+, Al3+, Cu2+, and by using UV radiation as power supply, the solution of SpO can acquire an “infinite” number of colours (reminding that two colours are different when just one of the three colour coordinates, R, G, B, assumes a different value) because there are plenty of photo-stationary states which are achievable. In the case of an analog addition of either HClO4 or AlCl3, the colour of the solution changes in chameleonic way from blue to cyan, to grey up to orange by increasing progressively the amount of chemical input. In the case of an analog addition of Cu(ClO4)2, the colour of the solution changes from blue to green, to yellow at different saturation levels. The simultaneous injection of two chemical inputs into the solution of SpO favours the achievement of photo-stationary states with further colour changes. In particular, if Al3+ and H+ are added together, both of them contribute to the formation of the same spectral band centred at 485 nm, whereas if H+ is added along with Cu2+, or Al3+ along with Cu2+, the former cation favours the appearance of the band with a maximum at 485 nm, whereas the latter gives rise to the most blue-shifted coloured band, having a maximum at 423 nm. Since the colour attributes change in a continuous way, the chromogenic properties of SpO can be exploited to process the infinite-valued fuzzy logic, having the number of equivalents of the species HClO4, AlCl3 and Cu(ClO4)2 as inputs, and the transmitted intensities of light at the different wavelengths in the visible region as output. To process fuzzy logic, it is necessary to build a Fuzzy Logic System (FLS). A FLS consists of three main elements:61,64 a fuzzifier, a fuzzy inference engine and a defuzzifier. If the Mamdani's method65 is chosen, in order to build the fuzzifier and defuzzifier, the granulation of all the variables involved must be performed by the operator.66 Each input is partitioned into four fuzzy sets, labelled as low (L), medium (M), high (H) and very high (VH) (whose shapes and positions are shown in Fig. 6: graph A for H+ and Cu2+, and graph B for Al3+). For the granulation of the output, the fuzzy nature of human colour perception24,67 is imitated. Human beings have three types of cones (the red, green and blue ones), which play like three spectral fuzzy sets, whereby colours are distinguished. Similarly, for the FLS based on SpO, the visible spectral region, representing the universe of discourse for the output, is partitioned in three fuzzy sets that are the colour-matching functions, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) , ȳ,
, ȳ, ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) , whereby the CIE (Commission Internationale de l'Éclairage) standardized the sensitivity of human eye in 1964 (see Fig. 6). The defuzzifier maps output fuzzy sets into crisp physical numbers, by transforming the transmittance spectra (T(λ)) recorded at the photostationary states, into values of the RGB colour coordinates, according to the procedure established by the CIE.49
, whereby the CIE (Commission Internationale de l'Éclairage) standardized the sensitivity of human eye in 1964 (see Fig. 6). The defuzzifier maps output fuzzy sets into crisp physical numbers, by transforming the transmittance spectra (T(λ)) recorded at the photostationary states, into values of the RGB colour coordinates, according to the procedure established by the CIE.49
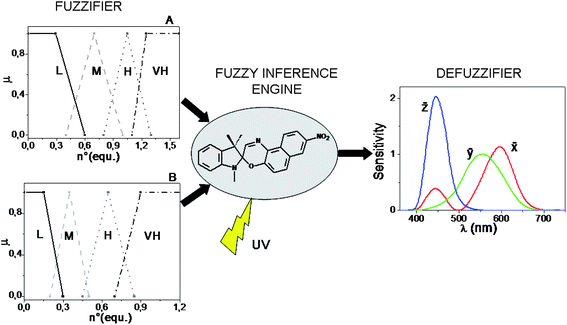 | ||
Fig. 6 Structure of the fuzzy logic systems built by the Mamdani's method and based on the chromogenism of SpO. The chemical inputs are partitioned in four fuzzy sets and the optical output in three fuzzy sets which are the colour-matching functions, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) , ȳ, , ȳ, ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) . . | ||
The third fundamental element of a FLS is the inference engine. It requires the formulation of fuzzy rules, i.e., linguistic statements of the type “IF…, THEN…” based on the experimental evidences. A FLS has been built with H+ and Al3+ as inputs and it is based on rules involving all the fundamental fuzzy logic operators (AND, OR, NOT); another FLS has been built with H+ and Cu2+ as inputs and it is based on rules involving only AND, NOT operators, because H+ and Cu2+ produces absorption bands in different regions of the visible spectrum.
Finally, the case of SpO is remarkable, because a single photochromic, acidichromic and metallochromic species can be used to implement complicated binary logic functions and all the fundamental fuzzy logic operators, at the same time. There are other molecules allowing to process both Boolean and fuzzy logic. The first examples proposed61,68 were based on fluorogenic compounds exhibiting smooth hyperbolic relations between the physicochemical inputs and the optical output (similarly to the input–output relations detected for the chromogenic SpO49). An example is the behaviour of carbonyl and nitrogen-heterocyclic compounds exhibiting proximity effects in their photophysics.69–71 If these molecules are electronically excited, a qubit is produced, defined by eqn (7).
| |ψ〉 = a|ψπ,π*〉 + b|ψn,π*〉 | (7) |
The two wave-functions of the linear combination, |ψπ,π*〉 and |ψn,π*〉, are relative to the two electronic excited states, (π, π*) and (n, π*), primarily associated with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C
O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N chemical groups. A few nanoseconds after photo-excitation, |Ψ〉 collapses into the (π, π*) or (n, π*) states, with probability a2 and b2 respectively, due to the interactions with the surrounding microenvironment. If it collapses into |ψπ,π*〉, the molecule can emit light, whereas if it collapses into |ψn,π*〉, the molecule is dark, since it thermally relaxes to the ground state bypassing the (π, π*) state. The values of the a and b coefficients depend on the coupling strength72 between the (π, π*) and (n, π*). The extent of their coupling is inversely proportional to the energy gap between them. The wider the energy gap between the (π, π*) and (n, π*) states, the weaker the coupling between them. When the two electronic states are weakly coupled and (π, π*) lies below (n, π*), the a coefficient of eqn (7) can be large. Therefore, the probability a2 that the molecular excited state will collapse into |ψπ,π*〉 will be high. If we consider a solution containing a huge number of molecules of either an aromatic carbonyl or an heterocyclic compound, a large a coefficient will mean a high fluorescence quantum yield (ΦF) for the macroscopic sample. It is possible to control the strength of the coupling and hence the values of the a and b coefficients through macroscopic physicochemical parameters, such as the temperature (T) and the hydrogen bond donating (HBD) ability of solvent.70 In general, high T favours the coupling, whereas a high HBD ability of the solvent reduces the coupling for an energetic arrangement of the excited states where the (π, π*) state lies below the (n, π*) state. Therefore, ΦF grows up by cooling (i.e. reducing T) and solubilising the compound into a solvent having high HBD ability, as shown for 6(5H)-phenanthridinone and Flindersine by Gentili.67 It is noteworthy that ΦF changes smoothly, in a hyperbolic rather than sigmoid manner. In agreement to what happens in electronics, the best accomplishments of fuzzy inference engines have been achieved so far by analogue electronic circuits,73 based on signals which vary smoothly, in linear or hyperbolic manner. On the other hand, the best operative conditions to process binary logic are sigmoid electrical signals, which vary steeply as in the McCulloch–Pitts neural model74 where the logistic function has a large λ gain parameter (see Fig. 1). The smooth dependence of ΦF on T and HBD ability of solvent for flindersine and 6(5H)-phenanthridinone has been exploited to implement the AND fuzzy logic operator.61
N chemical groups. A few nanoseconds after photo-excitation, |Ψ〉 collapses into the (π, π*) or (n, π*) states, with probability a2 and b2 respectively, due to the interactions with the surrounding microenvironment. If it collapses into |ψπ,π*〉, the molecule can emit light, whereas if it collapses into |ψn,π*〉, the molecule is dark, since it thermally relaxes to the ground state bypassing the (π, π*) state. The values of the a and b coefficients depend on the coupling strength72 between the (π, π*) and (n, π*). The extent of their coupling is inversely proportional to the energy gap between them. The wider the energy gap between the (π, π*) and (n, π*) states, the weaker the coupling between them. When the two electronic states are weakly coupled and (π, π*) lies below (n, π*), the a coefficient of eqn (7) can be large. Therefore, the probability a2 that the molecular excited state will collapse into |ψπ,π*〉 will be high. If we consider a solution containing a huge number of molecules of either an aromatic carbonyl or an heterocyclic compound, a large a coefficient will mean a high fluorescence quantum yield (ΦF) for the macroscopic sample. It is possible to control the strength of the coupling and hence the values of the a and b coefficients through macroscopic physicochemical parameters, such as the temperature (T) and the hydrogen bond donating (HBD) ability of solvent.70 In general, high T favours the coupling, whereas a high HBD ability of the solvent reduces the coupling for an energetic arrangement of the excited states where the (π, π*) state lies below the (n, π*) state. Therefore, ΦF grows up by cooling (i.e. reducing T) and solubilising the compound into a solvent having high HBD ability, as shown for 6(5H)-phenanthridinone and Flindersine by Gentili.67 It is noteworthy that ΦF changes smoothly, in a hyperbolic rather than sigmoid manner. In agreement to what happens in electronics, the best accomplishments of fuzzy inference engines have been achieved so far by analogue electronic circuits,73 based on signals which vary smoothly, in linear or hyperbolic manner. On the other hand, the best operative conditions to process binary logic are sigmoid electrical signals, which vary steeply as in the McCulloch–Pitts neural model74 where the logistic function has a large λ gain parameter (see Fig. 1). The smooth dependence of ΦF on T and HBD ability of solvent for flindersine and 6(5H)-phenanthridinone has been exploited to implement the AND fuzzy logic operator.61
Specific multi-switchable chromogenic and fluorogenic compounds exhibiting sharp spectral modifications after physical and chemical inputs have been proposed as moleculators,55,56,62,63i.e., as molecular scale calculators. The highest complexity of arithmetic operations is achieved in binary full adders and full subtractors. A 3-input full-adder is composed of one half-adder passing its sum digit to a second half-adder. The half-adder is composed of AND and XOR gates running in parallel to process the two input bits so that the AND gate outputs the carry digit and the XOR gate outputs the sum digit. A 3-input full-subtractor is composed of one half-subtractor passing its borrow digit to the second half-subtractor. A half-subtractor has parallel INHIBIT and XOR gates, which output the borrow and difference digits, respectively.
The first chromogenic molecule integrating both functions is fluorescein.75 Multiple protonation and deprotonation processes of fluorescein give rise to four distinct states: monocation, neutral, monoanion, and dianion. Each state is characterized by a specific absorption spectrum. Two analytical wavelengths have been selected: 447 and 474 nm. At 447 nm, the absorbance values of both monocation and monoanion are high, whereas at 474 nm the absorbance values of both monoanion and dianion are high. The neutral form has low values at both wavelengths. In order to implement the full adder, NaOH is used as input, the transmittance at 447 nm is assigned to the sum output, while the absorbance at 474 nm is assigned to the carry output. The operation starts from the monocation. The set of inputs is [0, 0, 0]. The monocation state is characterized by low transmittance at 447 nm and low absorption at 474 nm. It returns sum = 0 and carry = 0. Addition of one equivalent of NaOH yields the neutral form of fluorescein, which show high transmittance at 447 nm and low absorbance at 474 nm: sum = 1, carry = 0. Addition of the second equivalent of NaOH yields the monoanion, characterized by low transmittance at 447 nm and high absorbance at 474 nm: sum = 0 and carry = 1. Injection of the third equivalent of the strong base yields the dianion which has high transmittance at 447 nm and high absorbance at 474 nm: sum = 1 and carry = 1. To implement the full-subtractor, strong acid is assigned to the minuend while a strong base is assigned to the subtrahend and the pay-back. The absorbance values at 447 and 474 nm are selected as outputs. The initial state of the operations is the neutral form of fluorescein. It corresponds to low A values at both 447 and 474 nm: difference = 0 and borrow = 0. The impact of one equivalent of H+ gives the monocation having high A(447 nm) and low A(474 nm). It corresponds to diff. = 1 and borrow = 0. On the other hand the impact of one equivalent of OH− produces the monoanion having high A(447 nm) and high A(474 nm): diff. = 1 and borrow = 1. The addition of equimolar amounts of H+ and OH− gives the neutral form: diff. = 0 and borrow = 0.
In the literature55 there are other examples of chemically driven moleculators, similar to fluorescein. All of them require sequential addition of chemicals to perform calculations and to reset the device to its initial state. Their operating speed is restricted to the diffusion rate of the chemical inputs. Moreover, the constant increase of the volume of the solution containing the moleculator may be a concern for executing multiple arithmetic cycles. Finally, the processing power is still limited to a small number of bits. Much more promising are luminescent materials involving multi-photon photophysical events. In fact, these processes are usually very fast and reversible. An example is offered by a bichromophoric molecule: a rhodamine–azulene conjugate enabling the implementation of a reversible all-optical binary full-adder.76 Excitation of the rhodamine moiety with either hν1 or hν2 photons populates the S1(Rh) state, which efficiently transfers its energy to the lower S1(Az) state of azulene. S1(Az) generates a signal which represents the sum digit. The same output can be achieved by direct excitation of azulene with hν3. The carry output digit is represented by the emission from the S2 states of rhodamine or azulene. The possible combination of inputs are reported in Table 5. The emission from the S2 of rhodamine requires biphotonic absorption and emission from the S2 state of azulene needs an efficient intramolecular energy transfer.
| Inputs | Outputs | |||
|---|---|---|---|---|
| hν 1 | hν 2 | hν 3 | Sum S1(Az) | Carry S2 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 (S2(Rh)) |
| 0 | 1 | 1 | 0 | 1 (S2(Az)) |
| 1 | 0 | 1 | 0 | 1 (S2(Az)) |
| 1 | 1 | 1 | 1 | 1 (S2(Rh)) |
The chromogenic and fluorogenic compounds described so far, enable complicated logic functions and fundamental arithmetic, such as the addition and subtraction of three binary digits, to be implemented. Few photochromic, electrochromic and fluorogenic molecules have been proposed also as multiplexer and demultiplexer,77,78 encoders–decoders.79–81 All these logic operations, are combinatorial in nature, meaning that the history of input application has no consequences for the function of the device. When the output of a system depends on the current state, which is usually a function of the previous input, and the present input, the system processes sequential logic.82 Hence, sequential logic implies the existence of a memory function. This corresponds to the introduction of a feedback loop connecting the output of a logic gate back to one of its inputs. In conventional electronics, sequential logic is applied in the design of memory elements, such as flip-flops, latches and registers, and in protecting information by keypad locks. The first molecular keypad lock proposed is a pyrene–fluorescein dyad83 based on two chemical and one optical input signals and one optical output. What distinguishes this molecule from the other fluorogenic and chromogenic compounds used to implement logic gates is the fact that its output is dependent not only on the proper combination of the inputs but also on the correct order by which these inputs are applied. In other words, one needs to know the exact password (i.e., sequence of inputs) that opens this lock (entailing the emission of a strong fluorescence by the molecule). Later on, an all-photonic version of a molecular keypad lock based on triad with two distinct photochromic units and a fluorescent porphyrin reporter has been presented.84 The exclusive application of optical inputs and outputs enables remote operation and clean resetting without accumulation of the products of computation.
The first example of molecular set–reset latch is a surface-immobilized Os2+ polypyridyl complex.85 When the complex has osmium ion in its 2+ oxidation state, it exhibits a strong band in the blue (state 1), whereas when Os is in its 3+ oxidation state, the absorption almost disappears (state 0). The set input is Co2+, whereas the reset input is Cr6+. When the set input is high, the osmium complex writes and memorizes the binary state 1. On the other hand, when the reset input is high, the state 1 of the complex is erased and the state 0 is written and memorized. A low signal for set and reset preserves the current state of the complex. The switching can be repeated for at least 10 cycles without significant loss of performance and the retention time of the states is 10 minutes. Further improvements in the design of molecular elements of random access memory has been achieved by synthesizing an electrochromic Os-complex structurally similar to the previous one. When this Os-complex86 has been deposited on conductive layer, flip-flop and flip-flap-flop circuits have been implemented by electrical inputs and an optical output (the appearance and disappearance of a colour band). These layers can be cycled at least 1000 times without any significant data loss, and the response time is 200 times faster than the chemically addressable systems.
The multi-switchable chromogenic and fluorogenic compounds implementing complicated combinatorial and sequential logic elements operate in a wireless mode and their molecular structure limits their computational capabilities. Although the strategy described in this paragraph is extremely appealing and elegant, it lacks in versatility: a different molecule has to be designed, synthesized, and analyzed every single time a different complex logic function has to be performed. The alternative strategies, as already anticipated, are based on communication among molecules. They are presented in the next paragraph.
A bright example of physical communication among molecules is the phenomenon of light up-conversion by triplet–triplet annihilation (TTA). It involves a pair of light-emitting materials.87–89 The TTA up-conversion is a photophysical process involving usually a coloured coordination compound and an organic fluorophore, giving rise to the rare anti-Stokes emission, i.e., the emission of light having wavelengths shorter than those of the absorbed radiation. The coloured coordination compound plays the role of sensitizer (Se): it absorbs the low frequency photons and due to a high intersystem crossing quantum yield, it produces a huge number of triplet states characterized by long lifetimes (of the order of microseconds and more). If we remove atmospheric oxygen from the solution by bubbling nitrogen or argon, the triplet states of Se can phosphoresce. Conceiving the bubbling gas, either N2 or Ar, as input and the phosphorescence of Se as output, the YES logic function can be implemented when positive logic conventions are fixed for all the variables. In the presence of a properly chosen organic fluorophore (see the paper by Zhao and co-workers88 to find out which are the properties a good sensitizer and a good organic fluorophore should have in order to give a highly efficient up-conversion process), the triplet state of Se transfers its energy to the triplet state of the organic fluorophore (E), most often through a collisional mechanism. When at least two triplet states of E are produced, they can collide and annihilate, producing a singlet excited state of E (see Fig. 7). Since E is an organic fluorophore, it will relax to its ground state mainly by emitting light. The light emitted by E has frequencies larger than those of the radiation absorbed by Se. In Fig. 7, a specific case involving a palladium octaethyl-porphyrin (PdOEP) as sensitizer and tetraphenyl-pyrene (TPPy) as emitter is shown. PdOEP and TPPy converts green into violet light.90
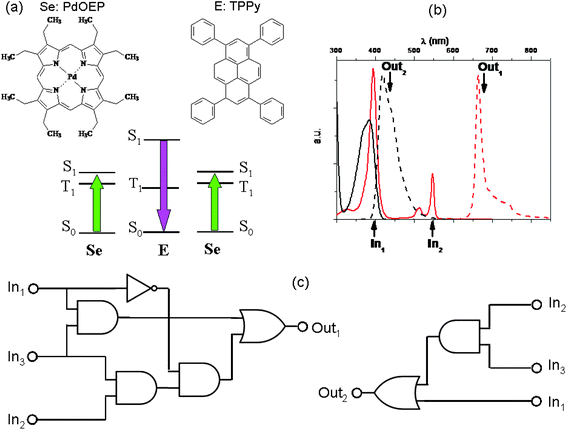 | ||
| Fig. 7 A TTA up-conversion process involving PdOEP as sensitizer (Se) and TPPy as emitter (E), whose molecular structures are in (a) along with a scheme of their relative energy levels. The pair PdOEP–TPPy convert green light into violet light. In (b) the continuous traces represent the absorption spectra (in black that of TPPY and in red that of PdOEP), whereas the dashed traces represent the emission spectra (black for TPPy and red for PdOEP). (c) If we choose λexc = 400 nm, λexc = 546 nm and N2 as the first (In1), second (In2) and third (In3) inputs, respectively, complicated binary logic circuits can be implemented with the phosphorescence of PdOEP (Out1) and the fluorescence signal of TPPy (Out2) as outputs. | ||
In the absence of oxygen, if radiations having wavelengths of 400 nm and 546 nm are used as inputs and the PdOEP phosphorescence and TPPy fluorescence are chosen as optical outputs, the OR logic gates can be implemented, based on positive logic conventions for all the optical variables (see Table 6).
| In1 | In2 | Out1 | Out2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
| OR | OR |
On the other hand, if green light (λexc = 546 nm) and nitrogen are used as inputs, the AND logic gates can be implemented using the PdOEP phosphorescence signal and the up-converted fluorescence of TPPy as outputs (see Table 7).
| In2 | In3 | Out1 | Out2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| AND | AND |
Combining the actions of the two optical inputs (i.e., the violet and green exciting light) with that of N2, and exploiting the phosphorence and fluorescence bands as outputs, complicated logic circuits can be implemented as shown in Fig. 7c and the truth tables are reported in Table 8. Seven simple logic elements AND, NOT, and OR are necessary to reproduce the functions performed by the pair of two simple light-emitting compounds, communicating through an effective intermolecular energy transfer.
| In1 | In2 | In3 | Out1 | Out2 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
It is amazing to notice that such mechanism of up-conversion is exploited by a genus of dragonfish living in deep sea: the Malocosteus.91 In deep sea, the residual sunlight and bioluminescence are spectrally very restricted with most radiation being in the region 450–500 nm. Not surprisingly, the vast majority of fishes has visual pigments whose absorption spectra have maxima in the blue region, providing a good match between environmental light and visual pigments. The exceptions are three genera of deep-sea dragonfish, Malacosteus, Aristostomias and Pachystomias, which have suborbital photophores producing far-red bioluminescence, whose spectrum has a maximum at 700 nm. Two of them, Aristostomias and Pachystomias, are provided with three very long-wave-shifted visual pigments allowing them to see their own bioluminescence. The third genus of dragonfish, Malacosteus, although it is devoid of the most bathochromic visual pigment, it can perceive its own far-red bioluminescence by an additional pigment which is a mixture of bacteriochlorophyll derivatives (Fig. 8).92 These additional pigments with absorption maxima around 670 nm play like photosensitizers which transfer their energy to the real visual pigments through an up-conversion process, similar to the one described for PdOEP and TPPy. This process of physical communication found in deep oceans is a remarkable hint to how to extend the spectrum of photosensitivity of artificial retinas.
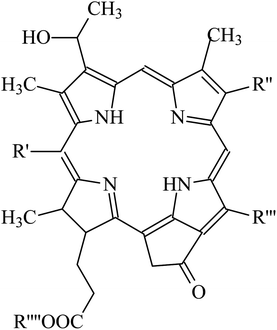 | ||
| Fig. 8 Structure of photosensitizer pigments present in Malacosteus niger (see the paper by Douglas et al.91 for more details about the identity of the R groups). | ||
An example of chemical communication between distinct chromogenic molecules, each having a limited number of states available, is reported by Raymo and Giordani.93 An acidichromic azopyridine (AZ) is dissolved in acetonitrile along with a spiropyran (SP) (see Fig. 9). AZ exists in two states: a purple-red protonated form (with an absorption band centred at 556 nm) and a orange deprotonated form (having an absorption band centred at 422 nm). SP under UV irradiation produces a photo-merocyanine (ME) which is a stronger base than AZ. Therefore, when SP is UV irradiated, the photogenerated ME deprotonates AZH+. Conversely, visible irradiation of the MEH+ promotes the ring closure of the merocyanine and the release of the proton to AZ. The switch SP transduces the two optical inputs, i.e., the UV radiation (In1) and the visible light (In2), into a chemical signal, i.e., the proton, that is exchanged with the two-state AZ switch and converted into a final optical output, i.e., the absorbance change at 556 nm. Since the species MEH+ is thermally stable, when the value of both inputs are zero (i.e., the system is not under irradiation), the system remembers the last state. This memory effect is the fundamental operating principle of sequential logic circuits82 (as we have seen at the end of the previous paragraph 3.a.1), which are used extensively to assemble the memory elements of modern microprocessors.
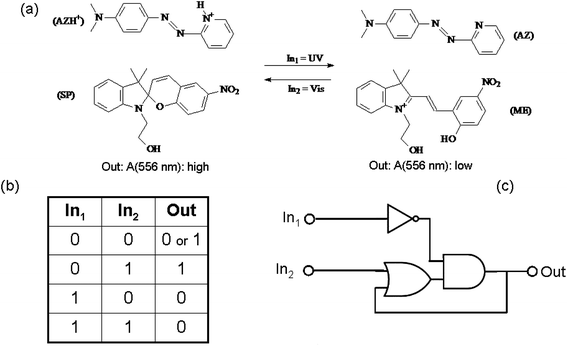 | ||
| Fig. 9 (a) Photoinduced proton transfer between the spiropyran (SP) and the azopyridine (AZ). (b) Truth table and (c) logic circuit associated with the behaviour of the molecular pair. | ||
A similar example of chemical communication based on proton transfer has been presented more recently by Raymo and coworkers.94 A reversible merocyanine-type photoacid communicates with a ruthenium polypyridine complex that functions as a pH-controlled three-state luminescent switch. Inputs of violet light modulate the luminescence output in the red/far-red region of the visible spectrum. Non-destructive reading is guaranteed because the green light used for excitation in the photoluminescence experiments does not affect the state of the gate. The reset is thermally driven and, thus, does not involve the addition of chemicals and accumulation of by-products. Owing to its reversibility and stability, this molecular device can afford many cycles of digital operation. It allows to implement the AND, OR and XNOR logic gates.
Effective chemical communication can be realized not only by protons, but also by electrons as shown by van der Boom.95 Two analogous osmium and ruthenium polypyridyl complexes covalently immobilized on two glass substrates can communicate by a metal ion (Fe3+/Fe2+) as an electron carrier coupled with optical readout. This process allows one system to detect the chemical oxidation state of other interfaces that are not in direct contact but are placed in the same chemical environment. The response time of the setup is sensitive to the substrate dimensions and the volume of the medium.
Chemical communication can be performed also by larger molecules. This occurs, for instance, when the computing elements are enzymes. A careful choice of enzymes and substrates allows complicated logic functions to be implemented.96,97 It is noteworthy the combination of four enzymes proposed by Willner and coworkers.98,99 In a solution containing acetylcholine esterase (AChE), choline oxidase (ChOx), microperoxidase-11 (MP-11), and glucose dehydrogenase (GDH), the inputs are four distinct substrates: acetylcholine (In1), butyrylcholine (In2), O2 (In3), and glucose (In4). The final output is the fluorescence signal of NADH. Acetylcholine or butyrylcholine are hydrolyzed by AChE to form choline that acts as the output of AChE OR gate. Choline produced by AChE, and O2 activate together ChOx enzymatic AND gate yielding betaine aldehyde and H2O2 as products. The other two enzymes, MP-11 and GDH perform the XOR operation on H2O2 and glucose: NADH is produced only when either H2O2 or glucose are oxidized.
Wealthy sources of inspiration for having new ideas on how to carry out complex logic functions based on proteins and other biomolecules are the intracellular and intercellular networks of biochemical reactions occurring in any living being.100 The cell has been defined as the smallest DNA-based molecular computer.101 The function of DNA is to store hereditary information and regulate the expression of this information. In other words, DNA is the memory and the software of the cell. The enzymes are the principal components of the hardware. In fact, enzymes turn on or off chemical reactions, just as transistors turn on or off electron flows in computer circuits. The chemicals are the information carriers as the electrons in microelectronic circuits. Traditionally, the enzymatic activity is described by the lock-and-key paradigm. The lock-and-key paradigm assumes that each protein (the lock) recognizes a specific type of molecule (the so-called substrate, i.e., the key) and then switches its state by making or breaking a precisely selected chemical bond.102 The recognition relies on selective supramolecular interactions between the enzymatic site and the substrate. There are enzymes whose activity is modelled by the Michaelis–Menten mechanism and whose rate of product formation grows in hyperbolic manner with the concentration of the substrate ([Sub]). On the other hand, there are allosteric enzymes, whose activity is influenced by ligands binding in sites different from the catalytic one, and whose rate of product formation grows in sigmoid manner with [Sub]. The first type of enzymes, following the Michaelis–Menten mechanism, is useful to process infinite-valued logic, like fuzzy logic, as we have already stressed previously. On the contrary, the allosteric enzymes are the ideal candidates to process crisp logics, like the binary one.67,103 To give rise to artificial system having the computational capabilities of cells, it is necessary to devise complex mixtures of interacting molecules; in other words, to draw our attention on systems chemistry. Systems chemistry is a new discipline that focus its attention on complex mixtures originating interesting and unexpected emergent properties, i.e., properties that result from the interactions between components and cannot be attributed to any of these components acting in isolation (a recent review is by Ludlow and Otto104). It seems clear that in complex mixtures, the lock-and-key model for proteins does not hold, because small molecules interact with many more proteins than one might expect.105 Proteins, rather being transistors, can be described as fuzzy sets: a substrate belongs to more than one protein and at different degrees in each of them.
The secret for observing emergent properties and hence high computational power is to create networks like the amazing one we have in our brain, made of neurons. Simple computing molecular switches can be mixed together inside the same pot, or otherwise a network can be built by disposing different elementary switches in distinct cells like if they were neurons. In the human nervous system, neurons communicate through chemicals (neurotransmitters); in microelectronics, the circuital elements are linked by properly designed electrical wires and communicate by flows of electrons. For molecular switches, confined in different cells, the integration can be quite easily performed by optical signals.106,107 For example, we know that the UV-induced electrocyclization reaction converting reversibly a spiropyran into a photo-merocyanine can be exploited to block a monochromatic optical signal falling in the visible range where the photo-generated isomer absorbs. This simple molecular switch can be used to implement the NOT logic function, based on optical input (UV) and output (visible). If such a photochromic species is dissolved in two distinct cells and these cells are configured in series respect to a visible probe beam, the NOR logic gate can be realized, based on two UV pumps as inputs (see Fig. 10). On the other hand, if the two cells operate in parallel, the NAND logic gate can be set up (see Fig. 10).
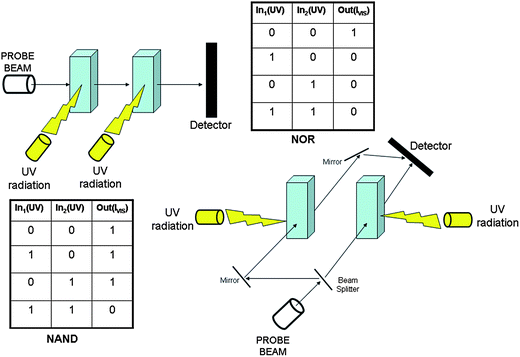 | ||
| Fig. 10 An array of two cells, each containing a solution of a spiropyran, can be used to implement the NOR or the NAND logic gate when they work in series or parallel, respectively. | ||
In principle, following this approach, quite complicated networks of cells containing molecular switches, and wired together through optical signals, can be designed.
Recently, Szaciłowski107 has described the computational power of different arrays of cells containing the nitroprusside ([Fe(CN)5NO]2−)–mercaptosuccinate (RS−) switch (Scheme 1):
 | ||
| Scheme 1 Equilibrium for the nitroprusside–mercaptosuccinate switch. | ||
A single cell works as an AND gate: only when both OH− and K+ are added into the solution the molecular switch changes from the OFF state to the ON state, characterized by a strong absorption band into the green region of the visible spectrum. The simplest array can be achieved by placing in series two or more cells, containing the switching element, and connecting them by a beam of green light. The set of cells has low absorbance at 520 nm only when all the cells have low absorbance, i.e., when in all cells the equilibrium is shifted to the reagents. High absorbance can be in turn obtained when in at least one cell the equilibrium is shifted to the product, which corresponds to OR operation on two outputs of AND gates. Since the logic state of any individual cell depends on the two chemical inputs (OH− and K+), the set of n cells in series can process 2n bits of input data. The logic of the system can be made more complicated by changing the arrangement of the cells. A two-dimensional system of four identical switching cells placed at the four corners of a square, with four sources of green light and four detectors, gives rise to a system with 24 = 16 different states possible. On every edge of the square, green light is absorbed if at least one of the cells is in the ON state. Four edges connecting four cells correspond to four 2-input AND gates and four OR gates (one gate for every edge of the square). A development towards further complexity in logic operations can be achieved by devising a three-dimensional system of switching elements. Eight identical cells can be placed at the corners of a cube, with 12 green light sources and 12 detectors and light guided along all 12 edges of the 2 × 2 × 2 cube. This system has 28 = 256 different states available. Every edge of the cube works like a circuit containing two AND gates and one OR gate. Larger arrays or other geometrical arrangements of the cells lead to increased complexity of logic operations.
So far, we have described multi-cell systems involving only one type of molecular switch. Of course, there is the possibility to devise networks of cells containing different molecular switches.108,109 An example is based on the photochemistry of two species: trans-chalcone and K3[Co(CN)6] complex.109 Under UV irradiation, trans-chalcone (Ct) isomerizes to the cis form, which only in acidic medium undergoes a ring-closure reaction yielding a yellow flavylium ion (AH+). On the other hand, the cyanocobaltate complex releases a basic CN− under UV irradiation. If the two species are mixed together in the same solution, a first pulse of UV radiation converts Ct in AH+ with the appearance of colour. A second UV pulse promotes the release of cyanide anions which increase the pH of the solution and hence the decomposition of the flavylium species and the disappearance of the coloured band. This finding reveals that the mixture behaves according to an XOR logic if the UV flashes are the inputs and the absorbance in the visible is the optical output. It has been proposed to exploit the photochemistry of Ct and K3[Co(CN)6] to build a minimal array of perceptrons, the artificial intelligence units used to mimic the behaviour of neurons (see Fig. 11).
In such a system, In1 and In2 are two equally intense pulses of UV radiation. Each pulse is subdivided in two equally intense beams. One beam of each pulse is sent to cell B containing a solution of a fluorophore emitting in the UV. Such emitted UV radiation is used to excite a solution of Ct and K3[Co(CN)6] contained in cell A. The other beam of each pulse hits cell C containing K3[Co(CN)6]. In such an array, when only one flash is unleashed, a beam is absorbed by cell C, whereas the other is absorbed by cell B which produces a second UV beam that conveyed in cell A triggers the conversion of Ct to AH+. When both UV flashes are fired, two beams reach cell B. The intensity emitted by the fluorophore in B doubles and also the amount of AH+ doubles. In cell C, the first beam promotes the release of a cyanide anion, whereas the second beam is transmitted to cell A where it causes the photoreaction of K3[Co(CN)6] with a consequent increase of the pH and back-conversion of the previously formed AH+ to Ct. The promise of such a system grounds on the possibility of changing the “weights” of the connecting signals (such as the splitting ratio of each radiation pulse or the composition of the solutions in the cells). This system traces the way for implementing networks of communicating cells, each containing simple switches, with the hope of reaching a sufficiently high level of complexity to observe emergent properties.
![A minimal artificial neural network involving a fluorescent compound in cell B, K3[Co(CN)6] in cell C and Ct + K3[Co(CN)6] in cell A. The communication among the cells occurs through optical signals: In1 and In2 are two UV pulses and the output is the absorbance in the blue region.](/image/article/2013/RA/c3ra44657c/c3ra44657c-f11.gif) | ||
| Fig. 11 A minimal artificial neural network involving a fluorescent compound in cell B, K3[Co(CN)6] in cell C and Ct + K3[Co(CN)6] in cell A. The communication among the cells occurs through optical signals: In1 and In2 are two UV pulses and the output is the absorbance in the blue region. | ||
A completely different hardware to set up chemical circuits processing complicated logic functions, is based on programmable microfluidic systems and active mass transport.110,111 In these systems, the microfluidic channels are the wires that distribute the chemical information, while the reaction chambers are places where the chemical logic gates work. Relatively complex logic functions, such as the half adder, have been implemented by fluorescein and rhodamine derivatives exploiting the sensitivity of their emission on physicochemical inputs.
3.b. The Belousov–Zhabotinsky reaction as a dynamical prototype of a neuron
The nonlinear dynamical properties of neurons in the brain can be imitated through particular chemical transformations such as the Belousov–Zhabotinsky (BZ) reaction, which, in the whole, is a catalytic oxidative bromination of malonic acid by bromate in acidic medium:112,113 | (8) |
Various metal ions or metallo-complexes, for example cerious ions or ferroin (i.e., tris-(1,10-phenantroline)-iron(II)), can serve as the catalyst. Although the chemistry of the BZ reaction does not share anything with the chemistry involved in the workings of a neuron (see paragraph 2), the BZ reaction can reproduce the main neural dynamical behaviours. A neuron is an example of a very far-from-equilibrium system, which, in its phase space, can trace a limit cycle or stand on a stable stationary state (see Fig. 12). In the former case, the neuron will show periodic spiking (Fig. 12b), whereas in the latter, it will be resting unless a strong perturbation will promote a temporary shift away from the initial condition, corresponding to the release of an action potential (Fig. 12a). The same holds for the BZ reaction.
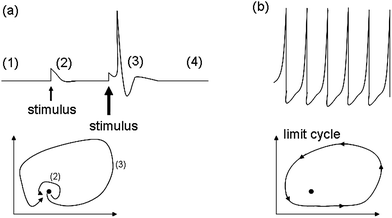 | ||
| Fig. 12 Possible dynamics of a neuron. In (a) a resting neuron (1) is perturbed by a (2) small stimulus, then by a large stimulus (3); in the latter case, before recovering the resting state, it fires an action potential. The graph, below the trace, represents the dynamics of the neuron in its hypothetical phase space: the fixed point corresponds to a steady state. In (b) a spiking neuron goes through a limit cycle in its phase space and it fires action potentials periodically. | ||
The mechanism of the BZ reaction, proposed by Field, Körös, and Noyes,114–116 is based on the existence of two sets of reactions. The first set (A) consists of non-radical reactions (see eqn (9)):
 | (9) |
The net effect of set A is removal of Br− and production of BrCH(COOH)2. Set A is relevant when the concentration of Br− is high (above the critical value of 5 × 10−6[BrO3−]) and the catalyst is present mainly in its reduced form (for instance Ce3+ in the case of the cerium-ion catalyst). The solution is red in the presence of the reduced form of ferroin, which can be used as redox indicator. When [Br−] is driven below its critical value, a new set of reactions becomes important, i.e., set B (eqn (10)):
 | (10) |
Set B is based on mono-electronic reactions and radicals. It involves an autocatalytic step (regarding HBrO2) and Ce4+ is produced. When set B dominates, the solution becomes blue coloured in the presence of the redox indicator. For oscillation to occur, a way must exist to turn off set B, i.e., to reset the system by reducing Ce4+ back to Ce3+. This is done by a third set of reactions, i.e., set C. The main reactions occurring in set C are reported in eqn (11):
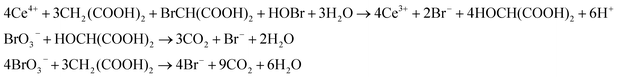 | (11) |
In set C, malonic acid is finally oxidized to CO2 and H2O; Ce4+ is consumed and Br− is again produced. When [Br−] becomes higher than the critical value, the reaction switches to set A, again.
The contour conditions (i.e., concentrations of the reagents, temperature, and flow rate in case the reaction is performed in an open system) determine if the BZ reaction is in oscillatory regime or it stays in a resting stationary condition. In the former case, the colour of the solution will switch from red to blue and again to red, periodically; in the latter case, the solution will maintain the red or blue colour depending on the electric potential of the solution (if the colour is red, it means that the elementary steps of set A occur; if the colour is blue, it means that the elementary steps of set B happen).
The BZ reaction has been used as computing element for many purposes, with the information encoded either in the time domain or as chemical concentrations. Examples of both approaches are presented in the next paragraphs.
By using the volumes of the KBr and AgNO3 solutions as inputs and ΔT as output, two different binary logic functions can be implemented after fixing positive logic conventions for all the variables.118 At low phase of addition, both Br− and Ag+ delay the appearance of the spike, that is they favour positive ΔT values. This means that the addition of Br− and Ag+ at low phase allows the OR gate to be implemented. On the other hand, when Ag+ is added at high phase, it always triggers a spike; i.e., it plays like an activator, whereas Br− is still an inhibitor. At high phase of addition, the “TRUE whenever KBr is true” logic function can be carried out. If the phases of KBr and AgNO3 addition are fixed as inputs and ΔT as output, after choosing positive logic conventions for the inputs and a negative logic convention for the output, the INHIBIT logic gate can be implemented.118 If we compare the computational power of the BZ reaction in time domain, with that of the multiswitchable chromogenic and fluorogenic compounds described in paragraph 3.a.1, we observe that the oscillatory BZ reaction is not a multiply configurable binary logic function like chromogenic and fluorogenic molecules usually are. However, an advantage in the use of the BZ reaction, carried out in an open system, consists in the constant renewal of the content of the solution, avoiding the accumulation of the products of the computation.
An analytic investigation of the dependences of ΔT on the volumes of the KBr and AgNO3 solutions and their phase of addition, reveals that such relations are smooth and almost linear.118 Therefore, these relations are suitable to process fuzzy logic. A few fuzzy logic systems can be built by using either V(KBr) and V(AgNO3) or φ(KBr) and φ(AgNO3) as inputs and ΔT as output. Since Ag+ behaves as either an activator or an inhibitor depending on the phase and the amount added, it is possible to generate FLSs whose inference engines are based on rules involving all the fundamental fuzzy logic operators: AND, OR and NOT. Therefore, the BZ reaction is the second example of chemical system allowing to implement the fundamental fuzzy logic functions, besides the case of SpO (see paragraph 3.a.1). The chromogenic SpO allows more complicated binary logic functions to be processed respect to the BZ reaction. However, the reset time of the BZ reaction is shorter than that of SpO: it requires a few tens of seconds (under the experimental conditions chosen by Gentili et al.118) respect to the hundreds of seconds the merocyanine (MC) needs to revert back thermally to SpO at room T.
The possibility of processing fuzzy logic by using the oscillatory BZ reaction suggests that a real pacemaker cell could process fuzzy logic in much the same fashion as the BZ reaction does, although the detailed workings of pacemakers or other oscillatory cells are quite different from those of an oscillating BZ reaction. Investigations on real pacemaker cells are needed to confirm or belie this hypothesis.
Since the amazing computational performances of our brain relies mainly on the emergent properties of neural networks, it is important to study the coupling between artificial neurons. In real neurons, signal transmission is typically unidirectional and takes place by discrete pulses of neurotransmitters at synapses. Therefore, the attention must be focused on pulse-coupled oscillators. When two ferroin-catalyzed BZ oscillators, operating in continuously fed stirred tank reactors (CSTRs), are pulse-coupled through symmetric, reciprocal release of either inhibitor or activator or mixed, and at variable time delay, many dynamical regimes can be achieved.120 Mutual inhibitory coupling can give rise to the following dynamical regimes (see Fig. 13a): anti-phase oscillations (a1) when the time delay (τ) is zero and the concentration of [Br−] is medium; in-phase oscillations (b1) when τ is large and [Br−] is small; irregular oscillations (c1) when τ is zero and [Br−] is large; suppression of oscillations (d1) in one artificial neuron when τ is zero and [Br−] is very large, with the suppressed oscillator in the reduced state. The mutual excitatory coupling generates different dynamical regimes: almost in-phase oscillations or the so-called master and slave condition (a2) when τ is zero and [Ag+] is low; bursting behaviour (b2) when τ is low and [Ag+] is high; bursting patterns cannot be observed (c2) if the time delay is reduced; at larger delay time, regular fast anti-phase oscillations (d2) have been observed; suppression of oscillations (e2) at very large [Ag+] and τ with the suppressed oscillator maintained in the oxidized state. The mixed excitatory–inhibitory coupling produces further patterns: the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 resonance (a3) when both [Br−] and [Ag+] are low; the 4
1 resonance (a3) when both [Br−] and [Ag+] are low; the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 resonance (b3) with a slightly higher [Ag+]; the 1
5 resonance (b3) with a slightly higher [Ag+]; the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (c3) and the 1
2 (c3) and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (d3) resonances when [Br−] is even larger and for an increasing [Ag+]; the suppression of the oscillations can be achieved in the CSTR where the inhibitor is injected when [Br−] is very high.
3 (d3) resonances when [Br−] is even larger and for an increasing [Ag+]; the suppression of the oscillations can be achieved in the CSTR where the inhibitor is injected when [Br−] is very high.
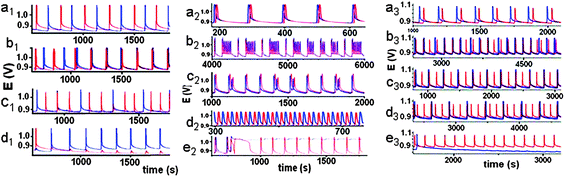 | ||
| Fig. 13 Dynamical regimes achievable in the case of mutual inhibitory coupling (from a1 to d1); mutual excitatory coupling (from a2 to e2); mixed coupling (from a3 to e3). The experimental details can be found in ref. 120. | ||
The many dynamical regimes depicted in Fig. 13 are examples of temporal patterns. They are achievable for different combinations of effectors and different delay times of their release. These temporal patterns constitute the reasoning code for neurons and their nets, according to the neuroscience axiom that “neurons that fire together, wire together”.121,122 The next step along this research path is to increase the number of coupled artificial neurons and study the emerging temporal patterns. The main drawback of this approach is its hybrid nature. In fact, the chemical coupling between the CSTRs is ruled by a silicon-based computer.
3.b.2.1 Open reactors with BZ or alternative bi-stable reactions connected by active mass transport. Networks of open bi-stable kinetic BZ reaction systems coupled by reciprocal active mass transfer (using peristaltic pumps) have been proposed as chemical computing devices.123 The state with high or low Ce4+ concentrations are assigned to logical “true” or “false”, respectively. A net of three feed-forward Continuous-flow Stirred Tank Reactors (CSTR) is needed to implement the fundamental binary logic functions AND, OR, NAND and NOR. Two CSTRs constitute the input layer (1 and 2 in Fig. 14) and the third CSTR (3 in Fig. 14) is the output. The states of the input reactors are switched manually by adjusting the flow rate arbitrarily. The output reactor is coupled to both input reactors, and the flow rate (kf3) is calculated according to the linear coupling equation:
| kf3 = w13[Ce4+]1 + w23[Ce4+]2 + b3 | (12) |
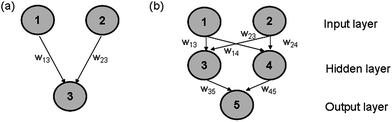 | ||
| Fig. 14 Feed-forward nets with (a) three CSTRs required to implement the AND, OR, NAND, NOR logic gates, and with (b) five CSTRs to implement the XOR and XNOR gates. | ||
The terms [Ce4+]1 and [Ce4+]2 represent the concentration of the Ce4+ in the first and second input CSTR, respectively.
A net of five feed-forward CSTRs are needed to implement the XOR and XNOR logic functions. Two CSTRs in the input layer, two in the hidden layer, and one in the output layer, have been coupled as indicated in Fig. 14 and according to the following equations,
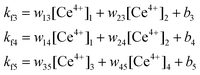 | (13) |
The chemical reaction network is a versatile basis for computation. In principle, it can be as powerful as a universal Turing machine.124 However, its main drawback is the low speed of information processing respect to the semiconductor technology. In order to approach a steady state in a reactor, less than three residence times are required. That means about 1 h in the experiments carried out by Lebender and Schneider.123 Since the state of a reactor belonging to a specific layer, depends on the state of all reactors in the previous layer, the larger the number of reactors, the longer the time to be awaited for achieving the final outcome. Networks of bi-stable chemical reactions have been proposed also to construct a binary decoder, a binary adder, and a stack memory.124 However, their most promising application concerns storing patterns and solving pattern recognition problems.125 The theoretical and experimental proofs presented by Ross and co-workers126–128 are based on the iodate–arsenous acid reaction rather than on the BZ one. However, the ideas presented can be extended also to the BZ reaction, because what is required is a bi-stable process. For the iodate–arsenous reaction, when iodate is in stoichiometric excess, the overall transformation is
| 2IO3− + 5H3AsO3 + 2H+ → I2 + 5H3AsO4 + H2O | (14) |
The autocatalysis in iodide results in bistable states of either low or high iodine concentration. The state of each reactor is determined visually by adding starch to the reactor inflows, the high iodine state being blue and the low iodine state colourless. Experimentally, a network of eight CSTRs coupled by mass transport have been realized to store and recognize patterns. The network is programmed by setting the pumping strengths between every pair (i and j) of CSTRs through a Hebbian type rule:
| kij = λθ[∑p(2Rpi − 1)(2Rpj − 1)] | (15) |
3.b.2.2 BZ reaction-diffusion processors. A tighter imitation of computational strategies of biological systems spurs the scientific community to devise alternative chemical artificial intelligent systems, based always on bi-stable reactions, involving not an active mass transfer system (controlled by silicon-based computers) but rather spontaneous diffusion. This is the idea of contriving reaction-diffusion computers.17 A reaction-diffusion computer is a spatially extended chemical system, which processes information using interacting growing patterns, excitable, sub-excitable and diffusive waves. In reaction-diffusion processors, information is encoded as concentration of chemicals and the computation is performed via the interaction of wave fronts. In paragraph 3.a.1, we have seen that in the case of chromogenic and fluorogenic materials, each molecule is a computing element, working in parallel and most often without communicating with the surrounding partners. In the case of BZ reaction-diffusion, the elementary computing elements are micro-volumes, contained in traditional chemical vessels: they work in parallel and are in communication with the closest neighbours due to the diffusion. The BZ reaction-diffusion processors can compute in geometrically constrained architectures, in free space, or encapsulated in elastic membranes.
3.b.2.2.a Geometrically constrained architectures. In geometrically constrained architectures, signal-carrier waves are generated in an excitable chemical medium and propagate along pre-determined channels. An excitable chemical medium is a system where an autocatalytic reaction such as the BZ occurs. The reagents are mixed in concentrations which maintain the overall system in a single stable stationary state. Small perturbations uniformly decay, whereas large perturbations can be enhanced by orders of magnitude and evolve for a long time before they finally vanish and the system approaches the stable state again.129 If such system is spatially distributed, then its local excitation can propagate in space in the form of a pulse of concentration. After an excitation, the system is refractory, which means it takes a certain recovery time before another excitation can take place (in the case of BZ reaction, an excitation is usually carried out by a silver wire). If we assume that the state that corresponds to a high concentration of a particular species (for example Ce4+ in the BZ) is the logical true state (or “1”) and the state corresponding to a low concentration is the logical false state (i.e. “0”), then a pulse describes a bit of information travelling in space. A resting neuron is a biochemical example of excitable system: if it receives strong perturbations in its dendrites, it fires an action potential and then rests again (see Fig. 12a).
In analogy with the structural constraints of either a nerve system or a micro-electronic processor, we can process information coded in travelling waves using an intentionally introduced geometrical structure. An asymmetric arrangement of two mesoporous glass plates with ferroin loaded at their surfaces (see Fig. 15), allows unidirectional transmission of chemical waves. The distance between the side of the plate A and the top of B is selected such that a pulse of excitation propagating in A and terminating at its right end gives sufficiently strong perturbation to excite the tip of B. For the same distance the excitation of the B plate generating a wave propagating from right up to the tip of B is too small to excite the side of A. This arrangement constitutes an example of chemical diode,130 whose alternative designs have been described in ref. 131 and 132.
 | ||
| Fig. 15 Scheme for a chemical diode based on unidirectional propagation of chemical waves. A and B are the excitable media, i.e., the glass plates with ferroin loaded on their surfaces. The waves propagate only from A to B and not vice versa. | ||
By using specific architectures constraining the chemical waves in excitable media, it is possible to implement also the fundamental binary logic gates.133–136 For example Tóth and Showalter used the narrow channels of two capillary tubes, disposed one in front of the other (see Fig. 16), as signal carriers in excitable BZ solutions.133 As the capillary tube size and the gap width was fixed, either the OR gate or the AND logic function were implemented by changing the concentration of bromate. Above a critical value of [BrO3−], waves initiated in the right or left compartment gave rise to wave initiation in the middle compartment at the tube exit. Below the critical value, no wave initiation was observed in the middle compartment for a single input wave.
 | ||
| Fig. 16 Schematic representation of two blue waves propagating through two capillary tubes and ending in a middle compartment where they interact. | ||
Using an excitable medium and simple structured circuits, it is possible to construct devices, that perform more complicated signal processing operations, for example excitation counters.137 The most successful application is the solution of the problem of finding the shortest path in the labyrinth.138 The labyrinth is made of excitable channels separated by regions that do not allow for interactions between pulses propagating in different channels. It is possible to verify if the distance between two selected points (Pi and Pf) in a labyrinth is shorter than an assumed value d. In order to solve this problem, one excites the medium at point Pi and observe if the wave appears at the point Pf before a certain time interval Δt. The excitation spreads out through the maze, separates at the junctions and pulses enter all possible paths. During the spreading, pulses of excitation can collide and annihilate, but the one that propagates along the shortest path has always unexcited medium in front. The speed (v) of a pulse propagating through the maze can be assumed to be constant if the influence of the corners can be neglected when compared with the time of propagation in the straight channels. The length of the shortest path will be less than d if Δt < d/v. This experiment is remarkable because it shows that an excitable medium confined in a labyrinth finds the shortest path in a highly parallel manner scanning all possible routes at the same time. The time required for the verification (roughly 40 min for the labyrinth described in ref. 138, where the waves propagated at a rate of 2.41 mm min−1) does not depend on the complexity of the maze structure, but only on the distance between the fixed points and the waves' velocity.
The main limitations in using computing excitable media in pre-defined structures are the rigid architectures limiting the operations and the problem of feeding the system of fresh solutions to assure continuous operations.
3.b.2.2.b Free space. A non-stirred layer of the BZ reaction can be regarded as a two-dimensional matrix of one-bit micro-volumetric processors, which work in parallel. Such system can be used for solving some computational problems. For example, it can be exploited to find the fastest path between two points (A and B) in an arbitrary velocity field.139 Of course, if we need to find the fastest path from A and B in a uniform space, it is just a straight line connecting these points. However, if the velocity is a function of the location in bidimensional space, i.e., v(x, y) (this field may be due to either a non-uniform distribution of the reagents or the presence of obstacles),140 the quickest path is not always a straight line. To find it, an excitation wave is triggered in A, and its propagation is recorded at desired time-interval until it reaches point B. The operation is repeated by triggering a wave in B. The intersection points between the wave fronts in the two propagation paths allow the quickest track from A to B to be traced. Ideally, each micro-volume of the layer is a processor exhibiting three possible states: “rest” (which corresponds to the reduced state of the catalyst), “excited” (which corresponds to the oxidized state), and “refractory” (it is the reduced state with a large concentration of bromide preventing back propagation of the wave). These micro-processors transfer their excitation state to the neighbouring elements. The characteristic rate of wave propagation is 0.05 mm s−1. If we assume that the linear dimension of each processor is of the order of 0.1 mm, each processor switches its state every 2 s. Assuming to have a squared dish with a side length of 8 cm, the number of processors is 640
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The computation rate will be of 320
000. The computation rate will be of 320![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 operations per second which is 1011 smaller than that of the fastest supercomputer, i.e., the Chinese Tianhe-2 reaching a rate of 33.86 petaFlop per s. Therefore, the difference in computational rate is striking and it spurs to find out ways to speed up the BZ reaction or discover new excitable media.
000 operations per second which is 1011 smaller than that of the fastest supercomputer, i.e., the Chinese Tianhe-2 reaching a rate of 33.86 petaFlop per s. Therefore, the difference in computational rate is striking and it spurs to find out ways to speed up the BZ reaction or discover new excitable media.
The BZ reaction can be transformed in photosensitive oscillating reaction when the catalyst is the complex ruthenium bipyridyl: [Ru(bpy)3]2+. The absorption of light by Ru2+ induces a dramatic change in its redox properties. In fact, the excited Ru2+ is a strongly reducing agent, able to reduce bromate to the inhibitor bromide. By illuminating the Ru-catalyzed BZ reaction carried out in unstirred free spaces, it is possible to control the propagation of wave front and manipulate the character of wave phenomena.141 If the reagents are in oscillatory regime and are not spread uniformly, the period of oscillations depends on the spatial coordinates, then a “phase wave” propagates over the layer, whose rate is inversely proportional to the phase gradient.142 If the reagents are in excitable regime, a “trigger wave” propagates through diffusion at constant velocity, after an initial perturbation. Trigger waves may also occur in oscillatory regime if a very high phase gradient has been established through a high concentration gradient of chemical substances.
In such a case the velocity of phase waves is very low and trigger waves dominate. By using light it is possible to control the composition of micro-volumes of the system and hence the velocity of waves, suppress oscillations, and let the phase and trigger waves to coexist in the same layer. For example, if a negative image is projected in a liquid layer where the Ru-catalyzed BZ reaction is going in oscillatory regime (the colour switches from orange to blue, and from blue to orange), initially no image appears. As time progresses, because the reaction is light-inhibited, the change of colour occurs first in the non-illuminated area and a positive image is produced. Then, because of auto-oscillations, the reverse takes place. Whereupon, the process repeats periodically. By increasing the intensity of light, the regions of the layer under illumination shift from an oscillatory to an excitatory regime. The regions under the dark remain in oscillatory regime. This situation favours the formation of waves along the contour of the image. They propagate towards the centre of the illuminated region. Such waves can also be used for image smoothing. If an image containing discontinuities of length l less than (1/2)v(Δt) (where v is the velocity of wave and Δt is the time of irradiation) is projected, it will be smoothed by wave propagation. This is a realization of an associative memory device: from an incomplete set of data, the whole pattern may be reconstructed. Therefore, the light-sensitive BZ reaction is a short-term memory, lasting from ten to several tens of periods (e.g. from 5 minutes up to 1 hour or more) depending on the state of the medium and the contrast of the image. The image processing properties of Ru-catalyzed BZ reaction are similar to some of human vision.143–145 For example, the “description of the general properties of an object” when the BZ is in oscillatory regime and under a slight intensity of light, and the “switching to the details of an image” when the intensity of illumination is higher. These properties of human vision are due to the “dark” biochemical processes which follow the first stage of light absorption. The light absorption by cones and rods is well-modelled by photochromic films.146
So far, we have seen that an autocatalytic reaction such as the BZ can proceed in different dynamical regime: oscillatory, excitable, unexcitable (wherein any perturbation simply decays until it disappears). In between the excitable and unexcitable regimes, there is a third level of excitability, named as sub-excitable. In a sub-excitable BZ medium, wave fragments develop, which behave like quasi-particles.147 They exhibit a rich dynamics of collisions.148 When two or more wave-fragments collide, they may fuse, annihilate, generate new wave fragments or change their trajectories. The trajectories of the wave fragments approaching a collision site represent input variables, and the trajectories of the patterns ejected from a collision, and travelling away from the collision site, represent the results of logical operations, i.e., the output variables. There are no predetermined stationary wires. Any trajectory of the travelling pattern is a momentarily wire. Any part of the space can be used as a wire. In this approach, the light-sensitive tris-bipyridine-Ru(II) catalyst has been immobilized on silica gel and then immersed in a solution containing the BZ reagents but catalyst-free, and connected to a CSTR in order to maintain a non-equilibrium state. With such a system, basic logic gates have been implemented149–151 through control of light intensity within each area of the reactor. Moreover, basic arithmetical circuits (i.e., binary counters, adders and multipliers) have been proposed through cellular-automaton models, wherein every resting cell of the automaton two-dimensional lattice takes an excited state if there are exactly two excited neighbours, whereas transitions from excited state to refractory state, and from refractory state to resting state are unconditional.152
3.b.2.2.c Encapsulating the BZ reaction in elastic membranes. A further development towards a closer imitation of real neurons has been accomplished quite recently by encapsulating the BZ reactants in nano-vesicles obtained by a mono-layer of lipids.153 The resulting artificial cells have some interesting parallels with real neurons. In fact, when two or more vesicles are pressed together in solution, the gap between the lipid layer forms a chemical junction similar to a synaptic cleft. Travelling waves can be generated when the BZ solution is in a sub-excitable mode and waves can be used as information signals. By exploiting networks of interconnected discs containing a uniform excitability level of the BZ reaction, it is possible to implement simple and composite logic gates, and memory elements. The photosensitive BZ dispersed in a water-in-oil microemulsion (with the surfactant sodium bis(2-ethylhexyl)sulfosuccinate) can store spatial information for up to an hour, even without replenishment of reactants as it has been demonstrated by Epstein and co-workers.154 Although the BZ vesicles are attracting as neuron-like computing and memory elements, they lack of some relevant peculiar properties characteristics of real neurons, such as multi- and dynamic connections, self-adaptation and longevity. In fact, the BZ vesicles so far prepared are connected only locally, they cannot be sustained beyond exhaustion of the reagents and any self-adaptation mechanism has not been so far devised. A real-world biological system, the Physarum polycephalum, has been proposed as an alternative to encapsulated BZ reaction,155 having properties a little bit closer to those of real neurons. Physarum polycephalum is a single cell with many nuclei which behave like an amoeba. In its vegetative phase (i.e., plasmodium), slime mold actively searches for nutrients. It propagates in similar ways to the waves in excitable or sub-excitable BZ medium, depending on the concentration of nutrients. Like chemical waves in excitable BZ medium, Physarum growing patterns fuse entirely in nutrient-rich conditions. When the substrate is poor on nutrients, plasmodium of Physarum exhibits mobile localizations, pseudopodia, similar to the wave-fragments of sub-excitable BZ medium. Like wave-fragments, pseudopodia collide and give reflection and repulsion. For a Physarum processor data are represented by nutrients and repellents, and the program is coded via disposal of data on the Petri dish. The result of the computation is represented by configuration of protoplasmic network formed by plasmodium. “Physarum computers” have been proposed to solve some computational problems such as shortest path in a labyrinth and spanning tree, based on Physarum foraging behaviour.
When a Physarum processor solves its computational problems, it leaves a trace of its solutions because tree-like structures of protoplasmic tubes are formed and they represent a static memory. This is an advantage respect to the BZ reaction because after the propagation of a chemical wave, the medium returns to a state that is macroscopically identical to the initial resting state. However, a Physarum processor is slower than a BZ one. In fact, in a BZ system, waves propagate with a rate of 2 mm min−1, whereas in plasmodium growing wave-fronts propagate with a speed of 0.1 mm min−1.
4. Outlook and conclusions
The best supercomputers of the TOP500 list are much faster in performing calculations than human brain. But calculations are not as much complex as human thoughts and a rate of 1016 calculations per second is not a recipe for cognition. Will we be able to exploit the best performances in processing power to accurately model human brain and create an artificial intelligence based upon that model? A novel approach developed at IBM, called “Cognitive Computing”,156 promises to operationalize vast collections of neuroscience data by leveraging large-scale computer simulations. In 2009, the Cognitive Computing group at IBM in collaboration with Lawrence Berkeley National Laboratory using the Dawn Blue Gene/P supercomputer, achieved the newsworthy milestone of cat-scale cortical simulations, roughly equivalent to 4.5% of human scale.156 Considering the trends in development of supercomputer technology, the human-scale cortical simulations appear within reach in a decade. What is impressive is that the power and space requirements of such simulations will be presumably many orders of magnitude greater than those of human brain (suffice to say that modern supercomputers fill rooms of more than 500 m2, whereas human brain has a volume of roughly 1.5 L). This disparity is due to the differences between the architecture of von Neumann supercomputers and that of the human nervous system. Supercomputers ground on digital, synchronous, serial, centralized, fast, hardwired, general-purpose, brittle electronic circuits, with a dichotomy between computation and memory. On the other hand, the human nervous system grounds on networks of neurons, working in mixed analog and digital modes, and in asynchronous, parallel, slow, distributed, reconfigurable, specialized, fault-tolerant manners, with memory and computation intertwined together. Yet the brain is fantastically more efficient than the electronic supercomputers: it can achieve five or six orders of magnitude more computation for each joule of energy consumed. In fact, in an electronic computer 96% of the machine's volume is used to transport heat, 1% is used for transporting information and just one-millionth of one per cent is used for transistors and other logic devices. On the other hand, the brain uses only 10% of its volume for energy supply and thermal transport, 70% for communication and 20% for computation.157 Therefore, it is compelling to devise new computing architectures drawing inspirations just from the human nervous system.These new architectures should come closer to the performances and the intelligence of human mind, able to integrate vague information from different sensory systems, form spatiotemporal associations and abstract concepts, and take decisions in complex situations. Chemists are contributing to this ambitious project both unveiling the chemistry of human nervous system and proposing surrogates of its sensory, computing and actuating elements. In this review, it has been shown that chromogenic and fluorogenic materials are excellent artificial sensory systems and the BZ reaction is a remarkable chemical model of neural dynamics. Chromogenic and fluorogenic molecules perceive physical and chemical stimuli: they can detect electromagnetic radiation, several chemicals, mechanical forces and temperature. Moreover, there are some of them which are sensitive to electric fields. In the human nervous system, the sensory cells catch the stimuli and transduce them into electrochemical signals which are sent to the afferent neurons, and finally to the brain. The chromogenic and fluorogenic materials collect the stimuli and use them to modify their molecular structures (determining a colour change) or to emit light. We have seen that either single multi-switchable compounds or molecules with a limited number of states available but communicating reciprocally, are good at processing the information of the stimuli. After completing the computing stage, they send optical signals. These optical signals are caught and decoded by human minds, which retrieve the results of the computations.
The BZ reaction can mimic unexcitable, sub-excitable, excitable and spiking neurons, depending on the contour conditions. Its tight resemblance with the neural dynamics allows pattern recognition problems to be solved. When it is Ru-catalyzed, the BZ reaction becomes photosensitive and acquires noticeable imaging properties.
Of course, all the results achieved so far are simply small steps towards the development of chemical artificial intelligence systems. Many more steps are needed for a tighter imitation of the human nervous system. A three-dimensional wetware containing encapsulated bistable reactions (like the BZ one) will be presumably the new generation of computing machines. They will not substitute current electronic supercomputers, but they will complete them. In fact, these new brain-like computing machines will reproduce, at least in part, the performances of the human nervous system. To confer sensory properties to the 3D wetware, chromogenic and fluorogenic materials will be used. They will be chosen with the aim of computing with words. Therefore, they will be selected to form fuzzy sets. The information of a stimulus will be encoded as a matrix of degrees of membership to the molecular fuzzy sets. The communication inside the wetware will be based on light and photo/chemical waves (see, for instance, the recent hydrodynamic photo-chemical waves involving a photochromic species as an effective and fast way to transfer information).158 To complete the functions of the artificial nervous system, actuators will be devised by using chromogenic and the BZ reaction embedded in specific matrices and in communication with the information processing elements of the artificial brain.
A success in this project of reverse engineering the human nervous system will bring a remarkable contribution to the worldwide goal of understanding more deeply the secrets of human mind and intelligence; Natural Complexity will be more intelligible and further ideas to solve Computational Complexity problems may become available.
Acknowledgements
The author gratefully acknowledges the financial support of the Ministero per l'Università e la Ricerca Scientifica e Tecnologica (Rome, Italy), the University of Perugia [PRIN 2010-2011, 2010FM738P].References
- http://www.top500.org .
- http://www.fujitsu.com .
- R. C. Merkle, Foresight Update, 1989, vol. 6, p. 1.
- R. C. Merkle, Foresight Update, 1988, vol. 4, p. 2.
- R. Kurzweil, The Singularity is near, Viking Penguin, 80 Strand London, England, 2005 Search PubMed.
- J. S. Albus, G. A. Bekey, J. H. Holland, N. G. Kanwisher, J. L. Krichmar, M. Mishkin, D. S. Modha, M. E. Raichle, G. M. Shepherd and G. Tononi, Science, 2007, 317, 1321 CrossRef CAS PubMed.
- C. R. Gallistel and A. King, Memory and the computational brain: Why cognitive science will transform neuroscience, Blackwell/Wiley, New York, 2009 Search PubMed.
- D. Marr, Vision. A Computational Investigation into the Human Representation and Processing of Visual Information, The MIT Press, 2010 Search PubMed.
- E. M. White, J. Yatvin, J. B. Grubbs III, J. A. Bilbrey and J. Locklin, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 1084 CrossRef CAS.
- D. Iqbal and M. H. Samiullah, Materials, 2013, 6, 116 CrossRef CAS.
- I. S. Gunes and S. C. Jana, J. Nanosci. Nanotechnol., 2008, 8, 1616 CrossRef CAS PubMed.
- D. Ratna and J. Karger-Kocsis, J. Mater. Sci., 2008, 43, 254 CrossRef CAS PubMed.
- Y. Zhao and T. Ikeda, Smart Light Responsive-Materials, Azobenzene Containing Polymers and Liquid Crystals, Wiley, Hoboken, NJ, USA, 2009 Search PubMed.
- C. Liu, H. Qin and P. T. Mather, J. Mater. Chem., 2007, 17, 1543 RSC.
- L. Suna, W. M. Huangb, Z. Dingb, Y. Zhaob, C. C. Wangb, H. Purnawalib and C. Tangb, Mater. Des., 2012, 33, 577 CrossRef PubMed.
- A. Lendlein and S. Kelch, Angew. Chem., Int. Ed., 2002, 41, 2034 CrossRef CAS.
- A. Adamatzky, J. Comput. Theor. Nanosci., 2011, 8, 295 CrossRef CAS PubMed.
- C. Koch and I. Segev, Methods in neuronal modeling: from ions to networks, MIT Press, Cambridge, Mass., 2nd edn, 1999 Search PubMed.
- G. Paxinos and J. K. Mai, The Human Nervous System, Elsevier, 2nd edn, 2004 Search PubMed.
- T. E. J. Behrens and O. Sporns, Curr. Opin. Neurobiol., 2011, 22, 1 Search PubMed.
- A. W. Burks, H. H. Goldstine and J. von Neumann, Preliminary discussion of the logical design of an electronic computing instrument, in John von Neumann, Collected works, ed. A. H. Taub, The Macmillan Co., New York, 1963, vol. V, pp. 34–79 Search PubMed.
- L. A. Zadeh, J. Stat. Plann. Infer., 2002, 105, 233 CrossRef.
- L. A. Zadeh, Inform. Contr., 1965, 8, 338 CrossRef.
- P. L. Gentili, International Journal of Unconventional Computing, 2013 Search PubMed , submitted.
- D. C. Knill and A. Pouget, Trends Neurosci., 2004, 27, 712 CrossRef CAS PubMed.
- E. Mach, Contributions to the Analysis of the Sensations (C. M. Williams, Trans.), Open Court Publishing Co., Chicago, IL, USA, 1980 Search PubMed.
- G. Coletti and R. Scozzafava, Fuzzy Set. Syst., 2004, 144, 227 CrossRef PubMed.
- D. Kersten, P. Mamassian and A. Yuille, Annu. Rev. Psychol., 2004, 55, 271 CrossRef PubMed.
- W. J. Ma, J. M. Beck and A. Pouget, Curr. Opin. Neurobiol., 2008, 18, 217 CrossRef CAS PubMed.
- J. Kåhre, The Mathematical Theory of Information, Kluwer Academic Publishers, Norwell (MA), USA, 2002 Search PubMed.
- C. W. Oyster, The Human Eye: Structure and Function, Sinauer Associates, Inc., Sunderland, MA, 1999 Search PubMed.
- C.-Y. Su, K. Menuz and J. R. Carlson, Cell, 2009, 139, 45 CrossRef CAS PubMed.
- B. Lindemann, Nature, 2001, 413, 219 CrossRef CAS PubMed.
- C. Kung, Nature, 2005, 436, 647 CrossRef CAS PubMed.
- R. J. Schepers and M. Ringkamp, Neurosci. Biobehav. Rev., 2010, 34, 177 CrossRef CAS PubMed.
- D. Julius and A. I. Basbaum, Nature, 2001, 413, 203 CrossRef CAS PubMed.
- C. B. Greenberg, Thin Solid Films, 1994, 251, 81 CrossRef CAS.
- C. M. Lampert, Mater. Today, 2004, 7, 28 CrossRef CAS.
- H. Bouas-Laurent and H. Dürr, Pure Appl. Chem., 2001, 73, 639 CrossRef CAS.
- P. L. Gentili, M. Nocchetti, C. Miliani and G. Favaro, New J. Chem., 2004, 28, 379 RSC.
- H. W. Verleur, A. S. Barker, Jr and C. N. Berglund, Phys. Rev., 1968, 172, 788 CrossRef CAS.
- M. R. di Nunzio, P. L. Gentili, A. Romani and G. Favaro, ChemPhysChem, 2008, 9, 768 CrossRef CAS PubMed.
- R. J. Mortimer, A. L. Dyer and J. R. Reynolds, Displays, 2006, 27, 2 CrossRef CAS PubMed.
- G. A. Niklasson and C. G. Granqvist, J. Mater. Chem., 2007, 17, 127 RSC.
- T. Ikeda and J. F. Stoddart, Sci. Technol. Adv. Mater., 2008, 9, 014104 CrossRef.
- P. R. Somani and S. Radhakrishnan, Mater. Chem. Phys., 2002, 77, 117 CrossRef.
- L. Leone, O. Crescenzi, A. Napolitano, V. Barone and M. d'Ischia, Eur. J. Org. Chem., 2012, 5136 CrossRef CAS.
- G. Favaro, C. Clementi, A. Romani and V. Vickackaite, J. Fluoresc., 2007, 17, 707 CrossRef CAS PubMed.
- P. L. Gentili, Phys. Chem. Chem. Phys., 2011, 13, 20335 RSC.
- P. Suppan and N. Ghoneim, Solvatochromism, Roy. Soc. Chem., Cambridge 1997 Search PubMed.
- J. B. Grimm, L. M. Heckman and L. D. Lavis, Fluorescence-based Biosensors: from concepts to applications, Book Series: Progress in Molecular Biology and Translational Science, 2013, vol. 113, p. 1 Search PubMed.
- G. M. Farinola and R. Ragni, Chem. Soc. Rev., 2011, 40, 3467 RSC.
- T. L. Dawson, Color. Technol., 2010, 126, 177 CAS.
- U. Isacsson and G. Wettermark, Anal. Chim. Acta, 1974, 68, 339 CrossRef CAS.
- K. Szaciłowski, Chem. Rev., 2008, 108, 3481 CrossRef PubMed.
- J. Andréasson and U. Pischel, Chem. Soc. Rev., 2010, 39, 174 RSC.
- U. Pischel, J. Andréasson, D. Gust and V. F. Pais, ChemPhysChem, 2013, 14, 28 CrossRef CAS PubMed.
- A. P. de Silva, H. Q. N. Gunaratne and C. P. McCoy, Nature, 1993, 364, 42 CrossRef.
- A. P. de Silva, H. Q. N. Gunaratne, T. Gunnlaugsson, A. J. M. Huxley, C. P. McCoy, J. T. Rademacher and T. E. Rice, Chem. Rev., 1997, 97, 1515 CrossRef CAS PubMed.
- A. P. de Silva and N. D. McClenaghan, Chem.–Eur. J., 2004, 10, 574 CrossRef PubMed.
- P. L. Gentili, Chem. Phys., 2007, 336, 64 CrossRef CAS PubMed.
- F. Raymo, Adv. Mater., 2002, 14, 401 CrossRef CAS.
- A. P. De Silva and S. Uchiyama, Nat. Nanotechnol., 2007, 2, 399 CrossRef CAS PubMed.
- J. M. Mendel, Proc. IEEE, 1995, 83, 345 CrossRef.
- E. H. Mamdani, IEEE Trans. Comput., 1977, 26, 1182 CrossRef.
- L. A. Zadeh, IEEE Software, 1994, 11, 48 CrossRef.
- P. L. Gentili, ChemPhysChem, 2011, 12, 739 CrossRef PubMed.
- P. L. Gentili, J. Phys. Chem. A, 2008, 112, 11992 CrossRef CAS PubMed.
- E. C. Lim, J. Phys. Chem., 1986, 90, 6770–6777 CrossRef CAS.
- P. L. Gentili, F. Ortica, A. Romani and G. Favaro, J. Phys. Chem. A, 2007, 111, 193 CrossRef CAS PubMed.
- P. L. Gentili, in Fuzzy Logic: Theory, Programming and Applications, ed. R. E. Vargas, Nova Science Publishers Inc., Hauppauge, NY, 2009 Search PubMed.
- W. Siebrand and M. Z. Zgierski, J. Chem. Phys., 1980, 72, 1641 CrossRef CAS.
- L. A. Zadeh, Comput. J., 1988, 83 Search PubMed.
- W. S. McCulloch and W. H. Pitts, Bull. Math. Biophys., 1943, 5, 115 CrossRef.
- D. Margulies, G. Melman and A. Shanzer, J. Am. Chem. Soc., 2006, 128, 4865 CrossRef CAS PubMed.
- O. Kuznetz, H. Salman, N. Shakkour, Y. Eichen and S. Speiser, Chem. Phys. Lett., 2008, 451, 63 CrossRef CAS PubMed.
- J. Andréasson, S. D. Straight, S. Bandyopadhyay, R. H. Mitchell, T. A. Moore, A. L. Moore and D. Gust, Angew. Chem., Int. Ed., 2007, 46, 958 CrossRef PubMed.
- M. Amelia, M. Baroncini and A. Credi, Angew. Chem., Int. Ed., 2008, 47, 6240 CrossRef CAS PubMed.
- J. Andréasson, S. D. Straight, T. A. Moore, A. L. Moore and D. Gust, J. Am. Chem. Soc., 2008, 130, 11122 CrossRef PubMed.
- P. Ceroni, G. Bergamini and V. Balzani, Angew. Chem., Int. Ed., 2009, 48, 8516 CrossRef CAS PubMed.
- H. Tian, Angew. Chem., Int. Ed., 2010, 49, 4710 CrossRef CAS PubMed.
- R. J. Mitchell, Microprocessor Systems: An Introduction, Macmillan, London, 1995 Search PubMed.
- D. Margulies, C. E. Felder, G. Melman and A. Shanzer, J. Am. Chem. Soc., 2007, 129, 347 CrossRef CAS PubMed.
- J. Andréasson, S. D. Straight, T. A. Moore, A. L. Moore and D. Gust, Chem.–Eur. J., 2009, 15, 3936 CrossRef PubMed.
- G. de Ruiter, E. Tartakovsky, N. Oded and M. E. van der Boom, Angew. Chem., Int. Ed., 2010, 49, 169 CrossRef CAS PubMed.
- G. de Ruiter, L. Motiei, J. Choudhury, N. Oded and M. E. van der Boom, Angew. Chem., Int. Ed., 2010, 49, 4780 CrossRef CAS PubMed.
- T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560 CrossRef CAS PubMed.
- J. Zhao, S. Ji and H. Guo, RSC Adv., 2011, 1, 937 RSC.
- A. Monguzzi, R. Tubino, S. Hoseinkhami, M. Campione and F. Meinardi, Phys. Chem. Chem. Phys., 2012, 14, 4322 RSC.
- M. Penconi, F. Ortica, F. Elisei and P. L. Gentili, J. Lumin., 2013, 135, 265 CrossRef CAS PubMed.
- R. H. Douglas, C. W. Mullineaux and J. C. Partridge, Philos. Trans. R. Soc. London, Ser. B, 2000, 355, 1269 CrossRef CAS PubMed.
- R. H. Douglas, J. C. Partridge, K. Dulai, D. Hunt, C. W. Mullineaux, A. Tauber and P. H. Hynninen, Nature, 1998, 393, 423 CrossRef CAS PubMed.
- F. M. Raymo and S. Giordani, Org. Lett., 2001, 3, 3475 CrossRef CAS PubMed.
- S. Silvi, E. C. Constable, C. E. Housecroft, J. E. Beves, E. L. Dunphy, M. Tomasulo, F. M. Raymo and A. Credi, Chem.–Eur. J., 2009, 15, 178 CrossRef CAS PubMed.
- T. Gupta and M. E. van der Boom, Angew. Chem., Int. Ed., 2008, 47, 2260 CrossRef CAS PubMed.
- R. Baron, O. Lioubashevski, E. Katz, T. Niazov and I. Willner, J. Phys. Chem. A, 2006, 110, 8548 CrossRef CAS PubMed.
- R. Baron, O. Lioubashevski, E. Katz, T. Niazov and I. Willner, Org. Biomol. Chem., 2006, 4, 989 CAS.
- T. Niazov, R. Baron, E. Katz, O. Lioubashevski and I. Willner, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 17160 CrossRef CAS PubMed.
- R. Baron, O. Lioubashevski, E. Katz, T. Niazov and I. Willner, Angew. Chem., Int. Ed., 2006, 45, 1572 CrossRef CAS PubMed.
- B. Li and L. You, Nature, 2011, 469, 171 CrossRef CAS PubMed.
- S. Ji, BioSystems, 1999, 52, 123 CrossRef CAS.
- M. Conrad, IEEE Spectrum, 1986, 55 CrossRef.
- D. Bray, Nature, 1995, 376, 307 CrossRef CAS PubMed.
- R. F. Ludlow and S. Otto, Chem. Soc. Rev., 2008, 37, 101 RSC.
- D. B. Kell, Nat. Chem. Biol., 2011, 7, 7 CrossRef CAS PubMed.
- F. M. Raymo and S. Giordani, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4941 CrossRef CAS.
- K. Szaciłowski, Chem.–Eur. J., 2004, 10, 2520 CrossRef PubMed.
- F. M. Raymo and S. Giordani, J. Am. Chem. Soc., 2002, 124, 2004 CrossRef CAS PubMed.
- F. Pina, M. J. Melo, M. Maestri, P. Passaniti and V. Balzani, J. Am. Chem. Soc., 2000, 122, 4496 CrossRef CAS.
- S. Kou, H. N. Lee, D. van Noort, K. M. K. Swamy, S. H. Kim, J. H. Soh, K.-M. Lee, S.-W. Nam, J. Yoon and S. Park, Angew. Chem., Int. Ed., 2008, 47, 872 CrossRef CAS PubMed.
- B.-Y. Chang, J. A. Crooks, K.-F. Chow, F. Mavré and R. M. Crooks, J. Am. Chem. Soc., 2010, 132, 15404 CrossRef CAS PubMed.
- B. P. Belousov, A periodic reaction and its mechanism, in Collection of Short Papers on Radiation Medicine, Medgiz, Moscow, 1959, pp. 145–152 Search PubMed.
- A. M. Zhabotinsky, Proc. Acad. Sci. USSR, 1964, 157, 392 Search PubMed.
- R. J. Field, E. Körös and R. M. Noyes, J. Am. Chem. Soc., 1972, 94, 8649 CrossRef CAS.
- R. J. Field and F. W. Schneider, J. Chem. Educ., 1989, 66, 195 CrossRef CAS.
- P. Ruoff, M. Varga and E. Körös, Acc. Chem. Res., 1988, 21, 326 CrossRef CAS.
- A. T. Winfree, Science, 1977, 197, 761 CAS.
- P. L. Gentili, V. Horvath, V. K. Vanag and I. R. Epstein, International Journal of Unconventional Computing, 2012, 8, 177 Search PubMed.
- P. Ruoff, J. Phys. Chem., 1984, 88, 2851 CrossRef CAS.
- V. Horvath, P. L. Gentili, V. K. Vanag and I. R. Epstein, Angew. Chem., Int. Ed., 2012, 51, 6878 CrossRef CAS PubMed.
- M. I. Rabinovich, P. Varona, A. I. Selverston and H. D. I. Abardanel, Rev. Mod. Phys., 2006, 78, 1213 CrossRef.
- P. Larimer and B. W. Strowbridge, Nature, 2007, 448, 652 CrossRef CAS PubMed.
- D. Lebender and F. W. Schneider, J. Phys. Chem., 1994, 98, 7533 CrossRef CAS.
- A. Hjelmfelt, E. D. Weinberger and J. Ross, Proc. Natl. Acad. U. S. A., 1991, 88, 10983 CrossRef CAS.
- A. Hjelmfelt and J. Ross, Proc. Natl. Acad. U. S. A., 1992, 89, 388 CrossRef CAS.
- A. Hjelmfelt, F. W. Schneider and J. Ross, Science, 1993, 260, 335 CrossRef CAS PubMed.
- A. Hjelmfelt and J. Ross, J. Phys. Chem., 1993, 97, 7988 CrossRef CAS.
- J.-P. Laplante, M. Pemberton, A. Hjelmfelt and J. Ross, J. Phys. Chem., 1995, 99, 10063 CrossRef CAS.
- J. Gorecki, J. N. Gorecka and Y. Igarashi, Nat. Comput., 2009, 8, 473 CrossRef.
- K. Agladze, R. R. Aliev, T. Yamaguchi and K. Yoshikawa, J. Phys. Chem., 1996, 100, 13895 CrossRef CAS.
- A. Toth, D. Horváth and K. Yoshikawa, Chem. Phys. Lett., 2001, 345, 471 CrossRef CAS.
- J. N. Gorecka, J. Gorecki and Y. Igarashi, J. Phys. Chem. A, 2007, 111, 885 CrossRef CAS PubMed.
- A. Tóth and K. Showalter, J. Chem. Phys., 1995, 103, 2058 CrossRef.
- O. Steinbock, P. Kettunen and K. Showalter, J. Phys. Chem., 1996, 100, 18970 CrossRef CAS.
- J. Sielewiesiuk and J. Górecki, J. Phys. Chem. A, 2001, 105, 8189 CrossRef CAS.
- K. Yoshikawa, I. N. Motoike, T. Ichino, T. Yamaguchi, Y. Igarashi, J. Górecki and J. N. Górecka, International Journal of Unconventional Computing, 2009, 5, 3 Search PubMed.
- J. Gorecki, K. Yoshikawa and Y. Igarashi, J. Phys. Chem. A, 2003, 107, 1664 CrossRef CAS.
- O. Steinbock, A. Tóth and K. Showalter, Science, 1995, 267, 868 CrossRef CAS PubMed.
- K. Agladze, N. Magome, R. Aliev, T. Yamaguchi and K. Yoshikawa, Physica D, 1997, 106, 247 CrossRef CAS.
- A. Adamatzky and B. de Lacy Costello, Naturwissenschaften, 2002, 89, 474 CrossRef CAS PubMed.
- L. Kuhnert, Nature, 1986, 319, 393 CrossRef CAS.
- L. Kuhnert, K. I. Agladze and V. I. Krinsky, Nature, 1989, 337, 244 CrossRef CAS.
- N. G. Rambidi, Supramol. Sci., 1998, 5, 765 CrossRef CAS.
- N. G. Rambidi and A. V. Maximychev, BioSystems, 1997, 41, 195 CrossRef CAS.
- N. G. Rambidi, K. E. Shamayaev and G. Yu. Peshkov, Phys. Lett. A, 2002, 298, 375 CrossRef CAS.
- A. Lewis, Y. Albeck, Z. Lange, J. Benchowski and G. Weizman, Science, 1997, 275, 1462 CrossRef CAS.
- I. Sendiña-Nadal, E. Mihaliuk, J. Wang, V. Pérez-Muñuzuri and K. Showalter, Phys. Rev. Lett., 2001, 86, 1646 CrossRef.
- A. Adamatzky and B. de Lacy Costello, Chaos, Solitons Fractals, 2007, 34, 307 CrossRef CAS PubMed.
- R. Toth, C. Stone, A. Adamatzky, B. de Lacy Costello and L. Bull, Chaos, Solitons Fractals, 2009, 41, 1605 CrossRef CAS PubMed.
- A. Adamatzky, Chaos, Solitons Fractals, 2004, 21, 1259 CrossRef CAS PubMed.
- R. Toth, C. Stone, A. Adamatzky, B. de Lacy Costello and L. Bull, J. Chem. Phys., 2008, 129, 184708 CrossRef PubMed.
- L. Zhang and A. Adamatzky, Chaos, Solitons Fractals, 2009, 41, 1191 CrossRef PubMed.
- J. Holley, A. Adamatzky, L. Bull, B. De Lacy Costello and I. Jahan, Nano Commun. Netw., 2011, 2, 50 CrossRef PubMed.
- A. Kaminaga, V. K. Vanag and I. R. Epstein, Angew. Chem., Int. Ed., 2006, 45, 3087 CrossRef CAS PubMed.
- A. Adamatzky, Physarum machine: Computers from slime mould, Series A, World Scientific Publishing, ISBN 978-981-4327-58-9, 2010, vol. 74 Search PubMed.
- D. S. Modha, R. Ananthanarayanan, S. K. Esser, A. Ndirango, A. J. Sherbondy and R. Singh, Commun. ACM, 2011, 54, 62 CrossRef.
- P. Ball, Nature, 2012, 492, 175 CrossRef PubMed.
- P. L. Gentili, M. Dolnik and I. R. Epstein, J. Phys. Chem. C Search PubMed , submitted.
Footnotes |
| † The superficial, inner somatosensory and vestibular systems own a 3D character. For them, the information of a 3D mechanical stimulus is encoded as a 3D tensor. |
| ‡ For example, near-sighted people, looking at far objects without glasses, have a visual perception which is significantly “prior probability” driven. |
| This journal is © The Royal Society of Chemistry 2013 |
