Molecular coolers: The case for [CuII5GdIII4]†
Stuart K.
Langley
a,
Nicholas F.
Chilton
a,
Boujemaa
Moubaraki
a,
Thomas
Hooper
b,
Euan K.
Brechin
*b,
Marco
Evangelisti
*c and
Keith S.
Murray
*a
aSchool of Chemistry, Monash University, Clayton, Victoria 3800, Australia. E-mail: keith.murray@monash.edu
bSchool of Chemistry, The University of Edinburgh, West Mains Road, Edinburgh, EH9 3JJ, UK. E-mail: ebrechin@staffmail.ed.ac.uk
cInstituto de Cienci a de Materiales de Aragón, CSIC-Universidad de Zaragoza, Departamento de Física de la Materia Condensada, 50009, Zaragoza, Spain. E-mail: evange@unizar.es
First published on 7th April 2011
Abstract
The use of triethanolamine (teaH3) in 3d/4f chemistry produces the enneanuclear cluster compound [CuII5GdIII4O2(OMe)4(teaH)4(O2CC(CH3)3)2(NO3)4]·2MeOH·2Et2O (1·2MeOH·2Et2O) whose molecular structure comprises a series of vertex- and face-sharing {GdIIICuII3} tetrahedra. Magnetic studies reveal a large number of spin states populated even at the lowest temperatures investigated. Combined with the high magnetic isotropy, this enables 1 to be an excellent magnetic refrigerant for low temperature applications.
Introduction
Magnetic refrigeration is a potential and realistic short-to-medium term application envisioned for polymetallic molecules built from paramagnetic metal ions; molecules often referred to as molecular nanomagnets (MNMs).1–3 The magnetocaloric effect (MCE) is based on the change of magnetic entropy upon application of a magnetic field and can be used for cooling applications via adiabatic demagnetisation. Recent studies have demonstrated that the MCE of isotropic MNMs can be enormous,4–7 and larger than that of lanthanide alloys8 and magnetic nanoparticles.9 The “recipe” required for the synthesis of such molecules was recently outlined.10 The “ideal” molecule should possess: (a) a large spin ground state, S. Magnetic entropy is related to the spin by Sm = Rln(2S + 1) [where R = gas constant] and thus the larger the S the larger the magnetic entropy. (b) Molecular isotropy (Dcluster = 0) — zero-field splitting (anisotropy) orders molecular Ms levels, thus decreasing magnetic entropy changes. (c) High spin degeneracy — the presence of low-lying excited states is controlled by the exchange interaction (J) between metal ions. Weak exchange equates to multiple low-lying excited states each of which can contribute to the magnetic entropy of the system via Sm = Rln(2S + 1). (d) A small molecular mass, mw.In other words we need to make low molecular mass ferro- or ferrimagnets displaying zero molecular anisotropy and exhibiting weak exchange interactions. This immediately points toward the use of lanthanide ions and, in particular, the f7 ion Gd3+ in the construction of homo- and heterometallic (Gd-3d) clusters. The inherently weak exchange mediated through the core-like f-orbitals of Gd3+ and its isotropic electronic configuration guarantee the presence of multiple low-lying [and hence field-accesible] spin states, negating the need for ferromagnetic exchange in homometallic f-block clusters. Heterometallic complexes (e.g.Gd3+-Mnn+, Gd3+-Cu2+etc) can be guaranteed to afford non-zero spin ground states on account of their differing dn/fn electron configurations and on the basis of literature precedents that show certain combinations, e.g.Gd3+-Cu2+, favour ferromagnetic exchange.11 Molecular isotropy can be controlled in two ways: (a) through the use of isotropic metal ions (Gd3+, Cu2+, Fe3+) since Dcluster is governed in the main by dsingle ion, or (b) through the synthesis of highly symmetric molecules since Dcluster = 0 in cubic (Oh, Td) symmetry.
To date, the molecule with largest enhancement of the MCE is a mixed-valent [MnII/III14] disc with values of −ΔSm as large as 25 J kg−1 K−1 for liquid-helium temperatures and ΔB0 = 7 T—almost a factor of 2 larger than that of [DyCo2] nanoparticles.9 Herein we present the first Cu2+-Gd3+ candidate, by showing that [CuII5GdIII4O2(OMe)4(teaH)4(O2CC(CH3)3)2(NO3)4]·2MeOH·2Et2O (1·2MeOH·2Et2O) displays a truly enormous enhancement of the MCE with −ΔSm reaching record values larger than 30 J kg−1 K−1. This cluster forms part of a family of isostructural CuII5LnIII4 clusters in which the anisotropic members, Ln = Tb, Dy and Ho, in contrast to Gd, display single molecule magnetism features (SMM).11
Results and discussion
The reaction of Cu(NO3)2·3H2O and Gd(NO3)3·6H2O with triethanolamine (teaH3) and trimethylacetic acid in a basic alcoholic solution leads to the formation of blue crystals of [CuII5GdIII4O2(OMe)4(teaH)4(O2CC(CH3)3)2(NO3)4]·2MeOH·2Et2O (1·2MeOH·2Et2O).‡ Compound 1 (Fig. 1A) crystallises in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with the asymmetric unit containing half the cluster which lies upon an inversion centre. The complex contains five CuII (Cu1–Cu3 and symmetry equivalent, s.e.) and four GdIII (Gd1, Gd2 and s.e.) ions; the CuII ions forming a planar ‘bow-tie’ arrangement, with the four GdIII ions forming a rectangle perpendicular to this (Fig. 1B). The metallic skeleton thus describes four vertex and face-sharing {GdCu3} tetrahedra (Fig. 1C). Two central trigonal bipyramidal μ5-O2− ions (O1 and s.e.) link the perpendicular Cu5 and Gd4 frameworks together. The central CuII ion (Cu1) is four coordinate and in a square planar geometry with a [CuO4] coordination sphere. The outer four CuII ions (Cu2, Cu3 and symmetry equivalents) are also four coordinate and square planar but with [CuO3N] coordination spheres and with an additional long (axial) contact to a non-bonded O-atom (O13 and s.e.) of a teaH ligand (∼2.4–2.7 Å). The GdIII ions are eight coordinate and in distorted square antiprismatic geometries, with [GdO8] coordination spheres. The two carboxylates and four methoxide ions each bridge in a μ-fashion across the short edge of the Gd4 rectangle, with one exception, O2(OMe−) and symmetry equivalent is μ3-bridging, the additional bond being to the central CuII ion. The NO3− ions each chelate to a GdIII ion at the four “outer” corners of the Gd4 rectangle. The doubly deprotonated μ3
with the asymmetric unit containing half the cluster which lies upon an inversion centre. The complex contains five CuII (Cu1–Cu3 and symmetry equivalent, s.e.) and four GdIII (Gd1, Gd2 and s.e.) ions; the CuII ions forming a planar ‘bow-tie’ arrangement, with the four GdIII ions forming a rectangle perpendicular to this (Fig. 1B). The metallic skeleton thus describes four vertex and face-sharing {GdCu3} tetrahedra (Fig. 1C). Two central trigonal bipyramidal μ5-O2− ions (O1 and s.e.) link the perpendicular Cu5 and Gd4 frameworks together. The central CuII ion (Cu1) is four coordinate and in a square planar geometry with a [CuO4] coordination sphere. The outer four CuII ions (Cu2, Cu3 and symmetry equivalents) are also four coordinate and square planar but with [CuO3N] coordination spheres and with an additional long (axial) contact to a non-bonded O-atom (O13 and s.e.) of a teaH ligand (∼2.4–2.7 Å). The GdIII ions are eight coordinate and in distorted square antiprismatic geometries, with [GdO8] coordination spheres. The two carboxylates and four methoxide ions each bridge in a μ-fashion across the short edge of the Gd4 rectangle, with one exception, O2(OMe−) and symmetry equivalent is μ3-bridging, the additional bond being to the central CuII ion. The NO3− ions each chelate to a GdIII ion at the four “outer” corners of the Gd4 rectangle. The doubly deprotonated μ3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η2
η2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η2
η2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η1
η1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η0 teaH ligands each encapsulate one CuII ion using two O-atoms and one N-atom and then attach it to the long rectangular edge of the Gd4 rectangle via their two μ-O-atoms. The non-bonding alcohol arms are protonated, two of which form H-bonds to solvent MeOH molecules and two of which form inter-molecular H-bonds to the NO3− ions of adjacent clusters. The latter interaction directs the formation 1-D H-bonded chains down the c-axis of the crystal.
η0 teaH ligands each encapsulate one CuII ion using two O-atoms and one N-atom and then attach it to the long rectangular edge of the Gd4 rectangle via their two μ-O-atoms. The non-bonding alcohol arms are protonated, two of which form H-bonds to solvent MeOH molecules and two of which form inter-molecular H-bonds to the NO3− ions of adjacent clusters. The latter interaction directs the formation 1-D H-bonded chains down the c-axis of the crystal.
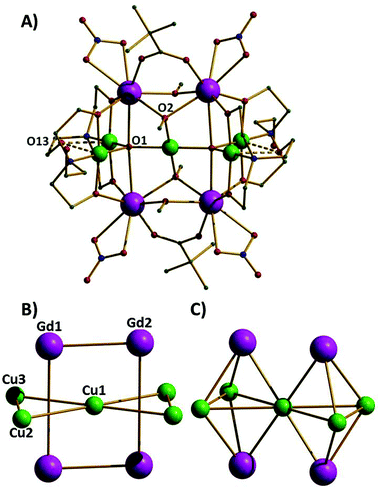 | ||
| Fig. 1 A) The molecular structure of complex 1. Colour code: Gd = purple, Cu = green, O = red, N = blue, C = grey. H-atoms are omitted for clarity. B) The metallic skeleton highlighting the two “interpenetrating” metal frameworks; the Cu5 “bow-tie” and the Gd4 rectangle. C) The metallic skeleton drawn to emphasise the four face- and vertex-sharing {Cu3Gd} tetrahedra. The Gd⋯Gd distances across the short and long rectangular edges are 3.735 Å and 5.279 Å, respectively. The Cu1⋯Cu2,3 distances are ∼3.5 Å; the Cu2⋯Cu3 distance is ∼3.1 Å and the Cu⋯Gd distance, ∼3.3 Å. Cu1–O1–Cu2, 123.88°, Cu1–O1–Cu3, 128.95°, Cu2–O1–Cu3, 107.05°. | ||
The DC magnetic susceptibility of 1 was collected in an applied field B0 = 0.01 T over the 2–300 K temperature range (Fig. 2). The room-temperature χMT value of 33.0 cm3 K mol−1 stays nearly constant with decreasing temperature down to ∼30 K, below which it increases significantly reaching a value of 48.6 cm3 K mol−1 at 2 K, indicating that dominant ferromagnetic pathways are present. The χMT value expected for an uncoupled [CuII5GdIII4] unit (g = 2.00) is 33.33 cm3 K mol−1, in good agreement with the experimental data at high temperatures. The magnetisation measurements (inset of Fig. 2) show a saturation value of 31.3 NμB at the lowest investigated temperature T = 2 K, suggesting a net spin state S = 31/2. This can be rationalised assuming the central CuII to be antiferromagnetically coupled to the outer Cu sites in the ‘bow-tie’. This is likely to occur as the average Cu(central)–O–Cu(outer) bond angle is ∼126° which will likely be antiferromagnetic and stronger than the outer Cu–O–Cu interactions (average angle of 107°) forcing the four Cu sites to align parallel to each other. The Cu⋯Gd interactions between the outer Cu ions and the Gd ions are likely weak and ferromagnetic, as has been noted for a number of Gd and Cu ions bridged by two O-atoms.12 The weak exchange promoted by the lanthanide ions will most likely lead to several spin states energetically close to an ill-defined ground state, a sought after situation for observing an enhanced MCE.5–7,10
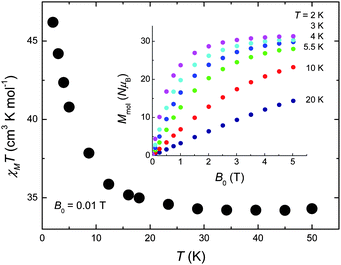 | ||
| Fig. 2 Temperature-dependence of χMT for 1 collected for B0 = 0.01 T. Inset: Field-dependence of the molar magnetisation for the indicated temperatures. | ||
We next turn to the evaluation of the magnetothermal properties of 1 by presenting its temperature-dependent heat capacity (C) collected for several field values (Fig. 3).
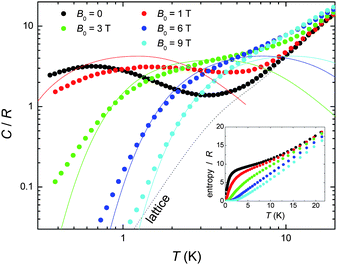 | ||
| Fig. 3 Temperature-dependence of the heat capacity C normalised to the gas constant R for 1 at several applied fields; the dotted line is the Debye fit to the lattice contribution, whereas the solid lines are the calculated Schottky contributions (see text). Inset: T-dependence of the entropy, as obtained from the C data. | ||
At high temperatures, the heat capacity is dominated by a non-magnetic contribution arising from thermal vibrations of the lattice, which is modelled with the well-known low-T Debye function (dotted line in Fig. 3) yielding a value of ΘD = 23 K for the Debye temperature, typical for this class of cluster compound.1 At low temperatures, the heat capacity is dependent upon the applied field. Indeed, the splitting of the molecular spin states results in a broad (Schottky-type) feature, which shifts to higher T by increasing the applied field. This behaviour can be explained using the same model which was suggested by the Mmol(T, B0) data, namely an antiferromagnetic core formed by the CuII spins (providing a net spin S[Cu] = 3/2, g = 2 at low temperatures) that weakly couples to the peripheral GdIII spins. As a comparison with the experimental data, Fig. 3 shows the contributions (solid lines for B0 = 1, 3, 6 and 9 T, respectively) that result by summing together the calculated Schottky curves arising from the field-split levels of a central S[Cu] = 3/2 net spin and four independent GdIII (S = 7/2, g = 2) spins. It can be seen that the higher fields promote a larger decoupling between the spin centres, yielding an increasingly better agreement. The relatively poorer agreement at lower fields and temperatures can likely be ascribed to the presence of low-lying excited spin states, in accordance with the interpretation of the Mmol(T,B0) data. From the experimental heat capacity, the temperature dependence of the entropy is obtained by integration, i.e. using Entropy(T) = ∫C(T)/TdT, and is depicted in the inset of Fig. 3 for several applied fields. One can notice the ∼9 R “plateau” for the zero-field entropy in the 2 < T < 8 K temperature range, which again can be understood within the frame of a model of four weakly coupled GdIII spins to a central S[Cu] = 3/2 core. Above 2–3 K, the Cu⋯Gd interactions are fully decoupled, therefore the expected entropy/R should be 4 x ln(8) + ln(4) = 9.7, in agreement with the experimental value reached at the plateau. Above approximately 8 K, the zero-field entropy content increases steadily because of the dominant lattice heat capacity (see Fig. 3).
We next evaluate the MCE of 1, i.e. both the magnetic entropy change ΔSm and adiabatic temperature change ΔTad from the temperature and field dependencies of the entropy.10 The results are summarised in Fig. 4. We report a record value of −ΔSm which reaches ∼31 J kg−1 K−1 at T = 3 K for ΔB0 = 9 T. This is what we could have expected considering the large net magnetic moment of the molecule, combined with the negligible anisotropy and the weak intra-cluster interactions that promote low-lying excited spin states.10 An added “pro” is the relatively small molecular mass (mw = 2141.8 g), which results from the relatively low ratio of ligands present. These being non-magnetic, contribute passively to the MCE. Likewise, the ΔTad is extraordinarily large (see bottom panel of Fig. 4). We refer particularly to the cooling rate K T−1, which goes from more than 1 K T−1 for ΔB0 = 9 T to well over 2 K T−1 for ΔB0 = 1 T, setting this material among the most efficient refrigerants for the liquid-helium temperature range.10 Finally, we note an excellent agreement between the −ΔSm obtained from the C data with that obtained by applying the Maxwell equation to the isothermal magnetisation curves (the asterisks in Fig. 4),10 suggesting that both independent procedures can be effectively used to characterise 1 with respect to its MCE.
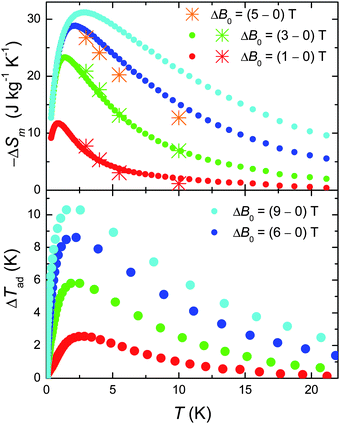 | ||
| Fig. 4 Top: T-dependencies of the magnetic entropy change as obtained from C (filled dots) and Mmol (asterisks) experimental data, for the indicated applied field changes. Bottom: T-dependencies of the adiabatic temperature change obtained from Cexperimental data, for the indicated applied field changes. | ||
Conclusions
The use of teaH3 in heterometallic 3d–4f chemistry has led to the isolation of an unusual but beautiful [CuII5GdIII4] cluster comprising a series of vertex- and face-sharing {GdCu3} tetrahedra. The low molecular mass, the constituent isotropic metal ions, the ferromagnetic CuII-GdIII interaction and the inherent weak exchange propagated by the lanthanide ions results in the population of numerous S states even at the lowest temperatures measured. This is reflected in a truly enormous enhancement of the MCE with −ΔSm values larger than 30 J kg−1 K−1; the largest value seen for any molecular compound. This clearly demonstrates that [CuII-GdIII] cluster compounds — for so long studied because of the ferromagnetic exchange between the 3d and 4f metal ions — can be successfully exploited for magnetic refrigeration.Acknowledgements
This work was supported by an ARC Discovery grant (KSM), the Spanish MICINN (contracts MAT2009-13977-C03 and CSD2007-00010); the EPSRC, Leverhulme Trust and the Royal Society of Chemistry (EKB).Notes and references
- M. Evangelisti, F. Luis, L. J. de Jongh and M. Affronte, J. Mater. Chem., 2006, 16, 2534 RSC.
- M. Evangelisti, A. Candini, A. Ghirri, M. Affronte, E. K. Brechin and E. J. L. McInnes, Appl. Phys. Lett., 2005, 87, 072504 CrossRef.
- R. Shaw, R. H. Laye, L. F. Jones, D. M. Low, C. Talbot-Eeckelaers, Q. Wei, C. J. Milios, S. Teat, M. Helliwell, J. Raftery, M. Evangelisti, M. Affronte, D. Collison, E. K. Brechin and E. J. L. McInnes, Inorg. Chem., 2007, 46, 4968 CrossRef CAS.
- M. Manoli, R. D. L. Johnstone, S. Parsons, M. Murrie, M. Affronte, M. Evangelisti and E. K. Brechin, Angew. Chem., Int. Ed., 2007, 46, 4456 CrossRef CAS.
- M. Evangelisti, A. Candini, M. Affronte, E. Pasca, L. J. de Jongh, R. T. W. Scott and E. K. Brechin, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79 Search PubMed.
- G. Karotsis, M. Evangelisti, S. J. Dalgarno and E. K. Brechin, Angew. Chem., Int. Ed., 2009, 48, 9928 CrossRef CAS.
- Y.-Z. Zheng, M. Evangelisti and R. E. P. Winpenny, Chem. Sci., 2011, 2, 99 RSC.
- (a) V. K. Pecharsky and K. A. Gschneidner, Jr, Phys. Rev. Lett., 1997, 78, 4494 CrossRef CAS; (b) F. X. Hu, B. G. Shen and J. R. Sun, Appl. Phys. Lett., 2000, 76, 3460 CrossRef CAS; (c) F. X. Hu, B. G. Shen, J. R. Sun, Z. H. Cheng, G. H. Rao and X. X. Zhang, Appl. Phys. Lett., 2001, 78, 3675 CrossRef CAS; (d) B. G. Shen, J. R. Sun, F. X. Hu, H. W. Zhang and Z. H. Chen, Adv. Mater., 2009, 21, 4545 CrossRef CAS; (e) N. A. de Oliveira, P. J. von Ranke, M. V. Tovar Costa and A. Troper, Phys. Rev. B: Condens. Matter, 2002, 66 Search PubMed; (f) N. H. Duc, D. T. Kim Anh and P. E. Brommer, Phys. B, 2002, 319, 1 CrossRef CAS; (g) N. K. Singh, P. Kumar, K. G. Suresh, A. K. Nigam, A. A. Coelho and S. Gama, J. Phys.: Condens. Matter, 2007, 19, 036213 CrossRef; (h) H. Wada, Y. Tanabe, M. Shiga, H. Sugawara and H. Sato, J. Alloys Compd., 2001, 316, 245 CrossRef CAS.
- S. Ma, W. B. Cui, D. Li, N. K. Sun, D. Y. Geng, X. Jiang and Z. D. Zhang, Appl. Phys. Lett., 2008, 92, 173113 CrossRef.
- M. Evangelisti and E. K. Brechin, Dalton Trans., 2010, 39, 4672 RSC.
- S. K. Langley, L. Ungur, N. F. Chilton, B. Moubaraki, L. F. Chibotaru and K. S. Murray, in preparation.
- See for example (a) A. Benelli, C. Benelli, A. Caneschi, R. Carlin, A. Dei and D. Gatteschi, J. Am. Chem. Soc., 1985, 107, 2560 CrossRef CAS; (b) M. Andruh, I. Ramade, E. Codjovi, O. Guillou, O. Kahn and J. C. Trombe, J. Am. Chem. Soc., 1993, 115, 1822 CrossRef CAS; (c) J. P. Costes, F. Dahan, A. Dupuis and J. P. Laurent, Inorg. Chem., 1997, 36, 3429 CrossRef CAS; (d) A. J. Blake, R. O. Gould, C. M. Grant, P. E. Y. Milne, S. Parsons and R. E. P. Winpenny, J. Chem. Soc., Dalton Trans., 1997, 485 RSC; (e) C. Benelli and D. Gatteschi, Chem. Rev., 2002, 102, 2369 CrossRef CAS; (f) M. Evangelisti, M. L. Khan, J. Bartolomé, L. J. de Jongh, C. Meyers, J. Leandri, Y. Leroyer and C. Mathonière, Phys. Rev. B: Condens. Matter, 2003, 68 Search PubMed; (g) B. W. Wang, S. D. Jiang, X. T. Wang and S. Gao, Sci. China, Ser. B: Chem., 2009, 52, 1739 CrossRef CAS.
- T. M. McPhillips, S. E. McPhillips, H. J. Chiu, A. E. Cohen, A. M. Deacon, P. J. Ellis, E. Garman, A. Gonzalez, N. K. Sauter, R. P. Phizackerley, S. M. Soltis and P. Kuhn, J. Synchrotron Radiat., 2002, 9, 401 CrossRef CAS.
- W. Kabsch, J. Appl. Crystallogr., 1993, 26, 795 CrossRef CAS.
- (a) G. M. Sheldrick, SHELXL-97, Program for refinement of crystal structures, University of Göttingen, Germany, 1997 Search PubMed; (b) A. L. Speck, Acta. Crystallogr. Sect. A, 1990, 46, C34.
Footnotes |
| † CCDC reference number 809026. For crystallographic data in CIF or other electronic format see DOI: 10.1039/c1sc00038a |
‡ [CuII5GdIII4O2(OMe)4(teaH)4(O2CC(CH3)3)2(NO3)4]·2MeOH·2Et2O (1·2MeOH·2Et2O). Cu(NO3)2·3H2O (0.2 g, 1 mmol) was dissolved in 20 ml of MeOH followed by the addition of triethanolamine (0.13 ml, 1 mmol), pivalic acid (0.05 g, 0.5 mmol) and triethylamine (0.5 ml, 3.5 mmol) to give a green/blue solution. To this Gd(NO3)3·6H2O (0.45 g, 1 mmol) was added to give a deep blue solution. This was then stirred for 4 h, allowed to stand and was then layered with diethyl ether. After 3–5 days blue crystals of 1 had formed. Yield: 102 mg, 39.2%. Anal. Calculated (found) for 1·2MeOH·2Et2O: Cu5Gd4C48H110O38N8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C, 24.49 (24.20); H, 4.71 (4.29); N, 4.76 (4.59). Selected ATR IR data (cm−1): 2957w, 2856s, 1559s, 1483s, 1457sh, 1423s, 1377w, 1360w, 1298s, 1251w, 1227w, 1155w, 1133w, 1083s,1022s, 916m, 896m, 817w.X-Ray crystallographic measurements were performed at 100(2) K at the Australian synchrotron MX1 beam-line as described elsewhere.13 The data collection and integration were performed within Blu-Ice13 and XDS14 software programs. The data collection and integration were performed within SMART and SAINT+ software programs, and corrected for absorption using the Bruker SADABS program. 1 was solved by direct methods (SHELXS-97) and refined (SHELXL-97) by full least matrix least-squares on all F2 data.15 Crystallographic details are available in the Supporting Information in CIF format.† CCDC number 809026. These data can be obtained free of charge from the Cambridge Crystallographic Data Centre viahttp://www.ccdc.cam.ac.uk/data_request/cif.Crystal data for 1: M, g mol−1 = 2354.16, Crystal system = Triclinic, P C, 24.49 (24.20); H, 4.71 (4.29); N, 4.76 (4.59). Selected ATR IR data (cm−1): 2957w, 2856s, 1559s, 1483s, 1457sh, 1423s, 1377w, 1360w, 1298s, 1251w, 1227w, 1155w, 1133w, 1083s,1022s, 916m, 896m, 817w.X-Ray crystallographic measurements were performed at 100(2) K at the Australian synchrotron MX1 beam-line as described elsewhere.13 The data collection and integration were performed within Blu-Ice13 and XDS14 software programs. The data collection and integration were performed within SMART and SAINT+ software programs, and corrected for absorption using the Bruker SADABS program. 1 was solved by direct methods (SHELXS-97) and refined (SHELXL-97) by full least matrix least-squares on all F2 data.15 Crystallographic details are available in the Supporting Information in CIF format.† CCDC number 809026. These data can be obtained free of charge from the Cambridge Crystallographic Data Centre viahttp://www.ccdc.cam.ac.uk/data_request/cif.Crystal data for 1: M, g mol−1 = 2354.16, Crystal system = Triclinic, P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , a = 11.050(2), b = 13.830(3), c = 14.030(3) Å, α = 78.80(3), β = 83.81(3), γ = 69.28(3)°, V/Å3 = 1965.4(8), T/K = 100(2), Z = 1, ρc/g cm−3 = 1.989, λb/Å = 0.7182, data measured = 12139, Ind. Reflns = 7056, Rint = 0.0315, Reflns with I > 2σ(I) = 6876, parameters = 477, restraints = 0, R1c, wR2c = 0.0398, 0.099, goodness of fit = 1.132, Largest residuals/e Å−3 = 1.09, −1.331. , a = 11.050(2), b = 13.830(3), c = 14.030(3) Å, α = 78.80(3), β = 83.81(3), γ = 69.28(3)°, V/Å3 = 1965.4(8), T/K = 100(2), Z = 1, ρc/g cm−3 = 1.989, λb/Å = 0.7182, data measured = 12139, Ind. Reflns = 7056, Rint = 0.0315, Reflns with I > 2σ(I) = 6876, parameters = 477, restraints = 0, R1c, wR2c = 0.0398, 0.099, goodness of fit = 1.132, Largest residuals/e Å−3 = 1.09, −1.331. |
| This journal is © The Royal Society of Chemistry 2011 |
