Enhanced water transportation on a superhydrophilic serial cycloid-shaped pattern†
Defeng
Yan
 a,
Yi
Lu
a,
Jinming
Liu
a,
Yang
Chen
a,
Yi
Lu
a,
Jinming
Liu
a,
Yang
Chen
 a,
Jing
Sun
a and
Jinlong
Song
a,
Jing
Sun
a and
Jinlong
Song
 *ab
*ab
aState Key Laboratory of High-performance Precision Manufacturing, Dalian University of Technology, Dalian, Liaoning 116024, China. E-mail: songjinlong@dlut.edu.cn
bKey Laboratory for Micro/Nano Technology and System of Liaoning Province, Dalian University of Technology, Dalian, Liaoning 116024, P. R. China
First published on 5th June 2023
Abstract
Spontaneous and directional water transportation (SDWT) is considered as an ideal water transportation method and has a great prospect in the aerospace and ship fields. Nonetheless, the existing SDWT has the limitation of a slow water transportation velocity because of its geometry structure configuration, which hinders the practical application of the SDWT. To overcome this limitation, we developed a new superhydrophilic serial cycloid-shaped pattern (SSCP) which was inspired by the micro-cavity shape of the Nepenthes. First, we experimentally found that the water transportation velocity on the SSCP was faster than that on the superhydrophilic serial wedge-shaped pattern (SSWP) and analyzed the faster water transportation mechanism. Then, the influence of the SSCP parameters on the transportation velocity was investigated by a single-factor experiment. In addition, the water transportation velocity on the SSCP was enhanced to 289 mm s−1 by combining the single-factor experiment, orthogonal optimization design, streamline junction transition optimization, and pre-wet pattern, which was the fastest in the SDWT. Moreover, the SSCP demonstrated its superior capability in long-distance water transportation, gravity resistant water transportation, heat transfer, and fog collection. This finding shows remarkable application prospects in the high-performance fluid transportation system.
1 Introduction
Water transportation widely occurs in nature and has extremely important applications in many engineering fields, such as lab-on-a-chip technology, water collection, heat transfer, and hydropower generation.1–5 Researchers divided the water transportation into active water transportation and spontaneous and directional water transportation (SDWT).6,7 The active water transportation requires an external energy input to realize water movement, which limits its application in some special fields.8 In contrast, the SDWT does not require an external energy input and is considered as an ideal water transportation method.9,10 Therefore, exploring different possibilities and potential principles of the SDWT has attracted scientists’ attention.In 1978, Greenspan predicted that a water droplet could spontaneously and directionally move to a more wettable area on a surface with a wettability gradient.11 Since then, scientists have made lots of efforts, but it was still difficult to realize the SDWT until 1992. In this year, Whitesides et al. first experimentally demonstrated that a water droplet could really realize the spontaneous and directional movement on a silicon surface with a surface energy gradient.12 In addition, researchers found that the increase of the water transportation velocity would help the SDWT technology to be applied in the aerospace and ship fields; for example, fast water transportation would improve the water vapour collection efficiency in the manned space station life support system or the seawater desalination system of the ship and the jet cooling efficiency of the heat electronics on a spacecraft.13–15 To enhance the water transportation velocity, researchers devoted many effective works and found that the surface with a structure gradient could also realize the SDWT and that the water transportation velocity was greatly enhanced.16–20 When a water droplet is placed at the narrow side of the superhydrophilic single wedge-shaped pattern which has a structure gradient, it would be quickly caught by the narrow side of the pattern and then spontaneously and directionally transported to the wide side of the pattern under Laplace pressure.21 Although the superhydrophilic single wedge-shaped pattern successfully demonstrated the transportation capability in the SDWT, the Laplace pressure difference of the water droplet significantly decreased due to the large end size, which meant that the single wedge-shaped pattern was not suitable for long-distance water transportation.22–25 To overcome this limitation, a superhydrophilic serial wedge-shaped pattern (SSWP), where the pattern consisted of several single wedge-shaped patterns connected in a head-to-tail arrangement, was proposed in our previous study, which was facilitated to decrease the fluid loss, resulting in the increase of the transportation distance.26,27 However, researchers found that once the water droplet moved to the junction of the SSWP, the droplet would encounter the resistance force from the pinning, resulting in the decrease of the water transportation velocity.27–29 Therefore, researchers devoted many effective efforts to optimize the junction transition, such as the arc junction transition, wedge junction transition, and streamlined junction transition, which could enhance the water transportation velocity. Despite this, the existing geometry structure of the pattern unit is still unsatisfactory, due to which the slow water transportation velocity still hinders the practical application of the SDWT. Therefore, it is necessary to propose a new strategy for the optimization of the geometry structure configuration that can realize high-velocity water transportation.
Herein, to overcome the limitation of the slow water transportation velocity during the SDWT processes, we proposed a superhydrophilic serial cycloid-shaped pattern (SSCP) inspired from the micro-cavity shape of the Nepenthes. We first experimentally demonstrated that the water transportation velocity on the SSCP was much faster than that on the SSWP under the same parameters and systematically analysed why the water droplet on the SSCP transported faster. To understand the influence of the SSCP parameters on the water transportation and to obtain the optimal parameter configuration, a single-factor experiment and orthogonal optimization design were performed, respectively. In addition, by the streamline junction transition and pre-wetting pattern strategy, the water transportation velocity was further enhanced on the SSCP. Based on the aforementioned optimal parameters, the SSCP exhibited superior application prospects for long-distance water transportation, gravity resistant water transportation, heat transfer, and fog collection, which provided a new avenue for high-performance fluid transportation.
2 Experiment section
2.1 Materials
Aluminum plates (Al, purity >99.5%) with a size of 3 cm × 10 cm and a thickness of 2 mm were bought from Shandong Metal Co. Ltd (China). Fluoroalkylsilane [FAS, C8F13H4Si(OCH2CH3)3] was purchased from Degussa Co. Ltd (Germany). Anhydrous ethanol and water-soluble red dye were bought from Dalian Bonuo Chemical Co. Ltd (China).2.2 Fabrication of samples
2.3 Sample characterization
The surface microstructures of the samples were characterized by using a scanning electron microscope (SEM, JSM-6360LV, Japan). The element compositions were characterized by using an X-ray photoelectron spectrometer (XPS, ESCALAB 250Xi, USA). The static water contact angle (CA, θw) was measured by using an optical contact angle meter (DSA100, Krüss, Germany) using a water droplet with a volume of 5 µL.31 The digital images and dynamic water transportation processes were recorded by using a digital camera (DSC-RX10M3, Sony, Japan). Water-soluble red dye was used for better visualization.2.4. Water transportation
Water transportation test equipment was assembled to test the transportation velocity of the water droplet on the superhydrophilic pattern, as shown in Fig. S2.† The distance between the needle and the Al plate was 10 mm, the water droplet volume used in the water transportation processes was 40 μL, and the water droplet was released on the superhydrophilic pattern by using a micro-dispensing pump (LSP02-2A, LongerPump). In the water transportation processes, the water bulge gradually became smaller with the water bulge movement along the superhydrophilic pattern. When the water bulge was too smaller, the water transportation velocity would significantly decrease, which resulted from the decrease of the Laplace pressure difference. Therefore, in this work, we calculated the average water transportation velocity of a 40 μL water droplet with a 50 mm transportation distance to evaluate whether the pattern was superior.2.5 Convective cooling of the superhydrophilic serial cycloid-shaped pattern surface
Convective cooling equipment was assembled to test the heat transfer capability of the SSCP and the SSWP. A heating plate with 10 W power was used to heat the superhydrophobic Al plate with the SSCP. Then, the water transported on the SSCP at a flux of ∼4 mL min−1 to take away the heat of the Al plate. The temperatures of two points on the Al plate were measured by using a multi-channel temperature monitor (DC5508U, China). As a comparison, the heat transfer capability of the SSWP with the same parameters was also tested.2.6 Fog collection
The samples were fixed on a holder at 20 °C ambient temperature and under 50% ambient relative humidity. An ultrasonic humidifier (AJ-H811, Aux group Co. Ltd, China) was used to generate the artificial fog flow, where the fog flow rate, fog velocity, fog humidity at the nozzle, nozzle diameter, and distance between the sample and the ultrasonic humidifier nozzle were 0.3 mL s−1, 1 m s−1, 100%, 5 cm, and 10 cm, respectively. The collected water mass was weighed by using a balance (JCS-Z1, Zhuheng Electronic Equipment Co. Ltd, China). The experimental fog collection rate We was We = mwater·ss−1·tf−1, where ss and tf are the sample area and the experimental fog collection time. The fog collection efficiency η was η = We/Wt, where Wt is the theoretical fog supply rate at the sample surface. In this fog collection system, Wt was 11.8 g cm−2 h−1.323 Results and discussion
3.1. The superhydrophilic serial cycloid-shaped pattern
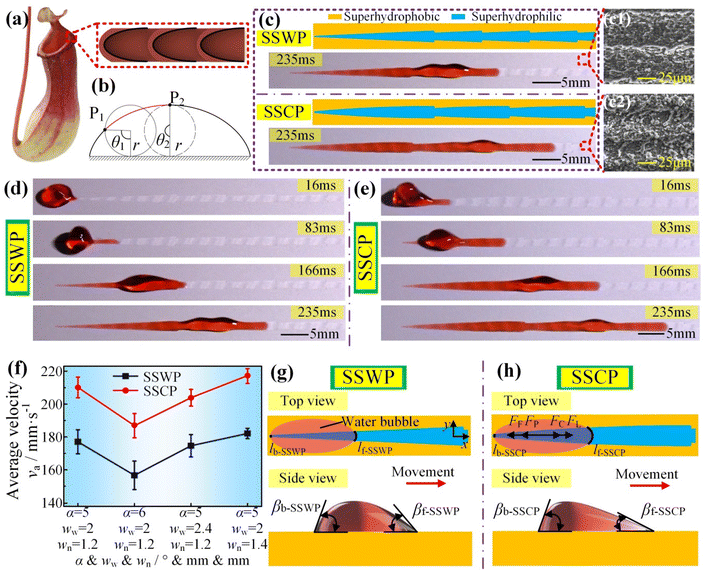
The lip of Nepenthes can realize the directional fluid transportation due to its unique arch-shaped micro-cavities, as shown in Fig. 1(a).33 Inspired by the micro-cavity shape of Nepenthes, we proposed a superhydrophilic serial cycloid-shaped pattern (SSCP) to enhance the water transportation velocity. The cycloid is a track formed by a point on a circle with a radius r which rolls on the horizontal plane without sliding. As shown in Fig. 1(b), we chose the part of the cycloid as the cycloid-shaped pattern, where the angle that the circle rolled from the origin position to the start position of the cycloid-shaped pattern was defined as the start rotation angle θ1; the angle that the circle rolled from the origin position to the end position of the cycloid-shaped pattern was defined as the end rotation angle θ2. We successfully fabricated a SSCP on a superhydrophobic Al plate by the first laser processing, low surface energy modification, and second laser processing (Fig. 1(c)). The microstructures of superhydrophobic region and superhydrophilic pattern were of a typical laser-processed morphology with micro/nano-scale particles, which were produced by the melting and re-solidification of Al (Fig. 1(c1) and (c2)).34 It was exciting that a 40 μL water droplet could transport the SSCP with a first unit pattern length Lf of 22.9 mm (a rolling circle radius r of 65.7 mm, a start rotation angle θ1 of 170°, and an end rotation angle θ2 of 180°), a wide side width ww of 2 mm, and a narrow side width wn of 1.2 mm. The average water transportation velocity va on the SSCP with 212 mm s−1 was obviously higher than that on the superhydrophilic serial wedge-shaped pattern (SSWP) with Lf of 22.9 mm, a wedge angle α of 5°, ww of 2 mm, and wn of 1.2 mm (176 mm s−1) which was the best parameter in previous research, as shown in Fig. 1(c) and Video S1.†27 The water droplet on the SSCP not only firstly reached the destination, but also was always faster than that on the SSWP during the transportation processes (Fig. 1(d) and (e)). We then calculated the va value of the 40 μL water droplet with a transportation length of 50 mm and found that the va value of the SSCP was always faster than that of the SSWP under the same Lf, ww, and wn, which meant that the SSCP had superior water transportation capability compared to the SSWP (Fig. 1(f)). To explain the aforementioned phenomenon, we analysed why the water transportation on the SSCP was faster than on the SSWP by force analysis. The schematics of the water transportation processes are shown in Fig. 1(g) and (h). For a water droplet placed on the superhydrophilic pattern, the driving force FL and FC from the Laplace pressure and the capillary effect and the resistance force FF and FP from the friction and the pinning were the main forces applied on the water droplet.27 The resultant force F was calculated by| F = FL + FC − FP − FF | (1) |
FL ∼ γlfcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βf − γlbcos βf − γlbcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βb βb | (2) |
3.2 Optimization of the superhydrophilic serial cycloid-shaped pattern
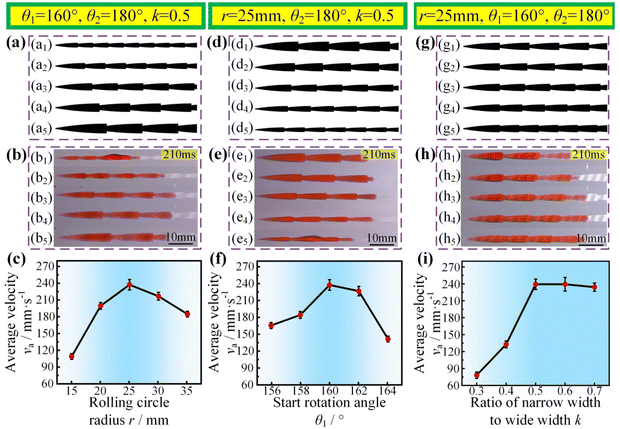
Since the proposed SSCP had a superior water transportation capability than the SSWP, we then investigated whether va could be further enhanced by optimizing the SSCP parameters, such as the rolling circle radius r, start rotation angle θ1, end rotation angle θ2, and ratio of the narrow width to the wide width k. From the pre-experiments, we found that the water transportation capability was better when the SSCP parameter ranges were 15 mm–35 mm for r, 156°–164° for θ1, 172°–180° for θ2, and 0.3–0.7 for k. We first investigated the influence of r on the water transportation velocity. Five SSCPs with the r = 15 mm & 20 mm & 25 mm & 30 mm & 35 mm, θ1 = 160°, θ2 = 180°, and k = 0.5 were fabricated on a superhydrophobic Al plate. It can be seen from Fig. 2(a) and (b) that, when r < 25 mm, the junction number increased with decreasing r, resulting in the increase of the resistance force from the pinning and the decrease of va. When r > 25 mm, the spreading area of the water droplet on the superhydrophilic pattern increased with increasing r, which meant that the water bubble became smaller quickly, indicating that the Laplace pressure difference of the water droplet significantly decreased. When r = 25 mm, the va value of the water droplet was about 238 mm s−1, which was faster than that under r = 15 mm & 20 mm & 30 mm & 35 mm (Fig. 2(c), Fig. S4(a), and Video S2†). Moreover, the influence of the SSCP parameters of θ1, θ2, and k on va has also been studied. θ1 had a large effect on the overall pattern width, similar to r, and the over-wide pattern indicated that the water droplet spread on the superhydrophilic pattern quickly, which resulted in the decrease of the Laplace force. The over-narrow track caused the increase of the junction number, resulting in the increase of the resistance force from the pinning, as shown in Fig. 2(d)–(f), Fig. S4(b), and Video S2.† Although θ2 also had an influence on va, that is va slightly increased with the increase of θ2, the variation of va was insignificant, as shown in Fig. S3, S4(c), and Video S2.† As in previous research, the water droplet would be blocked at the junction when k was over-small (Fig. S5(a) and S5(b)†).27 When 0.3 < k < 0.5, since ww was constant, wn decreased with decreasing k, resulting in the increase of the pinning force. When 0.5 < k < 0.7, the junction number increased slightly with the increase of k, resulting in a slight decrease of the water transportation velocity (Fig. 2(g)–(i), Fig. S4(d), and Video S2†). When k > 0.7, the difference between the front and the backside of the water bubble on the pattern was not obvious, which meant that the Laplace pressure of the water bubble was decreased with increasing k, resulting in the decrease of va (Fig. S5(c)†). In addition, the instantaneous water transportation flux of water droplets on the SSCP was also studied, as shown in Fig. S6.† Therefore, the variation law of the SSCP with the different parameters on the water transportation velocity and the better configuration parameters were obtained by the single-factor experiments.To obtain the optimal configuration parameters of the SSCP for further enhancing the water transportation velocity, an orthogonal optimization design was conducted.36 According to the aforementioned single-factor experiments, it can be seen that θ2 was insignificant on va; so r, θ1, and k were chosen as the influence factors in the orthogonal optimization design, and the parameter ranges were 20 mm–30 mm for r, 158°–162° for θ1, 0.4–0.6 for k, and 180° for θ2. The better configuration parameters verified by the single-factor experiments were used as the 0 level for the factor code of the orthogonal optimization design, and va was used as the response. The factor code table and experiment results are shown in Tables 1 and 2, respectively.
| Code | r/mm | θ 1/° | k |
|---|---|---|---|
| +1.682 | 30.00 | 162.00 | 0.60 |
| +1 | 27.97 | 161.19 | 0.56 |
| 0 | 25.00 | 160.00 | 0.50 |
| −1 | 22.03 | 158.81 | 0.44 |
| −1.682 | 20.00 | 158.00 | 0.40 |
| Sample | Factor and level combination | Response | ||
|---|---|---|---|---|
| r/mm | θ 1/° | K | ν a/mm s−1 | |
| 1 | 22.03 | 158.81 | 0.44 | 159.83 |
| 2 | 27.97 | 158.81 | 0.44 | 180.78 |
| 3 | 22.03 | 161.19 | 0.44 | 163.08 |
| 4 | 27.97 | 161.19 | 0.44 | 217.39 |
| 5 | 22.03 | 158.81 | 0.56 | 220.68 |
| 6 | 27.97 | 158.81 | 0.56 | 202.78 |
| 7 | 22.03 | 161.19 | 0.56 | 220.68 |
| 8 | 27.97 | 161.19 | 0.56 | 238.10 |
| 9 | 20.00 | 160.00 | 0.50 | 202.78 |
| 10 | 30.00 | 160.00 | 0.50 | 230.88 |
| 11 | 25.00 | 158.00 | 0.50 | 214.37 |
| 12 | 25.00 | 162.00 | 0.50 | 234.49 |
| 13 | 25.00 | 160.00 | 0.40 | 137.64 |
| 14 | 25.00 | 160.00 | 0.60 | 238.10 |
| 15 | 25.00 | 160.00 | 0.50 | 234.49 |
| 16 | 25.00 | 160.00 | 0.50 | 242.07 |
| 17 | 25.00 | 160.00 | 0.50 | 250.00 |
| 18 | 25.00 | 160.00 | 0.50 | 246.03 |
| 19 | 25.00 | 160.00 | 0.50 | 242.07 |
| 20 | 25.00 | 160.00 | 0.50 | 227.27 |
| 21 | 25.00 | 160.00 | 0.50 | 246.03 |
| 22 | 25.00 | 160.00 | 0.50 | 238.10 |
| 23 | 25.00 | 160.00 | 0.50 | 242.07 |
Analysis of variance (ANOVA) was conducted for the experimental results using Design-Expert software, as shown in Table S1.† We then established a regression model after eliminating the insignificant factor in Table S1† and obtained a fitted equation for the influence of r, θ1, and k on va, as follows
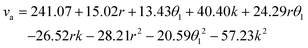 | (3) |
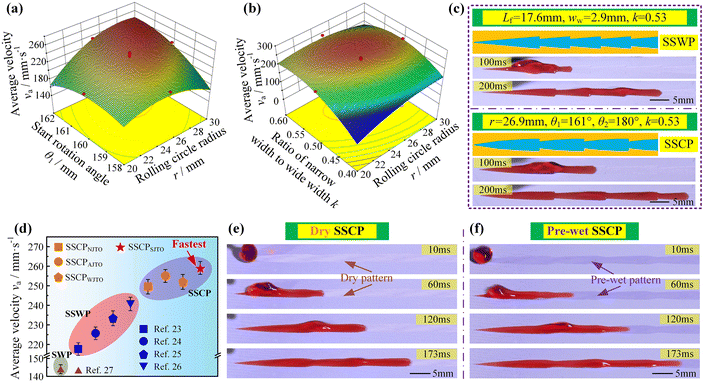
The obtained regression model was re-subjected to ANOVA. The ANOVA results are shown in Table S2.† It can be seen from the P value of Table S2† that the main influence order on va was k > r > θ1. Moreover, r and θ1, r and k had the interactive influence on va, which meant that the variation law of one factor on va might vary with the variation of the other one, as shown in Fig. 3(a) and (b). We then determined that the constraint condition on the optimization model was
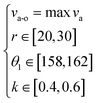 | (4) |
The previous literature showed that once a water droplet moved to the junction of the SSWP, it would be subjected to the resistance force from the pinning, resulting in the decrease of va.27 To decrease the influence of this resistance force in the water transportation processes, a series of optimization methods about the junction have been proposed to enhance water transportation capability, such as the arc junction transition, wedge junction transition, and streamline junction transition.27–29 Therefore, we applied the aforementioned optimization methods of the junction to the SSCP to enhance va, and the schematics of the SSWP and the SSCP after the junction optimization are shown in Fig. S10.† The experimental results showed that the junction transition optimizations really facilitated the increase of va, where the streamline junction transition optimization had the best effect on the improving va value and increased the va value from 250 mm s−1 to 259 mm s−1, as shown in Fig. 3(d) and Video S4.† However, we found that the influence of the geometry structure configuration on va was larger than that of the junction transition optimization, which showed that the va value of the SSCP without the junction transition optimization (SSCPNJTO) was also higher than that of the SSWP with the optimal junction transition optimization (SSWPSJTO). Strikingly, we found that va could be further enhanced by changing the external conditions. As shown in Fig. 3(e), the water droplet demonstrated va of 259 mm s−1 on the dry SSCP with the configuration parameters after the aforementioned optimizations. However, for the same configuration parameters, the arrival destination time decreased from 193 ms to 173 ms after pre-wetting the SSCP with 10 μL of water, showing the further enhancement of the va value from 259 mm s−1 to 289 mm s−1 (Fig. 3(f) and Video S5†). Ultimately, after a combination of the single-factor experiment, orthogonal optimization design, streamline junction transition optimization, and pre-wet pattern, the va value on the SSCP was enhanced to 289 mm s−1, which was the highest in the SDWT field.
3.3 Applications of the superhydrophilic serial cycloid-shaped pattern
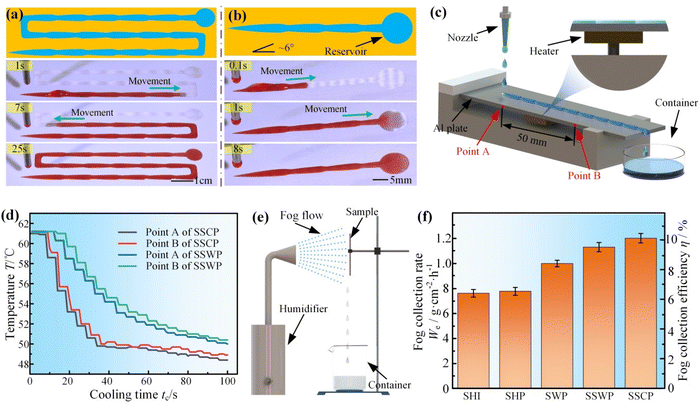
Since water could be transported faster on the SSCP, we then further explored other water transportation capabilities and applications of the SSCP using aforementioned optimal configuration parameters. As shown in Fig. 4(a), a long-distance SSCP with several right angles and a reservoir was fabricated on a superhydrophobic Al plate, and it could achieve the water long-distance transportation with ∼23 cm (Video S6†). In addition, the SSCP could even transport the water for a longer distance of ∼53 cm (Fig. S11 and Video S6†). Besides, a 40 μL water droplet could be spontaneously and directionally transported on an inclined SSCP with 6°; in this water transportation process, although gravity acted as a resistance force to impede the water movement, the water droplet still overcame gravity and was successfully transported to the reservoir at a height of ∼5.2 mm, as shown in Fig. 4(b) and Video S7.† Since water can be transported quickly, spontaneously, and directionally on the SSCP, it is promising for application on the spacecraft to cool the heat electronics. We heated a superhydrophobic Al plate with the SSCP and then cooled the Al plate by the directional water transportation on the SSCP, and measured the temperatures of point A and point B by using a multi-channel temperature monitor (Fig. 4(c)). As a comparison, the SSWP with the same parameters was also fabricated on the Al plate. Excitingly, point A and point B of the SSCP not only cooled faster than that of the SSWP, but also had a superior temperature drop of 12.5 °C than that of the SSWP with 10.9 °C, which resulted from the fact that the water was transported faster on the SSCP and could take away more heat (Fig. 4(d)). In addition, previous research studies verified that the patterned surface with a combination of the superhydrophobic surface and superhydrophobic surface was more efficient in fog collection than the entire superhydrophilic surface (SHI) and the entire superhydrophobic surface (SHP).37 Based on this, we conducted fog collection experiments and found that the SSCP had a higher fog collection rate and efficiency than the other pattern surface due to the larger area and faster water transportation velocity on the SSCP, which could make easier contact with the droplets on the superhydrophobic area and quickly transport the captured fog droplets to the pattern tail and shed the collected water from the collection surface easier, as shown in Fig. 4(e), (f), Fig. S12, and Video S8.†30,324. Conclusion
In summary, inspired by the micro-cavity shape of the Nepenthes, we have successfully overcome the limitation of the existing spontaneous and directional water transportation by proposing a superhydrophilic serial cycloid-shaped pattern (SSCP) via two-step laser processing and FAS modification. Specifically, we found that the water transportation velocity on the SSCP was faster on the superhydrophilic serial wedge-shaped pattern (SSWP) with the same parameters under the multiple parameters, and the mechanism of the faster water transportation velocity was that the water droplet had a larger driving force from the Laplace pressure on the SSCP. In addition, we investigated the influence of the SSCP parameters on the water transportation velocity, where the rolling circle radius, start rotation angle, and ratio of the narrow width to the wide width were significant on the water transportation velocity, while the end rotation angle was insignificant on the water transportation velocity. Moreover, after a combination of the single-factor experiment, orthogonal optimization design, streamline junction transition optimization, and pre-wet pattern, the water transportation velocity on the SSCP was enhanced to 289 mm s−1, which was the fastest in the spontaneous and directional water transportation field. Finally, the SSCP with the aforementioned optimizations showed that it could be applied in long-distance water transportation, gravity resistant water transportation, heat transfer, and fog collection, which resulted from its superior water transportation capability. The proposed SSCP will open a new avenue for the high-performance spontaneous and directional water transportation system.Author contributions
Defeng Yan: conceptualization, methodology, investigation, and writing – original draft. Yi Lu: data curation, validation, and visualization. Jinming Liu: investigation, methodology, and software. Yang Chen: methodology and formal analysis. Jing Sun: supervision. Jinlong Song: funding acquisition, resources, supervision, and writing – review & editing.This manuscript was written through contributions from all authors. All authors have given approval to the final version of the manuscript.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the National Natural Science Foundation of China (NSFC, 52175380) and the Fundamental Research Funds for the Central Universities (DUT21LAB120). The authors sincerely thank Qiao Liu from the Dalian Maritime University for her help in the orthogonal optimization design.References
- Y. Zheng, H. Bai, Z. Huang, X. Tian, F. Nie, Y. Zhao, J. Zhai and L. Jiang, Nature, 2010, 463, 640–643 CrossRef CAS PubMed.
- S. Feng, P. Zhu, H. Zheng, H. Zhan, C. Chen, J. Li, L. Wang, X. Yao, Y. Liu and Z. Wang, Science, 2021, 373, 1344–1348 CrossRef CAS PubMed.
- M. Aizudin, N. Alias, Y. Ng, M. Fadzuli, S. Ang, Y. Ng, R. Pottammel, F. Yang and E. Ang, Nanoscale, 2022, 14, 17871–17886 RSC.
- Y. Chen, D. Yan, R. Liu, Y. Lu, D. Zhao, X. Deng and J. Song, Nano Energy, 2022, 101, 107543 CrossRef CAS.
- Y. Wang, G. Wang, M. He, F. Liu, M. Han, T. Tang and S. Luo, Small, 2021, 17, 2103322 CrossRef CAS PubMed.
- X. Yang, K. Zhuang, Y. Lu and X. Wang, ACS Nano, 2021, 15, 2589–2599 CrossRef CAS PubMed.
- J. Elías-Maxil, J. van der Hoek, J. Hofman and L. Rietveld, Renewable Sustainable Energy Rev., 2014, 30, 808–820 CrossRef.
- J. Li and Z. Guo, Nanoscale, 2018, 10, 13814–13831 RSC.
- Y. Liu, H. Zhai, X. Li, N. Yang, Z. Guo, L. Zhu, C. Gao, Y. Hou and Y. Zheng, Nano Energy, 2022, 96, 107076 CrossRef CAS.
- J. Wu, K. Yin, L. Li, Z. Wu, S. Xiao, H. Wang, J. Duan and J. He, Nanoscale, 2020, 12, 4077–4084 RSC.
- H. Greenspan, J. Fluid Mech., 1978, 84, 125–143 CrossRef.
- M. K. Chaudhury and G. M. Whitesides, Science, 1992, 256, 1539–1541 CrossRef CAS PubMed.
- C. Yang, Y. Yu, X. Wang, L. Shang and Y. Zhao, Small, 2021, 18, 2104306 Search PubMed.
- L. Wang, K. Yin, Q. Deng, Q. Huang, J. He and J. Duan, Adv. Sci., 2022, 9, 2204891 CrossRef CAS PubMed.
- H. Bai, X. Wang, Z. Li, H. Wen, Y. Yang, M. Li and M. Cao, Adv. Mater., 2023, 2211596 CrossRef CAS PubMed.
- X. Leng, L. Sun, Y. Long and Y. Lu, Droplet, 2022, 1, 139–169 CrossRef.
- W. Zhao, Y. Jiang, W. Yu, Z. Yu and X. Liu, Small, 2022, 18, 2202906 CrossRef CAS PubMed.
- J. Xu, S. Xiu, Z. Lian, H. Yu and J. Cao, Droplet, 2022, 1, 11–37 CrossRef.
- L. Guo, S. Kumar, M. Yang, G. Tang and Z. Liu, Nanoscale, 2022, 14, 17871–17886 RSC.
- Y. Chen, J. Liu, Y. Zhou, Y. Li, Z. Yuan, D. Yan, S. Wu, D. Zhao and X. Liu, Adv. Mater. Interfaces, 2022, 10, 202201977 Search PubMed.
- Y. Hirai, H. Mayama, Y. Matsuo and M. Shimomura, ACS Appl. Mater. Interfaces, 2017, 9, 15814–15821 CrossRef CAS PubMed.
- D. Shi, Y. Chen, X. Chen, X. Chen, J. Gao, Y. He and C. Wong, ACS Appl. Mater. Interfaces, 2018, 10, 34735–34743 CrossRef CAS PubMed.
- Y. Jiang, C. Machado and K. Park, Droplet, 2023, 2, e55 CrossRef.
- Y. Tang, X. Yang, Y. Li and D. Zhu, Adv. Mater. Interfaces, 2021, 8, 2100284 CrossRef CAS.
- H. Bai, X. Wang, Z. Li, H. Wen, Y. Yang, M. Li and M. Cao, Adv. Mater., 2023, 35, 202211596 Search PubMed.
- J. Song, Z. Liu, X. Wang, H. Liu, Y. Lu, X. Deng, C. J. Carmalt and I. P. Parkin, J. Mater. Chem. A, 2019, 7, 13567–13576 RSC.
- Z. Liu, H. Liu, W. Li and J. Song, Chem. Eng. J., 2022, 433, 134568 CrossRef CAS.
- D. Xie, B. Y. Zhang, G. Wang, Y. Sun, C. Wu and G. Ding, Small Methods, 2022, 6, 2200812 CrossRef PubMed.
- Q. Liu, J. Zhang, P. Sun, J. Wang, W. Zhao, G. Zhao, N. Chen, Y. Yang, L. Li, N. He, Z. Wang and X. Hao, J. Mater. Chem. A, 2023, 11, 10164–10173 RSC.
- J. Liu, D. Yan, Y. Zhou, Y. Chen, X. Liu, D. Zhao, J. Liu and J. Sun, Colloids Surf., A, 2022, 647, 128999 CrossRef CAS.
- W. Pan, Q. Wang, J. Ma, W. Xu, J. Sun, X. Liu and J. Song, Adv. Funct. Mater., 2023, 230231 Search PubMed.
- D. Yan, Y. Chen, J. Liu and J. Song, Small, 2023, 2301745 CrossRef PubMed.
- H. Chen, P. Zhang, L. Zhang, H. Liu, Y. Jiang, D. Zhang, Z. Han and L. Jiang, Nature, 2016, 532, 85–89 CrossRef CAS PubMed.
- W. Pan, S. Wu, L. Huang and J. Song, Nanoscale, 2021, 13, 14023–14034 RSC.
- H. Ma, M. Cao, C. Zhang, Z. Bei, K. Li, C. Yu and L. Jiang, Adv. Funct. Mater., 2018, 28, 1705091 CrossRef.
- T. Movahedi and R. Norouzbeigi, J. Alloys Compd., 2019, 795, 483–492 CrossRef CAS.
- H. Bai, L. Wang, J. Ju, R. Sun, Y. Zheng and L. Jiang, Adv. Mater., 2014, 26, 5025–5030 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr02180g |
| This journal is © The Royal Society of Chemistry 2023 |