Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On scattered waves and lipid domains: detecting membrane rafts with X-rays and neutrons
Drew
Marquardt
ab,
Frederick A.
Heberle
cdg,
Jonathan D.
Nickels
cde,
Georg
Pabst
*ab and
John
Katsaras
*cdefg
aUniversity of Graz, Institute of Molecular Biosciences, Biophysics Division, NAWI Graz, Humboldtstr. 50/III, Graz, Austria. E-mail: georg.pabst@uni-graz.at; Tel: +43 316 380 4989
bBioTechMed-Graz, Graz, Austria
cOak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA. E-mail: katsarasj@ornl.gov; Tel: +1 865 274 8824
dJoint Institute for Neutron Sciences, Oak Ridge, Tennessee 37831, USA
eDepartment of Physics, University of Tennessee, Knoxville, Tennessee 37996, USA
fDepartment of Physics, Brock University, St. Catharines, Ontario L2S 3A1, Canada
gBredesen Center for Interdisciplinary Research and Graduate Education, University of Tennessee, Knoxville, Tennessee 37996, USA
First published on 21st September 2015
Abstract
In order to understand the biological role of lipids in cell membranes, it is necessary to determine the mesoscopic structure of well-defined model membrane systems. Neutron and X-ray scattering are non-invasive, probe-free techniques that have been used extensively in such systems to probe length scales ranging from angstroms to microns, and dynamics occurring over picosecond to millisecond time scales. Recent developments in the area of phase separated lipid systems mimicking membrane rafts will be presented, and the underlying concepts of the different scattering techniques used to study them will be discussed in detail.
1 Introduction
Biological membranes are complex, self-assembled composites of proteins, lipids and carbohydrates, whose hierarchical organization is fundamental to physiological processes. In particular, lateral organization of the lipid/protein layer of plasma membranes has not only attracted significant scientific interest, but also considerable controversy. The membrane raft paradigm invokes the existence of functional domains enriched in sphingolipids, cholesterol and proteins, such as glycophosphatidylinositol-anchored proteins that facilitate diverse cellular signaling and transport processes.1 However, proof of their existence in live cells has been elusive.2–4In contrast, domains are well-established in lipid-only model systems of plasma membranes.5,6 Such systems of reduced complexity allow for close scrutiny of the biophysical nature of lipid–lipid interactions and their potential in organizing lateral membrane structure. Over the years, a variety of experimental techniques have been applied to study the properties of lipid domains.7 In this tutorial review we focus on the ability of X-rays and neutrons to interrogate the properties of lipid domains, using either elastic or inelastic scattering. The present work can be seen as a follow-up to one of our previous review articles,8 which while briefly summarizing early scattering studies on lipid domains, was mainly focused on homogeneous lipid bilayers. Here we discuss progress in the field that has taken place over the past five years.
The review article is organized as follows. First, we give a brief introduction to lipid-only domains in model systems mimicking the plasma membrane. We then expand on the theory of elastic and inelastic scattering of lipid domains and describe some illustrative examples. Finally, we conclude and give an outlook as to what can be expected in this area of research in the near future.
2 Properties of membrane domains
Lipids in multi-component mixtures minimize free energies arising from their chemical structure, leading to differences in membrane structure, hydrocarbon chain packing and chain order, and hydrogen bond formation. For example, in a binary mixture of lipids (e.g., A and B), these interactions can be parameterized by9–11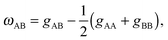 | (1) |
When discussing lateral membrane heterogeneity, it is useful to distinguish between four cases: (i) random (ideal) mixing; (ii) non-random mixing or compositional fluctuations (i.e., unstable domains); (iii) nanoscopic domains; and (iv) macroscopic domains. Domain stability and size depends on the line tension γ, which defines the free energy of the domain boundary (see e.g.ref. 15). That is, critical domain fluctuations occur at γ = 0. At small γ, nanoscopic domains are formed, whereas at large γ domains may grow to several microns in size.
Cholesterol is highly abundant in mammalian plasma membranes, and is a very peculiar membrane lipid. Although weakly amphiphilic, it has a finite solubility in phospholipid membranes, beyond which it precipitates from the bilayer as cholesterol monohydrate crystals.16 In bilayers composed of saturated or monounsaturated chains, cholesterol's solubility limit depends strongly on the phospholipid headgroup, and can be understood in terms of the “umbrella model”, where headgroups of neighboring lipids reorient to cover cholesterol's nonpolar surface, preventing its unfavorable exposure to water.17 The ability of different phospholipids to shield cholesterol should therefore depend not only on headgroup size, but also on chain packing considerations. Indeed, a 3- to 4-fold reduction in cholesterol solubility has been found in highly unsaturated PC bilayers composed of arachidonoyl (C20:4) or docosahexaenoyl (C22:6) chains at both the sn-1 and sn-2 positions,18 and several studies have shown that cholesterol preferentially interacts with membrane lipids composed of disaturated acyl chains.19
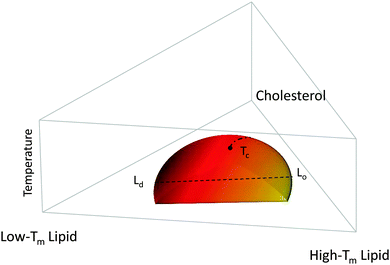
In binary lipid mixtures, cholesterol is well-known for its ordering effect on the fluid lamellar phase (Lα), leading to the liquid-disordered (Ld) and liquid-ordered (Lo) phases at low and high cholesterol contents, respectively. On the other hand, lamellar gel phases (Lβ) are disordered by cholesterol.10,20 (Note, that frequently Ld is used synonymously with Lα.) In describing the differences between these phases it is instructive to consider the two types of order that define the lamellar phases, namely translational or in-plane positional order (the spatial correlation between one lipid and another), and the chain configurational order of an individual lipid. These types of order are related to observables like the diffusion coefficient (translational order), hydrocarbon chain thickness and gauche/trans isomerization ratio (chain configurational order), all of which are strongly coupled in the Lα and Lβ phases. In other words, low translational order is accompanied by low configurational order within fluid phase bilayers, and vice versa in the case of gel phase bilayers. Cholesterol, however, has the unique property of decoupling these two types of order: the Lo phase has very high chain order, but lacks long-range positional order. Properties of the lamellar phases are summarized in Fig. 2.
Fig. 1 shows a typical compositional phase diagram for raft-like ternary lipid mixtures of low-melting lipids (mainly di- or monounsaturated lipids), high-melting lipids (long chain disaturated phosphatidylcholines or sphingomyelin) and cholesterol. In raft-like lipid mixtures, as shown in Fig. 1, Lo and Ld phases coexist over an extended range of compositions and temperatures. Since Lo and Ld are fluid phases, their γ is isotropic, leading to the formation of circular domains. Demixing occurs along tielines, and the Lo/Ld composition can be read off the tieline endpoints where they cross the phase coexistence boundary. The fraction of Lo or Ld changes along the tieline, and can be determined using the lever rule.6 The direction of tielines may differ from system to system, but in general shows that Ld domains contain most of the low-melting lipid, whereas Lo domains are enriched in the high-melting lipid, and moderately enriched (2- to 3-fold) in cholesterol.
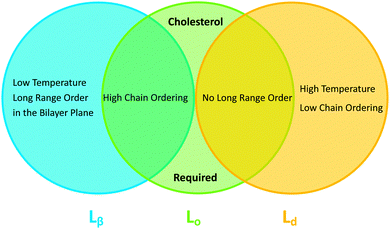 | ||
| Fig. 2 Venn diagram of properties shared between the gel (Lβ), liquid disordered (Ld) and liquid ordered (Lo) phases. | ||
At high temperatures, Lo melts into a pure Ld phase, giving the phase coexistence regime a dome-like structure. If this melting occurs at the peak of the “dome” it passes through a critical point Tc. Similarly, upon increasing cholesterol concentration, the Ld phase melts into an Lo phase. In this case, the tielines collapse into a single point, and the transition becomes second order. Thus, different critical transitions can be realized in ternary lipid mixtures, as shown in Fig. 1.
In the following section we describe how X-rays and neutrons can be used to probe overall domain size, as well as internal static and dynamic structures. For example, such information is needed for understanding how domains couple to protein partitioning and function. It is important to note that no bulky labels, which can potentially influence phase behavior,21–23 are needed for the scattering studies described herein.
3 General scattering theory
Even though X-rays are electromagnetic waves and neutrons particle waves, a single scattering theory is used to address both types of experiments. However, there are some important differences that must first be considered. To begin, X-rays interact with electrons, while neutrons interact with nuclei. Although not immediately obvious, X-ray scattering varies predictably with atomic number – heavy atoms scatter more strongly than lighter ones – while neutron scattering power varies erratically with atomic number. Importantly, however, neutrons are differentially sensitive to an element and its isotope(s). For example, hydrogen, which is ubiquitous in biological samples, has a coherent neutron scattering length bcohH = −3.7423 fm, while its stable isotope, deuterium, has bcohD = 6.674 fm. This difference between the two nuclei forms the basis of neutron contrast variation studies of biological materials. Therefore, by changing either the external contrast (by varying the H2O/D2O composition of the aqueous buffer), or by selectively deuterating specific parts of the biomolecule of interest,24 one can highlight or suppress static and dynamic structural features.Another important difference between X-ray and neutron scattering relates to instrumental resolution. The wavelength spread Δλ/λ at third generation synchrotron small-angle X-ray scattering (SAXS) beamlines is of the order of 0.01%, approximately 2 orders of magnitude finer than what is encountered at neutron beamlines. The main reason for this difference is the relatively low flux of neutron instruments, compared to X-rays, requiring monochromators capable of accepting a broader range of neutron wavelengths (i.e., less monochromatic beams). An obvious consequence of this, is that SAXS peaks are significantly sharper than peaks from small-angle neutron scattering (SANS) instruments. This offers the possibility to perform line-shape analysis using SAXS, resulting in the bilayer's elastic constant (see below). A less obvious result of tighter collimation and increased monochromicity relates to the beam coherence volume Vcoh, which is described in terms of partial coherence in the theory for optics.25Vcoh has a longitudinal component, i.e. parallel to the propagating wave train,
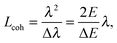 | (2) |
There is a third important difference between neutrons and X-rays. Neutron energies are typically on the order of meV, which are well within the range of thermally excited molecular motions, while X-rays are usually on the order of keV. Thus, while coherent inelastic X-ray scattering experiments on lipid membranes are feasible,28,29 neutrons are better suited for this purpose.30
3.1 Elastic X-ray and neutron scattering
In the case of elastic scattering there is no transfer of energy. It is therefore sufficient to consider the change in scattered intensity as a function of the momentum transfer vector, q. The magnitude of the scattering vector is given by q = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)/λ, where λ is the X-ray or neutron wavelength, and 2θ is the angle between the incoming and scattered beams (i.e., the scattering angle). Coherent elastic scattering of neutrons or X-rays provides information regarding spatial correlations of nuclei or electrons, respectively. However, unlike a crystal, where atoms are restricted to small thermal vibrations around well-defined positions, the inherent disorder of fluid lipid membranes prevents structure determination at atomic resolution. Thus it has proven useful to sum up the electrons or neutron scattering lengths per unit volume, and introduce the concept of the electron density profile (EDP) or neutron scattering length density (NSLD) profile (see Section 5).
sin(θ)/λ, where λ is the X-ray or neutron wavelength, and 2θ is the angle between the incoming and scattered beams (i.e., the scattering angle). Coherent elastic scattering of neutrons or X-rays provides information regarding spatial correlations of nuclei or electrons, respectively. However, unlike a crystal, where atoms are restricted to small thermal vibrations around well-defined positions, the inherent disorder of fluid lipid membranes prevents structure determination at atomic resolution. Thus it has proven useful to sum up the electrons or neutron scattering lengths per unit volume, and introduce the concept of the electron density profile (EDP) or neutron scattering length density (NSLD) profile (see Section 5).
Spatial correlations are contained in the amplitudes of the scattered wave or form factor F(q). F(q) is the sum of the coherent scattering length (bcoh) of all atoms in the sample (eqn (3)), and is proportional to the observed intensity of the scattered wave (eqn (4)):
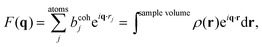 | (3) |
| I(q) ∝ |F(q)|2. | (4) |
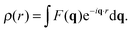 | (5) |
Two types of positional correlations can occur, which are accounted for by a modification of eqn (4):
| I(q) ∝ |F(q)|2S(q). | (6) |
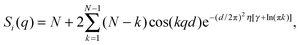 | (7) |
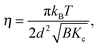 | (8) |
S p(q) and Si(q) are conceptually very different structure factors. Since nearest neighbors are typically much farther apart than bilayers in MLVs, contributions from Sp(q) will occur only at very low scattering angles and may even be neglected in data analysis by exempting the low-angle regime. Contributions from Si(q) in turn occur at higher q-values and cannot be omitted when analyzing MLV data. Certainly, inter-particle correlations also occur in concentrated MLV solutions. However, due to the strong scattering power of Si(q) as compared to Sp(q), such contributions are typically not observed.
3.2 Inelastic scattering
In contrast to the elastic scattering experiments described above, inelastic scattering results in the transfer of energy and momentum between the incident particle and the sample. Inelastic scattering of neutrons is ideal for studies of molecular motion in lipid bilayers, though its potential is relatively unexploited to date. The incident energy of neutrons typically used in inelastic scattering experiments is on the order of meV, comparable to the time scale of many processes in soft matter systems. For lipid bilayers, these include diffusion, vibration, molecular reorientation (e.g., methyl rotation), lipid rotation, bilayer undulation, and bilayer thickness fluctuation. Inelastic X-ray scattering experiments are also feasible in lipid bilayer systems, but their use has been restricted to the study of collective vibrational dynamics28,29 due to the coherent nature of X-ray scattering and their relatively high incident energies (0.1–100 keV). An alternative, indirect route to study membrane dynamics has been recently achieved using time-resolved elastic X-ray diffraction on multibilayers coupled to a surface acoustic wave generator.36 Thus, by taking advantage of the ps-time structure of highly brilliant photon pulses at synchrotron facilities, the response of membranes to external oscillatory excitation can be exploited.The goal of inelastic scattering experiments is to measure two quantities, namely the momentum transfer, q = kf − ki, and the energy transfer, ℏω = Ef − Ei. Here, ki and kf are the incident and scattered wave vectors, respectively, and Ei and Ef are the incident and scattered neutron energies, respectively. Through these two quantities, one can extract detailed information with respect to the frequency and geometry of atomic motions within a lipid bilayer.
The earliest inelastic scattering experiments were performed in the 1950s by Bertram Brockhouse37 at the then Chalk River Nuclear Laboratories using his newly developed triple-axis spectrometer. This novel way of measuring inelastic scattering enabled the measurement of scattered intensity at specific points in q and ω. A range of specialized spectrometers have subsequently been designed to optimize observation of scattered intensity simultaneously at multiple points in phase space, including time-of-flight,38 backscattering39 and neutron-spin-echo (NSE) spectrometers.40 This modern suite of instruments is able to probe motions on timescales ranging from 10−14 s to 10−7 s, and over length scales from 10−7 m to less than 10−10 m.
A quantitative description of inelastic scattering41–43 requires us to consider the basic quantity measured by neutron scattering experiments, namely the double differential cross-section:
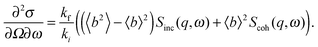 | (9) |
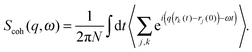 | (10) |
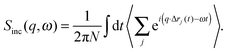 | (11) |
The most common type of inelastic scattering measurement for biological materials focuses on the incoherent scattering from hydrogen. Hydrogen has an incoherent scattering cross-section of 80.27 barns, 40 times greater than that of deuterium, and more than 100 times larger than the other elements typically found in lipid bilayers: C (0.001 barns); N (0.5 barns); O (0.0008 barns); and P (0.005 barns). Because of the large incoherent scattering from hydrogen, incoherent scattering experiments often use protiated or partially deuterated lipids, hydrated with D2O in order to isolate the scattered signal from the lipid component of interest within the sample.45–52 Naturally, this situation can be reversed to study the dynamics of hydration water using a deuterated bilayer.51,53,54
The scattered intensity is customarily reduced to a function of ω for a set of q values, analysis of which yields information about the confinement geometry and relaxation times of atomic motions within the sample.55 The geometric information for a given dynamic process is usually extracted from the ratio of elastic intensity to total scattered intensity, and is represented as a phenomenological quantity called the Elastic Incoherent Structure Factor or EISF(q,ω). Numerous functional forms of the EISF have been put forward in order to accurately model the various atomic motions probed by scattering experiments.56
The inelastic scattering associated with a given dynamic process, i, is often modeled with a Lorentzian function Γ(q,ω), which is scaled by a factor Pi representing the fraction of hydrogen atoms participating in the ith process. This inelastic contribution of each process is combined with the EISF and a delta function δ(ω) to account for elastic scattering, to generate a theoretical scattering function including n processes:
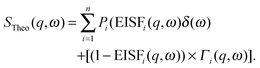 | (12) |
| SExp(q,ω) = DWF(q) × [STheo(q,ω) ⊗ R(q,ω) + B(q,ω)], | (13) |
Deuterated molecules are also useful to study inelastic coherent scattering by reducing the overwhelming incoherent signal from hydrogen. This class of experiment excels in studies of lattice dynamics,57,58 but can also be useful in the study of collective motions of soft matter.59–63 Treatment of coherent scattering data is somewhat more complicated due to its sensitivity to pair-correlations. On the other hand, this sensitivity is responsible for the key feature of inelastic coherent scattering measurements, namely the ability to observe which atomic spacings are preserved during a particular collective motion. Borrowing from the polymer64,65 and protein61 literature, this information can be accessed by plotting the scattered intensity as a function of q, at a set of ω values, and comparing to the static structure factor, S(q,0). When a set of atoms moves collectively, maintaining their relative spacing, they will give rise to excess intensity at the associated q value, which can be expressed as:
| S(q,ω) = A(ω) × S(q,0) × q2 + B(ω) × q2 + C. | (14) |
Analysis of neutron spin echo (NSE) data requires a different approach. The primary distinction of NSE, compared to the other inelastic techniques, is that it measures the intermediate scattering function, the ISF or I(q,t), rather than the dynamic structure factor, S(q,ω). The ISF is typically reported as I(q,t)/I(q,0) so that the quantity is normalized to 1. I(q,t) is simply the Fourier transform of the dynamic structure factor in the time domain. Another difference is that analysis of NSE results is typically performed in the time domain, using peak functions (rather than decay functions) to fit data.
Although NSE is capable of probing slow diffusive motions of lipids and bilayer thickness fluctuations, the most common spin echo experiments on lipid bilayers are direct measurements of bilayer undulation, allowing access to the bilayer's bending modulus.66–71 Typically, coherent scattering in the range 0.05 < q < 0.2 Å−1 is analyzed using a modification66,70,72 of the approach put forward by Zilman and Granek.73 Briefly, the ISF is fit in the time domain using a stretched exponential decay:
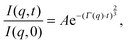 | (15) |
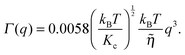 | (16) |
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) is the solvent viscosity, not to be confused with the Caillé parameter in eqn (8)). Eqn (16) implies that a plot of Γ(q)/q3 as a function of q will exhibit a constant value that is inversely proportional to the square root of Kc.
is the solvent viscosity, not to be confused with the Caillé parameter in eqn (8)). Eqn (16) implies that a plot of Γ(q)/q3 as a function of q will exhibit a constant value that is inversely proportional to the square root of Kc.
4 Sample geometries
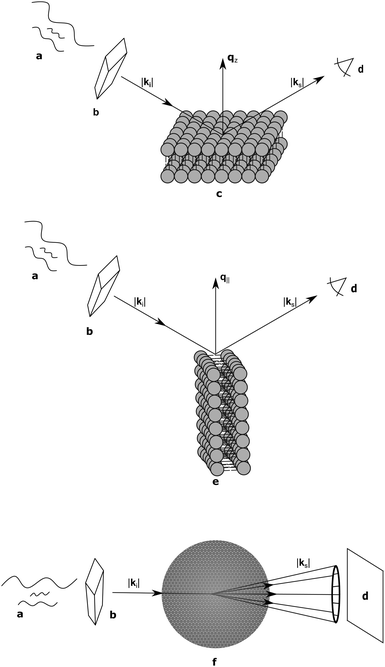
As discussed, lipid domains can be studied using a variety of scattering techniques, some of which demand unique sample preparations, conditions and geometries. From the standpoint of biological relevance, unilamellar vesicles (ULVs) are the most desirable mimics of a cellular membrane. Diffuse scattering from a dilute ULV suspension affords the possibility to extract the bilayer's continuous F(q) (eqn (4)), and often offers extended ranges for the scattering vector's transverse component (qz).Arguably the easiest method of sample preparation is that of MLVs, whereby a dry lipid mixture film is hydrated with water. Measurement of MLVs results in the presence of a F(q) and a Si(q) as a convolution of both the radial and in-plane heterogeneities of the bilayer structure. A great deal of information can be extracted from MLV samples, including (but not limited to) the bilayer's stiffness, and the presence of domains (Section 6).
Supported samples can be prepared as a single bilayer (typically examined with reflectometry) or as multilamellar stacks for interrogation by diffraction techniques. Although MLVs are themselves aligned bilayers, alignment on a solid substrate allows for the transverse and lateral structures to be examined independently (Fig. 3). The separation of qz and q∥ (the lateral scattering vector component) allows for the unambiguous assignment of scattering features arising from the different orientations. Like all systems, solid-supported bilayers suffer from some drawbacks. For example, supported lipid bilayers have proven difficult to fully hydrate,74,75 though recent advances in sample environments have achieved hydration levels of better than 99.6% as determined by lamellar repeat spacings.76 Perturbations attributed to bilayer–substrate interactions are limited to the first few bilayers, although much effort has been expended into functionalizing the substrate surface with a polymer cushion for use in single bilayer studies.77
The aforementioned sample conditions are characterized by low resolution data, however, improved structural data can be achieved by utilizing the neutron scattering method of contrast variation. The ability to change contrast conditions without resorting to bulky and unnatural probes that can alter the bilayer's physical properties is one clear advantage elastic neutron scattering has over other biophysical techniques, including X-ray scattering.78 Manipulating contrast is particularly important since the scattering intensity is proportional to the square of the SLD difference between the sample and solvent (medium). Contrast can be systematically changed by substituting one isotope of an element with another (discussed above). In the case of biological samples, the substitution of hydrogen for deuterium is commonly used to vary contrast. Scattering from individual components of the system, such as phase separated regions of a vesicle, can be suppressed through contrast matching with the solvent, allowing for the determination of lateral structure and composition. Contrast variation in a SANS experiment on lipid domains is illustrated below (Section 6.1) (Fig. 7).
5 Homogeneously mixed bilayers: a brief update
Although homogeneously mixed fluid bilayers lack long range in-plane atomic correlations, they do possess one-dimensional out-of-plane correlations. The structure of a homogeneous fluid bilayer can therefore be thought of as the time-averaged distribution of matter projected onto the bilayer normal. A scattering experiment provides a distorted reflection of this matter distribution, where features are reshaped by the relative interaction strength of the probe (neutrons or X-rays) with the lipid's chemical makeup. In this sense, the real-space scattering length density profiles obtained from different types of scattering experiments (i.e., X-ray data, or different contrast neutron data) are simply different representations of the bilayer's structure averaged over time/energy. While traditional bilayer structural analyses model SLD profiles of standalone scattering data,35,79–83 a model based on matter density distribution can easily combine different contrast data sets (i.e., X-ray and neutron) into a single global analysis, resulting in a more robust bilayer structure.White and coworkers were the first to exploit this fundamental link between the bilayer's different structural representations, in their development of the “composition space model”. Because individual atoms are not well-localized in a thermally disordered bilayer, they are best described by broad statistical averages. King and White84 proposed a coarse-grained lipid structure, where neighboring atoms are grouped into quasi-molecular distributions whose atomic number density profiles are described by simple functional forms (e.g., uniform or Gaussian distributions). A fully resolved fluid bilayer structure consists of a handful of such quasi-molecular distributions, typically 2–3 to describe the lipid headgroup, and 3–4 to describe the hydrocarbon chain region. Scattering length density profiles for different contrast data sets are then obtained by scaling the component number density distributions with an appropriate scattering length (i.e., the sum of individual atomic scattering lengths making up the distribution). Through the joint refinement of neutron and X-ray diffraction data, Wiener and White determined the fully resolved structure of a partially dehydrated fluid DOPC bilayer.85–89
Kučerka et al. extended this approach with their Scattering Density Profile (SDP) analysis (Fig. 4), which leverages the atomistic detail of MD simulations to guide the choice of atomic groupings, thereby maximizing the model's compatibility with different contrast X-ray and neutron data.90 For this model, which uses data from ULVs, eqn (3) becomes
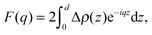 | (17) |
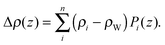 | (18) |
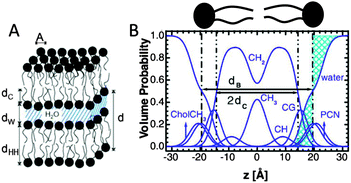 | ||
| Fig. 4 Description of membrane structure in terms of the SDP model. Panel A shows a schematic of a stack of membranes with the corresponding structural parameters: d – lamellar repeat distance; dB – bilayer thickness; dW – bilayer separation; dC – hydrocarbon chain length; dHH – headgroup-to-headgroup distance; and A – area per lipid. Panel B shows the volume distribution functions of quasimolecular distributions in terms of the SDP model. Figure adapted from ref. 91. | ||
Here Pi(z) represent the volume distributions of given molecular fragments, each described by a Gaussian or error function. A typical parsing scheme for a phosphatidylcholine bilayer would be, for example, the choline methyl (CholCH3), phosphate + CH2CH2N (PCN), carbonyl + glycerol (CG), hydrocarbon methylene (CH2) and terminal acyl chain methyl (CH3) groups. The Pi's are scaled by the contrast of their given scattering length densities, ρi, with water, ρW.
By combining SANS data at several D2O/H2O ratios (“external” contrasts) with SAXS data, Kučerka and coworkers obtained the first fully resolved bilayer structure from a vesicle suspension at full hydration. The SDP approach has since been used to determine structures for a wide range of biologically relevant lipids using fully hydrated fluid bilayers, including phosphatidylcholine,91,92 phosphatidylglycerol,93 phosphatidylserine,94 phosphatidylethanolamine,95 and cardiolipin.68 A major achievement of the SDP model is the robust determination of bilayer thickness, defined as
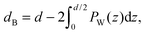 | (19) |
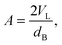 | (20) |
Recently, Heftberger et al.98 combined the SDP model with a Caillé structure factor (eqn (7)) to analyze MLVs in the Lα phase (Fig. 5). In this case, the scattered intensity is given by
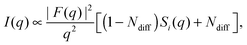 | (21) |
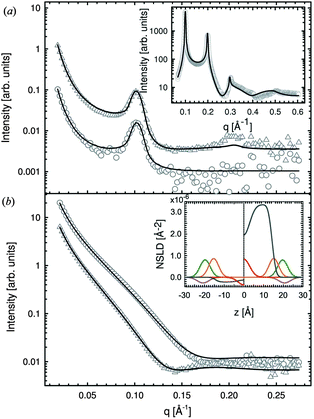 | ||
| Fig. 5 Joint analysis of SAXS (inset) and SANS data of POPC MLVs and ULVs. Panel A shows SANS data of POPC (circles) and chain deutrated POPC-d31 (triangles) MLVs. Panel B shows corresponding data for ULVs (same symbols). Figure is adapted from ref. 98. | ||
6 Phase separated bilayers
The importance of coherence volume Vcoh was mentioned in Section 3. For phase separated systems in particular, the domain size—or more precisely, the domain volume VD—with respect to Vcoh must be considered. If Vcoh ≥ VD, domain scattering contributions add coherently (Fig. 6 top). For ULVs exhibiting two-phase coexistence, the observed scattering intensity is thus given by:| I(q) ∝ |ϕAFA + (1 − ϕA)FB|2, | (22) |
| I(q) ∝ ϕA|FA|2 + (1 − ϕA)|FB|2 + Ĩ(q), | (23) |
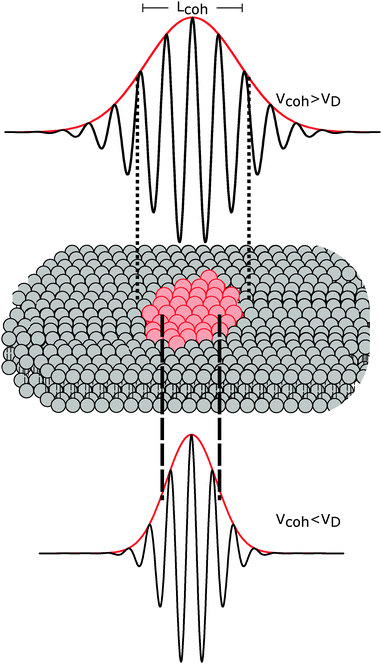 | ||
| Fig. 6 The influence of coherence volumes in detecting membrane domains. Coherence is represented as a 1D interferrogram with a given coherence length Lcoh (see also eqn (2)). For low wavelength spread and large Vcoh (top), scattering contributions from the domain and surrounding bilayer add coherently (eqn (22)). In this case, domain size, morphology, and configuration can in principle be determined in a small-angle scattering experiment. For multibilayer samples, Bragg peaks from distinct Lo and Ld lattices are averaged. At high wavelength spread (bottom), Vcoh < VD, resulting in incoherent addition of domain scattering contributions (eqn (23)), and a superposition of Ld and Lo Bragg peaks in a SAXS experiment, as demonstrated in Section 6.3. | ||
The effect of Vcoh was demonstrated by Armstrong et al.101 for dipalmitoyl phosphatidylcholine (DPPC) in the vicinity of its melting transition. Upon cooling from the liquid-disordered Ld phase, small gel-like domains begin to nucleate. Using neutron diffraction and oriented multibilayers, and by selectively detuning the pyrolytic graphite monochromator, the authors were able to decrease Lcoh from 242 Å to 30 Å. Only for Lcoh < 103 Å was phase coexistence observed.
With regard to domain size, another factor to consider is the overall ULV size. For 50–100 nm diameter ULVs, as studied by SANS (see Section 6.1), Vcoh > VD for Lo/Ld phase coexistence, allowing for in-plane structure (e.g., domain size and configuration) to be detected. In multibilayers, domains may grow to several microns. In such cases, Vcoh < VD. This gives rise to two lamellar lattices from which one can measure each domain's transverse structure (see Section 6.3). However, things may differ for lipid mixtures exhibiting nanoscopic domains,102 where domain size is of the order of Vcoh.
6.1 Elastic neutron scattering – SANS
Pencer et al. systematically addressed this problem by considering how the various SLD contrasts in a phase separated vesicle contribute to its total scattering signal.81 Approximating the vesicle structure as a series of concentric shells corresponding to the inner headgroups, hydrocarbon, and outer headgroups, the following SLDs are calculated:
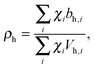 | (24) |
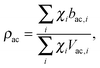 | (25) |
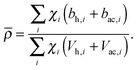 | (26) |
For ULVs, the total scattering 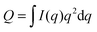 (also called the Porod invariant) can be decomposed into three additive contributions related to: (1) the SLD contrast between the average vesicle composition and the solvent; (2) the radial SLD contrast between the lipid headgroups and acyl chains; and (3) the lateral SLD contrast arising from domains having a different average acyl chain composition. Defining these three respective contributions as Q0, Qr, and Ql (i.e., Q = Q0 + Qr + Ql), Pencer et al.81 showed that
(also called the Porod invariant) can be decomposed into three additive contributions related to: (1) the SLD contrast between the average vesicle composition and the solvent; (2) the radial SLD contrast between the lipid headgroups and acyl chains; and (3) the lateral SLD contrast arising from domains having a different average acyl chain composition. Defining these three respective contributions as Q0, Qr, and Ql (i.e., Q = Q0 + Qr + Ql), Pencer et al.81 showed that
Q0 ∝ (![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) − ρm)2, − ρm)2, | (27) |
| Qr ∝ tf(1 − tf)(ρac − ρh)2, | (28) |
| Ql ∝ tfaf(1 − af)(ρLd − ρLo)2, | (29) |
An instructive example of such contrast matching is found in Heberle et al.,102 where the authors examined domain formation in a series of lipid mixtures including DSPC/DOPC/Chol in a 39/39/22 ratio. At 20 °C, this mixture separates into coexisting Ld and Lo phases, strongly enriched in DOPC and DSPC, respectively.22 Though DOPC and DSPC have similar acyl chain NSLDs (Table 1), a large contrast between Ld and Lo domains can nevertheless be generated by replacing DSPC with its chain perdeuterated counterpart, DSPC-d70. Because of its favorable partition into Lo domains, the use of DSPC-d70 results in a large increase in ρLo but only a small increase in ρLd, thereby enhancing the lateral scattering contribution Ql according to eqn (29). At the same time, the background homogeneous scattering Qhom is also affected, through changes in the average acyl chain and bilayer SLDs (ρac and ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) , respectively).
, respectively).
| Molecule | Chemical formula | b (fm) | V (Å3) | NSLD (fm Å−3) |
|---|---|---|---|---|
| a Ref. 104. b Ref. 91. c Ref. 105. d Ref. 106. | ||||
| PC headgroup | C10H18NO8P | 60.1 | 331a | 0.181 |
| DSPC chains | C34H70 | −35.8 | 1017b | −0.035 |
| DSPC-d70 chains | C34D70 | 692.9 | 1017b | 0.681 |
| DOPC chains | C34H66 | −20.8 | 1003c | −0.021 |
| POPC chains | C32H64 | −26.6 | 953b | −0.028 |
| Cholesterol | C27H46O | 13.3 | 630d | 0.021 |
| Water | H2O | −1.68 | 30.4 | −0.055 |
| Heavy water | D2O | 19.15 | 30.5 | 0.628 |
| 34.6% heavy water | H1.31D0.69O | 5.53 | 30.4 | 0.181 |
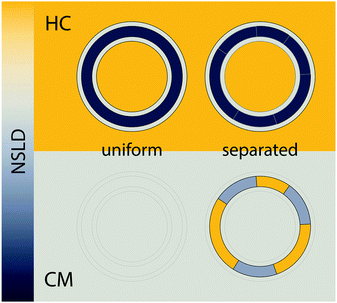
For the experiments described above, it is important to recognize that neither the domain nor the surrounding phase compositions are contrast matched to the solvent. Rather, it is the overall or average bilayer composition that is matched to solvent. This can be achieved by simple calculation provided lipid volumes are known (e.g., Table 1 and eqn (24)–(26)), or experimentally by measuring a solvent contrast series to determine the total scattering minimum.103 Importantly, this contrast matching scheme does not depend in any way on a priori knowledge of domain composition: by design, a well-mixed bilayer with no mesoscale domain structure (e.g., at temperatures above the upper miscibility transition) will exhibit minimal scattering. On the other hand, if the different lipid species segregate from each other into compositionally distinct domains, then neither phase is contrast matched to water, nor are they matched to each other. The resulting spatial contrasts (both lateral and transverse) result in increased scattering.
Fig. 8 shows a contour plot of Qhomvs. the fraction of DSPC-d70 (to total DSPC), and the solvent fraction of D2O calculated using eqn (24)–(29) and data from Table 1. A sharp minimum in Qhom is observed at 34.6% D2O and 65.9% DSPC-d70, precisely the point where the solvent and average bilayer NSLDs are matched to the PC headgroup. Using these experimental conditions, ρm ≅ ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) ≅ ρh ≅ ρac ≅ 0.181 fm Å−3: consequently, if the lipids are randomly mixed within the bilayer plane (e.g., at high temperature), a null scattering condition exists (Fig. 7, lower left). However, demixing of saturated and unsaturated lipids (i.e., DSPC and DOPC) causes lateral NSLD fluctuations that generate in-plane contrast (Fig. 7, lower right), resulting in increased scattering according to eqn (29).
≅ ρh ≅ ρac ≅ 0.181 fm Å−3: consequently, if the lipids are randomly mixed within the bilayer plane (e.g., at high temperature), a null scattering condition exists (Fig. 7, lower left). However, demixing of saturated and unsaturated lipids (i.e., DSPC and DOPC) causes lateral NSLD fluctuations that generate in-plane contrast (Fig. 7, lower right), resulting in increased scattering according to eqn (29).
 | ||
| Fig. 8 Optimizing experimental conditions for detecting domains in DSPC/DOPC/Chol. The relative homogeneous background scattering Qhom = Q0 + Qr, calculated from lipid NSLDs (Table 1) using eqn (24)–(29), is plotted vs. fraction of DSPC-d70 (to total DSPC) and the solvent fraction of D2O. A global contrast match point is observed at 34.6% D2O and 65.9% DSPC-d70 (“CM”, expanded in inset). Close to the contrast match point, Qhom is attenuated by >6 orders of magnitude relative to a fully protiated bilayer in 100% D2O solvent (“HC”). | ||
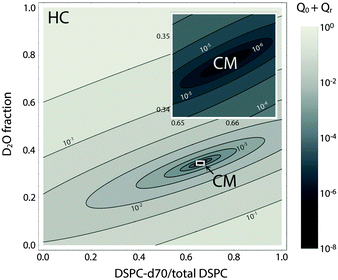
Fig. 9 shows the total scattering (i.e., the Porod invariant Q) for several 4-component lipid mixtures studied at bilayer contrast matching conditions.102 For mixtures containing DSPC and low-melting lipid (either POPC or DOPC) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, in addition to 22 mol% cholesterol, a marked increase in Q was observed with decreasing temperature, indicating domain formation. At fixed temperature, Q showed a systematic decrease as POPC replaced DOPC, consistent with a reduction in domain area fraction, and weaker DSPC partitioning between the Ld and Lo phases.107,108 In contrast, single phase mixtures showed low total scattering and little variation over the temperature range studied.
1 ratio, in addition to 22 mol% cholesterol, a marked increase in Q was observed with decreasing temperature, indicating domain formation. At fixed temperature, Q showed a systematic decrease as POPC replaced DOPC, consistent with a reduction in domain area fraction, and weaker DSPC partitioning between the Ld and Lo phases.107,108 In contrast, single phase mixtures showed low total scattering and little variation over the temperature range studied.
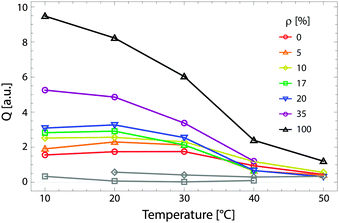 | ||
Fig. 9 Experimentally measured total scattering reveals domain formation in 4-component lipid mixtures. Shown is the Porod invariant 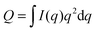 , plotted vs. temperature for DSPC/(DOPC + POPC)/Chol mixtures in a 0.39/0.39/0.22 molar ratio. Colors correspond to different values of the composition parameter ρ = χDOPC/(χDOPC + χPOPC) as indicated in the legend. Also shown are two single-phase control samples: DSPC/POPC/Chol 0.325/0.325/0.35 (gray diamond) and POPC/Chol 0.65/0.35 (gray square). Figure adapted from ref. 102. , plotted vs. temperature for DSPC/(DOPC + POPC)/Chol mixtures in a 0.39/0.39/0.22 molar ratio. Colors correspond to different values of the composition parameter ρ = χDOPC/(χDOPC + χPOPC) as indicated in the legend. Also shown are two single-phase control samples: DSPC/POPC/Chol 0.325/0.325/0.35 (gray diamond) and POPC/Chol 0.65/0.35 (gray square). Figure adapted from ref. 102. | ||
As a model-free method, the Porod invariant is a robust diagnostic tool for probing lateral bilayer inhomogeneities.102,109 However, this strength is at the same time a weakness – by collapsing the q-dependence of the scattering signal, any potential information regarding the size, shape, and spatial distribution of domains is lost. Elucidating these details requires modeling I(q), as will be discussed in the next section.
The scattered intensity of a vesicle containing multiple domains can be expressed as:
| I(q) = Ihom(q) + Iintra(q) + Iinter(q). | (30) |
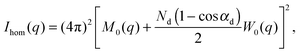 | (31) |
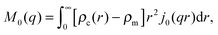 | (32) |
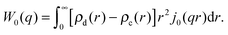 | (33) |
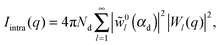 | (34) |
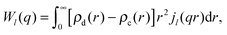 | (35) |
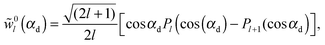 | (36) |
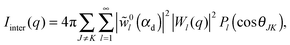 | (37) |
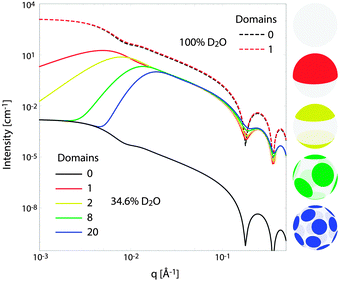
Fig. 10 illustrates the analytical model for typical experimental conditions (e.g., Table 1). For all theoretical curves, the average bilayer NSLD is identical (![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) = 0.18 fm Å−3), and differences in scattered intensity are due either to differences in solvent NSLD, or the presence (or absence) of domains. At 100% D2O (ρm = 0.636 fm Å−3, dashed curves), a large contrast exists between the solvent and bilayer; consequently, the homogeneous scattering dominates, and there is little apparent difference between uniform (black dashed) and phase-separated (red dashed) vesicles. However, consistent with the prediction of Fig. 8, the differences are greatly magnified near the contrast match point of 34.6% D2O (ρm = 0.181 fm Å−3, solid curves). While scattering from a uniformly mixed vesicle exhibits the same relative q-dependence at 100% and 34.6% D2O (black dashed and black solid curves, respectively), the total homogeneous intensity is attenuated by a factor of nearly 106 near the contrast match point (black solid curve).
= 0.18 fm Å−3), and differences in scattered intensity are due either to differences in solvent NSLD, or the presence (or absence) of domains. At 100% D2O (ρm = 0.636 fm Å−3, dashed curves), a large contrast exists between the solvent and bilayer; consequently, the homogeneous scattering dominates, and there is little apparent difference between uniform (black dashed) and phase-separated (red dashed) vesicles. However, consistent with the prediction of Fig. 8, the differences are greatly magnified near the contrast match point of 34.6% D2O (ρm = 0.181 fm Å−3, solid curves). While scattering from a uniformly mixed vesicle exhibits the same relative q-dependence at 100% and 34.6% D2O (black dashed and black solid curves, respectively), the total homogeneous intensity is attenuated by a factor of nearly 106 near the contrast match point (black solid curve).
Under these contrast matching conditions, phase separation into Ld (ρLd = 0.04 fm Å−3) and Lo (ρLo = 0.32 fm Å−3) domains—respectively depleted and enriched in chain-perdeuterated saturated lipid—results in a dramatic increase in scattered intensity (colored solid curves), compared to a uniformly mixed vesicle (black solid curve). Now, a distinct peak is evident in the low-q regime (q < 0.1 Å−1), which steadily shifts to higher q upon increasing the number of domains at a fixed total domain area fraction of 0.5 (i.e., decreasing the domain size, cf. yellow, green, and blue curves). This effect was previously observed experimentally.102,113 In the high-q regime (q > 0.1 Å−1), increased intensity or “liftoff” is observed near the minima between scattering lobes, which increases with increasing number of domains. Liftoff is typically interpreted as evidence for transbilayer asymmetry,82,114 but clearly can also originate from lateral SLD fluctuations, especially in SANS experiments where bilayers contain both protiated and deuterated lipids.
We conclude this section with a brief comment on isotopic labeling. It is well known that chain perdeuteration lowers the gel/fluid melting transition temperature by 2–4 °C for fully saturated lipids.115 However, with respect to Ld/Lo coexistence in ternary and quaternary mixtures, the effect of lipid perdeuteration has not been explored to our knowledge (i.e., it is unknown how the presence of perdeuterated species changes the locations of phase boundaries). In our own work with DSPC/DOPC/POPC/Chol mixtures, we find that corresponding protiated and deuterated samples exhibit remarkably similar phase behavior and domain size, as judged by fluorescence resonance energy transfer (FRET), electron spin resonance (ESR), and SANS.102,113 For these mixtures, there is no indication that the Lo phase forms more- or less-readily in perdeuterated versus protiated mixtures.
6.2 Inelastic neutron scattering
Inelastic neutron scattering offers an experimental method to probe the dynamics of lipid bilayers. As detailed in Section 3.2, there are two types of scattering from neutrons, coherent and incoherent, with coherent scattering relating to collective motions of pairs of atoms and incoherent scattering relating to the motions of individual atoms. Examples of the dynamics accessible through incoherent scattering experiments include localized motions connected to head group and acyl chain relaxations, rotation of the lipid molecule, and lateral diffusion in the plane of the bilayer.47,48,50–53,116–118Coherent scattering experiments are useful for probing collective vibrational motions and slower undulations of the entire bilayer. Collective vibrational features are relatively fast motions (<1 ps) connected to density fluctuations in the plane of the bilayer.63,119,120 The undulation motions of the bilayer are an especially interesting application of inelastic coherent neutron scattering because these motions can be related to the bending modulus of the bilayer. This has been demonstrated in homogenous lipid bilayers66,68,69 and subsequently used to show how the bending modulus is affected by a number of parameters including charge density,121 cholesterol content,67 and the presence of pore forming peptides.70 Coherent neutron scattering can also be used to investigate the mechanical properties of phase separated lipid bilayers in situ. In particular, by matching the SLD of one phase (e.g., Lo) to that of the solvent, it is possible to isolate the scattering from the other phase (e.g., Ld).
6.3 Elastic X-ray scattering
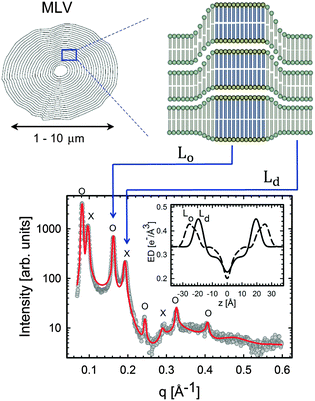 | ||
| Fig. 11 Lo/Ld phase coexistence as detected by SAXS. Like domains exhibit long-range alignment and consequently display two distinct lamellar lattices. Here o's indicate peaks associated with Lo domains and ×'s peaks associated with Ld domains. The inset to the scattering pattern of DSPC/DOPC/Chol in the phase coexistence regime shows the EDP of the two domains resulting from a global fit (red solid line). Figure taken from ref. 122. | ||
Heftberger et al.100 demonstrated that for MLVs, the scattered intensity can be modeled as:
| I(q) = (1 − cLd)ILo(q) + cLdILd(q), | (38) |
Having established the SDP analysis for MLVs98 (see above), it is reasonably straightforward to extend this model to coexisting domains. However, since each domain has a characteristic lipid composition (in the case of ternary mixtures, a high-Tm lipid, a low-Tm lipid and cholesterol) the underlying parsing scheme of quasi-molecular fragments must average over the contributions of each lipid, as illustrated in Fig. 12.
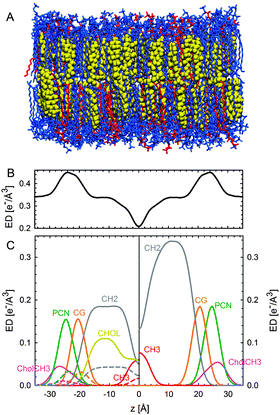 | ||
| Fig. 12 Parsing scheme of ternary lipid mixtures based on MD simulations of an Lo phase (panel A, DPPC lipids are drawn in blue, DOPC in red, and cholesterol in yellow). Panel B shows the electron density profile calculated from simulations, and panel C the electron densities of individual molecular groups. The left side panel shows the individual contributions of DPPC (solid lines) and DOPC (dashed lines) for the CholCH3, PCN, CG, CH2 and CH3 groups. The contribution of cholesterol is shown as a separate yellow line. The panel on the right shows the condensed parsing scheme after merging individual contributions. Figure taken from ref. 100 with permission. | ||
In order to establish this analysis, data from tieline endpoint samples were compared with tieline midpoint samples and were found to be in good agreement (within experimental uncertainty).100 Results of the in situ study of DOPC/DPPC/Chol and DOPC/DSPC/Chol showed that Lo domains are about 9–10 Å thicker than Ld phases (consistent with SANS measurements102), and that their area per lipid is about 20 Å2 smaller (Table 2). Due to the presence of a high-Tm lipid and the condensing effect of cholesterol, Lo phases are considerably more rigid than Ld domains. Thus, their Caillé parameter is about 65% smaller and the number of Bragg peaks is almost double that of those from the Ld phase. Further increase to the overall cholesterol concentration decreased the differences between Lo and Ld. This suggests that the Lo phase is saturated with cholesterol, and that additional cholesterol incorporates itself into the Ld phase.
Heftberger and co-workers100 additionally studied the temperature behavior of phase separated systems across the transition to a homogeneous phase (Fig. 1). In SAXS, this event is observed as a merging of the lamellar diffraction peaks (Fig. 13). Analysis of the corresponding diffraction patterns showed that melting of the Lo phase is associated with a decrease in bilayer thickness, and an increase in area per lipid and bending fluctuations. This is typical of fluid phase bilayers.91,123 In contrast, Ld shows the opposite behavior (i.e., increased dB, and a decrease in A and η).100 The most likely explanation for these findings is that at temperatures below Tc cholesterol diffuses from the Lo to the Ld phase. This process is accelerated as Tc is approached from below, in agreement with a previous NMR observation.124
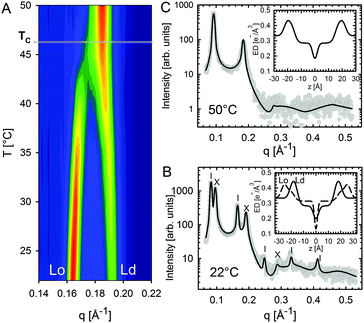 | ||
| Fig. 13 Melting of Lo domains in DOPC/DSPC/Chol. Panel A shows a contour plot of second order Bragg reflections associated with Lo and Ld phases. Above Tc, only a single lamellar lattice is observed. Panel B shows Bragg scattering from Lo (dashes) and Ld (crosses) domains at 22 °C. Panel C is the same system at 50 °C. Best fits are shown as solid lines. Inserts to both panels show the resulting ED profiles for Lo and Ld phases. Figure taken from ref. 100 with permission. | ||
The in situ analysis of coexisting phases detailed above relies on long-range positional correlations of like-domains in multibilayers. Such order has been directly observed using depth-resolved confocal microscopy,125 and poses a challenging scientific question: “Why are the observed domains in registry?” The answer to this question is intimately related to the forces present between the domains, which (in the case of neutral membranes) include van der Waals, hydration, and undulation repulsion forces.126
That SAXS is able to differentiate between coexisting Lo and Ld domains offers the possibility to distinguish between these interactions using osmotic stress experiments. In such experiments, osmotic pressure is induced by large neutral polymers, such as polyethylene glycol.127 Due to their size, the polymers are excluded from the interbilayer water layer, generating osmotic pressure that decreases bilayer separation. Bilayer separation as a function of osmotic pressure is then measured using SAXS (see e.g.ref. 128 and 129), and the data is fitted using functional forms of the interaction potentials, in turn yielding the underlying inter-membrane forces. However, when entropically driven bending undulations are present, the standard Derjaguin–Landau–Verwey–Overbeek (DLVO) paradigm (which allows for the treatment of solvent-mediated interactions) is, strictly speaking, not applicable.126 Instead, a mean-field/additivity approximation can be employed, where conformational fluctuation effects on the bare interaction potentials are included in a self-consistent manner.130–133 Moreover, through measurements of the Caillé parameter, the mean square fluctuations of the bilayer separation,
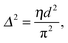 | (39) |
A different approach from the above is Monte Carlo (MC) simulations.135,136 Recently, Kollmitzer et al.137 explored this approach for coexisting Lo/Ld domains, by coupling MC simulations (Fig. 14) with an optimization routine that jointly fits osmotic pressure dependencies of dW and Δ. This allowed for the disentanglement of the different force contributions. Results (Fig. 14) for this analysis show only small differences in the van der Waals interactions between Lo and Ld. However, the other two interactions differed significantly. Lo phases show a rapid decay of undulation repulsion (i.e., reduced fluctuations compared to Ld phases), but a much slower decay in hydration repulsion. It is therefore clear that in the case of Ld domains, fluctuation forces dominate domain interactions over a broad range of distances, while hydration forces are most prominent in the Lo phase. Thus, there seems to be a delicate balance between hydration and fluctuation interactions which underlies domain alignment, an observation that should be considered in future theoretical treatments (Fig. 15).
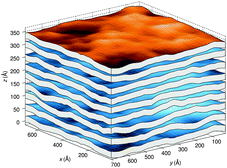 | ||
| Fig. 14 Real-space snapshots of equilibrium Ld simulations at a given osmotic pressure. Figure taken from ref. 137 with permission. | ||
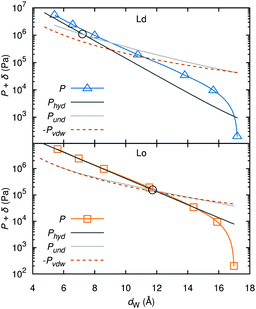 | ||
| Fig. 15 Deconstruction of the total osmotic pressure, P, into contributions of hydration, Phyd, van der Waals, PvdW, and undulation interactions, Pund, for coexisting Ld (upper) and Lo (lower) domains. Open black circles show the dW values at which the hydration and undulation pressures are equal. Figure taken from ref. 137 with permission. | ||
A further benefit of the above analysis is that the domain bilayer bending rigidity, Kc, can be derived from the fluctuation contributions. This is an important parameter with regard to the partitioning of proteins in either Lo or Ld domains.138,139 For DOPC/DSPC/Chol, Kollmitzer and co-workers137 reported Kc = 120 zJ for Lo and 44 zJ for Ld domains. In other words, Ld domains are about three times softer than Lo domains.
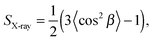 | (40) |
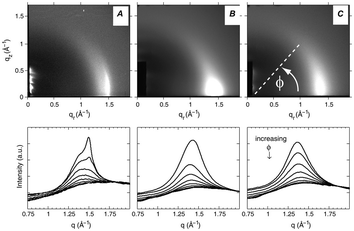 | ||
Fig. 16 WAXS scattering from: (A) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DOPC/DPPC; and (B and C) 1 1 DOPC/DPPC; and (B and C) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DOPC/DPPC/Chol (15 mol%), T = 25 °C and 45 °C (Tc ≃ 30 °C). The bottom row shows the corresponding I(q) plots with different ϕ-ranges (ϕ is the angle measured from the in-plane axis on the detector). Figure taken from ref. 142 with permission. 1 DOPC/DPPC/Chol (15 mol%), T = 25 °C and 45 °C (Tc ≃ 30 °C). The bottom row shows the corresponding I(q) plots with different ϕ-ranges (ϕ is the angle measured from the in-plane axis on the detector). Figure taken from ref. 142 with permission. | ||
7 Conclusions
Over the past 50 years neutron and X-ray scattering have contributed significantly to our knowledge of lipid membrane structure. With the advent of full q-range models – culminating in the SDP model – high-resolution structural information has been obtained. More recently, ULVs have been extensively used to interrogate phase separated systems, enabling new approaches for the study of static and dynamic structures. Importantly, inelastic scattering has developed to the point where it is possible to measure, in situ, the mechanical properties of nanoscopic domains populating ULVs. SANS on similar samples has provided unprecedented resolution of static domain structure and how domain size correlates with bilayer thickness mismatch between Lo and Ld domains.102 Recently, the effect of cholesterol and temperature on domain structure and bilayer elasticity,122,143 as well as inter-domain forces,137 have provided us with further insights into mechanisms that stabilize domains.It is hoped that future studies will explore questions including: the effect of membrane proteins on domains; ion-specific interactions; and the effect of bilayer asymmetry on domain structure and dynamics. In particular, bilayer asymmetry may change our current views on the role of lipids in plasma membranes.71,144 Ultimately, all of these efforts will fully be put to use to study the static and dynamic145 structure of live cells.
Acknowledgements
GP acknowledges financial support from the Austrian Science funds (FWF), project numbers P24459, P27083 and I1304. JDN is partially supported by the U.S. DOE BES through EPSCoR Grant No. DE-FG02-08ER46528. JK is supported through the Scientific User Facilities Division of the DOE Office of Basic Energy Sciences under US DOE Contract No. DE-AC05-00OR22725.References
- D. Lingwood and K. Simons, Science, 2010, 327, 46–50 CrossRef CAS PubMed.
- A. Kusumi, T. K. Fujiwara, R. Chadda, M. Xie, T. A. Tsunoyama, Z. Kalay, R. S. Kasai and K. G. N. Suzuki, Annu. Rev. Cell Dev. Biol., 2012, 28, 215–250 CrossRef CAS PubMed.
- M. L. Kraft, Mol. Biol. Cell, 2013, 24, 2765–2768 CrossRef CAS PubMed.
- E. Sevcsik, M. Brameshuber, M. Fölser, J. Weghuber, A. Honigmann and G. J. Schütz, Nat. Commun., 2015, 6, 6969 CrossRef CAS PubMed.
- G. W. Feigenson, Biochim. Biophys. Acta, 2009, 1788, 47–52 CrossRef CAS PubMed.
- D. Marsh, Biochim. Biophys. Acta, 2009, 1788, 2114–2123 CrossRef CAS PubMed.
- F. A. Heberle, R. S. Petruzielo, S. L. Goh, T. M. Konyakhina, D. G. Ackermann, J. J. Amazon and G. W. Feigenson, in Liposomes, Lipid Bilayers and Model Membranes, ed. G. Pabst, N. Kučerka, M.-P. Nieh and J. Katsaras, CRC Press, Boca Raton, FL, 2014, pp. 143–165 Search PubMed.
- G. Pabst, N. Kučerka, M.-P. Nieh, M. C. Rheinstädter and J. Katsaras, Chem. Phys. Lipids, 2010, 163, 460–479 CrossRef CAS PubMed.
- L. T. Hill, An Introduction to Statistical Thermodynamics, Dover Publications, New York, NY, 1986 Search PubMed.
- T. Heimburg, Thermal Biophysics of Membranes, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2007 Search PubMed.
- B. Brüning, E. Wald, W. Schrader, R. Behrends and U. Kaatze, Soft Matter, 2009, 5, 3340 RSC.
- P. F. Almeida, Biochim. Biophys. Acta, 2009, 1788, 72–85 CrossRef CAS PubMed.
- F. A. Heberle and G. W. Feigenson, Cold Spring Harbor Perspect. Biol., 2011, 3, a004630 Search PubMed.
- D. Marsh, Biochim. Biophys. Acta, Biomembr., 2010, 1798, 688–699 CrossRef CAS PubMed.
- P. I. Kuzmin, S. A. Akimov, Y. A. Chizmadzhev, J. Zimmerberg and F. S. Cohen, Biophys. J., 2005, 88, 1120–1133 CrossRef CAS PubMed.
- J. T. Buboltz and G. W. Feigenson, Biochim. Biophys. Acta, 1999, 1417, 232–245 CrossRef CAS.
- J. Huang, J. T. Buboltz and G. W. Feigenson, Biochim. Biophys. Acta, Biomembr., 1999, 1417, 89–100 CrossRef CAS.
- S. R. Wassall, M. R. Brzustowicz, S. R. Shaikh, V. Cherezov, M. Caffrey and W. Stillwell, Chem. Phys. Lipids, 2004, 132, 79–88 CAS.
- J. R. Silvius, Biophys. J., 2003, 85, 1034–1045 CrossRef CAS.
- O. G. Mouritsen and K. Jørgensen, Chem. Phys. Lipids, 1994, 73, 3–25 CrossRef CAS.
- A. G. Ayuyan and F. S. Cohen, Biophys. J., 2006, 91, 2172–2183 CrossRef CAS PubMed.
- J. Zhao, J. Wu, F. A. Heberle, T. T. Mills, P. Klawitter, G. Huang, G. Costanza and G. W. Feigenson, Biochim. Biophys. Acta, Biomembr., 2007, 1768, 2764–2776 CrossRef CAS PubMed.
- S. L. Veatch, S. S. W. Leung, R. E. W. Hancock and J. L. Thewalt, J. Phys. Chem. B, 2007, 111, 502–504 CrossRef CAS PubMed.
- Neutron scattering in biology: Techniques and applications, ed. J. Fitter, T. Gutberlet and J. Katsaras, Springer, Berlin and New York, 2006 Search PubMed.
- M. Born and E. Wolf, Principles of optics: Electromagnetic theory of propagation, interference and diffraction of light, Pergamon Press, Oxford and New York, 6th edn, 1980 Search PubMed.
- N. Bernhoef, A. Hiess, S. Langridge, A. Stunault, D. Wermeille, C. Vettier, G. H. Landler, M. Huth, M. Jourdan and H. Adrian, Phys. Rev. Lett., 1998, 81, 3419–3422 CrossRef.
- J. Felber, R. Gäler, R. Golub and K. Prechtl, Physica B, 1998, 252, 34–43 CrossRef CAS.
- S. H. Chen, C. Y. Liao, H. W. Huang, T. M. Weiss, M. C. Bellisent-Funel and F. Sette, Phys. Rev. Lett., 2001, 86, 740–743 CrossRef CAS.
- T. M. Weiss, P. J. Chen, H. Sinn, E. E. Alp, S. H. Chen and H. W. Huang, Biophys. J., 2003, 84, 3767–3776 CrossRef CAS.
- M. C. Rheinstädter, in Neutron scattering in biology, ed. J. Fitter, T. Gutberlet and J. Katsaras, Springer, Berlin and New York, 2006, pp. 263–286 Search PubMed.
- R. Klein, in Neutron, X-rays and light, ed. P. Lindner and T. Zemb, North-Holland, Amsterdam, 2002, pp. 351–379 Search PubMed.
- W. H. d. Jeu, B. I. Ostrovskii and A. N. Shalaginov, Rev. Mod. Phys., 2003, 75, 181–235 CrossRef.
- A. Caillé, C. R. Acad. Sci., Paris B, 1972, 274, 891–893 Search PubMed.
- R. Zhang, R. M. Suter and J. F. Nagle, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 5047–5059 CrossRef CAS.
- G. Pabst, M. Rappolt, H. Amenitsch and P. Laggner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 4000–4009 CrossRef CAS.
- T. Reusch, F. J. R. Schülein, J. D. Nicolas, M. Osterhoff, A. Beerlink, H. J. Krenner, M. Müller, A. Wixforth and T. Salditt, Phys. Rev. Lett., 2014, 113, 118102 CrossRef CAS.
- B. N. Brockhouse and A. T. Stewart, Phys. Rev., 1955, 100, 756–757 CrossRef CAS.
- J. Copley and T. Udovic, J. Res. Natl. Bur. Stand., 1993, 98, 71–87 CAS.
- H. Maier-Leibnitz, Nukleonik, 1966, 8, 61 CAS.
- F. Mezei, Z. Phys., 1972, 255, 146–160 CrossRef CAS.
- L. Van Hove, Phys. Rev., 1954, 95, 249–262 CrossRef CAS.
- M. Bée, Quasielastic neutron scattering: Principles and applications in solid state chemistry, biology, and materials science, Adam Hilger, Bristol, England and Philadelphia, 1988 Search PubMed.
- P. G. d. Gennes, Solid State Commun., 1963, 1, 132–137 CrossRef.
- G. Zaccai, Science, 2000, 288, 1604–1607 CrossRef CAS.
- W. Pfeiffer, T. Henkel, E. Sackmann, W. Knoll and D. Richter, Europhys. Lett., 1989, 8, 201–206 CrossRef CAS.
- K. Wood, A. Frölich, A. Paciaroni, M. Moulin, M. Härtlein, G. Zaccai, D. J. Tobias and M. Weik, J. Am. Chem. Soc., 2008, 130, 4586–4587 CrossRef CAS PubMed.
- C. L. Armstrong, M. D. Kaye, M. Zamponi, E. Mamontov, M. Tyagi, T. Jenkins and M. C. Rheinstädter, Soft Matter, 2010, 6, 5864 RSC.
- S. König, W. Pfeiffer, T. Bayerl, D. Richter and E. Sackmann, J. Phys. II, 1992, 2, 1589–1615 CrossRef.
- M. Rheinstädter, in Dynamics of Soft Matter, ed. V. García Sakai, C. Alba-Simionesco and S.-H. Chen, Springer US, Boston, MA, 2012, pp. 263–286 Search PubMed.
- M. Rheinstädter, T. Seydel, F. Demmel and T. Salditt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061908 CrossRef.
- J. Swenson, F. Kargl, P. Berntsen and C. Svanberg, J. Chem. Phys., 2008, 129, 45101 CrossRef CAS PubMed.
- J. Fitter, R. E. Lechner and N. A. Dencher, J. Phys. Chem. B, 1999, 103, 8036–8050 CrossRef CAS.
- S. König, E. Sackmann, D. Richter, R. Zorn, C. Carlile and T. M. Bayerl, J. Chem. Phys., 1994, 100, 3307 CrossRef PubMed.
- J. D. Nickels, H. O'Neill, L. Hong, M. Tyagi, G. Ehlers, K. L. Weiss, Q. Zhang, Z. Yi, E. Mamontov, J. C. Smith and A. P. Sokolov, Biophys. J., 2012, 103, 1566–1575 CrossRef CAS PubMed.
- G. H. Vineyard, Phys. Rev., 1958, 110, 999–1010 CrossRef CAS.
- G. B. J. Fitter, R. E. Lechner and N. A. Dencher, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 7600–7605 CrossRef.
- J. R. D. Copley and J. M. Rowe, Phys. Rev. Lett., 1974, 32, 49–52 CrossRef CAS.
- M. Nielsen, Phys. Rev. B: Solid State, 1973, 7, 1626–1635 CrossRef CAS.
- U. Buchenau, M. Prager, N. Nücker, A. J. Dianoux, N. Ahmad and W. A. Phillips, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5665–5673 CrossRef CAS.
- J. M. Carpenter and D. L. Price, Phys. Rev. Lett., 1985, 54, 441–443 CrossRef CAS.
- J. D. Nickels, S. Perticaroli, H. O'Neill, Q. Zhang, G. Ehlers and A. P. Sokolov, Biophys. J., 2013, 105, 2182–2187 CrossRef CAS PubMed.
- D. A. Neumann, J. R. D. Copley, R. L. Cappelletti, W. A. Kamitakahara, R. M. Lindstrom, K. M. Creegan, D. M. Cox, W. J. Romanow, N. Coustel, J. P. McCauley, N. C. Maliszewskyj, J. E. Fischer and A. B. Smith, Phys. Rev. Lett., 1991, 67, 3808–3811 CrossRef CAS.
- M. C. Rheinstädter, C. Ollinger, G. Fragneto, F. Demmel and T. Salditt, Phys. Rev. Lett., 2004, 93, 108107 CrossRef.
- U. Buchenau, A. Wischnewski, D. Richter and B. Frick, Phys. Rev. Lett., 1996, 77, 4035–4038 CrossRef CAS.
- D. Engberg, A. Wischnewski, U. Buchenau, L. Börjesson, A. J. Dianoux, A. P. Sokolov and L. M. Torell, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 9087–9097 CrossRef CAS.
- A. C. Woodka, P. D. Butler, L. Porcar, B. Farago and M. Nagao, Phys. Rev. Lett., 2012, 109, 058102 CrossRef.
- L. R. Arriaga, R. Rodríguez-García, I. López-Montero, B. Farago, T. Hellweg and F. Monroy, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 31, 105–113 CrossRef CAS PubMed.
- J. Pan, X. Cheng, M. Sharp, C.-S. Ho, N. Khadka and J. Katsaras, Soft Matter, 2015, 11, 130–138 RSC.
- Z. Yi, M. Nagao and D. P. Bossev, J. Phys.: Condens. Matter, 2009, 21, 155104 CrossRef PubMed.
- J.-H. Lee, S.-M. Choi, C. Doe, A. Faraone, P. A. Pincus and S. R. Kline, Phys. Rev. Lett., 2010, 105, 038101 CrossRef.
- J. Nickels, J. Smith and X. Cheng, Chem. Phys. Lipids, 2015 DOI:10.1016/j.chemphyslip.2015.07.012.
- M. C. Watson and F. L. Brown, Biophys. J., 2010, 98, L9–L11 CrossRef CAS PubMed.
- A. G. Zilman and R. Granek, Phys. Rev. Lett., 1996, 77, 4788–4791 CrossRef CAS.
- J. Katsaras, Biophys. J., 1997, 73, 2924–2929 CrossRef CAS.
- J. Katsaras, Biophys. J., 1998, 75, 2157–2162 CrossRef CAS.
- C. L. Armstrong, D. Marquardt, H. Dies, N. Kučerka, Z. Yamani, T. A. Harroun, J. Katsaras, A.-C. Shi and M. C. Rheinstaedter, PLoS One, 2013, 8, e66162 CAS.
- C. A. Naumann, O. Prucker, T. Lehmann, J. Rühe, W. Knoll and C. W. Frank, Biomacromolecules, 2002, 3, 27–35 CrossRef CAS PubMed.
- Liposomes, Lipid Bilayers and Model Membranes, ed. G. Pabst, N. Kučerka, M.-P. Nieh and J. Katsaras, CRC Press, Boca Raton, FL, 2014, pp. 199–216 Search PubMed.
- N. Kučerka, J. F. Nagle, S. E. Feller and P. Balgavý, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 051903 CrossRef.
- M. A. Kiselev, E. V. Zemlyanaya, V. K. Aswal and R. H. H. Neubert, Eur. Biophys. J., 2006, 35, 477–493 CrossRef CAS PubMed.
- J. Pencer, S. Krueger, C. P. Adams and J. Katsaras, J. Appl. Crystallogr., 2006, 39, 293–303 CrossRef CAS.
- M. R. Brzustowicz and A. T. Brunger, J. Appl. Crystallogr., 2005, 38, 126–131 CrossRef CAS.
- C. L. P. Oliveira, B. B. Gerbelli, E. R. T. Silva, F. Nallet, L. Navailles, E. A. Oliveira and J. S. Pedersen, J. Appl. Crystallogr., 2012, 45, 1278–1286 CrossRef CAS.
- G. I. King and S. H. White, Biophys. J., 1986, 49, 1047–1054 CrossRef CAS.
- M. C. Wiener, G. I. King and S. H. White, Biophys. J., 1991, 60, 568–576 CrossRef CAS.
- M. C. Wiener and S. H. White, Biophys. J., 1991, 59, 162–173 CrossRef CAS.
- M. C. Wiener and S. H. White, Biophys. J., 1991, 59, 174–185 CrossRef CAS.
- M. C. Wiener and S. H. White, Biophys. J., 1992, 61, 428–433 CrossRef CAS.
- M. C. Wiener and S. H. White, Biophys. J., 1992, 61, 434–447 CrossRef CAS.
- N. Kučerka, J. F. Nagle, J. N. Sachs, S. E. Feller, J. Pencer, A. Jackson and J. Katsaras, Biophys. J., 2008, 95, 2356–2367 CrossRef PubMed.
- N. Kučerka, M. P. Nieh and J. Katsaras, Biochim. Biophys. Acta, 2011, 1808, 2761–2771 CrossRef PubMed.
- N. Kučerka, J. Gallová, D. Uhríková, P. Balgavý, M. Bulacu, S.-J. Marrink and J. Katsaras, Biophys. J., 2009, 97, 1926–1932 CrossRef PubMed.
- J. Pan, D. Marquardt, F. A. Heberle, N. Kučerka and J. Katsaras, Biochim. Biophys. Acta, Biomembr., 2014, 1838, 2966–2969 CrossRef CAS PubMed.
- J. Pan, X. Cheng, L. Monticelli, F. A. Heberle, N. Kučerka, D. P. Tieleman and J. Katsaras, Soft Matter, 2014, 10, 3716–3725 RSC.
- N. Kučerka, B. van Oosten, J. Pan, F. A. Heberle, T. A. Harroun and J. Katsaras, J. Phys. Chem. B, 2015, 119, 1947–1956 CrossRef PubMed.
- F. A. Heberle, J. Pan, R. F. Standaert, P. Drazba, N. Kučerka and J. Katsaras, Eur. Biophys. J., 2012, 41, 1–16 CrossRef PubMed.
- D. Marsh, Chem. Phys. Lipids, 2010, 163, 667–677 CrossRef CAS PubMed.
- P. Heftberger, B. Kollmitzer, F. A. Heberle, J. Pan, M. Rappolt, H. Amenitsch, N. Kučerka, J. Katsaras and G. Pabst, J. Appl. Crystallogr., 2014, 47, 173–180 CAS.
- J. C. Fogarty, M. Arjunwadkar, A. P. Sagar and J. Pan, Biochim. Biophys. Acta, Biomembr., 2015, 1848, 662–672 CrossRef CAS PubMed.
- P. Heftberger, PhD thesis, Graz University of Technology, Austria, Graz, 2015.
- C. L. Armstrong, M. A. Barrett, A. Hiess, T. Salditt, J. Katsaras, A.-C. Shi and M. C. Rheinstaedter, Eur. Biophys. J. Biophys. Lett., 2012, 41, 901–913 CrossRef CAS PubMed.
- F. A. Heberle, R. S. Petruzielo, J. Pan, P. Drazba, N. Kučerka, R. F. Standaert, G. W. Feigenson and J. Katsaras, J. Am. Chem. Soc., 2013, 135, 6853–6859 CrossRef CAS PubMed.
- J. Pencer, T. T. Mills, N. Kucerka, M. P. Nieh and J. Katsaras, Methods Mol. Biol., 2007, 398, 231–244 CAS.
- S. Tristram-Nagle, Y. Liu, J. Legleiter and J. F. Nagle, Biophys. J., 2002, 83, 3324–3335 CrossRef CAS.
- S. Tristram-Nagle, H. I. Petrache and J. F. Nagle, Biophys. J., 1998, 75, 917–925 CrossRef CAS.
- A. I. Greenwood, S. Tristram-Nagle and J. F. Nagle, Chem. Phys. Lipids, 2006, 143, 1–10 CrossRef CAS PubMed.
- F. A. Heberle, J. Wu, S. L. Goh, R. S. Petruzielo and G. W. Feigenson, Biophys. J., 2010, 99, 3309–3318 CrossRef CAS PubMed.
- T. M. Konyakhina, J. Wu, J. D. Mastroianni, F. A. Heberle and G. W. Feigenson, Biochim. Biophys. Acta, Biomembr., 2013, 1828, 2204–2214 CrossRef CAS PubMed.
- R. S. Petruzielo, F. A. Heberle, P. Drazba, J. Katsaras and G. W. Feigenson, Biochim. Biophys. Acta, Biomembr., 2013, 1828, 1302–1313 CrossRef CAS PubMed.
- V. N. P. Anghel, N. Kučerka, J. Pencer and J. Katsaras, J. Appl. Crystallogr., 2007, 40, 513–525 CrossRef CAS.
- J. Pencer, T. Mills, V. Anghel, S. Krueger, R. M. Epand and J. Katsaras, Eur. Phys. J. E: Soft Matter Biol. Phys., 2005, 18, 447–458 CrossRef CAS PubMed.
- F. A. Heberle, V. N. Anghel and J. Katsaras, J. Appl. Crystallogr., 2015, 48, 1391–1404 Search PubMed.
- F. A. Heberle, M. Doktorova, S. L. Goh, R. F. Standaert, J. Katsaras and G. W. Feigenson, J. Am. Chem. Soc., 2013, 135, 14932–14935 CrossRef CAS PubMed.
- N. Kučerka, J. Pencer, J. N. Sachs, J. F. Nagle and J. Katsaras, Langmuir, 2007, 23, 1292–1299 CrossRef PubMed.
- J. Katsaras, R. F. Epand and R. M. Epand, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 3751–3753 CrossRef CAS.
- S. König, T. M. Bayerl, G. Coddens, D. Richter and E. Sackmann, Biophys. J., 1995, 68, 1871–1880 CrossRef.
- C. L. Armstrong, W. Häussler, T. Seydel, J. Katsaras and M. C. Rheinstädter, Soft Matter, 2014, 10, 2600–2611 RSC.
- V. K. Sharma, E. Mamontov, D. B. Anunciado, H. O'Neill and V. Urban, J. Phys. Chem. B, 2015, 119, 4460–4470 CrossRef CAS PubMed.
- J. S. Hub, T. Salditt, M. C. Rheinstädter and B. L. d. Groot, Biophys. J., 2007, 93, 3156–3168 CrossRef CAS PubMed.
- B. Brüning, M. C. Rheinstädter, A. Hiess, B. Weinhausen, T. Reusch, S. Aeffner and T. Salditt, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 31, 419–428 CrossRef PubMed.
- B. Brüning, R. Stehle, P. Falus and B. Farago, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 77 CrossRef PubMed.
- P. Heftberger, B. Kollmitzer, A. A. Rieder, H. Amenitsch and G. Pabst, Biophys. J., 2015, 108, 854–862 CrossRef CAS PubMed.
- G. Pabst, H. Amenitsch, D. P. Kharakoz, P. Laggner and M. Rappolt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 021908 CrossRef CAS.
- J. H. Davis and M. L. Schmidt, Biophys. J., 2014, 106, 1970–1978 CrossRef CAS PubMed.
- L. Tayebi, Y. Ma, D. Vashaee, G. Chen, S. K. Sinha and A. N. Parikh, Nat. Mater., 2012, 11, 1074–1080 CAS.
- J. N. Israelachvili, Intermolecular and surface forces, Academic Press, Burlington, MA, 3rd edn, 2011 Search PubMed.
- V. A. Parsegian, R. P. Rand, N. L. Fuller and D. C. Rau, Methods Enzymol., 1986, 127, 400–416 CAS.
- T. J. McIntosh and S. A. Simon, Biochemistry, 1993, 32, 8374–8384 CrossRef CAS.
- V. A. Parsegian and R. P. Rand, in Handbook of Biological Physics, ed. R. Lipowsky and E. Sackmann, Elsevier, Amterdam, 1995, pp. 643–690 Search PubMed.
- D. Sornette and N. Ostrowsky, J. Chem. Phys., 1986, 84, 4062 CrossRef CAS PubMed.
- E. A. Evans and V. A. Parsegian, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 7132–7136 CrossRef CAS.
- R. Podgornik and V. A. Parsegian, Langmuir, 1992, 8, 557–562 CrossRef CAS.
- K. R. Mecke, T. Charitat and F. Graner, Langmuir, 2003, 19, 2080–2087 CrossRef CAS.
- H. I. Petrache, N. Gouliaev, S. Tristram-Nagle, R. T. Zhang, R. M. Suter and J. F. Nagle, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 7014–7024 CrossRef CAS.
- N. Gouliaev and J. F. Nagle, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 881–888 CrossRef CAS.
- N. Gouliaev and J. F. Nagle, Phys. Rev. Lett., 1998, 81, 2610–2613 CrossRef CAS PubMed.
- B. Kollmitzer, P. Heftberger, R. Podgornik, J. F. Nagle and G. Pabst, Biophys. J., 2015, 108, 2833–2842 CrossRef CAS PubMed.
- D. Marsh, Biophys. J., 2007, 93, 3884–3899 CrossRef CAS PubMed.
- D. Marsh, Biophys. J., 2008, 94, 3996–4013 CrossRef CAS PubMed.
- D. M. Engelman and J. E. Rothman, J. Biol. Chem., 1972, 247, 3694–3697 CAS.
- T. T. Mills, S. Tristram-Nagle, F. A. Heberle, N. F. Morales, J. Zhao, J. Wu, G. E. Toombes, J. F. Nagle and G. W. Feigenson, Biophys. J., 2008, 95, 682–690 CrossRef CAS PubMed.
- T. T. Mills, G. E. Toombes, S. Tristram-Nagle, D. M. Smilgies, G. W. Feigenson and J. F. Nagle, Biophys. J., 2008, 95, 669–681 CrossRef CAS PubMed.
- B.-A. Brüning, S. Prévost, R. Stehle, R. Steitz, P. Falus, B. Farago and T. Hellweg, Biochim. Biophys. Acta, 2014, 1838, 2412–2419 CrossRef PubMed.
- D. Marquardt, B. Geier and G. Pabst, Membranes, 2015, 5, 180 CrossRef CAS PubMed.
- J. Nickels, M. Ohl, X. Cheng, C. Stanley, F. Heberle, R. F. Standaert and J. Katsaras, Biophys. J., 108 DOI:10.1016/j.bpj.2014.11.197.
| This journal is © The Royal Society of Chemistry 2015 |