Metal–organic frameworks based on tri- and penta-nuclear manganese(II) secondary building units self-assembled by a V-shaped silicon-containing dicarboxylate†
Angelica Vlada,
Mirela-Fernanda Zaltariova,
Sergiu Shovaa,
Ghenadie Novitchib,
Cyrille Train*bcd and
Maria Cazacu*a
a“Petru Poni” Institute of Macromolecular Chemistry, Aleea Gr. Ghica Voda 41A, 700487 Iasi, Romania. E-mail: mcazacu@icmpp.ro
bLaboratoire National des Champs Magnétiques Intenses, CNRS UPR 3228, 25 Rue des Martyrs, 38042, Grenoble, France. E-mail: cyrille.train@grenoble.cnrs.fr
cUniversité Grenoble-Alpes, F-38041 Grenoble, France
dInstitut Universitaire de France (IUF), 103, bd Saint-Michel, F-75005 Paris, France
First published on 7th April 2016
Abstract
A bent V-shaped silicon-containing linker, bis(p-carboxyphenyl)diphenylsilane (H2cpdps), has been used to synthesize two coordination polymers, [Mn5(cpdps)(HCOO)2(H2O)2(DMF)4]·6DMF (1) (DMF – dimethylformamide) and [Mn3(μ-H2O)2(Hcpdps)2(cpdps)2(DMF)2]·2DMF·12H2O (2). The crystal structure of both compounds was determined by single-crystal X-ray diffraction. In complex 1, pentanuclear manganese(II) secondary building units (SBUs) are held together by cpdps2− ligands to form a 2D (4,4) coordination polymer. Crystal 2 is built of trinuclear manganese(II) SBUs that are held together by cpdps2− and Hcpdps− ligands within a 2D (4,4) coordination polymer. The magnetic susceptibility measurements revealed antiferromagnetic exchange interactions between the paramagnetic manganese(II) ions (d5). The exchange interactions are ranging between −0.6 and −2.25 cm−1. Thermal analysis consisting in simultaneous thermogravimetry and automated FTIR analysis of the evolved gases permitted to evaluate the stability of the compounds and identify the main processes underlying decomposition. The void volumes accessible for particular guest molecules (CO2, H2O, Ar, N2) were theoretical estimated on the basis of the crystallographic data. Water vapor sorption capacity was measured experimentally in dynamic regime at room temperature.
1. Introduction
First-row transition metal coordination polymers (CPs) and metal–organic frameworks (MOFs) continue to attract the attention of researchers due to their potential application in different areas of science and industry.1–8 The metal ions and organic linkers determine the structure and properties of the polymeric materials. A large number of organic compounds, in particular many aromatic dicarboxylate ligands, have been designed and synthesized to create a wide variety of polymeric architectures with regular void spaces.9–12 The reaction of manganese(II) or manganese(III) salts/complexes with carboxylate ligands in the presence of other ancillary ligands or solvent molecules often results in linear trinuclear manganese clusters.13–17 These species can act as secondary building units (SBU's) to construct complex CPs and MOFs. It should be noted that manganese ions, dimeric, cyclic trimeric, tetrameric and higher nuclearity manganese clusters have also been exploited as nodes in the preparation of coordination polymers leading to new architectures with new physical properties.18–20 By using different aromatic semi-rigid V-shaped dicarboxylates, namely, 4,4′-oxybis(benzoic acid) (H2oba),21–26 4,4′-sulfonyldibenzoic acid (H2sdba),20,27–31 4-(4-carboxyphenylamino)-3,5-dinitrobenzoic acid (H2cpdba),32–34 4,4′-(hexafluoroisopropylidene)bis(benzoic acid) (H2hfbba)35,36 or benzophenone-4,4′-dicarboxylic acid (H2bpda)25 shown in Chart 1, as potential linkers, CPs with a variety of topologies and dimensionalities have been synthesized.21,22,25,30 By exploring the twist conformation of V-shaped ligands,35 as well as the potential chirality of amine nitrogen atom in H2cpdba,33 which can be locked by formation of coordination bonds via terminal carboxylate groups binding to manganese(II), chiral helical networks have been constructed.23,34 All these well-documented topologies were realized by making use of the binding flexibility of aromatic dicarboxylates (some of them contain other potential donor atoms), which adopt a variety of coordination modes,32 and different protonation states.29Taking into account the crucial role of the linkers for obtaining original architectures, we further extent our study using V-shaped aromatic dicarboxylates to template the formation of CPs. Herein, we report on the use of the silicon-containing linker, bis-(p-carboxyphenyl)diphenylsilane H2cpdps, (Chart 1) for the synthesis of two manganese(II) coordination polymers. This ligand is used for the first time to prepare manganese coordination compounds. Among other, it is expected that Si–C bond longer (from about 1.87 to about 1.90 Å) as compared with C–C (around 1.5 Å)37 in linker allowing greater conformational flexibility in coordination to metal ions, while somewhat polar nature thereof (due to electronegativity difference between Si and C) could increase H2 adsorption energies with a positive impact on hydrogen storage capacity of the resulted materials.38 In addition, the tetrahedral silicon centers are synthetically easier to achieve than analogous organic compounds. Thus, while there are a number (it is true that small) of publications in which silicon-containing carboxylic acids are used to prepare metal–organic frameworks (tetrakis-(4-carboxyphenyl)silane, di-(4-tolyl)-di-(4-carboxyphenyl)silane and (4-tolyl)-tris-(4-carboxyphenyl)silane, 5,5′-(dimethylsilanediyl)diisophthalic acid, 5,5′-[4,4′-(dimethylsilanediyl)bis(1,4-phenyl)bis-(ethine-1,2-diyl)]diisophthalic38–42), all being structurally different from our ligand and none of them containing Mn3/Mn5 SBUs, we have not found in the database CSD any similar structures with corresponding ligand containing carbon instead of silicon for comparison. The two compounds, namely [Mn5(cpdps)4(HCOO)2(H2O)2(DMF)4]·6DMF (1) and [Mn3(μ-H2O)2(Hcpdps)2(cpdps)2 (DMF)2]·2DMF·12H2O (2), were obtained under classical heating and solvothermal conditions in dimethylacetamide (DMA) and dimethylformamide (DMF), respectively. Compounds 1 and 2 are built around a pentanuclear and a trinuclear manganese(II) SBU respectively. The crystal structures of both compounds determined from single-crystal X-ray diffraction are described. The thermal stability, spectroscopic and magnetic properties of both crystalline materials, as well as their sorption ability are detailed thereafter.
2. Experimental section
2.1 Materials
Bis-(p-carboxyphenyl)diphenylsilane was prepared as described previously.43–45 Mn(NO3)2·4H2O, dimethylacetamide (DMA) and dimethylformamide (DMF) were purchased from Sigma Aldrich.2.2 Synthesis
It should be noted that, as confirmed by X-ray crystallography, both studied complexes contain statistically disordered co-crystallized solvent molecules, which are easily lost or replaced by water upon standing in air at room temperature. In addition, the amount and ratio of these solvents can vary for the samples obtained from each procedure. Therefore, non-significant differences found between experimental and theoretical values could be accepted.
2.3 Measurements
Fourier transform infrared (FTIR) spectra were recorded using a Bruker Vertex 70 FTIR spectrometer. Measurements were performed in KBr in the transmission mode in the range 400–4000 cm−1.Dynamic water vapor sorption (DVS) capacity of the samples was determined in the relative humidity (RH) range 0–90% by using a fully automated gravimetric analyzer IGAsorp produced by Hiden Analytical, Warrington (UK). Before being subjected to the adsorption process, the samples were kept in flowing dried nitrogen (250 mL min−1) at room temperature until the weight remained in equilibrium RH < 1%.
Magnetic susceptibility data (2–300 K) were collected on powdered samples using a SQUID magnetometer (Quantum Design MPMS-XL), applying a magnetic field of 0.1 T. All data were corrected for the contribution of the sample holder and the diamagnetism of the samples estimated from Pascal's constants.46,47 Magnetic data analysis was carried out by calculations of energy levels associated with the relevant isotropic spin Hamiltonians by using the MAGPACK program package.48
Thermogravimetrical analysis (TGA) and Differential Scanning Calorimetry (DSC) were performed with a Mettler Toledo TGA-DSC 1 STAReSystem in open alumina crucibles (capacity 70 μL) with samples weighing about 20 mg with a N2 flow of 50 mL min−1, and a heating rate of 10 °C min−1. The gases evolved during the heating process were analysed by infra-red spectroscopy using the Nicolet Fourier Transform Infra-Red (FTIR) spectrophotometer iS 50 IR. The FTIR spectra were recorded with 16 scans per spectrum at a resolution of 4 cm−1. The spectrometer is coupled to the TGA/DSC system through a heated (250 °C) 90 cm stainless steel transfer line with diameter of 5.0 mm. The entire system has been calibrated with monohydrate calcium oxalate according to literature49 and instruction of the manufacturer. To exploit the coupling between the two techniques, the Differential Thermogravimetry (DTG) curves are synchronized with Gram–Schmidt profiles, which represent the total variation of the IR spectrum relative to the initial spectrum.
X-ray diffraction data for 1 and 2 were collected with an Oxford-Diffraction XCALIBUR E CCD diffractometer equipped with graphite-monochromated MoKα radiation. Single crystals were positioned at 40 and 45 mm from the detector, and 545 and 334 frames were measured each for 4 and 30 s over 1° scan width for 1 and 2, respectively. The unit cell determination and data integration were carried out using the CrysAlis package of Oxford Diffraction.50 Both structures were solved by direct methods using Olex2 (ref. 51) software with the SHELXS structure solution program and refined by full-matrix least-squares on F2 with SHELXL-97.52 Atomic displacements parameters for non-hydrogen atoms were refined using an anisotropic model. Hydrogen atoms were placed in fixed, idealized positions and refined as rigidly bonded to the corresponding non-hydrogen atoms. The molecular plots were obtained using the Olex2 program. The positional parameters of the co-crystallized DMF and water molecules were refined in combination with PART and SADI restraints implemented in SHELXL-97 using anisotropic/isotropic model for non-H atoms. Table 1 provides a summary of the crystallographic data together with refinement details for 1 and 2. CCDC-1451812, 1451813.†
| a R1 = ∑||Fo| − |Fc||/∑|Fo|.b wR2 = {∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]}1/2.c GOF = {∑[w(Fo2 − Fc2)2]/(n − p)}1/2, where n is the number of reflections and p is the total number of parameters refined. | ||
|---|---|---|
| Empirical formula | C136H148Mn5N10O32Si4 (1) | C116H130Mn3N4O34Si4 (2) |
| Formula weight | 2821.70 | 2401.42 |
| Temperature/K | 200 | 173 |
| Crystal system | Triclinic | Monoclinic |
| Space group | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
C2/c |
| a/Å | 15.2389(6) | 26.5500(11) |
| b/Å | 15.9970(7) | 17.3564(5) |
| c/Å | 17.4713(7) | 30.9789(13) |
| α/° | 64.428(4) | 90.00 |
| β/° | 82.624(3) | 116.328(5) |
| γ/° | 68.486(4) | 90.00 |
| V/Å3 | 3571.9(3) | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 794.7(8) 794.7(8) |
| Z | 1 | 4 |
| Dcalc/mg mm−3 | 1.312 | 1.247 |
| μ/mm−1 | 0.538 | 0.403 |
| Crystal size/mm3 | 0.40 × 0.40 × 0.30 | 0.15 × 0.10 × 0.10 |
| θmin, θmax (°) | 10.22 to 51.36 | 3.38 to 52 |
| Reflections collected | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 308 308 |
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561 561 |
| Independent reflections | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 395[Rint = 0.0724] 395[Rint = 0.0724] |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 496[Rint = 0.0669] 496[Rint = 0.0669] |
| Data/restraints/parameters | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 395/48/818 395/48/818 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 496/9/731 496/9/731 |
| R1a (I > 2σ(I)) | 0.0792 | 0.0736 |
| wR2b (all data) | 0.2331 | 0.1994 |
| GOFc | 1.043 | 1.034 |
| Largest diff. peak/hole/e Å−3 | 1.58/−1.15 | 1.28/−1.99 |
3. Results and discussion
3.1 Synthesis
The reaction of Mn(NO3)2·4H2O with a silicon-containing dicarboxylic acid, namely bis(p-carboxyphenyl)diphenylsilane, in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio was performed in DMF under solvothermal conditions (140 °C, 72 h) producing [Mn5(cpdps)4(HCOO)2(H2O)2(DMF)4]·6DMF (1) and in DMA by heating at 140 °C for 72 h, followed by crystallization of the raw product in DMF for [Mn3(μ-H2O)2(Hcpdps)2(cpdps)2(DMF)2]·2DMF·12H2O (2) in 23.9% and 25.5% yields, respectively (Scheme 1).
1 molar ratio was performed in DMF under solvothermal conditions (140 °C, 72 h) producing [Mn5(cpdps)4(HCOO)2(H2O)2(DMF)4]·6DMF (1) and in DMA by heating at 140 °C for 72 h, followed by crystallization of the raw product in DMF for [Mn3(μ-H2O)2(Hcpdps)2(cpdps)2(DMF)2]·2DMF·12H2O (2) in 23.9% and 25.5% yields, respectively (Scheme 1).
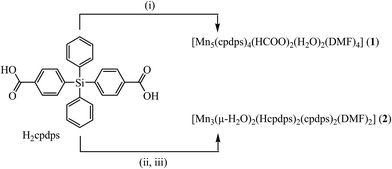 | ||
| Scheme 1 Reaction schemes leading to 1 and 2; conditions: (i) Mn(NO3)2·4H2O, DMF, solvothermal 140 °C, 72 h; (ii) Mn(NO3)2·4H2O, DMA, 140 °C, 72 h; (iii) crystallization in DMF. | ||
In IR spectra of manganese(II) complexes, the most useful characteristic bands are assigned to the asymmetric and symmetric stretching vibrations of COO−. The frequencies of these bands are responsive to the coordination modes of the carboxylate groups: ionic, monodentate, bidentate chelating or bidentate bridging coordination. As a result of coordination, the band at 1695 cm−1 in IR spectrum of H2cpdps assigned to the carboxylic acid C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration disappeared in IR spectra of the complexes and a new strong band attributed to νas(COO−) at 1537 cm−1 (1) and 1539 cm−1 (2) can be observed (Fig. S1†). The symmetric stretching vibration of this group gives rise to a band in the range 1470–1340 cm−1. The overlapped and hidden peak positions of νs(COO−) of the manganese(II) complexes 1 and 2 were determined with the second derivative of the spectra. The COO− stretching vibration region was deconvoluted by a curve-fitting method, and the areas were calculated with a 50% Lorentzian 50% Gaussian function. The curve-fitting analysis was performed with the OPUS 6.5 software. The procedure led to a best fit of the original curve with an error of less than 0.001 (Fig. S2†). The mode of the carboxylate binding in manganese(II) complexes was assigned from the magnitude of the separation between the carboxylate stretches Δexp = νas(COO−) − νs(COO−), the Δ values being compared with the Δ value of the sodium salt of H2cpdps. For the compound 1, the asymmetric and symmetric carboxylate stretches were observed at 1537 and 1388 cm−1, respectively (Fig. S2b†). The separation of the stretches, Δexp = 149 cm−1 is nearly equal with the Δsodium cpdps (147 cm−1) proving the bidentate bridging coordination of the carboxylate groups. The result is in good agreement with the crystal structure of the complex 1. For the compound 2, two νas(COO−) and νs(COO−) stretches were observed at 1576, 1539 cm−1 and 1388 cm−1, respectively (Fig. S2c†). The existence of two distinct vibration levels suggested different coordination modes of the carboxylate binding. The calculated Δ values are 151 cm−1 and 188 cm−1. The first value is an indicator of the bidentate bridging of the carboxylate coordination, while the second one of the monodentate carboxylate coordination, which is in good agreement with the structural analysis of this complex. The presence of the coordinated DMF molecules in both complexes was evidenced by the bands at 1657 cm−1 for 1 and 1661 cm−1 for 2, while those characteristic for phenyl-silicon and Mn–O bonds have been proven by the bands at 1105 and 1018 cm−1 and at 476 cm−1, respectively (Fig. S1†).53 The IR spectra of the complexes also exhibit a broad band at 3418 cm−1 (1) and 3414 cm−1 (2) assignable to the ν(O–H) vibration of the coordinated water molecules. The C–H stretching vibration bands occur in the region 3069–3009 cm−1, while the band at 1396 cm−1 is due to a combination of the C–O stretching and O–H deformation vibrations. The bands observed at 1427 cm−1 and 1416 cm−1 are characteristic for para-disubstituted benzene ring (Fig. S2†).54
O stretching vibration disappeared in IR spectra of the complexes and a new strong band attributed to νas(COO−) at 1537 cm−1 (1) and 1539 cm−1 (2) can be observed (Fig. S1†). The symmetric stretching vibration of this group gives rise to a band in the range 1470–1340 cm−1. The overlapped and hidden peak positions of νs(COO−) of the manganese(II) complexes 1 and 2 were determined with the second derivative of the spectra. The COO− stretching vibration region was deconvoluted by a curve-fitting method, and the areas were calculated with a 50% Lorentzian 50% Gaussian function. The curve-fitting analysis was performed with the OPUS 6.5 software. The procedure led to a best fit of the original curve with an error of less than 0.001 (Fig. S2†). The mode of the carboxylate binding in manganese(II) complexes was assigned from the magnitude of the separation between the carboxylate stretches Δexp = νas(COO−) − νs(COO−), the Δ values being compared with the Δ value of the sodium salt of H2cpdps. For the compound 1, the asymmetric and symmetric carboxylate stretches were observed at 1537 and 1388 cm−1, respectively (Fig. S2b†). The separation of the stretches, Δexp = 149 cm−1 is nearly equal with the Δsodium cpdps (147 cm−1) proving the bidentate bridging coordination of the carboxylate groups. The result is in good agreement with the crystal structure of the complex 1. For the compound 2, two νas(COO−) and νs(COO−) stretches were observed at 1576, 1539 cm−1 and 1388 cm−1, respectively (Fig. S2c†). The existence of two distinct vibration levels suggested different coordination modes of the carboxylate binding. The calculated Δ values are 151 cm−1 and 188 cm−1. The first value is an indicator of the bidentate bridging of the carboxylate coordination, while the second one of the monodentate carboxylate coordination, which is in good agreement with the structural analysis of this complex. The presence of the coordinated DMF molecules in both complexes was evidenced by the bands at 1657 cm−1 for 1 and 1661 cm−1 for 2, while those characteristic for phenyl-silicon and Mn–O bonds have been proven by the bands at 1105 and 1018 cm−1 and at 476 cm−1, respectively (Fig. S1†).53 The IR spectra of the complexes also exhibit a broad band at 3418 cm−1 (1) and 3414 cm−1 (2) assignable to the ν(O–H) vibration of the coordinated water molecules. The C–H stretching vibration bands occur in the region 3069–3009 cm−1, while the band at 1396 cm−1 is due to a combination of the C–O stretching and O–H deformation vibrations. The bands observed at 1427 cm−1 and 1416 cm−1 are characteristic for para-disubstituted benzene ring (Fig. S2†).54
Moreover, according to structural analysis, two molecules of formate are present in compound 1. Formic acid can indeed be generated during the solvothermal process by hydrolysis of DMF in presence of acid according to the reaction:55
| (CH3)2NCHO + H2O + H+ ⇔ (CH3)2NH2+ + HCOOH |
For 2, the use of DMA instead of DMF allowed using ambient pressure reaction to reach 140 °C and avoided the production of this extra-ligand.
3.2 Structural analysis
X-ray diffraction study of 1 reveals the presence of a pentanuclear [Mn5] neutral cluster, which sits on a crystallographic inversion center located on Mn1 atom (Fig. 1). Selected bond lengths and angles are summarized in Table 2. | ||
| Fig. 1 A view of pentanuclear [Mn5] cluster in the crystal structure of 1. Thermal ellipsoids are drawn at 50% probability level. Symmetry code: (i) 1 − x, −y, 1 − z. | ||
 | ||
| Fig. 2 2D (4,4) network of 1. Non-relevant H-atoms, as well as non-binding phenyl substituents are not shown for clarity. Blue = Mn, red = O, grey = C, yellow = Si. | ||
| a Symmetry code: (i) 1 − x, −y, 1 − z. | |||
|---|---|---|---|
| Mn1–O1 | 2.095(3) | Mn3–O9 | 2.305(3) |
| Mn1–O3 | 2.158(3) | Mn3–O10 | 2.264(4) |
| Mn1–O7 | 2.245(3) | Mn3–O12 | 2.140(4) |
| Mn2–O2 | 2.169(3) | Si1–C31 | 1.877(5) |
| Mn2–O4 | 2.127(3) | Si1–C34 | 1.868(6) |
| Mn2–O5 | 2.105(4) | Si1–C40 | 1.875(6) |
| Mn2–O7 | 2.194(3) | Si1–C46 | 1.870(5) |
| Mn2–O9 | 2.240(3) | Si2–C5 | 1.873(5) |
| Mn2–O11 | 2.219(6) | Si2–C8 | 1.877(5) |
| Mn3–O1w | 2.181(4) | Si2–C15 | 1.872(5) |
| Mn3–O6 | 2.128(4) | Si2–C21 | 1.874(5) |
| Mn3–O8 | 2.106(4) | ||
| O3Mn1O3i | 180.0 | O4Mn2O9 | 92.4(1) | O6Mn3O9 | 99.5(1) |
| O3Mn1O7i | 87.2(1) | O4Mn2O7 | 93.2(1) | O6Mn3O1w | 166.9(2) |
| O3Mn1O7 | 92.9(1) | O4Mn2O11 | 80.9(2) | O6Mn3O12 | 84.3(2) |
| O1Mn1O3i | 91.4(2) | O5Mn2O2 | 83.6(2) | O8Mn3O10 | 151.3(1) |
| O1Mn1O3 | 88.6(2) | O5Mn2O9 | 89.2(1) | O8Mn3O9 | 94.2(1) |
| O1Mn1O1i | 180.0 | O5Mn2O4 | 173.2(2) | O8Mn3O6 | 101.3(2) |
| O1Mn1O7i | 87.9(1) | O5Mn2O7 | 93.5(2) | O8Mn3O1w | 90.1(2) |
| O1Mn1O7 | 92.1(1) | O5Mn2O11 | 92.5(3) | O8Mn3O12 | 96.0(1) |
| O7Mn1O7i | 180.0 | O7Mn2O9 | 88.8(1) | O1wMn3O10 | 83.2(2) |
| O2Mn2O9 | 171.4(1) | O7Mn2O11 | 173.7(3) | O1wMn3O9 | 87.6(1) |
| O2Mn2O7 | 96.2(1) | O11Mn2O9 | 89.4(3) | O12Mn3O10 | 111.4 (1) |
| O2Mn2O11 | 86.2(3) | O10Mn3O9 | 57.7(1) | O12Mn3O9 | 168.2(1) |
| O4Mn2O2 | 94.3(1) | O6Mn3O10 | 90.3(2) | O12Mn3O1w | 86.5(2) |
| C5Si2C21 | 111.3(2) | C15Si2C8 | 111.1(2) | C40Si1C31 | 111.1(2) |
| C5Si2C8 | 106.7(2) | C21Si2C8 | 108.9(2) | C34Si1C31 | 109.1(2) |
| C15Si2C5 | 108.4(2) | C46Si1C31 | 108.0(2) | C34Si1C46 | 109.6(2) |
| C15Si2C21 | 110.4(2) | C46Si1C40 | 109.1(2) | C34Si1C40 | 109.9(3) |
All manganese ions display O6 octahedral coordination geometry slightly distorted for Mn1 and Mn2 centers and strongly distorted for Mn3 atom. The OMnO angles range from 86.2° to 94.9° for Mn1 and Mn2, respectively, while for Mn3 from 84.3° to 111.4° (Table 2). According to the bond valence analysis (Mn1 2.06, Mn2 1.99, Mn3 1.95) and the coordination geometry around the metal centers, the oxidation number of the three manganese centers is II.56–58 The Mn1⋯Mn2, Mn1⋯Mn3 and Mn2⋯Mn2i separations within pentanuclear cluster are of 3.6568(7), 5.7907(8) and 7.314(1) Å, respectively. The formation of pentanuclear cluster is insured by the coordination of ten carboxylate groups provided by four bis(p-carboxyphenyl)diphenylsilane and two formate ligands. All the carboxylate ligands fulfill a bridging function being coordinated in various modes. Both formate ions act as 1:2κ2O; 3κO-μ3 bridging ligands. The situation for the bis(p-carboxyphenyl)diphenylsilane ligands is more complicated. Four from the eight cpdps2− ligands are coordinated to Mn1–Mn2 and Mn2′–Mn3′ (symmetry code: 2 − x, −y, 1 − z) atoms in a 1κO; 2κO; 2′:3′κ2O; 3′κO-μ4 bridging mode while the remaining four exhibit a 1κO; 2κO; 2′κO; 3′κO-μ4 coordination mode. Accordingly, these ligands play a dual role, holding together the metal ions of the SBU and bridging the SBU together. Finally, the coordination sphere of both Mn2 and Mn3 is completed by one dimethylformamide molecule as ancillary monodentate ligands.
Further extension of this architecture in the crystal results into the formation of two-dimensional coordination network with a (4,4) topology (Fig. 3). It is to mention, that no CH–π or π–π interactions is present within the 2D architecture. In the crystal, the two-dimensional coordination polymers are packed to form a system of parallel channels along b crystallographic direction, which accommodate DMF and water solvate molecules (Fig. S3†).
 | ||
| Fig. 3 View of 2D (4,4) network in the crystal structure in 1. Non-binding phenyl substituents are not shown for clarity. See caption of Fig. 2 for color code. | ||
The crystal of 2 consists of a two-dimensional coordination network of general formula [Mn3(μ-H2O)2(Hcpdps)2(cpdps)2(DMF)2]·2DMF·12H2O comprising dipodal silicon-centered linkers and trinuclear [Mn3] SBU units. Each trinuclear cluster (Fig. 4) sits on a crystallographic inversion center located on Mn1 atom. Similar to pentanuclear cluster 1, based on bond valence analysis, three Mn ions in 2 are in +2 oxidation state (two crystallographic independent metal center Mn1 2.22, Mn2 1.94),56–58 so that the charge balance is in agreement with the formation of neutral species [Mn3(μ-H2O)2(Hcpdps)2(cpdps)2(DMF)2].
Six positive charges of three Mn2+ ions are balanced by the negative charges of six carboxylate groups originating from two double-deprotonated cpdps2− and two mono-deprotonated Hcpdps− silane linkers. Each manganese atom has a slightly distorted centers octahedral oxygenated coordination (Table 3). The four two doubly-deprotonated cpdps2− adopt 1κO; 2κO; 1′κO; 2′κO-μ4 coordination mode whereas the mono-deprotonated Hcpdps− adopt 1κO; 2κO; 2′κO-μ3 coordination mode. It is worth noting that the two carboxylate groups of mono-deprotonated Hcpdps− can accept the acidic proton so that the four acidic protons occupy their positions with 0.5 site occupancy factor (s.o.f). Accordingly, Mn1 is surrounded by two oxygen atoms from cpdps2− and two oxygen atoms from Hcpdps− forming the equatorial plane of its coordination octahedron. The coordination sphere is completed by one bridging water molecule and one terminal DMF molecule as monodentate ligands in trans positions (Fig. 4). Mn–O distances are typical for Mn2+ cation and lying in the range 2.114(3)–2.148(3) Å and 2.138(3)–2.234(3) Å for Mn1 and Mn2, respectively. The oxygen atoms of the mono-deprotonated ligand are engaged as acceptors in hydrogen bonding with coordinated aqua ligands (Fig. 4). These H-bonds further consolidate the [Mn3] SBU.
| a Symmetry code: (i) 3/2 − x, 1/2 − y, 1 − z; (ii) 1 − x, −y, 1 − z; (iii) 2 − x, −y, 1 − z. | |||
|---|---|---|---|
| Mn1–O1w | 2.148(3) | Si1–C5 | 1.865(4) |
| Mn1–O1 | 2.114(3) | Si1–C8 | 1.875(4) |
| Mn1–O5 | 2.137(3) | Si1–C15 | 1.881(4) |
| Mn2–O1w | 2.209(3) | Si1–C21 | 1.874(4) |
| Mn2–O2 | 2.140(3) | Si2–C31 | 1.877(4) |
| Mn2–O31 | 2.214(3) | Si2–C34 | 1.878(4) |
| Mn2–O6 | 2.138(3) | Si2–C41 | 1.875(4) |
| Mn2–O72 | 2.234(3) | Si2–C47 | 1.866(4) |
| Mn2–O9 | 2.174(3) | ||
| O1Mn1O1i | 180.0 | O2Mn2O3ii | 86.2(1) |
| O1Mn1O1w | 92.3(1) | O2Mn2O7iii | 172.1(1) |
| O1Mn1O1wi | 87.7(1) | O2Mn2O9 | 89.0(1) |
| O1Mn1O5 | 91.0(1) | O32Mn2O7iii | 85.9(1) |
| O1Mn1O5i | 89.0(1) | O6Mn2O1w | 93.6(1) |
| O1wMn1O1wi | 180.0 | O6Mn2O2 | 100.1(1) |
| O5Mn1O1w1 | 86.5(1) | O6Mn2O3ii | 173.6(1) |
| O5Mn1O1w | 93.5(1) | O6Mn2O7iii | 87.8(1) |
| O5Mn1O5i | 180.0 | O6Mn2O9 | 88.7(1) |
| O1wMn2O3ii | 87.0(1) | O9Mn2O1w | 177.2(1) |
| O1wMn2O7iii | 86.9(1) | O9Mn2O3ii | 90.6(1) |
| O2Mn2O1w | 92.2(1) | O9Mn2O7iii | 91.6(1) |
| C5Si1C8 | 105.2(2) | C31Si2C34 | 106.5(2) |
| C5Si1C15 | 108.4(2) | C41Si2C31 | 113.4(2) |
| C5Si1C21 | 112.8(2) | C41Si2C34 | 112.8(2) |
| C8Si1C15 | 111.2(2) | C47Si2C31 | 109.0(2) |
| C21Si1C8 | 108.7(2) | C47Si2C34 | 109.1(2) |
| C21Si1C15 | 110.6(2) | C47Si2C41 | 106.1(2) |
As in compound 1, the bis(p-carboxyphenyl)diphenylsilane ligands connect together the [Mn3] SBU, in such a way that each [Mn3] cluster is linked to four adjacent [Mn3] SBUs (Fig. 5). The same 2D (4,4) topology found in 1 is present in 2 but the arrangement is much more regular than for 1. The crystal structure packing essentially results from the packing of these 2D networks parallel to 110 planes (Fig. S4†). The removal of non-coordinated molecules shows the formation of the rectangular channels along the crystallographic 010 direction having a cross section of ca. 8.0–9.2 Å.
 | ||
| Fig. 5 View of 3D network in the crystal structure of 2. Non-relevant H-atoms, solvate DMF and water molecules as well as non-bonding phenyl substituents are not shown for clarity. | ||
3.3 Magnetic studies
The temperature dependence of the χT products of 1 and 2, where χ is the molar magnetic susceptibility per [Mn5] and [Mn3] SBU for 1 and 2 respectively measured under an applied magnetic field of 0.1 T, are shown in Fig. 6. At room temperature, the χT products are worth 20.59 cm3 K mol−1 for 1 and 12.27 cm3 K mol−1 for 2. These values are slightly lower than the expected value for five (21.884 cm3 K mol−1) and three (13.130 cm3 K mol−1) non-interacting MnII ions (S = 5/2, g = 2). Upon decreasing temperature, the χT product continuously decreases reaching 4.21 cm3 K mol−1 for 1 and 4.05 cm3 K mol−1 for 2 at 2.0 K. This evolution suggests the presence of dominant antiferromagnetic interactions in the compounds. Following the structural analysis, the magnetic properties should be governed by the well-separated pentanuclear and trinuclear linear clusters found in 1 and 2 respectively. Taking into account the isotropic character of MnII ions, the linear topology of both clusters and limiting the interaction to nearest-neighbours, the magnetic interactions in 1 and 2 can then be described by the following Hamiltonians:| Hp = −2Ja(S1S2 + S4S5) − 2Jb(S2S3 + S3S4) | (1) |
| Ht = −2Jc(S1S2 + S2S3) | (2) |
 | ||
| Fig. 6 χMT versus T plots for 1 and 2. The solid lines correspond to the simulation according to the Hamiltonians given in eqn (1) and (2) with Ja = −0.7 cm−1; Jb = −1.3 cm−1; g = 1.98 for 1 and Jc = −2.25 cm−1; g = 2.00 for 2. | ||
For 1, three sets of parameters reproduce well the thermal dependence of the magnetic susceptibility: (A) Ja = −0.7 cm−1, Jb = −1.3 cm−1, g = 1.98; (B) Ja = Jb = −1.0 cm−1, g = 1.98; (C) Ja = −1.5 cm−1, Jb = −0.5 cm−1, g = 1.98 (Fig. 6 and S5†). To discriminate between these three solutions, the simulation of the field dependence of the magnetization of 1 at 2.0, 3.0, 4.0 and 5.0 K was performed using the same Hamiltonian (eqn (1)). The best coincidence between calculated and experimental field dependence of the magnetization was found for Ja = −0.65 cm−1, Jb = −1.3 cm−1, g = 1.98 (Fig. S6†), which is consistent with solution (A).
With one interaction parameter, the case of 2 is much simpler. The best fit between theoretical and experimental data for the thermal dependence of the magnetic susceptibility was found for Jc = −2.25(2) cm−1, g = 2.00 (Fig. 6). Small intermolecular interactions (zj = −0.016 cm−1) are also used in order to better reproduce the experimental data at low temperature. The field dependence of the magnetization for 2 at 2.0, 3.0, 4.0 and 5.0 K can be fitted with the Brillouin function for a single S = 5/2 center confirming the antiferromagnetic character of the exchange interaction in 2 and indicating that mainly the S = 5/2 spin ground state is populated up to 5 K (Fig. S7†).
Magnetic interactions between MnII paramagnetic centers via carboxylate are most usually antiferromagnetic.59–64 Only in the case of κ2 bridging mode of coordination, ferromagnetic interaction was observed.65,66 The magnetostructural correlation has been reported for a series of trinuclear and dinuclear Mn(II) clusters with different carboxylic group functions.67,68 The constants of magnetic interaction usually have small values and the analysis of the data displays a considerable dispersion of values from the several structural parameters standpoint. Applying to compound 1 and 2, the quantitative correlation of exchange parameters with structural parameters of central atoms and bridging ligands cannot be relevant due to the presence of different bridging ligands between paramagnetic centers. Nevertheless, it is worth mentioning that the κ2 bridging modes of coordination present in 1 for both the Mn1–Mn2 and Mn2–Mn3 pairs tend to lower the exchange interaction compared to the situation observed in 2 where this bridging mode is absent.
3.4 Thermal analysis
TGA (Fig. 7) and coupled DTG-FTIR (Fig. 8) measurements were performed on both compounds in order to test the stability of the coordination networks and acquire a fine vision of their decomposition process through the identification of the gases evolved at each endothermic step of decomposition by direct comparison of the IR spectra of the evolved gas with database spectra of expected product of decomposition (Fig. S8 and S9† for 1 and 2, respectively).69–71 The results are gathered in Table 4. | ||
| Fig. 7 TGA and DTG curves of compounds 1 (red) and 2 (blue). The dotted zone is enlarged in the upper-right corner of the figure. | ||
 | ||
| Fig. 8 DTG and synchronized Gram–Schmidt and 2D IR spectra of the gases evolved during the heating of 1 (a) and 2 (b). | ||
| Processes (see Fig. 8, S8 and S9) | T1 | T2 | Tmax | Assignments | |
|---|---|---|---|---|---|
| 1 (Mn5) | a | 105.5 | 153.9 | 126.6 | Crystallisation DMF |
| a′ | 105.0 | 274.0 | 170.0 | Coordinated DMF | |
| b | 292.9 | 378.2 | 341.3 | H2O, C6H6 | |
| c | 404.6 | 449.8 | 428.3 | CO2, H2O, C6H6 | |
| d | 483.0 | CO2, C6H6 | |||
| 2 (Mn3) | a | 127.4 | 296.3 | 202.7 | Coordinated DMF |
| b | 300.0 | 352.4 | 328.9 | H2O, CO, CO2 | |
| c | 492.0 | CO2, Si(C6H5)4, C6H6 |
According of DTG curve (Fig. 7), the thermal decomposition of 2 occurs in three steps. The first step sharply starts just above 100 °C, peaks at 127 °C and lasts up to 300 °C with a gradual decrease of its intensity. The IR unambiguously analysis indicates that this step must be attributed to loss of DMF molecules (Fig. S8a†).
The percentage of weight loss indicates that coordinated DMF molecules (experimental value of 7.2 wt% compared to the theoretical 7.15 wt% calculated for desolvated formula of 2, e.g. [Mn3(μ-H2O)2(Hcpdps)2(cpdps)2(DMF)2]) are expelled from the compound at this stage. It should be noted that the departure of the solvated water and DMF molecules of 2 were not detected in the 25–300 °C temperature range. The absence of these molecules can be explained by an early departure of these loosely bonded molecules during the specific sample preparation which implies drying and crushing of the sample and thorough purging of TG/DCS-FTIR installation with N2. In the 300–360 °C temperature range, three components can be neatly detected in the gas phase: H2O, CO and CO2 (Fig. S8b†). According to the weight loss, this corresponds to the loss of bridging water molecules and partial decarboxylation of the silane ligand. Finally, during the last step of decomposition, in the 460–520 °C temperature range, the decomposition of the ligand is revealed by the presence of tetraphenylsilane (SiPh4), benzene and CO2 in the evolved gases (Fig. S8c†).
The thermal decomposition of 1 has similar stages. According to IR spectra, the first decomposition step (105–275 °C) is related to the departure of DMF molecules (Fig. S9a†). Two processes can be identified by the deconvolution of the DTG curve (inset of Fig. 7). The first part (105–155 °C) is sharp and takes place at the limit of the boiling temperature of DMF. It is assigned to crystallization DMF molecules. The second part which peaks at 170 °C but lasts up to 275 °C should be assigned to coordinated DMF. Similar two-steps departure of DMF molecules have been reported for [Nd2pdc3(DMF)2]DMF0.5·H2O.72 It should be noted that the loss of mass of DMF is less than expected from X-ray, probably due to the sample preparation as for compound 2. As for compound 2, the cracking of the ligand in the next decomposition steps is ascribed by the presence of CO2 and C6H6 in the gases evolved at higher temperatures (Fig. S9b–d†). It is worth mentioning the presence of water molecules in the gas evolved above 340 °C. These molecules originate from the bridging water molecules of the [Mn5] clusters and produced by the decomposition of the formate ions.73,74
3.5 Moisture behavior
An important aspect of which depends the MOFs suitability for certain practical applications is related to their behavior in wet environment. It has been found that most of MOFs are unstable in the presence of water, which could attack connectors within MOF sites, displacing the ligands and causing phase changes, loss of crystallinity and/or decomposition to reduce or destroy the porosity of the materials.75–77 In the case of water stable MOFs, the water sorption capacity can determine their applicability domain but also the stability of properties to environmental changes (e.g. temperature and humidity). In the gas storage and separation, it is most often desirable that the water vapor retention capacity is small, except in the case of CO2 when the sorption capacity and selectivity could be facilitated by the presence of water due to formation of more adsorptive sites toward CO2.78 On the contrary, there is currently a great interest for MOFs sorbents in water-based adsorption heat pumps. A water loading capacity, which to exceed 1 g H2O per g adsorbent is required for such application.79,80The water vapor sorption capacity of 1 and 2 compounds was thus investigated by recording room temperature sorption–desorption isotherms (Fig. 9) with equipment that we have available.
 | ||
| Fig. 9 Water vapour sorption–desorption isotherms at 25 °C registered for the thermal activated samples. | ||
Before this, the samples were first activated. There are several methods practiced and reported in the literature to activate the metal–organic frameworks: conventional heating and vacuum; solvent exchange; supercritical CO2 processing; freeze-drying; chemical treatment.81 We applied the first procedure consisting in heating the samples in vacuum at 120 °C (1) and 130 °C (2) for 24 h. Total removal of DMF molecules in the crystal structure of 1 and 2 has been checked and confirmed by IR technique, by the disappearance of the band at 1657 cm−1 for 1 and 1661 cm−1 for 2 attributed to the stretching frequency of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in dimethylformamide molecules. The water absence in activated samples is proved by the absence of characteristic band around 3400 cm−1 (Fig. S10†).
O in dimethylformamide molecules. The water absence in activated samples is proved by the absence of characteristic band around 3400 cm−1 (Fig. S10†).
Water vapor sorption capacity is determined both by the porosity of the material and the hydrophilic groups present in the structure, the ability to form hydrogen bonds and possible structural transitions.82 On the basis of the crystallographic data processed by Olex2 program it was theoretical estimated a total solvent accessible volume 27.3 and 30.9%, for the compounds 1 and 2, respectively. By using the Mercury software package, it is possible to differentiate the void volumes accessible for particular guest molecules such as water (Table 5) or various gases (CO2, Ar, N2) (Table S1†). The estimation was made after removal unbounded solvents. It can thus be seen that, in all cases, the solvent accessible volume is slightly greater for 2 as compared to 1 compound (Tables 5 and S1†). The solvent accessible surface values vary in the range 1.6% of unit cell volume for CO2 (compound 1) to 19.5% of unit cell volume for N2 (compound 2), while for water these values are 9.4 and 7.5% of unit cell volume in the case of compound 1 and 2, respectively. However, the experiment data showed that the water sorption for the compound 1 is higher than for compound 2. The more hydrophile nature of structure could be an explanation for this behavior of compound 1.
| Sample | Experimental water sorption resultsa | Solvent accessible surfaceb | ||
|---|---|---|---|---|
| Characteristic | Value | % of unit cell volume | Void volume (Å3) | |
| a On activated samples.b Estimated on the basis of the solvent accessible surface (mapped out by the centre of probe spheres) by using the Mercury software package after disordered crystallization solvent removal.c After desorption. | ||||
| 1 | Max. gained mass, wt% | 9.4 | 6.4 | 230 |
| Mass change, wt%c | 1.3 | |||
| 2 | Max. gained mass, wt% | 7.5 | 7.6 | 967 |
| Mass change, wt%c | 1.9 | |||
4. Conclusions
By using bis(p-carboxyphenyl)diphenylsilane (H2cpdps) as a V-shaped silicon-containing linker and Mn(NO3)2·4H2O as a first-row transition metal source, two different manganese(II) coordination polymers, namely [Mn5(cpdps) (HCOO)2(H2O)2(DMF)4]·6DMF (1) and [Mn3(μ-H2O)2(Hcpdps)2(cpdps)2(DMF)2]·2DMF·12H2O (2), have been obtained depending on reaction conditions: the first one under classical heating, the second under solvothermal conditions. Single-crystal X-ray diffraction analysis has revealed the presence of pentanuclear and trinuclear SBUs in 1 and 2, respectively embedded in a dicarboxylate-bridged 2D (4,4) coordination network. The good separation of the metallic SBU by rigid silicon-containing ligands opens new opportunities to study analogs of 1 and 2 with other transition metals. The analysis of temperature dependence of magnetic susceptibility indicates antiferromagnetic interactions between paramagnetic manganese(II) centers modulated by the coordination mode of the carboxylate bridges. FTIR-coupled thermal analysis showed in both cases multistep decomposition processes with sequential removal of crystallization and coordination solvent molecules followed by ligand decarboxylation and cracking processes at higher temperature. Theoretical estimation of volumes accessible for water and various gases revealed in all cases slightly higher values for the compound 2 when compared with compound 1. However the water sorption experiments showed sorption capacity values higher for 1 compared to 2 because of greater hydrophilic SBU proportion.Acknowledgements
This work was supported by a grant of the Romanian Ministry of Education and Scientific Research, CNCS – UEFISCDI, project number PN-II-ID-PCE-2012-4-0261. The authors acknowledge to Prof. Vladimir Arion from Inorganic Institute/University of Vienna for helpful discussions on the structures of these compounds.References
- J. J. Perry, J. A. Perman and M. J. Zaworotko, Chem. Soc. Rev., 2009, 38, 1400–1417 RSC.
- P. Dechambenoit and J. R. Long, Chem. Soc. Rev., 2011, 40, 3249–3265 RSC.
- A. Corma, H. Garcia and F. Xamena, Chem. Rev., 2010, 110, 4606–4655 CrossRef CAS PubMed.
- L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. Van Duyne and J. T. Hupp, Chem. Rev., 2012, 112, 1105–1125 CrossRef CAS PubMed.
- C. Wang, T. Zhang and W. B. Lin, Chem. Rev., 2012, 112, 1084–1104 CrossRef CAS PubMed.
- A. U. Czaja, N. Trukhan and U. Muller, Chem. Soc. Rev., 2009, 38, 1284–1293 RSC.
- M. D. Allendorf, C. A. Bauer, R. K. Bhakta and R. J. T. Houk, Chem. Soc. Rev., 2009, 38, 1330–1352 RSC.
- G. Givaja, P. Amo-Ochoa, C. J. Gomez-Garcia and F. Zamora, Chem. Soc. Rev., 2012, 41, 115–147 RSC.
- S. Y. Yang, H. B. Yuan, X. B. Xu and R. B. Huang, Inorg. Chim. Acta, 2013, 403, 53–62 CrossRef CAS.
- M. Li, Q. Ling, Z. Yang, B.-L. Li and H.-Y. Li, CrystEngComm, 2013, 15, 3630–3639 RSC.
- W. Q. Kan, B. Liu, J. Yang, Y. Y. Liu and J. F. Ma, Cryst. Growth Des., 2012, 12, 2288–2298 CAS.
- W.-Q. Kan, J. Yang, Y.-Y. Liu and J.-F. Ma, CrystEngComm, 2012, 14, 6271–6281 RSC.
- H. Asada, K. Hayashi, S. Negoro, M. Fujiwara and T. Matsushita, Inorg. Chem. Commun., 2003, 6, 193–196 CrossRef CAS.
- Y. G. Li, L. Lecren, W. Wernsdorfer and R. Clerac, Inorg. Chem. Commun., 2004, 7, 1281–1284 CrossRef CAS.
- R. A. Coxall, A. Parkin, S. Parsons, A. A. Smith, G. A. Timco and R. E. P. Winpenny, J. Solid State Chem., 2001, 159, 321–327 CrossRef CAS.
- B. S. Luisi, Z. Ma and B. Moulton, J. Chem. Crystallogr., 2007, 37, 743–747 CrossRef CAS.
- W.-X. Chen, G.-L. Zhuang, H.-X. Zhao, L.-S. Long, R.-B. Huang and L.-S. Zheng, Dalton Trans., 2011, 40, 10237–10241 RSC.
- C. C. Stoumpos, O. Roubeau, G. Aromi, A. J. Tasiopoulos, V. Nastopoulos, A. Escuer and S. P. Perlepes, Inorg. Chem., 2010, 49, 359–361 CrossRef CAS PubMed.
- C.-B. Ma, M.-Q. Hu, H. Chen, C.-N. Chen and Q.-T. Liu, Eur. J. Inorg. Chem., 2008, 33, 5274–5280 CrossRef.
- N. Li, L. A. Chen, F. Y. Lian, F. L. Jiang and M. C. Hong, Inorg. Chim. Acta, 2010, 363, 3291–3301 CrossRef CAS.
- C. Y. Sun, S. Gao and L. P. Jin, Eur. J. Inorg. Chem., 2006, 12, 2411–2421 CrossRef.
- P. Mahata, M. Prabu and S. Natarajan, Inorg. Chem., 2008, 47, 8451–8463 CrossRef CAS PubMed.
- W. H. Huang, L. Hou, B. Liu, L. Cui, Y. Y. Wang and Q. Z. Shi, Inorg. Chim. Acta, 2012, 382, 13–18 CrossRef CAS.
- G. L. Wen, Y. Y. Wang, H. Wang, E. K. Lermontova, C. Y. Guo and Q. Z. Shi, J. Mol. Struct., 2009, 928, 125–131 CrossRef CAS.
- J. H. He, D. R. Xiao, S. W. Yan, D. Z. Sun, H. Y. Chen, X. Wang, J. Yang, Z. L. Ye, R. Yuan and E. B. Wang, Solid State Sci., 2012, 14, 1203–1210 CrossRef CAS.
- J. Q. Liu, Y. Y. Wang, Y. N. Zhang, P. Liu, Q. Z. Shi and S. R. Batten, Eur. J. Inorg. Chem., 2009, 1, 147–154 CrossRef.
- C.-J. Wang, Y.-Y. Wang, J.-Q. Liu, H. Wang, Q.-Z. Shi and S.-M. Peng, Inorg. Chim. Acta, 2009, 362, 543–550 CrossRef CAS.
- S. W. Yan, G. J. Zhang, H. Y. Chen, S. C. Chang and F. T. Zhang, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2011, 67, M712 CAS.
- S. Bhattacharya, K. V. Ramanujachary, S. E. Lofland, T. Magdaleno and S. Natarajan, CrystEngComm, 2012, 14, 4323–4334 RSC.
- H. Y. Chen, D. R. Xiao, J. H. He, Z. F. Li, G. J. Zhang, D. Z. Sun, R. Yuan, E. B. Wang and Q. L. Luo, CrystEngComm, 2011, 13, 4988–5000 RSC.
- D. Xiao, R. Yuan, Y. Chai and E. Wang, Eur. J. Inorg. Chem., 2008, 16, 2610–2615 CrossRef.
- W. Li, H. P. Jia, Z. F. Ju and J. Zhang, Dalton Trans., 2008, 39, 5350–5357 RSC.
- J.-K. Sun, W. Li, L.-X. Cai and J. Zhang, CrystEngComm, 2011, 13, 1550–1556 RSC.
- W. Li, Z.-F. Ju, Q.-X. Yao and J. Zhang, CrystEngComm, 2008, 10, 1325–1327 RSC.
- X.-J. Jiang, S.-Z. Zhang, J.-H. Guo, X.-G. Wang, J.-S. Li and M. Du, CrystEngComm, 2009, 11, 855–864 RSC.
- X. Q. Wang, L. M. Liu, M. Conato and A. J. Jacobson, Cryst. Growth Des., 2011, 11, 2257–2263 CAS.
- J. Huheey and K. Cottrell, The Strengths of Chemical Bonds, Butterworths, London, 1958 Search PubMed.
- D. Frahm, F. Hoffmann and M. Froeba, CrystEngComm, 2013, 15, 9429–9436 RSC.
- J. B. Lambert, Z. Liu and C. Liu, Organometallics, 2008, 27, 1464–1469 CrossRef CAS.
- Z. Liu, C. L. Stern and J. B. Lambert, Organometallics, 2009, 28, 84–93 CrossRef CAS.
- R. P. Davies, P. D. Lickiss, K. Robertson and A. J. P. White, CrystEngComm, 2012, 14, 758–760 RSC.
- S. E. Wenzel, M. Fischer, F. Hoffmann and M. Froeba, Inorg. Chem., 2009, 48, 6559–6565 CrossRef CAS PubMed.
- M. Cazacu, A. Airinei and M. Marcu, Appl. Organomet. Chem., 2002, 16, 643–648 CrossRef CAS.
- I. K. Varma, K. Chander and R. C. Anand, Angew. Makromol. Chem., 1989, 168, 217–223 CrossRef CAS.
- M. Bruma, E. Hamciuc, B. Schulz, T. Kopnick, Y. Kaminorz and J. Robison, J. Appl. Polym. Sci., 2003, 87, 714–721 CrossRef CAS.
- P. Pascal, Ann. Chim. Phys., 1910, 19, 5–70 CAS.
- O. Kahn, Molecular Magnetism, VCH Publishers, Inc., New York, Weinheim, Cambridge, 1993 Search PubMed.
- J. J. Borras-Almenar, J. M. Clemente-Juan, E. Coronado and B. S. Tsukerblat, J. Comput. Chem., 2001, 22, 985–991 CrossRef CAS.
- M. Wagner and G. Widmann, Thermal analysis in practice, Mettler-Toledo, 2009 Search PubMed.
- CrysAlis RED, Version 1.171.34.76, Oxford Diffraction Ltd., 2003 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- G. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- K. Nakamoto, Infrared and Raman spectra of inorganic and coordination compounds, Wiley Online Library, 1986 Search PubMed.
- G. Socrates, Infrared and Raman characteristic group frequencies: tables and charts, John Wiley & Sons, 2004 Search PubMed.
- T. Cottineau, M. Richard-Plouet, J.-Y. Mevellec and L. Brohan, J. Phys. Chem. C, 2011, 115, 12269–12274 CAS.
- N. E. Brese and M. Okeeffe, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192–197 CrossRef.
- M. Okeeffe and N. E. Brese, J. Am. Chem. Soc., 1991, 113, 3226–3229 CrossRef.
- W. T. Liu and H. H. Thorp, Inorg. Chem., 1993, 32, 4102–4105 CrossRef CAS.
- K. Wieghardt, U. Bossek, B. Nuber, J. Weiss, J. Bonvoisin, M. Corbella, S. E. Vitols and J. J. Girerd, J. Am. Chem. Soc., 1988, 110, 7398–7411 CrossRef CAS.
- A. Caneschi, F. Ferraro, D. Gatteschi, M. C. Melandri, P. Rey and R. Sessoli, Angew. Chem., Int. Ed., 1989, 28, 1365–1367 CrossRef.
- S. V. Khangulov, P. J. Pessiki, V. V. Barynin, D. E. Ash and G. C. Dismukes, Biochemistry, 1995, 34, 2015–2025 CrossRef CAS PubMed.
- P. S. Mukherjee, S. Konar, E. Zangrando, T. Mallah, J. Ribas and N. R. Chaudhuri, Inorg. Chem., 2003, 42, 2695–2703 CrossRef CAS PubMed.
- P. Kar, Y. Ida, T. Ishida and A. Ghosh, CrystEngComm, 2013, 15, 400–410 RSC.
- C. B. Ma, C. N. Chen, Q. T. Liu, F. Chen, D. Z. Liao, L. C. Li and L. H. Sun, Eur. J. Inorg. Chem., 2004, 16, 3316–3325 CrossRef.
- V. Gomez, M. Corbella, M. Font-Bardia and T. Calvet, Dalton Trans., 2010, 39, 11664–11674 RSC.
- M. Wang, B. Wang and Z. Chen, J. Mol. Struct.: THEOCHEM, 2007, 816, 103–108 CrossRef CAS.
- V. Gomez and M. Corbella, Eur. J. Inorg. Chem., 2009, 29–30, 4471–4482 CrossRef.
- E. Escriva, L. Lezama, L. Soto, A. Sancho, J.-V. Folgado and C. Ramirez de Arellano, Polyhedron, 2014, 68, 319–323 CrossRef CAS.
- S. Materazzi and S. Vecchio, Appl. Spectrosc. Rev., 2013, 48, 654–689 CrossRef.
- S. Materazzi and S. Vecchio, Appl. Spectrosc. Rev., 2010, 45, 241–273 CrossRef.
- S. Materazzi, A. Gentili and R. Curini, Talanta, 2006, 68, 489–496 CrossRef CAS PubMed.
- R. Lyszczek, Thermochim. Acta, 2010, 509, 120–127 CrossRef CAS.
- P. J. Morando, N. H. Piacquadío, M. A. Blesa and C. O. Della Vedova, Thermochim. Acta, 1987, 117, 325–330 CrossRef CAS.
- D. Dollimore, Thermochim. Acta, 1991, 177, 59–75 CrossRef CAS.
- J. M. Taylor, R. Vaidhyanathan, S. S. Iremonger and G. K. H. Shimizu, J. Am. Chem. Soc., 2012, 134, 14338–14340 CrossRef CAS PubMed.
- H. Jasuja, J. Zang, D. S. Sholl and K. S. Walton, J. Phys. Chem. C, 2012, 116, 23526–23532 CAS.
- J.-H. Wang, M. Li and D. Li, Chem.–Eur. J., 2014, 20, 12004–12008 CrossRef CAS PubMed.
- S. Xian, J. Peng, Z. Zhang, Q. Xia, H. Wang and Z. Li, Chem. Eng. J., 2015, 270, 385–392 CrossRef CAS.
- C. R. Wade, T. Corrales-Sanchez, T. C. Narayan and M. Dinca, Energy Environ. Sci., 2013, 6, 2172–2177 CAS.
- A. Rezk, R. Al-Dadah, S. Mahmoud and A. Elsayed, Int. J. Heat Mass Transfer, 2012, 55, 7366–7374 CrossRef CAS.
- J. E. Mondloch, O. Karagiaridi, O. K. Farha and J. T. Hupp, CrystEngComm, 2013, 15, 9258–9264 RSC.
- F. Jeremias, D. Froehlich, C. Janiak and S. K. Henninger, New J. Chem., 2014, 38, 1846–1852 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1451812 and 1451813. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ra03969c |
| This journal is © The Royal Society of Chemistry 2016 |


