Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Co-assembly of cellulose nanocrystals and gold nanorods: insights from molecular dynamics modelling†
Jiaxin
Hou
ab,
William
Sampson
ab and
Ahu Gümrah
Dumanli
 *ab
*ab
aDepartment of Materials, The University of Manchester, Manchester, UK. E-mail: ahugumrah.parry@manchester.ac.uk
bHenry Royce Institute, The University of Manchester, Manchester, UK
First published on 6th November 2024
Abstract
A coarse-grained molecular dynamics model is developed to explore the co-assembly of cellulose nanocrystals (CNCs) and gold nanorods (AuNRs) under sedimentation conditions with varying volumetric concentration and particle-size ratios. Simulations and statistical analysis reveal a noticable preferential attachment of AuNRs on the surface of CNC clusters as the solid fraction of AuNRs was increased when the volumetric fraction of the AuNRs was low. Density-driven self-assembly under sedimentation forces is primarily driven by the AuNRs. This shift in the dominant mechanism from CNCs to AuNRs reveals the limits of multi-particle interactions and formation of ordered structures in binary particle systems. The fundamental insights provided in this work into the self-assembly process in complex particle systems are valuable for the design and control of the physical conditions to achieve desired ordered structures.
1 Introduction
Cellulose is the most abundant and renewable polysaccharide on Earth, and can be extracted from plants, bacteria, and certain marine organisms.1 Cellulose nanocrystals (CNCs) exhibit a rod-like structure, with a transverse dimension, D, around 5–20 nm and lengths in the range of 60 to 200 nm, depending on the source and extraction conditions. In dilute aqueous suspensions, particle–particle interactions between CNCs are governed by repulsive forces due to the half sulfate ester groups introduced during acid hydrolysis. In these suspensions, as the concentration of the CNCs are increased, a phase transition from isotropic to cholesteric phase takes place at a critical volume concentration, Cv, defined by Onsager's theory,2–4 between Cv = 3.3D/L and Cv = 4.5D/L, where D is the particle diameter and L is the length. Interestingly, such cholesteric order can be retained in dried films; in this dried state, the cholesteric periodicity-pitch, p, the distance within the pseudo-layers to make a full 360-degree turn to form a helicoidal structure is between 200 nm and 500 nm, giving rise to selective reflectance of light between UV and visible ranges according to the modified Bragg equation,λ = n·p·cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ, | (1) |
CNC self-assembly is a relatively robust process, compatible with host a range of particle systems. Different particles are therefore routinely added into the self-assembly media as a method of fabricating hybrid functional materials. In recent years, various particle systems, including small molecules such as organosilicates,5,6 gold nanorods,7 silver nanoparticles,8,9 carbon nanotubes and graphene,10 as well as polymers,11,12 have been shown to follow the self-assembly pathways of CNCs to produce multifunctional photonic structures.
Among these material combinations, co-assembly with gold nanonano particles (AuNPs) stands out. AuNPs possess remarkable physical, chemical and optical properties due to their surface plasmon resonances giving rise to enhanced scattering and absorption capabilities. In particular with their morphological proximity to CNCs and dual surface resonance frequencies, gold nanorods (AuNRs) have gained particular interest to integrate them into helicoidal order with the premise that such hybrid structures may give rise to the production of optical metamaterials.13 AuNRs have no intrinsic ability to self-assemble into such nanoarchitectures. Furthermore, micromachining techniques such as lithography have clear limitations such as scalability14 and the inability to produce sufficiently small nanostructures to attain the desired optical properties in the visible range.15,16 Therefore, co-assembly of AuNRs with cellulose nanocrystals has been suggested as a promising method to produce gold helicoids in the sub-visible wavelengths.7,17 Querjeta et al. and Cheng et al. both demonstrated hybrid chiroptical plasmonic responses from such co-assembled materials.7,18,19 However, these studies, which focused on the co-assembly of CNCs with either spherical Au nanoparticles or low aspect ratio AuNRs, for example, an aspect ratio of 2.520 and 2.9,7 demonstrated a concentration limit beyond which the CNC matrix could not accommodate the desired gold particle concentrations required to achieve a fully cholesteric response from the AuNRs.19,21,22 This limitation was most likely to be due to the surfactants used in the production of AuNRs. In addition of the influence of concentration, co-assembling CNCs with AuNRs possessing similar aspect ratio is also worth investigating. The mismatch of shape or size between CNCs and AuNRs might also lead to the fail in forming expected cholesteric structure. In this work, our models consist of AuNRs in different ARs and concentration would contribute to further experimental study.
To elucidate the fundamental reasons of the limits that arise in the co-assembly process, we report here an investigation into the dynamics of the self-assembly of a binary particle system of CNCs and AuNRs under sedimentation conditions through molecular dynamics (MD) simulations. To accurately simulate these interactions, the Gay–Berne (GB) potential has been used to describe anisotropic interactions between CNCs and AuNRs particles.23,24 Here we applied this method to investigate systems comprising varying concentrations of AuNRs and to examine the effects of different aspect ratios of AuNRs on co-assembly dynamics. Our simulations and subsequent analysis reveal a two-stage structure formation mechanism for the system composed of these two particle types. In the first stage, dissociated particles assemble into small clusters, which subsequently, aggregate into network structures. Further, our simulations demonstrate that a small fraction of AuNRs co-assembled with CNCs has little influence on the organisation of the structure. Notably, at low concentrations, AuNRs tend to attach to the surfaces of clusters formed by CNCs, whereas at higher concentrations, AuNRs played a more dominant role in self-assembly. A critical maximum loading was identified at a volume ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (CNC
2 (CNC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AuNRs). Nevertheless, AuNRs still associated preferentially with the network structure formed by the CNC particles. These findings shed new light on the co-assembly behaviour of CNCs in binary particle systems using AuNRs as a case study. Our work contributes valuable insights for understanding the co-assembly of multi-particle systems to guide the design and creation of chiroptical plasmonic materials with tailored structural properties.
AuNRs). Nevertheless, AuNRs still associated preferentially with the network structure formed by the CNC particles. These findings shed new light on the co-assembly behaviour of CNCs in binary particle systems using AuNRs as a case study. Our work contributes valuable insights for understanding the co-assembly of multi-particle systems to guide the design and creation of chiroptical plasmonic materials with tailored structural properties.
2 Methods
2.1 Molecular dynamics simulations
Molecular dynamics simulations of ellipsoidal self-assembly were performed using the large-scale atomic/molecular massively parallel simulator (LAMMPS).25 The simulations were employed in an orthogonal simulation cuboid, with a square base (x,y) of side 100, to avoid the finite size effect based on previous study on the macromolecular crowding of ellipsoidal particles26 and height (z) of 500. Periodic boundary conditions were applied in the x–y plane. CNCs and AuNRs were represented by a rigid ellipsoidal model. Around 30% CNC particles indeed have a twisted morphology.27 Yet when CNCs are dispersed in water suspension, the hydration layer of CNC particles due to surface charge makes the effective rod straight and smooth,28 which further reduced the anisotrpy in short axes. In addition, compared with spring-bead model, ellipsoidal model showed a better description of the shape of CNC particles. In addition, the ellipsoidal model allows for larger-scale molecular dynamics simulations due to the decrease of total particle number. CNCs had an aspect ratio (AR) of 10 and a fixed width of 2 and for AuNRs, aspect ratios of 2.5, 5, 7.5 and 10 with a fixed width of 2 were applied. These parameter values were guided by prior atomic force microscopy characterisation. The random start configurations, i.e. particles with random orientation and coordination, were completed by Mathematica by assigning random coordination and quaternion. Overlapped particles were removed. A canonical ensemble (NVT), was employed in the simulation, with fixed volume V and fixed temperature T in a vacuum condition. 3580 ellipsoidal particles were included in the emsembles. The number of ellipsoidal particles was calculated based on the aforementioned Cv, AR and a fixed crowding factor of 1. At this crowding factor, the expected colliding value between particles is 1.From Stokes’ law, we expect particles with different densities to have different settling velocities, which in turn influence the self-assembly dynamics. Meanwhile, Newton's second law and molecular dynamics simulation mean that particle attraction and repulsion forces are controlled by the density, ρ. To investigate the influence of density difference, a sedimentation force with g = 9.8 m s−2 was applied to all the CNCs and AuNRs particles in the simulations.
The system temperature was set to equilibrium at 5 in LJ units, giving the system a real temperature at around 287 K, and the simulations were performed for 6 × 106 steps with a time step of 0.001.
2.2 Gay–Berne potential for ellipsoidal nanoparticles
The Gay–Berne (GB) potential was used to model the co-assembly in the system. GB potential, a modified form of Leonard-Jones (LJ) potential, describes anisotropic interactions among ellipsoidal particles, it is worth noting that our particles do not possess any charges and introducing electrostatic interaction between CNCs and AuNRs will dramatically change the self-assembly behaviour. Recently, GB potential has been widely applied in the modelling of liquid crystal systems.29,30The GB potential started when Berardi, Fave and Zannoni31 introducing a general equation for the GB potential for biaxial ellipsoids. This ‘BFZ’ equation consists of three basic terms:
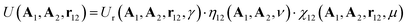 | (2) |
 | (3) |
In eqn (2), the first term has a typical LJ form and controls the distance dependence of the interaction:
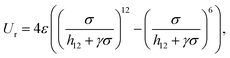 | (4) |
The second and third terms of eqn (2) control the interaction as a function of orientation and position and have the following forms:
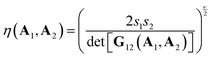 | (5) |
 | (6) |
Further,
| χ12(A1,A2,r12) = [2r12TB12−1(A1,A2)r12]μ, | (7) |
with
| B12(A1,A2) = A1TE1A1 + A2TE2A2. | (8) |
Finally,
 | (9) |
2.3 Kissing number analysis
The kissing number, or coordination number, provides the count of non-overlapping neighbours that touch the central particles in aggregated clusters. Here, we describe the methods employed in our simulations to define interparticle contact and hence to calculate the kissing number.A core–shell model was used to determine inter-particle contact, as shown in Fig. S1 (ESI†). The shell thickness was obtained by investigating some well-known packing structures, such as the close-packing of spheres and the close-packing of ellipsoid particles, as illustrated in Fig. S2 (ESI†). Our findings indicate that a shell thickness of 0.3 provides a balance between accuracy and computational efficiency, thereby ensuring reliable results. Periodic boundary conditions were employed so that particles at the cuboid side boundaries could identify their neighbouring particles.
To analyse the clusters assembled from ellipsoidal rods, all coordinates and orientation data were exported to the software Mathematica32 and the cluster structure was rebuilt and visualised. By generating 5000 points on the surface of each ellipsoid, an estimate of the shortest distance between two rods was computed using the ‘DistanceMatrix’ function in Mathematica to yield the minimum distance between points on a pair of ellipses. Integrating with the aforementioned criteria allowed the calculation of the average kissing number.
In heterogeneous systems comprising both AuNRs and CNCs, their different dimensions result in particle-dependent contributions to the kissing number. To address this, we introduced an ‘equivalent substitution method’ based on their aspect ratios, as shown in Fig. S3 (ESI†). We illustrate the approach by considering the kissing number between CNCs with parallel pairing, noting that such a configuration represents the most stable equilibrium state. In this state, a neighbouring pair of CNC particles, each with the same AR, possess a kissing number of 1. However, when a AuNR with an AR of 5 pairs with a CNC having an AR of 10, it only contributes 0.5 to the coordination number of the CNC, whereas the CNC contributes 2 to the AuNRs. This equivalent substitution method provides a unified assessment of particle contacts in the co-assembly, enabling an appropriately weighted evaluation of the overall structural stability and coordination characteristics within the heterogeneous system.
2.4 Solid fraction analysis
After completion of the self-assembly process, the porosity of the system, i.e., the complement of the solid fraction was determined. To compute the solid fraction, five slices parallel to the bottom substrate were obtained. Then the solid fraction of each slice was calculated using the fraction of the total area of the particles’ cross-section to that of the slice. Slices were selected only from the lower two-thirds of the thickness of the simulated structure, avoiding the influence of surface roughness.3 Results and discussion
3.1 Co-assembly of CNCs with AuNRs in vacuum – the effect of aspect ratio
To establish a baseline, we first analysed the co-assembly of the binary ellipsoidal particle systems made of CNCs with AuNRs in a vacuum without sedimentation forces. In each model, we maintained the volumetric ratio between the CNCs to AuNRs to be 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
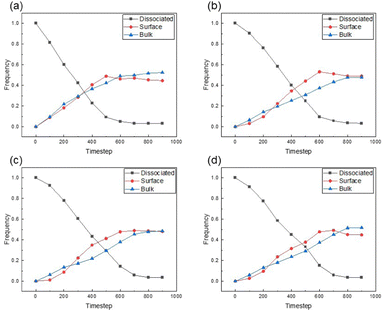
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, while varying the aspect ratio (AR) of AuNRs to the values of 2.5, 5, 7.5 and 10. Upon analysing the kissing number values, we identified three distinct particle categories: I. dissociated particles, characterised by kissing numbers below 2; II. surface particles, exhibiting kissing numbers ranging between 2 and 8; III. particles in the bulk, with kissing numbers greater than 8. Results are summarised in Fig. 1.
1, while varying the aspect ratio (AR) of AuNRs to the values of 2.5, 5, 7.5 and 10. Upon analysing the kissing number values, we identified three distinct particle categories: I. dissociated particles, characterised by kissing numbers below 2; II. surface particles, exhibiting kissing numbers ranging between 2 and 8; III. particles in the bulk, with kissing numbers greater than 8. Results are summarised in Fig. 1.
Fig. 1 and Fig. S4 (ESI†) reveal that, in the absence of sedimentation forces, the number frequency in dissociated, surface, and bulk particles are quite similar for all ARs of AuNR. This suggests that incorporating AuNRs, at a volume concentration of 10% into the self-assembling CNC media does not have a significant influence on the particle interactions responsible for assembling into the nematic structure. This confirms that the self-assembly of CNCs is a robust process ideal for hosting functional particles such as AuNRs. It is worth noting that a slight positive shift in the kissing number distributions of bulk-type particles was observed for the AuNRs with AR of 5. Such a shift arises from the equivalent substitution method. As mentioned above, the equivalent substitution assumes particles are parallel paired into a nematic structure in each cluster, yet in our simulations, intersecting configurations are observed between clusters. Such configuration leads to a significant increase in the frequency of bulk particles with low ARs, yet the overall self-assembly processes remain similar.
3.2 Co-assembly of CNCs with AuNRs under sedimentation force – the effect of aspect ratio
The self-assembly in vacuum conditions provided valuable insight and established a baseline for understanding the self-assembly of the binary particles and their pairing. In evaporation driven self assembly conditions, one should expect significant differences between the particle's sedimentation velocity considering the fluid dynamics and particles’ motion, thereby will also alter the dynamics of self-assembly. To better understand this effect, we incorporated a sedimentation force into the simulations of the binary particle systems.Fig. 2 shows the evolution of the distribution of dissociated, surface and bulk particles coordination number analysis during self-assembly under sedimentation conditions for systems of CNCs and AuNRs with different AR. Self-assembly of the ellipsoidal particles in this case consists of two stages. In the first stage, dissociated CNCs begin to form small clusters, where the primary transition involves the conversion from disassociated particles to surface particles, leading to a growth in the frequency of surface particles. Meanwhile, the increase in bulk particles is due to the motion towards the bottom and stack caused by sedimentation. In the end, these pre-clusters aggregate and stack, leading to the formation of larger nematic clusters where the orientation of the nematic domains forms a random network structure. Comparing these findings with our previous investigation on the self-assembly of single-type ellipsoidal particles representing CNCs only,26 it is significant that the presence of sedimentation conditions has accelerated the co-assembly process, thus increasing the frequency of bulk particles at earlier stages of the self-assembly process. Our simulations in vacuum conditions confirm the formation of nematic domains only, yet the introduction of sedimentation leads to the merge of such domains which yields a compressed final structure. Such scenarios have been observed experimentally that tactoids (temporarily formed during liquid crystal self assembly with an order of alignment) form and merge in random orientations.33
Notably, as shown in Fig. 2, under sedimentation conditions, an increase in the surface and bulk particle content was observed much earlier compared to the systems with no sedimentation shown in Fig. 1. Without the influence of sedimentation, the surface particles did not appear until 300 timesteps and the bulk particles first appear around 500 timesteps. This is primarily due to the boundary conditions we introduced at the bottom of our computational domain. During the sedimentation process, apart from following the molecular interactions imposed by the GB potential, the particles are also forced towards the bottom of the interaction volume, leading to increased interactions among particles and facilitating self-assembly.
We also observed that when the volume ratio of AuNRs in the system remained constant, the self-assembly process of the overall system exhibited remarkable similarity under sedimentation conditions, even with varying aspect ratios, as shown in Fig. 2. At the end of self-assembly, all four systems reached an equilibrium state where most of the dissociated particles have converted to either surface or bulk particles, with an approximate number ratio of 50/50.
Our subsequent analysis focused on the frequency of the AuNRs specifically in dissociated, surface and bulk positions, as shown in Fig. 3. This analysis highlighted that although the self-assembly of the binary particles ends with a 50/50 distribution between the surface and bulk, the specific ratios for occupying the surface of AuNRs were found to be 72/28. In addition, the AuNRs were inhomogeneously assembled onto the CNC network following their nematic order as shown in Fig. 4, which can be confirmed in the ESI† (Fig. S5), the radial distribution function (RDF) of the AuNRs. Compared with the cholesteric structure observed in experiments, the Gay–Berne potential does not include a chiral term. Thus the modelling exhibits a nematic network structure. Meanwhile, the induce of gravitational force quenched the system to further form the perfect nematic alignment, as observed by Hou et al.26
 | ||
| Fig. 3 Frequency change of dissociated, surface and bulk particles for AuNRs only during the different timescales of co-assembly for the binary particle group of CNCs of aspect ratio of 10 and AuNRs 10% by volume with an aspect ratio of 10, depicted in Fig. 2(d). | ||
Such a difference in particle positioning and distribution confirmed that CNCs are the primary structural drivers, dominating the coordination behaviour and contributing to the formation of the cluster core. In contrast, the AuNRs behaved like a guest component, occupying the surface of the clusters. We attribute this positional preference to the density difference between AuNR and CNC particles, where the higher density of AuNRs results in a slower motion, compared to the rapid aggregation of CNCs. Consequently, during cluster formation, CNCs pair more rapidly, forming the cluster core and causing AuNRs to preferentially attach to the cluster surfaces. This behaviour aligns well with previous experimental findings where the rod-like particles were shown to localise along parallel lines within the cholesteric layers of CNCs such as with AuNRs,7,19 Silver nanorods,9 and needle-like TiO2.34 It is consistent with the characteristics of colloidal particles in Brownian motion in fluids. In sedimentation conditions, the larger and denser particles are expected to settle faster in water.35,36 Our simulation conditions demonstrated that while particles were moving towards the substrate under sedimentation forces, they still interacted within their excluded volume as the colloidal behaviours of AuNRs were still influenced by the GB potential. With the combination of sedimentation and colloidal interactions, the co-assembled structures as well as the pre-assembled clusters in this binary particle system would most likely form a heterogeneous structure rather than ordered phases. While such alignment validates our work, this additional insight indicates the possibility of microscopic inhomogeneities caused by the secondary particles. Identification of these experimentally could prove time consuming and require a thorough high resolution TEM work including tomography, which was not conducted in previous studies.
3.3 Co-assembly of CNCs with AuNRs under sedimentation force – the effect of concentration
Co-assembly of the CNCs with AuNRs with varying concentrations has been demonstrated experimentally.37 However, in these studies, increasing the AuNRs concentration resulted in a decrease in the overall cholesteric order7 or disruption of the cholesteric phase forming random aggregates of AuNRs and CNCs.38 Such structural change results in loss of optical activity and circular dichroism in these films. To elucidate the effect of concentration, we constructed a binary particle system and systematically varied the concentration ratio of the AuNRs and CNCs in our molecular dynamics simulations. Our simulations suggest that as the concentration of AuNRs was increased, the previously observed microscopic inhomogeneities became more pronounced. Such phase disruption presents a barrier for the co-assembly to work successfully in experimental conditions from a sedimentation perspective alone.
Fig. 5 provides statistical analysis of the co-assembly behaviour under varying concentration ratios and with a sedimentation field applied. Similarly, even under sedimentation conditions, the influence of introducing a small amount of CNCs on the self-assembly behaviour of the entire system is negligible. However, as the concentration of gold nanoparticles gradually increases, the self-assembly dynamics of the overall system change, revealing a critical volume ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 as shown in Fig. 5(c) and (d). The increase in bulk particles is attributed to the size difference between the CNCs and the AuNRs. Due to the increase in the contents of smaller AuNRs, the co-assembled system tends to form a more densely packed structure, which can be evidenced by analysing the solid fraction, as shown in Fig. 6. Pure CNCs form a more porous structure, as shown in Fig. 7(a); however, after introducing AuNRs, these nanorods tend to occupy the vacancies within and between CNC clusters. Additionally, the sedimentation condition contributes to compressing the structure, resulting in a significant decrease in the percentage of surface-category particles in the system. Such a shift between the surface and bulk positioning of the gold particles confirms our previous hypothesis that a critical point, or maximum loading capacity, exists in this co-assembly system. Furthermore, once this critical value is exceeded, CNCs are not able to load extra gold nanoparticles and the entire co-assembly is seemingly dominated AuNRs.
1 as shown in Fig. 5(c) and (d). The increase in bulk particles is attributed to the size difference between the CNCs and the AuNRs. Due to the increase in the contents of smaller AuNRs, the co-assembled system tends to form a more densely packed structure, which can be evidenced by analysing the solid fraction, as shown in Fig. 6. Pure CNCs form a more porous structure, as shown in Fig. 7(a); however, after introducing AuNRs, these nanorods tend to occupy the vacancies within and between CNC clusters. Additionally, the sedimentation condition contributes to compressing the structure, resulting in a significant decrease in the percentage of surface-category particles in the system. Such a shift between the surface and bulk positioning of the gold particles confirms our previous hypothesis that a critical point, or maximum loading capacity, exists in this co-assembly system. Furthermore, once this critical value is exceeded, CNCs are not able to load extra gold nanoparticles and the entire co-assembly is seemingly dominated AuNRs.
 | ||
Fig. 5 Kissing number frequency for whole systems with various mixtures: (a) pure CNCs, (b) CNCs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AuNRs: 100 AuNRs: 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, (c) 1 1, (c) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and (d) 1 1, and (d) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The aspect ratio for CNCs and AuNRs are 10 and 2.5, respectively. 2. The aspect ratio for CNCs and AuNRs are 10 and 2.5, respectively. | ||
Fig. 7 also provided the individual structures formed under different concentration ratios. As we increased the gold nanoparticles in the system, the network structure persisted even in scenarios where gold nanoparticles were abundant and might be assumed to dominate the simulation system. Furthermore, gold nanoparticles persistently occupied the surface positions on CNC particles, as discussed before. Our colour mapping further confirmed the observation that the orientation of gold nanoparticles closely followed the orientation of the CNC particles to which they were attached. This structural analysis highlights the stability of the network structure formed by CNCs as a host matrix to AuNRs guests and shows the preferential attachment position of this binary system.
4 Conclusion
Our numerical investigation into the co-assembly of CNCs and AuNRs at varying concentration ratios and under sedimentation forces provided valuable insights into the determining mechanisms driving the structure. At a fixed concentration, when the aspect ratios of the AuNRs were changed, the self-assembly process remained similar in binary self-assembly media. In addition, the co-assembled structures within a binary system form a heterogeneous configuration where the AuNRs were distributed preferentially on the surface of the CNC clusters. This was mainly due to the inherent variances in particle density and size. In all simulations, AuNRs consistently occupy surface positions on CNC particles, demonstrating their preferential surface affinity. Moreover, the orientation of AuNRs follows that of the CNC particles to which they are attached, indicating a strong dependence. Furthermore, our study highlighted a critical loading threshold, beyond which CNCs can no longer load additional AuNRs, leading to structures dominated by the AuNRs in the co-assembling media and an increase in disorder. These insights deepen our understanding of the self-assembly behaviour in complex particle systems and help the design and control of the conditions driving self-assembly to achieve ordered structures.Data availability
Molecular dynamics simulation code for this article is available at the University of Manchester Data Repository at https://doi.org/10.48420/26312386.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Stefano Angioletti-Uberti for helpful insights into the use of LAMMPS and Mathematica. We also would like to thank to CSF3 facilities of the University of Manchester and ARCHER2 for supporting computational work. A. G. D. would like to acknowledge funding from bp through the bp-ICAM International Centre for Advanced Materials for her bp-ICAM Kathleen Lonsdale Research Fellowship and the Henry Royce Institute for Advanced Materials is funded through EPSRC grants EP/R00661X/1, EP/S019367/1, EP/P025021/1 and EP/P025498/1.References
- Y. Habibi, L. A. Lucia and O. J. Rojas, Chem. Rev., 2010, 110, 3479–3500 CrossRef CAS PubMed.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS.
- A. G. Dumanli, G. Kamita, J. Landman, H. van der Kooij, B. J. Glover, J. J. Baumberg, U. Steiner and S. Vignolini, Adv. Opt. Mater., 2014, 2, 646–650 CrossRef CAS PubMed.
- A. G. Dumanli, H. M. Van Der Kooij, G. Kamita, E. Reisner, J. J. Baumberg, U. Steiner and S. Vignolini, ACS Appl. Mater. Interfaces, 2014, 6, 12302–12306 CrossRef CAS PubMed.
- A. S. Terpstra, L. P. Arnett, A. P. Manning, C. A. Michal, W. Y. Hamad and M. J. MacLachlan, Adv. Opt. Mater., 2018, 6, 1800163 CrossRef.
- H. Gao, M. A. Soto, J. K. Szymkowiak, L. J. Andrew, W. Y. Hamad and M. J. MacLachlan, Dalton Trans., 2023, 52, 7136–7142 RSC.
- A. Querejeta-Fernández, G. Chauve, M. Methot, J. Bouchard and E. Kumacheva, J. Am. Chem. Soc., 2014, 136, 4788–4793 CrossRef PubMed.
- L. Liu, L. Wang, S. Luo, Y. Qing, N. Yan and Y. Wu, J. Mater. Sci., 2019, 54, 6699–6708 CrossRef CAS.
- G. Chu, H. Yin, H. Jiang, D. Qu, Y. Shi, D. Ding and Y. Xu, J. Phys. Chem. C, 2016, 120, 27541–27547 CrossRef CAS.
- K. K. Sadasivuni, A. Kafy, L. Zhai, H.-U. Ko, S. Mun and J. Kim, Small, 2015, 11, 994–1002 CrossRef CAS PubMed.
- C. Miao and W. Y. Hamad, Cellulose, 2013, 20, 2221–2262 CrossRef CAS.
- L. J. Andrew, C. M. Walters, W. Y. Hamad and M. J. MacLachlan, Biomacromolecules, 2023, 24, 896–908 CrossRef CAS PubMed.
- V. Amendola, R. Pilot, M. Frasconi, O. M. Maragò and M. A. Iat, J. Phys.: Condens. Matter, 2017, 29, 203002 CrossRef PubMed.
- A. G. Dumanli and T. Savin, Chem. Soc. Rev., 2016, 45, 6698–6724 RSC.
- R. Ogier, Y. Fang, M. Svedendahl, P. Johansson and M. Käll, ACS Photonics, 2014, 1, 1074–1081 CrossRef CAS.
- J. K. Gansel, M. Thiel, M. S. Rill, M. Decker, K. Bade, V. Saile, G. von Freymann, S. Linden and M. Wegener, Science, 2009, 325, 1513–1515 CrossRef CAS PubMed.
- A. Lukach, H. Therien-Aubin, A. Querejeta-Fernández, N. Pitch, G. Chauve, M. Méthot, J. Bouchard and E. Kumacheva, Langmuir, 2015, 31, 5033–5041 CrossRef CAS PubMed.
- A. Querejeta-Fernández, B. Kopera, K. S. Prado, A. Klinkova, M. Methot, G. Chauve, J. Bouchard, A. S. Helmy and E. Kumacheva, ACS Nano, 2015, 9, 10377–10385 CrossRef PubMed.
- Z. Cheng, Y. Ma, L. Yang, F. Cheng, Z. Huang, A. Natan, H. Li, Y. Chen, D. Cao and Z. Huang, et al. , Adv. Opt. Mater., 2019, 7, 1801816 CrossRef.
- J. Pérez-Juste, L. M. Liz-Marzán, S. Carnie, D. Y. Chan and P. Mulvaney, Adv. Funct. Mater., 2004, 14, 571–579 CrossRef.
- J. Majoinen, J. Hassinen, J. S. Haataja, H. T. Rekola, E. Kontturi, M. A. Kostiainen, R. H. Ras, P. Törmä and O. Ikkala, Adv. Mater., 2016, 28, 5262–5267 CrossRef CAS PubMed.
- Q. Liu, M. G. Campbell, J. S. Evans and I. I. Smalyukh, Adv. Mater., 2014, 26, 7178–7184 CrossRef CAS PubMed.
- P. Andrew, et al. , J. Chem. Soc., Faraday Trans., 1993, 89, 4069–4078 RSC.
- D. J. Cleaver, C. M. Care, M. P. Allen and M. P. Neal, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 559 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- J. Hou, W. Sampson and A. G. Dumanli, J. Chem. Phys., 2024, 160, 054905 CrossRef CAS PubMed.
- W. J. Orts, L. Godbout, R. H. Marchessault and J.-F. Revol, Macromolecules, 1998, 31, 5717–5725 CrossRef CAS.
- J. Araki and S. Kuga, Langmuir, 2001, 17, 4493–4496 CrossRef CAS.
- T. Margola, G. Saielli and K. Satoh, Mol. Cryst. Liq. Cryst., 2017, 649, 50–58 CrossRef CAS.
- S. Sarman, Y.-L. Wang and A. Laaksonen, Phys. Chem. Chem. Phys., 2019, 21, 292–305 RSC.
- R. Berardi, C. Fava and C. Zannoni, Chem. Phys. Lett., 1995, 236, 462–468 CrossRef CAS.
- Wolfram Research, Inc., Mathematica 14.0, https://www.wolfram.com.
- P.-X. Wang and M. J. MacLachlan, Philos. Trans. R. Soc., A, 2018, 376, 20170042 CrossRef PubMed.
- W. Zhang, X. Cheng, S. H. Chen and M. Anthamatten, Langmuir, 2023, 39, 9180–9185 CrossRef CAS PubMed.
- D. Ghernaout, A. I. Al-Ghonamy, A. Boucherit, B. Ghernaout, M. W. Naceur, N. A. Messaoudene, M. Aichouni, A. A. Mahjoubi and N. A. Elboughdiri, Am. J. Environ. Prot., 2015, 4, 1–15 Search PubMed.
- J. Gregory, Particles in water: properties and processes, CRC Press, 2005 Search PubMed.
- J. Van Rie and W. Thielemans, Nanoscale, 2017, 9, 8525–8554 RSC.
- D. Qu, J. Zhang, G. Chu, H. Jiang, C. Wu and Y. Xu, J. Mater. Chem. C, 2016, 4, 1764–1768 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00871e |
| This journal is © The Royal Society of Chemistry 2024 |