Crossed molecular beam experiments and theoretical simulations on the multichannel reaction of toluene with atomic oxygen

Abstract

Despite extensive experimental and theoretical studies on the kinetics of the O(³P) + C₇H₈ (toluene) reaction and a pioneering crossed molecular beam (CMB) investigation, the branching fractions (BFs) of the CH₃C₆H₄O(methylphenoxy) + H, C₆H₅O(phenoxy) + CH₃, and spin-forbidden C₅H₅CH₃ (methylcyclopentadiene) + CO product channels remain an open question, which has hampered the proper inclusion of this important reaction in the chemical modelling of various chemical environments. We report a CMB study with universal soft electron-ionization mass-spectrometric detection of the reactions O(³P,¹D) + toluene at the collision energy of 34.7 kJ mol⁻¹. From CMB data we have inferred the reaction dynamics and quantified the BFs of the primary products and the role of intersystem crossing (ISC). The CH₃-elimination channel dominates (BF = 0.69 ± 0.22) in the O(³P) reaction, while the H-displacement and CO-formation channels are minor (BF = 0.22 ± 0.07 and 0.09 ± 0.05, respectively), with ISC accounting for more than 50% of the reactive flux. Synergistic transition-state theory (TST)-based master equation simulations including nonadiabatic TST on ab initio coupled triplet/singlet potential energy surfaces were employed to compute the product BFs and assist in the interpretation of the CMB results. In the light of the good agreement between the theoretical predictions for the O(³P) + toluene reaction and the CMB results as well as the absolute rate constant as a function of temperature (T) (from literature), the so-validated computational methodology was used to predict channel-specific rate constants as a function of T at 1 atm.

---

1. Introduction

The investigation of reactive collisions involving more-complex systems than benchmark 3-/4-atom reactions requires a paradigm change, which implies focusing on the reaction mechanism and identifying the primary products and their relative yields (branching fractions, BFs), rather than measuring state-to-state differential cross sections (in general not reachable for polyatomic systems). These results, in addition to providing important information on the characteristics of the underlying potential energy surface (PES), have profound implications for the understanding of complex chemical environments where those reactions occur (e.g. combustion systems or plasmas, as well as the atmosphere of earth and other planets or the interstellar medium).

An important family of polyatomic multichannel reactions are those involving the ground state atomic oxygen, O(³P), and unsaturated hydrocarbons (UHs). For these reactions, there is an additional complication: they begin with the electrophilic O atom addition to the unsaturated bond(s) of the UH to form “chemically activated” triplet oxy-intermediate(s), which can evolve adiabatically on the triplet PES forming a series of primary products but also nonadiabatically via intersystem crossing (ISC) to the singlet PES.^1–12 The occurrence of ISC from the entrance triplet to the underlying singlet PES is caused by the presence of a low-lying singlet state of atomic oxygen, ¹D, the reactions of which start higher in energy with respect to ground state ³P and correlate with strongly bound singlet intermediates. Therefore, singlet and triplet PESs cross each other and ISC can occur leading to a variety of additional bimolecular product channels originating from the singlet PES. To characterize the mechanism of these reactions, the challenge is probing all possible competing product channels on the same footing and determining their BFs, thus assessing the extent of ISC.⁵

Experimentally, the most suitable method to tackle this challenge is the crossed molecular beam (CMB) scattering technique with universal mass spectrometric (MS) detection and time-of-flight (TOF) analysis.^2,5 When empowered by soft electron-ionization detection using tunable electron energy, as done in our laboratory,² or by soft photo-ionization detection using tunable VUV synchrotron radiation,¹³ the dissociative ionization of reactants, products, and background gases that has hampered the use of the CMB-MS method for this kind of study in the past is strongly mitigated or even suppressed.

Theoretically, these systems can be characterized using high-level electronic structure calculations of the stationary points of the PESs including their nonadiabatic couplings, statistical calculations of product BFs with inclusion of ISC, and kinetic computations of the total and channel-specific rate constants as a function of temperature.^8,9,11,12 Notably, for the simplest systems, such as those involving only three heavy atoms, quasi-classical-trajectory (QCT) calculations of product BFs on a full-dimensional PES were possible.^3,14 The comparison of the experimental product BFs with theoretically predicted ones, calculated at the collision energy of the CMB experiments, allows testing the reliability of the calculated PESs and of the theoretical methods used to predict the product BFs.^6,9,11,12 Once validated by experiment, theory can then be used to predict channel-specific rate constants as a function of temperature and pressure.^6,9,11,12

After combined experimental/theoretical investigations on a variety of O(³P) + UH reactions,^{1,3,6–9,11,12,16–20} we concluded that it is difficult to generalize the reaction mechanism because it is strongly affected by the occurrence of ISC, the extent of which depends on the PES details and triplet/singlet nonadiabatic couplings. A benefit of our experimental approach is that we use an atomic oxygen beam containing also a small amount of O(¹D) so that we can also obtain information on the reaction mechanism along the adiabatic singlet PES.^5–12,14

Recently, we have applied the same combined experimental/theoretical approach to reactions of atomic oxygen with small aromatic (benzene)^8,9 and heterocyclic (pyridine)¹¹ molecules. Aromatics are expected to retain their aromatic character when subjected to chemical attack. Instead, our work revealed that the O(³P) + C₆H₆ reaction can also occur via a ring-contraction mechanism involving ISC with a significant yield of CO + cyclopentadiene^8,9 with a BF of ca. 30%.⁹ For the reaction with the isoelectronic pyridine,¹¹ the ring-contraction channel leading to CO + pyrrole via ISC is largely dominant with a BF of 98%. This is the system with the largest contribution from ISC ever, a feature that theory explained with the occurrence of ISC in the entrance channel for the ipso-addition of O(³P) on the N atom.¹¹

In this work, we extend our combined experimental and theoretical approach to the reaction of O(³P) with toluene, the simplest alkylbenzene, with the aim of verifying whether the reaction mechanism and the ISC extent are in line with those of benzene. The O(³P) reaction with toluene is also of considerable interest per se, as toluene is the prototype of alkyl aromatic hydrocarbons, is a minor component of crude oil, is used as an octane booster in gasoline, is involved in the synthesis of PAHs, and is a chemical produced in large quantities and widely used as solvent.

In the past, the oxidation of toluene has been studied extensively from the kinetic standpoint^21–25 and also in combustion models.^26–29 There have been two previous studies using molecular beams, but the results were limited and inconclusive.^30,31

In this study, both the O(³P) + toluene and O(¹D) + toluene reactions have been characterized by using the CMB technique with MS detection and TOF analysis at a collision energy of E_c = 34.7 kJ mol⁻¹, using higher TOF resolution with respect to a previous study,³¹ and crucially exploiting soft electron ionization. The use of soft ionization was critical for observing the co-product (phenoxy) of the O/CH₃ exchange channel in a clean manner. To assist the interpretation of the experimental results, theoretical calculations of the triplet and singlet PESs were undertaken at the DFT and CCSD(T)-CBS levels, and then refined at the CASPT2 level for intermediates exhibiting multireference character and for the evaluation of the minimum energy crossing points (MECPs) between triplet and singlet PESs.^8,9,11 Rice–Ramsperger–Kassel–Marcus/master equation (RRKM/ME) calculations (with the inclusion of ISC) were performed to derive product BFs to be compared with the experimental BFs. Finally, the first channel-specific rate constants for this system were theoretically determined.

The paper is organized as follows. In Section 2 we describe the experimental and theoretical methods. In Section 3 we first report the PESs and then the experimental results and analysis. Section 4 summarizes the theoretical results of the ME simulations under CMB conditions and comparison with experiment. Discussion follows in Section 5. Conclusions are given in Section 6.

2. Methods

2.1 Experimental technique

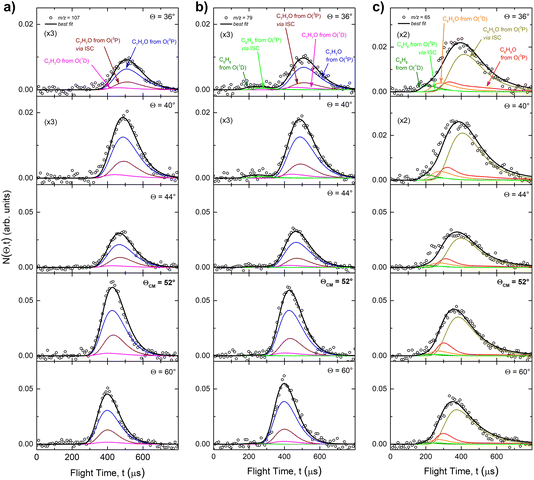
The experiments were carried out using a CMB apparatus featuring two continuous supersonic beam sources of the reactants crossing at 90°, a rotatable, triply-differentially pumped quadrupole MS detector with both hard (70 eV) and soft (17 eV) electron ionization, and a TOF system for determining the velocity distribution of reactants and products. The CMB apparatus has been described in some detail elsewhere.^2,5,32,33 The atomic oxygen beam was produced using a radio-frequency (RF) discharge supersonic beam source³⁴ in which a 5% O₂/He gas mixture, at the pressure of 85 mbar, was discharged through a 0.48 mm diameter water-cooled quartz nozzle at 300 W of RF power. The atomic oxygen beam mainly contains O(³P) and a small amount of O(¹D) (≤10%).³⁴ The molecular beam was generated by expanding 29 mbar of neat toluene (99.8% purity) through a 0.1 mm diameter stainless-steel nozzle. The toluene flask was immersed into a temperature-controlled bath (kept at 293 K) to avoid temperature fluctuations. Under these conditions, the reactant velocities were 2206 and 494 m s⁻¹, with speed ratios of 4.8 and 2.5 for the oxygen and toluene beam, respectively. The resulting E_c was 34.7 kJ mol⁻¹. Product laboratory (LAB) angular distributions, N(Θ), at selected mass-to-charge (m/z) ratios were acquired by modulating the toluene beam at 160 Hz for background subtraction. Product TOF distributions, N(Θ,t), were measured using the pseudo-random chopping TOF method at 10 μs per channel. Quantitative information on the reaction dynamics was derived from the raw data by moving from the LAB system to the center-of-mass (CM) frame, and by analyzing the product angular, T(θ), and translational energy,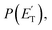 distributions, into which the CM product flux can be factorized.^2,5,34–36 The best-fit CM functions are actually derived by a forward convolution fit of the total product LAB angular and TOF distributions at each specific m/z ratio value according to the relation: 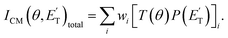The best-fit values of w_i allow one to derive the relative yield of the different reaction channels^2,33 (see the ESI†).

2.2 Theoretical methods

The theoretical investigation of the reaction of O(³P) and O(¹D) with toluene was performed adopting a well-established computational strategy previously used for the investigation of other bimolecular reactions.^35–38 The optimization of all stationary points was performed by locating the lowest stationary points (minima and transition states) at the ωB97X-D^39,40 level of theory in conjunction with the 6-311+G(d,p) basis set.^41–43 At the same level of theory we have computed the harmonic vibrational frequencies in order to check the nature of the stationary points, i.e., minimum if all the frequencies are real, or saddle point if there is one, and only one, imaginary frequency. The assignment of the saddle points was performed using intrinsic reaction coordinate (IRC) calculations.^44,45 Structures and Hessians of the MECPs between the triplet and the singlet PES were determined at the ωB97X-D/6-311+G(d,p) level using the methodology recently implemented in EStokTP.^9,46 The energy of all stationary points was then computed at the CCSD(T) level^47–49 using the more extended basis set aug-cc-pVTZ.^50–52 Both ωB97X-D and CCSD(T) energies were corrected to 0 K by adding the zero-point energy (ZPE) computed using harmonic vibrational frequencies evaluated at the ωB97X-D level. More accurate calculations were then performed at the CCSD(T) level corrected with a density-fitted (DF) MP2 extrapolation to the complete basis set (CBS) and with corrections for core electron excitations. The energies have been calculated as:

E_CBS = E(CCSD(T)/aug-cc-pVTZ) + [E(CCSD(T,core)/cc-pVTZ) − E(CCSD(T)/cc-pVTZ)] + [E(DF-MP2/CBS) − E(DF-MP2/aug-cc-pVTZ)],

where E(DF-MP2/CBS) is defined as:

E(DF-MP2/CBS) = E[(DF-MP2)/aug-cc-pVQZ] + 0.5772 × [E(DF-MP2/aug-cc-pVQZ) − E(DF-MP2/aug-cc-pVTZ)].

The E(DF-MP2/CBS) extrapolation was performed using Martin’s two-parameter scheme,⁵³ leading to an expected accuracy of about ±5 kJ mol⁻¹. These energies, simply labelled CBS despite also including core-valence correlation corrections, were used for the kinetic investigation described below.

The energies of key steps presenting strong multireference character were determined at the CASPT2/aug-cc-pVTZ level on ωB97X-D/6-311+G(d,p) structures. This was the case for all the O(³P) addition steps, the isomerization of the toluene oxides ¹W1, ¹W2, and ¹W3 (nomenclature according to Fig. 1), and the triplet–singlet minimum energy crossing points (MECPs). In the case of O(³P)-addition in ortho and ipso positions, the structures were also determined at the CASPT2 level employing the cc-pVTZ basis set. This additional set of calculations was necessary since the branching among the four possible O(³P) addition sites has a significant impact on the BF, so that calculations were performed at the highest level of theory computationally feasible for this system. CASPT2 calculations for the entrance channels were performed using a (10e,9o) active space and a two-states averaged wavefunction consisting of the (4e,3o) of O(³P) and the (6e,6o) of the π bonding and antibonding orbitals of the toluene aromatic ring. MECP energies were determined using a (8e,7o) active space and a two-states averaged wavefunction, consisting of the (2e,2o) electrons and orbitals of the radical centres, of the (4e,4o) π bonding and antibonding orbitals of the aromatic ring, and of the (2e,1o) oxygen lone pair. Energies for the isomerization reactions of the toluene oxides were determined using a (12e,11o) active space consisting of the (10e,9o) active space used for the addition reactions and of the (2e,2o) of the σ and σ* bonding and antibonding orbitals of the C–C bond of the three-membered ring of the reacting well.

Fig. 1 Schematic representation of the O(³P) + toluene triplet (a) and singlet (b–d) PESs, with ISC energies (for ipso, ortho, meta, and para initial addition). The main reaction pathways on the singlet PES are indicated in bold. Energies (kJ mol⁻¹, 0 K) computed at the CCSD(T)/CBS and CASPT2/aug-cc-pVTZ (with asterisk) levels are indicated.

Rate constants of all steps having a distinct transition state (TS) were determined with conventional transition-state theory (TST), using the rigid rotor harmonic oscillator approximation (RRHO) and treating the methyl torsional normal mode as a 1D hindered rotor. The rate constants for triplet–singlet ISC were determined using nonadiabatic TST (NA-TST) as implemented in EStokTP.⁴⁶ ISC probabilities were computed with Landau–Zener theory using averaged spin–orbit couplings (SOC) between singlet and triplet PESs determined with a Breit-Pauli Hamiltonian. The rate constants of four barrierless reactions involving the recombination of H and CH₃ with the methylphenoxy and phenoxy radicals were determined using variable reaction coordinate TST (VRC-TST).⁵⁴ In particular, rate constants were determined for methyl recombination with the phenoxy radical leading to the formation of ¹W4 and ¹W23 and atomic hydrogen, with the methylphenoxy radical leading to the formation of ¹W4, and ¹W25 or ¹W26 (see Section 3.1). While the details of these calculations will be reported in successive work dedicated to the pyrolysis of anisole and cresol,⁵⁵ here we briefly mention that the VRC-TST stochastic scan was performed using multifaceted spherical surfaces centered on pivot points placed along the axis of the breaking bond at the CASPT2 (2e,2o)/cc-pVDZ level. Correction potentials for geometry relaxation and energy were determined along the minimum energy path on structures optimized at the UωB97X-D/6-311+G(d,p) level determining energies at the CASPT2/aug-cc-pVTZ levels with large active spaces (inclusive of all π bonding and antibonding orbitals together and of the σ and σ* orbitals of the breaking bond). A 0.9 correction factor for recrossing was used to scale the VRC-TST rate constants.

The system reactivity was simulated under both CMB and thermal conditions integrating the master equation (ME) using our stochastic MC-RRKM code,⁵⁶ accounting explicitly for the coupling between the singlet and triplet PESs using NA-TST.⁵⁷ Four distinct ME simulations were performed, depending on whether the triplet PES is accessed, with reference to the methyl group, through addition to the ipso, ortho, meta, or para sites. The BF for addition at the four different sites for CMB simulations was determined at 300 K, thus assuming that the energy of the beam does not contribute to the density of states (DOS) at the TS. Simulations were performed for each examined condition until 10⁴ reactive events occurred. Thermal simulations were performed in the 300–2000 K temperature range at 1 bar in an Ar thermal bath. The intermolecular collisional energy transfer was calculated with Lennard-Jones collisional rates using σ = 6.1 Å and ε = 293.6 K Lennard-Jones parameters for all the isomers formed by atomic oxygen and toluene, σ = 3.54 Å and ε = 64.7 K for Ar, and a single exponential down model with an average downward energy computed as ΔE_down = 366(T/300)^0.47 cm⁻¹, determined following the procedures suggested by Jasper.⁵⁸

All DFT and CCSD(T) calculations were done using Gaussian 09 (ref. 59) while the CASPT2, CBS and SOC calculations were done with MOLPRO.^60,61 The analysis of the vibrational frequencies was performed using Molekel.^62,63

3. Results and discussion

3.1 Potential energy surfaces

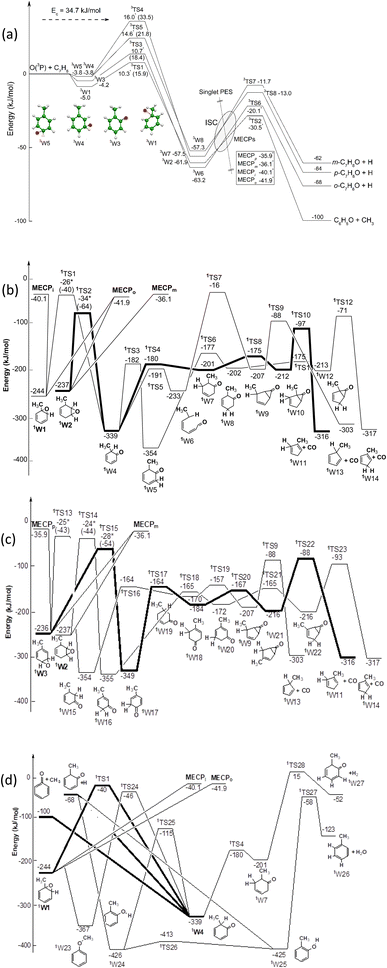
The triplet and singlet PESs originating from the addition of O(³P) to toluene are shown in Fig. 1a–d, respectively. The calculated energy values are reported rounded to the nearest kJ mol⁻¹ considering the accuracy of the calculations. However, for the addition transition states, van der Waals wells and MECPs (the energies of which are so critical for kinetic calculations and were obtained with a higher level of calculations) the values are reported rounded to the nearest tenth of a kJ mol⁻¹.

O(³P) can attack the toluene ring at four different sites: ipso, ortho, meta and para, giving rise to four different van der Waals adducts, ³W1, ³W3, ³W4 and ³W5, which are more stable than the reactants by 5.0, 4.2, 3.8 and 3.8 kJ mol⁻¹, respectively. These adducts can evolve to the more stable, covalently bound triplet diradical minima ³W2, ³W6, ³W7 and ³W8 by overcoming an energy barrier (from the van der Waals well) of 20.9 kJ mol⁻¹ for the ipso isomer, and 22.6, 25.6 and 37.3 kJ mol⁻¹ for the ortho, para, and meta isomers, respectively. The ³W2, ³W6, ³W7 and ³W8 intermediates have enough energy to overcome a relatively low energy barrier and dissociate to phenoxy + methyl, and o-, m-, p-methylphenoxy + H, respectively.

O(³P) can also abstract an H atom from the aromatic ring or from the methyl group. The abstraction of H from the ortho, meta and para carbon is endothermic by 39.1, 38.9, and 41.2 kJ mol⁻¹, respectively, while abstraction of H from CH₃ is exothermic by 55.0 kJ mol⁻¹. The last reaction, however, shows a barrier of 21.8 kJ mol⁻¹ at the CASPT2 level²⁸ (28.1 kJ mol⁻¹ at the CCSD(T) level), which is much larger than that (ca.10 kJ mol⁻¹) for the ipso- and ortho-addition pathways. Hence, at E_c = 34.7 kJ mol⁻¹, abstraction channels are expected to contribute little to the overall reactivity (4% at 300 K and 10% at 1000 K)²⁸ and thus are not included in the triplet PES of Fig. 1a.

The addition of O(¹D) to toluene leads to three different isomers, ¹W1, ¹W2 and ¹W3, with a similar stabilization. Fig. 1a–d shows three snapshots of the singlet PES with the MECPs indicated for ipso, ortho, meta, and para addition. O(¹D) has two unpaired electrons with opposite spin which can interact with the two electrons of the carbon atoms involved in π-bonding. This is why O(¹D) shows an η² coordination. These three isomers, through several isomerizations that imply overcoming relatively high energy barriers, can dissociate on the singlet PES to carbon monoxide and methylcyclopentadiene, in addition to methylphenoxy + H and phenoxy + CH₃. Other reaction pathways can lead to the formation of H₂O or H₂ (see bottom panel of Fig. 1b) but RRKM calculations indicated a negligible contribution.

3.2 Experimental results

According to our calculations, the open channels of the O(³P,¹D) + toluene reactions are:

O(³P) + C₆H₅CH₃ → o-CH₃C₆H₄O + H; ΔH⁰₀ = −68 kJ mol⁻¹ (1a)

O(³P) + C₆H₅CH₃ → p-CH₃C₆H₄O + H; ΔH⁰₀ = −64 kJ mol⁻¹ (1a′)

O(³P) + C₆H₅CH₃ → m-CH₃C₆H₄O + H; ΔH⁰₀ = −62 kJ mol⁻¹ (1a′′)

O(³P) + C₆H₅CH₃ → C₆H₅O + CH₃; ΔH⁰₀ = −100 kJ mol⁻¹ (2a)

O(³P) + C₆H₅CH₃ → C₅H₅CH₃ + CO; ΔH⁰₀ = −317 kJ mol⁻¹ (3a)

O(¹D) + C₆H₅CH₃ → o-CH₃C₆H₄O + H; ΔH⁰₀ = −258 kJ mol⁻¹ (1b)

O(¹D) + C₆H₅CH₃→ p-CH₃C₆H₄O + H; ΔH⁰₀ = −254 kJ mol⁻¹ (1b′)

O(¹D) + C₆H₅CH₃ → m-CH₃C₆H₄O + H; ΔH⁰₀ = −252 kJ mol⁻¹ (1b′′)

O(³P) + C₆H₅CH₃ → C₆H₅O + CH₃; ΔH⁰₀ = −290 kJ mol⁻¹ (2b)

O(³P) + C₆H₅CH₃ → C₅H₅CH₃ + CO; ΔH⁰₀ = −507 kJ mol⁻¹ (3b)

The reaction enthalpies (ΔH⁰₀) are those obtained from the present calculations at the CCSD(T)/CBS levels of theory. The exothermicities of the product channels in the O(¹D) reaction were determined by adding the oxygen ¹D-³P splitting of 190 kJ mol⁻¹.

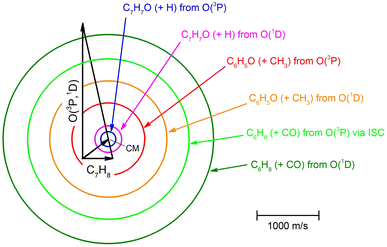
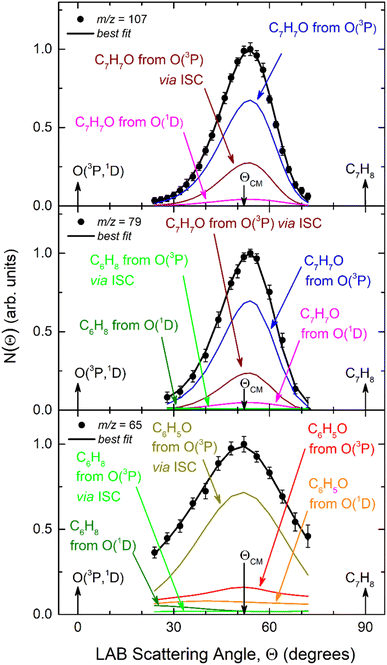
The velocity vector “Newton” diagram illustrating the kinematics of the reactive systems is depicted in Fig. 2. We detected reactive signals at m/z = 107 (C₇H₇O⁺), 106 (C₇H₆O⁺), 79 (C₆H₇⁺), and 65 (C₅H₅⁺). The measured relative intensities at the CM angle (θ_CM = 52°) for these m/z values (at an ionization energy of 17 eV) are 1.0, 0.07, 0.96, and 0.97, respectively. The product LAB angular distributions, N(Θ), acquired at m/z = 107, 79, and 65 are reported in Fig. 3 as solid dots (average of 4–5 angular scans, each with a counting time of 100 s per angle, with experimental error bars indicated). TOF distributions at five selected LAB angles are displayed in Fig. 4 for m/z = 107, 79, and 65. Measurements at m/z = 107 were done by using hard ionization (70 eV), while for m/z = 79 and 65 we resorted to soft ionization at 17 eV to mitigate/suppress the interferences from the background gas and elastic scattering. Data at m/z = 107 were also recorded at 17 eV for normalization purposes. TOF accumulation time per angle was 1 h (70 eV) at m/z = 107, while at m/z = 79 and 65 was 1 and 3 h, respectively (17 eV). The signal at m/z = 107 corresponds to the parent ion of the heavy co-product CH₃C₆H₄O (methylphenoxy, also known as a cresoxy radical, hereafter indicated as C₇H₇O) formed in the H-displacement channels 1a/1b. Upon ionization, cresoxy slightly fragments to m/z = 106 by loss of an H atom, while it significantly fragments to m/z = 79 by losing a CO group. The signal at m/z = 79 also originates from the −1 daughter ion of C₅H₅CH₃ (methylcyclopentadiene, hereafter indicated as C₆H₈), the co-product in the CO-forming channels 3a/3b. Finally, the signal at m/z = 65 corresponds to the (–CO) daughter ion of the phenoxy (C₆H₅O) co-product of the CH₃-elimination channels 2a/2b. The parent of phenoxy (m/z = 93) could not be probed in our experiment because of the strong elastic/inelastic signal at m/z = 93 (¹³CC₆H₈⁺) due to the presence of ¹³C (with its natural isotopic abundance) in toluene. In the evaluation of the branching fractions, it was assumed that the fragmentation of phenoxy to its daughter ion m/z = 65 is the same as was quantified in the CMB study on the O(³P,¹D) + C₆H₆ reactions under similar experimental conditions.⁹

Fig. 2 Velocity vector (Newton) diagram for O(³P,¹D) + toluene reactions at E_c = 34.7 kJ mol⁻¹. The color-coded circles delimit the maximum speed that the indicated primary products can attain in the CM frame when all the available energy (E_c − ΔH₀⁰) is channeled into product translational energy. Blue and magenta lines represent the heavy co-products (methylphenoxy, C₇H₇O) of the H-displacement channels from the O(³P) and O(¹D) reactions, respectively (the circles for the three C₇H₇O isomers are not distinguishable in this scale). Red and orange lines correspond to the heavy co-product (phenoxy, C₆H₅O) of the CH₃-elimination channels from the O(³P) and O(¹D) reactions, respectively. Green and olive lines correspond to the C₆H₈ (methylcyclopentadiene) co-product of the CO-formation channels from the O(³P) (via ISC) and O(¹D) reactions, respectively.

Fig. 3 LAB product angular distributions, N(Θ), for the O(³P,¹D) + C₇H₈ reactions at E_c = 34.7 kJ mol⁻¹, for m/z = 107, 79, and 65. The partial contributions of different products at the three different masses are indicated. The black line superimposed on the experimental data corresponds to the global best-fit calculated using the CM functions shown in Fig. 6. The distinct contributions to the calculated global N(Θ) are color-coded as in Fig. 2, and indicated with the formula of the corresponding product.

Fig. 4 Product TOF distributions measured at m/z = 107 (a), 79 (b), and 65 (c) at the indicated LAB angles Θ. The partial contributions of different channels are also indicated. The black line superimposed on the experimental data corresponds to the global best-fit calculated using the CM functions shown in Fig. 6. The distinct contributions to the calculated global N(Θ,t) are also shown (color-coded as in Fig. 2).

The use of soft ionization was critical for the m/z = 65 distributions because dissociative ionization of toluene to m/z = 65 is significant upon electron impact at 70 eV, while it becomes negligible at 17 eV. This is well illustrated in Fig. S1 of the ESI† where TOF spectra recorded at m/z = 65 for two different LAB angles at 70 and 17 eV are shown. As can be seen, when using 17 eV it is possible to measure in a clean manner the C₆H₅O distributions at its (−28) daughter ion, having suppressed the otherwise overwhelming contributions from elastically/inelastically scattered toluene.

The black curves in Fig. 3 and 4 represent the global best-fit for the LAB distributions at the indicated m/z data, while the labeled and color-coded curves represent the partial contributions from the various channels, when using the best-fit CM product angular, T(θ), and translational energy, 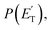distributions reported in Fig. 5 for the eight characterized contributions.

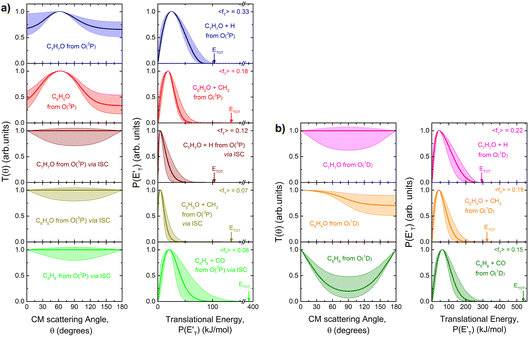Fig. 5 (a) LHS panels: best-fit CM angular distributions for the indicated products formed in the O(³P) + toluene reaction. (b) LHS panels: best-fit CM angular distributions for the indicated products formed in the O(¹D) + toluene reaction. In the RHS panels of (a) and (b) the total available energy, E_TOT, and its average fraction released as translational energy, 〈f_T〉, are shown. Color coding as in Fig. 2. The shaded areas embedding the best-fit function delimit the range of functions, which still provide an acceptable fit of the LAB distributions.

3.2.1 The m/z = 107 data: the H-displacement channels. Fig. 3 (top panel) shows the angular distribution obtained at m/z = 107. The distribution has a bell shape centered at the CM angle and extending in the 24–72° angular range. Fig. 4a shows the TOF spectra at selected LAB angles. They are characterized by a single broad peak centered at about 400 μs. At this m/z, the reactive signal can only derive from the daughter ions of the H-displacement channel heavy co-products, that is, o-, m-, and p-methylphenoxy radicals. Given the very small difference in the reaction enthalpy of the channels 1a, 1a′, and 1a′′, as well as in the case of 1b, 1b′, and 1b′′, it was not possible to distinguish the three isomers originating from both the triplet and singlet reactions. During the analysis, the signal at m/z = 107 was separated into three different contributions, two associated with the O(³P) reaction (of which one is associated with the adiabatic reaction on the triplet PES and the other to the nonadiabatic reaction via ISC) and one with the much more exothermic O(¹D) reaction. The two O(³P) contributions could be distinguished because the H-displacement channel occurs via a substantial exit barrier on the triplet PES, while the exit channel is barrierless in the singlet PES (see Fig. 1 and Discussion).

3.2.2 The m/z = 79 and 65 data: C₆H₅O + CH₃ and C₆H₈ + CO channels. The LAB angular and TOF distributions at m/z = 79 and 65 (see Fig. 3 and 4) indicate that the C₆H₅O + CH₃ and C₆H₈ + CO channels are open. At m/z = 79, the recorded signal mostly comes from the H-displacement channels, but a small fraction can be attributed to C₆H₈ (formed in the channels 3a and 3b) via its daughter ion (C₆H₇⁺). Indeed, the intensity of the recorded signal is slightly higher at angles around 30° with respect to the case of the m/z = 107 LAB angular distribution and some signal between 150 and 300 μs is visible in the TOF spectra at Θ = 36° and 40°. The fit of the TOF spectra at m/z = 65 at the same angles allowed us to separate two contributions: a faster one attributed to the O(¹D) reaction and a slower one that we have associated with the O(³P) reaction via ISC. The signal recorded at m/z = 65 is mostly given by the O/CH₃ exchange channels being associated with the daughter ion of C₆H₅O (phenoxy), which is known to strongly undergo dissociative ionization to C₅H₅⁺ by CO loss, as observed in the O(³P) + benzene reaction.⁹ The CH₃ channel was separated into three components, two associated with the O(³P) reaction (one occurring adiabatically on the triplet PES and another occurring via ISC) and one associated with the reaction of O(¹D) on the singlet PES (see Discussion).

3.2.3 Product angular and translational energy distributions in the CM frame. The best-fit CM angular and translational energy distributions for all the contributions are shown in Fig. 5. The characteristics of the CM distributions implicate different reaction mechanisms for the same set of primary products in the O(³P) and O(¹D) reactions, and for the adiabatic vs. ISC O(³P) pathways. More specifically, when comparing the T(θ) for the H-displacement channels from the O(³P) and O(¹D) reactions, the former, when occurring adiabatically on the triplet PES, is characterized by a sideways T(θ) function, suggesting that the H atom is emitted orthogonally to the collision plane with tight TSs on the triplet PES (see Discussion). At the same time, the other two components (from O(³P) via ISC and from O(¹D)) exhibit an isotropic distribution, which indicates that the H emission occurs without the need to reach a critical geometry associated with an exit TS on the singlet PES. Similarly, the mechanism of the CH₃-elimination channels is also different for the three components. The C₆H₅O CM angular distribution exhibits a sideways peak for the adiabatic reaction on the triplet PES, while the mechanism occurring via ISC is characterized by an isotropic T(θ). Similarly, the C₆H₅O product from O(¹D) has a slightly forward-biased T(θ) (osculating complex mechanism⁶⁴) because of the much higher amount of energy available.

The characteristics of the associated best-fit 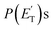have been pivotal to discriminate the different contributions. The peaking of the 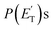for the methylphenoxy + H and phenoxy + CH₃ channels in the O(³P) reaction via ISC was found to be very close to zero, an indication that there are no exit barriers for these channels, as in the singlet PES. In contrast, the 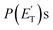associated with the adiabatic O(³P) reactions are characterized by a peak well displaced by 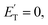a characteristic normally associated with an exit barrier, as is the case for the triplet PES. Consequently, the average fraction of the total energy released in translational energy, 〈f_T〉, is much larger for the adiabatic reactions with respect to those related to the ISC mechanisms (0.33 vs. 0.12 for the adiabatic vs. ISC mechanism in the H-displacement channel(s) and 0.18 vs. 0.07 for the CH₃-elimination channel). For the CO channel, 〈f_T〉 is 0.08 and 0.15 in the O(³P) reaction via ISC and the O(¹D) reaction, respectively, indicating that some electronic energy of the O atom is converted into product translational energy. We recall that 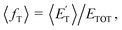where 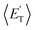is the average product translational energy defined as 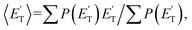and E_TOT = E_c − ΔH⁰₀.

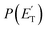3.2.4 Product branching fractions (BFs). After characterizing the best-fit T(θ) and functions for the various product channels, the BFs of each reaction channel were estimated using the procedure introduced by Schmoltner et al.⁶⁵ and widely employed by us in CMB investigations of a variety of multichannel reactions of O(³P).^{1–3,5–9,11,12,14–20} The experimental relative contributions for the competing product channels of the O(³P,¹D) + toluene reactions at E_c = 34.7 kJ mol⁻¹ are listed in Table 1, together with the BFs for the distinct O(³P) and O(¹D) reactions. The BFs are obtained by normalizing to unity the sum of the relative contributions of all O(³P) channels and all O(¹D) channels. For details on how the BFs were derived, see the ESI† and also ref. 5. In the same table the theoretical predictions from RRKM/ME simulations on the coupled triplet/singlet PES for the conditions of the CMB experiment are shown for comparison (see Section 4.2). As shown in Table 1, the experimental trend of BFs for the various channels of the O(³P) + toluene and O(¹D) + toluene reactions are found to be significantly different. For example, for O(³P) + toluene, the H-displacement channel 1a is substantial (global BF = 0.22 ± 0.09), while the analogous channel 1b for O(¹D) + toluene is minor (BF = 0.03 ± 0.02). Interestingly, the CH₃-elimination channel is dominant for O(³P), with global BF = 0.69 ± 0.20, and it is also substantial for O(¹D), with BF = 0.43 ± 0.13.

Table 1 Experimental branching fractions for the distinct O(³P) + C₇H₈ and O(¹D) + C₇H₈ reactions, obtained from the relative best-fit channel contributions (see text), compared with BFs predicted by RRKM/ME calculations on the coupled triplet/singlet PESs. Experimental uncertainties are between 25%–50% depending on the reactive channel (see text and the ESI)

Reactants	Primary products	PES involved	Relative contributions	Branching fractions
			CMB expt. (Ec = 34.7 kJ mol^−1)	CMB expt. (Ec = 34.7 kJ mol^−1)	Theory (RRKM/ME) (Ec = 34.7 kJ mol^−1)
O(^3P) + C7H8	C7H7O + H	Triplet	0.11	0.19 ± 0.07	0.34
		Singlet via ISC	0.02	0.03 ± 0.02	0.02
	C6H5O + CH3	Triplet	0.17	0.24 ± 0.08	0.16
		Singlet via ISC	0.26	0.45 ± 0.14	0.37
	C6H8 + CO	Singlet via ISC	0.06	0.09 ± 0.05	0.11
O(^1D) + C7H8	C7H7O + H	Singlet	0.01	0.03 ± 0.02	—
	C6H5O + CH3	Singlet	0.16	0.43 ± 0.13	—
	C6H8 + CO	Singlet	0.20	0.54 ± 0.27	—

---

On the other hand, if we compare channels 3a and 3b we find that the BF of the C₆H₈ (methylcyclopentadiene) + CO channel is very large for O(¹D) + toluene (BF = 0.54 ± 0.27), while it is much lower for O(³P) + toluene (BF = 0.09 ± 0.05). It should be noted that the BFs for the CO channels 3a and 3b are affected by the greatest uncertainty (50%), given the small signal associated with them. In the LAB distributions these channels are mainly visible in the TOFs at small angles (Θ = 36° and 40°) (see Fig. 4b and c). This is related to the fact that in CMB-MS experiments, where the number density of the scattered products is detected, heavy products that are scattered by a light co-product (such as a H atom) are strongly amplified in the LAB system because of the favorable Jacobian transformation (relating the LAB number density N(Θ) to the CM flux I(θ,u)) given by N(Θ) = I_CM(θ,u)v/u², where v and u are the LAB and CM product velocity, respectively.^5,33 For instance, while in the N(Θ) and N(Θ,t) at m/z = 79 of Fig. 3 and 4b, respectively, the experimental signal of the H-displacement channels appears dominant over the signal of the CO channels; in the CM the CO contribution becomes larger than that of H, with the ratio of the BFs of the channels (total H)/(total CO) being 0.26/0.14 (see Table 1).

By adding all contributions from the O(³P) reactions that proceed via ISC, we arrive at the conclusion that the fraction of spin-forbidden channels amounts to 57 ± 16% of the total reactive channels when using the experimental BFs, and 50% when using the theoretical BFs (see Table 1). This means that under CMB conditions ISC accounts for about 57% of the reactivity in the O(³P) + toluene reaction.

4. Theoretical results

4.1 O(³P) addition to toluene

The initial step of the O(³P) + C₇H₈ reaction is O(³P) addition to the toluene aromatic ring on the triplet PES (Fig. 1a). Four different addition sites are possible: ipso, on the methylated carbon, or in the ortho, meta, and para position with respect to the methyl group. The system reactivity is considerably influenced by the relative contributions of the possible addition sites, as isomerization and scrambling processes on the triplet PES are relatively slow with respect to bond fission and triplet-to-singlet ISC. Channel specific rate constants for the four addition reactions were, therefore, determined using conventional TST and the calculations of energy barriers at the CASPT2 level (using the geometries computed at the ωB97X-D level). It is found that addition in the ipso position is energetically favored, with a barrier of 10.3 kJ mol⁻¹ with respect to the reactants. Addition in the ortho, para, and meta positions is characterized by barriers of 10.7, 16.0, and 14.6 kJ mol⁻¹, respectively (see Fig. 1a). The total addition rate constant, calculated as a function of temperature, is compared with experimental data in Fig. 6.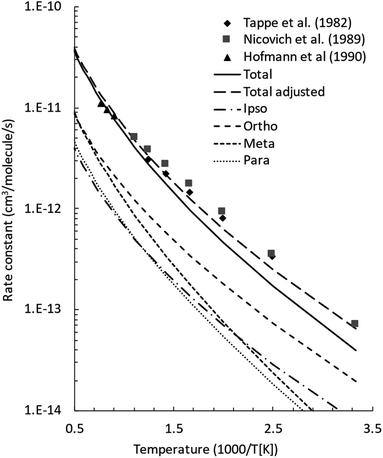

Fig. 6 Comparison between calculated (lines) and experimental (points) rate constants for O(³P) addition to toluene. The total adjusted rate was determined by decreasing the energy barrier for all addition channels by 1.2 kJ mol⁻¹, which is well within the uncertainty of the adopted theoretical model. Symbols: experimental rate constants from Tappe et al.,²⁴ Nicovich et al.,²³ and Hoffmann et al.²⁵

The agreement between the experimental and theoretical results for the total rate constant is quite good, with a maximum difference of ca. a factor of two at 300 K, and quantitative agreement at temperatures higher than 1000 K. It should be noted that quantitative agreement is also obtained at low temperatures if the energy barriers for addition are decreased by 1.2 kJ mol⁻¹, a correction factor that is well within the uncertainty of the theoretical level of the calculations. As can be seen from the distinct contribution of the total rate constant (Fig. 6), the fastest entrance channel is addition in the ortho position at all temperatures, with addition in the ipso position being the second fastest up to about 600 K. Above 600 K, the main reaction channels are addition in the ortho and meta positions, with similar rates.

4.2 Master equation simulations of product BFs under CMB conditions

The BFs used for the simulations of the CMB experiments were computed at 300 K. According to our previous studies on this reaction class, this temperature returns statistical thermal distributions that are able to appropriately describe the conditions of reacting molecules in the beam (see ref. 11 for a discussion on this point). The BFs so determined are 0.57, 0.22, 0.11, and 0.10 for addition in the ortho, ipso, meta, and para positions, respectively.

Following O(³P) addition on the triplet PES, two reaction channels are possible: decomposition or ISC. The decomposition channels lead to H loss for ortho, meta, and para addition, and to methyl loss for ipso addition. Isomerization reactions, such as H and CH₃ migrations to vicinal sites as well as H transfers leading to the formation of OH, are not competitive on the triplet PES. Similar to what was found for the O(³P) + benzene reaction,⁹ significant spin–orbit couplings of about 35 cm⁻¹ are found at the MECPs for the T1/S1 and T2/S0 PESs. MECP energies for T2/S0 and T1/S1 ISC are 21.8 and 26.8 kJ mol⁻¹ for ISC from the well accessed after ipso addition, and 22.2 and 25.1 kcal mol⁻¹ for ortho addition, respectively. ISC rates following meta- and para-addition channels were assumed to take place at rates equal to those computed for ortho addition. Energy barriers for H loss on the triplet PES following ortho, meta, and para addition are about 42 kJ mol⁻¹ with respect to the reacting well, while the energy barrier for methyl loss following ipso addition is only 33.5 kJ mol⁻¹ (from the ³W6, ³W7, ³W8, and ³W2 wells, respectively – see Fig. 1a).

The extent of ISC with respect to decomposition was determined through ME simulations computing the rate of ISC using NA-TST. It was found that following ortho, meta, and para addition under CMB conditions, about half of the reactive flux goes through ISC to the singlet PES, while the other half leads to H loss. In the case of ipso addition, only one fourth of the reactive flux undergoes ISC, as the main reaction channel is CH₃ loss.

The reactivity on the singlet PES is determined by the competition between three reaction channels: (i) decomposition to the methyl and phenoxy radicals, (ii) H loss, to form the methylphenoxy radical, and (iii) decomposition to CO and methylcyclopentadiene (see Fig. 1b). The fastest reaction is the barrierless decomposition to methyl + phenoxy, which is favored energetically over H loss by about 29 kJ mol⁻¹, and entropically because of the larger number of transitional degrees of freedom. Decomposition to methyl and phenoxy is also faster than decomposition to CO and methylcyclopentadiene, which is energetically favored by about 210 kJ mol⁻¹, because of the large energy barriers and tight nature of the transition states along the reaction path, most notably TS10, TS12, TS22, and TS23 (see Fig. 1b). In the ME simulation, the reactivity on the singlet PES was described by connecting the entrance triplet wells for ipso, ortho, meta, and para addition, to the ortho, meta, and para toluene oxides ¹W1, ¹W2, and ¹W3 (see Fig. 1b). While ISC from the ipso and para entrance wells can lead only to ¹W1 and ¹W3, respectively, ISC from the ortho and meta entrance wells can lead either to the ¹W1 or ¹W2 wells, or to the ¹W2 and ¹W3 wells, respectively. When two toluene oxide wells are accessible from the same MECP, it was decided in the ME simulations to split in half the ISC reactive flux, as ¹W1, ¹W2, and ¹W3 have similar energies (−244, −237, and −236 kJ mol⁻¹, respectively) and, following ISC, the evolution to the wells is expected to be a barrierless process with similar minimum energy paths. The ME simulations showed that following ISC to ¹W1 the main reaction channel is CH₃ loss, while upon ISC to ¹W2 about 80% of the reaction flux leads to CH₃ loss, and the remaining 20% is split equally between the H and CO decomposition channels. The reactivity on the singlet PES differs though for ISC to ¹W3. In this case, isomerization to the precursor for CH₃ loss, well ¹W4, is hindered by significant energy barriers. The main reaction channels are thus decomposition to CO and methylcyclopentadiene, which accounts for about 56% of the ISC flux, and H loss for 44%.

One important conclusion that can be drawn from this analysis of the system reactivity is that it is significantly influenced by the entrance channel. Addition in the proximity of the methyl substituent will in fact lead to methyl loss, which is the fastest channel on the triplet and singlet PESs for ipso addition, and the main channel if an isomerization reaction can efficiently lead to H transfer to the methyl-substituted carbon atom of the aromatic ring. This is, for example, one of the main reaction pathways, followed by addition in the ortho position, ISC to the singlet PES, and isomerization through ¹TS2. The system reactivity predicted through the ME simulations of the O(³P) + toluene reaction under CMB conditions is summarized in Table 1.

4.3 Thermal rate constants

Master equation simulations were performed under thermal conditions at 1 atm in the 300–2000 K temperature range. The BFs so determined for the main reaction channels are reported in Fig. 7, while rate constants fitted in the modified Arrhenius form are given in Table 2.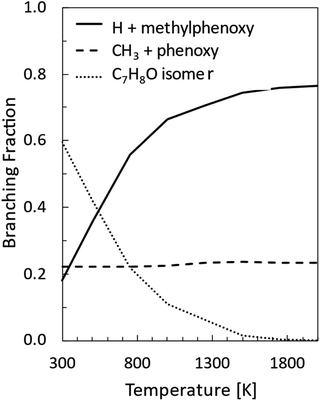

Fig. 7 Product branching fractions for the reaction between O(³P) and toluene computed as a function of temperature at 1 atm.

Table 2 Arrhenius fits in the form AT^α exp(−E_A/RT)^a

	log 10 (A)	a	E A (cal mol^−1)	R ^2	Fitting range (K)
a Units: cal, mol, s, cm^3. In the fitting, the rate constants for all the collisionally-stabilized wells were merged in a single isomer. The collisionally stabilized wells are mostly ^1W1, ^1W2, and ^1W3, or, at the higher temperatures, ^1W15, ^1W16, and ^1W17.
C7H8O isomer	−6.34 × 10^0	−1.64	4.15 × 10^3	0.99	300–1250
H + methylphenoxy	−1.55 × 10^1	1.63	3.34 × 10^3	0.99	300–2000
CH3 + phenoxy	−1.72 × 10^1	1.92	1.96 × 10^3	0.99	300–2000
CO + C6H8	5.33 × 10^1	−17.9	6.92 × 10^4	0.99	1000–2000

---

As was also found for the O(³P) + benzene reaction, at low temperatures the main reaction channel leads to the formation of C₇H₈O isomers through collisional stabilization. The main C₇H₈O isomers are the toluene oxide wells ¹W1, ¹W2, and ¹W3, and at the higher temperatures, the methyl cyclohexadienones ¹W15, ¹W16, and ¹W17 (see Fig. 1b). As the temperature increases, the reaction channels leading to the formation of the H and CH₃ radicals and their co-products, the methylphenoxy and phenoxy radicals, respectively, increase in relevance. In particular, the H-loss channels become dominant at combustion relevant temperatures, while the CH₃ channel BF is essentially temperature independent. It is also interesting to note that the channel leading to the formation of CO and methylcyclopentadiene is minor (<0.01) in the whole range of investigated conditions and is not reported in Fig. 7. The loss of relevance of this channel with respect to what was observed under CMB conditions is consistent with what was found for the O(³P) + benzene reaction⁹ and is determined by the prevalence of collisional stabilization at 1 atm in the low-temperature conditions in which it may be competitive with the homolytic decomposition channels.

5. Discussion

Little was known about the dynamics of the O(³P) + toluene reaction before the present study. An early dynamical study by Sloane³⁰ used effusive beams of reactants in a near single-collision environment and fixed mass spectrometer detector at E_c ≈ 4 kJ mol⁻¹. Products, detected via their appearance potentials using low-energy electrons, were observed at m/z = 108, 106, and 80 and were attributed to an addition complex (m/z = 108), benzaldehyde (m/z = 106), and an open-chain olefin (CH₂(CH)₄CH₂). Clearly, the stabilized adduct at m/z = 108 in this early study may have been from secondary collisions. No mass 107 product corresponding to the H-displacement channel was reported. Those results were found to be in poor agreement with the conclusions of a later CMB study by Baseman et al.³¹ with a rotating MS detector and TOF analysis at E_c = 38.5 kJ mol⁻¹, using a supersonic O atom beam and performed under truly single-collision conditions. That CMB study³¹ observed as primary products the CH₃ + phenoxy and H + cresoxy, with the CH₃ channel concluded to be dominant (BF = 0.99). Unfortunately, the detection of phenoxy (CH₃ channel) was severely hampered by the strong dissociative ionization to m/z = 65 of the toluene reactant under the experimental conditions of hard (200 eV) electron ionization. Regarding the H-abstraction channel, Hoffman et al.²⁵ investigated the title reaction behind incident shock waves at elevated temperatures (1100–1300 K) and estimated its upper limit to be about 10%.

By combining experimental evidence and a theoretical description, a clear picture of the reaction mechanism emerges. Firstly, the electrophilic oxygen atom can attack the ring on the carbon in the ortho, meta, and para positions (with respect to the carbon atom bonded to the CH₃ group), and in the ipso position, that is on the carbon bonded to the CH₃ group. According to the theoretical calculations, the energy of the minimum of the van der Waals interaction in the entrance channel, the entrance barrier, the minimum of the diradical intermediate, the exit barrier (toward H-elimination and CH₃-elimination), and the energy of the products, are all lowest for the ortho and ipso attack (see Fig. 1a). This is not surprising due to the inductive effect of the CH₃ group. Hence, theory and physical intuition indicate that the most probable methylphenoxy isomer co-product of the H-displacement channel on the triplet PES is ortho-methylphenoxy (channel 1a). Our experimental results (extent of 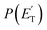distribution) do not allow distinguishing among the three methylphenoxy isomers because of the similar reaction enthalpies associated with channels 1a, 1a′, and 1a′′, which are within 6 kJ mol⁻¹ at the CCSD(T)/CBS level. The 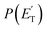distribution for the methylphenoxy + H channel peaks at 25 kJ mol⁻¹ (see Fig. 5) (with an average fraction of the total available energy released in translation 〈f_T〉 = 0.33, referring to the expected more abundant isomer, o-methylphenoxy) and this reflects a significant exit potential barrier. Indeed, this is corroborated by the calculated exit barrier on the triplet PES (Fig. 1a) (48 kJ mol⁻¹ for the dominant o-isomer, with respect to the products). Similarly, calculations also find a very significant exit potential barrier (69 kJ mol⁻¹ with respect to the products) on the triplet PES for the CH₃ elimination. The fact that 〈f_T〉 is only 0.18 (less than for the H-displacement) indicates that product internal excitation is 82% for the phenoxy + CH₃ products, and this high value could be due to the fact that CH₃ can carry internal excitation while the H atom cannot.

The entrance barrier for ipso attack is similar (lower by only 0.4 kJ mol⁻¹ at the CASPT2 level) to that for ortho attack and the stability of the triplet diradical intermediates is also very similar (−63.2 vs. −61.9 kJ mol⁻¹). In addition, the exit barrier for CH₃ elimination is significantly lower than for H displacement (−30.5 vs. −20.1 kJ mol⁻¹ from the ³W2 and ³W6 wells, respectively) and, moreover, the exothermicity of the CH₃-forming channel is significantly larger (−99.6 kJ mol⁻¹) than for the H-displacement channel (−68.2 kJ mol⁻¹). This suggests that the contribution of the CH₃-elimination channel with respect to the H-displacement channel on the triplet PES may well be comparable or even larger.

The entrance barriers of 10.7 kJ mol⁻¹ for ortho attack, and 10.3 kJ mol⁻¹ for ipso attack, calculated at the CASPT2 level, are lower than the barriers of 15.9 (T1) and 18.8 (T2) kJ mol⁻¹ calculated at the CASPT2 level for the related O(³P) + benzene reaction.⁹ This is in line with the room temperature global rate constant for O(³P) + toluene (k_298K = 7.14 × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹) being experimentally about 4.5 times larger than for O(³P) + benzene (k_298K = 1.58 × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹).

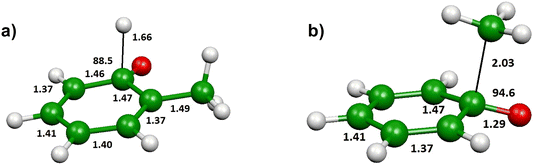
The shape of the T(θ) functions provides information on the reaction micromechanism. For instance, the pronounced sideways peaked T(θ) observed for both the H- and CH₃-forming channels (see Fig. 5a) on the triplet PES is related to the geometry of the decomposing transition states⁶⁴ and is nicely corroborated by the results of the electronic structure calculations. Fig. 8a depicts the calculated geometry of the exit transition state (³TS6) in the case of the most favorable oxygen attack (ortho). The H atom is released with the O–C–H angle being 88.5^o, meaning that the H atom is emitted orthogonally to the molecular plane, which is perfectly in line with the sideways shape of the derived T(θ) function for the C₇H₆O product (see Fig. 5). Notably, similar sideways scattering dynamics were also observed for the H-displacement channel in the reaction O(³P) + 1,3-butadiene.¹²

Fig. 8 (a) Optimized geometry of the transition state ³TS6 on the triplet PES leading via loss of H in the ortho position to formation of o-methylphenoxy + H products. (b) Optimized transition state ³TS2 on the triplet PES leading, via loss of CH₃ after ipso addition of the O atom, to phenoxy + CH₃ products. Bond lengths in Å, angles in degrees.

Fig. 8b shows the calculated geometry of the transition state ³TS2 for the CH₃ elimination on the triplet PES. As in case of the H-displacement channel, the CH₃ radical from the O(³P) + toluene reaction is emitted at the transition state orthogonally to the plane of the intermediate since the angle CH₃–C–O is 94.6°. Also in this case, this nicely correlated with the sideways shape of the derived T(θ) function for the C₆H₅O product (see Fig. 5).

The comparison of the CM angular distributions for the phenoxy product from the H-displacement channels 1a and 1b suggests different dynamics for the O(³P) and O(¹D) reactions. As mentioned above, the backward–forward symmetric T(θ) for the O(³P) reaction exhibits a clear sideways pattern, suggesting that the reaction occurs on the triplet PES via a long-lived complex mechanism and that the H atom is ejected nearly orthogonally to the plane of the ring at the exit transition state ³TS6 (see Fig. 1a and 8a).^64,66 Conversely, the H-displacement channel 1a for O(³P) + toluene via ISC exhibits similar dynamics to channel 1b, and with a very low 〈f_T〉 of 0.12 as expected for the barrierless decomposition of the singlet intermediate to H + methylphenoxy. The fact that for the O(¹D) H-displacement mechanism the 〈f_T〉 is not very small (0.22), even though there is not a barrier in the exit channel, indicates that part of the electronic energy of the O(¹D) atom is channeled into product translational energy.

A comment should be made about the 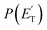distribution for the H- and CH₃-loss channels on the triplet PES. We notice that the 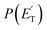for the methylphenoxy + H channel peaks at about 25 kJ mol⁻¹, while that for phenoxy + CH₃ peaks at about 19 kJ mol⁻¹. Notably, the height of the exit barrier (with respect to the products) is about 48 kJ mol⁻¹ and 69 kJ mol⁻¹ for the H- and CH₃-loss channels, respectively (see Fig. 1a). These high values indicate that the 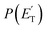should peak away from zero and that a significant fraction of the total available energy should be released as product translational energy.⁶⁴ Indeed, about 33% and 18%, respectively, of the total available energy goes into translational motion of the two co-products. This also indicates that about 67% and 82% of the energy is channeled into product internal excitation. We note that channel 3a leading to CO + C₆H₈ (methylcyclopentadiene) is minor (BF = 0.09 ± 0.05) in the reaction with O(³P), while it is the main channel in the O(¹D) reaction (BF = 0.54 ± 0.27). In contrast, in the reactions of O(³P,¹D) + benzene,⁹ the ring-contraction channels were found to be significant in both reactions of O(³P) (BF = 0.32) and O(¹D) (BF = 0.96). Since in the toluene reaction there is an additional competitive channel, the one associated with CH₃ elimination, we can conclude that the CH₃ substitution has the effect of protecting the aromatic ring, making its degradation less easy compared to the case of the O(³P) + benzene reaction.

The extent of ISC is, instead, very similar in the two cases, being 57% ± 16% for O(³P) + toluene and 52% ± 16% for O(³P) + benzene.⁹

Finally, it is interesting to observe that the BFs determined experimentally under CMB conditions are in good agreement with those theoretically estimated (see Table 1). This supports the predictive capability of the theoretical calculations of the channel-specific rate constants for the O(³P) + toluene reaction performed under thermal conditions. The only significant disagreement between experiments and computational estimates concerns the BF of the H + methylphenoxy channel on the triplet PES, which differs by almost a factor of two (see Table 1). The theoretical overestimate of the BF of the H-displacement channels with respect to CMB measurements (0.34 vs. 0.19) is, however, consistent with what was found in several other systems we investigated, such as O(³P) + propene⁶ and our recent study of O(³P) + 1,3 butadiene,¹² where the difference in BFs for the H channels was slightly larger than a factor of two. Among the possible causes for this disagreement, we believe that non-ergodic effects may be playing an important role, as ISC may take place before the C–H bonds of the entrance site are thermalized. A second cause is uncertainties in the calculations, as the reactivity of this system is significantly influenced by both the relative importance of the different addition sites and by the rate of ISC, whose determination is complicated by the multireference nature of the processes and the approximations on which NA-TST is based.

6. Conclusions

Although in past decades the O(³P) + toluene reaction had been extensively studied, the characterization of its detailed mechanism and dynamics, its primary product distribution and role of ISC, remained to be done. In the present work, the O(³P) + toluene reaction dynamics were investigated experimentally using the CMB scattering method at E_c = 34.7 kJ mol⁻¹, and the primary products and their BFs determined. The experimental results were analyzed with the support of high-level quantum chemical calculations of the underlying triplet/singlet PESs and statistical (RRKM/ME) simulations on these PESs with nonadiabatic effects (ISC) considered. The combined experimental/theoretical investigation of the O(³P) reaction with the simplest alkylbenzene adds to our recent effort to characterize the mechanism for the reactions of O(³P) with C2, C3, and C4 unsaturated hydrocarbons,^{1–3,5–7,12,15–20} with benzene,^8,9 pyridine,¹¹ and the simplest unsaturated nitriles.^67,68 It is also a gateway towards the investigation of other O(³P) reactions with more complex aromatics, including the prototype of PAHs, naphthalene.

Summarizing, the reaction mechanism of the O(³P) + toluene reaction sees the initial electrophilic attack of the O atom to the π-system of the aromatic ring (on a C atom in the ipso, ortho, meta, and para positions) on both the lowest triplet T1(³A′) and T2(³A′′) PESs, with formation of the corresponding triplet diradical intermediates. Each of these intermediates, under single-collision conditions can undergo competitive C–H and C–CH₃ bond cleavage on the ground triplet (T1) PES ³A′ and intersystem crossing at the MECPs for the T1/S1 and T2/S0 PESs to singlet toluene oxides isomers. Instead, on the singlet PES, competition between the following three reaction channels is dominant: decomposition to methyl + phenoxy radicals, decomposition with H loss to form the methylphenoxy radical, and decomposition to CO + methylcyclopentadiene (see Fig. 1b). The BFs of these product channels were determined theoretically under the CMB conditions and also as a function of temperature (from 300 to 2000 K) at 1 atm of pressure.

We have found that, under single-collision conditions at E_c = 34.7 kJ mol⁻¹, the reactive interaction of O(³P) with toluene mainly produces the radical channels phenoxy + CH₃ (overall BF = 0.69 ± 0.14) and methylphenoxy + H (overall BF = 0.22 ± 0.07), but it can also break apart the aromatic ring producing a small amount of methylcyclopentadiene + CO (BF = 0.09 ± 0.05) via ISC to the singlet PES. Because some of the observed products can only be formed via ISC, we have inferred the extent of ISC from the product BFs. Our data suggest that ISC is indeed highly relevant, accounting for 57 ± 16% of the product yield at the experimental E_c. It should be noted that this value is similar to that (52 ± 16%) observed in the reaction O(³P) + benzene at comparable E_c.⁹ As summarized in Table 1, experimental and theoretical BFs are in reasonable agreement, as well as the extent of ISC (experimentally 57 ± 16% and theoretically 50%). Significant differences between experimental and statistical BFs are mainly limited to the H-displacement channel occurring adiabatically on the triplet PES, a process known for its non-fully statistical character.

An important result produced by the combined experimental/theoretical study of the complex mechanism of the O(³P) + toluene reaction is that, once the theoretical statistical approach and description are reasonably validated by a satisfactory and encouraging comparison with the CMB experimental results, theory could be used to generate channel-specific rate constants as a function of temperature and pressure of interest in various media. In future work, we will apply the same approach to other reactions involving aromatic compounds with other substituents to verify their possible protective role toward the aromaticity of the reactants.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Work supported by MUR through PRIN 2017 Prot. 2017PJ5XXX (MAGIC DUST). We acknowledge financial support under the National Recovery and Resilience Plan (NRRP), Mission 4, Component 2, Investment 1.1, Call for tender No. 104 published on 02.02.2022 by the Italian Ministry of University and Research (MUR), funded by the European Union – NextGenerationEU – Project Title 20227W5CLJ Biomass gasification for hydrogen production (Bio4H2) – CUP J53D23001970006 – Grant Assignment Decree No. 961 adopted on 30.06.2023 by the Italian Ministry of University and Research (MUR) and Call for tender No. 1409 published on 14.09.2022 by the Italian Ministry of University and Research (MUR), funded by the European Union – NextGenerationEU – Project Title P20223H8CK Degradation of space-technology polymers by thermospheric oxygen atoms and ions: an exploration of the reaction mechanisms at an atomistic level (ThermOPoly) – CUP J53D23014440001 – Grant Assignment Decree No. 1386 adopted on 01.09.2023 by the Italian Ministry of University and Research (MUR).

References

1. P. Casavecchia, G. Capozza, E. Segoloni, F. Leonori, N. Balucani and G. G. Volpi, J. Phys. Chem. A, 2005, 109, 3527–3530.
2. P. Casavecchia, F. Leonori, N. Balucani, R. Petrucci, G. Capozza and E. Segoloni, Phys. Chem. Chem. Phys., 2009, 11, 46–65.
3. B. Fu, Y.-C. Han, J. M. Bowman, L. Angelucci, N. Balucani, F. Leonori and P. Casavecchia, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9733–9738.
4. C. A. Taatjes, D. L. Osborn, T. Selby, G. Meloni, A. J. Trevitt, E. Epifanovsky, A. I. Krylov, B. Sirjean, E. Danes and H. Wang, J. Phys. Chem. A, 2010, 114, 3355–3370.
5. P. Casavecchia, F. Leonori and N. Balucani, Int. Rev. Phys. Chem., 2015, 34, 161–204.
6. F. Leonori, N. Balucani, V. Nevrly, A. Bergeat, S. Falcinelli, G. Vanuzzo, P. Casavecchia and C. Cavallotti, J. Phys. Chem. C, 2015, 119, 14632–14653.
7. A. Caracciolo, G. Vanuzzo, N. Balucani, D. Stranges, P. Casavecchia, L. Pratali Maffei and C. Cavallotti, J. Phys. Chem. A, 2019, 123, 9934–9956.
8. C. Cavallotti, C. De Falco, L. P. Maffei, A. Caracciolo, G. Vanuzzo, N. Balucani and P. Casavecchia, J. Phys. Chem. Lett., 2020, 11, 9621–9628.
9. G. Vanuzzo, A. Caracciolo, T. K. Minton, N. Balucani, P. Casavecchia, C. de Falco, A. Baggioli and C. Cavallotti, J. Phys. Chem. A, 2021, 125, 8434–8453.
10. K. Ramasesha, J. D. Savee, J. Zádor and D. L. Osborn, J. Phys. Chem. A, 2021, 125, 9785–9801.
11. P. Recio, S. Alessandrini, G. Vanuzzo, G. Pannacci, A. Baggioli, D. Marchione, A. Caracciolo, V. J. Murray, P. Casavecchia, N. Balucani, C. Cavallotti, C. Puzzarini and V. Barone, Nat. Chem., 2022, 14, 1405–1412.
12. C. Cavallotti, A. Della Libera, P. Recio, A. Caracciolo, N. Balucani and P. Casavecchia, Faraday Discuss., 2022, 238, 161–182.
13. S. H. Lee, W. K. Chen and W. J. Huang, J. Chem. Phys., 2009, 130, 054301.
14. N. Balucani, F. Leonori, P. Casavecchia, B. Fu and J. M. Bowman, J. Phys. Chem. A, 2015, 119, 12498–12511.
15. F. Leonori, N. Balucani, G. Capozza, E. Segoloni, G. G. Volpi and P. Casavecchia, Phys. Chem. Chem. Phys., 2014, 16, 10008–10022.
16. G. Vanuzzo, N. Balucani, F. Leonori, D. Stranges, V. Nevrly, S. Falcinelli, A. Bergeat, P. Casavecchia and C. Cavallotti, J. Phys. Chem. A, 2016, 120, 4603–4618.
17. I. Gimondi, C. Cavallotti, G. Vanuzzo, N. Balucani and P. Casavecchia, J. Phys. Chem. A, 2016, 120, 4619–4633.
18. F. Leonori, A. Occhiogrosso, N. Balucani, A. Bucci, R. Petrucci and P. Casavecchia, J. Phys. Chem. Lett., 2012, 3, 75–80.
19. A. Caracciolo, G. Vanuzzo, N. Balucani, D. Stranges, P. Casavecchia, L. Pratali Maffei and C. Cavallotti, J. Phys. Chem. A, 2019, 123, 9934–9956.
20. A. Caracciolo, G. Vanuzzo, N. Balucani, D. Stranges, S. Tanteri, C. Cavallotti and P. Casavecchia, Chin. J. Chem. Phys., 2019, 32, 113–122.
21. G. R. H. Jones and R. J. Cvetanović, Can. J. Chem., 1961, 39, 2444–2451.
22. R. Atkinson and J. N. Pitts, Chem. Phys. Lett., 1979, 63, 485–489.
23. J. M. Nicovich, C. A. Gump and A. R. Ravishankara, J. Phys. Chem., 1982, 86, 1684–1690.
24. M. Tappe, V. Schliephake and H. G. Wagner, Z. Phys. Chem., 1989, 162, 129–145.
25. A. Hoffmann, M. Klatt and H. Gg. Wagner, Z. Phys. Chem., 1990, 168, 1–12.
26. K. Brezinsky, Prog. Energy Combust. Sci., 1986, 12, 1–24.
27. J. L. Emdee, K. Brezinsky and I. Glassman, J. Phys. Chem., 1992, 96, 2151–2161.
28. M. Pelucchi, C. Cavallotti, T. Faravelli and S. J. Klippenstein, Phys. Chem. Chem. Phys., 2018, 20, 10607–10627.
29. M. Derudi, D. Polino and C. Cavallotti, Phys. Chem. Chem. Phys., 2011, 13, 21308–21318.
30. T. M. Sloane, J. Chem. Phys., 1977, 67, 2267–2274.
31. R. J. Baseman, R. J. Buss, P. Casavecchia and Y. T. Lee, J. Am. Chem. Soc., 1984, 106, 4108–4111.
32. M. Alagia, N. Balucani, P. Casavecchia, D. Stranges and G. G. Volpi, J. Chem. Soc., Faraday Trans., 1995, 91, 575–596.
33. N. Balucani, G. Capozza, F. Leonori, E. Segoloni and P. Casavecchia, Int. Rev. Phys. Chem., 2006, 25, 109–163.
34. M. Alagia, V. Aquilanti, D. Ascenzi, N. Balucani, D. Cappelletti, L. Cartechini, P. Casavecchia, F. Pirani, G. Sanchini and G. G. Volpi, Isr. J. Chem., 1997, 37, 329–342.
35. A. Troiani, M. Rosi, S. Garzoli, C. Salvitti and G. de Petris, Int. J. Mass Spectrom., 2019, 436, 18–22.
36. A. Troiani, M. Rosi, C. Salvitti and G. de Petris, ChemPhysChem, 2014, 15, 2723–2731.
37. N. Balucani, D. Skouteris, C. Ceccarelli, C. Codella, S. Falcinelli and M. Rosi, Mol. Astrophys., 2018, 13, 30.
38. C. Salvitti, F. Pepi, A. Troiani, M. Rosi and G. de Petris, Molecules, 2023, 28, 132.
39. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
40. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
41. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
42. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294.
43. M. J. Frish, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265 , and references therein..
44. C. Gonzales and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154.
45. C. Gonzales and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523.
46. C. Cavallotti, M. Pelucchi, Y. Georgievskii and S. J. Klippenstein, J. Chem. Theory Comput., 2019, 15, 1122–1145.
47. R. J. Bartlett, Annu. Rev. Phys. Chem., 1981, 32, 359.
48. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479.
49. J. Olsen, P. Jorgensen, H. Koch, A. Balkova and R. J. Bartlett, J. Chem. Phys., 1996, 104, 8007.
50. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007.
51. D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1993, 98, 1358.
52. R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796.
53. J. M. Martin, Chem. Phys. Lett., 1996, 259, 669.
54. Y. Georgievskii and S. J. Klippenstein, J. Phys. Chem. A, 2003, 107, 9776–9781.
55. L. Pratali Maffei, A. Della Libera and C. Cavallotti, 2023, submitted.
56. A. Barbato, C. Seghi and C. Cavallotti, J. Chem. Phys., 2009, 130, 074108.
57. J. N. Harvey, Phys. Chem. Chem. Phys., 2007, 9, 331–343.
58. A. W. Jasper, Int. J. Chem. Kinet., 2020, 52, 387–402.
59. M. J. Frisch, et al., Gaussian 09, Revision D.01, 2013.
60. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242.
61. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller III, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107.
62. MOLEKEL 4.3, P. Flükiger, H. P. Lüthi, S. Portmann and J. Weber, Swiss Center for Scientific Computing, Manno, Switzerland, 2000–2002.
63. S. Portmann and H. P. Lüthi, Chimia, 2000, 54, 766.
64. W. B. Miller, S. A. Safron and D. R. Herschbach, Discuss. Faraday Soc., 1967, 44, 108–123.
65. A. M. Schmoltner, P. M. Chu and Y. T. Lee, J. Chem. Phys., 1989, 91, 5365–5373.
66. G. N. Robinson, R. E. Continetti and Y. T. Lee, J. Chem. Phys., 1990, 92, 275.
67. P. Liang, E. V. F. de Aragão, G. Pannacci, G. Vanuzzo, D. Marchione, P. Recio, D. Stranges, P. Casavecchia, N. Faginas Lago, L. Mancini, M. Rosi and N. Balucani, J. Phys. Chem. A, 2023, 127, 685–703.
68. G. Pannacci, L. Mancini, G. Vanuzzo, P. Liang, D. Marchione, M. Rosi, P. Casavecchia and N. Balucani, Phys. Chem. Chem. Phys., 2023, 25, 20194–20211.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3fd00181d

---