The role of density functional theory in decoding the complexities of hydrogen embrittlement in steels

Abstract

Hydrogen (H) is considered as the key element in aiding the initiated green energy transition. To facilitate this, efficient and durable technologies need to be developed for the generation, storage, transportation, and use of H. All these value chain stages require materials that can withstand continuous exposure to H. Once absorbed, H can eventually concentrate to critical levels in a stressed microstructure, inducing specific damage mechanisms and consecutive loss of mechanical properties. This is known as hydrogen embrittlement (HE). Being one of the most significant structural material types, steels are widely used throughout the H value chain. They can suffer from HE, and numerous attempts are made towards understanding and mitigating this complex phenomenon. While originating at a size scale of atoms, HE acts on multiple spatio-temporal scales, and combined efforts of experimental and modelling techniques are needed to deal with it. This perspective is devoted to assimilating the knowledge that can be generated by density functional theory (DFT) methods to understand interactions between H and iron-based materials, and to promote finding solutions to HE in metallic materials in general. We aim to provide a comprehensive understanding of the properties calculated using DFT that can help advance finding novel H-resistant high-strength materials that facilitate the green shift at sufficient performance levels to meet the growing future needs.

---

1. Introduction

The growing energy demands, and awareness of environmental pollution caused by the burning of conventional fossil fuels, have contributed to the technological development of alternative fuels and processes. As a sustainable fuel, hydrogen (H) is one of the top priorities in this scenario as it can be generated via a ‘green’ route, without harming the environment, utilizing solar energy through processes such as photocatalysis.¹ In effect, H as a feedstock can revolutionise key industries such as ammonia and steel production, as it can replace metallurgical coal, thus largely reducing CO₂ emissions. It can also help reduce the greenhouse gas emissions from the transportation sector.² However, although H is the most promising fuel towards decarbonising the planet, the cycle of producing green H from water electrolysis, transportation, and storage come with their own challenges.³ When H is replacing existing energy resources on a larger scale, it must be produced, stored, transported, and used in a safe, reliable, and economical manner. For the H value chain to be sustainable and reliable over time, all above components should be taken care of, and particularly infrastructure should be developed, i.e., pipelines and storage tanks, utilising appropriate structural materials.¹ These are most often built from different steel grades, like austenitic stainless steels and low-alloyed carbon steels.

Exposure to hydrogen can induce severe weakening of mechanical properties, such as plasticity weakening as H being the smallest atom on earth can easily enter the material as adsorbates on the surfaces, diffuse into the bulk, once stabilized inside the crystal structure can reduce the strength, ductility, and fracture toughness,⁴ eventually damaging the material. Hydrogen embrittlement (HE) is one of the severe hydrogen damage mechanisms that affects varied materials performance, and is a term most often associated with metallic materials like steels and their welds, as it can cause a sudden and unpredictable failure of a structure particularly the ones with high strength steels when used as structural materials and are in interaction with H.^5–15 Different materials and processes are involved in the hydrogen value chain, and the most important among them are the hydrogen production, distribution and storage¹⁶ as well as applications of hydrogen in various industries. These steps are mutually dependent and involve materials that will be exposed to H₂ over longer periods of time.

1.1. Production

The production of hydrogen is carried out by different methods and the most prevalent ones are steam-methane reforming and water splitting by methods such as electro and/or photocatalysis. A significant amount of research is being carried out to generate H in “greener” ways, such as thermochemical conversion of biomass into gas or liquids and to separate hydrogen from biological processes using microbes. Also, biogas, ethanol and natural gas are common feedstocks in H production processes.¹⁷ Modelling tools such as DFT go with experimental research to aid H production through sustainable and renewable routes as optimization of materials and processes is a key factor in catalytic reactions involved in H production.

1.2. Storage

The challenge in storage is to increase the efficiency and methods being used include storing H in different forms such as high-pressure gas phase, liquid storage at low temperatures, or solid storage through physical or chemical absorption. The materials commonly used in the high-pressure gaseous storage method include stainless steels and alloys such as 6061 and 7000 grads and Cr–Mo alloys susceptible to H-induced damage.¹⁸ For the solid storage, using metal hydrides, a bond will be formed between H molecules and metals in ground state temperature and pressure and hence this a safer method as H gas leakage or spontaneous blowing up of the container can be eliminated.

1.3. Transport

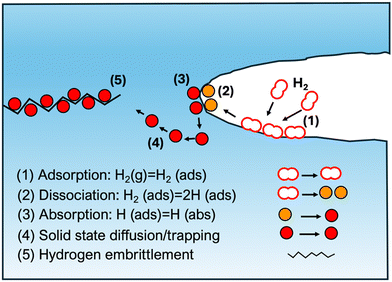
H is transported through pipelines and ferritic steels with different microstructures are utilized for this purpose, as microstructures are proposed to have an influence on the behaviour of the material concerned. Some of the compositions include pearlite, polygonal and quasi-polygonal ferrite, bainite and martensite. When it comes to the HE resistance of pipeline steels, the benchmark is to achieve a balance between the strength and the HE resistance capacity. Different strategies such as mixing H and methane or adding low mounts of carbon monoxide or carbon dioxide has shown to reduce the degradation effect of H and this is attributed to the reduced kinetics of H gas, at the surfaces owing to the presence of these gases.¹⁹

H may impact mechanical properties in several ways, once gotten into the metal-matrix in atomic form, for example by forming H molecules within internal defects, generating localized pressure, and eventually causing the material to crack.¹⁵Fig. 1 illustrates different distinctive steps of HE phenomenon. In the case of steels, a more organic process is the immature failure mechanism, wherein, H gets inside during formation and diffuses through the material to form higher concentrations building up local stress and leads to low stress brittle failure.¹⁵ A comprehensive understanding of H diffusion and embrittlement in materials, and specifically in atomistically complex-structured steels require combined investigations employing experimental techniques as well as modelling and simulation in different time and length scales to connect macroscopic and microscopic properties.⁵ Maybe the most relevant experimental methods for providing input for atomistic modelling is the application of cryo-APT (atom probe tomography) to provide elemental mapping at nearly atomic resolution.^20,21

Fig. 1 Introduction of hydrogen to materials, and the steps leading to hydrogen embrittlement.

Over the years, various modelling techniques such as quantum mechanical density functional theory (DFT), classical and ab initio molecular dynamics (MD), and probabilistic strategies such as Monte Carlo (MC) methods^6–14 have been employed to assess the effects of H in steels, that include but not limited to the complex problem of HE. Different MD approaches have shed light into the diffusion aspects of H in dislocations, and this happens mostly during transportation and storage processes.¹⁴ Interestingly, tackling HE by employing available first principles methods such as full-potential linearized augmented planewave method (FLAPW) has been a centre of interest in the ab initio researcher community.¹⁰ The initial investigations have been focusing on the bulk metals, but over the years, with the increase in computational power, accurate first principles calculations were carried out considering structures with more defect configurations such as grain boundaries (GB), vacancy defects and impurities, dislocations, surface, and interfaces.¹¹ Most importantly, the quantum mechanics-based methods such as DFT gained popularity due to their accuracy owing to the absence of empirical parameters. DFT, developed in its current form by W. Kohn and others in 1964 to deal with the complex electronic properties is based on the ground state electron density, which can be described as a function of only 3 spatial coordinates. In principle, it is an exact theory, governed by quantum mechanical laws that can accurately describe many atoms, many electron systems.²² During the past decades, DFT aided by the increasing supercomputing powers has emerged as a prime tool, not only in providing fundamental understanding of material properties but also in material design for future technologies such as that in energy sector. In this regard, we have successfully integrated DFT calculations with experimental investigations for calculating properties of steels and Fe-based materials. The investigations include but are not limited to the energetics of defect formation, non-metallic inclusions inherent to steels, and the role played by different exchange correlation functionals in accurately describing electronic properties.^23–29

Even though DFT finds it applications in varied areas of material science, diffusion and HE driven topics in steels are two areas in which it has tremendous impact in explaining the atomistic scale phenomena. This is mainly because diffusion of H in metals is often facilitated by point defects as it is much easier for H to occupy a vacancy site³⁰ than exchanging places with a lattice atom. Another possibility is an interstitial mechanism, wherein a self-interstitial can easily kick an impurity from a substitutional site and then migrate through an interstitial channel. However, interstitials are less abundant than vacancies as they have high formation energies and are less likely to form at ground state. Therefore, it is necessary to understand the formation and migration of native point defects and interstitials and the diffusion barriers that govern the energy of hopping of H impurities. DFT provides an efficient method to calculate the saddle point by employing postprocessing tools such as nudged elastic band (NEB) method, and by calculating total energy surfaces.³¹ Thanks to ab initio investigations dating back to the early 2000s, a clear idea of H – vacancy interactions in α-Fe were revealed¹² and those paved the fundamental knowledge for such advanced studies. The constructive interaction between H induced vacancy formation and further growth and clustering of H–V defect complexes cause mechanical degradation and the atomic scale interactions explained by DFT studies have been pivotal in this understanding.³² When it comes to the primary crystal structures of Fe (the ground state magnetic bcc and elevated temperature paramagnetic fcc phase³³), extensive DFT investigations has helped to understand the preference of H interstitial sites and trapping possibilities in presence of dopants and impurities.^13,34 Reduction of local plasticity and decohesion are two other important mechanisms that DFT has provided deep insights and tremendous impact.³⁵ Another prominent situation is at the surfaces of Fe, separation of H molecules into H atoms upon adsorption under favourable chemical conditions can occur. These atomic H can diffuse into the bulk regions, and DFT calculations based on the energetics of these phenomena can help to understand not only HE but also H storage and transportation.³⁶ Phase instability of the ferritic phase and ductile-to-brittle transition of the ferrite phase are two mechanisms that lead the way to HE. Even though HE continues to remain an attractive research problem due to the complexity to resolve it at high spatiotemporal resolutions, operando synchrotron experiments, when combined with DFT calculations can provide knowledge about the quasi-hydride formation and the possible phase transformation that can occur.³⁷ In this short perspective, we attempt to consolidate the scientific efforts being undertaken over the years to tackle HE by employing first principles DFT calculations. We hope that our article will serve as a guide to the vast scientific community working to solve the complex problem of HE, focussing especially on the beginners in this field, who aim to perform independent DFT calculations and/or investigations covering multiple length and time scales. After the brief introduction, the article is organized into three main topics (Sections 2–4). The first part deals with the methodology of DFT calculations, the third section will describe the extant knowledge base followed by a conclusion.

2. Computational methodology and the properties investigated with DFT

Let us have a look at the techniques and formalisms employed in ab initio studies so far as state-of-the-art DFT has been successfully employed to model various aspects of materials in general and is also used for modelling of H induced degradation phenomena in iron and steels.²² The plane wave basis and pseudopotential formalism are especially advantageous to calculate the defect properties of transition metals, where localized electronic states are present. To deal with the electronic exchange and correlations, generalized gradient approximation (GGA), which is a systematic improvement over local density approximation (LDA), proved to be accurate for steels, as it correctly predicts the bcc ferromagnetic phase as the ground state of iron at zero pressure compared to LDA.³⁸ Since the main constituent of steel is Fe and its alloys, the first principles calculations have been traditionally carried out using the standard exchange correlation functionals such as GGA. This is because the ferromagnetic bcc ground state for Fe is obtained by using GGA while the local density approximation (LDA) failed to describe the magnetic properties accurately.³⁹ However, when there are alloying elements present in Fe, such as N, approximations beyond GGA such as meta-GGA or GGA+U should be evoked to predict the properties in accurate detail.²⁵ For periodic DFT calculations, the accuracy of plane wave basis sets should be determined by converged values of kinetic energy cut off, as the electronic wave functions are determined by a liner combination of a set of basic functions. This basis set convergence is crucial to arrive at accurate forces during optimization. One of the foremost ingredients of a DFT calculation is the pseudopotentials, which describes the electron–ion interactions, and there are different methods available to construct various flavours of pseudopotentials, depends on the properties of the system at hand. The accuracy and quality of a pseudopotential is dependent on how well the calculated results match with accurate all electron calculations. Nevertheless, the possible inaccuracy that can creep in, owing to the nonlinear nature of exchange interactions of the valence and core electrons, is handled through appropriate core corrections. Having described the basics of a DFT calculation, the most important tool is the computational code, that should be chosen based on the basis sets, pseudo potentials, exchange–correlation functionals and algorithms to solve the Schrodinger equation. There exist a good number of first principles software packages in the public domain as well as those that are available for a small fee for the academic community.⁴⁰ When it comes to metals and associated degradation mechanisms, some of the important properties includes formation energy of vacancies with and without H and H-monovacancy complexes.⁴¹ H effects on vacancy clusterisation and potential vacancy contributions to HE and H-enhanced vacancy formation in alpha-Fe, as suggested in experiments have been elucidated and demonstrated evidence of H-enhanced anisotropic vacancy clusterisation.¹² DFT can help to understand the increasing concentration of vacancies and other defects by changing the size of the supercells and thereby calculating the formation energies of vacancies and vacancy complexes, which provides valuable information not directly deducible from experiments.⁴²

Once H enters the bulk steel material through diffusion, it accumulates inside the structure, eventually leading predominantly to two mechanisms such as HELP (hydrogen enhanced localized plasticity) and HEDE (hydrogen enhanced decohesion). The former reduces the activation energy for dislocation, increasing the formation of deformed localized regions, and promotes crack formation.^43,44 The latter increases the atomic decohesion, paving the way for cleavage along grain boundaries.^45,46 The concentration of H atoms in steel matrices is related to the presence of point defects as about 5 H atoms can be trapped in ferrite and 6 in austenite steels. Alternatively, the presence of H can reduce the vacancy formation energy and vacancy concentration can be increased. However, once the number of vacancies is in thermodynamic equilibrium, the H concentration is determined by chemical potential of H and temperature. In this situation, the total amount of H consists of trapped and dissolved H in interstitial sites, and the vacancy concentration will be determined by the chemical potential of H. Kinetic Montecarlo simulations have found that the presence of vacancies hinders the H diffusion, by acting as efficient H traps at low temperatures. Therefore, by tuning the concentration of defects and impurity atoms, the extent of H accumulation in steel matrices can be controlled.^47,48 Further, the possibility of changing the number and chemical species of nearest neighbour environment can be compared with experiments such as Atom Probe Tomography (APT)⁴² and the different real world defect formation scenarios can be mimicked in atomistic scale modelling and the formation energies of H traps can be calculated.⁴⁹ The mechanisms of H deeply buried inside carbide interfaces are difficult to monitor due to the inherent complexities such as the presence of strain fields, and combining DFT studies with experiments that can map the strain fields can obtain underlying atomic information.⁵⁰

Pipelines used for transportation of H are often subjected to H induced cracking, as they are made of high-strength steels. One way to check the degradation assessment of these steels is by determining the localized magnetic flux leakage, conducted by magnetizing the steel pipe to saturation flux density and then measuring the local flux leakage induced by imperfections surface morphology.⁵¹ H when in interaction with Fe, donates an electron to the Fe-d band, and it is found that when there is a change in magnetic field in ferromagnetic materials, the H prefer to diffuse to energetically favourable locations inside the magnetic domain structure. This causes lattice strain and reduces d-orbital overlap, eventually altering the shape and d-band filling characteristics. Such structural variations lead to entropy change in the system, implying that the H concentration and magnetic properties are closely connected to each other. Therefore, it can be concluded that the strength and microstructure of pipeline steels influence the H absorption characteristics. In the presence of surface anomalies, the magnetic flux density will increase, resulting in increased H absorption, increasing the probability of H induced degradation and embrittlement.⁵² Though DFT studies are not systematically done quantifying the relation between H induced degradation and magnetic properties, this is an avenue for future explorations. This is because DFT can accurately calculate the structural changes, energetics and magnetic properties of steel in the presence of H.

For a magnetic material, spin–orbit coupling (SOC) can arise from the peculiarities of crystal field interactions. Though SOC in steel in presence of H has not been studied in detail, SOC effects are included to extract the magnetic properties of Fe in general in DFT studies. The calculations conducted by incorporating the local spin density approximation (LSDA) and (GGA) have shown that the magnetic properties of Fe in presence of alloying elements are not significantly influenced by spin–orbit coupling. It is shown that the site projected spin magnetic moments of Fe remained about 2.23 μB with and without SOC. This is attributed to the absence of Jahn–Teller distortion and orbital quenching effects. These findings are also verified by the calculated Fermi contact hyperfine fields.³⁹

Role of DFT studies in describing the physical properties of Fe are exemplary and this extends beyond the traditional ground state properties such as structural and elastic parameters, magnetism, elastic properties and phase stability to estimating vibrational free energy properties. The stability of crystal structures can be assessed by calculating the phonons, in the presence of defects or impurity atoms.²⁶ These calculations helped to understand the discrepancy between H diffusion properties calculated in theoretical and experimental studies, and the contribution of phonons to free energy at high temperatures is identified to be crucial. However, at low temperatures tunnelling assisted diffusion of H is suggested as a probable mechanism.⁵³ Even though a sophisticated DFT code is a necessity to carry out the above computations, the resulting outputs such as the energies, wave functions and electron densities need further analysis to be compared to meaningful material properties. Therefore, there are also a bunch of post processing techniques and tools available. For example, nudged elastic band (NEB) calculations^54,55 are immensely powerful in calculating the H diffusion barriers⁵⁶ and PHONOPY is an effective tool for phonon analysis.^57,58 In short, DFT has been fundamental in bringing new insights into the design of hydrogen resistant advanced high strength steels.⁴² A comprehensive list of properties that can be obtained using DFT is listed in Table 1.

Table 1 The properties and phenomena that can be calculated with DFT for H–metal interactions

Parameter or phenomenon	Inferences
Vacancy formation energy	Hydrogen enhances vacancy formation in α Fe as well as promotes hydrogen enhanced vacancy clusterisation^12
Lattice parameters and volume	Dilation of steel matrix can be identified, which is not directly accessible to experiments.^59 Can deduce mechanical properties, information about local stress/strain field and associated deformation mechanisms.
Formation energy/solution energy/dissolution energy of H	The solution energy of H at different interstitial sites in bulk, interfaces, surfaces, and grain boundaries can give idea about stability, and effects of strain, and stress, e.g. Tensile strains facilitate dissolution while compressive strains suppress it.^50 H evolution potential can be calculated as a function of H chemical potential.^37
Elastic moduli	Mechanical properties: such as ductility, plasticity, and shear stability
Electronics structure analysis (density of states and band structure)	Understand orbital hybridization^60 between alloying elements and Fe that can influence HE, as this is related to the increased/decreased metallicity of the local environment. Stronger orbital hybridization will indicate stronger binding of H with alloying elements and Fe.^60
Charge density difference analysis and Bader charge	Qualitative and quantitative evaluation of charges reveal information related to metallicity and electron transfer between Fe and H and alloying elements. From this strength of the chemical bonding can be ascertained.^60
Energy barrier from nudged elastic band (NEB) or climbing image (CI) NEB	Information about H migration at surfaces, interfaces, grain boundaries.^31 H diffusion from the surface to the bulk regions can be identified. Can identify the dopants/alloying elements that can slow down the diffusion process and prevents embrittlement.
Surface energy	H can reduce the surface energy of bcc and fcc, and this information can help to predict the change of behaviour from ductile to brittle. Basically, surface energies calculated for both relaxed and unrelaxed surfaces help to understand the energetically favourable positions and configurations.^61
Interfacial energy	Interfacial energy is calculated by considering the energies of bulk atoms, the total energy of the interface, and the surface area. This gives clear indication about whether the interface formation is energetically favourable compared to the bulk.^61
Trap escape energy	The energy needed for H to escape from a given trap to bulk Fe. Applicable when H is present at the interface and is dependent on the migration energy of H.^61
Crack-formation mechanism	The work of separation calculated from DFT, can give an idea of the excess energy needed, e.g., for the separation of two grains along the interface, and indicates the energy difference between the fractured surfaces and the interface. The calculated work of separation can serve as indication of the brittleness of the interface.^62,63
Work of separation and segregation energies	Effect of hydrogen on the reversible work for grain boundary separation in a gaseous environment can be understood. The preference of H atoms to reside at the GB or the free surface depends on its energetic preferences, and this is calculated from DFT as the Gibbs free energy. H residing at the GB embrittles it, and idea of inter-granular or trans-granular fracture can be understood from calculating the work of separation of the GB and segregation energies.^64
Binding energy of H	The H atoms influence the mobility of dislocations mobility, and it is not straightforward to calculate this value from experiments, such as in thermal desorption spectroscopy the desorption peak for screw dislocations is insignificant compared to that of edge dislocations and grain boundaries. This value is calculated using DFT based on the binding energy.^65 Further information such as configuration relationship and information about local atomic environment can be obtained. Preference of H to occupy the nearest neighbour or next-nearest neighbour position to the alloying atom gives information about the H traps that can be formed inside the steel matrix in presence of different alloying elements. These results can be correlated to experiments such as APT.
Phonon calculations	Phonon analysis can be carried out as a post-processing analysis of ground state DFT calculations.^57,58 From calculated phonon frequencies, stability of the material in presence of alloying element and/or H can be ascertained.

---

3. HE and H-steel interactions addressed with DFT

3.1. Crystallographic structures, defects and dislocations

When discussing steels, the most important phases are martensite – corresponding to the magnetic ground state body centred tetragonal structure (bct) of Fe–C, body centred cubic structure (bcc) called ferrite, and austenite – the paramagnetic face centred cubic structure (fcc), and hexagonal close packing (hcp) martensitic structure, which has a high density of stacking faults due to lattice invariant deformation accompanied by a streak in the c-axis direction. Although fcc and bcc remain the most common structures in DFT calculations, in fcc Fe, the possibility of formation of H₂ molecule is ruled out from DFT calculations, while such a possibility exists in other fcc metals.⁶⁶ Evidently, the interaction of H is also different in above lattices and DFT has been very successful and accurate in estimating that out of the two interstitial sites (octahedral and tetrahedral), tetrahedral is the most favourable for H atoms in both ferrite and martensite lattices.⁶⁷ On the other hand, in austenite, it prefers to go to octahedral site.^31,68 Bcc Fe has been a susceptible system for HE, due to the smaller atomic packing factor (0.68) compared to fcc (0.74). In addition, the proximity of atomic sites in the nearest vicinity due to the smaller interatomic spacing allows for nearest neighbour H atom to hop easily between one site to another, leading to lower solubility and higher mobilities. This can lead to faster mobility of H atom towards the surface sites as well.⁶⁹ The long-standing problem of preference of H in bcc and fcc lattices is in fact solved by DFT results, as the occupation of H at bcc octahedral sites creates an anisotropic stress, favouring a tetragonal distortion, that drives to a phase transition to the fcc lattice (see Fig. 2).⁸ However, H at the tetrahedral sites only increases volume, due to more isotropic stress distribution. Both interstitial sites are very close in energy and through total energy calculations, it is possible to ascertain their energetic stability, and it has now been widely agreed that tetrahedral sites are the most favourable H interstitial site in bcc Fe. Furthermore, the magnetic effects also play a role in the H stabilization in steel matrices as ferromagnetic to paramagnetic transition involves a change in volume of the lattices.⁸ Therefore, DFT studies are crucial in capturing these interrelated phenomena occurring at the atomic scale. Fig. 2 (from ref. 8), showing the Bains transformation due to the presence of octahedral H in bcc Fe.

Fig. 2 The lattice transformation induced by H and the relation between lattice volume and magnetism in Fe. Reproduced from ref. 8 with permission from American Physical Society, copyright 2011.

Further, in presence of alloying elements, DFT studies have shown light into the effect of chemical environment of solubility of H in host lattices. It is seen that in Fe matrices, alloying elements such as Mn and C increase the solubility owing to the induced lattice expansion. The charge density calculations have successfully revealed the effect of H atoms in affecting the bond strength of crystal lattices when they are occupied at preferred interstitial locations as depicted in Fig. 3.⁶⁰

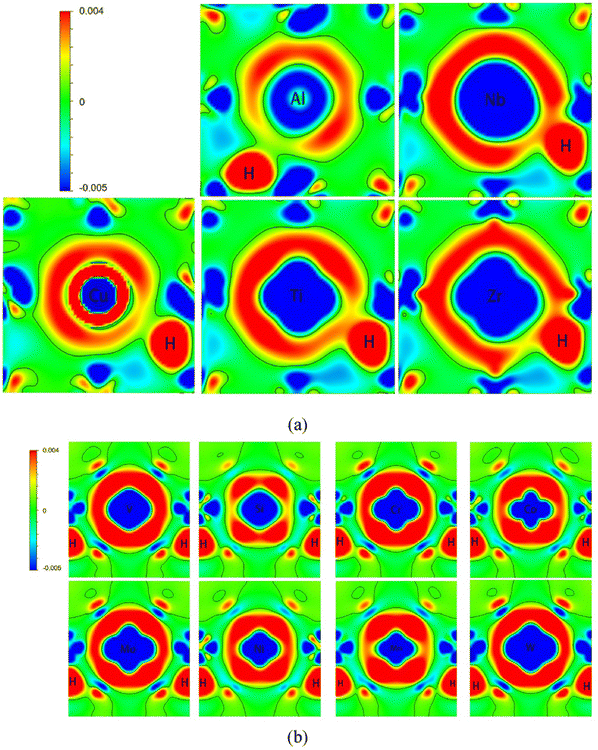Fig. 3 The differential charge density calculated for different scenarios when H is present in the interstitial locations in presence of different alloying elements such as Al, Nb, Cu, Mo in Fe matrices, (a) represents the second interstitial site for supercells alloyed with Al, Cu, Zr, Ti and Nb atoms, (b) third nearest interstitial site for supercells alloyed with Co, Cr, Mn, W, Mo, V, Si and Ni atoms. The accumulation and depletion of charges are represented in the colour coding. The charge density plots give idea about how the redistribution of charge is occurring between H and the alloying elements. Reproduced from ref. 60 with permission from Elsevier, copyright 2022.

The accumulation of H at dislocations and the shielding of dislocation interactions by H is difficult to study in-depth using first principles methods due to the computational cost, and continuum models cannot take chemical effects such as H–H interactions into account. Therefore, atomistic simulations of interaction between isolated dislocations and H are being carried out. This is being carried out by combining embedded atom (EAM) methods with Monte Carlo (MC) simulations. In this way, the binding energy of H atoms around the dislocation can be calculated self-consistently, considering the concentration aspects.⁵⁶ Furthermore, DFT based formation energy calculations were instrumental in providing information about the relation between phase changes and H induced degradation in austenitic and ferritic steels (Fig. 4).³⁷

Fig. 4 The formation energy of H atoms at the interstitial sites in Ni-rich FCC phase as a function of H chemical potential provide information about the interrelations between defect formation energy of H and the phase changes that can occur in both austenite and ferritic steels. (a) and (b) shows a comparison of how the formation energy of interstitial H in austenite and ferritic phases are dependent on the chemical potential and corresponding stability of both phases. (c) Indicates the solubility of H as a function of chemical potential and (d) shows the schematic picture of the austenite lattice with all available sites occupied with interstitial H atoms. Reproduced from ref. 37 under the terms of the Creative Commons CC-BY.

3.2. Surfaces, interfaces, and grain boundaries (GBs)

It is well established that the solubility of H in pristine Fe systems such as bcc and fcc structures is very low, even though H is more mobile than other impurities in transition metals. At room temperature, the diffusivity of H in pure bcc iron is about 1 × 10⁻⁴ cm² s⁻¹, compared to 1 × 10⁻¹⁶ cm² s⁻¹ for carbon and nitrogen. Spin polarized DFT calculations carried out in bcc Fe have shown that energetically stable site of H is on the Fe surface, rather than sub-surfaces or bulk and the H interstitial formation in bulk Fe is endothermic requiring additional energy to be supplied to the system.⁶⁹ More importantly, since the diffusion of H happens by hoping from one interstitial to another interstitial site, quantum mechanical methods were successful in deriving accurate estimate of the energy barriers. DFT has provided insights into the difference in solubilities of the most favoured octahedral interstitial to the less preferred tetrahedral site, through supercell calculations that allowed to recreate the exact dilutions. Efforts at the DFT front have suggested varied reasons for the site preference including charge transfer difference between the octahedral and tetrahedral sites, as well as reduced protonic electrostatic potential, that can provide more energetic stability.

The adsorption of H at (100), (110) and (111) surfaces of austenite steels have been quantitatively studied using DFT and it is seen that the adsorption energies are very close to each other with only 0.01 eV differences in energy, irrespective of the changes in atomic coordination numbers. This indicates that for a polycrystalline scenario, H will be adsorbed on to the steel surface, irrespective of the surface orientation.⁷⁰ Further, the 2D potential energy surfaces calculated using DFT indicated that, for the subsurface diffusion of H, more energy is needed for the H to move to the (111) surface, indicating that it might be possible to hinder the H diffusion pathways if the H exposure can be confined to the (111) surface.

Furthermore, the presence of intrinsic defects such as dislocations and grain boundaries (GBs) are inevitable in steels, and DFT calculations were attempted to calculate energetics of segregation effects of H at boundaries⁷¹ and low angle BCC boundaries are seen to attract H.^11,72–74 This is due to the more open bonding arrangements at the boundary than the bulk of the material, where more energy is needed to stabilize H. Nevertheless, it is found that in presence of other impurity atoms and/or C vacancies, H can be trapped away from the GB, into the deep bulk region of the steel matrix. More attempts are warranted in this area, as it is often difficult to understand the energy barriers for H to overcome the trap sites in the bulk and move towards the GB. Therefore, from DFT studies, it is understood that there is a competition between the bulk and GB trap sites for H and the presence of other alloying elements such as Mo, Nb, V, Ti etc., that can provide trap sites in presence of C atoms. It is now understood that the presence of GBs facilitates the segregation of H, and the presence of both high and low angle GBs are verified in steel matrices.

The presence of H at the GBs weakens the Fe bonds, leading to intergranular embrittlement, and investigations included both open GBs such as Σ5 [001] (310) and Σ11 [110] (113) and closed GBs such as Σ3 [110] (112) and Σ3 [110] (111).⁵⁶ The interstitial sites at the closed GBs more closely resemble respective bulk Fe structures in terms of solution energies and the values differed between bcc and fcc Fe indicating that the GB is attractive for H in bcc Fe while repulsive to H in fcc Fe. The migration barrier calculated using NEB methods showed that the migration barrier of the H atoms within the bcc Σ3 GB is 0.6 eV, larger than that in bulk bcc and hence attracts H. On the other hand, the corresponding fcc GB is mildly repulsive to H. For the open grain boundaries, the H must overcome larger migration barriers to move away from the GB, and the Σ11 GB act as an effective H trap with 0.4 eV larger migration barrier than bulk Fe.

DFT studies were conducted on some of the existing GB models such as coincidence cite lattice models (CSL) to simulate GBs and analysed the segregation behaviour, associated energetics as well as the charge transfer mechanisms at the GB interfaces.¹¹ There is a possibility of migration of H atoms to and from the GBs, surfaces, and bulk at varied circumstances. Recent DFT studies have uncovered the positive effects of alloying elements in trapping H and thus preventing embrittlement by quantifying the energy barriers when H moves from surface to the bulk regions.³⁶ It is ascertained since that the atomic coordination and arrangement of atoms in different surfaces of Fe vary according to the crystallographic orientation and H adsorption and diffusion are dependent on the surface energies, (see Fig. 5(A), from ref. 36).

Fig. 5 (A) The coordination of atoms along different crystallographic orientations are shown in the figure. A (a): geometry of (1 × 1 × 2) α-Fe surfaces. (b) α-Fe(001). (c) α-Fe(110). (d) α-Fe(111). (e) Calculated surface energies for the above surfaces. The adsorption, absorption and diffusion of H atoms are intimately connected to the nearest neighbour atoms and coordination number of the planes. Reproduced from ref. 36 with permission from Elsevier, copyright 2023. (B) The density of states (DOS) calculated for bulk and Fe surface and the changes in electronic structure brought by the presence of H. (a) and (b) represent calculated partial density of states of Fe on α-Fe(110) and that of H adsorbed on bulk α-Fe respectively. The DOS can serve as a valuable tool to provide information about the changes in orbital hybridization brought by the presence of H in the crystal lattice and the bonding characteristics. Reproduced from ref. 36 with permission from Elsevier, copyright 2023.

Further it is possible to elucidate the differences in electronic structure of the surfaces and bulk material in presence of H and the changes in density of states (DOS) obtained from DFT can be correlated to the bond length and charge information (refer to Fig. 5(B) from ref. 36). The DOS curve is a plot of the number of orbitals per unit volume per unit energy. A detailed discussion of the density of states of bulk and surface Fe with and without H is carried out by A. Juan et al.⁷⁵

For the bulk Fe, a significant amount of s and p orbitals disperses and penetrate the d bands, indicating that the d orbitals are more contracted. On the other hand, the bands at the surface are less dispersed and narrower. This is since the surface atoms have less near neighbour atoms compared to the bulk and therefore less orbitals available for overlap and this reduces the bandwidth. The surface bands are hence less dispersed and unoccupied compared to the bulk states.

The H atom normally occupies a 3-fold or 4-fold coordination at the Fe surface, and the presence of one H atom doesn't normally alter the DOS significantly, as the orbitals of Fe atoms dominate. At the surface, there will be a charge transfer from the Fe substrate to the H, and the H 1s orbitals predominantly interact with the 4s and 4p orbitals of Fe rather than with the 3d orbitals. In effect, a strong Fe–H bond is established, at the expense of a weakened Fe–Fe surface bond, and Fe–Fe bonding states are pushed down to the Fermi level. A visible change in the DOS in the presence of H at the Fe surface is that more antibonding states get populated and move to higher energies, weakening the Fe–Fe bonding.⁷⁶ H initially enters the surface regions and after chemical adsorption at the surface, it may diffuse to the sub-surface regions, and eventually reaches the bulk. The surface density of states, as presented in Fig. 5(B), depict the upward shifting of p orbitals of Fe, and this represents anti-bonding orbitals. It is also noticed that the presence of H at the bulk and surface results in an increase in Fe–Fe bond length, thus weakening the bond, and atoms at the bulk region are more prone to bond breaking compared to surface atoms.

The typical dissolution energy map of H at the GBs can be calculated and using the energy map it is possible to configure initial atomic configurations of GB and free surface (FS) with different number of H atoms (initial H excesses), according to a scheme whereby the lowest dissolution energy sites (strongest traps) are filled first and those with higher energies are filled next.⁷⁷ The dissolution energies for H at the bulk turned out to be positive, indicating that they are unstable at the bulk lattice interstitial sites.⁷⁷ However, the negative dissolution energies at the GB indicate that H stabilization is favourable. In both bulk and GB sites, dissolution energies decreased with Mn doping, and increased for Cr, Mo and Ni (see Fig. 6). The H diffusion barriers calculated using NEB method showed that H diffuses much slower in GBs than bulk like regions. The higher H diffusion barriers and lower dissolution energies for the GBs indicate that H will easily segregate the GBs leading to embrittlement. This is due to the structural differences between bulk and GB, and the two-dimensional character of the GBs. However, the addition of alloying elements such as Ni helped to reduce the segregation of H at the GBs as they influenced the diffusion barriers and changed the dissolution energies significantly. These results imply that for material design, suitable alloying elements can help prevent faster moving of H towards GB defects and prevent H embrittlement to some extent. DFT has also instrumental in understanding the binding of H to different sites at the screw dislocations, to identify the energetic preference varying from least to most stable positions.⁶⁵

Fig. 6 The dissolution energy of H in both bulk and GB of Fe in presence of alloying elements such as Cr, Mn, Ni and Mo. (a) Represents the H doped bcc Fe bulk. (b) Dissolution energies of H in bcc bulk. (c) Σ5 GB of Bcc Fe with H. (d) Dissolution energies of H in Σ5 GB of Bcc Fe. The dissolution energy calculated using DFT calculations shows that the dissolution energy for H at the GB is more favourable than the bulk region. Reprinted by permission from ref. 77 under the terms of the Creative Commons CC-BY.

3.3. The effect of H in clusters and precipitates

Since HE does not occur in ideal situations or in ideal bcc/fcc Fe matrices, it is important to consider the possible interactions between H and other metallic precipitates, as they are often the most efficient trapping sites,^78–83 possibly mitigating HE in advanced high-strength steels. Nanoprecipitates have been an interesting option to strengthen, and to trap H and prevent diffusing to defect areas in a microstructure.⁵⁶ A schematic representation of the absorption of H in steels and the proximity of H to the precipitate which is a steel inclusion is presented in Fig. 7.⁵⁹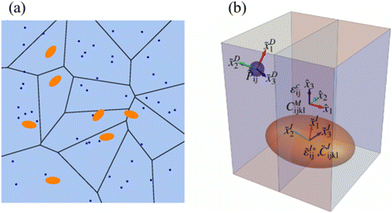

Fig. 7 A schematic picture of the presence of precipitates (inclusions) in steel and the presence of H absorption in near vicinity. (a) The blue dots represent h atoms, and the orange ellipses represent the carbide particles. (b) A schematic describing the model whereas the blue sphere is H atom and orange ellipsoid, the carbide particle, which is the inclusion. The global coordinates represent the semi axes of the ellipsoidal and the local coordinates represent the orientation of the point defect and inclusion respectively. Reproduced from ref. 59 with permission from American Physical Society, copyright 2021.

The multi-scale approach, which integrates atomistic, mesoscopic, and continuum-scale modelling to deal with H induced degradations, can be optimized through several key strategies such as, enhanced coupling between scales, advanced modelling and simulation techniques as well as validation and calibration with experimental data. The information exchange between atomistic and mesoscopic models can be improved by accurate interatomic potentials that can perform critical optimization step in improving the transfer of information between the atomistic and mesoscale models. This can involve developing more accurate interatomic potentials refined by machine learning (ML) methods, that capture the effect of H in steel structures. Further the gathered atomistic and microscopic information can be used in continuum models to describe mesoscale phenomena. At the continuum level, adaptive mesh refinement is a powerful tool to dynamically refine the regions with higher degradation caused by H accumulation. This will help to predict crack initiation and propagation.⁸⁴

The atomistic and continuum models can be further verified using experimental data, gathered from fracture toughness tests and slow strain rate tensile tests in H charged environments. Therefore, it is important to combine different time and length scales starting from the quantum mechanical DFT to capture atomistic insights and combine it with mesoscale methods to address HE in steels. In this direction, good understanding has been derived from DFT calculations on TiC precipitates considering surface calculations as these calculations also provided evidence that with the increase in carbide concentration, the amount of H segregated at dislocation interfaces decreases.⁵⁹ The advantage of considering nanocluster precipitates in surface calculations is owing to the possibility of engineering the atomic structure by introducing point defects and vacancies in the nanoclusters, such as introducing C vacancies in the TiC precipitates and the possibility of H diffusion through these vacancies, which will give idea about quantifying the activation barriers and energies inside the matrix.⁷⁸ Advanced microscopy techniques when combined with atomistic scale DFT simulations could shed light into fundamental phenomena occurring at incoherent interfaces when H encounters such nanoprecipitates.

The presence and distribution of carbide precipitates in the steel matrix significantly influences the absorption and trapping of H atoms. One of the strong H traps in steel are the steel/carbide interfaces, which possess lattice mismatch and associated strain fields promote H trapping, and the strength of which is associated with the density of dislocations.⁴² It is found that the increase in number of C vacancies in metal carbide precipitates can facilitate H trapping. First principles calculations have proved that the diffusion barrier for H atoms can be lowered by increasing the concentration of C vacancies both at the interface and at the interior of carbide precipitates, to reach the deep traps in the matrix.⁸⁵

Through DFT simulations, it possible to elucidate the H trapping behaviours of incoherent and semi coherent interfaces and can explain the diverse behaviours of H in different chemical environments such as the presence of carbon (C) vacancies, misfit dislocations and strains. In this scenario, the influence of increased number of C vacancies in H trapping and embrittlement is studied using DFT in combination with microstructural characterization experiments⁴² and it is ascertained that C vacancies can be a high-density H trap due to their high trapping energy.⁷⁸ Therefore, efforts were directed towards increasing the density of metal carbides inside the steel matrix and first principles simulations were undertaken to quantify H migration, and effect of C vacancies. Hence a viable strategy to increase the H trapping capacity is to engineer the metal carbides to encompass large numbers of accessible and strong C vacancies and by increasing the number density of metal carbides by methods such as interphase precipitation.

Fig. 8 depicts the influence of strain and associated changes in the stability of the material. The application of strain induces both compressive and tensile strain in the material depending on the material structure. Through DFT calculations, it is ascertained that tensile strain field promotes H trapping, while compressive strain prohibits H trapping, as it increases the solution energy of H in the matrix. Specifically, carbon/sulphur vacancies on the precipitate surface and strain of the matrix near the interface determine the hydrogen-trapping characteristics of the incoherent interfaces.

Fig. 8 The application of strain and corresponding changes in lattice expansion – that manifest as the volume changes can affect the stability of the material. These values are calculated as a function of solution energy. (a) and (b) Represents the solution energy and tetrahedral volume of two different precipitates in α-Fe, labelled as #2 and #3 Reproduced from ref. 50 under the terms of the Creative Commons CC-BY.

Precipitates such as carbides, carbonitrides, and nitrides are known to possess higher solution enthalpies than bulk Fe, due to their stable structures and H needs more energy to enter the structure, breaking the saturated covalent bonds. On the other hand, when there is an interface between a nitride and an Fe matrix, the presence of non-saturated covalent bonds makes it easier for H to settle. H easily bonds with C, better than with the metallic atoms at such interfaces. The segregation of H at these interfaces increases the decohesion and they are prone to HE.⁵⁶

The recent revolution in data science in different fields of science and technology is impacting steel research in general and HE research in particular. The severity of H embrittlement has been predicted with gradient boosting algorithms, by classifying the materials based on hydrogen embrittlement susceptibility using gradient boosting machine classification model, taking experimental data of (slow strain rate) tensile tests as input. The importance of this data analysis is that it could provide an embrittlement index that can serve as a determining parameter to predict failure of materials.⁸⁶ Combining ML with DFT is an efficient method to predict the effect of alloying elements on mechanical properties and HE. In most of the initial attempts, the input to ML models is gathered from existing experiments, and parameters that affect HE were identified, followed by correlation analysis between input features and the results will be used to train ML models. Since experimentally it is exceedingly difficult to map the solute H atoms, DFT models have helped to investigate the H situated at phase boundaries such as that of ferrite–metal carbide. It has been shown from DFT simulations that, even if C vacancies are present in transition metal carbides such as TiC, alloying elements such as V and N can reduce the H trapping efficiency of such carbide materials.⁸⁷ Mo is also a preferable alloying element in TiC, which helped to increase the migration barrier for H, also assisting the formation for C vacancies in the TiC matrix. Through DFT it was possible to quantify the vacancy formation energies and migration energy barriers for the H diffusion mechanism (see Fig. 9). Often, the presence of interfaces such as carbides needs the combined efforts of first principles methods and continuum models, and DFT outputs such as accurate lattice constants, and elastic constants serve as the input for such methods.⁸⁸ This is because in complex interfaces, the dilation of iron lattice caused by H atoms are not directly measurable using experiments, and that can be easily obtainable by combining DFT calculations with standard models for obtaining stress–strain relations. In the work of X. Tang et al.,⁸⁸ they had successfully obtained above mentioned material-specific quantities using DFT and then used those as inputs for continuum model to show that H atoms prefer to bind to precipitates, and these results aligned well with experimental observations.⁷⁸ The recent revolution in data science in different fields of science and technology is impacting steel research in general and HE research in particular. The severity of H embrittlement has been predicted with gradient boosting algorithms, by classifying the materials based on hydrogen embrittlement susceptibility using gradient boosting machine classification model, taking experimental data of tensile tests as input. The importance of this data analysis is that it could provide an embrittlement index that can serve as a determining parameter to predict failure of materials.⁸⁶ Combining machine learning (ML) with DFT is an efficient method to predict the effect of alloying elements on mechanical properties and HE. In most of the initial attempts, the input to ML models is gathered from existing experiments, and parameters that affect HE were identified, followed by correlation analysis between input features and the results will be used to train ML models. ML models such as random forest (RF), linear regression (LR), Bayesian ridge (BR) and support vector machine (SVM) are being used to understand the correlation between HE indexes and input features and which aids in improving the mechanical properties of steel to withstand the H exposure.⁸⁹ Instead of only relying on experimental data, the vast amount of data generated by DFT can aid the ML models and further predictions. ML models such as random forest (RF), linear regression (LR), Bayesian ridge (BR) and support vector machine (SVM) are being used to understand the correlation between HE indexes and input features and which aids in improving the mechanical properties of steel to withstand the H exposure.⁸⁹ Instead of only relying on experimental data, the vast amount of data generated by DFT can aid the ML models and further predictions.

Fig. 9 The changes brought about by the Mo addition to H diffusion, and the migration via C vacancies in TiC. (a) Represents the metal carbide interface with bcc Fe matrix, (b) represents the atomic coordination for the nearest neighbour configurations corresponding to the vacancy sites, (c) solution energy profiles for the vacancy configurations, (d) the representations of the metal carbide concentration, (e) 3-D model of the carbon-site-centered unit cells in the TiC bulk and at the ferrite-carbide interface, (f) C vacancy formation energy as a function of the Mo atoms and (g) H trapping energy in a C vacancy as a function of Mo atoms. Reproduced from ref. 42 under the terms of the Creative Commons CC-BY.

In this direction, DFT and MD studies have been combined with machine learning force field (MLFF) and neural network (NN) models to describe the static and dynamical property analysis of Fe–H systems.⁹⁰ Atomic energies calculated by DFT have been used to train the force fields and important insights into the H behaviour at GBs and how it affects crack propagation, have been obtained. In another attempt, a general-purpose neural network inter-atomic potential (NNIP) has been trained using DFT data to describe the interaction of H with various defects in alpha-Fe. It is shown that the NNIP is powerful tool to describe the properties of both α-Fe and interactions of H with both bulk Fe and defects such as surfaces, GBs, vacancies and screw dislocations.⁹¹ Therefore, it is worthwhile to note that the vast amount of DFT data existing in the steel research (energies, mechanical properties, and structural information to name a few) can be an alternative to/or combined with experimental data, wherever applicable for serving as an input for ML methods to predict HE.

4. Conclusion

Hydrogen embrittlement continues to be a challenge to the industries utilising steels due to the involvement of multi-time and length scales, and therefore fundamental research in this area will go on, using existing methods, and at the same time, encompassing new scientific advances. Density functional theory, in its reformed form has been used for decades both as an aid to experimental research and as an independent tool to deal with complex embrittlement phenomena. DFT forms the basis rung of the ladder that starts from the atomistic to continuum scale to deal with degradation of steel induced by hydrogen. In this short perspective article, we covered the effect of H in bulk phases of steels, surfaces and in other structural defects, from a DFT perspective and the material properties that are being investigated to quantify this degradation phenomenon. We envisage that, in the coming years, the vast amount of generated DFT data can aid in the development, testing and training of Machine learning models to better quantify the parameters that lead to hydrogen embrittlement and increased research efforts are needed in this direction.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this perspective.

Conflicts of interest

The authors state that there are no conflicts to declare.

Acknowledgements

AAS and VJ would like to thank Jane and Aatos Erkko (J&AE) Foundation and Tiina and Antti Herlin (TAH) Foundation for their financial supports on Advanced Steels for Green Planet project (AS4G) as well as the University of Oulu & The Research Council of Finland Profi 352788 for their funding of the H₂ Future project. SP would like to thank the JustH2Transit grant (#358422) from the Research council of Finland for financial support. AAS acknowledge EU/EURF/Teollisuuden Big Data project (A80437).

References

1. S. van Renssen, The hydrogen solution?, Nat. Clim. Change, 2020, 10, 799–801.
2. M. Yue, H. Lambert, E. Pahon, R. Roche, S. Jemei and D. Hissel, Hydrogen energy systems: a critical review of technologies, applications, trends and challenges, Renewable Sustainable Energy Rev., 2021, 146, 111180.
3. D. Castelvecchi, How the hydrogen revolution can help save the planet – and how it can’t, Nature, 2022, 611, 440–443.
4. I. M. Robertson, P. Sofronis, A. Nagao, M. L. Martin, S. Wang, D. W. Gross and K. E. Nygren, Hydrogen Embrittlement Understood, Metall. Mater. Trans. B, 2015, 46, 1085–1103.
5. H. Yu, A. Díaz, X. Lu, B. Sun, Y. Ding, M. Koyama, J. He, X. Zhou, A. Oudriss, X. Feaugas and Z. Zhang, Hydrogen Embrittlement as a Conspicuous Material Challenge—Comprehensive Review and Future Directions, Chem. Rev., 2024, 124, 6271–6392.
6. J. Sanchez, J. Fullea, M. C. Andrade and P. L. de Andres, Ab initio molecular dynamics simulation of hydrogen diffusion in α-iron, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 132102.
7. L. Ismer, T. Hickel and J. Neugebauer, Ab initio study of the solubility and kinetics of hydrogen in austenitic high Mn steels, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 094111.
8. A. Castedo, J. Sanchez, J. Fullea, M. C. Andrade and P. L. de Andres, Ab initio study of the cubic-to-hexagonal phase transition promoted by interstitial hydrogen in iron, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 094101.
9. Y. Tang and J. A. El-Awady, Atomistic simulations of the interactions of hydrogen with dislocations in fcc metals, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 174102.
10. L. Zhong, R. Wu, A. J. Freeman and G. B. Olson, Charge transfer mechanism of hydrogen-induced intergranular embrittlement of iron, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 13938–13941.
11. X. Zhou, D. Marchand, D. L. McDowell, T. Zhu and J. Song, Chemomechanical Origin of Hydrogen Trapping at Grain Boundaries in fcc Metals, Phys. Rev. Lett., 2016, 116, 075502.
12. Y. Tateyama and T. Ohno, Stability and clusterization of hydrogen-vacancy complexes in alpha-Fe: an ab initio study, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 174105.
13. U. Aydin, L. Ismer, T. Hickel and J. Neugebauer, Solution enthalpy of hydrogen in fourth row elements: systematic trends derived from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155144.
14. H. Kimizuka and S. Ogata, Slow diffusion of hydrogen at a screw dislocation core in alpha-iron, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 024116.
15. C. Interrante, G. Pressouyre and Creusot-Loire, Current solutions to hydrogen problems in steels: proceedings of the First International Conference on Current Solutions to Hydrogen Problems in Steels, Washington DC, November 1–5, 1982.
16. J. O. Abe, A. P. I. Popoola, E. Ajenifuja and O. M. Popoola, Hydrogen energy, economy and storage: review and recommendation, Int. J. Hydrogen Energy, 2019, 44, 15072–15086.
17. H. Ishaq, I. Dincer and C. Crawford, A review on hydrogen production and utilization: challenges and opportunities, Int. J. Hydrogen Energy, 2022, 47, 26238–26264.
18. B. Sun, H. Zhao, X. Dong, C. Teng, A. Zhang, S. Kong, J. Zhou, X.-C. Zhang and S.-T. Tu, Current challenges in the utilization of hydrogen energy-a focused review on the issue of hydrogen-induced damage and embrittlement, Adv. Appl. Energy, 2024, 14, 100168.
19. A. Laureys, R. Depraetere, M. Cauwels, T. Depover, S. Hertelé and K. Verbeken, Use of existing steel pipeline infrastructure for gaseous hydrogen storage and transport: a review of factors affecting hydrogen induced degradation, J. Nat. Gas Sci. Eng., 2022, 101, 104534.
20. Y.-S. Chen, H. Lu, J. Liang, A. Rosenthal, H. Liu, G. Sneddon, I. McCarroll, Z. Zhao, W. Li, A. Guo and J. M. Cairney, Observation of hydrogen trapping at dislocations, grain boundaries, and precipitates, Science, 2020, 367, 171–175.
21. Y.-S. Chen, C. Huang, P.-Y. Liu, H.-W. Yen, R. Niu, P. Burr, K. L. Moore, E. Martínez-Pañeda, A. Atrens and J. M. Cairney, Hydrogen trapping and embrittlement in metals – A review, Int. J. Hydrogen Energy, 2024 DOI:10.1016/j.ijhydene.2024.04.076.
22. J. Hafner, C. Wolverton and G. Ceder, Toward Computational Materials Design: The Impact of Density Functional Theory on Materials Research, 2006, vol. 31.
23. S. A. Aravindh, W. Cao, M. Alatalo, M. Huttula and J. Kömi, Adsorption of CO₂ on the ω-Fe(0001) surface: insights from density functional theory, RSC Adv., 2021, 11, 6825–6830.
24. S. A. Aravindh, A. A. Kistanov, M. Alatalo, J. Kömi, M. Huttula and W. Cao, Incorporation of Si atoms into CrCoNiFe high-entropy alloy: a DFT study, J. Phys.: Condens. Matter, 2021, 33, 135703.
25. A. A. S. Devi, J. Nokelainen, B. Barbiellini, M. Devaraj, M. Alatalo and A. Bansil, Re-examining the giant magnetization density in α′′-Fe₁₆N₂ with the SCAN+U method, Phys. Chem. Chem. Phys., 2022, 24, 17879–17884.
26. A. A. Sasikala Devi, S. Pallaspuro, W. Cao, M. Somani, M. Alatalo, M. Huttula and J. Kömi, Density functional theory study of ω phase in steel with varied alloying elements, Int. J. Quantum Chem., 2020, 120, 26223.
27. S. Pallaspuro, I. H. Miettunen, S. A. Aravindh, S. Ghosh, W. Cao, M. C. Somani and J. I. Kömi, The Multiphase Micro- and Nanostructures of 0.2 and 0.4C Direct-Quenched and Partitioned Steels, Mater. Sci. Forum, 2021, 1016, 1097–1102.
28. S. Ghosh, K. Rakha, A. Aravindh Sasikala Devi, S. Reza, S. Pallaspuro, M. Somani, M. Huttula and J. Kömi, A combined 3D-atomic/nanoscale comprehension and ab initio computation of iron carbide structures tailored in Q&P steels via Si alloying, Nanoscale, 2023, 15, 10004–10016.
29. H. Singh, T. Alatarvas, A. A. Kistanov, S. A. Aravindh, S. Wang, L. Zhu, B. Sarpi, Y. Niu, A. Zakharov, F. M. F. de Groot, M. Huttula, W. Cao and T. Fabritius, Unveiling interactions of non-metallic inclusions within advanced ultra-high-strength steel: a spectro-microscopic determination and first-principles elucidation, Scr. Mater., 2021, 197, 113791.
30. P. Nordlander, J. K. Norskov and F. Besenbacher, Trends in hydrogen heats of solution and vacancy trapping energies in transition metals, J. Phys. F: Met. Phys., 1986, 16, 1161–1171.
31. G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904.
32. M. Nagumo and K. Takai, The predominant role of strain-induced vacancies in hydrogen embrittlement of steels: overview, Acta Mater., 2019, 165, 722–733.
33. H. L. Zhang, S. Lu, M. P. J. Punkkinen, Q.-M. Hu, B. Johansson and L. Vitos, Static equation of state of bcc iron, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 132409.
34. M. L. Fullarton, R. E. Voskoboinikov and S. C. Middleburgh, Hydrogen accommodation in α-iron and nickel, J. Alloys Compd., 2014, 587, 794–799.
35. A. Tehranchi and W. A. Curtin, The role of atomistic simulations in probing hydrogen effects on plasticity and embrittlement in metals, Eng. Fract. Mech., 2019, 216, 106502.
36. L. Zhu, J. Luo, S. Zheng, S. Yang, J. Hu and Z. Chen, Understanding hydrogen diffusion mechanisms in doped α-Fe through DFT calculations, Int. J. Hydrogen Energy, 2023, 48, 17703–17710.
37. C. Örnek, M. Mansoor, A. Larsson, F. Zhang, G. S. Harlow, R. Kroll, F. Carlà, H. Hussain, B. Derin, U. Kivisäkk, D. L. Engelberg, E. Lundgren and J. Pan, The causation of hydrogen embrittlement of duplex stainless steel: phase instability of the austenite phase and ductile-to-brittle transition of the ferrite phase – Synergy between experiments and modelling, Corros. Sci., 2023, 217, 111140.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
39. G. Rahman, I. G. Kim, H. K. D. H. Bhadeshia and A. J. Freeman, First-principles investigation of magnetism and electronic structures of substitutional 3d transition-metal impurities in bcc Fe, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 184423.
40. Wikipedia, https://en.wikipedia.org/wiki/List_of_quantum_chemistry_and_solid-state_physics_software.
41. K. Ohsawa, K. Eguchi, H. Watanabe, M. Yamaguchi and M. Yagi, Configuration and binding energy of multiple hydrogen atoms trapped in monovacancy in bcc transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 094102.
42. P. Y. Liu, B. Zhang, R. Niu, S. L. Lu, C. Huang, M. Wang, F. Tian, Y. Mao, T. Li, P. A. Burr, H. Lu, A. Guo, H. W. Yen, J. M. Cairney, H. Chen and Y. S. Chen, Engineering metal-carbide hydrogen traps in steels, Nat. Commun., 2024, 15, 1–13.
43. D. P. Abraham and C. J. Altstetter, Hydrogen-enhanced localization of plasticity in an austenitic stainless steel, Metall. Mater. Trans. A, 1995, 26, 2859–2871.
44. H. K. Birnbaum and P. Sofronis, Hydrogen-enhanced localized plasticity—a mechanism for hydrogen-related fracture, Mater. Sci. Eng., A, 1994, 176, 191–202.
45. R. A. Oriani, Hydrogen Embrittlement of Steels, Annu. Rev. Mater. Sci., 1978, 8, 327–357.
46. A. R. Troiano, The Role of Hydrogen and Other Interstitials in the Mechanical BehavioBehaviour of Metals, Metallogr., Microstruct., Anal., 2016, 5, 557–569.
47. L. Zhu, J. Luo, S. Zheng, S. Yang, J. Hu and Z. Chen, Understanding hydrogen diffusion mechanisms in doped α-Fe through DFT calculations, Int. J. Hydrogen Energy, 2023, 48, 17703–17710.
48. U. K. Chohan, S. P. K. Koehler and E. Jimenez-Melero, Diffusion of hydrogen into and through γ-iron by density functional theory, Surf. Sci., 2018, 672–673, 56–61.
49. Y.-W. You, X.-S. Kong, X.-B. Wu, Y.-C. Xu, Q. F. Fang, J. L. Chen, G.-N. Luo, C. S. Liu, B. C. Pan and Z. Wang, Dissolving, trapping and detrapping mechanisms of hydrogen in bcc and fcc transition metals, AIP Adv., 2013, 3, 012118.
50. B. Zhang, Q. Zhu, C. Xu, C. Li, Y. Ma, Z. Ma, S. Liu, R. Shao, Y. Xu, B. Jiang, L. Gao, X. Pang, Y. He, G. Chen and L. Qiao, Atomic-scale insights on hydrogen trapping and exclusion at incoherent interfaces of nanoprecipitates in martensitic steels, Nat. Commun., 2022, 13, 1–11.
51. F. J. Sánchez, B. Mishra and D. L. Olson, Magnetization effect on hydrogen absorption in high-strength steels and its implications, Scr. Mater., 2005, 53, 1443–1448.
52. W. Pepperhoff and M. Acet, Constitution and Magnetism of Iron and its Alloys, Springer Berlin Heidelberg, Berlin, Heidelberg, 2001.
53. P. L. de Andres, J. Sanchez and A. Ridruejo, Hydrogen in α-iron: role of phonons in the diffusion of interstitials at high temperature, Sci. Rep., 2019, 9, 12127.
54. H. Jónsson, G. Mills and K. W. Jacobsen, Nudged elastic band method for finding minimum energy paths of transitions, Classical and Quantum Dynamics in Condensed Phase Simulation, 1998, pp. 385–404.
55. G. Mills, H. Jónsson and G. K. Schenter, Reversible work transition state theory: application to dissociative adsorption of hydrogen, Surf. Sci., 1995, 324, 305–337.
56. T. Hickel, R. Nazarov, E. J. McEniry, G. Leyson, B. Grabowski and J. Neugebauer, Ab Initio Based Understanding of the Segregation and Diffusion Mechanisms of Hydrogen in Steels, JOM, 2014, 66, 1399–1405.
57. A. Togo, First-principles Phonon Calculations with Phonopy and Phono3py, J. Phys. Soc. Jpn., 2023, 92, 012001.
58. A. Togo, L. Chaput, T. Tadano and I. Tanaka, Implementation strategies in phonopy and phono3py, J. Phys.: Condens. Matter, 2023, 35, 353001.
59. X. Tang, R. Salehin, G. B. Thompson and C. R. Weinberger, Long-range hydrogen-binding effects of carbide interfaces in iron, Phys. Rev. Mater., 2021, 5, 103603.
60. C. Wang, L. Cheng, X. Sun, X. Zhang, J. Liu and K. Wu, First-principle study on the effects of hydrogen in combination with alloy solutes on local mechanical properties of steels, Int. J. Hydrogen Energy, 2022, 47, 22243–22260.
61. S. Echeverri Restrepo, D. Di Stefano, M. Mrovec and A. T. Paxton, Density functional theory calculations of iron–vanadium carbide interfaces and the effect of hydrogen, Int. J. Hydrogen Energy, 2020, 45, 2382–2389.
62. M. W. Finnis, The theory of metal–ceramic interfaces, J. Phys.: Condens. Matter, 1996, 8, 5811.
63. A. Y. Lozovoi, A. T. Paxton and M. W. Finnis, Structural and chemical embrittlement of grain boundaries by impurities: a general theory and first-principles calculations for copper, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 155416.
64. M. Dadfarnia, A. Nagao, S. Wang, M. L. Martin, B. P. Somerday and P. Sofronis, Recent advances on hydrogen embrittlement of structural materials, Int. J. Fract., 2015, 196, 223–243.
65. M. Itakura, H. Kaburaki, M. Yamaguchi and T. Okita, The effect of hydrogen atoms on the screw dislocation mobility in bcc iron: a first-principles study, Acta Mater., 2013, 61, 6857–6867.
66. R. Nazarov, T. Hickel and J. Neugebauer, Ab initio study of H-vacancy interactions in fcc metals: implications for the formation of superabundant vacancies, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 144108.
67. D. E. Jiang and E. A. Carter, Diffusion of interstitial hydrogen into and through bcc Fe from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 064102.
68. W. A. Counts, C. Wolverton and R. Gibala, First-principles energetics of hydrogen traps in α-Fe: point defects, Acta Mater., 2010, 58, 4730–4741.
69. C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, First-principles calculations for point defects in solids, Rev. Mod. Phys., 2014, 86, 253–305.
70. U. K. Chohan, S. P. K. Koehler and E. Jimenez-Melero, Diffusion of hydrogen into and through γ-iron by density functional theory, Surf. Sci., 2018, 672–673, 56–61.
71. Y. A. Du, L. Ismer, J. Rogal, T. Hickel, J. Neugebauer and R. Drautz, First-principles study on the interaction of H interstitials with grain boundaries in α- and γ-Fe, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 144121.
72. H. Momida, Y. Asari, Y. Nakamura, Y. Tateyama and T. Ohno, Hydrogen-enhanced vacancy embrittlement of grain boundaries in iron, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 144107.
73. D. Di Stefano, M. Mrovec and C. Elsässer, First-principles investigation of hydrogen trapping and diffusion at grain boundaries in nickel, Acta Mater., 2015, 98, 306–312.
74. G. Henkelman, B. P. Uberuaga, H. Jónsson, B. P. Uberuaga and H. Jó, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904.
75. A. Juan and R. Hoffmann, Hydrogen on the Fe(110) surface and near bulk bcc Fe vacancies, Surf. Sci., 1999, 421, 1–16.
76. D. E. Jiang and E. A. Carter, Adsorption and diffusion energetics of hydrogen atoms on Fe(110) from first principles, Surf. Sci., 2003, 547, 85–98.
77. X. Fan, Z. Mi, L. Yang and H. Su, Application of DFT Simulation to the Investigation of Hydrogen Embrittlement Mechanism and Design of High Strength Low Alloy Steel, Materials, 2022, 16, 152.
78. K. Kawakami and T. Matsumiya, Numerical Analysis of Hydrogen Trap State by TiC and V4C3 in bcc-Fe, ISIJ Int., 2012, 52, 1693–1697.
79. Y. Tateyama and T. Ohno, Stability and clusterization of hydrogen-vacancy complexes in α Fe: an ab initio study, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 174105.
80. K. Kawakami and T. Matsumiya, Ab initio Investigation of Hydrogen Trap State by Cementite in bcc-Fe, ISIJ Int., 2013, 53, 709–713.
81. R. Shi, Y. Ma, Z. Wang, L. Gao, X.-S. Yang, L. Qiao and X. Pang, Atomic-scale investigation of deep hydrogen trapping in NbC/α-Fe semi-coherent interfaces, Acta Mater., 2020, 200, 686–698.
82. Y. Ma, Y. Shi, H. Wang, Z. Mi, Z. Liu, L. Gao, Y. Yan, Y. Su and L. Qiao, A first-principles study on the hydrogen trap characteristics of coherent nano-precipitates in α-Fe, Int. J. Hydrogen Energy, 2020, 45, 27941–27949.
83. C. Jones, V. Tuli, Z. Shah, M. Gass, P. A. Burr, M. Preuss and K. L. Moore, Evidence of hydrogen trapping at second phase particles in zirconium alloys, Sci. Rep., 2021, 11, 4370.
84. Z. Si, Hirshikesh, T. Yu and S. Natarajan, An adaptive phase-field simulation for hydrogen embrittlement fracture with multi-patch isogeometric method, Comput. Methods Appl. Mech. Eng., 2024, 418, 116539.
85. D. Di Stefano, R. Nazarov, T. Hickel, J. Neugebauer, M. Mrovec and C. Elsässer, First-principles investigation of hydrogen interaction with TiC precipitates in α-Fe, Phys. Rev. B, 2016, 93, 184108.
86. A. Campari, M. Darabi, A. Alvaro, F. Ustolin and N. Paltrinieri, A Machine Learning Approach to Predict the Materials’ Susceptibility to Hydrogen Embrittlement, Chem. Eng. Trans., 2023, 99, 193–198.
87. P. Hammer, L. Romaner and V. I. Razumovskiy, Hydrogen trapping in mixed carbonitrides, Acta Mater., 2024, 268, 119754.
88. X. Tang, G. B. Thompson and C. R. Weinberger, Long-range hydrogen-binding effects of carbide interfaces in iron, Phys. Rev. Mater., 2021, 5, 103603.
89. S.-G. Kim, S.-H. Shin and B. Hwang, Machine learning approach for prediction of hydrogen environment embrittlement in austenitic steels, J. Mater. Res. Technol., 2022, 19, 2794–2798.
90. B. Zhang, M. Asta and L.-W. Wang, Machine learning force field for Fe–H system and investigation on role of hydrogen on the crack propagation in α-Fe, Comput. Mater. Sci., 2022, 214, 111709.
91. F.-S. Meng, J.-P. Du, S. Shinzato, H. Mori, P. Yu, K. Matsubara, N. Ishikawa and S. Ogata, General-purpose neural network interatomic potential for the α-iron and hydrogen binary system: toward atomic-scale understanding of hydrogen embrittlement, Phys. Rev. Mater., 2021, 5, 113606.

---