Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Liquid-jet photoemission spectroscopy as a structural tool: site-specific acid–base chemistry of vitamin C†
Lukáš
Tomaník‡
 a,
Michele
Pugini
a,
Michele
Pugini
 b,
Karen
Mudryk
b,
Karen
Mudryk
 b,
Stephan
Thürmer
b,
Stephan
Thürmer
 c,
Dominik
Stemer
c,
Dominik
Stemer
 b,
Bruno
Credidio
b,
Bruno
Credidio
 b,
Florian
Trinter
b,
Florian
Trinter
 b,
Bernd
Winter
b,
Bernd
Winter
 *b and
Petr
Slavíček
*b and
Petr
Slavíček
 *a
*a
aDepartment of Physical Chemistry, University of Chemistry and Technology, Technická 5, 16628 Prague, Czech Republic. E-mail: Petr.Slavicek@vscht.cz
bMolecular Physics, Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany. E-mail: winter@fhi-berlin.mpg.de
cDepartment of Chemistry, Graduate School of Science, Kyoto University, Kitashirakawa-Oiwakecho, Sakyo-Ku, 606-8502 Kyoto, Japan
First published on 28th June 2024
Abstract
Liquid-jet photoemission spectroscopy (LJ-PES) directly probes the electronic structure of solutes and solvents. It also emerges as a novel tool to explore chemical structure in aqueous solutions, yet the scope of the approach has to be examined. Here, we present a pH-dependent liquid-jet photoelectron spectroscopic investigation of ascorbic acid (vitamin C). We combine core-level photoelectron spectroscopy and ab initio calculations, allowing us to site-specifically explore the acid–base chemistry of the biomolecule. For the first time, we demonstrate the capability of the method to simultaneously assign two deprotonation sites within the molecule. We show that a large change in chemical shift appears even for atoms distant several bonds from the chemically modified group. Furthermore, we present a highly efficient and accurate computational protocol based on a single structure using the maximum-overlap method for modeling core-level photoelectron spectra in aqueous environments. This work poses a broader question: to what extent can LJ-PES complement established structural techniques such as nuclear magnetic resonance? Answering this question is highly relevant in view of the large number of incorrect molecular structures published.
1 Introduction
Photoemission (PE) spectroscopy from the liquid phase was made possible via the liquid-microjet (LJ) technique,1 and has since become an increasingly applied tool for studying aqueous solutions as it directly probes the liquid's electronic structure.2–4 A growing body of experimental data in the field made us ask: can liquid-jet photoemission spectroscopy (LJ-PES) be used as a general structural tool in liquid-phase (and interface) chemistry? We are inspired by the ESCA (Electron Spectroscopy for Chemical Analysis) technique used for gaseous as well as solid-state samples and associated interfaces,5 where one determines chemical shifts in binding energies (BEs) of core-level electrons. As the core-level electrons are localized on a single atom, the observed shifts provide information on the specific chemical environment of the ionized atom. This approach can also be extended to liquids, where the PE spectrum, expressed in terms of BEs of the electrons, provides us with the full set of electronic-structure data on the studied solutes.6 For example, if we analyze all the aqueous-phase LJ-PES data up to May 2020, according to the list of publications in ref. 7, we obtain the following values for C 1s core-level BEs: 289.5–290.5 eV for the –CH2– group, 291–291.5 eV for the C–OH group, 293–293.7 eV for the –COO− group, and 293.9–295 eV for the –COOH group. This demonstrates that core-level LJ-PES can be sensitive enough to reveal a specific chemical environment of individual atoms in the molecule. The technique has additional advantages, e.g., the surface sensitivity of photoemission has been used to probe air–liquid interfaces8,9 or to study electrode–electrolyte interfaces.10–12Analogous to PE spectroscopy in the solid state, recent developments now enable the accurate determination of electron BEs in the liquid (typically aqueous) phase.13 In addition, Auger electrons emitted after subsequent decay of the core hole can reveal the liquid structure and associated electron (and nuclear) dynamics;14–16 we will not discuss this emission channel in the present work. One of the limiting factors for a wider-community application of LJ-PES as a chemical analysis tool can be the need for suitable X-ray sources, usually limited to synchrotron-based facilities. However, recent developments of laboratory-based sources relying on high-harmonic generation (HHG) promise to significantly ease access to table-top X-ray generation, possibly vastly increasing the number of studies in the near future.17–20
Utilizing chemical shifts revealed by photoelectrons from solution to gain structural insight appears to provide a promising complementary route to powerful structural analysis techniques such as nuclear magnetic resonance (NMR).21 It took many years for NMR to be fully developed and established as a conventional structural tool. Yet, even the well-established NMR has witnessed surprisingly frequent structural misassignments. This is especially the case for natural products, an important group of compounds in drug development. There are hundreds of reportedly misassigned structures of even medium-sized molecules.22–25 The present work should contribute to the development of LJ-PES as a complementary tool for chemical (structural) analysis for molecules solvated in liquids. It could extend the portfolio of techniques to analyze the structure of liquids from the perspective of individual atoms, i.e., useful to decipher molecular structure and speciation.
LJ-PES has been successfully applied, e.g., to study interactions of hydroxide ions (OH−) with water,26 different charge states of amino acids,27 or specific solvation structures of biomolecules.28,29 The technique could even trace minor conformational changes following solvation.30 Recently, we have demonstrated that when combined with theoretical modeling, LJ-PES is able to reveal acid–base transformations in complex cases.31 For example, in the case of the glucose molecule, we have shown that the specific deprotonation site out of five candidates in the molecule can be unequivocally assigned using C 1s core-ionization spectra when comparing with calculated spectra modeled for each hypothetical deprotonation center. Core-electron BEs contain site-specific information on the chemical environment, reflecting the molecular structure of the ionized site. We identified the real deprotonation center based on spectral shape and peak positions, i.e., only one of the modeled spectra matched the measured one. This proved the ability of the combined theoretical-experimental approach to site-specifically probe the acid–base chemistry of a molecule in an aqueous solution. The immediate follow-up question is how general such an approach is and whether the technique is also applicable in the case of multiple subsequent deprotonation events.
With that in mind, the current study focuses on the acid–base equilibria of vitamin C (L-ascorbic acid) revealed from LJ-PES. This vital water-soluble micronutrient has attracted much attention since the first pioneering studies of Albert Szent-Györgyi in the 1920s.32 Vitamin C's molecular structure, as shown in Fig. 1, is derived from glucose and exhibits versatile properties, enabling participation in numerous biochemical reactions, notably as an antioxidant.33,34 Its dual acidic and reducing nature allows it to donate protons and electrons, playing a pivotal role in cellular redox reactions, protecting biomolecules from oxidative stress. It also aids in iron absorption, collagen synthesis, neurotransmitter production, immune function, and regeneration of other antioxidants such as vitamin E.34–36
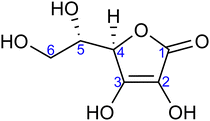 | ||
| Fig. 1 Molecular structure of L-ascorbic acid (vitamin C) in its fully protonated form. The numbering of carbon atoms, as used in this work, is indicated. | ||
Ascorbic acid as the molecular basis of vitamin C was identified by Szent-Györgyi between 1928 and 1932. In 1933, Walter Norman Haworth correctly deduced vitamin C's constitution based on chemical reactivity. The concepts of carbohydrate chemistry were well developed in the 1930s, and no alternative explanations, such as linear aldehyde structures, were considered. The story of vitamin C represents one of the final achievements of the classical era of structural elucidation before the field started to be dominated by various spectroscopies.37 The molecular structure of ascorbic acid can be considered in the form of different tautomers; see, e.g., structures A and B in Fig. 2, with the A form assigned as the correct one in aqueous solution by 13C NMR peak positions and splitting.38 Vitamin C's molecule exhibits four hydroxyl groups, thus representing a polyprotic system with multiple possible deprotonation sites. The first acidity constant is pKa1 = 4.17,39 and thus ascorbic acid is predominantly singly deprotonated at pH = 7, see Fig. 2. The deprotonation site is reported to be located at the –OH group at carbon site C3 based on pH-dependent chemical shifts in 13C NMR.38 With the second acidity constant being pKa2 = 11.57,39 ascorbic acid is doubly deprotonated in strongly alkaline solutions (Fig. 2) with the second deprotonation taking place at C2, again determined by 13C NMR.38
Here, we apply our combined experimental–theoretical approach using LJ-PES and ab initio modeling to probe the acid–base structure of vitamin C in an aqueous solution. We performed pH-dependent measurements of solutions at pH values of 2, 7, and 13 in order to be well below or above the respective pKa1 and pKa2 values. This means that we investigate a different acid–base structure in each solution – fully protonated at pH = 2, singly deprotonated at pH = 7, and doubly deprotonated at pH = 13 (Fig. 2). We show the versatility of core-level LJ-PES as a valuable tool to explore tautomeric forms and acid–base molecular structures as we site-specifically probe not only the single deprotonation, as in the case of our previous work on glucose, but also double deprotonation for the first time. As the accumulated empirical data do not allow for a theory-free determination of the chemical structure, we rely on ab initio theory. It is vital to employ a fast, reliable, and stable computational protocol to screen through a larger number of molecular structures. Therefore, the methodological aspects of the computations are explored. We present an efficient computational approach to model the spectra from a single molecular geometry based on the maximum-overlap method and compare the protocol to calculations from an ensemble of structures.
2 Methods
2.1 Experiments
LJ-PES measurements were performed at the P04 soft-X-ray beamline at PETRA III40 (DESY, Hamburg, Germany) using the EASI setup.41 A vacuum LJ of ∼26 μm diameter was ejected with a velocity of ∼25 m s−1via a fused-silica nozzle. A high-performance liquid chromatography (HPLC) pump was used for solution delivery with a constant flow rate of 0.8 ml min−1. The temperature of the ascorbic-acid aqueous solution after injection was estimated to be in the range of 279–283 K in the laminar region of the LJ, which typically extends for 5–10 mm from the capillary into vacuum.1,2 This laminar region is brought into overlap with the X-ray beam and the photoelectron detection axis. The liquid subsequently freezes and is collected by a liquid-nitrogen-cooled trap at the far end of the interaction chamber. A small metallic tube, placed into the main polyether ether ketone (PEEK) liquid-delivery line, enables electric grounding of the liquid or application of a defined bias voltage.Circularly polarized light from the beamline, with a focal size of 180 μm in the horizontal direction (parallel to the liquid jet) and 35 μm in the vertical direction (perpendicular to the liquid jet), intersected the jet perpendicular to the flow of the solution. The small focal size allowed for the spatial overlap with the liquid jet. Photoelectrons were detected in a backward-scattering detection geometry, corresponding to an angle of 130° with respect to the light propagation direction, i.e., near magic angle,41 thus minimizing any differential sensitivity to the photoelectron angular distributions. A single photon energy of 400.88 ± 0.02 eV was used for measuring all the C 1s PE spectra from the aqueous-phase ascorbic acid in this study, which corresponds to a (unbiased) kinetic energy of about 105 eV for C 1s electrons. C 1s spectra obtained at 850 eV photon energy, corresponding to a slightly increased probing depth into solution, from approximately 20 Å (∼7 solution layers) to 30 Å (∼10 layers),42 exhibit very similar shapes; see the ESI† for details. Calibration of the photon energy was done by measuring well-known absorption features of gas-phase N2,43 right before the solution spectra were measured. In all cases, the energy resolution of the P04 beamline was better than 250 meV. The energy resolution of the hemispherical analyzer was 100 meV, yielding a total energy resolution better than 270 meV. Experimental C 1s electron BEs reported in the present study refer to an absolute energy scale (against the vacuum level). This was determined as the energy distance between the position of the spectral low-energy cutoff and the position of the C 1s peak (both measured from a liquid jet biased with −64 V, thus accelerating the photoelectrons) and from the accurately known photon energy; this procedure of determining absolute electron BEs from liquids and (aqueous) solutions has been detailed in ref. 13. We estimate the resulting error for all stated BE values to be ±0.1 eV, which is a combination of fit errors and the accuracy of our measurements.
Commercially available L-ascorbic acid, C6H8O6 (Sigma-Aldrich, >99% purity), was dissolved in MilliQ (18.2 MΩ cm−1) water to prepare 0.5 M solutions. Ascorbic-acid aqueous solutions of 0.5 M concentration without prior pH adjustment were found to exhibit a pH of 2, which is well below the first acidity constant, pKa1 = 4.17,39 and all solute molecules are fully protonated. A small amount of NaCl (yielding 50 mM concentration) was added to ensure sufficient solution conductivity and minimize sample charging due to photoionization and the streaming potential.2 The conductivity is readily maintained for pH-adjusted solutions in the following. In order to shift the population to dominantly singly and doubly deprotonated ascorbic acid, the solution pH was adjusted to 7 and 13, respectively. This was done by addition of NaOH pellets into the aqueous solutions under constant magnetic stirring. The solution pH was monitored with a previously calibrated pH meter (VWR, pHenomenal 1100L).
2.2 Computational strategies
The interpretation of the liquid-phase PE spectra relies on electronic-structure calculations, which requires solving two issues: accurate calculation of BEs and proper treatment of solvation.44 Different flavors of density functional theory (DFT) are typically used to model the valence PE spectrum, e.g., by using a combination of DFT with time-dependent density functional theory45 or utilizing the ionization-potential theorem combined with optimally tuned range-separated hybrid functionals.46,47 Correlated ab initio calculations, e.g., using equation-of-motion coupled clusters (EOM-CC) theory typically provide more accurate results but at a higher computational price.48–50 An alternative strategy employs Green's function formalism.51,52 The calculations are more complicated for core-electronic levels, i.e., aiming at highly excited states of the ions. Here, the core-valence separation can be used in conjunction with EOM-CC,53,54 representing the state-of-the-art approach. Alternatively, the maximum-overlap method55 (MOM) can be used. MOM is based on modifying the convergence criteria to not only minimize eigenvalues but also to maximize overlap with the orbitals from the previous step. In this way, the approach prevents the variational collapse of the wavefunction and keeps the hole in the desired orbital. This represents an efficient and accurate approach as MOM can be combined with any electronic-structure method and includes full electronic relaxation. Based on our previous experience,31 we aim to utilize MOM in this way to describe core-level ionization in this study.The most efficient approach to cover the solvation effects is using the dielectric continuum model.56 It is mandatory to use its non-equilibrium form to separate the fast electronic and slow nuclear response.57,58 The specific solvent effects can be conveniently added within cluster-continuum models59,60 by including a few closest solvent molecules into the quantum-mechanical calculation explicitly, while the rest is represented by the dielectric continuum. However, when dealing with systems exhibiting highly concentrated charges, e.g., containing –O− groups, a large number of explicit solvent molecules may be required to achieve convergence.61,62 Alternatively, the QM/MM (quantum mechanics/molecular mechanics) or fragmentation techniques can be used.63,64
2.3 Calculations
The core-level BEs were calculated for optimized structures using the maximum-overlap method55 in its improved form, called initial maximum-overlap method,70 which yields better convergence. Here, we used the CAM-B3LYP functional with the aug-cc-pVTZ basis set71,72 for hydrogen atoms and the core-enhanced aug-cc-pCVTZ basis set73 for carbon and oxygen atoms. From our experience, this combination provides a very good accuracy (as we also demonstrate below in the present case) for an acceptable computational price. The solvent effects were included by non-equilibrium PCM,56,57 while partitioning the solvent response to slow (nuclear) and fast (electronic) responses to describe the rapid nature of the photoionization process. The same PCM parameters (UFF atomic radii, α = 1.1) as in the optimization described above were used. The calculations were performed in the Q-Chem package, version 6.0.74 The sample input is shown in the ESI.†
PE spectra were constructed from the calculated BEs as follows. Each energy value was broadened into a Gaussian function of the same intensity and width, and the Gaussian functions were summed to create the spectrum. The width of the Gaussian functions was set empirically for each protonation state to reproduce the experimentally observed spectral widths. Specifically, the standard-deviation value was set to 0.42, 0.45, and 0.52 eV for fully protonated, singly deprotonated, and doubly deprotonated molecules, respectively.
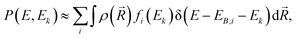 | (1) |
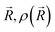 is the ground-state nuclear density and the electronic factor fi(Ek) is assumed in our study to be constant for all kinetic energies.78 Moreover, it has been shown that the number of sampled structures to represent
is the ground-state nuclear density and the electronic factor fi(Ek) is assumed in our study to be constant for all kinetic energies.78 Moreover, it has been shown that the number of sampled structures to represent 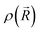 can be significantly lowered even to a single representative structure.79
can be significantly lowered even to a single representative structure.79
We used NEM here only for the fully protonated form (tautomer A), the singly deprotonated form at C3, and the doubly deprotonated form at C2 and C3. The geometries were sampled from a quantum mechanics/molecular mechanics simulation of a droplet containing the ascorbic-acid molecule in the respective protonation state and 1000 water molecules. The quantum part was applied to the ascorbic acid and was described at the B3LYP/6-31+G* level of theory with Grimme's D2 dispersion correction.80 The MM part modeling the water molecules was described by the TIP3P model.81 The temperature was kept constant at 280 K (close to the experimental conditions) during the simulation using the Nosé–Hoover thermostat.82,83 With this approach, we ignore nuclear quantum effects; however, they are usually not of significance for modeling PE spectra in the liquid phase.84 The initial droplet structure was created by the Packmol code,85 and the QM/MM simulation was performed with our ABIN code86 connected to Terachem, version 1.93.87,88 The total simulation length was 50 ps, with a time step of 0.5 fs. The first 10 ps were discarded as equilibrating period. From the remaining 40 ps, 100 geometries were sampled with equidistant steps of 400 fs. Geometries which contained the same number of explicit water molecules as in the single optimized geometry calculations were extracted, i.e., 0, 6, and 12 water molecules for fully protonated, singly deprotonated, and doubly deprotonated forms, respectively. These water molecules were again chosen to be the closest to the deprotonated –O− sites. The sampled geometries can be found in the ESI.†
The extracted 100 geometries for each protonated form were used as input for core-level binding-energy calculations employing exactly the same methodology as described for the single-geometry calculations. The resulting spectrum was again constructed from individual Gaussian functions with the same widths as detailed above.
3 Results and discussion
3.1 Core-level C 1s ionization for a site-specific probing of acid–base structure
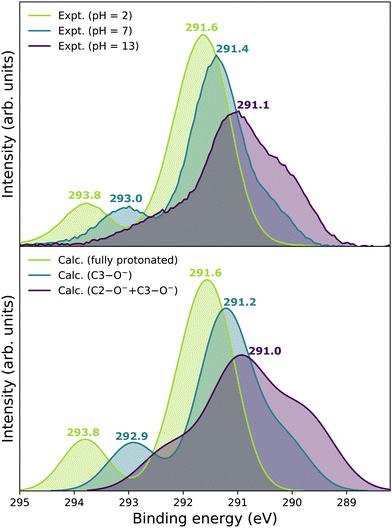
Our goal is to demonstrate the potential of LJ-PES for elucidating structural information. For this, we focus on the well-described example molecule of vitamin C and show that the chemical insight obtained from LJ-PES can be as good as the one achieved from NMR studies, with LJ-PES having the additional capabilities described in the introduction.Experimental and theoretical PE spectra for all three protonation states are presented in Fig. 3, panels A–C. Experimental spectra measured using a precise photon energy of 400.88 ± 0.02 eV are plotted in black and theoretical spectra are colored as indicated. We first focus on C 1s core-level PE spectra for pH = 2 (panel A) and pH = 7 (panel B), where the fully protonated and singly deprotonated forms of ascorbic acid are expected to be present.39 The results for pH = 13 (panel C), extending our approach to double deprotonation for the first time, are discussed later.
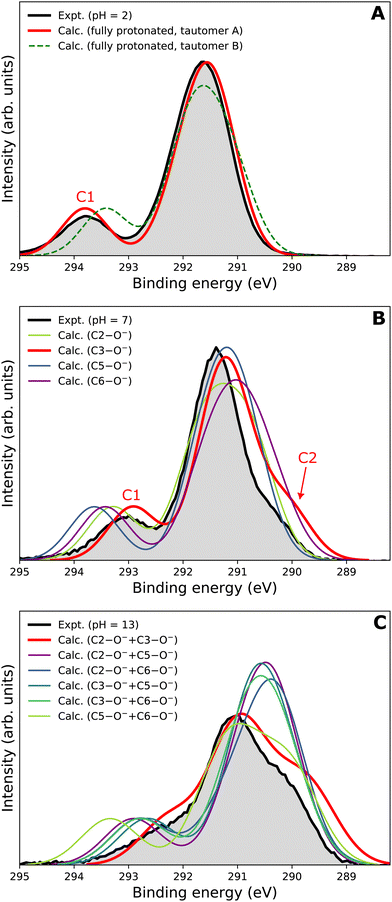 | ||
| Fig. 3 C 1s PE spectra of vitamin C at (A) pH = 2 (fully protonated), (B) pH = 7 (singly deprotonated), and (C) pH = 13 (doubly deprotonated); experimental spectra in black and calculated spectra in color as indicated in the legend. In panel A, spectra for two tautomers are modeled. In panels B and C, spectra for all possible deprotonation sites of tautomer A are modeled. The calculated spectrum with the best match is plotted in red in each panel. A quantification of the similarity between calculated and experimental spectra using KL (Kullback–Leibler) divergence can be found in the ESI† in Table S1. | ||
For a fully protonated molecule of vitamin C, we consider two tautomers (A and B, Fig. 2). The A form has been identified by NMR38 to be present in aqueous solution, and we show here that LJ-PES is capable of confirming this conclusion. The experimental PE spectrum for pH = 2 exhibits a main peak centered at BE = 291.6 eV and a smaller peak at BE = 293.8 eV. The experiment can be compared to our calculated spectra for the (fully protonated) A tautomer (red line) and the B tautomer (green dashed line). The modeled spectrum of the A tautomer agrees excellently with the experiment both in shape and position. From the theory, we can assign the smaller peak to ionization of the C1 site (see Fig. 1 and Table 1) while the main peak is from the combined signal of the other five carbon sites in the molecule. The main peak's position is in line with the previously published C 1s data for various systems containing the C–OH group ranging 291–291.5 eV, as mentioned in the Introduction, including the main peak of glucose C–OH centered at 291.5 eV.31 On the other hand, the modeled spectrum for the B tautomer exhibits discrepancies when compared to the experiment. With the positions of the smaller and main peaks at 293.4 eV and 291.6 eV, respectively, the energy separation between them is too small. Moreover, as the main peak is slightly broader, the relative intensities of the main and smaller peaks differ from the experiment. Therefore, we confirm that the A tautomer prevails in solution, and subsequent deprotonations will be considered for this structure.
| Carbon atoms | Experiment | Calculation |
|---|---|---|
| pH = 2 | ||
| C1 | 293.8 | 293.8 |
| C2–C6 | 291.6 | 291.6 |
| pH = 7 | ||
| C1 | 293.0 | 292.9 |
| C2 | 290.4 | 290.1 |
| C3–C6 | 291.4 | 291.2 |
| pH = 13 | ||
| C1 | 292.4 | 292.3 |
| C2–C3 | 290.1 | 289.8 |
| C4–C6 | 291.1 | 291.0 |
Let us now focus on a singly deprotonated form of vitamin C, with the deprotonation site assigned to the C3–OH site by NMR.38 The pH = 7 PE spectrum (panel B, black line) exhibits similar main and C1 peaks, but their positions have clearly changed with respect to pH = 2, with their maxima at BE = 291.4 eV and BE = 293.0 eV, respectively. Moreover, a shoulder at BE = 290.4 eV appears, originating from the C2 1s electron according to our calculations (Table 1). These observations indicate that vitamin C exists in a different form at pH = 7 compared to pH = 2; the good match with theory indicates that, indeed, a singly deprotonated form is present, as discussed in the following. The ascorbic-acid molecule has four –OH groups (at carbons C2, C3, C5, and C6) that could, in principle, deprotonate at relatively low pH (Fig. 2). Therefore, we modeled spectra for all four hypothetical acid–base forms using the cluster-continuum solvation model; results are shown in panel B of Fig. 3 for C2 (green), C3 (red), C5 (blue), and C6 (purple). When comparing the calculated spectra to the experiment, only one modeled deprotonation site (C3–O−) reproduces the experimentally observed features, with the additional shoulder at ≈290 eV being the most distinct one. Our calculation predicts positions of the main and the smaller peaks of 291.2 eV and 292.9 eV, respectively, i.e., an energetic distance of 1.7 eV, very close to the experimental energetic distance of 1.6 eV. Thus, we can safely assign the deprotonation center to the C3–OH site, consistent with the published NMR data.38
Interestingly, the high-BE peak originating from C1 is shifted by 0.8 eV upon the deprotonation at C3–OH, thus being influenced by an atom that is three chemical bonds away from the deprotonation site. A similar observation can be made for the C2 site, for which the chemical shift results in a distinguishable feature in the PE spectrum of the singly deprotonated molecule. This is well reproduced by our calculations and can be explained by two resonant structures,38 resulting in the –O− group attached to either C3 or C1, as shown in Fig. 4. Importantly, analogous shifts for C1 and C2 signals are also observed in 13C NMR pH-dependent spectra.38 This demonstrates that site-specific changes affect not only the observable LJ-PES chemical shift of the site itself but also of other atoms at a distance of a few chemical bond lengths.
3.2 Extending the structural assignment to double deprotonation
Next, we investigate whether our approach is also capable of probing two different acid–base sites selectively at the same time. As for the single deprotonation, this question has not escaped the attention of NMR spectroscopists, concluding that the deprotonation takes place at C2–OH and C3–OH.38Here, we investigate the PES spectrum for pH = 13, where double deprotonation of vitamin C is expected. The experimental spectrum (black) in panel C of Fig. 3 consists of a broad band with a maximum at BE = 291.1 eV, with a shoulder at BE = 290.1 eV, and another broad shoulder at BE = 292.4 eV. The spectrum is quite different from the one at pH = 7, and, in combination with our calculations (below), we find that the signal indeed comes from a doubly deprotonated molecule.
To interpret the experimental data, we again modeled all possible combinations of deprotonation for two sites to compare them with the experiment. We employed the cluster-continuum solvation model with 12 explicit water molecules placed around the deprotonated groups, as detailed in the Methods section. Calculated spectra for a total of six hypothetical combinations of double deprotonations (Fig. 2) are shown in panel C of Fig. 3. We observe that only one combination (C2–O− + C3–O−) reproduces all the experimental features. It exhibits the lowest energy separation between the main peak and the high-BE shoulder, similar to the broad high-BE shoulder observed in the experiment. That spectrum also reproduces the low-BE shoulder with a similar height ratio. Also, the main peak's calculated position of 291.0 eV is in very good agreement with the measured spectrum (Table 1). Thus, our approach directly enables us to uniquely assign the two deprotonation centers in the molecule to C2–O− and C3–O−. Our conclusion is in accordance with previously published results from NMR.38 To our knowledge, this is the very first time LJ-PES has been used to site-specifically probe double deprotonation acid–base sites. Although the double deprotonation of vitamin C has been previously probed by NMR, we highlight that LJ-PES augmented with theory can be used to derive the same structural information in this case, and in addition, promises to provide a plethora of complementary information, e.g., on electronic structure, electronic decay channels, speciation or intermolecular interactions.28,29,89
3.3 Fast and reliable ab initio interpretation of the experimental data
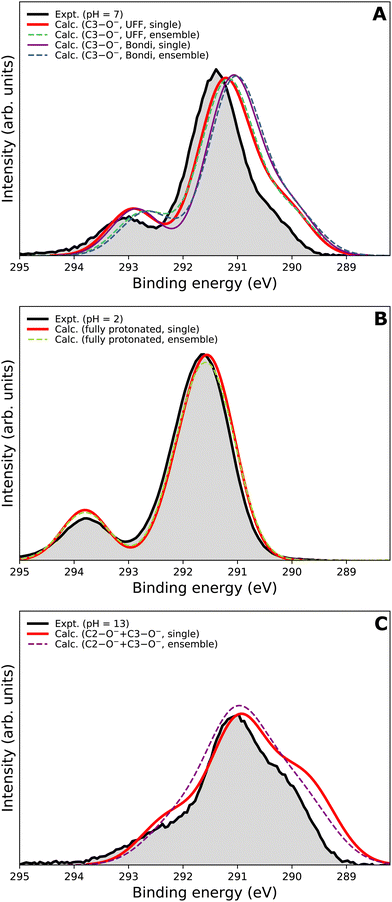
We now focus on the accuracy of our calculations. The so-far presented spectra were modeled using the maximum-overlap method based on a single structure for each protonation state. Therefore, the computations are inexpensive and relatively straightforward. Yet, they appear to be surprisingly accurate, as summarized in Table 1 and Fig. 5. All the peak positions are reproduced with an accuracy of 0.2 eV compared to the experiment, which has its own uncertainty of ≈0.1 eV. The small inaccuracies in our computations are attributed to multiple approximations, as described in the Calculations section, inevitably accompanying any theoretical effort to describe complex disordered systems of solvated molecules. We can compare our results to the typical accuracy of the state-of-the-art approach based on the equation-of-motion coupled clusters with single and double excitations (EOM-CCSD). With a small set of various gas-phase molecules, the reported mean average error (MAE) for calculated C 1s BEs was 0.68 eV, or 0.24 eV after shifting the values to eliminate systematic errors.90 For aqueous-phase glycine, the error was 0.05–0.22 eV when employing equilibrium averaging with an explicit solvent model based on EOM-CCSD with an effective fragment potential and solvent polarization correction.90 Our results thus indicate that the computational framework based on the maximum-overlap method combined with a suitably selected DFT approach is a powerful and efficient method for modeling core-level ionization. Although one could argue that the accuracy is based on an empirical combination of the CAM-B3LYP functional with a sufficiently large basis set and on possible cancellation of errors, we recommend this approach for modeling core-level electron ionization when aiming for high precision for a relatively low computational price. Before enough experimental data are collected to extract general trends, the above combination offers a pragmatic tool for the interpretation of the experimental data.The spectra modeled in this work using a single optimized geometry are accurate; however, this approach is not generally applicable to all systems as a single minimal structure might be an insufficient representation of the overall distribution. A more robust technique, such as the nuclear-ensemble method,75–77 can be used to sample an ensemble of initial structures from molecular dynamics. To provide a comparison, we also employed NEM to model the spectra. Specifically, we sampled 100 geometries from 40 ps long QM/MM dynamics and used them as input to our calculations for constructing the PE spectra.
We first focus on the singly deprotonated form of vitamin C. Panel A of Fig. 6 shows the calculated spectra from a single structure (denoted as ‘single’) as well as from an ensemble of 100 structures from molecular dynamics (denoted as ‘ensemble’). In addition, we also compare two PCM cavity radii specifications (UFF68 and Bondi91) each to provide insight into how much those parameters influence the overall modeled spectrum. The differences in the four modeled spectra in panel A of Fig. 6 are not large overall but clearly follow an interesting pattern, which is also distinctive for the main peak and for the small high-BE peak. For the main peak, a difference in position of ≈0.15 eV is caused by changing the cavity specification. This is, from our experience, a typical behavior. Interestingly, the main peak's position remains the same regardless of using a single structure or an ensemble of structures. The single-geometry approximation is thus reasonable in the present case. This is distinct from the behavior of the high-BE peak. A difference of ≈0.25 eV is seen between the single-structure and ensemble models, irrespective of the PCM cavity model. The ensemble model provides a slightly less accurate (compared to the experiment) peak position in this particular case. While the nuclear-ensemble approach is an approximation, we attribute the worse agreement with the experiment to the insufficiency of our molecular dynamics used for the sampling. Particularly, we used the QM/MM method with a QM zone containing the ascorbic-acid molecule and an MM zone containing solvating water molecules. Thus, we interpret the discrepancy as an insufficient description of the explicit solvent structure around the vitamin C molecule. This claim is further supported by the spectrum of the fully protonated form in panel B of Fig. 6, where no explicit water molecules from QM/MM dynamics were used and where the ‘single’ and ‘ensemble’ spectra match in both peak positions. In fact, both are virtually identical, confirming that the single geometry is a good representation of the system distribution. Consequently, a single-structure spectrum based on optimization to the energetic minimum can provide a more reliable result in some cases, such as for the singly deprotonated form discussed above.
In panel C of Fig. 6, the results for the doubly deprotonated form of ascorbic acid are shown. Although the position of the maximum is very similar, the spectral shape is slightly different. Specifically, the spectrum obtained from an ensemble of structures lacks the low-BE and, to some extent, also the high-BE shoulder. We again attribute this to the insufficiently described solvation structure by the QM/MM molecular dynamics used for the sampling. Thus, the single-geometry spectrum again reproduces the experimental spectral features more closely. In summary, a single microhydrated structure optimized on a sufficiently high level of theory provides a more accurate spectrum than an ensemble of structures sampled from molecular dynamics with a lower level of theory.
We emphasize that the computational price for the ‘ensemble’ spectra in the presented case is about one hundred times higher than that of the spectra from a single geometry. Thus, we find that the single geometry is an inexpensive yet accurate approach to modeling LJ-PE spectra of carbon core-level electrons.
4 Conclusions
We have reported the pH-dependent C 1s liquid-jet PE spectra of vitamin C in water. By performing measurements at pH = 2, pH = 7, and pH = 13, we obtained data for three different acid–base forms. The peaks’ origin was interpreted by assigning contributions of specific carbon atoms using electronic-structure calculations.We have demonstrated the applicability of a combined experimental–theoretical approach based on LJ-PES to probe tautomeric and acid–base molecular structure in aqueous solutions, using vitamin C as a prototype. A dominant tautomeric form of a fully protonated molecule has been determined. For the singly deprotonated molecule, we unequivocally assigned the deprotonation center to be C3–OH. Moreover, for the first time, the method has been extended to a double-deprotonation case, demonstrating the ability to selectively probe two acid–base centers simultaneously. This enabled us to identify the two deprotonation sites, C2–OH and C3–OH, in the double-deprotonated form of vitamin C in a highly alkaline solution.
These results are consistent with previous findings based on NMR spectroscopy. The two approaches thus provide comparable structural information. As NMR sometimes suffers from structural misassignments,22–25 there is room for the development of complementary structure-sensitive techniques. Furthermore, LJ-PES provides additional advantages as it simultaneously captures the full electronic structure and reflects molecular interactions, e.g., with the neighboring solvent molecules.28 Note also that a single LJ-PES measurement can probe the structure from the perspective of different atomic species (e.g., carbon and nitrogen) that can be helpful in the elucidation of complex structures. In the present case, probing the oxygen sites would be of little use due to the signal overlap with the aqueous solvent's oxygen. The LJ-PES technique can be conveniently expanded to studying air–water interfaces by varying the photon energy and thus the probing depth,92 exploring, e.g., specific acid–base behavior and speciation at the interface, relevant for atmospheric chemistry.
An interesting phenomenon observed in the present study is that deprotonation affects BEs of core-level electrons of an atom that is a few chemical bonds away from the deprotonation site. This may be surprising, considering the enormous ability of water to screen the electrostatic effects.93 Our observation is promising for a possible application of multivariate analysis techniques to the measured data to reconstruct the full molecular structure from LJ-PES.
We have presented an efficient computational approach to model C 1s photoelectron spectra in aqueous solution. It is based on a single optimized geometry and employs the maximum-overlap method with the CAM-B3LYP functional. With this, we achieved an accuracy of 0.2 eV for the modeled BEs. The computational protocol is inexpensive and relatively straightforward. Therefore, we recommend this approach as the first choice for calculating core-level BEs in aqueous solutions.
The high accuracy of the computational protocol is in line with our previous studies. Note that the calculated BEs are close to the experiment on an absolute scale. This finding is somewhat surprising in the present case for two reasons. First, the deprotonated forms of the ascorbic acid contain an –O− group with a highly concentrated charge. For calculations of the valence region, such a situation would usually require the inclusion of explicit solvent molecules in a large zone around the site.50 Second, the same computational treatment is required when dealing with multiply charged anions.62 In the present case, correct core-level energies are reproduced even with a minimalistic model assuming just a dielectric approximation of the environment and a few explicitly treated solvent molecules.
The present study further outlines the capabilities of liquid-phase photoemission spectroscopy for studying chemical and biochemical phenomena. In a broader sense, we attempt to bring LJ-PES's large potential to the awareness of experimental chemists. Both X-ray photoemission spectroscopy and nuclear magnetic resonance started to be developed in the 1950s, yet the former technique became almost exclusively a domain of solid-state physicists. We believe that LJ-PES could have played a more important role than NMR in an alternative history, and it is worth pursuing the paths it offers. The selectivity of the technique enables specific investigation of even complex systems,28 and a combination of information from different spectral regions provides full insight into the molecular structure in disordered systems. The need to interpret these data with the help of demanding electronic-structure calculations is one of the hurdles to a broader application of the technology. The present study focuses exclusively on the photoelectrons, yet further information can be retrieved from Auger and other second-order electrons (e.g., electrons stemming from intermolecular Coulombic decay89). The latter spectra, however, have been so far only rarely used for structural determination, even though they contain important additional information.29 More studies are, therefore, needed to extract empirical trends to make the approach theory-free, i.e., enable chemical and structural assignment on the basis of documented energies and spectral shapes.
The chemistry and acid–base properties of vitamin C are well-known. We used this system as a prototype with a large potential space of protonation states. We recall here that vitamin C was a favorite molecule of Linus Pauling, especially in his later years.94,95 While his views on the health effects of vitamin C were highly controversial, he is an undisputed titan of structural chemistry and the nature of a chemical bond.96,97 This work can be considered a homage to his lifelong achievements.
Author contributions
Lukáš Tomaník: conceptualization, methodology, investigation, writing – original draft, writing – review & editing, visualization. Michele Pugini: methodology, validation, formal analysis, investigation, data curation, writing – review & editing. Karen Mudryk: methodology, formal analysis, investigation, writing – review & editing. Stephan Thürmer: software, formal analysis, writing – review & editing. Dominik Stemer: investigation. Bruno Credidio: investigation. Florian Trinter: investigation. Bernd Winter: conceptualization, resources, writing – original draft, writing – review & editing, supervision, project administration, funding acquisition. Petr Slavíček: conceptualization, resources, writing – original draft, writing – Review & editing, supervision, project administration, funding acquisition.Data availability
Cartesian coordinates of optimized structures, sample input for calculating core-level ionization energies, and Cartesian coordinates of structures sampled from QM/MM dynamics are available in the ESI.† The raw data relevant to this work has been deposited at DOI: 10.5281/zenodo.10706227.Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. T. and P. S. appreciate the support of the Czech Science Foundation (EXPRO project no. 21-26601X). L. T. was supported in the later stage of the project by the outgoing grant of the Czech Science Foundation, grant number 24-12267O. M. P. and B. W. acknowledge funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 883759, AQUACHIRAL). F. T. and B. W. acknowledge support from the MaxWater initiative of the Max-Planck-Gesellschaft. F. T. acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project 509471550, Emmy Noether Programme. S. T. acknowledges support from the JSPS KAKENHI grant no. JP20K15229. This work was supported by the project “The Energy Conversion and Storage”, funded as project no. CZ.02.01.01/00/22 008/0004617 by Programme Johannes Amos Comenius, call Excellent Research.References
- M. Faubel, B. Steiner and J. P. Toennies, J. Chem. Phys., 1997, 106, 9013–9031 CrossRef CAS.
- B. Winter and M. Faubel, Chem. Rev., 2006, 106, 1176–1211 CrossRef CAS PubMed.
- B. Winter, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 601, 139–150 CrossRef CAS.
- R. Seidel, B. Winter and S. E. Bradforth, Annu. Rev. Phys. Chem., 2016, 67, 283–305 CrossRef CAS PubMed.
- K. Siegbahn, ESCA. Atomic, Molecular and Solid State Structure Studied by Means of Electron Spectroscopy, Almqvist & Wiksells Uppsala, Uppsala, 1967 Search PubMed.
- R. Signorell and B. Winter, Phys. Chem. Chem. Phys., 2022, 24, 13438–13460 RSC.
- R. Dupuy, C. Richter, B. Winter, G. Meijer, R. Schlögl and H. Bluhm, J. Chem. Phys., 2021, 154, 060901 CrossRef CAS PubMed.
- K. A. Perrine, K. M. Parry, A. C. Stern, M. H. C. V. Spyk, M. J. Makowski, J. A. Freites, B. Winter, D. J. Tobias and J. C. Hemminger, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13363–13368 CrossRef CAS PubMed.
- S. Ghosal, J. C. Hemminger, H. Bluhm, B. S. Mun, E. L. Hebenstreit, G. Ketteler, D. F. Ogletree, F. G. Requejo and M. Salmeron, Science, 2005, 307, 563–566 CrossRef CAS PubMed.
- C. H. Wu, R. S. Weatherup and M. B. Salmeron, Phys. Chem. Chem. Phys., 2015, 17, 30229–30239 RSC.
- S. Malmgren, K. Ciosek, M. Hahlin, T. Gustafsson, M. Gorgoi, H. Rensmo and K. Edström, Electrochim. Acta, 2013, 97, 23–32 CrossRef CAS.
- T. Reuss, S. S. Nair Lalithambika, C. David, F. Döring, C. Jooss, M. Risch and S. Techert, Acc. Chem. Res., 2023, 56, 203–214 CrossRef CAS PubMed.
- S. Thürmer, S. Malerz, F. Trinter, U. Hergenhahn, C. Lee, D. M. Neumark, G. Meijer, B. Winter and I. Wilkinson, Chem. Sci., 2021, 12, 10558–10582 RSC.
- B. Winter, U. Hergenhahn, M. Faubel, O. Björneholm and I. V. Hertel, J. Chem. Phys., 2007, 127, 094501 CrossRef PubMed.
- B. Winter, E. F. Aziz, N. Ottosson, M. Faubel, N. Kosugi and I. V. Hertel, J. Am. Chem. Soc., 2008, 130, 7130–7138 CrossRef CAS PubMed.
- D. Hollas, M. N. Pohl, R. Seidel, E. F. Aziz, P. Slavček and B. Winter, Sci. Rep., 2017, 7, 756 CrossRef PubMed.
- J. Li, J. Lu, A. Chew, S. Han, J. Li, Y. Wu, H. Wang, S. Ghimire and Z. Chang, Nat. Commun., 2020, 11, 2748 CrossRef CAS PubMed.
- L. Barreau, A. D. Ross, S. Garg, P. M. Kraus, D. M. Neumark and S. R. Leone, Sci. Rep., 2020, 10, 5773 CrossRef CAS PubMed.
- J. Nishitani, C. W. West and T. Suzuki, Struct. Dyn., 2017, 4, 044014 CrossRef PubMed.
- Z. Yin, Y.-P. Chang, T. Balčiūnas, Y. Shakya, A. Djorović, G. Gaulier, G. Fazio, R. Santra, L. Inhester, J.-P. Wolf and H. J. Wörner, Nature, 2023, 619, 749–754 CrossRef CAS PubMed.
- R. R. Ernst, G. Bodenhausen and A. Wokaun, Principles of Nuclear Magnetic Resonance in One and Two Dimensions, Oxford University Press, 1990 Search PubMed.
- H.-D. Yoo, S.-J. Nam, Y.-W. Chin and M.-S. Kim, Arch. Pharm. Res., 2016, 39, 143–153 CrossRef CAS PubMed.
- S.-M. Shen, G. Appendino and Y.-W. Guo, Nat. Prod. Rep., 2022, 39, 1803–1832 RSC.
- K. C. Nicolaou and S. A. Snyder, Angew. Chem., Int. Ed., 2005, 44, 1012–1044 CrossRef CAS PubMed.
- T. L. Suyama, W. H. Gerwick and K. L. McPhail, Bioorg. Med. Chem., 2011, 19, 6675–6701 CrossRef CAS PubMed.
- E. F. Aziz, N. Ottosson, M. Faubel, I. V. Hertel and B. Winter, Nature, 2008, 455, 89–91 CrossRef CAS PubMed.
- N. Ottosson, K. J. Børve, D. SpÅngberg, H. Bergersen, L. J. Sæthre, M. Faubel, W. Pokapanich, G. Öhrwall, O. Björneholm and B. Winter, J. Am. Chem. Soc., 2011, 133, 3120–3130 CrossRef CAS PubMed.
- L. He, L. Tomaník, S. Malerz, F. Trinter, S. Trippel, M. Belina, P. Slavíček, B. Winter and J. Küpper, J. Phys. Chem. Lett., 2023, 14, 10499–10508 CrossRef CAS PubMed.
- K. Mudryk, C. Lee, L. Tomaník, S. Malerz, F. Trinter, U. Hergenhahn, D. M. Neumark, P. Slavíček, S. Bradforth and B. Winter, J. Am. Chem. Soc., 2024, 146, 16062–16075 CrossRef CAS PubMed.
- S. Thürmer, R. Seidel, B. Winter, M. Ončák and P. Slavíček, J. Phys. Chem. A, 2011, 115, 6239–6249 CrossRef PubMed.
- S. Malerz, K. Mudryk, L. Tomaník, D. Stemer, U. Hergenhahn, T. Buttersack, F. Trinter, R. Seidel, W. Quevedo, C. Goy, I. Wilkinson, S. Thürmer, P. Slavíček and B. Winter, J. Phys. Chem. A, 2021, 125, 6881–6892 CrossRef CAS PubMed.
- A. Szent-Györgyi, Nobel Lecture, Nobel Foundation, 1937, https://www.nobelprize.org Search PubMed.
- Institute of Medicine, Dietary Reference Intakes for Vitamin C, Vitamin E, Selenium, and Carotenoids, The National Academies Press, Washington, DC, 2000.
- M. Davies, D. Partridge and J. Austin, Vitamin C: Its Chemistry and Biochemistry, Royal Society of Chemistry, 2007 Search PubMed.
- T. Ems, K. St Lucia and M. R. Huecker, Biochemistry, Iron Absorption, StatPearls Publishing, Treasure Island (FL), 2022 Search PubMed.
- N. Martıénez-Navarrete, M. Camacho, J. Martıénez-Lahuerta, J. Martıénez-Monzó and P. Fito, Food Res. Int., 2002, 35, 225–231 CrossRef.
- E. L. Hirst, in The Structure and Synthesis of Vitamin C (Ascorbic Acid) and its Analogues, ed. L. Zechmeister, Y. Asahina, C. Dhéré, K. Freudenberg, C. R. Harington, E. L. Hirst, F. Kuffner, H. Rudy, E. Spath, G. Tóth and G. Zemplén, Springer, Vienna, Vienna, 1939, pp. 132–159 Search PubMed.
- S. Berger, Tetrahedron, 1977, 33, 1587–1589 CrossRef CAS.
- T. W. Birch and L. J. Harris, Biochem. J., 1933, 27, 595 CAS.
- J. Viefhaus, F. Scholz, S. Deinert, L. Glaser, M. Ilchen, J. Seltmann, P. Walter and F. Siewert, Nucl. Instrum. Methods Phys. Res., Sect. A, 2013, 710, 151–154 CrossRef CAS.
- S. Malerz, H. Haak, F. Trinter, A. B. Stephansen, C. Kolbeck, M. Pohl, U. Hergenhahn, G. Meijer and B. Winter, Rev. Sci. Instrum., 2022, 93, 015101 CrossRef CAS PubMed.
- H. T. Nguyen-Truong, J. Phys.: Condens. Matter, 2018, 30, 155101 CrossRef PubMed.
- R. N. Sodhi and C. Brion, J. Electron Spectrosc. Relat. Phenom., 1984, 34, 363–372 CrossRef CAS.
- E. Pluhařová, P. Slavíček and P. Jungwirth, Acc. Chem. Res., 2015, 48, 1209–1217 CrossRef PubMed.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- E. Muchová and P. Slavček, J. Phys.: Condens. Matter, 2018, 31, 043001 CrossRef PubMed.
- U. Salzner and R. Baer, J. Chem. Phys., 2009, 131, 231101 CrossRef PubMed.
- A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- X. Feng, E. Epifanovsky, J. Gauss and A. I. Krylov, J. Chem. Phys., 2019, 151, 014110 CrossRef PubMed.
- D. Ghosh, A. Roy, R. Seidel, B. Winter, S. Bradforth and A. I. Krylov, J. Phys. Chem. B, 2012, 116, 7269–7280 CrossRef CAS PubMed.
- F. Aryasetiawan and O. Gunnarsson, Rep. Prog. Phys., 1998, 61, 237 CrossRef CAS.
- M. Govoni and G. Galli, J. Chem. Theory Comput., 2015, 11, 2680–2696 CrossRef CAS PubMed.
- M. L. Vidal, X. Feng, E. Epifanovsky, A. I. Krylov and S. Coriani, J. Chem. Theory Comput., 2019, 15, 3117–3133 CrossRef CAS PubMed.
- M. L. Vidal, A. I. Krylov and S. Coriani, Phys. Chem. Chem. Phys., 2020, 22, 2693–2703 RSC.
- A. T. B. Gilbert, N. A. Besley and P. M. W. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171 CrossRef CAS PubMed.
- J. M. Herbert, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1519 CAS.
- R. Cammi and J. Tomasi, Int. J. Quantum Chem., 1995, 56, 465–474 CrossRef.
- B. Jagoda-Cwiklik, P. Slavíček, L. Cwiklik, D. Nolting, B. Winter and P. Jungwirth, J. Phys. Chem. A, 2008, 112, 3499–3505 CrossRef CAS PubMed.
- J. R. Pliego and J. M. Riveros, J. Phys. Chem. A, 2001, 105, 7241–7247 CrossRef CAS.
- V. S. Bryantsev, M. S. Diallo and W. A. Goddard III, J. Phys. Chem. B, 2008, 112, 9709–9719 CrossRef CAS PubMed.
- L. Tomaník, E. Muchová and P. Slavíček, Phys. Chem. Chem. Phys., 2020, 22, 22357–22368 RSC.
- E. Pluhařová, M. Ončák, R. Seidel, C. Schroeder, W. Schroeder, B. Winter, S. E. Bradforth, P. Jungwirth and P. Slavíček, J. Phys. Chem. B, 2012, 116, 13254–13264 CrossRef PubMed.
- M. S. Gordon, D. G. Fedorov, S. R. Pruitt and L. V. Slipchenko, Chem. Rev., 2012, 112, 632–672 CrossRef CAS PubMed.
- J. M. Herbert, J. Chem. Phys., 2019, 151, 170901 CrossRef PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151–5158 CrossRef CAS.
- E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. I. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- G. M. J. Barca, A. T. B. Gilbert and P. M. W. Gill, J. Chem. Theory Comput., 2018, 14, 1501–1509 CrossRef CAS PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, I. DePrince, A. Eugene, J. DiStasio, A. Robert, A. Dreuw, B. D. Dunietz, T. R. Furlani, I. Goddard, A. William, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, I. Woodcock, H. Lee, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- R. Crespo-Otero and M. Barbatti, Theor. Chem. Acc., 2012, 131, 1237 Search PubMed.
- Š. Sršeň, J. Sita, P. Slavíček, V. Ladányi and D. Heger, J. Chem. Theory Comput., 2020, 16, 6428–6438 CrossRef PubMed.
- A. Prlj, E. Marsili, L. Hutton, D. Hollas, D. Shchepanovska, D. R. Glowacki, P. Slavíček and B. F. E. Curchod, ACS Earth Space Chem., 2022, 6, 207–217 CrossRef CAS PubMed.
- C. W. Dierking, F. Zurheide, T. Zeuch, J. Med, S. Parez and P. Slavíček, J. Chem. Phys., 2017, 146, 244303 CrossRef PubMed.
- Š. Sršeň and P. Slavíček, J. Chem. Theory Comput., 2021, 17, 6395–6404 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- M. Rubešová, V. Jurásková and P. Slavíček, J. Comput. Chem., 2017, 38, 427–437 CrossRef PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- D. Hollas, J. Suchan, O. Svoboda, M. Ončák and P. Slavíček, ABIN, v1.0, 2020 Search PubMed.
- I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed.
- A. V. Titov, I. S. Ufimtsev, N. Luehr and T. J. Martinez, J. Chem. Theory Comput., 2013, 9, 213–221 CrossRef CAS PubMed.
- T. Jahnke, U. Hergenhahn, B. Winter, R. Dörner, U. Frühling, P. V. Demekhin, K. Gokhberg, L. S. Cederbaum, A. Ehresmann, A. Knie and A. Dreuw, Chem. Rev., 2020, 120, 11295–11369 CrossRef CAS PubMed.
- A. Sadybekov and A. I. Krylov, J. Chem. Phys., 2017, 147, 014107 CrossRef PubMed.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- S. Thürmer, R. Seidel, M. Faubel, W. Eberhardt, J. C. Hemminger, S. E. Bradforth and B. Winter, Phys. Rev. Lett., 2013, 111, 173005 CrossRef PubMed.
- M. N. Pohl, E. Muchová, R. Seidel, H. Ali, Š. Sršeň, I. Wilkinson, B. Winter and P. Slavíček, Chem. Sci., 2019, 10, 848–865 RSC.
- L. Pauling, Science, 1968, 160, 265–271 CrossRef CAS PubMed.
- L. Pauling, How to Live Longer and Feel Better, Avon, 1987 Search PubMed.
- L. Pauling, Nobel Lecture, Nobel Foundation, 1954, https://www.nobelprize.org Search PubMed.
- L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, NY, 1960 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of optimized structures, sample input for calculating core-level ionization energies, and Cartesian coordinates of structures sampled from QM/MM dynamics. See DOI: https://doi.org/10.1039/d4cp01521e |
| ‡ Current address: Molecular Physics, Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany. |
| This journal is © the Owner Societies 2024 |