Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of synthesis and substitution on the structure and ionic transport properties of lithium rare earth metal halides†
Maximilian A.
Plass
 ab,
Sebastian
Bette
ab,
Sebastian
Bette
 a,
Nina
Philipp
ab,
Igor
Moundrakovski
a,
Nina
Philipp
ab,
Igor
Moundrakovski
 a,
Kathrin
Küster
a,
Robert E.
Dinnebier
a,
Kathrin
Küster
a,
Robert E.
Dinnebier
 a and
Bettina V.
Lotsch
a and
Bettina V.
Lotsch
 *ab
*ab
aMax-Planck-Institute for Solid-State Research, Heisenbergstrasse 1, 70569, Stuttgart, Germany. E-mail: b.lotsch@fkf.mpg.de
bDepartment of Chemistry, Ludwig-Maximilians-Universität München, Butenandtstraße 5-13, 81377 München, Germany
First published on 11th May 2023
Abstract
Lithium rare earth metal halides have emerged as attractive candidates for solid electrolytes in all-solid-state batteries due to their high ionic conductivities and stability against oxidation. Here, we study their electrochemical properties as a function of the synthesis procedure and post-synthetic treatment and report on the impact of iso- and aliovalent substitutions in the cation and anion sublattices of the lithium rare earth metal iodides Li3MI6. For selected compounds we have investigated the impact of the synthetic approach, i.e. of different solid-state synthesis protocols, and mechanochemical ball-milling without and with post-synthetic calcination on the resulting materials. Lithium rare earth metal iodides obtained from solid-state synthesis generally outperform the mechanochemical synthesized compounds in terms of ionic conductivity and activation energy for ion diffusion, but when mechanochemical ball-milling is combined with a post-synthetic calcination step, these iodides show similar ionic conductivites as their counterparts obtained from conventional solid-state synthesis. Furthermore, we report a series of new Li3MI6 compounds with M = Y, Sm, Gd–Lu, partially Cd2+-substituted Li3+yGd1−yCdyI6 and partially Cd2+-, Ca2+- and Zr4+-substituted Li3±yY1−yMII/IVyBr6−xIx phases. Using a combination of ssNMR, EIS and PFG-NMR we reveal the influence of structural parameters such as RE/Li radius ratio, intra-layer cation and stacking fault disorder on the ionic transport properties, obtained from in-depth PXRD analyses. We find that the ionic conductivity is strongly affected by the ratio of the RE/Li radius ratio as well as by the degree of intra-layer cation disorder. It ranges between 3.0 × 10−5 S cm−1 and 4.6 × 10−4 S cm−1 for M = Lu–Sm at 20 °C with activation energies between 0.20 eV to 0.33 eV. The combination of partial anion and cation substitution increases the ionic conductivity up to 3.0 × 10−3 S cm−1 and leads to a lower activation energy of 0.17 eV. This study highlights the impact of microstructural effects on the electrochemical properties of solid electrolytes. The rational design and modification of solid electrolytes, along with their comprehensive (micro)structural analysis is thus crucial to optimize their ionic transport properties for applications in all-solid-state batteries.
1 Introduction
All-solid-state batteries (ASSBs) have aspired to become the next-generation battery technology because of higher energy and power densities when combined with a lithium metal anode. In addition, ASSBs mitigate safety concerns in terms of flammability.1,2 Owing to their high ionic conductivities3–6 of up to 10−2 S cm−1, sulfide and thiophosphate solid electrolytes (SEs) are currently the most promising separators used in ASSBs. Nevertheless, sulfidic materials suffer from narrow electrochemical stability windows against high-voltage cathodes and elemental lithium.7 Contrary to this, halides show much wider electrochemical stability windows with higher stabilities against oxidation,8–12 while typically being prone to reduction when in contact with lithium metal anodes, as recently demonstrated for Li3YCl6 and Li3InCl6.10 In spite of concerns regarding their earth-abundance, halides are currently discussed as separators as well as protective coatings for thiophosphate solid electrolytes in cathode active materials, since they show relatively high ionic conductivities of up to 10−3 S cm−1.13–16 Specifically, lithium yttrium halides like Li3YCl6,17 Li3YBr6,13,14 Li3YCl3Br3 (ref. 15) and Li3Y1−xInxCl6 (ref. 16) have been investigated recently. In addition, a high ionic conductivity on the order of 10−3 S cm−1 at 300 K with an activation energy of around 0.26 eV, initially proposed by ab initio molecular dynamics simulations by Wang et al.11 for Li3HoBr6, has been experimentally verified by Shi et al.18 and Plass et al.19. So far, several lithium rare earth halide compounds including LiMF4,20,21 Li3ScF6,22 Li3MCl6,23 Li3MBr6,24 Li3ErI6 (ref. 25) and Li3HoI6,19 and sodium rare earth halides such as Na3MCl6, Na3MBr6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 and Na3MI6
26 and Na3MI6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 have already been reported or computationally predicted,28 including Li3ScI6 and Li3LaI6.
27 have already been reported or computationally predicted,28 including Li3ScI6 and Li3LaI6.
One approach to rationally engineer the ionic conductivity of SEs is the iso- or aliovalent substitution of one or more constituent elements. Aliovalent anion substitution in lithium argyrodites Li6PS5X with halides led to a decrease in anion site disorder and to an increase in lithium site disorder as the ionic radius of the substituted halide anion increases from X = Cl to Br and I. This decreasing anion site disorder is accompanied by a decrease in ionic conductivity.29 It was also shown that additional aliovalent cation substitution in the iodide substituted lithium argyrodite Li6+xP1−xGexS5I leads to an increase in anion site disorder and simultaneously increases the charge carrier concentration, and hence the ionic conductivity.30,31 Alternatively, decreasing the charge carrier concentration via aliovalent cation substitution led to an increasing vacancy concentration in Na3−xEr1−xZrxCl6 and, thus, again to an enhancement in ionic conductivity.32 Similar effects were also observed for Na3−xY1−xZrxCl6,33 Li3−xEr1−xZrxCl6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 or Li3−xYb1−xMxCl6 with M = Zr4+, Hf4+.35,36 In Na3GdBr6−xIx,27 Li3YCl6−xBrx37 and Li3HoBr6−xIx19 it was shown that isovalent anion substitution can be used to tune the ionic conductivity and its activation energy. While in Li3HoBr6−xIx an increase in iodine content led to a decrease in activation energy due to softening of the anion lattice, this is also accompanied by an increase in Li/rare earth (RE) site disorder, which led to a reduction of the ionic conductivity due to an increased electrostatic repulsion along the lithium conduction pathways. As a result of these competing effects (softening of the anion lattice vs. cation site disorder), an optimum of 2.7 × 10−3 S cm−1 at 20 °C for the ionic conductivity and of 0.18 eV for the activation energy was observed at different degrees of anion substitution. Alternatively, ion transport properties in solids can be controlled by using different synthetic protocols. For example, in Li3MCl6 with M = Er, Y17,38,39 higher ionic conductivities were achieved when the samples were solely ball-milled, compared to mechanochemical ball-milling (MCBM) with subsequent calcination. However, the exact reverse trend was already observed for Li3YBr6,38 where an increase in ionic conductivity was found after annealing of the material obtained from MCBM. This difference is rationalized by different structures of chlorides and bromides, where the ionic percolation pathways are affected differently by defects introduced via MCBM.
34 or Li3−xYb1−xMxCl6 with M = Zr4+, Hf4+.35,36 In Na3GdBr6−xIx,27 Li3YCl6−xBrx37 and Li3HoBr6−xIx19 it was shown that isovalent anion substitution can be used to tune the ionic conductivity and its activation energy. While in Li3HoBr6−xIx an increase in iodine content led to a decrease in activation energy due to softening of the anion lattice, this is also accompanied by an increase in Li/rare earth (RE) site disorder, which led to a reduction of the ionic conductivity due to an increased electrostatic repulsion along the lithium conduction pathways. As a result of these competing effects (softening of the anion lattice vs. cation site disorder), an optimum of 2.7 × 10−3 S cm−1 at 20 °C for the ionic conductivity and of 0.18 eV for the activation energy was observed at different degrees of anion substitution. Alternatively, ion transport properties in solids can be controlled by using different synthetic protocols. For example, in Li3MCl6 with M = Er, Y17,38,39 higher ionic conductivities were achieved when the samples were solely ball-milled, compared to mechanochemical ball-milling (MCBM) with subsequent calcination. However, the exact reverse trend was already observed for Li3YBr6,38 where an increase in ionic conductivity was found after annealing of the material obtained from MCBM. This difference is rationalized by different structures of chlorides and bromides, where the ionic percolation pathways are affected differently by defects introduced via MCBM.
In this study, we performed a systematic investigation of the influence of the synthetic protocol, of the size of the RE cation and of partial anion and cation substitution on the ionic transport properties in lithium rare earth iodides. Several lithium RE iodides Li3MI6 with M = Y, Sm, Gd–Lu (only M = Er25 and Ho19 were reported, while predictions28 exist for Sc, Y, La), as well as partially Cd2+-substituted Li3GdI6 and partially Cd2+-, Ca2+- and Zr4+-substituted Li3YBr3.5I2.5 were synthesized and characterized by powder X-ray diffraction (PXRD) and electrochemical impedance spectroscopy (EIS). For selected diamagnetic compounds, solid state nuclear magnetic resonance (ssNMR) and pulsed-field-gradient nuclear magnetic resonance (PFG-NMR) were used to connect (micro)structural properties with the Li diffusivities.
2 Results and discussion
In the following we delineate the structure–property relationships in the new lithium rare earth iodides Li3MI6. We compare the effect of different synthetic approaches (conventional solid-state synthesis (SSS), MCBM without and with subsequently annealing) on the microstructure as well as on the ion transport properties of selected lithium rare earth iodides. Next, we discuss the effect of complete isovalent cation substitution of the RE metal in Li3MI6. Finally, we present the impact of partial aliovalent cation substitution of the RE metal by main group (Ca2+) and transition metals (Cd2+, Zr4+) on the structural and transport properties.2.1 Influence of the synthetic approach on the structure and ionic transport properties
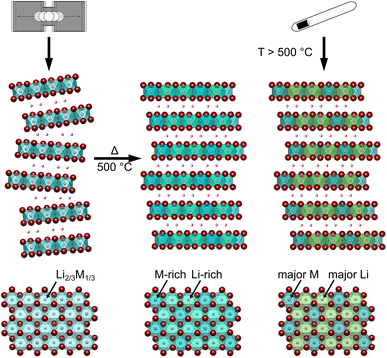
Lithium rare earth halides can be synthesized from the respective binary halides via SSS19 or MCBM.17,25,39 In SSS the heating temperature can either be set to the melting point of the respective alkali halide, of the eutectic mixture of alkali and rare earth halide or of the rare earth halide.40 Temperatures below the melting points of the alkali halides were reported to be insufficient for a homogeneous reaction. To probe the effect of the heating temperature of the SSS on structural and transport properties, we chose Li3YI6 as a model system. It was synthesized starting from LiI (melting point Tmp = 469 °C (ref. 41 and 42)) and YI3 (Tmp = 997 °C (ref. 41 and 42)), and its formation at low (750 °C) and high (1000 °C) temperatures of the eutectic mixture, are compared. Furthermore, we investigated the applicability and efficacy of MCBM for the synthesis of lithium rare earth iodides, using Li3YI6 and Li3TmI6 as representative examples. We carried out the MCBM process stepwise in order to track the formation of the lithium rare earth iodide. Finally, we performed a post-synthetic calcination at 500 °C for 60 h of the ball-milled Li3YI6 and Li3TmI6, since we have shown in our previous study19 that a calcination step at 500 °C with subsequent slow cooling to room temperature significantly reduces the disorder in the structures of lithium rare earth metal bromides and iodides.The sample synthesized from low temperature (LT) showed a higher purity of the obtained product than the high temperature (HT) sample (94 wt% vs. 90 wt%). We ascribe this difference in purity to the boiling retardation at HTs, which is accompanied by partial separation of the eutectic precursor melt (synthesis in a glassy carbon crucible) before the reaction is complete.
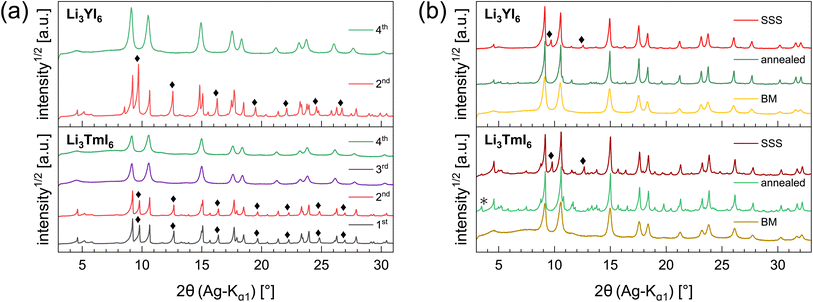
In the diffraction patterns of Li3TmI6 collected after the 1st and 2nd MCBM step (black and red lines at the bottom of Fig. 1a) TmI3-related reflections are clearly visible. There is no change – neither in the very sharp peak shape nor in the relative intensity of the peaks – during the first two low energy MCBM steps (1st: three 5 mm balls, 10.5 h, 10 Hz, 2nd: three 5 mm balls, 6 h, 15 Hz MCBM), suggesting that no noticeable conversion of the starting materials occurs at this stage. As the energy impact during milling is significantly increased (one 10 mm ball, 4.5 h, 30 Hz), the diffraction pattern clearly changes after the 3rd MCBM step (purple line in the bottom of Fig. 1a), where reflections attributed to TmI3 are absent. An additional MCBM step (one 10 mm ball, 9 h, 30 Hz) (green lines in Fig. 1a) only leads to slight changes in the peak shape. The reflections become slightly broadened and a hump in the background appears at around 7°, indicating that the solid phase begins to amorphize. For Li3YI6 the same behaviour can be observed (see top part of Fig. 1a). After subsequent annealing, reflections attributed to MOI (green lines and black asterisks in Fig. 1b) are present in the diffraction pattern of Li3TmI6. As lithium rare earth metal iodides are very sensitive towards oxidation, especially at elevated temperatures, even tiny oxygen impurities can lead to the formation of MOI during heating.
Additionally, we investigated the different steps of the synthesis via MCBM of Li3YI6 with ssNMR. The results are depicted in Fig. S11a to S11c and summarized in Table S8.† In contrast to the PXRD analysis, it can be seen that after the 3rd milling cycle LiI (shoulder at −4.4 ppm in Fig. S11a†) is still present, whereas this signal disappeared after the 4th milling step, which finally indicates a complete conversion of all starting materials. Thus, the disappearance of the lithium iodide related signal in the 7Li-ssNMR spectra can be seen as an additional indicator for the completeness of the reaction in Li3YI6. In the 89Y-ssNMR spectra of the HT-SSS (given in Fig. S11c†) two distinct signals can be observed. We tentatively assign these signals to highly disordered yttrium (broad signal at 627.7 ppm) and to an impurity of YI3 (narrow signal at 638.4 ppm). For the sample annealed after MCBM only one, but asymmetric signal at around 624 ppm is visible, indicating a complete conversion of the starting materials.
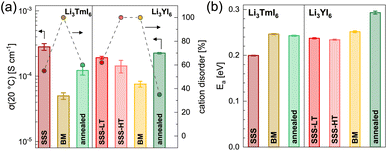
The HT synthesized Li3YI6 shows full intra-layer cation disorder and stacking fault disorder (see Fig. S6a†), whereas the LT synthesized sample exhibits significantly lower intra-layer cation disorder of only 62%. We assume that the high temperatures used in the SSS, which are close to the melting point of the MI3 reactants, facilitate entropy-driven cation mixing and thus trigger higher degrees of intra-layer cation disorder in the final product. The influence of the cooling rate needs to be investigated further, but for the isotypic Li3HoBr6 we did not observe a correlation between cooling rate and intra-layer cation disorder. After MCBM the few remaining reflections indicate that the product is highly disordered and the broad peak shape points to very small domain sizes. Furthermore, the reflections in the PXRD patterns of the ball-milled samples exhibit an unusual shape: reflections with h and k components are comparatively narrow, while 00l reflections, in contrast, exhibit a strong, symmetrical broadening (see Fig. S4a†). As there is no anisotropic broadening of the reflections, this effect is most likely caused by a pronounced anisotropic morphology of the crystalllite domains, i.e. by plate-like crystallites with a much higher lateral than vertical extension. Therefore, we used the full width at half maximum (FWHM) as a semi-quantitative measure for the aspect ratio. For all ball-milled samples, the vertical extension of the crystallites, determined from the FWHM of the associated reflections, is very small (between 2.5 nm and 3.8 nm), which corresponds to a thickness between three to five layers. In contrast, the broadening of the 104 reflection corresponds to coherent domain sizes between 14.4 nm and 15.3 nm, which almost approximate the lateral domain sizes. When comparing the diffraction data of Li3TmI6 after the 3rd and 4th MCBM step (see Fig. S4a†), it becomes clear that after conversion of the starting materials, additional MCBM leads to a decrease in both vertical and lateral domain sizes. Calcination after MCBM leads to a narrowing of the reflections (green lines in Fig. 1b) in PXRD. Furthermore, additional reflections appear in the range between 4.75° and 8.25°, indicating an ordering of the intra-layer cation substructure. Quantitative analysis of the diffraction patterns reveals that the domain sizes along the [001] (vertical) and [104] (approx. lateral) zone axes significantly increased (empty and filled bars in Fig. S4b†). Moreover, the shape of the domains tend to become more isotropic. In addition, subsequent calcination reduces the intra-layer cation disorder from 100% to 35% and 60% (filled circles in Fig. S4b†) in Li3YI6 and Li3TmI6, respectively. In direct comparison, the diffraction patterns of the lithium rare earth metal iodides of the ball-milled samples after subsequent annealing appear to be similar to the phases obtained from conventional SSS (Fig. 1b, green and red lines).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 and more details about the fitting procedure of the respective compounds are given in the ESI (see Fig. S17–S26 and Table S10†). While Li3YI6 synthesized from HT-SSS with full intra-layer cation disorder as well as stacking fault disorder showed an ionic conductivity of 1.4 × 10−4 S cm−1 at 20 °C, the LT-SSS with a reduced intra-layer cation disorder exhibited a slightly improved ionic conductivity of 1.9 × 10−4 S cm−1 and a similar activation energy for ion diffusion of 0.24 eV. For both Li3YI6 and Li3TmI6, the samples solely synthesized via MCBM showed the lowest ionic conductivities of 7.6 × 10−5 S cm−1 and 5.0 × 10−5 S cm−1, respectively, compared to the conventional SSS. Subsequent calcination of the ball-milled samples improves the ionic conductivity by a factor of two to three to 2.3 × 10−4 S cm−1 and 1.2 × 10−4 S cm−1 for Li3YI6 and Li3TmI6, respectively. The same trend was also observed for the isotypic Li3YBr6,38 where the ionic conductivity could be improved by annealing of the material obtained from MCBM. While for Li3TmI6 the conventional synthesis (24 h at 800 °C) led to a higher ionic conductivity and a lower activation energy for ion diffusion compared to MCBM without and with subsequent annealing at 500 °C for 60 h, in Li3YI6 MCBM with subsequent calcination led to a slightly improved ionic conductivity (due to the slightly lower intra-layer cation disorder), but an increased activation energy for ion diffusion of 0.29 eV compared to the SSS (24 h at 750 °C). The different behaviour of Li3YI6 and Li3TmI6 upon annealing may also result from the different ionic radii of the trivalent rare earth metal cations and the resulting larger ionic radii ratio of rVI(Y3+)/rVI(Li+) compared to rVI(Tm3+)/rVI(Li+). A larger ionic radii ratio implies a larger deviation of M3+ from Li+ in terms of size (see also Section 2.2) and likely leads to improved ordering upon annealing, and thus to a smaller degree of intra-layer cation disorder and higher ionic conductivities.
19 and more details about the fitting procedure of the respective compounds are given in the ESI (see Fig. S17–S26 and Table S10†). While Li3YI6 synthesized from HT-SSS with full intra-layer cation disorder as well as stacking fault disorder showed an ionic conductivity of 1.4 × 10−4 S cm−1 at 20 °C, the LT-SSS with a reduced intra-layer cation disorder exhibited a slightly improved ionic conductivity of 1.9 × 10−4 S cm−1 and a similar activation energy for ion diffusion of 0.24 eV. For both Li3YI6 and Li3TmI6, the samples solely synthesized via MCBM showed the lowest ionic conductivities of 7.6 × 10−5 S cm−1 and 5.0 × 10−5 S cm−1, respectively, compared to the conventional SSS. Subsequent calcination of the ball-milled samples improves the ionic conductivity by a factor of two to three to 2.3 × 10−4 S cm−1 and 1.2 × 10−4 S cm−1 for Li3YI6 and Li3TmI6, respectively. The same trend was also observed for the isotypic Li3YBr6,38 where the ionic conductivity could be improved by annealing of the material obtained from MCBM. While for Li3TmI6 the conventional synthesis (24 h at 800 °C) led to a higher ionic conductivity and a lower activation energy for ion diffusion compared to MCBM without and with subsequent annealing at 500 °C for 60 h, in Li3YI6 MCBM with subsequent calcination led to a slightly improved ionic conductivity (due to the slightly lower intra-layer cation disorder), but an increased activation energy for ion diffusion of 0.29 eV compared to the SSS (24 h at 750 °C). The different behaviour of Li3YI6 and Li3TmI6 upon annealing may also result from the different ionic radii of the trivalent rare earth metal cations and the resulting larger ionic radii ratio of rVI(Y3+)/rVI(Li+) compared to rVI(Tm3+)/rVI(Li+). A larger ionic radii ratio implies a larger deviation of M3+ from Li+ in terms of size (see also Section 2.2) and likely leads to improved ordering upon annealing, and thus to a smaller degree of intra-layer cation disorder and higher ionic conductivities.
We observed similar trends by using PFG-NMR for the characterization of the ionic transport properties. The results for the ball-milled and for the subsequently annealed Li3YI6 are depicted in Fig. S38.† The Arrhenius plots of the diffusion coefficients of the differently synthesized samples are given in Fig. S38b† and the extracted activation energies as well as diffusion coefficients at a given temperature are depicted in Fig. S38c.† Li3YI6 synthesized from SSS exhibits a lower activation energy compared to the MCBM and subsequently annealed sample. Similar to EIS, the sample obtained from MCBM shows a lower diffusion coefficient compared to the SSS, whereas MCBM with subsequent annealing leads to a similar diffusion coefficient.
2.2 Influence of complete isovalent cation substitution in Li3MI6 compounds
In order to investigate the influence of the rare earth metal cation on the electrochemical properties of Li3MI6 compounds, we have synthesized and characterized several new members of this class via a conventional SSS. The obtained new Li3MI6 compounds with M = Y, Sm, Gd–Lu are isostructural to Li3HoBr6−xIx.19 All attempts to synthesize Li3MI6 compounds with M = La, Ce or Pr at various temperatures were not successful as the reactants were still present. The diffraction patterns of the respective Li3MI6 compounds synthesized from conventional SSS are given in Fig. 5a. A linear trend of all lattice parameters consistent with the ionic radius of the respective RE metal can be observed and is depicted in Fig. S5.† Minor reflections (denoted with asterisks and diamonds in Fig. 5a) correspond to impurities of MOI and MI3, which usually occur during conventional SSS.19 In addition, all Li3MI6 also exhibit a high degree of stacking fault disorder of randomly oriented staggered honeycomb layers and a pronounced intra-layer cation disorder (see Fig. 5b). Furthermore, the intra-layer cation disorder tends to correlate with the ionic radius of the RE cation, i.e. the larger rVI(M3+) becomes, the lower the intra-layer cation disorder tends to be. This means that larger deviations between the ionic radii of lithium and the RE metal (represented by an increasing ionic radii ratio rVI(M3+)/rVI(Li+)) lead to a smaller degree of cation disorder within the mixed honeycomb layers in Li3MI6. In contrast, the stacking fault disorder does not tend to be affected by the size of the RE cation and exhibits full disorder, i.e. full randomization of the direction of the staggered stacking order, independent of the RE metal radius (except for Li3YbI6). The very low stacking fault disorder of Li3YbI6 most likely can be ascribed to the significantly lower heating temperature during SSS (see Table S1 and Fig. S6†) compared to the other Li3MI6.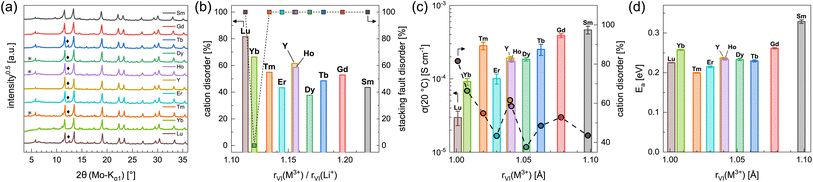 | ||
| Fig. 5 (a) PXRD diffraction patterns and (b) degrees of intra-layer cation disorder and stacking fault disorder obtained from Rietveld refinements of the different Li3MI6. Asterisks and diamonds correspond to impurities of MOI and MI3, respectively. In (c) ionic conductivities at 20 °C with intra-layer cation disorder and in (d) activation energies for ion diffusion obtained from EIS are shown as a function of the ionic radii43–45 of the rare earth metal cations. | ||
Using EIS we looked into ion diffusion within the different Li3MI6 compounds. The Arrhenius graphs, as well as the extracted ionic conductivities at 20 °C and the respective activation energies for ion diffusion of the different Li3MI6 are summarized in Fig. S16a,†5c and d. Here, a clear correlation of the ionic conductivity with the ionic radius of the RE metal in Li3MI6 can be observed. While Li3LuI6 with an intra-layer cation disorder of 82% exhibits an ionic conductivity of 3.0 × 10−5 S cm−1, it gradually increases by more than one order of magnitude with increasing size of the RE cation to 4.6 × 10−4 S cm−1 for Li3SmI6 having an intra-layer cation disorder of only 44%. In contrast, the activation energy for ion diffusion EEISa tends to stay constant for M = Lu–Tb (≈0.23 eV) and seems to increase for M = Tb–Sm (to 0.33 eV). In principle, the activation energy can be affected by several parameters such as cation disorder, volume of the diffusion paths, nature of the underlying anion sublattice or even microstructural effects. One approach to classify materials according to their activation energies is to look at their pre-exponential factors σ0 in the Arrhenius equation.46–48 By plotting the respective σ0 of the different Li3MI6 against their activation energies according to the Meyer–Neldel rule49–51 (see Fig. S27†), a Meyer–Neldel energy Δ0 of around 20 meV is observed for these lithium rare earth iodides. Since the observed Meyer–Neldel energy is close, but slightly lower than the thermal energy kBT (25 meV at 20 °C) Li3MI6 compounds cannot unambiguously be classified as type two materials, where Δ0 < kBT and σEISion is directly proportional to EEISa. Interestingly, Li3TmI6 shows a three times higher ionic conductivity (≈3 × 10−4 S cm−1) than expected according to its ionic radius and degree of intra-layer cation disorder, and exhibits the lowest activation energy for ion diffusion of 0.20 eV compared to the other Li3MI6 phases. To exclude that the higher conductivity is due to charge doping with Tm2+ according to Li3+yTmIII1−yTmIIyI6, X-ray photoelectron spectroscopy (XPS) measurements were performed and the obtained spectra are shown in Fig. S10.† Here, only features that can be related to Tm3+ could be observed and no signs of Tm2+ were found. A similar observation was made for Li3YbI6, which also shows a slightly higher ionic conductivity of 9.2 × 10−5 S cm−1 than one would expect from its ionic radius and degree of intra-layer cation disorder. We attribute this finding to the essentially complete absence of stacking faults in Li3YbI6, in contrast to all of its homologues.
2.3 Influence of partial aliovalent cation substitution
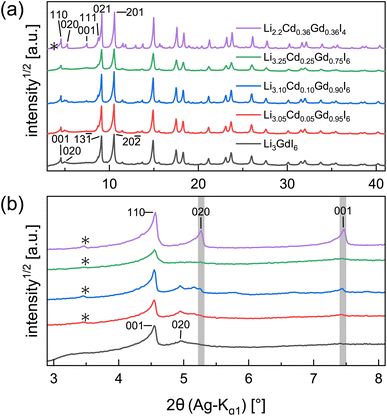
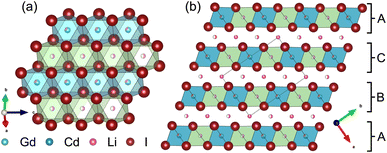
Partial aliovalent cation substitution is a common approach to rationally tune the ionic transport properties. This can either be done by introducing cations of lower charge to increase the concentration of the mobile charge carriers, or by incorporating cations of higher charge to increase the concentration of charge carrier vacancies. In literature, only the latter approach has been reported for similar compounds.32–36 Thus, we first focus on increasing the charge carrier concentration by substituting the RE metal cation by Cd2+ (similar ionic radius43–45 of Cd2+ compared to Gd3+) in Li3+yGd1−yCdyI6, since the structure of these compounds already possesses a high vacancy concentration within the empty honeycombs of the lithium inter-layer. The substitution of gadolinium with cadmium in the structure of Li3GdI6 does not lead to significant changes in the PXRD patterns, which are given in Fig. 6. Since no new reflections appear, the samples resulting from substitution can be considered as single-phase (see Fig. 6a). Due to the similar ionic radii the substitution does not lead to a significant shift of the peak positions. Close inspection of the diffraction pattern in which 50% of gadolinium was replaced by cadmium (violet pattern in Fig. 6b) reveals that new reflections arise that cannot be indexed with the monoclinic unit cell of Li3GdI6 anymore. Instead, the entire pattern can be indexed with a C-centered monoclinic unit cell that only shows 66% of the volume of Li3GdI6. Although the cell metrics differ significantly, both unit cells are closely related to each other (see Table S5†) as the main reflections are identical in the unsubstituted and in the 50% substituted (black and violet patterns in Fig. 6) sample. The crystal structure solution of the cadmium substituted compound indicates a Cd/Gd to I ratio of ≈1/6 as in the unsubstituted Li3GdI6. There are further similarities between the structure of the pure gadolinium and the cadmium-substituted compound. In both structures, all cations show an octahedral coordination environment (see Fig. 7), the iodide substructure exhibits a cubic close packing (ccp), and the general structural motif is a layered arrangement in an ABC-like fashion with a staggered stacking order. However, the constitution of the layers themselves differ. While in the layers of Li3GdI6 the GdI6/3-octahedra are surrounded by LiI6/3-octahedra resulting in a filled honeycomb motif as shown in Fig. 2, in the ∞[LixCd0.5−xGd0.5−xI6/3](0.5+3x)−-chains within the mixed layers along c as illustrated in Fig. 7a with light blue octahedra. Furthermore, these chains alternate with ∞[LiI6/3]2−-chains (green octahedra in Fig. 7a). The octahedral inter-layer voids are partially occupied by additional lithium ions as depicted by the magenta atoms in Fig. 7b. The crystal structure points to a variable phase composition with regard to the Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cd/Gd ratio of Li1.5+5xCd0.5−xGd0.5−xI4. It should be noted that there are no limitations for the Cd to Gd ratio, in principle. Hence, the occupational disorder apparent in the crystal structure would theoretically enable phase compositions of Li4I4 = LiI, Li2CdI4 (ref. 52) and LiGdI4, according to a sum formula of Li2−y+5x(CdyGd1−y)1−xI4 with 0 ≤ y ≤ 1 and 0 ≤ x ≤ 1. When applying gadolinium substitution degrees below 50%, the honeycomb motif of Li3GdI6 is still apparent as indicated by the presence of the 020 reflection at around 5° (red, blue and green patterns in Fig. 6). Weak reflections related to the 020 and 001 diffraction lines of the Li1.5+5xCd0.5−xGd0.5−xI4-type indicate that layers showing ∞[Lix(CdyGd1−y)1−xI6/3](y+3x)−-chains are apparent in the microstructure of these samples. As the main reflections do not show any splitting or shoulders, we assume that the distribution of cadmium is homogeneous among both layer types and that the coherent scattering domains of honeycomb- and chain-type motifs are crystallographically intergrown. Hence, we refined the patterns using two phases with constrained lattice parameters as given in Table S5,† but with individual crystallite size broadening parameters, in order to account for the extensions of the coherent scattering domains. When cadmium is added with 5 mol%, 10 mol% and 25 mol% we observed Li1.5+5xCd0.5−xGd0.5−xI4-type phases in fractions between 13 wt% to 18 wt%. If the amount of cadmium is increased to 75 mol% a multiphase sample containing CdI2, GdI3 and LiI besides Li2−y+5x(CdyGd1−y)1−xI4 (see Fig. S8†) was obtained. Due to extensive parameter correlation, we were not able to perform a meaningful quantitative analysis of the PXRD patterns.
Cd/Gd ratio of Li1.5+5xCd0.5−xGd0.5−xI4. It should be noted that there are no limitations for the Cd to Gd ratio, in principle. Hence, the occupational disorder apparent in the crystal structure would theoretically enable phase compositions of Li4I4 = LiI, Li2CdI4 (ref. 52) and LiGdI4, according to a sum formula of Li2−y+5x(CdyGd1−y)1−xI4 with 0 ≤ y ≤ 1 and 0 ≤ x ≤ 1. When applying gadolinium substitution degrees below 50%, the honeycomb motif of Li3GdI6 is still apparent as indicated by the presence of the 020 reflection at around 5° (red, blue and green patterns in Fig. 6). Weak reflections related to the 020 and 001 diffraction lines of the Li1.5+5xCd0.5−xGd0.5−xI4-type indicate that layers showing ∞[Lix(CdyGd1−y)1−xI6/3](y+3x)−-chains are apparent in the microstructure of these samples. As the main reflections do not show any splitting or shoulders, we assume that the distribution of cadmium is homogeneous among both layer types and that the coherent scattering domains of honeycomb- and chain-type motifs are crystallographically intergrown. Hence, we refined the patterns using two phases with constrained lattice parameters as given in Table S5,† but with individual crystallite size broadening parameters, in order to account for the extensions of the coherent scattering domains. When cadmium is added with 5 mol%, 10 mol% and 25 mol% we observed Li1.5+5xCd0.5−xGd0.5−xI4-type phases in fractions between 13 wt% to 18 wt%. If the amount of cadmium is increased to 75 mol% a multiphase sample containing CdI2, GdI3 and LiI besides Li2−y+5x(CdyGd1−y)1−xI4 (see Fig. S8†) was obtained. Due to extensive parameter correlation, we were not able to perform a meaningful quantitative analysis of the PXRD patterns.
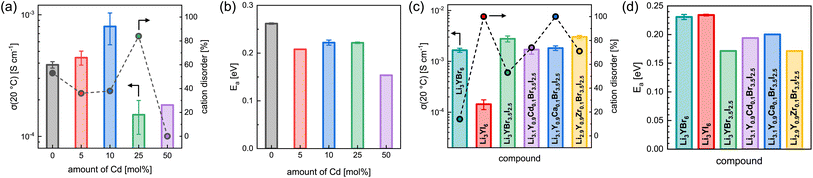
The effect of partial aliovalent cation substitution on the lithium ion transport properties in Li3+yGd1−yCdyI6 was investigated with the use of EIS and the results are given in Fig. 8a, b, S28–S31, and S16b.† As mentioned above, for small degrees of cadmium substitution of y ≤ 0.25 the honeycomb-type structure Li3+yGd1−yCdyI6 is more dominant and for higher substitution degrees with y ≥ 0.5 the chain-type structure Li2−y+5x(CdyGd1−y)1−xI4 is mainly formed. For y ≤ 0.25, when the honeycomb-type structure motif is the major phase, the ionic conductivity in Li3+yGd1−yCdyI6 could be doubled to 8.0 × 10−4 S cm−1 when y is increased to 0.1 (see Fig. 8a) compared to the unsubstituted Li3GdI6, whereas higher values of y led to a decline in ionic conductivity to 1.5 × 10−4 S cm−1 for y = 0.25. The increase in ionic conductivity for 0 < y ≤ 0.1 in Li3+yGd1−yCdyI6 can be ascribed to the simultaneous decrease of the intra-layer cation disorder (from 53% to 36% and 38%) and increased lithium charge carrier concentration. The subsequent decline in ionic conductivity for y = 0.25 originates from a drastically increased intra-layer cation disorder to 84%. Comparing the ionic conductivity of the honeycomb-type structure of the unsubstituted Li3GdI6 and of the substituted Li3.1Gd0.9Cd0.1I6 with the chain-type structure Li2.2Cd0.36Gd0.36I4, which showed an ionic conductivity of 1.8 × 10−4 S cm−1, it can be seen that the former structure motif tends to outperform the latter in terms of ionic conductivity. A similar trend is observed for the activation energy for ion diffusion, which is lowered from 0.26 eV for y = 0 to 0.22 eV for y = 0.1 as depicted in Fig. 8b, and suggesting that the electrostatic repulsion lithium ions encounter is reduced when Gd3+ is replaced with Cd2+. Interestingly, the chain-type structure Li2.2Cd0.36Gd0.36I4 showed an activation energy of only 0.15 eV and hence is significantly lower compared to the unsubstituted Li3GdI6 and to the substituted Li3.1Gd0.9Cd0.1I6, which presumably can be ascribed to the reduced electrostatic repulsion between lithium and Cd2+ compared to Gd3+ and to the different ordering within the chain-type structure. According to the Meyer–Neldel rule a similar Meyer–Neldel energy (20 meV) with Δ0 < kBT was observed for the Cd2+-substituted Li3GdI6 as for the other Li3MI6.
To better understand the different ionic conductivities of the different structure motifs, the nature of the underlying diffusion paths of the honeycomb- and chain-like structure were investigated using bond valence sum (BVS) calculations implemented in the softBV software.53,54 The bond valence energy landscape (BVEL) for lithium migration was calculated for Li2.2Cd0.36Gd0.36I4 and the obtained diffusion pathways are illustrated in Fig. S37.† The diffusion pathways within the honeycomb-type structure have already been discussed by Plass et al.19 for Li3HoBr6 and Li3HoI6 in detail, where extended 3D-percolation networks of the inter- and intra-layer lithium ions were observed. In the mixed chain-like layer (see Fig. S37a†) the lithium ion migration pathways predominantly connect the octahedral lithium sites on 4f in a 1D-fashion along c. The Li pathways are extended to 2D in the solely lithium (on 2a and 4f) occupied honeycomb inter-layer as depicted in Fig. S37b.† An extension of the BVEL to 2D within the mixed chain-like layer is only feasible where coincidentally two lithium ions occupy neighbouring octahedra of different [LixCd0.5−xGd0.5−xI6/3](0.5+3x)−∞-chains. Nevertheless, the lithium ion migration pathways of the mixed chain-like and solely lithium containing honeycomb layers are connected with each other along the stacking direction and thus the BVEL is extented to quasi-3D (see Fig. S37c†). Compared to the honeycomb-type structure, however, the ∞[LixCd0.5−xGd0.5−xI6/3](0.5+3x)−-chains in Li2.2Cd0.36Gd0.36I4 tend to limit the dimensionality of the lithium ion percolation network and thus the total number of possible diffusion opportunities is reduced, which is reflected in a lower lithium ion conductivity as observed by EIS.
2.4 Combining partial aliovalent cation and isovalent anion substitution
The findings of the partial aliovalent cation substitution for Li3+yGd1−yCdyI6 were combined with the findings of Plass et al.19 for partial isovalent anion substitution in Li3HoBr6−xIx, where a certain degree of substitution of bromide for iodide led to an enhancement of the ionic transport properties. Thus, mixed (aliovalent cation and isovalent anion) substituted lithium yttrium halides were investigated. To this end, we compare the unsubstituted lithium yttrium halides Li3YBr6 and Li3YI6, the isovalent anion substituted Li3YBr3.5I2.5 and the mixed substituted Li3+yY1−yMIIyBr3.5I2.5 and Li3−yY1−yMIVyBr3.5I2.5, where MII corresponds to a divalent metal cation like Cd2+ or Ca2+ (as a less toxic alternative), and MIV to a tetravalent metal cation like Zr4+. Aliovalent cation substitution in Li3YBr3.5I2.5 leads to the formation of an amorphous side phase (grey area depicted in Fig. S9a†). Nevertheless, a variation of the lattice parameters (see Fig. S9b†) as a function of the size of the dopant or of the mean metal–halide bond distances can be observed, which points to a successful incorporation of the divalent/tetravalent substituent into the lattice. Due to the strong parameter correlation of the average structure obtained from PXRD (substitution of the anion and cation lattice, as well as intra-layer cation and stacking fault disorder) some constraints had to be included and no quantitative information of the nature and amount of the amorphous side phase can thus be derived from PXRD.To obtain further insights into the nature of the amorphous side phase, ssNMR spectroscopy was performed; the 6Li- and 7Li-spectra of the different pure and substituted lithium yttrium halides are shown in Fig. S12a, S12b and the shifts of the respective signals are summarized in Table S9.† The main peaks in Li3YBr6 and Li3YI6 can be found at around −1.2 ppm and −3.9 ppm in the 6,7Li-ssNMR spectra, respectively. The shift of the main signal to lower frequencies in the ssNMR spectra of Li3YI6 compared to Li3YBr6 is in agreement with the increasing softness of the iodide anion and the resulting stronger shielding of the lithium ions. While in Li3YBr6 the signal is asymmetric, which indicates that this signal is a convolution of several contributions, in Li3YI6 an additional shoulder at around −3.7 ppm in the 6,7Li-ssNMR spectra can be observed, along with a minor impurity of LiI (asterisk at −4.5 ppm in Fig. S12a†). We tentatively ascribe this broad, but distinct shoulder in Li3YI6 to the inter-layer lithium, since the pronounced cation disorder within the RE/Li honeycomb-layer in Li3YI6 effectively decouples the inter- and intra-layer lithium ions and thus increases the 2D-character of the material. This is consistent with the larger inter-layer distance in Li3YI6 compared to Li3YBr6. As a consequence, the inter-layer lithium ions are less shielded, leading to the observed shoulder at higher frequencies. The anion substituted Li3YBr3.5I2.5 exhibits one asymmetric signal at around −1.9 ppm in the 6,7Li-ssNMR spectra, which is shifted to lower or to higher frequencies with respect to the unsubstituted Li3YBr6 or Li3YI6, respectively. The corresponding signal in the Cd2+ and Ca2+ substituted Li3+yY1−yMIIyBr3.5I2.5 can be found at a similar position in the 6,7Li-ssNMR spectra and is slightly shifted to higher frequencies in Li2.9Y0.9Zr0.1Br3.5I2.5. Similar to Li3YBr6 and Li3YBr3.5I2.5 the signals are asymmetric in the cadmium and calcium substituted compounds and most likely composed of multiple contributions. Furthermore, an additional, broad signal arises once a divalent or tetravalent dopant like Cd2+, Ca2+ or Zr4+ is introduced. These additional signals can be found at around −2.5 ppm, −2.2 ppm and −1.6 ppm in the respective 6,7Li-spectra. The fact that the broad signal of the inter-layer lithium in the zirconium substituted compound is slightly shifted to higher frequencies, whereas the ones of the cadmium and calcium substituted compounds are shifted to lower frequencies (with respect to the anion substituted Li3YBr3.5I2.5) can be explained with the concept of hard and soft acids and bases. According to the charge of the substituent (Zr4+ > Y3+ > Cd2+/Ca2+) and to the mean bond distance found in the respective binary bromides and iodides (dCa–X > dY–X ≈ dCd–X > dZr–X) the acidity and thus the deshielding effect of neighbouring metal cations on lithium decreases from Zr to Y to Cd and Ca. Thus, we tentatively assign these signals to the additional inter-layer Li in the Cd2+/Ca2+-doped compounds or to a signal resulting from Li depletion out of the mixed honeycomb into the Li inter-layers in the Zr-doped material. If or to what extent this signal may be attributed to an amorphous side phase, which could also be observed in PXRD, cannot be stated unambiguously.
The lithium ion transport within the mixed aliovalent cation and isovalent anion substituted lithium yttrium halides has been investigated with the use of EIS and the results of the measurements are given in Fig. 8c, d, S22, S32–S36, and S16c.† Similar to Li3HoBr6−xIx,19 Li3YBr6 exhibits a higher ionic conductivity of 1.7 × 10−3 S cm−1 (similar to Gombotz and Wilkening14) compared to the softer analogue Li3YI6 with 1.4 × 10−4 S cm−1, due to the significantly smaller degree of intra-layer cation disorder of only 14% in Li3YBr6. While the isovalent anion substituted Li3YBr3.5I2.5 exhibits a higher degree of intra-layer cation disorder of 53% compared to the pure bromide, the increase in ionic conductivity to 2.8 × 10−3 S cm−1, originating from the beneficial increase in lattice softening of the anion sublattice, still prevails. When the charge carrier concentration is increased additionally by incorporation of divalent metal cations such as Cd2+ or Ca2+, the intra-layer cation disorder is further increased to 74% and 100%, respectively, and the ionic conductivity slightly deteriorates accordingly to 1.7 × 10−3 S cm−1 and 1.8 × 10−3 S cm−1. If the vacancy concentration is increased by aliovalent substitution with a tetravalent metal cation like Zr4+, the intra-layer cation disorder is also increased to 71%. In contrast to the increase in charge carrier concentration for the divalent metal substitutions, the increased amount of lithium vacancies tends to be more beneficial in terms of ionic conductivity. In fact, Li2.9Y0.9Zr0.1Br3.5I2.5 exhibits a slightly enhanced ionic conductivity of up to 3.0 × 10−3 S cm−1. Similar effects can also be observed for the activation energy for lithium ion diffusion as summarized in Fig. 8b. While the pure lithium yttrium bromide or iodide show similar activation energies of 0.23 eV, it decreases to 0.17 eV for the anion substituted Li3YBr3.5I2.5. Again, increasing the charge carrier concentration by substituting with divalent metal cations such as Cd2+ or Ca2+ leads to a slight, but unfavorable increase of the activation energy to 0.19 eV and 0.20 eV compared to the solely anion substituted Li3YBr3.5I2.5. In contrast, increasing the vacancy concentration by substitution of the trivalent RE cation with tetravalent Zr4+ does not deteriorate the activation energy for ion diffusion, as Li2.9Y0.9Zr0.1Br3.5I2.5 exhibits a similar activation energy as Li3YBr3.5I2.5. Plotting the respective pre-exponential factors σ0 against Ea (blue squares in Fig. S27a†) a Meyer–Neldel energy Δ0 of 34 meV was obtained. Here, Δ0 deviates more strongly from the thermal energy and thus these mixed substituted lithium yttrium halides can be classified as type one materials with Δ0 > kBT and where the ionic conductivity and the activation energy show an inverse correlation. To obtain a comprehensive picture of the long-range lithium ion migration, lithium diffusivities were probed additionally by PFG-NMR in pure and substituted lithium yttrium halides. The obtained data are summarized in Fig. S39† and more details are provided in the ESI.† Both the activation energies and tracer diffusion coefficients obtained from PFG-NMR show very similar behaviour as the activation energies EEISa and ionic conductivities σEIStot obtained from EIS. Again, the unsubstituted Li3YBr6 exhibits a slightly smaller activation energy and a higher diffusion coefficient compared to the pure iodide. The anion substituted Li3YBr3.5I2.5 and mixed substituted Li2.9Y0.9Zr0.1Br3.5I2.5 show an even smaller activation energy ENMRa and an increased DNMRtr of 4.9 × 10−12 m2 s−1 and 6.1 × 10−12 m2 s−1, respectively. Substitution with divalent cadmium and calcium cations leads to an unchanged or slightly increased ENMRa and to a reduced DNMRtr of around 3 × 10−12 m2 s−1.
3 Conclusions
By evaluating the different synthetic approaches (SSS, MCBM with and without subsequent calcination), we can state that the synthesis via MCBM facilitates a quick, facile and energy efficient way to produce phase pure lithium rare earth metal iodides. The obtained products, however, exhibit fully disordered intra-layer cation substructures, as well as very small domain sizes, in particular perpendicular to the layer planes. The small vertical domain sizes of the balled-milled crystallites are attributed to facile cleavage of the materials with layered morphologies parallel to the layers, which are also soft due to the low charge density of the iodide anions. The microstructure of the ball-milled samples significantly reduces the ionic conductivity. Post-synthetic calcination at 500 °C leads to vastly increased domain sizes, especially in the vertical direction, and simultaneously reduces the intra-layer cation disorder leading to an improvement of the electrochemical properties compared to the solely ball-milled samples. In addition, we note that conventional SSS tends to result in lithium rare earth metal iodides with a lower degree of intra-layer cation disorder. Accordingly, they outperform their ball-milled counterparts in terms of ionic conductivity and activation energy for ion diffusion, even despite the fact that SSS conversion of lithium iodide and rare earth metal iodide is often incomplete.Furthermore, we report the synthesis and characterization of several new isostructural lithium rare earth metal iodides Li3MI6 with M = Y, Sm, Gd, Tb, Dy, Ho, Er, Tm, Yb and Lu. All Li3MI6 exhibit a high degree of stacking fault and intra-layer cation disorder as already observed for Li3HoBr6−xIx.19 While the degree of stacking fault disorder tends to have a minor influence on the ionic transport properties, the ionic conductivity in these iodides is strongly affected by the size of the RE cation and by the degree of intra-layer cation disorder. The ionic conductivity ranges from 3.0 × 10−5 S cm−1 for Li3LuI6 with 82% of intra-layer cation disorder to 4.6 × 10−4 S cm−1 for Li3SmI6 with an intra-layer cation disorder of 44%.
Small degrees of Cd2+ substitution in Li3+yGd1−yCdyI6 lead to an enhancement of the ionic conductivity from 3.9 × 10−4 S cm−1 for pristine Li3GdI6 to 8.0 × 10−4 S cm−1 for y = 0.1 and improve the activation energy for ion diffusion from 0.26 eV to 0.22 eV. An increase of the degree of substitution to Cd/Gd = 1 (corresponding to y = 0.5) leads to the formation of a chain-like ordering within the mixed layer and results in a composition of Li2.2Gd0.36Cd0.36I4, contrary to the honeycomb-type motifs found in the unsubstituted Li3MI6. As a consequence of the different ordering, the chain-type structure shows a decreased ionic conductivity of 1.8 × 10−4 S cm−1 due to the resulting more confined Li diffusion pathways.
Isovalent anion substitution in Li3YBr6−xIx leads to an overall improvement of the ionic transport properties. Additional aliovalent cation substitution with divalent metal cations in Li3+yY1−yMIIyBr3.5I2.5 (with MII = Cd2+ or Ca2+) leads to a slight diminishing of the ionic conductivity. In contrast, substitution with Zr4+ in Li3−yY1−yMIVyBr3.5I2.5 leads to a further improvement of the ionic conductivity to 3.0 × 10−3 S cm−1 in Li2.9Y0.9Zr0.1Br3.5I2.5.
Taking all the observed trends into account, the ionic transport properties in lithium rare earth iodides simultaneously depend on several parameters like it is schematically shown in Fig. 9.
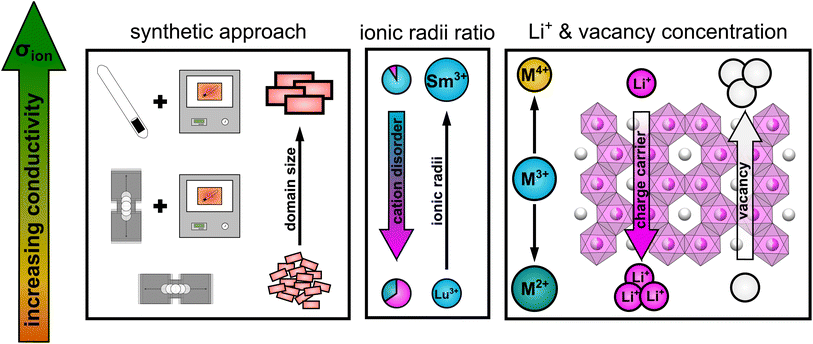 | ||
| Fig. 9 Schematic illustration of the influence of several parameters on the ionic conductivity in layered lithium rare earth iodides. | ||
(i) The packing of the anion sublattice defines the nature (size and shape) of the available diffusion pathways and the energy landscape that lithium ions encounter during diffusion. (ii) The charge carrier/vacancy concentration determines the amount of active charge carriers, where an increased vacancy concentration is found to be more effective than increasing the lithium ion concentration. Secondly, the BVELs are also affected by the size and charge of the countercations in the next nearest vicinity. (iii) Intra-layer cation disorder in the observed structures leads to an inhibition or blocking of diffusion paths, i.e. reducing the dimensionality of the lithium ion percolation network. The intra-layer cation disorder itself, i.e. occupational intermixing, can either be tuned by the synthetic approach or by the relative sizes of the cations and anions within the structure. (iv) Stacking fault disorder overall shows an unsignificant influence on the ionic transport properties in structures with an extensive 3D-percolation network, but becomes more dominant in structures with diffusion paths of lower or more confined dimensions.
Author contributions
The manuscript was written based on contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the BMBF cluster of competence FestBatt (03XPO177B), the DFG cluster of excellence e-conversion (EXC2089), the Max Planck Society and the Center for NanoScience. The authors thank Roland Eger and Claudia Kamella for the synthesis of the rare earth halide precursors. Christine Stefani is acknowledged for performing PXRD measurements. Open Access funding provided by the Max Planck Society.Notes and references
- B. V. Lotsch and J. Maier, J. Electroceram., 2017, 38, 128–141 CrossRef
.
- Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier, M. Armand and L. Chen, Energy Environ. Sci., 2018, 11, 1945–1976 RSC
.
- Y. Sun, K. Suzuki, S. Hori, M. Hirayama and R. Kanno, Chem. Mater., 2017, 29, 5858–5864 CrossRef CAS
.
- P. Bron, S. Johansson, K. Zick, J. Schmedt auf der Günne, S. Dehnen and B. Roling, J. Am. Chem. Soc., 2013, 135, 15694–15697 CrossRef CAS PubMed
.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed
.
- S. Harm, A.-K. Hatz, I. Moudrakovski, R. Eger, A. Kuhn, C. Hoch and B. V. Lotsch, Chem. Mater., 2019, 31, 1280–1288 CrossRef CAS
.
- Y. Zhu and Y. Mo, Angew. Chem., 2020, 132, 17625–17629 CrossRef
.
- W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder,
Chem. Mater., 2016, 28, 266–273 CrossRef CAS
.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Nat. Mater., 2019, 18, 1278–1291 CrossRef CAS PubMed
.
- L. M. Riegger, R. Schlem, J. Sann, W. G. Zeier and J. Janek, Angew. Chem., Int. Ed., 2021, 60, 6718–6723 CrossRef CAS PubMed
.
- S. Wang, Q. Bai, A. M. Nolan, Y. Liu, S. Gong, Q. Sun and Y. Mo, Angew. Chem., Int. Ed., 2019, 58, 8039–8043 CrossRef CAS PubMed
.
- A. M. Nolan, Y. Liu and Y. Mo, ACS Energy Lett., 2019, 2444–2451 CrossRef CAS
.
- R. Schlem, A. Banik, S. Ohno, E. Suard and W. G. Zeier, Chem. Mater., 2021, 33, 327–337 CrossRef CAS
.
- M. Gombotz and H. M. R. Wilkening, ACS Sustainable Chem. Eng., 2021, 9, 743–755 CrossRef CAS
.
- Z. Liu, S. Ma, J. Liu, S. Xiong, Y. Ma and H. Chen, ACS Energy Lett., 2021, 6, 298–304 CrossRef CAS
.
- X. Li, J. Liang, K. R. Adair, J. Li, W. Li, F. Zhao, Y. Hu, T. K. Sham, L. Zhang, S. Zhao, S. Lu, H. Huang, R. Li, N. Chen and X. Sun, Nano Lett., 2020, 20, 4384–4392 CrossRef CAS PubMed
.
- E. Sebti, H. A. Evans, H. Chen, P. M. Richardson, K. M. White, R. Giovine, K. P. Koirala, Y. Xu, E. Gonzalez-Correa, C. Wang, C. M. Brown, A. K. Cheetham, P. Canepa and R. J. Clément, J. Am. Chem. Soc., 2022, 144, 5795–5811 CrossRef CAS PubMed
.
- X. Shi, Z. Zeng, M. Sun, B. Huang, H. Zhang, W. Luo, Y. Huang, Y. Du and C. Yan, Nano Lett., 2021, 21, 9325–9331 CrossRef CAS PubMed
.
- M. A. Plass, S. Bette, R. E. Dinnebier and B. V. Lotsch, Chem. Mater., 2022, 34, 3227–3235 CrossRef CAS
.
- R. E. Thoma, G. D. Brunton, R. A. Penneman and T. K. Keenan, Inorg. Chem., 1970, 9, 1096–1101 CrossRef CAS
.
- C. Keller and H. Schmutz, J. Inorg. Nucl. Chem., 1965, 27, 900–901 CrossRef CAS
.
- A. Tyagi, J. Köhler, P. Balog and J. Weber, J. Solid State Chem., 2005, 178, 2620–2625 CrossRef CAS
.
- A. Bohnsack, F. Stenzel, A. Zajonc, G. Balzer, M. S. Wickleder and G. Meyer, Z. Anorg. Allg. Chem., 1997, 623, 1067–1073 CrossRef CAS
.
- A. Bohnsack, G. Balzer, H.-U. Güdel, M. S. Wickleder and G. Meyer, Z. Anorg. Allg. Chem., 1997, 623, 1352–1356 CrossRef CAS
.
- R. Schlem, T. Bernges, C. Li, M. A. Kraft, N. Minafra and W. G. Zeier, ACS Appl. Energy Mater., 2020, 3, 3684–3691 CrossRef CAS
.
- M. S. Wickleder and G. Meyer, Z. Anorg. Allg. Chem., 1995, 621, 457–463 CrossRef CAS
.
- A. Bohnsack and G. Meyer, Z. Anorg. Allg. Chem., 1997, 623, 837–843 CrossRef CAS
.
- Z. Xu, X. Chen, K. Liu, R. Chen, X. Zeng and H. Zhu, Chem. Mater., 2019, 31, 7425–7433 CrossRef CAS
.
- M. A. Kraft, S. P. Culver, M. Calderon, F. Böcher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909–10918 CrossRef CAS PubMed
.
- M. A. Kraft, S. Ohno, T. Zinkevich, R. Koerver, S. P. Culver, T. Fuchs, A. Senyshyn, S. Indris, B. J. Morgan and W. G. Zeier, J. Am. Chem. Soc., 2018, 140, 16330–16339 CrossRef CAS PubMed
.
- K. Hogrefe, N. Minafra, I. Hanghofer, A. Banik, W. G. Zeier and H. M. R. Wilkening, J. Am. Chem. Soc., 2022, 144, 1795–1812 CrossRef CAS PubMed
.
- W. G. Zeier, R. Schlem, A. Banik, M. Eckardt and M. Zobel, ACS Appl. Energy Mater., 2020, 3, 10164–10173 CrossRef
.
- E. A. Wu, S. Banerjee, H. Tang, P. M. Richardson, J.-M. Doux, J. Qi, Z. Zhu, A. Grenier, Y. Li, E. Zhao, G. Deysher, E. Sebti, H. Nguyen, R. Stephens, G. Verbist, K. W. Chapman, R. J. Clément, A. Banerjee, Y. S. Meng and S. P. Ong, Nat. Commun., 2021, 12, 1256 CrossRef CAS PubMed
.
- K.-H. Park, K. Kaup, A. Assoud, Q. Zhang, X. Wu and L. F. Nazar, ACS Energy Lett., 2020, 5, 533–539 CrossRef CAS
.
- S. Y. Kim, K. Kaup, K.-H. Park, A. Assoud, L. Zhou, J. Liu, X. Wu and L. F. Nazar, ACS Mater. Lett., 2021, 3, 930–938 CrossRef CAS
.
- J. Park, D. Han, H. Kwak, Y. Han, Y. J. Choi, K.-W. Nam and Y. S. Jung, Chem. Eng. J., 2021, 425, 130630 CrossRef CAS
.
- E. van der Maas, W. Zhao, Z. Cheng, T. Famprikis, M. Thijs, S. R. Parnell, S. Ganapathy and M. Wagemaker, J. Phys. Chem. C, 2023, 127, 125–132 CrossRef CAS PubMed
.
- T. Asano, A. Sakai, S. Ouchi, M. Sakaida, A. Miyazaki and S. Hasegawa, Adv. Mater., 2018, 30, 1803075 CrossRef PubMed
.
- R. Schlem, S. Muy, N. Prinz, A. Banik, Y. Shao-Horn, M. Zobel and W. G. Zeier, Adv. Energy Mater., 2020, 10, 1903719 CrossRef CAS
.
-
G. Meyer and L. R. Morss, Synthesis of Lanthanide and Actinide Compounds, Springer, Netherlands, Dordrecht, 1991, vol. 2 Search PubMed
.
-
Taschenbuch für Chemiker und Physiker, ed. R. Blachnik, Springer, Berlin, Heidelberg, 4th edn, 1998 Search PubMed
.
-
CRC Handbook of Chemistry and Physics, ed. J. R. Rumble, CRC Press/Taylor & Francis, 103rd edn, 2022 Search PubMed
.
- R. D. Shannon and C. T. Prewitt, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 925–946 CrossRef CAS
.
- R. D. Shannon and C. T. Prewitt, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 1046–1048 CrossRef CAS
.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef
.
- S. Muy, J. C. Bachman, H.-H. Chang, L. Giordano, F. Maglia, S. Lupart, P. Lamp, W. G. Zeier and Y. Shao-Horn, Chem. Mater., 2018, 30, 5573–5582 CrossRef CAS
.
- Y. Gao, N. Li, Y. Wu, W. Yang and S. Bo, Adv. Energy Mater., 2021, 11, 2100325 CrossRef CAS
.
- L. Zhou, Q. Zhang and L. F. Nazar, Chem. Mater., 2022, 34, 9634–9643 CrossRef CAS
.
- W. v Meyer and H. Neldel, Z. Tech. Phys., 1937, 18, 588 Search PubMed
.
-
R. W. Balluffi, S. M. Allen and W. C. Carter, Kinetics of Materials, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2005 Search PubMed
.
- A. Yelon, B. Movaghar and R. S. Crandall, Rep. Prog. Phys., 2006, 69, 1145 CrossRef CAS
.
- H. D. Lutz, Z. Zhang and A. Pfitzner, Solid State Ionics, 1993, 62, 1–3 CrossRef CAS
.
- L. L. Wong, K. C. Phuah, R. Dai, H. Chen, W. S. Chew and S. Adams, Chem. Mater., 2021, 33, 625–641 CrossRef CAS
.
- H. Chen, L. L. Wong and S. Adams, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 18–33 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2222205. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3ta01327h |
| This journal is © The Royal Society of Chemistry 2023 |