Ferroelectrically tunable magnetic skyrmions in two-dimensional multiferroics†
Zhonglin
He
,
Wenhui
Du
,
Kaiying
Dou
,
Ying
Dai
 *,
Baibiao
Huang
*,
Baibiao
Huang
 and
Yandong
Ma
and
Yandong
Ma
 *
*
School of Physics, State Key Laboratory of Crystal Materials, Shandong University, Shandanan Street 27, Jinan 250100, China. E-mail: daiy60@sina.com; yandong.ma@sdu.edu.cn
First published on 6th June 2023
Abstract
Magnetic skyrmions are topologically protected entities that are promising for information storage and processing. Currently, an essential challenge for future advances of skyrmionic devices lies in achieving effective control of skyrmion properties. Here, through first-principles and Monte-Carlo simulations, we report the identification of nontrivial topological magnetism in two-dimensional multiferroics of Co2NF2. Because of ferroelectricity, monolayer Co2NF2 exhibits a large Dzyaloshinskii–Moriya interaction. This together with exchange interaction can stabilize magnetic skyrmions with the size of sub-10 nm under a moderate magnetic field. Importantly, arising from the magnetoelectric coupling effect, the chirality of magnetic skyrmions is ferroelectrically tunable, producing the four-fold degenerate skyrmions. When interfacing with monolayer MoSe2, the creation and annihilation of magnetic skyrmions, as well as phase transition between skyrmion and skyrmion lattice, can be realized in a ferroelectrically controllable fashion. A dimensionless parameter κ′ is further proposed as the criterion for stabilizing magnetic skyrmions in such multiferroic lattices. Our work greatly enriches the two-dimensional skyrmionics and multiferroics research.
New conceptsMagnetic skyrmions have attracted increasing attention recently. To translate the compelling features of magnetic skyrmions into practical spintronic devices, it is crucial to achieve effective control of skyrmion properties, including density and morphology. Electric field via ferroelectric switching has been considered as a very efficient method, which can significantly reduce energy consumption. Nonetheless, the in situ ferroelectric control of skyrmion properties in 2D systems remains challenging. Herein, we report the discovery of topological magnetism in 2D multiferroics of Co2NF2. Arising from strong spin-orbit coupling and inversion symmetry breaking, a large DMI occurs in monolayer Co2NF2. This competing with ferromagnetic Heisenberg exchange interaction can stabilize magnetic skyrmions under a moderate magnetic field, with the size of sub-10 nm. Due to the magnetoelectric coupling effect, the switching of chirality of magnetic skyrmions is realized in monolayer Co2NF2 in a ferroelectrically controllable fashion, which yields the four-fold degenerate skyrmions. By interfacing with monolayer MoSe2, the ferroelectrically controllable creation-annihilation of magnetic skyrmions, as well as phase transition between skyrmion and skyrmion lattice, are obtained. |
Magnetic skyrmions are whirling spin textures exhibiting nontrivial topology in real space.1 Each skyrmion is characterized by a topological invariant Q = ±1 that measures the winding of the normalized local magnetization, m. This chiral spin configuration can be stabilized as a result of competing Heisenberg exchange interaction and Dzyaloshinskii–Moriya interaction (DMI).2–4 Since their first observation in B20 bulk MnSi5 and thin film Fe0.5Co0.5Si,6 magnetic skyrmions have attracted tremendous attention because of a variety of intriguing characteristics, such as topological robustness against continuous deformation, self-organized lattice form, and solitonic nature with current-driven motion.7–11 These exotic properties not only open up new opportunities for exploring nontrivial topological physics but also hold high potential for applications in future spintronics devices.12–14 Apart from conventional cubic B20 bulk crystals6 and thin films,15–17 in recent experiments, two independent groups have reported the observation of magnetic skyrmions in the van der Waals magnets Cr2GeTe618 and Fe3GeTe2,19 rendering two-dimensional (2D) magnetic materials a new category of skyrmion medium.20–25
To translate the compelling features of magnetic skyrmions into practical spintronic devices, it is crucial to achieve effective control of skyrmion properties, including density and morphology.26–28 For bulk compounds, the magnetic interactions are almost invariant. In contrast, magnetic skyrmions in heavy-metal/ferromagnet thin films are sensitive to various external stimuli, such as spin-transfer torque,29 electric field,30 and current gradient.31 Among them, electric field via ferroelectric (FE) polarization switching is considered a more effective method, which can significantly reduce energy consumption. Nonetheless, the in situ ferroelectric control of skyrmion properties in 2D systems remains challenging.32–34 Recently, 2D multiferroics, which simultaneously exhibit ferroelectricity and magnetism, have received increasing interest.35,36 In 2D multiferroic materials, the intrinsic inversion symmetry breaking gives rise to DMI, while the time-reversal symmetry breaking guarantees Heisenberg exchange interaction34. This quite naturally provides the possibility for the formation of magnetic skyrmions. Furthermore, through the magnetoelectric coupling effect, ferroelectrically tunable magnetic skyrmions are highly anticipated in such systems.
Here, based on first-principles calculations and Monte-Carlo (MC) simulations, we report the discovery of topological magnetism in 2D multiferroics of Co2NF2. Arising from strong spin-orbit coupling (SOC) and inversion symmetry breaking, a large DMI occurs in monolayer Co2NF2. This competing with ferromagnetic (FM) Heisenberg exchange interaction can stabilize magnetic skyrmions under a moderate magnetic field, with the size of sub-10 nm. Due to the magnetoelectric coupling effect, the switching of chirality of magnetic skyrmions is realized in monolayer Co2NF2 in a ferroelectrically controllable fashion, which yields the four-fold degenerate skyrmions. By interfacing with monolayer MoSe2, the ferroelectrically controllable creation-annihilation of magnetic skyrmions, as well as phase transition between skyrmion and skyrmion lattice, are obtained. Furthermore, we also unveil a dimensionless parameter κ′ as the criterion for assessing the formation of magnetic skyrmions in such multiferroic lattices. This work thus provides a novel avenue toward the design and control of magnetic skyrmions on 2D multiferroics.
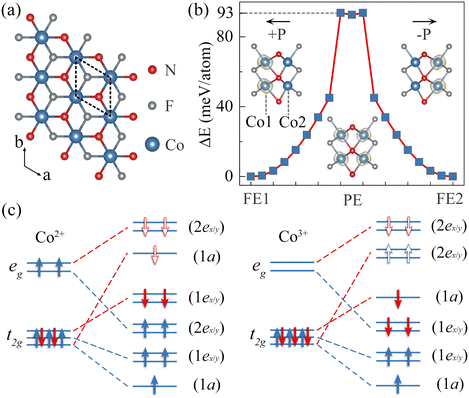
Fig. 1(a and b) show the crystal structure of monolayer Co2NF2. It exhibits a hexagonal lattice with P3m1 space group, and is composed of five triangular atomic layers stacked in the sequence of F-Co1-N-Co2-F. The lattice constant is optimized to be 2.87 Å, which agrees well with the previous work.37 To assess the stability of Co2NF2, we first calculate its phonon spectra. As shown in Fig. S1(a) (ESI†), except for the tiny imaginary frequencies around the Γ point, all branches are positive, suggesting the dynamical stability. The thermal stability of monolayer Co2NF2 is also investigated using ab initio molecular dynamics (AIMD) simulations. As illustrated in Fig. S1(b) (ESI†), after heating at 500 K for 5 ps, neither structure reconstruction nor bond breaking is found, which confirms that it is thermally stable as well.
In Co2NF2, as shown in Fig. 1(b), the N atomic layer favors a vertical displacement with respect to the central horizontal plane of Co dimers. This breaks the inversion symmetry and leads to an out-of-plane (OP) electric polarization. As the N atom can move vertically towards either Co1 or Co2 atoms and these two vertical displacements are energetically equivalent, the resulting two configurations can be considered as two FE states. To guarantee FE order in Co2NF2, we calculate the minimum energy path for the ferroelectric switching. The corresponding energy barrier is estimated to be 93 meV per atom, comparable to those of CuAP2S6 (A = In, Bi),38 SnX (X = S, Se),39 and Sc2CO2.40 This suggests the feasibility of ferroelectricity in Co2NF2. In addition to FE order, Co2NF2 prefers a spin-polarized phase with a magnetic moment of 3μB per unit cell. From the spin charge density shown in Fig. 1(b), we can see that the magnetic moment is mainly distributed on the Co atom lying further from the N atom, while another Co atom has no contribution to the magnetic moment. In this regard, the magnetic moment can be exchanged between the two Co atoms through ferroelectric transition, indicating that Co2NF2 is a multiferroic material with strong magnetoelectric coupling. For convenience of discussion, unless otherwise stated, Co2NF2 refers to the FE1 phase in the following.
To get insight into the magnetoelectric coupling in Co2NF2, we investigate the origin of its magnetism. The valence electronic configuration of the Co atom is 3d74s2. For the Co1 atom, it donates one valence electron to the surrounding N and F atoms, giving rise to the oxidation state of +2. Different from the Co1 atom, the vertical displacement of the N atom strengthens its bonding with Co2. As a result, the Co2 atom donates one more valence electron to the N atom compared with the Co1 atom, and thus possesses an oxidation state of +3. Under the octahedral crystal field, the d orbitals split into two manifolds, i.e., the higher doublet eg orbitals and the lower triplet t2g orbitals. As shown in Fig. 1(b), due to the distortion of the octahedral geometry and magnetic exchange field, eg and t2g orbitals further split. Because of the vertical displacement of the N atoms, the resulting orbitals are different for the Co1 and Co2 atoms, which is consistent with the projected density of states (PDOS) in Fig. S3 (ESI†). According to Hund's rule and the Pauli exclusion principle, the electronic configuration of Co12+ is t2g5eg2, generating a magnetic moment of 3μB per Co1 atom, as shown in Fig. 1(c). While for Co23+, the electronic configuration is t2g6eg0, suggesting the absence of a magnetic moment. Under ferroelectric transition, the coordination environments as well as the number of transferred electrons for Co1 and Co2 atoms are exchanged, which is accompanied by the exchange of magnetic moments on them. With these results in hand, we can easily understand the magnetoelectric coupling in Co2NF2.
For further exploring the magnetic properties of Co2NF2, we introduce a Heisenberg spin Hamiltonian:
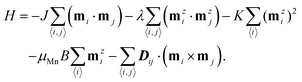 | (1) |
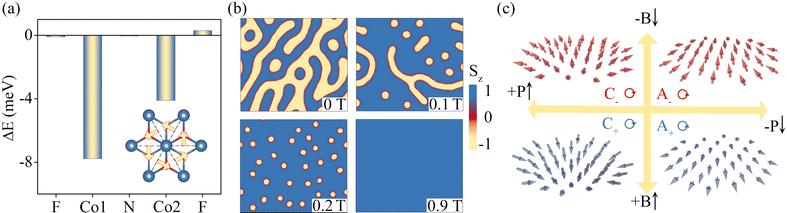
According to the Moriya's rule45, the DMI vector can be simplified as Dij = d‖ (uij × z) + dzz, where uij and z are the unit vector from site i to j and along the z direction. In view of the C3v symmetry, the OP component dz is arranged in a staggered pattern, rendering it negligible in Co2NF2.20,22 We therefore only consider the IP component d‖ of the DMI vector. To obtain d‖, we consider two spin-spiral configurations, i.e., the clockwise (CW) and anticlockwise (ACW) configurations (see Fig. S4(a), ESI†). The d‖ is calculated to be −1.01 meV. Based on the layer-resolved SOC energy difference (ΔE) between the two spin-spiral configurations shown in Fig. 2(a), it can be seen that ΔE is mainly contributed by the magnetic Co1 atom, which suggests that the DMI is dominated by the Rashba effect in Co2NF2. In addition to the magnetic Co1 atom, there is a moderate DMI contribution from the nonmagnetic Co2 atom, that is, the nonmagnetic Co2 atom also acts as a SOC-active site to induce spin-orbit scattering necessary for DMI, corresponding to the Fert–Levy mechanism.49 Therefore, the Fert–Levy mechanism also plays a nonnegligible role for forming DMI in Co2NF2. We wish to point out that different from the scalar magnetic parameters, the chirality of DMI vector Dij is tunable under FE transition. For example, when switching to the FE2 state, the sign of the IP component of the DMI vector is reversed, i.e., d‖ = 1.01 meV.
Concerning the NN isotropic exchange interaction and DMI of Co2NF2, the ratio between them is estimated to be |d‖/J| = 0.28. Note that 0.1 < |d‖/J| < 0.2 is usually considered as a criterion to stabilize magnetic skyrmions.20,22 The large |d‖/J| suggests the existence of spin spiral states (SS) in Co2NF2, which might transform into skyrmion lattice (SkL) phase through applying an external magnetic field.46 Notably, different from the skyrmion (SkX) phase that consists of isolated magnetic skyrmions, the SkL phase is composed of regular arrays of magnetic skyrmions. To verify this possibility, based on the magnetic parameters obtained from first-principles calculations, we perform the parallel tempering MC simulations to explore the spin textures in Co2NF2. Here, we introduce topological charge Q to characterize the nontrivial property of magnetic skyrmions, which is given by47
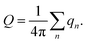 | (2) |
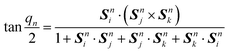 . Sni, jni and kni are the three spin vectors of the nth equilateral triangle in the ACW lattice. The spin texture of Co2NF2 under zero magnetic field is illustrated in Fig. 2(b). Intriguingly, although the ratio |d‖/J| is rather large, the isolated Néel-type magnetic skyrmions with nontrivial topological Q = ±1 is still observed near the labyrinth domains (see Fig. S4(b), ESI†). Such unexpected emergency of magnetic skyrmions in Co2NF2 under zero magnetic field can be attributed to its large magnetic anisotropy, which enhances the collinear spin arrangement.22,48 Moreover, the diameters of these magnetic skyrmions are found to be only ∼8 nm, which is highly desirable for device applications.
. Sni, jni and kni are the three spin vectors of the nth equilateral triangle in the ACW lattice. The spin texture of Co2NF2 under zero magnetic field is illustrated in Fig. 2(b). Intriguingly, although the ratio |d‖/J| is rather large, the isolated Néel-type magnetic skyrmions with nontrivial topological Q = ±1 is still observed near the labyrinth domains (see Fig. S4(b), ESI†). Such unexpected emergency of magnetic skyrmions in Co2NF2 under zero magnetic field can be attributed to its large magnetic anisotropy, which enhances the collinear spin arrangement.22,48 Moreover, the diameters of these magnetic skyrmions are found to be only ∼8 nm, which is highly desirable for device applications.
We then study the effect of an external magnetic field on the topological spin textures of Co2NF2. From Fig. 2(b) we can see that with increasing magnetic field from 0 to 0.1 T, the labyrinth domains shrink and more magnetic skyrmions emerge. When applying a magnetic field of 0.2 T, the labyrinth domains disappear completely, resulting in isolated magnetic skyrmions with Q = 1 embedded in the FM background. In this regard, the intriguing skyrmion (SkX) phase is realized in Co2NF2. Remarkably, the SkX phase can be preserved within a wide range of 0.2–0.9 T. Upon further increasing the magnetic field, the SkX phase transforms into the trivial FM phase. Therefore, except for the intriguing SkX phase, the expected SkL phase is absent in Co2NF2, which also results from its large magnetic anisotropy. Along with the evolution of topological spin textures, the diameter of the magnetic skyrmion is reduced with increasing the magnetic field. This phenomenon correlates to the fact that the magnetic field prefers to align spins. As for the density of magnetic skyrmions, as shown in Fig. S4(c) (ESI†), it first increases with the magnetic field and achieves the maximum of ∼0.05 per nm2 (44 per supercell) under the magnetic field of 0.5–0.65 T; with further increasing the magnetic field (0.65–0.9 T), it decreases rapidly and shrinks down to zero at 0.9 T, which corresponds to the trivial FM phase.
For the magnetic skyrmions in Co2NF2, as shown in Fig. 2(b), the core spin aligns antiparallel to the external magnetic field. With reversing the magnetic field, the core spin orientation of the magnetic skyrmions can be reversed, which would switch the signs of the topological charge, i.e., Q and -Q. Besides, as we mentioned above, the chirality of DMI vector Dij in Co2NF2 can be reversed under FE transition. As the chirality γ of the magnetic skyrmion is locked by the sign and direction of the DMI vector, the chirality of magnetic skyrmions in Co2NF2 is ferroelectrically controllable, i.e., γ and -γ. Based on these properties, the four-fold degenerate Néel-type magnetic skyrmions with (Q, γ) = (±1, ±1) are realized in Co2NF2, and these four states can be transformed into each other through FE and FM inversion, as illustrated in Fig. 2(c).
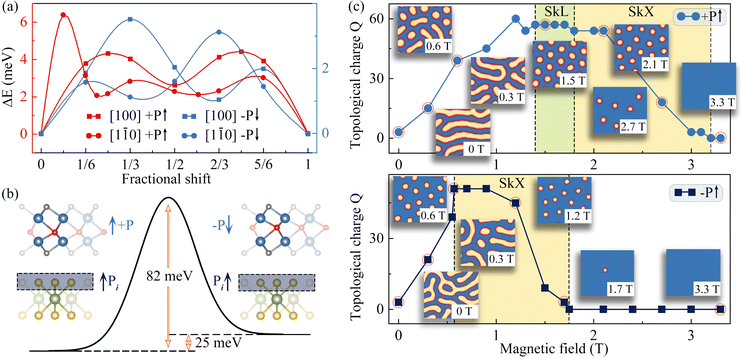
Considering the particular structure of Co2NF2, we propose a mechanism of coupling its multiferroics with a nonmagnetic substrate for realizing FE control of more skyrmion properties. We select monolayer MoSe2 as the nonmagnetic substrate and construct the Co2NF2/MoSe2 heterobilayer. Due to the significant difference in electronegativity between Se and F atoms, Co2NF2/MoSe2 is expected to exhibit a relatively strong interlayer coupling. This can lead to significant difference between the two FE states of Co2NF2, which is beneficial for enhancing the FE control of skyrmion properties. In Co2NF2/MoSe2, a √3 × √3 supercell of MoSe2 is used to match a 2 × 2 supercell of Co2NF2, which results in a rather small lattice mismatch of less than 1%. The binding energy of Co2NF2/MoSe2 as a function of normalized interlayer sliding is summarized in Fig. 3(a). We can see that the structure with N lying vertically above the Mo atom is the most stable configuration. In the following, we only consider this configuration (see Fig. S5ESI†). By interfacing with MoSe2, an interface dipole Pi pointing from MoSe2 to Co2NF2 is generated due to the different electronegativities of the interfaced atoms. The interface dipole Pi would interact with the FE polarization P, forming a dipole–dipole interaction in the form of – aP·Pi/r3, where a is a constant and r is the distance between the two dipoles. Clearly, the FE1 phase with P parallel to Pi tends to be lower in energy than FE2 with P antiparallel to Pi; see Fig. 3(b). And thus, the degeneracy of the two FE states is lifted in Co2NF2/MoSe2. As shown in Fig. 3(b), the FE switching barriers from FE1 (+ P↑) to FE2 (−P↓) and FE2 (−P↓) to FE1 (+P↑) phases are calculated to be 82 and 57 meV per atoms, respectively. These values are lower than that of freestanding Co2NF2, guaranteeing the feasibility of the FE order in Co2NF2/MoSe2.
Based on eqn (1), we calculate the magnetic parameters of these two FE states (+P↑ and −P↓) of Co2NF2/MoSe2 (see Table S1ESI†). It can be seen that, as compared with free-standing Co2NF2, KC for both +P↑ and −P↓ are substantially weakened (see ESI† for more details), while J and d‖ vary slightly. Based on these magnetic parameters, we conduct the parallel tempering MC simulations to investigate the spin textures of Co2NF2/MoSe2. Fig. 3(c) illustrates the evolutions of topological charge Q and spin textures of +P↑ and −P↓ as functions of magnetic field. It can be seen that +P↑ favors the SS phase under zero magnetic field. With increasing magnetic field, the labyrinth domains disappear and transform into SkL phase under 1.4–1.8 T. Upon increasing the magnetic field to 1.8–3.2 T, the ordered array of magnetic skyrmions is disrupted and SkX phase forms. Under the magnetic field larger than 3.2 T, the spin textures of +P↑ show a trivial FM phase. Different from +P↑, as shown in Fig. 3(c), isolated Néel-type magnetic skyrmions are observed near the labyrinth domains for −P↓ under zero magnetic field. When applying a magnetic field, the labyrinth domains shrink and more magnetic skyrmions emerge. Under 0.6–1.75 T, the labyrinth domains vanish completely and the SkX phase is favorable for −P↓. Upon increasing the magnetic field larger than 1.75 T, −P↓ prefers the trivial FM phase. Because these two FE states favor different topological spin textures under a magnetic field, the effective control of more skyrmion properties in a ferroelectrically controllable fashion is realized in Co2NF2/MoSe2. For example, the creation and annihilation of magnetic skyrmions is ferroelectrically controllable under 0.6–1.4 and 1.75–3.2 T, while under 1.4–1.75 T, the phase switching between SkX and SkL can be realized through FE transition. It should be noted that upon applying external strain, the bond length and angle would be changed, which could affect the magnetic parameters. Therefore, strain can also be applied to tune the skyrmion physics.25,50,51
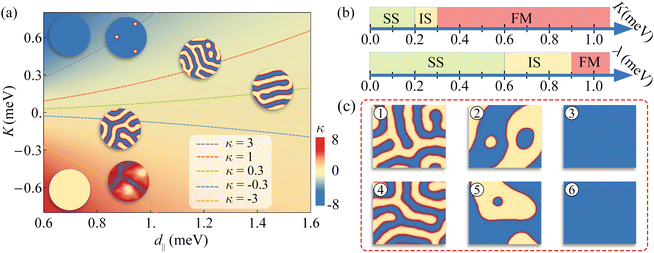
From the above, we can see that d‖ and K play important roles in realizing the topological magnetism. To get a deep insight into their combined effect, we investigated the evolution of spin textures as a function of d‖ and K. Fig. 4(a) displays the corresponding phase diagram. We find that a dimensionless parameter 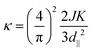 can be used to describe their combined effect on the topological spin texture.20,34 As shown in Fig. 4(a), for the spin textures around κ = 1, magnetic skyrmions appear around the labyrinth domains. Since
can be used to describe their combined effect on the topological spin texture.20,34 As shown in Fig. 4(a), for the spin textures around κ = 1, magnetic skyrmions appear around the labyrinth domains. Since 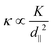 , the larger magnitude of κ (≫ 1) signifies the enhanced spin collinear arrangement, vanishing the labyrinth domains. For κ = 3 and κ = −3, the isolated magnetic skyrmions and meron pairs are, respectively, generated along with the reduction of labyrinth domains. With further increasing κ, the topological magnetism will be transformed into the trivial FM phase. For smaller magnitude of κ (≪ 1), the DMI plays a dominated role, giving rise to the SS phase.
, the larger magnitude of κ (≫ 1) signifies the enhanced spin collinear arrangement, vanishing the labyrinth domains. For κ = 3 and κ = −3, the isolated magnetic skyrmions and meron pairs are, respectively, generated along with the reduction of labyrinth domains. With further increasing κ, the topological magnetism will be transformed into the trivial FM phase. For smaller magnitude of κ (≪ 1), the DMI plays a dominated role, giving rise to the SS phase.
To verify the validation of dimensionless parameter κ in assessing the possibility for realizing magnetic skyrmions, we calculate κ for Co2NF2 and Co2NF2/MoSe2. As shown in Table S1 (ESI†), for Co2NF2, κ = 2.3 suggests that a SkX phase is stabilized according to the phase diagram shown in Fig. 4(a), which agrees well with MC simulations. However, according to the phase diagram shown in Fig. 4(a), κ = 1.0 indicates that +P↑ tends to form SkX phase, while κ = 0.6 suggests that −P↓ prefers SkL phase, which is quite different from the MC simulations. This discrepancy stems from the fact that λ is neglected. Fig. 4(b) and (c) display the evolution of spin textures as a function of λ and K, respectively. It can be seen that the ability of λ to enhance collinear arrangement is roughly equivalent to that of triple K. Therefore, we substitute the K term by K + 3 × λ and the expression of κ is transformed into 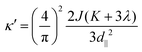 . It should be noted that the elaborations on the phase diagram of κ in Fig. 4(a) remain applicable to κ′. As shown in Table S1 (ESI†), κ′ is calculated to be 1.80 for monolayer Co2NF2, indicating the stabilization of the SkX phase in the presence of a magnetic field. For Co2NF2/MoSe2, +P↑ (κ′ = 0.2) tends to form SkL phase, while −P↓ (κ′ = 1.0) prefers SkX phase. The calculated κ′ agrees well with the MC simulations. Therefore, the dimensionless parameter κ′ can be considered as the criteria for assessing the formation of magnetic skyrmions in such multiferroic lattices.
. It should be noted that the elaborations on the phase diagram of κ in Fig. 4(a) remain applicable to κ′. As shown in Table S1 (ESI†), κ′ is calculated to be 1.80 for monolayer Co2NF2, indicating the stabilization of the SkX phase in the presence of a magnetic field. For Co2NF2/MoSe2, +P↑ (κ′ = 0.2) tends to form SkL phase, while −P↓ (κ′ = 1.0) prefers SkX phase. The calculated κ′ agrees well with the MC simulations. Therefore, the dimensionless parameter κ′ can be considered as the criteria for assessing the formation of magnetic skyrmions in such multiferroic lattices.
To summarize, we investigate the topological magnetism in 2D multiferroics of Co2NF2 on the basis of first-principles calculations and MC simulations. We find that Co2NF2 can exhibit magnetic skyrmions under moderate magnetic field, with the size of sub-10 nm. Arising from the magnetoelectric coupling effect, the chirality of magnetic skyrmions in monolayer Co2NF2 can be reversed via FE transition. Moreover, through interfacing with monolayer MoSe2, the ferroelectric control of more skyrmion properties is realized, such as the creation-annihilation of magnetic skyrmions and the phase transition between SkX and SkL. In addition, we introduce a dimensionless parameter κ′ as the criterion for assessing the formation of magnetic skyrmions in such multiferroic lattices.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work is supported by the National Natural Science Foundation of China (no. 12274261 and 12074217), Shandong Provincial Science Foundation for Excellent Young Scholars (no. ZR2020YQ04), Shandong Provincial Key Research and Development Program (Major Scientific and Technological Innovation Project) (no. 2019JZZY010302), Shandong Provincial QingChuang Technology Support Plan (no. 2021KJ002), and Taishan Young Scholar Program of Shandong Province.References
- B. Göbel, I. Mertig and O. A. Tretiakov, Beyond skyrmions: Review and perspectives of alternative magnetic quasiparticles, Phys. Rep., 2021, 895, 1 CrossRef
.
- H. Yang, A. Thiaville, S. Rohart, A. Fert and M. Chshiev, Anatomy of Dzyaloshinskii-moriya interaction at Co/Pt interfaces, Phys. Rev. Lett., 2015, 115, 267210 CrossRef PubMed
.
- J. Cho, N. H. Kim, S. Lee, J. S. Kim, R. Lavrijsen, A. Solignac, Y. Yin, D. S. Han, N. J. Van Hoof, H. J. Swagten and B. Koopmans, Thickness dependence of the interfacial Dzyaloshinskii-Moriya interaction in inversion symmetry broken systems, Nat. Commun., 2015, 6, 1 Search PubMed
.
- G. Beutier, S. P. Collins, O. V. Dimitrova, V. E. Dmitrienko, M. I. Katsnelson, Y. O. Kvashnin, A. I. Lichtenstein, V. V. Mazurenko, A. G. A. Nisbet, E. N. Ovchinnikova and D. Pincini, Band filling control of the Dzyaloshinskii-Moriya interaction in weakly ferromagnetic insulators, Phys. Rev. Lett., 2017, 119, 167201 CrossRef CAS PubMed
.
- S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii and P. Böni, Skyrmion lattice in a chiral magnet, Science, 2009, 323, 915 CrossRef PubMed
.
- X. Z. Yu, Y. Onose, N. Kanazawa, J. H. Park, J. H. Han, Y. Matsui, N. Nagaosa and Y. Tokura, Real-space observation of a two-dimensional skyrmion crystal, Nature, 2010, 465, 901 CrossRef CAS PubMed
.
- A. N. Bogdanov and C. Panagopoulos, Physical foundations and basic properties of magnetic skyrmions, Nat. Rev. Phys., 2020, 2, 492 CrossRef
.
- L. Caretta, M. Mann, F. Büttner, K. Ueda, B. Pfau, C. M. Günther, P. Hessing, A. Churikova, C. Klose, M. Schneider and D. Engel, Fast current-driven domain walls and small skyrmions in a compensated ferrimagnet, Nat. Nanotechnol., 2018, 13, 1154 CrossRef CAS PubMed
.
- J. Zang, M. Mostovoy, J. H. Han and N. Nagaosa, Dynamics of skyrmion crystals in metallic thin films, Phys. Rev. Lett., 2011, 107, 136804 CrossRef PubMed
.
- N. Kanazawa, S. Seki and Y. Tokura, Noncentrosymmetric magnets hosting magnetic skyrmions, Adv. Mater., 2017, 29, 1603227 CrossRef PubMed
.
- S. Seki, X. Z. Yu, S. Ishiwata and Y. Tokura, Observation of skyrmions in a multiferroic material, Science, 2012, 336, 198 CrossRef CAS PubMed
.
- A. Soumyanarayanan, M. Raju, A. L. Gonzalez Oyarce, A. K. Tan, M. Y. Im, A. P. Petrović, P. Ho, K. H. Khoo, M. Tran, C. K. Gan and F. Ernult, Tunable room-temperature magnetic skyrmions in Ir/Fe/Co/Pt multilayers, Nat. Mater., 2017, 16, 898 CrossRef CAS PubMed
.
- N. Nagaosa and Y. Tokura, Topological properties and dynamics of magnetic skyrmions, Nat. Nanotechnol., 2013, 8, 899 CrossRef CAS PubMed
.
- R. Wiesendanger, Nanoscale magnetic skyrmions in metallic films and multilayers: a new twist for spintronics, Nat. Rev. Mater., 2016, 1, 1 Search PubMed
.
- X. Z. Yu, N. Kanazawa, Y. Onose, K. Kimoto, W. Z. Zhang, S. Ishiwata, Y. Matsui and Y. Tokura, Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe, Nat. Mater., 2011, 10, 106 CrossRef CAS PubMed
.
- C. Moreau-Luchaire, C. Moutafis, N. Reyren, J. Sampaio, C. A. F. Vaz, N. Van Horne, K. Bouzehouane, K. Garcia, C. Deranlot, P. Warnicke and P. Wohlhüter, Additive interfacial chiral interaction in multilayers for stabilization of small individual skyrmions at room temperature, Nat. Nanotechnol., 2016, 11, 444 CrossRef CAS PubMed
.
- B. Satywali, V. P. Kravchuk, L. Pan, M. Raju, S. He, F. Ma, A. P. Petrović, M. Garst and C. Panagopoulos, Microwave resonances of magnetic skyrmions in thin film multilayers, Nat. Commun., 2021, 12, 1 CrossRef PubMed
.
- M. G. Han, J. A. Garlow, Y. Liu, H. Zhang, J. Li, D. DiMarzio, M. W. Knight, C. Petrovic, D. Jariwala and Y. Zhu, Topological magnetic-spin textures in two-dimensional van der Waals Cr2Ge2Te6, Nano Lett., 2019, 19, 7859 CrossRef CAS PubMed
.
- B. Ding, Z. Li, G. Xu, H. Li, Z. Hou, E. Liu, X. Xi, F. Xu, Y. Yao and W. Wang, Observation of magnetic skyrmion bubbles in a van der Waals ferromagnet Fe3GeTe2, Nano Lett., 2019, 20, 868 CrossRef PubMed
.
- J. Liang, W. Wang, H. Du, A. Hallal, K. Garcia, M. Chshiev, A. Fert and H. Yang, Very large Dzyaloshinskii-Moriya interaction in two-dimensional Janus manganese dichalcogenides and its application to realize skyrmion states, Phys. Rev. B, 2020, 101, 184401 CrossRef CAS
.
- C. Xu, J. Feng, S. Prokhorenko, Y. Nahas, H. Xiang and L. Bellaiche, Topological spin texture in Janus monolayers of the chromium trihalides Cr(I, X)3, Phys. Rev. B, 2020, 101, 060404 CrossRef CAS
.
- W. Du, K. Dou, Z. He, Y. Dai, B. Huang and Y. Ma, Spontaneous magnetic skyrmions in single-layer CrInX3 (X= Te, Se), Nano Lett., 2022, 22, 3440 CrossRef CAS PubMed
.
- W. Sun, W. Wang, J. Zang, H. Li, G. Zhang, J. Wang and Z. Cheng, Manipulation of magnetic skyrmion in a 2D van der Waals heterostructure via both electric and magnetic fields, Adv. Funct. Mater., 2021, 31, 2104452 CrossRef CAS
.
- S. Fragkos, P. Pappas, E. Symeonidou, Y. Panayiotatos and A. Dimoulas, Magnetic skyrmion manipulation in CrTe2/WTe2 2D van der Waals heterostructure, Appl. Phys. Lett., 2022, 120, 182402 CrossRef CAS
.
- D. Li, S. Haldar and S. Heinze, Strain-driven zero-field near-10 nm skyrmions in two-dimensional van der Waals Heterostructures, Nano Lett., 2022, 22, 7706 CrossRef CAS PubMed
.
- M. Schott, A. Bernand-Mantel, L. Ranno, S. Pizzini, J. Vogel, H. Béa, C. Baraduc, S. Auffret, G. Gaudin and D. Givord, The skyrmion switch: turning magnetic skyrmion bubbles on and off with an electric field, Nano Lett., 2017, 17, 3006 CrossRef CAS PubMed
.
- L. Wang, Q. Feng, Y. Kim, R. Kim, K. H. Lee, S. D. Pollard, Y. J. Shin, H. Zhou, W. Peng, D. Lee, W. Meng, H. Yang, J. H. Han, M. Kim, Q. Lu and T. W. Noh, Ferroelectrically tunable magnetic skyrmions in ultrathin oxide heterostructures, Nat. Mater., 2018, 17, 1087 CrossRef CAS PubMed
.
- X. Yu, D. Morikawa, Y. Tokunaga, M. Kubota, T. Kurumaji, H. Oike, M. Nakamura, F. Kagawa, Y. Taguchi, T. Arima, M. Kawasaki and Y. Tokura, Current-induced nucleation and annihilation of magnetic skyrmions at room temperature in a chiral magnet, Adv. Mater., 2017, 29, 1606178 CrossRef PubMed
.
- S. Komineas and N. Papanicolaou, Skyrmion dynamics in chiral ferromagnets under spin-transfer torque, Phys. Rev. B, 2015, 92(17), 174405 CrossRef
.
- P. J. Hsu, A. Kubetzka, A. Finco, N. Romming, K. Von Bergmann and R. Wiesendanger, Electric-field-driven switching of individual magnetic skyrmions, Nat. Nanotech., 2017, 12, 123 CrossRef CAS PubMed
.
- A. Hrabec, J. Sampaio, M. Belmeguenai, I. Gross, R. Weil, S. M. Chérif, A. Stashkevich, V. Jacques, A. Thiaville and S. Rohart, Current-induced skyrmion generation and dynamics in symmetric bilayers, Nat. Commun., 2017, 8, 1 CrossRef PubMed
.
- K. Dou, W. Du, Y. Dai, B. Huang and Y. Ma, Two-dimensional magnetoelectric multiferroics in a MnSTe/In2Se3 heterobilayer with ferroelectrically controllable skyrmions, Phys. Rev. B, 2022, 105, 205427 CrossRef CAS
.
- K. Huang, D. F. Shao and E. Y. Tsymbal, Ferroelectric control of magnetic skyrmions in two-dimensional van der Waals heterostructures, Nano Lett., 2022, 22, 3349 CrossRef CAS PubMed
.
- Q. Cui, Y. Zhu, J. Jiang, J. Liang, D. Yu, P. Cui and H. Yang, Ferroelectrically controlled topological magnetic phase in a Janus-magnet-based multiferroic heterostructure, Phys. Rev. Res., 2021, 3, 043011 CrossRef CAS
.
- J. J. Zhang, L. Lin, Y. Zhang, M. Wu, B. I. Yakobson and S. Dong, Type-II multiferroic Hf2VC2F2 MXene monolayer with high transition temperature, J. Am. Chem. Soc., 2018, 140, 9768 CrossRef CAS PubMed
.
- W. Sun, W. Wang, H. Li, G. Zhang, D. Chen, J. Wang and Z. Cheng, Controlling bimerons as skyrmion analogues by ferroelectric polarization in 2D van der Waals multiferroic heterostructures, Nat. Commun., 2020, 11, 1 CrossRef PubMed
.
- C. Huang, J. Zhou, H. Sun, F. Wu, Y. Hou and E. Kan, Toward room-temperature electrical control of magnetic order in multiferroic van der Waals materials, Nano Lett., 2022, 22, 5191 CrossRef CAS PubMed
.
- G. Yu, A. Pan and M. Chen, Interface engineering of ferroelectricity in thin films of thiophosphate ABP2X6 (A= Cu, Ag; B= In, Bi, Cr, V; X= S, Se), Phys. Rev. B, 2021, 104, 224102 CrossRef CAS
.
- M. Wu and X. C. Zeng, Intrinsic ferroelasticity and/or multiferroicity in two-dimensional phosphorene and phosphorene analogues, Nano Lett., 2016, 16, 3236 CrossRef CAS PubMed
.
- A. Chandrasekaran, A. Mishra and A. K. Singh, Ferroelectricity, antiferroelectricity, and ultrathin 2D electron/hole gas in multifunctional monolayer MXene, Nano Lett., 2017, 17, 3290 CrossRef CAS PubMed
.
- Y. Fang, S. Wu, Z. Z. Zhu and G. Y. Guo, Large magneto-optical effects and magnetic anisotropy energy in two-dimensional Cr2Ge2Te6, Phys. Rev. B, 2018, 98, 125416 CrossRef CAS
.
- P. W. Anderson, Antiferromagnetism. Theory of superexchange interaction, Phys. Rev., 1950, 79, 350 CrossRef
.
- J. B. Goodenough, Theory of the role of covalence in the perovskite-type manganites [La, M(II)]MnO3, Phys. Rev., 1955, 100, 564 CrossRef CAS
.
- J. Kanamori, Superexchange interaction and symmetry properties of electron orbitals, J. Phys. Chem. Solids, 1959, 10, 87 CrossRef CAS
.
- T. Moriya, Anisotropic superexchange interaction and weak ferromagnetism, Phys. Rev., 1960, 120, 91 CrossRef CAS
.
- A. Fert, N. Reyren and V. Cros, Magnetic skyrmions: advances in physics and potential applications. Nature Reviews, Materials, 2017, 2, 1 Search PubMed
.
- B. Berg and M. Lüscher, Definition and statistical distributions of a topological number in the lattice O(3) σ-model, Nuclear Phys. B, 1981, 190, 412 CrossRef
.
- Y. Zhou, Y. Wang, J. Cao, Z. Zeng, T. Zhou, R. Liao, T. Wang, Z. Wang, Z. Xia, Z. Ouyang and H. Lu, CoMOF5(pyrazine)(H2O)2 (M= Nb, Ta): two-layered cobalt oxyfluoride antiferromagnets with spin flop transitions, Inorg. Chem., 2021, 60, 13309 CrossRef CAS PubMed
.
- Z. Shao, J. Liang, Q. Cui, M. Chshiev, A. Fert, T. Zhou and H. Yang, Multiferroic materials based on transition-metal dichalcogenides: Potential platform for reversible control of Dzyaloshinskii-Moriya interaction and skyrmion via electric field, Phys. Rev. B, 2022, 105, 174404 CrossRef CAS
.
- F. Zhang, W. Mi and X. Wang, Spin-dependent electronic structure and magnetic anisotropy of 2D ferromagnetic Janus Cr2I3X3 (X= Br, Cl) monolayers, Adv. Electron. Mater., 2020, 6, 1900778 CrossRef CAS
.
- Z. Shen, C. Song, Y. Xue, Z. Wu, J. Wang and Z. Zhong, Strain-tunable Dzyaloshinskii-Moriya interaction and skyrmions in two-dimensional Janus Cr2X3Y3 (X, Y= Cl, Br, I, X≠ Y) trihalide monolayers, Phys. Rev. B, 2022, 106, 094403 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh00572k |
| This journal is © The Royal Society of Chemistry 2023 |