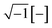Open Access Article
Open Access ArticleHarnessing cavity dissipation for enhanced sound absorption in Helmholtz resonance metamaterials†
Xinwei
Li
 a,
Xiang
Yu
a,
Xiang
Yu
 b,
Jun Wei
Chua
b,
Jun Wei
Chua
 a and
Wei
Zhai
a and
Wei
Zhai
 *a
*a
aDepartment of Mechanical Engineering, National University of Singapore, Singapore, 117575, Singapore. E-mail: mpezwei@nus.edu.sg
bDepartment of Mechanical Engineering, The Hong Kong Polytechnic University, 999077, Hong Kong, China
First published on 4th May 2023
Abstract
Helmholtz resonance, based on resonance through a pore-and-cavity structure, constitutes the primary sound absorption mechanism in majority of sound-absorbing metamaterials. Typically, enhancing sound absorption in such absorbers necessitates substantial geometrical redesign or the addition of dissipative materials, which is non-ideal considering the volume and mass constraints. Herein, we introduce a new approach – that is to simply reshape the cavity, without alterations to its overall mass and volume – to drastically enhance sound absorption. This is achieved by bringing the cavity walls close to the pores where additional thermoviscous dissipation along these boundaries can occur. Experimentally validated, with three sides of the cuboid cavity close to the pore and at a particular pore–cavity geometry, a 44% gain in maximum absorption is achieved compared to the original structure. Through numerical simulations, we fully elucidate structure–property relationships and their mechanisms, and propose analytical models for design and optimization. Ultimately, utilizing this concept, we demonstrate a heterogeneously porous broadband (1500 to 6000 Hz) absorber that exhibits an excellent average absorption coefficient of 0.74 at a very low thickness of 18 mm. Overall, we introduce a new and universal concept that could revolutionize the design principles of Helmholtz resonators, and demonstrate its potential for designing advanced sound-absorbing metamaterials.
New conceptsHelmholtz resonance, based on resonance through a narrow pore and cavity, constitutes the underlying functioning principle of the majority of acoustic metamaterials. Current methods to improve the sound absorption performance of such metamaterials generally include the introduction of additional volume and mass, which are non-ideal considering mass and volume constraints in engineering designs. Here, we introduce a novel approach to achieve Helmholtz resonators with enhanced sound absorption compared to the original structure by simply modifying the resonator cavity. Specifically, we reshape the Helmholtz resonator cavity so that three sides of the cavity walls immediately touch the boundaries of the pore. No changes to any other acoustical geometries, volume, or mass are required. At a particular pore diameter, the highest gain in maximum absorption measures up to a value of 44%. The underlying mechanism behind this enhanced absorption is attributed to the additional thermoviscous dissipation of the sound waves, which extends outwards from the dissipating pores onto the walls close to the pores. Overall, we revolutionize the design of Helmholtz resonators, and this concept is extendable to the design of acoustic metamaterials based on the same mechanism. |
1. Introduction
From the comfort of everyday lives, healthcare, to safe engineering operation, sound absorption is a crucial consideration in many aspects. Commercial sound-absorbing materials include micro-perforated panels, foams, fabric, and textile.1,2 They are effective in reducing echoes and reverberation; however, they have limitations in terms of low absorption capacity, limited bandwidth, structurally non-rigid, and without the potential as multifunctional materials. As modern engineering designs increasingly require multifunctional materials for achieving optimized space and mass efficiency, traditional commercial materials may not meet the necessary requirements. Metamaterials, with their unique properties not found in traditional materials, address this gap in requirements.3–6 In recent years, there has been growing interest in acoustic metamaterials and lattice structures as a new approach to sound absorption.7,8 These materials can be engineered to have unique acoustic properties tailored to specific applications, enabling them to be promising candidates as multifunctional sound absorbers.Acoustic metamaterials are mechanism-based architectured materials with properties not found in natural materials.7–10 Lattice structures, on the other hand, are periodic structures made up of repeated units consisting of struts,11 shells,12 plates,13 or hybrids.14,15 All these materials are fully customizable in terms of their physical properties, including mechanical properties and structural properties such as mass and porosity. Apart from it, these materials can also be designed to harness the negative effective density and bulk modulus that allow more flexible acoustic wave manipulation. For instance, they can harness the mechanism of local Helmholtz resonance to achieve effective sound absorption. As its name suggests, Helmholtz resonance takes place in Helmholtz resonators (HRs). Defined to be any structure consisting of a narrow pore (or neck) connected to a larger cavity,7 HRs were first conceptualized by physicist Hermann von Helmholtz in 1859. At the natural frequency of an HR, air molecules vibrate vigorously at the pore region. Sound energy dissipation then takes place via air friction and thermal dissipation across the viscous and thermal boundary layers of the pore (Fig. 1A). Therefore, an HR can effectively achieve high sound absorption near its resonant frequency, even at a thickness much smaller than the wavelength of the incoming wave. The resonance frequency of an HR can be conveniently estimated by three independent structural variables: the pore diameter, pore depth, and cavity volume. Owing to its simplicity in the design, HRs are amongst the most widely used sound absorbers. Also, Maa's proposition of the micro-perforated panel further contributed to the practical design of multi-layered Helmholtz resonance-based sound absorbers.16 Thus far, numerous acoustic metamaterials have been designed to incorporate the mechanism of multi-layer Helmholtz resonance. Examples include space-coiling structures,17 subwavelength and labyrinthine absorbers,18 sandwich panels,19,20 and tubular structures.21 In turn, numerous lattice structures also function as multi-layered HRs. These include dense truss lattices,14,22 plate lattices with pores,14,23–25 and layer-by-layered perforated plate lattices.15,26,27 As can be seen, Helmholtz resonance is regarded as one of the most effective and widely adopted mechanisms for sound absorption.
Therefore, novel methods to improve the performance of multi-layered HRs, e.g. better sound absorption while maintaining a low thickness, are often sought-after. Currently, additive methods are commonly used. These include increasing the number of cells along the thickness direction, introducing additional dissipative materials, and adopting ultra-flexible components in the HR. In general, an increased number of layers results in an increased depth that sound waves travels and hence the energy dissipation.28 Some researchers also introduced dissipative porous materials such as foams into the cavities of MLHRs.29 An additional degree of dissipation can be harnessed from the foams this way. In HRs, sound dissipation is independent of the material used for fabrication. However, if ultra-flexible components are incorporated in an HR (e.g., flexible films), an additional sound dissipation mechanism derived from structural damping by the physical vibration of the structure can be achieved.30,31 Beyond a single type of cell, at the multiscale level, combinations of heterogeneous cells with different pore and cavity geometries have been employed. Methods include incorporating heterogeneous cells in parallel,32 series,20 and hierarchically.21,33,34 Despite their effectiveness, these methods rely on additive steps and may not be practical for engineering applications where size and mass constraints are important factors to consider.
Herein, we propose a novel and revolutionary approach to the enhancement of sound absorption of HRs at its unit cell level. This approach consists of reshaping the cavity, bringing the cavity walls closer to the pores to allow for extended thermoviscous dissipation at the cavity (Fig. 1B). Experimentally validated, we reveal that up to 44% increase in the maximum absorption can be achieved when there are three sides of the cavity (quadrilateral cell) close to the pore. Through both finite element modelling and extensive experiments, we also characterized various structure–property relationships, elucidated their mechanisms, and provided analytical models to account for the altered acoustic impedances for optimization and design. We demonstrate the potential of this concept by constructing a heterogeneous broadband (1500 to 6000 Hz) absorber that achieves an average sound absorption coefficient of 0.74 at a low thickness of 18 mm. Overall, this study introduces a revolutionary design concept for Helmholtz resonators that has a promising potential for advanced sound-absorbing metamaterials.
2. Modified Helmholtz resonator concept
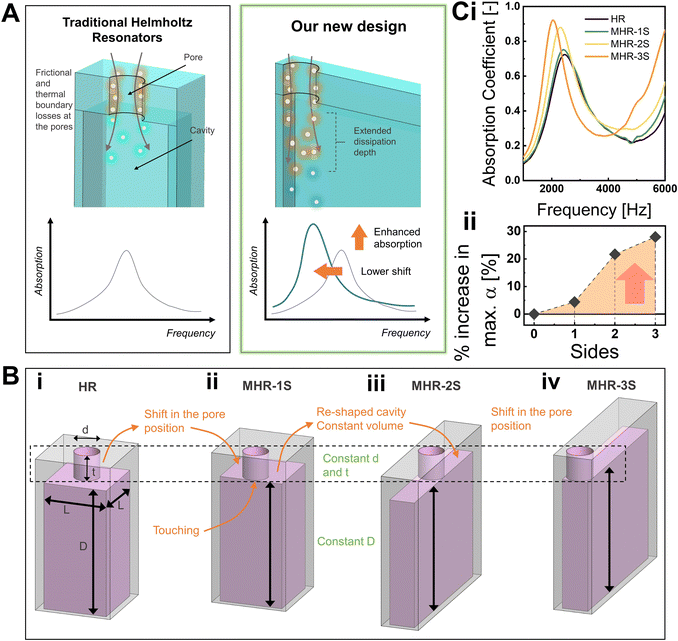
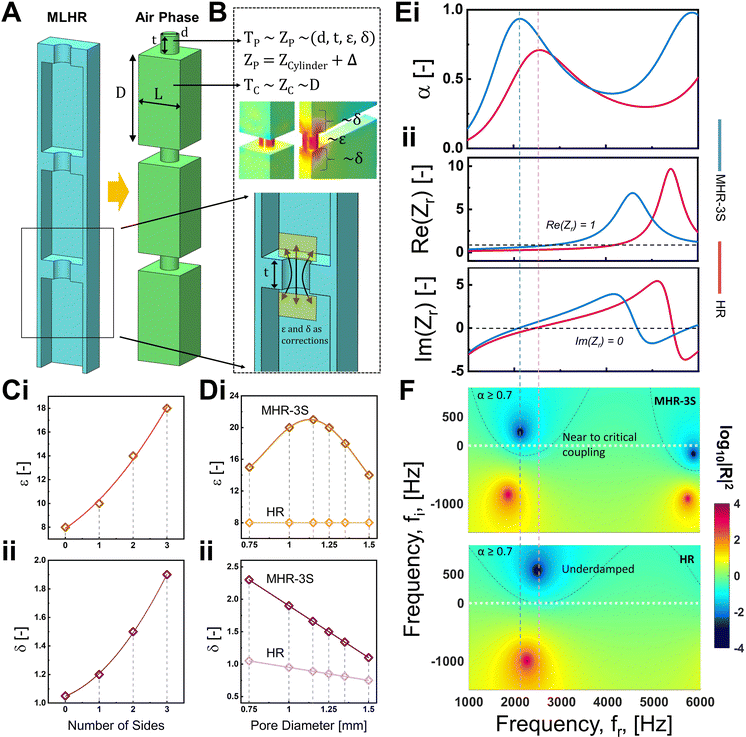
The schematic of our design concept is presented in Fig. 1B. Fig. 1Bi shows a unit cell of an HR and its inverse air phase as denoted by magenta. As shown, a traditional HR is based on a pore and an immediate cavity. Shown on the same figure, geometrical parameters of interest for acoustic properties include the pore diameter (d), pore thickness (t), cell width (L), and cavity depth (D). Together with the number of layers (for multi-layered HRs), these are the sole parameters defining the absorption behaviour of HRs. Fig. 1Bii–iv in turn depict the novel modified HR (MHR) that we conceptualize herein. Fig. 1Bii shows an MHR with one side (MHR-1S) of the wall in close proximity to the pore. Schematically illustrated, this design is achieved by strategically shifting the pore to one side of the cavity, such that the side of the pore is in contact with the cavity wall. No changes to any of the geometrical parameters are made. In turn, MHR with two sides (MHR-2S) is achieved by artificially engineering two cavity walls in contact with the pore circumference (Fig. 1Biii). To enable this configuration, the cavity is reshaped such that one side of its width (L) is made equal to the pore diameter (d). The total volume of the cavity and its depth (D) remain constant. MHR with three sides (MHR-3S) is then achieved by moving the pore to the edge of the cuboid cavity so that it touches three walls (Fig. 1Biv). For detailed illustrations, the exact dimensions of the MHR samples are given in Fig. S1, ESI.†3. Results and discussion
3.1. Influence of the cell walls
Following our MHR design, we conducted experiments to investigate the sound absorption properties of the HRs by using meta-structures composed of three layers of the unit cell. Herein, we designate the acoustical geometrical parameters, in millimetres, to be as follows: d = 1, t = 1, L = 2.5, and D = 5. The sound absorption coefficient (α) curves of the HR and MHRs, across a broad range of frequencies from 1000 to 6000 Hz, is shown in Fig. 1Ci. As shown, the absorption curves based on the Helmholtz resonance principle exhibit a Gaussian-like shape, characterized by a resonant frequency and an absorption peak. Consistent with our design principle and hypothesis, the maximum absorption is indeed observed to increase with the increasing number of sides. In addition, a slight shift towards a lower resonant frequency is observed. The percentage increase in the maximum α for the MHRs as compared to HR is plotted in Fig. 1Cii. It can be seen that MHR-3S displays a remarkable 28% increase in the maximum absorption when evaluated under the current geometrical parameters. It is worth noting that, according to the classical Helmholtz resonance theory, these absorption curves should not exhibit any differences.3.2. Influence of separation distance and pore size
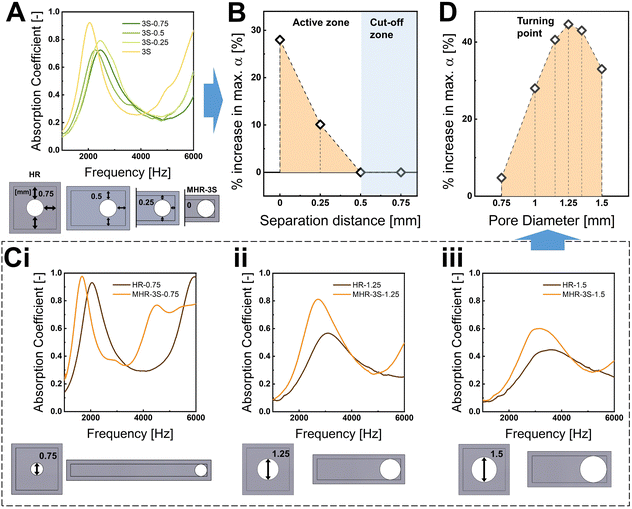
Having affirmed the effectiveness of our proximal cell wall concept, we next illustrate several structural–property relationships of the MHRs, specifically in relation to the pore morphology and absorption coefficient. Based on the findings in Fig. 1Ci, MHR-3S was identified as having the highest increase in absorption, and as a result, structures with three sides would be focused on in the subsequent sections for further analysis. We first aim to understand the relationship between the separation distance of the pore and the cavity walls and the extent of sound absorption enhancement. Fig. 2A reveals the sound absorption coefficient curves of MHR-3S with pores of varying distances from the cavity wall(s). For this study, d, t, and D of the structures are exactly the same as those in Section 3.1. For all cases, the furthest separation corresponds to the HR structure in which the pore is located at an equidistance of 0.75 mm from the nearest walls. A 0 mm separation then refers to the MHR-3S. The MHR structures studied are illustrated through the top view as shown in Fig. 2A. As observed, the maximum absorption increases with decreasing separation. A summary based on the plot of percentage increase of the maximum absorption, to the separation distance, is given in Fig. 2B. For the cases studied here, a cut-off distance of 0.5 mm, where pores placed beyond this separation display no improvements to absorption, is observed, after which, the absorption is expected to be increasing with decreasing separation. Next, the relationship between the pore sizes and the extent of enhancement is studied. Herein, MHR-3S of pore diameters from 0.75 to 1.5 mm, in varying step sizes, were investigated. Apart from the pore diameter, every other acoustical geometry is kept constant. Fig. 2C reveals the absorption coefficient curves of MHR-3S with pore diameters of 0.75, 1.25, and 1.5 mm. The corresponding structures are then revealed in the same figure. In line with the principles of Helmholtz resonance, a shift of the absorption maximum to a higher frequency and a reduction in intensity are observed with increasing pore diameters. A wider pore allows for increased airflow, decreasing the effective mass and stiffness of the air that is vibrating, leading to a higher resonant frequency. The decreasing intensity of absorption then attributes to the increasingly impedance mismatch of the acoustical parameters, to be detailed in section 3.5. A varying degree in the enhancement of the maximum absorption is observed. A clearer illustration is shown in the plot of the percentage increase and pore diameters in Fig. 2D. As observed, a quadratic behaviour with a maximum turning point at d = 1.25 mm exists. At this pore diameter, the gain in maximum absorption is also extremely high at 44%. The results for the additional data points used in Fig. 2D are shown in Fig. S2, ESI.† The exact dimensions of the HR and MHR used for studies in this section are given in Fig. S3 and S4, ESI.†3.3. Mechanism of enhancement
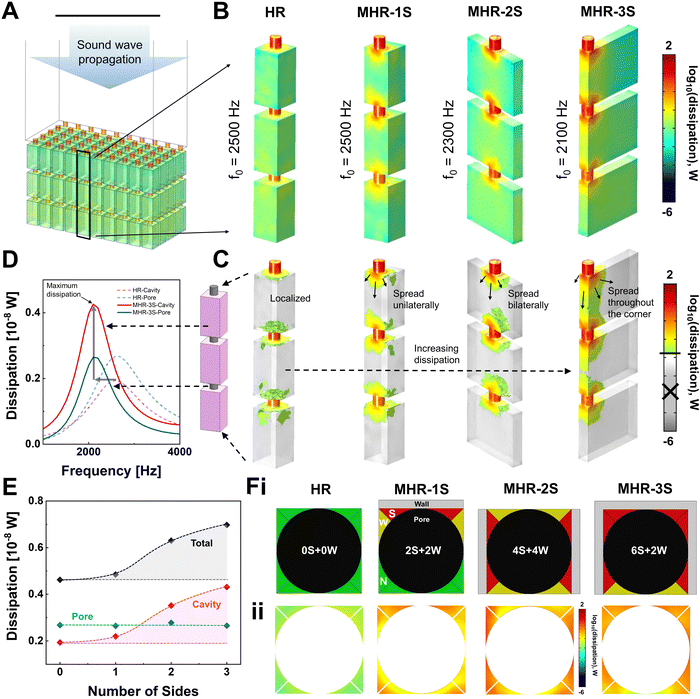
Following discussions on the sound absorption properties, we next illustrate their underlying mechanisms through finite element modelling (FEM) simulations using COMSOL Multiphysics. As mentioned in the introduction, sound energy dissipation takes place via a combined thermoviscous effect at the thermal and viscous boundary layers. Thus, the simulation model is defined according to the exact experimental setup with the conditions for thermoviscous dissipation applied in the MHR structures (Fig. 3A). Fig. 3B reveals the dissipation colour map at resonance for a single unit air column of the MHR structures with different numbers of sides. Colour-mapped in the logarithm scale, high intensity dissipation appears red while low intensity dissipation appears blue. A first impression is that high-dissipation is localized at or around the pores, consistent with the principle of Helmholtz resonance. Also, the area denoted by high dissipation increases drastically with increasing number of sides. A clearer visualization can be obtained in Fig. 3C, where only areas with high dissipation above 10−1.8 W are shown and those lower are greyed out. Essentially, the dissipation colour maps reveal that thermoviscous dissipation extends onto the immediate cavity walls in the MHRs. The number of sides this dissipation extends to corresponds to the number of sides in proximity to the pore. Therefore, the uptrend in dissipation intensity is observed from HR to MHR-3S (Fig. 3C). This elongation of dissipation also results in stronger wave interactions at longer wavelengths, resulting in a shift of the resonance peaks towards lower frequencies. Further probing into this phenomenon, we plot the dissipation curves of the pores and cavities of a single strand of air column for the HR and MHR-3S in Fig. 3D. As shown, there are no changes to the maximum dissipation in the pores with the introduction of sides. However, dissipation at the cavity increases drastically, from being initially lower than that of the pore, to being significantly higher. For both cases, a shift to the lower frequency is observed. An overall trend of the maximum dissipation (from the maximum turning point in the dissipation curves) with respect to the number of sides is shown in Fig. 3E. In agreements with the previously observed trends, no changes have been observed for the pore while the total and cavity dissipations increase steadily with increasing number of sides. It is worth noting that the total maximum dissipation is equal to the combined value of the dissipation in both the cavity and pore. Also, it is observed that the cavity dissipation exceeds the pore dissipation only when there are at least two sides. The individual dissipation curves used in Fig. 3E are shown in Fig. S5, ESI.†Next, we present a generalized rule for the intensity of dissipation based on our new “weak and strong” dissipation theory. This theory involves discretising the region surrounding a pore that is delineated by an immediate square. As shown in Fig. 3Fi, there are four corners in this pattern, which can be split into two identical halves, resulting in a total of eight sides. For each corner, we then classify it into two types of sides, strong (S) and weak (W). The S side is the one closest to the cavity wall while the W side is the one further, as exemplified in 1S in Fig. 3Fi. The sides without proximal cavity walls are then termed as non-contributing (N) sides. As can be seen, the number of S sides increases from HR to MHR-3S. Our S and W side theory is strongly supported by the dissipation intensity as observed from the top surface of the modelled air column (Fig. 3Fii), where S sides correspond to high dissipation and W sides to weaker dissipation. Another direct proof of our theory will be comparisons with a MHR-2S-Corner sample, where the pore is placed at a corner, as opposed to the centre. As compared, the maximum absorption coefficient of MHR-2S-Corner with 4S + 2W compares poorer to 2S with 4S + 4W. With both having two sides, the only difference comes from the number of W sides and thus this fully supports our theory. The absorption data and further details are included in Fig. S6, ESI.†
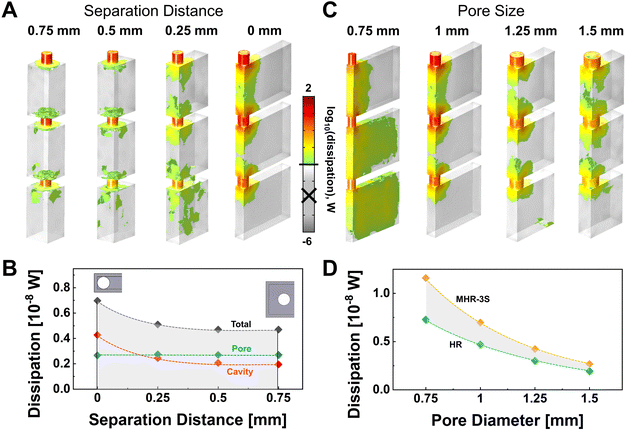
We also investigate the influence of the pore and cavity wall separation distance and pore sizes on thermoviscous dissipation. Fig. 4A depicts the dissipation colour map of the MHR-3S with varying separation distances where only regions of high dissipation above 10−1.8 W are shown. The results demonstrate that the intensity and area of high dissipation increase when the pore is placed closer to the cavity walls. The trend of maximum dissipation with respect to increasing proximity is then shown in Fig. 4B. Similar to observations found in Fig. 3E, there are no discernible changes observed for dissipation in the pores. In turn, dissipation increases, at an increasing rate, with the decreasing distance. Data also reveal that dissipation at the cavity exceeds that in the pores only when the gap is sufficiently small (around 0.125 mm in this case). Furthermore, it is shown that the cavity wall design is not meaningful if the gap is larger than 0.5 mm. Findings in Fig. 4A and B thus agree closely with the experimental absorption curves in Fig. 2B.
The colour maps and the maximum dissipation plot for the influence by pore sizes are shown in Fig. 4C and D, respectively. Both decreases in the maximum dissipation, and the relative increase in maximum dissipation from the MHR-3S structure, are observed. The higher dissipation energy at lower frequencies is owing to the waves of longer wavelengths interacting over a larger distance in the resonators. The maximum point observed at d = 1.25 mm (Fig. 2D) is then related to the matching acoustic impedance of that particular structure. The individual dissipation curves used in Fig. 4 are shown in Fig. S7 and S8, ESI.†
3.4. Analytical model
After demonstrating the mechanisms and the performances of the MHRs, we next propose analytical models that can both be used to effectively predict sound absorption coefficients and to extract critical acoustical parameters. Herein, the air volume inside the narrow pore is modelled using the equivalent-fluid approach35 while that of the overall pore–cavity structure is modelled using the transfer matrix method (TMM).36 Two transfer matrices are associated with an MLHR – that for the narrow pore, TP, and that for the cavity, TC. TP is related to the acoustic impedance of the pore, ZP, which is then related to the following geometrical parameters: d, t, L, and Φ (Fig. 5A and B). Φ refers to the surface porosity, a parameter dependent on d and L and is given by π(d/2)2/L2 herein. Table 1 shows some of the commonly occurring constants and variables used for the subsequent discussions. First, we derive the acoustic impedance of a pore, ZP: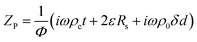 | (1) |
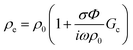 | (2) |
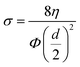 | (3) |
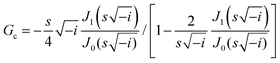 | (4) |
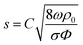 | (5) |
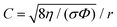 for a circular pore. J1 and J0 refer to the first and zeroth order Bessel functions, respectively.
for a circular pore. J1 and J0 refer to the first and zeroth order Bessel functions, respectively.
Eqn (1)–(5) provide a mathematical framework for calculating the standard acoustic impedance associated with a cylindrical pore. In eqn (1), the second and third terms are related to the resistance and mass reactance end corrections for the airflow through a narrow pore (represented using Δ in Fig. 5B), respectively. End corrections are necessary to account for the acoustical interactions beyond the vicinity of the pore. As can be noted from eqn (1)–(5), the acoustic impedance consists of a real and imaginary part corresponding to the acoustic resistance and mass reactance, respectively. The resistance is related to viscous losses, while the reactance is associated with the inertia of the vibrating air mass. Therefore, the real part determines the intensity of sound absorption, while the imaginary part determines the frequency at which resonance happens. The end correction is an important factor to describe these behaviours beyond the pore geometry. The resistance end correction takes into account the additional frictional viscous losses at the surface of the pore, while the reactance end correction accounts for the additional vibration depth extended outwards from the pore.
For the second term in eqn (1), Rs takes on an expression given by 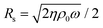 . The variable ε then describes the extent of the additional dissipation. The third term is described by a variable δ, which accounts for the added mass that vibrates with the pore. As noted, the structures proposed in this work are non-standard Helmholtz resonators. Indeed, as observed in Fig. 3B, thermoviscous dissipation extends outwards from the pore onto the cell walls for all of the cases, except HR. Therefore, we expect the end corrections to follow the trends of the physically observed dissipation and that they are non-trivial functions of the geometrical factors (number of sides, pore sizes, etc.). Herein, we derive the end corrections empirically via a best-fit of the analytically calculated absorption curves and the experimental data. The trends for both ε and δ, for the increasing number of sides and varying pore sizes, are shown in Fig. 5C and D, respectively. Fig. 5C shows that both ε and δ increase in a power-law manner as the number of sides increases. This is consistent with the observation in Fig. 3B, which demonstrates that the extension of thermoviscous dissipation increases with increasing number of sides. The increase in ε agrees well with the enhanced absorption coefficients (Fig. 1Cii) and the increased dissipation in the cavity (Fig. 3E). Similarly, the increase in δ, which signifies a prolonged dissipation depth, is also in agreements with the lower-frequency (i.e. longer wavelength) shift of the resonance peaks. In turn, Fig. 5Di reveals ε to be distinctly different from the previously mentioned trend. For the HR, ε shows to remain constant at a value of 8 regardless of the pore diameter. Not surprising, since dissipation is expected to be localized within (or near) the pore (Fig. 3B), no additional dissipation would be expected. In turn, there is a quadratic relationship between ε and pore diameter, with a distinct maximum turning point in MHRs. This trend is in turn in line with the trend of the increase in maximum absorption as observed in Fig. 2. δ then decreases linearly for both HR and MHR (Fig. 5Dii). However, the values of δ for the MHRs reveal to be both higher, and decrease at a faster rate, than that of the HR. It is worth noting that the value of δ in the HR is close to the typical value of 0.85 as derived by Ingard et al.37 for circular pores. The decline is then in good agreement with the trend presented in the same work.37 For the MHR case, the much higher δ is attributed to the extended dissipation owing to the presence of the walls (Fig. 4C). Indeed, MHR at a pore diameter of 0.75 mm shows an extremely high ratio of high-dissipation region. This ratio then decreases with increasing pore size. The explicit expressions of the end corrections are included in Table S1, ESI.† Following the analysis on end corrections, ZP is then fully substantiated. With ZP, the transfer matrix of the pore (TP) is then given as:
. The variable ε then describes the extent of the additional dissipation. The third term is described by a variable δ, which accounts for the added mass that vibrates with the pore. As noted, the structures proposed in this work are non-standard Helmholtz resonators. Indeed, as observed in Fig. 3B, thermoviscous dissipation extends outwards from the pore onto the cell walls for all of the cases, except HR. Therefore, we expect the end corrections to follow the trends of the physically observed dissipation and that they are non-trivial functions of the geometrical factors (number of sides, pore sizes, etc.). Herein, we derive the end corrections empirically via a best-fit of the analytically calculated absorption curves and the experimental data. The trends for both ε and δ, for the increasing number of sides and varying pore sizes, are shown in Fig. 5C and D, respectively. Fig. 5C shows that both ε and δ increase in a power-law manner as the number of sides increases. This is consistent with the observation in Fig. 3B, which demonstrates that the extension of thermoviscous dissipation increases with increasing number of sides. The increase in ε agrees well with the enhanced absorption coefficients (Fig. 1Cii) and the increased dissipation in the cavity (Fig. 3E). Similarly, the increase in δ, which signifies a prolonged dissipation depth, is also in agreements with the lower-frequency (i.e. longer wavelength) shift of the resonance peaks. In turn, Fig. 5Di reveals ε to be distinctly different from the previously mentioned trend. For the HR, ε shows to remain constant at a value of 8 regardless of the pore diameter. Not surprising, since dissipation is expected to be localized within (or near) the pore (Fig. 3B), no additional dissipation would be expected. In turn, there is a quadratic relationship between ε and pore diameter, with a distinct maximum turning point in MHRs. This trend is in turn in line with the trend of the increase in maximum absorption as observed in Fig. 2. δ then decreases linearly for both HR and MHR (Fig. 5Dii). However, the values of δ for the MHRs reveal to be both higher, and decrease at a faster rate, than that of the HR. It is worth noting that the value of δ in the HR is close to the typical value of 0.85 as derived by Ingard et al.37 for circular pores. The decline is then in good agreement with the trend presented in the same work.37 For the MHR case, the much higher δ is attributed to the extended dissipation owing to the presence of the walls (Fig. 4C). Indeed, MHR at a pore diameter of 0.75 mm shows an extremely high ratio of high-dissipation region. This ratio then decreases with increasing pore size. The explicit expressions of the end corrections are included in Table S1, ESI.† Following the analysis on end corrections, ZP is then fully substantiated. With ZP, the transfer matrix of the pore (TP) is then given as:
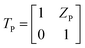 | (6) |
The acoustical properties of the cavity is then in turn only dependent on the cavity depth, D. The transfer matrix of the cavity (TC) is given as:
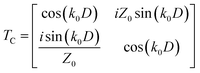 | (7) |
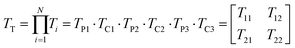 | (8) |
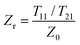 | (9) |
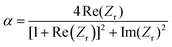 | (10) |
3.5. Influences to the acoustic impedance
With the derivation of Zr, important information on the acoustic impedance can be extracted. As can be seen from eqn (10), maximum absorption, i.e., α = 1, occurs when Re(Zr) = 1 and Im(Zr) = 0. Under such circumstances, perfect impedance matching, also known as critical coupling, takes place. In other words, to achieve good absorption, Re(Zr) and Im(Zr) should also be ideally as close to 1 and 0, respectively. The analytically modelled absorption curves and the Zr curves of both HR and MHR-3S are shown in Fig. 5Ei and Eii, respectively. It can be observed that the positions of the resonance peaks correspond to the point where the curve intersects the y-axis at Im(Zr) = 0. Also, the intersection point for MHR-3S occurs at a lower frequency, indicating a shift in the resonance peak towards lower frequencies. However, the Re(Zr) curve of MHR-3S is closer to Re(Zr) = 1 compared to HR within the vicinity of the resonance, indicating that MHR-3S has a more matching impedance. Next, the complex plane diagrams shown in Fig. 5Eiii are used to illustrate the extent of energy dissipation in the structures. Plotted in terms of the real (fr) and imaginary (fi) frequencies, the colour map in the complex plane maps out the reflection coefficient, |R|2. The reflection coefficient is related to α via the relationship: α = 1 − |R|2. A low |R|2 thus implies high absorption. The red and blue concentrations appearing on the colour map correspond to the conjugate pole and zero, respectively. When a conjugate zero is situated on the x-axis (i.e., when fi = 0), it indicates a state of critical coupling. If the conjugate zero is located above the x-axis, the system is considered underdamped, and if below, the system is said to be overdamped. As shown, the conjugate zeros for both structures are located at the same frequency as the absorption resonance peak and reasonably near to the Im(Zr) = 0 axis. Nonetheless, with the introduction of proximal cell walls, energy dissipation in the MHR-3S transitions into a more critically coupled state from the slightly underdamped state in the HR.3.6. Heterogeneous absorber
Having established improved sound dissipation brought about by the MHR design, we next demonstrate a proof-of-concept using a heterogeneously porous acoustic metamaterial. While homogeneous HRs display excellent absorption at one particular frequency,16 their heterogeneous counterparts display the potential for absorption across a broad bandwidth.15 Herein, we introduce structural heterogeneity by varying the pore diameters while keeping all other acoustical geometrical parameters (e.g. same t, D, L, and three layers of cells) constant. Specifically, we introduce four sections to this metamaterial, each consisting of MHR-3S unit cells with unique pore diameter that lies within the range of 0.75 – 1.5 mm. The relative acoustic impedance of each unit (Zr,i) is calculated through the same way as of eqn (1)–(9) using our proposed end correction factors. To calculate the total relative acoustic impedance (Zr,T) of a unit of the heterogeneous structure, the parallel summation rule is adopted to sum up the Zr,i of each ith individual section (Fig. 6A). Since the normal area of each unit cell is the same, the summation can be expressed as follows: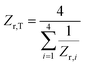 | (11) |
Similarly, the absorption coefficients are calculated using eqn (10). Here, the metric used for optimization is designated as the total number of points (in steps of 1 Hz) with α ≥ 0.7 across the frequency range of 1500 to 6000 Hz (Fig. 6A). The optimization criterion is then to find out the combination of pore diameters that results in the highest metric. Herein, the Genetic Algorithm was utilized for the search of this optimal combination, and the resulting set of optimized pore diameters are (0.75, 0.85, 1, and 1.5) mm (Fig. 6B). An illustration of a cubic cell of the optimized structure and its 3D printed structure, are shown in Fig. 6C. We then term it as the heterogeneous modified Helmholtz resonator absorber (HMHA). The analytically calculated and experimentally measured sound absorption coefficient curves of the HMHA are shown in Fig. 6D. Indeed, a broadband absorption behaviour, characterized by a generally smooth and high curve, is observed. Also, excellent correlation between the two curves is observed, further reinstating the validity of our proposed end correction relationships as shown in Fig. 5D. Through the entire frequency range, the average absorption coefficient is calculated to be 0.74 and 62% of the α points lie ≥ 0.7. The calculated Re(Zr) and Im(Zr) curves of HMHA and its constituents are shown in Fig. 6E. As observed, within most of the range, both curves of the HMHA lie much closer to their ideal values as compared to their constituents. It can also be said that the Re(Zr) and Im(Zr) curves of HMHA are based on a superposition of the regions of its constituents that are better impedance matched. The broadband behaviour is then attributed to the different resonance modes working in tandem. The complex plane diagram of HMHA is shown in Fig. 6F. A total of five pole-zero pairs can be found for this heterogeneous architecture. They all show to be reasonably close to the state of being critically coupled, albeit some are observed to be underdamped.
For comparisons, we also introduce a heterogeneous Helmholtz absorber (HHA), an analog to the HMHA but however based on pure HRs. The HHA is optimized through the same method under the same constraints and conditions, with the set of optimized pore diameters being (0.75, 0.75, 0.78, and 1.5) mm. Fig. 6G shows the sound absorption curve of HHA as compared to that of the HMHA. Indeed, the absorption curve of HMHA shows to be higher than that of the HHA across almost all frequency ranges. A metrical comparison is given in Fig. 6H. As shown, the average α, and the number of α points ≥0.7, are 20% and 17% higher in the HMHA, respectively. This result is consistent with the enhanced absorption observed in the homogeneous samples, and it further confirms the validity and potential extension of the concept to the design of broadband absorbers.
4. Further discussion
Herein, we have presented a novel concept, via a simple reshape of the cavity, to enhance the sound absorption coefficients of Helmholtz-resonance based absorbers. Since the extended dissipation depth is morphology independent (as long as requirements are fulfilled), our proposed method would also be extendable to all other HR related architectures. Our proposed method can be applied to a wide range of acoustic metamaterials, sandwich panels, and lattice structures, as they all rely on the principle of Helmholtz resonance. For instance, we have demonstrated the potentials of an acoustic metamaterial through our HMHA design. Modifications to sandwich panels are more straightforward. A strategic repositioning of the pores would suffice. Helmholtz resonance based lattice structures encompass dense trusses, plate lattices with pores, or layer-by-layer structures. For instance, cavity wall dissipation can be harnessed by modifications to the truss architecture, placement of pores near the edges of plates, or to introduce features to the cavity layers. Lattice structures also exhibit unique mechanical properties such as energy absorption, damage tolerance, or meta-behaviours. Our proposed concept has the potential to advance both acoustics and mechanical properties, offering a new design approach for lattice structures.With an average coefficient of 0.74 at a low thickness of 18 mm, our HMHA compares favourably in terms of absorption per unit thickness, to other metamaterials performing within the similar frequency range (Fig. 6I). It is worth noting that common absorbers usually display comparable or poor average coefficients, within a larger thickness of 20 to 30 mm. For instance, examples include a layer-by-layer lattice,15 hollow truss,22 bioinspired structure,26 window-foams,38 graded phononic crystals,39etc. Performance would be unfavourable if the HHA is considered instead. Since our concept is based on a simple reshape of the cavity without changes to the overall cell mass and volume required, our concept also promotes lightweight designs which calls for optimized absorption to thickness. Furthermore, we expect even greater performance improvements if heterogeneity in pore thickness, cavity depth, and cell size is considered in an HMHA-type absorber. Also, extended effective absorption frequency range can be achieved if MHR cells with a larger range of acoustical geometries are adopted.27,32
5. Conclusions
In conclusion, we introduce a novel approach to drastically enhance sound absorption in Helmholtz resonators by a simple reshaping of their cavity geometry – by bringing the cavity walls in close proximity to the pores. The experimental results demonstrate that for a cuboid cavity, the gain in the maximum absorption increases with an increasing number of sides where the cavity touches the pore. The further the pore is away from the cavity, the lower the gain in the maximum absorption. Also, we observed a non-linear relationship between the pore size and maximum gain in absorption, with the highest gain being 44% at a specific pore geometry. FEM analysis revealed that the enhanced dissipation is attributed to the additional thermoviscous dissipation that occurs when the cavity walls are in close proximity to the pores. We also developed an acoustic impedance based analytical model that can be used to predict and to optimize sound absorption properties. The effectiveness of our approach is demonstrated through an optimized heterogeneous broadband absorber that exhibited a high average absorption coefficient of 0.74 at a very low thickness of 18 mm over a broad frequency range of 1500–6000 Hz. Overall, this work introduces a universal concept that revolutionizes the design principles of Helmholtz resonators and demonstrates promising potential for advanced sound-absorbing metamaterials.Experimental
Numerical studies
Finite element analysis was performed to investigate the sound dissipation behaviour of the MHA structures using COMSOL Multiphysics. Similar to the experimental setup, the full impedance tube and the repeating lattice structure are modelled. The Pressure Acoustics module is applied to the impedance tube while samples are modelled with the Thermoviscous Acoustics module. The Thermoviscous Acoustics module utilizes the boundary layer theory to calculate and map the viscous flow and thermal losses. Color maps that represent the dissipated sound energy are generated by plotting the thermoviscous dissipation losses that are calculated within the domain. The default material properties of air provided in COMSOL were used. Full details of the COMSOL model are included in Fig. S11, ESI.† Analytical models based on the acoustic impedance were implemented using Matlab. Optimization using the Genetic Algorithm was carried out with the aid of the Optimization Toolbox in Matlab.3D printing
The MHA structures were fabricated using the Asiga Max X27 Digital Light Processing 3D printer from Asiga, Australia, with NovaStan from Nova3D as the photosensitive resin. Key printing parameters are as follows: a layer thickness of 100 μm, a light intensity of 5 mW cm−2, and a layer curing time of 1.5 s. After printing, the samples were cleaned in an isopropyl alcohol bath for approximately 15 minutes and post-cured in an Asiga Flash UV-curing chamber for 1 hour. An illustration of the as-printed samples used for sound absorption tests is included in Fig. S12, ESI.†Sound absorption tests
Sound absorption measurements were conducted using the two-microphone impedance tube technique in accordance with ISO 10534-2 standards. The BSWA SW477 series impedance tube with a 30 mm diameter and the BSWA MPA416 microphones were employed. Data acquisition was performed using the VA-Lab acoustical measurement software. The sound absorption tests were performed on cylindrical microlattice samples with a diameter of 30 mm. The reported results are based on a representative dataset obtained from five readings.Author contributions
X. Li: conceptualization, methodology, investigation, software, formal analysis, writing – original draft, and writing – review & editing. X. Yu: validation, supervision, and writing – review & editing. J. W. Chua: resources and investigation. W. Zhai: validation, supervision, writing – review & editing, funding acquisition, and project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the NUS Start-up Project (Project No. A-0009062-01-00).Notes and references
- M. Yang and P. Sheng, Annu. Rev. Mater. Res., 2017, 47, 83–114 CrossRef CAS.
- U. Berardi and G. Iannace, Build. Sci., 2015, 94, 840–852 Search PubMed.
- X. He and W. Cao, Opt. Mater. Express, 2023, 13, 413–422 CrossRef CAS.
- X. He, F. Lin, F. Liu and W. Shi, Opt. Mater. Express, 2022, 12, 73–84 CrossRef CAS.
- J. Peng, X. He, C. Shi, J. Leng, F. Lin, F. Liu, H. Zhang and W. Shi, Phys. E, 2020, 124, 114309 CrossRef CAS.
- X. He, F. Lin, F. Liu and W. Shi, Nanophotonics, 2022, 11, 4705–4714 CrossRef CAS.
- G. Liao, C. Luan, Z. Wang, J. Liu, X. Yao and J. Fu, Adv. Mater. Technol., 2021, 2000787 CrossRef CAS.
- N. Gao, Z. Zhang, J. Deng, X. Guo, B. Cheng and H. Hou, Adv. Mater. Technol., 2022, 2100698 CrossRef.
- M. Yang, S. Chen, C. Fu and P. Sheng, Mater. Horiz., 2017, 4, 673–680 RSC.
- F. Ma, C. Wang, Y. Du, Z. Zhu and J. H. Wu, Mater. Horiz., 2022, 9, 653–662 RSC.
- S. Lee, Z. Zhang and G. X. Gu, Mater. Horiz., 2022, 9, 952–960 RSC.
- B. Deng and G. J. Cheng, Mater. Horiz., 2021, 8, 987–996 RSC.
- T. Tancogne-Dejean, M. Diamantopoulou, M. B. Gorji, C. Bonatti and D. Mohr, Adv. Mater., 2018, 30, 1803334 CrossRef PubMed.
- X. Li, X. Yu, J. W. Chua, H. P. Lee, J. Ding and W. Zhai, Small, 2021, 2100336 CrossRef CAS PubMed.
- X. Li, X. Yu and W. Zhai, Adv. Mater., 2021, 33, 2104552 CrossRef CAS PubMed.
- D.-Y. Maa, J. Acoust. Soc. Am., 1998, 104, 2861–2866 CrossRef.
- J.-S. Chen, Y.-B. Chen, Y.-H. Cheng and L.-C. Chou, Phys. Lett. A, 2020, 384, 126887 CrossRef CAS.
- H. Zhao, Y. Wang, J. Wen, Y. W. Lam and O. Umnova, Appl. Acoust., 2018, 142, 11–17 CrossRef.
- Y. Tang, S. Ren, H. Meng, F. Xin, L. Huang, T. Chen, C. Zhang and T. J. Lu, Sci. Rep., 2017, 7, 43340 CrossRef PubMed.
- Y. Tang, F. Li, F. Xin and T. J. Lu, Mater. Des., 2017, 134, 502–512 CrossRef.
- J. Zhu, Y. Qu, H. Su, J. Zhang and G. Meng, Appl. Acoust., 2022, 187, 108496 CrossRef.
- X. Li, X. Yu and W. Zhai, Small, 2022, 2204145 CrossRef CAS PubMed.
- Z. Li, W. Zhai, X. Li, X. Yu, Z. Guo and Z. Wang, Virtual Phys. Prototyping, 2022, 17, 864–880 CrossRef.
- Z. Li, X. Li, J. W. Chua, C. H. Lim, X. Yu, Z. Wang and W. Zhai, Virtual Phys. Prototyping, 2023, 18, e2166851 CrossRef.
- Z. Li, X. Wang, X. Li, Z. Wang and W. Zhai, ACS Appl. Mater. Interfaces, 2023, 15, 9940–9952 CrossRef CAS PubMed.
- X. Li, X. Yu, M. Zhao, Z. Li, Z. Wang and W. Zhai, Adv. Funct. Mater., 2023, 33, 2210160 CrossRef CAS.
- Z. Li, X. Li, Z. Wang and W. Zhai, Mater. Horiz., 2023, 10, 75–87 RSC.
- X. Yang, P. Bai, X. Shen, S. To, L. Chen, X. Zhang and Q. Yin, Appl. Acoust., 2019, 146, 334–344 CrossRef.
- J. Zhang, T. Chen, B. Zhang and J. Zhu, Appl. Sci., 2022, 13, 78 CrossRef.
- A. Abbad, N. Atalla, M. Ouisse and O. Doutres, J. Sound Vib., 2019, 459, 114873 CrossRef.
- Y. Lee and E. Lee, Int. J. Mech. Sci., 2007, 49, 925–934 CrossRef.
- Z. Ren, Y. Cheng, M. Chen, X. Yuan and D. Fang, Mater. Des., 2022, 215, 110462 CrossRef.
- W. He, X. Peng, F. Xin and T. J. Lu, J. Sandwich Struct. Mater., 2021, 1099636221993880 Search PubMed.
- Z. Wang, Z. Guo, Z. Li and K. Zeng, Virtual Phys. Prototyping, 2023, 18, e2111585 CrossRef.
- T. Okuzono, T. Nitta and K. Sakagami, Acoust. Sci. Technol., 2019, 40, 221–224 CrossRef.
- N. Jiménez, J. Groby and V. Romero-García, The Transfer Matrix Method in Acoustics, Springer International Publishing, Cham, 2021, 103–164 Search PubMed.
- U. Ingard, J. Acoust. Soc. Am., 1953, 25, 1037–1061 CrossRef.
- X. Yu, Z. Lu and W. Zhai, Acta Mater., 2021, 206, 116666 CrossRef CAS.
- X. Zhang, Z. Qu, X. He and D. Lu, AIP Adv., 2016, 6, 105205 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh00428g |
| This journal is © The Royal Society of Chemistry 2023 |