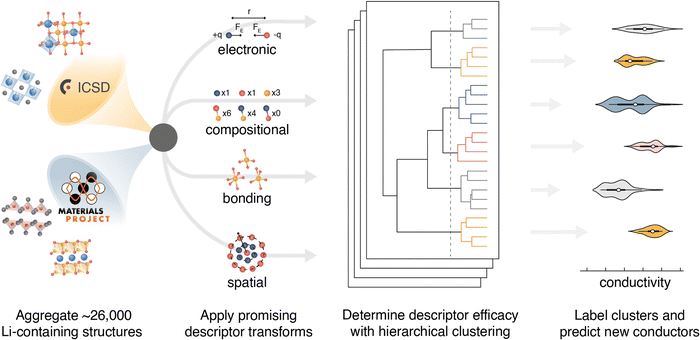
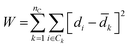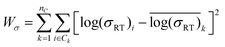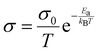Identification of potential solid-state Li-ion conductors with semi-supervised learning†
Forrest A. L.
Laskowski‡
a,
Daniel B.
McHaffie‡
b and
Kimberly A.
See
 *a
*a
aDivision of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, California 91125, USA. E-mail: ksee@caltech.edu
bDepartment of Applied Physics and Materials Science, California Institute of Technology, Pasadena, California 91125, USA
First published on 21st February 2023
Abstract
Despite ongoing efforts to identify high-performance electrolytes for solid-state Li-ion batteries, thousands of prospective Li-containing structures remain unexplored. Here, we employ a semi-supervised learning approach to expedite identification of superionic conductors. We screen 180 unique descriptor representations and use agglomerative clustering to cluster ∼26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Li-containing structures. The clusters are then labeled with experimental ionic conductivity data to assess the fitness of the descriptors. By inspecting clusters containing the highest conductivity labels, we identify 212 promising structures that are further screened using bond valence site energy and nudged elastic band calculations. Li3BS3 is identified as a potential high-conductivity material and selected for experimental characterization. With sufficient defect engineering, we show that Li3BS3 is a superionic conductor with room-temperature ionic conductivity greater than 1 × 10−3 S cm−1. While the semi-supervised method shows promise for identification of superionic conductors, the results illustrate a continued need for descriptors that explicitly encode for defects.
000 Li-containing structures. The clusters are then labeled with experimental ionic conductivity data to assess the fitness of the descriptors. By inspecting clusters containing the highest conductivity labels, we identify 212 promising structures that are further screened using bond valence site energy and nudged elastic band calculations. Li3BS3 is identified as a potential high-conductivity material and selected for experimental characterization. With sufficient defect engineering, we show that Li3BS3 is a superionic conductor with room-temperature ionic conductivity greater than 1 × 10−3 S cm−1. While the semi-supervised method shows promise for identification of superionic conductors, the results illustrate a continued need for descriptors that explicitly encode for defects.
Broader contextAll-solid-state batteries (ASSBs) could help to address energy storage needs for widespread renewable energy adoption as they may offer improved safety and performance over conventional Li-ion batteries. The discovery of novel solid-state electrolytes (SSEs) is necessary to meet the conductivity and stability requirements of ASSBs. In this work, we describe a method for identifying highly conductive SSEs and use this to screen over 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Li-containing materials. The utility of this approach is confirmed by demonstrating superionic conductivity in a candidate phase from our model. Included in this report is our database containing the experimental ionic conductivities of 1346 compounds digitized from over 300 publications. This repository will enable future data-driven efforts by the community to find high-performance SSEs, accelerating the development of improved energy storage technologies. Additionally, the described technique for assessing material descriptor efficacy and identifying novel materials can be broadly applied to expedite materials discovery in other emerging fields limited by data scarcity. 000 Li-containing materials. The utility of this approach is confirmed by demonstrating superionic conductivity in a candidate phase from our model. Included in this report is our database containing the experimental ionic conductivities of 1346 compounds digitized from over 300 publications. This repository will enable future data-driven efforts by the community to find high-performance SSEs, accelerating the development of improved energy storage technologies. Additionally, the described technique for assessing material descriptor efficacy and identifying novel materials can be broadly applied to expedite materials discovery in other emerging fields limited by data scarcity.
|
Identifying new materials that could improve solid-state ion battery prospects is an ongoing challenge. The search for an ideal solid-state Li electrolyte is a prime example. Research has focused on eight classes of materials: LISICON-type structures, argyrodites, garnets, NASICON-type structures, Li–nitrides, Li–hydrides, perovskites, and Li–halides.1 However, relatively few compounds with near-liquid–electrolyte conductivity (∼10−2 S cm−1) have been discovered. Notable examples include Li10GeP2S12 (LGPS),2 Li6PS5Br argyrodite,3 and Li7P3S11 ceramic-glass.1,4 Although promising discoveries, all three high-conductivity structures are unstable against the Li anode.5–10 While investigations to limit instability are ongoing,11,12 identification of additional superionic structures is desirable. Discovery of new structures that support superionic conductivity improves the odds of identifying or engineering a stable electrode|SSE interface. For example, engineering solutions that fail to stabilize the Li|argyrodite interface may prove more successful when applied to not-yet-discovered superionic conductors. The discovery of new superionic conductors may also enable stable architectures via multi-electrolyte approaches which have been proposed as more promising than single-electrolyte architectures for achieving stability against Li metal and cathode materials.13 High-performing structures that enable new battery chemistries may exist outside of the eight classes. However, exploration under the traditional Edisonian approach prioritizes small perturbations to well-known variable spaces.
Machine learning (ML) is a promising tool for expediting the discovery of useful solid-state materials. By representing prospective materials with physically meaningful descriptors, ML models can identify high-dimensional patterns in large datasets that are not readily apparent.14–20 Ongoing descriptor engineering21–26 has enabled discovery of battery components,27,28 electrocatalysts,15,29 photovoltaic components,16,30 piezoelectrics,31 new metallic glasses14 and new alloys.32 However, application of ML for discovery of SSEs and other emerging technologies can be challenging. Supervised ML approaches require empirical data for use as “labels”. For example, graph neural network (GNN) approaches have been successful in many domains but generally require thousands to tens of thousands of labels to avoid overfitting.33 By contrast, relatively few SSEs have been experimentally characterized compared to the ∼26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 known Li-containing structures.19,34–36 Characterized materials often exhibit ill-defined properties owing to the variety of synthetic approaches and non-standardized testing methods.37 Well-performing materials often contain charge-carrying defects that are not explicitly characterized or reported.38 Negative examples, i.e. materials with undesirable properties, are useful for ML models but are seldom reported.
000 known Li-containing structures.19,34–36 Characterized materials often exhibit ill-defined properties owing to the variety of synthetic approaches and non-standardized testing methods.37 Well-performing materials often contain charge-carrying defects that are not explicitly characterized or reported.38 Negative examples, i.e. materials with undesirable properties, are useful for ML models but are seldom reported.
Semi-supervised ML can guide synthetic prioritization of SSEs by overcoming the issues associated with label scarcity. Supervised ML requires labels because it infers correlation functions by mapping the input descriptors to the labels.39 Semi-supervised ML prioritizes comparison of descriptors to identify relationships between the descriptors in a dataset.36,39 The input materials are clustered (or grouped) by comparison of descriptors using a similarity metric. The clustering process does not consider labels, and thus circumvents the need for an abundant respository of labels. The resultant clusters can be labeled ex post facto to examine correlation between the descriptor and a physical property of interest. For semi-supervised ML, ideal descriptors result in a set of clusters where each cluster has similar labels and thus the label variance is minimized. Promising synthetic targets may then be identified by their membership in clusters that contain desirable labels.
A key insight of this work is that semi-supervised ML can be used to rank descriptors in terms of their correlation to physical properties of interest. Descriptors are representations of the input materials that encode the chemistry, composition, structure, and/or other system properties. An ideal descriptor should be a unique representation, a continuous function of the structure, exhibit rotational/translational invariance, and be readily comparable across all structures in the dataset.24–26 Recently, Zhang et al. demonstrated that a modified X-Ray diffraction (mXRD) descriptor lead to favorable clustering for Li SSEs.34 By labeling the resultant clusters with experimental room-temperature Li-ion conductivities, they identified 16 prospective fast-ion conductors. However, an ideal descriptor is not known a priori, and no comprehensive descriptor screening has yet been pursued for correlation with SSE properties. Descriptor screening is desirable for both experimentalists and computationalists. For experimentalists, ranking of descriptors affords insight into what aspects of materials are most correlated with target properties. For computationalists, descriptor rankings enable improved regression and supervised learning models by guiding the selection of input representation(s). Descriptor transformations for inorganic structures have been curated in a variety of software packages, including: Matminer,24 Dscribe,25 SchNet,40 and Aenet.41
Herein, we employ hierarchical agglomerative clustering to screen many descriptors, without assuming correlation to ionic conductivity. The performance of 20 descriptors is assessed for semi-supervised identification of Li SSEs. Each descriptor is paired with 9 structural simplification strategies, yielding a total of 180 unique representations per input structure. The approach is applied to a dataset of ∼26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Li-containing phases, encompassing all Li-containing structures contained in the Inorganic Crystal Structure Database (ICSD – v.4.4.0) and the Materials Project (MP – v.2020.09.08) database (Fig. 1). A set of 220 experimental room temperature ionic conductivities (σ25°C) are aggregated from literature reports and used as labels. Experimental labels are selected because they may bias models towards identifying structures that are synthetically tractable and processable. Descriptors that encode the spatial environment are found to be the most correlated with the ionic conductivity labels. Whereas descriptors that encode the electronic, compositional, or bonding environment have less predictive power. For the structural descriptors, simplifications that neglect the mobile ion perform best. The descriptor screening results suggest that ionic conductivity is most sensitive to the spatial environment of the framework lattice.
000 Li-containing phases, encompassing all Li-containing structures contained in the Inorganic Crystal Structure Database (ICSD – v.4.4.0) and the Materials Project (MP – v.2020.09.08) database (Fig. 1). A set of 220 experimental room temperature ionic conductivities (σ25°C) are aggregated from literature reports and used as labels. Experimental labels are selected because they may bias models towards identifying structures that are synthetically tractable and processable. Descriptors that encode the spatial environment are found to be the most correlated with the ionic conductivity labels. Whereas descriptors that encode the electronic, compositional, or bonding environment have less predictive power. For the structural descriptors, simplifications that neglect the mobile ion perform best. The descriptor screening results suggest that ionic conductivity is most sensitive to the spatial environment of the framework lattice.
Using the descriptors, the semi-supervised approach can identify potential fast solid-state Li-ion conductors. By selecting structures in clusters containing high conductivity labels, the ∼26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 input structures are down selected to just 212 promising structures. Application-based considerations, a semi-empirical bond valence site energy (BVSE) method42 and the Nudged Elastic Band (NEB) method are employed to rank the structures. From the ten highest ranking structures, Li3BS3 is selected for model validation. Synthesis of pure Li3BS3 yields a poor conductor. However, by employing defect engineering strategies we demonstrate that Li3BS3 is a superionic conductor with an ionic conductivity greater than 10−3 S cm−1.
000 input structures are down selected to just 212 promising structures. Application-based considerations, a semi-empirical bond valence site energy (BVSE) method42 and the Nudged Elastic Band (NEB) method are employed to rank the structures. From the ten highest ranking structures, Li3BS3 is selected for model validation. Synthesis of pure Li3BS3 yields a poor conductor. However, by employing defect engineering strategies we demonstrate that Li3BS3 is a superionic conductor with an ionic conductivity greater than 10−3 S cm−1.
Main text
Screening simplification-descriptor combinations
A set of 20 descriptors is selected for screening the semi-supervised learning approach (Table 1). The descriptors generally encode four types of information: the spatial environment, the chemical bonding environment, the electronic environment, and composition. All descriptors are implemented in Python using the Matminer24 or Dscribe25 libraries. The code is published to a GitHub repository and is available for download (https://github.com/FALL-ML/materials-discovery). Zhang et al. illustrated that structure simplification prior to learning can produce lower variance outcomes.34 Their mXRD descriptor was found to work best with the removal of all cations, all the anions replaced by a single representative anion, and the structure volume scaled to 40 Å3 per anion. Inspired by the previous success in using structure simplification, we screen eight structure simplifications in addition to the unperturbed structure. For simplifications the following categories of atoms are replaced with a representative specie: (1) cations are represented as Al, (2) anions are represented as S, (3) mobile ions are represented as Li, and (4) neutral atoms are represented as Mg. Categories of atoms are removed to yield the four simplifications: CAMN (all atoms retained), CAN (mobile ions removed), AM (cations and neutral atoms removed), and A (only anions retained). Four additional simplifications are formed by scaling each lattice volume to 40 Å3 per anion: CAMN-40, CAN-40, AM-40, and A-40.| Descriptor | Descriptor description | Ref. |
|---|---|---|
| Bond fraction | “Bag of bonds” approach described in Hansen et al. wherein pairwise nuclear charges and distances are encoded. | 43 |
| Band center | Estimation of band center from constituent atoms’ electronegativity values described by Butler et al. | 44 |
| Crystal structure analysis by voronoi decomposition (CAVD) | Calculation of the largest sphere that can pass through the lattice-sans-mobile-ion using Voronoi decomposition of structures. | 45 |
| Chemical ordering | Warren-Cowley-like ordering method to determine how different the structure's ordering is from random. | 46 |
| Density features | Calculates density, volume per atom, and the packing fraction. | 47 |
| Electronegativity difference | Composition-weighted calculation of the electronegativity difference between cations and anions. | 48 |
| Ewald energy | Sum of coulomb interaction energies across all lattice sites described by Ewald et al. | 49 |
| Global instability index | Averaged square root of the sum of squared differences over the bond valence sums. | |
| Jarvis | Diverse set of descriptors from the Jarvis-ML library. | 50 |
| Maximum packing efficiency | A measure of the void space within the unit cell. | 46 |
| Meredig | Composite descriptor from Meredig et al. | 51 |
| Modified XRD (mXRD) | Powder diffraction pattern calculated using Bragg's law. | 47 |
| Orbital field matrix | Descriptor that encodes the distribution of valence shell electrons for each input structure. | 52 |
| Oxidation states | Concentration weighted oxidation state statistics. | 48 |
| Radial distribution function | Radial distribution function for each structure. | 47 |
| Sine coulomb matrix | Coulomb matrix for periodic lattices, developed by Faber et al. | 53 and 54 |
| Smooth overlap of atomic positions (SOAP) | Geometric encoder that is rotationally/transitionally invariant through use of spherical harmonics and radial basis functions. Atoms are represented by a smeared Gaussian. | 25 |
| Structural complexity | The Shannon information entropy for a given structure. | 55 |
| Structure variance | Bond length and atomic volume variance for each structure. | 46 |
| Valence orbital | Structure-averaged number of valence electrons in each orbital. | 48 and 56 |
| Control | A control descriptor is not explicitly used. Instead, clustering outcomes are randomly assigned. For composite intracluster variance calculations, 100 control iterations are averaged. |
Agglomerative clustering is performed on all Li-containing structures from the ICSD and MP repositories. Agglomerative clustering is a “bottom-up” approach to clustering where each structure starts in its own cluster of one. Clusters are merged according to Ward's Minimum Variance criterion in Euclidean space, which minimizes the global descriptor variance:57
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) k is the average descriptor representation in cluster k. Each cluster merger results in the lowest variance set of clusters, relative to all other possible mergers. Other common linkage criteria (average, complete, and single linkages) and metrics (l1, l2, Manhattan, cosine) were screened but are found to result in clustering outcomes with larger W. For each simplification-descriptor combination, all clustering sets from 2–300 are computed. Physically relevant labels are applied to the resultant clustering sets to assess how well each simplification-descriptor combination performs. To compare between the 180 different simplification-descriptions combinations, the data is labeled with 155 experimental room temperature conductivity (σRT) values aggregated from the literature reports (see Sections I–IV, ESI†). A secondary label set is also screened, comprised of 6845 activation energies (Ea) computationally generated using a bond valence energy approach (see Section V, ESI†).
k is the average descriptor representation in cluster k. Each cluster merger results in the lowest variance set of clusters, relative to all other possible mergers. Other common linkage criteria (average, complete, and single linkages) and metrics (l1, l2, Manhattan, cosine) were screened but are found to result in clustering outcomes with larger W. For each simplification-descriptor combination, all clustering sets from 2–300 are computed. Physically relevant labels are applied to the resultant clustering sets to assess how well each simplification-descriptor combination performs. To compare between the 180 different simplification-descriptions combinations, the data is labeled with 155 experimental room temperature conductivity (σRT) values aggregated from the literature reports (see Sections I–IV, ESI†). A secondary label set is also screened, comprised of 6845 activation energies (Ea) computationally generated using a bond valence energy approach (see Section V, ESI†).
An ideal simplification-descriptor combination results in clustering where each cluster contains labels with similar σRT values. Ward's minimum variance method is applied to the conductivity labels as a measure of clustering efficacy:34
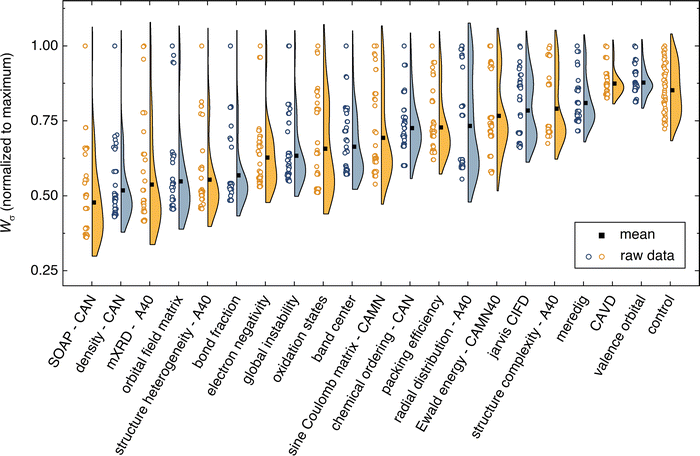
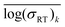 denotes the mean for all labels in cluster k. Since clusters containing only one label effectively drop out of the Wσ calculation, a frozen-state strategy is employed when needed (see Section IV, ESI†). Each descriptor's Wσ results are shown in Fig. 2 for the first 50 clustering outcomes (i.e. the Wσ is shown for each set of 2, 3, …, 49, and 50 clusters). For simplicity, only the best-performing simplification-descriptor combination is shown for each descriptor.
denotes the mean for all labels in cluster k. Since clusters containing only one label effectively drop out of the Wσ calculation, a frozen-state strategy is employed when needed (see Section IV, ESI†). Each descriptor's Wσ results are shown in Fig. 2 for the first 50 clustering outcomes (i.e. the Wσ is shown for each set of 2, 3, …, 49, and 50 clusters). For simplicity, only the best-performing simplification-descriptor combination is shown for each descriptor.
Using σ25°C labels, the best semi-supervised ML performance is attained when using the SOAP descriptor. SOAP is a spatial descriptor that employs smeared Gaussians to represent atomic positions for each crystal structure.25 Predictions using the SOAP descriptor have exhibited similar performance to state-of-the-art graph neural networks (GNNs) on a variety of materials science datasets.58 Optimization of SOAP hyper-parameters (radial cutoff, number of radial basis functions, degree of spherical harmonics) is explored in section VI of the ESI.† SOAP is found to perform best when combined with the CAN structure simplification. That is, the simplification where the mobile Li atoms are removed, and the remaining atoms are simplified into three representative species: cations, anions, and neutral atoms. SOAP outperforms all other descriptors for all depths of clustering. The SOAP descriptor can be modestly improved (2–3% decrease in Wσ) by mixing with other descriptors to make a 2nd-order SOAP descriptor (see Section VI, ESI†).
Semi-supervised identification of prospective Li-ion conductors
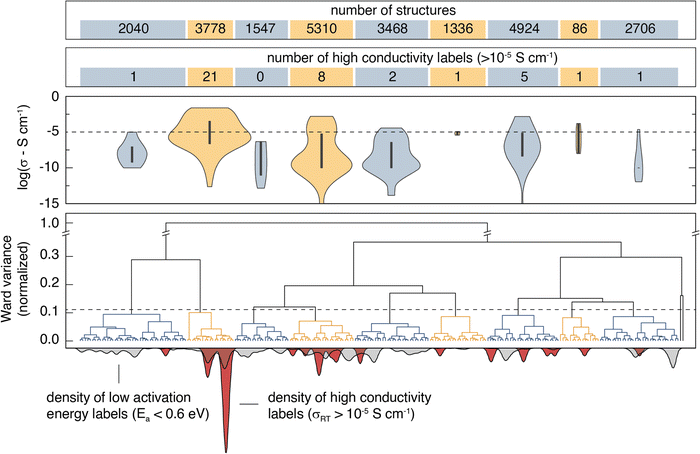
Agglomerative clustering with the 2nd-order SOAP descriptor is used to identify prospective ionic conductors. Wσ minimization is prioritized over WEa minimization because Ea alone is not necessarily a good predictor of conductivity; σ25°C may be affected by properties including the ionic carrier concentration, hopping attempt frequency, and the presence of concerted migration modes.59 The agglomerative dendrogram for the 2nd-order SOAP clustering is shown in Fig. 3, with the label densities plotted below. The agglomerative dendrogram is depicted to 241 clusters, after which the Wσ does not appreciably decrease. To facilitate discussion, an arbitrary cutoff is placed to yield 9 large clusters. The results show that although cluster #2 contains only 15% of the input structures, it accounts for over half of the high-conductivity (σ25°C > 10−5 S cm−1) labels. By the 17th clustering step, the densest cluster accounts for 6.2% of the structures while containing over half (52%) of the high-conductivity labels.Candidates for next-generation SSEs can be identified by evaluating clusters that either contain or are near high conductivity labels. Clusters #2, #4, and #7 are promising because they account for 85% of the high σ25°C labels. However, targeting these clusters would necessitate screening thousands of structures. Instead, we search from the 241st cluster depth, targeting all clusters that contain or are directly adjacent (i.e. the nearest cluster in the Euclidean feature space) to high σ25°C labels. The promising structures are further screened using calculated stability (E vs. Ehull) and band gap (Eg) properties from the Materials Project, and the BVSE Ea values. We select the structures that have (1) an Ehull of 70 meV or lower,60 (2) an Eg of at least 1 eV, and (3) a BVSE-calculated Ea below a conservative 0.6 eV. We note that while a true Eg value of 1 eV would be problematic for an SSE, the bandgaps reported on Materials Project are typically underestimated by about 40%.61 The approach identifies 212 structures as prospective ionic conductors. Climbing image nudged elastic band (CI-NEB) is employed to calculate the Ea for Li-ion hopping on the ten materials with the lowest BVSE-calculated Ea and an Ehull of 0 eV. The CI-NEB computational details can be found in Section VII (ESI†). The top 10 prospective structures are tabulated in Table 2.
| Compound | Space group | MP_ID | ICSD_ID | E vs. E hull (eV per atom) | E g (eV) | E a_calc (meV) | |
|---|---|---|---|---|---|---|---|
| BVSE | NEB | ||||||
| Li3VS4 |
P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (#215) 3m (#215) |
mp-760375 | 0 | 1.88 | 160 | 390 | |
| Na3Li3Al2F12 |
Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d (#230) d (#230) |
mp-6711 | 9923 | 0 | 7.85 | 230 | 340 |
| Li2Te |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (#225) m (#225) |
mp-2530 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 434 434 |
0 | 2.49 | 260 | 320 |
| LiAlTe2 |
I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d (#122) 2d (#122) |
mp-4586 | 280![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 226 226 |
0 | 2.46 | 260 | 310 |
| LiInTe2 |
I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d (#122) 2d (#122) |
mp-20782 | 658![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 016 016 |
0 | 1.49 | 270 | 450 |
| Li6MnS4 | P42/mmc (#137) | mp-756490 | 0 | 1.55 | 270 | 470 | |
| LiGaTe2 |
I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d (#122) 2d (#122) |
mp-5048 | 162![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 555 555 |
0 | 1.59 | 270 | 340 |
| Li3BS3 | Pnma (#62) | mp-5614 | 380![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 104 104 |
0 | 2.89 | 280 | 260 |
| KLi6TaO6 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (#166) m (#166) |
mp-9059 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 159 159 |
0 | 4.27 | 300 | 400 |
| Li3CuS2 | Ibam (#72) | mp-1177695 | 0 | 2.03 | 310 | 440 | |
The CI-NEB calculations generally agree with the BVSE calculated Ea values, suggesting favorable activation energies (<500 meV). Discrepancies between the two values may arise because BVSE does not allow framework ions to relax during Li+ migration and does not account for repulsive interactions between atoms of the mobile ion species. BVSE also does not capture cooperative conduction mechanisms or those involving the so-called paddlewheel effect. Despite these limitations, we note that the model identifies numerous diverse structures beyond those routinely explored. Table 1 includes four tellurides, a vanadium sulfide, and multiple transition–metal-containing structures. Of the structures in Table 1, 70% avoid the space groups for the best-performing SSEs discovered to date: LPS (62), LGPS (137), the argyrodites (216), and LLZO (230).
Experimental validation of the semi-supervised learning model: Li3BS3
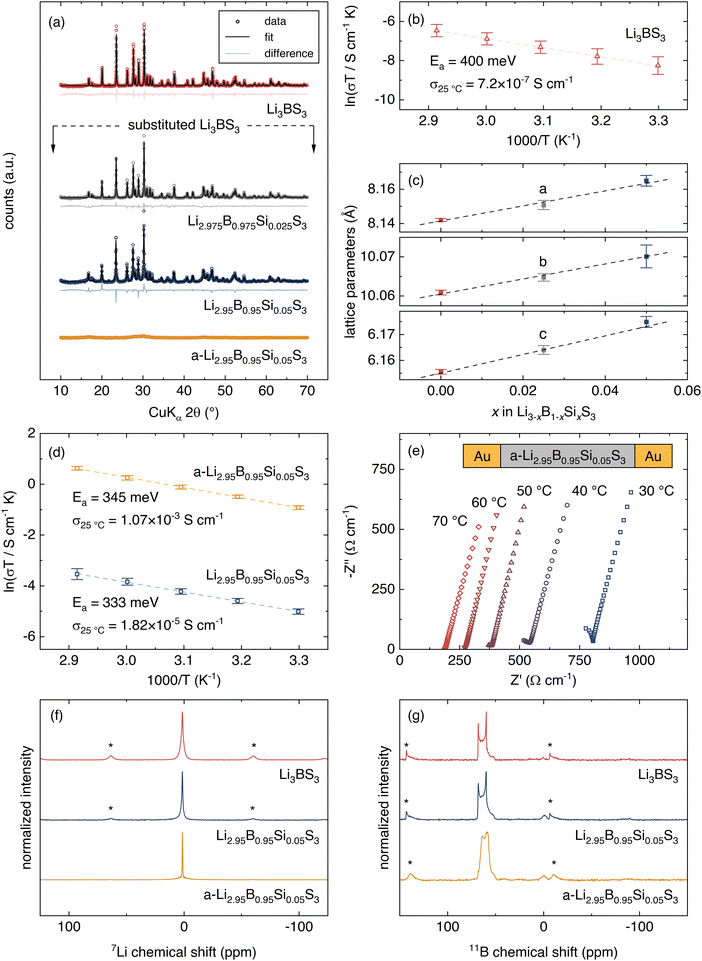
From the ten most promising candidates, Li3BS3 was selected for synthesis and characterization. Li3BS3 is noteworthy because it has been explored experimentally and computationally before. Experimentally, Vinatier et al. previously determined that Li3BS3 has a total DC conductivity of 2.5 × 10−7 S cm−1 with an activation energy of 700 meV.62 The DC measurement was not included in our label set because DC measurements cannot differentiate between ionic and electronic conductivity, so they were categorically discounted from the label set (see ESI,† I for more details on label selection). Although the conductivity and activation energy values reported by Vinatier et al. are underwhelming, there are promising theoretical reports. Density functional theory molecular dynamics (DFT-MD) simulations from Sendek et al.63 suggest that Li3BS3 should have a room temperature conductivity between 3.1 × 10−6 and 9.7× 10−3 S cm−1. Our NEB-calculated activation energy for Li3BS3 is 260 meV, corroborating a previous NEB result from Bianchini et al.64 Additionally, Li3BS3 is practically attractive because: (1) Li3BS3 contains no redox-active metals, (2) band edge calculations have suggested stability against metallic Li,65 (3) DFT-MD calculations have suggested a kinetic barrier for decomposition against metallic Li,63 and (4) the synthesis is reported.66 It is simpler to avoid redox active metals in the SSE as they may be reduced and oxidized at electrode interfaces. However, we note that Li0.5La0.5TiO3 is a widely studied SSE that contains redox active Ti67,68 so the compounds we report here that contain Mn, V, and Cu should not be categorically discounted. It is important to note that while studying Li3BS3 as a candidate Li-ion conductor for model validation, Kimura et al. reported that a so-called “Li3BS3 glass” exhibits an ionic conductivity of 3.6 × 10−4 S cm−1 at 25 °C.69Li3BS3 is prepared using solid-state synthesis from Li2S, B, and S precursors. The diffraction and quantitative Rietveld refinement are shown in Fig. 4a, indicating a phase pure material. Electrochemical impedance spectroscopy (EIS) is employed at various temperatures and the measured conductivity is plotted according to the Arrhenius-like relationship (Fig. 4b):
Aliovalent substitution of Li3BS3 is achieved by substituting Si for B. The XRD patterns and quantitative Rietveld refinements of Li2.975B0.975Si0.025S3 and Li2.95B0.95Si0.05S3 are shown in Fig. 4a. The lattice parameters from the refinements are plotted vs. stoichiometry with the Li3BS3 end-member in Fig. 4e. The linear trend shows that the materials obey Vegard's law and confirms that Si incorporates into the lattice as a solid-solution. Substitution to 7.5% Si continues the Vegard trend but unidentified impurities are apparent in the XRD pattern. With 5% Si substitution, the ionic conductivity is improved to 1.82(±0.21) × 10−5 S cm−1 and the activation energy is decreased to 333 ± 47 meV (Fig. 4d). All error bars reported for electrochemical measurements represent the standard deviation of three replicate cells. Kimura et al. demonstrated that extended ball milling of Li3BS3 causes amorphization and improves ionic conductivity, likely due to the introduction of defects.62,69 Extended ball milling is attempted on the 5%-substituted Li3BS3 to assess whether both defect engineering strategies are compatible. Planetary ball milling of the 5%-substituted Li3BS3 for 100 h achieves amorphization (a-Li2.95B0.95Si0.05S3), as verified by the lack of distinct peaks in the XRD pattern shown in Fig. 4a.
We find that amorphization significantly improves Li-ion conductivity. EIS measurements of a-Li2.95B0.95Si0.05S3 are shown in Fig. 4e. A high-frequency semicircle is partially resolved which may represent grain boundary or bulk ionic transport. A Warburg tail is evident at lower frequencies, indicating that electronic charge transfer is blocked. Although multiple high-frequency semicircles may exist (see Section VII, ESI†), a conservative estimate of the ionic conductivity is determined by linear fit of the Warburg tail and extrapolation to the x-intercept. The σ25°C of a-Li2.95B0.95Si0.05S3 is 1.07(±0.08) × 10−3 S cm−1 with an activation energy of 345 ± 2 meV (Fig. 4d). The electronic conductivity as measured by DC polarization is less than 4 × 10−10 S cm−1.
To determine if the local structure in the crystalline material is maintained after amorphization, we turn to 7Li and 11B NMR. If the local structure is not altered by amorphization, then it is likely that the ion diffusion pathways are similar. Comparing the ion diffusion pathways is important because the machine learning points to the structure of the crystalline Li3BS3 phase. The 7Li NMR spectra of Li3BS3, Li2.95B0.95Si0.05S3, and a-Li2.95B0.95Si0.05S3 are shown in Fig. 4d. All materials show a single resonance at the same chemical shift, suggesting that the Li local environment remains unchanged. The resonance width narrows significantly in the amorphous material due to the higher mobility. The 11B NMR measurements are shown in Fig. 4g. The 11B NMR for Li3BS3 and Li2.95B0.95Si0.05S3 show a single, quadrupolar environment that can be assigned to the [BS3]3− moieties.69,74 The signal from the a-Li2.95B0.95Si0.05S3 shows a similar signal to that of the crystalline phases but the shape changes, similarly to the previous measurement for amorphous Li3BS3.69 Li3BS3, Li2.95B0.95Si0.05S3, and a-Li2.95B0.95Si0.05S3 all exhibit a major peak at ∼60 ppm and a relatively minor peak ∼0 ppm. The major peak is assigned to trigonal planar [BS3]3− while the minor peak likely indicates a minor impurity with tetrahedrally coordinated B.75–77 The change in the shape of the 11B spectrum upon amorphization is likely due to an averaging of the quadrupolar couplings due to the fast Li dynamics. Thus, Li3BS3 and a-Li2.95B0.95Si0.05S3 have similar local structures and we can attribute the faster Li dynamics to the introduction of charge-carrying defects.
Although investigation of interfacial stability is beyond the scope of the model, we note that the Si-substituted Li3BS3 is a promising candidate for future investigations into interfacial stability. Work by Park et al. suggests that the (010) facet for Li3BS3 has a conduction band minimum 0.5 eV above the Li/Li+ couple.65 Since decomposition of Li3BS3 is likely to be mediated by electron injection from Li, their results suggest that thermodynamic stability can be engineered via orientation. From a kinetic perspective, high-temperature DFT-MD simulations show no mobility for B and S, suggesting large kinetic diffusion barriers.63 Since decomposition of Li3BS3 would entail the diffusion of these species, the reaction may be sluggish or wholly precluded. Interfacial stability has been previously demonstrated for a glassy electrode in the Li–B–S–Si–O phase space.78 This result may indicate that stability can be engineered into Si-substituted Li3BS3 by partial isovalent substitution of O for S. Finally, recently-synthesized Li–B–S–X (X = Cl, Br, I) quaternaries have exhibited promising conductivities.79 With similar elemental composition, the Si-substituted Li3BS3 may be a good candidate for a multi-electrolyte architecture with the halide-containing quaternaries.13
In addition to our experimental model validation, another of the predicted materials, KLi6TaO6, was recently synthesized with aliovalent Sn-substitution by Suzuki et al.80 With a reported ionic conductivity near 10−5 S cm−1, KLi6TaO6 is better than 70% of the SSEs in the semi-supervised labels. Further improvement may be possible via extended amorphization to introduce structural defects, as is observed for Li3BS3.
Conclusions
Identification of functional materials is critical for improving technologies. Here, we show the utility of using semi-supervised learning as a method for guiding next-generation materials discovery in emerging fields. The method's focus on identifying the relationships between descriptors, prior to labeling, enables understanding of compositional spaces where most inputs are unlabeled. We demonstrate how semi-supervised learning can be used to identify descriptors correlated with superionic conductivity in Li SSEs. By analyzing all Li-containing structures from the ICSD and MP database, we identify 212 materials that show promise as SSEs. All 212 structures exhibit a BVSE-predicted Ea below 0.6 eV.The results illustrate why careful screening of descriptors is useful when identifying new materials. While chemical intuition can be useful for descriptor selection, chemical intuition is often biased to favor previously investigated compositional spaces. For material discovery in emerging fields, the use of handpicked descriptors may miss complex phenomena that more generally describe the dataset. Descriptor screening reveals which material properties are correlated to a property of interest to help enhance chemical intuition. In the case of Li SSEs, spatial descriptors excel over compositional, bonding, and electronic descriptors: the Smooth Overlap of Atomic Positions (SOAP), modified X-ray diffraction (mXRD), and general density descriptors are within the top four models. For spatial descriptors, simplification of the input structure tends to improve clustering outcomes. Removing the mobile ions from the structure and simplifying the remaining atoms, i.e. the “CAN” simplification, is most effective. Thus, the placement of framework atoms, but not their precise identity, is most correlated with ionic conductivity. Specifying the mobile ion positions hurts the model performance, suggesting a low correlation of mobile ion positions with ionic conductivity.
Predictions from the semi-supervised method are promising starting points for the experimental identification of new superionic conductors but defects must be considered. The proposed materials are diverse, with the top thirty including halides, sulfides, tellurides, nitrides, oxides, and oxyhalides (see Section IX, ESI†). As a structure that falls outside of the eight routinely studied SSE classes, we demonstrate experimental characterization of Li3BS3 to confirm the utility of the approach. However, pure Li3BS3 exhibits poor ionic conductivity. Defects must be introduced into the material to achieve a superionic conductivity above 10−3 S cm−1, a value that surpasses most reported SSEs. We note that the defects are introduced while maintaining the local structure of the crystalline material and thus the ionic conduction pathways are likely similar. The need to introduce defects highlights the paramount importance that defects play when measuring real materials. Many of the highest-performing SSEs contain charge-carrying defects that are not explicitly encoded in their structure files. It is likely that some of the descriptors indirectly encode information about defects. By using experimental conductivity values as the evaluation metric, we may be prioritizing descriptors that encode information about a structure's ability to support charge-carrying defects. Although Li3BS3 is a poor conductor, it is clearly able to support charge-carrying defects. The large conductivity difference between pristine Li3BS3 and a-Li2.95B0.95Si0.05S3 highlights the importance of these defects. To improve predictive models and enhance chemical intuition, descriptors that explicitly encode defects are needed.
Now developed, the semi-supervised learning approach can serve as a template for material discovery beyond Li SSEs. The code is thoroughly documented following pythonic coding standards and made freely available on GitHub. Although the present effort focuses on Li SSEs, the approach is applicable to any material discovery space where labels are sparse. The discovery of new Li cathodes could be accomplished by using Li diffusivity, cathode capacity, and metal redox couple voltages as labels. The discovery of divalent SSEs (e.g. Mg2+, Ca2+, Zn2+) could foreseeably be accomplished in a similar manner. The semi-supervised learning strategy may accelerate identification of fast ionic conductors for ion exchange membranes, solid oxide fuel cells, and various sensor applications.
Methods
Data processing and semi-supervised learning
The ∼26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 input compositions are exported from the Inorganic Crystalline Structure Database (ICSD v.4.4.0) and Material's Project (MP – v.2020.09.08) as crystallographic information files (.cif). All structures containing Li are imported. Although transition metals could produce undesirable redox activity, transition metal-containing structures are not screened out. Some of the best-performing SSEs contain transition metals (e.g. LLZO and LLTO). Entries that exist in both ICSD and MP are merged. Data manipulations and structure simplifications are performed using the Python libraries NumPy (v1.19.1), Pandas (v1.0.5), ASE (v3.19.1), and Pymatgen (v2020.8.3). Descriptor transformations are performed using the Python libraries Pymatgen (v2020.8.3), Matminer (v0.6.3), and Dscribe. Agglomerative hierarchical clustering is performed using the Python library scipy (v1.5.0). All code has been successfully executed on a custom-built CPU with an AMD Ryzen Threadripper 3990x Processor and 256 GB of RAM, in Ubuntu 20.04 running on Windows Subsystem for Linux 2. All code is made available on the GitHub (https://github.com/FALL-ML/materials-discovery).
000 input compositions are exported from the Inorganic Crystalline Structure Database (ICSD v.4.4.0) and Material's Project (MP – v.2020.09.08) as crystallographic information files (.cif). All structures containing Li are imported. Although transition metals could produce undesirable redox activity, transition metal-containing structures are not screened out. Some of the best-performing SSEs contain transition metals (e.g. LLZO and LLTO). Entries that exist in both ICSD and MP are merged. Data manipulations and structure simplifications are performed using the Python libraries NumPy (v1.19.1), Pandas (v1.0.5), ASE (v3.19.1), and Pymatgen (v2020.8.3). Descriptor transformations are performed using the Python libraries Pymatgen (v2020.8.3), Matminer (v0.6.3), and Dscribe. Agglomerative hierarchical clustering is performed using the Python library scipy (v1.5.0). All code has been successfully executed on a custom-built CPU with an AMD Ryzen Threadripper 3990x Processor and 256 GB of RAM, in Ubuntu 20.04 running on Windows Subsystem for Linux 2. All code is made available on the GitHub (https://github.com/FALL-ML/materials-discovery).
CI-NEB
Migration barriers for Li-ion hopping are evaluated with the Climbing Image – Nudged Elastic Band (CI-NEB) method as implemented in the QuantumESPRESSO PWneb software package.81–84 Density-functional theory (DFT) calculations are performed using the Perdew–Burke–Ernzerfof (PBE) generalized gradient approximation functional and projector-augmented wave (PAW) sets.85,86 Convergence testing for the kinetic-energy cutoff of the plane-wave basis and the k-point sampling is performed for each structure to ensure an accuracy of 1 meV per atom. The lattice parameters and atomic positions of the as-retrieved structure are optimized. Supercells are created for each structure that are a minimum of 10 Å in each lattice direction to minimize interactions between periodic images of the mobile ion. To study the migration barrier in the dilute limit, a single Li vacancy is created in the boundary endpoint structures of each studied pathway. A uniform background charge is used to balance excess charge. Each boundary configuration is relaxed until the force on each atom is less than 3 × 10−4 eV Å−1. Images are created by linearly interpolating framework atomic positions between the initial and final boundary configurations. The initial pathway for the mobile ion is generated from the BVSE output minimum energy pathway to promote faster convergence of the NEB calculation. An NEB force convergence threshold of 0.05 eV Å−1 is used. The calculation is first converged using the default NEB algorithm and then restarted with the CI scheme to allow for the maximum energy of the pathway to be determined.Li3BS3 synthesis
Li3BS3 is synthesized by reaction of Li2S (Alfa Aesar, 99.9%), S8 (Acros Organics, >99.5%), and elemental B (SkySpring Nanomaterials, Inc. 99.99%). The reactants are first mixed stoichiometrically (300 rpm for 1 h) using a planetary ball mill (MSE PMV1-0.4L) in 50 mL ZrO2 jars with ZrO2 balls. Two grams of reactants are always combined with 2 large balls (10 mm diameter), 34 medium balls (5 mm diameter), and 8 grams of small balls (3 mm diameter). Loading of ball mill jars occurs in an Ar-filled glovebox (Mbraun) and the jars are sealed before removal. After the 1 h of milling, the precursor mixture is pumped back into the glovebox and 330–340 mg of the powder is loaded into carbon-coated vitreous silica ampoules (10 mm ID × 12 mm OD). The ampoules are evacuated (<10 mtorr) prior to sealing. Pure Li3BS3 is obtained via a four-step heating protocol in a Lindberg/Blue furnace: (1) ramp to 500 °C at 5 °C min−1, (2) hold at 500 °C for 12 h, (3) ramp to 800 °C at 5 °C min−1, and (4) hold at 800 °C for 6 h. The hot melt is then quenched from 800 °C into room-temperature water. Recovered ingots are typically covered in an amorphous shell. The shell is either sanded off or the ingot is ground into smaller pieces and the shell is manually removed.Substituted Li3BS3
Aliovalent substitution is accomplished by adding elemental Si (Acros, 99+%) into the precursor mixture prior to the 1 h mix. Si-Substitution stoichiometry assumed that each Si atom replaces one Li and B: Li3−xB1−xSixS3. Aside from the addition of Si, all steps are the same as for the synthesis of Li3BS3. Amorphization is accomplished via extended planetary ball milling in Ar of the 5% Si-substituted Li3BS3 (Li2.95B0.95Si0.05S3). Approximately 1 g of Li2.95B0.95Si0.05S3 is combined in a ZrO2 ball mill jar with 3 large balls (10 mm diameter), 51 medium balls (5 mm diameter), and 12 g of small balls (3 mm diameter). The powder is ground in a planetary ball mill (MSE PMV1-0.4L), under an Ar atmosphere, for 100 h.Material characterization
Li3BS3 materials are characterized using powder X-ray diffraction (XRD) and electrochemical impedance spectroscopy (EIS). XRD patterns are attained on a Rigaku Smartlab by scanning from 10° to 70° 2θ at 2 degrees per minute. The Smartlab employs a Cu-Kα source with a 20 kV accelerating voltage. For EIS measurements, 50–100 mg of powder is first hot-pressed (100 °C, 5 min) into a 1/4′′ diameter pellet. The pellet faces are polished using diamond lapping powder (Allied High Tech Products Inc.) in sequentially finer grits: 60, 30, 6, 0.5, and 0.1 microns. Au contacts are sputtered (90 s at 40 mA) onto the polished surfaces using a 108 Auto Sputter Coater (Cressington). Pellets are then assembled into a Swagelok 1/4′′ cell with stainless steel current collectors. After applying pressure with a hand vise (∼100 MPa), EIS data is collected on a VSP-300 with a Biologic low-current channel. All EIS data is collected to an upper frequency of 3 MHz. The lower frequency is case dependent, with a frequency cutoff selected such that the Warburg polarization feature is visible. 7Li and 11B MAS MAS NMR spectra were acquired using a Bruker DSX-500 spectrometer with a 4 mm ZrO2 rotor. The operating frequencies for 7Li and 11B are 190.5 and 160.5 MHz, respectively. The 7Li and 11B spectra were referenced to a 1 M LiCl aq. solution and BF3-OEt2, respectively. A spinning speed of 12 kHz was used, and the spectra were gathered after applying a single 0.5 μs to 15° pulse for both 7Li and 11B.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. The authors declare no competing financial interest.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. A. L. L. acknowledges the support of the Arnold and Mabel Beckman Foundation via a 2020 Arnold O. Beckman Postdoctoral Fellowship in Chemical Sciences. F. A. L. L. would also like to thank Andrew J. Martinolich for his guidance and insightful scientific input. The NEB computations presented here were conducted in the Resnick High Performance Computing Center, a facility supported by Resnick Sustainability Institute at the California Institute of Technology. K. A. S. acknowledges support from the David and Lucile Packard Foundation.References
- J. C. Bachman, et al., Inorganic Solid-State Electrolytes for Lithium Batteries: Mechanisms and Properties Governing Ion Conduction, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- N. Kamaya, et al., A lithium superionic conductor, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- P. Adeli, et al., Boosting solid-state diffusivity and conductivity in lithium superionic argyrodites by halide substitution, Angew. Chem., 2019, 131, 8773–8778 CrossRef.
- Y. Seino, T. Ota, K. Takada, A. Hayashi and M. Tatsumisago, A sulphide lithium super ion conductor is superior to liquid ion conductors for use in rechargeable batteries, Energy Environ. Sci., 2014, 7, 627–631 RSC.
- Y. Zhu, X. He and Y. Mo, First principles study on electrochemical and chemical stability of solid electrolyte–electrode interfaces in all-solid-state Li-ion batteries, J. Mater. Chem. A, 2016, 4, 3253–3266 RSC.
- W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder, Interface stability in solid-state batteries, Chem. Mater., 2016, 28, 266–273 CrossRef CAS.
- K. Kerman, A. Luntz, V. Viswanathan, Y.-M. Chiang and Z. Chen, Review—practical challenges hindering the development of solid state li ion batteries, J. Electrochem. Soc., 2017, 164, A1731 CrossRef CAS.
- S. Wenzel, et al., Direct observation of the interfacial instability of the fast ionic conductor Li10GeP2S12 at the lithium metal anode, Chem. Mater., 2016, 28, 2400–2407 CrossRef CAS.
- Y. Zhu, X. He and Y. Mo, Origin of outstanding stability in the lithium solid electrolyte materials: insights from thermodynamic analyses based on first-principles calculations, ACS Appl. Mater. Interfaces, 2015, 7, 23685–23693 CrossRef CAS PubMed.
- S. Wenzel, S. J. Sedlmaier, C. Dietrich, W. G. Zeier and J. Janek, Interfacial reactivity and interphase growth of argyrodite solid electrolytes at lithium metal electrodes, Solid State Ion, 2018, 318, 102–112 CrossRef CAS.
- Z. Ding, J. Li, J. Li and C. An, Review—interfaces: key issue to be solved for all solid-state lithium battery technologies, J. Electrochem. Soc., 2020, 167, 070541 CrossRef.
- S. Wang, et al., Interfacial challenges for all-solid-state batteries based on sulfide solid electrolytes, J. Materiomics, 2021, 7, 209–218 CrossRef.
- A. D. Sendek, G. Cheon, M. Pasta and E. J. Reed, Quantifying the Search for Solid Li-Ion Electrolyte Materials by Anion: A Data-Driven Perspective, J. Phys. Chem. C, 2020, 124, 8067–8079 CrossRef CAS.
- F. Ren, et al., Accelerated discovery of metallic glasses through iteration of machine learning and high-throughput experiments, Sci. Adv., 2018, 4, eaaq1566 CrossRef PubMed.
- K. Tran and Z. W. Ulissi, Active learning across intermetallics to guide discovery of electrocatalysts for CO2 reduction and H2 evolution, Nat. Catal., 2018, 1, 696–703 CrossRef CAS.
- S. Lu, et al., Accelerated discovery of stable lead-free hybrid organic-inorganic perovskites via machine learning, Nat. Commun., 2018, 9, 3405 CrossRef PubMed.
- D. Xue, et al., Accelerated search for materials with targeted properties by adaptive design, Nat. Commun., 2016, 7, 11241 CrossRef CAS PubMed.
- A. D. Sendek, et al., Holistic computational structure screening of more than 12000 candidates for solid lithium-ion conductor materials, Energy Environ. Sci., 2017, 10, 306–320 RSC.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine learning for molecular and materials science, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- Y. Liu, T. Zhao, W. Ju and S. Shi, Materials discovery and design using machine learning, J. Materiomics, 2017, 3, 159–177 CrossRef.
- A. Ziletti, D. Kumar, M. Scheffler and L. M. Ghiringhelli, Insightful classification of crystal structures using deep learning, Nat. Commun., 2018, 9, 2775 CrossRef PubMed.
- O. Isayev, et al., Universal fragment descriptors for predicting properties of inorganic crystals, Nat. Commun., 2017, 8, 15679 CrossRef CAS PubMed.
- K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Quantum-chemical insights from deep tensor neural networks, Nat. Commun., 2017, 8, 13890 CrossRef PubMed.
- L. Ward, et al., Matminer: an open source toolkit for materials data mining, Comput. Mater. Sci., 2018, 152, 60–69 CrossRef.
- L. Himanen, et al., DScribe: library of descriptors for machine learning in materials science, Comput. Phys. Commun., 2020, 247, 106949 CrossRef CAS.
- Y. Juan, Y. Dai, Y. Yang and J. Zhang, Accelerating materials discovery using machine learning, J. Mater. Sci. Technol., 2021, 79, 178–190 CrossRef.
- K. Suzuki, et al., Fast material search of lithium ion conducting oxides using a recommender system, J. Mater. Chem. A, 2020, 8, 11582–11588 RSC.
- Z. Wang, et al., Harnessing artificial intelligence to holistic design and identification for solid electrolytes, Nano Energy, 2021, 89, 106337 CrossRef CAS.
- M. Zhong, et al., Accelerated discovery of CO2 electrocatalysts using active machine learning, Nature, 2020, 581, 178–183 CrossRef CAS PubMed.
- Z. Wang, H. Zhang and J. Li, Accelerated discovery of stable spinels in energy systems via machine learning, Nano Energy, 2021, 81, 105665 CrossRef CAS.
- R. Yuan, et al., Accelerated discovery of large electrostrains in BaTiO3-based piezoelectrics using active learning, Adv. Mater., 2018, 30, 1702884 CrossRef PubMed.
- J. Li, et al., Accelerated discovery of high-strength aluminum alloys by machine learning, Commun. Mater., 2020, 1, 1–10 CrossRef.
- K. T. Butler, F. Oviedo and P. Canepa, Machine Learning in Materials Science, American Chemical Society, 2022, vol. 29 Search PubMed.
- Y. Zhang, et al., Unsupervised discovery of solid-state lithium ion conductors, Nat. Commun., 2019, 10, 1–7 CrossRef PubMed.
- Y. Liu, Q. Zhou and G. Cui, Machine learning boosting the development of advanced lithium batteries, Small Methods, 2021, 5, 2100442 CrossRef CAS PubMed.
- G. Forestier and C. Wemmert, Semi-supervised learning using multiple clusterings with limited labeled data, Inf. Sci., 2016, 361–362, 48–65 CrossRef.
- V. Thangadurai, S. Narayanan and D. Pinzaru, Garnet-type solid-state fast Li ion conductors for Li batteries: critical review, Chem. Soc. Rev., 2014, 43, 4714–4727 RSC.
- P. Gorai, T. Famprikis, B. Singh, V. Stevanović and P. Canepa, Devil is in the defects: electronic conductivity in solid electrolytes, Chem. Mater., 2021, 33, 7484–7498 CrossRef CAS.
- J. E. van Engelen and H. H. Hoos, A survey on semi-supervised learning, Mach. Learn., 2020, 109, 373–440 CrossRef.
- K. T. Schütt, et al., SchNet: a continuous-filter convolutional neural network for modeling quantum interactions, Adv. Neural Inf. Process. Syst., 2017, 30, 992–1002, DOI:10.48550/arXiv.1706.08566.
- N. Artrith and A. Urban, An implementation of artificial neural-network potentials for atomistic materials simulations: performance for TiO2, Comput. Mater. Sci., 2016, 114, 135–150 CrossRef CAS.
- S. Adams and R. P. Rao, in In structure and bonding, Bond Valences, ed. I. D. Brown and K. R. Poeppelmeier, Springer, Berlin, Heidelberg, 2014, vol. 158 Search PubMed.
- K. Hansen, et al., Machine learning predictions of molecular properties: accurate many-body potentials and nonlocality in chemical space, J. Phys. Chem. Lett., 2015, 6, 2326–2331 CrossRef CAS PubMed.
- M. A. Butler and D. S. Ginley, Prediction of flatband potentials at semiconductor–electrolyte interfaces from atomic electronegativities, J. Electrochem. Soc., 1978, 125, 228 CrossRef CAS.
- B. He, et al., CAVD, towards better characterization of void space for ionic transport analysis, Sci. Data, 2020, 7, 153 CrossRef CAS PubMed.
- L. Ward, et al., Including crystal structure attributes in machine learning models of formation energies via Voronoi tessellations, Phys. Rev. B, 2017, 96, 024104 CrossRef.
- S. P. Ong, et al., Python Materials Genomics (pymatgen): a robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- A. M. Deml, R. O’Hayre, C. Wolverton and V. Stevanović, Predicting density functional theory total energies and enthalpies of formation of metal-nonmetal compounds by linear regression, Phys. Rev. B, 2016, 93, 085142 CrossRef.
- P. P. Ewald, Die Berechnung optischer und elektrostatischer Gitterpotentiale, Ann. Phys., 1921, 369, 253–287 CrossRef.
- K. Choudhary, et al., The joint automated repository for various integrated simulations (JARVIS) for data-driven materials design, npj Comput. Mater., 2020, 6, 1–13 CrossRef.
- B. Meredig, et al., Combinatorial screening for new materials in unconstrained composition space with machine learning, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094104 CrossRef.
- T. L. Pham, et al., Machine learning reveals orbital interaction in materials, Sci. Technol. Adv. Mater., 2017, 18, 756–765 CrossRef PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Fast and accurate modeling of molecular atomization energies with machine learning, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- F. Faber, A. Lindmaa, O. A. von Lilienfeld and R. Armiento, Crystal structure representations for machine learning models of formation energies, Int. J. Quantum Chem., 2015, 115, 1094–1101 CrossRef CAS.
- S. V. Krivovichev, Structural complexity of minerals: information storage and processing in the mineral world, Mineral. Mag., 2013, 77, 275–326 CrossRef CAS.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, A general-purpose machine learning framework for predicting properties of inorganic materials, npj Comput. Mater., 2016, 2, 1–7 CrossRef.
- J. H. Ward, Hierarchical grouping to optimize an objective function, J. Am. Stat. Assoc., 1963, 58, 236–244 CrossRef.
- V. Fung, J. Zhang, E. Juarez and B. G. Sumpter, Benchmarking graph neural networks for materials chemistry, npj Comput. Mater., 2021, 7, 1–8 CrossRef.
- X. He, Y. Zhu and Y. Mo, Origin of fast ion diffusion in super-ionic conductors, Nat. Commun., 2017, 8, 15893 CrossRef CAS PubMed.
- W. Sun, et al., The thermodynamic scale of inorganic crystalline metastability, Sci. Adv., 2016, 2, e1600225 CrossRef PubMed.
- Electronic Structure. https://docs.materialsproject.org/methodology/materials-methodology/electronic-structure.
- P. Vinatier, M. Ménétrier and A. Levasseur, Structure and ionic conduction in lithium thioborate glasses and crystals, Phys. Chem. Glas, 2003, 44, 135–142 CAS.
- A. D. Sendek, et al., Combining superionic conduction and favorable decomposition products in the crystalline lithium–boron–sulfur system: a new mechanism for stabilizing solid li-ion electrolytes, ACS Appl. Mater. Interfaces, 2020, 12, 37957–37966 CrossRef CAS PubMed.
- F. Bianchini, H. Fjellvåg and P. Vajeeston, A first-principle investigation of the Li diffusion mechanism in the super-ionic conductor lithium orthothioborate Li3BS3 structure, Mater. Lett., 2018, 219, 186–189 CrossRef CAS.
- H. Park, S. Yu and D. J. Siegel, Predicting charge transfer stability between sulfide solid electrolytes and Li metal anodes, ACS Energy Lett., 2021, 6, 150–157 CrossRef CAS.
- P. Vinatier, P. Gravereau, M. Ménétrier, L. Trut and A. Levasseur, Li3BS3, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1994, 50, 1180–1183 CrossRef.
- L. Zhang, et al., Lithium lanthanum titanate perovskite as an anode for lithium ion batteries, Nat. Commun., 2020, 11, 3490 CrossRef CAS PubMed.
- A. G. Belous, G. N. Novitskaya, S. V. Polyanetskaya and Y. I. Gornikov, Investigation into complex oxides of La2/3−xLi3xTiO3 composition, Izv Akad Nauk SSSR Neorg Mater, 1987, 23, 470–472 CAS.
- T. Kimura, et al., Characteristics of a Li3BS3 thioborate glass electrolyte obtained via a mechanochemical process, ACS Appl. Energy Mater., 2022, 5, 1421–1426 CrossRef CAS.
- L. Zhou, N. Minafra, W. G. Zeier and L. F. Nazar, Innovative approaches to Li-argyrodite solid electrolytes for all-solid-state lithium batteries, Acc. Chem. Res., 2021, 54, 2717–2728 CrossRef CAS PubMed.
- W. Zhao, J. Yi, P. He and H. Zhou, Solid-state electrolytes for lithium-ion batteries: fundamentals, challenges and perspectives, Electrochem. Energy Rev., 2019, 2, 574–605 CrossRef CAS.
- V. Lacivita, N. Artrith and G. Ceder, Structural and compositional factors that control the Li-ion conductivity in LIPON electrolytes, Chem. Mater., 2018, 30, 7077–7090 CrossRef CAS.
- P. Knauth, Inorganic solid Li ion conductors: an overview, Solid State Ion, 2009, 180, 911–916 CrossRef CAS.
- D. Larink, H. Eckert and S. W. Martin, Structure and ionic conductivity in the mixed-network former chalcogenide glass system [Na2S]2/3[(B2S3)x(P2S5)1−x]1/3, J. Phys. Chem. C, 2012, 116, 22698–22710 CrossRef CAS.
- S.-J. Hwang, et al., Structural study of xNa2S + (1 − x)B2S3 glasses and polycrystals by multiple-quantum MAS NMR of 11B and 23Na, J. Am. Chem. Soc., 1998, 120, 7337–7346 CrossRef CAS.
- K. Kaup, et al., A lithium oxythioborosilicate solid electrolyte glass with superionic conductivity, Adv. Energy Mater., 2020, 10, 1902783 CrossRef CAS.
- B. Curtis, C. Francis, S. Kmiec and S. W. Martin, Investigation of the short range order structures in sodium thioborosilicate mixed glass former glasses, J. Non-Cryst. Solids, 2019, 521, 119456 CrossRef CAS.
- Y. Seino, et al., Synthesis and electrochemical properties of Li2S–B2S3–Li4SiO4, Solid State Ion, 2006, 177, 2601–2603 CrossRef CAS.
- K. Kaup, A. Assoud, J. Liu and L. F. Nazar, Fast Li-Ion Conductivity in Superadamantanoid Lithium Thioborate Halides, Angew. Chem., Int. Ed., 2021, 60, 6975–6980 CrossRef CAS PubMed.
- N. Suzuki, et al., Theoretical and experimental studies of KLi6TaO6 as a Li-ion solid electrolyte, Inorg. Chem., 2021, 60, 10371–10379 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- P. Giannozzi, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, et al., Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Dal Corso, Pseudopotentials periodic table: from H to Pu, Comput. Mater. Sci., 2014, 95, 337–350 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ee03499a |
| ‡ Co-authors with equal contribution. |
| This journal is © The Royal Society of Chemistry 2023 |