Nonlinear plexcitons: excitons coupled with plasmons in two-photon absorption†
Yichuan
Chen
,
Yuqing
Cheng
 and
Mengtao
Sun
and
Mengtao
Sun
 *
*
School of Mathematics and Physics, Beijing Advanced Innovation Center for Materials Genome Engineering, University of Science and Technology Beijing, Beijing 100083, China. E-mail: mengtaosun@ustb.edu.cn
First published on 11th April 2022
Abstract
The nonlinear optical properties of a D–A (donor–acceptor) conjugated organic molecule with polythiophene (PT) as the donor and indene-C60 bisadduct (IC60BA) as the acceptor are theoretically investigated, which exhibits a large two-photon absorption (TPA) cross-section up to 8000 GM at the wavelength of 780 nm. Combining surface plasmon resonances (SPRs) with nonlinear optics, nonlinear properties can be strongly enhanced. In this paper, an appropriate nonlinear plexciton method by the coupling of Au@Ag nanorods and an Ag film is designed, in which the TPA properties of the PT:IC60BA complex can be increased by 106 times. The angle dependence on polarization and incidence is investigated to obtain the maximum of plasmonic enhancement. Our results emphasize the physical mechanism of nonlinear plexcitons and provide a feasible method to improve the nonlinear properties of organic solar cell materials.
1. Introduction
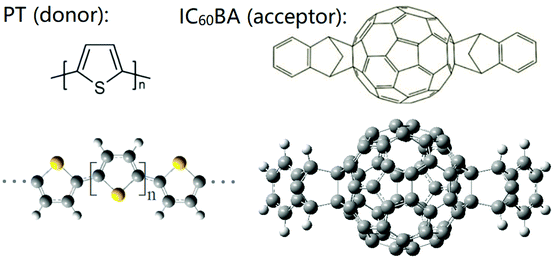
The development of ultrafast lasers promotes the research of nonlinear optics.1–7 Two-photon absorption (TPA) is a nonlinear absorption process.8 The discussion of TPA can be traced back to Göppert-Mayer's doctoral thesis in the 1930s,9 and practical experiments were carried out in the 1960s.10 Because of its high photon density and low light damage, TPA has wide applications in optical data storage,11 microprocessors,12,13 photodynamic therapy,14,15etc. However, TPA effects are usually weak as the reaction probability depends on square irradiance, which limits its optical performance. Recently, researchers combined the subwavelength electromagnetic field confinement properties of surface plasmon resonances (SPRs) with nonlinear optics, enabling weak nonlinear effects to be enhanced in micro–nano structures, and forming a new research field, named nonlinear surface plasmonic photonics.16 The localized electric field associated with localized surface plasmon resonances (LSPRs) can be intense enough to strongly modify the nonlinear properties near the surface of metallic nanoparticles. A prime instance is surface enhanced Raman scattering (SERS), where plasmonic excitations can enhance the inherently weak Raman scattering by orders of magnitude, even allowing for single-molecule detection.17 The plasmonic method can also work for enhancing the TPA response of molecules. Therefore, a plausible conjecture lies in the plasmonic-enhanced TPA properties of solar cells.Applying TPA to solar cells is promising because it offers an attractive possibility to overcome the Shockley–Queisser limit.18 Thus, it has generated a demand for developing solar cell materials with large TPA cross-sections. The research of organic TPA materials is the frontier of nonlinear optical materials.19,20 Organic molecules with conjugated structures are more prone to polarization in solar light, and their broad-spectrum absorption and efficient light-harvesting satisfy the TPA process.21–23 Therefore, for the selection of TPA organic solar cell (OSC) materials, fullerenes and their derivatives are appropriate. A polythiophene:indene-C60 bisadduct (PT:IC60BA) donor–acceptor (D–A) complex with polythiophene (PT) as the donor and indene-C60 bisadduct (IC60BA) as the acceptor was selected in our theoretical study. Such bulk-heterojunction polymer OSCs have attracted more and more attention owing to their high carrier mobility and strong absorption in the visible region.24,25Fig. 1 shows the molecular structures of PT and IC60BA. Considering their distinct conjugated systems, especially IC60BA as a fullerene derivative, the PT:IC60BA complex may exhibit significant nonlinear optical properties.
Constrained by unobvious optical nonlinearity, direct application of TPA materials to solar cells performs poorly. How to improve the nonlinear properties of materials has become a hot issue.26 One such concept is intermediate band (IB) solar cells, in which the TPA process involves a partially occupied IB that works as a “stepping stone” for optical transitions.27 IB solar cells can be achieved through quantum dots and highly mismatched alloys.28–30 However, it is challenging to establish an IB within a semiconductor material and the experimental photoelectric conversion efficiency is relatively low.31 In order to broadly and efficiently enhance optical nonlinearities, SPRs may be a feasible way. SPRs arise from the coherent oscillations of electrons near the surface of noble metals.32,33 The coupling of plasmons with excitons and the formation of plexcitons typically cause the enhancement of molecular properties.34 Employing the plasmonic effect to enhance molecular nonlinear properties, such as nonlinear plexcitons, may be more prominent in solar cells. Fofang et al. reported the nonlinear mechanism of plexcitons by studying the exciton–plasmon coupling in J-aggregate-Au nanoshell complexes.35 Manjavacas et al. theoretically investigated the nonlinear effects of plexcitons under strong optical pumping.36 Ovchinnikov et al. experimentally observed the nonlinear absorption enhancement of methylene blue based on the plasmonic coupling of Au/SiO2 core–shell nanoparticles.37 Furthermore, many studies have proven that nonlinear plasmonic effects are more likely to induce robust electric field enhancement.38–40 These studies demonstrate the feasibility and prospect of applying the plasmonic-enhanced two-photon absorption (PETPA) method to solar cells, where the TPA properties of photoactive materials may be strongly enhanced though nonlinear plexcitons.
In this work, we theoretically demonstrate the excellent TPA behavior of a PT:IC60BA D–A structure. The photoinduced CT and electron–hole coherence of different excitation processes in TPA are studied. A reasonable PETPA method is employed based on the theoretical framework. Through the plasmonic coupling between Au@Ag core–shell nanorods and an Ag metal film, the enhancement factor can reach up to the order of 106, which indicates that the TPA property in the OCS material is increased by 106 times. Furthermore, the incident angle or polarization direction is adjusted and the results show that the incident light at a small angle can obtain the most significant plasmonic enhancement. Our research provides theoretical guidance for designing high-efficiency solar cells based on nonlinear plexcitons.
2. Methods
All quantum calculations were performed using Gaussian 16. The ground state geometries of monomer and complex structures were optimized using density functional theory (DFT) with the B3LYP functional and the 6-31 g(d) basis set.41 The electronic transitions of structures were investigated with time-dependent DFT (TDDFT), the CAM-B3LYP functional, and the 6-31 g(d) basis set.42 Multiwfn program was used to draw the maps of the transition density matrix (TDM) and charge density difference (CDD).43Two-photon spectroscopy was studied visually by the program developed by Sun and Mu et al.44,45 The full data are obtained from the Gaussian package. The TPA cross-section can be defined as:
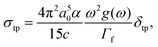 | (1) |
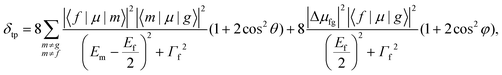 | (2) |
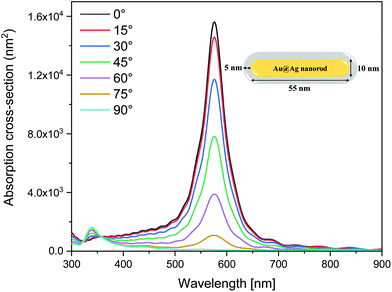
The plasmonic-enhanced TPA and electric field distribution of the nanostructure were simulated by the finite-difference time-domain (FDTD) method. The alloy nanorod comprised an Ag shell with a thickness of 5 nm coated on an Au core with a length of 55 nm and a diameter of 10 nm. The thicknesses of the molecular layer and the Ag film are 1.5 nm and 40 nm, respectively, which are arranged on a conductive glass substrate composed of an indium tin oxide (ITO) film and SiO2. The schematic diagram is shown in Fig. 2. The dielectric constants of Au, Ag and ITO were taken from ref. 48, 49 and 50, respectively, and the dielectric constant of the molecular layer was calculated using the Vienna ab initio simulation package (VASP). More details on the FDTD simulations are available in the ESI.†
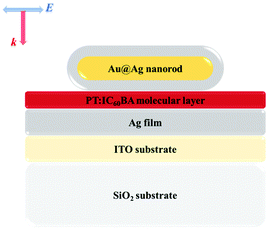 | ||
| Fig. 2 Schematic diagram of the plasmonic-enhanced TPA in OSCs, where the inset shows the initial light source orientation for all discussions in this paper. | ||
3. Results and discussion
The foundation of a solar cell material lies in its strong absorption in the visible region. Our previous work has discussed the linear optical performances of PT, IC60BA and their D–A structure in detail.51 The PT:IC60BA (n = 9) system composed of a PT molecule with a unit number (n) of nine and an IC60BA molecule can well represent the material's performance at the macro level.51 However, we noticed that, for the shorter molecular chain, the ground state structure of the complex is “semicircular”, which cannot represent the infinite length of the polymer, see the inset in Fig. 3(a). Therefore, we made an improvement by calculating the PT:IC60BA (n = 17) complex structure composed of one PT molecule with n = 17 and two IC60BA molecules, see the inset in Fig. 3(b). Their one-photon absorption (OPA) spectra are similar, proving that our calculations are correct, see Fig. 3. The absorption spectra show that the PT:IC60BA complex has a strong optical absorption from 400 to 500 nm, confirming its feasibility as a photoactive material. A weak redshift of the absorption peak for the longer chain is observed, which is explained in the ESI.†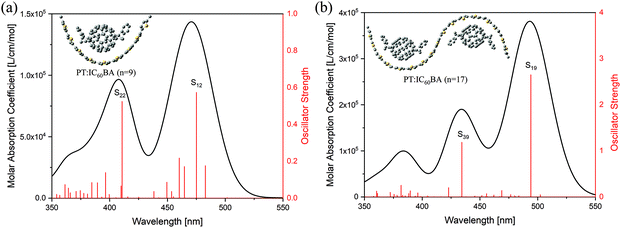 | ||
| Fig. 3 OPA spectra of (a) PT:IC60BA (n = 9) and (b) PT:IC60BA (n = 17), where the insets show the corresponding structures of the PT:IC60BA complex system. | ||
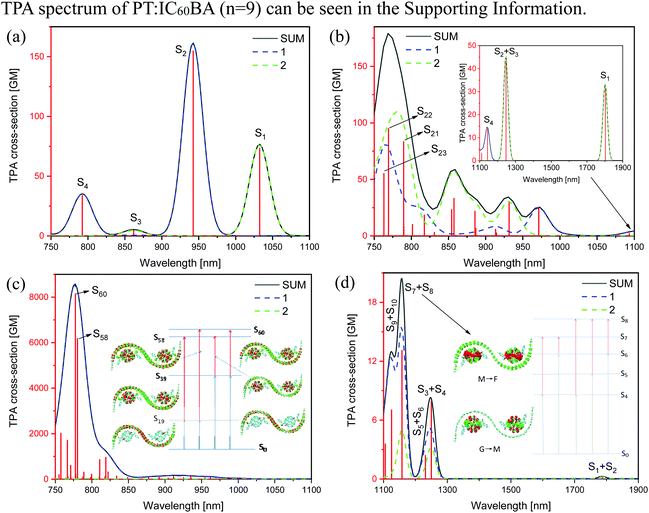
The fast and abundant electron transfer between molecules is particularly important for solar cells based on the D–A system. However, intermolecular CT excited states are generally weak in OPA, which significantly limits the efficiency of solar cells. In the process of TPA, the “three-state term” offers the opportunity for both efficient intermolecular CT and strong optical absorption, simultaneously. One of the origins of the nonlinear properties of PT and IC60BA has been demonstrated owing to the conjugated systems.52,53 To thoroughly explore the role of TPA in the PT:IC60BA D–A system, we investigated the TPA spectra of donor PT (n = 17) and acceptor IC60BA, respectively. Fig. 4(a) shows the TPA spectrum of the donor material. According to the characteristic of TPA, the excitation wavelength should be twice that of OPA. It can be seen that there are strong TPA excited states from 750 to 1000 nm, corresponding to S2 and S4 in the OPA spectrum, which are contributed from the “three-state terms” in eqn (2), where |〈f|μ|j〉|2|〈j|μ|g〉|2 and |Δμfg|2|〈f|μ|g〉|2 represent the “three state” and “two state” terms, respectively. Compared with the extremely weak absorption of S2 and S4 in the OPA spectrum,51 these excited states exhibit strong nonlinear optical properties in TPA. The near-infrared TPA cross-section of PT is consistent with previous reports.54–56Fig. 4(b) shows the TPA spectrum of the acceptor material, and the inset is the one in the long-wavelength region. The acceptor material has strong TPA response from 750 to 800 nm and the σmax value is 94 GM, which is similar to ref. 57. As a whole, the experimental and calculated TPA cross-sections of C60/C70 derivatives are in the range of 10−49–10−46 cm4 s per photon (1 GM = 10−50 cm4 s per photon).46,58,59 For S1 around 1800 nm, only a “one-step” transition is possible. Note that the S1 of IC60BA has a non-negligible TPA cross-section, which seems unreasonable, because with regard to the nonpolar molecule IC60BA,60 its permanent dipole moment is very small and S1 is weakly absorbing in the OPA spectrum.51 According to the “two-state term” formula |Δμfg|2|〈f|μ|g〉|2, its TPA cross-section of S1 should be small. In fact, IC60BA has a larger TPA cross-section in the short-wavelength region, see Fig. S2† in the ESI.† Although the short-wavelength TPA is strong, this is not the range of our study, and S1 is only a relatively strong peak in the wavelength range we observe. Fig. 4(c) shows that PT:IC60BA (n = 17) has a larger TPA cross-section up to 8000 GM compared with the bare IC60BA molecule from 750 to 850 nm, which mainly originates from the contributions of S58 and S60 around 780 nm. In the D–A system, the donor group, thiophene, is an effective “electron bridge” that increases the TPA cross-section.61,62 Moreover, the long-range excitation from the donor to acceptor could cause a huge TPA cross-section of the complex molecule.46 As shown in the inset of Fig. 4(c), S58 is the strong absorption by the “three-state terms” via two transition channels S0 → S19 → S58 and S0 → S39 → S58, and S60 is via two transition channels S0 → S19 → S60 and S0 → S39 → S60, respectively. Furthermore, the transitions from the ground state to the intermediate states are local excitation on thiophene, since almost all the electrons and holes are localized on the thiophene units (the red and green represent electrons and holes, respectively). For the transitions from the intermediate states to the final states, the maps of CDD show that electrons and holes are distributed on both the donor and acceptor, but it is difficult to analyze the degree of exciton delocalization, which will be discussed later. Fig. 4(d) shows the TPA spectrum of the complex in the region from 1100 to 1900 nm, which is mainly contributed from the acceptor, IC60BA. There are two near degenerate strong “three-state term” absorption peaks of S7 and S8, and their optical properties show the local excitation of IC60BA on the transitions from the ground state to the intermediate states; and on the transitions from the intermediate states to the final states, it is intermolecular CT. The TPA spectrum of PT:IC60BA (n = 9) can be seen in the ESI.†
The maps of CDD demonstrate the local excitation from the ground state to the intermediate states at S58 and S60 shown in Fig. 4(c), in which photoinduced excitons localized in the donor thiophene oligomer. In order to further reveal the degree of exciton delocalization, the TDM is employed, as shown in Fig. 5. It can be found that for the “three-state term” process at S58 and S60, the “first step” is the intramolecular local excitation. Electrons and holes form intense bound states due to the Coulomb interaction in adjacent units with larger exciton binding energy, which are typical Frenkel excitons. The large binding energy can facilitate light-harvesting.63 The “second step” is the intermolecular CT, which generates CT excitons. In general, CT excitons can cause large second-order nonlinear polarizabilities.64,65 These mixed Frenkel–CT excitons exhibit the properties of both types of contributing states: the Frenkel excitons provide a large oscillator strength, whereas the CT excitons cause a high sensitivity to the external electric field.65 Actually, hybridized Frenkel–CT exciton states have been used to analyze the TPA spectrum of the N,N-dimethylaminobenzylidene 1,3-indandione (DMABI) molecule.66,67 The S58 and S60 at around 780 nm can simultaneously satisfy the large TPA cross-section and efficient intermolecular CT. Therefore, applying SPRs to enhance the electric field at 780 nm can effectively improve the TPA performance and intermolecular CT of the PT:IC60BA material, which is of great significance to OCS based on this material. More details about TDM and CDD can be seen in the ESI.†
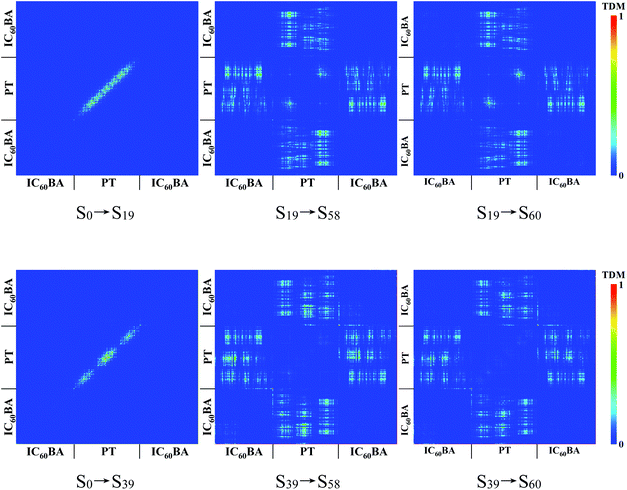 | ||
| Fig. 5 TDMs of different transition channels. The scale bar stands for the strength of electron–hole coherence. | ||
The PT:IC60BA complex molecule is known to have a huge nonlinear response at 780 nm. In a nonlinear optical process such as second harmonic generation (SHG),68 a nanometal absorbs two low-energy photons resulting in a near-field enhancement with the corresponding frequency, and simultaneously generates a high-energy photon with twice the energy, forming a dual-enhancement of the fundamental and double frequencies. This is a multiple SPR effect,69 and the enhancement factor (EF) can be estimated as70
| EF = |Min|2|Msc|1, | (3) |
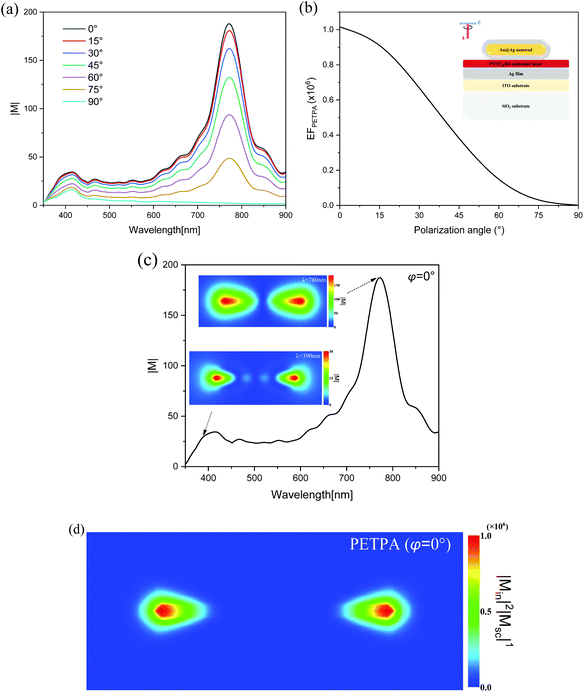
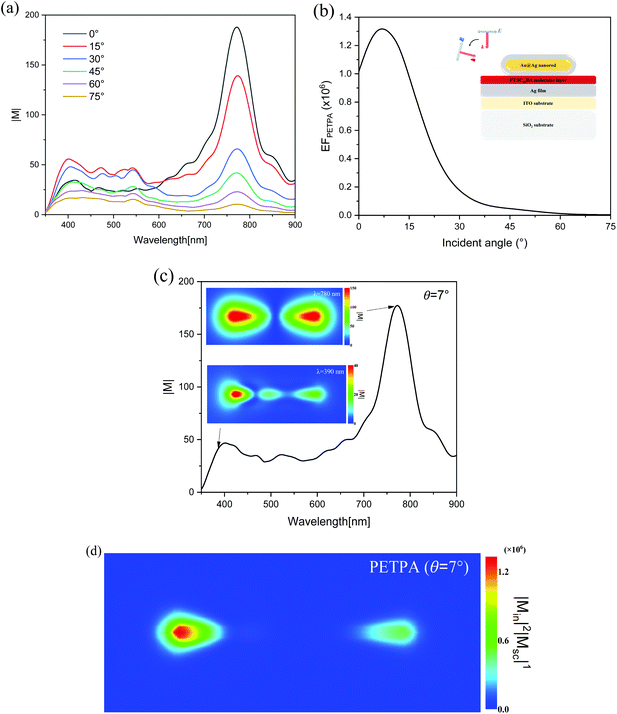
Fig. 7(a) shows the plasmonic-enhanced electric fields with different φ values in the molecular layer. There are two strong SPR peaks corresponding to the transverse and longitudinal modes of the Au@Ag nanorod at 390 nm and 780 nm, both of which decrease as the φ value increases. The strong electric field at the fundamental and double frequencies can significantly enhance the TPA in the molecular layer. However, the absorption spectra of the single Au@Ag nanorod shows that the transverse resonance will be enhanced as the φ value increases, which is different from the results in Fig. 7(a). Tcherniak et al. reported that hot electron–hole pairs can also create surface plasmons causing the transverse and longitudinal modes to be orthogonal to each other.73Fig. 7(b) shows the EF of PETPA versus φ. When φ = 0°, the strongest EF can be obtained, and as the φ value increases, the intensity of the EF decreases rapidly. When the polarization direction is perpendicular to the nanorod (φ = 90°), the enhanced TPA is almost invisible. Fig. 7(c) shows the enhanced electric field when φ = 0°, in which the maximum EF is obtained. The insets in Fig. 7(c) show the electric field distributions in the molecular layer at 390 and 780 nm. It can be seen that for the fundamental and double frequencies, the plasmons localized at both ends of the nanorod exhibit dipole behavior. Fig. 7(d) shows the distribution of PETPA in the molecular layer. The maximum EF at both ends of the nanorod can reach the order of 106, which indicates that the TPA properties can be enhanced about 106 times.
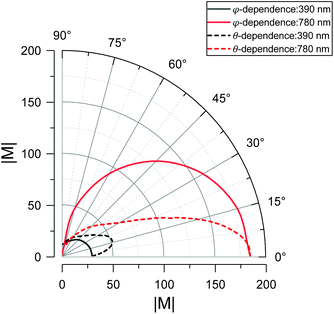
It is known that the increase of the polarization angle will lead to an almost linear decrease of the EF in the molecule. When φ = 0°, we change the incident angle θ, and the enhanced electric fields with different θ values are shown in Fig. 8(a). At the fundamental frequency of 780 nm, the electric field intensity decreases as the θ value increases. However, at the double frequency of 390 nm, as the θ value increases, the electric field intensity increases at the small θ value. Fig. 8(b) shows the relationship between the EF and θ in the molecular layer. It can be seen that the EF increases first and then decreases, reaching the maximum value around θ = 7°. Also, when changing θ, the overall decreasing trend of the EF is steeper than changing φ. For the maximum PETPA obtained when θ = 7° and φ = 0°, the electric field distributions of the fundamental and double frequencies are studied, as shown in the insets of Fig. 8(c). At 780 nm, a slight increase in the incident angle does not result in a drastic decrease for the enhanced electric field. At 390 nm, the electric field distribution varies greatly, and an asymmetric mode appears when the θ value is increased. This is because the change of the incident angle will cause the symmetry to be broken, and there is a decaying oscillation process when the wave vector propagates along the long axis, even the formation of stationary waves. Such a robust plasmon-aggregation behavior at one end usually exhibits better performance and broader applications.74,75 According to eqn (3), the EF when θ = 7° and φ = 0° is about 1.3 times stronger than that when θ = 0° and φ = 0° in the molecular layer, and the PETPA distribution also exhibits substantial agminated enhancement at one end, as shown in Fig. 8(d). Note that there is another configuration for increasing the incident angle while keeping the polarization angle and rotating the incident light around the longitudinal axis of the nanorod, which can be seen in Fig. S5 in the ESI.†
It is known that the properties of the coupling structure depend greatly on the angle of the light source, but the extent of dependence on different parameters is indefinite, such as the influence on the fundamental and double frequencies, and the dependence of the polarization and incident angles. To solve this, we compared the extent of angle dependence in polar coordinates. Fig. 9 shows the φ/θ dependence of the fundamental and double frequencies, and the curvature of the arc can indicate the dependence extent. For the fundamental frequency (red), the curvature of the dotted line is larger than the solid line, which means that θ influences the electric field more at the fundamental frequency. For the double frequency (black), the increase of θ will lead to the increase of the electric field, reaching the maximum at 15°. When the θ value increases continuously, the electric field will decrease rapidly compared with φ changes.
4. Conclusion
TPA spectroscopy analyses suggest that a PT:IC60BA complex has a large TPA cross-section. Through the coupling of Au@Ag nanorods and an Ag film, the EF of PETPA in the molecular layer can reach the order of 106, which means that its TPA properties can be increased by 106 times. Studies on the polarization and incident angle dependence show that the small incident angle can result in a stronger nonlinear plasmonic enhancement. Our results focus on the physical mechanism of nonlinear plexcitons and provide theoretical guidance for the plasmonic-enhanced nonlinear properties of OSC materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (91436102 and 11374353) and the Fundamental Research Funds for the Central Universities (06500067).References
- L. Cui, S. Zhu and M. Sun, External Electric Field Manipulating Sequential and Super-Exchange Charge Transfer in Donor-Bridge-Acceptor System in Two-Photon Absorption, Phys. E, 2021, 134, 114840 CrossRef CAS.
- Y. Gong, G.-L. Hou, X. Bi, N. Kuthirummal, A. A. Teklu, J. Koenemann, N. Harris, P. Wei, K. Devera and M. Hu, Enhanced Two-Photon Absorption in Two Triphenylamine-Based All-Organic Compounds, J. Phys. Chem. A, 2021, 125, 1870–1879 CrossRef CAS PubMed.
- A. Farenbruch, D. Fröhlich, D. Yakovlev and M. Bayer, Two-Photon Absorption and Second Harmonic Generation of 1s Para-and Orthoexcitons in Cu2o Coupled by a Magnetic Field, Phys. Rev. B, 2020, 102, 115203 CrossRef CAS.
- M. Kauranen and A. V. Zayats, Nonlinear Plasmonics, Nat. Photonics, 2012, 6, 737–748 CrossRef CAS.
- N. B. Grosse, J. Heckmann and U. Woggon, Nonlinear Plasmon-Photon Interaction Resolved by K-Space Spectroscopy, Phys. Rev. Lett., 2012, 108, 136802 CrossRef PubMed.
- S. Palomba and L. Novotny, Nonlinear Excitation of Surface Plasmon Polaritons by Four-Wave Mixing, Phys. Rev. Lett., 2008, 101, 056802 CrossRef PubMed.
- M. Jablan, Quasiclassical Nonlinear Plasmon Resonance in Graphene, Phys. Rev. B, 2020, 101, 085424 CrossRef CAS.
- M. Rumi and J. W. Perry, Two-Photon Absorption: An Overview of Measurements and Principles, Adv. Opt. Photonics, 2010, 2, 451–518 CrossRef CAS.
- M. Göppert-Mayer, Über Elementarakte Mit Zwei Quantensprüngen, Ann. Phys., 1931, 401, 273–294 CrossRef.
- W. K. C. Garrett and W. Kaiser, Two-Photon Excitation in Caf2: Eu2+, Phys. Rev. Lett, 1961, 7, 229–231 CrossRef.
- J. Lott, C. Ryan, B. Valle, J. R. Johnson III, D. A. Schiraldi, J. Shan, K. D. Singer and C. Weder, Two–Photon 3d Optical Data Storage Via Aggregate Switching of Excimer–Forming Dyes, Adv. Mater., 2011, 23, 2425–2429 CrossRef CAS PubMed.
- Z. Giedraityte, M. Tuomisto, M. Lastusaari and M. Karppinen, Three-and Two-Photon Nir-to-Vis (Yb, Er) Upconversion from Ald/Mld-Fabricated Molecular Hybrid Thin Films, ACS Appl. Mater. Interfaces, 2018, 10, 8845–8852 CrossRef CAS PubMed.
- Y. Chen and M. Sun, Two-Dimensional Ws2/Mos2 Heterostructures: Properties and Applications, Nanoscale, 2021, 13, 5594–5619 RSC.
- T. Rajh, N. M. Dimitrijevic, M. Bissonnette, T. Koritarov and V. Konda, Titanium Dioxide in the Service of the Biomedical Revolution, Chem. Rev., 2014, 114, 10177–10216 CrossRef CAS PubMed.
- F. Bolze, S. Jenni, A. Sour and V. Heitz, Molecular Photosensitisers for Two-Photon Photodynamic Therapy, Chem. Commun., 2017, 53, 12857–12877 RSC.
- J. Shi, Q. Guo, Z. Shi, S. Zhang and H. Xu, Nonlinear Nanophotonics Based on Surface Plasmon Polaritons, Appl. Phys. Lett., 2021, 119, 130501 CrossRef CAS.
- B. Sharma, R. R. Frontiera, A.-I. Henry, E. Ringe and R. P. Van Duyne, Sers: Materials, Applications, and the Future, Mater. Today, 2012, 15, 16–25 CrossRef CAS.
- A. Luque and A. Martí, The Intermediate Band Solar Cell: Progress toward the Realization of an Attractive Concept, Adv. Mater., 2010, 22, 160–174 CrossRef CAS PubMed.
- M. Albota, et al., Design of Organic Molecules with Large Two-Photon Absorption Cross Sections, Science, 1998, 281, 1653–1656 CrossRef CAS PubMed.
- O. Varnavski, X. Yan, O. Mongin, M. Blanchard-Desce and T. Goodson, Strongly Interacting Organic Conjugated Dendrimers with Enhanced Two-Photon Absorption, J. Phys. Chem. C, 2007, 111, 149–162 CrossRef CAS.
- X. Li, Z. Li and Y.-W. Yang, Tetraphenylethylene-Interweaving Conjugated Macrocycle Polymer Materials as Two-Photon Fluorescence Sensors for Metal Ions and Organic Molecules, Adv. Mater., 2018, 30, 1800177 CrossRef PubMed.
- T. G. Allen, et al., Highly Conjugated, Fused-Ring, Quadrupolar Organic Chromophores with Large Two-Photon Absorption Cross-Sections in the near-Infrared, J. Phys. Chem. A, 2020, 124, 4367–4378 CrossRef CAS PubMed.
- N. Tsuboya, R. Hamasaki, M. Ito, M. Mitsuishi, T. Miyashita and Y. Yamamoto, Nonlinear Optical Properties of Novel Fullerene–Ferrocene Hybrid Molecules, J. Mater. Chem., 2003, 13, 511–513 RSC.
- G. Zhao, Y. He and Y. Li, 6.5% Efficiency of Polymer Solar Cells Based on Poly(3-Hexylthiophene) and Indene-C60 Bisadduct by Device Optimization, Adv. Mater., 2010, 22, 4355–4358 CrossRef CAS PubMed.
- S. Nam, D. Khim, G. T. Martinez, A. Varambhia, P. D. Nellist, Y. Kim, T. D. Anthopoulos and D. D. C. Bradley, Significant Performance Improvement in N-Channel Organic Field-Effect Transistors with C60:C70 Co-Crystals Induced by Poly(2-Ethyl-2-Oxazoline) Nanodots, Adv. Mater., 2021, 33, 2100421 CrossRef CAS PubMed.
- R. Abbassi, A. Abbassi, M. Jemli and S. Chebbi, Identification of Unknown Parameters of Solar Cell Models: A Comprehensive Overview of Available Approaches, Renewable Sustainable Energy Rev., 2018, 90, 453–474 CrossRef.
- N. Ahsan, N. Miyashita, M. M. Islam, K. M. Yu, W. Walukiewicz and Y. Okada, Two-Photon Excitation in an Intermediate Band Solar Cell Structure, Appl. Phys. Lett., 2012, 100, 172111 CrossRef.
- A. Martí, E. Antolín, C. R. Stanley, C. D. Farmer, N. López, P. Díaz, E. Cánovas, P. G. Linares and A. Luque, Production of Photocurrent Due to Intermediate-to-Conduction-Band Transitions: A Demonstration of a Key Operating Principle of the Intermediate-Band Solar Cell, Phys. Rev. Lett., 2006, 97, 247701 CrossRef PubMed.
- N. López, L. A. Reichertz, K. M. Yu, K. Campman and W. Walukiewicz, Engineering the Electronic Band Structure for Multiband Solar Cells, Phys. Rev. Lett., 2011, 106, 028701 CrossRef PubMed.
- T. Li and M. Dagenais, Non-Resonant Below-Bandgap Two-Photon Absorption in Quantum Dot Solar Cells, Appl. Phys. Lett., 2015, 106, 171101 CrossRef.
- Y. Okada, et al., Intermediate Band Solar Cells: Recent Progress and Future Directions, Appl. Phys. Rev., 2015, 2, 021302 Search PubMed.
- T. Klar, M. Perner, S. Grosse, G. Von Plessen, W. Spirkl and J. Feldmann, Surface-Plasmon Resonances in Single Metallic Nanoparticles, Phys. Rev. Lett., 1998, 80, 4249 CrossRef CAS.
- O. Nicoletti, F. de La Peña, R. K. Leary, D. J. Holland, C. Ducati and P. A. Midgley, Three-Dimensional Imaging of Localized Surface Plasmon Resonances of Metal Nanoparticles, Nature, 2013, 502, 80–84 CrossRef CAS PubMed.
- N. T. Fofang, T.-H. Park, O. Neumann, N. A. Mirin, P. Nordlander and N. J. Halas, Plexcitonic Nanoparticles: Plasmon−Exciton Coupling in Nanoshell−J-Aggregate Complexes, Nano Lett., 2008, 8, 3481–3487 CrossRef CAS PubMed.
- N. T. Fofang, N. K. Grady, Z. Fan, A. O. Govorov and N. J. Halas, Plexciton Dynamics: Exciton−Plasmon Coupling in a J-Aggregate−Au Nanoshell Complex Provides a Mechanism for Nonlinearity, Nano Lett., 2011, 11, 1556–1560 CrossRef CAS PubMed.
- A. Manjavacas, F. J. García de Abajo and P. Nordlander, Quantum Plexcitonics: Strongly Interacting Plasmons and Excitons, Nano Lett., 2011, 11, 2318–2323 CrossRef CAS PubMed.
- O. V. Ovchinnikov, M. S. Smirnov, T. A. Chevychelova, A. I. Zvyagin and A. S. Selyukov, Nonlinear Absorption Enhancement of Methylene Blue in the Presence of Au/Sio2 Core/Shell Nanoparticles, Dyes Pigm., 2022, 197, 109829 CrossRef CAS.
- L. Sun, Y. Chen and M. Sun, Exploring Nonemissive Excited-State Intramolecular Proton Transfer by Plasmon-Enhanced Hyper-Raman Scattering and Two-Photon Excitation Fluorescence, J. Phys. Chem. C, 2022, 126, 487–492 CrossRef CAS.
- G. Spektor, D. Kilbane, A. Mahro, M. Hartelt, E. Prinz, M. Aeschlimann and M. Orenstein, Mixing the Light Spin with Plasmon Orbit by Nonlinear Light-Matter Interaction in Gold, Phys. Rev. X, 2019, 9, 021031 CAS.
- L. Cui, R. Li, T. Mu, J. Wang, W. Zhang and M. Sun, In Situ Plasmon-Enhanced Cars and Tpef for Gram Staining Identification of Non-Fluorescent Bacteria, Spectrochim. Acta, Part A, 2022, 264, 120283 CrossRef CAS PubMed.
- J. Tirado-Rives and W. L. Jorgensen, Performance of B3lyp Density Functional Methods for a Large Set of Organic Molecules, J. Chem. Theory Comput., 2008, 4, 297–306 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (Cam-B3lyp), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- T. Lu and F. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- X. Mu, J. Wang and M. Sun, Visualization of Photoinduced Charge Transfer and Electron–Hole Coherence in Two-Photon Absorption, J. Phys. Chem. C, 2019, 123, 14132–14143 CrossRef CAS.
- M. Sun, J. Chen and H. Xu, Visualizations of Transition Dipoles, Charge Transfer, and Electron-Hole Coherence on Electronic State Transitions between Excited States for Two-Photon Absorption, J. Chem. Phys., 2008, 128, 064106 CrossRef PubMed.
- S. Chakrabarti and K. Ruud, Intermolecular Interaction-Controlled Tuning of the Two-Photon Absorption of Fullerene Bound in a Buckycatcher, J. Phys. Chem. A, 2009, 113, 5485–5488 CrossRef CAS PubMed.
- X. Zhou, W.-Q. Li, B. Shao and W. Q. Tian, Nonlinear Optical Properties of Fullerene C96 (D3d) and Related Heterofullerenes, J. Phys. Chem. C, 2013, 117, 23172–23177 CrossRef CAS.
- P. B. Johnson and R.-W. Christy, Optical Constants of the Noble Metals, Phys. Rev. B: Solid State, 1972, 6, 4370 CrossRef CAS.
- E. D. Palik, Handbook of Optical Constants of Solids, Academic press, 1998, vol. 3 Search PubMed.
- R. J. Moerland and J. P. Hoogenboom, Subnanometer-Accuracy Optical Distance Ruler Based on Fluorescence Quenching by Transparent Conductors, Optica, 2016, 3, 112–117 CrossRef CAS.
- Y. Chen, Y. Cheng and M. Sun, Physical Mechanisms on Plasmon-Enhanced Organic Solar Cells, J. Phys. Chem. C, 2021, 125, 21301–21309 CrossRef CAS.
- S. A. Jenekhe, S. K. Lo and S. R. Flom, Third–Order Nonlinear Optical Properties of a Soluble Conjugated Polythiophene Derivative, Appl. Phys. Lett., 1989, 54, 2524–2526 CrossRef CAS.
- J. D. Perea, et al., Combined Computational Approach Based on Density Functional Theory and Artificial Neural Networks for Predicting the Solubility Parameters of Fullerenes, J. Phys. Chem. B, 2016, 120, 4431–4438 CrossRef CAS PubMed.
- M. M. Oliva, J. Casado, J. T. L. Navarrete, S. Patchkovskii, T. Goodson, M. R. Harpham, J. S. Seixas de Melo, E. Amir and S. Rozen, Do [All]-S,S’-Dioxide Oligothiophenes Show Electronic and Optical Properties of Oligoenes and/or of Oligothiophenes?, J. Am. Chem. Soc., 2010, 132, 6231–6242 CrossRef CAS PubMed.
- S. Pascal, S. David, C. Andraud and O. Maury, Near-Infrared Dyes for Two-Photon Absorption in the Short-Wavelength Infrared: Strategies Towards Optical Power Limiting, Chem. Soc. Rev., 2021, 50, 6613–6658 RSC.
- M. A. Ramírez-Gómez, et al., Physicochemical and Luminescent Properties of Copolymers Composed of Three Monomers: Polythiophenes Based on 3-Hexylthiophene and 3,4-Ethylenedioxythiophene, Int. J. Polym. Sci., 2017, 2017, 1918602 Search PubMed.
- X. Ouyang, H. Zeng and W. Ji, Synthesis, Strong Two-Photon Absorption, and Optical Limiting Properties of Novel C70/C60 Derivatives Containing Various Carbazole Units, J. Phys. Chem. B, 2009, 113, 14565–14573 CrossRef CAS PubMed.
- X. Zhou, A.-M. Ren and J.-K. Feng, Theoretical Investigation on the Two-Photon Absorption of C60, J. Mol. Struct.: THEOCHEM, 2004, 680, 237–242 CrossRef CAS.
- S. Jeon, et al., Linear and Nonlinear Optical Properties of Photoresponsive [60]Fullerene Hybrid Triads and Tetrads with Dual Nir Two-Photon Absorption Characteristics, J. Phys. Chem. C, 2013, 117, 17186–17195 CrossRef CAS PubMed.
- T. Ameri, T. Heumüller, J. Min, N. Li, G. Matt, U. Scherf and C. J. Brabec, Ir Sensitization of an Indene-C60 Bisadduct (Icba) in Ternary Organic Solar Cells, Energy Environ. Sci., 2013, 6, 1796–1801 RSC.
- H. Zhou, F. Zhou, S. Tang, P. Wu, Y. Chen, Y. Tu, J. Wu and Y. Tian, Two-Photon Absorption Dyes with Thiophene as Π Electron Bridge: Synthesis, Photophysical Properties and Optical Data Storage, Dyes Pigm., 2012, 92, 633–641 CrossRef CAS.
- M. R. Harpham, Ö. Süzer, C.-Q. Ma, P. Bäuerle and T. Goodson, Thiophene Dendrimers as Entangled Photon Sensor Materials, J. Am. Chem. Soc., 2009, 131, 973–979 CrossRef CAS PubMed.
- M. Knupfer, Exciton Binding Energies in Organic Semiconductors, Appl. Phys. A, 2003, 77, 623–626 CrossRef CAS.
- D. S. Chemla, Nonlinear Optical Properties of Organic Molecules and Crystals V1, Elsevier, 2012, vol. 1 Search PubMed.
- M. Hoffmann, K. Schmidt, T. Fritz, T. Hasche, V. M. Agranovich and K. Leo, The Lowest Energy Frenkel and Charge-Transfer Excitons in Quasi-One-Dimensional Structures: Application to Meptcdi and Ptcda Crystals, Chem. Phys., 2000, 258, 73–96 CrossRef CAS.
- S. Jur?enas, Exciton Spectroscopy in Polar Molecular Films and Crystals, Phys. Scr., 1999, T79, 159 CrossRef.
- S. Jursenas, A. Gruodis, G. Kodis, M. Chachisvilis, V. Gulbinas, E. A. Silinsh and L. Valkunas, Free and Self-Trapped Charge-Transfer Excitons in Crystals of Dipolar Molecules of N,N-Dimethylaminobenzylidene 1,3-Indandione, J. Phys. Chem. B, 1998, 102, 1086–1094 CrossRef CAS.
- J. Butet, P.-F. Brevet and O. J. F. Martin, Optical Second Harmonic Generation in Plasmonic Nanostructures: From Fundamental Principles to Advanced Applications, ACS Nano, 2015, 9, 10545–10562 CrossRef CAS PubMed.
- D. V. Voronine, Z. Zhang, A. V. Sokolov and M. O. Scully, Surface-Enhanced Fast Cars: En Route to Quantum Nano-Biophotonics, Nanophotonics, 2018, 7, 523–548 Search PubMed.
- X. Mi, Y. Wang, R. Li, M. Sun, Z. Zhang and H. Zheng, Multiple Surface Plasmon Resonances Enhanced Nonlinear Optical Microscopy, Nanophotonics, 2019, 8, 487–493 CAS.
- Y. Huang, Y. Fang and M. Sun, Remote Excitation of Surface-Enhanced Raman Scattering on Single Au Nanowire with Quasi-Spherical Termini, J. Phys. Chem. C, 2011, 115, 3558–3561 CrossRef CAS.
- J. J. Mock, R. T. Hill, A. Degiron, S. Zauscher, A. Chilkoti and D. R. Smith, Distance-Dependent Plasmon Resonant Coupling between a Gold Nanoparticle and Gold Film, Nano Lett., 2008, 8, 2245–2252 CrossRef CAS PubMed.
- A. Tcherniak, S. Dominguez-Medina, W.-S. Chang, P. Swanglap, L. S. Slaughter, C. F. Landes and S. Link, One-Photon Plasmon Luminescence and Its Application to Correlation Spectroscopy as a Probe for Rotational and Translational Dynamics of Gold Nanorods, J. Phys. Chem. C, 2011, 115, 15938–15949 CrossRef CAS.
- S. Zhang, H. Wei, K. Bao, U. Håkanson, N. J. Halas, P. Nordlander and H. Xu, Chiral Surface Plasmon Polaritons on Metallic Nanowires, Phys. Rev. Lett., 2011, 107, 096801 CrossRef PubMed.
- Y. Fang, Z. Li, Y. Huang, S. Zhang, P. Nordlander, N. J. Halas and H. Xu, Branched Silver Nanowires as Controllable Plasmon Routers, Nano Lett., 2010, 10, 1950–1954 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d1nr08163b |
| This journal is © The Royal Society of Chemistry 2022 |