Probing the hydration friction of ionic interfaces at the atomic scale†
Zibo
Li‡
 a,
Qian
Liu‡
a,
Deliang
Zhang
a,
Yin
Wang
b,
Yuge
Zhang
a,
Qiang
Li
a,
Qian
Liu‡
a,
Deliang
Zhang
a,
Yin
Wang
b,
Yuge
Zhang
a,
Qiang
Li
 *a and
Mingdong
Dong
*a and
Mingdong
Dong
 *b
*b
aKey Laboratory of Colloid and Interface Chemistry of the Ministry of Education, School of Chemistry and Chemical Engineering, Shandong University, Jinan 250100, China. E-mail: qiang@sdu.edu.cn
bInterdisciplinary Nanoscience Center (iNANO), Aarhus University, Aarhus C, DK-8000, Denmark. E-mail: dong@inano.au.dk
First published on 10th February 2022
Abstract
Despite the extensive studies conducted in exploring friction in the aqueous environment, the mechanism of hydration friction remains not well understood. Herein, we directly probed hydration friction on mica-electrolyte interfaces with different hydrated alkali cations through a combination of three-dimensional atomic force microscopy and friction force microscopy. The atomic scale imaging of the hydration layers at the mica surface in different electrolyte solutions clearly revealed a correlation between the alkali cations and the structure of the hydration layers. Our detailed analysis showed that the hydration force was much higher at high ionic concentrations than that at low concentrations. The hydration friction coefficient was found to follow the trend K+< Na+< Li+< Cs+, which contrasts with the Hofmeister series, indicating that the hydration friction depends not only on the hydration strength of the alkali cations but also on the arrangement of the alkali cations at the interface. The results of this study provide deep insights into the origins of hydration friction, with potential implications for the development of new boundary lubrication in aqueous media.
New conceptsUnderstanding the mechanism of hydration friction is fundamental in controlling and designing highly efficient boundary lubrication systems in aqueous and biological environments. However, the hydration friction mechanism at the micro-level remains unclear. In this work, using three-dimensional atomic force microscopy and friction force microscopy, we probed the hydration friction on the mica-electrolyte interface as a function of ion species and concentration. Our experimental results provided new insights into the mechanism of hydration friction due to our ability to measure the hydration force and friction force with a high sensitivity and resolution. We demonstrated the effects of electrolytes on the hydration layer structures and friction forces and revealed new insights into the interplay between these phenomena in determining the hydration friction at interfaces. Our results emphasize the critical role of an ionic interface on the hydration friction behavior at the nanoscale and the fundamental knowledge attained could be applied to understand more complex friction process in aqueous environments. |
Introduction
Hydration friction, which differs from the classical friction modes, provides a mighty framework for understanding, controlling and designing boundary lubrication systems in aqueous environments.1–3 Therefore, in recent years, extensive efforts have been made to study the friction in aqueous circumstances, whereby hydration layers are strongly attached to the charges they surround, such as ions at the interface.3,4 The hydration layer cannot be easily squeezed out even under a large pressure and can provide a shear response in a fluidic manner for the relative movement,4–6 thereby exhibiting a great lubrication effect. For instance, hydrated alkali cations confined between two contacted mica surfaces can decrease the friction coefficient to the order of magnitude of 10−4–10−3 under a contact pressure of ∼30 MPa.7To understand the effects of the surrounding ions, interface charge and polarizability on the hydration friction behaviors give deep insights into the mechanism of hydration friction; numerous experiments have been carried out in exploring the origins of hydration friction by employing a surface force balance (SFB) and a ball-on-disk tribometer.2,4,8–15 It has been demonstrated that an extremely low sliding friction could be achieved between charged surfaces in high-salt solutions,2,4,14 which is attributed to the formation of the hydration layers. However, there is little microscopic understanding of the hydration friction mechanism, especially the role of subnanometer hydration shells in the frictional dissipation process, which remains not well understood. This is due to the lack of suitable experimental techniques to characterize the nanostructures of the hydrated ions at the solid–liquid interfaces. Fortunately, three-dimensional atomic force microscopy (3D-AFM) with a high sensitivity and resolution has recently been developed to map the solid–liquid interfaces.16–21 The interfacial layer structures on crystalline surfaces and biological molecules in liquids have been successfully realized through 3D-AFM.22–37 On the other hand, friction force microscopy (FFM), a contact mode of AFM for nanotribology, has the ability to measure the friction with pico-Newton force resolution and record the atomic resolution imaging of the solid surface simultaneously,38 which might be helpful to probe the role of hydration layers in the hydration friction process.
The hydrophilic mica surface is the most commonly used substrate to establish a solid–liquid interface model owing to its atomically flat and net negatively charged surface. The electrostatic interactions between the alkali cations and interface charge of mica favors their attachment. Therefore, in this study, we explored the hydration friction on a mica surface with different hydrated alkali ions using a combination of 3D-AFM and FFM. Atomic resolution XZ imaging of the hydration layer on a mica surface several nanometers in depth was achieved by 3D-AFM. These hydration layer mappings allow us to systematically analyze the dependence of mechanical properties of the hydration layer on the ion species and concentrations. Moreover, we systematically characterized the nanoscale friction properties of mica in different electrolyte solutions by FFM. The coefficients of hydration friction (COFs) were found to follow the trend K+< Na+< Li+< Cs+. Combined with the hydration forces extracted from the XZ mapping, the hydration lubrication effects in different electrolyte solutions were well explained. This study not only provided in-depth insights into the mechanism of hydration layer friction but also shed light on the design of very efficient hydration lubrication systems in aqueous media.
Results and discussion
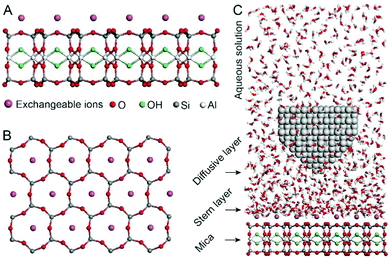
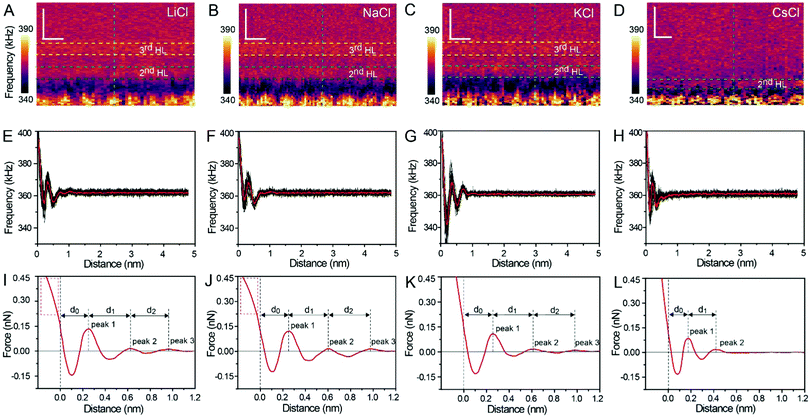
Fig. 1A and B show the mica lattice (001) surface and the corresponding cross-section view, the exchangeable ions on the surface play an important role in the formation process of the hydration layer. In an electrolyte solution, cations and water molecules can form a Stern layer and diffusion layer on the mica surface through electrostatic interaction, as shown in Fig. 1C, which is known as the hydration layer. The imaging measurements of the hydration layer were implemented by 3D-AFM. The AFM tip characterizes the XZ planes at the mica/electrolyte solution interface through executing a sequential series of force curves. During the tip laterally scanning, the vertical position (zt) of the tip is regulated in the form of a sine wave, which much be faster than the bandwidth of the tip-sample distance modulation. Herein, the force curves were obtained under a frequency modulation AFM (FM-AFM) feedback mode, and the force variation between the tip and sample (Fz) was detected as the frequency shift (Δf) of the cantilever caused by Fz. In each zt modulation cycle, both the trace and retrace Δf curves were recorded, and we adopted the trace Δf curves to construct the XZ Δf images in this study. It should be noted that when the solution concentration is 0.1–1 M, there is nearly no difference in the structure of the hydration layers. Similarly, when the concentration is higher than 1 M, the hydration layers will exhibit an epitaxial growth crystal structure.22 Therefore, in this work we chose the concentrations of 0.2 M and 4 M in order to make a more obvious comparison.The XZ mappings of the hydration layer in different electrolyte solutions at a low concentration (200 mM) and in pure water are shown in Fig. 2 and Fig. S1 (ESI†). In the case of LiCl, NaCl, and KCl, hydration layer mappings exhibit an atomic scale corrugation with a period of ∼0.52 nm at the bottom and two ultrathin layers above the atomic corrugation, as shown in Fig. 2A–C. In a previous report, it was demonstrated that the atomic corrugation corresponds to the monolayer of hydrated cations matched on the mica lattice, and the ultrathin layers correspond to the higher density hydration layers.22 Meanwhile, the layer of hydrated cations is the Stern layer (∼0.4 nm for Li+, Na+, K+ and ∼0.3 nm for Cs+) as labelled in Fig. S2 (ESI†). The dark area above the cation layers represents the local absence of water. Moreover, the first hydration layer is coordinated with the cation and could not be distinguished from the atomic corrugation, and the following layers with a ∼0.25 nm gap coincide with the maxima Δf caused by the second and third hydration layers. There are almost no anions at the interface. The hydration layer mapping of the CsCl solution (Fig. 2D) shows a significant difference compared with those of the cations mentioned above. The separation between the second hydration layer and the Cs+ layer is much smaller, and the third hydration layer is barely visible. This discovery proves that the hydration strength of Cs+ is very weak compared with those of Li+, Na+, and K+, which is consistent with previous reports.12,14,39,40 Fig. S1A (ESI†) shows the hydration layer mapping in pure water, where it can be seen that the cation layer is absent. It has been demonstrated that the cations are located closer in the hollow sites of a mica lattice compared with the water molecules, so there is a gap between the first hydration layer and the mica. Moreover, the second hydration layer is nearly invisible due to the absence of a cation hydration effect.
In order to quantitatively analyze the properties of the hydration layer, we have transformed the Δf curves into force curves. The Δf curves we adopted are all in the center of the cation as shown by the dashed lines marked in Fig. 2A–D, while the Δf curve is chosen randomly in the case of pure water. To increase the signal-to-noise ratio, 50 Δf curves were averaged to calculate the force curves, as shown in Fig. 2E–H and Fig. S1B (ESI†). Almost no background forces were found in our experiment in each averaged Δf curve, according to the almost horizontal part of the force curve. Therefore, the force curve was not need to calibrate, as reported in other literature.23,34 The Δf curves were transformed into force curves (Fig. 2I–L, and Fig. S1C, ESI†) by using the accurate formula developed for FM-AFM.41–43 The formula is shown below:
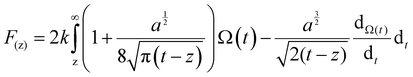 | (1) |
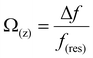 | (2) |
Fig. 2I–L show the force curves with alternated repulsive (F >0) and attractive (F <0) regions. The repulsive region corresponds to the adsorbed cation layer and local hydration layer, and the repulsive peak force decreases as the order of hydration layer increases. These values of the peak hydration force are comparable with the results reported in previous literature,21 which proves the reliability of our experiment. We define the position of the mica surface as the reference (z = 0), where the repulsion force is the same as the peak force of the second hydration layer as labelled in the force curves in Fig. 2I–L. It can be observed that the position of the peak force appears at larger distances compared with the position of the corresponding Δf maximum. In previous reports, it was explained that this phenomenon is because the force is proportional to the derivative with respect to the density of water.44
The force curves belonging to LiCl, NaCl, and KCl exhibit three obvious peak forces, while the force curves of CsCl and pure water exhibit two reduced peak forces. This result proves that Li+, Na+, and K+ have a stronger hydration strength. Moreover, at the leftmost end of the force curves of Li+ and Na+, the force curves have a clear tendency to bend to the left (the part framed by a red dashed rectangle in Fig. 2I and J), which may be caused by the detachment of cations from the mica surface as the force increases. But that's not the case with the force curves for K+ and Cs+. This phenomenon further proves that K+ and Cs+ can adsorb on the mica surface more stably due to the better lattice match between the cations and mica.
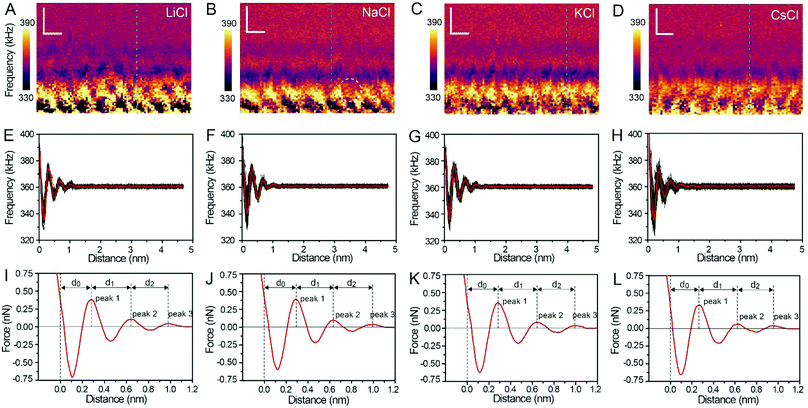
Fig. 3A–D show the XZ mappings at higher salt concentrations (4 M); a thicker and crystal-like nanostructure can be observed at the mica/electrolyte solution interface. This nanostructure is an epitaxial growth from the mica lattice with a lateral periodicity of ∼0.52 nm. It consists of alternated cation and anion layers parallel to the mica surface, and there is still a significant amount of water to balance the electrostatic interactions and stabilize the nanostructure.22 It is worth noting that there is a defect (marked by the white dashed circle) in Fig. 3B, which proves the reliability and accuracy of our experimental test. The corresponding Δf curves (the position of the selected Δf curves is labelled by the dashed lines in Fig. 3A–D) were also averaged, as shown in Fig. 3E–H, and further transformed into force curves (Fig. 3I–L). At high salt concentrations, the force curves exhibit three stronger peak forces compared with those at low salt concentrations, and the leftmost end of all the force curves has no tendency to bend to the left. This phenomenon indicates that at a high concentration many more ions assemble on the mica surface and form a more stable hydration layer. The decrease of the hydration ion radii in high concentrations results in the enhancement of the electrostatic interaction between the ions,40 and therefore the cations and anions can alternate epitaxial growth to form a relatively stable interface nanostructure, and these ions can be hydrated to fix water molecules.
The separations (labelled as d0, d1, and d2 in the force curves) between repulsive force peaks were extracted from the force curves and are summarized in Table 1 and Fig. S3 (ESI†). In the case of a low concentration electrolyte, it can be seen that d0 and d1 of CsCl are significantly reduced compared with those of LiCl, NaCl and KCl, owing to the greater hydration strength and the larger hydrated ionic radii of Li+, Na+, and K+. While in the case of a high concentration electrolyte, cations and anions alternately form an epitaxial growth nanostructure on the surface of the mica lattice, and the number of water molecules hydrated with ions is greatly reduced, which leads to the small difference between the hydrated ionic radii of Li+, Na+, K+, and Cs+. As a result, d0, d1 and d2 are nearly the same.
| Concentration | d 0 (nm) | d 1 (nm) | d 2 (nm) | |
|---|---|---|---|---|
| LiCl | 200 mM | 0.256 ± 0.02 | 0.370 ± 0.03 | 0.341 ± 0.05 |
| 4 M | 0.281 ± 0.01 | 0.361 ± 0.03 | 0.343 ± 0.04 | |
| NaCl | 200 mM | 0.254 ± 0.01 | 0.355 ± 0.02 | 0.369 ± 0.05 |
| 4 M | 0.284 ± 0.02 | 0.357 ± 0.04 | 0.349 ± 0.05 | |
| KCl | 200 mM | 0.252 ± 0.03 | 0.355 ± 0.03 | 0.370 ± 0.04 |
| 4 M | 0.287 ± 0.01 | 0.348 ± 0.05 | 0.358 ± 0.06 | |
| CsCl | 200 mM | 0.174 ± 0.01 | 0.246 ± 0.02 | — |
| 4 M | 0.260 ± 0.01 | 0.358 ± 0.03 | 0.345 ± 0.05 | |
| H2O | — | 0.228 ± 0.02 | 0.410 ± 0.05 | — |
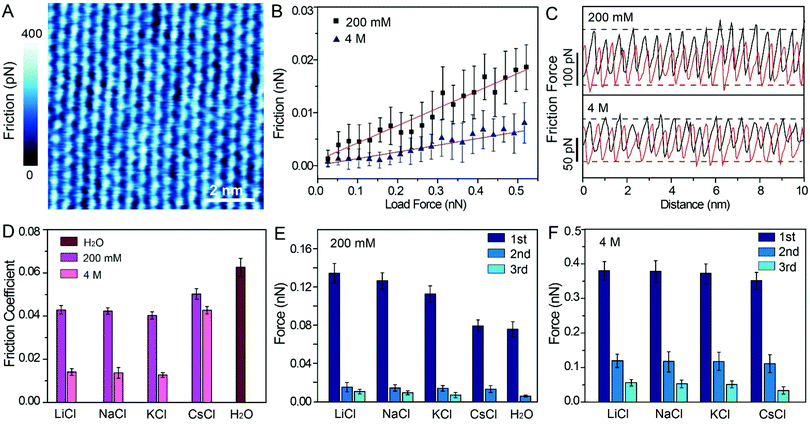
To probe the effects of hydrated cations on hydration friction, we then performed atomic resolution FFM in different electrolyte solutions. Fig. 4A exhibits the friction mapping in KCl solutions (200 mM) as an example. The dot-like pattern in Fig. 4A is arranged as a hexagonal structure with a ∼0.51 nm periodicity, which corresponds to the atomic scale corrugation at the bottom of the hydration layer map (Fig. 2A–D). Since the hydration repulsion of secondary and tertiary hydration layers is very weak (<150 pN), as shown in Fig. 2I–L, and there is almost no periodic corrugation in the secondary and tertiary hydration layers, so it can be proved that these dots are cations hydrated with the first hydration layer located on the mica lattice, which demonstrates that the tip was scanned over the first hydration layer.23 Friction force mappings are obtained with an increased load force to calculate the COFs, and extrinsic factors, such as experimental environment, AFM tip, and scan speed are kept constant. The friction force is calculated through dividing the friction signal difference between the forward and reverse scans by two. Fig. 4B shows the friction-load force curves recorded in KCl solution (200 mM, 4 M), and the friction-load force curves for LiCl, NaCl and CsCl solution are shown in Fig. S4 (ESI†). By linear fitting, the effective COFs can be obtained. As can be seen from the curves, the slope of a high concentration solution is smaller than that of a low concentration one, which indicates that the COFs are lower in a high electrolyte concentration. It should be noted that in order to exclude the potential impact of systematic change, the friction tests were conducted in a random sequence.
The representative friction loops obtained in the KCl solution (200 mM, 4 M) are shown in Fig. 4C, and the friction loops for the LiCl, NaCl, and CsCl solutions and pure water are shown in Fig. S5A–D (ESI†). The friction signals exhibit an atomic-scale stick-slip phenomenon, similar to that reported in previous publications for graphene and MoS2.45–48 It can be seen that, in the case of a high concentration solution, the difference between the trace and the retrace friction signals decreases compared with the that of a low concentration solution, which indicates less energy dissipation. Moreover, the reduction in energy dissipation is accompanied with the reduction of the local friction peak force. In order to quantify the energy dissipation, the values of the energy dissipation per unit cell and averaged peak friction force were calculated, and are plotted as shown in Fig. S5E and F (ESI†). One can clearly see that in the case of a high concentration electrolyte, both the energy dissipation and the mean friction peak force reduced significantly compared with those in the case of a low concentration electrolyte.
The most important finding in this study is that the frictional energy dissipation, when the AFM tip sliding across the mica surface with different hydrated cations, is considerably differed depending on the ion species and concentrations. According to our initial hypothesis, the energy dissipation would decrease due to the hydration lubrication effects, and the hydration lubrication capability of the cations may follow the Hofmeister sequence. Therefore, it can be inferred that Li+ may show the best lubricating cations, followed by Na+, K+, and Cs+. However, in this work, the COFs of different electrolyte solution suggest a disordered sequence: μK+ < μNa+ < μLi+ < μCs+, as shown in Fig. 4D.
For this abnormal phenomenon, we propose the following explanation. The hydrated cations are strongly located on the mica lattice sites, and simultaneously some hydrated cations are also absorbed on the negatively charged AFM tip. As the AFM tip scans the mica surfaces, the hydrated cations on the AFM tip and mica must slide past each other, and they must overcome an energy barrier (ΔE) originating from the hydration repulsion between the hydrated cations, as illustrated in Fig. S6 (ESI†). Thus, the hydrated cations will exert a hydration repulsion on the AFM tip.49–51 The force curves in Fig. 2, 3 and Fig. S1C (ESI†) were extracted from the trace Δf curves, so the peak hydration forces revealed the resistance of the hydration layer to the AFM tip. The greater the peak hydration force, the stronger the hydration layer. Therefore, the peak hydration force is used to represent the hydration capacity of the cations, and the values of each peak hydration forces are plotted in Fig. 4E and F. 1st, 2nd and 3rd represent the peak hydration forces, peak 1, peak 2 and peak 3, respectively, as labelled in the force curves in Fig. 2I–L, Fig. 3I–L and Fig. S1C (ESI†).
At low concentrations, Li+ has the larger peak hydration forces, leading to a greater frictional energy dissipation for the distortion of hydrated Li+, as the AFM tip slides past on the mica surface. The less strongly hydrated Na+ and K+ exhibit lower peak hydration forces (Fig. 4E) in sequence. For the cations with a larger hydration capacity (Li+, Na+, and K+), plenty of water molecules are hydrated with these cations and they have a great fluid response to the slipped tip. The hydrated cations can resist the rigid contact between the sliding tip and mica.7 Thus, these hydrated cations have some degree of hydration lubrication, which leading to a lower COF (Fig. 4D). While in the case of Cs+, the hydrated Cs+ has a smaller peak hydration force, and shows a higher COF compared with those of Li+, Na+ and K+. That is because there are very few water molecules hydrated with Cs+, which thus has little fluid response to the slipped tip. In pure water, the weakly hydrated layer cannot resist the rigid contact between the tip and mica, and causes the highest COF compared with those in the electrolyte solutions.
At high concentrations, the peak hydration forces are much stronger than those at low concentrations, and the difference of hydration repulsion between different ions is also reduced, as shown in Fig. 4F. These ions in the epitaxial growth nanostructure can be rapidly exchanged with the hydrated ions in the bulk solution, and one moment of this exchange behavior is captured, as shown in Fig. 3B (a defect has been circled to demonstrate the absence of ions). As shown in Fig. 3A–D, all the electrolyte solutions can form an epitaxial growth nanostructure, which guarantees a great fluid response to the slipped tip and resist rigid contact between the tip and mica. Therefore, the COFs of electrolyte solutions at high concentrations are obviously smaller than those in low concentrations, as shown in Fig. 4D.
Conclusions
To the best of our knowledge, this work overcomes earlier limitations and first explored the hydration friction mechanism at the atomic scale. We successfully imaged the hydration layer in electrolyte solutions on a mica surface at the atomic scale. At low electrolyte concentrations (200 mM), cations located on the mica lattice are topped by a few hydration layers. At high concentrations (4 M), the cations and anions alternate epitaxial growth on the mica lattice. In addition, the hydration force was found to be much higher at high concentrations than at low concentrations. Atomic scale friction mappings of mica in different electrolyte solutions were obtained through FFM, and the hydration lubrication effects of different alkali cations were well explained by combining the hydration forces. At low concentrations, Li+ caused the strongest resistance to tip slip due to the strongest hydration repulsion, followed by Na+ and K+. Cs+ showed a higher COF due to the weak hydration capacity to prevent rigid coupling between the tip and mica. At high concentrations, the electrolyte solution showed a much better lubrication effect relative to those in low concentrations, because the alkali cations in the epitaxial growth nanostructure provide a great fluid response to the slipped tip. This study is a supplement to the traditional hydration lubrication mechanism, and sheds lights on the design of new boundary lubrication systems in aqueous media.Materials and methods
Materials
The electrolyte solutions 200 mM and 4 M of LiCl, NaCl, KCl, CsCl were prepared by corresponding salt (≥99.9%, Shanghai Aladdin Bio-Chem Technology Co., Ltd) dissolved in the ultrapure water (18.0 MΩ). Muscovite mica discs (∼15 mm, Electron Microscopy China) were cleaved by adhesive tape for every AFM measurement.Hydration layer imaging
Hydration layer imaging was carried out on a commercial AFM (Cypher ES, Asylum Research). Silicon cantilevers with an Au reflex coating (ARROW-UHFAuD, Nanoword) were used for hydration layer imaging. The AFM tips were firstly immersed in a mixed solution (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in volume) of ultrapure water and isopropanol for one hour, then immersed in pure water for one hour, and finally treated by a UV-Ozone cleaner (ProCleanerTM Plus) for one hour to be hydrophilic and remove organic contaminants simultaneously. For a stable quantitative measurement of the force curve in an aqueous environment, the cantilever was excited by a blue drive (a photothermal excitation setup). The triangle cantilever used here had a gold backside coating, and the spring constant was 6 N m−1 through calibrating by Sader's method.52 The resonance frequency of the cantilever was 450 kHz in electrolyte solutions. For the hydration layer imaging, the Δf vs. distance curves were recorded as the tip approached the mica surface with a velocity of ∼1 Hz. When Δf reached the threshold value predetermined at the beginning, the approach process was stopped immediately and then reversed back to the starting position with the same speed. It should be noted that the threshold must be set reasonably to avoid damage to the tip and the sample, so as to ensure the continuous and stable measurement of the Δf curves.
1 in volume) of ultrapure water and isopropanol for one hour, then immersed in pure water for one hour, and finally treated by a UV-Ozone cleaner (ProCleanerTM Plus) for one hour to be hydrophilic and remove organic contaminants simultaneously. For a stable quantitative measurement of the force curve in an aqueous environment, the cantilever was excited by a blue drive (a photothermal excitation setup). The triangle cantilever used here had a gold backside coating, and the spring constant was 6 N m−1 through calibrating by Sader's method.52 The resonance frequency of the cantilever was 450 kHz in electrolyte solutions. For the hydration layer imaging, the Δf vs. distance curves were recorded as the tip approached the mica surface with a velocity of ∼1 Hz. When Δf reached the threshold value predetermined at the beginning, the approach process was stopped immediately and then reversed back to the starting position with the same speed. It should be noted that the threshold must be set reasonably to avoid damage to the tip and the sample, so as to ensure the continuous and stable measurement of the Δf curves.
Friction measurements
FFM measurement was also performed on a Cypher ES AFM. The height topography and friction mappings were obtained simultaneously with atomic-scale resolution. A rectangular cantilever (MSNL-10, Bruker) was selected for friction measurements. This cantilever has a normal and lateral spring constants of ∼0.02 N m−1 and ∼14 N m−1, respectively. During the FFM measurements, the cantilever scanning direction was kept perpendicular to the main axis, so the friction was quantified by the torsion of the cantilever. The cantilever was calibrated before each measurement. The FFM measurement was performed in a square region of 10 nm × 10 nm with a scan velocity of 10 Hz. The friction coefficient was acquired by fitting the friction vs. normal force curves linearly, as shown in Fig. 4B and Fig. S4 (ESI†). The maximum normal force between the tip and mica surfaces is 500 pN. Here, we used the Hertz contact theory to estimate the effective contact area through force-distance curves, as shown in Fig. S7 (ESI†). The maximum pressures between the tip and mica surfaces were ∼80 MPa (for a 200 mM solution) and ∼35 MPa (for a 4 M solution).Author contributions
Z. L. and Q. L. contributed equally. Q. L. and M. D. conceived and designed the experiments. Z. L. and Q. L. conducted the experiments and performed data analysis. D. Z., Y. W. and Y. Z. contributed to data analysis. Z. L. wrote the manuscript with contributions from all authors.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This study was supported by a Grant for Taishan Scholar Advantage Characteristic Discipline of Shandong Province, a Start-up Grant for QiLu Young Scholars of Shandong University, a Youth Fund from the Natural Science Foundation of Shandong Province (ZR2021QB045), the General Program from China Postdoctoral Science Foundation (2019M662325), a Grant from the Danish Council for Independent Research (9040-00219B), EU H2020RISE 2016-MNR4S Cell project.Notes and references
- U. Raviv, P. Laurat and J. Klein, Nature, 2001, 413, 51–54 CrossRef CAS PubMed
.
- U. Raviv and J. Klein, Science, 2002, 297, 1540 CrossRef CAS PubMed
.
- J. Klein, Friction, 2013, 1, 1–23 CrossRef CAS
.
- L. Ma, A. Gaisinskaya-Kipnis, N. Kampf and J. Klein, Nat. Commun., 2015, 6, 6060 CrossRef CAS PubMed
.
- W. H. Briscoe, S. Titmuss, F. Tiberg, R. K. Thomas, D. J. McGillivray and J. Klein, Nature, 2006, 444, 191–194 CrossRef CAS PubMed
.
- A. Gaisinskaya, L. Ma, G. Silbert, R. Sorkin, O. Tairy, R. Goldberg, N. Kampf and J. Klein, Faraday Discuss., 2012, 156, 217–233 RSC
.
- A. Gaisinskaya-Kipnis, L. Ma, N. Kampf and J. Klein, Langmuir, 2016, 32, 4755–4764 CrossRef CAS PubMed
.
- T. Han, C. Zhang and J. Luo, Langmuir, 2018, 34, 11281–11291 CrossRef CAS PubMed
.
- A. Schlaich, J. Kappler and R. R. Netz, Nano Lett., 2017, 17, 5969–5976 CrossRef CAS PubMed
.
- T. Han, C. Zhang, X. Chen, J. Li, W. Wang and J. Luo, J. Phys. Chem. C, 2019, 123, 20270–20277 CrossRef CAS
.
- R. M. Espinosa-Marzal, T. Drobek, T. Balmer and M. P. Heuberger, Phys. Chem. Chem. Phys., 2012, 14, 6085–6093 RSC
.
- S. Perkin, L. Goldberg, R. Fau-Chai, N. Chai, L. Fau-Kampf, J. Kampf, N. Fau-Klein and J. Klein, Faraday Discuss., 2009, 141, 399–413 RSC
.
- S. Perkin, L. Chai, N. Kampf, U. Raviv, W. Briscoe, I. Dunlop, S. Titmuss, M. Seo, E. Kumacheva and J. Klein, Langmuir, 2006, 22, 6142–6152 CrossRef CAS PubMed
.
- B. C. Donose, I. U. Vakarelski and K. Higashitani, Langmuir, 2005, 21, 1834–1839 CrossRef CAS PubMed
.
- R. Goldberg, L. Chai, S. Perkin, N. Kampf and J. Klein, Phys. Chem. Chem. Phys., 2008, 10, 4939–4945 RSC
.
- T. Fukuma and R. Garcia, ACS Nano, 2018, 12, 11785–11797 CrossRef CAS PubMed
.
- H.-L. Li, W.-N. Xu, F.-F. Jia, J.-B. Li, S.-X. Song and Y. Nahmad, Int. J. Miner., Metall. Mater., 2020, 27, 857–871 CrossRef CAS
.
- K. Miyata, J. Tracey, K. Miyazawa, V. Haapasilta, P. Spijker, Y. Kawagoe, A. S. Foster, K. Tsukamoto and T. Fukuma, Nano Lett., 2017, 17, 4083–4089 CrossRef CAS PubMed
.
- K. Umeda, K. Kobayashi, T. Minato and H. Yamada, Phys. Rev. Lett., 2019, 122, 116001 CrossRef CAS PubMed
.
- A. Labuda, K. Kobayashi, K. Suzuki, H. Yamada and P. Grütter, Phys. Rev. Lett., 2013, 110, 066102 CrossRef PubMed
.
- T. Fukuma, B. Reischl, N. Kobayashi, P. Spijker, F. F. Canova, K. Miyazawa and A. S. Foster, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 155412 CrossRef
.
- D. Martin-Jimenez, E. Chacon, P. Tarazona and R. Garcia, Nat. Commun., 2016, 7, 12164 CrossRef CAS PubMed
.
- K. Umeda, L. Zivanovic, K. Kobayashi, J. Ritala, H. Kominami, P. Spijker, A. S. Foster and H. Yamada, Nat. Commun., 2017, 8, 2111 CrossRef PubMed
.
- J. I. Kilpatrick, S.-H. Loh and S. P. Jarvis, J. Am. Chem. Soc., 2013, 135, 2628–2634 CrossRef CAS PubMed
.
- K. Kimura, S. Ido, N. Oyabu, K. Kobayashi, Y. Hirata, T. Imai and H. Yamada, J. Chem. Phys., 2010, 132, 194705 CrossRef PubMed
.
- K. Kobayashi, N. Oyabu, K. Kimura, S. Ido, K. Suzuki, T. Imai, K. Tagami, M. Tsukada and H. Yamada, J. Chem. Phys., 2013, 138, 184704 CrossRef PubMed
.
- D. Martin-Jimenez and R. Garcia, J. Phys. Chem. Lett., 2017, 8, 5707–5711 CrossRef CAS PubMed
.
- T. Fukuma, Y. Ueda, S. Yoshioka and H. Asakawa, Phys. Rev. Lett., 2010, 104, 016101 CrossRef PubMed
.
- H. Asakawa, S. Yoshioka, K.-I. Nishimura and T. Fukuma, ACS Nano, 2012, 6, 9013–9020 CrossRef CAS PubMed
.
- T. Fukuma, M. J. Higgins and S. P. Jarvis, Biophys. J., 2007, 92, 3603–3609 CrossRef CAS PubMed
.
- E. T. Herruzo, H. Asakawa, T. Fukuma and R. Garcia, Nanoscale, 2013, 5, 2678–2685 RSC
.
- K. Kuchuk and U. Sivan, Nano Lett., 2018, 18, 2733–2737 CrossRef CAS PubMed
.
- C.-W. Yang, K. Miyazawa, T. Fukuma, K. Miyata and I.-S. Hwang, Phys. Chem. Chem. Phys., 2018, 20, 23522–23527 RSC
.
- M. R. Uhlig, D. Martin-Jimenez and R. Garcia, Nat. Commun., 2019, 10, 2606 CrossRef PubMed
.
- M. R. Uhlig and R. Garcia, Nano Lett., 2021, 21, 5593–5598 CrossRef CAS PubMed
.
- D. J. Müller, A. C. Dumitru, C. Lo Giudice, H. E. Gaub, P. Hinterdorfer, G. Hummer, J. J. De Yoreo, Y. F. Dufrêne and D. Alsteens, Chem. Rev., 2021, 121, 11701–11725 CrossRef PubMed
.
- A. Viljoen, M. Mathelié-Guinlet, A. Ray, N. Strohmeyer, Y. J. Oh, P. Hinterdorfer, D. J. Müller, D. Alsteens and Y. F. Dufrêne, Nat. Rev. Methods Primers, 2021, 1, 63 CrossRef CAS
.
- R. Bennewitz, Mater. Today, 2005, 8, 42–48 CrossRef CAS
.
- I. U. Vakarelski and K. Higashitani, J. Colloid Interface Sci., 2001, 242, 110–120 CrossRef CAS
.
- I. U. Vakarelski, K. Ishimura and K. Higashitani, J. Colloid Interface Sci., 2000, 227, 111–118 CrossRef CAS PubMed
.
- J. E. Sader and S. P. Jarvis, Appl. Phys. Lett., 2004, 84, 1801–1803 CrossRef CAS
.
- J. N. Ladenthin, T. Frederiksen, M. Persson, J. C. Sharp, S. Gawinkowski, J. Waluk and T. Kumagai, Nat. Chem., 2016, 8, 935–940 CrossRef CAS PubMed
.
- F. Schulz, J. Ritala, O. Krejčí, A. P. Seitsonen, A. S. Foster and P. Liljeroth, ACS Nano, 2018, 12, 5274–5283 CrossRef CAS PubMed
.
- K. Miyazawa, N. Kobayashi, M. Watkins, A. L. Shluger, K.-I. Amano and T. Fukuma, Nanoscale, 2016, 8, 7334–7342 RSC
.
- S. Li, Q. Li, R. W. Carpick, P. Gumbsch, X. Z. Liu, X. Ding, J. Sun and J. Li, Nature, 2016, 539, 541–545 CrossRef CAS PubMed
.
- S. Zhang, T. Ma, A. Erdemir and Q. Li, Mater. Today, 2019, 26, 67–86 CrossRef CAS
.
- S. P. Koenig, N. G. Boddeti, M. L. Dunn and J. S. Bunch, Nat. Nanotechnol., 2011, 6, 543–546 CrossRef CAS PubMed
.
- S. Zhang, Y. Hou, S. Li, L. Liu, Z. Zhang, X.-Q. Feng and Q. Li, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 24452 CrossRef CAS PubMed
.
- R. An, X. Qiu, F. U. Shah, K. Riehemann and H. Fuchs, Phys. Chem. Chem. Phys., 2020, 22, 14941–14952 RSC
.
- A. M. Smith, K. R. J. Lovelock, N. N. Gosvami, T. Welton and S. Perkin, Phys. Chem. Chem. Phys., 2013, 15, 15317–15320 RSC
.
- P. K. Cooper, C. J. Wear, H. Li and R. Atkin, ACS Sustainable Chem. Eng., 2017, 5, 11737–11743 CrossRef CAS
.
- J. E. Sader, J. W. M. Chon and P. Mulvaney, Rev. Sci. Instrum., 1999, 70, 3967–3969 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nh00564b |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |