Investigating the innate selectivity issues of methane to methanol: consideration of an aqueous environment

Abstract

The higher reactivity of the methanol product over the methane reactant for the direct oxidation of methane to methanol is explored. C–H activation, C–O coupling, and C–OH coupling are investigated as key steps in the selective oxidation of methane using DFT. These elementary steps are initially considered in the gas phase for a variety of fcc (111) pristine metal surfaces. Methanol is found to be consistently more reactive for both C–H activation and subsequent oxidation steps. With an aqueous environment being understood experimentally to have a profound effect on the selectivity of this process, these steps are also considered in the aqueous phase by ab initio molecular dynamics calculations. The water solvent is modelled explicity, with each water molecule given the same level of theory as the metal surface and surface species. Free energy profiles for these steps are generated by umbrella sampling. It is found that an aqueous environment has a considerable effect on the kinetics of the elementary steps yet has little effect on the methane/methanol selectivity-conversion limit. Despite this, we find that the aqueous phase promotes the C–OH pathway for methanol formation, which could enhance the selectivity for methanol formation over that of other oxygenates.

---

Introduction

An efficient method for the direct conversion of methane (CH₄) to methanol (CH₃OH) remains an elusive goal within the field of catalysis. Both selectivity and activity are key issues that limit the industrial viability of this process.^1,2 The selectivity issues for this process can be deconstructed into two key areas. The first hurdle is the difficulty of forming the methanol product instead of other oxygenates. For example, bulk metals are adept oxidation catalysts, yet they make poor methane to methanol catalysts.^3,4 This is due to the tendency of surface CH₃ species to further dehydrogenate into CH/C species, which are more readily oxidizable compared to CH₃.^5,6 This causes CO₂ to (eventually) be formed directly, without methanol being an intermediary species. Even if complete selectivity towards forming the methanol product is realised, a second selectivity issue is encountered; the methanol product is more reactive than the methane reactant. Methanol, if the same mechanism is followed as methane, will subsequently be oxygenated into methanediol (CH₂OHOH), eventually undergoing further oxidation to CO₂.⁶

As C–H activation must occur before any form of methane functionalisation can take place, a great deal of theoretical interest has surrounded this elementary step.⁷ Across a wide range of materials and mechanisms, it was found that methanol is easier to activate with respect to methane, largely due to methanol's C–H bond being weaker than the C–H bond in methane.⁸ If it is assumed that C–H activation is the only step that affects the rate of oxidation, a selectivity–conversion limit arises; only small conversions are possible if significant overoxidation of the methanol product is to be avoided.⁹

Experimentally, this issue is avoided by oxidising methane in a stepwise manner.^10–16 Metal centres, typically Cu or Fe atoms supported in zeolites, are first oxidised. Once metal-oxo reaction centres are formed, methane is passed over the catalyst and activated. The formed methanol product is liberated from the metal centre upon washing. The methanol product is unable to be further oxidised, as it is physically anchored until washing. This allows the inherent issue with methanol being more reactive than methane to be overcome. However, completing this process in a stepwise manner does limit the industrial viability of this process.¹⁷ For this reason, furthering the understanding of what can affect the respective reactivity of methane and methanol in an asymmetric factor is vitally important for the further development of non-stepwise methane to methanol systems.

Moreover, an aqueous environment was found to be necessary for some methane to methanol processes.^18–22 Specifically, these processes oxidised methane in a continuous manner. The specific requirement of water was noted by Shan et al., where a variety of other solvents were found to be unsuitable for this process.¹⁹ Additionally, in the work of Liu et al., water was found to have a crucial role in promoting the activity of the catalyst.²² It was proposed that water was important for the formation of an active site that would selectively oxidise methane to methanol. From this series of experimental findings, it was suggested by Allegra et al. that water could prevent further oxidation of methanol. It was proposed that as the methanol has a stronger hydration energy than the methane reactant, water could act as a collector and stabilise the methanol product in the aqueous phase, preventing overoxidation.

Despite this, little research has been conducted theoretically to better understand the effects a water solvent has on the methane to methanol process, with only a few water molecules coordinated to active sites considered.^23–25 This is partly due to the requirement of an explicit model, where the water molecules are individually treated, so all of the water effects may be accurately studied.²⁶ Additional to the extra computational cost of considering the water molecules, computationally expensive ab initio molecular dynamics (AIMD) calculations may be carried out to obtain the respective water stabilised structures and the free energy profiles for different elementary steps in the aqueous phase.²⁷ These issues have limited the interest towards a better fundamental understanding of methane selective oxidation in an aqueous environment.

Herein, to more thoroughly comprehend the innate selectivity issues of the methane to methanol system, important elementary steps (C–H activation, C–O coupling, and C–OH coupling) are considered for both methane and methanol. First, these steps are considered in the gas phase with the total energy barriers calculated and compared for a variety of fcc (111) metal surfaces. Subsequently, AIMD calculations are performed for these elementary steps on the Pd(111) surface. Both gas and aqueous phase reactions are considered in these AIMD calculations, with free energy profiles generated by umbrella sampling (US).

Computational method

Spin-polarized density functional theory calculations were performed with the Perdew–Burke–Ernzerhof (PBE)²⁸ functional within the generalized gradient approximation (GGA) in the Vienna ab initio simulation package (VASP).^29–31 The projector-augmented wave (PAW) method was used to represent the core–valence electron interaction.^32,33 Structures were optimised until the forces on all atoms were below 0.05 eV Å⁻¹. Transition states were searched with the constrained minimization technique.^34,35 Structures were verified with frequency calculations, where no imaginary frequencies are associated with an initial or final state and one imaginary frequency is associated with the transition state.

For all DFT calculations, the cut-off energy of the plane wave basis set was 450 eV. The most stable (111) facet was used for all metal surfaces in a p(3 × 3) unit cell with a 15 Å vacuum region. All calculations were performed under low surface coverage to prevent adsorbates interacting with each other. For static calculations, the Brillouin zone was sampled with a 6 × 6 × 1 Monkhorst–Pack k-point grid.³⁶ For the AIMD calculations, a 2 × 2 × 1 k-point grid is used and the calculations are non-spin-polarized.

The time step interval for all molecular dynamics calculations was set to 1.0 fs. For modelling of the aqueous phase, an initial water box was first optimised with the TIP4P force field model in the LAMMPS package until convergence, where the density of water in the unit cell is set to 0.97 g cm⁻³ (1.0 g cm⁻³) - the experimental density of water at the operating conditions of 80 °C. This water structure was then optimised in the vacuum region of the Pd(111) slab for 50 000 steps until the average energy converged. The D3 correction method was employed to include the van der Waals interactions³⁷ to more accurately model the aqueous phase.³⁸ The canonical ensemble conditions were imposed with the Nosé–Hoover thermostat,³⁹ and the temperature was set to 353 K for all simulations. The free energy profiles were calculated using umbrella sampling, where the restricted coordinate was the distance between the two atoms for the respective bond breakage/formation step. No other restraints or biases were imposed on the system. The pathway was sampled between the initial state and the final state of the static calculations, where different R–R coordinate distances, of 0.1 Å intervals, were sampled for 10 ps and 20 ps each in the gas phase and aqueous phase, respectively. It is noted that more configurations may be sampled and the accuracy of the free energies may be improved if the AIMD simulation time was longer. We acknowledge that even 280 ps of simulation time may not be long enough to sample many configurations of water. A series of Gaussian bias constraints were used to sample the reaction coordinate.⁴⁰ The free energy profiles were rendered from the simulations using the weighted histogram analysis method (WHAM) code.^41,42

Results and discussion

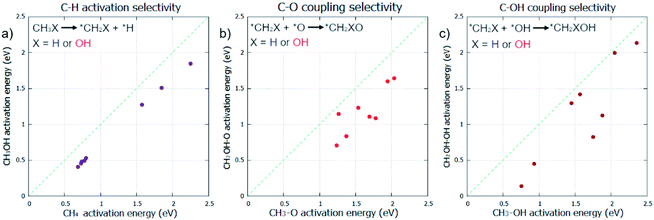
Initially, the selective oxidation of methane to methanol was considered in the gas phase. Whilst C–H activation is known to be more facile for methanol than methane,⁷ the selectivity of subsequent steps for selective oxidation still need thorough investigation. As the coupling of surface CH₃ with O/OH is known to be the dominant pathway for methanol formation from methane under oxidative conditions,^5,6 these steps in addition to C–H activation were also considered.

Pristine metal surfaces were chosen as the main catalyst class to investigate, due to their well understood mechanisms and proven ability as oxidation catalysts.⁴ Specifically, fcc metals that are contiguous in the periodic table (Ni, Cu, Rh, Pd, Ag, Ir, Pt, and Au) were selected for investigation. Three elementary steps are compared: C–H activation, for CH₄ and CH₃OH; C–O coupling, for CH₃ and CH₂OH; and C–OH coupling for CH₃ and CH₂OH. The comparison of the kinetics for these two different species helps to represent the selectivity of the reaction, where the reactivity of the methane reactant is measured against the methanol product. The surface mediated mechanism is considered for the C–H activation step.⁸

C–H activation in methane is found to be consistently more difficult compared with methanol (Fig. 1a) which is in agreement with our current understanding of methane/methanol selectivity.^7,9 However, our results also indicate that perhaps too much focus has been placed on this step; for many of the metals, C–O bond formation, in the form of C–O or C–OH coupling, have considerably higher activation energy barriers than those found for C–H activation (ESI1†). This could explain how C–H activation is readily reversible, evidenced by facile deuteration for many metals,⁴³ yet oxidation remains difficult; C–O bond formation may be the rate determining step for many methane to methanol catalysts, as suggested in other work.²³ The same trend observed for C–H activation is found for C–O and C–OH coupling as seen in Fig. 1b and c. CH₂OH species coupling with O/OH is consistently more kinetically favoured compared to CH₃. Even if carbon–oxygen bond formation is rate determining and C–H activation is reversible, our calculations suggest that preferential oxidation of methane over that of methanol is not possible if the reaction mechanism is followed by these other significant elementary steps. Methanol was found to be more reactive than methane for all elementary steps across all metals.

Fig. 1 Consideration of the reactivity of methane against methanol for different key elementary steps in the selective oxidation process for a variety of fcc metals (Ni, Cu, Rh, Pd, Ag, Ir, Pt, and Au). The selectivity is compared by reviewing the respective energy barriers if methane is used as a reactant or if methanol is used as a reactant. Points below the line suggest that methanol is preferentially reacted for this step and points above the line suggest that methane reacts preferentially. From left to right (a–c), the steps considered are: C–H activation (CH₃X → *CH₂X + *H); C–O coupling (*CH₂X + *O → *CH₂XO); and C–OH coupling (*CH₂X + *OH → *CH₂XOH), where X = H for methane or OH for methanol as reactants respectively.

Despite no selectivity being offered for any of the elementary steps in the gas phase, there remains an opportunity for some selectivity change by the reaction taking place in the aqueous phase. With methane and methanol having different affinities for water, water restructuring is a significant factor that could affect the respective reactivity of methane and methanol towards oxidation in an asymmetric fashion. As palladium is proven as an effective oxidation catalyst,^3,4 this metal surface was chosen to study the effects of an aqueous environment on all the previously studied key elementary steps (Fig. 1) for the oxidation of methane to methanol.

AIMD simulations allow explicit consideration of water and with long enough sampling and implemented biases, an accurate Helmholtz free energy profile for different elementary steps can be derived through umbrella sampling.²⁶ To allow comparison, gas phase AIMD calculations were first performed to obtain gas phase free energy profiles for both methane and methanol as reactants.

For the AIMD simulations of C–H activation, the barriers are with respect to the adsorbed methane/methanol surface species, counter to the molecule being in the gas phase, which was used as the initial state for the static calculations. This causes the free energy pathway to be substantially exothermic, due to the entropic contributions of molecular adsorption not being included in the energy pathway. As the C–H activation elementary step goes from one surface molecule to two surface species, entropy is considerably increased. This elementary process gives a Helmholtz free energy change of −1.15 eV and −1.24 eV for the C–H activation of methane and methanol in the gas phase with their energy barriers for these processes calculated as being 0.37 eV and 0.34 eV, respectively (Fig. 2a). Akin to the static calculations, there is preference for the activation of methanol over methane. This activation energy difference is considerably smaller than that found for the static calculations (0.26 eV as reported in ESI1†), but this can be partially attributed to the slightly stronger adsorption energy of methanol over methane.

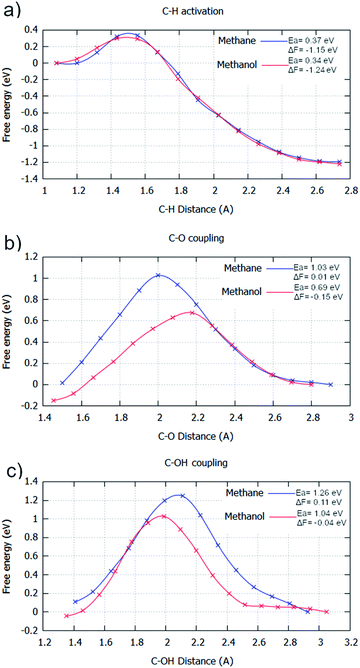Fig. 2 Free energy reaction profiles generated for different elementary steps where methane (blue) and methanol (red) are reactants, respectively. All steps are in the gas phase. The steps considered are: (a) C–H activation (CH₃X → *CH₂X + *H); (b) C–O coupling (*CH₂X + *O → *CH₂XO); and (c) C–OH coupling (*CH₂X + *OH → *CH₂XOH). The reaction coordinate is the distance between the two atoms involved with the bond formation or bond breaking. The profiles were generated by umbrella sampling, with the reaction coordinate sampled for 20 ps at 0.1 Å intervals between the optimised static calculation initial state and final state. All energies are in eV. Results are reported in tabular form alongside Fig. 4 in ESI2.†

For C–O coupling, the same trend is observed. For this elementary step, the barriers and energy changes of 1.03 eV and 0.01 eV for methane, and 0.69 eV and −0.15 eV for methanol were calculated (Fig. 2b). Activated methanol (CH₂OH) is greatly preferred to be oxidised over activated methane (CH₃), compounding the selectivity loss already caused by the C–H activation step.

C–O coupling is the dominant pathway for CH₃/CH₂OH oxidation,^5,6 due to O being the most dominant surface species, with only very small concentrations of OH being present on the surface. Despite this, some environments, such as aqueous conditions,⁴⁴ can encourage an increase in surface OH concentration. Due to this, C–OH coupling is also considered, as for some surfaces, C–OH coupling has significantly lower barriers than C–O coupling. For C–OH coupling in the gas phase, the barriers and energy changes of 1.26 eV and 0.11 eV for methane, and 1.04 eV and −0.04 eV for methanol, respectively, are observed (Fig. 2c). Even if OH radicals were the dominant surface species, methanol as a reactant is distinctly more reactive than methane, that no selectivity can be offered by this elementary step.

Whilst in the gas phase, methanol is more reactive than methane, there is an opportunity for an aqueous environment to change this selectivity. For static calculations, only implicit water models (such as the polarizable continuum model) that average the stabilising/destabilising effects of water uniformly across the reaction species can be used. However, these models fail to describe the coordination networks that water forms in the reaction solution, which are crucial to describe key reactivities of certain systems.^45–48

To model all of these solvent effects accurately, an explicit water model must be performed, where the water molecules in the aqueous phase are all considered individually. To this end, we performed AIMD calculations using the explicit water model and subsequently compared the results to the gas phase AIMD calculations. Fig. 3 displays the simulation cell used and the optimised water structure in the unit cell. It highlights that 4 layers of water are present through the density profile, suggesting a sufficient amount of water was considered to adequately describe the aqueous phase.

Fig. 3 Snapshot of the H₂O/Pd(111) interface with activated methane on the surface after 50 ps of simulation. A side view is shown on the left with the density profile of the last 10 ps of the simulation superimposed, where the average density of water is 1.0 kg m⁻³. The layers of water formed in solution are demonstrated. A top view is shown using a (2 × 2) supercell of the p(3 × 3) unit cell, showing the water structure in the unit cell.

For the aqueous phase, the general kinetics of the elementary processes undergo a remarkable change. The aqueous phase significantly maximises the energy barrier for all steps if considering methane as the reactant; water fails to stabilise the transition state species with respect to the intermediate species. There is an average barrier increase for elementary steps of 0.21 eV, with C–H activation and C–O coupling having substantial barrier increases of 0.27 eV and 0.32 eV with respect to the gas phase (Fig. 2/4 & ESI2†), respectively. However, C–OH coupling only has a minor increase of 0.04 eV. Curiously, this would cause the energy barriers for C–O coupling and C–OH coupling to become kinetically equivalent in the aqueous phase. This implies that the water environment could drive a mechanistic change for the selective oxidation of methane if enough build-up of surface OH occurs. This is possible from the hydrogen transfer from water to surface O species.³²

The calculated aqueous phase energetics suggest that water would impede the reactivity of methane oxidation considerably. Additionally, the C–H activation step becomes considerably less exergonic (Fig. 2a and 4a). This is due to the restricted free movement of surface species imposed by the liquid phase. In particular, surface species have a reduced translational entropic contribution to the free energy of a system in the aqueous phase compared to the gas phase caused by the restricted motion of molecules in the aqueous phase. Due to this, going from one surface species to two surface species (e.g. *CH₄ → *CH₃ + *H) does not contribute as much to the free energy change gained from entropy in the aqueous phase compared to the gas phase. For the C–O bond formation steps, considerable signs of water stabilisation are present for the initial state (Fig. 2b/c & 4b/c). The elementary steps go from slightly exergonic to considerably endergonic, becoming 0.53 eV and 0.11 eV more endergonic for C–O coupling and C–OH coupling, respectively. This can be explained by the coordination network of water with surface O/OH species, stabilising them on the surface.^26,45 This minimises the potential for these oxygen species to couple with formed surface CH₃ species, especially so for the atomic oxygen surface species. This can be observed in the simulation window close to the transition state. Water coordinates to the oxygen species throughout the transition state, impeding carbon oxygen bond formation (ESI4†).

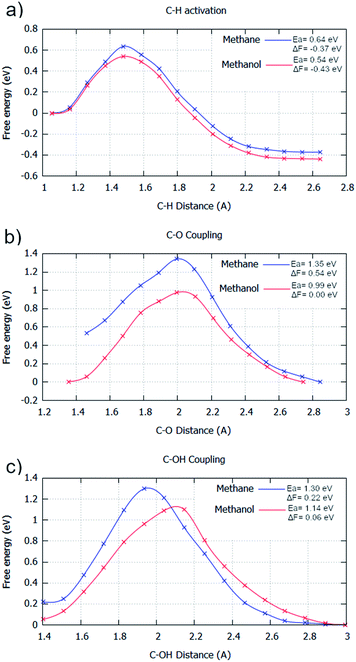Fig. 4 Free energy reaction profiles generated for different elementary steps where methane (blue) and methanol (red) are reactants, respectively. All steps are in the aqueous phase. The steps considered are: (a) C–H activation (CH₃X → *CH₂X + *H); (b) C–O coupling (*CH₂X + *O → *CH₂XO); and (c) C–OH coupling (*CH₂X + *OH → *CH₂XOH). The reaction coordinate is the distance between the two atoms involved with the bond formation or bond breaking. The profiles were generated by umbrella sampling, with the reaction coordinate sampled for 20 ps at 0.1 Å intervals between the optimised static calculation initial state and final state. All energies are in eV. Water was calculated explicitly. Results are reported in tabular form alongside Fig. 2 in ESI2.†

With the general kinetic effects studied for oxidising methane to methanol in the gas and aqueous phase, the subsequent excess oxidation of methanol product was also considered in the aqueous phase (Fig. 4). Identical to the gas phase, all significant elementary steps for selective oxidation are kinetically more accessible; only minor changes in the barrier difference for methane and methanol, being used as reactants respectively, are present when compared to the gas phase barrier differences. For C–H activation of methane, the barrier is 0.03 eV higher in the gas phase than methanol, whilst it is 0.10 eV higher in the aqueous phase (Fig. 4a). This is mirrored for C–O coupling, where the energy barrier difference between using methane or methanol as reactants, is close for both the gas and aqueous phases, with a gap of 0.34 eV and 0.36 eV found for the gas and aqueous phase respectively (Fig. 4b). For C–OH coupling, the energy barrier gap is slightly reduced in the aqueous phase, with an energy barrier difference of 0.22 eV for the gas phase and 0.16 eV for the aqueous phase (Fig. 4c).

The aqueous phase has a minimal effect on the selectivity–conversion relationship, but our calculations indicate that it does have a very profound effect on the selectivity of the reaction towards forming methanol. C–O and C–OH coupling become kinetically indiscriminate in the aqueous phase. The advantage offered by following a C–OH coupling mechanism is the removal of a methoxy (CH₃O) intermediate surface species. Whilst O–H coupling is a reasonably fast step, with a barrier calculated as being 0.59 eV, competing with this reaction is, however, the dehydrogenation of CH₃O to CH₂O, which has an effective barrier of 0.27 eV (ESI3†). Additional to having a much lower barrier, surface hydrogen is typically quickly oxidised under oxidative conditions, bottlenecking the rate of methanol formation, causing selectivity to be lost via formaldehyde. If the aqueous phase increases surface OH concentration and encourages a C–OH coupling pathway, the selectivity loss is minimised by only having one intermediate species (CH₃) on the pathway to methanol formation from methane.

We believe that the selectivity issues faced during the development of processes for the direct oxidation of methane to methanol will continue to affect these processes. However, we hope that our work will bring attention to the two kinds of selectivity problems that can be encountered for these catalysts. Our work suggests that the selectivity issues caused by the inherently increased reactivity of methanol over methane will continue to persist, regardless of the introduction of an aqueous environment.

Focus must be brought to how the effective barrier difference observed, between methane and methanol being used as reactants, respectively, is distinctly large. The average barrier difference was found to be 0.30 eV for C–H activation, 0.42 eV for C–O coupling, and 0.44 eV for C–OH coupling for the studied fcc metals (Fig. 1 & ESI1†). A very drastic effect would be required to be able to differentiate between methane and methanol to the degree required to negate this difference. The solvent effect of water was hoped to have some effect on this selectivity in an asymmetric fashion; however, our calculations indicate that it does not.

Beyond these general findings, better understanding of the effects of the aqueous phase will have important consequences for the development of electrocatalysts for methane to methanol.⁴⁹ Understanding the effects of the aqueous phase under a potential is crucial to describe and develop active and selective electrocatalysts.

Conclusions

Methanol is more reactive than methane as a reactant for all the elementary steps that we considered. We develop the understanding of this selectivity limit beyond that of C–H activation and demonstrate that this selectivity problem is also an issue for other crucial steps, namely C–O bond formation. Whilst it was hoped that water could offer selectivity through an asymmetric solvent effect for methane and methanol, our calculations suggest that this is not the case. The selectivity-conversion limit still remains a huge hurdle for an industrially viable method for direct methanol production from methane. However, we find that an aqueous environment does have a considerable effect on the kinetics and thermodynamics of methane selective oxidation. This could improve selectivity by driving the reaction pathway towards a C–OH coupling route instead of a C–O coupling route, minimising the selectivity loss to other oxygenates other than methanol.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful for computational support from the UK national high-performance computing service, ARCHER, for which access was obtained via the UKCP consortium and funded by EPSRC grant ref EP/P022561/1. We are grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1). We are grateful for access to the Queen's University Belfast Kelvin HPC service, which is partially funded by ESPRC (EP/T022175/1).

References

1. A. Olivos-Suarez, À. Szécsényi, E. Hensen, J. Ruiz-Martinez, E. Pidko and J. Gascon, ACS Catal., 2016, 6, 2965–2981.
2. P. Tomkins, M. Ranocchiari and J. van Bokhoven, Acc. Chem. Res., 2017, 50, 418–425.
3. R. Bunting, X. Cheng, J. Thompson and P. Hu, ACS Catal., 2019, 9, 10317–10323.
4. D. Ciuparu, M. Lyubovsky, E. Altman, L. Pfefferle and A. Datye, Catal. Rev., 2002, 44, 593–649.
5. M. Jørgensen and H. Grönbeck, ACS Catal., 2016, 6, 6730–6738.
6. J. Yoo, J. Schumann, F. Studt, F. Abild-Pedersen and J. Nørskov, J. Phys. Chem. C, 2018, 122, 16023–16032.
7. A. Latimer, A. Kulkarni, H. Aljama, J. Montoya, J. Yoo, C. Tsai, F. Abild-Pedersen, F. Studt and J. Nørskov, Nat. Mater., 2016, 16, 225–229.
8. A. Latimer, A. Kulkarni, H. Aljama, J. Montoya, J. Yoo, C. Tsai, F. Abild-Pedersen, F. Studt and J. Nørskov, Phys. Chem. Chem. Phys., 2017, 19, 3575–3581.
9. A. Latimer, A. Kakekhani, A. Kulkarni and J. Nørskov, ACS Catal., 2018, 8, 6894–6907.
10. V. Soboev, K. Dubkov, O. Panna and G. Panov, Catal. Today, 1995, 24, 251–252.
11. E. Starokon, M. Parfenov, S. Arzumanov, L. Pirutko, A. Stepanov and G. Panov, J. Catal., 2013, 300, 47–54.
12. C. Hammond, M. Forde, M. Rahim, A. Thetford, Q. He, R. Jenkins, N. Dimitratos, J. Lopez-Sanchez, N. Dummer, D. Murphy, A. Carley, S. Taylor, D. Willock, E. Stangland, J. Kang, H. Hagen, C. Kiely and G. Hutchings, Angew. Chem., 2012, 124, 5219–5223.
13. P. Vanelderen, R. Hadt, P. Smeets, E. Solomon, R. Schoonheydt and B. Sels, J. Catal., 2011, 284, 157–164.
14. E. Alayon, M. Nachtegaal, A. Bodi and J. van Bokhoven, ACS Catal., 2013, 4, 16–22.
15. D. Pappas, A. Martini, M. Dyballa, K. Kvande, S. Teketel, K. Lomachenko, R. Baran, P. Glatzel, B. Arstad, G. Berlier, C. Lamberti, S. Bordiga, U. Olsbye, S. Svelle, P. Beato and E. Borfecchia, J. Am. Chem. Soc., 2018, 140, 15270–15278.
16. T. Sheppard, C. Hamill, A. Goguet, D. Rooney and J. Thompson, Chem. Commun., 2014, 50, 11053–11055.
17. M. Ravi, M. Ranocchiari and J. van Bokhoven, Angew. Chem., 2017, 56, 16464–16483.
18. Y. Tang, Y. Li, V. Fung, D. Jiang, W. Huang, S. Zhang, Y. Iwasawa, T. Sakata, L. Nguyen, X. Zhang, A. Frenkel and F. Tao, Nat. Commun., 2018, 9, 1231.
19. J. Shan, M. Li, L. Allard, S. Lee and M. Flytzani-Stephanopoulos, Nature, 2017, 551, 605–608.
20. J. Xie, R. Jin, A. Li, Y. Bi, Q. Ruan, Y. Deng, Y. Zhang, S. Yao, G. Sankar, D. Ma and J. Tang, Nat. Catal., 2018, 1, 889–896.
21. W. Huang, S. Zhang, Y. Tang, Y. Li, L. Nguyen, Y. Li, J. Shan, D. Xiao, R. Gagne, A. Frenkel and F. Tao, Angew. Chem., 2016, 128, 13639–13643.
22. Z. Liu, E. Huang, I. Orozco, W. Liao, R. Palomino, N. Rui, T. Duchon, S. Nemšák, D. Grinter, M. Mahapatra, P. Liu, J. Rodriguez and S. Senanayake, Science, 2020, 368, 513–517.
23. R. Bunting, J. Thompson and P. Hu, Phys. Chem. Chem. Phys., 2020, 22, 11686–11694.
24. T. Yumura, Y. Hirose, T. Wakasugi, Y. Kuroda and H. Kobayashi, ACS Catal., 2016, 6, 2487–2495.
25. Z. Zhao, A. Kulkarni, L. Vilella, J. Nørskov and F. Studt, ACS Catal., 2016, 6, 3760–3766.
26. P. Rice, Y. Mao, C. Guo and P. Hu, Phys. Chem. Chem. Phys., 2019, 21, 5932–5940.
27. J. Carrasco, A. Hodgson and A. Michaelides, Nat. Mater., 2012, 11, 667–674.
28. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
29. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
30. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
31. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
32. P. Blöchl, O. Jepsen and O. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233.
33. A. Alavi, P. Hu, T. Deutsch, P. Silvestrelli and J. Hutter, Phys. Rev. Lett., 1998, 80, 3650–3653.
34. A. Michaelides and P. Hu, J. Am. Chem. Soc., 2001, 123, 4235–4242.
35. Z. Liu and P. Hu, J. Am. Chem. Soc., 2003, 125, 1958–1967.
36. H. Monkhorst and J. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
37. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
38. B. Santra, A. Michaelides, M. Fuchs, A. Tkatchenko, C. Filippi and M. Scheffler, J. Chem. Phys., 2008, 129, 194111.
39. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695.
40. G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1997, 23, 187.
41. S. Kumar, D. Bouzida, R. Swendsen, P. Kollman and J. Rosenberg, J. Comput. Chem., 1992, 13, 1011–1021.
42. S. Kumar, J. Rosenberg, D. Bouzida, R. Swendsen and P. Kollman, J. Comput. Chem., 1995, 16, 1339–1350.
43. A. Sattler, ACS Catal., 2018, 8, 2296–2312.
44. F. Xu, I. Fampiou, C. O'Connor, S. Karakalos, F. Hiebel, E. Kaxiras, R. Madixc and C. Friend, Phys. Chem. Chem. Phys., 2018, 20, 2196–2204.
45. D. Wang, T. Sheng, J. Chen, H. Wang and P. Hu, Nat. Catal., 2018, 1, 291–299.
46. Y. Mao and P. Hu, Sci. China: Chem., 2020, 63, 850–859.
47. X. Sun, P. Wang, Z. Shao, X. Cao and P. Hu, Sci. China: Chem., 2019, 62, 1686–1697.
48. Z. Wang and P. Hu, Sci. China: Chem., 2019, 62, 784–789.
49. J. C. Fornaciari, D. Primc, K. Kawashima, B. R. Wygant, S. Verma, L. Spanu, C. B. Mullins, A. T. Bell and A. Z. Weber, ACS Energy Lett., 2020, 5, 2954–2963.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc05402j

---