Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nano-imaging mass spectrometry by means of high-energy laser desorption ionization (HELDI)
Davide
Bleiner
 ab
ab
aUniversity of Zurich, Winterthurerstrasse 190, 8057 Zürich, Switzerland
bEmpa Materials Science & Technology, Überlandstrasse 129, CH 8600 Dübendorf, Switzerland. E-mail: davide.bleiner@empa.ch
First published on 8th February 2024
Abstract
Reduction of a sampled mass at the nano-scale degrades the sensitivity. Therefore, a theoretical analysis was carried out to assess the sample utilization efficiency, and the leeway for the enhancement of the sensitivity. High (photon)-energy laser desorption ionization (HELDI) is a novel microanalytical technique that uses XUV laser pulses to enhance and homogenize the sensitivity at the nano-scale, especially for light elements. While inspecting nanostructures in 3D, local heterogeneities are critical and are spotted only if the instrumental variance can be discerned from the compositional one. Such underlying information was found to be accessible when studying the data scatter distribution. Such an analytical method was applied to analyze functional thin films of photovoltaic kesterite materials, probed with HELDI hyphenated to time-of-flight mass spectrometry. The results indicated an enhanced analytical capability for imaging light elements and the ability to discern instrumental variances (random errors) from true compositional ones (heterogeneity).
1. Introduction
More than 95% of all matter is based on less than 10% of the periodic table. In particular, elements such as H, C, N, O, and S are the backbone of almost all chemistry. Light elements such as Li, Be, B, F, Na, and P provide unique properties to materials, life chemistry, and environmental cycles. These elements are, however, challenging from a microanalytical standpoint. Partly, this is due to their ubiquitous abundance, causing high background levels. On the other hand, device sensitivities are often a function of the host matrices, which makes quantitation hard. Furthermore, analyte detection in a spatially resolved mode limits the signal amplitude, especially in destructive methods, where signal accumulation is not possible.Spatially resolved analysis is often based on sample mapping, i.e. where a series of spots are collected hyperspectrally.1 In the case when the spot size is orders of magnitude smaller than the region of interest (ROI), smooth “chemical images” are obtained. Often spots of microns are collected on a ROI of 10–100 μm, such that the elemental images are “pixelated”. This limits the possibility to visualize the detailed diffusion and heterogeneity profiles of elements, especially in high gradient interfaces. In fact, the elemental heterogeneity of a functional material may degrade the localization and control of the electrical and optical properties. Unfortunately, starting from loose powder precursors, the preparation of materials can also lead to porosity, or crevices, which would favor elemental trapping and/or migration, especially of the mobile light elements. The microanalysis of these materials is thus important to visualize such a phenomenon, but it is generally challenging to address the chemical details of complex-fabrics nanostructures.
In fact, the collection of elemental signals across a porous fabric is obviously unstable. Previously, it was shown how such a phenomenon could provide chemical and textural information.2 For thin films (scales 10–100 nm), this is particularly challenging, since there is no microanalytical method able for directly accessing its length scales. In fact, some techniques are more suitable for surface analysis (scales < 10 nm), while other methods inspect the bulk (scales > 100 nm). The 10–100 nm gap is frequently either too thick or too thin for any direct quantitation in solid microanalysis.
When dealing with chemical visualization, it is important to distinguish between imaging and mapping.3 In imaging, i.e. microscopy, the heterogeneity is frozen while the entire field of view is acquired concomitantly. In mapping, fluctuation of the data response may be an effect either of the sample heterogeneity or of the shot-to-shot measurement. Thereafter, plotting a calibration curve is a complex problem in such a case. In fact, the assumption of linearity is valid only under the condition of perfect homogenization and matrix-match, which eliminate any compositional variance (i.e. no horizontal error bars).
Therefore, in the quantitative imaging of materials, one can deal with three sources of variance. First, the variance (i.e. noise) of the blank, which is associated with the random measurement error (σo2). Second, the quantitation variance, or repeatability, which is the associated compositional error (σ12). In principle, there is a covariance between the former and the latter. In solid microanalysis, however, heterogeneity is a further compositional variance (σ22), which is observed as a convoluted term with the compositional error. Defects, diffusion profiles, local enrichments or depletion are not accessible selectively, while they are non-covariant to the instrumental error. However, data scatter analysis can reveal such underlying information. While the present work focused on mass spectrometry, it is useful to survey briefly the microanalytical panorama of complementary methods.
For instance, X-ray fluorescence spectrometry, while providing modest access to light elements, is very robust for micro and bulk characterization.4–6 X-Ray photoemission spectrometry is extremely surface-sensitive, and does not have the depth dynamic range to investigate thin films down to the substrate.7 Secondary ion mass spectrometry is also an appreciated method for the microanalytical profiling of thin films, but it lacks a 3D capability, and has severe matrix effects.8,9 Laser ablation methods, with either optical emission (LIBS10–12 or the most recent LIXS13,14) or mass spectrometry (LA-ICP-MS15,16), are, in principle, suitable for the highly spatially resolved analysis of light and heavy elements, but the thick sampling in the micrometer length-scale hamper their use in combination for the nanostructured films of functionalized materials. Finally, glow discharge spectrometry offers excellent depth resolution, but the lateral resolution is quite coarse,17–19 which makes it unsuitable for elemental heterogeneity mapping.20
Extreme ultraviolet (XUV) laser pulses have been accomplished through single-pass amplified spontaneous emission (ASE) across a capillary discharge.21–23 Pulses at λ ∼ 46.9 nm can shrink the diffraction limit and allow accessing nano-scale lateral resolution.24–29 As a further advantage, the high-energy photon at ∼26 eV is just above the ionization energy of He, i.e. of any element in the periodic table. This implies direct single-photon desorption ionization.30 Henceforth, (high-energy, HE) laser desorption ionization (LDI) can dramatically enhance the sensitivity for direct solid microanalysis. The strong absorption cross-section permits improving the depth resolution to the nano-scale.28 As a combined effect, laser microanalysis using XUV pulses offers sub-micron-scale lateral and nano-scale depth resolution sampling, while effectively enabling the direct desorption and ionization of any element of the periodic table (elemental nano-tomography).
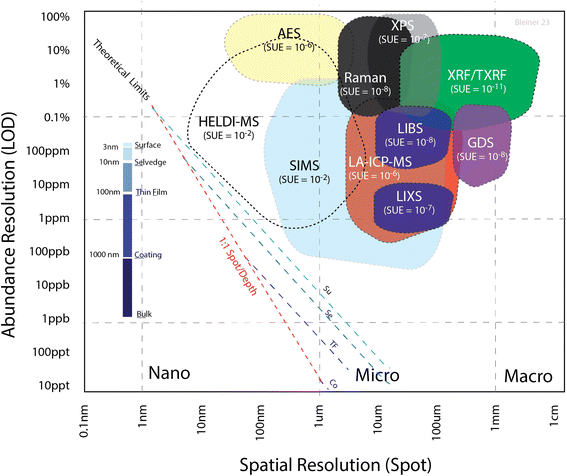
As discussed previously,27,31 there is a tradeoff between the spatial resolution and sensitivity. Fig. 1 summarizes the empirical range of the limit of detection (LOD) for a selection of microanalytical methods, as a function of the spot size. The theoretical limit was calculated from the number of atoms in a given volume, with the width as the spot size and height as the sampling depth. Considering an absolute limit of one atom out of the total number of sampled ones in the volume, the ratio gives the theoretical limit. This value is, in practice, degraded by the sample utilization efficiency (SUE), i.e. the proportion of sampled atoms contributing to the effective signal over the total number of sampled atoms. The fact that all these techniques were far from the theoretical limit (dashed lines, calculated for different depth ranges) suggests that the SUE has huge room for improvement, which should be a research priority in analytical science. Indeed, the SUE was estimated from the shown “cloud plot”, determining the vertical distance between the actual LOD (colored areas) and the corresponding theoretical limits (dashed line). The SUE for each of the analytical techniques is indicated in Fig. 1 next to the acronym of the analytical method. It should be also noted that this cloud plot shows the relative LODs. As pointed out elsewhere,32 in solid microanalysis, absolute and relative LODs can be more or less indicative limits for the various analytical techniques depending on the reference spatial resolution. Since the probed volume can change by several orders of magnitude among the various techniques, a poorer spatial resolution would degrade the absolute figures, even at a constant relative LOD. In the cloud plot (Fig. 1), the absolute LOD increased perpendicularly away from the dashed lines toward the upper right corner of the plot (from zeptograms to nanograms), while the relative LOD increased vertically from bottom up (Y axis).
Summarizing, the use of ion probes is plagued by matrix effects, which can be mitigated using photon probes, even though these are limited by diffraction to the micron scale. On the other hand, the utilization of ion signals (i.e., mass spectrometry) generally offers a better sensitivity. Finally, the use of electron probes offer nano-scale spatial resolution, but requires sample preparation for coating non-conductors. It is noteworthy that the utilization of XUV pulses, as in HELDI, combines the advantages of photons with those of electrons. Furthermore, the large photon energy and cross-section would predict a matrix-independent direct desorption/ionization. This is a preliminary requirement for substantial enhancement of the SUE in a fully quantitative mode.
The aim of this work was to apply HELDI-MS for the super-resolution (i.e. resolution beyond the diffraction limit) hyperspectral depth profiling of nanostructures, using advanced data-processing techniques, to spot defects and heterogeneities at the sub-micron scale. The quality of the chemical data is essential to implement successfully smart mapping procedures. This quality was accomplished here thanks to the microsampling with coherent XUV pulses.
The paper is organized as follows: Section 1 provides a topical introduction, Section 2 summarizes the experimental information to reproduce the results, Section 3 presents the observed data and discusses the insights that can be gained, and Section 4 summarizes the main conclusions.
2. Materials and methods
2.1 HELDI-mass spectrometry
High-energy (HE) photons are defined as those just above the elemental ionization energy. As helium shows the highest ionization energy (24.6 eV), any photon energy above that can, in principle, ionize any element. This direct ionization process is analytically advantageous, and can enable matrix-independent signal generation for mass spectrometry. The prompt photoemission triggered by HE photons in any matrix helps to minimize the desorption damage upon sampling. Laser desorption ionization (LDI) is well known in mass spectrometry.33 In particular, matrix-assisted LDI (MALDI34) is quite popular in organic mass spectrometry, but requires a complex sample preparation to enhance the coupling of the laser and target. In HELDI, in contrast, high photon energy in the XUV favors the strong coupling of radiation to the sample material as it is, without any need for sample preparation.The 3D analysis was carried out by means of combining a prototype XUV laser and a self-developed mass spectrometer.35 Argon discharge in a ceramic capillary generated coherent pulses (λ = 46.9 nm or 26 eV) with a deposited energy of approx. 3 μJ over a duration of about 1 ns (FWHM), such that the fluence was approx. 380 J cm−2. The pulse to pulse energy variance was <1%. The samples were mounted on a micrometric stage that could translate over the x and y axis to expose various positions of the sample (Fig. 2a). XUV microsampling is devoid from solid particles, as is also the case in traditional optical laser ablation, but produces an ion plume in the source of the mass spectrometer. In fact, the high photon energy ionizes the sample photolytically. The repeated delivery of pulses (2 Hz) to a specific spot permits retrieving a vertical depth-resolved profile. This mode of acquisition is called z-profiling. Shifting the sample under the laser pulse, gives a lateral surface-resolved profile. This mode of acquisition is called xy-profiling. The online mass spectrometry in the laser sampling gives a hyperspectral imaging. Fig. 2a shows the sample surface after the HELDI sampling was carried out.
2.2 Thin-film samples
The materials used for preparing the thin-film samples included a precursor solution of thiourea (99%+, Sigma-Aldrich), tin chloride dihydrate (SnCl2·2H2O, 98%, Sigma-Aldrich), zinc chloride (ZnCl2, 99.99%, Alfa Aesar), copper chloride dihydrate (CuCl2·2H2O, ≥99.99%, Sigma-Aldrich), and lithium chloride anhydrous (LiCl, 99%, Fluka) dissolved in dimethyl sulfoxide (DMSO, 99.9%, Alfa Aesar). A 200–300 nm thick SiOx alkali diffusion barrier layer was sputtered onto a 1 mm thick soda lime glass with a subsequent deposition of 1 μm of molybdenum. The precursor solution was spin coated onto the Mo layer and dried on a hotplate at 320 °C in air. The spin-coating and drying steps were repeated 12 times in order to obtain the desired precursor film thickness of 1.5 μm. The sample was annealed in a rapid thermal processing furnace (RTP Annealsys AS ONE 150) inside a closed graphite box with selenium pellets (800 mg). The temperature gradient employed for annealing was the three-stage process with holding at 300 °C, 500 °C, and 550 °C. CZTS (CuZnSn sulfide) tin films were deposited and implanted with Li, as this is known to enhance the photovoltaic efficiency. Fig. 2b shows the elemental distributions as obtained by means of energy dispersive X-ray spectrometry on a cross-section made with a focused ion beam.2.3 Hyperspectral data collection and processing
The 10 × 10 × 10 data point blocks (each point is a full MS spectrum) were processed by a self-written m-script (Matlab) that allowed extracting the underlying information to be visualized in a few seconds. The script performed a time-of-flight mass calibration of the raw signals based on a few reference peaks indicated by the user, which in the present work were at nominal mass-to-charge values of 6, 12, 23, 63, 80, 120 Da. The average mass spectra (and variances) were calculated layer by layer. After that, the spectra acquired across a 3D space were assembled in a 3D matrix. Plots could be extracted from the 3D matrix to visualize specific tomographic projections. In general, two types of projections are preferred: layers and cross-cuts. The former refers to the xy-planes parallel to the sample surface (layer at zero depth) depth-wise. Cross-cuts are the zy-planes showing the depth profile. In order to show all the zy-planes in one plot, the 3D matrix is “unfolded” like a paper map. This way one can observe next to each (every 10 points) the next zy-planes, which allows visually correlating the depth profiles in the third dimension.Based on the total collected signal, the script normalizes the elemental signals to obtain a semi-quantitative output. This implies a comparable sensitivity of all the elements because of the high-energy photoionization. Finally 3D elemental mappings are visualized and can be rotated and inspected to show the full block composition of the analyzed domain.
By plotting elemental intensities across a xyz-position grid (3D block), one can visualize the semi-quantitative distribution of elemental contents in the material (chemical tomography). The latter is affected by the material fabric (e.g. porosity, crevices), by the kinetics (e.g. interdiffusion), and impurities. Each of these factors has characteristic length-scales. Consequently, the local values in one specific xyz-position must be compositionally consistent with all neighboring data points in the 3D block. The direct plotting of the raw-data lacks any statistical or chemometrical ensemble-validation. In fact, it is essential to test the local value in the form of a data network consistency. Besides a better confidence, one can also gain length-scale insights, because connecting the measured dots allows retrieving insightful distributions (kernels). The sub-segmentation of the base scale (spot size), by means of adaptive smooth kernels, helps obtaining detailed profiles of the analytes. Therefore, this study first assessed chemometric methods, and then applied them to a real case in materials science of thin films.
2.4 Fundamental aspects
The convolution of σo and σ1 (see introduction) with σ2 causes the calibration plot to spread out. The mean counting produced by a given amount of analyte (i.e. the number of atoms) assumes a well-known shape dictated by the Poisson distribution. The latter tends to flatten out at a larger mean, until it becomes almost indistinguishable from a Gaussian curve. The exact values of the signal noise (σo) and repeatability (σ1) affect the sensitivity (S). The limit of detection (LOD) is thereafter calculated as follows:36,37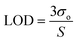 | (1) |
In a solid sample, one can write LOD ∼ σ1, as explained in detail here below. This is understood since the “limit of detection” is ultimately limited by the repeatability. Henceforth, one can determine the sensitivity from eqn (1) as a ratio of the noise and repeatability, as follows:
| S = 3σo/σ1. | (2) |
A classical calibration curve assumes that the data point is a delta function, i.e. a point with no concentration spread. The spread indicates the probability of finding a data point in different positions within given confidence intervals. Poisson statistics predicts such a point spread function for a counting statistics limited case. However, the occurrence of heterogeneity (σ2) can alter this model, as shown in Fig. 3, where only four reference points are plotted (see below). The distribution envelope is convex along the calibration line and transverse to it. As the points are higher in mean value, the absolute probability sinks, because the distribution flattens.
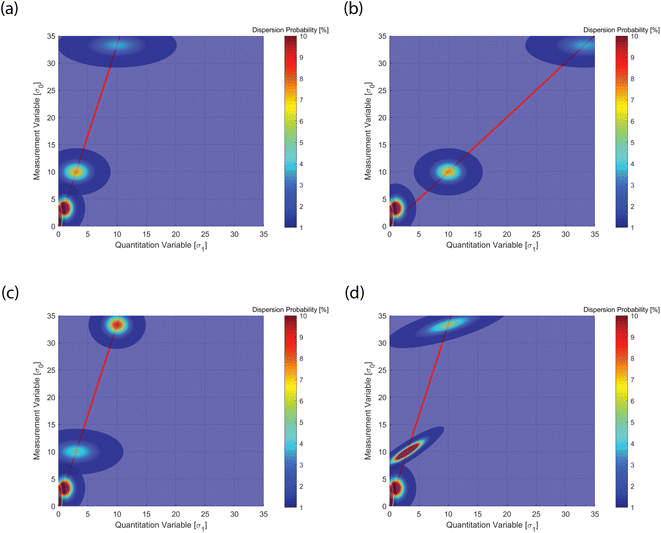 | ||
| Fig. 3 Point spread function of the four reference thresholds (LOB, LOD, LOQ, LOL) with values given in Table 1. (a) Set A in Table 1, standard case with values according to canonical definitions of the four limits; (b) set B visualizes a change in means for LOQ (μq = 10) and LOL (μq = 33.3); (c) set C visualizes a change in variances for LOQ (σ12 = 6) and LOL (σ12 = 2); (d) set D visualizes a change in the covariances for LOQ (cov01 = 2) and LOL (cov01 = 3). The four cases visualize how the calibration lines and data point spread function (PSF) are distributed in relation to the underlying sources of the statistics. See text for discussion. | ||
Fig. 3 was realized plotting a few important reference values for quantitation as indicated in the guideline protocols, and the associated calibration line. For instance ICH-Q2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 or CLSI EP17
38 or CLSI EP17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39 define three reference thresholds and Table 1 (case A) summarizes such thresholds, which are the basic “data points” in Fig. 3a. First, the limit of blank (LOB) is the “highest apparent analyte concentration expected to be found when replicates of a sample containing no analyte are tested”. The LOB is estimated as follows:
39 define three reference thresholds and Table 1 (case A) summarizes such thresholds, which are the basic “data points” in Fig. 3a. First, the limit of blank (LOB) is the “highest apparent analyte concentration expected to be found when replicates of a sample containing no analyte are tested”. The LOB is estimated as follows:
| LOB = μblank + 1.645σblank | (3) |
| LOB | LOD | LOQ | LOL | |
|---|---|---|---|---|
| Mean of signal | (A–D) 1.645 | (A–D) 3.3 | (A–D) 10 | (A–D) 33.3 |
| Mean of concentration | (A–D) 0 | (A–D) 1 | (A, C, D) 3 | (A, C, D) 10 |
| (B) 10 | (B) 33.3 | |||
| Variance of signal | (A–D) 1.645 | (A–D) 1.645 | (A–D) 1.645 | (A–D) 1.645 |
| Variance of concentration | (A–D) 0.1 | (A–D) 1 | (A, B, D) 3 | (A, B, D) 10 |
| (C) 6 | (C) 2 | |||
| Covariance between signal and concentration | (A–D) 0 | (A–D) 0 | (A, B, C) 0 | (A, B, C) 0 |
| (D) 2 | (D) 3 |
Second, the limit of detection (LOD) is defined as the threshold abundance needed to assess reliably the analyte occurrence in a qualitative analysis.37 The LOD may reside at quantitation values below the linear range, and therefore is not necessarily a point on the calibration line. The LOD is estimated as follows:
| LOD = μblank + 3.3σblank | (4) |
Thereafter, such a signal level corresponds to the norm (or unit) in the quantitation variable (X axis). The difference between the absolute versus relative LOD is very important in solid microanalysis, as discussed above.32 Finally, the limit of quantitation (LOQ) is defined as the threshold value for reliable quantitative analysis. Following a similar criterion as above (one-sided, 95%), the LOQ is estimated as follows:
| LOQ = μblank + 10σblank | (5) |
In terms of the quantitation variable (x axis), eqn (5) indicates that in the definition of the LOQ, the signal corresponds to 3 times the LOD (Fig. 3a). This pragmatic criterion is not globally adopted, and the analytical community has been lax in defining binding terms. Actually, the discussed analytical nomenclature is not officially coded for solid microanalysis, but workers have resorted to the available one for wet samples. However, it must be said that solid microanalysis has some peculiarities that do not facilitate a direct extrapolation. First, the blank is not easily estimated, as matrix-matched reference blanks are rare. Second, multipoint calibrations are not so easy, since it is difficult to get a series of matrix-matched solid standards of progressive concentration. Commonly in solid microanalysis, one relies on a bracketing calibration within the LOQ and an upper bound. The latter defines the limit of linearity (LOL). This is not the detector LOL, but the operative (calibrated) LOL. Adopting a similar criterion as above, the present work defined the LOL as the fourth upper point in Fig. 3 as follows:
| LOL = μblank + 33.3σblank | (6) |
In terms of the quantitation variable (x axis), the LOQ signal would correspond to 10-fold the LOD based on the adopted criterion (Fig. 3a). Obviously, one can have a dynamic range of calibration much larger than such an order of magnitude. In this work, the attention was on an extreme case, were outliers can more dramatically affect the calibration. Fig. 3 shows the mentioned four reference values, in order bottom up, LOB, LOD, LOQ, LOL, in four different cases, indicated as A (Fig. 3a), B (Fig. 3b), C (Fig. 3c), D (Fig. 3d) in Table 1. The dispersion40 is given by point spread functions (PSFs) that represent the scatter probabilities of the data points. These are the consequence of either measurement error or material heterogeneity. The values are characterized by five parameters, i.e. the mean (for x and y coordinates), variance (x and y) and covariance (this is symmetric, so only one value). First, the centroid of the points is associated with the mean values as coordinates: μquant, μsignal. Following the discussion above, these are given as follows (Table 1): LOB (0, 1.645), LOD (1, 3.3), LOQ (3, 10), and LOL (10, 33.3).
3. Results and discussion
Following the discussion above, Fig. 3 shows the multivariate point spread function (PSF) calibration plots. PSF is a well-established concept in optics and photonics. In Fig. 3a, one observes a basic case, where the canonical protocol values discussed above (eqn (3)–(6)) are shown, with zero covariance (see Table 1, set A). The latter implies no sample heterogeneity, only counting statistics. In Fig. 3b, the sensitivity (calibration slope) is reduced, while the PSF is identical to the former case (see Table 1, set B). In Fig. 3c, the quantitation variance is increased, while all the other values remain identical (see Table 1, set C). This causes a change in the PSF. This is not a consequence of changes in the sensitivity or instrumental error, but can be attributed to sample heterogeneities. Finally, in Fig. 3d, only the covariance is changed (see Table 1, set D). This has the effect of stretching the PSF, because of the enhanced correlation.Analysis of data point distributions is thus extremely insightful to distinguish data scatters in the PSF that could be attributed to instrumental or compositional variances. The latter can cause “bad” non-linearities in the ensemble data set, which are not to be considered as indicating poor measurement performance. In fact, this study highlights that detailed analysis of the data PSF can value the variance by aiding an educated assessment.
In order to quantify such effects, one needs descriptors associated with the data linearity (heterogeneity-bound regression spread) and the linearity slope (sensitivity-bound correlation). The former corresponds to the Pearson correlation coefficient,41 while the latter corresponds to the Spearman rank correlation coefficient.42 While the former reflects the scatter but not the regression slope, the latter assesses how monotonically steep a sensitivity curve is. Henceforth, the Pearson correlation coefficient in a PSF subset is a good metric for assessing the occurrence of heterogeneity, because in such a case the data do not scatter along the sensitivity slope. On the other hand, the Spearman rank correlation coefficient is a good metric of the variance associated with counting, because the PSF subset is scattered along the sensitivity slope. A comparison of the two descriptors is insightful to discern the source of variance, i.e. instrumental or compositional.
One may wonder, besides considering the analytical models, how many points are needed to populate the PSF within a certain confidence range to be able to discern. From probability theory, Chebyshev43,44 considered well-known inequality to express the probability of a deviation from the mean as k-times the standard deviation, as follows:
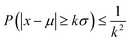 | (7) |
3.1 Heterogeneity analysis
In the case of compositionally structured samples, e.g. multilayer thin films, one has to consider that the external precision (spot to spot) dominates over the internal precision (random error). Therefore, σ2 is important to assess the heterogeneity of a material, induced either by design (layered composition) or by unwanted contamination during the material synthesis. The challenge is to discern statistically between signal variance consistent with measurement uncertainty and compositional heterogeneity. The latter is correlated to the layering and/or porosity. Therefore, one can compare the standard deviation σ1 at a given depth z (lateral signal heterogeneity) to that obtained over a fixed position xy (vertical signal heterogeneity). The latter is affected by the ablation depth and thin-film layering (material structure).To that purpose, the local sensitivity was determined here in the experimental data set, following the procedure discussed above. Thereafter, all the LODs in a 3D sampling matrix were determined for each laser spot, in order to build a population distribution. This procedure was consistent with the classical multipoint calibration, but was based on a larger ensemble of data points, rather than on a limited set of them.
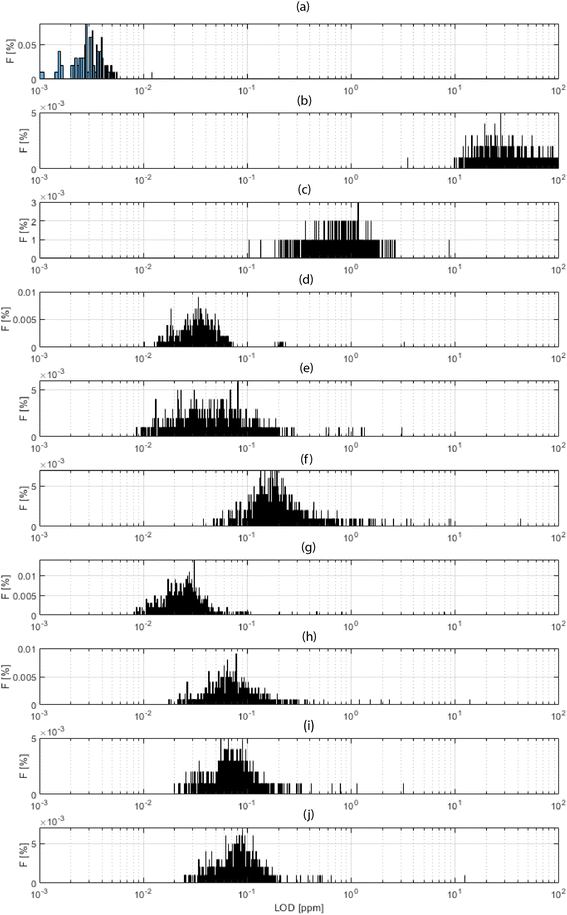
Fig. 4 shows a histogram for the distribution of the obtained LODs for each xyz shot in the 3D block, for a selection of elements. Fig. 4a shows the total ion current (TIC), which is a “fictive analyte” for a ceiling assessment of the ultimate LOD assuming the use of the entire collected signal. This upper-end value of the dynamic range lay in the 3 ppb domain. At the other extreme of the dynamic range, Fig. 4b shows the LOD calculated for the background equivalent concentration (BEC). This lower-end value lay in the range of 25 ppm. The range of these values, 3–25 ppm, thus indicated the bracketing range of sensitivities for HELDI mass spectrometry of any target analyte. Specifically, Fig. 4c–j show the LODs for a selection of major, minor and trace elements in the sample materials (see caption for details).
As the range of sensitivities was homogeneously restricted within less than one order of magnitude, one can conclude that TIC signal normalization would provide a very accurate semi-quantitative measure of the elemental concentrations. The efficient ionization mechanism of HELDI, thanks to the high photon energy as discussed above, is a major advantage to achieve a homogeneous distribution of semi-quantitative sensitivities.
Furthermore, the LOD distributions shown in Fig. 4 were characterized with respect to the mode and spread of the individual histograms. The histogram mode indicated the value for σ1. In fact, this mode was the most frequent response value, which was indicative of the sensitivity. On the other hand, the histogram standard deviation was related to σ2. In fact, the histogram spread was associated with the heterogeneity. Notably, if the analyte accumulated mainly in one layer, e.g. hydrogen on the surface, its 3D LOD could be dramatically affected by a drop of intensity in other parts of the sample.
Indeed, the case of H is worth a few more words (Fig. 4c). Its mode occurred at higher values than all the other analytes, and this was because of its poor concentration, mainly on the surface. As shown below, the concentration dropped rapidly over a few tens of nm. Impressively, the data clearly indicated that HELDI could spot surface H with an LOD of approx. <1 ppm. To the best of available knowledge, this analytical capability is unmatched by any other existing method.
Following the discussion in Section 3.1, the histograms shown in Fig. 4 permitted obtaining σ1 and σ2. In fact, if the distribution of the data was fully dictated by counting statistics (Poisson dispersion), the spot-to-spot variance would be given by the fluctuation of the measurement precision. Hence in this standard case, the spread (σ2) was equal to the mode (σ1). In the case of an overdispersed histogram45 (hyperskedastic or spread larger than the mode), one could conclude that the increase in spread of the data values was a consequence of the heterogeneity. In the theoretical opposite case (not observed here) of an underdispersed histogram (hyposkedastic spread much lower than the mode), one could conclude that the material suffered from contamination, i.e. a systematic bias shifted the data population. Following this analysis, the ratio σ2/σ1 is proposed to determine the level of heterogeneity of the 3D block analyzed. From a practical standpoint, this is an alternative method to the current comparison of the Pearson correlation and Spearman rank correlation mentioned above, and is simpler and more straightforward.
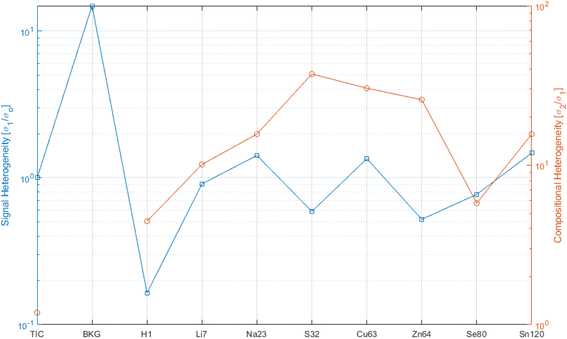
Fig. 5 shows the heterogeneity, with respect to the signal fluctuation (blue curve, LHS ordinate) and the compositional fluctuation (red curve, RHS ordinate), for a selection of analytes. For reference for the extreme ranges, again “fictive analytes”, such as TIC and the background (BKG), are shown for the signal fluctuation curve. One should look at the blue curve with respect to the threshold of 1. Lower values than this threshold indicate that the signal experienced its major charge along the vertical (depth) direction. This was the case for H that was highly concentrated on the surface, while it dropped rapidly over a depth of a few tens of a nm. All other analytes stayed close to 1, which indicates that the lateral and vertical signal fluctuation were comparable.
The red curve indicates how much compositional heterogeneity affected the various analytes. The case of H has been discussed. All other analytes indicated a compositional heterogeneity of 5 to 40. To a certain extent, this is the consequence of the material structure, where the analyte tends to reside mainly in the functional layer of the reference. Matrix elements, such as S, Cu, and Zn, were not localized in the functional layers. Henceforth, as a function of the porosity or impurity of the matrix, these analytes indicated larger values. Similarly, Na came from the SLG (soda lime glass) substrate. Li was introduced as an implanted ion, and therefor was less heterogeneous. Still the implanted dose control could be better, as shown by the case of H as homogeneous surface impurity.
3.2 Tomographic quantitation
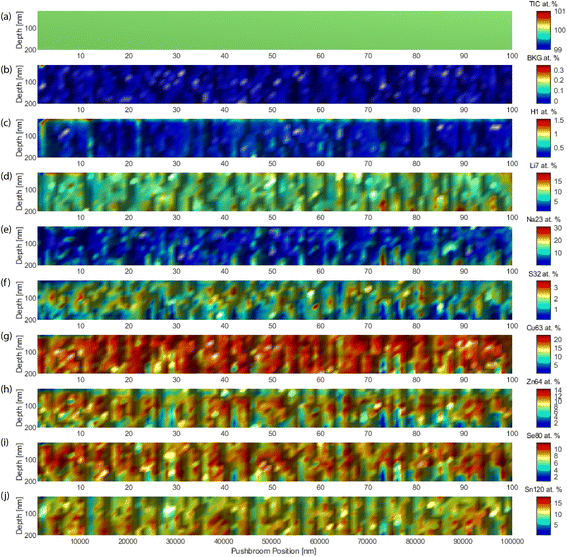
Fig. 6 shows the quantitative analyte distributions in cross-sections, with an edge side of 10 μm. The abscissa is the push-broom coordinate, which unfolds the 3D block every 10 points, the next ten points are plotted one layer more above the page, like unfolding a map. The granular structure and porosity of the material were evident. Careful observation highlighted the layered structure. The obtained concentrations (heat map color scales) were in agreement with the nominal concentration of the various analytes.3.3 Super-resolution by supervised learning
In order to enhance the details, a specific chemical visualization by means of supervised learning was deployed. The chemical visualization tested in this work was based on a convolution bootstrapping method. In this procedure, the block of data points was analyzed in smaller subgroups. Within such subgroups, the relations between pairs, i.e. in terms of covariance, were computed. As the code evaluated covariances between different alternatives, it also calculated standard errors, confidence intervals, etc. With this mathematical analysis, the hypothesis is tested, which was the function that best (minimization of the covariance) represented the distribution (concentration) of a given elemental signal. This was useful to enhance the resolution while statistically computing kernel functions between all pairs of data points xi and xj (for clarity here discussed in 1D, but the results were computed on xyz data collection blocks). Obviously, convolution is a straightforward image-processing technique that fits the raw value of a pixel according to the values of its surrounding pixels. The specific convolution kernel chosen is important to parametrize the supervised learning process.46 This can be parameterized in terms of the kernel parameters θ, which scales as a function of the correlation between two sample points; whereby the closer these points, the higher the expected correlation. The latter could be expected to degrade as a function of coordinate interspacing |xi − xj|, because, over a characteristic length-scale, the thin film will show heterogeneity. Hence, it is useful to express the covariance function as k(xi,xj|θ), using a Gaussian kernel defined as follows: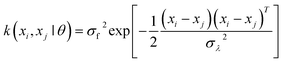 | (8) |
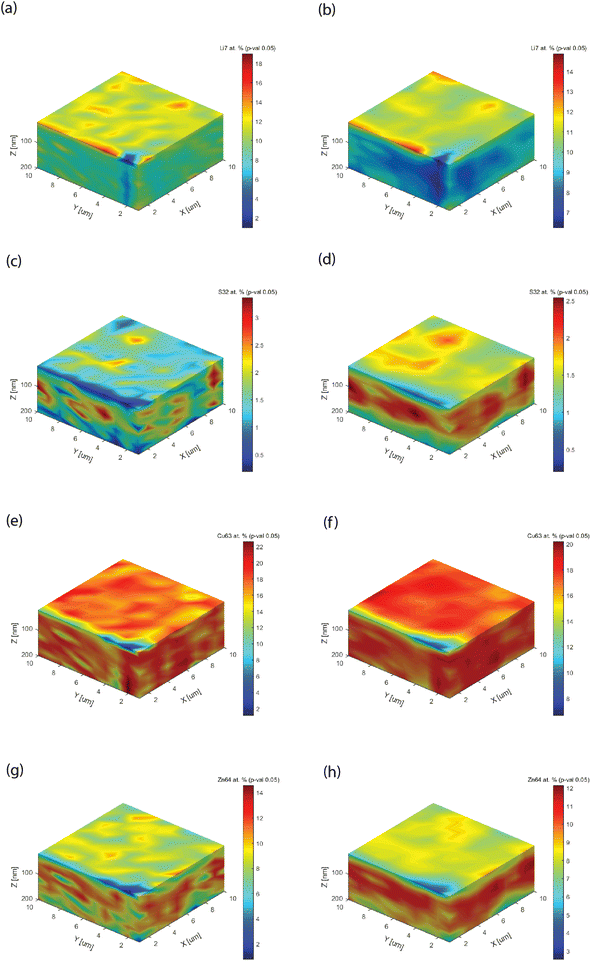
Fig. 7 shows the 3D block distribution, computed for two kernel sizes (showing how many data points are used for covariance analysis), a direct neighbor point size (k1 = 1) on x, y, and z, and a three-point size on each dimension (k2 = 3). These blocks can be rotated or dissected, as the internal parts (not shown) are also quantified. Increasing the kernel size makes the data processing more intensive, while averaging out the raw pixelation. If the kernel size is much larger than the characteristic heterogeneity (here k = 3), one will not notice any visualization change. Besides the graphical improvement of the chemical images, i.e. removal of pixelation, important technical improvements of the information could be observed. First, the leveling of the analyte concentration, as best shown in Fig. 7a and b (Li). An optimization of the analyte distribution allows improving the chromatic scale. Second, the appearance of a functional layer could be clearly observed, as shown in Fig. 7c and d as well as Fig. 7g and h. The examples are emblematic, because with a unit kernel size, the block showed a spotted structure. In Fig. 7e, one could also observe a spotted structure, but only with a larger kernel size can one notice the bulk matrix content (Fig. 7f) instead of a layer for Cu.
4. Conclusions
Direct solid microanalysis is a powerful analytical method to highlight compositional gradients in a material. Its quantitative approach is limited if a classical external calibration is adopted, due to the lack of blank assessment and matrix-matched calibration standards. It also becomes even less robust while reducing the observation length-scale down to the nano-scale. The fundamental aspects of this approach have been studied to identify the underlying information in the data scatter. Besides, shot noise, true scatter due to heterogeneity is highlighted. The multivariate convolution generated a point spread function of the single calibration points. The structure of such a spread, with respect to the shape and slope, permitted discerning instrumental variances from compositional ones. A detailed analysis, with quantitative descriptors (e.g. Pearson vs. Spearman) gave insights into 3D chemical imaging (chemical tomography). This model was implemented in XUV laser mass spectrometry, to retrieve super-resolution information by means of supervised learning procedures.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was funded with internal laboratory funding (KST 50203). The author is grateful to Dr Yaroslav Romanyuk for sharing samples of thin films.References
- J. M. Amigo, H. Babamoradi and S. Elcoroaristizabal, Hyperspectral image analysis. A tutorial, Anal. Chim. Acta, 2015, 896, 34–51 CrossRef CAS PubMed.
- G. Muller, F. Stahnke and D. Bleiner, Fast steel-cleanness characterization by means of laser-assisted plasma spectrometric methods, Talanta, 2006, 70(5), 991–995 CrossRef PubMed.
- A. Borgschulte, et al., Imaging the Chemistry of Materials Kinetics, Chimia, 2022, 76(3), 192 CrossRef CAS PubMed.
- K. H. Janssens, F. Adams and A. Rindby, Microscopic X-Ray Fluorescence Analysis, Wiley, Chichester, 2000, vol. 434 Search PubMed.
- A. A. Hummer and A. Rompel, The use of X-ray absorption and synchrotron based micro-X-ray fluorescence spectroscopy to investigate anti-cancer metal compounds in vivo and in vitro, Metallomics, 2013, 5(6), 597–614 CrossRef CAS PubMed.
- P. Lienemann and D. Bleiner, Elemental analysis with X-ray fluorescence spectrometry, in Short-Wavelength Imaging and Spectroscopy Sources, SPIE, 2012 Search PubMed.
- O. Sambalova, et al., Hard and soft X-ray photoelectron spectroscopy for selective probing of surface and bulk chemical compositions in a perovskite-type Ni catalyst, Surf. Interface Anal., 2020, 52(12), 811–817 CrossRef CAS.
- A. Priebe, et al., The matrix effect in TOF-SIMS analysis of two-element inorganic thin films, J. Anal. At. Spectrom., 2020, 35(6), 1156–1166 RSC.
- D. Bleiner, et al., FIB, TEM and LA-ICPMS investigations on melt inclusions in Martian meteorites-Analytical capabilities and geochemical insights, Talanta, 2006, 68(5), 1623–1631 CrossRef CAS PubMed.
- L. Radziemski and D. Cremers, A brief history of laser-induced breakdown spectroscopy: from the concept of atoms to LIBS 2012, Spectrochim. Acta, Part B, 2013, 87, 3–10 CrossRef CAS.
- J. D. Winefordner, et al., Comparing several atomic spectrometric methods to the super stars: special emphasis on laser induced breakdown spectrometry, LIBS, a future super star, J. Anal. At. Spectrom., 2004, 19(9), 1061–1083 RSC.
- K. Amal, et al., Comparison between single-and double-pulse LIBS at different air pressures on silicon target, Appl. Phys. B: Lasers Opt., 2006, 83, 651–657 CrossRef CAS.
- D. Qu, et al., High-precision mapping of fluorine and lithium in energy materials by means of laser-induced XUV spectroscopy (LIXS), Spectrochim. Acta, Part B, 2021, 181, 106214 CrossRef CAS.
- D. Bleiner, et al., Laser-induced XUV spectroscopy (LIXS): From fundamentals to application for high-precision LIBS, Spectrochim. Acta, Part B, 2023, 204, 106668 CrossRef CAS.
- R. E. Russo, Laser ablation research and development: 60 years strong, Appl. Phys. A: Mater. Sci. Process., 2023, 129(3), 168 CrossRef CAS.
- C. Neff, et al., Laser Ablation Inductively Coupled Plasma Mass Spectrometry–One Method, Many Applications, in European Winter Conference on Plasma Spectrochemistry, National Institute of Chemistry, Slovenia, 2023 Search PubMed.
- D. Zheng, P. Volovitch and T. Pauporté, What Can Glow Discharge Optical Emission Spectroscopy (GD-OES) Technique Tell Us about Perovskite Solar Cells?, Small Methods, 2022, 6(11), 2200633 CrossRef CAS PubMed.
- R. N. Owen, S. L. Kelly and A. G. Brenton, Towards a universal ion source: glow flow mass spectrometry, Int. J. Mass Spectrom., 2021, 466, 116603 CrossRef CAS.
- N. Hazel, J. Orejas and S. J. Ray, Evaluation of solution-cathode glow discharge atomic emission spectrometry for the analysis of nanoparticle containing solutions, Spectrochim. Acta, Part B, 2021, 176, 106040 CrossRef CAS.
- R. Muller, et al., Depth-Profiling Microanalysis of CoNCN Water-Oxidation Catalyst Using a lambda = 46.9 nm Plasma Laser for Nano-Ionization Mass Spectrometry, Anal. Chem., 2018, 90(15), 9234–9240 CrossRef CAS PubMed.
- J. J. Rocca, et al., Demonstration of a discharge pumped table-top soft-x-ray laser, Phys. Rev. Lett., 1994, 73(16), 2192–2195 CrossRef CAS PubMed.
- D. Bleiner, X-ray Lasers using a Plasma Medium: Tabletop Beams Got Brighter than Synchrotrons, in SPG Mitteilungen, Swiss Physical Society, Basel, 2022 Search PubMed.
- S. Heinbuch, et al., Desk-top size high repetition rate 46.9 nm capillary discharge laser as photoionization source for photochemistry applications, in Soft X-Ray Lasers and Applications VI, SPIE, 2005 Search PubMed.
- I. Kuznetsov, et al., Three-dimensional nanoscale molecular imaging by extreme ultraviolet laser ablation mass spectrometry, Nat. Commun., 2015, 6, 6944 CrossRef CAS PubMed.
- D. Bleiner, Tabletop Beams for Short Wavelength Spectrochemistry, Spectrochim. Acta, Part B, 2020, 105978 Search PubMed.
- D. Bleiner, The science and technology of X-ray lasers: a 2020 update, XVII International Conference on X-Ray Lasers, SPIE, 2021, vol. 11886 Search PubMed.
- D. Bleiner, L. Juha and D. Qu, Soft X-ray laser ablation for nano-scale chemical mapping microanalysis, J. Anal. At. Spectrom., 2020, 35(6), 1051–1070 RSC.
- D. Bleiner, et al., XUV laser mass spectrometry for nano-scale 3D elemental profiling of functional thin films, Appl. Phys. A: Mater. Sci. Process., 2020, 126(3), 1–10 CrossRef.
- D. Bleiner, et al., Evaluation of lab-scale EUV microscopy using a table-top laser source, Opt. Commun., 2011, 284(19), 4577–4583 CrossRef CAS.
- F. Dong, et al., Study of hydrogen-bonded and metal-oxide clusters using single photon ionization from a compact soft x-ray laser, in 2006 Conference on Lasers and Electro-Optics and 2006 Quantum Electronics and Laser Science Conference, IEEE, 2006 Search PubMed.
- D. Bleiner, et al., Spatially resolved quantitative profiling of compositionally graded perovskite layers using laser ablation-inductively coupled plasma mass spectrometry, J. Anal. At. Spectrom., 2003, 18(9), 1146–1153 RSC.
- N. Omenetto, et al., Absolute and/or relative detection limits in laser-based analysis: the end justifies the means, Fresenius' J. Anal. Chem., 1996, 355, 878–882 CrossRef CAS PubMed.
- K. Song and Q. Cheng, Desorption and ionization mechanisms and signal enhancement in surface assisted laser desorption ionization mass spectrometry (SALDI-MS), Appl. Spectrosc. Rev., 2020, 55(3), 220–242 CrossRef CAS.
- C. Keller, et al., Comparison of Vacuum MALDI and AP-MALDI Platforms for the Mass Spectrometry Imaging of Metabolites Involved in Salt Stress in Medicago truncatula, Front. Plant Sci., 2018, 9, 1238 CrossRef PubMed.
- Y. Arbelo and D. Bleiner, Tabletop extreme ultraviolet time-of-flight spectrometry for trace analysis of high ionization energy samples, Rapid Commun. Mass Spectrom., 2019, 33(14), 1196–1206 CrossRef CAS PubMed.
- H. P. Longerich, S. E. Jackson and D. Günther, Inter-laboratory note. Laser ablation inductively coupled plasma mass spectrometric transient signal data acquisition and analyte concentration calculation, J. Anal. At. Spectrom., 1996, 11(9), 899–904 RSC.
- Analytical Methods Committee AMCTB No. 92, The edge of reason: reporting and inference near the detection limit, Anal. Methods, 2020, 12(3), 401–403 RSC.
- ICH Quality Guidelines: An implementation Guide, ed. A. Teasdale, D. Elder and R. W. Nims, John Wiley & Sons, 2017 Search PubMed.
- D. A. Armbruster and T. Pry, Limit of blank, limit of detection and limit of quantitation, Clin. Biochem. Rev., 2008, 29(suppl. 1), S49 Search PubMed.
- Analytical Methods Committee, AMCTB No. 70, An analyst’s guide to precision, Anal. Methods, 2015, 7(20), 8508–8510 RSC.
- J. Benesty, J. Chen and Y. Huang, On the importance of the Pearson correlation coefficient in noise reduction, IEEE Trans. Audio Speech Lang. Process., 2008, 16(4), 757–765 Search PubMed.
- J. H. Zar, Significance testing of the Spearman rank correlation coefficient, J. Am. Stat. Assoc., 1972, 67(339), 578–580 CrossRef.
- J. G. Saw, M. C. Yang and T. C. Mo, Chebyshev inequality with estimated mean and variance, Am. Statistician, 1984, 38(2), 130–132 Search PubMed.
- A. W. Marshall and I. Olkin, Multivariate Chebyshev inequalities, Ann. Math. Stat., 1960, 1001–1014 CrossRef.
- J. M. Hilbe, Modeling Count Data, Cambridge University Press, 2014 Search PubMed.
- C. E. Rasmussen and C. K. Williams, Gaussian Processes for Machine Learning, Springer, 2006, vol. 1 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |