Achieving high color purity in multi-resonance thermally activated delayed fluorescence emitters through a substitution-driven design strategy†
Wanlin
Cai
 a,
Cheng
Zhong
b and
De-Yin
Wu
a,
Cheng
Zhong
b and
De-Yin
Wu
 *a
*a
aState Key Laboratory of Physical Chemistry of Solid Surface, Collaborative Innovation Center of Chemistry for Energy Materials, and Department of Chemistry, College of Chemistry and Chemical Engineering, Xiamen University, Xiamen, 361005, P. R. China. E-mail: dywu@xmu.edu.cn
bHubei Key Lab on Organic and Polymeric Optoelectronic Materials, Department of Chemistry, Wuhan University, Wuhan, Hubei 430072, P. R. China
First published on 8th June 2023
Abstract
To improve the visual quality and develop high-resolution displays, organic light-emitting diodes (OLEDs) with high color purity have garnered increasing attention. The color purity of OLEDs, which is determined by the full width at half-maximum of emission spectra, is associated with the vibronic coupling of emitters between the ground and emitting states. In this work, detailed theoretical analyses of the reorganization energy, which can characterize the strength of vibronic coupling, were conducted to clarify the color purity variations of B, O-doped polycyclic aromatic compounds with multi-resonance thermally activated delayed fluorescence (MR-TADF). The calculated results reveal that alterations in the bond length make the main contribution to the reorganization energies of these highly conjugated aromatic molecules. It is found that the origin of the large reorganization energy can be elucidated from the perspective of molecular orbitals (MOs). Moreover, the reorganization energy variations among these molecules can be rationalized by MO distribution. Based on these findings, we propose two substitution-driven design strategies to improve color purity. The first strategy involves introducing a neutral phenyl group to delocalize the orbital distribution, thereby weakening the bonding or antibonding character in frontier molecular orbitals of the bonds with a large reorganization energy. The second strategy entails the substitution at the position related to large reorganization energy with electron-donating or electron-withdrawing groups, thus decreasing the bond order difference between the MOs involved in the transition.
1. Introduction
Organic light-emitting diodes (OLEDs) have attracted extensive attention from both academia and industry owing to their excellent photoelectric properties and great potential in next-generation lighting devices.1–4 Despite numerous advantages of OLEDs, the broad emission property in most organic materials is unfavorable to high-definition displays with high color purity.5–7 This problem has become increasingly important and deserves further exploration. The major hurdle in achieving narrow emission is the vibronic coupling between the ground (S0) and emitting states, which is associated with the intensity of vibronic transitions (vibrational peaks) in the emission spectrum.8–11Although many fluorescence molecules can show narrow emission, only 25% of excitons of these materials can be utilized, which limits their further development.5,12 Metal complexes with theoretical 100% exciton utilization were also considered as potential molecules for achieving a small full width at half-maximum (FWHM).13,14 However, the use of noble metal complexes increases the cost and leads to environmental contamination. As a result, it is necessary to develop OLEDs based on pure organic molecules with high exciton utilization. From this perspective, third-generation OLEDs based on thermally activated delayed fluorescence (TADF) materials with a small energy gap between the lowest singlet excited state (S1) and the lowest triplet excited state (T1) are suitable candidates.3,15–17 The small energy gap can facilitate the up-conversion of triplet excitons to the S1 state, enabling efficient triplet exciton utilization. Unfortunately, conventional donor–acceptor type TADF emitters usually show broad emission with a typical FWHM of around 70–120 nm.5,7 This is because the small energy gap in conventional TADF emitters is achieved by minimizing the overlap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). Specifically, the HOMO is located on the donor, while the LUMO is located on the acceptor. This long-distance spatial separation enhances intramolecular charge transfer and thus increases vibronic coupling.18,19
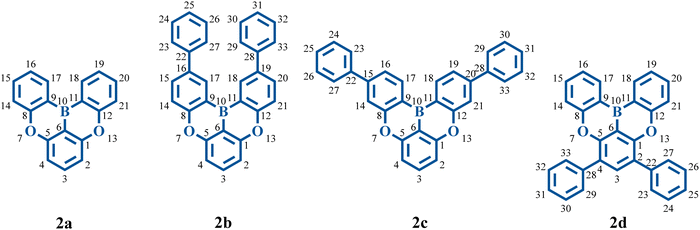
In 2015, Hatakeyama and colleagues proposed a solution strategy to address the broad emission problem mentioned above, named the multi-resonance TADF (MR-TADF), which presents a complementary distribution pattern of frontier molecular orbitals (FMOs) on adjacent atoms.20 This separated FMO distribution can make MR-TADF emitters present not only a small S1–T1 energy gap, but also an evident nonbonding molecular orbital (MO) character.20 This nonbonding character is associated with weak vibronic coupling between S1 and S0 states.18,21–25 The synthesized B, O-doped polycyclic aromatic compounds can show a narrow FWHM of around 30 nm.20 The molecular structures are shown in Fig. 1. It is interesting to note that introducing two phenyl rings at different positions of 2a (with a FWHM of 34 nm experimentally) results in different variations in color purity. The FWHM of 2b is reduced to 28 nm, while the FWHM of 2d is enlarged to 49 nm, and there is no apparent variation in 2c (with a FWHM of 33 nm). Since then, there has been a surge in the development of high-performance MR-TADF emitters.22,25–31 As the landmark molecules which lay down the basic skeleton of MR-TADF emitters, the nature of FWHM variations (vibronic coupling differences) in the four molecules remains to be clarified. Exclusive reliance on molecular rigidity and π-conjugation strength is insufficient to comprehend vibronic coupling.26 To better measure the strength of vibronic coupling, reorganization energy is commonly used.32–37 Moreover, research shows that the bond-order-bond-length (BOBL) relationship can provide valuable insights into reorganization energy.32,38,39
In this work, we aim to explore the underlying nature of color purity variations among the four molecules and establish an intuitive and reliable design rule for high color purity MR-TADF emitters. First, we performed the normal mode analysis and decomposed reorganization energy into internal coordinates. Next, we carefully elucidated the intuitive BOBL relationship under the MO framework to comprehend the origin of vibronic coupling and the role of the phenyl group in modulating vibronic coupling strength. It should be noted that MO theory is a powerful tool for chemists to use their chemical intuition to analyze problems. Finally, we explored the impact of substitution group electronic effects on vibronic coupling. This study can provide meaningful insights for chemists to design MR-TADF emitters.
2. Theoretical background and computational details
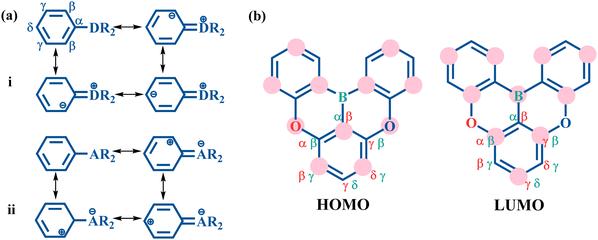
In the resonance representation, the electron donating group (D) increases the charge distribution at the ortho and para positions (Fig. 2a(i)). This corresponds to an increased HOMO distribution and a decreased LUMO distribution at the β and δ positions. In contrast, the electron withdrawing group (A) decreases the charge population at the ortho and para positions (Fig. 2a(ii)), which indicates a decreased HOMO distribution and an increased LUMO distribution at the β and δ positions. To illustrate the multi-resonance effect, the MR-TADF emitter 2a serves as an example (Fig. 2b). This effect is achieved by the combination of an electron donating O atom and an electron withdrawing B atom. The multi-resonance effect decreases the HOMO distribution at the α and γ positions of the O atom and at the β and δ positions of the B atom, and increases the HOMO distribution at the β and δ positions of the O atom and at the α and γ positions of the B atom. In the meantime, the multi-resonance effect results in an opposite change behavior in the LUMO distribution at these positions. As a result, the studied MR-TADF emitters can present separated frontier orbitals.For the studied four molecules shown in Fig. 1, the geometric optimizations and vibrational frequency calculations of S0 and S1 states were carried out using density functional theory (DFT) and time-dependent DFT (TDDFT), respectively, with the dispersion corrected PBE0-D3BJ functional and def2-SVP basis set.40–43 Note that TDDFT calculations are capable of providing a good description of S1 excitation energy.17 All these calculations were performed using the Gaussian 16 program with the polarizable continuum model (PCM) in the solvent of CH2Cl2.44–46
Under the harmonic oscillator approximation, the reorganization energy decomposed into contributions from vibrational normal modes can be represented by
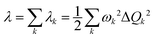 | (1) |
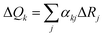 , where ΔRj is the displacement along the jth internal coordinate between the equilibrium positions of S1 and S0 states, and αkj is the combination coefficient.47 The vibronic coupling analyses mentioned above and emission spectra were calculated using the MOMAP program.48
, where ΔRj is the displacement along the jth internal coordinate between the equilibrium positions of S1 and S0 states, and αkj is the combination coefficient.47 The vibronic coupling analyses mentioned above and emission spectra were calculated using the MOMAP program.48
3. Results and discussion
3.1 Electronic transition properties
The electronic transition properties were used as the entry point to elucidate the complicated photophysical process. Compared with 2a, these molecules introduced with two phenyl rings (2b, 2c, and 2d) have smaller excitation energies (Table 1). The S1 excitation energy decreases in the order of 2a > 2b ≈ 2c > 2d. For the four molecules, S1 excitation is dominated by HOMO → LUMO transition. As shown in Fig. 3a, there is an apparent HOMO distribution on the C2, C4, C16, and C19 atoms of 2a, and this distribution on the C2 and C4 atoms is more noticeable than that on the C16 and C19 atoms. Therefore, the increase in the HOMO level resulting from the conjugation effect of the phenyl ring is more pronounced in 2d as compared with 2b (Fig. 3b). On the other hand, there is no HOMO distribution but a noticeable LUMO distribution on the C15 and C20 atoms of 2c. Therefore, the conjugation effect does not increase the HOMO level but decreases the LUMO level. On the whole, with the enlarged conjugation degree, 2b, 2c, and 2d present a smaller HOMO–LUMO gap and emission energy compared with 2a.| ΔEabsvert | ΔEad | ΔEemivert | ΔEL–H | Δq(Eox − Ered) | ΔEVIP–VEA | f | FWHM | |
|---|---|---|---|---|---|---|---|---|
| 2a | 3.52 | 3.39 | 3.28 | 4.04 | 3.76 | 3.83 | 0.20 | 33 |
| 2b | 3.35 | 3.23 | 3.16 | 3.87 | 3.59 | 3.65 | 0.28 | 27 |
| 2c | 3.37 | 3.23 | 3.11 | 3.83 | 3.57 | 3.61 | 0.46 | 36 |
| 2d | 3.26 | 3.10 | 2.94 | 3.64 | 3.41 | 3.39 | 0.13 | 48 |
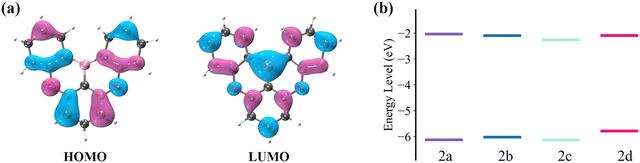 | ||
| Fig. 3 (a) HOMO and LUMO distribution (isovalue = 0.03 au) of 2a. (b) HOMO and LUMO levels for the four compounds, 2a, 2b, 2c, and 2d. | ||
Additionally, we also investigated the oxidation and reduction potentials and compared the oxidation–reduction energy gap (Δq(Eox − Ered)) to the HOMO–LUMO energy gap (ΔEL–H). As shown in Table 1, Δq(Eox − Ered) has a strong linear correlation with ΔEL–H. Assuming no structural relaxation and thermal correction to Gibbs free energy of the oxidation and reduction processes, the vertical ionization potential (VIP) is equal to qEox and vertical electron affinity (VEA) is equal to qEred, where q is the electron charge.49,50 According to Koopmans' theorem, VIP and VEA are approximately equal to the negative HOMO and LUMO energies, respectively.51,52 As a result, the structural relaxation and electron correlation make the main contribution to the difference between Δq(Eox − Ered) and ΔELUMO–HOMO.
3.2 Absorption and emission spectra
We then considered absorption and emission spectra from the view of theoretical calculations and give a detailed explanation of the relationship between color purity and vibronic coupling. According to the time-dependent perturbation theory, the Fermi golden rule can be conducted to estimate the spectrum. After the Born–Oppenheimer approximation and Condon approximation, the absorption and emission spectra can be described as53,54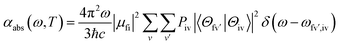 | (2) |
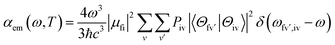 | (3) |
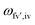 is the energy difference between the initial iv and final fv' vibronic states.
is the energy difference between the initial iv and final fv' vibronic states. 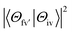 is the Franck–Condon factor (IFC), and determines the relative intensity of vibronic peaks. IFC can be evaluated as
is the Franck–Condon factor (IFC), and determines the relative intensity of vibronic peaks. IFC can be evaluated as 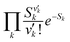 when v = 0, where Sk is the Huang–Rhys factor for the kth vibrational normal mode.53 Moreover, Sk = λk/ħωk, where λk is the reorganization energy used to characterize vibronic coupling strength. When the vibronic coupling is weak, the emission spectrum is dominated by the 0–0 vibronic transition, resulting in high color purity (small FWHM). In contrast, when the vibronic coupling is strong, the emission spectrum displays noticeable vibronic peaks, which broadens the spectrum and subsequently reduces color purity.55
when v = 0, where Sk is the Huang–Rhys factor for the kth vibrational normal mode.53 Moreover, Sk = λk/ħωk, where λk is the reorganization energy used to characterize vibronic coupling strength. When the vibronic coupling is weak, the emission spectrum is dominated by the 0–0 vibronic transition, resulting in high color purity (small FWHM). In contrast, when the vibronic coupling is strong, the emission spectrum displays noticeable vibronic peaks, which broadens the spectrum and subsequently reduces color purity.55
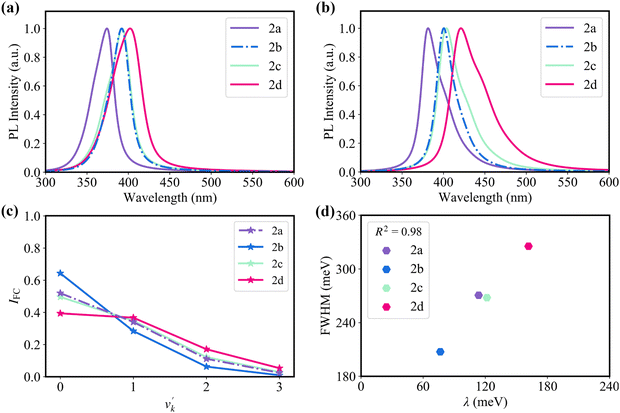
Fig. 4a and b show the simulated absorption and emission spectra for the four molecules. It shows that 2b, 2c, and 2d display red-shifted absorption and emission compared with 2a. The calculated maximum absorption peaks of 2a–2d are 374, 392, 392, and 402 nm, respectively. In the meantime, the calculated maximum emission peaks of 2a–2d are 381, 400, 404, and 420 nm, respectively, which is close to the experimental values of 398, 410, 410, and 436 nm.20 The emission spectra exhibit a near mirror image relationship with the absorption spectra. Since the bulk of the reorganization energy following electronic excitation arises from a stretching mode with an energy of about 1400 cm−1, we use this value as an effective frequency to clarify the relationship between the Franck–Condon factor and the reorganization energy of the studied four emitters (Fig. 4c).56 The Franck–Condon factors for the 0–v′ (from ν = 0 of S1 to v′ ≥ 1 of S0) transitions are positively proportional to the magnitude of reorganization energy. The relative intensity (I0–1/I0–0) of the 0–1 and 0–0 vibronic transitions increases in the order of 2b < 2a ≈ 2c < 2d. Note that the strength of 0–v′ vibronic peaks determines the FWHM of the spectrum.
Consistent with the above discussion, as shown in Fig. 4b and 4d, 2b with weak vibronic coupling (a small reorganization energy of 76.6 meV) exhibit high color purity (broad emission spectrum), while 2d with strong vibronic coupling (a large reorganization energy of 161.7 meV) exhibits low color purity (narrow emission spectrum).20 Here, we used a Lorentzian broadening of 900 cm−1 by considering environment effects to match experimental results (Fig. S7, ESI†).57,58 The coefficient of determination (R2) between reorganization energy and FWHM reaches 0.98 (Fig. 4d). As a consequence, to design high color purity MR-TADF emitters, we should pay attention to clarifying the nature of vibronic coupling and thus weakening it.
3.3 Analysis of the vibronic coupling between S1 and S0 states
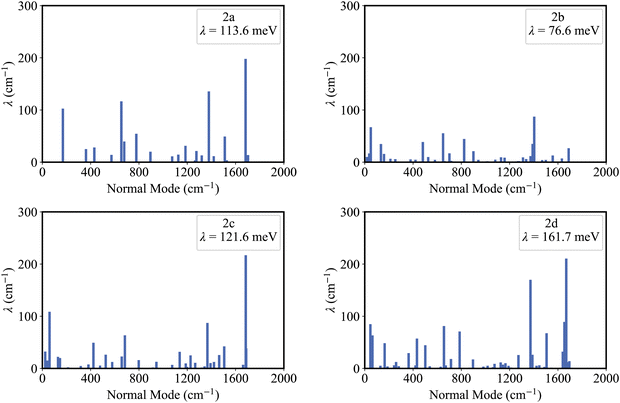
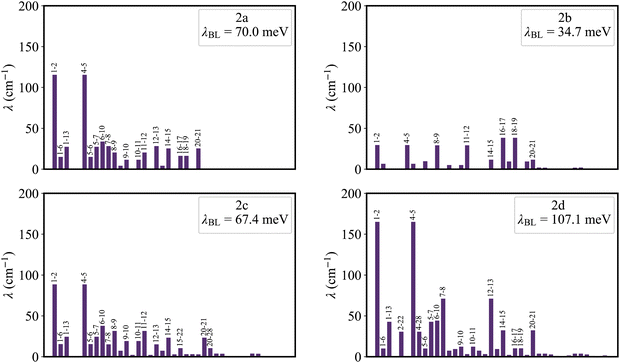
Fig. 5 shows that the reorganization energies of the studied molecules mainly come from the stretching modes (alterations in bond length) within the range of 1400–1700 cm−1. These normal modes with large reorganization energy make noticeable contributions to the vibronic peaks (low energy region) of emission spectra. The displacement vectors of these modes are given in Fig. S2–S5 (ESI†). In the internal coordinate representation, the reorganization energy originates from the alterations of bond lengths, bond angles, and dihedral angles. Fig. 6 shows the reorganization energy from bond length alterations (λBL), which corresponds to the aforementioned stretching modes. In particular, the C1–C2 and C4–C5 bonds in 2a make the major contribution to λBL, with a sum of 230.9 cm−1 (28.6 meV). The reorganization energy variations caused by the introduction of phenyl rings for 2b and 2d are −37.0 and 48.1 meV, respectively. It should be noted that these variations are primarily from λBL, contributing 95% for 2b (−35.3 meV) and 77% for 2d (37.1 meV). Moreover, the C1–C2 and C4–C5 bonds make a large contribution to the reorganization energy variations, −21.3 meV for 2b and 12.3 meV for 2d.To deeply understand the vibronic coupling, we employed the BOBL relationship under the MO framework to rationalize the magnitude of λBL. Based on the harmonic approximation, the reorganization energy in the BOBL relationship can be evaluated using the equation:37,38
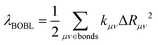 | (4) |
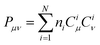 is associated with the number of electrons in the chemical bond. Here, ni is the occupation number of the ith molecular orbital, Ciμ and Ciν are the pz coefficients for the ith MO. For the HOMO → LUMO S1 excitation, the bond order difference between S1 and S0 states is
is associated with the number of electrons in the chemical bond. Here, ni is the occupation number of the ith molecular orbital, Ciμ and Ciν are the pz coefficients for the ith MO. For the HOMO → LUMO S1 excitation, the bond order difference between S1 and S0 states is 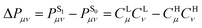 . Therefore, λBOBL can be estimated from
. Therefore, λBOBL can be estimated from 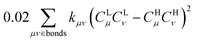 . In this work, we refer to CHμCHν and CLμCLν as the HOMO and LUMO bond orders, respectively, reflecting their contribution to Pμν. The general form for multi-MO transition excitation is
. In this work, we refer to CHμCHν and CLμCLν as the HOMO and LUMO bond orders, respectively, reflecting their contribution to Pμν. The general form for multi-MO transition excitation is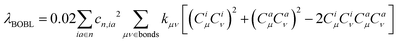 | (5) |
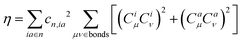 | (6) |
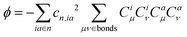 | (7) |
Accordingly, λBOBL is proportional to parameter κ(λBOBL ∝ κ), which is
| κ = η + 2ϕ | (8) |
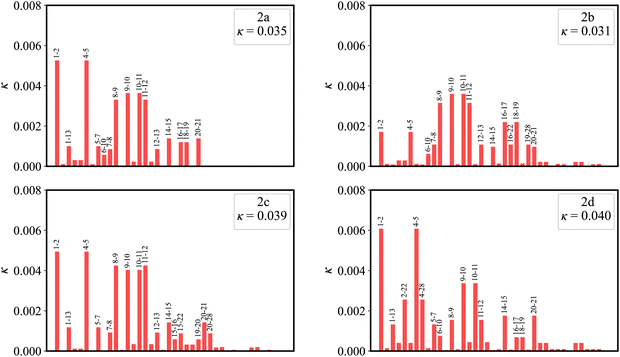
Fig. 7 plots the contribution of chemical bonds to κ in the four molecules. Taking 2a as an example, the C1–C2 and C4–C5 bonds present the largest value of κ in 2a, which indicates that the two bonds have large reorganization energy from the view of MO. This significant κ of the C1–C2 and C4–C5 bonds is an important source of the vibronic peaks in the emission spectrum. Here, this significant κ (associated with the bond order difference) can be attributed to the different distribution behavior of transition orbitals. The C1–C2 and C4–C5 bonds of 2a in the LUMO show the nonbonding character (Fig. 3a). However, due to the orbital antisymmetry of the HOMO, there is no HOMO distribution at the B atom, which means that the B atom cannot present efficient resonance character (decreasing the HOMO distribution at the β and δ positions and increasing the HOMO distribution at the α and γ position). Therefore, the two bonds in the HOMO show a noticeable bonding character. Moreover, based on the strong bonding character in the HOMO and the nonbonding character in the LUMO, the C1–C2 and C4–C5 bonds present large κ and reorganization energy.
3.4 Vibronic coupling variations caused by phenyl ring substitution
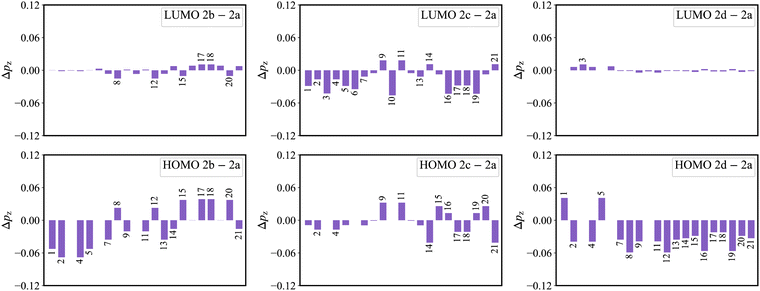
As shown in Fig. 3a, there is an evident HOMO distribution on the C16 and C19 atoms. Due to the conjugation effect of the phenyl group, the introduction of a phenyl ring to the C16 and C19 atoms (2b) gives rise to the delocalization in the HOMO, as evidenced by the HOMO distribution observed on the attached phenyl rings (Fig. S1, ESI†). This delocalized behavior is also reflected in the reduction of the HOMO distribution on the C1, C2, C4, and C5 atoms (Fig. 8). This reduction in the four atoms signifies a weakened bonding character of the C1–C2 and C4–C5 bonds in the HOMO, which further implies a weakened HOMO–LUMO bond order difference (associated with κ) of the two bonds in 2b. On the other hand, there is a noticeable LUMO distribution on the C15 and C20 atoms in 2a (Fig. 3a). The introduction of a phenyl ring to the C15 and C20 atoms (2c) reduces the LUMO distribution on the C1, C2, C4, and C5 atoms for the conjugation effect of the phenyl group. Note that there is a nearly nonbonding character of the C1–C2 and C4–C5 bonds in the LUMO. This decreased LUMO distribution on the C1, C2, C4, and C5 atoms in 2c does not affect the HOMO–LUMO bond order difference (associated with κ). As a result, 2b with a small κ shows a narrower emission spectrum (higher color purity) than 2a, while 2c shows the same FWHM (same color purity) as 2a.In the meantime, there is a noticeable HOMO distribution but no LUMO distribution on the C2 and C4 atoms in 2a (Fig. 3a). Upon the introduction of a phenyl ring to the C2 and C4 atoms (2d), the resonance effect of the phenyl group reduces the HOMO distribution on the C2 and C4 atoms while increasing it on the C1 and C5 atoms (Fig. 8). This results in a strengthened bonding character of the C1–C2 and C4–C5 bonds in the HOMO, indicating an increased HOMO–LUMO bond order difference (associated with κ) of the C1–C2 and C4–C5 bonds in 2d. Note that the newly introduced phenyl rings display an evident HOMO distribution, but no LUMO distribution is observed (Fig. S1, ESI†). The C2–C22 and C4–C28 bonds present the antibonding and nonbonding character in the HOMO and LUMO, respectively. This results in an evident bond order difference (associated with κ) of the C2–C22 and C4–C28 bonds. As a whole, due to the large κ of the C1–C2, C2–C22, C4–C5, and C4–C28 bonds, 2d with strong vibronic coupling exhibits a broader emission spectrum (lower color purity) compared with 2a.
From the discussion above, it is clear that we can weaken the vibronic coupling by delocalizing the MO distribution, thus decreasing the HOMO–LUMO bond order difference (associated with κ) of the bonds with a large reorganization energy.
3.5 Impact of substitution group electronic effects on vibronic coupling
To gain a deeper understanding of the impact of the electronic structure on vibronic coupling, we replaced the phenyl groups of 2b and 2d with various substituents. The selection of specific positions for substitution was driven by the observation that the substitution of phenyl rings on the C16/C19 (2b) and C2/C4 (2d) atoms significantly affects the vibronic coupling. Specifically, the substituents comprised electron-donating groups (D1: methoxy-substituted phenyl group, D2: pyrrolyl group, and D3: imidazolyl group) and electron-withdrawing groups (A1: trifluoromethyl-substituted phenyl group, A2: pyridyl group, and A3: pyrimidyl group) (Fig. 9). It is worth noting that the pyrrolyl group has a stronger electron-donating ability than the imidazolyl group, while the pyridyl group demonstrates a weaker electron-withdrawing ability compared with the pyrimidyl group.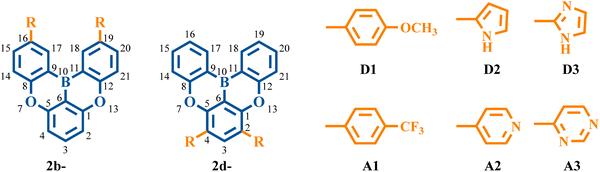 | ||
| Fig. 9 Chemical structures of 2b series and 2d series with different electron-donating and electron-withdrawing substituents. | ||
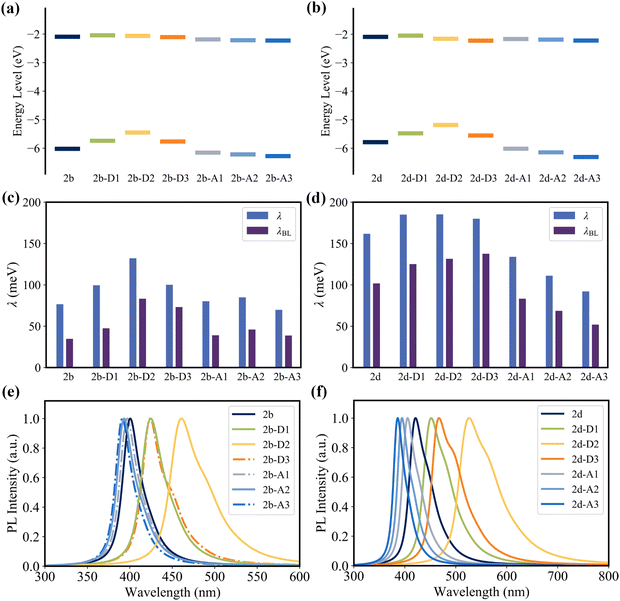
Since the C2, C4, C16, and C19 atoms of 2a present a noticeable HOMO distribution but no LUMO distribution (Fig. 3a), the substitution of the electron-donating groups and the electron-withdrawing groups can increase and decrease the HOMO level, respectively, while all of these substituent groups have a negligible impact on the LUMO level (Fig. 10a and b). As the orbital interaction strength is associated with the energy level difference of the two orbitals, the interaction between the HOMO of D1/D2/D3 and the HOMO of 2a is stronger than that between the LUMO of A1/A2/A3 and the HOMO of 2a. Consequently, 2b-D series (2b-D1, 2b-D2, and 2b-D2) and 2d-D series (2d-D1, 2d-D2, and 2d-D2) display significant red-shifted emission. In contrast, the 2b-A series (2b-A1, 2b-A2, and 2b-A2) and 2d-A series (2d-A1, 2d-A2, and 2d-A2) exhibit slight blue-shifted emission relative to 2b and 2d, respectively (Fig. 10e and f).
As shown in Fig. 10c and d, the majority of the 2b-D and 2b-A series of emitters present a larger reorganization energy compared with 2b. Meanwhile, a clear trend is observed as the reorganization energy decreases in the order of 2d-D series > 2d > 2d-A series. The coefficient of determination (R2) between reorganization energy and FWHM of the fourth emitters can reach 0.99 (Fig. S22, ESI†). The FWHM values of 2b, 2b-D series, and 2b-A series were calculated to be 207, 237, 289, 249, 212, 217, and 203 meV, respectively. The FWHM values of the 2d, 2d-D series and 2d-A series were calculated to be 325, 348, 351, 352, 291, 261, and 237 meV, respectively.
For the 2b-D series, the electron-donating groups significantly decrease the HOMO distribution on the C1, C2, C4, and C5 atoms (Fig. S18, ESI†), thus decreasing the HOMO–LUMO bond order difference (due to the smaller HOMO bond order) and reorganization energy of the C1–C2 and C4–C5 bonds (Fig. S14, ESI†). However, the strong electron-donating ability of these groups gives rise to an aggravated HOMO distribution in the newly introduced electron-donating groups (Fig. S10, ESI†), resulting in a large HOMO–LUMO bond order difference and reorganization energy of the bonds of the newly introduced groups (Fig. S14, ESI†). Overall, the strong electron-donating ability increase the reorganization energy. Similarly, the bonds of the newly introduced electron-donating groups in the 2d-D series present noticeable reorganization energy (Fig. S15, ESI†), which makes the main contribution to the increase in reorganization energy from the 2d to 2d-D series.
It should be noted that the strength of orbital interactions decreases as the orbital levels move farther apart. In the case of the 2b-A series, the electron-withdrawing groups with lower HOMO levels present weaker conjugation ability to decrease the HOMO distribution on the C1, C2, C4, and C5 atoms compared with the phenyl groups of 2b (Fig. 8 and Fig. S19, ESI†). Consequently, this results in a larger HOMO–LUMO bond order difference (due to the larger HOMO bond order) and reorganization energy of the C1–C2 and C4–C5 bonds in the 2b-A series compared with 2b (Fig. 6 and Fig. S14, ESI†). In contrast, for the 2d-A series, the electron-withdrawing groups have a weaker resonance effect to enhance the HOMO bond order compared with the phenyl group of 2d. Simultaneously, the electron-withdrawing group increases the LUMO distribution on the C2 and C4 atoms (Fig. S21, ESI†), thus increasing the LUMO bond order. Consequently, the 2d-A series present a smaller HOMO–LUMO bond order difference (due to the smaller HOMO bond order and the larger LUMO bond order) and reorganization energy of the C1–C2 and C4–C5 bonds compared with 2d.
From the discussion above, to decrease the reorganization energy associated with the strong bonding character in the HOMO, we can substitute the position related to large reorganization energy with an electron-withdrawing group. This substitution can weaken the HOMO bonding character and enhance the LUMO bonding character, thereby decreasing the HOMO–LUMO bond order difference.
4. Conclusion
In this work, a series of theoretical analyses of the reorganization energy (the vibronic coupling) were studied to elucidate the color purity of four MR-TADF emitters. It is found that bond length alterations provide the dominant contribution to the reorganization energy variations from 2a to 2b and 2d, where the C1–C2 and C4–C5 bonds make a large contribution to the reorganization energy variations. Here, the large reorganization energy of the two bonds can be interpreted as the noticeable κ (associated with the HOMO–LUMO bond order difference), which can be further attributed to the strong bonding character in the HOMO.We confirmed that it is feasible to rationalize the reorganization energy variations under the MO framework. In the case of 2b, the conjugation effect of the phenyl group weakens the HOMO bonding character of the C1–C2 and C4–C5 bonds, leading to a decrease in the reorganization energy. Therefore, 2b shows a narrower emission spectrum (higher color purity) compared with 2a. In contrast, the HOMO bonding character of the two bonds in 2d is strengthened by the resonance effect of the phenyl group, which makes a large contribution to the increase in the reorganization energy. This results in the broad emission spectrum (low color purity) of 2d. It should be noted that the strong electron-donating ability of the 2b-D series and 2d-D series can give rise to the aggravated HOMO distribution on the newly introduced electron-donating groups, thus increasing the reorganization energy of the bonds of the newly introduced electron-donating groups. In the case of the 2b-A series, the electron-withdrawing groups present a weaker ability to decrease the HOMO bonding character of the two bonds compared with the phenyl groups of 2b. For the 2d-A series, the substitution of the electron-withdrawing group weakens the HOMO bonding character and enhances the LUMO bonding character of the two bonds, which results in a small HOMO–LUMO bond order difference and reorganization energy. This also offers potential to improve the color purity.
For the design of MR-TADF emitters with high color purity, in addition to using the resonance effect to enhance the nonbonding character, two substitution-driven design strategies can be employed. The first strategy involves introducing a neutral phenyl group to delocalize the orbital distribution, thereby weakening the bonding or antibonding character in frontier molecular orbitals of the bonds with a large reorganization energy. The second strategy entails substitution at the position related to a large reorganization energy with electron-donating or electron-withdrawing groups, thus decreasing the HOMO–LUMO bond order difference.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work is supported by the National Natural Science Foundation of China (22032004, 22021001, and 21533006).References
- H. Yersin, A. F. Rausch, R. Czerwieniec, T. Hofbeck and T. Fischer, The triplet state of organo-transition metal compounds. Triplet harvesting and singlet harvesting for efficient OLEDs, Coord. Chem. Rev., 2011, 255, 2622–2652 CrossRef CAS.
- P. K. Samanta, D. Kim, V. Coropceanu and J.-L. Brédas, Up-conversion intersystem crossing rates in organic emitters for thermally activated delayed fluorescence: impact of the nature of singlet vs triplet excited states, J. Am. Chem. Soc., 2017, 139, 4042–4051 CrossRef CAS PubMed.
- Z. Y. Yang, Z. Mao, Z. L. Xie, Y. Zhang, S. W. Liu, J. Zhao, J. Xu, Z. G. Chi and M. P. Aldred, Recent advances in organic thermally activated delayed fluorescence materials, Chem. Soc. Rev., 2017, 46, 915–1016 RSC.
- Z. G. Shuai and Q. Peng, Organic light-emitting diodes: theoretical understanding of highly efficient materials and development of computational methodology, Natl. Sci. Rev., 2017, 4, 224–239 CrossRef CAS.
- J. M. Ha, S. H. Hur, A. Pathak, J.-E. Jeong and H. Y. Woo, Recent advances in organic luminescent materials with narrowband emission, NPG Asia Mater., 2021, 13, 1–36 CrossRef.
- J.-M. Teng, Y.-F. Wang and C.-F. Chen, Recent progress of narrowband TADF emitters and their applications in OLEDs, J. Mater. Chem. C, 2020, 8, 11340–11353 RSC.
- V. V. Patil, H. L. Lee, I. Kim, K. H. Lee, W. J. Chung, J. Kim, S. Park, H. Choi, W. J. Son and S. O. Jeon, Purely spin-vibronic coupling assisted triplet to singlet up-conversion for real deep blue organic light-emitting diodes with over 20% efficiency and y color coordinate of 0.05, Adv. Sci., 2021, 8, 2101137 CrossRef CAS PubMed.
- W. L. Cai, H. Z. Zhang, X. Yan, A. C. Zhao, R. X. He, M. Li, Q. X. Meng and W. Shen, What accounts for the color purity of tetradentate Pt complexes? A computational analysis, Phys. Chem. Chem. Phys., 2019, 21, 8073–8080 RSC.
- C. Adamo and D. Jacquemin, The calculations of excited-state properties with Time-Dependent Density Functional Theory, Chem. Soc. Rev., 2013, 42, 845–856 RSC.
- D. Jacquemin, E. Brémond, I. Ciofini and C. Adamo, Impact of vibronic couplings on perceived colors: two anthraquinones as a working example, J. Phys. Chem. Lett., 2012, 3, 468–471 CrossRef CAS PubMed.
- S. A. Ahmad, J. Eng and T. J. Penfold, Rapid predictions of the colour purity of luminescent organic molecules, J. Mater. Chem. C, 2022, 10, 4785–4794 RSC.
- S. Y. Byeon, D. R. Lee, K. S. Yook and J. Y. Lee, Recent progress of singlet-exciton-harvesting fluorescent organic light-emitting diodes by energy transfer processes, Adv. Mater., 2019, 31, 1803714 CrossRef PubMed.
- G. S. M. Tong, K. T. Chan, X. Chang and C.-M. Che, Theoretical studies on the photophysical properties of luminescent pincer gold (III) arylacetylide complexes: the role of π-conjugation at the C-deprotonated [C^N^C] ligand, Chem. Sci., 2015, 6, 3026–3037 RSC.
- G. Baryshnikov, B. Minaev and H. Ågren, Theory and calculation of the phosphorescence phenomenon, Chem. Rev., 2017, 117, 6500–6537 CrossRef CAS PubMed.
- X.-K. Chen, D. Kim and J.-L. Brédas, Thermally activated delayed fluorescence (TADF) path toward efficient electroluminescence in purely organic materials: molecular level insight, Acc. Chem. Res., 2018, 51, 2215–2224 CrossRef CAS PubMed.
- R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha and T. Wu, et al., Design of efficient molecular organic light-emitting diodes by a high-throughput virtual screening and experimental approach, Nat. Mater., 2016, 15, 1120–1127 CrossRef PubMed.
- S. Y. Lin, Q. Ou and Z. G. Shuai, Computational selection of thermally activated delayed fluorescence (TADF) molecules with promising electrically pumped lasing property, ACS Mater. Lett., 2022, 4, 487–496 CrossRef CAS.
- S. Madayanad Suresh, D. Hall, D. Beljonne, Y. Olivier and E. Zysman-Colman, Multiresonant thermally activated delayed fluorescence emitters based on heteroatom-doped nanographenes: recent advances and prospects for organic light-emitting diodes, Adv. Funct. Mater., 2020, 30, 1908677 CrossRef CAS.
- A. Pershin, D. Hall, V. Lemaur, J.-C. Sancho-Garcia, L. Muccioli, E. Zysman-Colman, D. Beljonne and Y. Olivier, Highly emissive excitons with reduced exchange energy in thermally activated delayed fluorescent molecules, Nat. Commun., 2019, 10, 597 CrossRef CAS PubMed.
- H. Hirai, K. Nakajima, S. Nakatsuka, K. Shiren, J. Ni, S. Nomura, T. Ikuta and T. Hatakeyama, One-step borylation of 1, 3-diaryloxybenzenes towards efficient materials for organic light-emitting diodes, Angew. Chem., Int. Ed., 2015, 54, 13581–13585 CrossRef CAS PubMed.
- Y.-C. Chang and I. Chao, An important key to design molecules with small internal reorganization energy: strong nonbonding character in frontier orbitals, J. Phys. Chem. Lett., 2010, 1, 116–121 CrossRef CAS.
- T. Hatakeyama, K. Shiren, K. Nakajima, S. Nomura, S. Nakatsuka, K. Kinoshita, J. Ni, Y. Ono and T. Ikuta, Ultrapure blue thermally activated delayed fluorescence molecules: efficient HOMO–LUMO separation by the multiple resonance effect, Adv. Mater., 2016, 28, 2777–2781 CrossRef CAS PubMed.
- S. M. Pratik, V. Coropceanu and J.-L. Brédas, Purely organic emitters for multiresonant thermally activated delay fluorescence: design of highly efficient sulfur and selenium derivatives, ACS Mater. Lett., 2022, 4, 440–447 CrossRef CAS.
- Z. Pei, Q. Ou, Y. Z. Mao, J. Yang, A. l d l Lande, F. Plasser, W. Z. Liang, Z. G. Shuai and Y. H. Shao, Elucidating the electronic structure of a delayed fluorescence emitter via orbital interactions, excitation energy components, charge-transfer numbers, and vibrational reorganization energies, J. Phys. Chem. Lett., 2021, 12, 2712–2720 CrossRef CAS PubMed.
- D. Hall, K. Stavrou, E. Duda, A. Danos, S. Bagnich, S. Warriner, A. M. Slawin, D. Beljonne, A. Köhler and A. Monkman, Diindolocarbazole–achieving multiresonant thermally activated delayed fluorescence without the need for acceptor units, Mater. Horiz., 2022, 9, 1068–1080 RSC.
- Y. W. Zhang, D. D. Zhang, J. B. Wei, Z. Y. Liu, Y. Lu and L. Duan, Multi-resonance induced thermally activated delayed fluorophores for narrowband green OLEDs, Angew. Chem., Int. Ed., 2019, 58, 16912–16917 CrossRef CAS PubMed.
- Y. C. Xu, C. L. Li, Z. Q. Li, Q. Y. Wang, X. L. Cai, J. B. Wei and Y. Wang, Constructing charge-transfer excited states based on frontier molecular orbital engineering: narrowband green electroluminescence with high color purity and efficiency, Angew. Chem., Int. Ed., 2020, 59, 17442–17446 CrossRef CAS PubMed.
- S. Oda, B. Kawakami, R. Kawasumi, R. Okita and T. Hatakeyama, Multiple resonance effect-induced sky-blue thermally activated delayed fluorescence with a narrow emission band, Org. Lett., 2019, 21, 9311–9314 CrossRef CAS PubMed.
- Y. Yuan, X. Tang, X. Y. Du, Y. Hu, Y. J. Yu, Z. Q. Jiang, L. S. Liao and S. T. Lee, The design of fused amine/carbonyl system for efficient thermally activated delayed fluorescence: novel multiple resonance core and electron acceptor, Adv. Opt. Mater., 2019, 7, 1801536 CrossRef.
- D. M. Sun, S. M. Suresh, D. Hall, M. Zhang, C. F. Si, D. B. Cordes, A. M. Slawin, Y. Olivier, X. H. Zhang and E. Zysman-Colman, The design of an extended multiple resonance TADF emitter based on a polycyclic amine/carbonyl system, Mater. Chem. Front., 2020, 4, 2018–2022 RSC.
- Y. W. Zhang, G. M. Li, L. Wang, T. Y. Huang, J. B. Wei, G. Y. Meng, X. Wang, X. Zeng, D. D. Zhang and L. Duan, Fusion of Multi-Resonance Fragment with Conventional Polycyclic Aromatic Hydrocarbon for Nearly BT. 2020 Green Emission, Angew. Chem., Int. Ed., 2022, 134, e202202380 Search PubMed.
- W.-C. Chen and Y.-C. Chang, Rational design of organic semiconductors with low internal reorganization energies for hole and electron transport: position effect of aza-substitution in phenalenyl derivatives, Phys. Chem. Chem. Phys., 2021, 23, 18163–18172 RSC.
- W. C. Huang, W. J. Xie, H. J. Huang, H. Zhang and H. G. Liu, Designing organic semiconductors with ultrasmall reorganization energies: insights from molecular symmetry, aromaticity and energy gap, J. Phys. Chem. Lett., 2020, 11, 4548–4553 CrossRef CAS PubMed.
- X. Zeng, X. Wang, Y. W. Zhang, G. Y. Meng, J. B. Wei, Z. Y. Liu, X. Q. Jia, G. M. Li, L. Duan and D. D. Zhang, Nitrogen-Embedded Multi-Resonance Heteroaromatics with Prolonged Homogeneous Hexatomic Rings, Angew. Chem., Int. Ed., 2022, 134, e202117181 Search PubMed.
- C.-C. Wu, E. Y. Li and P.-T. Chou, Reducing the internal reorganization energy via symmetry controlled π-electron delocalization, Chem. Sci., 2022, 13, 7181–7189 RSC.
- J.-W. Huang, Y.-C. Hsu, X. Wu, S. Wang, X.-Q. Gan, W.-Q. Zheng, H. Zhang, Y.-Z. Gong, W.-Y. Hung and P.-T. Chou, Influence of charge transfer strength on emission bandwidth for multiple-resonance emitters via systematically tuning the acceptor–donor assembly, J. Mater. Chem. C, 2022, 10, 7866–7874 RSC.
- W.-C. Chen and Y.-C. Cheng, Elucidating the magnitude of internal reorganization energy of molecular excited states from the perspective of transition density, J. Phys. Chem. A, 2020, 124, 7644–7657 CrossRef CAS PubMed.
- S. Larsson, A. Klimkāns, L. Rodriguez-Monge and G. Duškesas, Reorganization energies in organic π systems, J. Mol. Struct. THEOCHEM, 1998, 425, 155–159 CrossRef CAS.
- J. P. Paolini, The bond order—bond length relationship, J. Comput. Chem., 1990, 11, 1160–1163 CrossRef CAS.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: the PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. Tomasi, B. Mennucci and R. Cammi, Quantum mechanical continuum solvation models, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, Geometries and properties of excited states in the gas phase and in solution: theory and application of a time-dependent density functional theory polarizable continuum model, J. Chem. Phys., 2006, 124, 094107 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone and G. A. Petersson, et al., Gaussian 16 Rev. A.03, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- H. Geng, Y. L. Niu, Q. Peng, Z. G. Shuai, V. Coropceanu and J.-L. Brédas, Theoretical study of substitution effects on molecular reorganization energy in organic semiconductors, J. Chem. Phys., 2011, 135, 104703 CrossRef PubMed.
- Y. L. Niu, W. Q. Li, Q. Peng, H. Geng, Y. P. Yi, L. J. Wang, G. J. Nan, D. Wang and Z. G. Shuai, Molecular materials property prediction package (MOMAP) 1.0: a software package for predicting the luminescent properties and mobility of organic functional materials, Mol. Phys., 2018, 116, 1078–1090 CrossRef CAS.
- M. Isegawa, F. Neese and D. A. Pantazis, Ionization energies and aqueous redox potentials of organic molecules: comparison of DFT, correlated ab initio theory and pair natural orbital approaches, J. Chem. Theory Comput., 2016, 12, 2272–2284 CrossRef CAS PubMed.
- C. F. Wang, L. Q. Ouyang, X. F. Xu, S. Braun, X. J. Liu and M. Fahlman, Relationship of ionization potential and oxidation potential of organic semiconductor films used in photovoltaics, Sol. RRL, 2018, 2, 1800122 CrossRef.
- R. Kar, J. W. Song and K. Hirao, Long-range corrected functionals satisfy Koopmans' theorem: calculation of correlation and relaxation energies, J. Comput. Chem., 2013, 34, 958–964 CrossRef CAS PubMed.
- J.-L. Brédas, Mind the gap!, Mater. Horiz., 2014, 1, 17–19 RSC.
- C.-K. Lin, M.-C. Li, M. Yamaki, M. Hayashi and S. H. Lin, A theoretical study on the spectroscopy and the radiative and non-radiative relaxation rate constants of the S01A1–S11A2 vibronic transitions of formaldehyde, Phys. Chem. Chem. Phys., 2010, 12, 11432–11444 RSC.
- S. H. Lin, C. H. Chang, K. K. Liang, R. Chang, Y. J. Shiu, J. M. Zhang, T. S. Yang, M. Hayashi and F. C. Hsu, Ultrafast dynamics and spectroscopy of bacterial photosynthetic reaction centers, Adv. Chem. Phys., 2002, 1–88 CAS.
- W. L. Cai, A. C. Zhao, K. Ren, R. X. He, M. Li and W. Shen, Understanding the mechanisms of white light emission of a tetradentate Pt complex in various surrounding environments, J. Phys. Chem. C, 2019, 123, 17968–17975 CrossRef CAS.
- F. C. Spano, The spectral signatures of Frenkel polarons in H-and J-aggregates, Acc. Chem. Res., 2010, 43, 429–439 CrossRef CAS PubMed.
- J. Gierschner, H.-G. Mack, H.-J. Egelhaaf, S. Schweizer, B. Doser and D. Oelkrug, Optical spectra of oligothiophenes: vibronic states, torsional motions, and solvent shifts, Synth. Met., 2003, 138, 311–315 CrossRef CAS.
- Y. L. Niu, Q. Peng, C. M. Deng, X. Gao and Z. G. Shuai, Theory of excited state decays and optical spectra: application to polyatomic molecules, J. Phys. Chem. A, 2010, 114, 7817–7831 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3qm00280b |
| This journal is © the Partner Organisations 2023 |