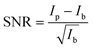High-efficiency X-ray emission spectroscopy of cold-compressed Fe₂O₃ and laser-heated pressurized FeCO₃ using a von Hámos spectrometer

Abstract

X-ray spectroscopy of iron-bearing compounds under high pressure and high temperature is an important tool to understand geological processes in the deep Earth. However, the sample environment using a diamond anvil cell complicates spectroscopic measurements and leads to long data acquisition times. We present a setup for resonant and non-resonant X-ray emission spectroscopy and showcase its capabilities for in situ studies at high pressure and high temperature. Spin-state imaging of laser-heated FeCO₃ at 75 GPa via Kβ_1,3 emission spectroscopy demonstrates the great potential of this setup with measurement times within seconds for robust spin-state analysis results. The results of Kβ_1,3 emission spectroscopy of cold-compressed Fe₂O₃ reveal a two-step spin transition with the ζ-phase between 57 GPa and 64 GPa, having iron in different spin states at the different iron sites. The phase transition via ζ- to Θ-phase causes a delocalization of the electronic states, which is supported by 1s2p resonant X-ray emission spectroscopy.

---

1 Introduction

The study of iron in iron-bearing compounds at extreme conditions with spectroscopic methods is of high relevance, as iron is the most abundant transition metal in the Earth's deep mantle. Due to its complex electronic structure, it plays a key role in a variety of geological processes. Iron is present in different oxidation states as ferrous (Fe²⁺) and ferric (Fe³⁺) iron and can undergo a spin transition from high spin (HS) to low spin (LS) or vice versa, depending on its local environment and the thermodynamic conditions. Numerous studies have addressed the pressure induced spin transition in iron-bearing compounds.^1–6 This transition can influence many physical and chemical properties⁷ such as sound velocity,⁸ conductivity,⁹ compressibility,¹⁰ material transport^11–14 or element partitioning.^15–19 Thus, a detailed understanding of the electronic structure of iron-bearing compounds in situ at extreme conditions, i.e., high temperature and high pressure, is crucial to understand and interpret the material's properties and chemistry of the interior of the Earth and other terrestrial planets. Besides Mössbauer spectroscopy^20–22 and X-ray absorption spectroscopy,^4,23 X-ray emission spectroscopy, resonant^24,25 and non-resonant,^5,6,25–30 is widely used to determine spin state, covalency, oxidation state, electronic structure and structural changes.

The thermodynamic conditions in the vicinity of the core-mantle-boundary reach 136 GPa and 3000 K. Such static high-pressure-high-temperature (HPHT) conditions can only be achieved by laser-heated diamond anvil cells (LHDACs) (Anzellini et al.³¹ and references therein) or X-ray heating, exploiting fs X-ray pulses from an X-ray free electron laser.^30,32–34 However, X-ray emission spectroscopy of samples contained in such highly absorbing environment is extremely challenging, as the diamond anvils or gaskets reduce the intensity of the incident and scattered X-rays significantly and often require relatively long measuring times. Here, we present applications for fast resonant and non-resonant X-ray emission spectroscopy ((R)XES) at lower mantle conditions, utilizing a wavelength dispersive von Hámos spectrometer⁶ in combination with a dedicated sample preparation. The preparation process is specifically optimized to experiments that require non-X-ray-transparent gasket materials, e.g., rhenium, while the setup itself can also be applied to transparent gasket materials with even higher efficiency.

In the first part, results of laser-heated FeCO₃ at 75 GPa will be presented to showcase the capabilities of the setup regarding fast Kβ_1,3 and valence-to-core (vtc) emission spectroscopy, which allows for in situ spin-state imaging. In the second part, results of cold-compressed Fe₂O₃ up to 75 GPa will be shown, using XES and RXES to analyze the development of the electronic structure with pressure. Both systems gained significant attention during the past years.

The iron-bearing carbonate, siderite (FeCO₃) undergoes a pressure-induced spin transition from HS to LS at around 43 GPa.^2,3,5,6 Interestingly, FeCO₃ was found to exhibit a complex chemistry for pressures above 50 GPa and temperatures above 1400  K. At given P–T conditions two phases with tetrahedrally coordinated carbon form, tetrairon(III) orthocarbonate (Fe₄³⁺C₃O₁₂) and diiron(II) diiron(III) tetracarbonate (Fe₂²⁺Fe₂³⁺C₄O₁₃).^21,35–41 Recently, it has been shown experimentally that in both phases iron is in HS state at lower mantle pressure and temperature.^29,30

Fe₂O₃ is an ideal showcase to discuss the capabilities of this setup for samples under cold compression. While Badro et al.²⁶ presented the first measurements of Kβ_1,3 and vtc emission from Fe₂O₃ under pressure, finding a HS to LS transition and a bond length change indicated by Kβ′′ intensity, more detailed studies are scarce. RXES on Fe₂O₃ was discussed several times in the past^42–44 for ambient conditions, but data of compressed Fe₂O₃ do not exist from our knowledge. However, this system is well characterized using X-ray diffraction, Mössbauer spectroscopy and theoretical approaches.^{4,20,22,26,42,44–57}

Fe₂O₃ can be found in various crystalline phases depending on the pressure and temperature conditions, as recently shown in detail by Bykova et al.²⁰ They report α-Fe₂O₃, which is fully in HS state with iron in octahedral coordination, to be stable up to 54 GPa at cold compression with a subsequent phase transition to triclinic ζ-Fe₂O₃. The ζ-phase is a mixture of two distinct iron sites with LS iron on the octahedral site and HS iron on the trigonal-prismatic site that transforms to orthorombic Θ-Fe₂O₃ at a pressure of 67 GPa, fully in LS state with trigonal-prismatic coordination. These findings are supported by Sanson et al.,⁴ as they also find a mixed average spin state at a pressure of around 50 GPa using X-ray absorption near edge structure measurements. Furthermore, Greenberg et al.²² report a pressure induced insulator-metal transition, i.e., localized and delocalized electronic states in the α- and Θ-phase, respectively. The ζ-phase was found to exhibit localized as well as delocalized electrons. When laser heating the sample at high pressure additional phases appear such as ι- and η-Fe₂O₃, depending on the pressure range. Here, we focus on the phase transitions observed under cold compression.

2 Experimental

2.1 Sample environment

The materials used were single crystalline siderite (FeCO₃) (synthesis described in Cerantola et al.²) and commercially available hematite (Fe₂O₃) (Sigma-Aldrich, 99.995% trace metal basis). The pressure was applied by a BX90 type diamond anvil cell (DAC) with an enlarged radial opening angle (BX90-RD) with argon as pressure transmitting medium to ensure quasi-hydrostatic conditions. The diamond setup consisted of a standard diamond (ST) on the downstream side and a Boehler-Almax (BA) shaped miniature diamond (MD)⁵⁸ on the upstream side. The usage of an MD instead of a regular sized BA diamond increases the intensity on the sample by a factor of 2 and 15 for incident energies of 10 400 eV and 7100 keV, respectively, by reducing the beampath through the diamond from 1720 μm to 500 μm. The pressure was determined by optical Raman spectroscopy via the diamond's Raman peak shift.⁵⁹ Rhenium plates with an initial thickness of 200 μm were used as gasket material. To ensure data acquisition in a horizontal scattering angle of ∼70°, a special indentation procedure was applied. First, the gasket was indented to a thickness of 40–50 μm. Second, the gasket was flipped around and indented to the final thickness of 20–30 μm. Finally, the rhenium bulge caused by the indentation procedure was ground off before drilling the sample chamber. Due to the different shapes of the diamonds, the ST will penetrate deeper into the gasket material. Thus, after flipping the gasket, the ST side of the gasket is less indented than the other one in the final setup. Furthermore, the BA anvil is flatter than the ST anvil, i.e., pavilion angles of 25° and 39°, respectively, and thus provides a wider indented hole. The flipping process results in an enlarged field of view of the spectrometer onto the sample between rim of the gasket and edge of the diamond for efficient data acquisition in ∼70° horizontal scattering angle. Furthermore, beveled diamonds increase the size of the indented plateau and thus improve the measurement geometry for small culet sizes. In this scattering geometry the emission radiation only passes through ∼500 μm instead of 2275 μm (ST) or 1720 μm (BA) of diamond in case of forward scattering. This increases the intensity by a factor of ∼56 and ∼237 (ST) or ∼16 and ∼43 (BA) for Kβ and Kα emission, respectively.

2.2 X-ray emission setup

The measurements were performed at beamline P01 at PETRA III (DESY).⁶⁰ The incident beam was focused to 7  ×  7 μm² (FWHM) using a Kirkpatrick–Baez mirror system and monochromatized utilizing a double crystal monochromator, exploiting the Si(111) crystals for XES and the Si(311) crystals for RXES measurements. This provides an incident energy resolution of 1.0 eV and 0.2 eV at 7100 eV, respectively. For non-resonant XES, the incident energy was fixed to 10 400 eV, which is a good compromise between transmission through the upstream diamond and interaction with the sample. Furthermore, choosing an energy below 10 500 eV prevents detection of strong Compton scattering signal during data acquisition, detected via higher order reflection (Si(660)), which results in a reduced background. In case of RXES the incident energy was varied with a step size of 0.2 eV in the pre-edge region, i.e., between 7108 eV and 7120 eV and larger step sizes afterwards to measure the X-ray absorption near-edge structure region for normalization. The flux on the sample was ∼8 × 10¹³ ph s⁻¹ for XES and ∼1.2 × 10¹³ ph s⁻¹ for RXES measurements. At each incident energy a full emission spectrum was acquired using a wavelength dispersive von Hámos spectrometer⁶¹ in combination with a Pilatus 100 K area detector⁶ having a pixel size of 172  ×  172 μm². The von Hámos spectrometer can be equipped with 4 cylindrically bent analyzer crystals with a focusing radius of 500 mm. The choice of the analyzer depends on the emission-energy range to be detected. In this study Si(111) and Si(110) analyzer crystals were used exploiting Si(333) and Si(440) reflections for Kα and Kβ emission, respectively, with an energy resolution of the spectrometer of ∼0.5 eV and ∼0.6 eV, dominated by the pixel size of the detector. The detector was energy calibrated by elastically scattered photons of known incident energies via higher order reflections, i.e., Si(555) and Si(660) for Kα and Kβ XES, respectively. This setup allows for data acquisition in a single shot fashion. A sketch of the scattering geometry is shown in Fig. 1. As the geometric constraints of the spectrometer settings, i.e., height of the analyzer array and detector position for Kα and Kβ emission detection are similar, a combination of both types of analyzer crystals makes two-color measurements feasible. The spectrometer was positioned at a horizontal scattering angle of ∼70°.

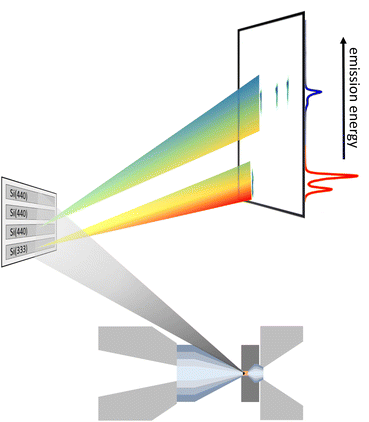Fig. 1 Representation of the scattering geometry for a two-color experiment using one Si(333) and three Si(440) reflections measuring the Fe Kα (red) and Kβ emission (blue), respectively.

For in situ experiments at HPHT conditions, a portable double-sided Yb:YAG laser system dedicated for the setup at beamline P01 at PETRA III was used. The laser provides a maximum output power of 100 W at a wavelength of 1070 nm. The complete laser-heating setup is described in detail by Spiekermann et al.⁶² For the experiments discussed here, one-sided heating was performed on the downstream side of the sample. The temperature was determined by a Planck fit of the grey body radiation detected from the hot spot of the sample.

2.3 Data analysis

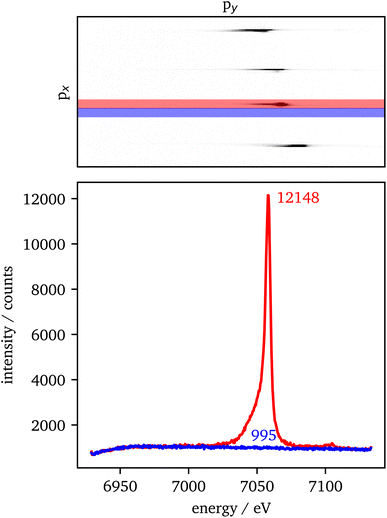
The data extraction is illustrated in Fig. 2. For each crystal with the same scattering geometry, a region of interest (ROI) is defined that includes all of the sample's intensity, but should be as small as possible to reduce the background in the data. To extract the background from the data, the ROI is shifted in p_x (blue) next to the data ROI (red). Both ROIs are summed up individually in p_x direction. Afterwards, the background is subtracted from the data and the p_y-scale is energy calibrated as explained in the experimental setup. For the RXES measurements, an XES spectrum is analyzed for each incident energy and merged to a 2D image with the incident energy on the x-axis and the energy transfer on the y-axis.

Fig. 2 (Top) Detector image with signal of 4 analyzer crystals using the Si(440) reflection for a 2 minutes measurement of Fe₂O₃ at 75 GPa. The red and blue shaded areas define the ROI for the signal and background intensity, respectively. Both ROIs have the same size of 10 pixels in p_x-direction. (Bottom) Integrated intensities of the ROIs with maximum intensity and the background within the plot. The background was averaged in a small eV range around the maximum position. The values result in a SNR of ∼354.

An estimation of the data quality provides the signal-to-noise ratio (SNR), which is calculated here by

with the maximum intensity I_p and the intensity of the background I_b. The background intensity is calculated at the same energy position but using the background ROI. Fig. 2 shows an example for a 2 minutes measurement of Fe₂O₃ at 75 GPa.

The spin state is analyzed using the Integral of the Absolute Difference (IAD) method.⁶³ Therefore, the spectra are shifted in emission energy so that their center-of-gravity (COG) is positioned at 7055 eV to account for energy scale uncertainties of data that are measured during different experiments. The IAD value is then calculated in the energy range between 7030 eV and 7070 eV with a spectrum of FeCO₃ measured at 75 GPa as LS reference. As an error estimation the IAD value between FeCO₃ measured at 75 GPa and 82 GPa is used, i.e., Fe being in LS state in both samples. The resulting IAD value is ∼8% of a complete spin transition. Moreover, the position of the First Momentum (M₁) is calculated considering the intensity of the Kβ_1,3 emission down to 50% of its maximum value.⁶⁴

RXES measurements are analyzed via constant emission energy (CEE) and constant incident energy (CIE) cuts. The CEE-cuts are calculated for an energy range of ∼1.1 eV (3 pixel), whereas the CIE-cuts are analyzed for each incident energy, i.e., 0.2 eV steps.

3 Results

3.1 X-ray emission at pressure and temperature: FeCO₃

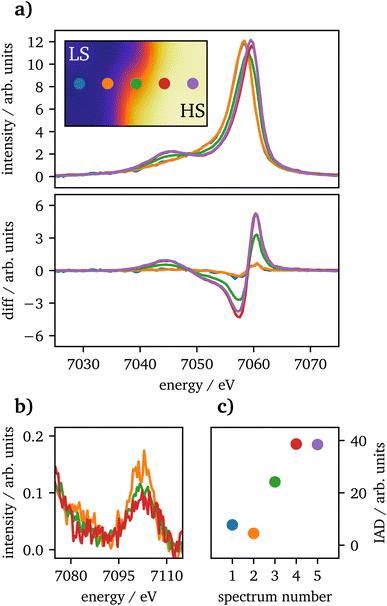
Spin-state imaging²⁹ was performed in situ on laser-heated FeCO₃ at 75 GPa. The sample was heated to 2800 ± 300 K on one side. During spin-state imaging, the step size was 7 μm in between measurements. Fig. 3(a) shows Kβ_1,3 XES spectra for a traverse across the heated sample, ranging from the unheated part to the heating spot. Each spectrum was measured for 5 minutes. Underneath the XES spectra the difference to the unheated sample at 75 GPa for IAD analysis is shown, measured prior to the heating process. The data exhibit a consistent trend from LS to HS state, while going from the cold to the hot part of the sample. Furthermore, in (b) the vtc regions of each spectrum is plotted. The short measurement times of only 5 minutes do not allow for a dedicated analysis of the vtc. However, a clear trend in the Kβ_2,5-peak can be detected as the peak's position is shifting to higher emission energies along with decreasing intensity, related to the changes in Fe–O bonding distance. Since the first and last spectra were measured at the rim of the sample, the data quality is insufficient even for a qualitative analysis and are therefore not shown in the graph.

Fig. 3 (a) Kβ_1,3 XES spectra for laser-heated FeCO₃ at 75 GPa for a traverse across the sample going from the unheated part to the heating spot with increasing spin state. Data acquisition was performed for 5 minutes in total, separated into 1 minute measurements. The inset shows the spin distribution on the sample with the dots indicating the measurement position. Difference to the LS reference, i.e., long measurement of the unheated sample, is shown underneath the spectra. In (b) the corresponding vtc spectra are shown, the first and last spectrum are missing due to the low data quality. (c) IAD values corresponding to the spectra shown in (a) with the same color code.

3.2 X-ray emission at pressure: Fe₂O₃

3.2.1 Non-resonant X-ray emission. Fe Kβ XES of Fe₂O₃ was performed in a pressure range of 11 GPa to 75 GPa during two different experiments. Selected emission spectra are shown in Fig. 4(a) for the Kβ_1,3 emission. The IAD results are shown in (b) along with the IAD value of FeCO₃ at 82 GPa, which serves as an error estimation. Up to a pressure of 42 GPa, the sample is in HS state within the error. For higher pressures, the IAD values drop to around 40% of their previous values. Between 57 GPa and 64 GPa the spin state is constant and drops again at 75 GPa. However, the sample might not be completely in a LS state at the highest pressure.

Fig. 4 (a) Selected Kβ_1,3 spectra of Fe₂O₃ between 11 GPa and 75 GPa. The difference to the LS reference is shown underneath the spectra. (b) IAD values for all pressures along with the reference value for FeCO₃ at 82 GPa in gray. Open symbols represent the second experiment. The gray line is a guide to the eye.

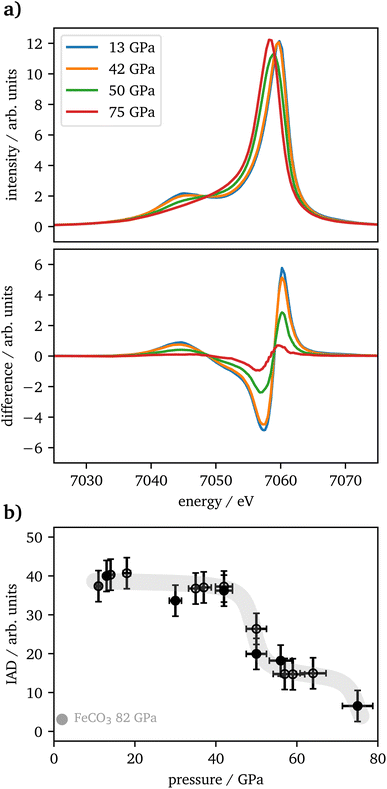
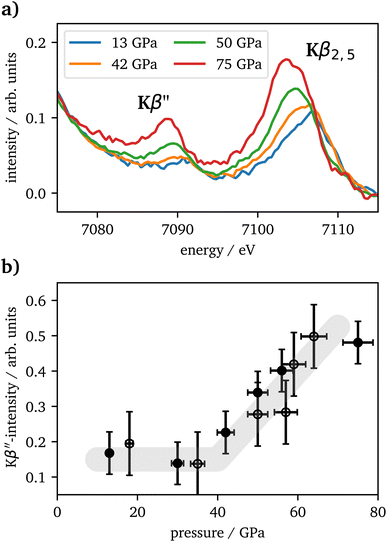
The vtc spectra are shown in Fig. 5(a) for the same pressures as in Fig. 4(a). The Kβ′′ peak originates from the hybridization between oxygen 2s and iron 3d states and its intensity is connected to the Fe–O bonding distance.⁶⁵ It's integrated intensity is shown in Fig. 5(b) for all pressures. Up to 42 GPa, no significant change was observed in the data. At higher pressures the Kβ′′'s peak-intensity is significantly increasing, which is indicative for a decreased Fe–O bonding distance, starting with the onset of the spin changes.

Fig. 5 (a) Selected vtc spectra of Fe₂O₃ between 11 GPa and 75 GPa. (b) Integrated Kβ′′-intensities for all pressures. Open symbols represent the second experiment. The gray line is a guide to the eye.

3.2.2 Resonant X-ray emission. 1s2p RXES maps were measured for selected pressures up to 75 GPa. Results for pressures in the vicinity of the phase transition at 50 GPa will be discussed within this paragraph (spectra for all pressures are presented in the ESI, Fig. S1†). The RXES data are shown in Fig. 6. The RXES maps with a zoom on the Kα₁ emission in the pre-edge region are visualized in (a) with the resulting CEE-cuts in (b). At 46 GPa, the sample is in HS state and octahedral coordination as the CEE-cuts contain both electronic states for this phase, ⁵T_2g and ⁵E_g.⁶⁶ The peak positions at 46 GPa are at 7112.4 ± 0.1 eV and 7114.2 ± 0.1 eV, which results in a crystal field splitting of 1.8 ± 0.1 eV. With the onset of the spin-state changes at higher pressures, the electronic structure changes drastically with a shift of the pre-edge peaks to lower incident energies. At 50 GPa the ⁵T_2g and ⁵E_g transitions are still observable but an underlying new feature is rising, which replaces the Fe³⁺ HS features at 57 GPa completely. The CEE-cut of 50 GPa can be reproduced with a reasonable accuracy by a mixture of 46 GPa and 57 GPa. The best fit between 7110 eV and 7116 eV results in an abundance of 57% of the HS spectrum and is in mutual agreement with the spin-state results of ∼50%.

Fig. 6 (a) RXES planes of Fe₂O₃ at high pressures of 46 GPa, 50 GPa and 57 GPa. (b) CEE-cuts of the pre-edge region are shown and shifted vertically for clarity. The grey dashed line is a superposition of 46 GPa and 57 GPa with 57% abundance of the HS spectrum. (c) CIE-cuts of each pressure in the pre-edge region, shifted vertically with increasing incident energy. The colored dots indicate the maximum position for each CIE-cut and are visualized in (d), shifted vertically for clarity.

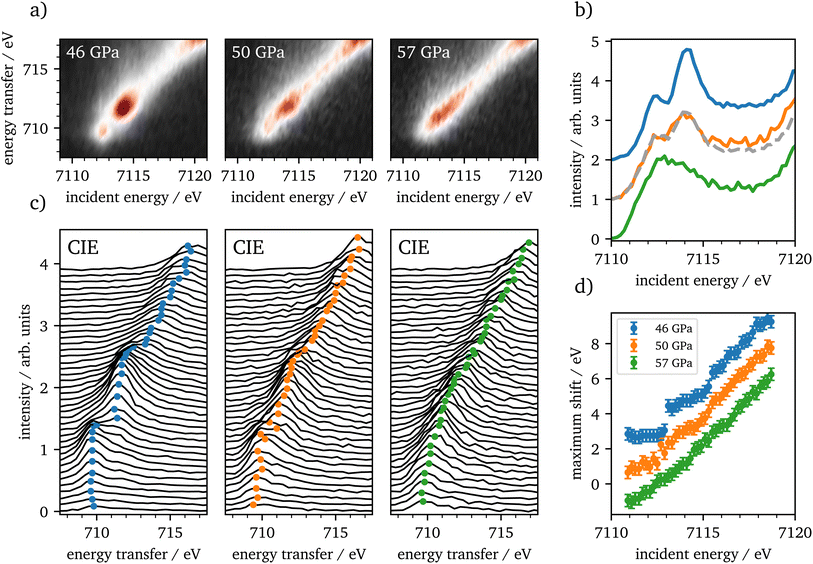
CIE-cuts for the pre-edge region are visualized in Fig. 6(c) and support the previous findings. The colored dots indicate the maximum positions of the emission, which are also shown in (d). A constant energy transfer can be indicative for localized states, whereas a linear dispersion can indicate delocalized states.^44,67–69 Nevertheless, this assignment is not unambiguous.⁷⁰ The data in (d) show that the ⁵T_2g and ⁵E_g transitions in 46 GPa and 50 GPa are discrete localized states and the states at higher incident energies are delocalized via bridging hybridization to neighbouring Fe atoms (Fe₁(3d)-O(2p)-Fe₂(4p)) (ref. 67 and references therein). At 57 GPa the maxima of the pre-edge region are almost completely dispersing with the incident energy, except for a small energy region at the onset of the pre-edge region.

4 Discussion

4.1 FeCO₃

Laser-heated FeCO₃ in the given pressure range undergoes a phase transition into Fe₄³⁺C₃O₁₂ and Fe₂²⁺ Fe₂³⁺C₄O₁₃.^21,35–41 Recently Albers et al.²⁹ and Kaa et al.³⁰ have shown experimentally, that both phases are in HS state. The findings in this study are in accordance with the spin changes for laser-heated FeCO₃. However, as the sample was not post-characterized after temperature quenching, an exact phase transition could not be verified. Nevertheless, the LS and HS state regions in the sample were conserved after temperature quenching (not shown). Thus, a transition into Fe₄³⁺C₃O₁₂ and Fe₂²⁺ Fe₂³⁺C₄O₁₃ is likely.

4.2 Fe₂O₃

Kβ_1,3-XES measurements of Fe₂O₃ show a drop in spin state between 46 GPa and 57 GPa with intermediate spin values in between and a subsequent further drop between 64 GPa and 75 GPa. The IAD values in the intermediate plateau are at 40% of the maximum value, whereas a transition of one iron site should result in an IAD value of 50%. This might be based on a symmetry reduction of the trigonal-prismatic HS site, as seen also for FeO, which undergoes a transition from octahedral to rhombohedral distorted coordination under pressure. The resulting Kβ_1,3 peak-shape change results in an IAD value of around 20% of a complete HS–LS transition²⁵ and, translated to this case, would perfectly fit the difference of 10% to the expected value, as only half of the iron is impacted by the distortion. These findings are in good agreement with recently published literature.^4,20,22

At around 50 GPa a transition from the α-phase (hematite) into the ζ-phase with a perovskite structure occurs, incorporating two distinct iron sites, an octahedral LS site (A) and a trigonal-prismatic HS site (B). Mössbauer spectroscopy results published by Bykova et al.²⁰ show a constant decrease of magnetic components in favor of non-magnetic components, but the lack of sufficient data points allows no final assignment to the phase transition from α-Fe₂O₃via ζ-Fe₂O₃ to Θ-Fe₂O₃, which was reported in detail by their XRD data. Sanson et al.⁴ and Greenberg et al.²² report a completed phase transition into the ζ-phase at around 56 GPa with a subsequent plateau to 80 GPa or 62 GPa, respectively.

At higher pressures Bykova et al.²⁰ and Greenberg et al.²² both report the transition into the Θ-phase with an Aba2-structure having all iron in LS-state and trigonal-prismatic coordination. Bykova et al.²⁰ see a completed transition already at 75 GPa whereas Greenberg et al.²² report around 70% of the high-pressure phase to be present at this pressure. In contrast, Sanson et al.⁴ find this transition on a structural level but see no further drop in spin state and thus conclude the sample is already completely in LS state at 56 GPa which is in contradiction to our findings indicating a plateau of mixed spin state for iron on the different sites. Based on the IAD values in our study, we cannot decide whether iron is not completely in LS state in accordance with Greenberg et al.²² or in full LS state according to Bykova et al.²⁰

The vtc spectra show a significantly increased Kβ′′ intensity with the onset of the phase transition at pressures >42 GPa. Based on structural data reported by Bykova et al. and Greenberg et al.,^20,22 the Fe–O distance is substantially decreasing with pressure due to the phase transition into the ζ-phase, which results in an increased hybridization with the oxygen 2s states. Thus, our results are in accordance with the findings of the literature. As there is again only one data point within the stability region of the Θ-phase, one can only speculate about the further development of the Kβ′′ intensity.

The RXES data show iron in the HS state up to 46 GPa, which is in accordance with recent literature.^4,20,22 Up to 46 GPa the crystal field splitting is constantly increasing as shown in Table 1. At the onset of the spin-state changes in the Kβ_1,3-XES measurements, CEE- and CIE-cuts change significantly. The measurements at 50 GPa are well reproduced by a linear combination of 46 GPa and 57 GPa with an abundance of around 57% of the HS spectrum. In combination with the XES results this verifies that the phase transition occurs on a broad range of about 10 GPa, as reported by Greenberg et al.²² Furthermore, the CIE-cuts show a transition from discrete localized ⁵T_2g and ⁵E_g states at 46 GPa into potentially delocalized states at 57 GPa, that show continuum-like character. At the onset of the pre-edge region we observe at least one localized transition, which is constant in energy transfer. At higher incident energies, states dominate that are not well separated. This may indicate the delocalized nature of these excitations. However, overlapping discrete localized states might also be present, but are covered by the delocalized states. Nevertheless, our results support the findings of Greenberg et al.²² of a site-selective delocalization in ζ-Fe₂O₃.

Table 1 Crystal field splitting values for different pressures of α-Fe₂O₃. The error of each measurement is estimated with ±0.1 eV

Pressure/GPa	CEE-split/eV	CIE-split/eV
11	1.59	1.83
35	1.70	1.90
46	1.78	1.97

---

4.3 Setup

The setup used in 70°-scattering geometry significantly increased the SNR for iron Kα and Kβ emission spectroscopy. During laser heating, the data acquisition lasted for 5 minutes per spectrum, which was separated into 5 images of each 1 minute integration time for further analyzes. The 1 minute spectra along with their SNRs are shown in the ESI, Fig. S2.†

In Fig. 7 IAD values and ΔM₁ of each 1 minute spectrum are analyzed and compared to the summed spectra with 5 minute integration time. The results are in good agreement between both integration times for most of the data. The only outlier is the first position (blue) in which the IAD values of the 1 minute spectra are considerably higher than the sum of all spectra. In these spectra, the data quality is significantly lower, as they were taken from the rim of the sample, which results in a lower intensity of emitted X-rays, due to the probed sample volume. The black crosses show the SNR of each measurement and verify the lower data quality of the blue spectra. Furthermore, the IAD value is calculated using the absolute difference to the LS reference, hence, low-quality data with a high amount of LS in the spectra are systematically overrated, as only the noise will be summed up. Another source of error is the shift to the same COG, as low-quality data might be shifted to a slightly incorrect value which is then be transmitted into the IAD value.

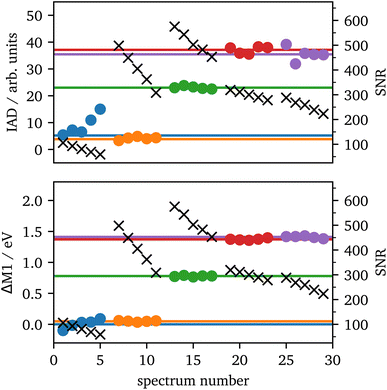Fig. 7 IAD (top) and First Momentum (bottom) analysis of each 1 minute (dots) and their corresponding 5 minutes (lines) spectrum for the spectra from Fig. 3 with the same color code. The black crosses (right scale) show the SNRs for each 1 minute measurement.

Contrary, ΔM₁ analysis is highly stable even for low-quality data. Fig. 7 shows the ΔM₁-shifts for all 1 minute and 5 minutes spectra with the first spectrum as reference. All data points of the 1 minute spectra are in accordance with their corresponding 5 minute spectrum.

Based on these results, we can conclude that spectra with an SNR >100 provide a high-quality spin-state analysis with robust results. Prior to laser heating, the sample has a peak intensity of ∼13 000 counts with a background of ∼500 counts for each crystal and an integration of 10 pixels orthogonal to the energy axis within one minute. This provides a SNR of around ∼560 for one crystal. When extrapolated to a minimal SNR of 100, this results in a minimal data acquisition time for consistent spin-state measurements of around 2 seconds for a single crystal and 1 second if four crystals are summed up. However, the exact signal from a cell depends on various factors such as the accuracy of gasket preparation, the size of the sample, the quality of shielding the incident photons or the type of upstream diamond⁵⁸ and varies between different samples, DACs and experiments. The discussed sample may be close to the ideal configuration and thus, longer measurement times should be assumed. For comparison, the measurement of Fe₂O₃ at 75 GPa provided a SNR of around 350 per crystal within two minutes, which results in a data acquisition time of 10 seconds and 5 seconds for one and four crystals, respectively.

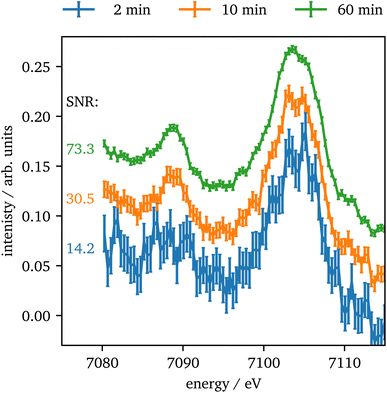
In contrast to Kβ_1,3, the intensity of the vtc emission is significantly lower by a factor of ∼80 for Kβ_2,5 emission and thus, longer data acquisition times are required. In Fig. 8 the vtc region of Fe₂O₃ at 75 GPa is shown for different integration times and four crystals summed up. The data show, that even after 2 minutes the signal is strong enough to identify Kβ′′ and Kβ_2,5 emission and after 10 minutes the data quality allows for a reasonable determination of the peak's position and intensity. With higher integration times the data quality improves more and more slowly. The data quality might be further improved by binning of consecutive data points as discussed via Fig. S3 in the ESI.†

Fig. 8 Vtc spectra of Fe₂O₃ at 75 GPa for different integration times. The SNRs are calculated for the maximum of the Kβ_2,5 emission with the background averaged between 7100 eV and 7110 eV. The data have been offset by 0.05 units for clarity.

A substantial improvement of this setup was the utilization of mini diamonds on the upstream side. At 10 400 eV, the incident energy for Kβ_1,3-XES, the transmission through the upstream diamond is more than doubled. However, the most important improvement is achieved for RXES measurements. At an incident energy of 7100 eV the intensity gains a factor of 15 compared to a regular sized BA diamond of 1720 μm. The substantially increased SNR and thus decreased data acquisition time allows for RXES measurements with an incident energy resolution of 0.2 eV in about 2 hours for samples with a high iron content such as Fe₂O₃. The extent of the improved data quality allows also for in situ RXES when combined with a long term stable laser-heating system. Apart from that, the scattering geometry allows for simultaneous 1s2p and 1s3p RXES measurements as indicated in Fig. 1. However, this increases the data acquisition times again, as the intensity of Kβ emission is significantly lower than Kα emission and only one crystal provides Kα emission instead of four. Contrary, the higher emission energy of the Kβ_1,3 peak results in a decreased absorption of the downstream diamond. All in all, this leads to a roughly equal intensity of Kα and Kβ emission when using one Si(111) and three Si(110) analyzer crystals.

5 Conclusion

We combined a wavelength dispersive von Hámos spectrometer and an area detector along with a dedicated sample preparation to allow high-quality (resonant) X-ray emission spectroscopy. To showcase the great potential of this setup, in situ spin-state imaging of laser-heated FeCO₃ at 75 GPa and XES (including vtc) as well as RXES measurements of cold-compressed Fe₂O₃ up to 75 GPa were performed.

In situ spin-state imaging of laser-heated FeCO₃ shows a spatially separated spin-state distribution of LS in the unheated and HS in the heated area of the sample, likely due to a decomposition of FeCO₃ into Fe₄C₃O₁₂ and Fe₄C₄O₁₃.²⁹

The spin-state development of Fe₂O₃ shows a decrease in IAD value in the ζ-phase with a significant further drop at 75 GPa, i.e., in the Θ-phase. The IAD value in the ζ-phase of 40% of the α-phase's value is likely based on a symmetry reduction from octahedral to trigonal-prismatic coordination on the HS site. These findings are in great accordance with the results of Bykova et al.²⁰ and Greenberg et al.,²² but show differences to Sanson et al.⁴ at higher pressures. The vtc intensity is significantly increasing after the onset of the phase transition, which is due to the changing Fe–O bonding distances and in line with structural data. The RXES measurements support the findings by Greenberg et al.²² of delocalized states in the high-pressure phases.

The derived SNR for short measurement times provides an estimate for future experiments and one can evaluate the feasibility of experiments, e.g., for samples with a low iron content or beamlines with lower photon flux. There are different approaches for an improvement of the SNR of a measurement, which have a different impact on the result. A total increase of signal and background, e.g., by increasing the measurement time or the photon flux on the sample, is scaling with the square root of the intensity, whereas on improvement of the signal by the sample itself, e.g., by improving the opening angle of the cell or the iron content, is scaling linearly.

The setup's great potential for future applications is the combination of 1s2p and 1s3p RXES to extend the amount of information within a measurement. Furthermore, the combination of 1s2p with in situ laser-heating of iron-bearing samples will be feasible. Moreover, in situ spin-state imaging will be established as a standard tool for analyzes of the electronic structure of iron under extreme conditions.

Author contributions

CA, MT, MW and CS designed the research. CA, RS, NT, LL, GS, JK, HG and MS conducted the experiments. LL and GS implemented the laser-heating device. CA analyzed the data. CA and CS wrote the manuscript with contributions of all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. Parts of this research were carried out at PETRA III beamlines P01 and P02.2. Beamtime was allocated for proposals I-20191002, I-20200600, I-20200519, I-20211259 and H-20010185. We thank Conrad Hagemeister for technical support at P01. We are grateful for gas loading at DeutschesGeoForschungsZentrum. This work was financially supported by the DFG via STE 1079/4-1 and WI 2000/17-1 within the DFG-FOR2125 CarboPaT and STE 1079/2-1. We acknowledge Delta (Dortmund, Germany) for providing synchrotron radiation for commissioning of the spectrometer at BL9.

Notes and references

1. J. F. Lin, V. V. Struzhkin, S. D. Jacobsen, M. Y. Hu, P. Chow, J. Kung, H. Liu, H. K. Mao and R. J. Hemley, Nature, 2005, 436, 377–380.
2. V. Cerantola, C. McCammon, I. Kupenko, I. Kantor, C. Marini, M. Wilke, L. Ismailova, N. Solopova, A. Chumakov, S. Pascarelli and L. Dubrovinsky, Am. Mineral., 2015, 100, 2670–2681.
3. J. Müller, S. Speziale, I. Efthimiopoulos, S. Jahn and M. Koch-Müller, Am. Mineral., 2016, 101, 2638–2644.
4. A. Sanson, I. Kantor, V. Cerantola, T. Irifune, A. Carnera and S. Pascarelli, Phys. Rev. B, 2016, 94, 014112.
5. C. Weis, C. Sternemann, V. Cerantola, C. J. Sahle, G. Spiekermann, M. Harder, Y. Forov, A. Kononov, R. Sakrowski, H. Yavaş, M. Tolan and M. Wilke, Sci. Rep., 2017, 7, 16526.
6. C. Weis, G. Spiekermann, C. Sternemann, M. Harder, G. Vankó, V. Cerantola, C. J. Sahle, Y. Forov, R. Sakrowski, I. Kupenko, S. Petitgirard, H. Yavaş, C. Bressler, W. Gawelda, M. Tolan and M. Wilke, J. Anal. At. Spectrom., 2019, 34, 384–393.
7. J.-F. Lin, S. Speziale, Z. Mao and H. Marquardt, Rev. Geophys., 2013, 51, 244–275.
8. N. B. Zhang, Y. Cai, X. H. Yao, X. M. Zhou, Y. Y. Li, C. J. Song, X. Y. Qin and S. N. Luo, AIP Adv., 2018, 8, 075028.
9. K. Ohta, S. Onoda, K. Hirose, R. Sinmyo, K. Shimizu, N. Sata, Y. Ohishi and A. Yasuhara, Science, 2008, 320, 89–91.
10. Y. Okuda, K. Ohta, R. Sinmyo, K. Hirose and Y. Ohishi, Phys. Chem. Miner., 2020, 47, 40.
11. D. J. Bower, M. Gurnis, J. M. Jackson and W. Sturhahn, Geophys. Res. Lett., 2009, 36, L10306.
12. M. H. Shahnas, W. R. Peltier, Z. Wu and R. Wentzcovitch, J. Geophys. Res.: Solid Earth, 2011, 116, B08205.
13. K. Vilella, S.-H. Shim, C. G. Farnetani and J. Badro, Earth Planet. Sci. Lett., 2015, 417, 57–66.
14. Y. Li, K. Vilella, F. Deschamps, L. Zhao and P. J. Tackley, Geophys. Res. Lett., 2018, 45, 5918–5928.
15. R. Sinmyo, K. Hirose, D. Nishio-Hamane, Y. Seto, K. Fujino, N. Sata and Y. Ohishi, J. Geophys. Res.: Solid Earth, 2008, 113, B11204.
16. T. Irifune, T. Shinmei, C. A. McCammon, N. Miyajima, D. C. Rubie and D. J. Frost, Science, 2010, 327, 193–195.
17. R. Sinmyo and K. Hirose, Phys. Chem. Miner., 2013, 40, 107–113.
18. C. Prescher, F. Langenhorst, L. S. Dubrovinsky, V. B. Prakapenka and N. Miyajima, Earth Planet. Sci. Lett., 2014, 399, 86–91.
19. H. Piet, J. Badro, F. Nabiei, T. Dennenwaldt, S.-H. Shim, M. Cantoni, C. Hébert and P. Gillet, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 11127–11130.
20. E. Bykova, L. Dubrovinsky, N. Dubrovinskaia, M. Bykov, C. McCammon, S. V. Ovsyannikov, H. P. Liermann, I. Kupenko, A. I. Chumakov, R. Rüffer, M. Hanfland and V. Prakapenka, Nat. Commun., 2016, 7, 10661.
21. V. Cerantola, E. Bykova, I. Kupenko, M. Merlini, L. Ismailova, C. McCammon, M. Bykov, A. I. Chumakov, S. Petitgirard, I. Kantor, V. Svitlyk, J. Jacobs, M. Hanfland, M. Mezouar, C. Prescher, R. Rüffer, V. B. Prakapenka and L. Dubrovinsky, Nat. Commun., 2017, 8, 15960.
22. E. Greenberg, I. Leonov, S. Layek, Z. Konôpková, M. P. Pasternak, L. Dubrovinsky, R. Jeanloz, I. A. Abrikosov and G. K. Rozenberg, Phys. Rev. X, 2018, 8, 31059.
23. V. Cerantola, M. Wilke, I. Kantor, L. Ismailova, I. Kupenko, C. McCammon, S. Pascarelli and L. S. Dubrovinsky, Am. Mineral., 2019, 104, 1083–1091.
24. J.-F. Lin, Z. Mao, I. Jarrige, Y. Xiao, P. Chow, T. Okuchi, N. Hiraoka and S. D. Jacobsen, Am. Mineral., 2010, 95, 1125–1131.
25. C. Albers, N. Thiering, R. Sakrowski, H. Gretarsson, J. Kaa, M. Sundermann, M. Tolan, M. Wilke and C. Sternemann, J. Phys.: Conf. Ser., 2022, 2380, 012128.
26. J. Badro, V. V. Struzhkin, J. Shu, R. J. Hemley, H.-K. Mao, C. C. Kao, J.-P. Rueff and G. Shen, Phys. Rev. Lett., 1999, 83, 4101–4104.
27. J. Badro, G. Fiquet, F. Guyot, J.-P. Rueff, V. V. Struzhkin, G. Vankó and G. Monaco, Science, 2003, 300, 789–791.
28. J. Badro, J.-P. Rueff, G. Vankó, G. Monaco, G. Fiquet and F. Guyot, Science, 2004, 305, 383–386.
29. C. Albers, R. Sakrowski, L. Libon, G. Spiekermann, B. Winkler, C. Schmidt, L. Bayarjargal, V. Cerantola, S. Chariton, N. Giordano, H. Gretarsson, J. Kaa, H.-P. Liermann, M. Sundermann, N. Thiering, M. Tolan, M. Wilke and C. Sternemann, Phys. Rev. B, 2022, 105, 085155.
30. J. M. Kaa, C. Sternemann, K. Appel, V. Cerantola, T. R. Preston, C. Albers, M. Elbers, L. Libon, M. Makita, A. Pelka, S. Petitgirard, C. Plückthun, V. Roddatis, C. J. Sahle, G. Spiekermann, C. Schmidt, A. Schreiber, R. Sakrowski, M. Tolan, M. Wilke, U. Zastrau and Z. Konôpková, Phys. Rev. Res., 2022, 4, 033042.
31. S. Anzellini and S. Boccato, Crystals, 2020, 10, 459.
32. J. Meza-Galvez, N. Gomez-Perez, A. S. Marshall, A. L. Coleman, K. Appel, H. P. Liermann, M. I. McMahon, Z. Konôpková and R. S. McWilliams, J. Appl. Phys., 2020, 127, 195902.
33. H.-P. Liermann, Z. Konôpková, K. Appel, C. Prescher, A. Schropp, V. Cerantola, R. J. Husband, J. D. McHardy, M. I. McMahon, R. S. McWilliams, C. M. Pépin, J. Mainberger, M. Roeper, A. Berghäuser, H. Damker, P. Talkovski, M. Foese, N. Kujala, O. B. Ball, M. A. Baron, R. Briggs, M. Bykov, E. Bykova, J. Chantel, A. L. Coleman, H. Cynn, D. Dattelbaum, L. E. Dresselhaus-Marais, J. H. Eggert, L. Ehm, W. J. Evans, G. Fiquet, M. Frost, K. Glazyrin, A. F. Goncharov, H. Hwang, Z. Jenei, J. Y. Kim, F. Langenhorst, Y. Lee, M. Makita, H. Marquardt, E. E. McBride, S. Merkel, G. Morard, E. F. O'Bannon III, C. Otzen, E. J. Pace, A. Pelka, J. S. Pigott, V. B. Prakapenka, R. Redmer, C. Sanchez-Valle, M. Schoelmerich, S. Speziale, G. Spiekermann, B. T. Sturtevant, S. Toleikis, N. Velisavljevic, M. Wilke, C. S. Yoo, C. Baehtz, U. Zastrau and C. Strohm, J. Synchrotron Radiat., 2021, 28, 688–706.
34. H. Hwang, T. Kim, H. Cynn, T. Vogt, R. J. Husband, K. Appel, C. Baehtz, O. B. Ball, M. A. Baron, R. Briggs, M. Bykov, E. Bykova, V. Cerantola, J. Chantel, A. L. Coleman, D. Dattlebaum, L. E. Dresselhaus-Marais, J. H. Eggert, L. Ehm, W. J. Evans, G. Fiquet, M. Frost, K. Glazyrin, A. F. Goncharov, Z. Jenei, J. Kim, Z. Konôpková, J. Mainberger, M. Makita, H. Marquardt, E. E. McBride, J. D. McHardy, S. Merkel, G. Morard, E. F. O'Bannon III, C. Otzen, E. J. Pace, A. Pelka, C. M. Pépin, J. S. Pigott, V. B. Prakapenka, C. Prescher, R. Redmer, S. Speziale, G. Spiekermann, C. Strohm, B. T. Sturtevant, N. Velisavljevic, M. Wilke, C. S. Yoo, U. Zastrau, H.-P. Liermann, M. I. McMahon, R. S. McWilliams and Y. Lee, J. Phys. Chem. Lett., 2021, 12, 3246–3252.
35. E. Boulard, A. Gloter, A. Corgne, D. Antonangeli, A.-L. Auzende, J.-P. Perrillat, F. Guyot and G. Fiquet, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5184–5187.
36. E. Boulard, N. Menguy, A.-L. Auzende, K. Benzerara, H. Bureau, D. Antonangeli, A. Corgne, G. Morard, J. Siebert, J.-P. Perrillat, F. Guyot and G. Fiquet, J. Geophys. Res.: Solid Earth, 2012, 117, B02208.
37. E. Boulard, D. Pan, G. Galli, Z. Liu and W. L. Mao, Nat. Commun., 2015, 6, 6311.
38. J. Liu, J.-F. Lin and V. B. Prakapenka, Sci. Rep., 2015, 5, 7640.
39. M. Merlini, M. Hanfland, A. Salamat, S. Petitgirard and H. Müller, Am. Mineral., 2015, 100, 2001–2004.
40. M. Merlini, V. Cerantola, G. D. Gatta, M. Gemmi, M. Hanfland, I. Kupenko, P. Lotti, H. Müller and L. Zhang, Am. Mineral., 2017, 102, 1763–1766.
41. C. Sanloup, J. M. Hudspeth, V. Afonina, B. Cochain, Z. Konôpková, G. Lelong, L. Cormier and C. Cavallari, Front. Earth Sci., 2019, 7, 72.
42. H. Yamaoka, M. Oura, M. Taguchi, T. Morikawa, K. Takahiro, A. Terai, K. Kawatsura, A. M. Vlaicu, Y. Ito and T. Mukoyama, J. Phys. Soc. Jpn., 2004, 73, 3182–3191.
43. F. de Groot, P. Glatzel, U. Bergmann, P. A. van Aken, R. A. Barrea, S. Klemme, M. Hävecker, A. Knop-Gericke, W. M. Heijboer and B. M. Weckhuysen, J. Phys. Chem. B, 2005, 109, 20751–20762.
44. P. Glatzel, A. Mirone, S. G. Eeckhout, M. Sikora and G. Giuli, Phys. Rev. B, 2008, 77, 115133.
45. J. S. Olsen, C. S. Cousins, L. Gerward, H. Jhans and B. J. Sheldon, Phys. Scr., 1991, 43, 327–330.
46. M. P. Pasternak, G. Kh. Rozenberg, G. Yu Machavariani, O. Naaman, R. D. Taylor and R. Jeanloz, Phys. Rev. Lett., 1999, 82, 4663–4666.
47. J. Badro, G. Fiquet, V. V. Struzhkin, M. Somayazulu, H.-K. Mao, G. Shen and T. Le Bihan, Phys. Rev. Lett., 2002, 89, 205504.
48. G. Kh Rozenberg, L. S. Dubrovinsky, M. P. Pasternak, O. Naaman, T. Le Bihan and R. Ahuja, Phys. Rev. B, 2002, 65, 064112.
49. H. Liu, W. A. Caldwell, L. R. Benedetti, W. Panero and R. Jeanloz, Phys. Chem. Miner., 2003, 30, 582–588.
50. S. Ono, T. Kikegawa and Y. Ohishi, J. Phys. Chem. Solids, 2004, 65, 1527–1530.
51. A. V. Kozhevnikov, A. V. Lukoyanov, V. I. Anisimov and M. A. Korotin, J. Exp. Theor. Phys., 2007, 105, 1035–1042.
52. S.-H. Shim, A. Bengtson, D. Morgan, W. Sturhahn, K. Catalli, J. Zhao, M. Lerche and V. Prakapenka, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 5508–5512.
53. E. Ito, H. Fukui, T. Katsura, D. Yamazaki, T. Yoshino, Y. Aizawa, A. Kubo, S. Yokoshi, K. Kawabe, S. Zhai, A. Shatzkiy, M. Okube, A. Nozawa and K.-I. Funakoshi, Am. Mineral., 2009, 94, 205–209.
54. L. Dubrovinsky, T. Boffa-Ballaran, K. Glazyrin, A. Kurnosov, D. Frost, M. Merlini, M. Hanfland, V. B. Prakapenka, P. Schouwink, T. Pippinger and N. Dubrovinskaia, High Pressure Res., 2010, 30, 620–633.
55. E. Bykova, M. Bykov, V. Prakapenka, Z. Konôpková, H. P. Liermann, N. Dubrovinskaia and L. Dubrovinsky, High Pressure Res., 2013, 33, 534–545.
56. J. Tuček, L. Machala, S. Ono, A. Namai, M. Yoshikiyo, K. Imoto, H. Tokoro, S. I. Ohkoshi and R. Zbořil, Sci. Rep., 2015, 5, 15091.
57. M. Nowakowski, J. Czapla-Masztafiak, J. Szlachetko and W. M. Kwiatek, Chem. Phys., 2017, 493, 49–55.
58. S. Petitgirard, G. Spiekermann, C. Weis, C. Sahle, C. Sternemann and M. Wilke, J. Synchrotron Radiat., 2017, 24, 276–282.
59. Y. Akahama and H. Kawamura, J. Appl. Phys., 2006, 100, 043516.
60. H.-C. Wille, H. Franz, R. Röhlsberger, W. A. Caliebe and F.-U. Dill, J. Phys.: Conf. Ser., 2010, 217, 012008.
61. L. v. Hámos, Ann. Phys., 1933, 409, 716–724.
62. G. Spiekermann, I. Kupenko, S. Petitgirard, M. Harder, A. Nyrow, C. Weis, C. Albers, N. Biedermann, L. Libon, C. J. Sahle, V. Cerantola, K. Glazyrin, Z. Konôpková, R. Sinmyo, W. Morgenroth, I. Sergueev, H. Yavaş, L. Dubrovinsky, M. Tolan, C. Sternemann and M. Wilke, J. Synchrotron Radiat., 2020, 27, 414–424.
63. G. Vankó, T. Neisius, G. Molnár, F. Renz, S. Kárpáti, A. Shukla and F. M. de Groot, J. Phys. Chem. B, 2006, 110, 11647–11653.
64. S. Lafuerza, A. Carlantuono, M. Retegan and P. Glatzel, Inorg. Chem., 2020, 59, 12518–12535.
65. G. Spiekermann, M. Harder, K. Gilmore, P. Zalden, C. J. Sahle, S. Petitgirard, M. Wilke, N. Biedermann, C. Weis, W. Morgenroth, J. S. Tse, E. Kulik, N. Nishiyama, H. Yavaş and C. Sternemann, Phys. Rev. X, 2019, 9, 011025.
66. T. E. Westre, P. Kennepohl, J. G. Dewitt, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1997, 119, 6297–6314.
67. G. Vankó, F. M. F. de Groot, S. Huotari, R. J. Cava, T. Lorenz and M. Reuther, arxiv.org/abs/0802.2744, 2008.
68. A. Kotani, J. Electron Spectrosc. Relat. Phenom., 2000, 110–111, 197–212.
69. T. Idé and A. Kotani, J. Phys. Soc. Jpn., 2000, 69, 1895–1906.
70. P. Glatzel, M. Sikora and M. Fernández-García, Eur. Phys. J.: Spec. Top., 2009, 169, 207–214.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ja00014a

---