Open Access Article
Open Access ArticleBenchmarking quantum chemical methods for accurate gas-phase structure predictions of carbonyl compounds: the case of ethyl butyrate†
Lilian W.
Sutikdja
a,
Ha Vinh Lam
Nguyen
 *bc,
Dragan
Jelisavac
a,
Wolfgang
Stahl‡
a and
Halima
Mouhib
*bc,
Dragan
Jelisavac
a,
Wolfgang
Stahl‡
a and
Halima
Mouhib
 *d
*d
aInstitute of Physical Chemistry, RWTH Aachen University, Landoltweg 2, D-52074, Aachen, Germany
bUniv Paris Est Creteil and Université Paris Cité, CNRS, LISA, F-94010, Créteil, France. E-mail: lam.nguyen@lisa.ipsl.fr
cInstitut Universitaire de France (IUF), F-75231, Paris cedex 05, France
dDepartment of Computer Science, VU Bioinformatics, Vrije Universiteit Amsterdam, De Boelelaan 1111, 1081 HV, Amsterdam, The Netherlands. E-mail: h.mouhib@vu.nl
First published on 9th February 2023
Abstract
High-resolution spectroscopy techniques play a pivotal role to validate and efficiently benchmark available methods from quantum chemistry. In this work, we analyzed the microwave spectrum of ethyl butyrate within the scope of a systematic investigation to benchmark state-of-the-art exchange–correlation functionals and ab initio methods, to accurately predict the lowest energy conformers of carbonyl compounds in their isolated state. Under experimental conditions, we observed two distinct conformers, one of Cs and one of C1 symmetry. As reported earlier in the cases of some ethyl and methyl alkynoates, structural optimizations of the most abundant conformer that exhibits a C1 symmetry proved extremely challenging for several quantum chemical levels. To probe the sensitivity of different methods and basis sets, we use the identified soft-degree of freedom in proximity to the carbonyl group as an order parameter. The results of our study provide useful insight for spectroscopists to select an adapted method for structure prediction of carbonyl compounds based on their available computational resources, suggesting a reasonable trade-off between accuracy and CPU cost. At the same time, our observations and the resulting sets of highly accurate experimental constants from high-resolution spectroscopy experiments give an appeal to theoretical groups to look further into this seemingly simple family of chemical compounds, which may prove useful for the further development and parametrization of theoretical methods in computational chemistry.
1 Introduction
With the increasing accuracy of quantum chemical calculations and available computational resources, significant advances have been achieved in characterizing and quantifying molecular interactions within the fields of physical chemistry and chemical physics.1,2 Still, theoretical approaches are continuously improved, aiming to predict even more precisely experimental outcome without any prior knowledge of the desired result. In this respect, several blind challenges in numerical quantum chemistry have already been successfully established, such as the GöBenCH,3,4 HyDRA,5 Fe-MAN,6 or the SAMPL67,8 benchmarks. These challenges target important physical chemical properties, like van der Waals interactions, hydrogen bonding and proton transfer, to identify methodological limitations and bottlenecks, and to push forward the development of new methodologies and composite schemes. Such projects are crucial to foster collaborations between experimental and theoretical groups and to ensure the cross-talking between different disciplines.9 Within the studies of small to medium sized molecules, rotational spectroscopy has long manifested itself as the method of choice to characterize the structure and dynamics of isolated systems.10–12 Hereby, insight from quantum chemistry as a complementary tool is required to efficiently assign the experimental data, which, at the same time, provide highly accurate sets of experimental constants that can be used in return to benchmark quantum chemical methodologies.11,13,14 The development of theoretical methods has long been focused on providing accurate characterization of molecular structure and non-covalent interactions.15 While for several classes of molecules, routine functionals and ab initio methods can predict rotational constants for assignment guidance with results within 1% deviation to the experimental ones,16 some molecular systems still turn out to be extremely challenging for numerical quantum chemistry methods.13 This is often the case when weak inter- and intra-molecular interactions such as van der Waals interactions play a pivotal role in stabilizing one conformer over the others,11 as well as in flexible molecules of biological interest.17 On rarer occasions, even seemingly simple molecular targets turn out to exhibit some soft-degree of freedom, e.g., within a broad potential energy well, that cannot be properly captured by routine quantum chemical methods. Well-documented cases, for instances, are ethyl and methyl alkynoates.18–21 These fruit esters have been shown to possess an extreme soft-degree of freedom around the C–C single bond in proximity to the CO carbonyl group. While in the case of methyl and ethyl esters, equilibrium rotational constants predicted for Cs conformers at any level of theory are often close to the experimentally determined ones with a deviation of about 1% or better, it is not the case for C1 conformers where dihedral angle predictions vary strongly (at least ±15°) from the experimental value.13,18,19 The predicted structures then strongly depend on the method and basis set applied. Fluctuations like this are far too large to be explained by the numerical accuracy of available quantum chemical methods and complicate the assignment of experimental spectra. Interestingly, this is not observed for the respective aldehyde analogues of these esters, which are well-described using conventional methods such as the B3LYP22,23 functional from density functional theory (DFT) or the ab initio method based on Møller–Plesset perturbation theory of second order (MP2).24In the present work, we studied the structures of ethyl butyrate (C3H7–COO–C2H5), a small member of the ethyl ester family, in its isolated state in the gas-phase. Consistent with our previous studies,18,19 assignment guidance using optimizations at the MP2/6-311++G(d,p) level of theory was very problematic for the lowest energy conformer of C1 symmetry. A joint study of microwave spectroscopy and X-ray crystallography on ethyl 2-methylbutyrate had pointed out the problem to be the plasticity of the dihedral angle around the carbonyl group.25 One of the two observed dihedral angle values (of about 20°) in the crystal corresponds to the conformer identified in the gas-phase, while the second dihedral angle value in the crystal (of about 60°) corresponds to the optimized structure at the MP2/6-311++G(d,p) level of theory. Using Fourier Transform MicroWave (FTMW) spectroscopy, we identified two conformers of ethyl butyrate with different symmetry point groups (Cs and C1) under molecular jet conditions. The resulting highly accurate sets of spectroscopic constants were used for comparison with theoretical values predicted by different DFT and ab initio methods utilizing different basis sets. This exhaustive benchmark study allows us to identify the most reliable functionals and basis sets to aid spectroscopists with the assignment of their experimental spectra. We also compare our results with previous benchmarks on related carbonyl compounds available in the literature.
2 Quantum chemical calculations
2.1 Conformational analysis
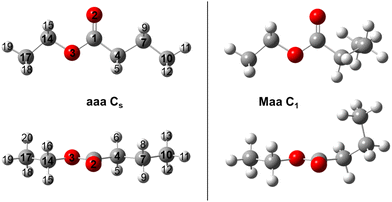
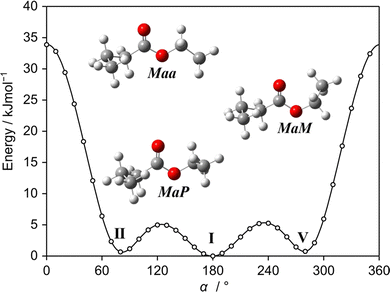
To sample the conformational space of ethyl butyrate, 27 starting geometries were optimized at the MP2/6-311++G(d,p) level of theory using the Gaussian 16 package.26 To create these geometries, the dihedral angles ϑ1 = ∠(C10, C7, C4, C1), ϑ2 = ∠(C7, C4, C1, O3) and ϑ3 = ∠(C1, O3, C14, C17) were set to 180°, 60° and −60°, respectively. The atoms are numbered according to Fig. 1. Rotating the two methyl groups does not generate new conformers. The rotation around the C1–O3 bond by varying the dihedral angle ϑ = ∠(C4, C1, O3, C14) results in two stable geometries: syn (ϑ = 0°) and anti (ϑ = 180°). Since syn esters are known to be much higher in energy27 and are not present in our jet-cooled experimental spectra, we only followed-up on the conformational analysis on anti esters by setting ϑ = 180° for all starting geometries. The MP2/6-311++G(d,p) level was chosen as base for our conformational analysis because of its reasonable performance in many previous investigations.28–31After completion of the optimizations, a total of 14 conformers remained. Harmonic frequency calculations confirmed them to be true minima. The theoretical results, including the rotational constants, dipole moment components and relative energies, are presented in Table S1 in the ESI.† They are all close in energy with a difference not exceeding 4 kJ mol−1. Only conformer aaa, shown on the left-hand side of Fig. 1, belongs to the Cs point group. The others, including the most stable conformer Maa illustrated on the right-hand side of Fig. 1, form enantiomeric pairs belonging to the C1 point group. Conformers Maa and aaa are eventually observed in the experimental spectrum. Their Cartesian coordinates are shown in Table S2 (ESI†).
The dihedral angles ϑ1, ϑ2 and ϑ3 are essentially 180° for the aaa conformer. In the Maa conformer, the angle ϑ1 is 66.1°, which is a typical value referring to the gauche orientation (denoted as M, the enantiomer to Maa is denoted as Paa) of the propyl methyl group. The angle ϑ3 ≈ 180° refers to a normal anti orientation (noted as a) of the ethyl methyl group. The angle ϑ2 of 146.5°, noticeably different from 180°, refers to a tilt angle of Θ = 180° − |ϑ2| = 34.5° of the entire propyl group out of the COO plane. Many previous investigations on carbonyl containing molecules have revealed an exceptional soft-degree of freedom around the angle Θ when an alkyl chain is attached to the ester functional group. The bond connecting these two moieties is extremely flexible and predictions become very sensitive to the applied quantum chemical method and basis set. Although this applies foremost to esters, as shown for a series of methyl alkynoate like methyl butyrate,32 methyl valerate,20 methyl hexanoate21 and many ethyl esters like ethyl valerate18 and ethyl isovalerate,19 it also concerns ketones like the series of linear aliphatic ketones33–36 and 2-propionyl thiophene.37 However, the effect seemingly is much stronger in esters, with predicted values of Θ ranging from 20° to 50°, than it is in ketones where values between 5° and 25° are reported.
2.2 Basis set variations
We shall see in the next section on microwave spectroscopy that the MP2/6-311++G(d,p) level is not able to provide rotational constants that are sufficiently precise to guide the assignment of conformer Maa, which possesses a C1 symmetry, as mentioned in the introduction. At this point, it is clear that identifying a quantum chemical level to provide accurate structures for carbonyl compounds requires a systematic benchmark of different combinations of methods and basis sets. Therefore, we selected several exchange–correlation functionals from DFT, namely B3LYP22,23 (with and without Grimme's dispersion corrections D338 to demonstrate changes induced by these corrections, and with and without Becke–Johnson damping BJ39), Head–Gordon's ωB97X-D,40 Truhlar's M06-2X,41 Minesota MN15,42 as well as the ab initio MP2 method,24 to benchmark their performance on predicting the structures of the two assigned conformers Maa and aaa of ethyl butyrate. Although the CCSD(T) method43 is widely accepted as the golden standard in quantum chemistry, we intentionally do not include optimizations at this computationally expensive level of theory, as this method is too time-consuming to be suitable for the conformational sampling of molecules with hundreds of potential conformers. A total of 21 different Pople44 and Dunning45 basis sets are used in combination with these methods. The predicted rotational constants are compared with those deduced from the experimental spectrum. Our main emphasis is to monitor the predicted values using the angle Θ as an order parameter to directly estimate the impact of Θ on the rotational constants. The optimized values of Θ as well as the resulting rotational constants obtained using the selected methods are listed in Tables S3 and S4 in the ESI.†3 Microwave spectroscopy
3.1 Measurements
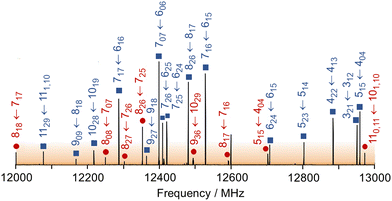
The microwave spectra of ethyl butyrate were recorded using two molecular jet FTMW spectrometers operating in the frequency range 2–40 GHz.46,47 The substance was purchased from Merck Schuchardt OHG, Hohenbrunn, Germany, and used without further purification. A mixture of 1% ethyl butyrate in helium at a total pressure of 1 bar was expanded into the cavity.A survey spectrum was measured at the beginning in the frequency range of 10.0–14.0 GHz where a series of spectra were overlapped at a frequency increment of 0.25 MHz. A 1 GHz portion is illustrated in Fig. 2, indicating the line positions. The observed lines were then remeasured at higher resolution where they appear as Doppler doublets. The line frequencies can be determined with an accuracy of about 4 kHz.
3.2 Spectral assignment
By analyzing the spectrum, we found 117 lines belonging to one conformer and 172 lines to another. The standard deviations obtained with the program XIAM48 are around 4 kHz for both conformers. The results of the fits are presented in Table 1. The frequency lists of all fitted transitions along with their observed-minus-calculated deviations are given in Tables S5 and S6 in the ESI.†| Par.a | Unit | Maa-C1 | aaa-Cs |
|---|---|---|---|
| a All parameters refer to the principal axis system. Watson's A reduction in Ir representation was used. The errors in parentheses are in the unit of the last significant digits. b Number of lines. c Standard deviation of the fit. | |||
| A | MHz | 5238.14891(36) | 6328.28789(48) |
| B | MHz | 903.763789(48) | 806.593698(94) |
| C | MHz | 869.264390(56) | 732.371867(93) |
| Δ J | kHz | 0.23804(12) | 0.02045(40) |
| Δ JK | kHz | −5.5646(13) | −0.1935(23) |
| Δ K | kHz | 76.474(32) | 17.609(40) |
| δ J | kHz | −0.052236(64) | 0.003093(41) |
| δ K | kHz | 1.0527(96) | −0.1449(87) |
| N | 172 | 117 | |
| σ | kHz | 3.9 | 4.1 |
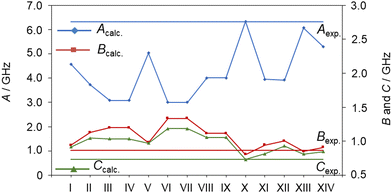
The conformer associated with the 117-line-fit should possess a Cs point group symmetry since no c-type transitions were observed. By comparing the experimentally deduced rotational constants with those of the 14 conformers given in Table S1 in the ESI,† as visualized in Fig. 3, this conformer should be the aaa conformer of Cs symmetry, which exhibits a fully extended conformation of the alkyl chain. The second moment Pcc is 16.362 uÅ2, corresponding to the typical value of 16 uÅ2 for a molecule with a planar heavy atom arrangement and five pairs of hydrogen atoms out-of-plane. The nomenclature a, P, M is used to describe the different rotamers with respect to the dihedral angles throughout the alkyl chain of ethyl butyrate and has been described in more details for isoamyl acetate.49
For the other conformer, 13 c-type lines were found. Therefore, it must have a C1 symmetry and exhibits transient chirality. All centrifugal distortion constants are about ten times larger than the other observed conformer featuring Cs symmetry. The intensities of the C1 conformer lines are stronger than those of the Cs conformer, as shown exemplary in the broadband scan given in Fig. 2. This scan portion captures a total of 15 transitions of the C1 conformer which includes a set of R-branch a-type transitions of J = 7 ← 6 and two Q-branch series of b-type transitions. The Cs conformer is represented by a total of 8 transitions, dominated by R-branch a-type transitions of J = 8 ← 7.
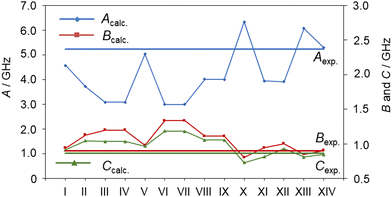
Without any prior knowledge on ethyl esters and carbonyl compounds, the assignment of the observed C1 conformer is by far less obvious, especially if relying solely on a comparison of the sets of rotational constants obtained at the MP2/6-311++G(d,p) level of theory. At first sight, it seems that the rotational constants predicted for conformer XIV (aPM) match the experimental values best, which is illustrated in Fig. 4 (see also Table S1, ESI†). However, conformer XIV has a relative energy value of 3.54 kJ mol−1 higher than the predicted global minimum and is the highest in energy. Based on our experience with the experimental setup, it is unlikely to observe conformer aPM (XIV) while not observing conformer Maa (I). This is further reflected by the observed line intensities, which indicate that the C1 conformer is more abundant in the spectrum and therefore likely to be energetically more favorable than the Cs conformer. However, as shown in previous studies on related carbonyl containing molecules, the drastic changes on the rotational constants, especially the A rotational constant, are observed upon varying the level of theory for the optimization, as shown in Table S3 of the ESI.† This allows us to identify the second conformer to be conformer Maa (I).
Using our experimental setup, we often observed the most abundant C1 conformer and could almost always identify the Cs-type conformer, even though its relative energy compared to other predicted conformers may be higher (see Table S1, ESI†, which presents the relative energies of the 14 conformers of ethyl butyrate predicted at the MP2/6-311++G(d,p) level of theory). We can therefore not rule out that some of the weaker unassigned lines remaining in the spectrum belong to other conformers, but their experimental spectra are obviously weaker than that of the Cs conformer. One possible reason is the relaxation of the non-observed conformers during the supersonic expansion to the Maa or aaa conformers. The potential energy curve shown in Fig. 5 obtained by varying the dihedral angle α = ∠(C1,O3,C14,C17) (for atom numbering see Fig. 1) captures conformer I (Maa), conformer II (MaP) and conformer V (MaM). The interconversions of conformer II (MaP) and conformer V (MaM) to conformer I (Maa) require relatively low barriers of 5.0 kJ mol−1 (420 cm−1) and 5.3 kJ mol−1 (443 cm−1), respectively, supporting this hypothesis.
4 Discussion
After successfully mapping the two sets of experimental rotational constants to the Cs aaa and C1 Maa conformers, we applied the experimental results to benchmark many different combinations of methods and basis sets for each conformer. We used several DFT functionals as well as the two ab initio methods MP2 and CCSD, although we retained from varying the basis set with CCSD. This method is computationally expensive and is not necessary to sample the conformational landscape of average-sized molecules for classical rotational spectroscopic studies. In many earlier works, optimizations with the MP2 and B3LYP methods in combination with Pople triple zeta basis sets were frequently used throughout the microwave spectroscopic community. Indeed, for small to medium-sized organic molecules, the MP2 method usually yields reliable structures with rotational constants in good agreement with experimental ones (<1% deviation). Although optimizations with the MP2 method are often understood to be more accurate than with the B3LYP functional, B3LYP has proved itself to perform better for some aromatic species and is computationally less expensive. Nowadays, it is commonly used in combination with Grimme's D3 dispersion corrections which significantly improve the predicted structures, especially when weak intramolecular interactions are crucial to stabilize the most abundant conformers.11 In recent years, with increasing computational capabilities and number of available exchange–correlation methods to study the electronic structures of organic compounds, spectroscopists aim to include optimizations using additional methods such as the Truhlar's M06-2X or Head–Gordon's ωB97X-D functionals, which are also well-adapted for gas-phase structural studies, or Yu's MN15 local exchange–correlation functional, which was parametrized to accurately predict noncovalent binding. The adequate choice of method should be verified within the available literature of structurally related species and benchmarking. In the case of the Cs conformer, the Θ angle is correctly predicted to be zero degrees (see Table S4 in the ESI†). The observed-minus-calculated absolute deviations of the rotational constants are unrelated to the soft-degree of freedom around Θ, resulting in reasonably well-optimized structures. Generally, for Cs conformers, predicted sets of rotational constants at any level of theory should be sufficiently good to guide the experimental assignment of microwave spectra. This is not the case for the C1 conformer and we choose the angle Θ as our order parameter to monitor the accuracy of the different theoretical approaches. This generally impacts the A rotational constant in particular. At this point it should be mentioned, that we are directly comparing experimental constants X0 (X = A, B, C) from the vibrational ground-state with the equilibrium constants Xe obtained from quantum chemical calculations, and the good match is based on error compensations. An extract of Table S3 (ESI†) for the C1 conformer is shown in Table 2. As can be seen from the optimized values in Table 2, Θ varies between 12° and 35°. Such large fluctuations of approximately 23° exceed the expected numerical error that may arise when optimizing the same conformer with different methods. The predicted theoretical angle which best reproduces the experimental finding would be of approximately 20°.25 For ethyl butyrate, this is the case at several levels of theory such as B3LYP-D3/6-311++G(d,p), ωB97X-D/6-311G(d,p), or MP2/cc-pVTZ. However, the obtained values are not consistent with the usual basis set extrapolation limit. There is no systematic improvement on the optimized angle throughout the basis set variation. Nevertheless, it can be compensated with the errors between the Xe and X0 rotational constants. To compare the validity of some methods for different molecular targets of interest, we optimized the C1 conformers of several carbonyl compounds previously observed under the same experimental conditions. Five levels of theory are used: MP2/6-311++G(d,p), MP2/cc-pVDZ, B3LYP-D3BJ/cc-pVDZ, as well as B3LYP/cc-pVDZ and B3LYP-D3BJ/6-311++G(d,p) to test the performance of dispersion functions and methods, respectively. An overview of the results is depicted in Fig. 6 and summarized in Table S7 in the ESI.† Note that the choice of these levels is not random, but based on exhaustive benchmarking already performed for methyl valerate (2),20 methyl hexanoate (3),21 and the series of methyl alkyl ketones (7–10).33–36| Level of theory | ΔA | ΔB | ΔC | ΣΔ | Θ | ΔA | ΔB | ΔC | ΣΔ | Θ |
|---|---|---|---|---|---|---|---|---|---|---|
| B3LYP | B3LYP-D3 | |||||||||
| 6-311G(d,p) | 135.6 | −15.8 | −20.9 | 172.2 | 14.1 | 200.9 | −10.0 | −18.6 | 229.6 | 12.1 |
| 6-311++G(d,p) | −158.2 | −11.1 | −7.6 | 177.0 | 21.8 | −72.0 | −6.1 | −5.4 | 83.6 | 19.3 |
| cc-pVDZ | 166.5 | −16.9 | −23.9 | 207.3 | 12.6 | 218.3 | −11.1 | −21.2 | 250.6 | 10.8 |
| aug-cc-pVDZ | −110.4 | −14.0 | −12.0 | 136.4 | 20.5 | −43.9 | −8.3 | −8.9 | 61.1 | 18.5 |
| cc-pVTZ | 32.0 | −12.5 | −13.5 | 57.9 | 17.5 | 101.7 | −6.8 | −11.0 | 119.4 | 15.5 |
| aug-cc-pVTZ | −82.5 | −10.5 | −8.3 | 101.3 | 20.5 | −1.4 | −5.2 | −6.0 | 12.6 | 18.2 |
| B3LYP-D3BJ | CAM-B3LYP-D3BJ | |||||||||
| 6-311G(d,p) | 99.0 | −7.1 | −11.7 | 117.8 | 15.1 | 237.0 | −1.3 | −9.1 | 247.4 | 12.5 |
| 6-311++G(d,p) | −227.3 | −0.2 | 5.2 | 232.7 | 23.5 | −27.6 | 2.3 | 3.3 | 33.2 | 19.5 |
| cc-pVDZ | 128.3 | −8.6 | −14.9 | 151.8 | 13.6 | 262.7 | −2.5 | −12.0 | 277.3 | 11.2 |
| aug-cc-pVDZ | −183.6 | −3.1 | 0.9 | 187.6 | 22.4 | −4.9 | 0.0 | 0.1 | 5.0 | 18.9 |
| cc-pVTZ | −19.0 | −2.8 | −2.7 | 24.5 | 18.8 | 137.0 | 1.9 | −1.5 | 140.3 | 16.0 |
| aug-cc-pVTZ | −150.7 | 0.2 | 4.2 | 155.1 | 22.2 | 27.3 | 3.6 | 3.8 | 34.8 | 18.8 |
| PBE0 | PBE0-D3 | |||||||||
| 6-311G(d,p) | 16.6 | −15.1 | −18.3 | 50.0 | 16.0 | −4.6 | −11.1 | −14.3 | 30.1 | 16.3 |
| 6-311++G(d,p) | −319.7 | −8.1 | −2.1 | 329.8 | 24.8 | −375.4 | −2.1 | 5.1 | 382.7 | 25.9 |
| cc-pVDZ | 40.2 | −16.5 | −21.3 | 78.0 | 14.7 | 21.8 | −12.8 | −17.7 | 52.3 | 14.8 |
| aug-cc-pVDZ | −266.8 | −11.9 | −7.2 | 285.9 | 23.4 | −326.1 | −5.9 | 0.1 | 332.1 | 24.6 |
| cc-pVTZ | −88.8 | −12.1 | −11.2 | 112.1 | 19.4 | −122.5 | −7.5 | −6.1 | 136.0 | 20.1 |
| aug-cc-pVTZ | −236.8 | −8.7 | −4.0 | 249.6 | 23.3 | −295.0 | −2.8 | 3.2 | 301.0 | 24.5 |
| M06-2X | MN15 | |||||||||
| 6-311G(d,p) | 285.7 | 1.8 | −7.9 | 295.4 | 11.2 | 266.0 | 2.9 | −5.7 | 274.7 | 11.7 |
| 6-311++G(d,p) | 121.4 | 3.8 | −0.2 | 125.4 | 15.6 | 110.3 | 4.6 | 1.4 | 116.2 | 15.9 |
| cc-pVDZ | 312.4 | 1.1 | −9.9 | 323.4 | 10.1 | 283.2 | 0.4 | −9.1 | 292.7 | 10.8 |
| aug-cc-pVDZ | 141.0 | 2.3 | −2.4 | 145.8 | 15.2 | 132.0 | 2.4 | −1.7 | 136.1 | 15.4 |
| cc-pVTZ | 238.4 | 3.5 | −3.4 | 245.4 | 13.2 | 229.8 | 6.2 | −0.1 | 236.1 | 13.4 |
| aug-cc-pVTZ | 174.9 | 4.2 | −0.4 | 179.5 | 14.9 | 183.5 | 7.3 | 2.8 | 193.7 | 14.7 |
| ωB97X-D | MP2 | |||||||||
| 6-311G(d,p) | −110.1 | 2.6 | 5.4 | 118.1 | 21.3 | −236.0 | 15.2 | 20.8 | 272.1 | 24.3 |
| 6-311++G(d,p) | 129.5 | −1.8 | −6.5 | 137.7 | 15.2 | −666.5 | 37.6 | 47.2 | 751.3 | 34.7 |
| cc-pVDZ | 162.8 | −4.3 | −10.7 | 177.8 | 13.6 | 21.5 | 0.6 | −3.7 | 25.8 | 16.2 |
| aug-cc-pVDZ | −87.4 | −0.5 | 1.4 | 89.4 | 20.6 | −543.0 | 20.6 | 32.1 | 595.7 | 30.9 |
| cc-pVTZ | 43.5 | 0.8 | −0.2 | 44.5 | 18.0 | −105.6 | 15.3 | 17.6 | 138.5 | 21.4 |
| aug-cc-pVTZ | −38.1 | 2.6 | 4.0 | 44.7 | 20.1 | −259.3 | 20.4 | 27.2 | 306.8 | 25.1 |
| Experiment | 5238.1 | 903.8 | 869.3 | 5238.1 | 903.8 | 869.3 | ||||
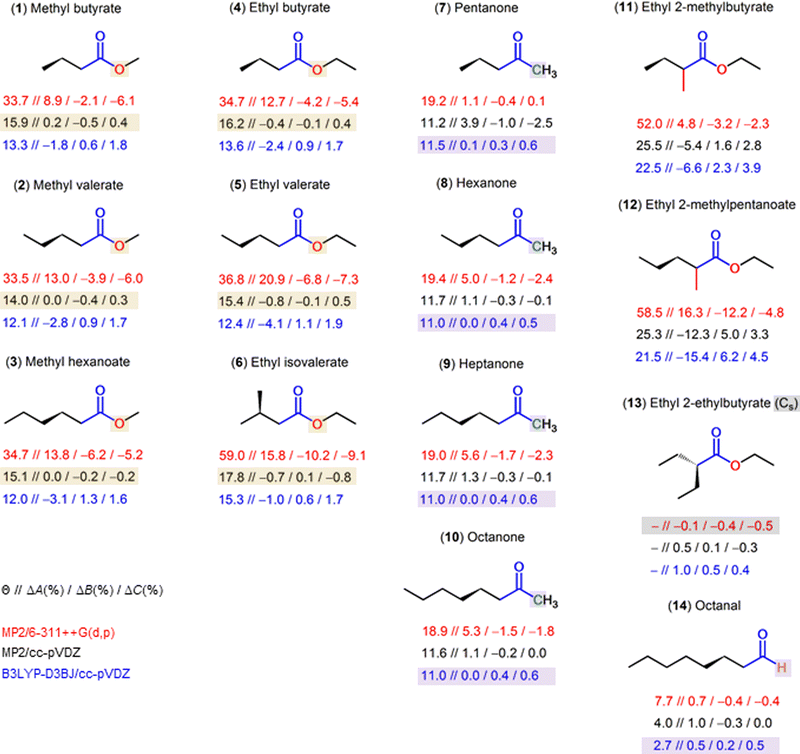 | ||
| Fig. 6 Overview of different carbonyl compounds investigated to probe for the sensitivity of the dihedral predictions at the MP2/6-311++G(d,p) (red values), MP2/cc-pVDZ (black values) and B3LYP-D3BJ/cc-pVDZ (blue values) levels of theory. The given values are Θ//ΔA(%)/ΔB(%)/ΔC(%). The percentage deviations are calculated as (Xexp. − Xcalc.) 100%/Xexp., with X = A, B, C. B3LYP/cc-pVDZ and B3LYP-D3BJ/6-311++G(d,p) calculations were also carried out with values in Table S7 in the ESI† to test the performance of dispersion functions and methods, respectively. (1) Methyl butyrate,32 (2) methyl valerate,20 (3) methyl hexanoate,21 (4) ethyl butyrate (this work), (5) ethyl valerate,18 (6) ethyl isovalerate,19 (7) pentan-2-one,33 (8) hexane-2-one,34 (9) heptan-2-one,35 (10) octan-2-one,36 (11) ethyl 2-methylbutyrate,25 (12) ethyl 2-methylpentanoate,13 (13) ethyl 2-ethylbutyrate,50 (14) octanal.51 | ||
From the results shown in Fig. 6, we propose a method that yields reliable structures and can be used for future investigations on related molecules. This is extremely important for experimentalists, as it allows to tune the experimental set up and facilitates the assignment of the experimental spectra. For the most stable C1 conformer of esters exhibiting the Θ-problem, i.e., those with the CH2–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–O center moiety (molecules 1–6 in Fig. 6), MP2/cc-pVDZ is the level of choice. The error in the Θ angle of around 14° to 18° calculated at this level compensates the Xe − X0 error in a way that the Xe rotational constants become very close to the X0 rotational constants. For ketones with the Θ-problem, i.e., those with the CH2–(C
O)–O center moiety (molecules 1–6 in Fig. 6), MP2/cc-pVDZ is the level of choice. The error in the Θ angle of around 14° to 18° calculated at this level compensates the Xe − X0 error in a way that the Xe rotational constants become very close to the X0 rotational constants. For ketones with the Θ-problem, i.e., those with the CH2–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–C center moiety (molecules 7–10 in Fig. 6), the B3LYP-D3BJ/cc-pVDZ level is the most suitable one. The calculated Θ angle is around 11° at both the MP2/cc-pVDZ and the B3LYP-D3BJ/cc-pVDZ levels, but exchanging the oxygen in esters by a carbon atom requires another error compensation in methods, so that a method change is needed to yield Xe rotational constants that are close to X0 ones. In calculations with predicted results close to the experimental values, the Θ angle is always around 11°–12°. Finally, if a hydrogen atom in the CH2–(C
O)–C center moiety (molecules 7–10 in Fig. 6), the B3LYP-D3BJ/cc-pVDZ level is the most suitable one. The calculated Θ angle is around 11° at both the MP2/cc-pVDZ and the B3LYP-D3BJ/cc-pVDZ levels, but exchanging the oxygen in esters by a carbon atom requires another error compensation in methods, so that a method change is needed to yield Xe rotational constants that are close to X0 ones. In calculations with predicted results close to the experimental values, the Θ angle is always around 11°–12°. Finally, if a hydrogen atom in the CH2–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–O center moiety is substituted, for example in the case of ethyl 2-methylbutyrate (11)25 and ethyl 2-methylpentanoate (12),13 neither the MP2/cc-pVDZ level nor the B3LYP-D3BJ/cc-pVDZ level retains its good agreement with experiments. Obviously, another method/basis set error compensation is required. Therefore, we performed the method/basis set variation on ethyl 2-methylbutyrate (11) and ethyl 2-methylpentanoate (12) with the results on the predicted rotational constants and Θ angles shown in Tables S8 and S9 in the ESI.† In both cases, the ωB97X-D/aug-cc-pVTZ level seems to be a good choice. Also quite recommendable are the B3LYP-D3/6-311+(+)G(df,pd) or B3LYP-D3/6-311+(+)G(3df,3pd) levels. They all predict the Θ angle to be around 35°–40°. Diffuse functions are necessary for all Pople basis sets, since omitting them leads to a tremendous decrease of the prediction accuracy on the A rotational constant. However, if substituting the hydrogen atoms in the CH2–(C
O)–O center moiety is substituted, for example in the case of ethyl 2-methylbutyrate (11)25 and ethyl 2-methylpentanoate (12),13 neither the MP2/cc-pVDZ level nor the B3LYP-D3BJ/cc-pVDZ level retains its good agreement with experiments. Obviously, another method/basis set error compensation is required. Therefore, we performed the method/basis set variation on ethyl 2-methylbutyrate (11) and ethyl 2-methylpentanoate (12) with the results on the predicted rotational constants and Θ angles shown in Tables S8 and S9 in the ESI.† In both cases, the ωB97X-D/aug-cc-pVTZ level seems to be a good choice. Also quite recommendable are the B3LYP-D3/6-311+(+)G(df,pd) or B3LYP-D3/6-311+(+)G(3df,3pd) levels. They all predict the Θ angle to be around 35°–40°. Diffuse functions are necessary for all Pople basis sets, since omitting them leads to a tremendous decrease of the prediction accuracy on the A rotational constant. However, if substituting the hydrogen atoms in the CH2–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–O center moiety results in a Cs configuration, as in the case of ethyl 2-ethylbutyrate (13),50 the MP2/6-311++G(d,p) level delivers very satisfactory results, as it does in the Cs conformer cases of many other molecules including all those presented in Fig. 6. Almost all levels of theory do not experience difficulty in predicting rotational constants for ethyl 2-ethylbutyrate with deviation often not exceeding 1–2%. Finally, in molecules where the Θ-problem does not occur for C1 conformers, for example octanal (14)51 that contains the CH2–(C
O)–O center moiety results in a Cs configuration, as in the case of ethyl 2-ethylbutyrate (13),50 the MP2/6-311++G(d,p) level delivers very satisfactory results, as it does in the Cs conformer cases of many other molecules including all those presented in Fig. 6. Almost all levels of theory do not experience difficulty in predicting rotational constants for ethyl 2-ethylbutyrate with deviation often not exceeding 1–2%. Finally, in molecules where the Θ-problem does not occur for C1 conformers, for example octanal (14)51 that contains the CH2–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–H moiety, good agreements can also be achieved at almost all levels, but the B3LYP-D3BJ/cc-pVDZ level recommended for ketones (CH2–(C
O)–H moiety, good agreements can also be achieved at almost all levels, but the B3LYP-D3BJ/cc-pVDZ level recommended for ketones (CH2–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–C) works also very well.
O)–C) works also very well.
At this stage, the nature of these low torsional barriers around the C1–C4 bond still remains speculative. However, there are several tentative explanations that can be made and could be verified further in future studies. An over-simplistic explanation could be that the MP2 method overestimates the intramolecular interaction of the studied molecules which, especially in the case of the esters, then results in an overstatement of the Θ angle and skews the accuracy of the prediction. Another possibility could be the remarkably low torsional potential that is observed around the dihedral Θ, as also observed in benzyl cyanide52 and 4-methyl-5-vinylthiazole.53 We previously proposed a tentative explanation that relates to the local symmetry of the C–COO–C environment. For this purpose, we shall consider the case of an acetate anion, nitromethan, or toluene. In all three cases, we observe a local C3v symmetry of the CH3 group and a local C2v symmetry of the OCO, ONO, or CCC moiety, respectively, which results in a six-fold potential around the dihedral angle. In such cases, the barrier heights to internal rotation of the methyl group are extremely low, and the methyl group of toluene or that of nitromethane acts almost as a free rotor with barriers of 4.9 cm−154 and 2.1 cm−1,55 respectively. If we move to less symmetrical frames such as acetates, the COOR group no longer possesses C2v symmetry. However, it still resembles C2v and the resulting three-fold potential exhibits a rather low barrier of around 100 cm−1,56,57 except in some cases where conjugation effects may impact the electronic surrounding of the ester COO-moiety.58–60 Coming to the alkyl ester family, the C3v symmetry is also lost due to the alkyl chain, but still resembles C3v locally. This could then result in the low torsional barriers observed in this (C3v)–(C2v)-like molecular family.
It is also interesting that the centrifugal distortion constants of the Maa conformer are much higher than those of the aaa conformer. This is consistent with the observation in several molecules that exhibit a soft-degree of freedom around the angle Θ (cf. molecules (1–5) and (7–10) in Fig. 6). In all these cases, the centrifugal distortion constants of the C1 conformer(s) are larger than those of the Cs conformer. We have no explanation for this observation, but a possible reason is the use of a semi-rigid Hamiltonian model, where the fitted centrifugal distortion constants need to compensate the large amplitude motion around the angle Θ.
5 Conclusion
We identified two different conformers of ethyl butyrate under molecular jet conditions, one of Cs and one of C1 symmetry. For the Cs conformer, the rotational constants perfectly matched those predicted at the MP2/6-311++G(d,p) level of theory. The relative deviations for all rotational constants are below 1%, and the existence of an ab-mirror plane is further supported by the absence of c-type lines and the order of magnitude of the centrifugal distortion constants. From our experience on related systems, the second observed conformer could be matched to the global minimum of the potential energy surface of ethyl butyrate. Subsequently, a systematic benchmark of several exchange–correlation functionals and basis sets was carried out to identify the sensitivity of the soft-degree of freedom with respect to the applied quantum chemical levels. From the results of this benchmark, we concluded that for esters with the CH2–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–O center moiety, MP2/cc-pVDZ is the level of choice to predict the rotational constants for the most stable C1 conformer. It is B3LYP-D3BJ/cc-pVDZ for ketones (CH2–(C
O)–O center moiety, MP2/cc-pVDZ is the level of choice to predict the rotational constants for the most stable C1 conformer. It is B3LYP-D3BJ/cc-pVDZ for ketones (CH2–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–C center moiety) and aldehydes (CH2–(C
O)–C center moiety) and aldehydes (CH2–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–H). For all Cs conformers, the MP2/6-311++G(d,p) level is recommended. Altogether, our benchmark showed that the predicted C1 structures fluctuate strongly around the experimental structures in the gas-phase. Although our results confirm the existence of a soft-degree of freedom around the C–C bond in proximity to the carbonyl moiety of ethyl butyrate and related molecules, we can only hypothesize on the nature of this low torsional barrier. As we cannot observe a systematic improvement on selected functional using Grimme's dispersion correction D3, it is unlikely that the effect arises from intra-molecular dispersion interactions that could stabilize the C1 conformer. In future, rapidly evolving experimental progress will allow us to move towards faster data acquisition of molecular targets of increasing size and complexity. This makes the accessibility to low-cost computational methods and composite schemes important,61–64 and it is essential to continuously develop and improve available numerical quantum chemistry methods.
O)–H). For all Cs conformers, the MP2/6-311++G(d,p) level is recommended. Altogether, our benchmark showed that the predicted C1 structures fluctuate strongly around the experimental structures in the gas-phase. Although our results confirm the existence of a soft-degree of freedom around the C–C bond in proximity to the carbonyl moiety of ethyl butyrate and related molecules, we can only hypothesize on the nature of this low torsional barrier. As we cannot observe a systematic improvement on selected functional using Grimme's dispersion correction D3, it is unlikely that the effect arises from intra-molecular dispersion interactions that could stabilize the C1 conformer. In future, rapidly evolving experimental progress will allow us to move towards faster data acquisition of molecular targets of increasing size and complexity. This makes the accessibility to low-cost computational methods and composite schemes important,61–64 and it is essential to continuously develop and improve available numerical quantum chemistry methods.
Author contributions
Lilian W. Sutikdja: investigation, data curation, formal analysis, visualization, writing – review & editing. Ha Vinh Lam Nguyen: investigation, formal analysis, visualization, validation, writing – original draft preparation, resources. Dragan Jelisavac: investigation, data curation, formal analysis, writing – review & editing. Wolfgang Stahl: conceptualization, investigation, validation, supervision, resources. Halima Mouhib: investigation, formal analysis, validation, writing – original draft preparation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Agence Nationale de la Recherche ANR (project ID ANR-18-CE29-0011) and by the European Union (ERC, 101040480-LACRIDO). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. Part of the simulations were performed with computing resources granted by the RWTH Aachen University under project rwth0506.References
- M. Jusot, D. Stratmann, M. Vaisset, J. Chomilier and J. Cortés, J. Chem. Inf. Model., 2018, 58, 355 CrossRef PubMed.
- J. Liu and X. He, Phys. Chem. Chem. Phys., 2020, 22, 12341 RSC.
- H. C. Gottschalk, A. Poblotzki, M. Fatima, D. A. Obenchain, C. Pérez, J. Antony, A. A. Auer, L. Baptista, D. M. Benoit, G. Bistoni, F. Bohle, R. Dahmani, D. Firaha, S. Grimme, A. Hansen, M. E. Harding, M. Hochlaf, C. Holzer, G. Jansen, W. Klopper, W. A. Kopp, M. Krasowska, L. C. Kröger, K. Leonhard, M. M. Al-Mogren, H. Mouhib, F. Neese, M. N. Pereira, M. Prakash, I. S. Ulusoy, R. A. Mata, M. A. Suhm and M. Schnell, J. Chem. Phys., 2020, 152, 164303 CrossRef CAS PubMed.
- H. C. Gottschalk, A. Poblotzki, M. A. Suhm, M. M. Al-Mogren, J. Antony, A. A. Auer, L. Baptista, D. M. Benoit, G. Bistoni, F. Bohle, R. Dahmani, D. Firaha, S. Grimme, A. Hansen, M. E. Harding, M. Hochlaf, C. Holzer, G. Jansen, W. Klopper, W. A. Kopp, L. C. Kröger, K. Leonhard, H. Mouhib, F. Neese, M. N. Pereira, I. S. Ulusoy, A. Wuttke and R. A. Mata, J. Chem. Phys., 2018, 148, 014301 CrossRef PubMed.
- T. L. Fischer, M. Bödecker, A. Zehnacker-Rentien, R. A. Mata and M. A. Suhm, Phys. Chem. Chem. Phys., 2022, 24, 11442 RSC.
- https://qmbench.net/challenges/feman/feman .
- P. Pracht, R. Wilcken, A. Udvarhelyi, S. Rodde and S. Grimme, J. Comput.-Aided Mol. Des., 2018, 32, 1139 CrossRef CAS PubMed.
- M. Işık, A. S. Rustenburg, A. Rizzi, M. R. Gunner, D. L. Mobley and J. D. Chodera, J. Comput.-Aided Mol. Des., 2021, 35, 131 CrossRef PubMed.
- C. Puzzarini and J. F. Stanton, Phys. Chem. Chem. Phys., 2023, 25, 1421 RSC.
- Q. T. Saragi, M. Juanes, J. L. Abad, R. Pinacho, J. E. Rubio and A. Lesarri, Spectrochim. Acta, Part A, 2022, 267, 120531 CrossRef PubMed.
- I. Uriarte, A. Insausti, E. J. Cocinero, A. Jabri, I. Kleiner, H. Mouhib and I. Alkorta, J. Phys. Chem. Lett., 2018, 9, 5906 CrossRef CAS PubMed.
- D. Loru, I. Peña and M. E. Sanz, Phys. Chem. Chem. Phys., 2019, 21, 2938 RSC.
- R. Dahmani, H. Sun and H. Mouhib, Phys. Chem. Chem. Phys., 2020, 22, 27850 RSC.
- C. Puzzarini, M. Biczysko, V. Barone, I. Peña, C. Cabezas and J. L. Alonso, Phys. Chem. Chem. Phys., 2013, 15, 16965 RSC.
- M. Piccardo, E. Penocchio, C. Puzzarini, M. Biczysko and V. Barone, J. Phys. Chem. A, 2015, 119, 2058 CrossRef CAS PubMed.
- H. Mouhib, W. Stahl, M. Lüthy, M. Büchel and P. Kraft, Angew. Chem., Int. Ed., 2011, 50, 5576 CrossRef CAS PubMed.
- S. R. Domingos, C. Pérez, C. Medcraft, P. Pinacho and M. Schnell, Phys. Chem. Chem. Phys., 2016, 18, 16682 RSC.
- H. Mouhib and W. Stahl, Chem. Phys. Chem., 2012, 13, 1297 CrossRef CAS PubMed.
- H. Mouhib, D. Jelisavac, L. W. Sutikdja, E. Isaak and W. Stahl, J. Phys. Chem. A, 2011, 115, 118 CrossRef CAS PubMed.
- H. V. L. Nguyen, M. Andresen and W. Stahl, Phys. Chem. Chem. Phys., 2021, 23, 2930 RSC.
- N.-N. Dang, H.-N. Pham, I. Kleiner, M. Schwell, J.-U. Grabow and H. V. L. Nguyen, Molecules, 2022, 27, 2639 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Paar, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- C. Merkens, T. Stadtmüller, U. Englert, H. Mouhib and W. Stahl, Z. Naturforsch., 2014, 69b, 303 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Inc., Wallingford CT, 2016 Search PubMed.
- M. Oki and H. Nakanishi, Bull. Chem. Soc. Jpn., 1970, 43, 2558 CrossRef CAS.
- L. Tulimat, H. Mouhib, H. V. L. Nguyen and W. Stahl, J. Mol. Spectrosc., 2020, 373, 111356 CrossRef CAS.
- R. Kannengießer, W. Stahl and H. V. L. Nguyen, J. Phys. Chem. A, 2016, 120, 5979 CrossRef PubMed.
- M. Andresen, M. Schwell and H. V. L. Nguyen, J. Mol. Struct., 2022, 1247, 131337 CrossRef CAS.
- V. Van, W. Stahl, M. T. Nguyen and H. V. L. Nguyen, Can. J. Phys., 2020, 98, 538 CrossRef CAS.
- A. O. Hernandez-Castillo, C. Abeysekera, B. M. Hays, I. Kleiner, H. V. L. Nguyen and T. S. Zwier, J. Mol. Spectrosc., 2017, 337, 51 CrossRef CAS.
- M. Andresen, I. Kleiner, M. Schwell, W. Stahl and H. V. L. Nguyen, J. Phys. Chem. A, 2018, 122, 7071 CrossRef CAS PubMed.
- M. Andresen, I. Kleiner, M. Schwell, W. Stahl and H. V. L. Nguyen, Chem. Phys. Chem., 2019, 20, 2063 CAS.
- M. Andresen, I. Kleiner, M. Schwell, W. Stahl and H. V. L. Nguyen, J. Phys. Chem. A, 2020, 124, 1353 CrossRef CAS PubMed.
- M. Andresen, D. Schöngen, I. Kleiner, M. Schwell, W. Stahl and H. V. L. Nguyen, Chem. Phys. Chem., 2020, 19, 2206 CrossRef PubMed.
- C. Dindic, W. Stahl and H. V. L. Nguyen, Phys. Chem. Chem. Phys., 2020, 22, 19704 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerig, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032 RSC.
- G. E. Scuseria, A. C. Scheiner, T. J. Lee, J. E. Rice and H. F. Schaefer III, J. Chem. Phys., 1987, 86, 2881 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef.
- J.-U. Grabow, W. Stahl and H. Dreizler, Rev. Sci. Instrum., 1996, 67, 4072 CrossRef CAS.
- I. Merke, W. Stahl and H. Dreizler, Z. Naturforsch., 1994, 49a, 490 CrossRef.
- H. Hartwig and H. Dreizler, Z. Naturforsch., 1996, 51a, 923 CrossRef.
- L. W. Sutikdja, D. Jelisavac, W. Stahl and I. Kleiner, Mol. Phys., 2012, 110, 2883 CrossRef CAS.
- R. Hakiri, N. Derbel, W. Stahl and H. Mouhib, Chem. Phys. Chem., 2020, 21, 20 CrossRef CAS PubMed.
- K.-N. Truong, L. B. Weger, W. Stahl and H. Mouhib, Chem. Phys. Chem., 2017, 18, 2631 CrossRef CAS PubMed.
- Q. T. Tran, A. Errouane, S. Condon, C. Barreteau, H. V. L. Nguyen and C. Pichon, J. Mol. Spectrosc., 2022, 388, 111685 CrossRef CAS.
- S. Khemissi, M. Schwell, I. Kleiner and H. V. L. Nguyen, Mol. Phys., 2022, 120, e2052372 CrossRef.
- H. D. Rudolph, H. Dreizler, A. Saeschke and P. Z. Wendling, Z. Naturforsch., 1967, 22a, 940 CrossRef.
- G. O. Sørensen, T. Pedersen, H. Dreizler, A. Guarnieri and A. P. Cox, J. Mol. Struct., 1983, 97, 77 CrossRef.
- L. W. Sutikdja, W. Stahl, V. Sironneau, H. V. L. Nguyen and I. Kleiner, Chem. Phys. Lett., 2016, 663, 145 CrossRef CAS.
- H. V. L. Nguyen and I. Kleiner, Phys. Sci. Rev., 2022, 7, 679 Search PubMed.
- A. Jabri, V. Van, H. V. L. Nguyen, W. Stahl and I. Kleiner, Chem. Phys. Chem., 2016, 17, 2660 CrossRef CAS PubMed.
- H. V. L. Nguyen and W. Stahl, J. Mol. Spectrosc., 2010, 264, 120 CrossRef CAS.
- L. Ferres, L. Evangelisti, A. Maris, S. Melandri, W. Caminati, W. Stahl and H. V. L. Nguyen, Molecules, 2022, 27, 2730 CrossRef CAS PubMed.
- J. Lupi, S. Alessandrini, C. Puzzarini and V. Barone, J. Chem. Theory Comput., 2021, 17, 6974 CrossRef CAS PubMed.
- G. Ceselin, V. Barone and N. Tasinato, J. Chem. Theory Comput., 2021, 17, 7290 CrossRef CAS PubMed.
- A. Melli, F. Tonolo, V. Barone and C. Puzzarini, J. Phys. Chem. A, 2021, 125, 9904 CrossRef CAS PubMed.
- H. Ye, S. Alessandrini, M. Melosso and C. Puzzarini, Phys. Chem. Chem. Phys., 2022, 24, 23254 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Cartesian coordinates, results of the basis set variations and benchmarks, lists of fitted frequencies along with their residuals. See DOI: https://doi.org/10.1039/d2cp05774c |
| ‡ Deceased. |
| This journal is © the Owner Societies 2023 |