Open Access Article
Open Access ArticleVisualizing screening in noble-metal clusters: static vs. dynamic†
Rajarshi
Sinha-Roy
 *abcf,
Pablo
García-González
*abcf,
Pablo
García-González
 df,
Xóchitl
López-Lozano
df,
Xóchitl
López-Lozano
 e and
Hans-Christian
Weissker
e and
Hans-Christian
Weissker
 *af
*af
aAix-Marseille University, CNRS, CINAM, Marseille 13288, France. E-mail: hans-christian.weissker@univ-amu.fr
bLaboratoire des Solides Irradiés, École Polytechnique, CNRS, CEA/DRF/IRAMIS, Institut Polytechnique de Paris, Palaiseau F-91128, France
cUniversité de Lyon, Université Claude Bernard Lyon 1, CNRS, Institut Lumière Matière, F-69622, VILLEURBANNE, France. E-mail: rajarshi.sinha-roy@univ-lyon1.fr
dDepartamento de Física Teórica de la Materia Condensada and Condensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, E-28049 Madrid, Spain
eDepartment of Physics & Astronomy, The University of Texas at San Antonio, One UTSA circle, 78249-0697 San Antonio, TX, USA
fEuropean Theoretical Spectroscopy Facility (ETSF), Web: https://www.etsf.eu/
First published on 10th December 2022
Abstract
The localized surface-plasmon resonance of metal nanoparticles and clusters corresponds to a collective charge oscillation of the quasi-free metal electrons. The polarization of the more localized d electrons opposes the overall polarization of the electron cloud and thus screens the surface plasmon. By contrast, a static electric external field is well screened, as even very small noble-metal clusters are highly metallic: the field inside is practically zero except for the effect of the Friedel-oscillation-like modulations which lead to small values of the polarization of the d electrons. In the present article, we present and compare representations of the induced densities (i) connected to the surface-plasmon resonance and (ii) resulting from an external static electric field. The two cases allow for an intuitive understanding of the differences between the dynamic and the static screening.
Introduction
The response of noble-metal clusters to an external electric field is characterized by the reaction of the metals' electrons. In particular, the well-known effect of the surface plasmon (localized surface-plasmon resonance, LSPR), which dominates the optical absorption spectra of many clusters in the visible and ultraviolet ranges, corresponds to a collective charge oscillation that can be excited by an external field. On the other hand, in the presence of a static external electric field, a static surface polarization is induced that would expel any fields inside the nanoparticle if the latter behaved like a perfect classical metal.1 Clearly, this leads to differences in the role of the noble metals' d electrons.It is well known that the basic band structure of the coinage metals/noble metals is rather similar. The delocalized electrons form the metallic sp band, whereas a completely filled shell of atomic d electrons, which are more localized in space around the atoms, produces the d bands. In the static case, with its approximately vanishing internal fields, the localized d electrons react mostly to the Friedel-oscillation-like density variations of the delocalized electron cloud. They are, therefore, visible in isosurface or color-coded slab representations of the systems, which is why we have likened them to “sensors” in the past.2
The d-band edge lies about 4 eV below the Fermi energy in silver and about 2 eV below the Fermi energy in gold and copper. Interband transitions from the d bands, i.e., transitions across the Fermi energy into unoccupied states, start at roughly these energies and are clearly seen in the absorption spectra of the bulk metals.3 Likewise, the polarizability of the d electrons plays an essential role for the optical response at the nanoscale, in particular leading to the screening of the surface plasmons in the noble-metal clusters.4–7
The effect of the noble-metal d electrons on the overall optical response has been taken into account on different levels:
(1) A semiempirical dielectric approximation was implemented into jellium models,4,6,8–10 where the dynamical polarizability of the d electrons is accounted for by an effective dielectric function εd(ω). This allowed, in particular, for the description of the size-dependence of the plasmon energies in noble-metal clusters due to the size-dependent influence of different surface effects, viz., the electron spill-out and the reduced screening of the d electrons in a surface layer of the cluster. This approach also served to understand the behavior of the dispersion relation of surface plasmons at noble-metal surfaces.11–13
(2) In later works,5,14 d electrons were introduced as point dipoles depending on the surrounding density and introduced in an averaged manner into a jellium model. Nevertheless, as in the dielectric approximation, the response of the d electrons is treated at a different level of theory than that of the valence-electrons.
(3) Newer calculations7,15–20 describe the electron–core interaction using suitable pseudopotentials,21 effective core potentials, or PAWs22 in the framework of Time-Dependent Density-Functional Theory (TDDFT)23 or sometimes quantum-chemistry methods.24 As a consequence, the d and the sp electrons are treated explicitly at the same level of theory, whereas the more strongly bound core electrons below are considered as negligible for the optical response and compounded into the pseudopotential.
In present-day calculations of metal clusters, TDDFT has mostly become the method of choice. More generally, plasmonic features in a wide variety of situations have been described by TDDFT, ranging from bulk plasmons in metals25 and semiconductors26 to plasmons in molecules27 and metal clusters.28 In addition, the correspondence between the classical and the quantum results was analyzed in ref. 29.
In particular, the real-time formalism of TDDFT30,31 obtains the evolution of the induced densities, which provides an intuitive way of understanding the processes involved in the excitations. As the d electrons are more localized than the metals' sp electrons, it is easy to distinguish the two in representations of the induced densities even without explicit analysis using projections, because small spatial shifts lead to smaller differences for the smooth, extended sp contributions compared to the more strongly peaked d-state densities.7,16,31
In earlier work, we have used snapshots and animations32,33 from δ-kick RT-TDDFT calculations30 to discuss the electron dynamics. This approach is, however, really useful only if the electron dynamics is dominated by one mode,33 otherwise, the superposition of different modes complicates the interpretation enormously. We have then, in order to resolve contributions of different frequencies to the absorption spectra, used a Fourier transform analysis of the time-dependent density for each space point, so as to obtain electronic oscillation modes belonging to particular frequencies and representing individual peaks in the spectra.31
In the present article, we illustrate and discuss in an intuitive manner the differences in the reaction of the d electrons in the dynamic (plasmonic) case and in the static case, thereby emphasizing their role in the screening in the clusters.
Methods
As model structures, we use the icosahedral Ag309 quasi-spherical silver cluster from the series of icosahedral closed-shell clusters that we have extensively studied before.2,34 In addition, a silver nanorod of 263 atoms is used. This type of rods based on 5-fold symmetry axes has likewise been studied extensively before.29,35–37 These decahedral rods are model structures based on a stacking and shell-wise expansion of decahedral base clusters like the Au13. Such decahedral shapes are competitive for some materials and sizes.38 In addition to the pentagonal rods, rod-like structures cut-out of the fcc bulk material have been used in the discussion of aspect-ratio dependence and general shifts of surface-plasmon energies.39,40The Ag309 was relaxed using the VASP code.41,42 The Ag263 rod was not relaxed.
The electronic states and the optical spectra have been calculated using DFT and TDDFT with the real-space code octopus.43 Norm-conserving Troullier–Martins pseudopotentials44 were used which include the d electrons in the valence, that is, with 11 valence electrons for each atom. The gradient-corrected PBE exchange–correlation functional45 has been used. The real-space grid spacing was set to 0.18 Å, the radius of the spheres around each atom that make up the calculation domain was set to 5 Å.
Optical spectra were calculated using the Yabana–Bertsch time-evolution formalism30 of TDDFT using the real-space code octopus43 and the gradient-corrected PBE exchange–correlation potential. The ETRS propagator (“enforced time-reversal symmetry”) was used. Propagation time was 25 fs.
In order to analyze the electronic modes contributing to the individual features in the absorption spectra, we used the Fourier-transform analysis of the time-dependent induced density from a δ-kick RT-TDDFT calculation that some of the present authors recently presented and analyzed in detail.31 The time-dependent induced densities for each 25th time-step were used to perform the Fourier transformation at each of the grid points. The grid spacing (0.18 Å), the interval between two consecutive time-steps (dt = 0.0024ħ eV−1), and the total time of evolution (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 × dt) were chosen to be the same as in the octopus simulation for the corresponding spectra. A damping of 0.0037 atomic units of energy (≈0.1 eV) was chosen for the exponential window function during the Fourier transform.
500 × dt) were chosen to be the same as in the octopus simulation for the corresponding spectra. A damping of 0.0037 atomic units of energy (≈0.1 eV) was chosen for the exponential window function during the Fourier transform.
The modes of the induced density corresponding to the optical absorption at a given energy ω are shown as the Fourier sine coefficients which were written out for 100 equally spaced frequency points between 0 and 0.27 atomic units of energy (i.e., up to 7.35 eV). We show the sine coefficients of the Fourier transform because, for a well resolved excitation peak in the absorption spectrum centered at a given energy ω, they correspond to the induced densities at T/4, T being 2π/ω.31
Static calculations
Using the real-space code octopus,43 we calculate both the the field-free ground state and the ground state with a constant and homogeneous external electric field E = 0.2 eV Å−1 = 0.00389 Eh/(eaB), where Eh is the Hartree energy and aB is the Bohr radius. The field, which is arbitrary but small enough to guarantee a linear response of the electron system, is applied along one of the five-fold symmetry axes in all cases. The same pseudopotentials, PBE functional, grid spacing and radius as in the dynamic calculations were used.Results: static vs. dynamic screening
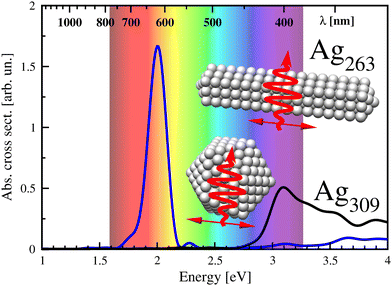
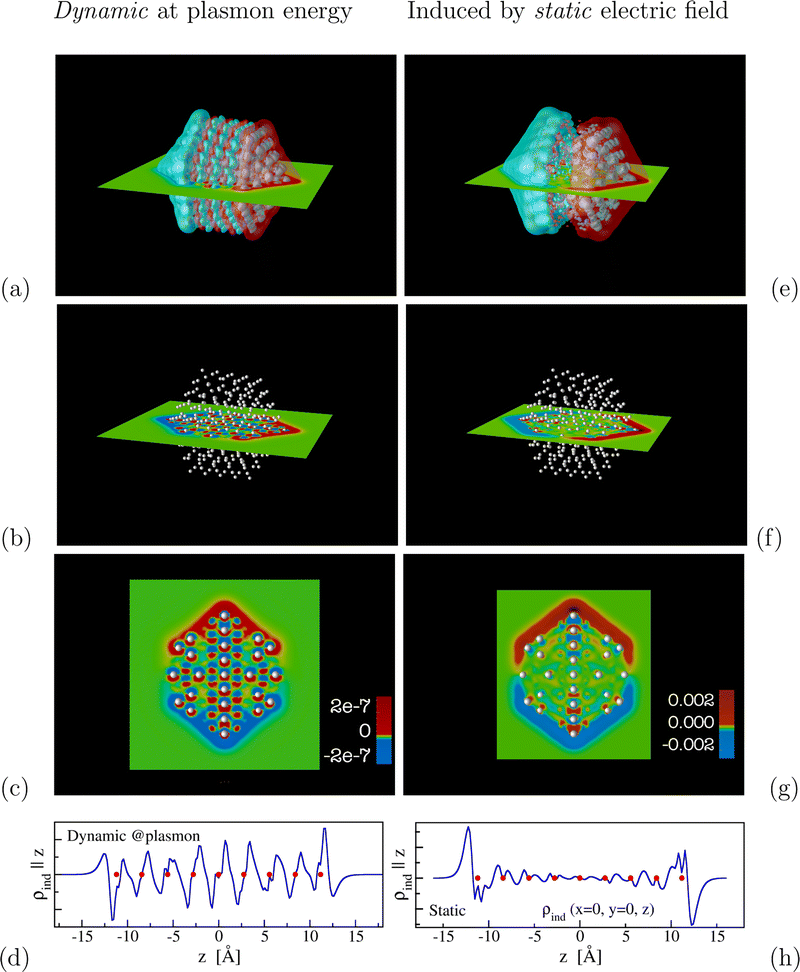
We consider first the icosahedral quasi-spherical 309 atom silver cluster Ag309, the spectrum of which is shown in Fig. 1. In the left column of Fig. 2, the dynamic response at the surface plasmon energy is shown, i.e., the induced density obtained by the Fourier-transform tool described in the Methods section. The calculations using the PBE functional have a number of shortcomings. In particular, they underestimate the SPR energies,46 but the qualitative picture is well represented. A comparison with the long-range-corrected LB94 functional for a smaller silver rod is shown in the ESI.† The expected dipole mode of the collective charge oscillation that characterizes the LSPR in spherical or quasi-spherical clusters is clearly visible, in particular when the induced density of the system is represented using isosurfaces of a rather small density in Fig. 2(a), such that the pictured contributions belong mainly to the delocalized sp electrons. The influence of the different isovalues is discussed below and illustrated in Fig. 4.This surface mode of the delocalized electrons is connected with the d electrons that oscillate with the same frequency (which is not their resonance frequency) but out of phase with the surface contribution. This polarization, opposing the surface mode, is nothing else but the dynamical screening by the d electrons as mentioned above.5,6,16,31,33 In particular, around each atom we observe the localized contribution opposed to the surface mode. This is even more clearly seen in the color-coded slab representation of the same system in Fig. 2(b) and (c) where around each of the atoms that sit on the slab, the polarization opposing the field of the outer electron cloud is clearly visible by the change of colors opposite to that of the latter. Finally, the same is seen in the density line profile in Fig. 2(d) where clearly each atom sits approximately at a zero point within an interval of increasing density, illustrating the same situation.
The situation is very different for the static response, i.e., the induced density due to a static, homogeneous external electric field, shown in Fig. 2(e–h). Even though the overall picture as seen from outside the structure is likewise an overall dipole, the density is very different here. We have studied this situation in detail in order to discuss the metallicity of noble-metal clusters.2 If the NPs were classical perfect metals, the interior fields would be strictly zero, with surface charges compensating any imposed fields inside. In particular, if a cavity existed in such a structure, it would be invisible to a static electric field. Using the overall static polarizability of the clusters as a measure, we have shown previously that the NPs of about 300 atoms are clearly metallic—as little as one layer of atoms is sufficient to produce about 96% of the polarization of the corresponding compact structure.2 The static screening is, in fact, very close to that of a classical perfect metal. Nonetheless, the structures exhibit the Friedel-oscillation-like modulations of the density as they are well known to occur at metallic surfaces and in clusters. These density variations, as they occur for simple metals and jellium models alike, are also present in the noble-metal clusters. Clearly, they concern the delocalized electron density of the sp bands. By contrast, the d electrons act somewhat as “sensors” there, in the sense that they react to the local surrounding density and, therefore, make the density variations easily visible in the representations of the induced density. Naturally, unlike in the dynamic case, here the d electrons are not systematically opposing the (surface) dipole polarization of the delocalized electron cloud.2 Furthermore, as the field inside the cluster is largely screened, i.e., the field inside roughly vanishes, there is little contribution by the d electrons to the static response. This is most clearly seen in the density line profile along the central axis of the cluster shown in Fig. 2(h) which shows rather small variations compared to the dynamic case (as referred to the scale of the induced-density maxima at the surfaces).
The situation is even clearer in the second example that we use here: that of a quasi-1d structure, the nanorod Ag263. It has two advantages over the quasi-spherical cluster: (1) the structure is quasi-one-dimensional and the induced densities are, therefore, easier to interpret than the ones above where the shape (facets…) renders the picture more intricate, and (2) the fact that the LSPR is strongly red-shifted compared to the spherical structure.29,36,37 The optical absorption spectrum is shown in Fig. 1. This separates the excitation further from the interband transitions and makes the interpretation clearer.
The dynamic response at the surface-plasmon frequency (cf., the spectrum in Fig. 1) is shown in the left-hand side of Fig. 3(a–f), alongside the static density induced by a homogeneous static external electric field in Fig. 3(g–l). Again, low-density iso-surfaces of both situations show an overall dipole. To highlight the effect of the d electrons, we show two different slabs, one cutting through the center axis of the rod, the other parallel to this axis but cutting through the plane defined by the three parallel lines of atoms at the rod's surface.
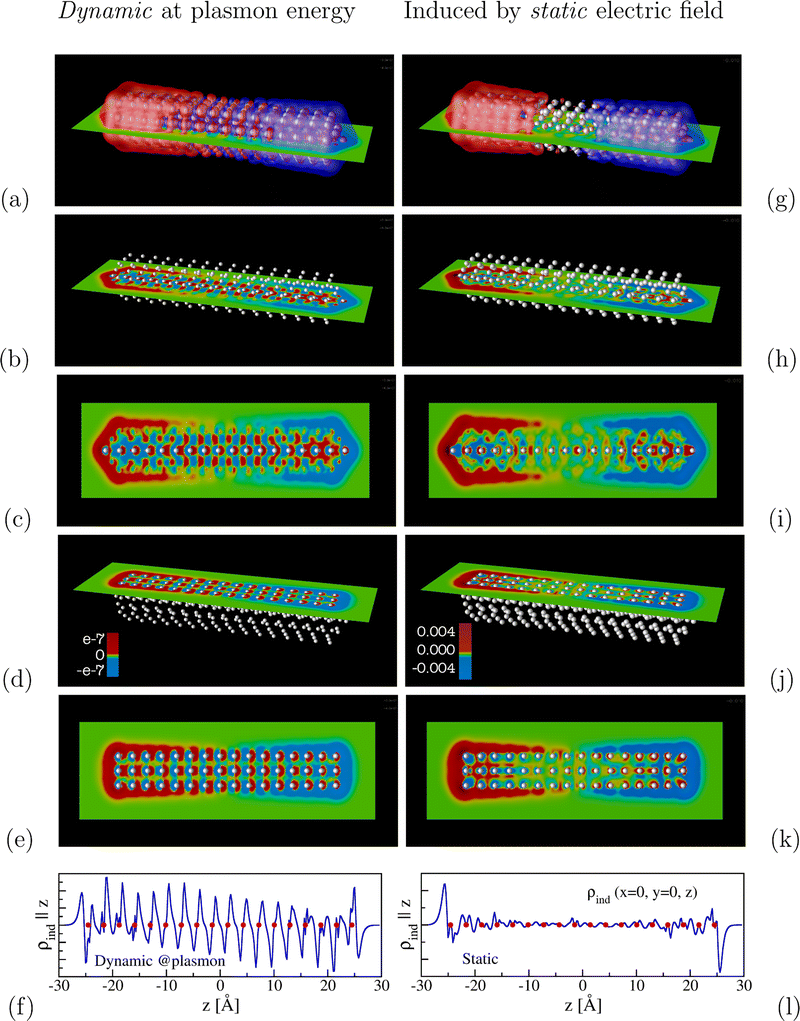 | ||
| Fig. 3 Representations of the induced densities of an optical excitation at the SPR frequency and as reaction to a static electric field as in Fig. 2 for the nanorod Ag263. The color-coded slab representations of the second and the fourth rows are shown from a perpendicular view angle in the third and the fifths rows for better visibility. | ||
Even more clearly than in the quasi-spherical clusters discussed above, we see here that around each of the atoms, the polarization opposes the fields created by the dipole SPR mode. By contrast, in the static case, we see very clearly the strong suppression of the field at the center of the rod, best seen in Fig. 3(i) and (l).
Intricacies: isovalues and snapshots
The importance of the iso values for how the different contributions can be visualized is illustrated in Fig. 4. There, for the same Ag263 nanorod, the iso-surfaces at the plasmon energy are shown for different values of the induced density. Clearly, for the smallest values, the dipole character of the movement of the delocalized electron cloud is visible. An increase of the density values make the contributions of the d electrons clearly visible around each atom. This is a practically important point which has been tacitly used all along this article: the approximate analysis of the interaction of d and sp electrons in noble-metal clusters is possible without an explicit analysis of the wavefunctions' character (projection). But this shows likewise that in the use of iso-surfaces for the visualization of induced densities, care must be taken to make sure that the effects to be discussed are appropriately exposed using appropriate density values. | ||
| Fig. 4 Induced density of the Ag263 rod after the same optical excitation as shown in Fig. 3, i.e., showing the oscillation at the plasmon frequency. The density of the isosurfaces is progressively increasing, (a) 1 × 1010, (b) 1 × 108, (c) 5 × 108, and (d) 1 × 107. The lowest value in (a) highlights the overall dipole mode of the delocalized electrons, whereas with increasing density values, the induced dipoles of the d states around the atoms with opposite polarization become clearly visible. | ||
In addition, to make the link with previous studies, we comment on the differences of the induced densities obtained using the Fourier analysis compared to the snapshots taken out of the trajectories of δ-kick calculations customarily used to calculate optical spectra.
Compared to the snapshots of induced densities from δ-kick calculations (hereafter referred to simply as snapshots) that we have used in the past,32,33,37 the Fourier analysis allows for much cleaner representations. In the δ-kick calculations, all excitable modes are excited, leading to a superposition of all the respective density oscillations. If there is one dominant mode, with all the rest essentially negligible, one can still draw useful conclusions based on the snapshots out of the trajectories, an example being the rod-like structures that have a very strong resonance for excitation along the long axis which dominates all the response, although even there the pictures are not as “clean” as when the FT analysis is used.37
However, looking for instance at spherical clusters (i.e., those most commonly found in experiment), the situation is more intricate. The surface plasmon is fragmented and, in addition, rather close to the onset of the interband transitions from the d electrons. This difference can be seen clearly in Fig. S2 of the ESI,† where we show spectra obtained with a much longer time evolution and the resulting much smaller broadening. While for the rod, a single resonance is dominant compared to all other contributions, in the quasi-spherical Ag147, the plasmon is partially fragmented and multiple modes appear close to it. This impacts the snapshots, as we can see clearly in Fig. 5 where two snapshots are compared taken at moments of maximal overall dipole moment. The snapshots are much more fuzzy and thus much more difficult to meaningfully interpret. In addition to the fuzziness, the large differences between the two snapshots taken at different times show that the procedure is rather arbitrary and error prone, in particular if one is tempted to analyze the snapshots in view of an expected result. We note that the multiple modes will influence the Fourier analysis as well if their energetic separation in the spectrum is smaller than the energy window corresponding to the evolution time used, for a detailed discussion we refer to reader to ref. 31.
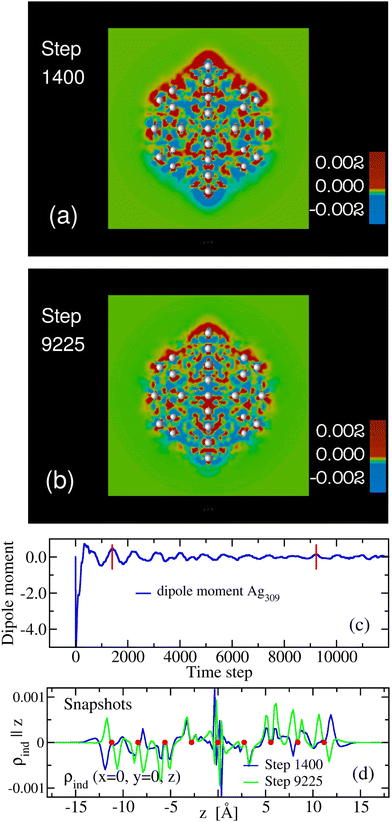 | ||
| Fig. 5 (a and b) Slab representations of two snapshots taken out of the trajectory of the δ -kick calculation of Ag309. They have been taken at steps 1400 and 9225 of the time evolution, as indicated by the read lines in graph (c) showing the dipole moment as a function of time. The two instants correspond to maximal dipole moments along the evolution. (d) Induced density along the z axis, ρind(x = 0, y = 0, z) (i.e., parallel to the excitation direction) for the two snapshots. Clearly, the two snapshots are both much more fuzzy than the Fourier result (Fig. 2(c)). In addition, both the line densities (d) and the slabs show that the densities are very different at the two points in time, even though they have both been taken at instants of maximal overall dipole moment. This shows that the use of snapshots is problematic for situations where more than one mode of any significance are excited, as it is the case for the Ag309 at/around the SPR. | ||
Conclusion
In conclusion, we have shown and discussed representations of the induced densities of noble-metal clusters excited at the surface-plasmon frequency and in a static electric field. These representations allow for a direct understanding of, in particular, the role played by the d electrons. In the dynamic case, the screening of the surface mode as seen by the opposite polarization around the atom locations is highlighted. In the static case, where the metallic screening largely suppresses any internal fields, the d electrons react to the Friedel-oscillation-like variations of the density of the delocalized sp electrons. In addition, our illustrations provide a reminder that the density values chosen for isosurface drawings need to be carefully chosen in order to ensure pertinent representations. In particular, a choice of low densities shows very similar overall dipole polarizations for both the dynamic and the static cases, whereas in reality the two situations are very different due to the metallic screening and the reaction of the d electrons. Moreover, we highlight the need to complement the isosurfaces by slab representations when the interior of the density “clouds” plays a role. Our representations provide an clear picture of the physical situation which, in turn, facilitates the intuitive understanding of the d electron screening.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been carried out in part thanks to the support of the A*MIDEX grant (no. ANR-11-IDEX-0001-02) funded by the French Government “Investissements d'Avenir” program. We acknowledge support from the French National Research Agency (Agence Nationale de Recherche, ANR) in the frame of the projects “FIT SPRINGS”, ANR-14-CE08-0009 and “SchNAPSS”, ANR-21-CE09-0021. The work has used HPC resources from GENCI-IDRIS (Grant 2020-096829). Moreover, HCW and RSR would like to acknowledge the contribution of the International Research Network IRN Nanoalloys (CNRS). PGG acknowledges funding from the Spanish MCINN through the “María de Maeztu” programme for Units of Excellence in R&D (CEX2018-00805-M) and the research grant PID2021-126964OB-I00.References
- J. D. Jackson, Classical electrodynamics, Wiley, New York, NY, 2nd edn, 1975 Search PubMed.
- R. Sinha-Roy, P. García-González and H.-Ch. Weissker, How metallic are noble–metal clusters? Static screening and polarizability in quantum-sized silver and gold nanoparticles, Nanoscale, 2020, 12, 4452–4458 RSC.
- P. B. Johnson and R. Christy, Optical Constants of the Noble Metal, Phys. Rev. B: Solid State, 1972, 6, 4370–4379 CrossRef CAS.
- A. Liebsch, Surface-plasmon dispersion and size dependence of Mie resonance: Silver versus simple metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 11317–11328 CrossRef CAS PubMed.
- L. Serra and A. Rubio, Core Polarization in the Optical Response of Metal Clusters: Generalized Time-Dependent Density-Functional Theory, Phys. Rev. Lett., 1997, 78, 1428–1431 CrossRef CAS.
- E. Cottancin, G. Celep, J. Lermé, M. Pellarin, J. Huntzinger, J. Vialle and M. Broyer, Optical Properties of Noble Metal Clusters as a Function of the Size: Comparison between Experiments and a Semi-Quantal Theory, Theor. Chem. Acc., 2006, 116, 514 Search PubMed.
- H.-Ch. Weissker, O. Lopez-Acevedo, R. L. Whetten and X. López-Lozano, Optical Spectra of the Special Au144 Gold-Cluster Compounds: Sensitivity to Structure and Symmetry, J. Phys. Chem. C, 2015, 119, 11250–11259 CrossRef CAS.
- J. Tiggesbäumker, L. Köller, K.-H. Meiwes-Broer and A. Liebsch, Blue shift of the Mie plasma frequency in Ag clusters and particles, Phys. Rev. A, 1993, 48, R1749–R1752 CrossRef PubMed.
- G. Toscano, J. Straubel, A. Kwiatkowski, C. Rockstuhl, F. Evers and H. Xu, Asger Mortensen, N.; Wubs, M. Resonance shifts and spill-out effects in self-consistent hydrodynamic nanoplasmonics, Nat. Commun., 2015, 6, 7132 CrossRef PubMed.
- A. Campos, N. Troc, E. Cottancin, M. Pellarin, H.-Ch. Weissker, J. Lermé, M. Kociak and M. Hillenkamp, Plasmonic quantum size effects in silver nanoparticles are dominated by interfaces and local environments, Nat. Phys., 2019, 15, 275–280 Search PubMed.
- A. Liebsch, Surface plasmon dispersion of Ag, Phys. Rev. Lett., 1993, 71, 145–148 CrossRef CAS PubMed.
- J.-S. Kim, L. Chen, L. L. Kesmodel, P. García-González and A. Liebsch, Surface plasmon dispersion of Cl/Ag(111), Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, R4402–R4405 CrossRef CAS.
- A. Liebsch, Prediction of a Ag multipole surface plasmon, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 3803–3806 CrossRef CAS.
- F. Xuan and C. Guet, Core-polarization-corrected random-phase approximation with exact exchange for dipole surface plasmons in silver clusters, Phys. Rev. A, 2016, 94, 043415 CrossRef.
- K. Yabana and G. F. Bertsch, Optical response of small silver clusters, Phys. Rev. A, 1999, 60, 3809–3814 CrossRef CAS.
- M. Kuisma, A. Sakko, T. P. Rossi, A. H. Larsen, J. Enkovaara, L. Lehtovaara and T. T. Rantala, Localized surface plasmon resonance in silver nanoparticles: Atomistic first-principles time-dependent density-functional theory calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 115431 CrossRef.
- R. Schira and F. Rabilloud, Localized Surface Plasmon Resonance in Free Silver Nanoclusters Agn, n = 20-147, J. Phys. Chem. C, 2019, 123, 6205–6212 CrossRef CAS.
- R. Sinha-Roy, X. López-Lozano, R. L. Whetten and H.-Ch. Weissker, Crucial Role of Conjugation in Monolayer-Protected Metal Clusters with Aromatic Ligands: Insights from the Archetypal Au144L60 Cluster Compounds, J. Phys. Chem. Lett., 2021, 12, 9262–9268 CrossRef CAS PubMed , PMID: 34533967.
- S. Malola, L. Lehtovaara, J. Enkovaara and H. Häkkinen, Birth of the Localized Surface Plasmon Resonance in Monolayer-Protected Gold Nanoclusters, ACS Nano, 2013, 7, 10263–10270 CrossRef CAS PubMed.
- N. A. Sakthivel, M. Stener, L. Sementa, A. Fortunelli, G. Ramakrishna and A. Dass, Au-279(SR)(84): The Smallest Gold Thiolate Nanocrystal That Is Metallic and the Birth of Plasmon, J. Phys. Chem. Lett., 2018, 9, 1295–1300 CrossRef CAS PubMed.
- E. Luppi, H.-Ch. Weissker, S. Bottaro, F. Sottile, V. Veniard, L. Reining and G. Onida, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 245124 CrossRef.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- E. Runge and E. Gross, Density-Functional Theory for Time-Dependent Systems, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- V. Bonacic-Koutecky, J. Pittner, M. Boiron and P. Fantucci, An accurate relativistic effective core potential for excited states of Ag atom: An application for studying the absorption spectra of Agn and Agn+ clusters, J. Chem. Phys., 1999, 110, 3876–3886 CrossRef CAS.
- S. Huotari, M. Cazzaniga, H.-C. Weissker, T. Pylkkänen, H. Müller, L. Reining, G. Onida and G. Monaco, Dynamical response function in sodium studied by inelastic x-ray scattering spectroscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075108 CrossRef.
- H.-Ch. Weissker, J. Serrano, S. Huotari, E. Luppi, M. Cazzaniga, F. Bruneval, F. Sottile, G. Monaco, V. Olevano and L. Reining, Dynamic structure factor and dielectric function of silicon for finite momentum transfer: Inelastic x-ray scattering experiments and ab initio calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085104 CrossRef.
- S. Bernadotte, F. Evers and C. R. Jacob, Plasmons in molecules, J. Phys. Chem. C, 2013, 117, 1863–1878 CrossRef CAS.
- C. Yu, R. Schira, H. Brune, B. von Issendorff, F. Rabilloud and W. Harbich, Optical properties of size selected neutral Ag clusters: electronic shell structures and the surface plasmon resonance, Nanoscale, 2018, 10, 20821–20827 RSC.
- R. Sinha-Roy, P. García-González, H.-Ch. Weissker, F. Rabilloud and A. I. Fernández-Domínguez, Classical and ab Initio Plasmonics Meet at Sub-nanometric Noble Metal Rods, ACS Photonics, 2017, 4, 1484–1493 CrossRef CAS.
- K. Yabana and G. F. Bertsch, Time-dependent local-density approximation in real time, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 4484–4487 CrossRef CAS PubMed.
- R. Sinha-Roy, P. García-González, X. López Lozano, R. L. Whetten and H.-Ch. Weissker, Identifying Electronic Modes by Fourier Transform from δ -Kick Time-Evolution TDDFT Calculations, J. Chem. Theory Comput., 2018, 14, 6417–6426 CrossRef CAS PubMed.
- H.-Ch. Weissker, R. L. Whetten and X. López-Lozano, Optical response of quantum-sized Ag and Au clusters - cage vs. compact structures and the remarkable insensitivity to compression, Phys. Chem. Chem. Phys., 2014, 16, 12495–12502 RSC.
- H.-Ch. Weissker and X. López-Lozano, Surface plasmons in quantum-sized noble–metal clusters: TDDFT quantum calculations and the classical picture of charge oscillations, Phys. Chem. Chem. Phys., 2015, 17, 28379–28386 RSC.
- H.-Ch. Weissker and C. Mottet, Optical properties of pure and core-shell noble–metal nanoclusters from TDDFT: The influence of the atomic structure, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 165443 CrossRef.
- H. E. Johnson and C. M. Aikens, Electronic Structure and TDDFT Optical Absorption Spectra of Silver Nanorods, J. Phys. Chem. A, 2009, 113, 4445–4450 CrossRef CAS PubMed , PMID: 19296635.
- E. B. Guidez and C. M. Aikens, Diameter Dependence of the Excitation Spectra of Silver and Gold Nanorods, J. Phys. Chem. C, 2013, 117, 12325–12336 CrossRef CAS.
- X. Lopez-Lozano, H. Barron, C. Mottet and H.-Ch. Weissker, Aspect-ratio- and size-dependent emergence of the surface-plasmon resonance in gold nanorods - an ab initio TDDFT study, Phys. Chem. Chem. Phys., 2014, 16, 1820–1823 RSC.
- F. Baletto, R. Ferrando, A. Fortunelli, F. Montalenti and C. Mottet, Crossover among structural motifs in transition and noble–metal clusters, J. Chem. Phys., 2002, 116, 3856–3863 CrossRef CAS.
- G. Piccini, R. W. A. Havenith, R. Broer and M. Stener, Gold Nanowires: A Time-Dependent Density Functional Assessment of Plasmonic Behavior, J. Phys. Chem. C, 2013, 117, 17196–17204 CrossRef CAS.
- R. W. Burgess and V. J. Keast, TDDFT Study of the Optical Absorption Spectra of Bare Gold Clusters, J. Phys. Chem. C, 2014, 118, 3194–3201 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mat. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- N. Tancogne-Dejean, M. J. T. Oliveira, X. Andrade, H. Appel, C. H. Borca, G. Le Breton, F. Buchholz, A. Castro, S. Corni and A. A. Correa, et al., Octopus, a computational framework for exploring light-driven phenomena and quantum dynamics in extended and finite systems, J. Chem. Phys., 2020, 152, 124119 CrossRef CAS PubMed.
- N. Troullier and J. L. Martins, Efficient pseudopotentials for plane-wave calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. M. Aikens, S. Li and G. C. Schatz, From Discrete Electronic States to Plasmons: TDDFT Optical Absorption Properties of Ag n (n = 10, 20, 35, 56, 84, 120) Tetrahedral Clusters, J. Phys. Chem. C, 2008, 112, 11272 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04316e |
| This journal is © the Owner Societies 2023 |