Metal cluster plasmons analyzed by energy-resolved photoemission†
N.
Iwe
 a,
K.
Raspe
a,
K.
Raspe
 a,
F.
Martinez
a,
L.
Schweikhard
b,
K.-H.
Meiwes-Broer
ac and
J.
Tiggesbäumker
a,
F.
Martinez
a,
L.
Schweikhard
b,
K.-H.
Meiwes-Broer
ac and
J.
Tiggesbäumker
 *ac
*ac
aInstitute of Physics, University of Rostock, 18059, Rostock, Germany. E-mail: josef.tiggesbaeumker@uni-rostock.de
bInstitute of Physics, University of Greifswald, 17489, Greifswald, Germany
cDepartment Life, Light and Matter, University of Rostock, 18059, Rostock, Germany
First published on 21st December 2022
Abstract
The optical response of size-selected metal clusters is studied by wavelength-dependent photoemission and energy-resolved photoelectron detection. Relative photodetachment cross sections giving information on the plasmon are determined for the example of closed-shell Ag91−. Notably, the peak energy of this anion (3.74 eV) is higher than the small particle limit in Mie theory of 3.5 eV. Different methods to extract cross sections from the spectra are applied. In particular, we compare the results obtained by integrating the full electron yields to analyses based on evaluating specified binding energy windows. The approach opens up new possibilities to conduct studies on Landau fragmentation as a result of multielectron excitations.
1 Introduction
Novel properties of matter arising from unique structures at the nanoscale are of high interest for scientific research and applications.1 Composites which comprise nanoparticles offer interesting opportunities to build up functional materials, which, e.g., provide an effective coupling between nanooptics and catalysis.2 In particular, the optical response of metal nanoparticles, i.e. the Mie plasmon resonance,3 and their use in nanoplasmonics is appealing, because it may be used for improved light guiding and trapping, e.g. in thin-film solar cells4 and for nanoscale focusing in tapered waveguides,5 or nanoscale antennas.6 In order to exploit the possibilities in the context of complex materials, it is essential to explore the optical properties of the elementary building blocks, which includes the plasmonics of free metal clusters. By controlling particle size and charge state, unique optical fingerprints can be realized, that provide avenues to design dedicated materials.The electronic properties of metal particles7 and fullerenes8,9 can be well-described by the response of nearly-free electrons within the context of the jellium model. Alkali clusters, e.g., show a collective resonance of the valence electrons down to cluster sizes of N = 8.10,11 It is well-known that the plasmon energies ħωalkali show a red-shift as a function of decreasing radius R.12–14 This phenomenon is related to the electron spill-out δ.15 In a first order treatment, the resulting increase in the static polarizability α from the classical metallic sphere result R3 to (R + δ)3 leads to a ratio between the plasmon frequency of the alkali clusters ωalkali(R) and the small particle limit ħωMie of16
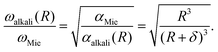 | (1) |
Within Mie theory3 the value of ωMie can be calculated from the optical constants.17Eqn (1) well-describes the size-dependence of the plasmon energy in alkali clusters. The optical response has been studied as function of ellipsoidal deformation,18,19 temperature20 and oxidation.21 Calculations on different theoretical levels are capable to reproduce the experimental findings.22–25
Coinage metals and in particular silver particles are also known to exhibit distinct plasmon resonances. Due to the influence of the d-electrons, however, the optical constants modify17 and the peak in silver shifts from the free-electron value ωMie to ℏωAgMie = 3.5 eV.26 In contrast to alkali clusters, AgN+ shows a blue-shift of the resonance with decreasing N, that can be understood, when taking into account the reduced sd-screening near the particle surface.27–29 One finds27:
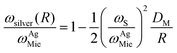 | (2) |
Even up to date, the method of choice to measure optical spectra of anionic clusters is to record photodepletion yields.31 The corresponding signals are extracted by measuring photoreaction yields, that is
| AgN− + ħω → AgN + e− → AgN−m− + Agm | (3) |
A drawback of the photodepletion method is that essential details of the cluster response are lost, i.e., the coupling to the electronic system triggered by the photoabsorption is not accessible. In contrast, recording the corresponding photoelectron spectra will provide this information.
In this contribution, we record photoelectron spectra of silver cluster anions of size N = 91 in order to obtain relative photodetachment cross sections, i.e. differential cross sections with respect to the energy of the emitted photoelectrons. To the best of our knowledge, such a treatment was not utilized before to obtain an extended characterization of the plasmonic response of metal clusters. Further, the method presented here will enable us to capture the optical response of a broader class of systems, namely polyanionic clusters.
2 Experimental setup
Details about the experimental setup have been published elsewhere.32 Briefly, a magnetron-based gas aggregation source is used to produce a molecular beam of clusters, which contains negatively charged silver cluster anions.33 After size-selection, the particles enter a digital radio frequency ion trap,34 where the anions are accumulated using argon buffer gas cooling. By pulsed extraction at a rate of 10 Hz, the anions are transferred into the interaction region, where light from a tunable laser system illuminates the cluster bunch. An optical parametric oscillator (OPO) laser system delivers nanosecond light pulses between Eph = 3.52–4.11 eV at pulse energies on the order of 1 μJ. The OPO process, however, comes along with considerable pulse-to-pulse fluctuations. Therefore, electron signals and pulse energies are monitored on a shot-to-shot basis. This allows for a compensation of pulse fluctuations in the data evaluation, thus ensuring the determination of reliable response cross sections. Photon fluxes are adjusted with respect to changes in the photodetachment cross sections. The entire energy-resolved photoelectron signals are obtained by a magnetic bottle electron spectrometer.35 Special care was taken in the calibration procedure to minimize artificial electron binding energy shifts, when changing the laser wavelength.323 Results
The photoelectron measurements were conducted on Ag91−. This particular size was chosen for two reasons: (i) according to jellium calculations a metal cluster having Ne = 92 valence electrons represents a closed-shell system.15 Such magic clusters are expected to have a spherical shape and thus should reveal only a single plasmon peak.16 (ii) The onset of photoemission, characterized by the electron affinity EA = 3.03 eV,36 is low compared to larger cluster anions.36 Thus, an excitation energy range, which extents to lower Eph can be captured to determine detachment cross sections. Fig. 1a shows the electron spectrum taken at Eph = 3.76 eV. The onset of photoemission is found at an electron binding energy Ebin of around 2.95 eV, followed by a first peak at 3.07 eV and a second one at Ebin = 3.42 eV. The overall structure compares well with previous studies of other groups.37 At a binding energy of almost 3.6 eV the signal decreases substantially, which originates from the low detection efficiency of the spectrometer for slow electrons, We take this into account by defining a minimum detection threshold for the electron kinetic energy of Et = 0.23 eV (Fig. 1). Thus, signals for Ebin > Eph − Et are excluded from further evaluation.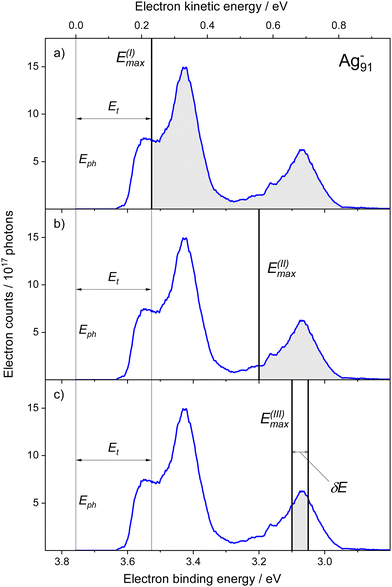 | ||
| Fig. 1 Experimental photoelectron energy spectrum of Ag91− (blue line), obtained at Eph = 3.76 eV. The panels (a–c) illustrate three different methods to analyze the spectrum and determine relative photodetachment cross sections, see corresponding shaded regions. (a) The signals are integrated up to a photon-energy dependent binding energy value of E(I)max = Eph − Et. Et marks the energy range, where the transmission of the spectrometer decreases significantly (Method I). Note that the excluded binding energy range may contain substantially more electrons than registered in the above plot (Fig. S1, ESI†) (b) irrespective of the photon energy, the electron yields are summed up to a selected maximum binding energy value E(II)max (Method II); (c) the spectrum is integrated only within a selected narrow binding energy region, i.e. [E(III)max − δE; E(III)max] (Method III). | ||
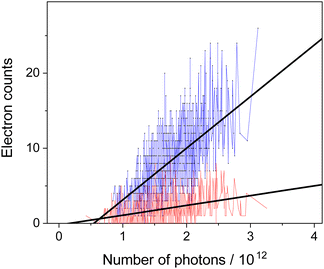
The single-shot data acquisition, where both, the laser pulse energy and the photoelectron yield, are recorded, enables us to analyze the data as shown in Fig. 2: a linear function is fitted to the number of electrons detected and plotted versus the number of photons. From the resulting slopes relative photodetachment cross section are determined. Note that conducting the analysis in such a way has the advantage, that offsets in the determination of the pulse energies and/or electron counts (e.g. due to dark counts of the detector), see intersections with the ordinate, have no effect on the extracted cross sections.
In the core of the subsequent evaluation, we concentrate on the photon energy dependent cross sections, which are also a function of the binding-energy range. For this reason, we specify three methods and analyze:
• The entire photoelectron spectra up to the highest accessible Ebin, i.e. E(I)max = Eph − Et (Fig. 1a).
• The photoelectron spectra up to a predefined maximum binding energy E(II)max (Fig. 1b).
• The photoelectron spectra only within a selected energy window δE, i.e. in the range [E(III)max − δE; E(III)max] (Fig. 1c).
Note that only E(I)max depends on Eph, whereas E(II)max and E(III)max are constant values to be defined.
3.1 Method I
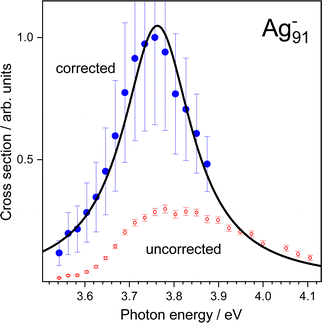
Evaluation of the entire spectrum (Method I) allows for a comparison to corresponding photodepletion experiments, whereby one has to take into account that photo-induced cluster fragmentation is not captured. The cross sections σI from wavelength-dependent measurements are shown in Fig. 3 (open symbols). Inspecting σI, a clear increase in the optical response is obtained at energies between Eph = 3.58 eV and 3.78 eV. The cross sections show a broad feature, that decreases slowly for energies above 3.85 eV. Backed by results obtained by photodepletion,30,38 photoionization39,40 and photoabsorption26,41,42 experiments on unsupported Ag clusters and nanoparticles, the feature can be assigned to a collective response of the valence electrons. As indicated in Fig. 1, electrons having kinetic energies below Et are excluded from the analysis, due to the reduced detection efficiency with respect to low energy electrons. Consequently, the cross-section values may be largely underestimated especially at lower photon energies, leading to an artificial peak shift towards higher energies. In fact, in photodepletion restricted to electron emission (see eqn (3)), the entire electron spectrum has to contribute when determining the optical response. In order to obtain more reliable values, a representative photoelectron spectrum taken at the highest photon energy of Emaxph = 4.11 eV is used to “complete” the spectra recorded at photon energies Eph < Emaxph − Et = 3.88 eV. We thereby assume no qualitative change of the spectra with Eph. Thus, one can estimate the fraction of the electron yield Y within the critical energy window [Eph − Et; Eph] and correct the previously obtained cross sections with a corresponding factor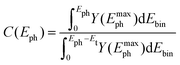 | (4) |
Conducting the analysis in such a way leads to the corrected cross sections presented in Fig. 3 (closed symbols). Fitting a Lorentz profile to the data results in a plasmon peak position at 3.76 eV. By consideration of the correction procedure, the cross sections increase by up to a factor of eight, which is due to the large proportion of electrons located at high binding energies above 3.3 eV (Fig. S1, ESI†). One should therefore note that a significant number of low energy electrons showing up in the binding energy region [Eph − Et; Eph] may lead to a noticeable shift of the cross section values. Possible qualitative changes of the spectra with photon energy are also not covered. These contributions, however, could have a significant impact on the resulting cross sections and hence represent a drawback of the procedure.
3.2 Method II
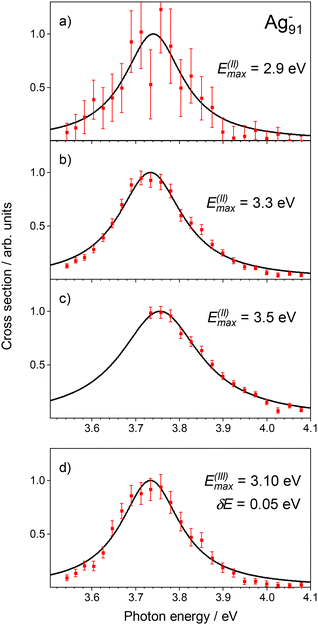
While Method I represents a complex data analysis, the results allow for a direct comparison with other depletion experiments. However, the approach comes along with some disadvantages. In order to bypass the correction procedure and thus avoid systematic errors in the detection method, it is advisable to concentrate on a limited energy range in the evaluation (Fig. 1b). In the implementation of Method II, we assume that the selected range of Ebin adequately maps the cross sections. Electron signals are evaluated up to a predefined binding energy E(II)max. Excitation energies are thereby restricted to Eph ≥ Emax + Et. This ensures that the specified binding energy window is fully covered for all Eph.Resulting detachment cross sections σII for selected E(II)max values are presented in Fig. 4. We notice, that:
• all energy windows show a similar development of σII.
• choosing the value of E(II)max too small leads to significant uncertainties with respect to σII due to lower statistics (a).
• the statistical uncertainty reduces when increasing the energy window (a–c). However, cross sections at lower excitation energies are not captured for too large E(II)max (c).
3.3 Method III
Finally, the electron spectra were evaluated by using Method III. The procedure is similar to Method II, but now the energy window is tuned to specific needs, i.e. [ E(III)max −δE; E(III)max], see Fig. 1c. This enables us to resolve photon energy dependencies of the cross sections for different binding energy regions. In order to illustrate Method III, a δE = 50 meV broad slice of the low binding energy peak is selected, see Fig. 1, and analyzed with respect to electron detachment. The corresponding cross sections are presented in Fig. 4d. Clearly, the development of the data points as obtained by Method I (Fig. 3) and II (Fig. 4a–c) is well-reproduced although the energy window used for the evaluation is significantly restricted.Fig. 5 summarizes the collective resonance energies determined by applying Methods I–III. Although different evaluation techniques are used, the Methods II and III provide a reliable plasmon energy of 3.73 eV. Note that analyzing different regions of the low binding energy peak using Method III shows almost no shift of the plasmon. Clearly, the plasmon energy of Ag91− neither depends on the chosen values of Emax nor on the method applied. As long as the envelope of the resonance is sufficiently sampled, a conclusive fit curve can be obtained, see also Fig. 4. The plasmon energy value obtained by Method I of 3.76 eV, is only about 30 meV higher, which is probably a result of the increased uncertainty due to the correction as discussed.
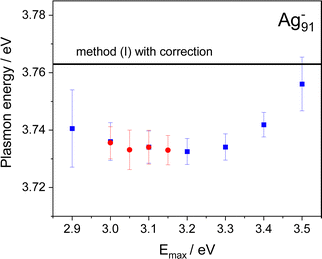 | ||
| Fig. 5 Comparison of the plasmon energy obtained from the different data evaluation methods described in the text. The photoelectron signal was either analyzed up to Ebin = E(II)max (blue square) or in separated binding energy windows [E(III)max − δE; E(III)max] (δE = 50 meV) (red circles), see Fig. 4. The low-energy cutoff of the spectrometer limits the electron transmission, which requires a correction procedure for Method I, see Fig. 3 and text for details. The solid line shows the corresponding corrected value, when using the entire electron signal. Note that when determining the error margins, only statistical errors were taken into account. | ||
4 Discussion
In our photoreaction experiment on Ag91− only a single reaction pathway, i.e. photodetachment of electrons, is considered, but other processes may contribute as well. This raises the issue of the coupling of the collective electron motion to single particle states termed Landau damping.43 Indeed, fluorescence as a corresponding plasmon decay channel has been found, however, for only a few clusters like Ag8.44 This process requires excited-state lifetimes on the order of nanoseconds. Such exceptional long lifetimes are not expected for metal clusters in general due to the high density of electronic states. This statement is supported by experiments on supported Ag clusters, where lifetimes in the femtosecond regime have been reported.45 The excess energy may also dissipate into other internal degrees of freedom, potentially leading to the evaporation of atoms. Indeed, in plasmon measurements on Na91−, photofragmentation has been identified as competing decay channel to photodetachment.31 Moreover, at higher photon energies, photoemission is almost suppressed. If the excitation leads to a heating of the electron system, single electron emission does not take place. The coupling of the electronic excitation to vibrational modes finally results in an evaporation of atoms, which has been observed for small silver clusters on time scales extending up to several milliseconds.46–48 Time-dependent local-density approximation (TDLDA) calculations on NaN have shown that Landau damping contributes beyond N = 92.22 In our experiments, we cannot exclude photofragmentation.49 Probably, the increase in the density of single electron states with cluster size50 favors extensive Landau damping into many electron–hole states. Further energy dissipation into vibratioal modes finally triggers cluster fragmentation. Analyzing photoemission signals in specific energy ranges may provide further insights into relaxation pathways. With the availability of ultrashort laser pulses51 it has even become possible to trace the electronic response on ultrafast time scales, i.e. conducting time-resolved photoelectron spectroscopy.52,53The plasmon energies of free, supported and embedded silver nanoparticles have been studied in detail experimentally39,54–57 as well as by theory.58–66 By considering the respective matrix shifts, experiments on size-selected Ag clusters embedded in rare gases confirm the results obtained in the molecular beam.57 An interesting dependence is obtained, when comparing clusters of different charge state, keeping the relevant number of valence electrons constant. In Ag839,40 and Ag9+38 the position hardly shifts, whereas in Ag7− the plasmon lowers in energy by 0.68 eV with respect to Ag9+ and centers at 3.34 eV.30 Interestingly, our result for Ag91− (3.73 eV) overshoots the small particle limit ħωAgMie of 3.5 eV and tends to coincide with the result of 3.74 eV expected for Ag91+ (eqn (2)). Possibly, the Ag cluster charge state has hardly any influence on the plasmon energies in this size range, which is in contrast to the behavior of sodium clusters of similar size.14,31 Followup experiments on the cluster anion size dependence are under way, which will clarify, whether the plasmon energies in larger AgN− indeed develop similar to those of cationic systems.27 Evidence for the applicability of eqn (2) to larger systems, independent of their charge state, stems from photoabsorption measurements on unsupported 2 nm silver nanoparticles.41
All methods described in the present work can be applied in parallel, since the values are determined after the data sets have been recorded. Method I is closest to photodepletion and thus provides the traditional measure of the absorption cross sections. However, for a full analysis, measurements on the competing decay channel of photofragmentation have to be conducted, too. To get access to the entire photoelectron signal, the detection efficiency of magnetic bottle spectrometers at low electron energies has to be improved. This can be accomplished by accelerating the electrons by a weak electrostatic potential.32,67 Method II is based on the assumption that photodetachment fully reflects in the evolution of the weakly bound electrons and that therefore the evaluated signals are good measures of the actual cross sections. As an advantage, only the signals close to the detachment energy threshold are evaluated. Compared to Method I, the yields in the selected low binding energy region depend to a lesser extent on spectrometer transmission. As demonstrated by Fig. 4 and 5, the analysis allows to adjust E(II)max in a proper way. In our experiment on Ag91− (EA = 3.03 eV), which covers a photon energy range between 3.52 and 4.11 eV, EIImax = 3.3 eV is an appropriate choice. Method III in principle allows to study the wavelength dependence of selected photoelectron peaks. It is well-known from other experiments, that inelastic energy loss, shake-up, and autodetachment can modify the spectra.68 Method III reveals the differential cross section with respect to the photoelectron energy and, thus, in principle allows for investigating such processes.
5 Conclusions
In summary, a procedure has been described, which allows to determine relative photodetachment cross sections of silver cluster anions in various ways, providing information on the optical response with respect to direct photoemission. The methods of evaluation are not restricted to metal nanoparticles but can be applied to other systems as well. For example, the present studies could be extended to the optical response of polyanionic molecules, which are relevant to photochemistry.69 In contrast to photodepletion, photoelectron spectroscopy allows to separate direct electron emission from processes like fragmentation, which develop on longer time scales. Evaluating plasmon-induced photoemission is thereby of utmost importance for applications like photocatalysis70 and photovoltaics.71 Understanding the fundamentals of plasmon decay into hot electrons in metal nanoparticles and nanostructures offers promising prospects for efficient energy conversion of light.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Madlen Müller for helpful discussions. S. Lochbrunner provided us with a tunable laser system. The Deutsche Forschungsgemeinschaft (TI 210-10) is gratefully acknowledged for financial support.References
- E. Roduner, Size matters: Why nanomaterials are different, Chem. Soc. Rev., 2006, 35, 583–592 RSC.
- M. Valenti, M. P. Jonsson, G. Biskos, A. Schmidt-Ott and W. A. Smith, Plasmonic nanoparticle-semiconductor composites for efficient solar water splitting, J. Mater. Chem. A, 2016, 4, 17891–17912 RSC.
- G. Mie, Beiträge zur Optik trüber Medien, speziell kolloidaler Metalllösungen, Ann. Phys., 1908, 25, 377–445 CrossRef CAS.
- C. Clavero, Plasmon-induced hot-electron generation at nanoparticle/metal-oxide interfaces for photovoltaic and photocatalytic devices, Nat. Photonics, 2014, 8, 95–103 CrossRef CAS.
- M. I. Stockman, Nanofocusing of Optical Energy in Tapered Plasmonic Waveguides, Phys. Rev. Lett., 2004, 93, 137404 CrossRef PubMed.
- V. Giannini, A. I. Fernández-Domínguez, S. C. Heck and S. A. Maier, Plasmonic Nanoantennas: Fundamentals and Their Use in Controlling the Radiative Properties of Nanoemitters, Chem. Rev., 2011, 111, 3888–3912 CrossRef CAS PubMed.
- Metal clusters, Wiley series in theoretical chemistry, ed. W. Ekardt, John Wiley & Sons Ltd, Chichester, 1999 Search PubMed.
- G. F. Bertsch, A. Bulgac, D. Tomanek and Y. Wang, Collective plasmon exitation in C60 Clusters, Phys. Rev. Lett., 1991, 67, 2690 CrossRef CAS PubMed.
- I. V. Hertel, H. Steger, J. de Vries, B. Weisser, C. Menzel and B. Kamke, et al., Giant plasmon excitation in free C60 and C70 molecules studied by photoionization, Phys. Rev. Lett., 1992, 68, 784–787 CrossRef CAS PubMed.
- K. Selby, M. Vollmer, J. Masui, V. Kresin, W. de Heer and W. D. Knight, Surface plasma resonances in free metal clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 5417 CrossRef CAS PubMed.
- S. Pollack, C. R. C. Wang and M. M. Kappes, On the optical response of Na20 and its relation to computational prediction, J. Chem. Phys., 1991, 94, 2496–2501 CrossRef CAS.
- C. Bréchignac, P. Cahuzac, N. Kebaili, J. Leygnier and A. Sarfati, Collective Resonances in Large Potassium Cluster Ions, Phys. Rev. Lett., 1992, 68, 3916–3919 CrossRef PubMed.
- C. Bréchignac, P. Cahuzac, J. Leygnier and A. Sarfati, Optical Response of large Lithium Clusters: Evolution towards the bulk, Phys. Rev. Lett., 1993, 70, 2036–2039 CrossRef PubMed.
- T. Reiners, C. Ellert, M. Schmidt and H. Haberland, Size Dependence of the Optical Response of Spherical Sodium Clusters, Phys. Rev. Lett., 1995, 74, 1558–1561 CrossRef CAS PubMed.
- W. Ekardt, Work function of small metal particles: Self consistent spherical jellium-background model, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 1558–1564 CrossRef CAS.
- W. A. de Heer, The Physics of Simple Metal Clusters: Experimental Aspects and Simple Models, Rev. Mod. Phys., 1993, 65, 611 CrossRef CAS.
- F. Abeles, Optical Properties of Solids, North-Holland Publishing, London, 1972 Search PubMed.
- K. Selby, V. Kresin, J. Masui, M. Vollmer, W. A. de Heer and A. Scheidemann, et al., Photoabsorption spectra of sodium clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 4565 CrossRef CAS PubMed.
- C. Bréchignac, P. Cahuzac, F. Carlier, M. deFrutos and J. Leygnier, Optical Excitation in small ionized sodium Clusters: Closed-Shell and Open-Shell systems, Chem. Phys. Lett., 1992, 189, 28–34 CrossRef.
- C. Ellert, M. Schmidt, C. Schmitt, T. Reiners and H. Haberland, Temperature Dependence of the Optical Response of Small, Open Shell Sodium Clusters, Phys. Rev. Lett., 1995, 75, 1731–1734 CrossRef CAS PubMed.
- H. Fallgren, K. M. Brown and T. P. Martin, Photoabsorption spectra of CsN O and CsN clusters, Z. Phys. D: At., Mol. Clusters, 1991, 19, 81 CrossRef CAS.
- W. Ekardt, Size-dependent photoabsorption and photoemission of small metal particles, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 6360 CrossRef CAS PubMed.
- V. Bonacic-Koutecký, P. Fantucci and J. Koutecký, Theoretical interpretation of the photoelectron detachment spectra of Na2 − 5 and of the absorption spectra of Na3, Na4, and Na8 clusters, J. Chem. Phys., 1990, 93, 3802–3825 CrossRef.
- P. G. Reinhard, O. Genzken and M. Brack, From sum rules to RPA: 3. Optical dipole response in metal clusters, Ann. Phys., 1996, 5, 576–607 CAS.
- J. M. Pacheco and J. L. Martins, Ab initio pseudopotential calculation of the photo-response of metal clusters, J. Chem. Phys., 1997, 106, 6039–6044 CrossRef.
- K. P. Charlé, L. König, S. Nepijko, I. Rabin and W. Schulze, The Surface Plasmon Resonance of Free and Embedded Ag-Clusters in the Size Range 1,5 nm<D< 30 nm, Cryst. Res. Technol., 1998, 33, 1085–1096 CrossRef.
- J. Tiggesbäumker, L. Köller, K. H. Meiwes-Broer and A. Liebsch, Blue Shift of the Mie Plasma Frequency in Ag Clusters and Particles, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 48, R1749–R1752 CrossRef PubMed.
- K. Baishya, J. C. Idrobo, S. Öğüt, M. Yang, K. A. Jackson and J. Jellinek, First-principles absorption spectra of Cun (n = 2 − 20) clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245402 CrossRef.
- B. Anak, M. Bencharif and F. Rabilloud, Time-dependent density functional study of UV-visible absorption spectra of small noble metal clusters (Cun, Agn, Aun, n = 2-9, 20), RSC Adv., 2014, 4, 13001–13011 RSC.
- J. Tiggesbäumker, L. Köller and K. H. Meiwes-Broer, Bound-free collective electron excitations in negatively charged silver clusters, Chem. Phys. Lett., 1996, 260, 428–432 CrossRef.
- T. Reiners and H. Haberland, Plasmon Enhanced Electron and Atom Emission from a Spherical Sodium Cluster: Na91−, Phys. Rev. Lett., 1996, 77, 2440–2443 CrossRef CAS PubMed.
- K. Raspe, M. Müller, N. Iwe, R. N. Wolf, P. Oelßner and F. Martinez, et al., A versatile setup for studying size and charge-state selected polyanionic nanoparticles, Rev. Sci. Instrum., 2022, 93, 043301 CrossRef CAS PubMed.
- H. Haberland, 1. In: History, Some Basics, and an Outlook, John Wiley & Sons, Ltd, 2017, p. 1–21 Search PubMed.
- F. Martinez, S. Bandelow, C. Breitenfeldt, G. Marx, L. Schweikhard and A. Vass, et al., Upgrades at ClusterTrap and latest results, Int. J. Mass Spectrom., 2014, 365–366, 266–274 CrossRef CAS.
- P. Kruit and F. H. Read, Magnetic field paralleliser for 2π electron-spectrometer and electron-image magnifier, J. Phys. E: Sci. Instrum., 1983, 16, 313 CrossRef CAS.
- N. Iwe, K. Raspe, M. Müller, F. Martinez, L. Schweikhard and K. H. Meiwes-Broer, et al., Size and charge-state dependence of detachment energies of polyanionic silver clusters, J. Chem. Phys., 2021, 155, 164303 CrossRef CAS PubMed.
- O. Kostko, Photoelectron spectroscopy of mass-selected sodium, coinage metal and divalent metal cluster anions. University of Freiburg, 2007 Search PubMed.
- J. Tiggesbäumker, L. Köller, H. O. Lutz and K. H. Meiwes-Broer, Giant resonances in silver-cluster photofragmentation, Chem. Phys. Lett., 1992, 190, 42–47 CrossRef.
- F. Federmann, K. Hoffmann, N. Quaas and J. P. Toennies, Spectroscopy of extremly cold silver clusters in helium droplets, Eur. Phys. J. D, 1999, 9, 11–14 CrossRef CAS.
- T. Diederich, J. Tiggesbäumker and K. H. Meiwes-Broer, Spectroscopy on rare gas-doped silver clusters in helium droplets, J. Chem. Phys., 2002, 116, 3263–3269 CrossRef CAS.
- H. Hövel, S. Fritz, A. Hilger, U. Kreibig and M. Vollmer, Width of cluster plasmon resonances: Bulk dielectric functions and chemical interface damping, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 18178–18188 CrossRef PubMed.
- E. Loginov, L. F. Gomez, N. Chiang, A. Halder, N. Guggemos and V. V. Kresin, et al., Photoabsorption of AgN(N∼ 6 − 6000) Nanoclusters Formed in Helium Droplets: Transition from Compact to Multicenter Aggregation, Phys. Rev. Lett., 2011, 106, 233401 CrossRef PubMed.
- S. Saito, G. F. Bertsch and D. Tománek, Collective electronic excitations in small metal clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 6804–6807 CrossRef PubMed.
- F. Federmann, K. Hoffmann, N. Quaas and J. D. Close, Rydberg states of silver: Excitation dynamics of doped helium droplets, Phys. Rev. Lett., 1999, 83, 2548–2551 CrossRef CAS.
- J. Lehmann, M. Merschdorf, W. Pfeiffer, A. Thon, S. Voll and G. Gerber, Surface Plasmon Dynamics in Silver Nanoparticles Studied by Femtosecond Time-Resolved Photoemission, Phys. Rev. Lett., 2000, 85, 2921–2924 CrossRef CAS PubMed.
- U. Hild, G. Dietrich, S. Krückeberg, M. Lindinger, K. Lützenkirchen and L. Schweikhard, et al., Time-resolved photofragmentation of stored silver clusters Agn+, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 2786–2793 CrossRef CAS.
- K. Hansen, A. Herlert, L. Schweikhard and M. Vogel, Dissociation energies of silver clusters Agn+, n = 14, 15, 16, 18, Int. J. Mass Spectrom., 2003, 227(1), 87–96 CrossRef CAS.
- L. Schweikhard, G. Dietrich, U. Hild, S. Krückeberg, K. Lützenkirchen and C. Walther, Pulsed photodissociation in an ion cyclotron resonance trap: extending the time range for unimolecular dissociation studies of metal clusters, Rapid Commun. Mass Spectrom., 1997, 11, 1624–1626 CrossRef CAS.
- Y. Shi, V. A. Spasov and K. M. Ervin, Competitive fragmentation and electron loss kinetics of photoactivated silver cluster anions: Dissociation energies of Agn− (n = 7-11), J. Chem. Phys., 1999, 111, 938–949 CrossRef CAS.
- R. Kubo, Electronic Properties of Metallic Fine Particles. I, J. Phys. Soc. Jpn., 1962, 17, 975–986 CrossRef CAS.
- G. Mourou, Nobel Lecture: Extreme light physics and application, Rev. Mod. Phys., 2019, 91, 030501 CrossRef CAS.
- D. M. Neumark, Time-resolved photoelectron spectroscopy of molecules and clusters, Annu. Rev. Phys. Chem., 2001, 52, 255–278 CrossRef CAS PubMed.
- J. R. R. Verlet, Femtosecond spectroscopy of cluster anions: insights into condensed-phase phenomena from the gas-phase, Chem. Soc. Rev., 2008, 37, 505–517 RSC.
- B. A. Collings, K. Athanassenas, D. M. Rayner and P. A. Hackett, Optical spectroscopy of Ag7, Ag9+, and Ag9. A test of the photodepletion method, Chem. Phys. Lett., 1994, 227, 490–495 CrossRef CAS.
- A. Terasaki, T. Majima, C. Kasai and T. Kondow, Photon-trap spectroscopy of size-selected free cluster ions: direct measurement of optical absorption of Ag9+, Eur. Phys. J. D, 2009, 52, 43–46 CrossRef CAS.
- T. Lünskens, P. Heister, M. Thämer, C. A. Walenta, A. Kartouzian and U. Heiz, Plasmons in supported size-selected silver nanoclusters, Phys. Chem. Chem. Phys., 2015, 17, 17541–17544 RSC.
- C. Yu, R. Schira, H. Brune, B. von Issendorff, F. Rabilloud and W. Harbich, Optical properties of size selected neutral Ag clusters: electronic shell structures and the surface plasmon resonance, Nanoscale, 2018, 10, 20821–20827 RSC.
- L. Serra and A. Rubio, Optical response of Ag clusters, Z. Phys. D: At., Mol. Clusters, 1997, 40, 262–264 CrossRef CAS.
- V. Kasperovich and V. V. Kresin, Ultraviolet photoabsorption spectra of silver and gold nanoclusters, Philos. Mag. B, 1998, 78, 385–396 CrossRef CAS.
- V. Bonačić-Koutecký, V. Veyret and R. Mitric, Ab initio study of the absorption spectra of AgN (N = 5 − 8) clusters, J. Chem. Phys., 2001, 115, 10450–10460 CrossRef.
- E. Cottancin, G. Celep, J. Lermé, M. Pellarin, J. R. Huntzinger and J. L. Vialle, et al., Optical Properties of Noble Metal Clusters as a Function of the Size: Comparison between Experiments and a Semi-Quantal Theory, Theor. Chem. Acc., 2006, 116, 514–523 Search PubMed.
- K. Baishya, J. C. Idrobo, S. Öğüt, M. Yang, K. Jackson and J. Jellinek, Optical absorption spectra of intermediate-size silver clusters from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075439 CrossRef.
- F. Rabilloud, UV-visible absorption spectra of metallic clusters from TDDFT calculations, Eur. Phys. J. D, 2013, 67, 18 CrossRef.
- M. Kuisma, A. Sakko, T. P. Rossi, A. H. Larsen, J. Enkovaara and L. Lehtovaara, et al., Localized surface plasmon resonance in silver nanoparticles: Atomistic first-principles time-dependent density-functional theory calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 115431 CrossRef.
- J. T. Titantah and M. Karttunen, Ab initio calculations of optical properties of silver clusters: cross-over from molecular to nanoscale behavior, Eur. Phys. J. B, 2016, 89, 125 CrossRef.
- G. U. Kuda-Singappulige and C. M. Aikens, Excited-State Absorption in Silver Nanoclusters, J. Phys. Chem. C, 2021, 125, 24996–25006 CrossRef CAS.
- M. Mucke, M. Förstel, T. Lischke, T. Arion, A. M. Bradshaw and U. Hergenhahn, Performance of a short magnetic bottle electron spectrometer, Rev. Sci. Instrum., 2012, 83, 063106 CrossRef CAS PubMed.
- J. Li, X. Li, H. J. Zhai and L. S. Wang, Au20: A Tetrahedral Cluster, Science, 2003, 299, 864–867 CrossRef CAS PubMed.
- L. Brus, Noble Metal Nanocrystals: Plasmon Electron Transfer Photochemistry and Single-Molecule Raman Spectroscopy, Acc. Chem. Res., 2008, 41, 1742–1749 CrossRef CAS PubMed.
- W. Hou and S. B. Cronin, A Review of Surface Plasmon Resonance-Enhanced Photocatalysis, Adv. Funct. Mater., 2013, 23, 1612–1619 CrossRef CAS.
- S. Pillai and M. A. Green, Plasmonics for photovoltaic applications, Sol. Energy Mater. Sol. Cells, 2010, 94, 1481–1486 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03830g |
| This journal is © the Owner Societies 2023 |