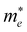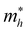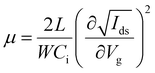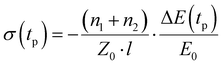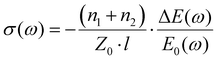Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Grain engineering for improved charge carrier transport in two-dimensional lead-free perovskite field-effect transistors†
Shuanglong
Wang
a,
Sabine
Frisch
b,
Heng
Zhang
a,
Okan
Yildiz
a,
Mukunda
Mandal
a,
Naz
Ugur
a,
Beomjin
Jeong
a,
Charusheela
Ramanan
 ac,
Denis
Andrienko
ac,
Denis
Andrienko
 a,
Hai I.
Wang
a,
Hai I.
Wang
 a,
Mischa
Bonn
a,
Mischa
Bonn
 a,
Paul W. M.
Blom
a,
Paul W. M.
Blom
 a,
Milan
Kivala
a,
Milan
Kivala
 b,
Wojciech
Pisula
b,
Wojciech
Pisula
 *ad and
Tomasz
Marszalek
*ad and
Tomasz
Marszalek
 *ad
*ad
aMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: pisula@mpip-mainz.mpg.de; marszalek@mpip-mainz.mpg.de
bOrganisch-Chemisches Institut, Centre for Advanced Materials, Ruprecht-Karls-Universität Heidelberg, 69120 Heidelberg, Germany
cDepartment of Physics and Astronomy, Faculty of Sciences, Vrije Universiteit Amsterdam, De Boelelaan 1081, 1081 HV Amsterdam, Netherlands
dDepartment of Molecular Physics, Faculty of Chemistry, Lodz University of Technology, Zeromskiego 116, 90-924 Lodz, Poland
First published on 9th August 2022
Abstract
Controlling crystal growth and reducing the number of grain boundaries are crucial to maximize the charge carrier transport in organic–inorganic perovskite field-effect transistors (FETs). Herein, the crystallization and growth kinetics of a Sn(II)-based 2D perovskite, using 2-thiopheneethylammonium (TEA) as the organic cation spacer, were effectively regulated by the hot-casting method. With increasing crystalline grain size, the local charge carrier mobility is found to increase moderately from 13 cm2 V−1 s−1 to 16 cm2 V−1 s−1, as inferred from terahertz (THz) spectroscopy. In contrast, the FET operation parameters, including mobility, threshold voltage, hysteresis, and subthreshold swing, improve substantially with larger grain size. The optimized 2D (TEA)2SnI4 transistor exhibits hole mobility of up to 0.34 cm2 V−1 s−1 at 295 K and a higher value of 1.8 cm2 V−1 s−1 at 100 K. Our work provides an important insight into the grain engineering of 2D perovskites for high-performance FETs.
New conceptsOne of the main obstacles in achieving a reliable operation of perovskite transistors at room temperature is severe ion migration, which can screen the applied gate field, resulting in poor field-effect behavior and large dual-sweeping hysteresis. Grain engineering controlled by film deposition parameters is one of the new approaches to improve charge carrier transport and understand the relation between crystallization and ion migration. Such processing conditions, like substrate temperature, are usually not considered as a powerful tool to control surface morphology and microstructure. In this work, the hot-casting method is used for an effective modulation of grain size and grain boundary number, in order to improve in-plane charge carrier transport in a perovskite film. Additionally, a close correlation between the density of the grain boundaries, charge carrier transport, and ion migration is established. We believe that the grain engineering proposed herein is a major breakthrough for developing operationally stable room-temperature perovskite transistors. |
Introduction
Over the past decade, organic–inorganic hybrid metal halide perovskites have emerged as an exciting new class of semiconducting materials.1,2 Their simple low-temperature solution processing, combined with unique photophysical properties such as tunable bandgap, high optical absorption coefficient, large charge carrier diffusion length and superior photoluminescence quantum yield, has led to a wide range of optoelectronic applications, including solar cells, light-emitting diodes, lasers and photodetectors.3–6 Perovskite semiconductors have also been employed in thin-film field-effect transistors (FETs), which provide an ideal and versatile platform to study their electronic properties. Despite the relatively high intrinsic charge carrier mobility of these semiconductors, the fabrication of reliable perovskite FETs with high performance at room temperature (RT) has remained an enormous challenge.7–10One of the fundamental obstacles is the ion migration in perovskite thin-film FETs under bias, which can partially or even completely screen the applied gate electric field.11 Consequently, charge carrier transport over long macroscopic distances is obstructed, resulting in low RT field-effect mobilities. Furthermore, the ion migration causes significant hysteresis of polycrystalline FETs due to the non-stoichiometric ratio in the precursor solution, as well as grain boundaries and other structural defects in the formed film.12 Two-dimensional (2D) hybrid perovskite semiconductors displayed natural advantages in suppressing ion movement in the FET devices due to the quantum and dielectric confinement effects.13 Kagan and co-workers were the first to report 2D perovskite FETs based on a (C6H5C2H4NH3)2SnI4 ((PEA)2SnI4) semiconducting layer operating at RT.14 Sn is a promising substitute for Pb due to it's non-toxic nature and smaller atomic mass, which could produce higher charge mobility in perovskite thin films due to less Fröhlich interaction.15 Qin et al. investigated the charge transport properties in PEA-based 2D layered Sn–Pb perovskite films and the results showed that there is no field-effect mobility for (PEA)2PbI4 perovskite FET at RT.16 So far, many strategies have been proposed to enhance the device performance including controlling the crystallization process, regulating the film microstructure and adjusting the phase orientation. These approaches involve self-assembled monolayers, non-stoichiometry engineering, mixed solvents, and additives and result additionally in the reduction of ion migration.17,18 FETs may also benefit from the perovskite layers parallelly oriented to the substrate, which should substantively reduce charge-transport resistance in the in-plane direction and dramatically improve the device performance.19 However, a simple, robust and general approach to effectively control the crystal orientation in layered 2D perovskites for FET applications is still lacking. Increasing grain size is another important strategy to improve the device performance. The growth of large grains decreases charge transport barriers and structural defects that increase the efficiency of perovskite solar cells have been reported.20 Very recently, high mobility 2D tin-based perovskite FETs were realized by employing π-conjugated bulky cations and optimized annealing temperatures to reach large grain sizes up to 500 μm.21 However, the complicated synthesis of large cations might impede their potential application. For this reason, small and simple cations bear high potential for 2D perovskite FETs.
The precursor compounds and solution deposition have a strong impact on the charge carrier properties of perovskites. Thiophene derivatives have been widely used as organic semiconductors as well as spacers and passivators in perovskite electronics, resulting in high device performances.22,23 Chiu et al. performed theoretical simulations and found the reduced dielectric constant of TEA compared to benchmark organic cation PEA in 2D tin perovskite, leading to narrower band gaps and improved dielectric confinement, making TEA suitable for efficient optoelectronic device applications.24 This gives us the motivation to select the TEA organic spacer for the studies on the correlation between grain size and FET performance. Here, rational grain engineering by the hot-casting method is applied for Sn(II)-based 2D perovskite thin films to drastically reduce the ion migration that limits the device performance of FETs. We show that hot-casting is an efficient approach to precisely control the crystallization and growth kinetics of 2-thiopheneethylammonium tin iodide ((TEA)2SnI4) enabling large grain sizes. While the local charge carrier mobility improves moderately with larger grain size, the performance of the perovskite FETs is increased considerably due to a reduced density of grain boundaries that lower the charge trapping and ion migration. The insights into the role of grain boundaries in charge carrier transport and ion migration of (TEA)2SnI4 are important for the development of high-performance 2D perovskite-based FET devices.
Results and discussion
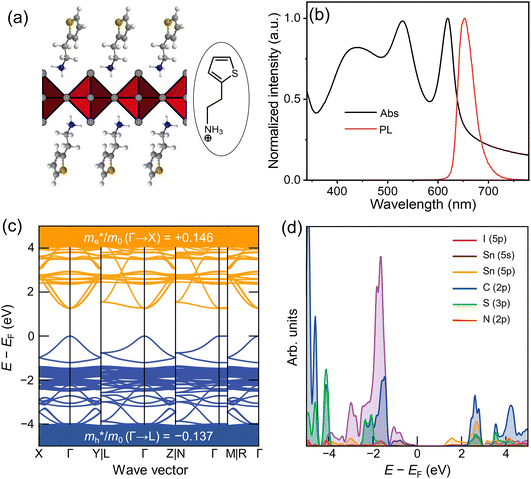
Fig. 1(a) shows the chemical structure of the organic spacer TEA (synthesis details are presented in the Experimental section). The optical properties of (TEA)2SnI4 thin films with traditional spin-coating at RT were investigated by UV-vis absorption and steady-state photoluminescence measurements as shown in Fig. 1(b), which confirm the formation of the target perovskite structure.25 The absorption peak located at 440 nm (corresponding to 2.82 eV) is attributed to the high-energy exciton transition energy levels. The absorption peak located at 529 nm (2.34 eV) is assigned to the charge transfer from TEA+ organic cations to adjacent [SnI4]2− octahedron layers, whereas the sharp absorption centered at 619 nm (2.00 eV) is attributed to the intrinsic exciton absorption of the tin iodide lattice.26 The (TEA)2SnI4 exhibits strong photoluminescence at room temperature with the corresponding PL peak located at 649 nm (1.91 eV).Density functional theory (DFT) calculations were carried out to decipher the effect of incorporating the thiophene-based TEA ligand as the organic spacer within the octahedral [SnI6]4− sheets on the overall electronic properties of the 2D-perovskite semiconductor. The calculated lattice parameters for (TEA)2SnI4 reveal a distance of 31.5 Å for adjacent double interlayers along the c-axis direction, as shown in Fig. S1 (ESI†). The band structure of (TEA)2SnI4 (Fig. 1(c)) suggests a direct bandgap of 1.25 eV at PBE at the Γ-point. The density of states plot in Fig. 1(d) indicates that both the valence band maximum (VBM) at 1.80 eV and the conduction band minimum (CBM) at 3.05 eV are mainly located at the inorganic layers. Specifically, the Sn 5s and I 5p orbitals contribute to the VBM, while the CBM is primarily composed of the Sn 5p orbital. The effective masses of electron (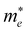 ) and hole (
) and hole (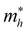 ), in units of the rest mass of the free electron (m0), were also calculated from the band structure in Fig. 1(c) using parabolic fitting of the band edges. Based on the DFT calculations, the computed
), in units of the rest mass of the free electron (m0), were also calculated from the band structure in Fig. 1(c) using parabolic fitting of the band edges. Based on the DFT calculations, the computed 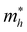 and
and 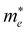 value of 0.137 m0 and 0.146 m0 (with m0 as the electron rest mass) was used for the calculation of the hole mobility in the subsequent THz analysis.27
value of 0.137 m0 and 0.146 m0 (with m0 as the electron rest mass) was used for the calculation of the hole mobility in the subsequent THz analysis.27
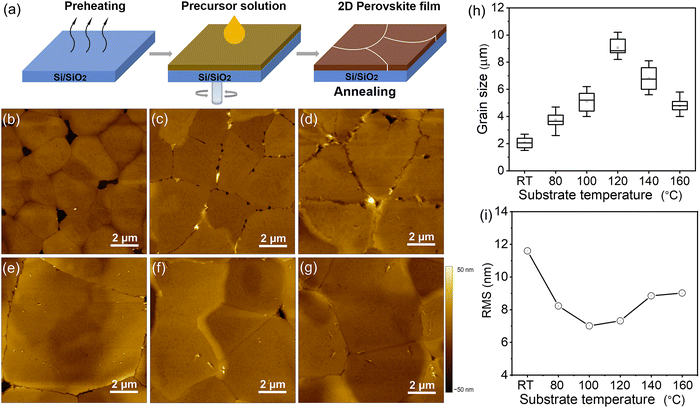
Previously, we have developed several methods to precisely control the grain size and optimize the charge carrier transport in organic semiconductors.28–30 Similar to organic semiconductors, the thin-film morphology is a critical factor for efficient and stable charge transport in perovskite FETs.31 To correlate the morphology formation and crystallization kinetics of (TEA)2SnI4 with the behavior of FETs, hot-casting was applied to tune the grain size of the thin films. Fig. 2(a) schematically describes the hot-casting process for deposition of (TEA)2SnI4 thin films. In contrast to the procedure reported in the literature, the approach involves spin-coating a mixture of organic cation TEA and tin iodide (SnI2) solution onto a hot substrate maintained at a temperature range from RT to 160 °C to obtain a uniform film. This process was modified to the reported method to ensure continuity (pinhole-free structure) and homogeneity of the obtained film and to control the lateral grain size and film roughness, which finally determine the charge carrier transport in (TEA)2SnI4 FETs. Atomic force microscopy (AFM) was used to evaluate the role of substrate temperature on the (TEA)2SnI4 film morphology deposited on the Si/SiO2 substrate. Fig. 2(b)–(g) illustrates grain structures obtained at different substrate temperatures from RT to 160 °C. As evident from the AFM image, (TEA)2SnI4 deposited at RT creates 2 μm small grains surrounded by pinholes. The grain size is substantially enlarged when the substrate temperature is increased to 120 °C resulting in a more compact and uniform surface morphology. Additional AFM images with a larger scan size of 50 × 50 μm further confirm the lower density of pinholes in the optimized films compared to conventional RT cast films, as shown in Fig. S2 (ESI†). Histograms of the grain size distribution in Fig. 2(h) reveal that with increasing temperature from RT to 120 °C the grain size increases from 2 μm to 9 μm, while further T rise leads to its reduction. Optical microscopy images further confirm larger grains in the hot casted films compared to RT cast ones (Fig. S3, ESI†). Therefore, the optimal growth conditions for large grains at 120 °C can be attributed to a low number of nucleation sites allowing a prolonged growth of the (TEA)2SnI4 crystals. As the substrate temperature further increases, a larger number of nuclei precipitate from the supersaturation solution due to the fast solvent vaporization, yielding smaller crystal grains.32 Increasing the grain size is of great importance for perovskite FETs because the grain boundaries act as trap centers for charge carriers and pathways for ion migration, which is one of the key reasons for the limited device performance of perovskites.33 In that case, the presence of grain boundaries generates a potential barrier for carrier transport across the active channel of the FET. Large grains together with a low density of boundaries minimize the concentration of mobile ions leading to efficient charge carrier transport and stable device performance. In addition, the film root mean square roughness (RMS) is reduced when hot-casting is applied (Fig. 2(i)). The (TEA)2SnI4 films processed at 100 °C and 120 °C show the smoothest film surface with low RMS values of 7.04 and 7.26 nm. The flattened surface is beneficial to reduce the roughness-induced charge scattering effects and to improve the effective contact between the perovskite semiconducting film and electrodes.34
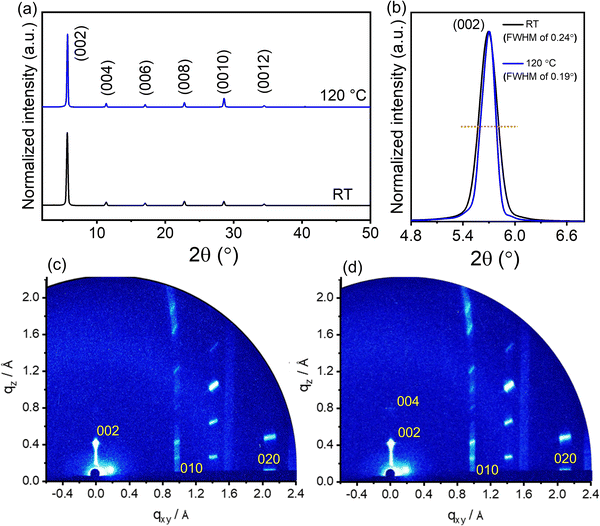
The role of deposition temperature on the crystal structure of the 2D (TEA)2SnI4 thin films was further investigated by X-ray diffraction (XRD) and grazing incidence wide-angle X-ray scattering (GIWAXS). The XRD patterns of the two films cast at RT and 120 °C in Fig. 3(a) exhibit typical (00l) diffractions (l = 2, 4, 6, 8, 10, and 12), confirming a layered and well-ordered structure of the (TEA)2SnI4 films. The interlayer spacing of 15.6 Å is consistent with the DFT calculations in Fig. S1 (ESI†). The diffraction peak intensity is only slightly higher for the optimized film processed at 120 °C compared to the RT deposited one. The full width at half-maximum (FWHM) of the (002) diffraction peak slightly differs and decreases from 0.24° for RT to 0.19° for the substrate temperature of 120 °C (Fig. 3(b)). The slightly changed diffraction intensity and FWHM value indicate a similar out-of-plane crystallinity for the (TEA)2SnI4 films cast at RT and 120 °C. For films cast at 140 °C, additional peaks appear in the XRD spectra, as shown in Fig. S4 (ESI†), that are assigned to SnI2. This suggests that the film fabricated at temperatures beyond 140 °C does not fully convert from the source compounds to the complete semiconducting perovskite phase, which is also detrimental to the crystallinity and device operation. Fig. S5 (ESI†) shows the PL spectra of the (TEA)2SnI4 films prepared at RT and 120 °C. The PL intensity of the hot cast film is higher in comparison to the RT cast one indicating slightly reduced trap states in the optimized hot-casting film.29Fig. 3(c) and (d) show the GIWAXS patterns of the thin films processed at RT and 120 °C. The diffraction peak with the highest intensity is assigned to the interlayer spacing (002). The in-plane (010) and (020) reflections are attributed to Sn–I and I–Sn–I bonds with corresponding d-spacings of 2.9 Å and 5.8 Å (Fig. S6, ESI†), in agreement with the literature.35 The crystal lattice parameters are summarized in Table S1 (ESI†). The octahedral structure of the [SnI4]2− sheet exhibits the 120 peak (4.1 Å) for I–I bonds, as shown in Fig. S6b and c (ESI†). The inorganic part [SnI4]2− is organized parallel to the substrate surface, which is beneficial for the in-plane charge transport of FETs. To understand the influence of the substrate temperature on the crystallite size, the coherence length (CL) is calculated for the (010) and (020) reflections. Interestingly, the films processed at RT and 120 °C reveal identical CL010 and CL020 values of ∼132 nm and ∼19 nm, respectively. Despite a significant difference in grain size (Fig. 1(c)–(h)), surprisingly, the substrate temperature does not significantly affect the crystal lattice parameters and crystallinity.
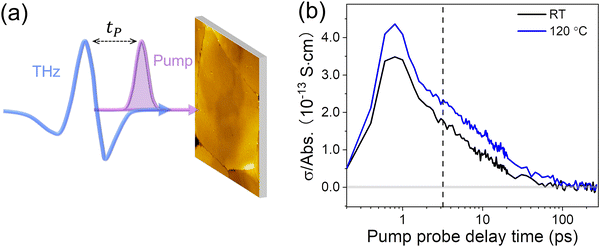
To investigate how deposition temperature and thus film morphology affect the local charge carrier transport in (TEA)2SnI4 perovskites, we conducted contact-free, optical pump-Terahertz (THz) probe (OPTP) spectroscopy. Unlike the FET devices, where the charge carriers are transported over the macroscopic dimension of the transistor channel, the mobility inferred from THz spectroscopy represents an intrinsic, local (∼10 nm) value due to the ultrafast oscillating nature of the THz electric field (∼1 ps).36 The local probe length is substantially smaller than the grain sizes of our samples. In a typical OPTP measurement, as schematically shown in Fig. 4(a), a 400 nm pulse with a duration of ∼50 femtoseconds (fs) is employed to excite charge carriers from the valence to the conduction band. The photoconductivity σ dynamics is then probed by a ∼picoseconds (ps) THz pulse by controlling pump–probe delay time tP. At a given pump–probe delay, σ is directly proportional to the pump-induced THz absorption ΔE by σ ∝ −ΔE/E0. Fig. 4(b) compares the photoconductivity dynamics for films deposited at RT and 120 °C. The fast 1 ps rise corresponds to the generation of free carriers in the film, followed by decay with a lifetime in the range of 10's of ps. Given the time scale, we tentatively attribute the decay dynamics to charge trapping at defects. In principle, the photoconductivity of free carriers σ is defined by σ = neμ = (Nabsφ) eμ, with n the carrier density, μ the charge carrier mobility, Nabs the absorbed photon density, φ the photon-to-charge conversion efficiency, and e the elementary charge. For a better comparison, we divide the photoconductivity by the absorbed photon density Nabs. By assuming the same photon-to-charge conversion efficiency φ, such a normalization provides a direct comparison of the conductivity per charge carrier, i.e., the mobility of the samples under different treatments (σ/Nabs ∝ μ). As shown in Fig. 4(b), we observe ∼25% higher charge carrier mobility for (TEA)2SnI4 films cast at 120 °C in comparison to that deposited at RT. The estimated charge carrier mobility at the peak of the photoconductivity is ∼13 and ∼16 cm2 V−1 s−1 for samples prepared at RT and 120 °C, respectively, by assuming 100% photon-to-charge conversion efficiency (i.e., Nabs = n, or φ = 100%). It should be noted that the estimated mobility represents the lower boundary of charge carrier mobility, as in reality φ ≤ 100%. Further analysis on the frequency-resolved photoconductivity based on the Drude–Smith model seems to point out the critical role of charge scattering time in determining the carrier mobilities in (TEA)2SnI4 films (see details in Fig. S7, ESI†). As such, we conclude that the hot casted film lowers the density of the charge scattering centers, very likely due to the slightly improved crystallinity as observed by GIWAXS. It should also be noted that the improvement of the local charge carrier mobility remains in a moderate range as the grain size is sufficiently large to play a minor role in dictating the local carrier mobility by THz spectroscopy.
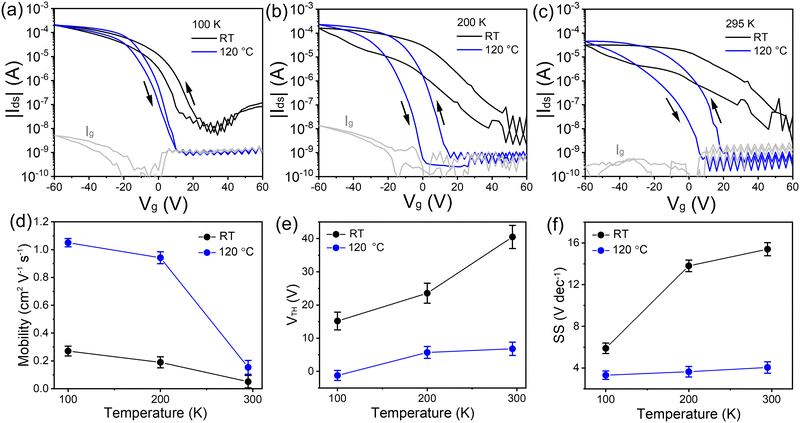
To further understand the role of grain size and crystallinity on the macroscopic charge carrier transport in FETs, the (TEA)2SnI4 perovskite films processed at different temperatures were integrated in bottom-gate top-contact devices. Ultraviolet photoemission spectroscopy (UPS) was performed to analyze the electronic structure of (TEA)2SnI4, as shown in Fig. S8 (ESI†). The valence-band maximum (VBM) and conduction-band minimum (CBM) are determined to be 5.27 and 3.37 eV, respectively. The energy alignment of the (TEA)2SnI4 film at the Au/perovskite interface ensures an efficient hole injection into the active layer.37 The hole transfer characteristics in Fig. 5(a)–(c) were recorded at Vds = −60 V with Vg scanning from +60 V to −60 V for (TEA)2SnI4 FETs fabricated at RT and 120 °C. The corresponding output curves of the FETs are shown in Fig. S9 (ESI†). The device characteristics were measured at three typical temperatures of 100 K, 200 K, and 295 K. FETs cast at RT show weak p-type field modulated conduction and a high OFF current, especially at 295 K. The threshold voltage (VTH) of 40 V is determined in the linear region and forward direction of the transfer curves. The hole mobility (μh) of 0.04 cm2 V−1 s−1 at 295 K is extracted from the linear region of the square root of the transfer curve (forward sweep). In contrast, an overall improved device operation is observed for the 120 °C hot-cast (TEA)2SnI4 FETs. We defined ΔVhys to analyse the degree of the hysteresis in the transfer characteristics for |Ids| = 1 μA under both sweeping directions. FETs hot-cast at 120 °C show ΔVhys of 21 V at RT, which is smaller than 30 V of the RT processed device. The reduced hysteresis is related to the suppressed ion movement as a consequence of lower density of grain boundaries and reduced traps at the perovskite/dielectric interface. Furthermore, a significantly reduced OFF current, enhanced ON–OFF current ratio (Ion/off) over 104 and improved gate modulation are observed for the hot-cast FETs. The optimized devices reveal higher ON current, which again confirms that the larger grain size dominantly facilitates the charge transport in the FET channel. It is worth noting that the optimized device showed significantly decreased OFF current, which originates from the leakage current Ig of the device leading to poor modulation of the gate voltage.38 The corresponding Ig of the RT- and hot-cast transistors operated at 295 K are shown in Fig. S10 (ESI†). The Ig of the optimized hot-cast FET is reduced more than one order of magnitude compared to the RT-cast device leading to a higher Ion/off of the hot-cast FETs. The hole mobility μh in the optimized FET at 295 K increases almost 4-fold to 0.15 cm2 V−1 s−1 accompanied by a notably decreased VTH of 6.6 V and smaller subthreshold swing (SS) of 4.05 V dec−1. We further calculated the interface trap density (Nt) at the dielectric/perovskite interface from SS using the following equation39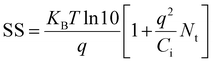 , with Ci the areal capacitance of the dielectric layer; q the elementary charge; KB the Boltzmann constant; and T the absolute temperature. Accordingly, the Nt of RT prepared FETs was calculated to be 1.88 × 1013 cm−2 eV−1, which was notably reduced to ∼4.8 × 1012 cm−2 eV−1 for the 120 °C cast FETs. These results suggest that the hot-cast strategy improves the film quality at the perovskite/dielectric interface such as order and morphology, contributing to the lower SS value and reduced interface trap density.40 The reduced defects are further evidenced by transient absorption spectroscopy measurement (see more details in Fig. S11, ESI†). However, the experimentally determined charge mobility is under these conditions much lower than that extracted from the THz measurements. The large difference implies a critical role of grain boundaries and ion migration on charge carrier transport in FETs.20 In general, ion migration can be significantly suppressed by lowering the temperature leading to smaller hysteresis of the transfer curves, as illustrated also in this case in Fig. 5(b) and (c). The better device performance with smaller dual-sweep hysteresis is obtained at lower temperature for both (TEA)2SnI4 films. Specifically, at 100 K, FETs cast at both temperatures, RT and 120 °C, reveal enhanced mobilities of 0.27 cm2 V−1 s−1 and 1.05 cm2 V−1 s−1, respectively, with the hot-cast FET mobility is only an order of magnitude lower than the local mobility measured using the THz setup. The reason for the poor mobility of the RT cast (TEA)2SnI4 perovskite FETs can therefore be attributed to the large number of grain boundaries and low quality of the perovskite/dielectric interface. As mentioned before, the ion migration is induced by tin vacancies due to oxidation of Sn2+, which can be preferentially moved at grain boundaries.41 Considering the varied density of grain boundaries in the (TEA)2SnI4 films cast at different temperatures and the above analysis, two primary mechanisms take place in the FET devices. At low operation temperature, at which ion migration is suppressed to a great extent, the grain boundaries act mainly as trap centers for the charge carriers. This is the primary reason for the better hot-casting FET performance. As the operating temperature increases, grain boundaries facilitate ion drift, screening of the gate potential, and finally hindering of the gate modulation of the electronic current. Therefore, for FETs with large grain sizes, Vth shifts only slightly to higher voltages with higher temperatures, while for the devices with small grains, this shift is much more pronounced.42
, with Ci the areal capacitance of the dielectric layer; q the elementary charge; KB the Boltzmann constant; and T the absolute temperature. Accordingly, the Nt of RT prepared FETs was calculated to be 1.88 × 1013 cm−2 eV−1, which was notably reduced to ∼4.8 × 1012 cm−2 eV−1 for the 120 °C cast FETs. These results suggest that the hot-cast strategy improves the film quality at the perovskite/dielectric interface such as order and morphology, contributing to the lower SS value and reduced interface trap density.40 The reduced defects are further evidenced by transient absorption spectroscopy measurement (see more details in Fig. S11, ESI†). However, the experimentally determined charge mobility is under these conditions much lower than that extracted from the THz measurements. The large difference implies a critical role of grain boundaries and ion migration on charge carrier transport in FETs.20 In general, ion migration can be significantly suppressed by lowering the temperature leading to smaller hysteresis of the transfer curves, as illustrated also in this case in Fig. 5(b) and (c). The better device performance with smaller dual-sweep hysteresis is obtained at lower temperature for both (TEA)2SnI4 films. Specifically, at 100 K, FETs cast at both temperatures, RT and 120 °C, reveal enhanced mobilities of 0.27 cm2 V−1 s−1 and 1.05 cm2 V−1 s−1, respectively, with the hot-cast FET mobility is only an order of magnitude lower than the local mobility measured using the THz setup. The reason for the poor mobility of the RT cast (TEA)2SnI4 perovskite FETs can therefore be attributed to the large number of grain boundaries and low quality of the perovskite/dielectric interface. As mentioned before, the ion migration is induced by tin vacancies due to oxidation of Sn2+, which can be preferentially moved at grain boundaries.41 Considering the varied density of grain boundaries in the (TEA)2SnI4 films cast at different temperatures and the above analysis, two primary mechanisms take place in the FET devices. At low operation temperature, at which ion migration is suppressed to a great extent, the grain boundaries act mainly as trap centers for the charge carriers. This is the primary reason for the better hot-casting FET performance. As the operating temperature increases, grain boundaries facilitate ion drift, screening of the gate potential, and finally hindering of the gate modulation of the electronic current. Therefore, for FETs with large grain sizes, Vth shifts only slightly to higher voltages with higher temperatures, while for the devices with small grains, this shift is much more pronounced.42
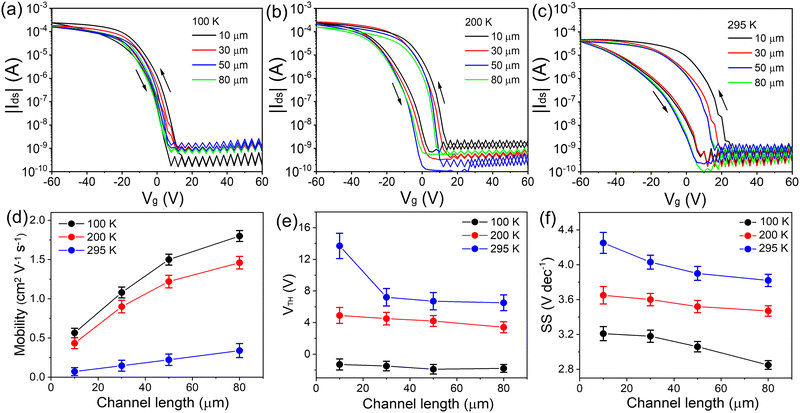
Notably, the device performance of the hot-cast films is further improved by using longer channel lengths. Fig. 6 shows the device performance of 120 °C hot-cast (TEA)2SnI4 FETs for various channel lengths (10, 30, 50 and 80 μm). The corresponding output curves are shown in Fig. S12 (ESI†). Upon the increase of the channel length, the operational parameters of the FETs are improved at both room and low temperature. When the channel length is enlarged from 10 μm to 80 μm for devices measured at 295 K, the charge carrier mobility increases from 0.08 cm2 V−1 s−1 to 0.34 cm2 V−1 s−1, and at the same time a reduction of VTH from 14 V to 7 V and of SS from 4.3 V dec−1 to 3.7 V dec−1 is obtained. On the other hand, Ion/off is almost independent of channel length. A similar enhancement in charge carrier mobility, as well as VTH and SS values is observed at 100 K. The maximum mobility of 1.8 cm2 V−1 s−1 is achieved for the device at 100 K with the channel length of 80 μm. The higher device performance is ascribed to the reduced contribution of the contact resistance (Rc) relative to the total resistance.43 The plot of R·W as a function of channel length is presented in Fig. S13 (ESI†). The normalized Rc·W of 1.53 × 104 Ω·cm was obtained for the 120 °C hot-cast (TEA)2SnI4 FET at 295 K by using the transmission-line method.39 To better understand the correlation between the channel length and ion movement, we utilized impedance spectroscopy to explore the processes in transistors with various channel lengths at 295 K. Fig. S14 (ESI†) compares the real parts of the dielectric constant for (TEA)2SnI4 FETs with different channel lengths as a function of frequency. The dielectric constant for the transistor with the channel length of 80 μm slightly increases at low-frequency. The devices with shorter channels show a significantly higher dielectric response in the low-frequency region in comparison to devices with larger channel lengths because of the accumulation of mobile ions at the electrodes. Such electrode polarization is in fact typical for perovskite-based devices and can significantly influence the spatial distribution and response behavior of the charge carriers within the active perovskite film.44 When the positive ions accumulate at the negatively charged electrode interface, charge carrier extraction is blocked by the accumulated ions. Meanwhile, an ion-induced electric field is formed with the direction opposite to the external electric field, which impedes charge carrier transport.45 As the channel length increases, the polarization effect has a lower impact on the total channel resistance resulting in high performance of the devices, which is consistent with the observed reduction in hysteresis for longer channel lengths.
Conclusion
We studied the device behavior of 2D lead-free perovskite FETs based on (TEA)2SnI4 thin films. The hot-casting strategy was employed to control the growth kinetics and morphology of the perovskite film to enhance the charge carrier transport and mitigate ion migration in the FET devices. An optimized substrate temperature was identified for the growth of large grains. Since film crystallinity remains identical for all deposition temperatures, only a moderate increase in the local charge carrier mobility of 16 cm2 V−1 s−1 at room temperature, is observed, as confirmed by THz spectroscopy. On the other hand, the device parameters such as mobility, threshold voltage, subthreshold swing and hysteresis significantly improve in devices with larger grains, as well as in devices with an increased channel length or/and low operation temperature. The reduced grain boundaries enabled drastic mitigation of the ion migration and the corresponding screening effects of the effective applied electric field in the device. Devices with maximum hole mobility of 0.34 cm2 V−1 s−1 at 295 K and 1.8 cm2 V−1 s−1 at 100 K are obtained. Our results highlight the importance of suppressing mobile ions by reducing grain boundaries and trap densities by controlling the film morphology to ensure high performance perovskite FETs.Experimental section
Materials synthesis
All chemical reagents and solvents were used without further purification. Tin(II) iodide (SnI2, 99.999%), N,N-dimethylformamide (DMF, anhydrous, 99.8%), and dimethyl sulfoxide (DMSO, anhydrous, ≥99.9%) were purchased from Sigma-Aldrich. Silicon wafers were ordered from Ossila. The synthesis of TEAI follows a variation of published methods.46 2-(Thiophen-2-yl)ethan-1-amine (1.00 g, 7.86 mmol) was dissolved in 160 mL MeOH. The solution was cooled to 0 °C and aqueous HI solution (57%, 2.00 g, 15.7 mmol) was added dropwise. After 3 h of stirring at RT, the reaction was stopped and the solvents were removed under reduced pressure. The crude product was washed several times with Et2O. The desired compound was obtained as a colorless solid (2.00 g, 7.86 mmol) (Fig. S15 and S16, ESI†). 1H NMR (300 MHz, (CD3)2SO, rt) δ 7.76 (br s, 3H), 7.42 (dd, J = 5.0, 1.4 Hz, 1H), 7.03–6.96 (m, 2H), 3.07 (s, 4H) ppm. 13C NMR (76 MHz, (CD3)2SO, rt): δ 138.9, 127.3, 126.0, 124.8, 27.2 ppm. Elemental analysis (%) calcd. for C6H10INS: C 28.25, H 3.95, N 5.49; found C 28.29, H 3.99, N 5.72.2D perovskite thin film preparation
The 2D perovskite (TEA)2SnI4 precursor solution with the concentration of 0.1 M was prepared in a stoichiometric ratio of TEAI and SnI2 (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) by dissolving TEAI and SnI2 in mixed DMF/DMSO solvent (1
1) by dissolving TEAI and SnI2 in mixed DMF/DMSO solvent (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The solution was stirred overnight at 60 °C in a glove box and cooled to room temperature before use. The as-prepared fresh precursor solution was spin-coated with a 0.2 μm PTFE filter at 4000 rpm for 60 s and annealed at 100 °C for 10 min. For the detailed hot-casting process, the substrate is heated to a certain temperature (from 80 °C to 160 °C) on a hot plate. During spin-coating, we transfer the hot substrate to the spin coater chuck and start the spin coating process. After that, the solution is immediately drop cast onto the substrate. The films were then annealed at 100 °C for 10 min.
1). The solution was stirred overnight at 60 °C in a glove box and cooled to room temperature before use. The as-prepared fresh precursor solution was spin-coated with a 0.2 μm PTFE filter at 4000 rpm for 60 s and annealed at 100 °C for 10 min. For the detailed hot-casting process, the substrate is heated to a certain temperature (from 80 °C to 160 °C) on a hot plate. During spin-coating, we transfer the hot substrate to the spin coater chuck and start the spin coating process. After that, the solution is immediately drop cast onto the substrate. The films were then annealed at 100 °C for 10 min.
Device fabrication and measurement
The bottom-gate top-contact configuration was employed for the FET devices. The heavily p-doped bare Si/SiO2 wafers (1.5 × 2 cm) were used as the substrates and cleaned in an ultrasonic bath with deionized water, acetone, and isopropyl alcohol and then blown dry with N2. The substrates were treated with oxygen plasma for 3 min and then transferred into a glove box for the perovskite film deposition. This was followed by the deposition of the 2D perovskite semiconductor layer as described above. The SiO2 layer was adopted as a dielectric layer. Finally, the source and drain electrodes were deposited with the thickness of 50 nm by gold thermal evaporation through a shadow mask (from Ossila) to construct L × 1000 μm (length × width) transistor channels with various L values (10, 30, 50, and 80 μm). The device characterization was performed using a semiconductor parameter analyzer (Keithley 4200-SCS) in a low-temperature probe station. The transfer characteristics were collected in pulse mode, and the output characteristics were measured in continuous mode. In the pulse mode, Vg was applied over a short impulse of 1 s. The temperature-dependent measurements were performed using a Desert Cryogenics low-temperature probe station. Mobility values of FETs are extracted with the following equation:where L, W, and Ci are the channel length and width and the unit capacitance of the oxide dielectric, respectively.
Characterization
The NMR spectra were recorded with a Bruker Avance 300 NMR spectrometer (Bruker, 300 MHz for 1H and 76 MHz for 13C) at room temperature. Chemical shifts (δ) are reported in parts per million (ppm) and are referenced to the residual solvent signal as an internal reference ((CD3)2SO: 2.50 ppm for 1H, 39.5 ppm for 13C). Coupling constants (J) are given in Hz and the apparent resonance multiplicity is reported as s (singlet), br s (broad singlet), dd (doublet of doublets), or m (multiplet). Elemental analysis was carried out on a Vario MICRO cube (Elementar). The thin film morphology was characterized by a Leica POM and a Bruker Dimension Icon FS AFM in tapping mode at room temperature The grain size statistics are determined by Gwyddion software for 15 grains in different areas for the perovskite thin film with each hot-casting temperature. GIWAXS measurements were performed by means of a solid anode X-ray tube (Siemens Kristalloflex X-ray source, copper anode X-ray tube operated at 35 kV and 20 mA), Osmic confocal MaxFlux optics, X-ray beam with pinhole collimation, and a MAR345 image plate detector. The coherence length (CL) is calculated for reflection peaks with the Scherrer equation. The film XRD patterns were recorded using a Rigaku D/MAX 2600 V with Cu Kα (λ = 1.5406 Å) radiation. The interlayer distance was calculated by Bragg's law: 2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = nλ, where θ = 5.66° and n = 2, respectively. Thin film absorption spectra were recorded on an Agilent UV-Vis-NIR Cary-5000 spectrometer in transmission mode. The PL spectra were recorded with a HORIBA Jobin-Yvon Fluorolog 3-22 Tau-3 using a photomultiplier tube (PMT) as the detector and FluorEssence (version 3.9.0.1; Origin version 8.6001) software. Photoluminescence quantum yield was measured using the aforementioned Fluorolog-3 with an integrating sphere (F-3018 from Horiba Jobin Yvon) under nitrogen flow to avoid the degradation of perovskite samples. For UPS characterization, to avoid any charging during the measurement, Si wafers were coated with Cr/Au (2 nm/80 nm) as a conductive layer by thermal evaporation. Then, samples were transferred into the UPS chamber and measurements were carried out at a base pressure of 10−9 mbar. UPS measurements were conducted with a Kratos Axis UltraDLD spectrometer (Kratos, Manchester, England). Illumination at 21.22 eV was provided by the He(I) emission line from a helium discharge lamp. Photoelectron emission was collected at 0° from the surface normal of the samples. The spectra were taken at three different spots to confirm that the spectra are reproducible and the irradiation exposure time was kept under one minute. Transient absorption spectroscopy was measured using a Helios-Fire pump–probe setup (Ultrafast Systems). This is paired with a regeneratively amplified 1030 nm laser (Light Conversion Pharos, 200 fs, 200 uJ), set at an effective repetition rate of 1 kHz via an internal pulse picker. A small portion (20%) of the 1030 nm fundamental is directed to an optical delay line, and, subsequently, to a sapphire crystal to generate the broadband probe light. The remaining 80% of the 1030 nm fundamental is directed to an optical parametric amplifier (Light Conversion, Orpheus-F) to generate the pump pulse at 529 nm. Global analysis of TA data was done using the R-package TIMP software,47 with the graphical interface Glotaran 1.5.1.48 Impedance measurements were performed with the FET configuration by connecting the source and drain electrodes using a computer-controlled Solartron impedance analyzer under ac voltage of 100 mV in a vacuum chamber.
θ = nλ, where θ = 5.66° and n = 2, respectively. Thin film absorption spectra were recorded on an Agilent UV-Vis-NIR Cary-5000 spectrometer in transmission mode. The PL spectra were recorded with a HORIBA Jobin-Yvon Fluorolog 3-22 Tau-3 using a photomultiplier tube (PMT) as the detector and FluorEssence (version 3.9.0.1; Origin version 8.6001) software. Photoluminescence quantum yield was measured using the aforementioned Fluorolog-3 with an integrating sphere (F-3018 from Horiba Jobin Yvon) under nitrogen flow to avoid the degradation of perovskite samples. For UPS characterization, to avoid any charging during the measurement, Si wafers were coated with Cr/Au (2 nm/80 nm) as a conductive layer by thermal evaporation. Then, samples were transferred into the UPS chamber and measurements were carried out at a base pressure of 10−9 mbar. UPS measurements were conducted with a Kratos Axis UltraDLD spectrometer (Kratos, Manchester, England). Illumination at 21.22 eV was provided by the He(I) emission line from a helium discharge lamp. Photoelectron emission was collected at 0° from the surface normal of the samples. The spectra were taken at three different spots to confirm that the spectra are reproducible and the irradiation exposure time was kept under one minute. Transient absorption spectroscopy was measured using a Helios-Fire pump–probe setup (Ultrafast Systems). This is paired with a regeneratively amplified 1030 nm laser (Light Conversion Pharos, 200 fs, 200 uJ), set at an effective repetition rate of 1 kHz via an internal pulse picker. A small portion (20%) of the 1030 nm fundamental is directed to an optical delay line, and, subsequently, to a sapphire crystal to generate the broadband probe light. The remaining 80% of the 1030 nm fundamental is directed to an optical parametric amplifier (Light Conversion, Orpheus-F) to generate the pump pulse at 529 nm. Global analysis of TA data was done using the R-package TIMP software,47 with the graphical interface Glotaran 1.5.1.48 Impedance measurements were performed with the FET configuration by connecting the source and drain electrodes using a computer-controlled Solartron impedance analyzer under ac voltage of 100 mV in a vacuum chamber.
Computational details
Density functional calculations were performed with the Vienna Ab initio Simulation Package (VASP, version 6.1) employing the PBE exchange-correlation functional.49,50 The valence-core interactions were described with the projected augmented wave (PAW) method.51 A plane-wave kinetic energy cutoff of 520 eV, an energy convergence criterion of 10−5 eV together with forces of each atom smaller than 0.01 eV Å−1 were used during geometry relaxation. The van der Waals interactions were considered for geometric optimizations by employing Grimme's D3 method.52 The structural relaxation was done by sampling the Brillouin zone over a 3 × 3 × 1 k-point grid centered at the Γ point, while a 9 × 9 × 3 mesh was used for the density of states (DOS) calculation. The initial structure of the compound was obtained from Lin et al. and the optimized structure and the corresponding lattice parameters were obtained by using the above protocol.24 The high-symmetry k-path of the triclinic unit cell suggested by Setyawan et al. was used to calculate the band structure.53 Visualization and post-processing of the DOS and band structures were performed using the VESTA and sumo packages.54,55Optical pump-THz probe (OPTP) spectroscopy
The OPTP setup is driven by a commercial, regenerative amplified, mode-locked Ti:sapphire femtosecond laser with a 1 kHz repetition rate. The pulse duration is around 50 fs, and the central wavelength is ∼800 nm. A single-cycle THz pulse is generated by optical rectification on a 1 mm thick ZnTe crystal. The THz electrical field is probed in the time domain with an 800 nm sampling pulse using the electro-optic effect in a second ZnTe crystal, by varying the time delay between THz and the sampling beam with an optical delay stage. For the pump–probe measurements, excitation by a 400 nm light pulse is used. It is produced by second harmonic generation based on 800 nm light by a beta barium borate (BBO) crystal. The pump–probe delay is controlled by a second optical delay stage. The photoconductivity (σ(tp)) dynamics is monitored by probing the relative change in the peak field of the THz pulse (−ΔE(tp)/E0) induced by photoexcitation, thanks to the linear proportionality of these two quantities within the thin-film approximation:36Here, ΔE(tp) = Epump(tp) − E0 is the pump-induced THz electric field changes, and tp is the pump–probe delay. n1 and n2 are the refractive indices of the media before and after the sample (in our work, n1 and n2 are 1 and 1.95 for vacuum and fused silica, respectively), Z0 = 377 Ω is the impedance of free space, and l = 50 nm is the film thickness.
Frequency-domain photoconductivity spectra
The frequency-domain photoconductivity spectra are obtained at a specific pump–probe delay time by Fourier transforming the complete time-domain ΔE(t) and E0(t) (where t represents the sampling-probe delay time) into frequency-domain ΔE(ω) and E0(ω), and applying thin film approximation as in OPTP measurement:In this study, the time-domain data are collected at 3 ps after photoexcitation by simultaneously moving the pump and sampling stage.
Author contributions
T. M. conceived the idea; T. M., and W. P. supervised the study; S.-L. W. prepared the samples and fabricated the devices. S. F. synthesized the organic cations under the supervision of M. K.; O. Y. carried out GIWAXS measurement and data analysis under the supervision of T. M.; H. Z. performed THz measurement and analyzed the data with support from H. W.; M. M. conducted the DFT calculations and analyzed the data with support from D. A.; N. U., and C. R performed transient absorption spectroscopy measurement; B. J. provided helpful discussion; M. B. and P. B. coordinated the work. S.-L. W. prepared the manuscript with support from all co-authors; all authors discussed the results and contributed to this work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. Wang thanks the China Scholarship Council (CSC, 201906890035) for financial support. M. Mandal acknowledges postdoctoral support from the Alexander von Humboldt Foundation. T. Marszalek acknowledges the Foundation for Polish Science financed by the European Union under the European Regional Development Fund (POIR.04.04.00-00-3ED8/17). The authors thank Dr Hao Wu for the help with UPS measurements. This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – project number 424708673 and by the KAUST Office of Sponsored Research (OSR). Open Access funding provided by the Max Planck Society.References
- Q. Dong, Y. Fang, Y. Shao, P. Mulligan, J. Qiu, L. Cao and J. Huang, Science, 2015, 347, 967–970 CrossRef CAS PubMed.
- P. N. Rudd and J. Huang, Trends Chem., 2019, 1, 394–409 CrossRef CAS.
- A. Mei, X. Li, L. Liu, Z. Ku, T. Liu, Y. Rong, M. Xu, M. Hu, J. Chen, Y. Yang and M. Grätzel, Science, 2014, 345, 295–298 CrossRef CAS PubMed.
- N. Wang, L. Cheng, R. Ge, S. Zhang, Y. Miao, W. Zou, C. Yi, Y. Sun, Y. Cao, R. Yang and Y. Wei, Nat. Photonics, 2016, 10, 699–704 CrossRef CAS.
- H. Zhu, Y. Fu, F. Meng, X. Wu, Z. Gong, Q. Ding, M. V. Gustafsson, M. T. Trinh, S. Jin and X. Y. Zhu, Nat. Mater., 2015, 14, 636–642 CrossRef CAS PubMed.
- S. F. Leung, K. T. Ho, P. K. Kung, V. K. Hsiao, H. N. Alshareef, Z. L. Wang and J. H. He, Adv. Mater., 2018, 30, 1704611 CrossRef PubMed.
- W. Yu, F. Li, L. Yu, M. R. Niazi, Y. Zou, D. Corzo, A. Basu, C. Ma, S. Dey, M. L. Tietze and U. Buttner, Nat. Commun., 2018, 9, 1–10 CrossRef PubMed.
- S. Jana, E. Carlos, S. Panigrahi, R. Martins and E. Fortunato, ACS Nano, 2020, 14, 14790–14797 CrossRef PubMed.
- S. P. Senanayak, M. Abdi-Jalebi, V. S. Kamboj, R. Carey, R. Shivanna, T. Tian, G. Schweicher, J. Wang, N. Giesbrecht, D. D. Nuzzo and H. E. Beere, Sci. Adv., 2020, 6, 4948 CrossRef PubMed.
- X. J. She, C. Chen, G. Divitini, B. Zhao, Y. Li, J. Wang, J. F. Orri, L. Cui, W. Xu, J. Peng and S. Wang, Nat. Electron., 2020, 3, 694–703 CrossRef CAS.
- Y. Lin, Y. Bai, Y. Fang, Q. Wang, Y. Deng and J. Huang, ACS Energy Lett., 2017, 2, 1571–1572 CrossRef CAS.
- Y. Chen, Y. Sun, J. Peng, J. Tang, K. Zheng and Z. Liang, Adv. Mater., 2018, 30, 1703487 CrossRef PubMed.
- J. C. Blancon, A. V. Stier, H. Tsai, W. Nie, C. C. Stoumpos, B. Traore, L. Pedesseau, M. Kepenekian, F. Katsutani, G. T. Noe and J. Kono, Nat. Commun., 2018, 9, 1–10 CrossRef CAS PubMed.
- C. R. Kagan, D. B. Mitzi and C. D. Dimitrakopoulos, Science, 1999, 286, 945–947 CrossRef CAS PubMed.
- L. M. Herz, ACS Energy Lett., 2017, 7, 1539–1548 CrossRef.
- C. Q. Qin, Z. Fan, Q. Liang, L. Xin, H. Y. Ji, L. T. Li, Y. F. Hu, Z. D. Lou, Y. B. Hou and F. Teng, Adv. Electron. Mater., 2021, 10, 2100384 CrossRef.
- T. Matsushima, S. Hwang, A. S. Sandanayaka, C. Qin, S. Terakawa, T. Fujihara, M. Yahiro and C. Adachi, Adv. Mater., 2016, 28, 10275–10281 CrossRef CAS PubMed.
- H. Zhu, A. Liu, K. I. Shim, J. Hong, J. W. Han and Y. Y. Noh, Adv. Mater., 2020, 32, 2002717 CrossRef CAS PubMed.
- C. Jie, Y. Zhou, Y. P. Fu, J. Pan, O. F. Mohammed and O. M. Bakr, Chem. Rev., 2021, 121, 12112–12180 CrossRef PubMed.
- W. Nie, H. Tsai, R. Asadpour, J. C. Blancon, A. J. Neukirch, G. Gupta, J. J. Crochet, M. Chhowalla, S. Tretiak, M. A. Alam and H. L. Wang, Science, 2015, 347, 522–525 CrossRef CAS PubMed.
- A. Liang, Y. Gao, R. Asadpour, Z. Wei, B. P. Finkenauer, L. Jin, J. Yang, K. Wang, K. Chen, P. Liao and C. Zhu, J. Am. Chem. Soc., 2021, 143, 15215–15223 CrossRef CAS PubMed.
- C. Ni, Y. Huang, T. Zeng, D. Chen, H. Chen, M. Wei, A. Johnston, A. H. Proppe, Z. Ning, E. H. Sargent and P. Hu, Angew. Chem., Int. Ed., 2020, 132, 14081–14087 CrossRef.
- D. Lu, G. Lv, Z. Xu, Y. Dong, X. Ji and Y. Liu, J. Am. Chem. Soc., 2020, 142, 11114–11122 CrossRef CAS PubMed.
- J. T. Lin, C. C. Liao, C. S. Hsu, D. G. Chen, H. M. Chen, M. K. Tsai, P. T. Chou and C. W. Chiu, J. Am. Chem. Soc., 2019, 141, 10324–10330 CrossRef CAS PubMed.
- R. Li, C. Yi, R. Ge, W. Zou, L. Cheng, N. Wang, J. Wang and W. Huang, Appl. Phys. Lett., 2016, 109, 151101 CrossRef.
- Z. Wang, F. Wang, B. Zhao, S. Qu, T. Hayat, A. Alsaedi, L. Sui, K. Yuan, J. Zhang, Z. Wei and Z. A. Tan, J. Phys. Chem. Lett., 2020, 11, 1120–1127 CrossRef CAS PubMed.
- M. Dyksik, H. Duim, X. Zhu, Z. Yang, M. Gen, Y. Kohama, S. Adjokatse, D. K. Maude, M. A. Loi, D. A. Egger and M. Baranowski, ACS Energy Lett., 2020, 5, 3609–3616 CrossRef CAS.
- K. Zhang, T. Marszalek, P. Wucher, Z. Wang, L. Veith, H. Lu, H. J. Räder, P. M. Beaujuge, P. W. Blom and W. Pisula, Adv. Funct. Mater., 2018, 28, 1805594 CrossRef.
- K. Zhang, M. Borkowski, P. Wucher, P. M. Beaujuge, J. J. Michels, P. W. Blom, T. Marszalek and W. Pisula, Adv. Electron. Mater., 2021, 7, 2100397 CrossRef CAS.
- O. Yildiz, Z. Wang, M. Borkowski, G. Fytas, P. W. Blom, J. J. Michels, W. Pisula and T. Marszalek, Adv. Funct. Mater., 2021, 32, 2107976 CrossRef.
- F. Paulus, C. Tyznik, O. D. Jurchescu and Y. Vaynzof, Adv. Funct. Mater., 2021, 31, 2101029 CrossRef CAS.
- D. B. Kim, S. Lee, C. H. Jang, J. H. Park, A. Y. Lee and M. H. Song, Adv. Mater. Interfaces, 2020, 7, 1902158 CrossRef CAS.
- Z. Li, C. Xiao, Y. Yang, S. P. Harvey, D. H. Kim, J. A. Christians, M. Yang, P. Schulz, S. U. Nanayakkara, C. S. Jiang and J. M. Luther, Energy Environ. Sci., 2017, 10, 1234–1242 RSC.
- Q. Chen, H. Zhou, Z. Hong, S. Luo, H. S. Duan, H. H. Wang, Y. Liu, G. Li and Y. Yang, J. Am. Chem. Soc., 2014, 136, 622–625 CrossRef CAS PubMed.
- Y. Gao, Z. Wei, P. Yoo, E. Shi, M. Zeller, C. Zhu, P. Liao and L. Dou, J. Am. Chem. Soc., 2019, 141, 15577–15585 CrossRef CAS PubMed.
- R. Ulbricht, E. Hendry, J. Shan, T. F. Heinz and M. Bonn, Rev. Mod. Phys., 2011, 83, 543 CrossRef CAS.
- S. Shao, W. Talsma, M. Pitaro, J. Dong, S. Kahmann, A. J. Rommens, G. Portale and M. A. Loi, Adv. Funct. Mater., 2021, 31, 2008478 CrossRef CAS.
- F. Zhang, Q. Zhang, X. Liu, Y. Hu, Z. Lou, Y. Hou and F. Teng, ACS Appl. Mater. Interfaces, 2021, 13, 4272–4284 Search PubMed.
- Y. Reo, H. Zhu, J. Y. Go, K. I. Shim, A. Liu, T. Zou, H. Jung, H. Kim, J. Hong, J. W. Han and Y. Y. Noh, Chem. Mater., 2021, 33, 2498–2505 CrossRef CAS.
- S. P. Senanayak, B. Yang, T. H. Thomas, N. Giesbrecht, W. Huang, E. Gann, B. Nair, K. Goedel, S. Guha, X. Moya and C. R. McNeill, Sci. Adv., 2017, 3, 1601935 CrossRef PubMed.
- R. Lin, K. Xiao, Z. Qin, Q. Han, C. Zhang, M. Wei, M. I. Saidaminov, Y. Gao, J. Xu, M. Xiao and A. Li, Nat. Energy, 2019, 4, 864–873 CrossRef CAS.
- J. Chen, T. Shi, X. Li, B. Zhou, H. Cao and Y. Wang, Appl. Phys. Lett., 2016, 108, 053302 CrossRef.
- T. Matsushima, S. Hwang, S. Terakawa, T. Fujihara, A. S. Sandanayaka, C. Qin and C. Adachi, Appl. Phys. Express, 2017, 10, 024103 CrossRef.
- R. Su, Z. Xu, J. Wu, D. Luo, Q. Hu, W. Yang, X. Yang, R. Zhang, H. Yu, T. P. Russell and Q. Gong, Nat. Commun., 2021, 12, 1–11 CrossRef PubMed.
- S. Zhang, Z. Y. Lin, E. Shi, B. P. Finkenauer, Y. Gao, A. J. Pistone, K. Ma, B. M. Savoie and L. Dou, Adv. Mater., 2021, 33, 2105183 CrossRef.
- C. Ni, Y. Huang, T. Zeng, D. Chen, H. Chen, M. Wei, A. Johnston, A. H. Proppe, Z. Ning, E. H. Sargent and P. Hu, Angew. Chem., Int. Ed., 2020, 132, 14081–14087 CrossRef.
- K. M. Mullen and I. H. M. van Stokkum, J. Stat. Softw., 2007, 18(3), 1–46 Search PubMed.
- J. J. Snellenburg, S. Laptenok, K. M. Mullen and I. H. M. van Stokkum, J. Stat. Softw., 2012, 49(3), 1–22 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- W. Setyawan and S. Curtarolo, Comput. Mater. Sci., 2010, 49, 299–312 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- A. M. Ganose, A. J. Jackson and D. O. Scanlon, Int. J. Open Source Softw. Process., 2018, 3, 717 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2mh00632d |
| This journal is © The Royal Society of Chemistry 2022 |