Open Access Article
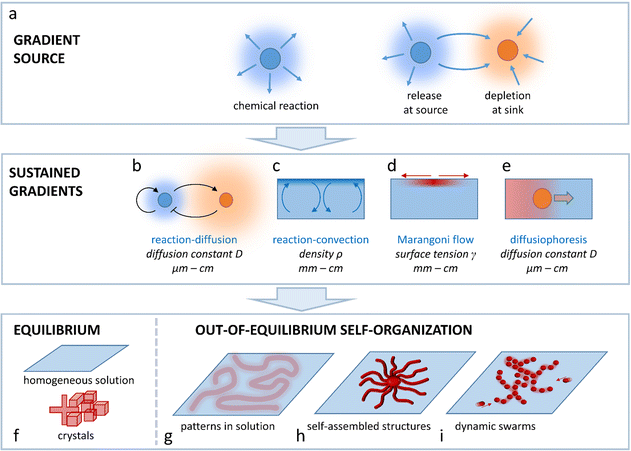
Open Access ArticleSpatial programming of self-organizing chemical systems using sustained physicochemical gradients from reaction, diffusion and hydrodynamics
Anne-Déborah C.
Nguindjel†
,
Pieter J.
de Visser†
,
Mitch
Winkens†
and
Peter A.
Korevaar
 *
*
Institute for Molecules and Materials, Radboud University, Nijmegen, The Netherlands. E-mail: p.korevaar@science.ru.nl
First published on 29th September 2022
Abstract
Living organisms employ chemical self-organization to build structures, and inspire new strategies to design synthetic systems that spontaneously take a particular form, via a combination of integrated chemical reactions, assembly pathways and physicochemical processes. However, spatial programmability that is required to direct such self-organization is a challenge to control. Thermodynamic equilibrium typically brings about a homogeneous solution, or equilibrium structures such as supramolecular complexes and crystals. This perspective addresses out-of-equilibrium gradients that can be driven by coupling chemical reaction, diffusion and hydrodynamics, and provide spatial differentiation in the self-organization of molecular, ionic or colloidal building blocks in solution. These physicochemical gradients are required to (1) direct the organization from the starting conditions (e.g. a homogeneous solution), and (2) sustain the organization, to prevent it from decaying towards thermodynamic equilibrium. We highlight four different concepts that can be used as a design principle to establish such self-organization, using chemical reactions as a driving force to sustain the gradient and, ultimately, program the characteristics of the gradient: (1) reaction–diffusion coupling; (2) reaction–convection; (3) the Marangoni effect and (4) diffusiophoresis. Furthermore, we outline their potential as attractive pathways to translate chemical reactions and molecular/colloidal assembly into organization of patterns in solution, (dynamic) self-assembled architectures and collectively moving swarms at the micro-, meso- and macroscale, exemplified by recent demonstrations in the literature.
1. Introduction
The spontaneous emergence of shape, structure and patterns is one of the most fascinating processes in life.1,2 At small length scale, a living cell combines a vast amount of molecular building blocks into functional architectures, for example the cytoskeleton that enables the cell to move and divide.3 Primitive unicellular organisms employ the cytoskeleton to achieve highly dynamic shape transformations at the macroscale. For example, Physarum polycephalum slime molds self-organize into networks to explore their surroundings, and reconfigure to optimize food acquisition and distribution.4 Social amoebae Dictyostelium discoideum colonies collectively aggregate from a dynamic swarm of individually moving cells into fruiting bodies,5 and multicellular organisms generate structures of increasing complexity over the course of embryonic development.6 Importantly, the bottom-up emergence of functional structures in life is entirely driven by chemical and physical principles, which transduce molecular interactions into structures at length scales well beyond the molecular building blocks. Recreating such self-organization – spontaneous emergence of patterns and structures as directed by internal processes, rather than external control – from integrated chemical reactions, assembly pathways and physicochemical phenomena is one of the biggest fundamental challenges in systems chemistry.7–10 To this end, de novo-designed chemical systems based on a minimalistic set of elements allow us to elucidate the general principles that are essential for self-organization of supramolecular structures, crystals, colloids and soft matter. At the same time, these insights offer new potential in novel classes of synthetic matter that display ‘life-like’ behaviour, i.e. operate autonomously and interact with cues from their environment. Bottom-up control in such systems will allow them to morph into functional structures, adapt to changing circumstances, and ultimately enable intelligent systems with potential in e.g. diagnostics, interactive biomaterials or molecular computing.Non-covalent, reversible associations embedded in the design of the building blocks provide a powerful tool to program assembly processes. Under thermodynamic control, the assemblies will spread out into a homogeneous solution, or form equilibrium structures, such as supramolecular assemblies or crystals (Fig. 1). Developing ‘life-like’ systems however involves a paradigm where self-organization occurs out-of-equilibrium.11–15 For example, the construction of the cells’ cytoskeleton shows how coupling of assembly steps to chemical reactions drives self-organization in time and space.16 First, the tubulin building blocks are activated by a chemical fuel, guanosine triphosphate (GTP), in order to assemble into microtubules. Over time, hydrolysis of GTP occurs, and tubulin becomes inactive again. Hence, the self-organization of the microtubules relies on the supply of fresh GTP, which enables the cell to control the build-up and disassembly of the cytoskeleton. The transient nature of microtubule assemblies has inspired the development of synthetic systems17,18 – varying from 1D nanofibers19–23 to colloidal assemblies24 and macroscale gels25 – that form and fall apart over time, as programmed by the kinetics of the underlying chemical reactions.
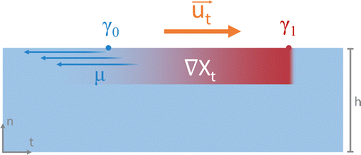
This Perspective addresses the challenge to arrive at spatial programmability in the out-of-equilibrium organization of matter that is of interest to systems chemistry, ranging from supramolecular assemblies to colloids, hydrogels, crystalline structures and flow patterns in chemical reaction networks. In general, such organization requires the spontaneous emergence of concentration gradients that provide a spatial differentiation in the system. To avoid decay back to thermodynamic equilibrium (e.g. a homogeneous solution, emulsion, or non-organized dispersion of colloids), these gradients need to be sustained under out-of-equilibrium conditions. Such sustainment requires at first a gradient source; a chemical reaction that takes place in solution, a source element that releases a chemical compound, or a sink element that depletes the compound. Even though patterns can emerge around gradient sources that are a priori localized at a fixed position, in an entirely self-organizing system, one needs a mechanism by which the production, release or depletion of the compound gets localized such, that the gradient of this compound is sustained. In this Perspective, we outline four physicochemical principles that enable design strategies to arrive at sustained gradients in solution-based systems: reaction–diffusion coupling (Fig. 1b), reaction–convection (Fig. 1c), the Marangoni effect (Fig. 1d) and diffusiophoresis (Fig. 1e). We selected these principles as they provide unique pathways to direct the self-organization of systems that either comprise concentration patterns in solution (Fig. 1g), self-assembled structures (Fig. 1h) or dynamic swarms of colloids or (micro)droplets (Fig. 1i), at the micro-, meso- or macroscale.
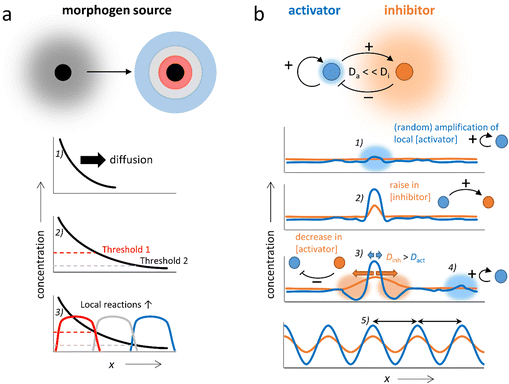
2. Reaction–diffusion systems
The coupling of chemical reactions and diffusion lends itself towards the construction of self-organizing systems. In nature, pattern formation in processes such as embryonic development has been rationalized by two concepts, which may take place in conjunction: Wolpert's positional information, and Turing instability.26–29 In Wolpert's concept, gradients of chemicals (morphogens) are locally amplified to establish spatial differentiation, dividing the area in which the gradient is present into multiple zones with large differences in terms of chemical composition (Fig. 2a). This is accomplished by local regulatory interactions, which rely on gene networks that combine repression, (auto)activation and cross-regulation of multiple genes. In Turing's mechanism, a homogeneous system spontaneously generates patterns with repetitive structure.12,30–35 These Turing patterns can be achieved via as little as two components; the activator which promotes the production of both components (positive feedback), and the inhibitor which inhibits the production of the activator (negative feedback) and has a high diffusion rate compared to the activator (i.e. Da ≪ Di, Fig. 2b). Starting off from a homogeneous solution with activator and inhibitor, even the slightest local increase in the activator concentration (1) amplifies both the local activator and inhibitor concentration in a self-sustaining fashion (2). While the peak in activator concentration remains localized due to its low Da, the inhibitor rapidly diffuses away from the activation site, suppressing production of the activator in neighboring areas (3). Outside of this area, new peaks in activator concentration eventually arise (4). Finally, the entire solution is divided into a periodic pattern of high and low activator concentration, their spacing regulated by the combination of reaction and diffusion kinetics inherent to the chemical network (5).The first experimental demonstration of a Turing pattern in a synthetic system was provided by Castets et al. in the chlorite-iodide-malonic acid (CIMA) reaction, where starch, used as indicator in the gel, provides a selective complexation and thereby generates the required distinction in diffusion rates between the activator (iodide) and the inhibitor (chlorite).36–39 Furthermore, Turing patterns have been reported in the ferrocyanide–iodate–sulphite reaction40–42 and, under specific conditions, in the Belousov–Zhabotinsky (BZ) reaction.43–45 In this reaction that naturally displays reaction–diffusion patterns, oscillation results from the autocatalytic oxidation of a redox catalyst by bromate ions (activator), a process that is inhibited by bromide ions. A reducing agent (e.g. malonic acid) restarts the cycle, by reducing the catalyst again. Classically, the BZ reaction provides waves at the cm-scale that spiral through the reaction medium in an unstirred batch configuration. However, Epstein et al. showed how the classical BZ reaction can be further tailored in water-in-oil micro-emulsions.46,47 Here, differentiation in diffusivity is obtained as polar species are transferred via the aqueous micro-droplets, whereas non-polar intermediates are transferred more rapidly as they diffuse through the oil-based continuous phase, resulting into a large diversity of spatial organizations, including Turing patterns in the 100 micrometer-range.48
Even though most of these pattern-forming reactions are found by chance,49 it is clear that the emergence of reaction–diffusion patterns relies on the kinetic reaction rate constants and diffusion constants involved,41,50,51 and various models have been developed to simulate reaction–diffusion patterns.11,52–55 Furthermore, generic design principles have been proposed, such as a stepwise method through which an oscillatory reaction occurring in a homogeneous, well-mixed solution can be translated into reaction–diffusion patterns in open one-side-fed reactors.56,57 To this end, a complexing agent is introduced which selectively binds the activator to decrease its diffusion rate (a strategy that was suggested earlier by Lengyel and Epstein38), as well as an antagonist reaction to control its accumulation. All in all, examples of complexity emerging from reaction–diffusion systems have been demonstrated which range from nano- and microscale structures to patterns that span centimeters, and from “static” Turing patterns to dynamic patterns that continuously change over time.49,58–63 Here, we highlight some of the more recent strategies that have been developed to couple reaction and diffusion and generate self-organizing structures and patterns.
2.1 Reaction–diffusion systems as a means to create complex structure
First, we discuss approaches to self-organize complex static structures with distinct topologies and functionalities that are otherwise difficult to achieve. Recently, Wu et al. reported the synthesis of Cu2+-loaded Turing membranes, which improve ionic conductivity in zinc-based batteries.64 To create these membranes, a homogeneous solution of polybenzimidazole (PBI) is cast in a thin film on a substrate, and immersed in a CuCl2 solution in N,N-dimethylacetamide (DMAc) (Fig. 3a and b). Cu2+ ions dissociate from the DMAc solvent, and coordinate with the pyridine moiety in the PBI polymer chains. The PBI–Cu2+ complex now functions as the activator for the membrane formation, as further diffusion of reactants towards the activated site is accelerated by local depletion of PBI and Cu2+, generating a cross-linked polymer network. At the same time, DMAc molecules that are released from Cu2+ ions that have been associated to PBI diffuse away from the active site – much faster than the PBI–Cu2+ complex. Thereby, DMAc functions as an inhibitor, and sequesters Cu2+ at neighboring locations where PBI–Cu2+ has not formed yet. Together, the PBI–Cu2+ activator and DMAc inhibitor generate Turing patterns of PBI–Cu2+: the crests and troughs that emerge in the initially homogeneous PBI-film have a typical feature size of approximately 100 μm.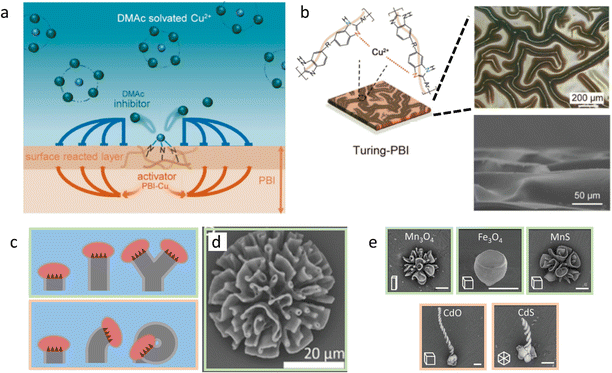 | ||
| Fig. 3 Complex static structures emerge from reaction–diffusion. (a) DMAc functions as the inhibitor in a Turing-like reaction–diffusion system, resulting in patterned PBI-Cu membranes (b). Reprinted (adapted) with permission from ref. 64. Copyright 2021 American Chemical Society. (c) Various polycrystalline biomorphic structures grow from reaction–diffusion triggered BaCO3–SiO2 co-precipitation. Due to the narrow pH range in which passivating SiO2 precipitation takes place, crystal formation is affected by the acidic growth front. This causes the structures to ‘blossom’ towards the bulk solution if it has high pH (top) and ‘curl’ inwards if bulk pH is lower (bottom). (d) BaCO3–SiO2 co-precipitate structure that is formed in the blossoming regime. (e) Ion-substituted structures, exemplifying the shapes obtained in either the blossoming (top row) or curling (bottom row) regime. Reproduced from ref. 72 with permission from the Wiley-VCH publishing group, Copyright 2020. | ||
Furthermore, inorganic structures with biomorphic shapes such as corals, vases and helices can be generated upon coupling the precipitation reactions of barium carbonate (BaCO3) nanocrystals and amorphous silica (SiO2). García-Ruiz showed how polycrystalline biomorphic structures grow when CO2 diffuses into an aqueous solution of sodium metasilicate (Na2SiO3) and barium chloride (BaCl2).65,66 These chemicals participate in the following (overall) precipitation reactions:
| Ba2+ + CO2 + H2O → BaCO3 + 2H+ | (1) |
| SiO32− + 2H+ → SiO2 + H2O | (2) |
2.2 Reaction–diffusion systems with sustained oscillations
In addition to static patterns, reaction–diffusion coupling can be exploited in self-organizing systems that display spatiotemporal dynamics. The BZ reaction offers an attractive pathway to translate spatiotemporally oscillating concentration gradients into (functional) responses at material-level. This reaction is unique due to its ability to sustain oscillations for hundreds of cycles in a closed system, which manifest as expanding ring-shaped pulses (‘target patterns’) or spirals.73 Furthermore, inclusion of photo-responsive catalysts allows external control over the dynamics of the system via light exposure.74,75For example, Yoshida et al. have exploited the BZ reaction to direct biomimetic hydrogels that are able to move without any external driving force.76 An oscillating hydrogel was produced by including a Ru(bpy)3 catalyst – which can participate in the BZ reaction – into a poly(NIPAAm-co-Ru(bpy)3-co-AMPS) polymer network. Upon immersion of the gel in the catalyst-free BZ reaction medium, the BZ reaction starts and the catalyst inside the hydrogel oscillates between Ru(III) and Ru(II) oxidation states. These oxidation states, in turn, influence the hydrophilicity of the gel, and thereby drive its periodical swelling (Ru(III)) and deswelling (Ru(II)), which results into peristaltic motion of the gel (Fig. 4).77 Alternatively, walking motion can be achieved using gels that swell asymmetrically due to an internal gradient in Ru(bpy)3 and AMPS concentration, and self-oscillating polymer brushes – polymer chains grafted onto a glass substrate – can be used to transport nanoscale objects.76,78 Using a similar poly(NiPAAm-co-Ru(bpy)3-co-AMPS) hydrogel immersed in catalyst-free BZ-solution, Lu et al.79 exploit the catalyst's photosensitivity. When weakly illuminated, the frequency of oscillations in the gel increases with light intensity, while above a certain intensity threshold, stronger illumination reduces the oscillation frequency instead. When placed inside a capillary of which the left and right halves are illuminated with different intensities, the authors were able to cause both photophobic and phototropic motion of the gel, as the imbalance between oscillation frequencies in the weakly and brightly illuminated parts of the gel dictated its movement.
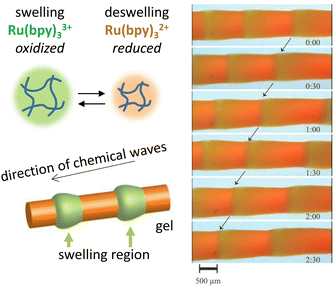 | ||
| Fig. 4 Functional oscillating systems based on the Belousov–Zhabotinsky (BZ) reaction. By incorporating the BZ reaction into a hydrogel, the hydrophilicity change resulting from Ru2+–Ru3+ switching can be exploited to cause periodic swelling and deswelling, giving rise to peristaltic motion. Reproduced from ref. 77 with permission from the Wiley-VCH publishing group, Copyright 2008. | ||
Additionally, BZ reactions can be used as a basis for chemical communication amongst compartmentalized systems such as micro-droplets or -particles.80–82 For example, Litschel et al. used this concept to create a synthetic ‘central pattern generator’, a motif found in the nervous system that produces pulses which alternatively travel down the left and right sides of its spinal column, inducing cyclic muscle contractions.83 A microfluidic device was created that comprises a linear array of nanoliter wells, connected via microchannels and loaded with the BZ reagent solution. Coupling of the BZ reactions in neighboring wells occurs either by diffusion of the hydrophobic inhibitor Br2 through the PDMS walls (inhibitory coupling), or by water-soluble species, which can propagate oscillations along the microchannels (excitatory coupling). A photosensitive catalyst was included to suppress spontaneous oscillation by initially exposing the wells to light. As a result, BZ oscillations selectively start when the light is turned off at the beginning of the array (the ‘pacemaker’), which excites the subsequent wells, such that traveling waves of BZ oscillations progress down the array. Even if the two parallel arrays are excited simultaneously, their inhibitory coupling upon exchange of Br2 through the PDMS walls causes a phase-shift, such that they end up oscillating out of phase. One can envision such a system being coupled to previously mentioned examples of contracting BZ-gels, creating synthetic analogues of muscles that constantly contract and relax upon actuation by neural signals.
2.3 In vitro reaction–diffusion systems based on biomolecules
The impressive complexity that can be established from chemical systems such as the BZ reaction – which relies on a fixed reaction network topology – has inspired the bottom-up design of reaction networks based on biomolecules. The sequentially programmable nature of DNA strands allows precise control over the topology of the reaction network and thereby reaction and diffusion rates. As a result, it becomes possible to translate the high degree of control inherent to DNA programming into macroscale spatial patterns and sustained out-of-equilibrium gradients. This concept has been exploited by various research groups,84–88 who implemented toehold-mediated DNA strand displacement reactions into reaction–diffusion networks. Such reactions require a partially hybridized complex of two DNA strands, to which a single complementary DNA strand is then added as an input. This input strand now displaces one of the original (partly bound) DNA strands, which is released as the output – a reaction that is driven by the gain in number of hydrogen bonds. The release of the output strands can be followed by functionalizing them with a fluorescent probe that is inactive when in close contact to a quencher in the DNA hybrid, and displays strong fluorescence when the output strand is free in solution.For example, Chen et al. reported a system where rapidly diffusing activator (input) strands displace fluorescent signal strands from reporter hybrids.84 Subsequently, the signal strands can be sequestered by slowly diffusing inhibitor hybrids. Various fluorescent patterns can then be generated from gels with a homogeneous loading of these reporter hybrids. For example, single and concentric rings spread outward from a cavity in the gel that contains both activator and inhibitor strands, while destructive interference patterns appear when one cavity is filled with activator and another with inhibitor, and constructive interference is observed when orthogonal activators are added into separate cavities. Zenk et al. reported a setup that generates sustained DNA concentration gradients and patterns.85 In their design, single and double DNA strands diffuse from opposite liquid reservoirs into a hydrogel, and release an output DNA strand via strand-displacement. Throughout the system, ‘recapturer complexes’ are present at constant concentration in order to sequester the output strands. Together, this constant production and depletion of the output strands maintains a stable, yet out-of-equilibrium concentration profile in the hydrogel. This approach provides the foundation for the experimental realization of (programmed) DNA-based pattern generating systems which thus far have only been demonstrated in silico, such as the pattern-processing modules used by Scalise et al. in their simulations.86
In addition to these DNA strand displacement reactions, Zadorin et al. have demonstrated how positional information can be established in DNA-based systems with chemical reactions that produce and deplete DNA strands.87 In the example highlighted in Fig. 5a, autocatalysis of activator DNA strand A1 is established via template strand TA1. Upon binding of the activator, TA1 templates the extension of A1 into a strand that comprises two sequences of A1 – a reaction that is catalyzed by DNA polymerase. Next, a nicking enzyme cleaves the extended strand such that two A1 strands are released from this autocatalytic system. Finally, A1 is converted into waste when DNA polymerase acts upon it while it is bound to repressor strand R1. By combining autocatalysis and inhibition, a weak gradient in repressor strand can be transferred into a strong, almost stepwise increase in A1 concentration – in analogy to Wolpert's scenario – with the repressor R1 functioning as the morphogen. By coupling two orthogonal autocatalytic motifs via a morphogen that contains both repressor strands, a ‘French flag pattern’ with three chemically distinct zones can be generated based on a single morphogen gradient (Fig. 5b). This gradient is then exploited to selectively bind colloidal beads in a particular area via DNA hybridization.
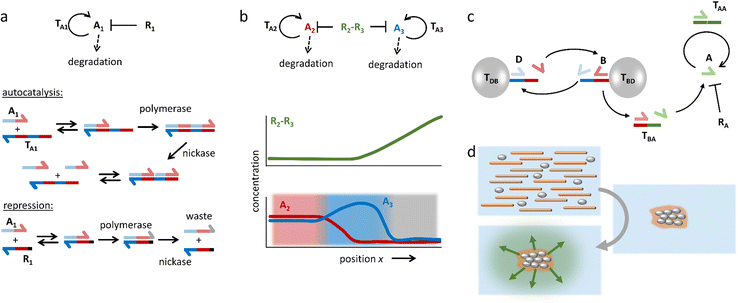 | ||
| Fig. 5 DNA-based reaction–diffusion systems. (a) DNA reaction networks for autocatalysis, repression and degradation. (b) A bifunctional repressor strand functions as the morphogen in a demonstration of DNA-based positional information. The repressor gradient is amplified by the autocatalytic reactions, resulting in three zones with distinct chemical compositions, i.e. a ‘French flag pattern’.87 (c) A DNA-based density-dependent autocatalytic reaction is triggered as a network of beads, microtubules and kinesin motors contracts. (d) As a result, a fluorescent front is initiated from the sites where a critical bead density is reached.88 | ||
Self-organization processes in life, such as embryonic development, often involve a coupling of chemical as well as mechanical systems. Such coupling can pave the way towards new control mechanisms in artificial self-shaping materials. In work by Senoussi et al., DNA reaction networks were implemented in active matter-based gels that, upon contraction, initiate propagating reaction fronts.88 To this end, two different types of microbeads are functionalized at their surface, each with one type of single DNA strand, where bead type B templates the formation of the activator for bead type D, and vice versa (Fig. 5c). These beads are loaded into a solution with an activator strand-degrading exonuclease, as well as microtubules and kinesin motors, which together form an active gel that concentrates the microbeads upon contraction. When the microbeads are brought close together, they easily exchange their activator strands in cross-catalysis. Next, activator species B is coupled to a motif (TBA) that enables autocatalysis of activator A. As a result, an autocatalytic front of A emerges, which is triggered from the location where the active gel has started to contract (Fig. 5d).
Finally, the spatiotemporal patterns that emerge from the Min protein system provide an intriguing platform to study in vitro pattern formation. The Min protein system is a biological reaction–diffusion system in Escherichia coli that comprises the MinD and MinE proteins, and forms patterns that localize the middle plane to assist in bacteria cell division. MinD switches from a solubilized monomeric state in solution to a membrane-bound dimeric state upon binding ATP (Fig. 6a). MinD at the membrane sequesters MinE from the solution, which elevates the ATPase activity of MinD. As result ATP is hydrolyzed to ADP, and MinD dissociates from the membrane again. In the reaction–diffusion patterns that emerge from this system, MinD serves as the activator, and MinE as the inhibitor. To introduce external control, comparable to the photocatalytic BZ reactions, Glock et al. introduced an azobenzene-bound peptide derived from MinE. This peptide binds to MinD when the azobenzene moiety is in the cis state, activating its ATPase activity and thereby triggering its dissociation from the membrane (Fig. 6b).89 Importantly, the binding and unbinding of the peptide-azobenzene derivative to MinD can be controlled by promoting the cis or trans state upon exposure to UV and blue light, respectively. Notably, entrainment of the spatiotemporal patterns of the MinDE system was obtained after periodic illumination by UV, which remained stable for more than 20 illumination cycles (Fig. 6c). When the periodic illumination was stopped, the spatiotemporal patterns returned to their ground state after a few oscillations. The relative simplicity of this network and the manipulation technique offers possibilities for control of nonlinear dynamics of natural reaction–diffusion systems. This opens pathways to establish patterns in synthetic biology contexts, such as the development of a synthetic cell.
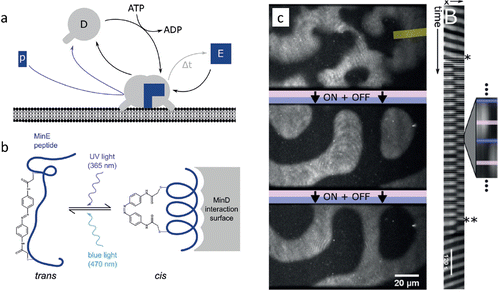 | ||
| Fig. 6 Entrainment of Min-protein patterns based on a photoswitchable MinE peptide. (a) Monomeric MinD in solution forms a dimer that attaches to the membrane upon binding ATP. (b) Upon illumination with UV, the MinE peptide associates with membrane-bound MinD, causing hydrolysis of ATP followed by release of MinD from the membrane. (c) Periodic illumination of the sample synchronizes the patterns with the light pulses. Reproduced from ref. 89 with permission from the Wiley-VCH publishing group, Copyright 2018. | ||
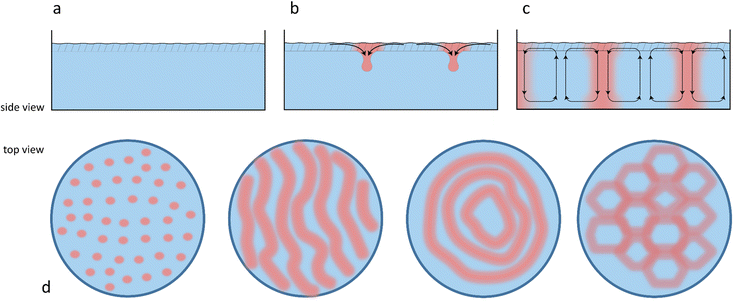
3. Reaction–convection systems
Chemical reactions can also give rise to self-organization by affecting the local physical properties of the solution, e.g. generate imbalances in density or surface tension (vide infra).90–93 Such chemo-hydrodynamic coupling enables simple A + B → C reactions, or even A → B reactions to drive the self-organization of concentration patterns that spontaneously emerge in an initially homogeneous solution. When buoyancy is the driving factor, these patterns rely on the convection patterns that are driven by local variations in the density of dissolved compounds in solution. Here, a chemical reaction produces a high-density product on top of a low-density reactant solution, or a low-density product at the bottom of a high density reactant solution, such that a convective flow emerges to negate this density instability. The high-density solution is transported downward while a counterbalancing flow is directed upward. Depending on the physical characteristics of the system, e.g. the fluid viscosity and liquid depth, convection patterns are generated with regions of upward and downward flow, as schematically shown in Fig. 7. Comparable convection patterns emerge in liquid systems that are heterogeneously heated, due to the well-known Rayleigh–Bénard instability. The difference between these two buoyancy driven convection phenomena is the mechanism through which the density variations arise: solutal expansion due to a chemical reaction versus thermal expansion due to heating.Solutal buoyancy convection is described by the solutal Rayleigh number, the ratio between the rate of convective transport due to solutal buoyancy and the rate of diffusive transport:
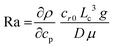 | (1) |
Importantly, if Ra ≫ Rac, strong convection causes a rapid equilibration of the system, resulting in a limited lifetime of the convection patterns. Hence, experimental systems with intermediate Ra values are required to establish solutal buoyancy convection patterns.
3.1 Self-organization emerging from reaction–convection systems in solution
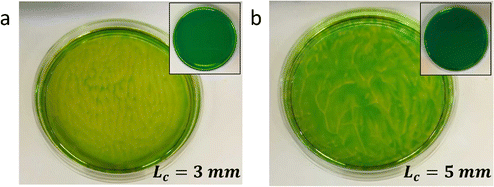
Typically, generating the density gradient requires an interface. For example, Avnir et al. reported convection patterns in Petri dishes with solutions of pH indicators methyl orange or phenolphthalein.95,97 Upon subjecting these solutions at the air–water interface to an ammonia vapour, which increases the pH in the top of the solution, the solution becomes denser in the top, and convection patterns form with concentric rings and mosaic structures. These observations also exemplify that studying reaction–convection patterns is most convenient when either the reactants or products are coloured. Additionally, convection patterns were shown to emerge from density-based instabilities in chemical waves generated by the chlorite–thiosulfate reaction,98 whereas in the iodate arsenic acid reaction99 and the iron(II)–nitric acid reaction,100 density gradients are generated that add a convective component to the progression of reaction–diffusion fronts through solution. Furthermore, convection patterns emerge when hydrodynamic, typically density-related, instabilities are generated at the horizontal interface of two phases with reagents that are enclosed in a Hele-Shaw cell, for example through an acid–base reaction101,102 or the dissolution of CO2 from the gas phase into a NaOH solution.103Experiments in our lab with the pH indicator bromothymol blue showed similar convection patterns (Fig. 8). We have activated a photoacid generator to decrease the pH in the top layer of the solution upon exposure to UV. Starting from pH ≈ 8, the acidification resulted in a change of the pH indicator bromothymol blue from green to yellow. Convection patterns emerged over the course of 5 to 10 minutes, varying in shape from stripes (Fig. 8a) to branches and dots (Fig. 8b). Intriguingly, we observed that the patterns can be varied by varying the depth of the solution, i.e. Lc.
Surprisingly, despite the abundance of chemical reactions that potentially give rise to density differences, the implementation of chemo-hydrodynamic effects in chemical systems as a design principle, rather than a phenomenon as such, is quite rare. However, recent theoretical studies emphasize the untapped potential of reaction–convection: self-generated convection can accelerate chemical reactions,104 and enhance nonlinear kinetics such as chemical oscillations.105
To engineer self-organizing convection patterns in solution, careful design of the chemical reactions is important. Enzymatic reactions with a constant production rate – in order to generate a steady density gradient – can relatively easily be tuned via the enzyme concentration. Furthermore, it is relatively easy to spatially restrict the region of chemical activity by immobilizing the enzyme(s), e.g. at the top or at the bottom of a reaction container. For example, Zhang et al. use an enzymatic reaction network comprised of two enzymes, glucose oxidase (GOx) and horseradish peroxidase (HRP).106 GOx utilizes atmospheric oxygen at the top of the reaction container to oxidize glucose into gluconic acid and hydrogen peroxide. Due to gluconic acid being ∼0.2% more dense than glucose, a vertical density gradient emerges.107 The patterns are visualized via hydrogen peroxide, a side product of the glucose oxidation. HRP uses hydrogen peroxide to oxidize 2,2′-azino-bis(3-ethylbenzothiazoline-6-sulfonic acid) (ABTS) into ABTS˙+. This green product visualizes the solutal buoyancy convection patterns. The patterns that appear were demonstrated to depend strongly on the liquid depth and evolve over time into different configurations.
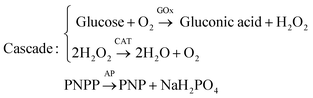
Apart from self-organization into convection cells of various geometrical shapes, solutal buoyancy convection can be tailored to self-organize flow patterns into so-called chemical pumps.108–111 By immobilizing enzymes at fixed locations in a container, substrates and products can be ‘pumped’ over centimetre-long distances if the density differences between substrates and products are large enough. The pump velocity is governed by the substrate concentrations and the reaction rate. Intricate flow patterns can be designed by combining sequential enzymatic reactions. For example, Maiti et al. engineered a bifurcating flow pattern using three different enzymes: glucose oxidase (GOx), catalase (CAT) and acid phosphatase (AP).110 These three enzymes were separately immobilized in pieces of agarose gel and spaced apart 6–7 mm in a triangular configuration inside a reaction container. GOx and CAT take part in a reaction cascade while AP catalyses a separate reaction:
3.2 Reaction–convection systems to shape self-assembled structures
Aside from self-organizing convection patterns of molecularly dissolved compounds in solution, convection can be applied to direct the organization of self-assembled structures. Leira-Iglesias et al. provide a demonstration of solutal buoyancy to affect the macroscopic organization of a supramolecular polymer.112 During the self-assembly of perylene diimide (PDI) based monomers, the assemblies aligned due to solutal buoyancy convection, driven by a 0.2% density mismatch between the PDI monomer and the PDI assemblies in solution. Depending on whether or not the polymerization was initiated by seeding with a small amount of PDI assemblies, the resultant PDI polymers aligned inside a centimeter-sized patch of outward pointing lines, or in multiple millimeter-sized polygon-shaped patches. Furthermore, inorganic solid structures with complex morphologies can emerge from a combination of reaction–diffusion, convection and precipitation reactions, resulting in chemical gardens and biomorphs.113,114 Finally, the concept of viscous fingering results in chemo-hydrodynamic structures at the interface of two liquids, when the low-viscosity fluid enters the more viscous fluid phase.115,116 Whereas the emergence of these fingers does not require a chemical reaction as such, it is shown how the viscous fingering amongst a low- and high-viscosity interface with the respective reagents can shape the structures that are formed upon the deprotonation of a polymer,117 the assembly of wormlike micelles,118 or crystallization.1194. Marangoni flow systems
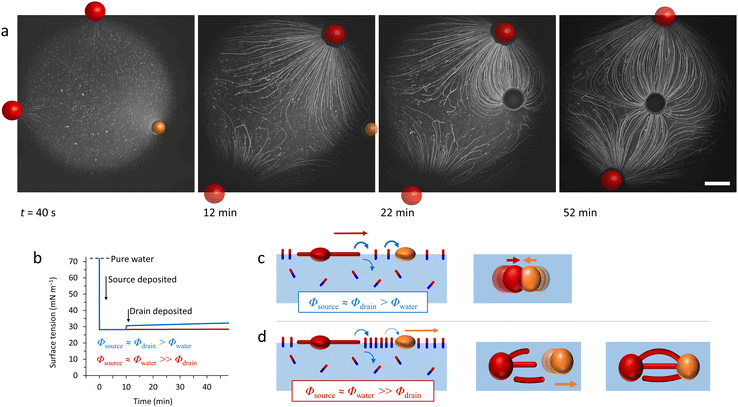
Surface tension gradients are an attractive design principle to establish organization at gas–liquid or liquid–liquid interfaces in out-of-equilibrium systems, via a simple chemical reaction (e.g. A → B, or A + B → C).120 When an imbalance in surface tension is present, a mass transfer, named the Marangoni effect, occurs from the region of low surface tension towards the region of high surface tension.121 Two types of Marangoni effect are generally described: thermo-capillary Marangoni flows are obtained when inhomogeneous heating of an interface leads to local changes in surface tension, while soluto-capillary Marangoni flows are established by the inhomogeneous repartition of a single surfactant in the system, or multiple surface active compounds with distinct surface tension properties. Regardless of their origin, these gradients induce tangential shear stresses at the interface, which in turn generate flow once the shear stress overcomes the viscous stress.122,123 This balance is represented as follows: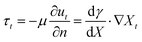 | (2) |
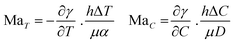 | (3) |
Marangoni flows are used in a wide variety of systems, and the examples selected here outline the diversity of approaches to create complex spatial organization. We focus on flows induced by the soluto-capillary effect, as – contrary to thermally-induced flows – they can be controlled by chemical reactions, and thereby offer a greater ability to program Marangoni flow in self-organizing systems.
4.1 Generating and sustaining surface tension gradients under non-equilibrium conditions
Surface tension gradients can be generated at 2D liquid–liquid or gas–liquid interfaces or in 3D systems at the interface of spherical droplets dispersed in solution.124–126 In each configuration, the Marangoni flow displays characteristic range, velocities and duration that depend on the chemistry and the geometry of the system.A supramolecular approach was used by Cheng et al. in their attempt to extend the lifetime of a Marangoni flow induced by a gradient of sodium dodecyl sulfate (SDS) at an air–water interface.134 Similar to the boat experiments presented above, SDS is gradually released in solution from a hydrogel source, giving rise to a Marangoni flow sustained for approximatively 45 s, before the surface tension is evened out. The system is altered to prevent interfacial saturation with the introduction of cyclodextrin as a complexation agent in the medium. By sequestering the surfactant in a supramolecular complex that readily dissolves in the bulk solution, the system is sustained far from equilibrium. The simultaneous release and capture of SDS dramatically extends the time for which the Marangoni flow is sustained by a factor 50.
To further control the way the flow is established and the period for which it is sustained (and so for which ΔC > 0), chemical reactions that impact the surface tension are particularly useful. Here, instead of relying on deposition, a gradient is established from an initially homogeneous interface by introducing reactions that locally produce or consume surface active compounds. The chemistry of fatty acid compounds is mainly used in such examples, because their acid/base properties are directly coupled with their surface activity. Indeed, the difference in surface tension between the protonated (high γ) vs. the deprotonated (low γ) forms of these compounds is significant enough to generate instabilities, meaning that the presence of a pH gradient can eventually lead to Marangoni flow. Lagzi et al.135 and later Suzuno et al.136 take advantage of the properties of 2-hexyldecanoic acid to solve mazes at a liquid-air interface. In both examples, a pH gradient is established in a solution containing the fatty acid by placing a hydrogel pre-soaked in concentrated acid at the exit of the maze. In that setting, protons diffuse away from the hydrogel source and the subsequent protonation of the fatty acid occurs unevenly at the interface, giving rise to a Marangoni flow that drags objects floating at velocities up to 10 mm s−1 directly towards the maze exit within seconds.
In a work recently published by our research group, the need for an external source of protons is eliminated upon using a photochemical reaction.137 Starting from a homogeneous aqueous solution containing a photoacid generator and the surface active sodium oleate, a pH gradient is established upon local irradiation of the interface (Fig. 10a). The rapid acidification of the medium leads to the protonation of oleate into oleic acid. Apart from displaying a higher surface tension than its deprotonated counterpart, oleic acid tends to phase-separate into oil droplets, which enhances the gradient. We have demonstrated that the Marangoni flow, by continuously bringing unreacted photoacid and oleate towards the irradiated area could sustain itself over extended periods of time of up to 30 minutes. Moreover, careful investigation into the ratio of sodium oleate over photoacid introduced in the system demonstrated that the flow velocity and duration could be accurately controlled.
 | ||
| Fig. 10 (a) Self-sustained Marangoni flow at a 2D air–water interface, triggered by local UV exposure. Photoacid generator 1-(2-nitrophenyl)ethyl sulfate (NPE sulfate) produces an acid, which protonates the surfactant oleate. Thereby, the surface tension increases at the site of UV exposure, where phase separated oleic acid droplets accumulate. Adapted from ref. 137 with permission from the Wiley-VCH publishing group, Copyright 2021. (b) Propulsion of octanol droplets in an aqueous solution (i.e. 3D system): an asymmetric occupation of lipid (of which the formation is catalyzed by the octanol-water interface) at the droplet interface results into an internal Marangoni flow in the droplet, which drives their propulsion. Adapted from ref. 147. | ||
Considerable advantages of chemistry-induced gradients can be anticipated with the way chemical reactions can be coupled with one another into networks. The reversibility of acid/base chemistry can also be an asset in efforts to increase the complexity of the system and possibly generating feedback loops.
Over the past decade, photoswitches have gained traction for their ability to remotely modify surface properties, because of their light sensitivity and their high reversibility.138,139 In a variety of studies, amphiphilic molecules containing a photoswitchable azobenzene moiety have been synthetized to control interfacial mass transfer. These systems, exemplified by the work of Diguet et al., rely on the drastic change in surface activity displayed by the trans (low γ) and cis (high γ) isomers (in some cases +10 mN m−1)140 to generate stimuli-responsive Marangoni flows.141 In a work by Lv et al., the trajectory of polystyrene microparticles present at an air–water interface is manipulated by using such a photoswitch.142 Upon light activation (laser irradiation at 442 nm) of an interface covered with the trans surfactant, local cis isomerisation leads to the transport and trapping of the particles at the beam location. The use of multiple laser beams in close proximity reveals the possibility to manipulate adjacent surface tension gradients to control the positioning of multiple particles.
Self-propulsion of droplets immersed in a micellar continuous phase can also occur when the micelles present in the system are able to partially solubilize the droplet phase. This phenomenon is exemplified by Izri et al. where water droplets are immersed in solutions of squalane and monoolein.145 Monoolein, which acts as a surfactant, ensures the stability of the emulsion by covering the droplets interface. When its concentration exceeds the critical micelle concentration (CMC), surfactant molecules present at the water-squalane interface migrate to the bulk to join the newly formed micelles, which in turn begin to solubilize water in the squalene running phase, thereby displaying the above mentioned symmetry breaking. A surface tension gradient emerges at the droplets interface because they are no longer homogeneously covered with surfactant, and self-propulsed motion is observed with velocities ranging between 10 and 50 μm s−1.
In a similar system, Thutupalli et al. demonstrate that chemical reactions involving monoolein at water droplets interface can be at the origin of self-propulsion and collective behaviour.146 The aqueous droplets, immersed in squalane and monoolein, contain bromine, or reagents leading to bromine formation. At the droplet interface, bromine readily reacts with the monoolein double bond, to form a less active brominated surfactant. The subsequent surface tension imbalance results in active droplets, of which the internal and external velocity fields can be computed by taking into account the relation between surface tension and the bromination density. Collective behaviour, signified here by the polar alignment of the velocities of neighbouring droplets, is observed experimentally and explored theoretically, revealing that the interaction of self-propulsed droplets in a high density environment may lead to the formation of ordered structures.
In a work performed by Babu et al., another type of chemical system is used to trigger the motion of organic droplets.147,148 The authors show that the lipid-forming reaction between 1-hexanethiol and 2-methacryloyloxyethyl phosphorylcholine can be exploited to induce the propulsion of octanol droplets immersed in an aqueous medium (Fig. 10b). The lipid formation is catalysed by the octanol–water interface, leading to a homogeneous lipid coverage of the octanol droplets. Over time, the lipid concentration increases in the medium and they begin to self-assemble into micelles that partially solubilize the octanol in water. The recruitment of lipids into micelles results in a non-homogeneous coverage of the droplets and thus in symmetry breaking which leads to internal Marangoni flow. This work demonstrates that for a specific droplet/surfactant couple, a critical propulsion concentration, beyond the CMC value, needs to be reached to observe motion in the system.
Lastly, a recent study by Cheon et al. demonstrates that the self-propulsion of oil droplets in micellar solutions can be drastically enhanced by the addition of silica particles.149 They hypothesize that the adsorption of these particles at the rear of the droplet interface helps to further polarize the droplet and thereby enhance the Marangoni induced-propulsion. While the precise mechanism is not clarified yet, this effect is observed for a wide range of surfactants and oil and so, opens new perspective in the domain of self-propelled droplets.
4.2 Examples of self-organized systems using surface tension gradients
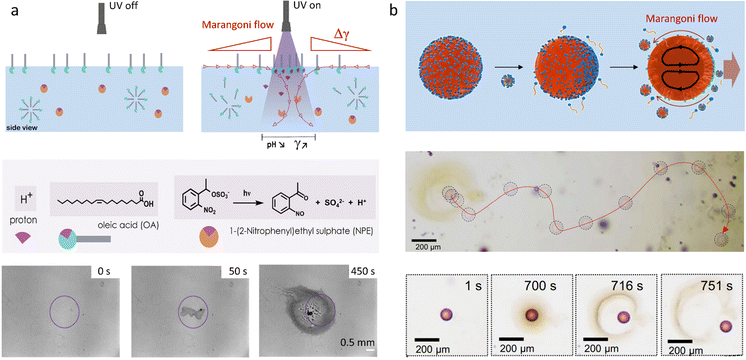
When it comes to the Marangoni effect, self-organization seems particularly likely to emerge in systems relying on a two-body interaction or the collective behaviour of multiple objects placed at a fluid interface. Even though such ‘two-body’ systems all depend on the difference in surface property of two distinct objects, they encompass a wide variety of complex interactions to drive the self-organization.In a source-sink configuration, the surface tension gradient is sustained by the interaction between an object that generates a Marangoni flow (source) and another one that absorbs surface active compounds (sink). Our research group has used such dynamics to obtain self-organized patterns between source and drain droplets deposited at an 2D air–water interface.150 Here, source droplets composed of the surfactant tetraethyleneglycol monododecyl ether (C12E4) are used not only to generate a surface tension gradient by releasing the surfactant, but also for their ability to grow centimetre-long, multi-lamellar wire-like structures called myelin figures. We showed that to form patterns, the positioning of these sources can be mediated by the presence of liquid organic droplets that act as sinks by absorbing C12E4 from the air–water interface (Fig. 11a). The resulting Marangoni flow accelerates the growth of the myelin figures from the source droplet, while simultaneously directing them towards the sink droplets. Upon adsorption at the sink, the myelin figures impose a force on the sink droplet, drawing it towards the source until the attractive force is balanced with the repelling Marangoni flow (Fig. 11b and c).151 Along with a kinetic model, we demonstrated experimentally that the composition of the sink determines its capacity for surfactant uptake, and thereby on the self-organization of the myelins-droplet networks.
 | ||
| Fig. 11 Self-organized source-sink system driven by Marangoni flows. (a) Optical microscopy recordings of an air–water interface where a newly deposited oleic acid sink droplet (orange) positions itself between two C12E4 source droplets (red). The interaction between the three floating droplets is mediated by the attractive and repulsive forces originating from the local surface tension gradients at the interface. The source droplets grow myelins and release surfactant molecules in solution, inducing a surface tension gradient. The repelling Marangoni flow that they generate is balanced by the sink droplet that absorbs the surfactant and tethers to the myelins, leading to self-organization into a linear pattern. The scale bar is 2 mm. (b) Simulation of the dynamic surface tension based on C12E4 release rate from the source (Φsource), its absorption rate by the sink (Φdrain) and its desorption from the interface (Φwater). The blue curve represents a situation where the deposition of the sink induces a local surface tension gradient because it absorbs the surfactant faster than it desorbs from the interface. In opposition, the red curve shows a situation where the desorption is faster than the absorption. (c) The schemes present the impact of the dynamic surface tension on the droplets’ positioning. The top, absorption-dominant situation leads to attraction between source and sink. The bottom, desorption-dominant situation leads to repulsion of the sink away from the source, followed by tethering of the myelins to the sink, which keeps the sink in position. Adapted from ref. 150. | ||
A different type of source-sink configuration is developed by Meredith et al. where organic droplets immersed in an aqueous Triton X-100 micellar solution display predator-prey behaviour (Fig. 12a).152 In this 3D system, the difference in micellar solubilisation rate between droplets of 1-bromooctane (BOct) and ethoxynonafluorobutane (EFB), respectively used as source and sink, is exploited to give rise to complex chase dynamics. In a first step, the BOct predator droplets deplete their surroundings from Triton X-100 by recruiting the surfactant to form BOct-filled micelles (Fig. 12b). This produces a gradient of filled micelles that tends to repel other predator droplets, as the depletion of surfactant generates an asymmetric surfactant occupation at the droplet interface, which drives its motion away from the other BOct droplet. On the contrary, EFB prey droplets are able to have non-reciprocal interactions with their predators because they are resistant to micellar solubilisation and thus induce no repulsion. When EFB preys are in proximity to their BOct predators, they primarily interact with the filled micelle gradient by taking up the BOct that they carry, emptying the previously filled micelles. The adsorption of these newly-formed empty micelles at the front of BOct droplets triggers the internal Marangoni propulsion that is at the origin of the chase, as the prey droplet flees from the predator towards regions with an even lower concentration of solubilized oil. This dynamic behaviour is sustained by the gradient in BOct-filled micelles and can therefore be modulated by the Triton X-100 concentration in the aqueous phase. Increasing the density of predators and prey in a system also leads to self-assembled clusters displaying remarkably complex interactions based on the same non-reciprocal exchanges.
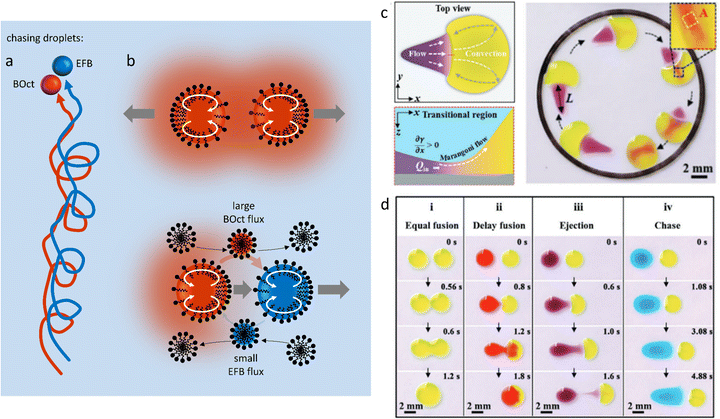 | ||
| Fig. 12 Self-organized motion in two-body systems. (a) Chase dynamics between BOct (red) and EFB (blue) droplets immersed in a micellar Triton X-100 solution. The BOct predator droplet chases after the EFB prey droplet. Once the predator has caught the prey they keep moving as a pair in the solution. (b) The scheme details the non-reciprocal mechanism behind the chase: (1) BOct is solubilized in the Triton micelles, creating a repelling gradient of filled micelles around it (top scheme). (2) BOct-filled micelles diffuse in the solution and the transported oil is taken up by the EFB droplets, releasing new free micelles at the back of the prey. (3) The free micelles are adsorbed at the front of the predator droplets, triggering the Marangoni propulsion of the predator towards the prey (bottom scheme). (4) The preys also escape the predator by using Marangoni propulsion, moving towards areas rich in empty micelles.152 (c) Self-driven droplet vehicle actuated by the Marangoni effect. The vehicle is made of two droplets (head in yellow, tail in purple) adsorbed on a solid substrate. The surface tension difference between head (high γ) and tail (low γ) generates a convective flow that enables the vehicle to move into a confined space until the tail merges with the head. (d) Table recapitulating the type of vehicle interaction (fusion, delay fusion, ejection, chase) that can be obtained when the surface tension of the tail droplet is decreased while the head droplet is kept constant. (c and d) Reproduced from ref. 154 with permission from the Wiley-VCH publishing group, Copyright 2021. | ||
Self-driven droplet vehicles developed by Cira et al.,153 and further explored by Li et al.154 are fascinating examples of the versatility present in two-body systems. These vehicles consist of two liquid droplets with distinct surface tensions at their air–liquid interface, that are deposited on a solid substrate, one serving as head and the other as tail (Fig. 12c). When in contact, the convective flow that is generated because of the surface tension difference between the two liquids constitutes the driving force of the vehicles (Fig. 12d), and Li et al.154 demonstrate that this surface tension difference must exceed 5 mN m−1 while the size ratio of the droplets (Dhead/Dtail) must be above 1.6 to display propulsion. Interestingly, they revealed that increasing Δγ did not systematically induce an increase in propulsion velocity and that the latter was in fact determined by the surface tension coefficient ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) /Δγ, where
/Δγ, where ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) represents the average of the initial γhead and γtail, and Δγ is the difference between the initial γhead and γtail. Finally, they show that by carefully choosing the liquids, the vehicles can efficiently deposit colloidal particles at solid surfaces into patterns at the microscale.
represents the average of the initial γhead and γtail, and Δγ is the difference between the initial γhead and γtail. Finally, they show that by carefully choosing the liquids, the vehicles can efficiently deposit colloidal particles at solid surfaces into patterns at the microscale.
In a work published by Liu et al., decanol droplets are driven through complex pathways at a liquid interface by surface tension gradients induced with organic solvent vapours.155 The decanol droplets are deposited on aqueous ethanol solutions while carbon tetrachloride (CCl4) vapour is released from droplets suspended on a glass substrate placed a few millimetres above the interface (Fig. 13a). The CCl4 vapour locally increases the surface tension and therefore generates Marangoni flows that attract the decanol droplets, towards the vapour-rich area. Intriguingly, the use of multiple droplets at the interface reveals the possibility to generate dynamic droplet patterns. Here, CCl4 is placed on the glass substrate to form the letter T, H or U, and when placed over the interface, the decanol droplets organize according to that shape while maintaining a distance between one another. This out-of-equilibrium process is controlled by the attractive Marangoni flow, driven by the CCl4 vapour, and the repulsive interaction between the decanol droplets, which is driven by the outward Marangoni flow when the droplets are in close contact. Together, this shows promise for the emergence of collective effects in multi-droplets systems.
 | ||
| Fig. 13 Collective behaviour in multi-droplets systems. (a) Decanol droplets at air–water interface self-organize into various letter-shaped patterns under the influence of CCl4 vapours. The latter are used to increase the local surface tension of the interface and subsequently attract the decanol droplets. The patterns are then sustained by the simultaneous action of the Marangoni effect and the repulsion exerted by each droplet. Reprinted (adapted) with permission from ref. 155. Copyright 2019 American Chemical Society. (b) Dynamic self-organized patterns are observed when ethyl salicylate droplets are deposited over an aqueous SDS solution. The initially random arrangement (I) evolves to successively form a ring (II), a chain-like structure (III) and eventually a compact cluster (IV). The organic droplets partially solubilize in the surfactant-rich medium over time, each generating its own Marangoni flow. The transformation of the patterns is therefore understood to be the result of the complex interaction between the local surface tension gradients produced by each individual droplet, and capillary interaction. The scale bar is 10 mm. Reprinted from Colloids and Surfaces A, 566, J. Čejková, K. Schwarzenberger, K. Eckert, S. Tanaka, Dancing performance of organic droplets in aqueous surfactant solutions, 141–147, Copyright 2019, with permission from Elsevier. | ||
In experiments involving TiO2 particles at a silicon oil–water interface, Wittmann et al. observed Marangoni-induced collective motion upon UV irradiation of the system.156 The particles are adsorbed onto the interface because of the presence of the surfactant Triton X and they catalyse the photo-degradation of H2O2 in the aqueous solution. They report that the spherical particles, which individually display no motility due to their symmetry, are able to collectively move towards an area exposed to UV when they are present as a monolayer, indicating that a collective effect is at the origin of the phenomenon. Throughout their investigation, they rule out possible thermal or phoretic effects and argue that the inhomogeneous repartitioning of the particles at the oil–water interface along with the interface response to the photochemical activity is responsible for symmetry-breaking events leading to a Marangoni flow. The system appears to be maintained in an out-of-equilibrium state by continuous UV exposure, and therefore continuous H2O2 decomposition, as the particles’ motion is interrupted as soon as the irradiation is stopped. Additionally, they demonstrate the existence of a particle density dependence on flow behaviours. In low density settings, the TiO2 particles gather in the irradiated area within seconds and then immediately bounce away from it while in high density settings, they gather and accumulate in the irradiated area to form a stable cluster.
Intriguing collective effects are observed by Tanaka et al., and further explored by Čejková et al. when droplets of decanol or ethyl salicylate (ES) are respectively deposited at the interface of sodium decanoate or SDS aqueous solutions.157,158 The organic droplets first display individual random motion, but then evolve into self-organized dynamic clusters. Three consecutive cluster configurations are showcased in both systems (Fig. 13b). First, a geometrical configuration is obtained where the droplets arrange themselves into a semi-static pattern, circular for ES droplets and squared for the decanol droplets. Over time, these patterns become less stable and eventually collapse, followed by the emergence of a second configuration. Here, the cluster appears to be oscillating because droplets form chain-like structures where they continuously permutate with one another. In the third configuration, the droplets merge via capillary attraction into compact clusters that remain static for hours. The complex interaction between each droplet and the surfactant solution seems to be at the origin of the unique configurations displayed in both systems. Indeed, a study of the decanol droplets in decanoate solution reveals that partial dissolution of the droplets in the medium decreases the local surface tension and thus generates a Marangoni flow away from them. In this context, it is hypothesized that the varying intensity of the Marangoni flow generated from each droplet mediates the interaction, repulsive or attractive, between the members of the cluster.
5. Diffusiophoresis systems
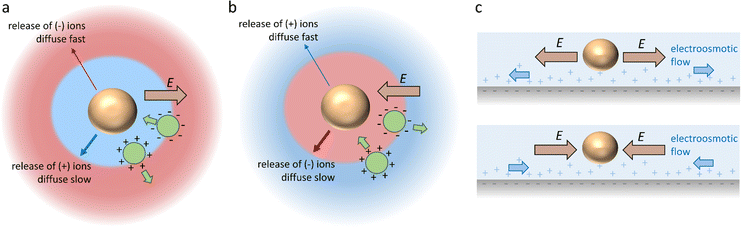
Diffusiophoresis is well-established as a mechanism to drive the directional motion of objects, such as colloidal particles, up or down concentration gradients in solution, with speeds that are impossible to establish with Brownian motion (up to 1–10 μm s−1).159 This opens perspectives to direct self-organization. The motion of a particle up or down a solute concentration gradient is driven by the favourable or unfavourable interaction between solute and particle. In electrolyte-based (ionic) gradients, diffusiophoresis typically generates faster particle velocities compared to non-electrolyte gradients.159 Furthermore, self-diffusiophoresis, where particles migrate along self-generated gradients, typically involves electrolytes.160 In many self-organizing systems where electrolyte gradients induce the motility of charged colloidal particles, the velocity of the particles is dominated by the electric field that spontaneously emerges in a concentration gradient of ions with different diffusion coefficients. For example, for an ammonia solution, D(NH4+) = 1.96 × 10−9 m2 s−1, and D(OH−) = 5.27 × 10−9 m2 s−1, and therefore, OH− diffuses faster down the ammonia concentration gradient that is released from the spherical source in Fig. 14a. Thereby, an electric field arises that concomitantly slows down OH− diffusion and speeds up NH4+, in order to enhance local electro-neutrality in the solution. This electric field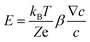 drives charged particles, with zeta potential ζp, with a speed
drives charged particles, with zeta potential ζp, with a speed 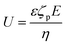 down the electric field. Here, β represents the diffusivity difference factor: for symmetric Z:Z electrolytes (i.e., equally charged cations and anions), β = (D+ − D–)/(D+ + D–), where D+ and D– represent cation and anion diffusivity, respectively. ε is the dielectric permittivity of the medium, η the viscosity of the medium, and ∇c/c the relative concentration gradient of the electrolyte (in m−1). This relationship implies that an ammonia gradient decreasing along the x-axis (dc/dx < 0) causes a negatively charged particle (ζp < 0) to move up the concentration gradient (U < 0), since β < 0 for NH4+/OH−, and a positively charged particle to move down the gradient. Vice versa, upon release of an electrolyte with a cation diffusing faster than the anion (β > 0), a positive particle will move up the concentration gradient, and a negatively charged particle will move down the gradient (Fig. 14b). Alternatively, if an electrolyte gradient with unequal diffusion constants of cat- and anions is established along a charged substrate, the counter ions of this substrate will be exposed to the electric field that is generated by the differential ion diffusion. As a result, an electroosmotic flow emerges along the substrate, as schematically shown in Fig. 14c.
down the electric field. Here, β represents the diffusivity difference factor: for symmetric Z:Z electrolytes (i.e., equally charged cations and anions), β = (D+ − D–)/(D+ + D–), where D+ and D– represent cation and anion diffusivity, respectively. ε is the dielectric permittivity of the medium, η the viscosity of the medium, and ∇c/c the relative concentration gradient of the electrolyte (in m−1). This relationship implies that an ammonia gradient decreasing along the x-axis (dc/dx < 0) causes a negatively charged particle (ζp < 0) to move up the concentration gradient (U < 0), since β < 0 for NH4+/OH−, and a positively charged particle to move down the gradient. Vice versa, upon release of an electrolyte with a cation diffusing faster than the anion (β > 0), a positive particle will move up the concentration gradient, and a negatively charged particle will move down the gradient (Fig. 14b). Alternatively, if an electrolyte gradient with unequal diffusion constants of cat- and anions is established along a charged substrate, the counter ions of this substrate will be exposed to the electric field that is generated by the differential ion diffusion. As a result, an electroosmotic flow emerges along the substrate, as schematically shown in Fig. 14c.
5.1 Self-organization by electrolyte diffusiophoresis
Electrolyte diffusiophoresis has been demonstrated to drive the motion of a wide variety of charged particles along electrolyte gradients, where the path of the particles is determined by the concentration profile.161 For example, Squires et al. have demonstrated how hydrogels that slowly release electrolytes serve as beacons that attract or repel charged colloidal micro-particles over distances as long as 1 mm.162 In pH gradients that are sustained by complementary hydrogel couples that release base and acid, respectively, 1 μm-sized negative polystyrene particles were transferred at speeds larger than 2 μm s−1 over a distance of approx. 1 mm from the acid to the base source, resulting into emerging flow patterns as shown in Fig. 15a. These observations highlight the strong contribution of OH− and H+ to the electric fields that are generated, since both OH− (D = 5.27 × 10−9 m2 s−1) and H+ (D = 9.31 × 10−9 m2 s−1) diffuse significantly faster than their respective counter-ions (typically D ≈ 1 × 10−9 m2 s−1). Additionally, the acid-base reaction sustains the diffusion of acid and base from the respective sources.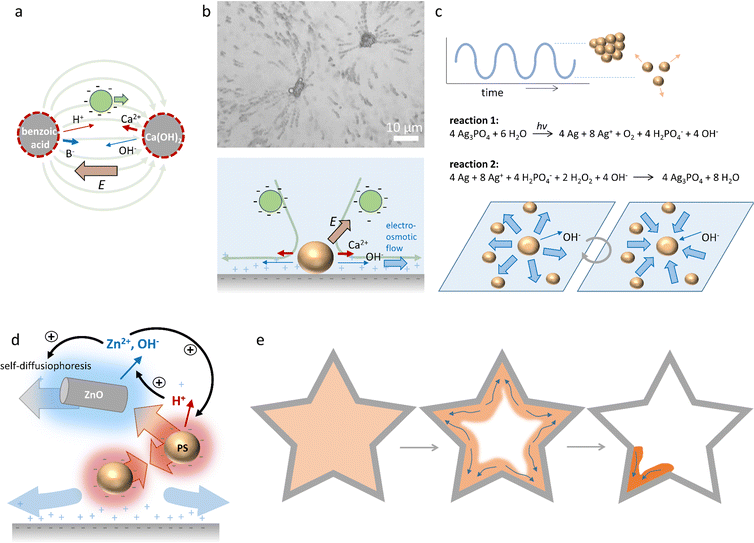 | ||
| Fig. 15 Self-organisation driven by diffusiophoresis. (a) Motion pattern of negatively charged tracer particles along a sustained pH gradient between benzoic acid and Ca(OH)2 sources.162 (b) Electroosmotic flow drives the motion of tracer particles amongst CaCO3 microparticles on a negatively charged substrate. Reprinted (adapted) with permission from ref. 163. Copyright 2012 American Chemical Society. (c) Oscillatory clustering and dispersion of Ag3PO4 microparticles in an aqueous H2O2 solution, where reaction (1) and (2) alternate and drive the electroosmotic flow.170 (d) Diffusiophoretic colloidal swarms based on ZnO nanorods and sulfonated polystyrene microbeads, that are coupled via an ion exchange reaction that provide positive and negative feedback to ZnO/polystyrene clustering. (e) Collective swarm behaviour of ZnO/polystyrene particles (orange) that accumulate in the edge of the geometry (grey) with the highest curvature.171 | ||
Furthermore, McDermott et al.163 reported self-generated flow patterns that emerge from calcium carbonate micropumps, where CaCO3 microparticles slowly dissolve and generate an ionic gradient of Ca2+, HCO3− and OH− ions in the surrounding solution. Due to the high diffusion constant of OH−, an electric field of 1–10 V cm−1 is generated, which is oriented away from the CaCO3 microparticles. This electric field attracts negatively charged sulfate-functionalized polystyrene tracer particles towards the CaCO3 microparticles. Interestingly, as the tracer particles approach the surface underneath the CaCO3 microparticles, they are rapidly ejected radially outward in solution, as shown in Fig. 15b. The flow pattern of the tracer particles exemplifies the electroosmotic flow, which originates from the electric field that is generated around the dissolving CaCO3 microparticles, and exerts its influence on the counterions of the negatively charged substrate.
In addition to particles that move in external concentration gradients, self-organization of dynamic colloidal swarms can emerge from a homogeneous dispersion of particles via autophoresis.160 Here, the colloids self-generate a gradient of ions, which provides the electric field that is required for their propulsion and leads to organized collective behaviour. This concept has been exploited in self-assembly,164,165 dynamic clustering,166 schooling167,168 and predator-prey behaviour of colloidal systems.169 Recently, it has been shown that autophoretic systems can be classified as being either self-diffusiophoretic, when a net ion production occurs, or self-electrophoretic, when the net ion production is zero (i.e., ions are released at one side of the particle, and consumed at the other side).160 Self-diffusiophoretic colloids tend to move slower in a denser population, and form clusters that grow over time, whereas the motility of self-electrophoretic colloid clusters is independent of their density, and results in dynamic clusters with limited sizes.160
Collective, oscillatory behaviour of colloidal swarms has been reported by Altemose et al.170 Silver orthophosphate microparticles (Ag3PO4) are dispersed in an aqueous hydrogen peroxide (H2O2) solution that is exposed to continuous UV illumination. Two opposing reactions occur: (1) reduction of silver ions (Ag+) to silver metal (Ag) under UV illumination, and (2) oxidation of Ag to Ag+ by H2O2 (Fig. 15c). As OH−, which is formed upon the photo-reduction, has a higher diffusion coefficient than the positive ions that are produced, an electric field is generated which is directed away from the Ag3PO4 microparticles. This electric field acts on the positive counterions of the underlying glass substrate, resulting in an electroosmotic flow away from individual Ag3PO4 microparticles, which drives their mutual repulsion in the swarm. However, the re-oxidation (reaction (2)) consumes OH−, and thereby reverses the electroosmotic flow. This causes the Ag3PO4 microparticles to attract each other and form compacted clusters. At the onset of the experiment, microparticles form stable clusters in the presence of H2O2 and UV, and after approx. 5–10 min, instabilities emerge that cause the clusters to disperse. Subsequently, the combination of both reactions causes the microparticles to periodically cluster and disperse. Intriguingly, these oscillations can be synchronized among neighbouring clusters through the diffusion of ions, and oscillation frequencies can be controlled via the H2O2 concentration.
Recently, Wu et al.171 reported diffusiophoretic colloidal swarms inspired by a microbial symbiosis system, where the waste product of one chemical species is the nutrient that drives the motility of the other, and vice versa (Fig. 15d). To this end, ZnO nanorods and sulfonated polystyrene microbeads are coupled via an ion exchange reaction. ZnO nanorods release Zn2+ and OH− in solution, resulting in self-diffusiophoresis that propels the nanorods with velocities up to 2 μm s−1. As the polystyrene microbeads are negatively charged, they are attracted via electrophoresis along the Zn2+ gradient towards the ZnO nanorods. At the same time, the porous polystyrene microbeads take up Zn2+ and release H+via an ion exchange reaction. The H+ gradient that is generated around the negatively charged PS beads causes them to attract each other via an electroosmotic flow at the substrate. Furthermore, the high H+ concentration around the PS bead clusters lowers the local pH, which enhances Zn2+ release as the polystyrene beads approach the ZnO nanorods. Together, the ion exchange between ZnO nanorods and polystyrene microbeads generates a positive feedback that enhances the motility of both. However, close to the glass substrate, underneath the ZnO nanorods/polystyrene microbeads conglomerates, an outward electroosmotic flow is generated, which disassembles the aggregates. Together, the dynamic coupling of the ZnO nanorod/polystyrene microbead system through interconnected ion-exchange reactions allows for hierarchical and dynamic swarm behaviour (Fig. 15e). The clustering of the aggregates is enhanced when high concentrations of Zn2+ and H+ accumulate at the edge of the sample chamber. As a result, the ZnO and polystyrene particles accumulate at all edges and corners present in the geometry of the system. Over the course of the accumulation, the highest curvature confines the ions most successfully. Once a threshold accumulation is reached, the mixture acts as a collective swarm and all colloids migrate towards the sharpest corner – in analogy to the quorum sensing routines displayed by microorganisms.
6. Outlook
The examples of self-organization highlight the potential of reaction–diffusion coupling, reaction–convection, the Marangoni effect and diffusiophoresis to sustain physicochemical gradients, which are critical to shape concentration patterns in solution, drive the self-assembly of out-of-equilibrium structures, or direct the organization of colloidal swarms. Importantly, the emergence of a stable gradient, rather than an uncontrolled system, requires a subtle balance of opposing effects, such as activation and inhibition, solute production and convection, or release and depletion of surfactants or electrolytes. This imposes limits on the parameter window where self-organization can be obtained (e.g. kinetic rate and diffusion constants, differences in density, surface tension, etc.). As a result, finding a new chemical system with a particular topology of feedback relations amongst chemical reactions and physicochemical principles that gives rise to self-organizing gradients is typically a serendipitous endeavour. And whereas moving particles driven by Marangoni flow or diffusiophoresis can easily be observed under the microscope (or even with the naked eye), reaction–diffusion or reaction–convection patterns that emerge in a homogeneous solution can easily be overlooked if the chemicals involved cannot be distinguished based on colour. In this regard, the development of DNA- and enzyme-based reaction networks – rather than exploiting reaction topologies of chemical systems that cannot be easily modified – opens new potential to follow a model-driven approach and design feedback relationships that can be implemented in the synthetic network topology. We note that the robustness and diversity of self-organizing modes can be expanded by combining different types of gradients – that are typically used in different physical environments, e.g. Marangoni flow with diffusiophoresis172 or buoyancy.91We anticipate that molecular systems which translate chemical reactions into gradients can strengthen the link between systems chemistry – i.e. the study of multicomponent molecular networks and their emergent properties – and advanced materials that operate at the micro-, meso- or macroscale.173–175 Whereas classical responsive systems such as hydrogels typically respond to a single parameter (e.g. swelling/contraction upon pH change), sustained physicochemical gradients allow integration of multiple chemical input signals into a specific self-organizing response.176,177 This might be exploited to direct the bottom-up construction of morphogenetic materials, for example in interactive biomaterials that adapt their form or texture in concert with bio-molecular cues from the surrounding tissue. Alternatively, self-organization can generate read-out patterns in diagnostic systems that distinguish and report signal inputs derived from complex samples. Furthermore, in chemical systems that solve computational problems, such as maze-solving,178 logic operations179 or pattern recognition,180 the information is typically transferred via diffusion among the ‘computing cores’ where chemical reactions take place that represent the computational steps. Whereas spread of molecular signals via diffusion by itself is uncontrolled, self-organizing gradients can autonomously determine how chemical input signals are guided, for example via reaction–diffusion waves, traveling droplets, growing filaments or organizing colloidal swarms, amongst the computing cores, and ultimately be transferred into material-based responses. Taken together, we foresee that self-organization emerging from chemical systems presents new potential to process complex molecular information into matter-based functional behaviour.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank the Dutch Research Council (NWO, START-UP grant no. 740.018.003) as well as the Dutch Ministry of Education, Culture and Science (Gravitation program 024.001.035) for financial support.References
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- P. Ball, The Self-Made Tapestry: Pattern Formation in Nature, Oxford University Press, Oxford, 2001 Search PubMed.
- T. Wittmann, A. Hyman and A. Desai, Nat. Cell Biol., 2001, 3, E28–E34 CrossRef CAS PubMed.
- A. Tero, S. Takagi, T. Saigusa, K. Ito, D. P. Bebber, M. D. Fricker, K. Yumiki, R. Kobayashi and T. Nakagaki, Science, 2010, 327, 439–442 CrossRef CAS.
- T. Gregor, K. Fujimoto, N. Masaki and S. Sawai, Science, 2010, 328, 1021–1025 CrossRef CAS PubMed.
- P. J. Keller, Science, 2013, 340, 1234168 CrossRef.
- G. Ashkenasy, T. M. Hermans, S. Otto and A. F. Taylor, Chem. Soc. Rev., 2017, 46, 2543–2554 RSC.
- H. S. Azevedo, S. L. Perry, P. A. Korevaar and D. Das, Nat. Chem., 2020, 12, 793–794 CrossRef CAS PubMed.
- B. A. Grzybowski and W. T. S. Huck, Nat. Nanotechnol., 2016, 11, 585–592 CrossRef CAS PubMed.
- E. Mattia and S. Otto, Nat. Nanotechnol., 2015, 10, 111–119 CrossRef CAS PubMed.
- I. Prigogine and R. Lefever, J. Chem. Phys., 1968, 48, 1695–1700 CrossRef.
- G. Nicolis and I. Prigogine, Proc. Natl. Acad. Sci. U. S. A., 1981, 78, 659–663 CrossRef CAS.
- G. Nicolis and I. Prigogine, Self-Organization in Nonequilibrium Systems, Wiley, New York, 1977 Search PubMed.
- L. Pismen, Patterns and Interfaces in Dissipative Dynamics, Springer Verlag Berlin, Heidelberg, 2006 Search PubMed.
- L. Onsager, Phys. Rev., 1931, 37, 405–426 CrossRef CAS.
- M. Kirschner and T. Mitchison, Cell, 1986, 45, 329–342 CrossRef CAS.
- S. M. Morrow, I. Colomer and S. P. Fletcher, Nat. Commun., 2019, 10, 1–9 CrossRef CAS PubMed.
- K. K. Nakashima, J. F. Baaij and E. Spruijt, Soft Matter, 2018, 14, 361–367 RSC.
- G. Ragazzon and L. J. Prins, Nat. Nanotechnol., 2018, 13, 882–889 CrossRef CAS PubMed.
- E. te Brinke, J. Groen, A. Herrmann, H. A. Heus, G. Rivas, E. Spruijt and W. T. S. Huck, Nat. Nanotechnol., 2018, 13, 849–855 CrossRef CAS PubMed.
- J. Boekhoven, W. E. Hendriksen, G. J. M. Koper, R. Eelkema and J. H. van Esch, Science, 2015, 349, 1075–1079 CrossRef CAS PubMed.
- M. Kumar, N. L. Ing, V. Narang, N. K. Wijerathne, A. I. Hochbaum and R. V. Ulijn, Nat. Chem., 2018, 10, 696–703 CrossRef CAS PubMed.
- A. Mishra, D. B. Korlepara, M. Kumar, A. Jain, N. Jonnalagadda, K. K. Bejagam, S. Balasubramanian and S. J. George, Nat. Commun., 2018, 9, 1–9 CrossRef.
- R. K. Grötsch, C. Wanzke, M. Speckbacher, A. Angı, B. Rieger and J. Boekhoven, J. Am. Chem. Soc., 2019, 141, 9872–9878 CrossRef.
- T. Heuser, E. Weyandt and A. Walther, Angew. Chem., Int. Ed., 2015, 54, 13258–13262 CrossRef CAS.
- A. M. Turing, Philos. Trans. R. Soc., B, 1952, 52, 153–197 Search PubMed.
- L. Wolpert, J. Theor. Biol., 1969, 25, 1–47 CrossRef CAS.
- J. B. A. Green and J. Sharpe, Development, 2015, 142, 1203–1211 CrossRef CAS.
- J. Briscoe and S. Small, Development, 2015, 142, 3996–4009 CrossRef CAS PubMed.
- F. Brauns, G. Pawlik, J. Halatek, J. Kerssemakers, E. Frey and C. Dekker, Nat. Commun., 2021, 12, 1–11 CrossRef.
- A. N. Landge, B. M. Jordan, X. Diego and P. Müller, Dev. Biol., 2020, 460, 2–11 CrossRef CAS.
- J. Halatek, F. Brauns and E. Frey, Philos. Trans. R. Soc., B, 2018, 373, 20170107 CrossRef.
- S. Kondo and T. Miura, Science, 2010, 329, 1616–1620 CrossRef CAS.
- R. Sheth, L. Marcon, M. F. Bastida, M. Junco, L. Quintana, R. Dahn, M. Kmita, J. Sharpe and M. A. Ros, Science, 2014, 338, 1476–1480 CrossRef.
- A. D. Economou, A. Ohazama, T. Porntaveetus, P. T. Sharpe, S. Kondo, M. A. Basson, A. Gritli-Linde, M. T. Cobourne and J. B. A. Green, Nat. Genet., 2012, 44, 348–351 CrossRef CAS PubMed.
- V. Castets, E. Dulos, J. Boissonade and P. De Kepper, Phys. Rev. Lett., 1990, 64, 2953–2956 CrossRef CAS.
- I. Lengyel and I. R. Epstein, Science, 1991, 251, 650–652 CrossRef CAS PubMed.
- I. Lengyel and I. R. Epstein, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 3977–3979 CrossRef CAS.
- K. Asakura, R. Konishi, T. Nakatani, T. Nakano and M. Kamata, J. Phys. Chem. B, 2011, 115, 3959–3963 CrossRef CAS PubMed.
- K. J. Lee, W. D. McCormick, Q. Ouyang and H. L. Swinney, Science, 1993, 261, 192–194 CrossRef CAS.
- K.-J. Lee, W. D. McCormick, J. E. Pearson and H. L. Swinney, Nature, 1994, 369, 215–218 CrossRef.
- I. Szalai and P. De Kepper, Chaos, 2008, 18, 026105 CrossRef PubMed.
- A. M. Zhabotinsky, Biofizika, 1964, 9, 306–311 Search PubMed.
- A. N. Zaikin and A. M. Zhabotinsky, Nature, 1970, 225, 535–537 CrossRef CAS.
- A. T. Winfree, Science, 1972, 175, 634–636 CrossRef CAS PubMed.
- V. K. Vanag and I. R. Epstein, Phys. Rev. Lett., 2001, 87, 228301 CrossRef CAS.
- I. R. Epstein and V. K. Vanag, Chaos, 2005, 15, 47510 CrossRef.
- T. Bánsági, V. K. Vanag and I. R. Epstein, Science, 2011, 331, 1309–1312 CrossRef PubMed.
- V. K. Vanag and I. R. Epstein, Chaos, 2008, 18, 026107 CrossRef PubMed.
- J. E. Pearson, Science, 1993, 261, 189–192 CrossRef CAS.
- V. K. Vanag and I. R. Epstein, Phys. Chem. Chem. Phys., 2009, 11, 897–912 RSC.
- P. Gray and S. K. Scott, Chem. Eng. Sci., 1984, 39, 1087–1097 CrossRef CAS.
- A. Gierer and H. Meinhardt, Kybernetik, 1972, 12, 30–39 CAS.
- J. Schnakenberg, J. Theor. Biol., 1979, 81, 389–400 CrossRef CAS PubMed.
- R. J. Field and R. M. Noyes, J. Chem. Phys., 1974, 60, 1877–1884 CrossRef CAS.
- J. Horváth, I. Szalai and P. De Kepper, Acc. Chem. Res., 2018, 51, 3183–3190 CrossRef.
- J. Horváth, I. Szalai and P. De Kepper, Science, 2009, 324, 772–775 CrossRef.
- Y. Kuramoto, Chemical Oscillations, Waves and Turbulence, Springer, Berlin, 1984 Search PubMed.
- I. R. Epstein and B. Xu, Nat. Nanotechnol., 2016, 11, 312–319 CrossRef CAS PubMed.
- V. K. Vanag and I. R. Epstein, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 14635–14638 CrossRef CAS PubMed.
- B. A. Grzybowski, Chemistry in Motion: Reaction–Diffusion Systems for Micro- and Nanotechnology, John Wiley & Sons, Ltd, Chichester, 2009 Search PubMed.
- M. Fialkowski, K. J. M. Bishop, R. Klajn, S. K. Smoukov, C. J. Campbell and B. A. Grzybowski, J. Phys. Chem. B, 2006, 110, 2482–2496 CrossRef CAS PubMed.
- G. Ertl, Science, 1991, 254, 1750–1755 CrossRef CAS PubMed.
- J. Wu, C. Yuan, T. Li, Z. Yuan, H. Zhang and X. Li, J. Am. Chem. Soc., 2021, 143, 13135–13144 CrossRef CAS.
- J. M. García-Ruiz, S. T. Hyde, A. M. Carnerup, A. G. Christy, M. J. Van Kranendonk and N. J. Welham, Science, 2003, 302, 1194–1197 CrossRef PubMed.
- J. M. García-Ruiz, E. Melero-García and S. T. Hyde, Science, 2009, 323, 362–365 CrossRef PubMed.
- P. Knoll, E. Nakouzi and O. Steinbock, J. Phys. Chem. C, 2017, 121, 26133–26138 CrossRef CAS.
- P. Knoll and O. Steinbock, Isr. J. Chem., 2018, 58, 682–692 CrossRef CAS.
- W. L. Noorduin, A. Grinthal, L. Mahadevan and J. Aizenberg, Science, 2013, 340, 832–837 CrossRef CAS PubMed.
- C. N. Kaplan, W. L. Noorduin, L. Li, R. Sadza, L. Folkertsma, J. Aizenberg and L. Mahadevan, Science, 2017, 355, 1395–1399 CrossRef CAS PubMed.
- M. H. Bistervels, M. Kamp, H. Schoenmaker, A. M. Brouwer and W. L. Noorduin, Adv. Mater., 2022, 34, 2107843 CrossRef CAS PubMed.
- H. C. Hendrikse, A. van der Weijden, M. Ronda-Lloret, T. Yang, R. Bliem, N. R. Shiju, M. van Hecke, L. Li and W. L. Noorduin, Adv. Mater., 2020, 32, 1–7 CrossRef PubMed.
- I. R. Epstein, V. K. Vanag, A. C. Balazs, O. Kuksenok, P. Dayal and A. Bhattacharya, Acc. Chem. Res., 2012, 45, 2160–2168 CrossRef CAS.
- O. Steinbock, V. Zykov and S. C. Müller, Nature, 1993, 366, 322–324 CrossRef CAS.
- T. Sakurai, E. Mihaliuk, F. Chirila and K. Showalter, Science, 2002, 296, 2009–2012 CrossRef CAS PubMed.
- R. Yoshida and T. Ueki, NPG Asia Mater., 2014, 6, e107 CrossRef CAS.
- S. Maeda, Y. Hara, R. Yoshida and S. Hashimoto, Angew. Chem., Int. Ed., 2008, 47, 6690–6693 CrossRef CAS.
- S. Maeda, Y. Hara, T. Sakai, R. Yoshida and S. Hashimoto, Adv. Mater., 2007, 19, 3480–3484 CrossRef CAS.
- X. Lu, L. Ren, Q. Gao, Y. Zhao, S. Wang, J. Yang and I. R. Epstein, Chem. Commun., 2013, 49, 7690–7692 RSC.
- K. Torbensen, F. Rossi, S. Ristori and A. Abou-Hassan, Lab Chip, 2017, 17, 1179–1189 RSC.
- A. F. Taylor, M. R. Tinsley, F. Wang, Z. Huang and K. Showalter, Science, 2009, 323, 614–617 CrossRef CAS PubMed.
- I. R. Epstein, Chem. Commun., 2014, 50, 10758–10767 RSC.
- T. Litschel, M. M. Norton, V. Tserunyan and S. Fraden, Lab Chip, 2018, 18, 714–722 RSC.
- S. Chen and G. Seelig, Soft Matter, 2020, 16, 3555–3563 RSC.
- J. Zenk, D. Scalise, K. Wang, P. Dorsey, J. Fern, A. Cruz and R. Schulman, RSC Adv., 2017, 7, 18032–18040 RSC.
- D. Scalise and R. Schulman, Technology, 2014, 02, 55–66 CrossRef.
- A. S. Zadorin, Y. Rondelez, G. Gines, V. Dilhas, G. Urtel, A. Zambrano, J. C. Galas and A. Estevez-Torres, Nat. Chem., 2017, 9, 990–996 CrossRef CAS PubMed.
- A. Senoussi, J. C. Galas and A. Estevez-Torres, Sci. Adv., 2021, 7, 1–10 Search PubMed.
- P. Glock, J. Broichhagen, S. Kretschmer, P. Blumhardt, J. Mücksch, D. Trauner and P. Schwille, Angew. Chemie, 2018, 130, 2386–2390 CrossRef.
- M. A. Budroni, F. Rossi and L. Rongy, ChemSystemsChem, 2022, 4, e202100023 CrossRef CAS.
- M. A. Budroni, L. Rongy and A. De Wit, Phys. Chem. Chem. Phys., 2012, 14, 14619–14629 RSC.
- A. De Wit, K. Eckert and S. Kalliadasis, Chaos, 2012, 22, 37101 CrossRef CAS.
- I. Mutabazi, J. E. Wesfreid and E. Guyon, Dynamics of Spatio-temporal Cellular Structures, Springer, New York, 2006 Search PubMed.
- R. Tiani, A. De Wit and L. Rongy, Adv. Colloid Interface Sci., 2018, 255, 76–83 CrossRef CAS PubMed.
- D. Avnir and M. L. Kagan, Chaos, 1995, 5, 589–601 CrossRef CAS PubMed.
- S. Chandrasekhar, Hydrodynamic and Hydromagnetic Stability, Oxford, Clarendon press, 1961 Search PubMed.
- D. Avnir and M. Kagan, Nature, 1984, 307, 717–720 CrossRef CAS.
- I. Nagypal, G. Bazsa and I. R. Epstein, J. Am. Chem. Soc., 1986, 108, 3635–3640 CrossRef CAS.
- J. Masere, D. A. Vasquez, B. F. Edwards, J. W. Wilder and K. Showalter, J. Phys. Chem., 1994, 98, 6505–6508 CrossRef CAS.
- G. Bazsa and I. R. Epstein, J. Phys. Chem., 1985, 89, 3050–3053 CrossRef CAS.
- C. Almarcha, P. M. J. Trevelyan, P. Grosfils and A. De Wit, Phys. Rev. Lett., 2010, 104, 44501 CrossRef CAS PubMed.
- K. Eckert, M. Acker and Y. Shi, Phys. Fluids, 2003, 16, 385–399 CrossRef.
- V. Loodts, C. Thomas, L. Rongy and A. De Wit, Phys. Rev. Lett., 2014, 113, 114501 CrossRef CAS PubMed.
- R. K. Manna, K. Gentile, O. E. Shklyaev, A. Sen and A. C. Balazs, Langmuir, 2022, 38, 1432–1439 CrossRef CAS PubMed.
- O. E. Shklyaev, V. V. Yashin, S. I. Stupp and A. C. Balazs, Commun. Phys., 2020, 3, 1–9 CrossRef.
- Y. Zhang, S. Tsitkov and H. Hess, Nat. Catal., 2018, 1, 276–281 CrossRef.
- M. A. Bees, A. J. Pons, P. G. Sørensen and F. Sagués, J. Chem. Phys., 2001, 114, 1932–1943 CrossRef CAS.
- K. Gentile, S. Maiti, A. Brink, B. Rallabandi, H. A. Stone and A. Sen, Langmuir, 2020, 36, 7948–7955 CrossRef CAS.
- S. Sengupta, D. Patra, I. Ortiz-Rivera, A. Agrawal, S. Shklyaev, K. K. Dey, U. Córdova-Figueroa, T. E. Mallouk and A. Sen, Nat. Chem., 2014, 6, 415–422 CrossRef CAS PubMed.
- S. Maiti, O. E. Shklyaev, A. C. Balazs and A. Sen, Langmuir, 2019, 35, 3724–3732 CrossRef CAS PubMed.
- I. Ortiz-Rivera, H. Shum, A. Agrawal, A. Sen and A. C. Balazs, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 2585–2590 CrossRef CAS.
- J. Leira-Iglesias, A. Tassoni, T. Adachi, M. Stich and T. M. Hermans, Nat. Nanotechnol., 2018, 13, 1021–1027 CrossRef CAS.
- E. Nakouzi and O. Steinbock, Sci. Adv., 2016, 2, e1601144 CrossRef.
- L. M. Barge, S. S. S. Cardoso, J. H. E. Cartwright, G. J. T. Cooper, L. Cronin, A. De Wit, I. J. Doloboff, B. Escribano, R. E. Goldstein, F. Haudin, D. E. H. Jones, A. L. Mackay, J. Maselko, J. J. Pagano, J. Pantaleone, M. J. Russell, C. I. Sainz-Díaz, O. Steinbock, D. A. Stone, Y. Tanimoto and N. L. Thomas, Chem. Rev., 2015, 115, 8652–8703 CrossRef CAS PubMed.
- A. De Wit and G. M. Homsy, J. Chem. Phys., 1999, 110, 8663–8675 CrossRef CAS.
- L. A. Riolfo, Y. Nagatsu, S. Iwata, R. Maes, P. M. J. Trevelyan and A. De Wit, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 15304 CrossRef CAS.
- Y. Nagatsu, K. Matsuda, Y. Kato and Y. Tada, J. Fluid Mech., 2007, 571, 475–493 CrossRef CAS.
- T. Podgorski, M. C. Sostarecz, S. Zorman and A. Belmonte, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 16202 CrossRef PubMed.
- F. Haudin, J. H. E. Cartwright, F. Brau and A. De Wit, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17363–17367 CrossRef CAS.
- M. A. Budroni, V. Upadhyay and L. Rongy, Phys. Rev. Lett., 2019, 122, 244502 CrossRef CAS PubMed.
- A. A. Nepomnyashchy, M. G. Velarde and P. Colinet, Interfacial Phenomena and Convection, Chapman and Hall/CRC, New York, 2014 Search PubMed.
- A. S. Basu and Y. B. Gianchandani, J. Micromech. Microeng., 2008, 18, 115031 CrossRef.
- T. Battal, C. D. Bain, M. Weiß and R. C. Darton, J. Colloid Interface Sci., 2003, 263, 250–260 CrossRef CAS PubMed.
- C. C. Maass, C. Krüger, S. Herminghaus and C. Bahr, Annu. Rev. Condens. Matter Phys., 2016, 7, 171–193 CrossRef CAS.
- R. Seemann, J.-B. Fleury and C. C. Maass, Eur. Phys. J.: Spec. Top., 2016, 225, 2227–2240 CAS.
- N. J. Suematsu and S. Nakata, Chem. – Eur. J., 2018, 24, 6308–6324 CrossRef CAS PubMed.
- Y. Xu, N. Takayama, H. Er and S. Nakata, J. Phys. Chem. B, 2021, 125, 1674–1679 CrossRef CAS PubMed.
- Y. Karasawa, T. Nomoto, L. Chiari, T. Toyota and M. Fujinami, J. Colloid Interface Sci., 2018, 511, 184–192 CrossRef CAS PubMed.
- Y. S. Ikura, R. Tenno, H. Kitahata, N. J. Suematsu and S. Nakata, J. Phys. Chem. B, 2012, 116, 992–996 CrossRef CAS.
- Y. Karasawa, S. Oshima, T. Nomoto, T. Toyota and M. Fujinami, Chem. Lett., 2014, 43, 1002–1004 CrossRef CAS.
- S. Soh, K. J. M. Bishop and B. A. Grzybowski, J. Phys. Chem. B, 2008, 112, 10848–10853 CrossRef CAS PubMed.
- L. J. Burton, N. Cheng and J. W. M. Bush, Int. Comput. Biol., 2014, 54, 969–973 CrossRef CAS.
- Y. Watahiki, T. Nomoto, L. Chiari, T. Toyota and M. Fujinami, Langmuir, 2018, 34, 5487–5494 CrossRef CAS PubMed.
- M. Cheng, D. Zhang, S. Zhang, Z. Wang and F. Shi, CCS Chem., 2019, 1, 148–155 CAS.
- I. Lagzi, S. Soh, P. J. Wesson, K. P. Browne and B. A. Grzybowski, J. Am. Chem. Soc., 2010, 132, 1198–1199 CrossRef CAS PubMed.
- K. Suzuno, D. Ueyama, M. Branicki, R. Tóth, A. Braun and I. Lagzi, Langmuir, 2014, 30, 9251–9255 CrossRef CAS PubMed.
- A.-D. C. Nguindjel and P. A. Korevaar, ChemSystemsChem, 2021, 3, e2100021 CAS.
- B. A. Cicciarelli, T. A. Hatton and K. A. Smith, Langmuir, 2007, 23, 4753–4764 CrossRef CAS PubMed.
- S. Chen, R. Costil, F. K.-C. Leung and B. L. Feringa, Angew. Chem., Int. Ed., 2021, 60, 11604–11627 CrossRef CAS PubMed.
- T. Shang, K. A. Smith and T. A. Hatton, Langmuir, 2003, 19, 10764–10773 CrossRef CAS.
- A. Diguet, R.-M. Guillermic, N. Magome, A. Saint-Jalmes, Y. Chen, K. Yoshikawa and D. Baigl, Angew. Chem., Int. Ed., 2009, 48, 9281–9284 CrossRef CAS PubMed.
- C. Lv, S. N. Varanakkottu, T. Baier and S. Hardt, Nano Lett., 2018, 18, 6924–6930 CrossRef CAS PubMed.
- M. Schmitt and H. Stark, Phys. Fluids, 2016, 28, 12106 CrossRef.
- Y. Xiao, S. Zarghami, K. Wagner, P. Wagner, K. C. Gordon, L. Florea, D. Diamond and D. L. Officer, Adv. Mater., 2018, 30, 1801821 CrossRef.
- Z. Izri, M. N. van der Linden, S. Michelin and O. Dauchot, Phys. Rev. Lett., 2014, 113, 248302 CrossRef PubMed.
- S. Thutupalli, R. Seemann and S. Herminghaus, New J. Phys., 2011, 13, 73021 CrossRef.
- D. Babu, R. J. H. Scanes, R. Plamont, A. Ryabchun, F. Lancia, T. Kudernac, S. P. Fletcher and N. Katsonis, Nat. Commun., 2021, 12, 2959 CrossRef CAS.
- D. Babu, N. Katsonis, F. Lancia, R. Plamont and A. Ryabchun, Nat. Rev. Chem., 2022, 6, 377–388 CrossRef.
- S. I. Cheon, L. B. C. Silva, A. S. Khair and L. D. Zarzar, Soft Matter, 2021, 17, 6742–6750 RSC.
- A. van der Weijden, M. Winkens, S. M. C. Schoenmakers, W. T. S. Huck and P. A. Korevaar, Nat. Commun., 2020, 11, 1–10 CrossRef PubMed.
- M. Winkens and P. A. Korevaar, Langmuir, 2022, 38, 10799–10809 CrossRef CAS PubMed.
- C. H. Meredith, P. G. Moerman, J. Groenewold, Y. J. Chiu, W. K. Kegel, A. van Blaaderen and L. D. Zarzar, Nat. Chem., 2020, 12, 1136–1142 CrossRef CAS.
- N. J. Cira, A. Benusiglio and M. Prakash, Nature, 2015, 519, 446–450 CrossRef CAS.
- Z. Li, H. Li, A. Li, Z. Liu, Z. Zhang, K. Li, Y. Qiao and Y. Song, Adv. Mater. Interfaces, 2021, 8, 2101309 CrossRef CAS.
- D. Liu, A. Mahmood, D. Weng and J. Wang, Langmuir, 2019, 35, 16146–16152 CrossRef CAS PubMed.
- M. Wittmann, M. N. Popescu, A. Domínguez and J. Simmchen, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 15 CrossRef CAS.
- S. Tanaka, S. Nakata and T. Kano, J. Phys. Soc. Jpn., 2017, 86, 101004 CrossRef.
- J. Čejková, K. Schwarzenberger, K. Eckert and S. Tanaka, Colloids Surf., A, 2019, 566, 141–147 CrossRef.
- D. Velegol, A. Garg, R. Guha, A. Kar and M. Kumar, Soft Matter, 2016, 12, 4686–4703 RSC.
- Y. Peng, P. Xu, S. Duan, J. Liu, J. L. Moran and W. Wang, Angew. Chem., Int. Ed., 2022, 61, e202116041 CAS.
- W. Wang, W. Duan, S. Ahmed, A. Sen and T. E. Mallouk, Acc. Chem. Res., 2015, 48, 1938–1946 CrossRef CAS.
- A. Banerjee and T. M. Squires, Sci. Adv., 2019, 5, eaax1893 CrossRef CAS PubMed.
- J. J. McDermott, A. Kar, M. Daher, S. Klara, G. Wang, A. Sen and D. Velegol, Langmuir, 2012, 28, 15491–15497 CrossRef CAS PubMed.
- R. Niu, T. Palberg and T. Speck, Phys. Rev. Lett., 2017, 119, 028001 CrossRef PubMed.
- R. Niu, A. Fischer, T. Palberg and T. Speck, ACS Nano, 2018, 12, 10932–10938 CrossRef CAS PubMed.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303 CrossRef CAS.
- A. Bricard, J. B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98 CrossRef CAS PubMed.
- W. Duan, R. Liu and A. Sen, J. Am. Chem. Soc., 2013, 135, 1280–1283 CrossRef CAS.
- M. Ibele, T. E. Mallouk and A. Sen, Angew. Chem., Int. Ed., 2009, 48, 3308–3312 CrossRef CAS PubMed.
- A. Altemose, M. A. Sánchez-Farrán, W. Duan, S. Schulz, A. Borhan, V. H. Crespi and A. Sen, Angew. Chemie, 2017, 129, 7925–7929 CrossRef.
- C. Wu, J. Dai, X. Li, L. Gao, J. Wang, J. Liu, J. Zheng, X. Zhan, J. Chen, X. Cheng, M. Yang and J. Tang, Nat. Nanotechnol., 2021, 16, 288–295 CrossRef CAS PubMed.
- P. Bacchin, K. Glavatskiy and V. Gerbaud, Phys. Chem. Chem. Phys., 2019, 21, 10114–10124 RSC.
- H. W. H. van Roekel, B. J. H. M. Rosier, L. H. H. Meijer, P. A. J. Hilbers, A. J. Markvoort, W. T. S. Huck and T. F. A. de Greef, Chem. Soc. Rev., 2015, 44, 7465–7483 RSC.
- R. Merindol and A. Walther, Chem. Soc. Rev., 2017, 46, 5588–5619 RSC.
- B. A. Grzybowski, K. Fitzner, J. Paczesny and S. Granick, Chem. Soc. Rev., 2017, 46, 5647–5678 RSC.
- C. Kaspar, B. J. Ravoo, W. G. van der Wiel, S. V. Wegner and W. H. P. Pernice, Nature, 2021, 594, 345–355 CrossRef CAS PubMed.
- A. Walther, Adv. Mater., 2020, 32, 1905111 CrossRef CAS PubMed.
- O. Steinbock, Á. Tóth and K. Showalter, Science, 1995, 267, 868–871 CrossRef CAS.
- O. Steinbock, P. Kettunen and K. Showalter, J. Phys. Chem., 1996, 100, 18970–18975 CrossRef CAS.
- J. M. Parrilla-Gutierrez, A. Sharma, S. Tsuda, G. J. T. Cooper, G. Aragon-Camarasa, K. Donkers and L. Cronin, Nat. Commun., 2020, 11, 1442 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally. |
| This journal is © the Owner Societies 2022 |