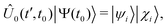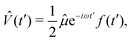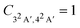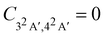Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum coherence in molecular photoionization
Marco
Ruberti
 *a,
Serguei
Patchkovskii
b and
Vitali
Averbukh
*a,
Serguei
Patchkovskii
b and
Vitali
Averbukh
 c
c
aImperial College London, Department of Physics, South Kensington Campus, London SW7 2AZ, UK. E-mail: m.ruberti11@imperial.ac.uk
bMax-Born Institute, Max-Born-Straße 2A, 12489 Berlin, Germany. E-mail: Serguei.Patchkovskii@mbi-berlin.de
cImperial College London, Department of Physics, South Kensington Campus, London SW7 2AZ, UK. E-mail: v.averbukh@imperial.ac.uk
First published on 2nd August 2022
Abstract
The study of onset and decay, as well as control of ultrafast quantum coherence in many-electron systems is in the focus of interest of attosecond physics. Interpretation of attosecond experiments detecting the ultrafast quantum coherence requires application of advanced theoretical and computational tools combining many-electron theory, description of the electronic continuum, including in the strong laser field scenario, as well as nuclear dynamics theory. This perspective reviews the recent theoretical advances in understanding the attosecond dynamics of quantum coherence in photoionized molecular systems and outlines possible future directions of theoretical and experimental study of coherence and entanglement in the attosecond regime.
The process of photoionization is a perfect example of breakup of a quantum system into a series of distinct sub-systems, namely the photoelectron drifting away and the parent ion that is left behind. In the case of atomic photoionization, the remaining parent ion can in general consist of a bound or highly-excited many-electron system, while in the molecular case additional breakup of the nuclear quantum system, such as fragmentation, can also be triggered during the process.
1 Ionic coherence: formal theory
Two interrelated, fundamental quantum-mechanical concepts characterize the many-body dynamics that is triggered by photoionization: quantum coherence and quantum entanglement. From a quantum mechanical point of view, maximal quantum electronic coherence within each of the photoelectron and parent-ion sub-systems that are formed upon photoionization implies that, at large separations between the two, the total, time-dependent, N-electron wavefunction of the photoionized system ΨN (x1,…, xi,…, xN; R, t) is separable in the degrees of freedom of the two formed sub-systems. Note that here the parameter R stands for the nuclear coordinates. (When nuclear dynamics are relevant, R becomes a dynamical variable as well, on equal footing with xi. This case will be considered below, in Section 4.) Therefore, the wavefunction of the composite N-electron system can be written, at least to a good approximation, as the anti-symmetrized product of a (N − 1)-electron wavefunction (in principle fully correlated) describing the parent-ion, i.e. only dependent on ionic degrees of freedom, and a one-electron wavefunction describing the photoelectron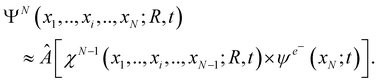 | (1) |
However, the product Ansatz of eqn (1) is valid only if the photoelectron and the parent-ion systems are not entangled and, as a result, the quantum coherence is at maximum within each subsystem. In fact, the total bipartite system is in general described by a time-dependent density matrix ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t). Each of the separate sub-systems is itself described by a reduced density matrix that is obtained by tracing out the extra degrees of freedom pertaining to the other, unobserved, sub-system. In the case of the parent ion, the so-called reduced ionic density matrix (R-IDM) reads as
(t). Each of the separate sub-systems is itself described by a reduced density matrix that is obtained by tracing out the extra degrees of freedom pertaining to the other, unobserved, sub-system. In the case of the parent ion, the so-called reduced ionic density matrix (R-IDM) reads as
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) R-IDM (t) = Tre− ( R-IDM (t) = Tre− (![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t)), (t)), | (2) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t) that actually describes a photoionized system, i.e. where, at least at times t when the photoelectron is sufficiently far away from the parent-ion, one of the electronic degrees of freedom (the one that will be identified as pertaining to the photoelectron) is associated to single-electron states that are physically distinguishable (e.g. for energy/momentum and spatial separation) from the ones occupied by the remaining (N − 1) electrons.
(t) that actually describes a photoionized system, i.e. where, at least at times t when the photoelectron is sufficiently far away from the parent-ion, one of the electronic degrees of freedom (the one that will be identified as pertaining to the photoelectron) is associated to single-electron states that are physically distinguishable (e.g. for energy/momentum and spatial separation) from the ones occupied by the remaining (N − 1) electrons.
Even in the case where the total density matrix ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t) corresponds to a pure state, i.e.
(t) corresponds to a pure state, i.e. ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t) = |ΨN〉〈ΨN|, the partial trace operation gives rise in general to a mixed quantum state for the resulting sub-system. The operator of eqn (2) can be projected onto a basis of many-electron states of the parent-ion. For example, in the basis of eigenstates of the ionic Hamiltonian |EN−1I〉 we obtain:
(t) = |ΨN〉〈ΨN|, the partial trace operation gives rise in general to a mixed quantum state for the resulting sub-system. The operator of eqn (2) can be projected onto a basis of many-electron states of the parent-ion. For example, in the basis of eigenstates of the ionic Hamiltonian |EN−1I〉 we obtain:
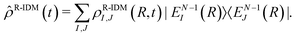 | (3) |
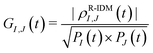 | (4) |
| ϕI,J(t) = arg(ρR-IDMI,J(t)), | (5) |
Spectral decomposition of the R-IDM
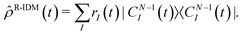 | (6) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) R-IDM (t) ×
R-IDM (t) × ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) R-IDM(t)), while the entanglement between the parent-ion and the photoelectron can be measured by the von Neumann entropy of entanglement
R-IDM(t)), while the entanglement between the parent-ion and the photoelectron can be measured by the von Neumann entropy of entanglement 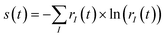 . The more entangled the two subsystems are, the more mixed (i.e. with less quantum coherence) the state of each of them is. This can be easily seen by comparing eqn (1) and (6): maximal coherence requires the parent-ion to be described by a pure state, i.e. by a well-defined (N − 1)-electron wavefunction, which can be expressed in any arbitrary basis as a specific fully coherent linear superposition of the basis states. Therefore, the spectral decomposition of eqn (6) must only have one ri term different from zero (and consequently equal to 1). This requirement automatically gives us a minimum value for the entropy of entanglement, equal to 0, and a maximum value for the purity, equal to 1. Finally, it is important to note that both of these “global” quantities are independent of the specific basis set used.
. The more entangled the two subsystems are, the more mixed (i.e. with less quantum coherence) the state of each of them is. This can be easily seen by comparing eqn (1) and (6): maximal coherence requires the parent-ion to be described by a pure state, i.e. by a well-defined (N − 1)-electron wavefunction, which can be expressed in any arbitrary basis as a specific fully coherent linear superposition of the basis states. Therefore, the spectral decomposition of eqn (6) must only have one ri term different from zero (and consequently equal to 1). This requirement automatically gives us a minimum value for the entropy of entanglement, equal to 0, and a maximum value for the purity, equal to 1. Finally, it is important to note that both of these “global” quantities are independent of the specific basis set used.
2 Coherence in attosecond science
In the last four decades, traditional synchrotron photoionization experiments have allowed the community to address the properties of individual, incoherently populated eigenstates of the ionized system. Indeed, a narrow-bandwidth synchrotron radiation couples each molecular ionized state to an outgoing electron wave of well-defined energy. Thus, the total wavefunction of the photoionized N-electron system is highly entangled and cannot be represented as a separable product of ionic and free-electron states.The alternative large-bandwidth photoionising laser sources based on the high-order harmonic generation (HHG) and X-ray free electron laser (FEL) technologies have been actively developed over the recent two decades,1 however until recently they have been suffering from drawbacks that hindered their use in exploring the onset and the effects of the ionic coherence. While the attosecond HHG sources have the required bandwidth for coherently exciting series of atomic or molecular ionic states, they lacked the intensity required for both creating and probing the excited coherent superpositions. On the other hand, the much more intense X-ray FEL sources lacked the bandwidth required to create the ionic coherence across, e.g. 10 eV energy range. Recently, the spectacular developments of both HHG sources2 and X-ray FELs3 has led to the emergence of new-generation attosecond light pulses which can coherently excite and probe a system of interest over a broad range of photon energies. These pulses allow one to produce the quantum electronic coherences that characterize the partially-entangled state of the ionized electron and parent-ion sub-systems, as well as to explore new, spectacular physical effects which result from the non-stationary quantum superpositions of ionized atomic and molecular states, such as molecular hole migration.4
It is the set of quantities from eqn (4) and (5) that determine the ultrafast correlated dynamics that is triggered by the photoionization process and that eventually couple with the adiabatic and non-adiabatic nuclear dynamics in the ionic system. One particular example is the so-called charge migration which results from electronic correlation and assumes a coherent superposition of all the states resulting from removal of an electron from a specific hole orbital. The partially coherent superposition of such molecular ionic eigenstates can be accompanied by an ultrafast electron dynamics which has been predicted to feature a migration of the positive charge across the molecular-ion backbone, on a sub- to few-femtosecond (fs) timescale (hole migration).4 On longer timescales, this purely electronic coherent dynamics is potentially subject to decoherence5,6 due to coupling to the slower nuclear motion degree of freedom, which acts as a bath and could eventually lead to the final localization of the positive charge.
At the heart of modern attosecond science is the study of the coherent many-electron dynamics resulting from photoionization by means of attosecond pump–probe spectroscopy techniques.7,8 Since molecular bonds are more likely to break in the regions with higher density of the electronic hole, ultrafast charge redistribution underpinned by electronic coherence in the cation leads the way to photoionization-induced, charge-directed reactivity on attosecond timescales. In turn, this opens up the possibility of steering the molecular reaction dynamics at a very early stage of its quantum evolution by using the electronic degrees of freedom before the dephasing occurs. Exploiting the quantum electronic coherences, rather than just the eigenstates populations, provides a novel opportunity to control photochemical reactions, previously unavailable on the much longer (femto/pico-second) timescales intrinsic to nuclear dynamics. Moreover, since electronic redistribution initiates all photochemical change,9 the study of quantum electronic coherence and entanglement in photoionization is also of fundamental interest for understanding the basic processes eventually leading to photosynthesis and radiation damage. Here it is important to note that, although natural photosynthetic processes are triggered by incoherent light, ultrafast pump–probe techniques based on fully-coherent light sources represent a strong tool to investigate the evolution of quantum coherence and energy transport in photosynthetic systems and shed light on their fundamental light-harvesting mechanisms.
The goals of the attosecond community can be briefly summarized as follows:
• Prepare ultrafast quantum coherence.
• Probe ultrafast quantum coherence.
• Control ultrafast quantum coherence.
In order to realize the full potential impact of attosecond science, a close integration of theoretical and experimental efforts is crucial. On the one hand, attosecond experiments frequently ionize the system, leading to an entangled ion–photoelectron pair. The resulting entanglement limits the coherence that we can observe when we perform measurements on each of the two sub-systems. On the other hand, attosecond experiments, that investigate the type of ultrafast dynamics that can be triggered in the parent ion, rely on the existence of coherence in the latter sub-system, i.e. a well-defined phase relationship (see eqn (4) and (5)) between the various components of the quantum state that can give rise to a time-dependent interference pattern when an observable sensitive to the coherences is measured in the laboratory. Because of the complexity of the photoionization dynamics involved, the capability to model laser-induced many-electron processes from first principles is absolutely key to predict new physical phenomena, and to guide experimental efforts towards their observation and characterization.
In addition, theoretical prediction of quantum coherences in photoionization is essential not only for our fundamental understanding of the physics underlying photochemical transformations at ultrashort timescales, but also for applying concepts of quantum information (QI) to the field of ultrafast dynamics. Most importantly, doing so can provide us with new routes to control photo-physical/chemical processes, i.e. it opens the way to harnessing these fundamental, inherently quantum mechanical concepts in order to develop control strategies of chemical reactivity of photoionized molecules.
To date, a full quantum information perspective on attoscience is still missing and the role of electron nuclear coupling in this respect is thus far mostly unexplored. There are many open questions yet to be answered including: how would an interaction with, or a measurement performed on, the photoelectron affect or correlate, respectively, with the chemical process in the ion that this electron left behind?
3 Theoretical methodology and applications
All this has called for the development, in the last decade, of new theoretical and computational methodologies capable of answering fundamental questions on coherence and entanglement in ultrafast photoionization dynamics. In general, in order to calculate the ionization-induced quantum electronic coherences, it is essential for these methodologies to explicitly describe the photoionization process and preferably include in the theoretical description the following required “ingredients”:• A complete description of the full N-electron quantum system, starting from the initial state of the neutral molecule, and capturing the entanglement between the (N − 1)-electron ion and the photoelectron after the photoionization process. This must be done by tracking the time evolution of the N-electron wavefunction, whose ionized part can be written in general as
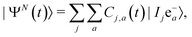 | (7) |
• A time-dependent description of the photoionization process in order to capture the ultrafast formation and loss of quantum coherence.
• An accurate prediction of the ionization quantum amplitudes corresponding to each of the (most physically-relevant) many-electron states of the parent ion (ionization channels), as a function of the parameters (e.g. frequency and intensity) of the ionizing laser pulse.
• Accounting for the effect of the interchannel couplings between the emitted electron and the parent ion, i.e. for correlation effects in the continuum. This type of residual interaction between the parent-ion and the photoelectron is different with respect to the so-called intrachannel coupling, where the photoelectron experiences the potential created by the charge distribution of the specific fixed cationic state, insofar as the state of the parent-ion is also allowed to change as a result of it. It is important to note that it is the interchannel coupling term that causes the loss of coherence in the parent-ion during the departure of the emitted electron.
From a theoretical point of view, the major challenge in modelling the formation of ionic coherence in the process of attosecond and strong-field ionization of a molecular system consists of solving the multi-centre (with respect to the single-centre atomic case), multi-channel, many-electron problem in the presence of a laser field. This is key to revealing the physical mechanisms contributing to the formation of the cationic wavefunction through the external field and electron correlation, and needs to be done across a wide energy window, which is defined by the interaction with the ionising pulse, and which leads one to face several computational difficulties. Here we refer to the electron correlation, as standard in quantum chemistry, as to the effect of electron-electron repulsion that is not accounted for within the Hartree–Fock (self-consistent field) approximation.10 First, standard methods of electronic structure calculation are poorly adapted to the description of continuum electrons. Second, attosecond (HHG and pump–probe) experiments typically involve tunneling/multi-photon ionization as well as (sequential) double ionization, which are even more difficult to take into account. Finally, molecular systems are characterized by a larger size, a higher number of degrees of freedom and, in general, a lower symmetry with respect to atoms, which poses additional demands on the computation. This is why, until recently, the density matrix characterising the ionic state emerging from attosecond ionization could not be predicted theoretically or characterized experimentally in the general molecular case – but only in some atomic cases,11,12 for which a very recent experimental work has also reported the experimental reconstruction of the density matrix of the photoelectron sub-system.13
3.1 Low-frequency strong-field regime
In recent years, simulation of coherence formation in infrared (IR)-driven strong-field ionization (SFI) has been performed, by solving the time-dependent Schrodinger equation (TDSE), both for atomic systems by the group of Santra et al.,14 using the time-dependent (TD) configuration interaction singles (CIS) method for electronic structure, and for molecular systems by Ruberti and Averbukh15 using the first-order version of TD B-spline algebraic diagrammatic construction (ADC) method, i.e. TD B-spline ADC(1).In the low-frequency, SFI regime, it is possible to identify at least three different physical mechanisms that, interplaying with each other, contribute to the formation and destruction of quantum electronic coherence in the parent ion system during the photoionization process. These are:
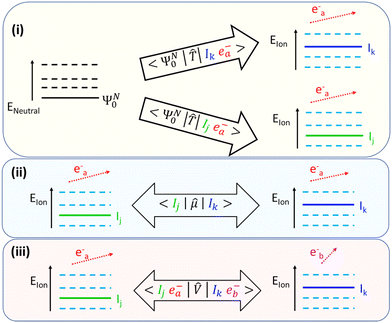
• The presence of distinct, single-channel, laser-driven non-perturbative transitions (multi-photon or tunnel) that can excite an electron to the same continuum state and, at the same time, leave the parent-ion system in different (j, k) internal states. The Hamiltonian terms responsible for this process are:
〈ΨN0|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |Ij/kea−〉 ≠ 0 and 〈Ij/kea−| |Ij/kea−〉 ≠ 0 and 〈Ij/kea−|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |Ij/keb−〉 ≠ 0, |Ij/keb−〉 ≠ 0, | (8) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) is the electric dipole operator. In a simple orbital picture, these mechanisms correspond to a non-zero amplitude for an electron to be excited, by the electric field of the laser pulse, from different, initially occupied (hole) orbitals into the same final orbital in the continuum of its energy spectrum. The terms in eqn (8) are Hamiltonian terms, that are independent of the intensity of the laser field. However, what does strongly depend on the strength of the laser field is what type of dynamics and transitions these Hamiltonian matrix elements lead to: non-perturbative multi-photon or tunnelling ionization in the strong-field regime, perturbative single to a few-photon transitions in the weak field regime.
is the electric dipole operator. In a simple orbital picture, these mechanisms correspond to a non-zero amplitude for an electron to be excited, by the electric field of the laser pulse, from different, initially occupied (hole) orbitals into the same final orbital in the continuum of its energy spectrum. The terms in eqn (8) are Hamiltonian terms, that are independent of the intensity of the laser field. However, what does strongly depend on the strength of the laser field is what type of dynamics and transitions these Hamiltonian matrix elements lead to: non-perturbative multi-photon or tunnelling ionization in the strong-field regime, perturbative single to a few-photon transitions in the weak field regime.
• Rabi-like dynamics in the parent-ion: resonant or nearly-resonant laser-driven transitions between different states of the parent-ion that are coupled to each other by an electric dipole matrix element:
δa,b〈Ij|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |Ik〉 ≠ 0. |Ik〉 ≠ 0. | (9) |
• Residual Coulomb interaction between the parent-ion and the photoelectron as the latter is still in the proximity of the former. In particular, the interaction of the liberated electron with the ionic hole state, from which it originates, is referred to as intrachannel interaction and leads, for large electron-ion distances, to the 1/r behaviour typical of the Coulomb potential. If the liberated electron is influenced by other molecular orbitals (ionic states) the interaction is referred to as interchannel coupling:
〈Ijea−|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) |Ikeb−〉 ≠ 0, |Ikeb−〉 ≠ 0, | (10) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) represents the direct and exchange terms of the two-particle Coulomb interaction. It is the latter scenario that can produce transitions in the parent-ion and directly impact on the coherence between the ionic states involved.
represents the direct and exchange terms of the two-particle Coulomb interaction. It is the latter scenario that can produce transitions in the parent-ion and directly impact on the coherence between the ionic states involved.
A schematic representation of these mechanisms can be seen in Fig. 1. An important feature of SFI is the strong (exponential) dependence of the ionization amplitude for a specific ionic state on the value of its ionization potential. As a result, during this ionization process, only the first few lowest-excited states of the parent-ion are effectively populated. In small to medium-sized molecules, these states are characterized by a relatively small amount of electron correlation and, as a consequence, they are reasonably well described within the Koopman's picture of ionization,10 according to which singly-ionized states are obtained by removing an electron from one of the occupied orbitals in the Hartree–Fock (HF) ground state of the neutral molecule.
Therefore, in the long-wavelength, strong-field regime, the complexity given by the non-perturbative nature of the laser-molecule interaction is tempered by the fact that the modelling of the electronic structure in the outer-valence energy region of the spectrum can often be greatly simplified by adopting a single-hole description. Orbital relaxation and electron correlation in the strong-field regime can also be included without much difficulty, using a non-orthogonal, time-dependent resolution in ion states (TD-RIS) approach.16,17
3.2 High-frequency regime
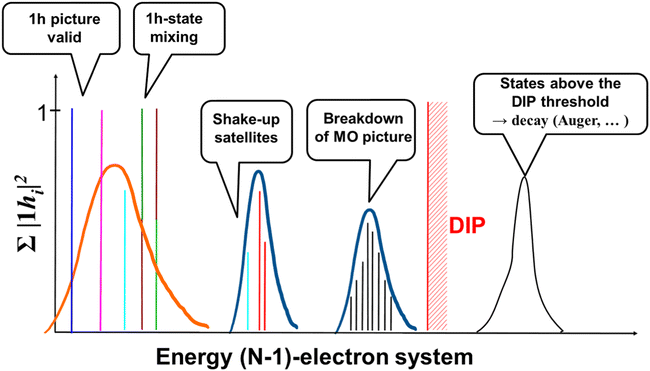
The situation is radically different in the XUV and soft X-ray regimes, where the photon energy is such that more deeply-bound electronic states, i.e. higher excited states of the parent ion, can be accessed by absorption of a single or a few photons. In spite of the perturbative nature of the photoionization process at these shorter wavelengths (at least for laser intensity of the order of 1015 W cm−2 or less), calculation of the quantum electronic coherences in the ionic sub-system requires a more accurate treatment of electron correlation effects, which dominate in the inner-valence energy region of the ionic spectrum. Moreover, things are made more complicated also by the higher density of states in the region close to the double ionization potential (DIP) threshold and by the fact that each of these states of the parent-ion has to be coupled to a continuum of states for the photoelectron sub-system. All these aspects make the accurate prediction of the reduced ionic density matrix upon attosecond XUV ionization of a polyatomic molecule very challenging.A typical electronic energy spectrum of a molecular ion in the fixed-nuclei approximation, which extends beyond the DIP threshold, is shown in Fig. 2. Each line in the spectrum represents an ionic eigenstate and is located at the corresponding ionization energy. The values of the spectral intensities reflect the contribution of the one-hole (1h) configurations to the ionic states. In the absence of electron correlation, i.e., within the range of validity of the Koopman's theorem, one indeed obtains a series of lines with a height of 1 for each occupied HF molecular orbital. This is often accurate in the outer-valence energy region, i.e. close to the first ionization potential of the system. As the energy of the ionic states increases the effect of electron correlation also becomes more important: this can either give rise to hole-mixing, where eigenstate are linear combinations of different 1h states, to the formation of shakeup satellites and ultimately, in the inner-valence energy region to the complete breakdown of the molecular orbital (MO) picture (see Fig. 2). In terms of electronic configurations, description of electron correlation in the modelling of the cation implies the inclusions of all the ionic two-hole–one-particle (2h–1p) configurations. Within advanced descriptions, such as the one given by the second (ADC(2)x) and third (ADC(3)) order methods of the ADC hierarchy,18 electron correlation in the description of the ionic system manifests itself in individual ionic states as a reduction of the spectral intensity line height (with the “missing” part reflecting the contribution of 2h1p configurations) and, related with the latter, as the appearance of additional (satellite) lines in the spectrum. A 2h1p configuration indeed describes the removal of an electron from a particular orbital accompanied by the excitation of another electron to an initially unoccupied orbital.
As a result, two more “ingredients” can be added to the previous list:
• Description of electron correlation, i.e. shakeup states, correlation satellites.
• Description of the electronic relaxation that happens due to the change in the mean-field potential that each electron experiences upon creation of a hole in a deeply-bound orbital.
Among the most promising new theoretical methods that have recently been developed to achieve this goal, we would highlight the time-dependent first-order perturbation theory, static-exchange density–functional–theory (DFT) method developed by P. Decleva and collaborators,7 its multi-reference extension developed by Ponzi et al.19 and applied to attosecond molecular ionization dynamics by Martin and collaborators,20 the XCHEM method by Martin and collaborators,21 the real-time non-equilibrium Green's function methods (NEGF) as implemented in the CHEERS code by Perfetto et al.,22 the molecular R-matrix with-time approach by Benda et al.,23 the TD B-spline ADC method by Ruberti and Averbukh,24,25 and finally the TD B-spline restricted correlation space (RCS)-ADC by Ruberti.26,27 For a more comprehensive list of such methods we refer the reader to ref. 28.
In particular, the TD B-spline ADC method extends the ab initio ADC approach, originally developed to describe bound state dynamics,18 to the realm of ultrafast ionization dynamics, combining the accurate description of electron correlation of quantum chemistry with the full account of the continuum dynamics of the photoelectron, while the RCS technique26 crucially turns first-principles modeling of coherence and entanglement in photoionization of polyatomic molecular systems into a tractable problem. RCS–ADC is based on the separation of the orbital space into correlation and ionization spaces26 and naturally bridges the gap between multi-configurational ab initio techniques and closed-coupling schemes based on a limited number of essential, physically relevant ionic states, combining the key advantages of both.
Approaches of this kind allow one to accurately predict the mixed state of the ionized system prepared by attosecond ionization of a molecular system.27 Within TD B-spline RCS–ADC, complete theoretical characterization of the atto-ionized many-electron state and photo-induced attosecond charge dynamics is achieved by calculating the reduced ionic density matrix (R-IDM) of the bipartite ion-photoelectron system, with full inclusion of the correlated ionic shakeup states, and its interaction with yet another ionising laser pulse probing its dynamics.29
The power of this approach is apparent in the Schmidt decomposition of the R-IDM. In fact, the latter unveils the many-electron dynamics triggered by the pump and allows for the identification of the key pure-state channels involved in the quantum coherent many-electron dynamics.29 Most importantly, the methodology can be applied to the simulation of complete numerical pump–probe experiments of ultrafast dynamics in molecular systems.15,29,30 This is because the hierarchies of both ADC and RCS–ADC methods extend across different ionization stages.
Another wavefunction method is XCHEM,21 which uses a Close-Coupling approach based on a Restricted-Active-Space Self-Consistent-Field (RAS-SCF) description of electron correlation and on the use of a mixed basis set comprising both Gaussian type orbitals and B-splines. This method, which, as well as the ADC-based methods, includes a description of electron correlation effects in the continuum, has so far been applied to the time-independent description of photoionization in small molecules.31 The static-exchange DFT method7 provides an effective single-particle description of the photoionization dynamics, as well as a more basic description of electron correlation effects through the use of exchange–correlation functionals in the calculation of the ground-state Kohn–Sham (KS) orbitals. The multi-reference static-exchange scattering method19 improves the description of electron correlation with respect to ref. 7 by considering the multi-configurational character of the parent-ion wavefunction. However, both methods neglect interchannel couplings in the electronic continuum and their first-order perturbation theory implementation is limited to description of weak-field, single-photon ionization processes. Finally, NEGF theory allows one to describe the many-body problem from first principles by using effectively-single-particle approaches.22 Dynamical correlation effects are added to the Hartree–Fock dynamics through a many-body self-energy. The real-time implementation of the method is potentially suitable for applications to describe non-perturbative ionization dynamics. The description of the photoelectron system is limited by the use of KS continuum states a in planewave or grid basis set.
Within single-photon absorption, coherence between different single holes in the outer-valence part of the spectrum, where the energy separation between the different ionic states can be of the order of a few eV, typically requires ultra-short, attosecond laser pulses with a time duration of the order of hundreds of attoseconds.
In the inner-valence energy region, longer pulses in the few-femtoseconds range can already be capable of exciting coherently either a single hole and its shakeup satellite states, or a series of correlated states in a breakdown of the molecular orbital (MO) picture scenario (see Fig. 2). This is because of the higher density of states in the inner-valence energy region. A particular type of coherent excitation is the one pictured by the so-called sudden ionization approximation, whose validity strictly requires the photon energy to be much higher than the ionization thresholds of the system. In the sudden ionization picture, a high frequency pulse “suddenly” removes an electron from one occupied orbital in the inner-valence region. As a consequence of electron correlation, this implies the coherent population of each of the ionic eigenstates with a non-zero amplitude on the 1h configuration corresponding to the created hole.
Finally, it is worth noting that the creation of quantum coherence between states lying above the DIP can give rise to coherent dynamics super-imposed on the non-radiative (Auger) decay of such states, a phenomenon that we can call “Auger wavepackets”.
In perturbative XUV ionization, direct (in this case mainly single-photon) transitions into the same continuum state and inter-channel couplings (see panel (i) and (iii) of Fig. 1, respectively) are the dominating mechanisms that contribute to the build-up of the ionic coherence. The latter always leads to an overall decrease of ionic purity and a corresponding increase of the entropy of entanglement. Increasing the intensity can also potentially introduce new mechanisms of coherence formation in the XUV regime: these include not only the dipole transitions between the populated ionic states and multi-photon ionization, but also Raman-type transitions mediated by the core-ionized states and/or the continuum.
Finally, in order to achieve a complete theoretical description of the quantum coherent dynamics triggered during the photoionization of a molecular system, the last key “ingredient” is:
• Description of the coupling between the electronic and nuclear dynamics. This is in principle a very challenging task, because the possible existence of several electronic coherences among excited electronic states requires one to model non-adiabatic nuclear dynamics across the several, correspondent, potential energy surfaces.
Before proceeding, in the next section, to discuss the correlations between electronic and nuclear degrees of freedom, we would like to remark that a deeper understanding of the mechanisms that characterize the dynamics of the quantum attosecond coherences is also key to the interpretation and the design of new experimental protocols aiming at probing such coherences, such as single-photon laser enabled Auger decay (spLEAD),32,33 X-ray attosecond transient absorption29 and X-ray time-resolved Auger and photoelectron spectroscopies.30,34 Crucial features, which are highly desirable for such new schemes, are, on the one hand, the chemical-site and ionic-state selectivity and, on the other hand, extremely high temporal resolutions up to the attosecond regime.
4 Correlations between electronic and nuclear degrees of freedom in ionization
Electronic-state coherences, discussed in the preceding section, are the most important, but not the only coherence effects relevant to attosecond and strong-field photoionization. All isolated systems possess the centre-of-mass degrees of freedom, as well as electronic- and nuclear-spin degrees of freedom. Molecules additionally possess rotational and vibrational degrees of freedom. Potentially, all of these degrees of freedom can become correlated to the electronic degrees of freedom, leading to non-trivial dynamical and spectroscopic consequences.Here, we will concentrate on the vibrational motion, which occurs on the time scale closest to that of the electron dynamics. We will however note in passing that correlations between the centre-of-mass motion and ultrafast electronic dynamics, which are routinely neglected in the attosecond domain, can offer a sensitive, non-destructive probe of the electron dynamics.35,36
4.1 Vibrational dynamics
In order to qualitatively understand the origin of the nuclear-motion effects in broad-band, coherent photoelectron spectra, it is helpful to adopt the time-dependent perspective. A delightful exposition of these ideas can be found in a classic review by Heller.37 The simplest-possible, near-trivial example is one-photon ionization, which we find instructive to explore in some detail. We choose to closely follow the textbook by Tannor,38 however casting the expressions in the S-matrix form commonly used in analytical strong-field applications.39,40 Unless mentioned otherwise, we use Hartree atomic units me = |e| = ħ = 1 below.Because we are now interested in correlations between electronic and nuclear dynamics, it is necessary to venture into the realm of non-adiabatic vibronic dynamics (see e.g. ref. 41–44). For our purposes, it is sufficient to work within the Born-Huang Ansatz45 and to ignore the challenges42,46 arising due to state intersections. A more careful treatment is necessary in the general case, which however would be out of scope of this perspective. Some of the possibilities would include using diabatic representation,43 the “complete adiabatic” Ansatz,47,48 and the related exact-factorization approach.49
The lowest-order total (electronic and nuclear) wavefunction response to a time-dependent perturbation ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (t) is given by:38,40,50
(t) is given by:38,40,50
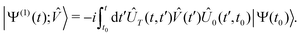 | (11) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) vanishes at all earlier times. The propagators Û0 and ÛT are symbolically represented by exponentiation of the corresponding Hamiltonians Ĥ0 and ĤT = Ĥ0 +
vanishes at all earlier times. The propagators Û0 and ÛT are symbolically represented by exponentiation of the corresponding Hamiltonians Ĥ0 and ĤT = Ĥ0 + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (for brevity, we choose to omit the time index where it is unambiguous from the context):
(for brevity, we choose to omit the time index where it is unambiguous from the context):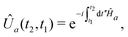 | (12) |
The general eqn (11) can be reduced to a computationally tractable form by introducing a sequence of approximation, as discussed in detail elsewhere.38,50,51 Briefly, by choosing the energy origin at the energy of the initial state Ψ, which is assumed to be an eigenfunction of Ĥ0, and using the Born–Oppenheimer factorization for the initial state, we obtain:
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) can normally be treated within the dipole approximation:
can normally be treated within the dipole approximation:where ω is the carrier frequency, f(t) is a slowly-varying envelope, the counter-rotating, stimulated-emission term
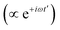 has been dropped, and operator
has been dropped, and operator ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) absorbs the field polarization properties and the choice of the interaction gauge. Finally, approximating ÛT by Û0, neglecting non-adiabatic contributions42,43 to Ĥ0, projecting Ψ(1)(t) onto a time-independent target electronic state ψf, and rearranging the terms, we recover the expected38,50 result for the vibronic wavepacket propagating on the electronic potential energy surface f:
absorbs the field polarization properties and the choice of the interaction gauge. Finally, approximating ÛT by Û0, neglecting non-adiabatic contributions42,43 to Ĥ0, projecting Ψ(1)(t) onto a time-independent target electronic state ψf, and rearranging the terms, we recover the expected38,50 result for the vibronic wavepacket propagating on the electronic potential energy surface f: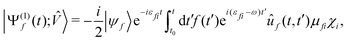 | (13) |
μfi(R) = 〈ψf|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |ψi〉. |ψi〉. | (14) |
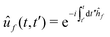 | (15) |
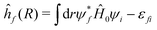 | (16) |
Eqn (13) represents bound and dissociative nuclear wavepacket on an equal footing.37 It is applicable to both bound-to-bound and ionizing electronic transitions. In the latter case, electronic dynamics in the continuum, which is the subject of the preceeding sections, appears as an additional integration over the target states f. Furthermore, the general form of the eqn (13) is preserved for multiphoton and strong-field transitions,38 although the definitions of the specific operators may need to be modified. It therefore forms the perfect departure point for the discussion below.
4.2 Broadband, 1-photon ionization
We advance by examining the familiar example of 1-photon ionization. Except for the (presently immaterial) normalization choice of the target states, the same treatment applies to 1-photon excitation. Because we are ultimately interested in coherent electronic dynamics, we will consider a coherent, two-colour perturbation: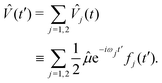 | (17) |
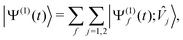 | (18) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) j〉, wavepacket component on electronic surface f produced by perturbation component
j〉, wavepacket component on electronic surface f produced by perturbation component ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) j, is given by eqn (13).
j, is given by eqn (13).
Because we assume that only the electronic state of the system is observed, we need to form the reduced density matrix ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) of the system, with the vibrational degrees of freedom traced out, exactly as we did for the photoelectron in eqn (3):
of the system, with the vibrational degrees of freedom traced out, exactly as we did for the photoelectron in eqn (3):
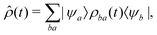 | (19) |
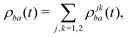 | (20) |
ρjkba(t) = 〈Ψ(1)b(t); ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) j|ψb〉〈ψa|Ψ(1)a(t); j|ψb〉〈ψa|Ψ(1)a(t); ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) k〉, k〉, | (21) |
Substituting Ψ(1) from eqn (13), rearranging the terms, changing the time variables, neglecting the difference between fj(t′ + τ) and fj(t′) for the slowly-varying envelope fj, and considering the limit of t → ∞, t0 → −∞, we obtain:37,50
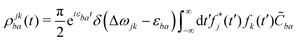 | (22) |
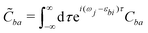 | (23) |
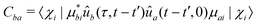 | (24) |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ba is its Fourier transform. In deriving eqn (22) we used the invariance of propagator û with respect to time origin and the relation
ba is its Fourier transform. In deriving eqn (22) we used the invariance of propagator û with respect to time origin and the relation 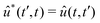 . For brevity, we suppress the arguments of
. For brevity, we suppress the arguments of 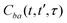 and
and 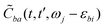 in the expressions above. (Note that ωj − εbi = ωk − εai due to the presence of the δ-function term in eqn (22).)
in the expressions above. (Note that ωj − εbi = ωk − εai due to the presence of the δ-function term in eqn (22).)
The individual terms in eqn (22) have a transparent physical interpretation. The δ(Δωjk − εba) term reflects energy conservation. The 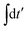 integral is, up to a constant, the fluence of the ionizing laser pulse. Finally, the
integral is, up to a constant, the fluence of the ionizing laser pulse. Finally, the ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ba term reflects the vibrational density of states available at the target energy.
ba term reflects the vibrational density of states available at the target energy.
The effects of ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ba on the reduced density matrix are qualitatively different for the diagonal (population) and off-diagonal (coherence) terms. It is therefore useful to examine the two separately. For the diagonal term, the nuclear propagators ûa and ûb in eqn (24) coincide. The observation-time argument (t − t′) therefore drops out, and the resulting autocorrelation function depends only on the time difference τ between the two ionization times. The time-dependent phase factors in eqn (22) also cancel, leading to:
ba on the reduced density matrix are qualitatively different for the diagonal (population) and off-diagonal (coherence) terms. It is therefore useful to examine the two separately. For the diagonal term, the nuclear propagators ûa and ûb in eqn (24) coincide. The observation-time argument (t − t′) therefore drops out, and the resulting autocorrelation function depends only on the time difference τ between the two ionization times. The time-dependent phase factors in eqn (22) also cancel, leading to:
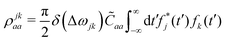 | (22a) |
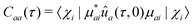 | (24a) |
The situation is quite different for the off-diagonal elements of the density matrix, describing the electronic coherence. This is clearly seen by rewriting eqn (24) in an equivalent form:6,52
| Cba (Δt,τ) = 〈ûb(Δt,τ)μbiχi|ûa (Δt,0)μaiχi〉 | (24b) |
In very small molecules, where the vibrational motion remains low-dimensional, periodic revivals of the cross-correlation function Cba, and therefore the electronic wavepacket motion, can be expected to persist for many vibrational periods.53,54 A similar situation can be expected when the electronic wavepacket evolves on electronic surfaces which are nested either due to the symmetry reasons, or accidentally. In all other systems, we should expect the cross-correlation function to decay rapidly, leading to a suppression of the electronic wavepacket dynamics.
We should emphasize that the coupled vibronic dynamics discussed above is fully coherent; no “true” decoherence due to interaction with the environment is included in our model. The electronic and nuclear wavefunctions remain entangled throughout. The reason the electronic dynamics described by the off-diagonal reduced density-matrix elements “disappears”, is the loss of overlap between the nuclear wavepackets. This is turn prevents factorization of the electronic and nuclear components of the wavefunction, and suppresses interference between the electronic eigenstates.
We also note that the time-domain, cross-correlation treatment of the reduced electronic coherence, exemplified by the eqn (22), (23) and (24b), is fundamentally different from the approach considered in ref. 5 and 55. The latter treatment assumes, as its very departure point, that electronic and nuclear wavefunctions are factorizable, neglecting the entanglement between the two. As the result, the treatment of ref. 5 and 55 only accounts for the structural inhomogeneity of the electronic transition, giving the upper bound for the electronic coherence lifetime due to nuclear motion. On the other hand, the approaches taken by ref. 6 and 52 fully account for the electronic–nuclear entanglement, are equivalent to our treatment above, and reach conclusions similar to ours.
4.3 An example: coherent hole dynamics in glycine cation
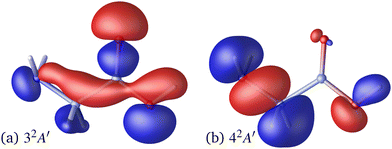
Following the seminal work by Kuleff, Breidbach, and Cederbaum,4,56 electron–hole dynamics in glycine cation provides the paradigmal example of attosecond electron dynamics in molecular systems. It is therefore fitting to examine the effect nuclear motion has on these dynamics.We limit ourselves to the case of the 32A′, 42A′ state pair, which has large contributions due to electron removal from the Hartree–Fock molecular orbital 14a′ of the neutral species.56 The corresponding Dyson orbitals (see Fig. 3) have norms of 0.852 and 0.877 respectively, confirming that these are 1h-type states. In the fixed-nuclei approximation, sudden removal of an electron from the 14a′ orbital induces hole dynamics with the period of ≈3.6 fs, lasting for at least tens of femtoseconds.56 In our calculations the two states are separated by ≈1.19 eV, corresponding to the natural oscillation period of ≈3.47 fs, in a good agreement with ref. 56.
We calculate the nuclear correlation functions on quadratic potential energy surfaces, determined at the occupation-restricted multiple active space configuration-interaction singles [ORMAS-CI(S)]57/cc-pVDZ58 level, with the ROHF ground-state wavefunction used as the reference. We perform the expansion in the vicinity of the RHF/cc-pVDZ optimized geometry of the ground-state, neutral glycine. All quantum-chemistry calculations used GAMESS-US code.59,60
The nuclear dynamics is performed in the basis of the products of the harmonic vibrational states of the neutral species, using an internally-developed code.61,62 The implementation relies on a binary-tree representation of Franck-Condon factors63 for efficient, sparse storage of vibrational wavepackets. The electronic potential-energy surfaces are implemented within the quadratic vibronic-Hamiltonian approach,64 fitted to ab initio energy points. Non-adiabatic and electric–dipole coupling terms, although available in the code, were neglected presently. Wavepackets were propagated using the 4th-order Runge-Kutta integrator with the time step of 0.02 atomic units, independently on the 32A′ and 42A′ surfaces. Atomic masses of the most-abundant isotopes were used in the simulations. (In passing, we note that much more general and powerful wavefunction-dynamics packages, such as MCTDH,65 are readily available. Our choice here is driven more by familiarity and personal convenience than any technical advantage.) While this level of theory is far from reaching spectroscopic accuracy, it suffices to illustrate the main features of the dynamics, at least semi-quantitatively.
The 10-atomic glycine molecule possesses 24 vibrational degrees of freedom, which makes a full-dimensional, quantum simulation of vibrational dynamics quite challenging. We instead choose to include the 14 degrees of freedom, along which the quadratic forcefields of the parent neutral and the two cations differ significantly. Ionization event is expected to trigger nuclear motion along these modes. The list of the “activated” modes is given in Table 1. Along the remaining normal modes, the neutral and cationic energy surfaces remain almost-perfectly nested. Dynamics along these modes can be neglected at short times. None of the “activated” modes are dominant, with each giving an incremental effect on the auto- and cross-correlation functions. Such behaviour appears to be universal for sufficiently-large molecules.52
| No. | Symm. | ω | T | 32A′ | 42A′ | Dominant character |
|---|---|---|---|---|---|---|
| 7 | a′′ | 87 | 383 | ✓ | CC torsion | |
| 8 | a′′ | 267 | 125 | ✓ | ✓ | CN torsion |
| 14 | a′ | 910 | 36.7 | ✓ | CC stretch | |
| 16 | a′ | 1048 | 31.8 | ✓ | ✓ | NH2 rock |
| 17 | a′ | 1228 | 27.2 | ✓ | ✓ | CN stretch |
| 19 | a′ | 1301 | 25.6 | ✓ | ✓ | COH bend/CH2 rock |
| 20 | a′ | 1328 | 25.1 | ✓ | ✓ | COH bend/CH2 rock |
| 22 | a′ | 1555 | 21.4 | ✓ | CO(H) stretch | |
| 23 | a′ | 1567 | 21.3 | ✓ | CH2 scissor | |
| 24 | a′ | 1806 | 18.5 | ✓ | NH2 scissor | |
| 25 | a′ | 2022 | 16.5 | ✓ | ✓ | CO stretch |
| 26 | a′ | 3209 | 10.3 | ✓ | CH2 symm. stretch | |
| 28 | a′ | 3724 | 8.96 | ✓ | NH2 symm. stretch | |
| 30 | a′ | 4086 | 8.16 | ✓ | ✓ | OH stretch |
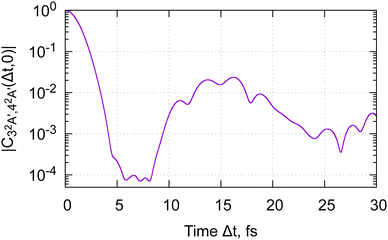
The calculated magnitude of the cross-correlation function 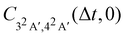 (eqn (24b), where we have taken μbi = μai = 1) is shown in Fig. 4. We are restricting ourselves to the case of zero inter-surface wavepacket delay τ, as appropriate for the sudden preparation of the vibronic wavepacket. In the simulation, we allowed maximum of nmax = 2 vibrational quanta per normal mode, for the total of (1 + nmax)14 ≈ 4.8 × 106 vibrational basis functions. To check convergence of the results, we have performed test calculations with nmax = 3 (2.7 × 108 basis functions), which we continued to Δt = 6 fs. We further evaluated the full-dimensional cross-correlation functions up to Δt = 3 fs while allowing excitation up to nmax = 3 in each of the 24 normal modes (2.8 × 1014 basis functions). The results of the test calculations qualitatively agree with data in Fig. 4, confirming that our model is adequate for discerning the main features of the dynamics.
(eqn (24b), where we have taken μbi = μai = 1) is shown in Fig. 4. We are restricting ourselves to the case of zero inter-surface wavepacket delay τ, as appropriate for the sudden preparation of the vibronic wavepacket. In the simulation, we allowed maximum of nmax = 2 vibrational quanta per normal mode, for the total of (1 + nmax)14 ≈ 4.8 × 106 vibrational basis functions. To check convergence of the results, we have performed test calculations with nmax = 3 (2.7 × 108 basis functions), which we continued to Δt = 6 fs. We further evaluated the full-dimensional cross-correlation functions up to Δt = 3 fs while allowing excitation up to nmax = 3 in each of the 24 normal modes (2.8 × 1014 basis functions). The results of the test calculations qualitatively agree with data in Fig. 4, confirming that our model is adequate for discerning the main features of the dynamics.
As we can see from Fig. 4, the nuclear cross-correlation function decays below 5% of the initial value after 3 fs. In the case of glycine cation, both nuclear surfaces remain bound. As long as the external sources of decoherence can be neglected, the dynamics therefore remains periodic, and the cross-correlation function (and the electronic–hole dynamics) will eventually revive. Due to the large number of the normal modes accessed by the dynamics, and their disparate characteristic times (see Table 1), the full-revival time is expected to be quite long – certainly in excess of 380 fs, the period of the C–C torsion mode. Due to the number of modes involved in the dynamics, partial revivals are expected to be weak. Indeed, in our simulation, the largest revival is at the 2% level, reached 14 fs after the start of the dynamics.
We therefore conclude that the coherent electronic wavepacket oscillation upon sudden preparation of the 32A′, 42A′ state pair in glycine cation is expected to disappear within 3 fs. We can expect to observe at most a single, decaying oscillation of these electronic dynamics, even under the ideal experimental conditions. This conclusion is at stark variance with the result obtained for the frozen nuclei, where pronounced charge oscillations are predicted to persist for tens of femtoseconds, with hardly any decay.56 Thus, even though the nuclear displacements and velocities reached on a few-femtosecond time scales remain minuscule in absolute terms, their effect on the electronic dynamics is profound, and can't be neglected.
We note that coherent electronic dynamics in the glycine cation was previously examined using Ehrenfest dynamics,66 obtaining electronic dephasing times similar to ours. On the other hand, the study,55 also using Ehrenfest dynamics, found nuclear motion effects to be negligible for short-time electronic dynamics, and only become visible beyond 15 fs. The reasons for the discrepancy between the conclusions reached by ref. 55 and 66 are not immediately apparent.
We can reasonably suspect that the rapid-dephasing scenario generally applies to valence electronic wavepackets in medium-sized molecules.52 As long as the components of the electronic wavepacket modify the bonding situation in different parts of the molecule, the ensuing nuclear dynamics will rapidly drive apart the nuclear wavepackets evolving on different electronic eigensurfaces. The sheer volume of the available vibrational phase space will then ensure that the vibrational revival does not occur before the system has a chance do decohere due to interactions with the environment.
Naturally, other scenarios can and will arise, where the electronic wavepacket is confined to a manifold of nested states, so that the nuclear-wavefunction coherence, together with the electron–hole dynamics could persist for longer times. As we have seen on the example above, the existence of such long-lived electronic oscillations is by no means guaranteed, and must be investigated, individually for each specific case.
4.4 Other types of electronic transitions
Although our analysis of nuclear-motion effects has focussed on 1-photon ionization, very similar results apply for other atto- and femto-second electronic transitions. Thus, the nuclear autocorrelation function Caa (τ) (eqn (24c)) modulates the high-harmonics yield in molecules,67 as beautifully demonstrated in PACER (“Probing attosecond dynamics by chirp-encoded recollisions”) experiments.68,69 It has been recently shown that the short-time autocorrelation functions can be extracted directly from the intensity-dependent HHG spectra for medium-sized molecules,70 without resorting to elaborate theory modeling. These femtosecond nuclear dynamics in turn give access to the local potential-energy surface parameters of the transiently-created cations,67,71 despite their fleeting, sub laser-cycle existence.The nuclear autocorrelation function has also been shown to make an appearance in the strong-field streaking spectra of molecules,72 creating a potentially very rich source of information on atto- and femto-second vibronic dynamics. We can further expect the nuclear autocorrelation to play a role in all processes whether the observables can be expressed in terms of the diagonal part of the electronic reduced density matrix.
Similarly, the nuclear cross-correlation is expected to modulate the attosecond electronic wavepacket dynamics in molecules, regardless of the specific preparation mechanism. It has been long used in the theory of molecular Raman transitions,38,73 and was recently applied to modeling the dephasing of attosecond electronic dynamics in molecules.6,52 We expect it to appear wherever molecular observables are determined by an electronic coherence.
5 Coherence in high-intensity high-frequency ionization
Broad-band ionization with attosecond X-ray pulses can lead to coherent population of a series of outer-valence-, inner-valence- or core-ionized states spanning energy ranges of 10 s of eV. In the perturbative regime, such as has been considered by us here in relation to high-frequency (XUV, X-ray) ionization so far, the relative populations of and coherences between these states are defined by the pulse shape, bound-continuum dipole moments and the subtle many-electron effects of loss of coherence due to break-up of an N-electron system. Within this perturbative picture, applying higher intensity ionising pulses will simply lead to a proportional increase of the populations of the ionized states, without changing their relative populations or degrees of coherence. However, it is well-established that multi-level systems driven by non-resonant high frequency, high-intensity fields exhibit fast transitions between the levels once the interaction energy associated with the bound–bound transitions exceeds the inter-level spacing, see ref. 74 and 75: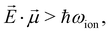 | (25) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) is the electric field amplitude,
is the electric field amplitude, 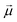 is the transition dipole and ħωion is the energy spacing between the two coupled bound levels. Therefore, ionising pulse of sufficient intensity can lead to redistribution of populations among the ionized states. This redistribution is expected to be strongly intensity-dependent and cannot be accounted for by the traditional perturbation theory where the interaction energy in the units of level spacing is a small parameter. On the contrary, the inverse perturbative treatment becomes possible in this case, in which the level spacing is much smaller than the interaction energy.74,75 We postulate that transition to this regime signifies the onset of strong-field X-ray physics.
is the transition dipole and ħωion is the energy spacing between the two coupled bound levels. Therefore, ionising pulse of sufficient intensity can lead to redistribution of populations among the ionized states. This redistribution is expected to be strongly intensity-dependent and cannot be accounted for by the traditional perturbation theory where the interaction energy in the units of level spacing is a small parameter. On the contrary, the inverse perturbative treatment becomes possible in this case, in which the level spacing is much smaller than the interaction energy.74,75 We postulate that transition to this regime signifies the onset of strong-field X-ray physics.
This suggested strong-field regime can be reached at much lower intensities than would be necessary for reaching any appreciable values of the ponderomotive potential on the scale of the ionization energy, as required by for the strong-field dynamics at the low (e.g. IR) field frequencies. As an order of magnitude estimation, one can think of ionic states separated by several eV (≈0.1 a.u.) with transition dipole moments of the order of 0.1 a.u. driven by the ionising field of the frequency of several hundreds of eV (≈10 a.u.). In this case, the interaction energy exceeds the level spacing for the electric field strength of the order of 1 a.u., at which the ponderomotive potential for the high frequency field is still negligible. This does not mean, however, that the suggested high-frequency strong-field regime is guaranteed to be observable. The main competing perturbative process that can obscure the suggested strong-field dynamics is the sequential multiple ionization. Indeed, apart from driving the non-resonant transitions between the ionized states, as assumed above, the high-frequency field can also lead to further ionization of the system. For hard X-ray fields and relatively long (e.g. 100 fs) pulses, multiple ionization clearly dominates at intensities of about 1019 W cm−2 and higher, as has been shown in a series of studies by Santra and co-workers, see e.g. ref. 76. Using soft X-rays would lower this intensity threshold due to larger photoionization cross-sections, which could be partly mitigated by using the presently available sub-fs X-ray pulses.3 The precise window of intensities available for the strong-field high-frequency photoionization dynamics proposed here remains to be established.
6 Conclusions
In conclusion, the partial loss of quantum coherence in the course of a break-up of an atomic or molecular system interacting with a short pulse of ionising radiation, as well as the decay of the remaining quantum coherence by both purely electronic and electronic-nuclear mechanisms are central issues in attosecond physics. Due to the complexity of the problem, involving many-electron dynamics, coupling of electronic and nuclear degrees of freedom, as well as strong laser field effects, theoretical description of the onset and decay of coherence in attosecond ionization is still very much an open problem. Spectacular successes have been made in the theoretical modelling of purely electronic dynamics within frozen nuclei approximation, even in the most complicated cases of the breakdown of the molecular orbital picture of the ionization. Similarly, the role of nuclear dynamics (including, at the simplest level, the role of finite distribution of nuclear coordinates due to zero-point energy) is presently well-understood for the cases of simple (Koopmans-like) spectrum of the ionized states. Combining the two, however, as is necessary for example for the description of attosecond ionization in the inner-valence region of polyatomic molecules, has not yet been achieved and should be subject of future studies. The theoretical advances towards understanding the quantum coherence in attosecond photoionization allow one, for the first time, to look at the photoionization problem from the point of view of the quantum information theory. Quantifying the interplay between quantum entanglement and quantum coherence in photoionization will therefore form another avenue of future research. Finally, while a good understanding of the mechanisms underlying the quantum coherence in photoionization by high-intensity low-frequency fields has been achieved, the more notion of a high-intensity field in the opposite, high-frequency regime is yet to be defined. One possible definition has been proposed here. Further theoretical and experimental work needs to be done in order to verify the validity of this proposition.Author contributions
All authors contributed equally to the conceptualization of this work. The contributions to the writing were as follows: M. R. wrote Sections 1–3, S. P. wrote Section 4, V. A. wrote Sections 5 and 6. All authors contributed to the reviewing and the editing of the whole manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Marco Ruberti acknowledges support from the Quantum entanglement in attosecond ionization EPSRC grant EP/V009192/1.Notes and references
- F. Krausz and M. Ivanov, Rev. Mod. Phys., 2009, 81, 163–234 CrossRef.
- A. S. Johnson, D. R. Austin, D. A. Wood, C. Brhamsan, D. Gregory, K. B. Holzner, S. Jarosch, E. W. Larsen, S. Parker, C. S. Struber, P. Ye, J. W. G. Tisch and J. P. Marangos, Sci. Adv., 2018, 4, eaar3761 CrossRef PubMed.
- J. Duris, S. Li, T. Driver, E. G. Champenois, J. P. MacArthur, A. A. Lutman, P. R. Z. Zhang, J. W. Aldrich, R. Coffee, G. Coslovich, F.-J. Decker, J. M. Glownia, G. Hartmann, W. Helml, A. Kamalov, J. Knurr, J. Krzywinski, M.-F. Lin, J. P. Marangos, M. Nantel, A. Natan, J. T. ONeal, N. Shivaram, P. Walter, A. L. Wang, J. J. Welch, T. J. A. Wolf, J. Z. Xu, M. F. Kling, P. H. Bucksbaum, A. Zholents, Z. Huang, J. P. Cryan and A. Marinelli, Nat. Photonics, 2020, 14, 30 CrossRef CAS.
- J. Breidbach and L. S. Cederbaum, J. Chem. Phys., 2003, 118, 3983 CrossRef CAS.
- V. Despré, A. Marciniak, V. Loriot, M. C. E. Galbraith, A. Rouzée, M. J. J. Vrakking, F. Lépine and A. I. Kuleff, J. Phys. Chem. Lett., 2015, 6, 426 CrossRef PubMed.
- M. Vacher, M. J. Bearpark, M. A. Robb and J. P. Malhado, Phys. Rev. Lett., 2017, 118, 083001 CrossRef PubMed.
- F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. D. Camillis, S. Anumula, F. Frassetto, L. Poletto, A. Palacios, P. Decleva, J. B. Greenwood, F. Martin and M. Nisoli, Science, 2014, 346, 336 CrossRef CAS PubMed.
- P. M. Kraus, B. Mignolet, D. Baykusheva, A. Rupenyan, L. H. F. Penka, G. Grassi, O. I. Tolstikhin, J. Schneider, F. Jensen, L. B. Madsen, A. D. Bandrauk, F. Remacle and H. J. Worner, Science, 2015, 350, 790 CrossRef CAS PubMed.
- M. Nisoli, P. Decleva, F. Calegari, A. Palacios and F. Martín, Chem. Rev., 2017, 117, 10760 CrossRef CAS PubMed.
- A. Szabo and N. S. Ostlund, Modern quantum chemistry: Introduction to advanced electronic structure theory, Dover Publications, Mineola, NY, 1996 Search PubMed.
- E. Goulielmakis, Z.-H. Loh, A. Wirth, R. Santra, N. Rohringer, V. S. Yakovlev, S. Zherebtsov, T. Pfeifer, A. M. Azzeer, M. F. Kling, S. R. Leone and F. Krausz, Nature, 2010, 466, 739 CrossRef CAS PubMed.
- S. Pabst, L. Greenman, P. J. Ho, D. A. Mazziotti and R. Santra, Phys. Rev. Lett., 2011, 106, 053003 CrossRef PubMed.
- C. Bourassin-Bouchet, L. Barreau, V. Gruson, J.-F. Hergott, F. Quéré, P. Salières and T. Ruchon, Phys. Rev. X, 2020, 10, 031048 CAS.
- S. Pabst, M. Lein and H. J. Wörner, Phys. Rev. A, 2016, 93, 023412 CrossRef.
- M. Ruberti, P. Decleva and V. Averbukh, J. Chem. Theory Comput., 2018, 14, 4991–5000 CrossRef CAS PubMed.
- M. Spanner and S. Patchkovskii, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 80, 063411 CrossRef.
- M. Spanner and S. Patchkovskii, Chem. Phys., 2013, 414, 10–19 CrossRef CAS.
- J. Schirmer, Many-Body Methods for Atoms, Molecules and Clusters, Springer, 2018, vol. 94 Search PubMed.
- A. Ponzi, M. Sapunar, C. Angeli, R. Cimiraglia, N. Doslic and P. Decleva, J. Chem. Phys., 2016, 084307 CrossRef PubMed.
- J. Delgado, M. Lara-Astiaso, J. González-Vázquez, P. Decleva, A. Palacios and F. Martin, Faraday Discuss., 2021, 228, 349 RSC.
- C. Marante, M. Klinker, I. Corral, J. Gonzalez-Vazquez, L. Argenti and F. Martin, J. Chem. Theory Comput., 2017, 13, 499 CrossRef CAS PubMed.
- E. Perfetto and G. Stefanucci, J. Phys: Condens. Matter, 2018, 30, 465901 CrossRef CAS PubMed.
- J. Benda, J. D. Gorfinkiel, Z. Masin, G. S. J. Armstrong, A. C. Brown, D. D. A. Clarke, H. W. van der Hart and J. Wragg, Phys. Rev. A, 2020, 102, 052826 CrossRef CAS.
- M. Ruberti, V. Averbukh and P. Decleva, J. Chem. Phys., 2014, 141, 164126 CrossRef CAS PubMed.
- V. Averbukh and M. Ruberti, in Attosecond Molecular Dynamics, ed. M. Vrakking and F. Lepine, Royal Society Chemistry, Cambridge, 2018, vol. 13 of Theoretical and Computational Chemistry series, pp. 68–102 Search PubMed.
- M. Ruberti, J. Chem. Theory Comput., 2019, 15, 3635–3653 CrossRef CAS PubMed.
- M. Ruberti, Phys. Chem. Chem. Phys., 2019, 21, 17584–17604 RSC.
- G. S. J. Armstrong, M. A. Khokhlova, M. Labeye, A. S. Maxwell, E. Pisanty and M. Ruberti, Eur. Phys. J. D, 2021, 75, 209 CrossRef CAS PubMed.
- M. Ruberti, Faraday Discuss., 2021, 228, 286–311 RSC.
- D. Schwickert, M. Ruberti, P. Kolorenč, S. Usenko, A. Przystawik, K. Baev, I. Baev, M. Braune, L. Bocklage, M. Czwalinna, S. Deinert, S. Düsterer, A. Hans, G. Hartmann, C. Haunhorst, M. Kuhlmann, S. Palutke, R. Röhlsberger, J. Rönsch-Schulenburg, P. Schmidt, S. Toleikis, J. Viefhaus, M. Martins, A. Knie, D. Kip, V. Averbukh, J. Marangos and T. Laarmann, Sci. Adv., 2022, 8, eabn6848 (1–11) Search PubMed.
- M. Klinker, C. Marante, L. Argenti, J. Gonzalez-Vazquez and F. Martin, J. Phys. Chem. Lett., 2018, 9, 756 CrossRef CAS PubMed.
- B. Cooper and V. Averbukh, Phys. Rev. Lett., 2013, 111, 083004 CrossRef PubMed.
- D. You, K. Ueda, M. Ruberti, K. Ishikawa, P. Carpeggiani, T. Csizmadia, L. Gulyas, N. Harshitha, G. Sansone, P. Maroju, K. Kooser, C. Callegari, M. Di Fraia, O. Plekan, R. Richter, L. Giannessi, E. Allaria, G. De Ninno, M. Trovo, L. Badano, B. Diviacco, D. Gauthier, N. Mirian, G. Penco, P. Rebernik, S. Spampinati, C. Spezzani, S. Di Mitri, G. Gaio and K. Prince, New J. Phys., 2019, 21, 113036 CrossRef CAS.
- T. Barillot, O. Alexander, B. Cooper, T. Driver, D. Garratt, S. Li, A. A. Haddad, A. Sanchez-Gonzalez, M. AgÅker, C. Arrell, M. J. Bearpark, N. Berrah, C. Bostedt, J. Bozek, C. Brahms, P. H. Bucksbaum, A. Clark, G. Doumy, R. Feifel, L. J. Frasinski, S. Jarosch, A. S. Johnson, L. Kjellsson, P. Kolorenč, Y. Kumagai, E. W. Larsen, P. Matia-Hernando, M. Robb, J.-E. Rubensson, M. Ruberti, C. Sathe, R. J. Squibb, A. Tan, J. W. G. Tisch, M. Vacher, D. J. Walke, T. J. A. Wolf, D. Wood, V. Zhaunerchyk, P. Walter, T. Osipov, A. Marinelli, T. J. Maxwell, R. Coffee, A. A. Lutman, V. Averbukh, K. Ueda, J. P. Cryan and J. P. Marangos, Phys. Rev. X, 2021, 11, 031048 CAS.
- A. W. Bray, U. Eichmann and S. Patchkovskii, Phys. Rev. Lett., 2020, 124, 233202 CrossRef CAS PubMed.
- U. Eichmann, H. Rottke, S. Meise, J.-E. Rubensson, J. Soderstrom, M. Agaker, C. Sathe, M. Meyer, T. M. Baumann, R. Boll, A. De Fanis, P. Grychtol, T. Mazza, J. Montano, V. Music, Y. Ovcharenko, D. E. Rivas, S. Serkez, R. Wagner, S. Eisebitt and M. Ilchen, Science, 2020, 369, 1630 CrossRef CAS PubMed.
- E. J. Heller, Acc. Chem. Res., 1981, 14, 368–375 CrossRef CAS.
- D. J. Tannor, Introduction to quantum mechanics: a time-dependent perspective, University Science Books, Mill Valley, CA, 2006 Search PubMed.
- S. V. Popruzhenko, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 204001 CrossRef.
- D. B. Milosevic, G. G. Paulus, D. Bauer and W. Becker, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, R203–R262 CrossRef CAS.
- H. Köppel, W. Domcke and L. S. Cederbaum, Adv. Chem. Phys., 1984, 57, 59–246 Search PubMed.
- D. Yarkony, Rev. Mod. Phys., 1996, 68, 985–1013 CrossRef CAS.
- D. R. Yarkony, Chem. Rev., 2012, 112, 481–498 CrossRef CAS PubMed.
- T. Yonehara, K. Hanasaki and K. Takatsuka, Chem. Rev., 2011, 112, 499–542 CrossRef PubMed.
- M. Born and K. Huang, Dynamical theory of crystal lattices, Oxford University Press, USA, 1998 Search PubMed.
- C. A. Mead, Rev. Mod. Phys., 1992, 64, 51–85 CrossRef CAS.
- L. A. Nafie, J. Chem. Phys., 1983, 79, 4950–4957 CrossRef CAS.
- L. A. Nafie, J. Phys. Chem. A, 2004, 108, 7222–7231 CrossRef CAS.
- A. Abedi, N. T. Maitra and E. K. U. Gross, Phys. Rev. Lett., 2010, 105, 123002 CrossRef PubMed.
- K. C. Kulander and E. J. Heller, J. Chem. Phys., 1978, 69, 2439–2449 CrossRef CAS.
- O. Smirnova and M. Ivanov, in Attosecond and Free electron Laser Science, ed. T. Schulz and M. Vrakking, Wiley-VCH, 2014, ch. 7, pp. 201–256 Search PubMed.
- C. Arnold, O. Vendrell and R. Santra, Phys. Rev. A, 2017, 95, 033425 CrossRef.
- T. Latka, V. Shirvanyan, M. Ossiander, O. Razskazovskaya, A. Guggenmos, M. Jobst, M. Fieß, S. Holzner, A. Sommer, M. Schultze, C. Jakubeit, J. Riemensberger, B. Bernhardt, W. Helml, F. Gatti, B. Lasorne, D. Lauvergnat, P. Decleva, G. J. Halász, A. Vibók and R. Kienberger, Phys. Rev. A, 2019, 99, 063405 CrossRef CAS.
- W. Hu, B. Gu and I. Franco, J. Chem. Phys., 2018, 148, 134304 CrossRef PubMed.
- M. Lara-Astiaso, A. Palacios, P. Decleva, I. Tavernelli and F. Martín, Chem. Phys. Lett., 2017, 683, 357–364 CrossRef CAS.
- A. Kuleff, J. Breidbach and L. Cederbaum, J. Chem. Phys., 2005, 123, 044111 CrossRef PubMed.
- J. Ivanic, J. Chem. Phys., 2003, 119, 9364–9376 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- M. Schmidt, K. Baldridge, J. Boatz, S. Elbert, M. Gordon, J. Jensen, S. Koseki, N. Matsunaga, K. Nguyen, S. Su, T. Windus, M. Dupuis and J. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- M. S. Gordon and M. W. Schmidt, in Theory and Applications of Computational Chemistry, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, ch. 41, pp. 1167–1189 Search PubMed.
- S. Patchkovskii and M. S. Schuurman, J. Phys. Chem. A, 2014, 118, 12069–12079 CrossRef CAS PubMed.
- S. Patchkovskii and M. S. Schuurman, Phys. Rev. A, 2017, 96, 053405 CrossRef.
- D. Gruner and P. Brumer, Chem. Phys. Lett., 1987, 138, 310–314 CrossRef CAS.
- M. S. Schuurman and D. R. Yarkony, J. Chem. Phys., 2007, 127, 094104 CrossRef PubMed.
- G. A. Worth, H. D. Meyer, H. Köppel, L. S. Cederbaum and I. Burghardt, Intl. Rev. Phys. Chem., 2008, 27, 569–606 CrossRef CAS.
- I. Polyak, A. J. Jenkins, M. Vacher, M. E. F. Bouduban, M. J. Bearpark and M. A. Robb, Mol. Phys., 2018, 116, 2474–2489 CrossRef CAS.
- M. Lein, Phys. Rev. Lett., 2005, 94, 053004 CrossRef PubMed.
- S. Baker, J. Robinson, C. Haworth, H. Teng, R. Smith, C. Chirila, M. Lein, J. Tisch and J. Marangos, Science, 2006, 312, 424–427 CrossRef CAS PubMed.
- A. Zair, T. Siegel, S. Sukiasyan, F. Risoud, L. Brugnera, C. Hutchison, Z. Diveki, T. Auguste, J. W. G. Tisch, P. Salieres, M. Y. Ivanov and J. P. Marangos, Chem. Phys., 2013, 414, 184–191 CrossRef CAS.
- D. R. Austin, A. S. Johnson, F. McGrath, D. Wood, L. Miseikis, T. Siegel, P. Hawkins, A. Harvey, Z. Masin, S. Patchkovskii, M. Vacher, J. P. Malhado, M. Y. Ivanov, O. Smirnova and J. P. Marangos, Sci. Rep., 2021, 11, 2485 CrossRef CAS PubMed.
- S. Patchkovskii, Phys. Rev. Lett., 2009, 102, 253602 CrossRef PubMed.
- M. Kowalewski, K. Bennett, J. R. Rouxel and S. Mukamel, Phys. Rev. Lett., 2016, 117, 043201 CrossRef PubMed.
- S. Lee and E. J. Heller, J. Chem. Phys., 1979, 71, 4777–4788 CrossRef CAS.
- M. Y. Ivanov and P. B. Corkum, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 48, 580–590 CrossRef CAS PubMed.
- V. Averbukh, O. E. Alon and N. Moiseyev, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 64, 033411-1-13 CrossRef.
- L. Inhester, K. Hanasaki, Y. Hao, S.-K. Son and R. Santra, Phys. Rev. A, 2016, 94, 023422-1-8 CrossRef.
| This journal is © the Owner Societies 2022 |

![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)