Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Using core-hole reference states for calculating X-ray photoelectron and emission spectra
Andreas
Dreuw
 a and
Thomas
Fransson
a and
Thomas
Fransson
 *b
*b
aInterdisciplinary Center for Scientific Computing, Heidelberg University, Im Neuenheimer Feld 205, Heidelberg 69120, Germany
bDepartment of Theoretical Chemistry and Biology, KTH Royal Institute of Technology, Stockholm 10691, Sweden. E-mail: thofra@kth.se
First published on 28th April 2022
Abstract
For the calculation of core-ionization energies (IEs), X-ray photoelectron spectra (XPS), and X-ray emission spectra (XES), a commonly applied approach is to use non-Aufbau reference states with a core-hole as either final (IE and XPS) or initial (XES) state. However, such reference states can introduce numerical instabilities in post-HF methods, relating to the denominator of the energy corrections involved. This may become arbitrarily close to zero if a negative virtual orbital is present, e.g. a core-hole, leading to near-singularities. The resulting instabilities lead to severe convergence issues of the calculation schemes and, in addition, can strongly affect both energies and intensities, with oscillator strengths seen to reach values up to 4 × 107. For the K-edge we propose freezing the highest-energy virtual orbitals which contribute to any denominator below a threshold of 0.1 Hartree. Stable and reliable spectra are then produced, with minimal influence due to freezing energetically high-lying virtual orbitals (typically removing <5% of the total number of MOs). The developed protocol is here tested for Møller–Plesset perturbation theory and for the algebraic diagrammatic construction scheme for the polarization propagator, and it is also relevant for coupled cluster theory and other related methods.
1 Introduction
For the investigation of the electronic and atomic structure of molecular materials, X-ray spectroscopies provides a number of highly element-specific probes, capable of addressing occupied states, unoccupied states, local bond character, and more.1 Included here are X-ray photoelectron spectroscopy (XPS), which probes core-electron binding energy, and X-ray emission spectroscopy (XES), for which the fluorescence decay of core-ionized or core-excited molecules provides information on occupied states. Focusing on the use of core-ionized energies (i.e. non-resonant XES), X-ray emission occurs after core-ionization when a valence electron re-fills the initial core-hole, and thus grants insight into the valence states.1–3 If resonant energies are used instead, one obtains resonant inelastic X-ray scattering (RIXS), which yields information on both occupied and unoccupied states.For modeling XPS (and X-ray absorption spectroscopy, XAS), the core–valence separation (CVS) approximation has emerged as an efficient and at the same time accurate approach, in which the valence–valence excitations are excluded from excited-state eigenvalue equations by construction, and the resulting excited-state equations involve only excitations containing the core orbital(s) of interest.4–8 However, as XES and RIXS involve the transition of valence electrons into core-holes, the CVS approximation is no longer applicable, and other schemes have to be applied. A major challenge in simulating core spectroscopies is the correct description of the drastic electronic relaxation effects occurring during the creation of a core-hole and its refilling (effectively changing the local atomic charge by one unit), and the absolute performance of above methods is largely tied into how well this effect is considered. However, absolute and relative performances are two different measures, and the latter can be good even if the former is poor.9
The computation of core-ionization and -excitation energies can often be considered by constructing the ground state and the individual core-ionized or core-excited final states separately via tweaked ground state methods. The corresponding core-ionization or core-excitation energies are then obtained as differences of the total energies of the final and initial states. These so-called Δ-methods comprise, for instance, self-consistent-field theory (ΔSCF),10,11 complete-active-space SCF (ΔCASSCF),12 Møller–Plesset perturbation theory (ΔMP),13 and coupled cluster approaches (ΔCC).14,15 Furthermore, the use of a core-hole reference state can also be used for modeling XAS, as is done using the static exchange (STEX) method.16 An advantage is that the electronic relaxation effects are explicitly taken into account in the respective calculations. However, the computation of full core-ionization or core-excitation spectra is extremely tedious, if not impossible due to increasing convergence issues for energetically higher lying final states. Furthermore, the limited use of correlated Δ-methods, in particular ΔCC methods, is attributed to convergence problems of CC equations for the core-ionized or core-excited state due to the presence of a core-hole.15,17 Here certain doubly excited configurations, in which an occupied valence orbital is coupled to the core-hole, and another occupied valence orbital to a high-lying virtual orbital, exhibit very small orbital energy differences, which then lead to numerical instabilities in the solution of CC amplitude equations, for example.
For the simulation of complete X-ray emission spectra, i.e. for the calculation of several emission energies and their corresponding intensities, one can again start from an explicitly core-ionized state by tweaking a suitable ground state method to converge onto this state. Subsequently, the valence-to-core transitions are computed as “excited” states with negative excitation energies and oscillator strengths using, for example, established linear response theory.1,18–20 The core-ionized reference determinant belongs to the class of so-called non-Aufbau references, since it possesses a vacancy in an inner electronic shell, thus violating the Aufbau principle. This procedure yields full X-ray emission spectra corresponding to one particular core-hole in one single calculation, avoiding the need for separate calculations for each valence-to-core transition. This computational procedure has already been successfully employed within time-dependent DFT (TDDFT),18,19,21 equation of motion coupled cluster singles and doubles (EOM-CCSD),18,21–23 and the algebraic diagrammatic construction (ADC) scheme.24 In principle, one can exploit this procedure to start from a non-Aufbau reference state also for the computation of other X-ray spectroscopies such as RIXS25 and transient XAS.26 However, when using such reference states for response and equation-of-motion theories, the convergence issues related to near-singularities from certain doubly excited configurations with near-zero energy difference are again present. These lead to numerical instabilities in the solution algorithms and to spurious results for transition energies and oscillator strengths, as will be shown below.
In this paper, these instabilities will be discussed in the context of ΔMP treatments of XPS, and ADC calculations of XES. A method for removing these instabilities is presented and illustrated, and we posit that this approach will also be useful for other post-HF methods—most notably for coupled cluster theory. First, we illustrate how the instabilities affect ionization energies (IE) and X-ray emission energies and intensities for the K-edge of neon, utilizing a number of different basis sets. A scheme for removing these instabilities is presented, in which effective core potentials (ECPs) are used for all non-hydrogen atoms save one. A core-hole is then constructed on this atom, and specific virtual orbitals are frozen in the post-HF calculations. This approach is tested for different basis sets and energy thresholds, showing a smooth convergence for the K-edge of light elements. Complications are shown to occur for the L-edge of heavier elements, and the approach is thus not recommended there. Finally, using this approach we consider the X-ray emission spectra of a number of medium-sized molecules, obtaining good agreement with experimental measurements.
2 Theory and methods
An approach to converge SCF calculations incorporating a core-hole is using the maximum overlap method (MOM).27–30 In the MOM, the wave function is optimized with overlap to previous iterations in mind, rather than from energetic arguments. With this non-Aufbau approach, core-holes and other energetically higher wave functions can be obtained. Alternative approaches of forming a core-hole reference state are available, including the initial maximum overlap method (IMOM),31 state-targeted energy projection (STEP),32 and square gradient minimization (SGM).33 Core-hole states converged this way can be used to estimate ionization energies (IE) via the ΔSCF approach, or as the initial state of an X-ray emission spectrum calculation. There, the converged core-hole wave function is used as a reference of iterative diagonalization schemes, e.g. the Davidson algorithm, for which the valence-to-core transitions occur as the first (negative) eigenvalues.18,19,22,24Using Møller–Plesset perturbation theory, the energy correction at second order in perturbation theory can be expressed as
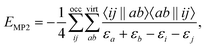 | (1) |
The algebraic diagrammatic construction scheme for the polarization propagator is a size-extensive and Hermitian computational method for excited (correlated) electronic states.34–37 Here a perturbation expansion of the polarization operator using the Møller–Plesset (MP) partitioning leads to algebraic expressions for the elements of the ADC matrix components. An intuitive way to construct the ADC matrix and the associated working equations is provided by the intermediate state representation (ISR) approach,35,38,39 introducing a Hamiltonian matrix shifted by the ground state energy (E0) on the basis of a set of intermediate excited states. The nth order ADC approximation (ADC(n)) contains entities of excitation classes required for the consistent description of properties to order n of perturbation theory. Additionally, singular matrix blocks can be expanded to higher order in an ad hoc manner, which can potentially yield improved results at lower computational cost than for a full order expansion. An example of this is the ADC(2)-x model, in which the 2p2h block is expanded to first order, while a strict formulation of ADC(2) only contains orbital energy differences in the diagonal. These methods are utilized in this study, as well as the third order (in energy) method ADC(3/2), which utilizes second-order property gradients.
3 Computational details
The geometries of the molecules were optimized at the frozen-core MP2 level of theory,40 using cc-pVTZ basis sets,41 as implemented in Q-Chem 5.2.42 Property calculations were run using several different Pople43 and Dunning41 basis sets, including core-polarizing functions for the latter.44 Effective core potentials (ECP) of the Stuttgart–Cologne type45 were used where stated. Convolution of the obtained energies and intensities using a Lorentzian function was performed to facilitate the analysis and comparison to experimental spectra, using a half-width at half-maximum of 0.4 eV.The coupled cluster calculations were carried out in Q-Chem 5.2,42 and the ADC results were obtained using the adcc software package,46 using SCF results obtained from pyscf.47,48 MP2 denominator evaluations were performed at the Python level, with an example script found in the adcc repository.49
4 Results and discussion
We first illustrate the effects of instabilities on ionization energies, emission energies and intensities, focusing on neon using progressively larger basis sets. A method for selecting and freezing intruding virtual orbitals is then presented, with tests to determine a suitable threshold for K-edge studies on light elements. The performance of this protocol is illustrated for ammonia and methanol, followed by a discussion on issues related to heavier elements. Finally, an illustration of the performance of ADC(2), ADC(2)-x, and ADC(3/2) for reproducing experimental X-ray emission spectra is presented.4.1 Instability from progressively larger basis sets
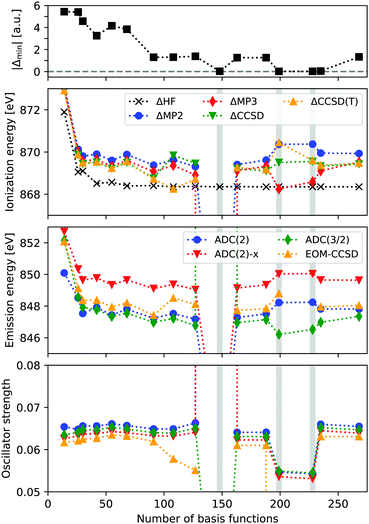
In Fig. 1 the ionization energy (IE), X-ray emission energy and intensity of neon is reported, as a function of basis set size. IEs are calculated from total energy differences, using HF, MP2, MP3, CCSD, and CCSD(T). Emission energies and intensities are obtained from EOM-CCSD and ADC(n) calculations on the core-hole reference state, focusing on the transition from the HOMO. The basis sets used are cc-pV nN (n = 2–9), considering both the contracted and uncontracted versions. The top panel shows the value of the smallest absolute denominator (|Δmin|) for each basis set.We see that the ΔHF calculations are stable and reach an IE of around 868.4 eV, which compares reasonably well with the experimental value of 870.09 eV. The correlated results are generally higher in energy by about 1 eV, and when accounting for relativistic effects (∼0.9 eV), these results are within a few tenths of an eV from experimental values. However, for the uncontracted cc-pV6Z calculations convergence issues occur for CCSD, and the MP2 and MP3 IE are far below experimental results, with 857.8 and −25.5 eV, respectively. For the cc-pV8Z basis sets there are some abnormal results as well. Looking at the X-ray emission spectra, we obtain unphysical excitation energies and intensities for these three basis sets, in particular when using uncontracted cc-pV6Z. These erroneous excitation energies range from 836.1 to 245.8 eV, and intensities from 0.00 to 7.32.
The unphysical results are thus present for some of the basis sets, but it is not simply a function of the total basis set size. Rather, it occurs when MP2 denominators become close to zero, with the three unstable calculations featuring |Δmin| of 0.019–0.024 a.u. A fourth basis set (cc-pV9Z) yields |Δmin| = 0.043 a.u., while the remaining calculations all have |Δmin| > 1.0 a.u.
4.2 Removing intruding denominators
When using a core-hole reference state, the core-hole provides an unoccupied orbital with a large negative value. In eqn (1), this corresponds to, e.g., εa ≪ 0, with which there are now the following possibilities for Δ to become arbitrarily close to zero:1. Core-hole (a) coupling to valence orbital (i), and other valence orbital (j) to high-lying virtual orbital (b).
2. Core-hole (a) coupling to higher-lying core orbital (i), and valence orbital (b) to lower-lying virtual orbital (b).
The second scenario can most easily be removed by using effective core potentials (ECPs) or by freezing outer core-orbitals—provided that they belong to a different element (see below). For removing the first class of denominators we use the following protocol:
1. Perform SCF on the (neutral) ground state.
2. Using the above wave function as initial guess to perform SCF optimization of a core-hole state, constrained with, e.g., the MOM approach.
3. Extract orbital energies.
4. Iterate over all possible denominators, tagging the highest-energy virtual orbital associated with |Δmin|.
5. If |Δmin| is smaller than some threshold, save tag (orbital index) and remove from further denominator iterations (here by temporarily setting corresponding energy to a very high value). Iterate until remaining |Δmin| is larger than the threshold.
6. Freeze the tagged MOs for subsequent post-HF calculation.
The sorting protocol and examples of X-ray emission spectrum calculations can be found in the adcc repository.49 The current version includes all possible denominators in step 5, in order to always identify the lowest denominator. For practical purposes, only permutations including the core-hole are likely needed to avoid the instabilities. Note that similar schemes, where certain denominators were excluded from the correlated calculation, have been applied within a coupled cluster framework,15,17 and the issue and potential solutions have also been discussed for Z-averaged perturbation theory.50 It was also noted that Δ-based schemes using second-order approaches might not perform better than ΔSCF methods (with ΔMP2 overestimating the IE10,50), but better results are seen for higher-order theory,15 as a result of the improved inclusion of electron correlation.
4.3 Determining denominator threshold
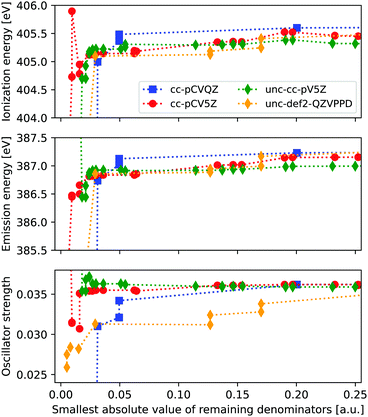
From Fig. 1 we see that clear issues are present for |Δmin| ≤ 0.024 a.u., while values of 0.043 a.u. and above appear to provide more stable results. In order to more systematically determine a suitable threshold for freezing virtual orbitals, we consider the ionization energies and X-ray emission spectra of ammonia when removing one virtual orbital at a time, considering four different basis sets. Results are shown in Fig. 2, with IE and XES considered using MP3 and ADC(3/2), and plotted as a function of remaining |Δmin|.We observe clear stabilization when |Δmin| becomes larger, with significant instabilities for values below 0.05 a.u. When determining a suitable denominator threshold, there is a balance between removing sufficiently many virtual orbitals to avoid near-singularities, and not restricting virtual orbital space too much. For the uncontracted def2-QZVPPD basis set, there is some remaining shift in intensity within the energy window shown, but the difference is kept reasonably small. Beyond this energy window the trends continue to be relatively smooth, but they will eventually reach the point where all virtual orbitals are frozen and no correlation is possible. From these results we propose that a threshold of 0.1 a.u. is a good compromise between avoiding instabilities and not restricting the virtual orbital space too much, noting that this threshold here corresponds to freezing 2–5% of the total number of MOs.
Note that the IEs are calculated by comparing the total energy of the neutral and core-hole calculations when freezing the same MOs. In principle, the ground state calculation can be run without freezing any MOs. The difference in the obtained IE when using above threshold is ≤0.21 eV, and either approach is thus likely to work.
4.4 Evaluate approach for second-row elements
In Table 1 the IE and X-ray emission spectra of ammonia are shown, using four different basis sets and the freezing protocol. Four different thresholds (ΘΔ) of 0.000 (i.e. not freezing any MOs), 0.025, 0.050, and 0.100 a.u. are used. If several thresholds yield the same selection of frozen virtual orbitals, they are all collected under the largest relevant value of ΘΔ. For cc-pCVDZ and cc-pCVTZ |Δmin| > 1.66 a.u., and the IE and X-ray emission spectra are stable.| cc-pCVDZ | cc-pCVTZ | cc-pCVQZ | cc-pCV5Z | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| θ Δ | 0.100 | 0.100 | 0.000 | 0.025 | 0.100 | 0.000 | 0.025 | 0.050 | 0.100 | |
| |Δmin| | 1.666 | 1.661 | 0.002 | 0.029 | 0.200 | 0.004 | 0.027 | 0.062 | 0.133 | |
| n rem | 5 | 9 | 8 | 13 | 16 | |||||
| MP2 | IE | 405.30 | 405.66 | 405.19 | 405.53 | 405.68 | 405.66 | 405.68 | 405.68 | 405.63 |
| μ CH | 2.222 | 2.094 | 2.613 | 2.157 | 2.073 | 1.9745 | 2.0823 | 2.0831 | 2.0836 | |
| MP3 | IE | 405.37 | 405.72 | 358.11 | 391.51 | 405.60 | 400.93 | 405.13 | 405.14 | 405.35 |
| ADC(2) | E | 394.45 | 394.74 | 394.28 | 394.54 | 394.45 | 394.69 | 394.69 | 394.69 | 394.53 |
| I | 0.047 | 0.047 | 0.000 | 0.024 | 0.047 | 0.040 | 0.050 | 0.051 | 0.048 | |
| μ | 1.255 | 1.189 | 1.244 | 1.180 | 1.172 | 1.1782 | 1.1815 | 1.1816 | 1.1791 | |
| E | 388.39 | 388.82 | 388.40 | 388.66 | 388.56 | 388.82 | 388.82 | 388.82 | 388.67 | |
| I | 0.037 | 0.037 | 8.587 | 0.021 | 0.037 | 0.069 | 0.036 | 0.036 | 0.037 | |
| μ | 3.189 | 3.010 | 3.031 | 2.980 | 2.973 | 2.9898 | 2.9958 | 2.9958 | 2.9744 | |
| E | 376.15 | 376.60 | 376.21 | 376.45 | 376.38 | 376.63 | 376.63 | 376.63 | 376.47 | |
| I | 0.002 | 0.002 | 0.343 | 0.045 | 0.003 | 0.001 | 0.001 | 0.001 | 0.001 | |
| μ | 2.730 | 2.560 | 2.606 | 2.534 | 2.530 | 2.5277 | 2.5338 | 2.5340 | 2.5321 | |
| ADC(3/2) | E | 393.74 | 393.65 | 379.83 | 380.94 | 393.24 | 389.13 | 392.83 | 392.85 | 393.03 |
| I | 0.046 | 0.046 | 0.000 | 0.019 | 0.046 | 0.035 | 0.049 | 0.049 | 0.047 | |
| E | 387.55 | 387.59 | 377.95 | 379.82 | 387.23 | 383.48 | 386.82 | 386.84 | 387.01 | |
| I | 0.036 | 0.036 | 0.000 | 0.001 | 0.036 | 0.065 | 0.035 | 0.036 | 0.036 | |
| E | 380.05 | 379.91 | 377.80 | 377.95 | 379.84 | 379.86 | 379.87 | 379.87 | 379.87 | |
| I | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
For cc-pCVQZ the smallest MO is 0.002 a.u., and large discrepancies in primarily ΔMP3 and oscillator strengths are visible. Removing denominators below 0.025 a.u., the energies and properties stabilize, but the intensities are still noticeable different from those of the smaller basis sets. The values stabilize with larger threshold values, freezing 9 out of 174 orbitals. Similar trends are present for cc-pCV5Z, although the discrepancies are not as large as for cc-pCVQZ, which is likely due to the smaller |Δmin| of the latter. This is particularly the case for the intensities, for which cc-pCVQZ takes clearly unphysical values of up to 8.6. Comparing the spectra when using our recommended threshold of 0.1 a.u., we note that ADC(2)/ADC(3/2) cc-pCVDZ results are within 0.33/0.71 eV from cc-pCV5Z, with intensities varying by at most 0.001. The corresponding values for cc-pCVTZ and cc-pCVQZ are 0.20/0.62 and 0.10/0.22 eV, or 0.001 and 0.002 in absolute intensity. Compared to experimental emission energies of 395.05 ± 0.1 and 388.80 ± 0.2 eV,51 the cc-pCV5Z results are within 0.1–0.3 eV for ADC(2), and 1.6–1.8 eV for ADC(3/2), when including a rigid shift of 0.21 eV to account for relativistic effects.
In terms of initial and final state properties, we note that the difference in dipole moment when including all virtual orbitals and when using a threshold varies more for the initial state than for the final state, with the MP2 initial state dipole moments varying by up to 30%, while the ADC(2) final state dipole moment varying by at most 6%. This implies that the issues are more influential for the initial (core-hole) state than for the final state, as will be discussed more below.
Table 2 shows the convergence of IE and X-ray emission spectra for the oxygen K-edge of methanol, for which denominators close to zero can be formed from coupling to the occupied carbon 1s. This is clearly a larger concern than coupling to high-lying virtual orbitals, with all of the smallest denominators containing the carbon 1s. The discrepancies in energies and intensities reach 2 × 104 eV and 4 × 107, respectively. Removing these denominators by either freezing the carbon 1s, or using ECP, yields reasonable results for the two smaller basis sets, while two virtual orbitals contributing to small denominators are still present for cc-pCVQZ. Freezing also these two virtual orbitals yields results in good agreement with the two other basis sets. We note that the u6-311G** and cc-pCVTZ results using frozen core orbitals or ECP are very similar, with some larger discrepancies when comparing the cc-pCVQZ results using either option. We recommend using ECP for all non-hydrogen atoms except for the probed one, as this both lowers computational costs and has the advantage of localizing the core-hole to one atomic site, which has been seen to yield results in better agreement with experimental results than using a delocalized core-hole.52,53 Comparing the three different basis sets, intensities differ by at most 0.002, while transition energies are within 0.29/0.44 eV for ADC(2)/ADC(3/2) calculations using u6-311G**, and 0.13/0.42 eV for cc-pCVTZ, as compared to the cc-pCVQZ results. Compared to experiment results,54 the cc-pCVQZ results are within 0.0–0.2 eV when using ADC(2), and 1.4–1.9 eV when using ADC(3/2).
| u6-311G** | cc-pCVTZ | cc-pCVQZ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Full | fc | ECP | Full | fc | ECP | Full | fc | ECP | ECP + ΘΔ | ||
| |Δmin| | 0.046 | 1.502 | 1.003 | 0.002 | 1.402 | 1.402 | 0.000 | 0.016 | 0.014 | 0.171 | |
| n rem | 2 | ||||||||||
| MP2 | IE | 538.72 | 538.71 | 538.73 | 539.15 | 539.15 | 539.15 | 539.22 | 539.21 | 539.23 | 539.14 |
| μ CH | 2.365 | 2.365 | 2.379 | 2.292 | 2.293 | 2.301 | 3.247 | 2.013 | 2.021 | 2.291 | |
| MP3 | IE | 538.64 | 538.64 | 538.66 | 539.04 | 539.04 | 539.05 | 520.90 | 529.19 | 528.96 | 538.85 |
| ADC(2) | E | 527.43 | 527.43 | 527.45 | 527.74 | 527.74 | 527.75 | 527.76 | 527.77 | 527.77 | 527.62 |
| I | 0.047 | 0.047 | 0.047 | 0.046 | 0.046 | 0.046 | 0.028 | 0.038 | 0.031 | 0.048 | |
| μ | 3.102 | 3.105 | 3.099 | 3.035 | 3.040 | 3.041 | 3.203 | 3.109 | 3.114 | 3.071 | |
| E | 525.60 | 525.60 | 525.60 | 525.94 | 525.94 | 525.95 | 525.98 | 525.99 | 526.00 | 525.85 | |
| I | 0.030 | 0.030 | 0.030 | 0.029 | 0.029 | 0.029 | 5 × 104 | 0.402 | 0.454 | 0.030 | |
| μ | 3.514 | 3.517 | 3.510 | 3.476 | 3.484 | 3.493 | 3.703 | 3.580 | 3.593 | 3.534 | |
| E | 523.12 | 523.12 | 523.12 | 523.49 | 523.50 | 523.51 | 523.54 | 523.552 | 523.56 | 523.41 | |
| I | 0.022 | 0.022 | 0.022 | 0.022 | 0.023 | 0.023 | 1 × 105 | 0.213 | 0.237 | 0.023 | |
| μ | 4.187 | 4.185 | 4.164 | 3.944 | 3.939 | 3.917 | 4.143 | 3.970 | 3.948 | 3.870 | |
| ADC(3/2) | E | 526.72 | 526.72 | 526.72 | 526.71 | 526.71 | 526.71 | 2 × 104 | 517.96 | 517.77 | 526.28 |
| I | 0.053 | 0.053 | 0.053 | 0.053 | 0.053 | 0.053 | 4 × 107 | 0.045 | 0.039 | 0.055 | |
| E | 524.54 | 524.54 | 524.54 | 524.54 | 524.54 | 524.53 | 6 × 103 | 515.97 | 515.79 | 524.12 | |
| I | 0.044 | 0.044 | 0.044 | 0.043 | 0.044 | 0.044 | 2 × 104 | 0.772 | 0.876 | 0.045 | |
| E | 520.74 | 520.74 | 520.73 | 520.83 | 520.82 | 520.82 | 909.65 | 513.04 | 513.04 | 520.42 | |
| I | 0.033 | 0.033 | 0.033 | 0.033 | 0.034 | 0.034 | 0.032 | 0.000 | 0.000 | 0.034 | |
Returning to the initial and final state dipole moments, we see that the former varies by up to 40% when comparing calculations with and without near-singularities, but only by up to 10% for the final state. This again implies that the final state of the unstable calculations is not very far away from the correct final state, when compared to the initial state. This is not very surprising, as the correlated core-hole calculation attempts to correct for the core-hole by approaching a valence-hole configuration, while the final state is an actual valence-hole configuration. The large variations in particularly transition moments are thus considered to be more due to unphysical initial states.
4.5 Heavier elements
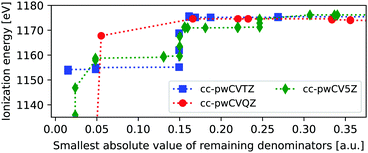
For heavier elements the core-hole can couple to outer core orbitals of the same atom, in addition to the possible near-singularities discussed above. These MOs can, evidently, not be frozen, as they are needed to capture the full relaxation of the ionization process, and are thus more problematic than the previously discussed near-singularities. In Fig. 3 we show the ΔMP3 IE of the L1-edge of zinc, as obtained using three different basis sets and removing one virtual orbital at a time. The variations in ionization energies are much more pronounced than for neon, and remain also for higher values of |Δmin|.For the K-edge the smallest value of |Δmin| is 0.96 a.u., and no instabilities are thus observed there, since the 1s is well separated in energy from the remaining occupied state, and only combinations with very high-energy virtual orbitals can yield near-singularities. By comparison, the 2s energies are close to 2p, such that many different permutations involving low-energy virtual orbitals can yield near-singularities. This is seen by noting that the energies of the removed virtual orbitals range from −0.19 to 40.21 a.u., thus including the low-energy virtual orbital space. Relatively stable energies are obtained at a threshold of about 0.2 au, but between 5 and 19% of all MOs were frozen, yielding an influence on the ground state MP3 energy of 0.08–0.34 Hartree.
As such, we currently do not recommend using the freezing protocol for probing the L1-edge, at least not without more extensive tests. We note that the L1-edge is less used for experimental studies, as the L2,3-edge provides more information. This edge requires spin–orbit couplings, which are currently not available within the adcc package.
4.6 Comparison to experiment
Finally, we evaluate the performance of the ADC hierarchy for calculating X-ray emission spectra of molecules ranging in size from methanol to nitrobenzene, with results presented in Fig. 4. Three different carbon, one nitrogen, four oxygen, and one fluorine K-edge are considered, including comparison to experimental measurements.54–57 These results have been obtained using ECPs for all non-hydrogen atoms except the probed one, and using a denominator threshold of 0.1 a.u. Only a limited number of virtual orbitals are frozen in these calculations, excluding at most 4.7% of the total number of MOs. Two different basis sets are considered, with u6-311G** results marked with full lines and colored areas, and cc-pCVTZ with dashed lines, showing only a small difference. For the carbon edge of fluorobenzene and ethanol, the spectrum contributions from the different carbon atoms are marked by alternating area colors.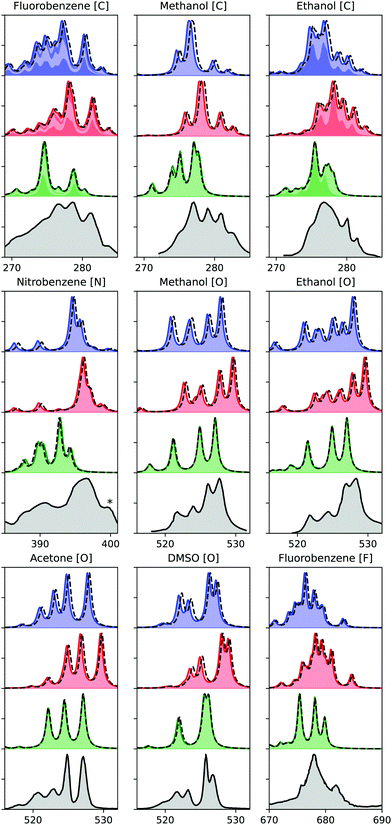 | ||
| Fig. 4 K-edge X-ray emission spectra calculated using (from the top) ADC(2), ADC(2)-x, and ADC(3/2), as compared to experiment (bottom).54–57 Experimental spectra constructed from original sources using WebPlotDigitizer,60 except for methanol and ethanol, where Ref.18 was used. Theoretical spectra shifted by 0.11, 0.21, 0.37, 0.61 eV for C, N, O, and F, respectively. Asterix in the experimental spectrum of nitrobenzene indicates a multielectron feature. Theoretical results plotted with a full line and area obtained with u6-311G**, and dashed line indicates results obtained with cc-pCVTZ, augmented with core-polarizing functions for the atom probed. Nitrobenzene cc-pVTZ results obtained with cc-pVDZ for non-neighbour atoms. | ||
The theoretical results are obtained using only equilibrium structures and broadened with a uniform broadening protocol, so some disagreement in particular in spectrum broadening is to be expected. Including ground state and core-hole dynamics would likely improve the agreement with experimental measurements,24,58 but this is beyond the scope of the present study. Because of this lack of a more detailed treatment of the spectra, we also refrain from a more quantitative comparison of our results. With that in mind, we observe generally good agreement with experimental results in terms of relative features for both ADC(2) and ADC(2)-x, while ADC(3/2) performs worse in both relative energies and intensities. In terms of absolute energies, ADC(2) yields results in best agreement with experimental results. These observations are in line with a previous study on smaller molecules, where ADC(2) and ADC(2)-x were noted to yield similar error spreads, and ADC(2) provided the best agreement in absolute terms.24 The relative error of ADC(2)-x was seen to be slightly smaller than of ADC(2), and looking more closely on Fig. 4, we do note that ADC(2)-x performs slightly better in terms of relative features. As such, focusing on relative features, ADC(2)-x yields results in best agreement with experimental measurements for both XAS and XES, while for valence properties ADC(2) and ADC(3/2) both perform better.59 This discrepancy is due to the different effects of error cancellation for the different spectroscopies, where the ad hoc extension of the 2p2h-block in ADC(2)-x over-emphasizes the double excited configurations, which thus better account for the strong relaxation involved in core properties.
4.7 Outlook
Our protocol is seen to work well for the K-edge of light elements, and is likely equally applicable to the K-edge of heavier elements. Moving to the L-edge and above is more difficult, and our approach should only be used with care for such studies. For the K-edge, we expect that this approach will work equally well for other post-HF methods such as coupled clusters, for which the numerical instabilities have been noted previously,15,17 and similar denominator screening approaches have been used for IE calculations.15 Potential alternative approaches include more fine-tuned removal of intruding terms (e.g. removing only specific denominators), shifting singularities from the energy axis by introducing an imaginary shift, use of quasi-degenerate perturbation theory, and more. However, we note that the presented approach typically only removes a small number of MOs, achieves stable results, and is straightforward to implement.The use of non-Aufbau reference states is also adopted for other property calculations, including doubly core-ionized states,61 resonant inelastic X-ray scattering (RIXS)25 and transient X-ray absorption spectroscopy (TR-XAS).26 For RIXS the reference state is core-excited, and the same issues of near-singularities are thus expected. The approach presented here should thus work for these calculations as well. For TR-XAS the initial state is typically a low-lying valence-excited state, such that any virtual orbitals would only be expected to adopt small negative energies. The potential influence and stability of such spectrum calculations due to near-singularities is beyond the scope of the present study.
4.8 Conclusions
Instabilities in the calculation of ionization energies and X-ray emission spectra using MP and ADC theory are discussed and seen to be a result from denominators in the energy correction becoming arbitrarily close to zero. These near-singularities originate from denominators containing a highly negative virtual orbital energy, corresponding to the core-hole, which can yield close to zero values when coupled to either a high-lying virtual or a higher-lying core MO. Physically, these near-singularities are related to a fundamental issue with using post-HF methods with non-Aufbau reference states, as these methods attempt to compensate for the high-energy initial state by filling up the core-hole. Note that the issues are primarily there for the core-hole state, and the final state for an X-ray emission spectrum calculation is usually not as affected. This is illustrated by considering the dipole moment of the initial and final states.A simple protocol for removing these issues is proposed and shown to perform well, in which ECPs are used for other (non-hydrogen) atoms, and the highest-lying virtual orbitals contributing to small absolute denominators are discarded. A threshold of |Δmin| > 0.1 a.u. is shown to provide stable results for the K-edge of second-row elements, and is suitable also for heavier elements. This approach typically only removes a small fraction of all virtual orbitals (up to 5%), and provides stable energies and intensities. For the L-edge and above, the approach may not be suitable, as the smaller energy difference between the different L-edges yield denominators close to zero in energy also when including low-lying virtual orbitals. The sorting protocol and an example focusing on ADC calculations of the X-ray emission spectrum of ammonia is available in the adcc repository,49 and we note that it is likely to work equally well for other correlated methods, e.g. coupled cluster.
With this scheme established, the performances of ADC(2), ADC(2)-x, and ADC(3/2) for the calculation of X-ray emission spectra are evaluated for systems ranging from methanol to nitrobenzene. It is seen that while ADC(2) is in better agreement with experimental results in terms of absolute energies, ADC(2)-x exhibits the best relative performance, while ADC(3/2) is in poorer agreement in particular in terms of relative features. Furthermore, a 6-311G** basis set with decontracted 1s basis function for the element in investigation is seen to yield almost identical results to that when using cc-pVTZ with core-polarizing functions on the probed atom. These observations are consistent with previous results, which focused on smaller molecules.24
Conflicts of interest
There are no conflicts to declare.Acknowledgements
T. F. acknowledges financial support from the Air Force Office of Scientific Research (Grant FA8655-20-1-7010). Calculations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre (NSC), Sweden.References
- P. Norman and A. Dreuw, Chem. Rev., 2018, 118, 7208–7248 CrossRef CAS PubMed.
- X-Ray Absorption and X-Ray Emission Spectroscopy: Theory and Applications, ed. J. A. van Bokhoven and C. Laberti, John Wiley & Sons, 2016 Search PubMed.
- P. Glatzel and U. Bergmann, Coord. Chem. Rev., 2005, 249, 65–95 CrossRef CAS.
- L. S. Cederbaum, W. Domcke and J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 206 CrossRef CAS.
- A. Barth and L. S. Cederbaum, Phys. Rev. A: At., Mol., Opt. Phys., 1981, 23, 1038 CrossRef CAS.
- J. Wenzel, M. Wormit and A. Dreuw, J. Comput. Chem., 2014, 35, 1900–1915 CrossRef CAS PubMed.
- J. Wenzel, A. Holzer, M. Wormit and A. Dreuw, J. Chem. Phys., 2015, 142, 214104 CrossRef PubMed.
- M. L. Vidal, X. Feng, E. Epifanovsky, A. I. Krylov and S. Coriani, J. Chem. Theory Comput., 2019, 15, 3117–3133 CrossRef CAS PubMed.
- T. Fransson, I. E. Brumboiu, M. L. Vidal, P. Norman, S. Coriani and A. Dreuw, J. Chem. Theory Comput., 2021, 17, 1618 CrossRef CAS PubMed.
- N. A. Besley, A. T. B. Gilbert and P. M. W. Gill, J. Chem. Phys., 2009, 130, 124308 CrossRef PubMed.
- M. A. Ambroise and F. Jensen, J. Chem. Theory Comput., 2019, 15, 325 CrossRef CAS PubMed.
- H. Ågren and H. J. A. Jensen, Chem. Phys., 1993, 172, 45 CrossRef.
- J. Shim, M. Klobukowski, M. Barysz and J. Lesczynski, Phys. Chem. Chem. Phys., 2011, 13, 5703 RSC.
- S. Sen, A. Shee and D. Mukherjee, J. Chem. Phys., 2018, 148, 054107 CrossRef PubMed.
- X. Zheng and L. Cheng, J. Chem. Theory Comput., 2019, 15, 4945–4955 CrossRef CAS PubMed.
- H. Ågren, V. Carravetta, O. Vahtras and L. G. M. Pettersson, Chem. Phys. Lett., 1994, 222, 75–81 CrossRef.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1995, 102, 6735–6756 CrossRef CAS.
- N. A. Besley and F. A. Asmuruf, Phys. Chem. Chem. Phys., 2010, 12, 12024–12039 RSC.
- Y. Zhang, S. Mukamel, M. Khalil and N. Govind, J. Chem. Theory Comput., 2015, 11, 5804–5809 CrossRef CAS PubMed.
- I. P. E. Roper and N. A. Besley, J. Chem. Phys., 2016, 144, 114104 CrossRef PubMed.
- J. D. Wadey and N. A. Besley, J. Chem. Theory Comput., 2014, 10, 4557–4564 CrossRef CAS PubMed.
- N. A. Besley, Chem. Phys. Lett., 2012, 542, 42–46 CrossRef CAS.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1995, 102, 6735 CrossRef CAS.
- T. Fransson and A. Dreuw, J. Chem. Theory Comput., 2019, 15, 546–556 CrossRef CAS PubMed.
- A. E. A. Fouda, G. I. Purnell and N. A. Besley, J. Chem. Theory Comput., 2018, 14, 2586–2595 CrossRef CAS PubMed.
- S. Tsuru, M. L. Vidal, M. Papai, A. I. Krylov, K. B. Møller and S. Coriani, Struct. Dyn., 2021, 8, 024101 CrossRef CAS PubMed.
- P. G. Lykos and H. N. Schmeising, J. Phys. Chem., 1961, 35, 288 CrossRef CAS.
- H. F. King, R. E. Stanton, H. Kim, R. E. Wyatt and R. G. Parr, J. Chem. Phys., 1967, 47, 1936 CrossRef CAS.
- P. S. Bagus and H. F. Schaefer, J. Chem. Phys., 1971, 55, 1474 CrossRef CAS.
- A. T. B. Gilbert, N. A. Besley and P. M. W. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171 CrossRef CAS PubMed.
- G. M. J. Barca, A. T. B. Gilbert and P. M. W. Gill, J. Chem. Theory Comput., 2018, 14, 1501 CrossRef CAS PubMed.
- K. Carter-Fenk and J. M. Herbert, J. Chem. Theory Comput., 2020, 16, 5067 CrossRef CAS PubMed.
- D. Hait and M. Head-Gordon, J. Chem. Theory Comput., 2020, 16, 1699 CrossRef CAS PubMed.
- J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416 CrossRef CAS.
- J. Schirmer and A. B. Trofimov, J. Chem. Phys., 2004, 120, 11449–11464 CrossRef CAS PubMed.
- M. Wormit, D. R. Rehn, P. H. Harbach, J. Wenzel, C. M. Krauter, E. Epifanovsky and A. Dreuw, Mol. Phys., 2014, 112, 774 CrossRef CAS.
- A. Dreuw and M. Wormit, WIREs Comput. Mol. Sci., 2015, 5, 82–95 CrossRef CAS.
- J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 4647 CrossRef CAS PubMed.
- F. Mertins and J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 53, 2140–2152 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons and A. L. Dempwolff, et al. , J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS.
- A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuß, Mol. Phys., 1993, 80, 1431–1441 CrossRef CAS.
- M. F. Herbst, M. Scheurer, T. Fransson, D. R. Rehn and A. Dreuw, WIREs Comput. Mol. Sci., 2020, e1462 Search PubMed.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, WIREs Comput. Mol. Sci., 2018, 8, 1340 Search PubMed.
- Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry, N. S. Blunt, N. A. Bogdanov, G. H. Booth, J. Chen, Z.-H. Cui and J. J. Eriksen, et al. , J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed.
- See https://github.com/adc-connect/adcc.
- I. Ljubic, J. Chem. Theory Comput., 2014, 10, 2333 CrossRef CAS PubMed.
- J. Nordgren, H. Ågren, L. O. Werme, C. Nordling and K. Siegbahn, J. Phys. B: At. Mol. Phys., 1976, 9, 295–302 CrossRef CAS.
- P. S. Bagus and H. F. Schaefer, J. Chem. Phys., 1972, 56, 224 CrossRef CAS.
- L. S. Cederbaum and W. Domcke, J. Chem. Phys., 1977, 66, 5084 CrossRef.
- J.-E. Rubensson, N. Wassdahl, R. Brammer and J. Nordgren, J. Electron Spectrosc. Relat. Phenom., 1988, 47, 131–145 CrossRef CAS.
- V. D. Yumatov, A. V. Okotrub, G. G. Furin and N. F. Salakhutdinov, Russ. Chem. Bull., 1997, 46, 1389 CrossRef CAS.
- V. D. Yumatov, N. V. Davydova and G. G. Furin, Russ. Chem. Bull., 2006, 55, 1346 CrossRef CAS.
- K. M. Lange and E. F. Aziz, Chem. Soc. Rev., 2013, 42, 6840 RSC.
- A. A. E. Fouda and N. A. Besley, J. Comput. Chem., 2020, 41, 1–10 CrossRef PubMed.
- P. H. Harbach, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 064113 CrossRef PubMed.
- A. Rohatgi, Webplotdigitizer: Version 4.5, 2021, https://automeris.io/WebPlotDigitizer Search PubMed.
- J. Lee, D. W. Small and M. Head-Gordon, J. Chem. Phys., 2019, 151, 214103 CrossRef PubMed.
| This journal is © the Owner Societies 2022 |