Electron and ion spectroscopy of the cyclo-alanine–alanine dipeptide

Abstract

The VUV photoionisation and photofragmentation of cyclo-alanine–alanine (cAA) has been studied in a joint experimental and theoretical work. The photoelectron spectrum and the photoelectron–photoion coincidence (PEPICO) measurements, which enable control of the energy being deposited, combined with quantum chemistry calculations, provide direct insight into the cAA molecular stability after photoionisation. The analysis of the ion-neutral coincidence experiments with the molecular dynamics simulations and the exploration of the potential energy surface allows a complete identification of the fragmentation pathways. It has been found that the fragmentation always starts with the ring opening through the C–C bond cleavage, followed by release of neutral CO or HNCO moieties.

---

1 Introduction

Amino acids are the building blocks of peptides, enzymes and proteins. By the combination of a relatively limited number of these elementary constituents an enormous variety of systems, with the most diverse structures and functionalities can be realized, both via biotic and abiotic^1–5 natural processes, as well as by ad-hoc designed bioengineering⁶ strategies. The simplest combination of two amino acids, a dipeptide, is achieved via the formation of peptide bonds between the carboxylic and amino groups of the two respective amino acids and the elimination of one or two water molecules, resulting in a linear or cyclic structure, respectively. Already at this stage, a large variety of combinations can be envisaged, providing an essential opportunity to investigate the electronic and molecular structures of these prototypal oligopeptides, where the most detailed experimental and quantum mechanical methods can still be exploited to provide deeper insight into their intrinsic properties. While almost all amino acids have been investigated in the gas phase by valence and core photoemission spectroscopy^7–12 as well as by mass spectrometry,‡^13–15 so far studies of both linear¹⁶ and cyclo^17–19 dipeptides, are quite scarce. This is probably due to the thermal lability of most of these biomolecules which can undergo structural changes during the desorption, particularly in linear dipeptides.^13,20–24

Nevertheless, the driving force for the investigation of dipeptides spans from the need to answer fundamental questions concerning the origin of life^19,25 and the biological activities of larger peptides and proteins,²⁶ to their exploitation in therapeutic²⁷ and technological applications.^28–30

Cyclo-alanine–alanine (cAA) is one of the simplest cyclo dipeptides. It is built on a 2,5-diketopiperazine (DKP) six-member ring structure with the two metyhyl groups (CH₃) as side chains. In a recent publication¹⁹ we focused on a specific cAA fragmentation channel proposing reactive mechanisms which allow this dipeptide not only to withstand VUV radiation, but also to provide the seed for chain elongation in both cyclic and linear structures. This mechanism predicted by molecular dynamics simulations and potential energy surface exploration, was based on the experimental observation of the fragment of mass/charge, m/z 71, attributed to a peculiar ‘amino acid-like’ structure of [A–H–OH]. This fragment is the core of the A amino acid in a peptide sequence and was proposed¹⁹ as a possible intermediate for peptide formation in the early stages of the chemical evolution of life.

In this work we present a comprehensive investigation of the VUV photoionisation and photofragmentation of cAA by joint experimental (photoelectron spectroscopy, photoelectron–photoion and ion-neutral fragment coincidence experiments) and quantum chemistry calculations.

2 Methods

2.1 Experimental methods

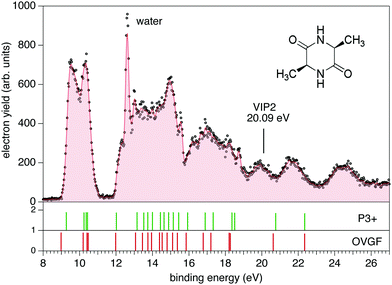
The photoemission and electron–ion coincidence experiments were performed at the CIPO beamline³¹ of the Elettra synchrotron radiation facility, using a monochromatic photon beam of 60 eV and an end-station equipped with a 150 mm radius hemispherical electron energy analyser (VG 220i) and a time-of-flight (TOF) ion mass spectrometer. The two spectrometers are mounted opposite to each other at approximately 55° with respect to the linearly polarized photon beam, in order to cancel out any angular effect in the measurements. They have been operated independently for photoelectron (PE) spectroscopy or photoion mass spectrometry (MS) measurements, or ‘in conjunction’ for photoelectron–photoion coincidence (PEPICO) experiments. For the PE measurements, the TOF is switched off in order to have the interaction region free from possible residual fields due to the penetration of the high voltage applied to the drift tube. The electron analyzer, recently refurbished to host a 2D position sensitive detector (PSD) built by Sincrotrone Trieste,^32,33 is characterized by an acquisition window and an energy resolution of about 10% and 2% of the pass energy, respectively. The PE spectrum reported in Fig. 1 has been measured with a pass energy of 10 eV, an overall energy resolution of about 200 meV and an acquisition time of 10 s per point.

Fig. 1 (top panel) The photoelectron spectrum of cAA measured at 60 eV photon energy (black dots) and the 3 point smoothed data (filled area). Some contamination caused by water degassing from the sample produces the feature at 12.62 eV due the H₂O⁺ ground state. Broader bands of lower intensity are located at 14.74 and about 18.51 eV due to the H₂O⁺ A and B states, respectively. Schematic of the cAA sample is reported in the top-right corner. The calculated vertical double ionisation potential (VIP2) at 20.09 eV is also shown. (bottom panels) The valence spectrum calculated with the P3+ and OVGF/6-311G(d,p) methods is reported as vertical bars of different colors.

For MS measurements, the repeller and extractor electrodes of the TOF spectrometer are polarized with antisymmetric voltages (Directed Energy Inc., model PVM4210) to produce a field up to 370 V cm⁻¹. At the time resolution of our experiments, the synchrotron photon beam can be considered as a continuous source, therefore the ion extraction has been operated in pulsed mode. The trigger for the extraction is provided by a 1 kHz pulse generator in the MS measurements, while in the PEPICO mode the extraction is triggered by either the detection of a photoelectron or a pulse running at a frequency of 100 Hz. The latter is used for the measurement of the so-called ‘random mass spectrum’, due to ions residing in the interaction zone and uncorrelated with the detected photoelectron, to be subtracted from the measured electron–ion coincidence spectrum. The cAA sample (C₆H₁₀N₂O₂, mass m = 142 amu), which is a powder at standard ambient temperature and pressure, has been introduced in the vacuum chamber in a crucible and sublimated at a temperature of 87 °C. During sublimation, MS measurements were used to monitor the thermal stability and purity of the sample (results not shown).

The PEPICO experiments reported in Fig. 2 have been performed at the fixed photon energy of 60 eV, with an analyser pass energy of 30 eV. The coincidence measurement is performed by scanning the electron kinetic energy (KE) over the range of interest in steps of 2.7 eV to provide sufficient overlap between two adjacent KE settings. The entire scan is repeated several times to improve the statistics. Schematically, the coincidence data acquisition is based on a 8-channels time-to-digital converter (TDC) that records the arrival times of the signals from the four ends of the PSD of the electron detector and the one from the ion detector. As already mentioned, the ion extraction can be switched on either by the detection of an electron or by a random pulse. These two signals are combined into an OR logic unit whose output controls the power supplies for repeller/extraction voltages. The output of this OR unit as well as an analogue signal of an OR unit where an arbitrary time delay is added to the random trigger are recorded into two other separate TDC channels, providing respectively the time-zero for the scale of the ions's flight time and a flag to sort ‘true + random’ and ‘random’ coincidence events. All signals in the TDC unit are measured relative to a master 1 Hz pulse.

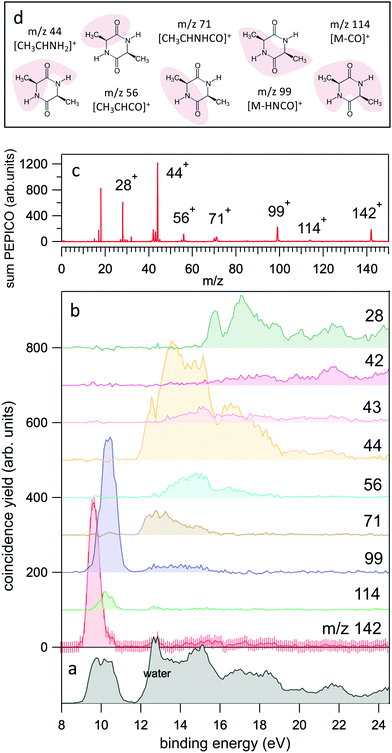Fig. 2 (a and b) The yields of the most intense fragments in the PEPICO spectra reported versus molecular binding energy. For the case of the parent ion, m/z 142, the uncertainty is also shown as an indication of the expected accuracy. The sum of all PEPICO fragments is reported in the bottom panel. The presence of water (outgassed from the sample) is clearly visible. (c) The mass spectrum of cAA obtained as sum of all PEPICO spectra measured in the binding energy range 8–25 eV. (d) A pictorial view of the main fragments. For the detailed discussion and calculation of the structures the reader should refer to Fig. 5–7.

The post processing of these raw data provides, among other information not relevant to the present publication, (i) the x, y coordinates of each electron hit on the PSD (converted to electron KE) that has one – and only one – ion detected within a defined time window and the arrival time of the ion and (ii) the mass spectrum generated by a random pulse. These sorted electron/random coincidence data are binned according to selected electron KE and ion flight time intervals. After the normalization to their respective number of triggers, they are subtracted from each other, providing the random subtracted PEPICO spectra at all selected electron KE.

The next step in the data analysis consists of identifying the m/z fragments and their yield obtained by integrating the area over the region of approximately m/z ± 0.5 in the PEPICO spectra. The area of these fragments can finally be reported versus the binding energy, BE = hv − KE, see ref. 19 and Fig. 2 of the present paper where a larger set of fragments is shown.

In the PEPICO experiments the ion signal is typically two orders of magnitude larger than that of electrons, due to the high angular and energy selectivity in the electron spectrometer. Typical acquisition times on a PEPICO experiments are in the order of 24 h. This is determined by the low count rate of the energy selected electrons in the hemispherical analyzer.

The ion-neutral coincidence experiments have been performed at the CNR-ISM in Rome, using a Wiley-McLaren TOF mass spectrometer equipped with a rare gas discharge lamp (see ref. 34 and 35 and the ESI† of ref. 36). Briefly, the TOF spectrometer is operated in a continuous extraction mode, with DC electric fields of 700 and 1575 V cm⁻¹ in the extraction (1 cm long) and acceleration (2 cm long) regions, respectively. The free flight region in the drift tube is 22.5 cm long. A channel electron multiplier mounted behind the mesh of the repeller of the TOF spectrometer detects all photoelectrons released in the photoionisation events. The electron signal triggers a TDC that, being operated in multihit mode, measures the flight time of any charged/neutral particle that, impinging on a pair of one inch microchannel plates (MCP), has sufficient kinetic energy to produce electrons on the surface of the MCP. The discharge lamp has been operated with He, Ne and Ar gases, producing a main emission line at 21.22 eV, 16.85 eV and 11.62 eV, respectively. The presence of an unquantified contribution of other wavelengths cannot be excluded as the radiation was not monochromatised.

This set-up has been used to investigate the delayed emission of neutral fragments³⁷ in cAA. Throughout this article, the notation ‘molecular ion’ will refer to the unfragmented cAA⁺ molecular cation, while the notation ‘parent ion’ will refer to a generic ion that, undergoing fragmentation, produces a ‘daughter ion’. Indeed, in a two-body fragmentation of a singly charged ion, a parent ion (P_ion) breaks into a daughter ion (D_ion) and a neutral fragment (N_frag). While ions can be handled by electric fields, neutrals cannot. Nevertheless, if they travel towards the TOF spectrometer and hit the MCP detector with sufficient impact energy, they can be detected.³⁸ In our set-up, with constant DC extraction fields, any ion begins its travel towards the TOF immediately at the time of birth, being extracted, accelerated and then launched into the drift tube. Qualitatively, it is easy to visualize that when dissociates in a region where it is subject to an accelerating field then (i) the flight time of D_ion (having a smaller m/z) will be shorter than the nominal flight time of P_ion while (ii) N_frag will continue its travel in a free flight at a constant speed unaffected by any electric field in the TOF spectrometer and may or may not reach the MCP and be detected after at a flight time longer than the nominal flight time of P_ion. The‘nominal flight time’ corresponds to a prompt dissociation. Therefore the decay rate of a fragmentation process^39,40 produces a distribution of correlated partners (D_ion, N_frag) that, ideally, can be measured in a coincidence experiment and encode the information on the position/time in the TOF spectrometer where the fragmentation occurred. By taking into account the geometry and operating conditions of the TOF spectrometer, ion trajectory simulations predict (see Section S1 in the ESI†) a residence time in the extraction/acceleration regions of the TOF in the range 880–940 ns for m/z 142 (cAA⁺ molecular ion) and 385–415 ns for m/z 28. Even though these results can be taken as an indication of the measurable time for the dissociation events, in practice, the capability of the experiment to detect these processes will crucially depend on the instrumental response of the MCP, which is known to be a complicated function of energy and angle of incidence, mass and charge of the particle as well as of the applied bias voltage and the physical characteristics of the MCP itself.³⁸

The results for cAA are reported in Fig. 3, which displays the 2D map of the arrival times of the first (TOF₁, that will always be the ion) and second (TOF₂, that can be either an uncorrelated ion or a correlated N_frag) particle. Therefore, in addition to the vertical and horizontal lines due to uncorrelated events, a large number of ‘traces’ is observed. According to the qualitative discussion above, these ‘traces’ connect the correlated arrival times of D_ion and N_frag due to the delayed fragmentation events. As a general feature, they originate at the coordinate (TOF₁ = TOF₂) of P_ion – which corresponds to ‘delayed fragmentation’ events happening in the drift tube of the time of flight spectrometer – and converge, asymptotically, to the TOF₁ of D_ion. Moving away from the origin, the intensity of the ‘traces’ becomes fainter, because these events correspond to ‘early fragmentations’. In these events the N_frag is very slow and therefore less effectively detected. In order to assign the dissociation channels we performed a simulation using a custom made procedure in Igor Pro⁴¹ software, see Section S1 in the ESI† for the details. The results of these simulations are reported together with the experimental data in Fig. 3. The fragmentation paths responsible of the ‘traces’ are indicated by the notation P_ion → D_ion. The experimental data in Fig. 3 are the sum of different acquisitions performed at photon energies 21.22, 16.85 and 11.62 eV to improve the statistics. The experimental data acquired at each photon energy are reported in Section S1 in the ESI.†

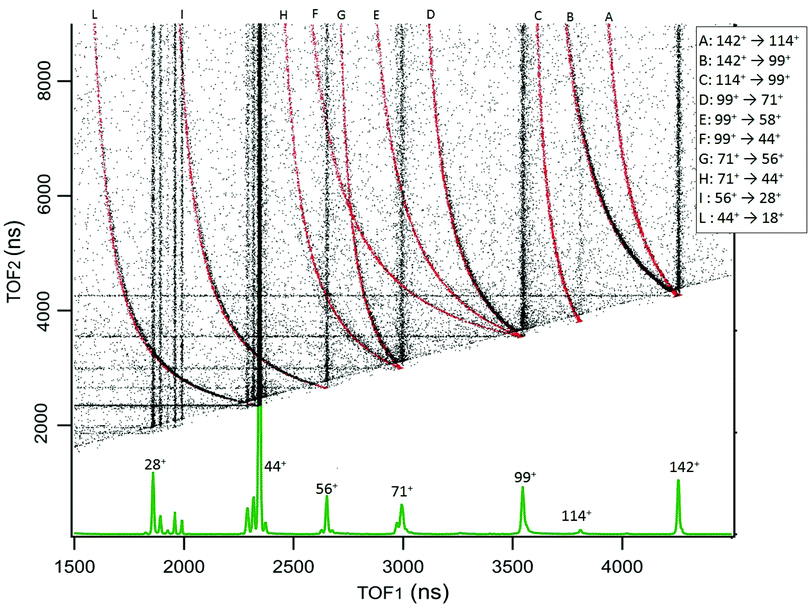Fig. 3 The 2D coincidence map for cAA reports the arrival times of the first, TOF₁, and the second, TOF₂, particle as measured by the TDC. The experimental data, reported in black, are the sum of different acquisitions performed at photon energies 21.22, 16.85 and 11.62 eV, added up to improve the statistics. The individual maps are shown in Fig. S1 of the ESI.† At the bottom, the mass spectrum measured at 21.22 eV is shown and the main fragments are indicated. In the 2D coincidence map many ‘traces’ provide evidence of delayed fragmentation processes. These have been simulated by a custom made Igor Pro⁴¹ procedure in order to provide unambiguous assignment of the P_ion → D_ion + N_frag reaction paths, see text and Section S1 in the ESI.† The results of these simulations are superimposed in red and labeled by capital letters assigned in the legend.

2.2 Computational details

Quantum chemistry calculations were performed for the simulation of both the photoemission of electrons and the production of different charged fragments after ionisation. First, photoelectron spectra were estimated calculating ionisation potentials using the electron propagation theory (EPT) of correlated electron,^42,43 in particular using the quasiparticle methods OVGF⁴⁴ and P3+.^45,46 These methods provide a significant improvement over the results obtained with the Koopman's theorem. In both cases, OVGF and P3+, the simulations are based upon the diagonal matrix elements in the canonical HF orbital basis of the self-energy operator in electron propagator theory.⁴⁷ The atomic basis set used in these simulations is 6-311G(d,p).⁴⁸

Ab initio Molecular Dynamics (AIMD) simulations and potential energy surface calculations were performed using density functional theory (DFT), in order to obtain dynamical and energetic information on the fragmentation after ionisation. For the AIMD trajectories we used the Atom-centered Density Matrix Propagation formalism (ADMP),^49–51 an extended Lagrangian molecular dynamics method that propagates simultaneously the nuclei and the electronic density, and employs atom-centered Gaussian basis functions. The ADMP simulations were performed using a time step of Δt = 0.1 fs and a fictitious electron mass of μ = 0.1 amu, thus ensuring adiabaticity. One hundred trajectories propagated up to 500 fs were calculated for the most stable conformer of the singly-charged cycle-Alanine–Alanine taking into consideration two different internal energies, 10 and 15 eV, using the B3LYP functional^52–54 in combination with the 6-31++G(d,p) basis set.^48,55 The AIMD calculations were done using the optimized geometry of the neutral molecule and considering a Franck–Condon transition in the ionisation. In each trajectory, we randomly distributed the internal energy over the nuclear degrees of freedom of the cationic molecule and we propagated the dynamics in its electronic ground state. With this approximation we are thus assuming that the electronic excitation in the ionisation is rapidly transferred to the nuclei. In spite of the state-selected kind of ionisation in the experiment, the main patterns of the fragmentation are correctly described with this approximation⁵⁶. We analyzed the channels that have been populated in the ADMP simulations: in the last step of each trajectory we considered two fragments separated if the smallest distance between all their atoms exceeded 3 Å. After identification of each fragment, we performed a Mulliken population analysis in the atoms and we thus obtain the total charge in each fragment. The AIMD simulations only explore the first few hundred femtoseconds after ionisation, nevertheless, several processes, relevant to the dissociation of the molecule, could take place in longer timescales. Therefore, we complemented the ADMP molecular dynamics with Potential Energy Surface calculations at the B3LYP/6-311++G(d,p) level of theory. The combination of AIMD with potential energy surface exploration has been used with success in the past to study the fragmentation dynamics of ionized molecules and clusters of different nature.^56–63 EPT, ADMP and DFT calculations were performed by using the Gaussian16 program⁶⁴. The strength of the bonds were characterized with the Quantum Theory of Atoms in Molecules (QTAIM),⁶⁵ using the AIMAll code.⁶⁶ QTAIM is a Quantum Chemical Topology (QCT) method used to analyze different descriptors of Bond Critical Points (BCP) to assess the nature of the chemical bond.⁶⁷

3 Results and discussion

The PE spectrum of cAA over the binding energy region 8–24 eV measured at 60 eV photon energy is shown in Fig. 1, where it is compared to the theoretical predictions of the OVGF and P3+ models for the orbital ionisation energies shown in the figure as vertical bars. The spectroscopic pole strength of these orbitals are always larger than 0.85, which indicates that a single-particle approximation in this region is appropriate. The spectrum presents a distinct structure, with many similarities to the spectra of other similar cyclo dipeptides, and is characterized by a few partially resolved bands in the range 9–11 eV followed, after a gap of about 1 eV, by several broader bands at BE > 12 eV.

The DKP ring structure of the lower, almost energetically degenerate, conformers of cAA has a boat shape, like in other symmetric cyclo dipeptides,^17,18 see Fig. S3 in the ESI.† The geometry of the different conformers, as observed in several amino acids^7,9 as well as in aromatic cyclo dipeptides⁶⁸ results in different electronic density of states. However, the predicted differences in the energies of electronic levels become negligible when convoluted to the experimental resolution, indicating a scarse sensitivity of the PE spectroscopy to molecular conformation. We therefore compare the experimental spectrum with the calculation of the electronic structure of the lowest energy conformer.

The OVGF model has been successfully used in the past to predict IE and electron spectra of biomolecules, which well match the experiments once a shift of a few hundreds of meV is applied¹⁷. In the present case overall both the OVGF and P3+ models provide a good representation of the PE spectrum and catch the main features in the region up to about 18 eV with no shift. There are small differences in the position of the bands between the two models, with the OVGF predicting the IE about 0.3 eV lower than the experimental results and overestimating the separation of the states contributing to the first bands. In the inner valence region, BE > 18 eV, both models overestimate the ionisation energy of the main bands, due to the increasing contribution of two-electron processes in this binding energy region, as witnessed by the calculated vertical double ionisation potential at 20.09 eV.

The BE region <11 eV in cAA contains four molecular orbitals organized in two distinct bands. In the most simple cyclo dipeptide cGG these orbitals are dominated by the 2p electron lone pairs of the oxygen atoms in the C=O moieties in the DKP ring.¹⁸ In more complex cyclo dipeptides, like the ones with either aromatic amino acids,⁶⁸ a pyrrolidine ring fused to the DKP ring¹⁷ or an imidazole ring¹⁸ as side chain, a larger number of orbitals contributes in this lower BE region, partially or completely localised on the side chain ring of the amino acid. In the A amino acid the first contribution of orbitals localized on the methyl group appear well above 13 eV binding energy.⁷⁰ It is therefore reasonable to observe how the outermost region of the PE spectrum, similarly to the cGG case, is dominated by only four orbitals related to the DKP ring. The Hartree–Fock representation of the main molecular orbitals (Fig. S4 in the ESI†) confirms these features. The outer orbitals are mainly combinations of lone pair orbitals in the oxygen atom, π orbitals in the C=O bonds and σ orbitals in the C–N bonds.

The relative stability of systems evolving from amino acids to oligo and poly-peptides is an interesting topic. In peptides of increasing length, a complex relation between molecular survival and molecular size has been observed under VUV irradiation.⁷¹ The comparison between amino acid considered as isolated units or ‘assembled’ into dipeptides represents the simplest case. The gap between the HOMO and LUMO orbitals is often used as an indicator of the kinetic stability of the species with respect to any further chemical reaction.⁷² In the cyclo dipeptides the HOMO–LUMO gap has been observed to decrease as the side group becomes larger¹⁷ thus, for instance, it decreases of about 0.61 eV going from cGG to cPhePhe. In the present calculations we found that, despite the side group of cAA, the methyl moiety, is larger than the single H atom in cGG, the HOMO–LUMO gap of cAA is 0.14 eV larger than the one of cGG, indicating a slightly higher kinetic stability and lower chemical reactivity of cAA with respect to cGG.

A comparison of the ionisation energies of the cyclic dipeptides measured up to now and of their constituent amino acids is shown in Table 4. It can be observed that they follow the same trend, indicating the role of the side chain of the amino acid building the cyclo peptide in determining its physico-chemical properties. In the case of the series of cyclic dipeptides cGPhe, cTrpTyr and cTrpTrp⁶⁸ it has been observed that even though orbitals localized on the aromatic side chain largely contribute to the frontier orbitals of the dipeptide, the ionisation energy of the dipeptide is not smaller than the one of the constituent amino acids as expected for the case of a molecule of increased size. This observation has been interpreted⁶⁸ as a signature of a stability effect induced by the structure of the DKP on the orbitals of the aromatic ring of the side chain. The data collected in Table 1, where dipeptides with different side chains are considered, appears to be consistent with this observation, although they do not allow a general statement. For example, the cAA dipeptide has the same ionisation energy of the A amino acid within the experimental uncertainty.

Table 1 The experimental ionisation energies (IE) of several cyclo dipeptides and of their constituent amino acids are reported. Unless stated otherwise, these are all vertical ionisation energies

Cyclo-dipeptide	IE (eV)	Amino acid	IE (eV)
a Present authors, private communications from unpublished data. b Present work, determined by fitting. c Ref. 18. d Ref. 68. e Ref. 69, adiabatic value. f Ref. 8. g Ref. 9. h Estimated from Fig. 3 in ref. 70.
cGG^a	9.91 ± 0.01	G^g	10.0 ± 0.1
cGA^a	9.62 ± 0.01	G^g	10.0 ± 0.1
		A^h	9.74
cAA^b	9.53 ± 0.05	A^h	9.74
cGPhe^d	9.54 ± 0.02	Phe^f	9.5 ± 0.1
		G^g	10.0 ± 0.1
cHistG^c	9.41 ± 0.02	His^e	8.2 ± 0.1
		G^g	10.0 ± 0.1
cPhePhe^c	8.93 ± 0.02	Phe^f	9.5 ± 0.1
cTrpPro^c	8.28 ± 0.04	Trp^f	7.8 ± 0.1
		Pro^g	8.9 ± 0.1
cTrpTyr^d	8.18 ± 0.04	Trp^f	7.8 ± 0.1
		Tyr^f	8.5 ± 0.1
cTrpTrp^d	7.97 ± 0.04	Trp^f	7.8 ± 0.1

---

In the BE range 8–24 eV we performed PEPICO measurements to investigate the cAA state-selected photofragmentation, see Fig. 2 where the yield of the main fragments is reported vs binding energy. These spectra display features quite commonly observed in small polyatomic molecules,^12,36,73,74 where increasingly smaller fragments represent the fragmentation products at higher excitation energy, E_exc = BE − IP. In cAA the molecular ion at m/z 142 (or 142⁺) is measured as an intact unit exclusively in the region of the HOMO orbital, rapidly becoming unstable already from the region of the HOMO−1 state onwards, where it is fragmented into either 114⁺ or 99⁺, assigned respectively to the CO and HNCO loss channels (see Table 2). These two channels, even though opening at similar energies, present very different branching ratios, clearly favouring the HNCO-loss over the CO-loss. These three species, molecular ion and its daughter ions 114⁺ and 99⁺, are the only ones observed in the BE region <11 eV.

Table 2 Statistics of the ADMP molecular dynamics simulations for cAA⁺: percentage of all channels for both internal energies. The mass over charge ratio (m/z) of the charged fragments in each channel is also given

(cAA)^+
Channel	m/z	10 eV %	15 eV %
H10C6N2O2^+	142	86.0	48.0
CH3CHCONHCHCH3^+/HNCO	99	5.0	17.0
CH3CHCO^+/CH3CHNH/HNCO	56	1.0	7.0
CH3CHCO/CH3CHNH^+/HNCO	43	0.0	2.0
CH3CHNH/CH3CHNH^+/2CO	43	1.0	5.0
CH3CHNHCOCH(CH3)NH^+/CO	114	0.0	3.0
CH3CHNHCO^+/CH3CHNH/CO	71	0.0	4.0
CH3CHNHCOCHNH^+/CH3	127	5.0	6.0
COCH(CH3)CHNHCO^+/CH3CHNH	99	2.0	0.0
COCH(CH3)CHNHCOCH(CH2)NH/H	141	0.0	1.0
CH3CHNHCOH^+/CH3CHN/CO	72	0.0	1.0
CH3CHCONHCHCH2^+/HNCO/H	98	0.0	1.0
CH3CHNHCOCHNH^+/CH3/CO	99	0.0	1.0
NH2CHCH3^+/CH3CHNCO/CO	44	0.0	1.0
NHCHCO^+/CH3CHNH/CH3/CO	56	0.0	1.0
CONHCH(CH3)CO^+/CH3CHN/H	99	0.0	1.0
CHNH^+/CH3CHNH/CH3/2CO	28	0.0	1.0

---

In the region of BE > 12 eV, a larger number of smaller fragments, i.e. 71⁺, 56⁺, 44⁺–42⁺ and 28⁺ to cite the most relevant, can be released, with different branching ratios and a less defined state selectivity, particularly for the smaller fragments at m/z ≤ 44.

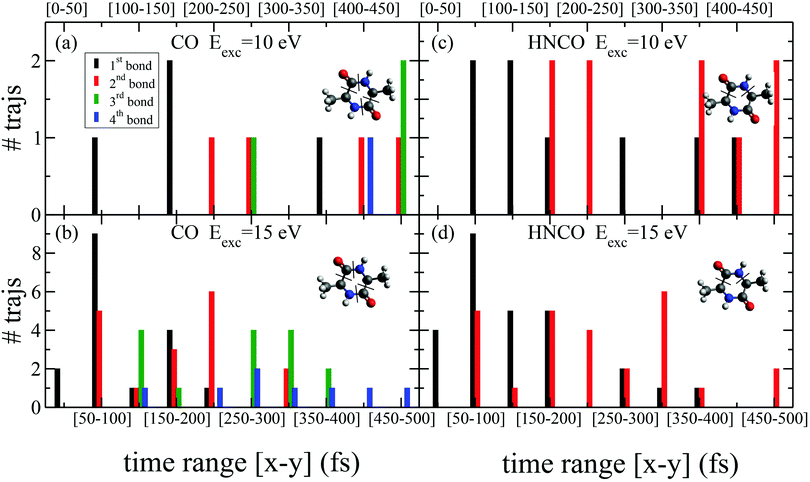
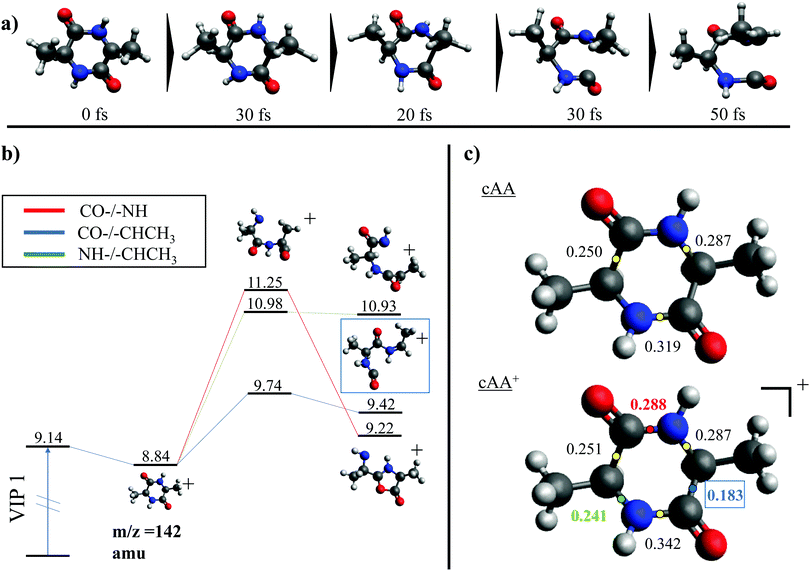
While the pathways of formation and the reactivity of fragment 71⁺ have been already presented in a previous publication,¹⁹ in the following we will discuss the general picture on cAA⁺ molecular fragmentation. To this purpose, we have performed ab initio molecular dynamics (MD) simulations at two internal excitation energies, namely 10 and 15 eV. Statistics on the populated channels during the first 500 fs after ionisation are given in Table 2. With low excitation energy, E_exc = 10 eV, 86% of the trajectories are ‘non-reactive’; i.e. they do not produce any fragment, although the initial cAA⁺ could undergo isomerization. This percentage is reduced to 48% when E_exc = 15 eV. Most of the fragmentation observed in the MD simulations corresponds to the release of HNCO and/or CO moieties. Exceptions in the reactive trajectories, meaning those trajectories involving the formation of new molecules and thus showing cleavage of one or several chemical bonds, are those showing production of CH₃ or H, although with extremely low rates. Fig. 4 presents a temporal analysis of the bond cleavage in those trajectories that lead to HNCO and CO fragments. Both cases exhibit broad distributions. At E_exc = 15 eV, the first bond break, which corresponds to ring opening, occurs mainly within the first 100–150 fs, and the second one (thus leading to the release of the fragment) is observed typically in the range 250–350 fs. In the case of CO loss, breaking of the third and fourth bonds corresponds to the release of a second CO molecule. Further analysis on the ring opening process is given in Table 3, where we observe that the most probable process starts with the CO–CHCH₃ bond cleavage, which amounts to almost 85% of the reactive trajectories at E_exc = 15 eV. The results of the MD simulations are qualitatively in agreement with the mass spectra, i.e. they show all main fragments experimentally observed. Even though the MD statistics distribution of Table 2 cannot be directly compared to the experimental intensities in the PEPICO (Fig. 2) and ion-neutral (Fig. 3) spectra, both of these measurements show how the molecular ion follows two possible fragmentation pathways, in each one producing a neutral moiety and a cationic fragment, 114⁺ and 99⁺, respectively. These fragments are observed in Fig. 2 and the fragmentation channels are identified in Fig. 3 with the notation 142⁺ → 114⁺ and 142⁺ → 99⁺. Notice that ∼95% of the fragmentation channels observed in the MD simulations involve the direct formation of neutral CO or HNCO as a first step. These two neutral fragments are of special interest as they have been identified as potential prebiotic activating agents, low-molecular weight organic compounds that act as free energy carriers to induce biomolecular self-organization.^75–77 By ‘direct formation’ we indicate that, in the mechanism leading to these two fragments, the first two bonds that break lead to either the release of neutral CO or HNCO. Furthermore, in the molecular dynamics simulations it was observed that in 96% of the reactive trajectories, the first bond to break was one of the C–C bonds in the ring, CO–CHCH₃ bond. Fig. 5a shows an example of a typical trajectory following this bond cleavage. Fig. 5b shows the energetic profile for ionisation followed by ring opening through cleavage of each of the three different bond types in the DKP ring: CO–NH, CO–CHCH₃ and NH–CHCH₃. The energy profile indicates a different lability among the three bond-types in the ionized cAA⁺. To assess the strength in these bonds we performed a Bader analysis for both neutral and singly-ionized cAA using the QTAIM formalism.⁷⁸Fig. 5c shows how, before ionisation, the strength of each bond type is very similar and equal between the same bond type, as indicated by the value of their density at the bond critical point. Nevertheless, after ionisation, the charge acts by widening the gap between the strength of the three different bonds and also between the same bonds type, identifying again the CO−CHCH₃ bond as the most reactive. Notice that cleavage of this bond corresponds to the lowest energy barrier and is the most populated one in the molecular dynamics (see statistics of first bond breaking in Table 3).

Fig. 4 Statistics of bond breaking in the molecular dynamics simulations that lead to HNCO and CO losses, with two different internal excitation energy values (E_exc = 10 and 15 eV). Histograms summing up those trajectories that present bond breaking within time intervals of 50 fs. We consider that a bond is broken when it reaches a distance of 3 Å for the first time in the trajectory. For HNCO production two bond breaks are shown (when the second is broken HNCO is released). For CO production, four bonds are given: the first two correspond to the release of one CO molecule and the third and fourth to the second CO molecule loss.

Table 3 Percentage of reactive trajectories (those producing two or more fragments) that start with the breaking of different bonds

First bond breaking	10 eV %	15 eV %
CO–/–CHCH3	64.3	84.6
CH3–/–CH	35.7	13.5
CH2–/–H	0.0	1.9

---

Fig. 5 (a) Snapshots of an example trajectory of the ab initio Molecular Dynamics simulations showing the cAA ring opening in time. (b) Different energetic barriers for the break up of the three different bonds in cAA. Relative energies are given in eV, referred to the neutral molecule and were obtained at a B3LYP/6-311++G(d,p) level of theory. (c) Bader's QTAIM analysis for the neutral and singly charged cAA. The numbers correspond to the values for the density at the bond critical points, determining the strength of the chemical bond. This analysis was performed using the QTAIM formalism and the density obtained at the B3LYP/6-311++G(d,p) level of theory.

After cleavage of the CO−CHCH₃ bond, the direct formation of HNCO and CO allows us to explain the most relevant peaks highlighted in the PEPICO experiments and observed in the ion-neutral coincidence map, i.e. 114⁺ and 99⁺, as directly correlating to the parent molecular ion. The corresponding mechanisms are shown in Fig. 6 and 7. In the former, we appreciate that release of HNCO implies a barrier located at 9.65 eV with respect to the neutral cAA. The fragment produced, 99⁺, can further evolve leading to CH₃CH₂CHO⁺ (58⁺). This fragmentation channel, labelled 99⁺ → 58⁺, is a complex mechanism that involves several hydrogen transfers and the break-up of the peptide NH–CO bond. The complete path, including minima and transition states in this process, is detailed in Fig. S5 in the ESI.† Mechanisms involving multiple hydrogen transfers have been previously proposed to explain the fragmentation dynamics in other ionized molecules in the gas phase.^60,62 In Fig. 6 we also observe the formation of CO through a barrier at 10.18 eV leading to fragment 114⁺. This can further evolve to produce CH₃CHNH₂⁺ (44⁺) and CH₃CHNH⁺ (43⁺). Notice that in the pathway towards production of CH₃CHNH₂⁺ the highest barrier is the one at 10.18 eV with respect to neutral cAA, and the exit channel is at 9.41 eV (almost degenerated with the ionisation at 9.14 eV); this implies an energetically quite accessible mechanism and is the reason behind the dominance of the peak at m/z 44 in the mass spectra (Fig. 2); in the PEPICO this fragment peak appears at relatively low energy (∼11 eV) and is dominant in a wide energy range. In contrast, fragment 43⁺ presents very low intensity and appears at BE larger than 12 eV. This can be explained again with simple energetic arguments, as the mechanism leading to fragment CH₃CHNH⁺ in Fig. 6 involves high-energy barriers.

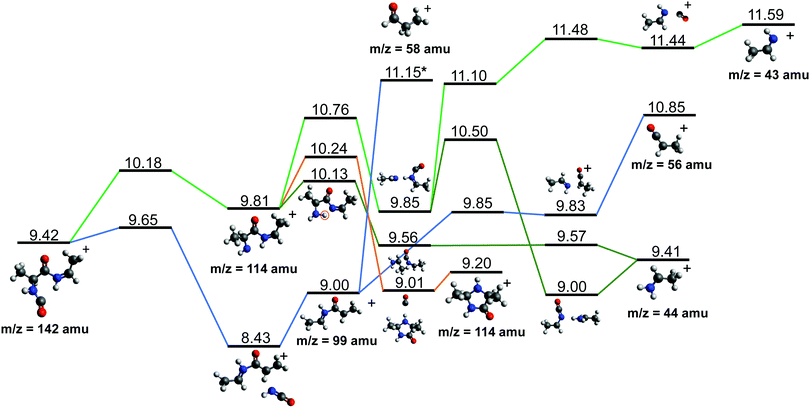Fig. 6 Two different paths after the most probable ring opening CO−/−CHCH₃ (see Fig. 5a). The green paths follows the direct formation of CO and its evolution while the lower blue path follows the evolution after the release of HNCO. Relative energies are given in eV, referred to the neutral molecule and were obtained at a B3LYP/6-311++G(d,p) level of theory. The blue path leading to fragment 58⁺, indicated with a *, is presented and further discussed in Section S4 in the ESI.†

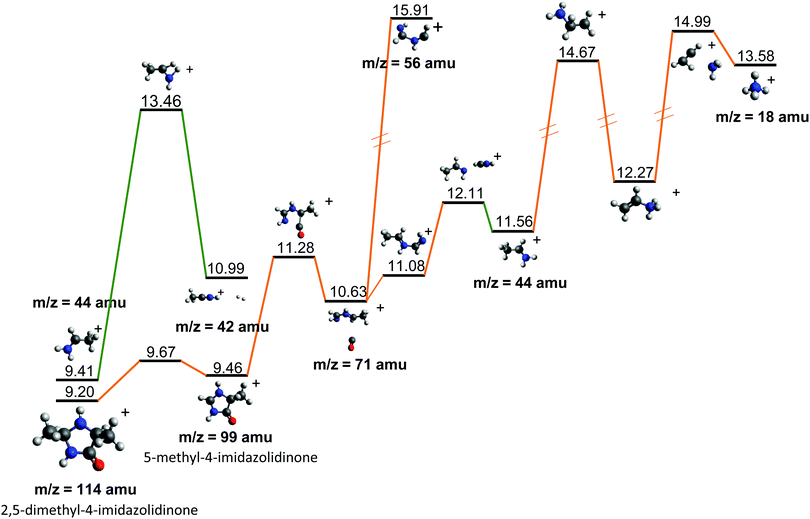Fig. 7 Further evolution of the Potential Energy Surface starting from fragments 44⁺ and 114⁺, both observed after the fragmentation of cAA⁺ (see Fig. 5 and 6). Relative energies are given in eV, referred to the neutral molecule and were obtained at a B3LYP/6-311++G(d,p) level of theory.

Fragment 114⁺ can also rearrange to form a 4-imidazolidinone(2,5-dimethyl-4-imidazolidinone⁺), a type of organic molecule recently proposed as relevant intermediates in peptide macrocyclization.³⁵ This path also implies a relatively low energy barrier (10.24 eV with respect to neutral cAA) and the product (at 9.20 eV) is also almost degenerated with the ionized cAA (9.14 eV). However, despite its energetic accessibility, fragment 114⁺ presents very weak intensity in the recorded PEPICO spectra (Fig. 2). The difference in intensity between 44⁺ (NH₂CHCH₃⁺) and 114⁺ (2,5-dimethyl-4-imidazolidinone⁺) can be understood by analyzing the fragmentation of these species, given in Fig. 7. Formation of fragment 42⁺ (NH₂CHCH₃⁺) arises from the direct release of neutral H₂ from NH₂CHCH₃⁺ through a quite high energy barrier of more than 4 eV, located at 13.46 eV with respect to neutral cAA, thus explaining its appearance over 14 eV in the PEPICO spectra (Fig. 2) and why peak at m/z 44 is quite intense. The degradation channel of 2,5-dimethyl-4-imidazolidinone⁺, on the other hand, leads to the sequential appearance of several molecular moieties: 5-methyl-4-imidazolidinone⁺ (99⁺), NHCHNHCHCH₃⁺ (71⁺), CH₃CHNH₂⁺ (44⁺), and NH₄⁺ (18⁺). In this path, it is necessary to overcome a low barrier for the production of fragment 99⁺, which explains why fragment 114⁺ appears to be particularly fragile, and, as a consequence, of very low intensity in the mass spectra.

The sequential fragmentation pathways presented in Fig. 5–7 provide insight into the experimental ion-neutral map in Fig. 3, where each path has its corresponding mechanism in the potential energy surface. In particular, further that the channels m/z 142⁺ → 114⁺ and/or 99⁺, we clearly identified the evolution of m/z 114⁺ → 99⁺; 99⁺ → 71⁺, 58⁺ and 44⁺, as well as the fragmentation of these smaller ions, 71⁺ → 56⁺ and 44⁺; 56⁺ → 28⁺; 44⁺ → 18⁺. Even though the present ion-neutral coincidence measurements cannot validate the entire sequential evolution as illustrated in the potential energy surfaces (as for example in m/z 142⁺ → 114⁺ → 99⁺ → 71⁺ → 44⁺ → 18⁺) each individual step is present in the coincidence map in Fig. 3. We note however that while the model assumes a statistical distribution of the energy in the ionic ground state, the measurements were performed at several photon energies above the molecular ionisation threshold. Thus effects due to the formation of excited electronic states of the ion and, in the valence region, also the resonant excitation of autoionizing neutral states embedded in the continuum can contribute to the measured fragmentation patterns. To evaluate the importance of those processes, the photon energy dependence of the fragmentation patterns and corresponding decay rate would need to be explored, which is beyond the scope of the present study.

4 Conclusions

An extensive investigation of the photoionisation and photofragmentation of cAA in the VUV photon energy range has been performed by PE spectroscopy, PEPICO and ion-neutral coincidence experiments accompanied by quantum chemistry calculation of the photoelectron spectrum, ab initio molecular dynamics simulations and potential energy surface exploration of the most important fragmentation channels. The analysis of the photoemission spectrum has outlined the relative stability of the cAA cyclo dipeptide with respect to the constituent A amino acid as well as with respect to other cyclo dipeptides, in general revealing a complex interplay between the molecular orbitals of the DKP ring and of the side chain of the constituent amino acid in determining the frontier orbitals of the dipeptide. In the case of cAA the molecular orbitals of the DKP ring dominate the frontier orbitals. The PEPICO experiments have shown that already in the lower energy molecular bands (BE < 11 eV) the parent ion dissociates into fragment 114⁺ and 99⁺, as also observed in the ion-neutral coincidence measurements, with a clear dominance of fragment 99⁺ over 114⁺. Consistently, the molecular dynamics simulations have shown a large variety of sequential fragmentation mechanisms, initiated by the ring opening through the CO–CHCH₃ bond cleavage followed by the release of neutral CO or HNCO fragments. The analysis of the molecular bond strength of neutral and singly-ionized cAA has allowed to identify how, after ionisation, the CO–CHCH₃ bond becomes indeed the most reactive one. The exploration of the potential energy surface for the production and evolution of these two fragments has shown how a nearly barrierless process leads to the fragmentation of 114⁺, contrary to fragment 99⁺ whose fragmentation requires overtaking a much higher energy barrier, thus explaining the low intensity of 114⁺ with respect to 99⁺ in the mass spectra.

In the region BE > 12 eV several smaller fragments are observed. The observation of smaller fragments over a broad range of BEs is most likely due to the existence of different fragmentation patterns leading to the same fragments. Nevertheless, all fragments in the PEPICO spectrum have been assigned and sequential paths of fragmentation have been proposed. Most of these paths have been observed also in ion-neutral coincidence measurements that correlate the formation of a daughter ion to a specific parent ion in a delayed fragmentation process, providing an excellent support to the theoretical calculation, which in turn allows interpreting the coincidence map.

The release of neutral carbon monoxide (CO) and isocyanic acid (HNCO),⁷⁹ have been also observed in the fragmentation of urea,^80,81 uracil,^82–84 thymine⁸⁵ and larger samples like flavins.⁸⁶ Together with the theoretically predicted rearrangement of the molecular ion into a 4-imidazolidinone structure,³⁵ these represent particularly relevant channels: in addition to the already discussed path leading to the release of charged fragments in the so-called ‘amino acid-like’ structure, [A–H–OH]⁺, with a peculiar predicted reactivity,¹⁹ these neutral and charged fragments are crucial in astrochemistry, confirming how cyclo dipeptides may have played a role as prebiotic molecules.

Author contributions

P. B., J. C., R. R., H. Z., M. H. S., and L. A. performed the experiments. P. B. and J. C. analyzed the data. D. B.-L. carried out the simulations and analyzed the theoretical results. P. B., S. D.-T., D. B.-L., and L. A. conceived the project and prepared the original draft of the manuscript. All authors thoroughly reviewed the manuscript and contributed to the final version, suggesting comments for the presentation and discussion of the results.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This article is based upon work from COST action CA18212 – Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology). The authors acknowledge the generous allocation of computer time at the Centro de Computación Científica at the Universidad Autónoma de Madrid (CCC-UAM). This work was partially supported by MICINN (Spanish Ministry of Science and Innovation) project PID2019-110091GB-I00 funded by MCIN/AEI/10.13039/501100011033, the “María de Maeztu” (CEX2018-000805-M) Program for Centers of Excellence in RD, MAECI Italy-Sweden project “Novel molecular tools for the exploration of the nanoworld”, and PRIN 20173B72NB project “Predicting and controlling the fate of bio-molecules driven by extreme-ultraviolet radiation”. D. B.-L. acknowledges the FPI grant associated with MICINN project CTQ2016-76061-P. H. Z. acknowledges the Swedish Research Council for the individual project grant with contract no. 2020-03437. M. H. S. acknowledges the Swedish Research council (Grant No. 2016-03675) and the Carl Trygger Foundation (Grant No. 17:436).

Notes and references

1. A. Shimoyama and R. Ogasawara, Origins Life Evol. Biospheres, 2002, 32, 165–179.
2. R. Pascal, L. Boiteau and A. Commeyras, Top. Curr. Chem., 2005, 69–122.
3. M. Frenkel-Pinter, M. Samanta, G. Ashkenasy and L. J. Leman, Chem. Rev., 2020, 120, 4707–4765.
4. N. Lahav, D. White and S. Chang, Science, 1978, 201, 67–69.
5. L. Bedoin, S. Alves and J.-F. Lambert, ACS Earth Space Chem., 2020, 4, 1802–1812.
6. H. Liu, M. Cao, Y. Wang, B. Lv and C. Li, Crit. Rev. Biotechnol., 2020, 40, 231–246.
7. I. Powis, E. E. Rennie, U. Hergenhahn, O. Kugeler and R. Bussy-Socrate, J. Phys. Chem. A, 2003, 107, 25–34.
8. O. Plekan, V. Feyer, R. Richter, M. Coreno and K. C. Prince, Mol. Phys., 2008, 106, 1143–1153.
9. O. Plekan, V. Feyer, R. Richter, M. Coreno, M. de Simone, K. C. Prince and V. Carravetta, J. Phys. Chem. A, 2007, 111, 10998–11005.
10. W. Zhang, V. Carravetta, O. Plekan, V. Feyer, R. Richter, M. Coreno and K. C. Prince, J. Chem. Phys., 2009, 131, 07B611.
11. O. Plekan, V. Feyer, R. Richter, M. Coreno, M. de Simone, K. Prince and V. Carravetta, Chem. Phys. Lett., 2007, 442, 429–433.
12. J. Chiarinelli, P. Bolognesi, A. Domaracka, P. Rousseau, M. C. Castrovilli, R. Richter, S. Chatterjee, F. Wang and L. Avaldi, Phys. Chem. Chem. Phys., 2018, 20, 22841–22848.
13. H. J. Svec and G. A. Junk, J. Am. Chem. Soc., 1964, 86, 2278–2282.
14. S. Simon, A. Gil, M. Sodupe and J. Bertrán, THEOCHEM, 2005, 727, 191–197.
15. H.-W. Jochims, M. Schwell, J.-L. Chotin, M. Clemino, F. Dulieu, H. Baumgärtel and S. Leach, Chem. Phys., 2004, 298, 279–297.
16. V. Feyer, O. Plekan, R. Richter, M. Coreno, K. C. Prince and V. Carravetta, J. Phys. Chem. A, 2009, 113, 10726–10733.
17. A. P. W. Arachchilage, F. Wang, V. Feyer, O. Plekan and K. C. Prince, J. Chem. Phys., 2010, 133, 174319.
18. A. P. Wickrama Arachchilage, F. Wang, V. Feyer, O. Plekan and K. C. Prince, J. Chem. Phys., 2012, 136, 124301.
19. D. Barreiro-Lage, P. Bolognesi, J. Chiarinelli, R. Richter, H. Zettergren, M. H. Stockett, L. Carlini, S. Diaz-Tendero and L. Avaldi, J. Phys. Chem. Lett., 2021, 12, 7379–7386.
20. D. Gross and G. Grodsky, J. Am. Chem. Soc., 1955, 77, 1678–1680.
21. V. Badelin, E. Y. Tyunina, G. Girichev, N. Giricheva and O. Pelipets, J. Struct. Chem., 2007, 48, 647–653.
22. A. S. Noguerola, B. Murugaverl and K. J. Voorhees, J. Am. Soc. Mass Spectrom., 1992, 3, 750–756.
23. A. D. Hendricker and K. J. Voorhees, J. Anal. Appl. Pyrol., 1996, 36, 51–70.
24. L. Carlini, J. Chiarinelli, G. Mattioli, C. Mattea, V. Valentini, A. De Stefanis, E. Bauer, P. Bolognesi and L. Avaldi, J. Phys. Chem. B, 2021 , submitted.
25. J. Ying, R. Lin, P. Xu, Y. Wu, Y. Liu and Y. Zhao, Sci. Rep., 2018, 8, 1–8.
26. P. Milne, A. Hunt, K. Rostoll, J. Van Der Walt and C. Graz, J. Pharm. Pharmacol., 1998, 50, 1331–1337.
27. A. Zorzi, K. Deyle and C. Heinis, Curr. Opin. Chem. Biol., 2017, 38, 24–29.
28. X. Yan, P. Zhu and J. Li, Chem. Soc. Rev., 2010, 39, 1877–1890.
29. M. A. Ziganshin, A. S. Safiullina, S. A. Ziganshina, A. V. Gerasimov and V. V. Gorbatchuk, Phys. Chem. Chem. Phys., 2017, 19, 13788–13797.
30. T. Govindaraju, M. Pandeeswar, K. Jayaramulu, G. Jaipuria and H. S. Atreya, Supramol. Chem., 2011, 23, 487–492.
31. A. Derossi, F. Lama, M. Piacentini, T. Prosperi and N. Zema, Rev. Sci. Instrum., 1995, 66, 1718–1720.
32. G. Cautero, R. Sergo, L. Stebel, P. Lacovig, P. Pittana, M. Predonzani and S. Carrato, Nucl. Instrum. Methods Phys. Res., Sect. A, 2008, 595, 447–459.
33. R. H. Menk, M. Antonelli, G. Brajnik, J. Bufon, C. Dri, D. Giuressi, A. Gubertini, C. Nichetti, G. Pinaroli and P. Pittana, et al. , AIP Conf. Proc., 2019, 060071.
34. A. Cartoni, P. Bolognesi, E. Fainelli and L. Avaldi, J. Chem. Phys., 2014, 140, 184307.
35. V. Adebomi, R. D. Cohen, R. Wills, H. A. H. Chavers, G. E. Martin and M. Raj, Angew. Chem., Int. Ed., 2019, 58, 19073–19080.
36. P. Bolognesi, A. Casavola, A. Cartoni, R. Richter, P. Markus, S. Borocci, J. Chiarinelli, S. Toši, H. Saadeh and M. Masič, et al. , J. Chem. Phys., 2016, 145, 191102.
37. S. Martin, R. Brédy, A.-R. Allouche, J. Bernard, A. Salmoun, B. Li and L. Chen, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 062513.
38. R. Rispoli, E. De Angelis, L. Colasanti, N. Vertolli, S. Orsini, J. Scheer, A. Mura, A. Milillo, P. Wurz and S. Selci, et al. , Opt. Eng., 2013, 52, 051206.
39. T. Baer, B. Sztáray, J. P. Kercher, A. Lago, A. Bödi, C. Skull and D. Palathinkal, Phys. Chem. Chem. Phys., 2005, 7, 1507–1513.
40. B. Sztáray, A. Bodi and T. Baer, J. Mass Spectrom., 2010, 45, 1233–1245.
41. Wavemetrics Inc., Igor Pro, https://www.wavemetrics.com.
42. J. V. Ortiz, The Electron Propagator Picture of Molecular Electronic Structure, 1997.
43. J. Ortiz, Toward an Exact One-Electron Picture of Chemical Bonding, Academic Press, 1999, vol. 35, pp. 33–52.
44. J. V. Ortiz, Int. J. Quantum Chem., 2005, 105, 803–808.
45. M. Díaz-Tinoco, O. Dolgounitcheva, V. G. Zakrzewski and J. V. Ortiz, J. Chem. Phys., 2016, 144, 224110.
46. H. H. Corzo, A. Galano, O. Dolgounitcheva, V. G. Zakrzewski and J. V. Ortiz, J. Phys. Chem. A, 2015, 119, 8813–8821.
47. J. Linderberg and Y. Öhrn, Propagators in Quantum Chemistry, John Wiley & Sons, Ltd, 2004.
48. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
49. H. B. Schlegel, J. M. Millam, S. S. Iyengar, G. A. Voth, A. D. Daniels, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 114, 9758–9763.
50. S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 115, 10291–10302.
51. H. B. Schlegel, S. S. Iyengar, X. Li, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2002, 117, 8694–8704.
52. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
53. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
54. A. J. Cohen and N. C. Handy, Mol. Phys., 2001, 99, 607–615.
55. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
56. S. Maclot, R. Delaunay, D. G. Piekarski, A. Domaracka, B. A. Huber, L. Adoui, F. Martín, M. Alcamí, L. Avaldi, P. Bolognesi, S. Díaz-Tendero and P. Rousseau, Phys. Rev. Lett., 2016, 117, 073201.
57. M. Capron, S. Diaz-Tendero, S. MacLot, A. Domaracka, E. Lattouf, A. Lawicki, R. Maisonny, J. Y. Chesnel, A. Mery, J. C. Poully, J. Rangama, L. Adoui, F. Martin, M. Alcami, P. Rousseau and B. A. Huber, Chem. – Eur. J., 2012, 18, 9321–9332.
58. S. Maclot, D. G. Piekarski, A. Domaracka, A. Mery, V. Vizcaino, L. Adoui, F. Martín, M. Alcamí, B. A. Huber, P. Rousseau and S. Díaz-Tendero, J. Phys. Chem. Lett., 2013, 4, 3903–3909.
59. D. G. Piekarski, R. Delaunay, S. Maclot, L. Adoui, F. Martín, M. Alcamí, B. A. Huber, P. Rousseau, A. Domaracka and S. Díaz-Tendero, Phys. Chem. Chem. Phys., 2015, 17, 16767–16778.
60. N. G. Kling, S. Daz-Tendero, R. Obaid, M. R. Disla, H. Xiong, M. Sundberg, S. D. Khosravi, M. Davino, P. Drach, A. M. Carroll, T. Osipov, F. Martn and N. Berrah, Nat. Commun., 2019, 10, 2813.
61. B. Oostenrijk, D. Barreiro, N. Walsh, A. Sankari, E. P. MÅnsson, S. Maclot, S. L. Sorensen, S. Díaz-Tendero and M. Gisselbrecht, Phys. Chem. Chem. Phys., 2019, 21, 25749–25762.
62. M. McDonnell, A. C. LaForge, J. Reino-González, M. Disla, N. G. Kling, D. Mishra, R. Obaid, M. Sundberg, V. Svoboda, S. Díaz-Tendero, F. Martín and N. Berrah, J. Phys. Chem. Lett., 2020, 11, 6724–6729.
63. P. Rousseau, D. G. Piekarski, M. Capron, A. Domaracka, L. Adoui, F. Martn, M. Alcam, S. Daz-Tendero and B. A. Huber, Nat. Commun., 2020, 11, 3818.
64. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
65. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press: Oxford, England, 1990, vol. l.
66. T. A. Keith, AIMAll (Version 19.10.12), aim.tkgristmill.com, TK Gristmill Software, Overland Park KS, USA, 2019.
67. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
68. E. Molteni, G. Mattioli, P. Alippi, L. Avaldi, P. Bolognesi, L. Carlini, F. Vismarra, Y. Wu, R. B. Varillas and M. Nisoli, et al. , Phys. Chem. Chem. Phys., 2021 10.1039/D1CP04050B.
69. K. R. Wilson, L. Belau, C. Nicolas, M. Jimenez-Cruz, S. R. Leone and M. Ahmed, Int. J. Mass Spectrom., 2006, 249, 155–161.
70. H. Farrokhpour, F. Fathi and A. N. De Brito, J. Phys. Chem. A, 2012, 116, 7004–7015.
71. D. Egorov, R. Hoekstra and T. Schlathölter, Phys. Chem. Chem. Phys., 2017, 19, 20608–20618.
72. D. Manolopoulos, J. May and S. Down, Chem. Phys. Lett., 1991, 181, 105.
73. P. Bolognesi, J. Kettunen, A. Cartoni, R. Richter, S. Tosic, S. Maclot, P. Rousseau, R. Delaunay and L. Avaldi, Phys. Chem. Chem. Phys., 2015, 17, 24063–24069.
74. A. Cartoni, A. Casavola, P. Bolognesi, M. Castrovilli, D. Catone, J. Chiarinelli, R. Richter and L. Avaldi, J. Phys. Chem. A, 2018, 122, 4031–4041.
75. L. Boiteau and R. Pascal, Origins Life Evol. Biospheres, 2011, 41, 23–33.
76. G. Danger, R. Plasson and R. Pascal, Chem. Soc. Rev., 2012, 41, 5416–5429.
77. A. Pross, Toward a general theory of evolution: Extending Darwinian theory to inanimate matter, 2011, http://www.jsystchem.com/content/2/1/1.
78. J. Andrés, L. Gracia, P. González-Navarrete and V. S. Safont, Comput. Theor. Chem., 2015, 1053, 17–30.
79. L. Le Roy, K. Altwegg, H. Balsiger, J.-J. Berthelier, A. Bieler, C. Briois, U. Calmonte, M. R. Combi, J. De Keyser and F. Dhooghe, et al. , Astron. Astrophys., 2015, 583, A1.
80. I. Corral, O. Mó, M. Yáñez, J.-Y. Salpin, J. Tortajada and L. Radom, J. Phys. Chem. A, 2004, 108, 10080–10088.
81. A. Eizaguirre, O. Mó, M. Yáñez, J. Tortajada and J.-Y. Salpin, J. Phys. Chem. B, 2013, 117, 2088–2095.
82. A. M. Lamsabhi, M. Alcamí, O. Mó, M. Yáñez, J. Tortajada and J.-Y. Salpin, ChemPhysChem, 2007, 8, 181–187.
83. C. Trujillo, A. M. Lamsabhi, O. Mó, M. Yáñez and J.-Y. Salpin, Int. J. Mass Spectrom., 2011, 306, 27–36.
84. E. Rossich-Molina, J.-Y. Salpin, R. Spezia and E. Martínez-Núñez, Phys. Chem. Chem. Phys., 2016, 18, 14980–14990.
85. H.-W. Jochims, M. Schwell, H. Baumgärtel and S. Leach, Chem. Phys., 2005, 314, 263–282.
86. L. Giacomozzi, C. Kjær, S. Brøndsted Nielsen, E. K. Ashworth, J. N. Bull and M. H. Stockett, J. Chem. Phys., 2021, 155, 044305.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of the ion-neutral fragment coincidence simulations; lowest energy conformers; and HF molecular orbitals. See DOI: 10.1039/d1cp05811h

‡ The cited references represent just a few examples, far from being an exhaustive review of the vast amount of work present in the literature

---