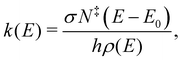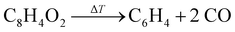Formation of phenylacetylene and benzocyclobutadiene in the ortho-benzyne + acetylene reaction†
Morgan N.
McCabe
 a,
Patrick
Hemberger
a,
Patrick
Hemberger
 b,
Dario
Campisi‡
b,
Dario
Campisi‡
 c,
Jeger C.
Broxterman
c,
Jeger C.
Broxterman
 a,
Engelbert
Reusch
d,
Andras
Bodi
a,
Engelbert
Reusch
d,
Andras
Bodi
 b and
Jordy
Bouwman§¶||
b and
Jordy
Bouwman§¶||
 *a
*a
aLaboratory for Astrophysics, Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands. E-mail: jordy.bouwman@colorado.edu; Fax: +31 7 1527 8432
bLaboratory for Synchrotron Radiation and Femtochemistry, Paul Scherrer Institute, 5232 Villigen, Switzerland
cLeiden Observatory, Leiden University, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands
dInstitute of Physical and Theoretical Chemistry, University of Würzburg, Am Hubland, D-97074 Würzburg, Germany
First published on 3rd January 2022
Abstract
Ortho-benzyne is a potentially important precursor for polycyclic aromatic hydrocarbon formation, but much is still unknown about its chemistry. In this work, we report on a combined experimental and theoretical study of the o-benzyne + acetylene reaction and employ double imaging threshold photoelectron photoion coincidence spectroscopy to investigate the reaction products with isomer specificity. Based on photoion mass-selected threshold photoelectron spectra, Franck–Condon simulations, and ionization cross section calculations, we conclude that phenylacetylene and benzocyclobutadiene (PA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BCBdiene) are formed at a non-equilibrium ratio of 2
BCBdiene) are formed at a non-equilibrium ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively, in a pyrolysis microreactor at a temperature of 1050 K and a pressure of ∼20 mbar. The C8H6 potential energy surface (PES) is explored to rationalize the formation of the reaction products. Previously unidentified pathways have been found by considering the open-shell singlet (OSS) character of various C8H6 reactive intermediates. Based on the PES data, a kinetic model is constructed to estimate equilibrium abundances of the two products. New insights into the reaction mechanism – with a focus on the OSS intermediates – and the products formed in the o-benzyne + acetylene reaction provide a greater level of understanding of the o-benzyne reactivity during the formation of aromatic hydrocarbons in combustion environments as well as in outflows of carbon-rich stars.
1, respectively, in a pyrolysis microreactor at a temperature of 1050 K and a pressure of ∼20 mbar. The C8H6 potential energy surface (PES) is explored to rationalize the formation of the reaction products. Previously unidentified pathways have been found by considering the open-shell singlet (OSS) character of various C8H6 reactive intermediates. Based on the PES data, a kinetic model is constructed to estimate equilibrium abundances of the two products. New insights into the reaction mechanism – with a focus on the OSS intermediates – and the products formed in the o-benzyne + acetylene reaction provide a greater level of understanding of the o-benzyne reactivity during the formation of aromatic hydrocarbons in combustion environments as well as in outflows of carbon-rich stars.
1 Introduction
Polycyclic aromatic hydrocarbons (PAHs), organic molecules that contain two or more fused aromatic rings, are abundant on Earth and ubiquitous in the interstellar medium (ISM). Terrestrially, these molecules have natural and anthropogenic sources (via combustion) and are of concern as their accumulation in the environment can lead to health issues.1,2 In the ISM, PAHs are detected as a family of molecules by the characteristic emission bands in the 3–20 μm mid-infrared (mid-IR) spectral region.3–5 These mid-IR emission bands have been reported towards many sources including H II regions, planetary nebula, and reflection nebula.6Numerous studies have been conducted to simulate combustion environments and to reveal the PAH and soot formation mechanisms.1,7–12 These combustion studies also provide a basis for understanding PAH formation in the ISM, as it is assumed that PAHs are formed under the combustion-like conditions in the outflow of carbon-rich stars.5,13 However, the formation of the second aromatic ring, a critical step in the growth of aromatic molecules, has yet to be explained.14 New mechanisms, such as reactions involving o-benzyne, may contribute to growth of PAHs and the formation of a second ring.
The structure and reactivity of o-benzyne have been studied in some detail. Spectroscopic measurements characterized o-benzyne's structure, with IR stretching modes indicating the presence of a carbon–carbon triple bond, albeit with a lower frequency than the average for the bond type.15 Further, computational studies confirmed that the species largely exhibits aryne character, due to the presence of a large singlet–triplet energy gap, with the singlet species being lower in energy. However, o-benzyne retains some small amount (ca. 10%) of biradical character, as confirmed by rotational spectroscopy.16,17 Recently, o-benzyne was detected toward the Taurus Molecular Cloud TMC-1,18 marking its first ever detection in the ISM. In addition, o-benzyne has recently awakened the interest of the combustion chemistry community, as it was shown that phenyl radicals can decompose to o-benzyne under combustion-relevant conditions.19 Moreover, o-benzyne self-reactions were shown to result in PAHs.20 Due to its presence in the ISM and its potential role in combustion chemistry, o-benzyne may play a significant role in closing the gap between current PAH and soot formation models and the observed PAH abundance and rates of formation.14,21,22
A few studies have aimed to understand gas-phase o-benzyne reactions with both closed-shell and radical reactants.23–26 A combined experimental and computational study by Friedrichs et al.27 probed the products of o-benzyne's reaction with the small unsaturated hydrocarbons acetylene (C2H2), ethene (C2H4), and propene (C3H6). Computationally, they found 40–50 kJ mol−1 entrance barriers to the o-benzyne + hydrocarbon reactions. Furthermore, while their mass spectrometric approach did not allow for isomer-specific product assignment, they concluded based on computational results that both polycylic and branched monocyclic reaction products are accessible. In addition, Friedrichs et al. proposed an “edge-on” and a “concerted” pathway for the o-benzyne + acetylene association reaction with the final product dependent on the favored angle of attack. In the absence of isomer-specific data, the dominant product formation mechanism remained unclear.
Computational studies to determine reaction pathways and accurate energies for reactions with o-benzyne are uniquely challenging. Specifically, the reactions between o-benzyne and hydrocarbons are likely to involve biradical intermediates with open-shell singlet (OSS) character, and as a result, care needs to be taken to describe these systems appropriately. Closed-shell single-determinant wave functions are insufficient to represent the wave function of these molecules because of the presence of independent radical centers. Potential energy surface exploration using multireference approaches with large enough basis sets is an intractable pursuit in these comparably large systems. Luckily, studies have shown that OSS energies can also be approximated based on OSS and triplet energies quite reliably, allowing for a straightforward density functional theory (DFT) description of these species.28–30
The aim of this work is to determine the reaction mechanism and final isomeric products of the acetylene + o-benzyne reaction by double imaging photoelectron photoion spectroscopy31 (i2PEPICO) at the Swiss Light Source. Photoion mass-selected threshold photoelectron spectra offer an isomer-selective and sensitive detection tool to identify reactive intermediates in gas mixtures, and reveal reaction mechanisms, as also applied in catalysis and combustion environments.32,33 DFT computational chemistry methods are employed to yield insights into the potential energy surface and the reaction mechanism at play taking into account the OSS character of the biradical species. Finally, statistical modelling is performed to reveal the isomerization reaction dynamics and put the measured isomer branching ratios into context. With the combined application of these methods, we identify the products of the acetylene + o-benzyne reaction and obtain a clear understanding of the reaction mechanism.
2 Experimental
The o-benzyne + acetylene reaction was studied using a pyrolysis microreactor connected to the CRF-PEPICO setup at the vacuum ultraviolet (VUV) beamline of the Swiss Light Source (SLS) at Paul Scherrer Institute (PSI) in Villigen, Switzerland. The VUV beamline, the i2PEPICO detection chamber34,35 and the pyrolysis reactor36 have been described in much detail elsewhere and only a summary of the relevant experimental details is provided here.Benzocyclobutenedione (BCBdione) was synthesized following the method by South and Liebeskind37 and used as o-benzyne precursor. The solid BCBdione sample was placed in between a small aluminum pellet and glass wool in a 0.25 inch diameter sample container tube. The tube had a 100 μm pinhole at the end, situated at the entrance of the pyrolysis microreactor. The sample container tube was mounted in a copper block, of which the temperature was stabilized at 60 °C using water cooling and heating with a Huber minichiller. As shown in a previous study, the vapor pressure of BCBdione is sufficient at this temperature to create a stable o-benzyne signal, while being low enough to suppress bimolecular o-benzyne chemistry.25 The reactant gas, neat acetylene (≥99.5% stabilized with acetone, Carbagas), flowed through the sample container and picked up the BCBdione vapor.
The resulting gas-phase mixture of acetylene and BCBdione expanded through the pinhole at the end of the sample container tube and into the pyrolysis microreactor. The microreactor consists of a ∼4 cm long SiC tube with an inner diameter of 1 mm and is resistively heated over a length of ∼2 cm using DC power. The temperature was estimated from the electrical power, based on previous surface temperature measurements as recorded using a thermocouple for a similar SiC reactor tube with equidistant electrodes. Temperatures were varied between 700–1200 K with an absolute uncertainty on the order of ±100 K, but with a small relative error between measurements.
The gas pressure in the sample tube containing the precursor was measured at 0.25–0.35 bar while flowing acetylene at a rate of 30 sccm. The gas expands through the pyrolysis reactor into the source chamber. The pressure in the source chamber was 5 × 10−4 mbar during gas flow. The pressure and residence time in the reactor tube can be inferred from these conditions based on computational fluid dynamics and are on the order of 20 mbar and 10–100 μs, respectively.38–40 The effusive beam containing reactants and products exiting the pyrolysis reactor was skimmed by a 2 mm skimmer, forming a molecular beam in the i2PEPICO detection chamber. The background pressure of the detection chamber was ∼ 10−6 mbar during measurements with a baseline pressure of ca. one order of magnitude lower.
Synchrotron radiation was generated using a bending magnet and dispersed by a 150 grooves per mm grating. The dispersed light was focused at the 200 μm exit slit, situated in a differentially pumped rare gas filter and resulting in a resolution of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1500. The gas filter was filled with 10 mbar of a mixture of Kr, Ar, and Ne over an optical length of 10 cm to filter out high harmonic radiation of the grating above 14 eV. The monochromatized ionizing VUV synchrotron radiation intersects the molecular beam in the i2PEPICO detection chamber. The detection chamber is connected to the beamline, and the ionization region is 50 cm downstream from the exit slit. The electron–ion pairs formed in an ionization event are accelerated in opposite directions using a 218 V cm−1 field and are recorded in delayed coincidence. Electrons are velocity map imaged on a RoentDek delay line detector, and their arrival time serves as the start time for the time-of-flight (TOF) measurement of the associated cation. A second RoentDek detector on the opposite end records the position and arrival time of the space focused ions. Coincidence data were recorded over a photon energy range of 7.4–9.4 eV using a step size of 10 meV and an integration time of 60 s per energy point. These data were then used to construct the mass-selected threshold photoelectron spectra (ms-TPES) of the reaction products. Isomer-resolved product assignments are made based on the ms-TPES data in conjunction with reference and/or simulated spectra.
1500. The gas filter was filled with 10 mbar of a mixture of Kr, Ar, and Ne over an optical length of 10 cm to filter out high harmonic radiation of the grating above 14 eV. The monochromatized ionizing VUV synchrotron radiation intersects the molecular beam in the i2PEPICO detection chamber. The detection chamber is connected to the beamline, and the ionization region is 50 cm downstream from the exit slit. The electron–ion pairs formed in an ionization event are accelerated in opposite directions using a 218 V cm−1 field and are recorded in delayed coincidence. Electrons are velocity map imaged on a RoentDek delay line detector, and their arrival time serves as the start time for the time-of-flight (TOF) measurement of the associated cation. A second RoentDek detector on the opposite end records the position and arrival time of the space focused ions. Coincidence data were recorded over a photon energy range of 7.4–9.4 eV using a step size of 10 meV and an integration time of 60 s per energy point. These data were then used to construct the mass-selected threshold photoelectron spectra (ms-TPES) of the reaction products. Isomer-resolved product assignments are made based on the ms-TPES data in conjunction with reference and/or simulated spectra.
2.1 Computational methods
Wherever possible, isomeric assignments are based on reference threshold photoelectron spectra. Otherwise, for species without a published photoelectron spectrum, adiabatic ionization energies (IEs) were calculated at the CBS-QB3 level of theory using the program Gaussian 1641 to support the interpretation of the experimental observations. Furthermore, TPE spectra were simulated by calculating Franck–Condon factors in the double harmonic approximation. For the Franck–Condon simulations, geometry optimizations and frequency calculations for the neutral and ionic ground state of the species were conducted with DFT using the B3LYP/6-311++G(d,p)42–46 level of theory. Franck–Condon factors were calculated from these vibrational normal modes using ezSpectrum.47 The resulting stick spectra were convoluted with a Gaussian function with a full-width-at-half-maximum of 0.032 eV to simulate the rotational envelope and facilitate comparison with the experimental data.In order to estimate the relative abundances of the isomers present in the ms-TPES, eZDyson was used to calculate absolute photoionization cross sections for each isomer.48 Dyson orbitals were obtained using equation of motion for ionization potential with coupled cluster singles and doubles (EOM-IP-CCSD)49,50 with the correlation consistent polarized triple zeta basis set (cc-pVTZ)51 basis set, using Q-Chem 4.3.52 The continuum state of the photoelectron was taken into account to compute photoionization cross sections, which were then combined with Franck–Condon simulations of the nuclear wave function overlap to predict relative TPES intensities of the isomers. Thus, we only rely on relative signal intensities to estimate the relative abundance of the isomers contributing to the photoelectron spectrum.
Potential energy surface (PES) calculations were performed in order to provide insight into the energy landscape of the acetylene + o-benzyne reaction. Relaxed coordinate scans were conducted at the M06-2X/6-311++G(d,p)46,53 level of theory and stationary points were located. M06-2X was chosen as it provides accurate energies when studying reactions involving large hydrocarbons.54–56 Due to fact that the reaction starts from the closed-shell but in part biradical o-benzyne, some of the intermediates exhibit biradical character. To treat this properly using DFT, unrestricted singlet wave functions were calculated for the biradical intermediates by mixing the highest occupied and lowest unoccupied α orbitals in the initial guess of the wave function to destroy spatial symmetry of the α and β sets of orbitals. The wave function was thus allowed to converge to an open-shell singlet solution. The energy of OSS species was determined using the Ziegler–Cramer correction by calculating twice the OSS energy minus the triplet energy at the same geometry.29,30 This was done in instances where the mixing of the singlet and triplet states is comparable, as indicated by a spin expectation value 〈S2〉 ≈ 1. Lastly, Complete Active Space Self-Consistent Field (CASSCF)57 calculations were preformed along the entrance pathways (see ESI†) to confirm the entrance barriers and therewith obtain insights into the association mechanism at play.
The product distribution in the pyrolysis microreactor is determined by the radical precursor formation, the bimolecular kinetics of the association reaction, the competition between fast re-thermalization and the system exploring the adduct's potential energy surface, as well as the short reaction time, determined by the 10–100 μs residence time in the reactor. This means that non-equilibrium product distributions can result from fast cooling after exothermic reactions. To put the experimentally determined isomer distribution of the products into context, unimolecular microcanonical rate curves were calculated by Rice–Ramsperger–Kassel–Marcus (RRKM) theory using a computer program broadly validated in modeling unimolecular dissociative photoionization and developed by Sztáray et al.58 The model provides microcanonical rates for unimolecular reactions based on the reactant density of states and the transition state numbers of states via the equation:
3 Results
Mass spectra and mass-selected threshold photoelectron spectra for the reactions of o-benzyne with acetylene recorded at selected pyrolysis temperatures are presented first. Comparing the TPES data with reference data or with Franck–Condon simulated spectra allows us to identify the species with isomer specificity. Next, the potential energy surface, computed at the M06-2X/6-311++G(d,p) level of theory, is discussed to support the experimental findings.3.1 Mass spectrometry
Mass spectra are depicted in Fig. 1 comparing the products for (A) acetylene only and (B) acetylene + BCBdione recorded at a photon energy of 10.0 eV.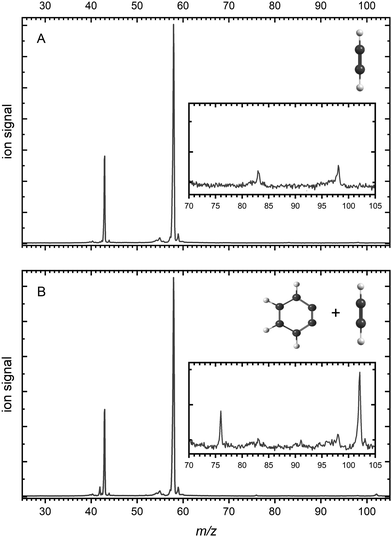 | ||
| Fig. 1 Mass spectra recorded at a photon energy of 10.0 eV and a microreactor temperature of 1026 K and 996 K (respectively) for (A) neat acetylene and (B) neat acetylene + BCBdione (1%). | ||
As can be seen from Fig. 1A as well as the inset, a number of peaks are present in the mass spectrum of pyrolyzed acetylene. In Fig. 1A, strong signals are seen at m/z 58 and m/z 43 and are attributed to the acetone ((CH3)2CO+) and the acetyl cation (CH3CO+), the latter being a dissociative ionization fragment of acetone (see ESI† for further details).59 Acetone is present in our gas flow as it is added to acetylene gas bottle as an inhibitor. Acetylene (m/z 26) is not seen in the mass spectrum, as it was recorded using a photon energy well below its ionization potential of 11.4 eV.60 In the inset, two peaks can be seen at m/z 83 and m/z 98 and are confirmed to be trace contaminants present and are not involved in the reactions occuring during pyrolysis (see ESI† for further details).
BCBdione was used as a precursor as it has previously been shown to be a clean source of o-benzyne via:25,37
3.2 Threshold photoelectron spectroscopy
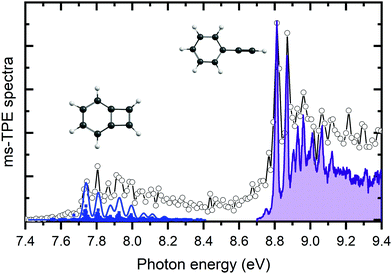
The m/z 102 ms-TPES was recorded over the 7.4–9.4 eV range with a 10 meV step size to assign the reaction products and is shown in Fig. 2. Two distinct, vibrationally resolved bands are present, the first starting at 7.74 eV and the second at 8.82 eV. Literature reference data were used to assign the vibronic structure starting at 8.82 eV. A clear match is apparent with the previously recorded ms-TPES of phenylacetylene (PA) taken from Hemberger et al.61 and shown in purple. The onset also matches well with the previously reported ionization energy of PA of 8.825 eV.62 Benzocyclobutadiene (BCBdiene) may be responsible for the signal at 7.74 eV, with a previously reported IE of 7.87 eV63 obtained by photoelectron spectroscopy. The IE found by Koenig et al.63 is notably higher in energy than the onset seen here; the difference in energy is likely due to the lower resolution of the photoelectron spectrum taken at the time.In order to determine if BCBdiene is indeed responsible for the m/z 102 signal, we turn to quantum chemical computations and Franck–Condon simulations to assign the spectrum. Using CBS–QB3 and G4 levels of theory, the adiabatic IE of BCBdiene is predicted at 7.75 eV and 7.76 eV, respectively, in very good agreement with the onset of the ms-TPES band. The B3LYP/6-311++G(d,p) optimized ground state structure of the neutral and the cation were subsequently used in a Franck–Condon simulation. The resulting stick spectrum was then convoluted with a 32 meV FWHM Gaussian profile to account for the rotational envelope and the experimental energy resolution to facilitate comparison with the recorded spectrum. From Fig. 2, it is clear that the simulated spectrum of BCBdiene matches very well with the vibronic structure seen in the experiment, leading us to conclude that BCBdiene is indeed the product from the reaction. A zoom in of the BCBdiene ms-TPE spectrum is shown in the ESI,† where further information is provided on the vibrational normal modes responsible for the observed progression. From our data we conclude that the ionization energy is 7.74 ± 0.04 eV, which is significantly lower than the value of Koenig et al.,63 also cited in the NIST Chemistry Webbook.64
Photoionization cross section calculations with ezDyson based on the EOM-IP-CCSD/cc-pVTZ Dyson orbitals show that the ionization cross sections to the ground cation states of BCBdiene and PA agree to within 3% for electrons with less than 300 meV kinetic energy. Thus, the relative TPES peak intensities will be determined by the nuclear wave function overlap between the neutral and the final cation rovibrational state and the relative abundance of the two products in the sample stream. Therefore, based on the predicted intensities from the Franck–Condon simulations, we conclude that the products form approximately in a ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of PA to BCBdiene, respectively, under our experimental conditions. As will be shown later, the non-equilibrium product distribution indicates that the less stable BCBdiene is collisionally stabilized in the microreactor faster than it is converted to the more stable PA.
1 of PA to BCBdiene, respectively, under our experimental conditions. As will be shown later, the non-equilibrium product distribution indicates that the less stable BCBdiene is collisionally stabilized in the microreactor faster than it is converted to the more stable PA.
3.3 Potential energy surface calculations
The acetylene + o-benzyne (C8H6) potential energy surface (PES) was explored using DFT and the results are shown in Fig. 3. An entrance barrier of 55 kJ mol−1 (T1) was found to form the biradical intermediate (INT1) at −71 kJ mol−1. From this initial adduct, the reaction path branches with the lower energy biradical pathway proceeding through a series of small rotational barriers; T3 (〈S2〉 = 1) at −49 kJ mol−1, INT2 (〈S2〉 = 1) at −76 kJ mol−1, and finally through T4 (〈S2〉 = 1) at −59 kJ mol−1 for ring closure, forming BCBdiene at −288 kJ mol−1. Alternatively, we have also located a closed-shell singlet pathway, initiated by the formation of a [2 + 1] closed-shell intermediate (INT3) at 16 kJ mol−1 by crossing a barrier of 56 kJ mol−1 (T6), which also proceeds to BCBdiene. However, this pathway is unlikely to compete with the lower energy biradical pathway. The third pathway from the initial adduct (INT1) proceeds via a hydrogen transfer to the radical site on the ring, forming PA (−387 kJ mol−1). This route also requires overcoming a transition state energy of 36 kJ mol−1. BCBdiene may also isomerize to PAvia a hydrogen transfer over T5 at −2 kJ mol−1.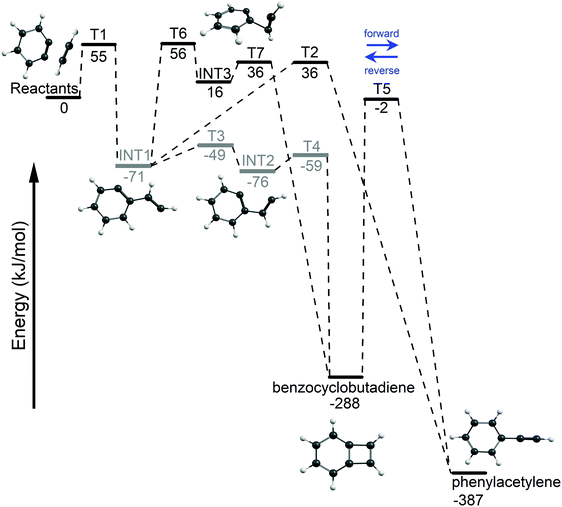 | ||
| Fig. 3 The potential energy surface for the acetylene + o-benzyne reaction using M06-2X/6-311++G(d,p). Open-shell intermediates and transition states are indicated in gray. | ||
In addition to density functional calculations at using the M06-2X functional, the G4 composite method65 was also applied to refine the potential energy surface and obtain improved energetics. For closed-shell species, the agreement between the DFT and G4 results was generally good (with energies varying by no more than 10 kJ mol−1), but G4 could not be applied consistently to describe open-shell singlet intermediates and transition states. Consequently, all energies are reported at the M06-2X/6-311++G(d,p) level of theory.
3.4 Kinetic modeling
RRKM theory was used to provide insight into the product branching for the two reactions. To this end, microcanonical rates were calculated as a function of the internal energy for the interconversion of the BCBdiene and PA products of the acetylene + o-benzyne reaction (Fig. 4).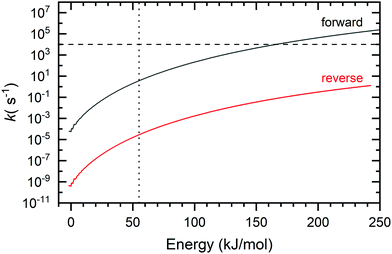 | ||
| Fig. 4 Forward and reverse rate constants for crossing T5 between PA and BCBdiene (see Fig. 3 for reference). The dotted vertical line indicates the minimum energy present needed for the reaction to proceed. The horizontal line indicates the average residence time of molecules inside the pyrolysis microreactor. | ||
The rate-limiting transition state, T5, connects the two species (see Fig. 3). The forward rate curve shown in Fig. 4 depicts the PA formation rate constant starting from the BCBdiene isomer, while the reverse rate curve shows the rate constant in the opposite direction. The vertical dotted line in this figure indicates the minimum energy needed for the o-benzyne + C2H2 association reaction to proceed, i.e., the energy of the association transition state T1 to form the initial adduct. The horizontal line in the figure shows an estimate of the inverse residence time of molecules in the pyrolysis microreactor.38
The lowest energy pathway on the potential energy surface leads to BCBdiene. However, there is enough energy in the system to cross the barrier T5 leading to PA. The RRKM rates provide us insights into the equilibration between the two products on the time scale of the reactor. The reaction from BCBdiene leading to PA is several orders of magnitude faster than the reverse. Hence, on the time scale on which reactions occur in our reactor, the excess energy drives the reaction forward to form PA in larger abundance. However, even at the highest internal energies, the forward rate is still commensurate with the residence time in the microreactor. Based on the isomerization free energy, the BCBdiene abundance should be negligible in equilibrium. Combined with the experimentally observed 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of PA
1 ratio of PA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BCBdiene, this implies that a fraction of BCBdiene is stabilized upon rethermalization in the microreactor, while a slightly larger fraction proceeds to form PA.
BCBdiene, this implies that a fraction of BCBdiene is stabilized upon rethermalization in the microreactor, while a slightly larger fraction proceeds to form PA.
4 Discussion and conclusion
The results presented here can be compared with the study by Friedrichs et al.,27 who suggested that the formation of phenylacetylene was dependent on a single “concerted” route, with an estimated barrier of over 70 kJ mol−1. The reported energy of the transition state involved in this pathway was deemed “less reliable” as the optimization did not fully converge, yet the suggested route was assumed to exist based on similar reactions between o-benzyne and other unsaturated hydrocarbons. It was concluded that BCBdiene is the primary product of the reaction, although the authors proposed that subsequent isomerization may take place. This could, however, not be confirmed as the study was limited to recording mass spectrometric data only. Moreover, the authors had not presented a mechanism for the isomerization of BCBdiene to PA.By applying i2PEPICO spectroscopy, we are now able to provide isomer-specific detection of the reaction products, allowing us to elucidate these key questions posed earlier. Based on the estimated photoionization cross sections combined with Franck–Condon factors, we have shown that, under our experimental conditions, PA is the favored reaction product with an estimated 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 branching ratio with respect to BCBdiene. Our PES calculations accounted for open-shell singlets explicitly, and allowed us to locate two additional routes for the formation of PA in the title reaction. Furthermore, a subsequent isomerization step was located, which accounts for the conversion of BCBdiene to PA. Kinetic modeling was employed to show that the dynamic competition between this isomerization step and the re-thermalization and, thus, stabilization of BCBdiene can explain the limited, 67% conversion of BCBdiene to the preferred PA product in the SiC microreactor.
1 branching ratio with respect to BCBdiene. Our PES calculations accounted for open-shell singlets explicitly, and allowed us to locate two additional routes for the formation of PA in the title reaction. Furthermore, a subsequent isomerization step was located, which accounts for the conversion of BCBdiene to PA. Kinetic modeling was employed to show that the dynamic competition between this isomerization step and the re-thermalization and, thus, stabilization of BCBdiene can explain the limited, 67% conversion of BCBdiene to the preferred PA product in the SiC microreactor.
The results of this study yield insights into the role of o-benzyne in the growth of aromatic molecules. The association reaction of o-benzyne with acetylene first has to overcome a sizeable entrance barrier of 55 kJ mol−1. Afterwards, this bimolecular reaction produces a mix of a polycyclic species and an open-chain isomer of C8H6 composition, favoring the open-chain species PA. It may proceed in hot environments, such as in combustion and in outflows of carbon-rich stars, but, due to the high entrance barrier, it is highly unlikely to contribute to growth of aromatic molecules in cold regions of the ISM. Moreover, the polycyclic BCBdiene is formed by (collisional) stabilization, and the system is expected to shift more towards equilibrium, i.e., towards PA, if the reaction time is not constrained. Although the system possesses sufficient internal energy to dissociate, collisional stabilization may not be essential for the survival of the adduct: the dissociation will proceed slower than the reverse isomerization step, which may lengthen the lifetime of the adduct to allow for IR-fluorescence, which could contribute to the stabilization of the C8H6 products. Further collisional stabilization may not occur in low-density interstellar molecular clouds. On the whole, this suggests reactions of o-benzyne with radicals are more likely the driving force behind the formation of larger poly-ringed species, at least in the ISM, as they are barrierless and proceed via addition–elimination mechanisms.12,25
Conflicts of interest
There are no conflicts to declare.Acknowledgements
JB acknowledges the Netherlands Organisation for Scientific Research (Nederlandse Organisatie voor Wetenschappelijk Onderzoek, NWO) for a Vidi grant (grant number 723.016.006) which was used to support this work. This work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative (e-infra 46011 and EINF-997). The i2PEPICO experiments were performed at the VUV beamline at the Swiss Light Source (Paul Scherrer Institute, 5232 Villigen, Switzerland). PH and AB gratefully acknowledge funding by the Swiss Federal Office of Energy (BFE Contract Number SI/501269-01).Notes and references
- H. Richter and J. B. Howard, Prog. Energy Combust. Sci., 2000, 26, 565–608 CrossRef CAS.
- C. A. Menzie, B. B. Potocki and J. Santodonato, Environ. Sci. Technol., 1992, 26, 1278–1284 CrossRef CAS.
- L. J. Allamandola, A. G. G. M. Tielens and J. R. Barker, Astrophys. J., 1985, 290, L25–L28 CrossRef CAS.
- A. Leger and J. L. Puget, Astron. Astrophys., 1984, 137, L5–L8 CAS.
- A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337 CrossRef CAS.
- E. Peeters, S. Hony, C. Van Kerckhoven, A. Tielens, L. J. Allamandola, D. M. Hudgins and C. W. Bauschlicher, Astron. Astrophys., 2002, 390, 1089–1113 CrossRef CAS.
- M. Frenklach and E. D. Feigelson, Astrophys. J., 1989, 341, 372 CrossRef CAS.
- Z. Mansurov, Combust., Explos. Shock Waves, 2005, 41, 727–744 CrossRef.
- M. Schenk, N. Hansen, H. Vieker, A. Beyer, A. Gölzhäuser and K. Kohse-Höinghaus, Proc. Combust. Inst., 2015, 35, 1761–1769 CrossRef CAS.
- T. Yang, T. P. Troy, B. Xu, O. Kostko, M. Ahmed, A. M. Mebel and R. I. Kaiser, Angew. Chem., Int. Ed., 2016, 55, 14983–14987 CrossRef CAS PubMed.
- L. Zhao, R. I. Kaiser, W. Lu, B. Xu, M. Ahmed, A. N. Morozov, A. M. Mebel, A. Hasan Howlader and S. F. Wnuk, Nat. Commun., 2019, 10, 3689 CrossRef PubMed.
- D. E. Couch, A. J. Zhang, C. A. Taatjes and N. Hansen, Angew. Chem., Int. Ed., 2021, 60, 27230–27235 CrossRef CAS PubMed.
- I. Cherchneff, J. R. Barker and A. G. G. M. Tielens, Astrophys. J., 1992, 401, 269 CrossRef CAS.
- K. O. Johansson, M. P. Head-Gordon, P. E. Schrader, K. R. Wilson and H. A. Michelsen, Science, 2018, 361, 997–1000 CrossRef CAS PubMed.
- J. G. Radziszewski, B. A. Hess and R. Zahradnik, J. Am. Chem. Soc., 1992, 114, 52–57 CrossRef CAS.
- A. C. Scheiner, H. F. Schaefer and B. Liu, J. Am. Chem. Soc., 1989, 111, 3118–3124 CrossRef CAS.
- R. D. Brown, P. D. Godfrey and M. Rodler, J. Am. Chem. Soc., 1986, 108, 1296–1297 CrossRef CAS.
- J. Cernicharo, M. Agúndez, R. I. Kaiser, C. Cabezas, B. Tercero, N. Marcelino, J. R. Pardo and P. de Vicente, Astron. Astrophys., 2021, 652, L9 CrossRef CAS.
- A. Comandini, S. Abid and N. Chaumeix, J. Phys. Chem. A, 2017, 121(31), 5921–5931 CrossRef CAS PubMed.
- F. Hirsch, E. Reusch, P. Constantinidis, I. Fischer, S. Bakels, A. M. Rijs and P. Hemberger, J. Phys. Chem. A, 2018, 122, 9563–9571 CrossRef CAS PubMed.
- A. Keller, R. Kovacs and K.-H. Homann, Phys. Chem. Chem. Phys., 2000, 2, 1667–1675 RSC.
- A. D’Alessio, A. D’Anna, P. Minutolo, L. Sgro and A. Violi, Proc. Combust. Inst., 2000, 28, 2547–2554 CrossRef.
- A. Comandini and K. Brezinsky, J. Phys. Chem. A, 2012, 116, 1183–1190 CrossRef CAS PubMed.
- A. Comandini, S. Abid and N. Chaumeix, J. Phys. Chem. A, 2017, 121, 5921–5931 CrossRef CAS PubMed.
- M. N. McCabe, P. Hemberger, E. Reusch, A. Bodi and J. Bouwman, J. Phys. Chem. Lett., 2020, 11, 2859–2863 CrossRef CAS PubMed.
- A. Matsugi and A. Miyoshi, Phys. Chem. Chem. Phys., 2012, 14, 9722–9728 RSC.
- G. Friedrichs, E. Goos, J. Gripp, H. Nicken, J.-B. Schönborn, H. Vogel and F. Temps, Z. Phys. Chem., 2009, 223, 387–407 CrossRef CAS.
- C. Wentrup, Aust. J. Chem., 2010, 63, 979–986 CrossRef CAS.
- W. T. G. Johnson, M. B. Sullivan and C. J. Cramer, Int. J. Quantum Chem., 2001, 85, 492–508 CrossRef CAS.
- D. Kvaskoff, H. Lüerssen, P. Bednarek and C. Wentrup, J. Am. Chem. Soc., 2014, 136, 15203–15214 CrossRef CAS PubMed.
- T. Baer and R. P. Tuckett, Phys. Chem. Chem. Phys., 2017, 19, 9698–9723 RSC.
- P. Hemberger, J. A. van Bokhoven, J. Pérez-Ramírez and A. Bodi, Catal. Sci. Technol., 2020, 10, 1975–1990 RSC.
- P. Hemberger, A. Bodi, T. Bierkandt, M. Köhler, D. Kaczmarek and T. Kasper, Energy Fuels, 2021, 35, 16265–16302 CrossRef CAS.
- B. Sztáray, K. Voronova, K. G. Torma, K. J. Covert, A. Bodi, P. Hemberger, T. Gerber and D. L. Osborn, J. Chem. Phys., 2017, 147, 013944 CrossRef PubMed.
- A. Bodi, P. Hemberger, T. Gerber and B. Sztáray, Rev. Sci. Instrum., 2012, 83, 083105 CrossRef PubMed.
- D. W. Kohn, H. Clauberg and P. Chen, Rev. Sci. Instrum., 1992, 63, 4003–4005 CrossRef CAS.
- M. S. South and L. S. Liebeskind, J. Org. Chem., 1982, 47, 3815–3821 CrossRef CAS.
- Q. Guan, K. N. Urness, T. K. Ormond, D. E. David, G. B. Ellison and J. W. Daily, Int. Rev. Phys. Chem., 2014, 33, 447–487 Search PubMed.
- S. Grimm, S.-J. Baik, P. Hemberger, A. Bodi, A. M. Kempf, T. Kasper and B. Atakan, Phys. Chem. Chem. Phys., 2021, 23, 15059–15075 RSC.
- M. V. Zagidullin, R. I. Kaiser, D. P. Porfiriev, I. P. Zavershinskiy, M. Ahmed, V. N. Azyazov and A. M. Mebel, J. Phys. Chem. A, 2018, 122, 8819–8827 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 59, 1200 CrossRef.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- S. Gozem and A. I. Krylov, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, e1546 Search PubMed.
- S. Gozem, A. O. Gunina, T. Ichino, D. L. Osborn, J. F. Stanton and A. I. Krylov, J. Phys. Chem. Lett., 2015, 6, 4532–4540 CrossRef CAS PubMed.
- J. Paldus and X. Li, in A Critical Assessment of Coupled Cluster Method in Quantum Chemistry, John Wiley & Sons, Ltd, 1999, pp. 1–175 Search PubMed.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- Y. Shao, L. F. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. B. Gilbert, L. V. Slipchenko, S. V. Levchenko, D. P. O'Neill, R. A. DiStasio, R. C. Lochan, T. Wang, G. J. O. Beran, N. A. Besley, J. M. Herbert, C. Y. Lin, T. Van Voorhis, S. H. Chien, A. Sodt, R. P. Steele, V. A. Rassolov, P. E. Maslen, P. P. Korambath, R. D. Adamson, B. Austin, J. Baker, E. F. C. Byrd, H. Dachsel, R. J. Doerksen, A. Dreuw, B. D. Dunietz, A. D. Dutoi, T. R. Furlani, S. R. Gwaltney, A. Heyden, S. Hirata, C.-P. Hsu, G. Kedziora, R. Z. Khalliulin, P. Klunzinger, A. M. Lee, M. S. Lee, W. Liang, I. Lotan, N. Nair, B. Peters, E. I. Proynov, P. A. Pieniazek, Y. M. Rhee, J. Ritchie, E. Rosta, C. D. Sherrill, A. C. Simmonett, J. E. Subotnik, H. L. Woodcock, W. Zhang, A. T. Bell, A. K. Chakraborty, D. M. Chipman, F. J. Keil, A. Warshel, W. J. Hehre, H. F. Schaefer, J. Kong, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 3172–3191 RSC.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- P. A. Jensen, M. Leccese, F. D. S. Simonsen, A. W. Skov, M. Bonfanti, J. D. Thrower, R. Martinazzo and L. Hornekær, Mon. Not. R. Astron. Soc., 2019, 486, 5492–5498 CrossRef CAS.
- D. Campisi, F. D. S. Simonsen, J. D. Thrower, R. Jaganathan, L. Hornekær, R. Martinazzo and A. G. G. M. Tielens, Phys. Chem. Chem. Phys., 2020, 22, 1557–1565 RSC.
- D. Campisi and A. Candian, Phys. Chem. Chem. Phys., 2020, 22, 6738–6748 RSC.
- B. O. Roos, P. R. Taylor and P. E. Sigbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- B. Sztáray, A. Bodi and T. Baer, J. Mass Spectrom., 2010, 45, 1233–1245 CrossRef PubMed.
- J. Bouwman, A. Bodi, J. Oomens and P. Hemberger, Phys. Chem. Chem. Phys., 2015, 17, 20508–20514 RSC.
- K. Kimura, S. Katsumata and Y. Achiba, Handbook of HeI photoelectron spectra of fundamental organic molecules ionization energies, Ab Initio assignments, and valence electronic structure for 200 molecules, Japan scientific societies Press; Halsted Press, Tokyo; New York, 1981 Search PubMed.
- P. Hemberger, A. J. Trevitt, T. Gerber, E. Ross and G. da Silva, J. Phys. Chem. A, 2014, 118, 3593–3604 CrossRef CAS PubMed.
- J. M. Dyke, H. Ozeki, M. Takahashi, M. C. R. Cockett and K. Kimura, J. Chem. Phys., 1992, 97, 8926–8933 CrossRef CAS.
- T. Koenig, D. Imre and J. A. Hoobler, J. Am. Chem. Soc., 1979, 101, 6446–6447 CrossRef CAS.
- NIST, NIST Chemistry WebBook, National Institute of Standards and Technology, Gaithersburg MD, 20899, 2009, vol. NIST Standard Reference Database Number 69.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp05183k |
| ‡ Present address: Chemistry Department, The University of Chicago, 5735 S Ellis Ave, Chicago, IL 60637, USA. |
| § Present address: Laboratory for Atmospheric and Space Physics, University of Colorado, Boulder, CO 80303, USA. |
| ¶ Present address: Department of Chemistry, University of Colorado, Boulder, CO 80309, USA. |
| || Present address: Institute for Modeling Plasma, Atmospheres, and Cosmic Dust (IMPACT), University of Colorado, Boulder, CO 80303, USA. |
| This journal is © the Owner Societies 2022 |