Experimental validation of high thermoelectric performance in RECuZnP2 predicted by high-throughput DFT calculations†
Jan-Hendrik
Pöhls
 ab,
Sevan
Chanakian‡
ab,
Sevan
Chanakian‡
 c,
Junsoo
Park
c,
Junsoo
Park
 d,
Alex M.
Ganose
d,
Alexander
Dunn
d,
Alex M.
Ganose
d,
Alexander
Dunn
 d,
Nick
Friesen
a,
Amit
Bhattacharya
a,
Brea
Hogan
e,
Sabah
Bux
e,
Anubhav
Jain
d,
Arthur
Mar
*a and
Alexandra
Zevalkink
d,
Nick
Friesen
a,
Amit
Bhattacharya
a,
Brea
Hogan
e,
Sabah
Bux
e,
Anubhav
Jain
d,
Arthur
Mar
*a and
Alexandra
Zevalkink
 *c
*c
aDepartment of Chemistry, University of Alberta, Edmonton, AB T6G 2G2, Canada. E-mail: arthur.mar@ualberta.ca
bDepartment of Physics, McGill University, Montreal, QC H3A 2T8, Canada
cDepartment of Chemical Engineering and Materials Science, Michigan State University, East Lansing, MI 48824, USA. E-mail: alexzev@msu.edu
dEnergy Technologies Area, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
eThermal Energy Conversion Research and Advancement Group, Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
First published on 4th November 2020
Abstract
Accurate density functional theory calculations of the interrelated properties of thermoelectric materials entail high computational cost, especially as crystal structures increase in complexity and size. New methods involving ab initio scattering and transport (AMSET) and compressive sensing lattice dynamics are used to compute the transport properties of quaternary CaAl2Si2-type rare-earth phosphides RECuZnP2 (RE = Pr, Nd, Er), which were identified to be promising thermoelectrics from high-throughput screening of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 disordered compounds. Experimental measurements of the transport properties agree well with the computed values. Compounds with stiff bulk moduli (>80 GPa) and high speeds of sound (>3500 m s−1) such as RECuZnP2 are typically dismissed as thermoelectric materials because they are expected to exhibit high lattice thermal conductivity. However, RECuZnP2 exhibits not only low electrical resistivity, but also low lattice thermal conductivity (∼1 W m−1 K−1). Contrary to prior assumptions, polar-optical phonon scattering was revealed by AMSET to be the primary mechanism limiting the electronic mobility of these compounds, raising questions about existing assumptions of scattering mechanisms in this class of thermoelectric materials. The resulting thermoelectric performance (zT of 0.5 for ErCuZnP2 at 800 K) is among the best observed in phosphides and can likely be improved with further optimization.
000 disordered compounds. Experimental measurements of the transport properties agree well with the computed values. Compounds with stiff bulk moduli (>80 GPa) and high speeds of sound (>3500 m s−1) such as RECuZnP2 are typically dismissed as thermoelectric materials because they are expected to exhibit high lattice thermal conductivity. However, RECuZnP2 exhibits not only low electrical resistivity, but also low lattice thermal conductivity (∼1 W m−1 K−1). Contrary to prior assumptions, polar-optical phonon scattering was revealed by AMSET to be the primary mechanism limiting the electronic mobility of these compounds, raising questions about existing assumptions of scattering mechanisms in this class of thermoelectric materials. The resulting thermoelectric performance (zT of 0.5 for ErCuZnP2 at 800 K) is among the best observed in phosphides and can likely be improved with further optimization.
New conceptsThis investigation of RECuZnP2 (RE = rare earth) is the first in-depth study of transport properties in quaternary CaAl2Si2-type compounds, a promising class of thermoelectric materials. This study demonstrates that the combined application of DFT calculations with advanced physics-based scattering calculations delivers new insight on the underlying mechanisms of thermoelectric transport. The results directly challenge the usual assumption that acoustic phonon scattering is the limiting factor of electron transport in most thermoelectric materials; instead, polar-optical phonon scattering is likely more important than previously believed. Moreover, the calculations shed light on the unexpectedly low lattice thermal conductivity in RECuZnP2: despite high bulk moduli and speeds of sound, strongly anharmonic bonding can significantly reduce the thermal conductivity. These insights on the mechanisms of electron and heat transport have broader implications to the materials science community, by guiding researchers to discover more efficient thermoelectric materials in applying new concepts to optimize their properties. The low computational cost of these methods could also herald an exciting era of DFT-guided materials discovery. |
Introduction
More than half of the world's energy produced by nonrenewable sources is wasted as a non-usable form of thermal energy. Part of the lost useful energy could be recovered by converting heat into electrical energy using thermoelectric materials. However, the high costs and low efficiencies of commercial thermoelectric materials limit affordable applications. The efficiency is proportional to the thermoelectric figure of merit, zT = S2T/(ρκ), which depends on the Seebeck coefficient S, the electrical resistivity ρ, the thermal conductivity κ (having electronic, κel, and phononic, κph, contributions) and the absolute temperature T.1 Optimizing thermoelectric efficiency is a complicated balancing act because the factors are dependent of each other.The search for high-performance thermoelectric materials can be accelerated by high-throughput screening of candidates evaluated by density functional theory (DFT) calculations.2–8 Based on ongoing screening of the electrical properties (viz., power factor, PF = S2/ρ) for over 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 disordered inorganic compounds taken from the Inorganic Crystal Structure Database (ICSD),9 the phosphides RECuZnP2 (RE = trivalent rare-earth metal) have emerged as promising candidates. These compounds are quaternary derivatives of a family of AM2X2 compounds that adopt the trigonal CaAl2Si2-type structure and exhibit electrical and thermal properties suitable for thermoelectric materials (e.g., Mg3Sb2,10–12 EuCd2Sb213). Despite restrictions on the formation of these AM2X2 compounds (requiring a valence electron count of 16 and a d0, d5, or d10 configuration for M), they are numerous and diverse. The A cation is commonly divalent but can be monovalent or trivalent with appropriate substitution of the other components to maintain the electron count, as exemplified by RECuZnP2, which contains Cu+ and Zn2+ mixed on the M site (Fig. S3, ESI†).14–16
000 disordered inorganic compounds taken from the Inorganic Crystal Structure Database (ICSD),9 the phosphides RECuZnP2 (RE = trivalent rare-earth metal) have emerged as promising candidates. These compounds are quaternary derivatives of a family of AM2X2 compounds that adopt the trigonal CaAl2Si2-type structure and exhibit electrical and thermal properties suitable for thermoelectric materials (e.g., Mg3Sb2,10–12 EuCd2Sb213). Despite restrictions on the formation of these AM2X2 compounds (requiring a valence electron count of 16 and a d0, d5, or d10 configuration for M), they are numerous and diverse. The A cation is commonly divalent but can be monovalent or trivalent with appropriate substitution of the other components to maintain the electron count, as exemplified by RECuZnP2, which contains Cu+ and Zn2+ mixed on the M site (Fig. S3, ESI†).14–16
In general, semiconducting compounds containing light atoms such as C, N, or P often exhibit excellent electrical properties,17 but they would be expected to have stiff bonds, leading to high thermal conductivities. However, some metal phosphides have been predicted to show low lattice thermal conductivities,18–20 suggesting that lightweight compounds should not be dismissed so easily. The transport properties of many CaAl2Si2-type compounds remain largely uninvestigated, especially of nitride and phosphide members,21–28 as well as those containing a trivalent A cation. Given that site disorder would also lower thermal conductivity, we hypothesize that the phosphides RECuZnP2 are attractive candidates for thermoelectric materials.
To test this hypothesis and to validate the predictions from the computational screening, three RECuZnP2 (RE = Pr, Nd, Er) compounds were synthesized and their thermoelectric properties were measured. These experimental results were compared with first-principles calculations of electron and phonon transport properties to gain insight on the scattering mechanisms that determine thermoelectric performance.29,30 In particular, starting solely from first-principles input, the ab initio scattering and transport (AMSET) software package was used to compute carrier lifetimes arising from acoustic deformation potential (ADP), polar-optical phonon (POP), and ionized impurity (IMP) scattering processes. In a recent study,31 AMSET was applied to 16 simple semiconductors and demonstrated excellent agreement against both experimental measurements on single crystals and state-of-the-art calculations (Electron–Phonon Wannier, EPW) of electronic mobility and Seebeck coefficient. However, unlike other methods whose computational expense limits their use to small highly-symmetric systems, AMSET can be applied to complex compounds (including disordered ones such as RECuZnP2) and in a high-throughput manner, enabling information about scattering to be extracted for a wide variety of materials. We evaluate how well this new computational approach agrees with the experimental results on RECuZnP2 and whether other related phosphides may be feasible thermoelectric materials.
Results and discussion
Synthesis
Samples of RECuZnP2 (RE = Pr, Nd, Er) were prepared by high-temperature reactions of the elements. Powder X-ray diffraction (XRD) confirmed that they crystallize in the CaAl2Si2-type structure [space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (no. 164)] (Fig. S1, ESI†), with lattice parameters that agree with those reported previously (Table S1, ESI†).14 They were densified into pressed pellets by spark plasma sintering for property measurements.
m1 (no. 164)] (Fig. S1, ESI†), with lattice parameters that agree with those reported previously (Table S1, ESI†).14 They were densified into pressed pellets by spark plasma sintering for property measurements.
Elastic properties
The intrinsic lattice thermal conductivity of a material depends on its elastic properties, which were calculated and measured for RECuZnP2 compounds (Table 1).32 On progressing from the Pr to the Er member, the stiffness increases slightly (as gauged by the bulk, Young's, and shear modulus), consistent with smaller lattice parameters and shorter bond lengths,14 but the Poisson ratio does not change significantly. For PrCuZnP2 and ErCuZnP2, the average speed of sound, vavg = (vL + 2vT)/3, is about 3650 m s−1, which is higher than typically found in other CaAl2Si2-type compounds (e.g., Mg3Sb2, 2800 m s−1; EuZn2Sb2, 2400 m s−1);33 to date, only CaMg2Sb2 has a comparable value of 3200 m s−1.34 In general, the thermoelectric properties of stiffer CaAl2Si2-type compounds, namely phosphides and arsenides, are not as well studied as the antimonide members.26,35,36 Filling this gap will help clarify the relationship between bonding and properties in these compounds.| Compound | B [GPa] | E [GPa] | G [GPa] | ν | v L [m s−1] | v T [m s−1] |
|---|---|---|---|---|---|---|
| PrCuZnP2 (exp.) | 87 | 126 | 50 | 0.26 | 5170 | 2940 |
| PrCuZnP2 (comp.) | 87 | 142 | 58 | 0.23 | 5340 | 3180 |
| NdCuZnP2 (comp.) | 88 | 143 | 58 | 0.23 | 5300 | 3140 |
| ErCuZnP2 (exp.) | 95 | 142 | 57 | 0.25 | 5080 | 2910 |
| ErCuZnP2 (comp.) | 94 | 147 | 59 | 0.24 | 5080 | 2970 |
Electrical transport properties
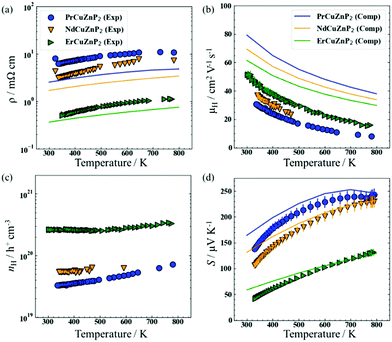
The electrical resistivity (ρ), Hall mobility (μH), Hall carrier concentration (nH), and Seebeck coefficient (S) of RECuZnP2 compounds were measured experimentally as a function of temperature and compared with calculated results (Fig. 1).For all samples, the resistivity increases with higher temperature and the carrier concentration is >1019 cm−3 (Fig. 1(a) and (c)), implying that these compounds are highly degenerate p-type semiconductors. Substitution with a heavier RE component (from Pr to Er) lowers the resistivity by an order of magnitude, due primarily to an increase in carrier concentration in ErCuZnP2 relative to the two other compounds. The higher carrier concentration could be the result of sample processing or suggest that cation vacancies have a lower formation energy in ErCuZnP2.37
The hole mobility is relatively low for RECuZnP2 samples, ranging from 37 to 50 cm2 V−1 s−1 at 300 K on progressing from RE = Pr to Er (Fig. 1(b)), compared to other rare-earth-containing compounds with the CaAl2Si2-type structure (e.g., EuZn2Sb2, 250 cm2 V−1 s−1;38 YbZn2Sb2, 130 cm2 V−1 s−1;39 EuMg2Bi2, 192 cm2 V−1 s−1).40 The mobility reported previously in the related phosphide YbCuZnP2 is even lower (11 cm2 V−1 s−1 at 300 K).26 Given that the mobility, μ = (e·τe)/m*, depends on the competing effects of effective mass m* and relaxation time τe, first-principles calculations were carried out to gain insight on their roles. The electronic band structures, calculated using DFT with the Heyd–Scuseria–Ernzerhof (HSE06) exchange–correlation functional,41 reveal that the RECuZnP2 compounds are small band gap semiconductors (Eg = 0.52 eV (Nd), 0.54 eV (Pr), 0.73 eV (Er)) with the valence band maximum at the Γ point (Fig. S4, ESI†). Note, experiments indicate that the materials are paramagnetic above room temperature (>0.3 K for ErCuZnP2).14 For each compound, the conductivity effective mass mc* was evaluated at the experimental carrier concentration and is the weighted average of three bands that nearly converge at the Γ point.42 At 300 K, the value of mc* for ErCuZnP2 (0.43 me) is larger than for NdCuZnP2 (0.38 me) and PrCuZnP2 (0.36 me). To check for contributions from bands below the band edge, mc* was also evaluated as a function of chemical potential;43 ErCuZnP2 retains the highest mc* regardless of chemical potential. These values are similar to the only other report of mc* for a CaAl2Si2-type compound, namely p-type Mg3Sb2 (0.34 me at a carrier concentration of 1019 cm−3).44
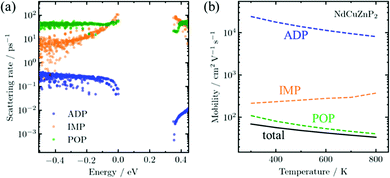
To understand the scattering physics in more detail, it is of interest to calculate the transport properties, which requires electronic band structures as the primary input. Although existing methods to evaluate electron–phonon scattering such as Electron–Phonon Wannier (EPW)45 can yield accurate scattering rates, they are not feasible for complex compounds due to their high computational cost. As the first application of AMSET31 to examine new thermoelectric materials, scattering rates and carrier mobilities were calculated for RECuZnP2 using the momentum relaxation time approximation.46 Three scattering mechanisms were considered: ionized impurities, acoustic deformation potential, and polar-optical phonons.
The AMSET results were obtained at the experimental temperature-averaged Hall carrier concentrations. The mobilities are shown for all three compounds in Fig. S5 (ESI†) and highlighted for NdCuZnP2 in Fig. 2. The chief mechanisms that are predicted to limit the mobilities are polar-optical phonon and, to a lesser extent, ionized impurity scattering. In contrast, acoustic deformation scattering is not predicted to affect the hole transport significantly, given the small absolute valence band deformation potentials (∼1.4 eV) and stiff elastic constants (Table 1). This is rather surprising, because the experimental temperature dependence of the hole mobility (Fig. S7, ESI†) suggests that acoustic scattering is the dominant mechanism, as would be commonly assumed for thermoelectric materials used in mid-to-high temperature ranges.47 In fact, acoustic scattering as a dominant mechanism is contradicted by many recent state-of-the-art computational studies, which indicate that polar-optical phonon scattering is the most important mechanism in many classes of high-performance heteropolar thermoelectric materials (e.g., SnSe, PbTe, half- and full-Heusler compounds),48–51 as is the case here for RECuZnP2.
To confirm that the presence of f-electrons and disorder of the Cu/Zn site in RECuZnP2 do not engender unusual features, analogous AMSET calculations were carried out for the related simpler compound CaZn2P2. The results confirm that polar-optical phonon scattering also dominates in CaZn2P2 (Fig. S6, ESI†), suggesting that this mechanism is important in other CaAl2Si2-type compounds. CaZn2P2 is predicted to have a lower hole mobility than RECuZnP2 because of its higher mc* (0.47 me at n = 1019 cm−3) and smaller dielectric constants, leading to reduced electronic screening. The present AMSET results suggest that further understanding of the scattering mechanisms in CaAl2Si2-type compounds is required to develop concepts to improve their thermoelectric performance.
Compared to the experimentally measured mobilities for RECuZnP2, the computed values are overestimated (Fig. 1(b)); however, the AMSET values should be considered as upper limits as the input DFT calculations were performed using completely ordered structures and boundary scattering, or other mesoscale imperfections not taken into account. The predicted trend in mobility as a function of RE substitution is opposite to that observed. However, the experimental mobility of the samples can be controlled by many factors (e.g., impurities, porosity, grain boundaries, pores, etc.), and may not reflect inherent differences in the electronic structure. In particular, the Er-containing samples have a larger grain size, as evidenced by the powder XRD patterns, which reveal narrower peaks compared to those for the Pr- and Nd-containing samples (Fig. S2, ESI†). The computed resistivities, evaluated at the temperature-averaged experimental Hall carrier concentrations, show reasonable agreement with the experimental values (Fig. 1(a)), but they are somewhat underestimated, due to the overestimation of mobility.
The measured Seebeck coefficients of RECuZnP2 are positive, increase with higher temperature, and are inversely proportional to carrier concentration (Fig. 1(d)). For the Pr- and Nd-containing samples, saturation occurs around 780 K due to minority carrier activation, whereas for the Er-containing sample, a maximum is reached at 860 K (as seen more clearly in the high-temperature data shown in Fig. S9, ESI†). The Goldsmid-Sharp band gap energy (Eg = 2e|Smax|Tmax) is similar for PrCuZnP2 (0.36 eV) and NdCuZnP2 (0.38 eV), but much lower for ErCuZnP2 (0.23 eV), contradicting the trend in computed band gaps. This disagreement likely arises because the Goldsmid-Sharp approximation breaks down for highly degenerate samples,42 as is the case here. Nevertheless, the computed and experimental Seebeck coefficients agree well with each other in terms of magnitude and temperature dependence.
The density of states effective mass mDOS* was estimated from the experimental Seebeck coefficients using the single parabolic band (SPB) model52 and the three scattering mechanisms (IMP, ADP, POP) proposed above, as shown in Fig. S9 (ESI†). The selected type of scattering affects the magnitude of the estimated value of mDOS*, but not the predicted dependence of S on nH (Fig. S10(b), ESI†). Regardless of scattering mechanism, mDOS* increases with higher temperature, indicating a greater number of valence bands or flatter band dispersion (Fig. S8, ESI†). Furthermore, mDOS* is virtually independent of the RE component. A similar observation was noted in AZn2Sb2 compounds, for which substitution of the divalent A component has no effect on mDOS*;53 these previous reports made use of an SPB model with transport assumed to be limited by acoustic phonon scattering. If the same assumption is applied to the present compounds containing trivalent cations, the mDOS* values (0.9 me at 373 K and 1.1 me at 673 K) are significantly higher than the average reported in other p-type CaAl2Si2-type compounds (0.6 me).26,33,53 If, instead, the dominant mechanism in RECuZnP2 is assumed to be polar optical scattering, as suggested by the AMSET results above, then the mDOS* values become comparable to those of other p-type CaAl2Si2-type compounds, assuming that they are dominated by acoustic phonon scattering.
Thermal transport properties
The total thermal conductivity, which consists of electronic and phononic contributions, κ = κel + κph, was measured for RECuZnP2 compounds. The electronic thermal conductivity κel was estimated from the Wiedemann–Franz law, κel = Leff (T/ρ), and the lattice thermal conductivity κph was obtained by subtracting κel from κ. The effective Lorenz number Leff can be calculated from the SPB model, but it is important to note that the choice of scattering mechanism directly affects Leff, and thus κph (see ESI† for details and Fig. S11 for comparison of various assumptions of scattering type). Because polar-optical phonon scattering was shown above to be the most important, it was chosen to calculate Leff. The total thermal conductivity κ of ErCuZnP2 is nearly twice that of NdCuZnP2 and PrCuZnP2 (Fig. 3(a)), mainly because it has a larger electronic contribution. The lattice thermal conductivities κph of these compounds are remarkably low (Fig. 3(b)), comparable to that of previously reported YbCuZnP2.26 As the temperature increases, the values of κph decrease due to Umklapp scattering, and at high temperatures, they approach the so-called “glassy limit,” which is roughly 0.9 W m−1 K−1 based on the experimental speed of sound for ErCuZnP2. Given their high speeds of sound, the low κph values for RECuZnP2 compounds are rather unexpected. Table 2 shows that these κph values are comparable to those of compounds having 30% lower speeds of sound (e.g., EuZn2P2,54 CaMg2Bi255).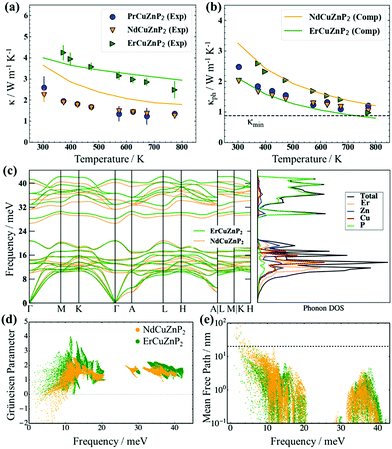 | ||
| Fig. 3 (a) Experimental (symbols) and computed (solid lines) total thermal conductivities and (b) lattice thermal conductivities of RECuZnP2 compounds. (c) Phonon dispersion and DOS curves reveal stiffer phonons in ErCuZnP2 than in NdCuZnP2. (d) Computed mode Grüneisen parameters and (e) phonon mean free paths indicate stronger anharmonicity and smaller average mean free path in ErCuZnP2 than in NdCuZnP2. (Dashed line indicates the grain size limiting the thermal conductivity in NdCuZnP2.) Note that the calculation for PrCuZnP2 did not converge; see ESI† for details. | ||
| Compound | Density | v avg | Grüneisen parameter | κ ph,exp | Ref. |
|---|---|---|---|---|---|
| PrCuZnP2 | 5.70 | 3900 | 1.1 | This work | |
| NdCuZnP2 | 5.82 | 3880 | 1.5 | 1.0 | This work |
| ErCuZnP2 | 6.67 | 3680 | 1.7 | 1.0 | This work |
| YbCuZnP2 | 6.64 | 0.9-1.0 | 26 | ||
| CaZn2P2 | 3.93 | 4190 | 1.0 | 26 | |
| CaMg2Sb2 | 3.87 | 3210 | 1.4 | 1.6 | 34 and 57 |
| Mg3Sb2 | 4.04 | 2790 | 1.8;1.8–2.2 | 0.6 | 34, 58 and 59 |
| CaMg2Bi2 | 5.66 | 2480 | 1.5 | 1.2 | 55 |
| CaZn2Sb2 | 5.40 | 2480 | 1.8 | 1.9 | 60 |
| EuZn2Sb2 | 6.78 | 2400 | 1.1 | 54 | |
| CaCd2Sb2 | 5.95 | 2380 | 1.7 | 0.7 | 61 and 62 |
| SrZn2Sb2 | 5.68 | 2320 | 1.2 | 63 | |
| YbMn2Sb2 | 6.71 | 2070 | 2.2 | 64 |
To shed light on the relative influence of phonon velocity and relaxation time on κph, DFT calculations using compressive sensing lattice dynamics (CSLD)29 were performed to determine the phonon dispersion curves (Fig. 3(c)). The phonon DOS curve reveals that the acoustic and low-frequency optical modes are dominated by RE, Cu, and Zn atoms, whereas the high-frequency modes are dominated by the lighter P atoms. Examining the phonon dispersion curves shows that ErCuZnP2 has the highest group velocity, but it also exhibits stronger anharmonicity, as indicated by the higher mode-averaged Grüneisen parameter of 1.73 (compared to 1.47 for NdCuZnP2). The Grüneisen parameters are slightly lower than that of Mg3Sb2 and lie within the range of CaAl2Si2-type and other Zintl compounds.34,55,58,60,61 Given its higher anharmonicity, ErCuZnP2 is predicted to have lower κph than NdCuZnP2 (Fig. 3(d)). This prediction contradicts the experimental trend in κph. The computed κph value for ErCuZnP2 is lower than the experimental value, which is surprising given that grain boundaries are not considered in the calculation. It is possible that our “experimental” κph values are slightly overestimated due to an underestimate of Leff and thus κe. Even if Leff is similarly overestimated for all three compounds, the impact on the “experimental” κph for ErCuZnP2 would be the greatest, because it has an order of magnitude higher electrical conductivity than the Pr- or Nd-analogues.
In contrast, the computed κph value for NdCuZnP2 is overestimated relative to the experimental value, the discrepancy potentially arising from impurities, grain boundaries, or point defect scattering (e.g., Cu/Zn disorder, notwithstanding the small mass contrast) which are not included in the calculations. To gauge the effects of grain boundary scattering, the lattice thermal conductivity was also calculated as a function of mean free path (Fig. S13, ESI†). Grain sizes of 25 ± 5 nm in NdCuZnP2 would scatter the majority of acoustic phonons (above the dashed line shown in Fig. 3(e)), reproducing the experimental κph value. The thermal conductivity was computed by combining the lattice thermal conductivity derived from lattice dynamics (Fig. 3(b)) and the electronic thermal conductivity derived from electron scattering calculations. In general, the computed and experimental thermal conductivities agree reasonably (Fig. 3(a)).
Thermoelectric figure of merit
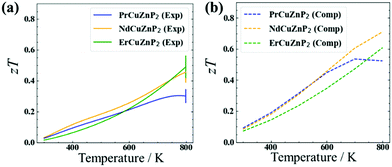
The electrical and thermal transport properties were combined to evaluate the experimental and computed thermoelectric figures of merit zT (Fig. 4). The experimental figure of merit rises to nearly 0.5 at 780 K for ErCuZnP2 and NdCuZnP2, with the trend suggesting further increase at higher temperature, and reaches a maximum of 0.3 at 773 K for PrCuZnP2. These values are nearly comparable to previously reported zT of YbCuZnP2, which reaches a peak zT of 0.6 at 1000 K.26 Given the temperature dependence, it is likely that the performance of the present compounds will surpass YbCuZnP2, ranking them among the best phosphide thermoelectrics yet.19,26 The experimental and computed figures of merit agree reasonably well with each other, particularly for ErCuZnP2. The small discrepancies can be traced mainly to the neglect of the imperfect crystallinity of the samples, e.g., grain boundary and disorder scattering in the calculation of hole mobilities. When grain boundary scattering is included in PrCuZnP2 and NdCuZnP2, the computed electronic and thermal properties are slightly closer to experiment, but there is only a minor effect on zT (see details in ESI† and Fig. S14).The thermoelectric measurements were made on unoptimized samples, meaning that there is room for improvement. Because the thermoelectric figure of merit zT is strongly related to carrier concentration nH, this dependence was examined in more detail at 673 K (Fig. S12, ESI†). When the AMSET model was applied, the results suggest that the figure of merit for ErCuZnP2 can be significantly improved by doping to achieve a carrier concentration to about 5 × 1019 cm−3 or potentially by using single-crystal samples. A similar trend of zT vs. nH was obtained when the SPB model was applied. Assuming polar-optical phonon scattering vs. acoustic phonon scattering leads to major differences in the dependence of mobility and Leff on carrier concentration and chemical potential, and thereby the figure of merit (Fig. S10(a), S11, and S12(a), ESI†). In particular, the mobility is nearly independent of carrier concentration under polar-optical phonon scattering, consistent with the relatively carrier-independent mobility in CaAl2Si2-type compounds. This leads to a prediction of a higher optimum carrier concentration if the predictions from AMSET are correct, and polar-optical phonon scattering is dominant in this system.
Conclusions
Based on a high-throughput screening of >20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compounds, the phosphides RECuZnP2 (RE = Pr, Nd, Er) were predicted to be promising thermoelectric materials that are unconventional candidates because lightweight compounds are not normally considered. These predictions were validated by experimental measurements, which indicated that their thermoelectric performance is promising even before optimization by appropriate doping. First-principles calculations coupled with advanced scattering models of electronic and phononic properties successfully modelled the experimental transport of these compounds, notwithstanding their complex crystal structures. The hole transport in these compounds is predicted to be mostly limited by polar-optical phonon scattering, suggesting that polar-optical phonon scattering may be more widespread than previously thought, which has important consequences for strategies used to optimize the thermoelectric figure of merit. The lattice thermal conductivities of RECuZnP2 compounds are quite low, despite their stiff elastic moduli and high speeds of sound. In particular, for ErCuZnP2, strong anharmonicity may be responsible for low κph values that approach the glassy limit (about 1 W m−1 K−1). This study is a promising indicator that AMSET and CSLD are sufficiently robust to screen the thermoelectric properties of complex materials that have been traditionally avoided in high throughput studies. This methodology of using first-principles calculations to identify and explore electron/hole scattering can be extended generally and has implication to all classes of thermoelectric and other functional materials.
000 compounds, the phosphides RECuZnP2 (RE = Pr, Nd, Er) were predicted to be promising thermoelectric materials that are unconventional candidates because lightweight compounds are not normally considered. These predictions were validated by experimental measurements, which indicated that their thermoelectric performance is promising even before optimization by appropriate doping. First-principles calculations coupled with advanced scattering models of electronic and phononic properties successfully modelled the experimental transport of these compounds, notwithstanding their complex crystal structures. The hole transport in these compounds is predicted to be mostly limited by polar-optical phonon scattering, suggesting that polar-optical phonon scattering may be more widespread than previously thought, which has important consequences for strategies used to optimize the thermoelectric figure of merit. The lattice thermal conductivities of RECuZnP2 compounds are quite low, despite their stiff elastic moduli and high speeds of sound. In particular, for ErCuZnP2, strong anharmonicity may be responsible for low κph values that approach the glassy limit (about 1 W m−1 K−1). This study is a promising indicator that AMSET and CSLD are sufficiently robust to screen the thermoelectric properties of complex materials that have been traditionally avoided in high throughput studies. This methodology of using first-principles calculations to identify and explore electron/hole scattering can be extended generally and has implication to all classes of thermoelectric and other functional materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Canada First Research Excellence Fund (CFREF, through the Future Energy Systems Research Institute at the University of Alberta, Project T12-P01) and the Natural Sciences and Engineering Research Council of Canada (NSERC, through Discovery Grant RGPIN-2018-04294). JHP acknowledges the FRQNT PBEEE postdoctoral fellowship. This work was supported by the NASA Science Missions Directorate under the Radioisotope Power Systems Program's Thermoelectric Technology Development Project. Synthesis-related tasks performed by SC and AZ were supported by the National Science Foundation (NSF) award number 1709158. SC's contributions are based upon work supported by the National Science Foundation Graduate Research Fellowship Program award number DGE-1848739. Computational efforts by JP, AG, AD, and AJ were funded by the U.S. Department of Energy (DOE), Office of Basic Energy Sciences, Early Career Research Program. This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DEAC02-05CH11231. Lawrence Berkeley National Laboratory is funded by the DOE under award DE-AC02-05CH11231. The authors would like to thank George Nakatsukasa and Gregory Gerig at JPL for their work in measuring the thermal diffusivity and Seebeck coefficients of the samples presented in this work.Notes and references
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105 CrossRef CAS.
- P. Gorai, E. S. Toberer and V. Stevanovic, Phys. Chem. Chem. Phys., 2016, 18, 31777 RSC.
- L. Bjerg, G. K. H. Madsen and B. B. Iversen, Chem. Mater., 2011, 23, 3907 CrossRef CAS.
- G. K. H. Madsen, J. Am. Chem. Soc., 2006, 128, 12141 CrossRef.
- J. He, M. Amsler, Y. Xia, S. S. Naghavi, V. I. Hegde, S. Hao, S. Goedecker, V. Ozoliņš and C. Wolverton, Phys. Rev. Lett., 2016, 177, 046602 CrossRef.
- J. Carrete, N. Mingo, S. Wang and S. Curtarolo, Adv. Funct. Mater., 2014, 24, 7427 CrossRef CAS.
- H. Zhu, G. Hautier, U. Aydemir, Z. M. Gibbs, G. Li, S. Bajaj, J.-H. Pöhls, D. Broberg, W. Chen, A. Jain, M. A. White, M. Asta, G. J. Snyder, K. Persson and G. Ceder, J. Mater. Chem. C, 2015, 3, 10554 RSC.
- U. Aydemir, J.-H. Pöhls, H. Zhu, G. Hautier, S. Bajaj, Z. M. Gibbs, W. Chen, G. Li, S. Ohno, D. Broberg, S. D. Kang, M. Asta, G. Ceder, M. A. White, K. Persson, A. Jain and G. J. Snyder, J. Mater. Chem. A, 2016, 4, 2461 RSC.
- G. Bergerhoff, I. Brown and F. Allen, Crystallographic Databases, International Union of Crystallography, Chester, 1987 Search PubMed.
- H. Tamaki, H. K. Sato and T. Kanno, Adv. Mater., 2016, 28, 10182–10187 CrossRef CAS.
- K. Imasato, S. D. Kang and G. J. Snyder, Energy Environ. Sci., 2019, 12, 965–971 RSC.
- X. Shi, T. Zhao, X. Zhang, C. Sun, Z. Chen, S. Lin, W. Li, H. Gu and Y. Pei, Adv. Mater., 2018, 31, 1903387 CrossRef.
- H. Zhang, L. Fang, M.-B. Tang, H.-H. Chen, X.-X. Yang, X. Guo, J.-T. Zhao and Y. Grin, Intermetallics, 2010, 18, 193 CrossRef CAS.
- P. E. R. Blanchard, S. S. Stoyko, R. G. Cavell and A. Mar, J. Solid State Chem., 2011, 184, 97 CrossRef CAS.
- A. T. Nientiedt, H. Lincke, U. Ch Rodewald, R. Pöttgen and W. Jeitschko, Z. Naturforsch., B: J. Chem. Sci., 2011, 66b, 221–226 Search PubMed.
- J. Prakash, M. C. Schäfer and S. Bobev, Acta Crystallogr., 2015, C71, 894–899 Search PubMed.
- Y. Kumashiro, M. Hirabayashi, T. Koshiro and Y. Okada, J. Less-Common Met., 1988, 143, 159–165 CrossRef CAS.
- J.-H. Pöhls, A. Faghaninia, G. Petretto, U. Aydemir, F. Ricci, G. Li, M. Wood, S. Ohno, G. Hautier, G. J. Snyder, G.-M. Rignanese, A. Jain and M. A. White, J. Mater. Chem. C, 2017, 5, 2050 RSC.
- J. Nuss, U. Wedig, W. Xie, P. Yordanov, J. Bruin, R. Hübner, A. Weidenkaff and H. Takagi, Chem. Mater., 2017, 29(16), 6956–6965 CrossRef CAS.
- W. D. Thompson, R. Vaddi and B. E. White Jr., J. Alloys Compd., 2016, 687, 813–820 CrossRef CAS.
- P. Klüfers and A. Mewis, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1977, 32, 753–756 Search PubMed.
- P. Klüfers and A. Mewis, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1977, 32, 353–354 Search PubMed.
- H.-O. Fischer and H.-U. Schuster, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1977, 35, 1322–1323 Search PubMed.
- S. L. Brock, J. E. Greedan and S. M. Kauzlarich, J. Solid State Chem., 1994, 113, 303–311 CrossRef CAS.
- V. Ponnambalam and D. T. Morelli, J. Electron. Mater., 2014, 43, 1875–1880 CrossRef CAS.
- V. Ponnambalam, S. Lindsey, W. Xie, D. Thompson, F. Drymiotis and T. M. Tritt, J. Phys. D: Appl. Phys., 2011, 44, 155406 CrossRef.
- A. C. Payne, A. E. Sprauve, M. M. Olmstead, S. M. Kauzlarich, J. Y. Chan, B. A. Reisner and J. W. Lynn, J. Solid State Chem., 2002, 163, 498–505 CrossRef CAS.
- O. Reckeweg, C. Lind, A. Simon and F. J. DiSalvo, Z. Naturforsch., B: J. Chem. Sci., 2002, 58, 159–162 Search PubMed.
- F. Zhou, W. Nielson, Y. Xia and V. Ozoliņš, Phys. Rev. Lett., 2014, 113, 185501 CrossRef.
- J. J. Kuo, U. Aydemir, J.-H. Pöhls, F. Zhou, G. Yu, A. Faghaninia, F. Ricci, M. A. White, G.-M. Rignanese, G. Hautier, A. Jain and G. J. Snyder, J. Mater. Chem. A, 2019, 7, 2589 RSC.
- E. S. Toberer, A. Zevalkink and G. J. Snyder, J. Mater. Chem., 2011, 21, 15843–15852 RSC.
- A. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Pearsson and A. Jain, 2020, arXiv:2008.09734v1 [cond-mat.mtrl-sci].
- W. Peng, S. Chanakiana and A. Zevalkink, Inorg. Chem. Front., 2018, 5, 1744–1759 RSC.
- W. Peng, G. Petretto, G.-M. Rignanese, G. Hautier and A. Zevalkink, Joule, 2018, 2, 1879–1893 CrossRef CAS.
- S. M. Kauzlarich, C. L. Condron, J. K. Wassei, T. Ikeda and G. J. Snyder, J. Solid State Chem., 2009, 182, 240–245 CrossRef CAS.
- Y. Hinuma, T. Hatakeyama, Y. Kumagai, L. A. Burton, H. Sato, Y. Muraba, S. Iimura, H. Hiramatsu, I. Tanaka, H. Hosono and F. Oba, Nat. Commun., 2016, 7, 11962 CrossRef CAS.
- G. S. Pomrehn, A. Zevalkink, W. G. Zeier, A. van de Walle and G. J. Snyder, Angew. Chem., Int. Ed., 2014, 53, 3422–3426 CrossRef CAS.
- H. Zhang, J.-T. Zhao, Y. Grin, X.-J. Wang, M.-B. Tang, Z.-Y. Man, H.-H. Chen and X.-X. Yang, J. Chem. Phys., 2008, 129, 164713 CrossRef.
- F. Gascoin, S. Ottensmann, D. Stark, S. M. Haile and G. J. Snyder, Adv. Funct. Mater., 2005, 15, 1860 CrossRef CAS.
- A. F. May, M. A. McGuire, D. J. Singh, J. Ma, O. Delaire, A. Huq, W. Cai and H. Wang, Phys. Rev. B, 2012, 85, 035202 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- Z. M. Gibbs, F. Ricci, G. Li, H. Zhu, K. Persson, G. Ceder, G. Hautier, A. Jain and G. J. Snyder, npj Comput. Mater., 2017, 32, 8 CrossRef.
- F. Ricci, W. Chen, U. Aydemir, G. J. Snyder, G.-M. Rignanese, A. Jain and G. Hautier, Sci. Data, 2017, 4, 170085 CrossRef CAS.
- J. Zhang, L. Song and B. B. Iversen, npj Comput. Mater., 2019, 5, 76 CrossRef.
- J. Noffsinger, F. Giustino, B. D. Malone, C.-H. Park, S. G. Louie and M. L. Cohen, Comput. Phys. Commun., 2010, 181, 2140–2148 CrossRef CAS.
- S. Poncé, W. Li, S. Reichardt and F. Giustino, Rep. Prog. Phys., 2020, 83, 036501 CrossRef.
- Y. Pei, H. Wang and G. J. Snyder, Adv. Mater., 2012, 24, 6125–6135 CrossRef CAS.
- J. Cao, J. D. Querales-Flores, A. R. Murphy, S. Fahy and I. Savić, Phys. Rev. B, 2018, 98, 205202 CrossRef.
- J. Ma, Y. Chen and W. Li, Phys. Rev. B, 2018, 97, 205207 CrossRef CAS.
- J. Zhou, H. Zhu, T.-H. Liu, Q. Song, R. He, J. Mao, Z. Liu, W. Ren, B. Liao, D. J. Singh, Z. Ren and G. Chen, Nat. Commun., 2018, 9, 1721 CrossRef.
- J. Park, Y. Xia and V. Ozoliņš, Phys. Rev. Appl., 2019, 11, 014058 CrossRef CAS.
- A. F. May, E. S. Toberer, A. Saramat and G. J. Snyder, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 125205 CrossRef.
- E. S. Toberer, A. F. May, B. C. Melot, E. Flage-Larsen and G. J. Snyder, Dalton Trans., 2010, 39, 1046 RSC.
- Y. Takagiwa, Y. Sato, A. Zevalkink, I. Kanazawa, K. Kimura, Y. Isoda and Y. Shinohara, J. Alloys Compd., 2017, 703, 73–79 CrossRef CAS.
- C. Sun, X. Shi, L. Zheng, B. Chen and W. Li, J. Materiomics, 2019, 5, 567–573 CrossRef.
- M. de Jong, W. Chen, T. Angsten, A. Jain, R. Notestine, A. Gamst, M. Sluiter, C. K. Ande, S. Van Der Zwaag, J. J. Plata, C. Toher, S. Curtarolo, G. Ceder, K. A. Persson and M. Asta, Sci. Data, 2015, 2, 150009 CrossRef CAS.
- M. Wood, U. Aydemir, S. Ohno and G. J. Snyder, J. Mater. Chem. A, 2018, 6, 9437–9444 RSC.
- J. Zhang, L. Song, M. Sist, K. Tolborg and B. B. Iversen, Nat. Commun., 2018, 9, 4716 CrossRef.
- Z. Ren, J. Shuai, J. Mao, Q. Zhu, S. Song, Y. Ni and S. Chen, Acta Mater., 2018, 143, 265–271 CrossRef CAS.
- T. A. Wubieneh, P. C. Wei, C. C. Yeh, S. Chen and Y.-Y. Chen, J. Electron. Mater., 2016, 45, 1942–1946 CrossRef CAS.
- T. Pandeya and A. K. Singh, Phys. Chem. Chem. Phys., 2015, 17, 16917–16926 RSC.
- Q.-G. Cao, H. Zhang, M.-B. Tang, H.-H. Chen, X.-X. Yang, Y. Grin and J.-T. Zhao, J. Appl. Phys., 2010, 107, 053714 CrossRef.
- H. Zhang, M.-B. Tang, W. Schnelle, M. Baitinger, Z.-Y. Man, H.-H. Chen, X.-X. Yang, J.-T. Zhao and Y. Grin, J. Electron. Mater., 2010, 39, 1772–1776 CrossRef CAS.
- K. Guo, Q.-G. Cao, X.-J. Feng, M.-B. Tang, H.-H. Chen, X. Guo, L. Chen, Y. Grin and J.-T. Zhao, Eur. J. Inorg. Chem., 2011, 4043–4048 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0mh01112f |
| ‡ J.-H. Pöhls and S. Chanakian contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |