Origin of pressure-induced band gap tuning in tin halide perovskites

Abstract

Structural and optical high-pressure study of FASnBr₃ (FA = formamidinium) revealed a cubic to orthorhombic phase transition near 1.4 GPa accompanied by a huge band gap red-shift from 2.4 to 1.6 eV, which is followed by a blue-shift of ∼0.2 eV upon further pressure increase. DFT calculations indicate that the variation in band gap is related to changes in Sn–Br bond length alternation, with an equalization of such difference predicted at high pressure. Extending the calculations to analogous lead-free systems provides a unifying mechanistic picture of pressure-induced band gap tuning in tin halide perovskites, which is correlated to the variation of specific structural parameters. These results represent a solid guide to predict and modulate the pressure-response of metal halide perovskites based on the knowledge of their structural properties at ambient pressure.

---

Introduction

Metal halide perovskites (MHPs) possess unique electronic and optical properties and have been the subject of tremendous experimental and computational efforts focused on understanding the mechanisms that dominate their functionalities. This huge work had unveiled relevant correlations between phase composition and structural features affecting optical properties and charge carrier dynamics.^1,2 Despite these efforts, challenges still exist in the fundamental understanding of structure–property relationships that govern the wide tunability of MHPs. Due to their soft lattice, MHPs are highly sensitive to mechanical deformation, resulting in changes of their electronic structure and physical properties. In this regard, in situ high-pressure (HP) research has proven to be a powerful tool with great potential for the engineering of MHPs.^3–7

3D perovskites have been the subject of intense HP study with strong focus on lead-based systems, namely MAPbX₃ (MA = methylammonium) compounds (where X = Cl, Br and I), as well as FAPbI₃, FAPbBr₃ (FA = formamidinium) and CsPbBr₃.^8–18 Numerous experimental and computational results have revealed the existence of some common pressure-induced features. These features include band gap (E_g) red-shift upon initial compression, which is followed by a blue-shift that correlates to the occurrence of a structural phase transition to a more distorted crystal structure.^3,4 Concerning the microscopic mechanisms proposed for lead halide perovskites, it appears that the first red-shift is typically correlated to a shortening of the Pb–X bond length, resulting in increased orbital coupling. The subsequent blue-shift is related to local deformations in the crystal structure, connected with the bending of the Pb–X–Pb bond angles, which tend to reduce orbital coupling.⁷ Moreover, all of the lead halide perovskites investigated under pressure have shown that significant amorphization of the lattice occurs within the blue-shift regime of the band gap.^3,4 However, systematic studies that couple HP experiments with computational modelling tools are still scarce, and additional insights into the mechanistic features of HP effects are still required.

We recently conducted HP investigations of Sn-based systems, which have been much less extensively investigated with respect to their lead counterpart, despite the huge interest toward lead-free perovskites.^19,20 In particular, we reported the structural and optical properties of MASnBr₃ and CsSnBr₃, where large red shifts of 0.4 eV for MASnBr₃ and 0.2 eV for CsSnBr₃ were observed by ∼1.5 GPa, followed by large blue shifts of 0.3 and 0.5 eV, respectively.²⁰ Using density functional theory (DFT) calculations, it was then possible to determine the underlying mechanism affecting the band gap evolution with pressure, the key role of metal–halide bond lengths for CsSnBr₃ and of cation orientation for MASnBr₃. These results highlight the impact of different A-cations on the pressure response.²⁰ Triggered by these results, clearly correlating the observed trends to local lattice properties, we extended the HP study to FASnBr₃ by virtue of its peculiar structural features, and also to confirm the mechanistic picture we obtained on MASnBr₃ and CsSnBr₃.^20,21 Previously, we reported that FASnBr₃ is characterized by a distorted structure with partly uncoupled SnBr₃ units, and that its 3D structure originates from a dynamical averaging of quasi-0D structures.²¹ Such structural characteristics make FASnBr₃ a useful system to probe the extent of pressure effects on the electronic structure and to correlate these effects to local metal–halide bond distances.

In view of the above considerations, in this paper we present the results of a high-pressure structural and optical properties investigation of FASnBr₃. The high-pressure experiments are carried out using diamond anvil cells (DAC), and are readily comparable with our previous results on MASnBr₃ and CsSnBr₃. This systematic experimental and computational work provides the first unifying mechanistic picture of pressure induced effects on lead-free MHPs.

Results and discussion

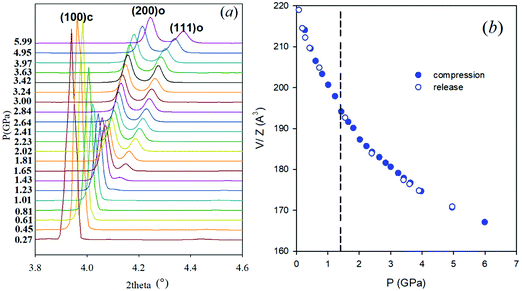
Synchrotron X-ray powder diffraction data were collected in a DAC using helium as pressure transmitting medium up to 6 GPa. Fig. 1a reports the evolution with pressure of the cubic (100) reflection. Full patterns are reported in the ESI,† Fig. S1. FASnBr₃ is cubic (space group Pm3̄m) at ambient conditions as previously reported, and this structure is retained up to ∼1.4 GPa. The pressure increase induces splitting of some of the main reflections (see for example the peaks around 4° in Fig. 1a), consistent with the formation of an orthorhombic phase, with metric 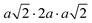, and space group Pnma. Examples of refinements are reported in Fig. S2 (ESI†). No further phase transition nor evidence of amorphization was observed with pressure.

Fig. 1 Experimental XRD patterns (λ = 0.41116 Å) across the (100) reflection of the parent cubic phase as a function of pressure (reported in GPa on the left) (a) and corresponding lattice volume trend as a function of pressure (b). Dashed line highlights phase transition (see text for details).

Surprisingly, no temperature or pressure resolved studies have been performed so far on this compound. It follows that comparisons are available only with analogous compounds replacing one of the elements involved, e.g. MA for FA, Sn with Pb, or Br with I.

The same Pnma orthorhombic phase was observed in FAPbBr₃ at pressures above 2 GPa and cooling below 100 K.^18,22 Similarly, Schueller et al. showed that the orthorhombic Pnma phase is stable at low temperature for FASnI₃.²² However, both studies reported intermediate phases (tetragonal P4/mbm at low temperature, and cubic Immm at high pressure), which are not observed here. FASnBr₃ exhibits similar behaviour to MASnBr₃, though the phase transformation involves a less distorted high-pressure phase. Indeed, the orthorhombic phase of MASnBr₃ shows a doubling of all cell axis to produce the metric 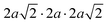. Other than that, the structural high-pressure behaviour of FA and MA compounds is very similar.²⁰ Another peculiarity of the ASnBr₃ (A = MA, FA) system is the important splitting of the a and c axes, leading to a much more pronounced orthorhombic distortion than in the Pb and I counterparts, where the distortion is generally within 0.1 Å.^18,22

The unit cell volume trend was determined from XRD pattern refinements, both during compression and pressure release, as shown in Fig. 1b. The phase transition process is fully reversible and no discontinuity in unit cell volume was observed. Details on data refinement together with lattice parameters and volume as a function of P are reported in the ESI,† Fig. S3 and S4. No evidence of amorphization was found in the XRD patterns, in analogy with other Sn-based MHPs, differing from the behavior of all the lead-containing phases.^3,4,20 After pressure release, the XRD pattern of FASnBr₃ is cubic and clearly crystalline (see Fig. S5 and S6, ESI† for raw data and refinement).

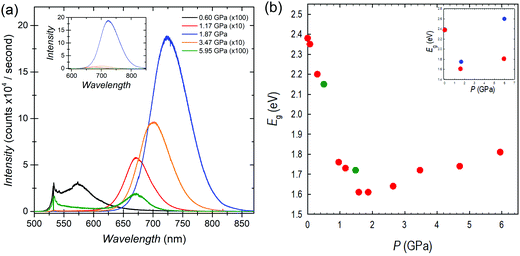
The optical properties of FASnBr₃ under pressure were measured using both photoluminescence (PL) and optical absorption spectroscopy. The high-pressure PL spectra and the band gap extracted from absorption spectroscopy for FASnBr₃ are reported in Fig. 2a and b, respectively. Selected optical absorption spectra are reported in Fig. S7–S9 (ESI†).

Fig. 2 (a) PL spectra with pressure for FASnBr₃. PL intensity varies by orders of magnitude and spectra have been scaled as indicated. The inset shows the unscaled intensity. Raman and Raleigh laser light scattering are apparent for spectra with low PL intensities. (b) Trend of band gap vs. pressure for FASnBr₃ under compression (red circles) and decompression (green circles); inset: comparison between experimental (red circles) and calculated data (blue circles). Data points at 0 GPa are overlapping.

No detectable PL emission was observed at room temperature from ambient pressure up to about 0.3 GPa, even using a 405 nm laser for excitation. This is not unusual since many tin-based MHPs have very low emissions at ambient conditions due to the possible presence of defects. Above this pressure, a weak PL signal becomes evident in the spectra. With further pressure increase, the PL intensity increases exponentially, and as in other systems under pressure, the PL peak shifts to the red.²⁰ Above 1.9 GPa, the PL trend reverses and a blue-shift coupled to a rapid decrease in PL intensity is observed. This pressure range of PL-trend change is consistent with the interval where the cubic to orthorhombic phase transition is observed. Above the transition pressure, the PL intensity diminishes significantly and is no longer detectable between 6–11 GPa. All PL trends are reversible with decreasing pressure.

The optical band gap extracted from absorption measurements confirms the ambient pressure value of about 2.4 eV for FASnBr₃.²¹ With increasing pressure there is continuous red-shift of the band gap, which drops to ∼1.6 eV at 1.87 GPa. Above this pressure, the trend reverses, as observed in the PL, and the optical gap increases with pressure. These results are consistent with the XRD data indicating a phase transition in this pressure range, i.e. between 1.58 and 1.87 GPa, where the maximum wavelength of the absorption should be present. Above 1.87 GPa, the E_g continues to increase until 6.5–7.4 GPa, with band gap decreasing to approximately ∼2.2 eV. Finally, absorption data collected under decompression confirm the observed trends are reversible with slight hysteresis (see ESI†).

As shown in Fig. 2b, the overall variation of E_g (ΔE_g) from ambient pressure to the phase transition is close to 0.8 eV, passing from about 2.4 to 1.6 eV. Such a high jump in the band gap as a function of pressure has never been observed in any 3D metal halide perovskite under pressure. In Pb-based MHPs, the first red-shift, coupled to the structural phase transitions, is generally of the order of 0.03 eV, while we demonstrated that passing to Sn-containing perovskites such ΔE_g value tends to increase to about ∼0.2 eV and ∼0.4 eV for CsSnBr₃ and MASnBr₃, respectively.²⁰ In both these last cases, the lowest value of the E_g was around 1.6 eV and occurred within about 2 GPa and in correspondence of the first structural phase transition. Therefore, the present data shows a record red-shift achieved in less than 2 GPa for FASnBr₃, but even more important, a very interesting evidence is that in these three systems, irrespective to the value of the ambient pressure band gap, the lowest value reached during compression is always around 1.6 eV (before band gap reversing or to blue-shift).²⁰

In order to gain further insights into this peculiar behavior of FASnBr₃, and to provide a unifying mechanistic picture correlating the E_g variation across the three systems (i.e., including CsSnBr₃ and MASnBr₃), we investigated the band gap evolution of FASnBr₃ with pressure using density functional theory (DFT) calculations.

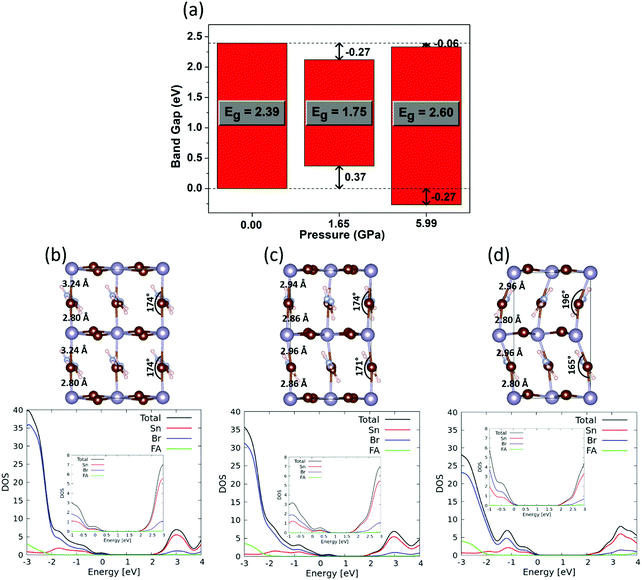
We started by optimizing the structures of FASnBr₃ at ambient pressure and at the pressure with the lowest and the highest band gap, i.e. 0, 1.65 and 5.99 GPa. For the ambient pressure, we have considered tetragonal lattice by rotating the experimental cubic lattice parameters. The optimized tetragonal and cubic structures show similar structural parameters (see Fig. S10 in the ESI†). Such structural adaptation has been done for better comparison of structural properties (bond lengths, bond angles and organic cation's rotation) at ambient pressure with that of the high pressure orthorhombic structure. The band gap evolution matches nicely with the experimental trends (see inset of Fig. 2b), showing a substantial band gap narrowing with increasing pressure followed by a band gap opening with further pressure increase, in close agreement with optical measurements. To understand the shifting of band edges with pressure, we have aligned the density of states (DOS) as shown in Fig. 3a and in the bottom panel of Fig. 3b–d.

Fig. 3 (a) Alignment of band edges under different pressure. Optimized structures and density of states (DOS) at (b) ambient (c) 1.65 GPa and (d) 5.99 GPa. The band edges have been determined from the corresponding eigenvalues. Alignment of the band edges have been done with respect to the lowest-energy peak of carbon of FA and the valence band edge of the ambient pressure DOS has been set to zero.

Optimized structure of FASnBr₃ at ambient pressure (Fig. 3b) shows that the Sn–Br bond distances alternate between short and long, at 2.80 and 3.24 Å, respectively. As mentioned above, we previously described that FASnBr₃ possesses a dynamical average of a short-long Sn–Br bond distance at shorter time scale and behaves as a quasi 0D perovskite, resulting in a high band gap of 2.39 eV.²¹ Since the band gap is the result of the metal halide connectivity, a more equalized pattern of Sn–Br bond distances, i.e. a more continuous 3D-connected perovskite, should result in a lower the band gap compared to a partly decoupled network of SnBr₃ units. With increasing pressure (Fig. 3c), the alternating short-long nature of Sn–Br bond length tends to equalize (2.86 vs. 2.94 Å) and the overlap between Sn and Br increases, resulting in a band gap reduction to 1.75 eV with a concomitant destabilization of the valence band (VB). It is interesting to notice from Table 1 that lowest band gap under moderate pressure is almost identical for FASnBr₃ (1.61 eV), MASnBr₃ (1.62 eV) and CsSnBr₃ (1.59 eV), however, the magnitude of the band gap lowering (ΔE_g) from ambient pressure gradually decreases from FASnBr₃ to CsSnBr₃. Since the Sn–Br bond distances are almost equivalent for FASnBr₃, MASnBr₃ and CsSnBr₃ at moderate pressure, the band gap values are similar for all three cases. However, the highest band gap variation from ambient pressure (∼0.8 eV) is found for FASnBr₃ due to its greatest variation in short-long Sn–Br distances (0.45 Å). Such short-long bond distance variation decreases moving from MASnBr₃ (0.25 Å) to CsSnBr₃ (0.01Å), resulting in smaller ΔE_g values for MASnBr₃ (∼0.4 eV) and CsSnBr₃ (∼0.2 eV) under pressure, as confirmed experimentally.²⁰ Therefore, ∼1.6 eV represents a lower bound for the band gap of Sn-based cubic perovskites under pressure, irrespective of the organic or inorganic cation.

Table 1 Short and long Sn–Br bond lengths and experimental band gaps under different pressure domains. Values for MASnBr₃ and CsSnBr₃ have been taken from ref. 21

Pressure domain	Systems	Sn–Br bond distance (Å)	Exp. band gap (eV)
Ambient	FASnBr3	2.80, 3.24	2.39
	MASnBr3	2.83, 3.08	2.00
	CsSnBr3	2.90, 2.91	1.79
Moderate (0.9–1.6 GPa)	FASnBr3	2.86, 2.94	1.61
	MASnBr3	2.85, 2.95	1.62
	CsSnBr3	2.87, 2.87	1.59

---

With a further increase of pressure, one would expect that all Sn–Br lengths in FASnBr₃ will eventually equalize, leading to a further reduction of band gap. This trend, however, is different from experimental observations. High pressure induces a significant alteration of the FA cation orientation, which in turn causes tilting of the metal–halide bond (Fig. 3d) along with the reappearance of alternating short-long Sn–Br bond lengths (2.80 and 2.96 Å). As a result, the metal halide orbital mixing is reduced, and the VB shifts toward lower energy by 0.64 eV with a concomitant increase of E_g. Notably, the higher absolute band gap in DFT compared with the experimental value at 5.99 GPa (see inset of Fig. 2b) is due to the presence of substantial structural flexibility of this kind of material. For such a distorted orthorhombic geometry, there could be a sizeable difference in the instantaneous structure from the time scale and experimental XRD structures (i.e., thermal averaged structure). Moreover, the dynamic disorder of the organic cation strongly influences the inorganic lattice and has important consequences on the electronic properties.²³ Since the motivation of this work is to investigate the band gap evolution and its origin under pressure, the matching of the absolute values of the band gap with the experiment is not worth considering.

Therefore, in the moderate pressure domain, bond length shortening and the equalization of non-equivalent Sn–Br bond lengths, play the key roles in band gap reduction. At higher pressure, octahedral tilting and cation displacement start to play the central role leading to band gap increase upon further compression. While we previously described the relative weights of the two mechanisms in driving the red- and blue-shifts as a function of pressure, the overall picture drawn from these new data nicely and reliably correlates the ΔE_g changes of the red-shift to the relative bond length changes with pressure, and provide a unifying mechanistic picture for understanding pressure-induced phenomena in tin-halide perovskites.²⁰

Conclusions

In this study we report the first structural and optical high-pressure experiments on FASnBr₃ halide perovskite coupled with DFT calculations. Measurements up to ∼6 GPa in DACs under hydrostatic conditions reveal an impressive 0.8 eV red-shift of the band gap from ambient pressure to the cubic to orthorhombic phase transition (i.e., within ∼1.8 GPa). This trend is followed by a blue-shift of the band gap up to 6 GPa. While analogous trends have been observed in some related systems, the overall band gap changes in those cases are about one order of magnitude lower.^3,4 The mechanism of this unprecedented change in the optical properties of FASnBr₃ halide perovskite is explained by local structural changes by means of DFT calculations, which also provides a comparison with MASnBr₃ and CsSnBr₃. These last two lead-free MHPs show similar pressure-induced variations with a common value of about 1.6 eV for the lowest E_g reported, corresponding to the first structural phase transition. However, the extent of band gap tuning from ambient conditions to the common value of 1.6 eV, changes for the three systems and scales with the magnitude of short-long Sn–Br bond distances, as determined by computational modelling. At the lowest common band gap of about 1.6 eV, the Sn–Br short-long bond distances are almost equivalent for FASnBr₃, MASnBr₃ and CsSnBr₃, and the variation in these distances from the ambient pressure values is what governs the magnitude band gap reduction.

The present experimental and computational data allow us to define a unifying mechanistic picture that governs the optical properties in a series of lead-free MHPs under pressure, and reveal a common lower boundary for the band gap under pressure, irrespective of the organic or inorganic cation. Such results enable predictions of which MHPs are most sensitive to pressure-induced tuning of optical properties through the knowledge of ambient-pressure structural features. We believe that the approach reported in this paper may become a guide to further experimental and modelling work in high-pressure research on MHPs.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

The authors acknowledge the ESRF for provision of beam T. A. S. acknowledges support from the National Science Foundation, Division of Material Research (NSF-DMR) under award number 1809756. A. M., E. M. and F. D. A. acknowledge support from the European 531 Union's Horizon 2020 research and innovation programme under Grant Agreement No. 764047 of the Espresso project. F. D. A. thanks the from the Ministero Istruzione dell’Università e della Ricerca (MIUR) and the University of Perugia through the program “Dipartimenti di Eccellenza 2018–2022” (grant AMIS); and Distinguished Scientist Fellowship Program (DSFP) of King Saud University, Riyadh, Saudi Arabia.

References

1. J. Huang, Y. Yuan, Y. Shao and Y. Yan, Nat. Rev. Mater., 2017, 2, 17042.
2. L. M. Herz, Annu. Rev. Phys. Chem., 2016, 67, 65–89.
3. M. Szafrański and A. Katrusiak, J. Phys. Chem. Lett., 2017, 8, 2496–2506.
4. P. Postorino and L. Malavasi, J. Phys. Chem. Lett., 2017, 8, 2613–2622.
5. M. Li, T. Liu, Y. Wang, W. Yang and X. Lu, Matter Radiat. Extremes, 2020, 5, 018201.
6. A. Jaffe, Y. Lin and H. I. Karunadasa, ACS Energy Lett., 2017, 2, 1549–1555.
7. X. Lu, W. Yang, Q. Jia and H. Xu, Chem. Sci., 2017, 8, 6764–6776.
8. K. Wang, R. Liu, Y. Qiao, J. Cui, B. Song, B. Liu and B. Zou, 2015, arXiv:1509.03717.
9. A. Jaffe, Y. Lin, C. M. Beavers, J. Voss and W. L. Mao, ACS Cent. Sci., 2016, 2, 201–209.
10. S. Jiang, Y. Fang, R. Li, H. Xiao, J. Crowley, C. Wang, T. J. White, W. A. Goddard, Z. Wang and T. Baikie, Angew. Chem., Int. Ed., 2016, 55, 6540–6544.
11. F. Capitani, C. Marini, S. Caramazza, P. Postorino, G. Garbarino, M. Hanfland, A. Pisanu, P. Quadrelli and L. Malavasi, J. Appl. Phys., 2016, 119, 185901.
12. M. Szafranski and A. Katrusiak, J. Phys. Chem. Lett., 2016, 7, 3458–3466.
13. I. P. Swainson, M. G. Tucker, D. J. Wilson, B. Winkler and V. Milman, Chem. Mater., 2007, 19, 2401–2405.
14. Y. Wang, X. Lu, W. Yang, T. Wen, L. Yang, X. Ren, L. Wang, Z. Lin and Y. Zhao, J. Am. Chem. Soc., 2015, 137, 11144–11149.
15. L. Wang, K. Wang, G. Xiao, Q. Zeng and B. Zou, J. Phys. Chem. Lett., 2016, 7, 5273–5279.
16. P. Wang, J. Guan, T. K. Galeschuk, Y. Yao, C. F. He, S. Jiang, S. Zhang, Y. Liu, M. Jin, C. Kin and Y. Song, J. Phys. Chem. Lett., 2017, 8, 2119–2125.
17. L. Zhang, Q. Zeng and K. Wang, J. Phys. Chem. Lett., 2017, 8, 3752–3758.
18. L. Wang, K. Wang and B. Zou, J. Phys. Chem. Lett., 2016, 7, 2556–2562.
19. W. Ke and M. G. Kanatzidis, Nat. Commun., 2019, 10, 965.
20. M. Coduri, T. A. Strobel, M. Szafranski, A. Katrusiak, A. Mahata, F. Cova, S. Bonomi, E. Mosconi, F. De Angelis and L. Malavasi, J. Phys. Chem. Lett., 2019, 10, 7398–7405.
21. A. Pisanu, A. Mahata, E. Mosconi, M. Patrini, P. Quadrelli, C. Milanese, F. De Angelis and L. Malavasi, ACS Energy Lett., 2018, 3, 1353–1359.
22. E. C. Schueller, G. Laurita, D. H. Fabini, C. C. Stoumpos, M. G. Kanatzidis and R. Seshadri, Inorg. Chem., 2018, 57, 695–701.
23. C. Quarti, E. Mosconi and F. De Angelis, Phys. Chem. Chem. Phys., 2015, 17, 9394.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and computational details. See DOI: 10.1039/d0ma00731e

---